The Chinese Meteorological Society
Article Information
- LUO, Siqiong, Xuewei FANG, Shihua LYU, et al., 2017.
- Improving CLM4.5 Simulations of Land–Atmosphere Exchange during Freeze–Thaw Processes on the Tibetan Plateau. 2017.
- J. Meteor. Res., 31(5): 916-930
- http://dx.doi.org/10.1007/s13351-017-6063-0
Article History
- Received May 26, 2016
- in final form May 19, 2017
2. School of Atmospheric Sciences, Plateau Atmosphere and Environment Key Laboratory of Sichuan Province, Chengdu University of Information Technology, Chengdu 610225;
3. Collaborative Innovation Center on Forecast and Evaluation of Meteorological Disasters, Nanjing University of Information Science & Technology, Nanjing 210044;
4. Changzhou Meteorological Bureau, Changzhou 213000
The bidirectional interactions between the land surface and the atmosphere play important roles in the weather and climate. Many sensitivity studies using global climate models have shown that the global and regional climates are very sensitive to processes with different properties that occur on the land surface. Owing to the complexity of land–atmosphere interactions and the limitation of observations, in recent years, land surface models have become a major tool for studies of land–atmosphere interactions (Bonan, 1996; Gao et al., 2004; Yang et al., 2004; Lawrence et al., 2008; Luo et al., 2009a; Chen et al., 2014a; Wang et al., 2017). The numerical expression of land surface processes is important in both climate and weather forecast models.
Soil (including bare soil and soil under vegetation) is the most important underlying surface. It has quite different thermal and hydraulic properties, causing quite different behavior in heat and moisture transport, and thus has an important effect on land–atmosphere interactions. Soil thermal conductivity is one of the key thermal properties in numerical models and is used to determine soil temperature and soil heat flux (Gao et al., 2003; Gao, 2005). In general, soil thermal conductivity is defined based on mineral soil parameterizations that are dependent on soil texture (Johansen, 1975; Farouki, 1986). Soil sand, clay, and silt percentages are provided as a model input dataset to characterize soil texture. Peter-Lidard et al. (1998) found that the parameterization scheme developed by Johansen (1975) provided the best overall prediction results for sands and fine-grained soils available in the literature. This parameterization scheme normalizes the actualthermal conductivity data with respect to the thermal conductivity of dry and saturated fine soils and sands, accounting for the effects of the mineral content through the thermal conductivity of solid particles and the effects of the degree of saturation and the grain-size distribution based on empirical relationships. However, Farouki (1986) found that the methods, which were developed mostly for fine-grained soils and sands, were generally not suitable for dry or nearly dry soil. Furthermore, based on nearly 200 tests on unfrozen and frozen compacted base-course samples and solid rock, Côté and Konrad (2005a) found that the thermal conductivity was strongly influenced by the water content, the porosity of the samples, and the mineralogy of the solid particles of the materials. The Johansen (1975) parameterization scheme is generally not suitable for base-course materials (Côté and Konrad, 2005a). The organic matter, which is prevalent in soils in most vegetated regions of the world and strongly impacts surface energy fluxes, air temperature (Peter-Lidard et al., 1998), soil temperature (Beringer et al., 2001; Yi et al., 2006), and soil moisture (Letts et al., 2000; Zheng et al., 2015), however, is not typically included in the land-surface schemes used in land surface models and global climate models (Lawrence and Slater, 2008a).
The Tibetan Plateau (TP), with an average elevation of more than 4000 m above sea level, is the highest and the most extensive plateau in the world (Liu and Chen, 2000). Many studies have indicated that the TP has strong land–atmosphere interactions. Permafrost and seasonal frozen ground are extensive in the TP, and their seasonal freeze–thaw processes lead to variations in the surface moisture conditions and energy balance (Yang et al., 2007; Wang et al., 2008; Guo et al., 2011b; Fang et al., 2016). Suitable soil thermal and hydraulic parameterization schemes for the TP are major components of land surface models and climate models. In the TP, the soil genesis layer is shallow and contains large soil particles and a high content of broken stones and gravel. Luo et al. (2009b) investigated the soil texture of the central TP using 57 soil samples collected from 16 sites and found an average gravel mass proportion (particle size > 2 mm) of 22.92% based on 18 soil samples. Soil mixed with gravel has different thermal and hydrological properties compared with fine soil (particle size < 2 mm). However, the soil thermal conductivity parameterization schemes in commonly used land surface models do not consider the effects of gravel. Luo et al. (2008) found that the Common Land Model (CoLM) with Farouki’s scheme (Farouki, 1981) tended to overestimate the thermal conductivity in the TP. Based on the soil thermal conductivity parameterization schemes of Johansen (1975), Farouki (1981), Côté and Konrad (2005b), and the observed soil texture in central TP, a new soil thermal conductivity parameterization scheme was established and verified by Luo et al. (2009b). The results showed that in both unfrozen and frozen soil, the calculated soil thermal conductivity of Luo’s scheme was better than that of Farouki (1981). In addition, the soil temperature simulation of CoLM with calculated soil thermal conductivity was shown to be better than that of the original CoLM (Luo et al., 2009b). This scheme has also been applied to the Community Land Model (CLM) and ecosystem model, resulting in improved predictions of soil temperature and soil volumetric water content compared with the original model (Yi et al., 2013, 2014; Wang et al., 2015). Furthermore, soil stratification is a typical phenomenon beneath alpine meadows, with dense roots and soil organic matter within the topsoil, and controls the profile of soil moisture in the central and eastern TP (Yang et al., 2009). The cold conditions on the TP lead to slow decomposition of soil organic carbon (SOC), readily resulting in the accumulation of dense roots and high SOC content in the topsoil layer. Recently, soil was investigated based on 77 soil profiles at 34 stations; it was found that the topsoil of alpine grasslands contained higher SOC content than the underlying soil layers, which led to higher soil porosity values and lower thermal conductivity and bulk density values in the topsoil (Chen Y. Y. et al., 2012). A new parameterization scheme was then developed by Chen Y. Y. et al. (2012) to take the impacts of SOC into account. The new parameterization accurately estimated the soil thermal conductivity values under both low and high SOC content (Chen Y. Y. et al., 2012). The new scheme was also applied to the Noah land surface model, and the resulting soil moisture profile dynamics were better captured by including the modified SOC (Gao et al., 2015; Zheng et al., 2015).
In this study, we sought to further improve the most recent version of CLM (i.e., CLM4.5) by focusing on its ability to simultaneously determine the duration of freeze–thaw periods, together with soil temperature, soil moisture, and surface energy during freeze–thaw processes. Based on consideration of the gravel and organic matter in the soil, data from two typical sites on the TP (Zoige and Madoi) were selected. Following this introduction, Section 2 describes CLM4.5 and the proposed improvements; Section 3 describes the measurements and model configuration; Section 4 discusses the results from three simulation experiments; and conclusions are presented in Section 5.
2 Model 2.1 Description of CLM4.5CLM simulates the partitioning of mass and energy from the atmosphere, redistributes the mass and energy of the land surface, and then exports the fresh water and heat to the oceans (Swenson and Lawrence, 2012). It is the land component of the Community Climate System Model and the Community Earth System Model (Lawrence et al., 2011). The latest version, CLM4.5, is an upgraded version of CLM4.0, including revisions to parameterizations and use of additional data sources. The biogeophysical processes in CLM4.0 include: solar and longwave radiation interactions with the vegetation canopy and soil; momentum and turbulent fluxes from the canopy and soil; heat transfer in soil and snow; hydrology of canopy, soil, and snow; and stomatal physiology and photosynthesis (Lawrence et al., 2011). A detailed description of how these processes are parameterized can be found in the CLM4.0 technical description (Oleson et al., 2010). The main parameterizations revised in CLM4.5 include: new hydraulic properties of frozen soils and the introduction of an ice impedance function (Swenson et al., 2012); a new snow cover fraction parameterization (Swenson and Lawrence, 2012); a completely revised lake model (Subin et al., 2012); a revised canopy radiation scheme; and revisions to the photosynthetic parameters (Bonan et al., 2011). In addition, CLM4.5 uses U.S. Geological Survey global data, including 25 different plant functional types (PFTs) at 30-s intervals, and 17 kinds of soil types from the Food and Agriculture Organization and the State Soil Geographic datasets that determine the soil thermal and hydrological properties. Biogeophysical processes in CLM are simulated for each sub-grid land unit, column, and PFT independently, and each sub-grid unit maintains its own prognostic variables. Detailed information can be found in the technical description of CLM4.5 published by the NCAR (Oleson et al., 2013). The performance of previous versions of CLM for the TP region has been confirmed as well (Chen et al., 2012, 2014a, b, c ; Xiong et al., 2014; Wang et al., 2015).
2.2 Organic and thermal conductivity parameterization 2.2.1 Organic soil incorporated in CLM4.5The thermal and hydraulic properties of organic soil differ from those of mineral soil. Since the release of CLM4.0, the organic matter content in the soil has been taken into account in the land model while calculating the thermal and hydrological physical parameters of soil (Lawrence and Slater, 2008). The soil layer organic matter fraction fom used in CLM4.5 is defined as
| ${f_{{\rm{om}}}} = \frac{{{\rho _{{\rm{om}}}}}}{{{\rho _{{\rm{om}},\max }}}},$ | (1) |
where ρom is the soil carbon density for the soil layer, and ρom, max = 130 kg m–3 is the bulk density of peat.
2.2.2 Thermal conductivity in CLM4.5The thermal conductivity parameterization in CLM4.5 is mainly based on the research of Farouki (1986). Thermal conductivity λ (W m–1 K–1) is expressed as
| ${λ} = \left\{ {\begin{array}{*{20}{c}}{{K\!_{\rm{e}}}\,\,{{λ} _{{\rm{sat}}}} + (1 - {K\!_{\rm{e}}}){{λ} _{{\rm{dry}}}},\quad\;\;{S_{\rm{r}}} > 1 \times {{10}^{ - 7}}},\\{{{λ} _{{\rm{dry}}}}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\quad{S_{\rm{r}}} \leqslant 1 \times {{10}^{ - 7}}},\end{array}} \right. $ | (2) |
where λsat and λdry are soil thermal conductivities under saturation and dry conditions, Ke is the Kersten number, and Sr is the wetness of the soil with respect to saturation. Thermal saturated soil conductivity λsat (W m–1 K–1) is determined by the thermal conductivities of soil solid, liquid water, and ice constituents, as follows:
| ${{λ} _{{\rm{sat}}}} = {{λ} _{\rm{s}}}^{1 - {\theta _{{\rm{sat}}}}}{{λ} _{{\rm{liq}}}}^{\frac{{{\theta _{{\rm{liq}}}}}}{{{\theta _{{\rm{liq}}}} + {\theta _{{\rm{ice}}}}}}{\theta _{{\rm{sat}}}}}{{λ} _{{\rm{ice}}}}^{{\theta _{{\rm{sat}}}}(1 - \frac{{{\theta _{{\rm{liq}}}}}}{{{\theta _{{\rm{liq}}}} + {\theta _{{\rm{ice}}}}}})},$ | (3) |
where θsat is the volumetric water content at saturation (porosity); θliq is the liquid water content of soil; θice is the ice content in soil; λliq = 0.57 W m–1 K–1 and λice = 2.29 W m–1 K–1 are the thermal conductivities of water and ice, respectively; and λs is the soil solid thermal conductivity, which varies with the mineral soil and organic matter content
| ${{λ} _{\rm{s}}} = (1 - {f_{{\rm{om}}}}){{λ} _{{\rm{s}},\min }} + {f_{{\rm{om}}}}{{λ} _{{\rm{s}},{\rm{om}}}},$ | (4) |
where λs,om = 0.25 W m–1 K–1. The thermal conductivity of mineral soil solids is determined by the soil texture, as follows:
| ${{λ} _{{\rm{s}},\min }} = \frac{{{{λ} _{{\rm{sand}}}}({\%}{\rm{sand}}) + {{λ} _{{\rm{clay}}}}({\%} {\rm{clay}})}}{{({\%} {\rm{sand}}) + ({\%} {\rm{clay}})}},$ | (5) |
where λsand (= 8.8 W m–1 K–1) and λclay (= 2.92 W m–1 K–1) are the thermal conductivities of sand and clay, respectively; and %sand and %clay are the percentage contents of sand and clay, respectively. The thermal conductivity of dry soil in Eq. (1) is
| ${{λ} _{{\rm{dry}}}} = (1 - {f_{{\rm{om}}}}){{λ} _{{\rm{dry}},\min }} + {f_{{\rm{om}}}}{{λ} _{{\rm{dry}},{\rm om}}}.$ | (6) |
The thermal conductivity of dry mineral soil λdry,min is determined by the bulk density ρd = 2700(1 – θsat) as
| ${{λ} _{{\rm{dry}},\min }} = \frac{{0.135{\rho _{\rm{d}}} + 64.7}}{{2700 - 0.947{\rho _{\rm{d}}}}},$ | (7) |
and λdry,om (= 0.05 W m–1 K–1) is the dry thermal conductivity of organic matter. The Kersten number Ke is a function of the degree of saturation Sr and the phase of water:
| ${K\!_{\rm{e}}} = \left\{ {\begin{array}{*{20}{c}}{\log {S_{\rm{r}}} + 1 \geqslant 0,\;\;T \geqslant {T_{\rm{f}}}},\\{{S_{\rm{r}}},\,\,\;\;\;\;\;\;\;\;\;\;\;\quad\quad T < {T_{\rm{f}}}},\end{array}} \right.$ | (8) |
where
Recently, a new soil organic matter fraction scheme was developed by Chen Y. Y. et al. (2012). In this scheme, the organic matter fraction is defined according to the volumetric content and calculated by considering the general soil and gravel. Commonly, the mass of soil is measured without gravel. However, as mentioned, gravel is a considerable component of alpine grassland soils over the TP; therefore, it cannot be ignored when the soil organic matter fraction is calculated. The new scheme accurately estimates the soil thermal conductivity values under both low and high organic matter. The mean biases were reduced to –0.01 to –0.06 W m–1 K–1 in four alpine grassland stations on the TP (Chen Y. Y. et al., 2012). In this study, the soil layer organic matter fraction fom in CLM4.5 was changed to
| ${f_{{\rm{om}}}} = {V_{{\rm{soc}}}} = \frac{{{\rho _{\rm{p}}}(1 - {\theta _{{\rm{m}},{\rm{sat}}}}){m\!_{{\rm{soc}}}}}}{{\left( {{\rho _{{\rm{om}},\max }}(1 - {m\!_{{\rm{soc}}}}) + {\rho _{\rm{p}}}(1 - {\theta _{{\rm{m}},{\rm{sat}}}}){m\!_{{\rm{soc}}}} + (1 - {\theta _{{\rm{m}},{\rm{sat}}}})\frac{{{\rho _{{\rm{om}},\max }}{m_{\rm{g}}}}}{{(1 - {m_{\rm{g}}})}}} \right)}},$ | (9) |
where ρp (= 2700 kg m–3) is mineral density, θm,sat is the mineral soil porosity, msoc is the organic carbon mass content, and mg is the gravel mass proportion. The volumetric water content at saturation θsat(θsat = (1 – fom)θsat,min
Based on Johansen’s scheme (Johansen, 1975) and Côté’s scheme (Côté and Konrad, 2005b), the Luo scheme (Luo et al., 2009b) improved the thermal conductivity scheme of soil to provide a more accurate calculation of soil thermal conductivity for the TP. In Luo’s scheme, the thermal conductivity of mineral soil solids λs and the thermal conductivity of dry soil λdry are calculated as follows:
| $\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{{λ} _{\rm{s}}} = {λ} _{\rm{q}}^{\rm{\delta }}{λ} _{\rm{o}}^{1 - {\rm{\delta }}},$ | (10) |
| ${{λ} _{{\rm{dry}}}} = \chi \times {10^{ - {\rm{\eta }}{{\rm{\theta }}_{{\rm{sat}}}}}}.$ | (11) |
Based on Luo’s scheme, the modified soil layer organicmatter fraction fom in Eq. (9) was incorporated into the parameter calculations. The calculations of soil thermal properties in CLM4.5 were changed as follows:
| $\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{{λ} _{\rm{s}}} = {{λ} _{\rm{q}}}^{\rm{\delta }}{{λ} _{\rm{o}}}^{1 - {\rm{\delta }} - {f_{{\rm{om}}}}}{{λ} _{{\rm{s}},{\rm{om}}}}^{{f_{{\rm{om}}}}},$ | (12) |
| ${{λ} _{{\rm{dry}}}} = (1 - {f_{{\rm{om}}}})\chi \times {10^{ - {\rm{\eta }}{{\rm{\theta }}_{{\rm{sat}}}}}} + {{λ} _{{\rm{dry}},{\rm{om}}}} \times {f_{{\rm{om}}}},$ | (13) |
| $\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{K\!_{\rm{e}}} = \frac{{\kappa {S_{\rm{r}}}}}{{1 + (\kappa - 1){S_{\rm{r}}}}},$ | (14) |
where Ke is the Kersten number, λq (= 7.7 W m–1 K–1) is the thermal conductivity of quartz, λo (= 2.0 W m–1 K–1) is assigned to all the other forming minerals, and δ is the quartz content that determines 50% of the sand content (Peter-Lidard et al., 1998; Sun, 2005; Luo et al., 2009b). The parameters χ, η, and κ account for the soil particle shape effect and the contents of gravel and coarse sands, respectively (Côté and Konrad, 2005b). Normally, gravel percentages are not provided as a model input dataset to characterize soil texture in land surface models. Considering the similar thermal properties of gravel with coarse base-course materials, the χ, η, and κ variables for sand were replaced by those for gravel. The variables according to the six investigated soil textures of the central TP are listed in Table 1 (Luo et al., 2009b).
| Soil type | χ | η | κ | |
| Unfrozen | Frozen | |||
| Sand | 1.70 | 1.80 | 4.60 | 1.70 |
| Loamy sand, sandy loam | 0.75 | 1.20 | 3.55 | 0.95 |
| Silt loam, loam, silty clay loam, silt | 0.75 | 1.20 | 1.90 | 0.85 |
The simulations were conducted for two typical sites, Zoige and Madoi, in the Yellow River source region (YRSR) on the TP (Fig. 1). The YRSR is a mosaic transition zone of seasonal frozen ground and areas of discontinuous and continuous permafrost (Jin et al., 2009). In recent years, the temperature of frozen ground has continually increased and the depth of frozen ground has gradually decreased (Jin et al., 2009; Xue et al., 2009; Luo et al., 2016, 2017). The climate of the region is characterized by humid, sub-humid, and semi-arid zones (Zheng et al., 2010).
The Zoige Alpine Wetland Ecosystem Research Station (Northwest Institute of Eco-Environment and Resources, Chinese Academy of Sciences; 33°89′N, 102°14′E, altitude of 3423 m) is located in the Gannan Tibetan Autonomous Prefecture, Gansu Province, China. Generally, the climate at this observation site is cold and damp, with wet and mild summers and dry and cold winters. The mean annual temperature is 1.9°C and the mean annual precipitation amount is 593 mm (during 1981–2010), according to the climatic data measured at a meteorological station (34°00′N, 102°08′E, altitude of 3471 m) located approximately 14 km north of the Zoige site. Detailed descriptions of the underlying surface conditions and observational information for the Zoige site are provided byShang et al. (2015) and Wang et al. (2016). A brief review is provided as follows. The vegetation in this area is typical alpine meadow with a canopy height of 0.2 m in summer and 0.1 m in winter. The topography is flat, and homogenous and the soil is silt–clay–loam comprising 29.8% sand, 66.7% silt, and 3.5% clay in the 40-cm top. The sensible and latent heat fluxes were measured by using an eddy covariance (EC) system, consisting of a three-dimensional sonic anemometer (CSAT3, Campbell Scientific, Inc., Logan, UT, USA) and an open-path fast response infrared gas analyzer (LI-7500, LI-COR Biosciences Inc., Lincoln, NE, USA). The longwave and shortwave radiation were measured at a height of 1.5 m with a four-component net radiometer (CNR-1, Kipp and Zonen, Delſt, Nether-lands). The air temperature and relative humidity sensors (HMP-45C, Vaisala, Helsinki, Finland) were installed at a height of 3.2 m. Precipitation was measured by using a weighing gauge (T200B, Geonor, Norway). Soil temperature and soil volumetric water content were measured in 5 layers (5, 10, 20, 40, and 80 cm) with CS107 temperature probes (Campbell Scientific, Inc.) and CS616 time-domain reflectometer probes (Campbell Scientific, Inc.), respectively. Soil heat flux was measured by using heat flux plates (HPF01, Wohlwend Engineering, Sennwald, Switzerland) buried at 2 and 7 cm below the soil surface.
The second site, Madoi (35°01′N, 97°39′E, altitude of 4272 m), is situated near Zaling lake and Eling lake, Qinhai Province, China. A cold and semi-arid continental climate prevails in the lake basin. The mean annual temperature is –3.7°C, and the mean annual precipitation amount is 321 mm (during 1953–2012), according to data from China’s National Climate Center (Li et al., 2015). Detailed descriptions of the underlying surface conditions and observational information at the Madoi site are provided by Li et al. (2015). A brief review is provided as follows. The vegetation in this area is also typical alpine meadow, with a canopy height of 0.05 m. The soil contains large amounts of gravel and rock fragments. The sensible and latent heat fluxes were also measured by using an EC system, mounted at a height of 3.2 m above the land surface, and the sensor signals were recorded by using a data logger (CR3000, Campbell Scientific, Inc.) at a 10-Hz frequency. The longwave and shortwave radiation were measured by using a net radiometer (CNR-1/CNR-4, Kipp and Zonen) located 1.5 m above the ground. The soil water content and temperature were measured at soil depths of 5, 10, 20, 40, and 80 cm with CS616 and 109L, respectively (Campbell Scientific, Inc.). The air temperature and relative humidity sensors (HMP-45C) were also installed at a height of 3.2 m. Precipitation was measured by using a weighing gauge (T200B, Geonor, Norway). Soil heat flux was measured by using heat flux plates (HPF01) buried within 5–10 cm.

|
| Figure 1 The Tibetan Plateau, Yellow River source region, and the locations of the Zoige and Madoi sites denoted by ZS and GS, repectively. |
For the control experiment, offline simulation experiments were conducted on the TP with CLM4.5 (hereafter referred to as the CTL experiment). The offline experiment used atmospheric forcing data for the Zoige and Madoi sites, and the simulation time was from 1 January 2009 to 31 August 2010 at Zoige, and from 1 June 2013 to 31 July 2014 at Madoi. Zoige data collected prior to September 2009 were eliminated during analysis of the results (equal to an eight-month spin-up in the model), and Madoi data before August 2013 were eliminated (equal to a two-month spin-up in the model). Atmospheric forcing variables required in CLM4.5 to conduct the offline experiment included air temperature, wind speed, humidity, air pressure, rainfall rate, and downward shortwave radiation. Data based on the observations at the two sites described above were used. The time step in the model was set to 30 min. Soil texture, organic matter, and gravel were determined based on observations of the soil samples collected from the Zoige and Madoi sites (Table 2). Other surface parameters were based on the model default values. In order to obtain a more intuitive comparison between simulated and observed soil temperature and humidity values, the simulated results were compared with the observed values by linear interpolation.
We used the thermal conductivity parameterization scheme of Luo (hereafter referred to as the LUO experiment) and the improved organic matter and thermal conductivity parameterization scheme (hereafter referred to as the NEW experiment). All other model settings were the same as those in the CTL experiment.
| Layer | z (m) | zh (m) | Zoige | Madoi | ||||||
| Soil texture* (%) | Organic matter (kg m–3) | Gravel (%) | Soil texture (%) | Organic matter (kg m–3) | Gravel (%) | |||||
| Sand | Clay | Sand | Clay | |||||||
| 1 | 0.0175 | 0.0071 | 32.40 | 2.70 | 119.93 | 0 | 35.20 | 30.00 | 85.00 | 6.14 |
| 2 | 0.0451 | 0.0280 | 32.40 | 2.70 | 119.93 | 0 | 42.17 | 25.50 | 75.12 | 6.14 |
| 3 | 0.0906 | 0.0623 | 32.40 | 2.70 | 119.93 | 0 | 69.23 | 14.03 | 37.26 | 27.09 |
| 4 | 0.1656 | 0.1189 | 26.30 | 3.80 | 66.11 | 0 | 76.44 | 13.59 | 35.02 | 42.92 |
| 5 | 0.2891 | 0.2122 | 30.20 | 3.80 | 42.30 | 0 | 85.42 | 9.42 | 16.28 | 36.00 |
| 6 | 0.4930 | 0.3661 | 35.50 | 3.30 | 26.83 | 0 | 96.51 | 2.47 | 2.63 | 27.95 |
| 7 | 0.8289 | 0.6198 | 56.30 | 1.70 | 7.12 | 0 | 97.13 | 1.82 | 1.41 | 52.02 |
| 8 | 1.3828 | 1.0380 | 68.35 | 2.50 | 2.16 | 0 | 96.18 | 2.96 | 1.33 | 19.49 |
| 9 | 2.2961 | 1.7276 | 87.11 | 2.48 | 0.00 | 0 | 95.72 | 3.20 | 0.00 | 22.73 |
| 10 | 3.4331 | 2.8647 | 92.01 | 1.71 | 0.00 | 0 | 95.60 | 2.95 | 0.00 | 46.94 |
| *Soil texture was measured for soil without the gravel; therefore, %silt = 1 – %sand – %clay. | ||||||||||
The simulation results from the original and modified models were compared with the observed data on the basis of three key statistical measures: bias (Bias), standard error of the estimate (SEE), and correlation coefficient (Corr). The methods used to calculate Bias, SEE, and Corr are shown as follows:
| $\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{\rm{Bias}} = \sum\limits_{i = 1}^n {\frac{{{M_i} - {O_i}}}{n}} ,$ | (15) |
| $\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{\rm{SEE}} = \sqrt {\frac{{\sum\limits_{i = 1}^n {{{\left( {{M_i} - {O_i}} \right)}^2}} }}{{n - 2}}},$ | (16) |
| ${\rm{Corr}} = \frac{{\sum\limits_{i = 1}^n {({M_i} - \overline M )({O_i} - \overline O )} }}{{\sqrt {\sum\limits_{i = 1}^n {{{({M_i} - \overline M )}^2}} } \sqrt {\sum\limits_{i = 1}^n {{{({O_i} - \overline O )}^2}} } }},$ | (17) |
where Mi is simulated data, Oi is observation data, n is the total number of data,
Four freeze–thaw periods were presented according to the soil temperature: the freezing period (soil column experiences freezing processes); the completely frozen period (maximum daily soil temperature below 0°C); the thawing period (soil column profile experiences thawing processes); and the completely thawed period (minimum daily soil temperature remains above 0°C). Moreover, ground diurnal freeze–thaw cycles were believed to have occurred when the daily maximum soil temperature was above 0°C and the minimum soil temperature was below 0°C. In order to avoid the potential impact of random weather processes on the determination of the freeze–thaw period, the occurrence of three consecutive days meeting a chosen set of criteria was used as an indicator of the transition, and the first day was recorded as the start date of the next freeze–thaw period (Guo et al., 2011a, b).
Based on the above classifications, four freeze–thaw periods at the Zoige and Madoi sites at a depth of 5 cm below the surface are listed in Table 3. Based on the observational dataset, at Zoige (Madoi), the duration of the freezing period was 13 (27) days from 5 to 17 November 2009 (6 October to 1 November 2013); the duration of the completely frozen period was 81 (145) days from 18 November 2009 to 6 February 2010 (2 November 2013 to 26 March 2014); the duration of the thawing period was 88 (47) days from 7 February to 5 May 2010 (27 March to 12 May 2014); and the duration of the completely thawed period was 118 (80) days from 6 May to 31 August 2010 (13 May to 31 July 2014).
In the CTL experiment, the freezing and completely frozen periods occurred earlier than in the observed data, and their durations were extended at the Zoige site, while the freezing and thawing periods occurred earlier than the observed periods, and their durations were also extended at the Madoi site. Compared with the CTL experiment, the LUO and NEW experiments performed better with respect to simulating the starting dates of the freezing and completely frozen periods at these two sites. The NEW experiment also performed better with respect to simulating the duration of the four periods, especially for the freezing and completely frozen periods.
| Completely thawed | Freezing | Completely frozen | Thawing | |
| Zoige | ||||
| OBS | 9.1–11.4/65 5.6–8.31/118 | 11.5–11.17/13 | 11.18–2.6/81 | 2.7–5.5/88 |
| CTL | 9.1–10.26/56 4.15–8.31/139 | 10.27–11.10/15 | 11.11–2.17/99 | 2.18–4.14/56 |
| LUO | 9.1–10.30/60 4.16–8.31/138 | 10.31–11.18/19 | 11.19–1.19/62 | 1.20–4.15/86 |
| NEW | 8.1–10.31/61 4.15–8.31/139 | 11.1–11.15/15 | 11.16–1.16/62 | 1.17–4.14/88 |
| Madoi | ||||
| OBS | 8.1–10.5/66 5.13–7.31/80 | 10.6–11.1/27 | 11.2–3.26/145 | 3.27–5.12/47 |
| CTL | 8.1–9.26/57 5.13–7.31/80 | 9.27–11.13/48 | 11.14–2.21/100 | 2.22–5.12/80 |
| LUO | 8.1–9.27/58 5.21–7.31/72 | 9.28–11.16/51 | 11.17–2.21/97 | 2.22–5.20/88 |
| NEW | 8.1–9.27/58 5.24–7.31/69 | 9.28–11.9/43 | 11.10–2.21/104 | 2.22–5.23/91 |
| OBS, observed; CTL, control experiment; LUO, LUO parameterization scheme; NEW, NEW parameterization scheme. | ||||
Figures 2 and 3 show the temporal and spatial variation in the daily mean soil thermal conductivity based on the CTL, LUO, and NEW results for the Zoige and Madoi sites. The soil thermal conductivity was low and relatively stable in the completely frozen period, but high and variable in the completely thawed period. The soil thermal conductivity values in the CTL experiment were the highest during the entire simulation period at these two sites. Previous research has shown that soil thermal conductivity values calculated by using the Farouki scheme were higher than the actual values on the TP (Luo et al., 2009b). Compared with the CTL experiments, the soil thermal conductivity values in the LUO and NEW experiments were relatively similar. The value for the LUO experiment was approximately half the value obtained in the CTL experiments, which was consistent with previous results (Luo et al., 2009b). At Zoige, no obvious differences occurred among the LUO and NEW experiments; however, at Madoi, the soil thermal conductivity values in the NEW scheme were distinctly smaller due to the soil containing a high gravel content (Table 2). As illustrated in Table 2, the soil contains high gravel content at the Madoi site, especially at the depth of 80 cm.
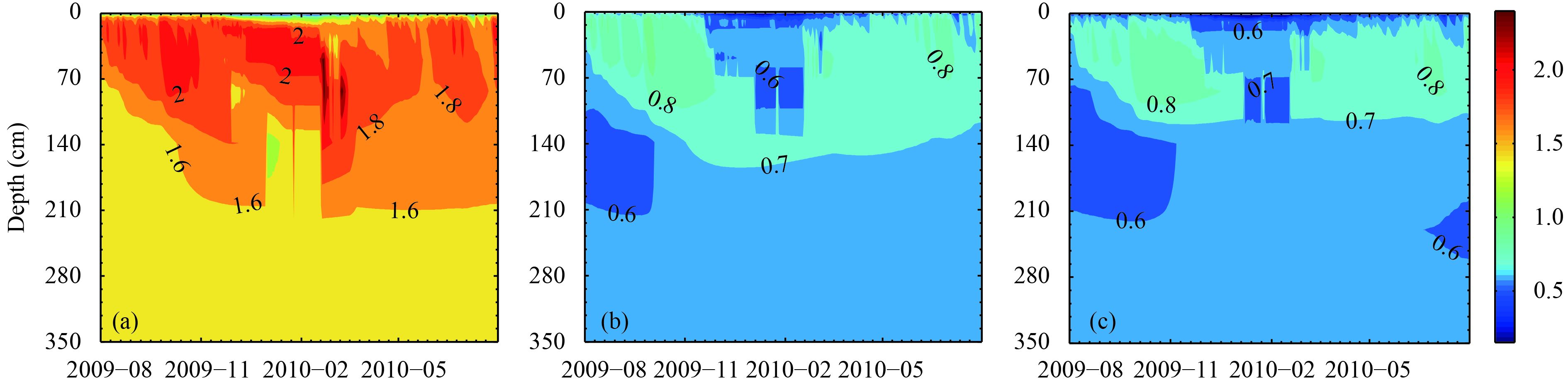
|
| Figure 2 Time–depth evolution of the simulated daily soil thermal conductivity (W m–1 K–1) from the (a) CTL, (b) LUO, and (c) NEW experimemts at the Zoige site. |
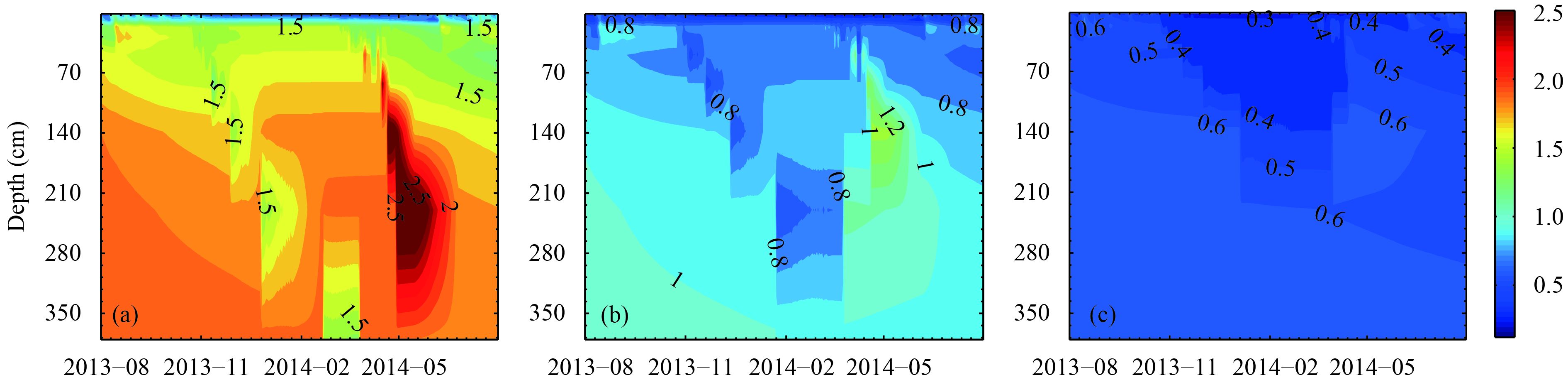
|
| Figure 3 As in Fig. 2, but at the Madoi site. |
Figure 4 compares observed data to the CTL, LUO, and NEW results for soil temperature at four soil depths (10, 20, 40, and 80 cm) at the Zoige site. In the CTL experiment, there was a significant underestimation during the freezing and completely frozen periods, but a significant overestimation during the thawing period, at these four depths. The high soil thermal conductivity value in the CTL experiment may have led to the release of more heat to the air during the freezing period and greater absorption of heat from the air during the thawing period (Fig. 8d). Therefore, the soil temperature may have been underestimated during the freezing and overestimated during thawing. Compared with the CTL experiment, the LUO and NEW experiments indicated some improvement during the freezing, completely frozen, and thawing periods. During the freezing period, the soil released less heat to the air, and soil temperature was higher than in the CTL experiment. Moreover, the thawing period in the LUO and NEW experiments was advanced by approximately 30 days compared with the CTL experiment (Table 3), and the simulated soil temperature was higher than that in the CTL experiment. On average, in these three periods, more substantial improvements occurred, where the Bias was reduced from –0.63°C in the CTL experiment to 0.15°C in the LUO experiment and 0.13°C in the NEW experiment; SEE was reduced from 2.04°C to 1.90°C and 1.85°C, and the Corr increased from 0.70 to 0.70 and 0.71, respectively. However, during the completely thawed period, the Bias increased, especially in May and June 2010 (Figs. 4c, d). Throughout the whole year, the Bias and SEE for the observed data decreased, but the Corr decreased (Table 4). Overall, the LUO and NEW experiments improved the soil temperature simulation, effectively reduced the cold SEE by 7% and 10% during the freezing, completely frozen, and thawing periods, and reduced the cold SEE by 6% and 4%, respectively, throughout the whole year.
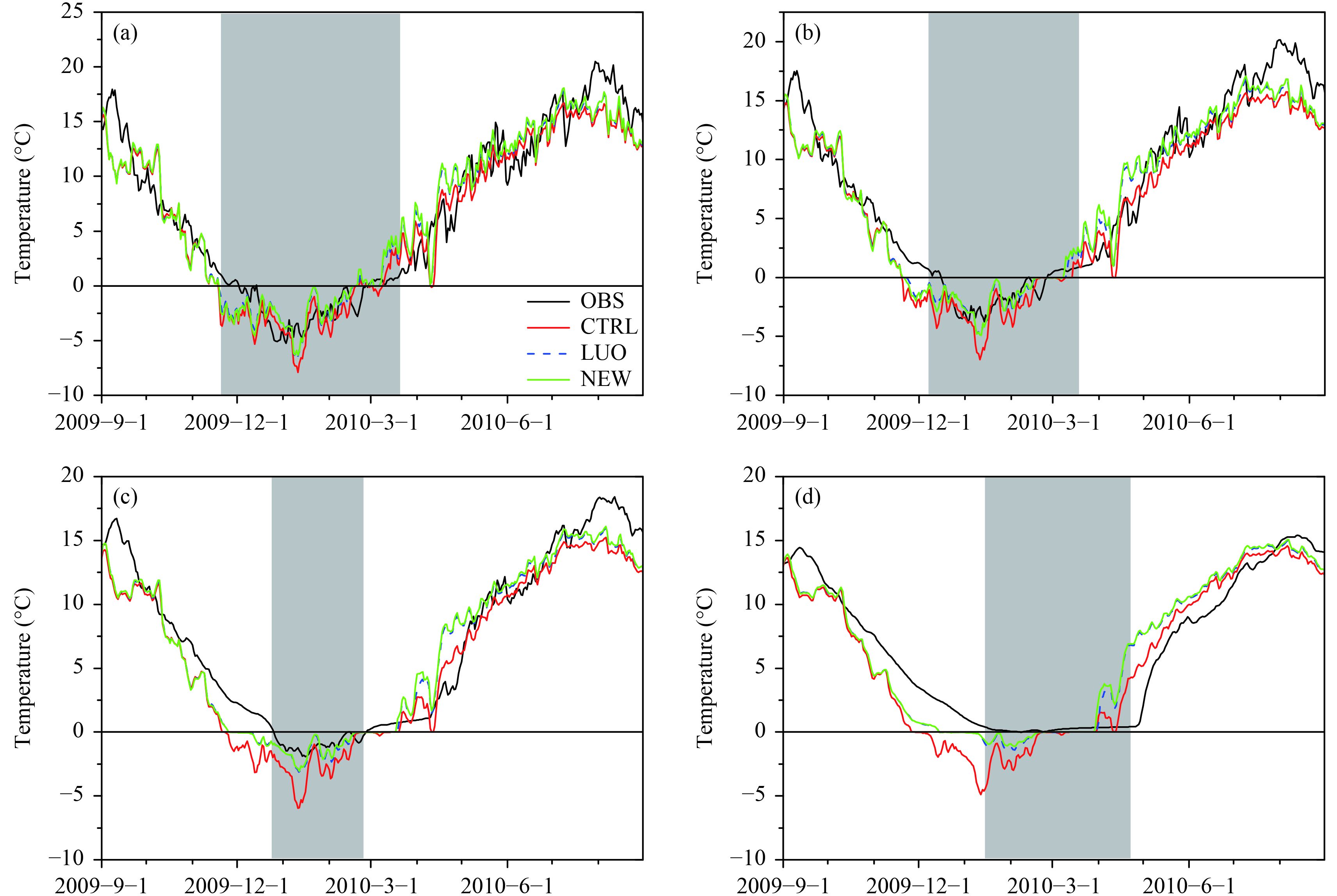
|
| Figure 4 Observed and simulated daily soil temperature (°C) at (a) 10 cm, (b) 20 cm, (c) 40 cm, and (d) 80 cm at the Zoige site. Shaded areas in the figure denote the duration of the freezing, completely frozen, and thawing periods, based on observed soil temperature. |
Figure 5 displays the daily simulated and observed soil temperature at different depths at the Madoi site. In the CTL experiment, the model tended to underestimate soil temperature at the four depths during the freezing period, but overestimated soil temperature during the thawing period. Compared with CTL, the LUO and NEW experiments improved soil temperature at these four depths and effectively decreased the Bias, especially in the case of NEW. In the three freeze–thaw periods and throughout the whole year, the Bias and SEE of the observed data decreased significantly, and the Corr (with respect to the observed data) increased (Table 4). For example, throughout the whole year, the Bias, SEE, and Corr were –0.07°C, 2.22°C, and 0.96 at the depth of 80 cm in CTL, compared with –0.03°C, 1.36°C, and 0.98, respectively, in NEW. The soil temperature in NEW clearly improved, mainly due to the more accurate soil conductivity that was calculated with gravel included. As illustrate inTable 2, the soil contains a high gravel content at the Madoi site, especially at the depth of 80 cm. Overall, the LUO and NEW experiments improved the soil temperature simulation and effectively decreased cold biases throughout the whole year, especially in NEW. The average cold SEE reduced by 1% in LUO and 5% in NEW in the three freeze–thaw periods, and decreased by 8% in LUO and 20% in NEW throughout the whole year.

|
| Figure 5 As in Fig. 4, but at the Madoi site. |
| Depth (cm) | Bias (°C) | SEE (°C) | Corr | ||||||
| CTL | LUO | NEW | CTL | LUO | NEW | CTL | LUO | NEW | |
| Zoige | |||||||||
| 10* | –0.63 | 0.23 | 0.18 | 1.99 | 2.04 | 1.88 | 0.61 | 0.56 | 0.60 |
| 20* | –0.79 | –0.43 | –0.34 | 2.23 | 1.89 | 1.78 | 0.71 | 0.70 | 0.72 |
| 40* | –0.85 | 0.03 | 0.17 | 1.92 | 1.51 | 1.53 | 0.61 | 0.64 | 0.66 |
| 80* | –0.25 | 0.77 | 0.52 | 2.02 | 2.17 | 2.19 | 0.86 | 0.88 | 0.87 |
| Ave* | –0.63 | 0.15 | 0.13 | 2.04 | 1.90 | 1.85 | 0.70 | 0.70 | 0.71 |
| 10** | –0.75 | –0.12 | –0.01 | 2.42 | 2.41 | 2.50 | 0.95 | 0.95 | 0.94 |
| 20** | –1.38 | –0.64 | –0.52 | 2.38 | 2.14 | 2.12 | 0.97 | 0.96 | 0.96 |
| 40** | –1.37 | –0.60 | –0.50 | 2.20 | 1.99 | 2.03 | 0.97 | 0.96 | 0.95 |
| 80** | –0.83 | –0.04 | 0.04 | 2.22 | 2.16 | 2.21 | 0.94 | 0.93 | 0.92 |
| Ave** | –1.08 | –0.35 | –0.25 | 2.31 | 2.18 | 2.22 | 0.96 | 0.95 | 0.94 |
| Madoi | |||||||||
| 10* | 0.66 | 0.08 | –0.18 | 2.66 | 2.63 | 2.52 | 0.84 | 0.85 | 0.86 |
| 20* | 0.93 | 0.25 | –0.03 | 2.68 | 2.67 | 2.53 | 0.81 | 0.82 | 0.82 |
| 40* | 0.95 | 0.26 | –0.03 | 2.72 | 2.70 | 2.57 | 0.81 | 0.82 | 0.82 |
| 80* | 0.77 | 0.15 | –0.18 | 2.91 | 2.86 | 2.77 | 0.84 | 0.85 | 0.85 |
| Ave* | 0.83 | 0.19 | –0.11 | 2.74 | 2.72 | 2.60 | 0.83 | 0.84 | 0.84 |
| 10** | 0.81 | 0.59 | 0.04 | 2.67 | 2.67 | 2.45 | 0.95 | 0.95 | 0.96 |
| 20** | 0.67 | 0.53 | –0.03 | 2.41 | 2.41 | 2.08 | 0.96 | 0.97 | 0.97 |
| 40** | 0.52 | 0.46 | –0.03 | 2.13 | 2.00 | 1.63 | 0.97 | 0.97 | 0.98 |
| 80** | –0.07 | –0.04 | –0.03 | 2.22 | 1.62 | 1.36 | 0.96 | 0.98 | 0.98 |
| Ave** | 0.48 | 0.39 | –0.01 | 2.36 | 2.18 | 1.88 | 0.96 | 0.97 | 0.97 |
| *Statistical results in the freezing, completely frozen, and thawing periods; **statistical results in the whole year. | |||||||||
Figure 6 shows the daily simulated and observed liquid water content at different depths at the Zoige site. In the CTL experiment, there was a substantial underestimation of the soil liquid water content at the four depths, especially in the completely frozen period. The first date of soil freezing occurred approximately 10–30 days earlier, while the first date of soil thawing occurred approximately 15–30 days earlier at these four depths in the CTL experiment. The liquid water content at all four depths decreased earlier than the observed during the freezing period and increased earlier than the observed during the thawing period. The liquid water content was lower than observed because soil temperature was lower than the observed during the freezing and completely frozen periods. Compared with CTL, the LUO and NEW experiments produced wetter soil conditions at these four depths and effectively decreased dry biases, especially in the completely frozen period because of the improved soil temperature. The LUO and NEW experiments delayed the first date of soil freezing substantially, especially in NEW at the depths of 40 and 80 cm. From Table 5, it is seen that the liquid water content in NEW was a better fit to the observtions. In one year, the Bias and SEE associated with the observed data decreased significantly. For example, the average Bias and SEE of these four depths were 0.005 and 0.055, respectively, in NEW. These values were smaller than those (0.032 and 0.068, respectively) in CTL. The liquid water content was higher in NEW than in CTL and LUO throughout the whole year because of the volumetric water content at saturation θsat (figure omitted), and the water holding capability in NEW was greater than that in CTL and LUO. There was no significant improvement in the average Corr between simulations and observations (0.81, 0.80, and 0.79 for CTL, LUO, and NEW, respectively). Overall, the LUO and NEW experiments improved the simulation of liquid water content and decreased the underestimation throughout the whole year, especially in NEW. The average SEE reduced by 3% in LUO and 8% in NEW in the three freeze–thaw periods, and reduced by 9% in the LUO experiment and 10% throughout the NEW experiment in the whole year.

|
| Figure 6 As in Fig. 4, but for soil liquid water content (m3 m–3). |
Figure 7 compares the observed data to the CTL, LUO, and NEW liquid water content results at the Madoi site. As illustrated in Table 2, at the Madoi site, topsoil from the surface to 30 cm in depth also contains high organic matter, and the underlying soil layers contain higher gravel content than the top soil layers. In the CTL experiment, the soil freeze and thaw dates were also advanced at the four studied depths of the Madoi site. At 10 cm, the CTL experiment overestimated the soil liquid water content during the whole simulation period. Notably, the NEW experiment presented substantial improvements, where the Bias decreased and the Corr increased during the freezing, completely frozen, and thawing periods. As illustrated in Table 5, the average SEE reduced by 2% in NEW in the three freeze–thaw periods. However, the NEW experiment increased the overestimation during the completely thawed period (Fig. 7). Consequently, the SEE increased by 11%, although the Corr improved throughout the whole year. In NEW, the liquid water content was higher than that in CTL and LUO throughout the whole year because of the volumetric water content at saturation θsat, i.e., the water holding capability in NEW was higher than that in CTL and LUO. Therefore, optimization concerning the numerical description of the hydraulic and thermal properties during the freeze–thaw process on the TP is needed in future studies.
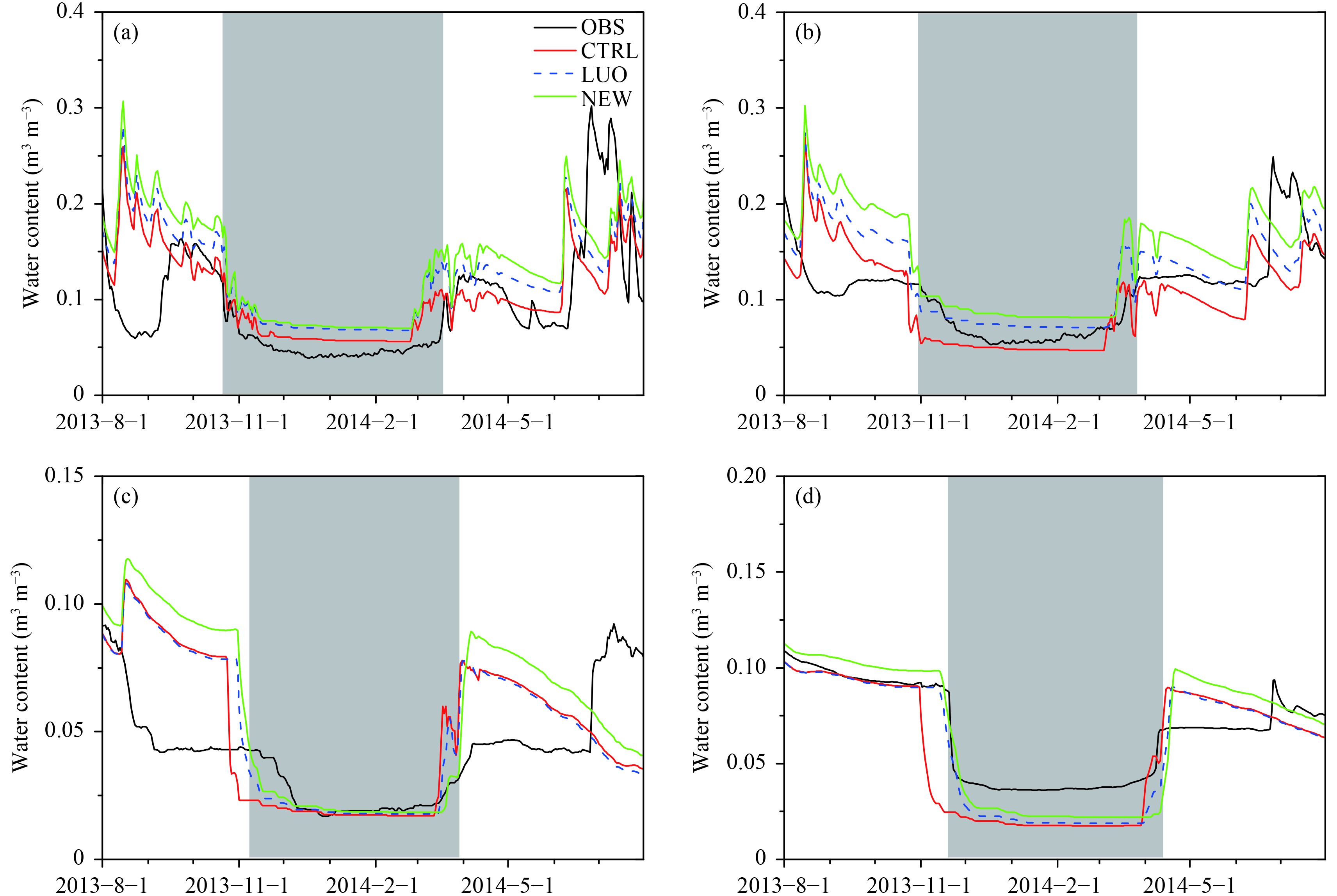
|
| Figure 7 As in Fig. 6, but at the Madoi site. |
| Depth (cm) | Bias (m3 m–3) | SEE (m3 m–3) | Corr | ||||||
| CTL | LUO | NEW | CTL | LUO | NEW | CTL | LUO | NEW | |
| Zoige | |||||||||
| 10* | –0.031 | –0.022 | 0.019 | 0.065 | 0.066 | 0.062 | 0.69 | 0.63 | 0.60 |
| 20* | –0.016 | –0.004 | 0.020 | 0.051 | 0.051 | 0.047 | 0.68 | 0.68 | 0.65 |
| 40* | –0.017 | –0.007 | 0.023 | 0.051 | 0.049 | 0.047 | 0.48 | 0.54 | 0.61 |
| 80* | –0.024 | –0.014 | 0.016 | 0.069 | 0.063 | 0.061 | 0.79 | 0.80 | 0.83 |
| Ave* | –0.022 | –0.012 | 0.020 | 0.059 | 0.057 | 0.054 | 0.66 | 0.66 | 0.67 |
| 10** | –0.054 | –0.057 | –0.027 | 0.082 | 0.088 | 0.075 | 0.86 | 0.83 | 0.81 |
| 20** | –0.021 | –0.015 | –0.006 | 0.060 | 0.058 | 0.058 | 0.82 | 0.81 | 0.80 |
| 40** | –0.046 | –0.041 | –0.005 | 0.071 | 0.059 | 0.044 | 0.81 | 0.84 | 0.83 |
| 80** | –0.008 | 0.004 | 0.032 | 0.059 | 0.043 | 0.068 | 0.75 | 0.72 | 0.72 |
| Ave** | –0.032 | –0.029 | –0.018 | 0.068 | 0.062 | 0.061 | 0.81 | 0.80 | 0.79 |
| Madoi | |||||||||
| 10* | –0.039 | –0.033 | 0.004 | 0.068 | 0.069 | 0.062 | 0.82 | 0.76 | 0.78 |
| 20* | –0.031 | –0.023 | 0.014 | 0.058 | 0.059 | 0.058 | 0.81 | 0.83 | 0.86 |
| 40* | –0.029 | –0.022 | 0.015 | 0.059 | 0.058 | 0.057 | 0.82 | 0.84 | 0.87 |
| 80* | –0.033 | –0.028 | 0.005 | 0.062 | 0.066 | 0.066 | 0.83 | 0.85 | 0.88 |
| Ave* | –0.033 | –0.027 | 0.010 | 0.062 | 0.063 | 0.061 | 0.82 | 0.82 | 0.85 |
| 10** | 0.021 | 0.031 | 0.029 | 0.055 | 0.061 | 0.061 | 0.49 | 0.51 | 0.52 |
| 20** | 0.017 | 0.031 | 0.036 | 0.054 | 0.061 | 0.062 | 0.49 | 0.51 | 0.54 |
| 40** | –0.012 | 0.018 | 0.034 | 0.038 | 0.037 | 0.046 | 0.60 | 0.62 | 0.64 |
| 80** | 0.009 | 0.006 | 0.024 | 0.029 | 0.026 | 0.028 | 0.48 | 0.49 | 0.53 |
| Ave** | 0.015 | 0.022 | 0.031 | 0.044 | 0.046 | 0.049 | 0.52 | 0.53 | 0.56 |
| *Statistical results in the freezing, completely frozen, and thawing periods; **statistical results in the whole year. | |||||||||
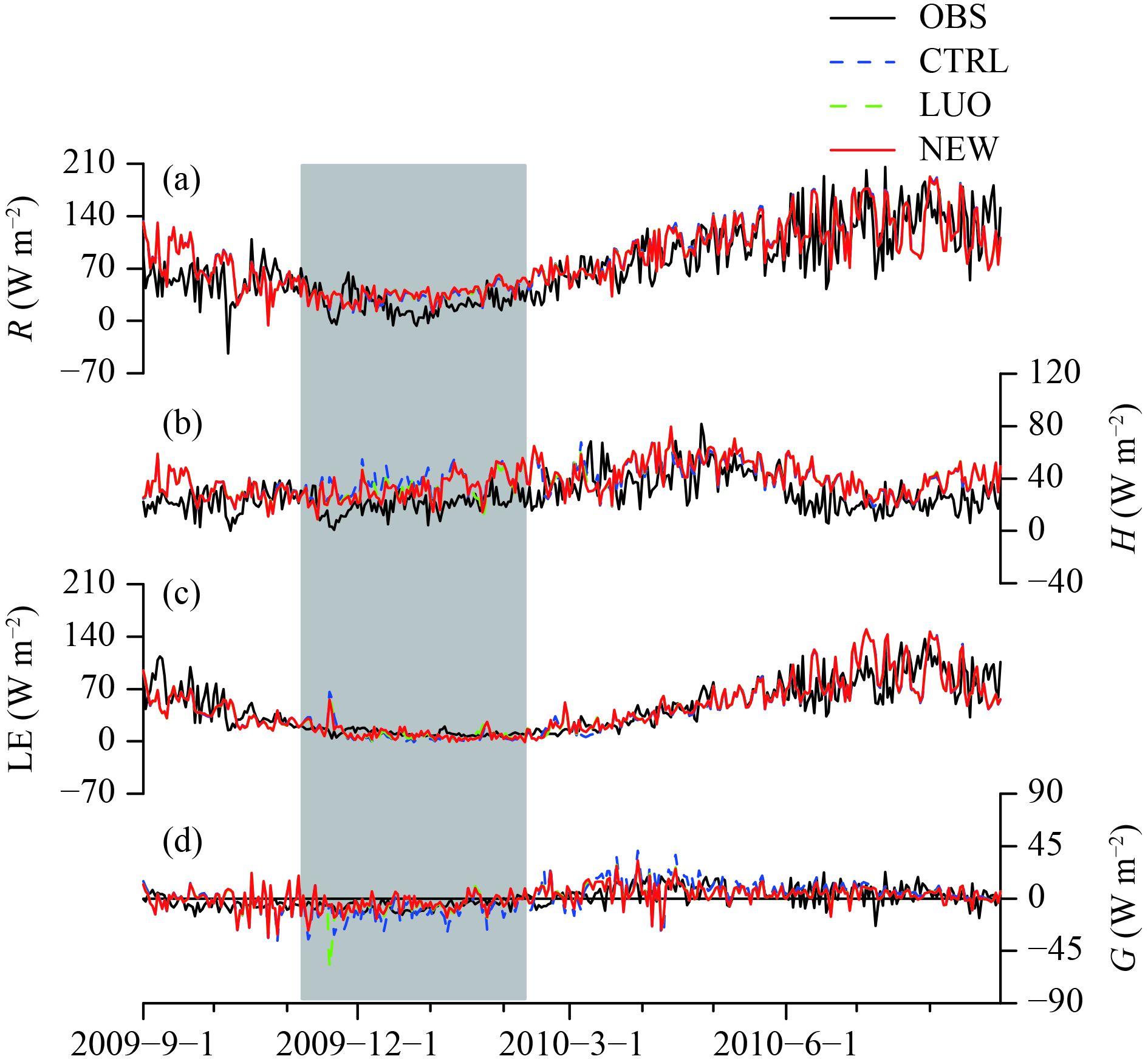
|
| Figure 8 Observed and simulated daily energy flux (W m–2) at the Zoige site: (a) net radiation (R), (b) sensible heat flux (H), (c) latent heat flux (LE), and (d) surface soil heat flux (G). Shaded areas denote the duration of the freezing, completely frozen, and thawing periods, based on observed soil temperature at a depth of 5 cm. |
Figure 8 illustrates the simulated and observed net radiation, sensible heat flux, latent heat flux, and surface soil heat flux at the Zoige site. In the three freeze–thaw periods, although the Bias and SEE were very small with respect to the simulated and observed data, the Bias and SEE associated with the observed data decreased significantly, especially in the NEW experiment (Table 6). Throughout the whole year, there was an overestimation of net radiation, and the bias was 9.80 W m–2. The LUO and NEW experiments decreased this Bias to 9.46 and 9.18 W m–2, respectively. The simulated heat fluxes from the three experiments matched with the observations, but higher than the observations in magnitude (Fig. 8b). The Bias between the simulation and the observation in CTL, LUO, and NEW was 10.85, 10.58, and 10.41 W m–2, respectively. The Corr was 0.36, 0.44, and 0.43, respectively. As shown in Fig. 8c, the CTL, LUO, and NEW experiments also captured the seasonal pattern of latent heat flux. The Bias of the original simulation associated with the observation was –1.78 W m–2, while the modified simulation resulted in values of –0.65 and –0.40 W m–2. In all cases, their Corr was 0.80. In the CTL experiment, the soil surface heat fluxes were underestimated (negative values decreased, absolute values increased) during the freezing and the completely frozen periods, but were overestimated during the thawing period. This agrees with the findings presented in Section 4.2, i.e., the soil temperature was underestimated during freezing and overestimated during thawing. The LUO and NEW experiments produced a much better simulation, with the peak of soil surface heat flux being well simulated. The Bias of the simulations and observations was 1.18, 0.84, and 0.87 W m–2, respectively. As a whole, these results indicate that the estimations of net radiation, sensible heat flux, latent heat flux, and soil surface heat flux were much improved by the new organic matter and thermal conductivity parameterization used for the Zoige site. The average SEE for these four variables reduced by 10%, 11%, 47%, and 12% in the three freeze–thaw periods, and by 1%, 3%, 2%, and 16%, respectively, throughout the whole year.
As shown in Table 6, at Madoi, the Bias and SEE relative to the observed data in the NEW experiment also decreased significantly in the three freeze–thaw periods, and throughout the whole year. In CTL, there was an underestimation of net radiation and overestimation of sensible and latent heat fluxes. The soil surface heat flux was also underestimated during the freezing and completely frozen periods, and overestimated during the thawing period (Fig. 9). In LUO, the Bias of net radiation and surface heat flux reduced, but that for sensible and latent heat fluxes increased. In NEW, except for an increase in the Bias of sensible heat flux throughout the whole year, the Bias of all other variables reduced. The relatively wetter soils in NEW decreased the latent heat flux throughout the whole year. The average SEE for these four variables decreased by 1%, 7%, 25%, and 34% in the three freeze–thaw periods, and the average SEE for latent heat flux and soil surface heat flux by 10% and 27%, respectively, throughout the whole year. As a result of the improved parameterization schemes, the NEW experiment generally captured the observed daily energy variations well, except for the slightly overestimated sensible heat flux throughout the whole year.
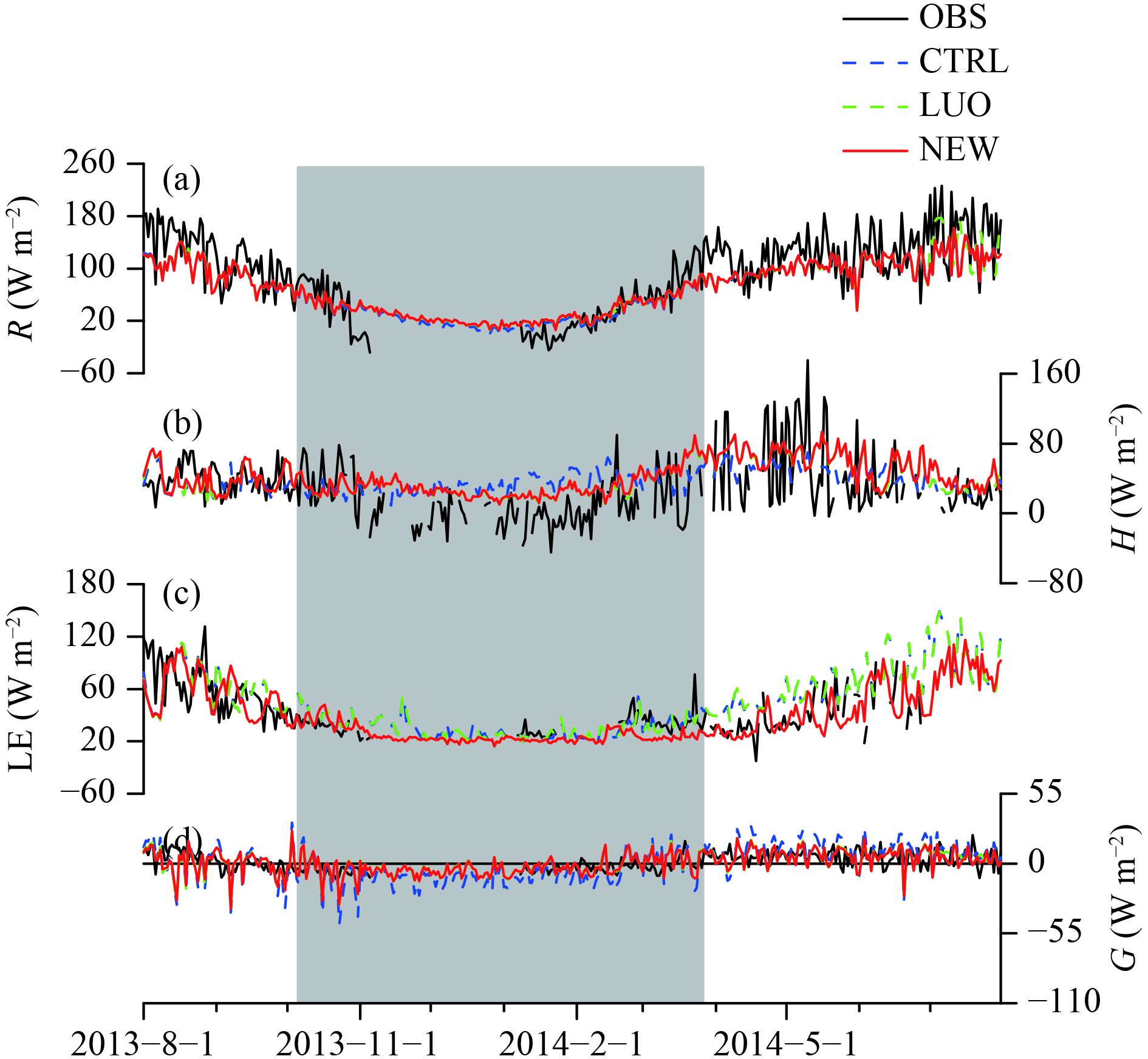
|
| Figure 9 As in Fig. 8, but for the Madoi site. |
| Component | Bias (W m–2) | SEE (W m–2) | Corr | ||||||
| CTL | LUO | NEW | CTL | LUO | NEW | CTL | LUO | NEW | |
| Zoige | |||||||||
| R* | –0.04 | –0.03 | 0.00 | 0.07 | 0.07 | 0.06 | 0.84 | 0.82 | 0.80 |
| H* | –0.02 | –0.01 | 0.00 | 0.07 | 0.07 | 0.06 | 0.73 | 0.74 | 0.71 |
| LE* | –0.06 | –0.04 | 0.00 | 0.09 | 0.06 | 0.05 | 0.69 | 0.82 | 0.82 |
| G* | –0.04 | 0.00 | 0.01 | 0.07 | 0.04 | 0.06 | 0.72 | 0.86 | 0.84 |
| R** | 9.80 | 9.46 | 9.18 | 34.21 | 34.04 | 33.99 | 0.75 | 0.75 | 0.75 |
| H** | 10.85 | 10.58 | 10.41 | 17.95 | 17.38 | 17.42 | 0.36 | 0.44 | 0.43 |
| LE** | –1.78 | –0.65 | –0.40 | 21.90 | 21.59 | 21.47 | 0.80 | 0.80 | 0.80 |
| G** | 1.18 | 0.84 | 0.87 | 12.11 | 10.08 | 10.15 | 0.42 | 0.35 | 0.38 |
| Madoi | |||||||||
| R* | –7.11 | –4.84 | –4.12 | 31.75 | 31.69 | 31.43 | 0.85 | 0.85 | 0.85 |
| H* | 19.81 | 19.54 | 18.83 | 40.90 | 38.38 | 38.07 | 0.39 | 0.52 | 0.52 |
| LE* | 10.06 | 10.32 | –6.28 | 22.11 | 22.51 | 16.50 | 0.08 | 0.06 | 0.09 |
| G* | –1.02 | 1.47 | 1.20 | 12.85 | 8.82 | 8.43 | 0.45 | 0.38 | 0.41 |
| R** | –17.08 | –14.85 | –15.62 | 40.48 | 41.07 | 40.63 | 0.78 | 0.75 | 0.78 |
| H** | 10.95 | 12.45 | 13.91 | 35.31 | 35.28 | 35.61 | 0.22 | 0.33 | 0.34 |
| LE** | 9.83 | 10.13 | –5.01 | 28.36 | 28.87 | 25.44 | 0.51 | 0.50 | 0.57 |
| G** | 1.29 | 0.48 | 0.33 | 13.33 | 10.03 | 9.71 | 0.37 | 0.28 | 0.30 |
| *Statistical result in the freezing, completely frozen, and thawing periods; **statistical result in the whole year; R, net radiation; H, sensible heat flux; LE, latent heat flux; and G, surface soil heat flux. | |||||||||
Soil surfaces, comprising both bare soil and soil under vegetation have different thermal and hydraulic properties, cause different behavior in heat and moisture transport, and have an important influence on land–atmosphere interactions. In the TP, the soil genesis layer is shallow and contains large soil particles and a high content of broken stones and gravel. The soil stratification within the TP is typically that of alpine meadows containing organic matter in the topsoil layer. By considering the gravel and organic matter in the soil, an improved soil parameterization with organic and thermal conductivity schemes was introduced into CLM4.5. The ability of the model to simultaneously simulate the duration of freeze–thaw periods, soil temperature, soil moisture, and surface energy during freeze–thaw processes was validated based on the data from the Zoige and Madoi sites over the TP.
The results indicate that the NEW parameterization performed better with respect to simulating the duration of the four periods, especially the freezing and completely frozen periods. The NEW experiment improved soil temperature and decreased cold biases effectively because of smaller soil thermal conductivity values. The average SEE reduced by 4% for the Zoige site and by 20% for the Madoi site. The water holding ability was higher than that in the original experiments, which effectively decreased the dry biases of soil liquid water content; the average SEE reduced by 10% at the Zoige site, but overestimation occurred at the Madoi site. The net radiation, latent heat flux and soil surface heat flux simulations for both sites were much improved by the new organic matter and thermal conductivity parameterization scheme, whereas the sensible heat flux may have been overestimated during the study period. Therefore, optimization of the numerical description of the hydraulic and thermal properties of the freeze–thaw processes on the TP is still necessary in future studies.
Acknowledgments. The observation data were provided by the Zoige Alpine Wetlands Ecosystem Research Station and the Madoi Grassland Station. We acknowledge computing resources and time at the Supercomputing Center, Big Data Center, Northwest Institute of Eco-Environment and Resources, Chinese Academy of Sciences. Special thanks are given to the anonymous reviewers and the editor for their very constructive comments.
| Beringer, J., A. H. Lynch, F. S. Chapin III, et al., 2001: The representation of arctic soils in the land surface model: The importance of mosses. J. Climate, 14, 3324–3335. DOI:10.1175/1520-0442(2001)014<3324:TROASI>2.0.CO;2 |
| Bonan, G. B., 1996: A Land Surface Model (LSM version 1.0) for Ecological, Hydrological, and Atmospheric Studies: Technical Description and User’s Guide. NCAR Technical Note NCAR/TN-417+STR, doi: 10.5065/D6DF6P5X. |
| Bonan, G. B., P. J. Lawrence, K. W. Oleson, et al., 2011: Improving canopy processes in the community land model version 4 (CLM4) using global flux fields empirically inferred from fluxnet data. J. Geophys. Res., 116(G2). DOI:10.1029/2010JG001593 |
| Côté, M. Konrad, 2005a: Thermal conductivity of base-course materials. Canad. Geotech. J., 42, 61–78. DOI:10.1139/t04-081 |
| Côté, M. Konrad, 2005b: A generalized thermal conductivity model for soils and construction materials. Canad. Geotech. J., 42, 443–458. DOI:10.1139/t04-106 |
| Chen, B. L., S. H. Lü, and S. Q. Luo, 2012a: Simulation analysis on land surface process at maqu station in the Qinghai–Xizang Plateau using community land model. Plateau Meteor., 31, 1511–1522. |
| Chen, B. L., S. Q. Luo, S. H. Lü, et al., 2014a: Effects of the soil freeze–thaw process on the regional climate of the Qinghai–Tibet Plateau. Climate Res., 59, 243–257. DOI:10.3354/cr01217 |
| Chen, B. L., S. Q. Luo, S. H. Lü, et al., 2014b: Validation and comparison of the simulation at Zoigê station during freezing and thawing with land surface model CLM. Climatic Environ. Res., 19, 649–658. DOI:10.3878/j.issn.1006-9585.2014.13013 |
| Chen, B. L., S. Q. Luo, S. H. Lü, et al., 2014c: Simulation and improvement of soil temperature and moisture at zoige station in source region of the Yellow River during freezing and thawing. Plateau Meteor., 33, 337–345. |
| Chen, Y. Y., K. Yang, W. J. Tang, et al., 2012: Parameterizing soil organic carbon’s impacts on soil porosity and thermal parameters for eastern Tibet grasslands. Sci. China Earth Sci., 55, 1001–1011. DOI:10.1007/s11430-012-4433-0 |
| Fang, X. W., S. Q. Luo, S. H. Lyu, et al., 2016: A simulation and validation of CLM during freeze–thaw on the Tibetan Plateau. Adv. Meteor., 2016, 9476098. DOI:10.1155/2016/9476098 |
| Farouki, O. T., 1981: The thermal properties of soils in cold regions. Cold Regions Sci. Technol., 5, 67–75. DOI:10.1016/0165-232X(81)90041-0 |
| Farouki, O. T., 1986: Thermal Properties of Soils. Series on Rock and Soil Mechanics, Trans. Tech. Publ., Clausthal-Zellerfeld, Germany, Vol. 11, 12–28. |
| Gao, Y. H., K. Li, F. Chen, et al., 2015: Assessing and improving Noah-MP land model simulations for the central Tibetan Plateau. J. Geophys. Res., 120, 9258–9278. DOI:10.1002/2015JD023404 |
| Gao, Z. Q., 2005: Determination of soil heat flux in a Tibetan short-grass prairie. Bound.-Layer Meteor., 114, 165–178. DOI:10.1007/s10546-004-8661-5 |
| Gao, Z. Q., X. G. Fan, and L. G. Bian, 2003: An analytical solution to one-dimensional thermal conduction-convection in soil. Soil Science, 168, 99–107. DOI:10.1097/00010694-200302000-00004 |
| Gao, Z. Q., N. Chae, J. Kim, et al., 2004: Modeling of surface energy partitioning, surface temperature, and soil wetness in the Tibetan prairie using the simple biosphere model 2 (SiB2). J. Geophys. Res., 109(D6). DOI:10.1029/2003JD004089 |
| Guo, D. L., M. X. Yang, and H. J. Wang, 2011a: Sensible and latent heat flux response to diurnal variation in soil surface temperature and moisture under different freeze/thaw soil conditions in the seasonal frozen soil region of the central Tibetan Plateau. Environ. Earth Sci., 63, 97–107. DOI:10.1007/s12665-010-0672-6 |
| Guo, D. L., M. X. Yang, and H. J. Wang, 2011b: Characteristics of land surface heat and water exchange under different soil freeze/thaw conditions over the central Tibetan Plateau. Hydrol. Processes, 25, 2531–2541. DOI:10.1002/hyp.8025 |
| Jin, H. J., R. X. He, G. D. Cheng, et al., 2009: Changes in frozen ground in the source area of the Yellow River on the Qinghai–Tibet Plateau, China, and their eco-environmental impacts. Environ. Res. Lett., 4, 045206. DOI:10.1088/1748-9326/4/4/045206 |
| Johansen, O., 1975: Thermal conductivity of soils. Ph. D. dissertation, O US Army Cold Regions Research and Engineering Lab, Trondheim, Norway, 236 pp. |
| Lawrence, D. M., and A. G. Slater, 2008: Incorporating organic soil into a global climate model. Climate Dyn., 30, 145–160. DOI:10.1007/s00382-007-0278-1 |
| Lawrence, D. M., A. G. Slater, V. E. Romanovsky, et al., 2008: Sensitivity of a model projection of near-surface permafrost degradation to soil column depth and representation of soil organic matter. J. Geophys. Res., 113(F2). DOI:10.1029/2007JF000883 |
| Lawrence, D. M., K. W. Oleson, M. G. Flanner, et al., 2011: Parameterization improvements and functional and structural advances in version 4 of the community land model. J. Adv. Model. Earth Sys., 3. DOI:10.1029/2011MS00045 |
| Letts, M. G., N. T. Roulet, N. T. Comer, et al., 2000: Parametrization of peatland hydraulic properties for the Canadian land surface scheme. Atmos.–Ocean, 38, 141–160. DOI:10.1080/07055900.2000.9649643 |
| Li, Z. G., S. H. Lyu, Y. H. Ao, et al., 2015: Long-term energy flux and radiation balance observations over Lake Ngoring, Tibetan Plateau. Atmos. Res., 155, 13–25. DOI:10.1016/j.atmosres.2014.11.019 |
| Liu, X. D., and B. D. Chen, 2000: Climatic warming in the Tibetan Plateau during recent decades. Int. J. Climatol., 20, 1729–1742. DOI:10.1002/(ISSN)1097-0088 |
| Luo, S. Q., S. H. Lü, Y. Zhang, et al., 2008: Simulation analysis on land surface process of BJ site of central Tibetan Plateau using colm. Plateau Meteor., 27, 259–271. |
| Luo, S. Q., S. H. Lü, and Y. Zhang, 2009a: Development and validation of the frozen soil parameterization scheme in common land model. Cold Regions Sci. Technol., 55, 130–140. DOI:10.1016/j.coldregions.2008.07.009 |
| Luo, S. Q., S. H. Lü, Y. Zhang, et al., 2009b: Soil thermal conductivity parameterization establishment and application in numerical model of central Tibetan Plateau. Chinese J. Geophy., 52, 919–928. |
| Luo, S. Q., X. W. Fang, S. H. Lyu, et al., 2016: Frozen ground temperature trends associated with climate change in the Tibetan Plateau three river source region from 1980 to 2014. Climate Res., 67, 241–255. DOI:10.3354/cr01371 |
| Luo, S. Q., X. W. Fang, S. H. Lyu, et al., 2017: Interdecadal changes in the freeze depth and period of frozen soil on the Three Rivers Source Region in China from 1960 to 2014. Adv. Meteor., 2017, 5931467. DOI:10.1155/2017/5931467 |
| Oleson, K. W., D. M. Lawrence, G. B. Bonan, et al., 2010: Technical Description of Version 4.0 of the Community Land Model (CLM). NCAR Technical Note NCAR/TN-478+STR, doi: 10.5065/D6FB50WZ. |
| Oleson, K. W., D. M. Lawrence, G. B. Bonan, et al., 2013: Technical Description of Version 4.5 of the Community Land Model (CLM). NCAR Technical Note NCAR/TN-503+STR, 420 pp, doi: 10.5065/D6RR1W7M. |
| Peter-Lidard, C. D., E. Blackrurn, X. Liang, et al., 1998: The effect of soil thermal conductivity parameterization on surface energy fluxes and temperatures. J. Atmos. Sci., 55, 1209–1224. DOI:10.1175/1520-0469(1998)055<1209:TEOSTC>2.0.CO;2 |
| Shang, L. Y., Y. Zhang, S. H. Lü, et al., 2015: Energy exchange of an alpine grassland on the eastern Qinghai–Tibetan Plateau. Sci. Bull., 60, 435–446. DOI:10.1007/s11434-014-0685-8 |
| Subin, Z. M., W. J. Riley, and D. Mironov, 2012: An improved lake model for climate simulations: Model structure, evaluation, and sensitivity analyses in CESM1. J. Adv. Model. Earth Sys., 4, 2001. DOI:10.1029/2011MS000072 |
| Sun, S. F., 2005: Physical, Biochemical Mechanism and Parametric Model of Land Surface Processes. China Meteorological Press, Beijing, 84 pp. (in Chinese) |
| Swenson, S. C., and D. M. Lawrence, 2012: A new fractional snow-covered area parameterization for the community land model and its effect on the surface energy balance. J. Geophys. Res., 117(D21), D21107. DOI:10.1029/2012JD018178 |
| Swenson, S. C., D. M. Lawrence, and H. Lee, 2012: Improved simulation of the terrestrial hydrological cycle in permafrost regions by the community land model. J. Adv. Model. Earth Sys., 4, M8002. DOI:10.1029/2012MS000165 |
| Wang, C. H., R. Shi, and H. C. Zuo, 2008: Analysis on simulation of characteristic of land surface in western Qinghai–Xizang Plateau during frozen and thawing. Plateau Meteor., 27, 239–248. |
| Wang, C., Z. G. Wei, Z. C. Li, et al., 2017: Testing and improving the performance of the Common Land Model: A case study for the Gobi landscape. J. Meteor. Res., 31, 625–632. DOI:10.1007/s13351-017-6080-z |
| Wang, S. Y., Y. Zhang, S. H. Lü, et al., 2016: Biophysical regulation of carbon fluxes over an alpine meadow ecosystem in the eastern Tibetan Plateau. Int. J. Biometeor., 60, 801–812. DOI:10.1007/s00484-015-1074-y |
| Wang, X. J., M. X. Yang, G. J. Pang, et al., 2015: Simulation and improvement of land surface processes in nameqie, central Tibetan Plateau, using the community land model (CLM3.5). Environ. Earth Sci., 73, 7343–7357. DOI:10.1007/s12665-014-3911-4 |
| Xiong, J. S., Y. Zhang, S. Y. Wang, et al., 2014: Influence of soil moisture transmission scheme improvement in CLM4.0 on simulation of land surface process in Qinghai–Xizang Plateau. Plateau Meteor., 33, 323–336. |
| Xue, X., J. Guo, B. S. Han, et al., 2009: The effect of climate warming and permafrost thaw on desertification in the Qinghai–Tibetan Plateau. Geomorphology, 108, 182–190. DOI:10.1016/j.geomorph.2009.01.004 |
| Yang, K., T. Koike, H. Ishikawa, et al., 2004: Analysis of the surface energy budget at a site of Game/Tibet using a single-source model. J. Meteor. Soc. Japan, 82, 131–153. DOI:10.2151/jmsj.82.131 |
| Yang, K., Y. Y. Chen, and J. Qin, 2009: Some practical notes on the land surface modeling in the Tibetan Plateau. Hydr. Earth Sys. Sci., 13, 687–701. DOI:10.5194/hess-13-687-2009 |
| Yang, M. X., T. D. Yao, X. H. Gou, et al., 2007: Diurnal freeze/thaw cycles of the ground surface on the Tibetan Plateau. Chinese Sci. Bull., 52, 136–139. DOI:10.1007/s11434-007-0004-8 |
| Yi, S. H., M. A. Arain, and M. K. Woo, 2006: Modifications of a land surface scheme for improved simulation of ground freeze–thaw in northern environments. Geophys. Res. Lett., 33, L13501. DOI:10.1029/2006GL026340 |
| Yi, S., N. Li, B. Xiang, et al., 2013: Representing the effects of alpine grassland vegetation cover on the simulation of soil thermal dynamics by ecosystem models applied to the Qinghai–Tibetan Plateau. J. Geophys. Res., 118, 1186–1199. DOI:10.1002/jgrg.20093 |
| Yi, S., K. Wischnewski, M. Langer, et al., 2014: Freeze/thaw processes in complex permafrost landscapes of northern Siberia simulated using the tem ecosystem model: Impact of thermokarst ponds and lakes. Geosci. Model Dev., 7, 1671–1689. DOI:10.5194/gmd-7-1671-2014 |
| Zheng, D. H., R. van der Velde, Z. B. Su, et al., 2015: Augmentations to the noah model physics for application to the yellow river source area. Part I: Soil water flow. J. Hydrometeor., 16, 2659–2676. DOI:10.1175/JHM-D-14-0198.1 |
| Zheng, J. Y., Y. H. Yin, and B. Y. Li, 2010: A new scheme for climate regionalization in China. Acta Geogr. Sinica, 65, 3–12. |
 2017, Vol. 31
2017, Vol. 31


