The Chinese Meteorological Society
Article Information
- KOU, Xingxia, Xiangjun TIAN, Meigen ZHANG, et al., 2017.
- Accounting for CO2 Variability over East Asia with a Regional Joint Inversion System and Its Preliminary Evaluation . 2017.
- J. Meteor. Res., 31(5): 834-851
- http://dx.doi.org/10.1007/s13351-017-6149-8
Article History
- Received August 30, 2016
- in final form June 21, 2017
2. State Key Laboratory of Atmospheric Boundary Layer Physics and Atmospheric Chemistry, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029;
3. International Center for climate and Environment Sciences, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029;
4. School of Atmospheric Sciences, Nanjing University, Nanjing 210093;
5. School of Atmospheric Sciences, Chengdu University of Information Technology, Chengdu 610225
Atmospheric carbon dioxide (CO2) is one of the major long-lived greenhouse gases, and its steady increase is accepted to be the major reason for global warming. The increasing CO2 is primarily a result of fossil-fuel burning, land-use change, and other human activities, but it is tempered by uptake from natural reservoirs: the ocean and the terrestrial biosphere (Bousquet et al., 2000; Strassmann et al., 2008; Le Quéré et al., 2009). Despite decades of research, there remain significant uncertainties in the estimation of surface CO2 sources and sinks. Investigating and understanding the regional CO2 sources and sinks is of great importance for the reliable prediction of future atmospheric CO2 levels and the associated climate change (Mays et al., 2009; Miyazaki, 2009; McKain et al., 2012).
Atmospheric CO2 concentration observations provide crucial information about the spatiotemporal pattern of CO2 surface fluxes. By assimilating information from atmospheric observations, inverse modeling is used to interpret the measurements and has led to substantial improvements in the understanding of CO2 surface fluxes, with atmospheric transport models providing the links between fluxes and concentrations (e.g., Baker et al., 2006; Maki et al., 2010; Kang et al., 2012; Jiang et al., 2013; Saeki et al., 2013; Huang et al., 2014; Peng et al., 2015). In CO2 flux inversion studies, global chemical transport models (CTMs) have been widely used to adjust surface CO2 fluxes through assimilating information from atmospheric observations (Gurney et al., 2004, 2009; Deng et al., 2007; Peters et al., 2007; Stephens et al., 2007; Feng et al., 2009). For example, Peters et al. (2007) developed CarbonTracker (a global CO2 flux inversion system) by incorporating the ensemble Kalman filter (EnKF) into the TM5 global transport model to assimilate natural CO2 fluxes at the ecological scale. Feng et al. (2009) developed an EnKF-based inversion system to estimate global eight-day CO2 surface fluxes based on the GEOS-Chem transport model from satellite measurements. In response to the “signal-to-noise” problem (i.e., the strong and quite uncertain interference from the biosphere–atmosphere and ocean–atmosphere exchange), most inversion studies have focused on optimizing biospheric fluxes and ocean fluxes at the ecological scale (Peters et al., 2005, 2007; Feng et al., 2009; Jiang et al., 2013; Peylin et al., 2013), while ignoring the uncertainties related to anthropogenic and other CO2 emissions. However, uncertainty in the estimation of anthropogenic emission inventories likely exists due to inaccurately documented statistical fuel consumption data (Andres et al., 2012; Guan et al, 2012; Kort et al, 2012).
With increasing scientific and political interest in regional aspects of the carbon cycle, there is a strong impetus to reduce uncertainties in estimates of regional CO2 surface emissions and concentrations at fine spatiotemporal scales (Wunch et al., 2009; Pillai et al., 2011). East Asia, as one of the major terrestrial carbon sinks of the Northern Hemisphere, has experienced distinct changes in land-use conditions (mainly deforestation) and accumulated impacts of fossil-fuel emissions in the last four decades, and thus atmospheric CO2 is a prominent climatic issue in this region (Engelen et al., 2009; Piao et al., 2009; Zhao et al., 2012; Liu M. et al., 2013; Zhang et al., 2014). Previous CO2 regional modeling studies have produced some encouraging results with high-resolution regional CTMs (Ahmadov et al., 2009; Ballav et al., 2012; Kou et al., 2013, 2015; Liu Z. et al., 2013). Considering that there are certain characteristics that are unique to regional atmospheric CO2 simulation, as compared to global CTMs, e.g., the significance of the diurnal and synoptic cycle, the extremely uneven spatial distribution, the transport mechanisms, and the model errors, further study is thus necessary to gain an insight into inverse modeling with regional CTMs. A comprehensive regional air quality modeling system—the Regional Atmospheric Modeling System and Community Multiscale Air Quality (RAMS-CMAQ) model (Zhang et al., 2002)—was used to simulate atmospheric CO2 concentrations over East Asia, and demonstrated its potential to facilitate interpretations of CO2 observations and resolve fine-scale features (Kou et al., 2013, 2015). The present work will focus on developing a regional inversion system by incorporating an assimilation framework into CMAQ to resolve regional CO2 fluxes at fine spatiotemporal scales over East Asia.
The core algorithm used in our study is a hybrid method: the proper orthogonal decomposition-based ensemble four-dimensional variational data assimilation (POD-4DVar) approach. The POD-4DVar takes advantage of the EnKF and 4D-Var (i.e., the flow-dependent background error covariance estimation and the simultaneous assimilation of observations at multiple times), and its effectiveness has been demonstrated in both an idealized model and the WRF (Tian et al., 2008, 2011; Liu, et al., 2015; Zhang et al., 2015). Also, by incorporating POD-4DVar into GEOS-Chem, a joint carbon assimilation system, Tan-Tracker (“Tan” means carbon in Chinese), has been developed to optimize CO2 fluxes and concentrations simultaneously with atmospheric observations, and the results indicated the good potential of POD-4DVar in global CO2 fluxes inversion (Nassar et al., 2010; Tian et al., 2014). Joint assimilation implies that CO2 concentrations and surface CO2 fluxes are both model state variables, and any useful observation information taken in the current assimilation cycle could be utilized effectively in the following assimilation cycle. Furthermore, the simultaneous assimilation of CO2 concentration and CO2 fluxes can further decrease the uncertainty related to CO2 initial concentrations at the grid scale. Additionally, a flux persistence forecasting model has also been designed to solve the “signal-to-noise” problem, such that natural and anthropogenic surface CO2 fluxes could be estimated as a whole.
The regional surface CO2 flux inversion system presented in this paper is developed by incorporating the Tan-Tracker assimilation framework into CMAQ to resolve fine-scale CO2 fluxes and variability. CMAQ acts as the major contribution to the observation operator for linking the surface fluxes with CO2 observations. For simplicity, this system is referred to as TT-R (i.e., Tan-Tracker-Region). This paper reports the first step made towards the goal of a fine-scale 4D CO2 reanalysis, and explores the strategy for assimilating atmospheric CO2 into a regional CTM over East Asia. Observing system simulation experiments (OSSEs) are designed to evaluate the ability of TT-R in optimizing CO2 fluxes with artificial ground-based measurements. A description of the regional CO2 assimilation system, including the POD-4DVar assimilation algorithm and the coupling with CMAQ, is given in Section 2, followed in Section 3 by discussion on the ground-based observation assimilation OSSEs as part of a preliminary evaluation of the inversion system. A summary and conclusions are provided in Section 4.
2 Framework of the regional carbon data assimilation system (TT-R) 2.1 Regional carbon assimilation frameworkThe ultimate goal of the regional assimilation system is to estimate the first-guess net CO2 surface flux, expressed as
In this study, a set of linear multiplication factors λ is used to describe net surface fluxes, following previous studies (Peters et al., 2005, 2007). The ith ensemble member of the surface CO2 fluxes,
| ${F_i}(x,y,t) = {\lambda _{i,r}}(x,y,t){F^*}(x,y,t),$ | (1) |
where

|
| Figure 1 Flowchart of the TT-R joint data assimilation system, in which C represents CO2 concentrations, F represents surface CO2 fluxes, and λ represents linear scaling factors of fluxes for each assimilation time and each grid. The superscript a refers to analysis, b to background, and m to samples. F* denotes the first-guess flux series. |
Figure 2 demonstrates the construction of the sampling window and assimilation window in TT-R. In the background simulation, CMAQ integrates over the assimilation window La (i.e., the sum of the optimized window, the lag window, and the observational window; Fig. 2) to prepare the background CO2 concentration fields (Cb) derived by the background fluxes (Fb) [see Eq. (2)] and thus prepare the background joint vector (λb, Cb)T. In the rth cycle, the measurements in the rth observational window would be utilized to assimilate the state variables (λ, C)T of the rth optimized window:
| ${F^{\rm b}}(x,y,t) = {\lambda ^{\rm b}}(x,y,t){F^*}(x,y,t),(t = 1,...,{L_{\rm a}}).$ | (2) |

|
| Figure 2 Schematic diagram of the sampling window, assimilation window, optimized window, lag window, and observational window in the joint assimilation framework. |
Correspondingly, in the sampling run, CO2 concentrations are simulated continuously by CMAQ using Fb [see Eq. (3)] with initial Cb over the sampling window to produce the sampling CO2 concentration series
| ${F^{\rm b}}(x,y,t) = {\lambda ^{{\rm b},r}}(x,y,t){F^*}(x,y,t),(t = 1,...,{L_{\rm s}}).$ | (3) |
Next, the 4D moving sampling strategy (Wang et al., 2010) is used to produce the sampling vector (λm, Cm)T as follows:
| ${(\lambda _i^{\rm m},C_i^{\rm m})^{\rm T}} = \left[ {\begin{array}{*{20}{c}}{\lambda _i^{\rm m}}\\ \vdots \\{\lambda _{i + {L_{\rm{a}}} - 1}^{\rm m}}\\{C_i^{\rm m}}\\ \vdots \\{C_{i + {L_{\rm{a}}} - 1}^{\rm m}}\end{array}} \right],$ | (4) |
where
With the identity operator chosen as the surface CO2 flux dynamical sub-model (Peters et al., 2005, 2007; Peng et al., 2015), the large-scale joint sampling vectors (λ, C)T are regarded as the prognostic variables of this regional carbon assimilation system:
| ${M\!_F} = I\left( {I \! :{\rm{ identity}}\;{\rm{matrix}}} \right).$ | (5) |
This flux persistence forecasting model [Eq. (5)] is developed based on previous studies (e.g., Peters et al., 2007) and supposes that the background scaling factors
| ${\lambda ^{\rm b}}(t + 1) = \frac{1}{{{L_{{\rm{opt}}}}}}\sum\limits_{i = 1}^{{L_{{\rm{opt}}}}} {\lambda _i^{\rm a}} ,$ | (6) |
where Lopt is the optimized window length.
MF (the surface CO2 flux dynamical model) is thus used in this study to construct the joint dynamical model,
| $M = \left[ {\begin{array}{*{20}{c}}I\\{{\rm{CMAQ}}}\end{array}} \right],$ | (7) |
with CMAQ. By employing H (the observation operator) in the simulated CO2 concentrations
| $C_{{\rm{obs}},i}^{\rm m} = H(C_i^{\rm m}),$ | (8) |
| $C_{{\rm{obs}}}^{\rm b} = H({C^{\rm b}}).$ | (9) |
Therefore, the background vector (λb, Cb)T, the ensemble vector (λm, Cm)T, the observation operator H, and the atmospheric CO2 observations Cobs will be inputs to the POD-4DVar assimilation algorithm, which generates the assimilated (λa, Ca)T and the assimilated fluxes
In summary, TT-R works as follows (Fig. 1): (1) It is initiated by two CMAQ simulations, the background simulation and the sampling simulation, forced by the background fluxes over the assimilation and sampling windows (see Fig. 2). In the background run, CMAQ integrates over the assimilation window to produce the background CO2 concentration field Cb, and thus prepares the background joint vector (λb, Cb)T. The sampling run is utilized to prepare the joint ensemble vectors using a 4D moving strategy over the sampling window so that the background error covariance is updated at each assimilation cycle. (2) With the background and ensemble vectors in addition to the observations, the scaling factors λ and C are updated by the POD-4DVar algorithm through comparison of the simulated and observed CO2 according to the 4DVar cost function. (3) The assimilated flux is calculated as
The POD-4DVar approach is developed from conventional 4DVar assimilation. By minimizing the incremental format of the standard 4DVar cost function J(x'), an optimum increment
| $\begin{aligned}J({{\bf{x}}'}) & = \frac{1}{2}{\left( {{{\bf{x}}'}} \right)^{\rm T}}{{\bf{B}}^{ - 1}}\left( {{{\bf{x}}'}} \right) \\ & + \frac{1}{2}{\left[ {{y'}({{\bf{x}}'}) - {\bf{y}}_{\rm obs}^{'}} \right]^{\bf{T}}}{{\bf{R}}^{ - 1}}\left[ {{y'}({{\bf{x}}'}) - {\bf{y}}_{\rm obs}^{'}} \right],\end{aligned}$ | (10) |
where
| $\!\!\!\!\!{{\bf{y}}'} = {y'}({{\bf{x}}'}) = \left[ {\begin{array}{*{20}{c}}{{{({{\bf{y}}_1})}'}}\\{{{({{\bf{y}}_2})}'}}\\ \vdots \\{{{({{\bf{y}}_S})}'}}\end{array}} \right],$ | (11) |
| $\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{\bf{y}}_{{\rm{obs}}}^{'} = \left[ {\begin{array}{*{20}{c}}{{\bf{y}}_{{\rm{obs}},1}^{'}}\\{{\bf{y}}_{{\rm{obs}},2}^{'}}\\ \vdots \\{{\bf{y}}_{{\rm{obs}},S}^{'}}\end{array}} \right],$ | (12) |
| ${({y_k})'} = {y_k}({x^{\rm b}} + x') - {y_k}({x^{_{\rm b}}}),$ | (13) |
| $\!\!\!\!\!\!\!\!\!y{'_{{\rm{obs}},k}} = {y_{{\rm{obs}},k}} - {y_k}({x^{_{\rm b}}}),$ | (14) |
| $\!\!\!\!\!\!\!\!\!\!\!\!\!\!{y_k} = {H_k}\left( {{M_{{t_0} \to {t_k}}}(x)} \right),$ | (15) |
and
| ${\bf{R}} = \left[ {\begin{array}{*{20}{c}}{{{\bf{R}}_1}} & 0 & \cdots & 0\\0 & {{{\bf{R}}_2}} & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots \\0 & 0 & \cdots & {{{\bf{R}}_S}}\end{array}} \right].$ | (16) |
In the given equations, k represents the observational time, S indicates the sum of observational steps throughout the observational window, b denotes background fields, the superscript T refers to a transpose, Hk stands for the observation operator, Rk represents the observational error covariance, and B refers to the background error covariance.
By using the background matrices xb, the observational increments
| ${x^{\rm a}} \!\!=\! {x^{\rm b}} \!+\! {x'}{\bf{V}}\!\!{\left[ {(N \!\!-\! 1){\bf{I}} \!+\! {\bf{P}}_y^{\bf{T}}{{\bf{R}}^{ - 1}}\!{{\bf{P}}_y}} \right]^{ - 1}}{\bf{P}}_y^{\bf{T}}{{\bf{R}}^{ - 1}}\mathbf{y}_{\text{obs}}^{\prime }, \quad\,\,\,\,\,\,$ | (17a) |
and the analysis error covariance Pa is given as
| ${{\bf{P}}^{\rm a}} = {{\bf{P}}_x}{\bf{P}}_{\rm a}^*{\bf{P}}_x^{\bf{T}},$ | (17b) |
where
Specifically, in TT-R,
| ${\bf{y}}{'_{\!\!{\rm{obs}},k}} = {{\rm{C}}_{{\rm{obs}},k}} - {\rm{C}}_{{\rm{obs}}}^{\rm b},$ | (18) |
and
| ${\bf{y}}' = {\rm{C}}_{\rm obs}^{\rm m} - {\rm{C}}_{\rm obs}^{\rm b},$ | (19) |
where
| $H = \left[ {\begin{array}{*{20}{c}}{{H_1}} & 0 & \cdots & 0\\0 & {{H_2}} & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots \\0 & 0 & \cdots & {{H_S}}\end{array}} \right].$ | (20) |
As mentioned above, both CO2 concentrations and fluxes are treated as model states to be assimilated, which implies
| ${x^{\rm b}} = {({\lambda ^{\rm b}},{C^{\rm b}})^{\rm T}},$ | (21) |
and
| $x' = {\left( {{\lambda ^{\rm m}},{C^{\rm m}}} \right)^{\rm{T}}} - {\left( {{\lambda ^{\rm b}},{C^{\rm b}}} \right)^{\rm{T}}},$ | (22) |
in TT-R.
Thus, the coupling between the regional assimilation framework with the POD-4DVar assimilation algorithm has been realized through Eqs. (18)–(22) (see Fig. 1).
2.3 Localization schemesThe localization strategy is necessary to ameliorate the spurious long-range correlations due to the limited ensemble members. Previous studies have found that the covariance decreases in a complex but close to exponential manner with distance between model states and observations (Houtekamer and Mitchell, 1998; Gaspari and Cohn, 1999; Greybush et al., 2011). Similar to other ensemble-based assimilation systems, the following widely-recognized filter function is used in this regional assimilation system:
| ${\rho _h}[i,j] = {{{D}}_0}({d_{i,j}}/{d_0}),$ | (23) |
and
| $\!\!\!\!\!\!{D_0}(r) = \left\{ {\begin{array}{*{20}{c}}{ - \frac{1}{4}{r^5} + \frac{1}{2}{r^4} + \frac{5}{8}{r^3} - \frac{5}{3}{r^2} + 1, \qquad\qquad\qquad\qquad\quad 0 \leqslant r \leqslant 1}\\\!\!\!{\frac{1}{{12}}{r^5} - \frac{1}{2}{r^4} + \frac{5}{8}{r^3} + \frac{5}{3}{r^2} - 5r + 4 - \frac{2}{3}{r^{ - 1}},\qquad\qquad{\rm{ 1 < }}r \leqslant 2}\\\!\!\!\!\!\!\!\!\!\!\!{0, \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\, 2 < r}\end{array}} \right.,$ | (24) |
where
Consequently, with the covariance localization scheme, the final POD-4DVar analysis solution xa can be formulated as follows:
| $\begin{aligned}{x^{\rm a}} & = {x^{\rm b}} + {\rho _h}\circ \left\{ {x'{\bf{V}}} \right.\left[ {(N - 1){\bf{I}}} \right.\\& {\left. { + {\bf{P}}_y^T{{\bf{R}}^{ - 1}}{{\bf{P}}_y}} \right]^{ - 1}}\left. {{\bf{P}}_y^T{{\bf{R}}^{ - 1}}} \right\}{\mathbf{y}_{_{\text{obs}}}^{\prime }}.\end{aligned}$ | (25) |
where the Schur product is denoted by
In this section, the performance of the regional assimilation system is preliminarily assessed through a group of ground-based observation assimilation OSSEs. The net CO2 flux is strongly influenced by the seasonal growth and decay of terrestrial ecosystems in East Asia. The primary purpose of this paper is to introduce a regional inversion system, TT-R, to refine regional CO2 surface fluxes and fine-scale CO2 variability, so numerical experiment results are presented for two single months (i.e., January and July 2010, in representation of winter and summer) over East Asia. The regional joint assimilation system will form a foundation for more comprehensive studies of CO2 uncertainties and variabilities in the future, which will be achieved by analyzing results for a longer time span with more observational data.
3.1 CMAQ configurationThe regional atmospheric CO2 transport model used in the regional surface flux inversion system was developed based on CMAQ and was extended to include CO2 simulation with RAMS providing the 3D meteorological fields (Zhang et al., 2002; Kou et al., 2013, 2015). In this study, the model domain for CMAQ was 6654 km × 5440 km on a rotated polar stereographic map projection centered at 35.0°N, 116.0°E, with a 64 km × 64 km horizontal grid cell, and covered the whole area of East Asia (as shown in Fig. 3). The model system has 15 vertical layers in the σz-coordinate system, unequally spaced from the ground to approximately 23 km, with approximately 9 layers concentrated in the lowest 2 km of the atmosphere to resolve the planetary boundary layer (PBL). The output time step is one hour.
The CO2 volume fraction is transported as a tracer in this model, with prescribed surface CO2 fluxes including fossil-fuel emissions Fff [Regional Emission inventory in Asia; horizontal resolution: 0.25° × 0.25°; temporal resolution: monthly;Kurokawa et al. (2013)], biomass burning Ffire [Global Fire Emissions Database; horizontal resolution: 0.5° × 0.5°; temporal resolution: monthly;van der Werf et al. (2010)], ocean–atmosphere CO2 exchange Foce, and biosphere–atmosphere exchangeFbio [Carbon Tracker 2011 optimized estimation (CT2011_oi); global resolution: 3° × 2°; temporal resolution: three-hourly;Peters et al. (2007); data available at http://carbontracker.noaa.gov]. The boundary conditions and initial fields of atmospheric CO2 volume fraction were also obtained by interpolation of CT2011_oi:
| $\begin{aligned}{F^0}(x,y,t) & = {F_{{\rm{bio}}}}(x,y,t) + {F_{{\rm{oce}}}}(x,y,t) \\ & + {F_{{\rm{ff}}}}(x,y,t) + {F_{{\rm{fire}}}}(x,y,t).\end{aligned}$ | (26) |
Compared to the large uncertainty in the estimation of natural fluxes, wintertime is mainly dominated by fossil-fuel emissions in the model domain, and even a tiny amount of uncertainty in fossil-fuel emissions is equivalent to the total exchange from bioflux and ocean flux (Table 1). January was chosen as the experimental period to assess the regional assimilation system during wintertime. A set of OSSEs were designed to evaluate the regional assimilation system, including in-depth analyses of assimilated fluxes and concentrations. In addition, a series of numerical experiments were conducted to investigate the sensitivity of assimilation parameters (e.g., optimized window, ensemble size, and covariance localization).
| Fossil fuel | Biomass burning | Bioflux | Ocean flux | Total flux | |
| January | 338.34 | 19.69 | 67.50 | –9.78 | 415.75 |
| July | 314.56 | 0.79 | –344.48 | 0.50 | –28.63 |
The prior prescribed net surface flux F0 [Eq. (26)] was assumed as the “true” surface flux in the following OSSEs, and the artificial “true” CO2 concentrations C0 were simulated continuously by CMAQ using the prior “true” flux F0 from 26 December 2009 to 31 January 2010 (starting at 0000 UTC 26 December).
The prescribed first-guess fluxes F* were then created by using
| ${F^*}(x,y,t) = (1.8 + \delta (x,y,t)){F^0}(x,y,t),$ | (27) |
where δ is a set of random numbers of standard normal distribution at each grid during the assimilation period. Then, the “simulated concentrations” Cf(x, y, z, t) in OSSEs were obtained by a parallel free integration of the CMAQ simulation forced by first-guess fluxes F* without any data assimilation.
With the observation operator, the “artificial” CO2 observations were produced every hour by sampling the hourly “true” CO2 concentrations with addition of a small amount of random noise (with error variance of 0.01 ppm2) over the observational sites. Due to the sparseness of ground-based measurements in East Asia, several ground-based observations from the World Data Centre for Greenhouse Gases [WDCGG; AMY (Lee and Kim, 2013), UUM (Conway, 2013), and WLG (Zhou, 2013)] and Chinese Ecosystem Research Network (CERN; Mt. Dinghu and Fukang) with hourly artificial observed data were chosen in the current inversion system for the representation of the following sub-regions: (1) Korean peninsula and Japan (AMY); (2) North China and South Mongolia (UUM); (3) West China (WLG); (4) Southeast China (Mt. Dinghu); and (5) Northwest China (Fukang). The geographical information of these five observation stations is presented in Table 2; they could generally be classified as inland, mountain, and coastal stations. The locations of the observation sites are given in Fig. 3a. The five chosen sites of this OSSE design performed like “single-observation experiments,” and then a group of single-observation-based OSSEs were carried out to evaluate the regional assimilation system more broadly.
| Station | Latitude (°N) | Longitude (°E) | Altitude (m) | Country | General site description |
| 1. AMY (Anmyeon-do) | 36.53 | 126.32 | 47.0 | Korea | Coastal |
| 2. UUM (Ulaan Uul) | 44.45 | 111.08 | 914.0 | Mongolia | Inland (grassland) |
| 3. WLG (Mt. Waliguan) | 36.30 | 100.90 | 3810.0 | China | Inland (plateau) |
| 4. DH (Mt. Dinghu) | 23.17 | 112.50 | 90.0 | China | Mountain (subtropical forest) |
| 5. FK (Fukang) | 44.28 | 87.92 | 460.0 | China | Inland (desert) |
The performance of TT-R was assessed through a set of ground-based observation assimilation OSSEs. All the assimilation processes were initiated by CMAQ with the first-guess F* and conducted by assimilating the hourly “pseudo-observations” in the assimilation cycle. Similar to the initialization for other regional inversion systems, the scaling factors began from
The experiments were performed in a pseudo-data environment, so that the “true” concentrations and fluxes were known and the results of the inversion tests could be evaluated against them. A description of the artificial “true” simulation and assimilation concentrations and fluxes is now demonstrated to reveal the strengths and weaknesses of the regional inversion system. We start by describing the impacts of assimilating artificial measurements Cobs on the CO2 simulations by TT-R. Figures 3a–dshow the monthly-averaged horizontal distributions of the true, simulated, and assimilated near-surface CO2 concentrations, and the difference between the assimilation and the simulation in January 2010. The CMAQ simulation could represent the fine-scale spatiotemporal variability of CO2, while generally retaining the large-scale spatial patterns, compared to global simulations (Kou et al., 2015). CO2 concentrations above 420 ppm were found over the Sichuan basin, North China, and the coastal regions of Southeast China, where human activities have intensified (Fig. 3a). This spatiotemporal variability was concordant with the CO2 surface flux distribution pattern (Fig. 5a).

|
| Figure 3 Monthly-averaged horizontal distributions of CO2 concentrations (ppm) near the surface in January 2010. (a) C0: simulation with prior true fluxes F0; (b) Cf: simulation with first-guess fluxes F*; (c) Ca: assimilations; and (d) Ca–Cf. The locations of the five CO2 monitoring sites (black dots—AMY, WLG, UUM, DH, and FK) are presented in (a). The grey square denotes the WLG region. |
As shown in Figs. 3a–d, the monthly-averaged CO2 concentrations Cf (simulated with the first-guess CO2 fluxes F*) were much larger than the artificial true CO2 concentrations C0 (forced by the prior CO2 fluxes F0) near the surface in January 2010. Generally, the simulated values Cf were greater than the monthly-averaged artificial observations. The areas of CO2 concentrations above 420 ppm were considerably larger than those of the true distribution C0. After assimilation, the analysis field Ca (Fig. 3c) was much closer to C0 around the observation sites. As shown in Fig. 3d, the monthly differences between Ca and Cf ranged from –3 to 2 ppm, indicating that the trend in analyzed concentrations was approaching the true conditions. It should also be noted that the assimilation reduced the bias, but did not significantly change the spatial pattern due to the small number of observations.
The assimilated CO2 concentrations were then compared with the artificial “true” values interpolated to the observation locations, in order to further evaluate the performance of TT-R. Examples of daily mean CO2 concentrations from the true, simulation, and assimilation are demonstrated in Fig. 4 for the five observational sites (AMY, UUM, WLG, DH, and FK). Over the first few days, the assimilated CO2 diverged from the simulated fields, generally moving closer to the observations, implying that a spin-up time of about six days is required for the regional assimilation system to respond. The spin-up time for different assimilation systems indicates that the long lifetime of atmospheric CO2 and the limited number of observations need to be taken into account in the regional joint assimilation framework (Tian et al., 2014; Peng et al., 2015). As shown in Fig. 4, assimilated CO2 concentrations were generally in better agreement with the artificial “true” CO2 concentrations than the simulated values. The AMY station showed a distinctly different variation of CO2 compared to WLG, despite the geographical location of both stations being at a similar latitude (approximately 36.4°N). This implies that the regional inversion system is capable of reproducing the local conditions.
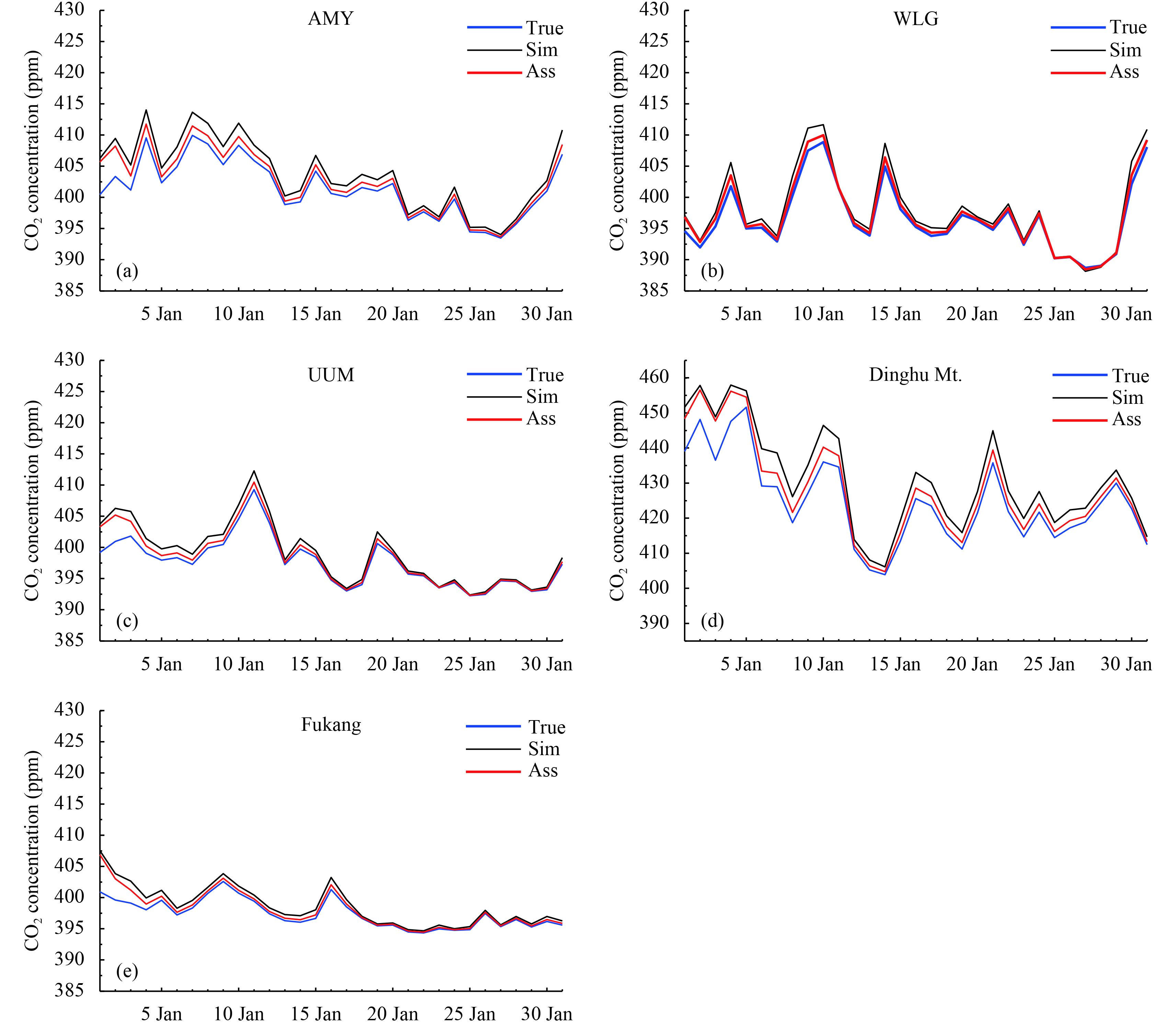
|
| Figure 4 Daily-averaged assimilation (red), simulation (black) and artificial “true” (blue) surface CO2 concentrations (in ppm) from 1 January to 31 January 2010 at stations (a) AMY, (b) WLG, (c) UUM, (d) Mt. Dinghu, and (e) Fukang. |
The horizontal distribution of the prior “true” CO2 flux retained features from both the biosphere–atmosphere flux and anthropogenic emissions (Fig. 5a). The biosphere acts as a source that further amplifies the CO2 net flux on the basis of growing fossil-fuel emissions during wintertime (Liu et al., 2012; Jiang et al., 2013). The first-guess fluxes were about 1.8 times larger than the prior fluxes with a set of random numbers (Fig. 5b). Figure 5d demonstrates that the monthly averaged analysis increment of fluxes exhibited a similar spatial pattern to the concentration increments (Fig. 3d), since both CO2 concentrations and the flux scaling factors were simultaneously assimilated under the joint assimilation framework. The shape of the increment depends on both the local sensitivity and the observation innovation (Tangborn et al., 2013). A typical difference (i.e.,

|
| Figure 5 Monthly-averaged horizontal distributions of surface CO2 fluxes (μmolem–2 s–1) near the surface in January 2010. (a) F0: prior true fluxes, (b) F*: the first-guess fluxes, (c) Fa: assimilated fluxes, and (d) Fa – F*. |
The daily averaged surface fluxes at five ground-based stations were summarized in Fig. 6. The five stations, located from south to north in the model domain with different land-use conditions, cover both urban regions (e.g., the Mt. Dinghu in the Pearl River Delta region) and rural regions (e.g., Fukang station in the deserts of Northwest China, WLG over the Tibetan Plateau, UUM in the semi-arid grassland, and AMY in the coastal region). Due to the impact of local fossil-fuel emissions, temporal variations of CO2 surface fluxes and concentrations were particularly high at the urban site of DH, compared to the other remote sites. As can be seen in Fig. 6, the regional inversion system demonstrated certain potential in reproducing the surface CO2 fluxes at urban sites dominated by anthropogenic emissions. Considering complex land-cover and topographical conditions in urban areas, the capability of the regional inversion system in fossil-fuel verification from metropolitan regions needs to be further assessed. Moreover, the first-guess surface CO2 fluxes F* in this study were greater than the prior “true” fluxes F0. Attributing the overestimation of analyzed fluxes to errors in regional CTMs transport in the PBL, large background bias, inadequate ground-based observation, as well as the assimilation parameters, would lead to drastically different conclusions.

|
| Figure 6 As in Fig. 4, but for daily-averaged surface CO2 fluxes (μmolem–2 s–1). |
In addition, the root-mean-square error (RMSE) of the assimilated CO2 concentration and fluxes was evaluated in order to obtain a more quantitative picture of how the assimilation affects the accuracy of the surface-layer CO2. The RMSE results indicated a consistent decrease in both CO2 concentration and fluxes when the continuous ground-based observations were assimilated compared to the simulated ones. This decrease was particularly apparent at the AMY, WLG, and DH stations, where the mean RMSE of the CO2 concentration and fluxes at the assimilation sites decreased by about 0.5–1.5 ppm and 0.02–0.18 μmolem–2 s–1, respectively. Moreover, relatively larger analyzed RMSEs appeared at DH compared to the remote stations, where the RMSEs of first-guess fluxes were larger. The monthly-analyzed RMSE was almost less than 0.1 μmolem–2 s–1 at most of the stations (Fig. 7b), indicating an improved daily mean CO2 flux after assimilation. Conversely, the lower bias of analyzed fluxes could be partly attributed to the reduced uncertainty of the initial CO2 concentrations in the joint assimilation framework (Tian et al., 2014; Peng et al., 2015).

|
| Figure 7 Comparison of monthly mean RMSEs for the assimilated and simulated CO2 (a) concentrations (ppm) and (b) fluxes (μmolem–2 s–1) at stations AMY, WLG, UUM, DH, and FK. |
Moreover, the WLG region (indicated by the grey square in Fig. 3a) was further investigated due to its unique geographical location and high international popularity. The Mt. Waliguan site is one of the 23 global baseline stations of the World Meteorological Organization’s Global Atmosphere Watch network, and the only one in the hinterland of the Eurasian continent (Zhou, 2013). The CO2 concentrations at WLG region are mostly influenced by long-range transport and local biospheric flux. Figure 8a shows that the posteriori uncertainties of the analyzed surface CO2 fluxes in the WLG region are gradually reduced by assimilation of CO2 measurements. Furthermore, Fig. 8b indicates the time series of the daily mean scaling factors. All scaling factors could be created and then updated when this regional inversion system continued to assimilate observations at each assimilation cycle. The daily-averaged scaling factor also decreased and signaled the values approaching the artificial “true” flux, with small fluctuations during the latter half of January.
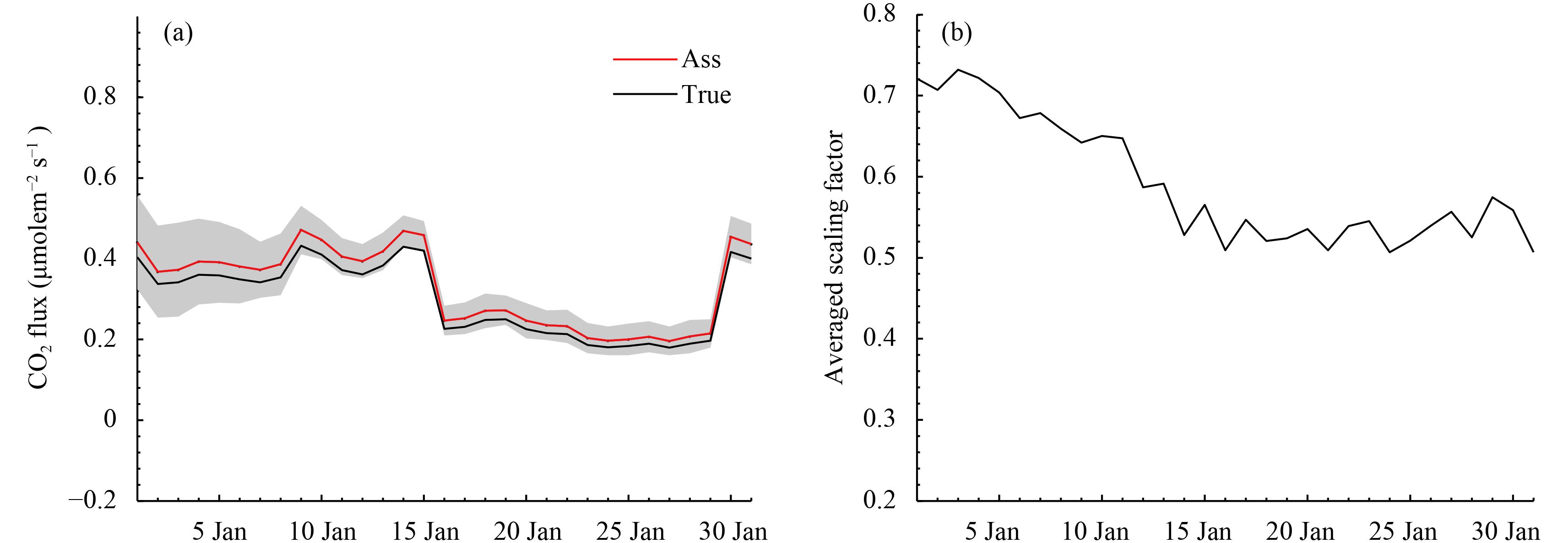
|
| Figure 8 Time series of the daily-averaged (a) posteriori uncertainties (shaded areas) of the assimilated surface fluxes (μmolem–2 s–1) and (b) averaged scaling factors, in the WLG region (shown in Fig. 3a) from 1 January to 31 January 2010. |
Previous studies have mostly tended to focus on the annual and/or seasonal timescales (Tian et al., 2014; Zhang et al., 2014), while our regional inversion system assimilates CO2 concentrations and fluxes on the hourly timescale. The biosphere, acting as a source or sink pending on the relative strengths of the uptake of atmospheric CO2 by photosynthesis and the CO2 released by respiration, is regarded as the leading factor for surface CO2 diurnal variation in remote regions (Jia et al., 2015). The diurnal effect imposes a regional extreme of CO2 concentrations in the boundary layer when abundant vegetation is present. Figure 9 shows a typical diurnal CO2 concentration and flux variation for 0000–2300 Local Standard Time (LST) 18 January at the WLG site. The artificial true simulations reproduced the diurnal cycle of CO2 concentrations reasonably well at WLG, with a daytime trough due to the bioflux variation during day and night. As shown in Fig. 9, surface CO2 fluxes at WLG presented obvious diurnal variability dominated by terrestrial bioflux, with relatively little influence from human activity. In general, the strong diurnal cycle was captured fairly well by the regional inversion system, with a reduced bias compared to the background profiles.
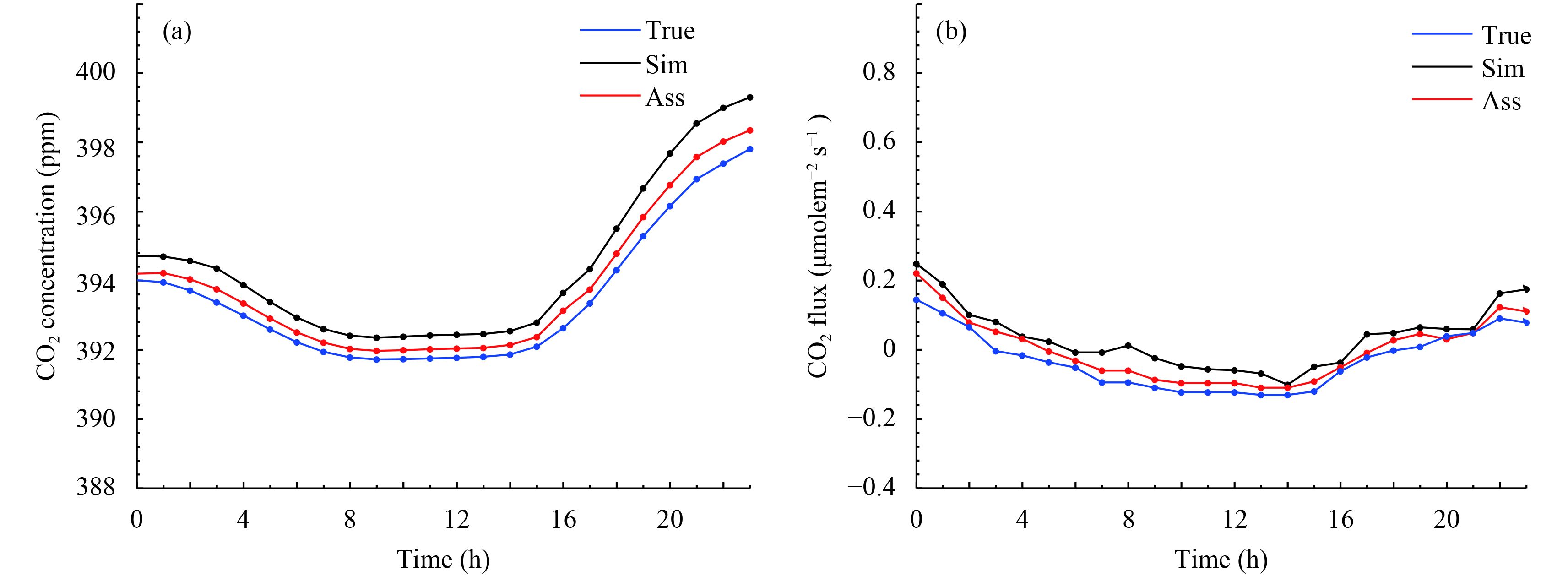
|
| Figure 9 Diurnal cycle of the assimilation (red), background (black), and artificial true (blue) CO2 (a) concentrations (ppm) and (b) fluxes (μmolem–2 s–1) for 0000–2300 LST 18 January at station WLG, where bioflux dominated the net surface fluxes. |
Considering that surface CO2 fluxes are most closely connected to atmospheric CO2 observations, the performance of the inversion system in reproducing the diurnal profiles is quite encouraging. A comparison of the simulated and assimilated results suggested that observations helped to offset the background bias but would not lead to distinctly different surface CO2 variation based on the prior data. Moreover, the ground-based observations had a limited zone of impact due to the covariance localization technique used and the sparse observation, and thus any improvements made around the monitoring sites could only have contributed to the nearby sites. As a result, it was difficult for the small number of observations to spread the fine-scale features of the CO2 pattern over the model domain. This would have been particularly true in the regions where there was little direct impact of the observations, and thus flux assessments needed to be limited to the relevant areas in the present study. In addition, the spin-up time (about six days) required for the assimilation system to respond indicated that the long lifetime of atmospheric CO2 and limited number of observations need to be taken into account in the regional joint assimilation framework.
3.2.3 Parameter sensitivity experiments and discussionA series of numerical experiments were conducted to investigate the sensitivity of assimilation parameters (i.e., the ensemble size N, optimized window length Lopt, and horizontal localization radius R). The default optimized window Lopt was 3 h, the ensemble size N was 145, and the standard localization radius R was 320 km. As previously stated, the optimized window was a newly introduced parameter. Considering that information from observations is propagated through the POD-4DVar analysis and transported through the CMAQ simulation within a limited response zone, the surface fluxes averaged in the WLG region (indicated by the grey square in Fig. 3a) are presented in Fig. 10. The regional inversion system worked rather well for Lopt = 3 h. The assimilated CO2 fluxes deviated occasionally from the true CO2 fluxes, with several random fluctuations, when Lopt ≥ 6 h. This is perhaps attributable to the influence of significant CO2 diurnal variation in the regional simulation, which would undermine the linear assumption between the observation perturbations and the model perturbations when the POD technique is adopted. While a much smaller Lopt with comparable improvements would be computationally more expensive, a certain length of the optimized window (about 3 h) could generally guarantee a reliable performance of this regional inversion system.
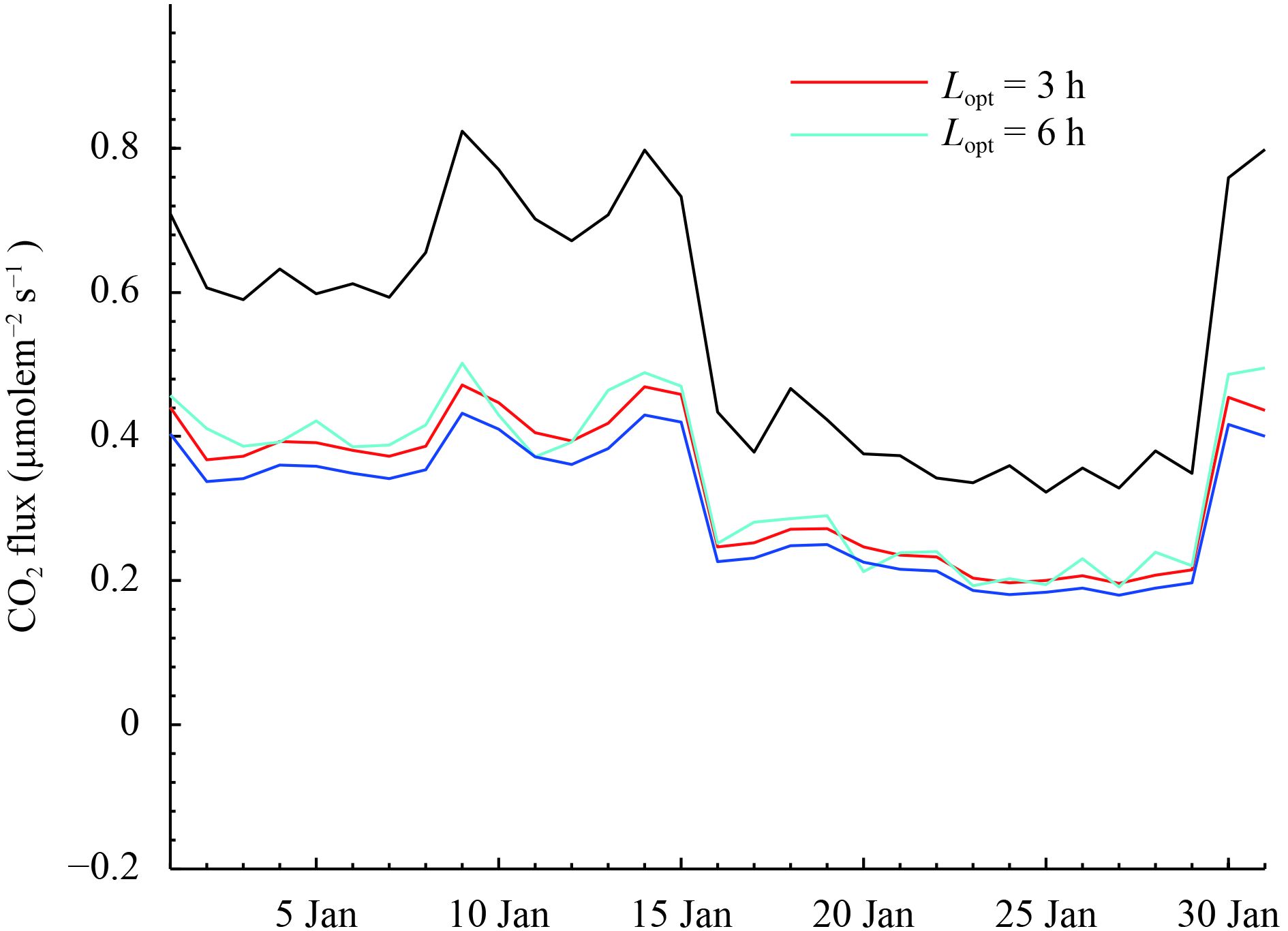
|
| Figure 10 Time series of daily mean CO2 fluxes averaged in the WLG region (shown in Fig. 3a) from 1 to 31 January 2010 with different optimized window lengths (Lopt = 3 or 6 h). The black and blue lines represent the first-guess and artificial “true” fluxes, respectively. |
The impact of sample size on the results of TT-R was evaluated by conducting another group of experiments with ensemble sizes N = 49, 97, and 145, respectively. Figure 11 compares the different ensemble sizes in the daily averaged assimilated flux over the WLG region. Better performance was found in the case of N = 145 compared to N = 49 or 97. It is clear that samples with a larger ensemble size would be more representative for general conditions, and a reliable performance of TT-R requires an ensemble size of approximately 100. However, this is associated with greater computational expense. This finding is consistent with the ensemble-based assimilation studies of Tian et al. (2011, 2014).

|
| Figure 11 As in Fig. 10, but for ensemble size N = 49, 97, and 145. |
From the perspective of the covariance localization, another group of experiments were also performed to assess the sensitivity of the regional inversion system to different horizontal radii. The differences among the sensitivity experiments with a horizontal radius R = 320, 450, and 640 km are very clear (see Fig. 12). As suggested by previous studies (Peng et al., 2015), we chose 320 km as the default horizontal radius. The regional inversion system performed well with a horizontal localization radius of approximately 320 km. The time series of assimilated daily CO2 fluxes with 640 km showed considerable deviation from the artificial “true” flux. Moreover, it is impossible to systematically change the values of λ in large areas after assimilating observations. Therefore, the results indicate that horizontal localization has a significant influence on the assimilated results for TT-R and should be carefully assessed.

|
| Figure 12 As in Fig. 10, but for covariance localization radii R = 320, 450, and 640 km. |
As mentioned above, a flux persistence forecasting model was further designed to solve the “signal-to-noise” problem, such that natural and anthropogenic surface CO2 fluxes could be estimated as a whole at the grid scale. Generally, the biosphere acts as a sink in summer, since in the growing season the uptake of atmospheric CO2 by photosynthesis exceeds CO2 released by respiration (Table 1). Thus, we designed another set of OSSEs during summertime with more observations to further study the effect of the assimilation system in different CO2 flux situations.
3.3.1 Experimental designThe prior prescribed net surface flux F0 in Eq. (26) was also assumed as the true surface flux in the following OSSEs, and the artificial “true” CO2 concentrations C0 were simulated continuously by CMAQ using the prior “true” flux F0 from 26 June to 31 July 2010 (starting at 0000 UTC 26 June).
The prescribed first-guess fluxes F* were then created by using Eq. (27), and the rest procedures were basically the same as in the winter case (see Section 3.2.1).
In this case, 60 ground-based observations with hourly artificial observed data were chosen to further evaluate the regional CO2 inversion system with different densities of the artificial observation network. Figure 13 shows locations of the 60 measurement sites used for the summer CO2 assimilation experiment. These ground-based stations were scattered randomly over the model domain and only the geographical position information was used to produce the artificial “observation” in the following OSSEs. The previous five chosen sites performed like “single-observation experiment”, and the assimilation effects were too far away from each other to influence others. In this section, we focus in particular on discussing the effect of observation distribution changes before and after assimilation.

|
| Figure 13 Locations of 60 CO2 observation stations (black dots) in the model domain. |
The performance of TT-R was assessed through a set of more intensive ground-based observation assimilation OSSEs. The basic experimental design (e.g., the CMAQ configuration, etc.) was exactly the same as that adopted in the previous OSSEs. Following the results of the parameter sensitivity experiments, the lag window was five days, and the optimized and observational windows were both three hours. The ensemble size N was 145 and the localization radius was 320 km in all OSSEs. Numerical experiment results for a single month (i.e., July 2010) over East Asia are presented.
3.3.2 Experimental resultsWe started by investigating the impacts of assimilating observations on CO2 simulations and fluxes by the regional inversion system. Moreover, we made a free run of the CMAQ simulation without any assimilation. As shown in Figs. 14a, the monthly-averaged simulated CO2 concentrations Cf forced by the surface CO2 fluxes F* were compared with those of the assimilated CO2 concentrations Ca near the surface in July 2010. As expected, the inversion system ingested the observations and exerted impacts over the nearby areas, and the resulting differences between Ca and Cf ranged from –5 to 3 ppm in the south and east of China. As shown in Fig. 14b, the differences between assimilated and first-guess fluxes were –0.05–0.05 μmolem–2 s–1. Compared to the five-station experiment in winter, the 60 sites used in this OSSE could systematically change the values of CO2 concentration and flux in large areas over the model domain. The results also indicated that horizontal localization has a significant influence on the assimilated results for TT-R and should be carefully assessed. In addition, observation error should be carefully checked to guarantee the quality of the assimilated data.

|
| Figure 14 Monthly-averaged horizontal distributions of CO2 concentrations and fluxes near the surface in July 2010. (a) Ca–Cf (ppm) and (b) Fa–F* (μmolem–2 s–1). |
To comprehensively evaluate the performance of this regional inversion system, the RMSEs for the daily gridded (64 km × 64 km) TT-R-assimilated CO 2 concentrations from 1 to 31 July 2010 are shown in Figs. 15a, b. Moreover, the relevant RMSEs for the assimilated (optimized) CO2 fluxes are also illustrated in Figs. 15c, d. Compared with the RMSEs in the winter case, larger RMSEs in summer can be found in the north and south of East Asia. This could be attributed to the strong and quite uncertain interference from the terrestrial–atmosphere CO2 exchange. Encouragingly, the RMSEs of TT-R-assimilated CO2 concentration were mostly maintained at a relatively low level (≤ 10 ppm), and large RMSEs only arose in a very small area over central China. Thus, the uncertainty in the initial CO2 concentration fields could affect the assimilation of fluxes, and the design of simultaneously assimilating concentrations and fluxes in this study improved the final performance of Tan-Tracker-Region. In addition, the hybrid assimilation algorithm (i.e., POD-4DVar) also contributed greatly to this regional inversion system.
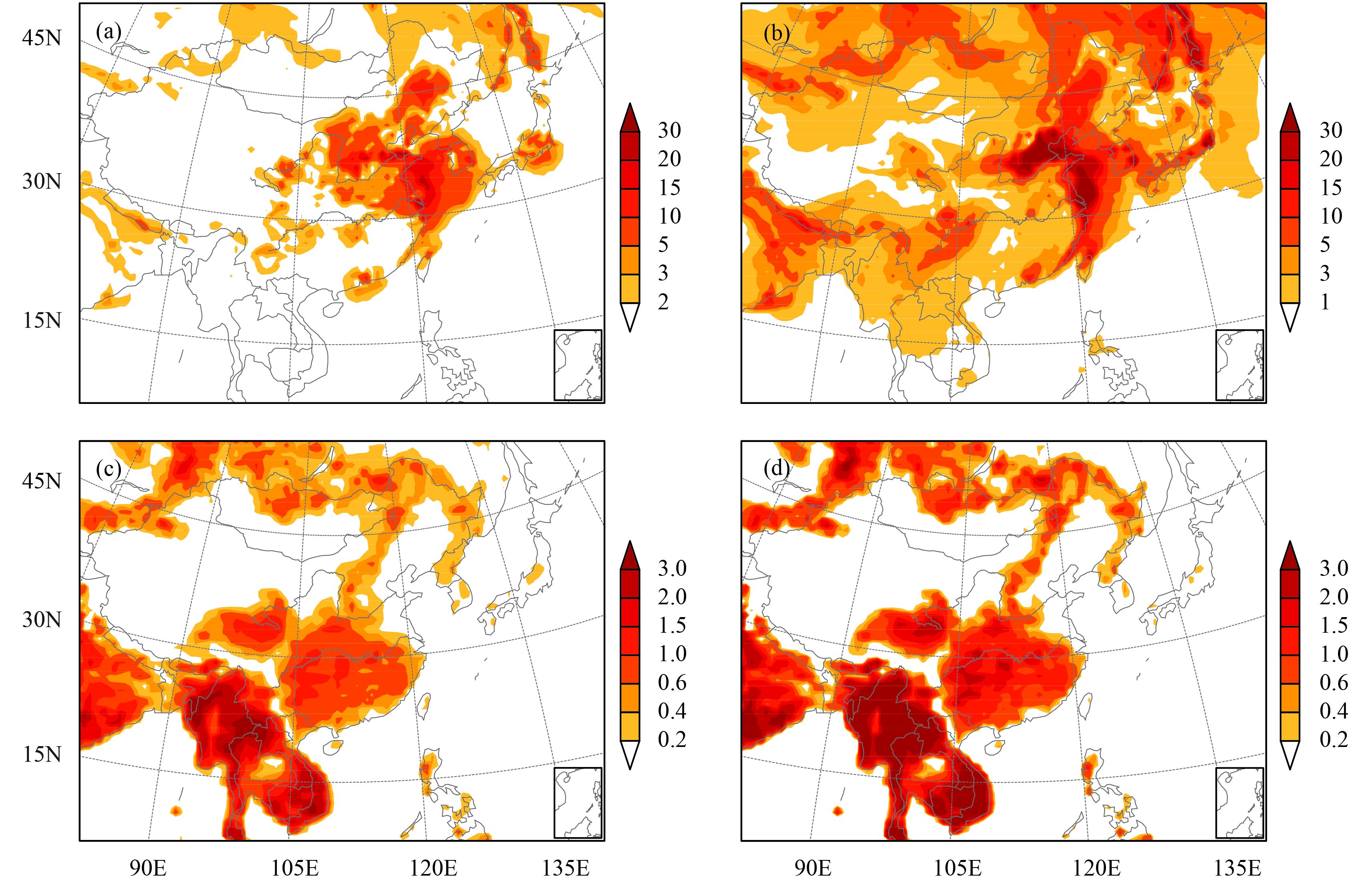
|
| Figure 15 RMSEs for the daily-averaged (a) assimilated CO2 concentrations (ppm), (b) simulated CO2 concentrations (ppm), (c) assimilated CO2 fluxes (μmolem–2 s–1), and (d) first-guess CO2 flux (μmolem–2 s–1) during 1–31 July 2010. |
The above results indicated that more observation sites would be useful to systematically improve the estimation of CO2 concentration and flux in large areas over the model domain. Moreover, the Indochina Peninsula in the model domain acts as a source in summer and sink in winter. This distinctly different seasonal variation of CO2 flux should be noted, since photosynthesis is restrained during the rainy season, while respiration is subject to favorable conditions (Yu et al., 2013). The first-guess flux displays large RMSEs over Southeast Asia, and the improvements were very small due to the lack of observations in this area. This would have been particularly true in the regions where there was little direct impact of the observation, and thus flux assessments needed to be limited to the relevant areas in the present study.
While the regional inversion system in this study represents an encouraging approach to CO2 flux inversion, further efforts should be made on satellite observations, which we intend to present in future studies. Due to the lack of reliable CO2 flux estimations, we need to seek indirect ways to evaluate the real data assimilations of fluxes in the future (Chevallier et al., 2014).
4 Summary and conclusionsA regional surface CO2 flux inversion system (TT-R) was developed based on the joint POD-4DVar assimilation framework with CMAQ acting as the CTM to resolve fine-scale CO2 variability over East Asia. The POD-4DVar approach is the core algorithm for the joint assimilation framework. CMAQ acts as the major contribution for linking the surface fluxes (fossil-fuel emissions, biomass burning, ocean flux, and biosphere–atmosphere exchange) and CO2 concentrations. A persistence dynamical model is used to forecast surface CO2 flux scaling factors and help avoid the “signal-to-noise” problem, such that surface CO2 fluxes can be assimilated as a whole at the grid scale with better use of observation information. Simultaneous assimilation of CO2 concentrations and surface CO2 fluxes was applied to help reduce the uncertainty in initial CO2 concentrations.
A set of OSSEs were designed to assess the system’s performance for assimilation of CO2 concentrations and fluxes with artificial ground-based measurements, which were chosen from several WDCGG stations (AMY, UUM, and WLG) and CERN stations (Mt. Dinghu and Fukang), due to the sparseness of ground-based measurements in East Asia. The comparison between the assimilated and true CO2 concentrations and fluxes indicated that TT-R reproduced temporal and spatial CO2 variations reasonably well, but with a higher bias in some regions, implying strong effects of background bias, model transport errors in the boundary layer, and inadequate ground-based observations.
The regional inversion system assimilated surface CO2 concentrations and fluxes on the hourly timescale, and the diurnal variation of CO2 at the WLG station was fairly well captured by the inversion system, with reduced bias compared to the background values, demonstrating the good potential of TT-R in assimilating CO2 fluxes and concentrations at finer spatiotemporal scales. It should also be noted that the assimilation reduced the bias but did not significantly change the spatial pattern, due to the sparse localization of observation sites. Careful analyses of the results suggested that assimilation parameters used in the global inversion system needed to be regulated to adapt to the unique characteristics of regional transport models. Certain assimilation parameter choices (e.g., an optimized window length of approximately 3 h, an ensemble size of approximately 100, and a standard horizontal localization radius of approximately 320 km) could generally guarantee the reliable performance of TT-R. Due to the strong diurnal variation and spatial heterogeneity in the CMAQ simulation, the performance of the regional inversion system could be affected.
Moreover, because all observations can be artificially obtained in OSSEs, the performance of Tan-Tracker-Region was further evaluated through different densities of the artificial observation network in different CO2 flux situations. Sixty ground-based stations were scattered randomly over the model domain and only the geographical position information was used to produce the artificial “observation” in the following OSSEs. Results indicated that more observation sites were useful to systematically improve the estimation of CO2 concentration and flux in large areas over the model domain.
The work presented here could also serve as a basis for future research in which thorough estimation of CO2 flux variability over East Asia can be achieved with the regional inversion system. The Chinese carbon satellite (TanSat) was launched on 22 December 2016, and China has become the third state with a carbon satellite (following America and Japan). In future work, we intend to apply our proposed Tan-Tracker-Region on TanSat as well as GOSAT measurements of CO2.
Acknowledgments. We thank the two anonymous reviewers for their helpful comments. CarbonTracker results used in the model as initial fields and boundary conditions were provided by NOAA ESRL, Boulder, Colorado, USA (http://carbontracker.noaa.gov). We express deep gratitude to the research team and support staff for providing their data on the website.
| Ahmadov, R., C. Gerbig, R. Kretschmer, et al., 2009: Comparing high resolution WRF-VPRM simulations and two global CO2 transport models with coastal tower measurements of CO2. Biogeosciences, 6, 807–817. DOI:10.5194/bg-6-807-2009 |
| Andres, R. J., T. A. Boden, F.-M. Bréon, et al., 2012: A synthesis of carbon dioxide emissions from fossil-fuel combustion. Biogeosciences, 9, 1845–1871. DOI:10.5194/bg-9-1845-2012 |
| Baker, D. F., S. C. Doney, and D. S. Schimel, 2006: Variational data assimilation for atmospheric CO2. Tellus B, 58, 359–365. DOI:10.1111/j.1600-0889.2006.00218.x |
| Ballav, S., P. K. Patra, M. Takigawa, et al., 2012: Simulation of CO2 concentration over East Asia using the regional transport model WRF-CO2. J. Meteor. Soc. Japan, 90, 959–976. DOI:10.2151/jmsj.2012-607 |
| Bousquet, P., P. Peylin, P. Ciais, et al., 2000: Regional changes in carbon dioxide fluxes of land and oceans since 1980. Science, 290, 1342–1346. DOI:10.1126/science.290.5495.1342 |
| Chevallier, F., P. I. Palmer, L. Feng, et al., 2014: Toward robust and consistent regional CO2 flux estimates from in situ and spaceborne measurements of atmospheric CO2. Geophys. Res. Lett., 41, 1065–1070. DOI:10.1002/2013GL058772 |
| Conway, T. J., 2013: Atmospheric CO2 Monthly Concentration Data, Ulaan Uul, World Data Centre for Greenhouse Gases. Japan Meteorology Agency, Tokyo. [Available online at http://ds.data.jma.go.jp/gmd/wdcgg/.] |
| Deng, F., J. M. Chen, M. Ishizawa, et al., 2007: Global monthly CO2 flux inversion with a focus over North America . Tellus B, 59, 179–190. DOI:10.1111/j.1600-0889.2006.00235.x |
| Engelen, R. J., S. Serrar, and F. Chevallier, 2009: Four-dimensional data assimilation of atmospheric CO2 using AIRS observations . J. Geophys. Res., 114(D3), D03303. DOI:10.1029/2008JD010739 |
| Feng, L., P. I. Palmer, H. Bösch, et al., 2009: Estimating surface CO2 fluxes from space-borne CO2 dry air mole fraction observations using an ensemble Kalman filter . Atmos. Chem. Phys., 9, 2619–2633. DOI:10.5194/acp-9-2619-2009 |
| Gaspari, G., and S. E. Cohn, 1999: Construction of correlation functions in two and three dimensions. Quart. J. Roy. Meteor. Soc., 125, 723–757. DOI:10.1002/qj.49712555417 |
| Greybush, S. J., E. Kalnay, T. Miyoshi, et al., 2011: Balance and ensemble Kalman filter localization techniques. Mon. Wea. Rev., 139, 511–522. DOI:10.1175/2010MWR3328.1 |
| Guan, D. B., Z. Liu, Y. Geng, et al., 2012: The gigatonne gap in China’s carbon dioxide inventories. Nat. Climate. Change, 2, 672–675. DOI:10.1038/nclimate1560 |
| Gurney, K. R., R. M. Law, A. S. Denning, et al., 2004: Transcom 3 inversion intercomparison: Model mean results for the estimation of seasonal carbon sources and sinks. Global Biogeochem. Cy., 18, GB1010. DOI:10.1029/2003GB002111 |
| Gurney, K. R., D. L. Mendoza, Y. Y. Zhou, et al., 2009: High resolution fossil fuel combustion CO2 emission fluxes for the United States . Environ. Sci. Technol., 43, 5535–5541. DOI:10.1021/es900806c |
| Houtekamer, P. L., and H. L. Mitchell, 1998: Data assimilation using an ensemble Kalman filter technique. Mon. Wea. Rev., 126, 796–811. DOI:10.1175/1520-0493(1998)126<0796:DAUAEK>2.0.CO;2 |
| Huang, Z. K., Z. Peng, H. N. Liu, et al., 2014: Development of CMAQ for East Asia CO2 data assimilation under an EnKF framework: A first result . Chinese Sci. Bull., 59, 3200–3208. DOI:10.1007/s11434-014-0348-9 |
| Jia, B. H., Z. H. Xie, Y. Y. Zeng, et al., 2015: Diurnal and seasonal variations of CO2 fluxes and their climate controlling factors for a subtropical forest in Ningxiang . Adv. Atmos. Sci., 32, 553–564. DOI:10.1007/s00376-014-4069-4 |
| Jiang, F., H. W. Wang, J. M. Chen, et al., 2013: Nested atmospheric inversion for the terrestrial carbon sources and sinks in China. Biogeosciences, 10, 5311–5324. DOI:10.5194/bg-10-5311-2013 |
| Kang, J. S., E. Kalnay, T. Miyoshi, et al., 2012: Estimation of surface carbon fluxes with an advanced data assimilation methodology. J. Geophys. Res., 117(D24), D24101. DOI:10.1029/2012JD018259 |
| Kort, E. A., C. Frankenberg, C. E. Miller, et al., 2012: Space-based observations of megacity carbon dioxide. Geophys. Res. Lett., 39, L17806. DOI:10.1029/2012GL052738 |
| Kou, X. X., M. G. Zhang, and Z. Peng, 2013: Numerical simulation of CO2 concentrations in East Asia with RAMS-CMAQ . Atmos. Oceanic Sci. Lett., 6, 179–184. DOI:10.3878/j.issn.1674-2834.13.0022 |
| Kou, X. X., M. G. Zhang, Z. Peng, et al., 2015: Assessment of the biospheric contribution to surface atmospheric CO2 concentrations over East Asia with a regional chemical transport model . Adv. Atmos. Sci., 32, 287–300. DOI:10.1007/s00376-014-4059-6 |
| Kurokawa, J., T. Ohara, T. Morikawa, et al., 2013: Emissions of air pollutants and greenhouse gases over Asian regions during 2000–2008: Regional Emission inventory in ASia (REAS) version 2. Atmos. Chem. Phys., 13, 11019–11058. DOI:10.5194/acp-13-11019-2013 |
| Le Quéré, C., M. R. Raupach, J. G. Canadell, et al., 2009: Trends in the sources and sinks of carbon dioxide. Nat. Geosci., 2, 831–836. DOI:10.1038/ngeo689 |
| Lee, H., and S. H. Kim, 2013: Atmospheric CO2 Monthly Concentration Data, Anmyeon-Do, World Data Centre for Greenhouse Gases. Japan Meteorology Agency, Tokyo. [Available online at http://ds.data.jma.go.jp/gmd/wdcgg/.] |
| Liu, J. J., I. Fung, E. Kalnay, et al., 2012: Simultaneous assimilation of AIRS Xco2 and meteorological observations in a carbon climate model with an ensemble Kalman filter . J. Geophys. Res., 117(D5), D05309. DOI:10.1029/2011JD016642 |
| Liu, M., H. Wang, H. Wang, et al., 2013: Refined estimate of China’s CO2 emissions in spatiotemporal distributions . Atmos. Chem. Phys., 13, 10873–10882. DOI:10.5194/acp-13-10873-2013 |
| Liu, Y., and X. L. Zou, 2015: Impact of 4DVAR assimilation of AIRS total column ozone observations on the simulation of Hurricane Earl. J. Meteor. Res., 29, 257–271. DOI:10.1007/s13351-015-4058-2 |
| Liu, Z., R. P. Bambha, J. P. Pinto, et al., 2013: Toward verifying fossil fuel CO2 emissions with the CMAQ model: Motivation, model description and initial simulation . J. Air Waste Manag. Assoc., 64, 419–435. DOI:10.1080/10962247.2013.816642 |
| Maki, T., M. Ikegami, T. Fujita, et al., 2010: New technique to analyze global distributions of CO2 concentrations and fluxes from non-processed observational data . Tellus B, 62, 797–809. DOI:10.1111/j.1600-0889.2010.00488.x |
| Mays, K. L., P. B. Shepson, B. H. Stirm, et al., 2009: Aircraft-based measurements of the carbon footprint of Indianapolis. Environ. Sci. Technol., 43, 7816–7823. DOI:10.1021/es901326b |
| McKain, K., S. C. Wofsy, T. Nehrkorn, et al., 2012: Assessment of ground-based atmospheric observations for verification of greenhouse gas emissions from an urban region. Proc. Natl. Acad. Sci. USA, 109, 8423–8428. DOI:10.1073/pnas.1116645109 |
| Miyazaki, K., 2009: Performance of a local ensemble transform Kalman filter for the analysis of atmospheric circulation and distribution of long-lived tracers under idealized conditions. J. Geophys. Res., 114(D19), D19304. DOI:10.1029/2009JD011892 |
| Nassar, R., D. B. A. Jones, P. Suntharalingam, et al., 2010: Modeling global atmospheric CO2 with improved emission inventories and CO2 production from the oxidation of other carbon species . Geosci. Model Dev., 3, 689–716. DOI:10.5194/gmd-3-689-2010 |
| Peng, Z., M. G. Zhang, X. X. Kou, et al., 2015: A regional carbon data assimilation system and its preliminary evaluation in East Asia. Atmos. Chem. Phys., 15, 1087–1104. DOI:10.5194/acp-15-1087-2015 |
| Peters, W., J. B. Miller, J. Whitaker, et al., 2005: An ensemble data assimilation system to estimate CO2 surface fluxes from atmospheric trace gas observations . J. Geophys. Res., 110(D24), D24304. DOI:10.1029/2005JD006157 |
| Peters, W., A. R. Jacobson, C. Sweeney, et al., 2007: An atmospheric perspective on North American carbon dioxide exchange: CarbonTracker. Proc. Natl. Acad. Sci. USA, 104, 18925–18930. DOI:10.1073/pnas.0708986104 |
| Peylin, P., R. M. Law, K. R. Gurney, et al., 2013: Global atmospheric carbon budget: Results from an ensemble of atmospheric CO2 inversions . Biogeosciences, 10, 6699–6720. DOI:10.5194/bgd-10-5301-2013 |
| Piao, S. L., J. Y. Fang, P. Ciais, et al., 2009: The carbon balance of terrestrial ecosystems in China. Nature, 458, 1009–1013. DOI:10.1038/nature07944 |
| Pillai, D., C. Gerbig, R. Ahmadov, et al., 2011: High-resolution simulations of atmospheric CO2 over complex terrain-representing the Ochsenkopf mountain tall tower . Atmos. Chem. Phys., 11, 7445–7464. DOI:10.5194/acpd-11-6875-2011 |
| Saeki, T., S. Maksyutov, M. Sasakawa, et al., 2013: Carbon flux estimation for Siberia by inverse modeling constrained by aircraft and tower CO2 measurements . J. Geophys. Res., 118, 1100–1122. DOI:10.1002/jgrd.50127 |
| Stephens, B. B., K. R. Gurney, P. P. Tans, et al., 2007: Weak northern and strong tropical land carbon uptake from vertical profiles of atmospheric CO2. Science, 316, 1732–1735. DOI:10.1126/science.1137004 |
| Strassmann, K. M., F. Joos, and G. Fischer, 2008: Simulating effects of land use changes on carbon fluxes: Past contributions to atmospheric CO2 increases and future commitments due to losses of terrestrial sink capacity . Tellus B, 60, 583–603. DOI:10.1111/j.1600-0889.2008.00340.x |
| Tangborn, A., L. L. Strow, B. Imbiriba, et al., 2013: Evaluation of a new middle–lower tropospheric CO2 product using data assimilation . Atmos. Chem. Phys., 13, 4487–4500. DOI:10.5194/acp-13-4487-2013 |
| Tian, X. J., Z. H. Xie, and A. G. Dai, 2008: An ensemble-based explicit four-dimensional variational assimilation method. J. Geophys. Res., 113(D21), D21124. DOI:10.1029/2008JD010358 |
| Tian, X. J., Z. H. Xie, and Q. Sun, 2011: A POD-based ensemble four-dimensional variational assimilation method. Tellus A, 63, 805–816. DOI:10.1111/j.1600-0870.2011.00529.x |
| Tian, X. J., Z. H. Xie, Y. Liu, et al., 2014: A joint data assimilation system (Tan-Tracker) to simultaneously estimate surface CO2 fluxes and 3-D atmospheric CO2 concentrations from observations . Atmos. Chem. Phys., 14, 13281–13293. DOI:10.5194/acp-14-13281-2014 |
| van der Werf, G. R., J. T. Randerson, T. Randerson, L. Giglio, et al., 2010: Global fire emissions and the contribution of deforestation, savanna, forest, agricultural, and peat fires (1997–2009). Atmos. Chem. Phys., 10, 11707–11735. DOI:10.5194/acp-10-11707-2010 |
| Wang, B., J. J. Liu, S. D. Wang, et al., 2010: An economical approach to four-dimensional variational data assimilation. Adv. Atmos. Sci., 27, 715–727. DOI:10.1007/s00376-009-9122-3 |
| Wunch, D., P. O. Wennberg, G. C. Toon, et al., 2009: Emissions of greenhouse gases from a North American megacity. Geophys. Res. Lett., 36, L15810. DOI:10.1029/2009gl039825 |
| Yu, G. R., X. J. Zhu, Y. L. Fu, et al., 2013: Spatial patterns and climate drivers of carbon fluxes in terrestrial ecosystems of China. Global Change Biol., 19, 798–810. DOI:10.1111/gcb.12079 |
| Zhang, B., X. J. Tian, J. H. Sun, et al., 2015: PODEn4DVar-based radar data assimilation scheme: Formulation and preliminary results from real-data experiments with advanced research WRF (ARW). Tellus A, 67, 26045. DOI:10.3402/tellusa.v67.26045 |
| Zhang, H. F., B. Z. Chen, I. T. van der Laan-Luijk, et al., 2014: Estimating Asian terrestrial carbon fluxes from CONTRAIL aircraft and surface CO2 observations for the period 2006–2010 . Atmos. Chem. Phys., 14, 5807–5824. DOI:10.5194/acp-14-5807-2014 |
| Zhang, M. G., I. Uno, S. Sugata, et al., 2002: Numerical study of boundary layer ozone transport and photochemical production in East Asia in the wintertime. Geophys. Res. Lett., 29, 40-1–40-4. DOI:10.1029/2001GL014368 |
| Zhao, Y., C. P. Nielsen, and M. B. McElroy, 2012: China’s CO2 emissions estimated from the bottom up: Recent trends, spatial distributions, and quantification of uncertainties . Atmos. Environ., 59, 214–223. DOI:10.1016/j.atmosenv.2012.05.027 |
| Zhou, L. X., 2013: Atmospheric CO2 Monthly Concentration Data, Mt. Waliguan, World Data Centre for Greenhouse Gases. Japan Meteorology Agency, Tokyo. [Available online at http://ds.data.jma.go.jp/gmd/wdcgg/.] |
 2017, Vol. 31
2017, Vol. 31


