The Chinese Meteorological Society
Article Information
- Seyedeh Atefeh MOHAMMADI, Majid AZADI, Morteza RAHMANI . 2017.
- Comparison of Spatial Interpolation Methods for Gridded Bias Removal in Surface Temperature Forecasts. 2017.
- J. Meteor. Res., 31(4): 791-799
- http://dx.doi.org/10.1007/s13351-017-6135-1
Article History
- Received August 7, 2016
- in final form January 4, 2017
2. Atmospheric Science and Meteorological Research Center, Tehran 16385-14977, Iran;
3. Faculty of Basic and Advanced Technologies in Biology, University of Science and Culture, Tehran 14619-68151, Iran
Since recent decades, numerical weather prediction (NWP) models have been used routinely to forecast the future weather events (e.g., Li et al., 2015; Wang et al., 2015; Li et al., 2016). Inevitably, the output of all NWP models involves some substantial errors that impact on the quality and operational utility of the forecasts. The errors arise mainly from the difference between the land use and topography used in the model and the real world, imperfections in the model itself, and the deficiencies in generating the initial conditions, and have two components of random and systematic errors. The model improvements and the developments in data assimilation methods for generating the initial conditions may be effective on the reduction of the random component. On the other hand, statistical methods can be used to remove the systematic error that is mostly the larger component of total error at the surface where often there are substantial deficiencies in specified surface parameters and model physics (Hacker and Rife, 2007). As such, total error in the near surface fields such as 2-m temperature forecasts can be significantly reduced by removing the systematic error.
The systematic error or bias in NWP model outputs could be removed by using historical bias data. For this purpose, several statistical post-processing techniques have been proposed. The most popular methods that need long data archive for training period are model output statistics (MOS) (Glahn and Lowry, 1972; Wilks and Hamill, 2007) and perfect prognosis method (PPM) (Klein et al., 1959). Other methods that use short term training period include Kalman filtering (Homleid, 1995; Galanis and Anadranistakis, 2002; Roeger et al., 2003), running mean error (Stensrud and Skindlov, 1996), the neural network-based methods (Marzban, 2003; Yuval and Hsieh, 2003), and some other methods (e.g., Lam et al., 2011; Acharya et al., 2013; Sweeney et al., 2013). Using historical observation data for bias removal makes these techniques applicable only at observation locations and so they are not directly applicable to other points of interest. However, many end users of weather forecasts require bias corrected forecasts at any location that rarely coincides with the observation sites. Consequently, it is necessary to remove bias on the model grid where there is usually no observation data.
As there is no observation or bias data on the grid points, bias can be removed by using historical information of the bias in neighboring observation stations. The issue of interpolating past biases from neighboring observation stations to a given grid point has been addressed in some earlier works. For example, Yussouf and Stensrud (2006) used Cressman scheme (Cressman, 1959) to interpolate 12-day mean bias values at observation stations to a given location. Gel (2007) compared three methods named as local observation-based (LOB), classification and regression trees and alternating conditional expectations (CART–ACE), and LOB–CART–ACE, which is a natural combination of two previous methods for gridded bias correction in mesoscale weather forecasting. Hacker and Rife (2007) proposed two error covariance models to estimate the bias of near-surface temperature on a mesoscale grid. Mass et al. (2008) interpolated biases at observing locations to model grid points that have similar elevation and/or land-use characteristics.
All of the above mentioned methods interpolate biases at observation stations to the point of interest, but Glahn et al. (2009) interpolated MOS predictions (not bias) at observation sites to the model grid using a modified version of Cressman (1959) method. Similarly, in this paper, the bias corrected surface temperature forecasts are interpolated from observation stations to any given location.
For this purpose, four interpolation techniques are used for interpolating surface temperature that take into account the topography information. They are based on weighted-averaging with different approaches to calculate the weights and lapse rates. The first method is the inverse distance squared weighting with a constant lapse rate (IDSW-CLR) for temperature. The second method called GIDS-LR is the gradient plus inverse distance squared (GIDS) with linear regression to calculate the lapse rate. GIDS has been used with success for climate data interpolation (Nalder and Wein, 1998). In GIDS, a multiple linear regression based on latitude, longitude, and altitude of points is modeled to calculate the lapse rate. Moreover, an alternative method such as classification and regression tree (CART) is examined for lapse rate calculation. Therefore, the third method is GIDS-CART which incorporates nonlinear relationships between the temperature as the predictand and longitude, latitude, and altitude of a point as the predictors to calculate the lapse rate. The fourth technique (Kriging-CLR) is an ordinary Kriging method with a constant lapse rate used for the elevation adjustment. Finally, the results of using proposed techniques in bias correction of the weather research and forecasting (WRF) model (Skamarock et al., 2008) 48-h surface temperature forecasts are compared with each other.
The reminder of this paper is organized as follows. Section 2 supplies the general framework of the applied interpolation schemes. Section 3 reports the used data and methods. The verification and comparison results are presented in Section 4, and conclusions are finally drawn in Section 5.
2 MethodologyFor spatial interpolation of bias corrected temperature, three aspects should be considered (Stahl et al., 2006): (1) the approach of choosing the neighboring observation stations, (2) the method of calculating the lapse rate to adjust for elevation, and (3) the method used for interpolating the data. In the following, the above mentioned three aspects used here, are presented.
2.1 NeighborhoodIn fact, there is no optimal instruction for choosing an appropriate neighborhood, but some theoretical rules of thumb can be useful. Here, we have used the semivariogram that can provide an insight into estimating a radius of vicinity.
In geostatistics (e.g., Cressie, 2015), a semivariogram is a function for describing the spatial correlation of the observation data and is defined as
|
$\gamma \left(h \right) = \frac{1}{{2N \!\! \left(h \right)}}\mathop \sum \limits_{i = 1}^{N\left(h \right)} {\left[ {Z \!\! \left({{x_k} + h} \right) - Z \!\! \left({{x_k}} \right)} \right]^2}, $
|
(1) |
where γ(h) is the semivariogram of variable Z at lag distance h and N(h) is the number of pairs of points separated by lag h. Semivariogram increases when the distance between locations grows up to the distance called range at which the observations are uncorrelated. Thus, the range value is taken to be the radius of circle in which the appropriate neighbors used for interpolation exist.
2.2 Lapse rateIn general, temperature decreases with altitude and hence, the rate of temperature change with height (lapse rate) is an effective factor in determining temperature (Nalder and Wein, 1998). As the point of interest and its neighboring observation stations do not necessarily have similar altitude, the temperature change with elevation has to be taken into account in the interpolation procedure. The most common constant lapse rate value found in the literature is 6 ℃ km–1 (Dodson and Marks, 1997; Liston and Elder, 2006), but Courault and Monestiez (1999) claimed that this value corresponds to the free atmosphere, which is not proximate to the surface, and also varies in different seasons. Hence, they obtained the lapse rate by linear regression performed between temperature and elevation.
Similarly, in this study, a constant lapse rate is used in IDSW-CLR and Kriging-CLR methods whose lapse rate is estimated from the relationship between temperature and elevation. For the two other methods, adjustments for elevation have been made by using temperature gradients based on the geographical coordinates of the points that will be explained in the next subsection.
2.3 Prediction algorithmsTo remove the systematic errors associated with the surface temperature forecast on a regular grid, the temperature forecasts are first bias corrected by using the running mean error method (Stensrud and Skindlov, 1996) at observation sites and then, corrected temperature forecasts are interpolated to the desired grid points.
Four various weighted-average interpolation methods are applied to estimate the temperature forecasts at desired gird points. To enhance the interpolation accuracy, temperature variation with height is taken into account by considering the lapse rate. The interpolation methods differ from each other primarily in the way the weights and lapse rate are calculated by employing two approaches to calculate weights and three approaches for lapse rate calculation.
In the following, T is temperature, d is the distance between the prediction point and observation point, n is the number of data points in local neighborhood of a prediction point, h is the elevation, and subscripts g and i refer to the grid prediction and observation point, respectively.
2.3.1 IDSW-CLR method
In this method, temperatures are first converted to sea level equivalent by using a constant lapse rate as:
|
${T^{\rm sea}} = T + {c \cdot h}, $
|
(2) |
where Tsea is temperature at sea level and c is the constant lapse rate. Then, the bias corrected temperatures of neighboring observation stations are interpolated to the given grid point by using weighted averaging with the weights calculated with inverse distance squared as:
|
$T_g^{{\rm{sea}}} = \frac{{\sum\limits_{i = 1}^n {\left\{ {{{\left( {\displaystyle\frac{1}{{{d_i}}}} \right)}^2}\left( {T_i^{{\rm{sea}}}} \right)} \right\}} }}{{\sum\limits_{i = 1}^n {{{\left( {\displaystyle\frac{1}{{{d_i}}}} \right)}^2}} }}.$
|
(3) |
Then, the interpolated temperature at grid points are converted to the elevation of the prediction point with a constant lapse rate:
|
${T_g} = T_g^{\rm sea} - {c \cdot h_g}.$
|
(4) |
2.3.2 Kriging-CLR method
This method uses the same approach for elevation adjustment as used in the IDSW-CLR method. Hence, temperatures are first adjusted to sea level prior to the interpolation as explained above. Similar to IDSW-CLR, the interpolation method is a weighted averaging method, but the weights are computed by using Kriging scheme.
Kriging is a geostatistical interpolation method that is mathematically related to regression analysis (Cressie, 2015). Generally, this method is a weighted average of the known data points surrounding the estimation point. The ordinary Kriging estimator can be defined as:
|
$T_g^{\rm sea} = {m_g} + \mathop \sum \limits_{i = 1}^n {\lambda _i}\left({T_i^{\rm sea} - {m_i}} \right), $
|
(5) |
where λ and m are the Kriging weight and expected value (mean), respectively. Rather than an arbitrary weighting function, Kriging assigns weights by minimizing the variance of the estimator. The reader is referred to Stein (1999) for full details.
2.3.3 GIDS-LR method
The GIDS is first proposed by Nalder and Wein (1998) for spatial interpolation of climatic data. This method is a weighted average interpolation that adjustment for elevation is made by using the multiple linear regression based on the geographical coordinates of the points. It first fits a multiple linear regression whose predictor variables are longitude (x), latitude (y), and altitude (h) of the observing points:
|
$\hat T = {a_0} + {a_1}x + {a_2}y + {a_3}h.$
|
(6) |
The fitted temperature at each observation station and prediction point are used to estimate the temperature gradient. The predicted temperature is then calculated by weighted averaging of the temperature at known points adjusted by their corresponding temperature gradient, with inverse distance squared weights. The GIDS-LR can be formulated as follows:
|
${T_g} = \frac{{\sum\limits_{i = 1}^n {\left\{ {{{\left( {\displaystyle\frac{1}{{{d_i}}}} \right)}^2}\left( {{T_i} + \left( {{{\hat T}_g} - {{\hat T}_i}} \right)} \right)} \right\}} }}{{\sum\limits_{i = 1}^n {{{\left( {\displaystyle\frac{1}{{{d_i}}}} \right)}^2}} }}.$
|
(7) |
2.3.4 GIDS-CART method
This method has similar interpolation approach to the GIDS-LR method, except that
Generally, CARTs suffer from high variance that can be decreased by applying random forest method proposed by Breiman (2001) to improve the predictive performance of trees. Random forest is an ensemble learning method that builds a number of trees on bootstrapped training samples, and then averages the resulting predictions. Moreover, in a random forest, each node is split by using a random subset of the predictors to de-correlate the trees. Here, the random forest is used with spatial predictors such as longitude, latitude, and altitude of the points.
3 Application 3.1 DataThe data are 48-h WRF forecasts of the surface temperature initialized daily at 1200 UTC from 15 September through 31 December 2011 over Iran. The initial conditions of the forecasts are provided by Global Forecast System (GFS) forecasts with a one-degree horizontal resolution. WRF was run with two nested domains, with the larger domain covering the south–west Middle East from 10° to 51° north and from 20° to 80° east and the inner domain covers Iran from 23° to 41° north and from 42° to 65° east. The spatial resolutions are 45 and 15 km for the coarser and finer domains, respectively.
The model forecasts for the inner domain are bilinearly interpolated to the observation stations. Observational data used in this study consist of observations of the surface temperature measured at 1200 UTC at 306 irregularly spaced synoptic meteorological stations scattered across Iran as shown in Fig. 1.

|
| Figure 1 Synoptic meteorological stations scattered across Iran. |
The training period is a sliding training window of the most recent 15 days prior to the forecast day. The test period included all the days from 19 September 2011 to 28 February 2012.
3.2 SemivariogramThe semivariogram is used to estimate the appropriate size of a neighborhood. Figure 2 shows the estimated semivariogram of post-processed forecasts at 306 observation sites. The range value is estimated 7.61 degree (approximately 800 km), which implies that the observation stations within a 800-km radius of grid point vicinity could be used for bias correction while those stations located outside of this range are not correlated and thus, may not make any improvement.

|
| Figure 2 Semivariogram of bias corrected forecasts at 306 observation sites. |
Both IDSW-CLR and Kriging-CLR methods are adjusted for elevation using a constant lapse rate. Accordingly, a linear regression model is fitted between the observed temperature and elevation as:
|
$T = a + b \cdot h, $
|
(8) |
where a is the intercept and b is the proposed constant lapse rate. The training period data are used to employ Eq. (8). Using available data sample, the slope coefficient b is estimated to be 5.6 ℃ km–1. This constant lapse rate is used to convert the temperature to sea level equivalent prior to interpolation. However, the results of some experiments show that the interpolated temperatures are not sensitive to the various lapse rate values ranging from 4.5 to 6.5 ℃ km–1.
3.4 VerificationSince the correct value at the grid points is not known, the methods' performance is assessed by using the cross validation approach. For every day of the test period, each observation station, in turn, is excluded from the list of observation stations, and the withheld observation station is considered as a given point which is proposed to be bias corrected in the absence of its historical information. Eventually, the prediction error is computed with mean absolute error (MAE), root mean squared error (RMSE), and mean error (ME) or the bias.
4 ResultsFigure 3 presents the error distribution of the raw and bias corrected forecasts graphically using the box-and-whisker plots over the test period. As can be seen, the mean error of the raw forecast is –1.4℃ while it has been decreased to about zero after bias correction. Similar results could be seen for other methods, though the error variance of the Kriging-CLR and GIDS-CART methods are slightly less than the others.

|
| Figure 3 Box-and-whisker plots of the error for the raw and bias corrected forecasts. The boxes show the median, the first and third quartiles, and whiskers indicate 1.5 × IQR (interquartile range) below the first quartile and above the third quartile. |
An important cause of the systematic error existence in the output of NWP models is the difference between the topography used in the model and in the real world. In our domain of study, central and southern parts of the country are covered with desert and have more or less flat terrain, so we expect lesser differences the model and real world topography and land use. But North, West, and Northwest Iran are covered with complex topography.
More specifically, the chance of having a difference between the model and real world topography and land use, and thus systematic error for near-surface variables, in regions with complex topography (north, west, and northwest of the country with higher elevations) is higher compared to flat terrain. Hence, some correlation is expected between the systematic error and the topography. As seen in Fig. 4, the MAEs in the higher altitudes are almost larger than those in the lower altitudes representing more flat terrain, and the correlation coefficient between MAE and terrain height is 0.4. After statistical post-processing, the systematic error is removed and we expect a lower correlation coefficient between MAE and topography, which is out to be 0.03. In other words, the spatial dependency of the errors is decreased after employing any of the four post-processing methods.

|
| Figure 4 MAEs of (a) raw forecasts, and corrected forecasts using (b) IDSW-CLR, (c) Kriging-CLR, (d) GIDS-LR, and (e) GIDS-CART, at different altitudes. |
Figure 5 shows the MAE of the bias corrected forecasts using the four methods and also the raw forecasts in six different months. As seen, there is a slightly increasing trend in the MAE of the raw forecasts from September to February, which are the cold months of the winter. This result is natural since the error of the NWP models for surface temperature is generally larger during winter time compared to the error during other seasons (Warner, 2011). However, after removing the bias using either of the four methods (Fig. 5), errors of the post-processed forecasts are almost similar for all months. Thus, the temporal dependency of the errors is decreased after employing the statistical post-processing methods.

|
| Figure 5 MAE of the raw forecasts and corrected forecasts using IDSW-CLR, Kriging-CLR, GIDS-LR, and GIDS-CART in different months from September 2011 to February 2012. |
The calculated values for MAE, RMSE, improvement to hurt ratio, and RMSE skill score (RMSESS) of the raw and bias corrected forecasts are presented in Table 1 over the test period. The RMSESS is calculated as 1 – RMSE/RMSEref, with RMSE of the raw forecast as the reference value. The improvement to hurt ratio is computed by the fraction of cases with more than 2℃ improvement in the absolute bias, to cases with more than 2℃ deterioration in the absolute bias (Gel, 2007). In Table 1, Kriging-CLR method has better performance than the other methods, and makes 26% RMSE reduction relative to the raw forecast.
| Methods | MAE | RMSE | Hurt ratio improved | RMSESS |
| IDSW-CLR | 2.09 | 2.72 | 1.92 | 0.17 |
| Kriging-CLR | 1.83 | 2.40 | 2.93 | 0.27 |
| GIDS-LR | 1.92 | 2.48 | 2.47 | 0.24 |
| GIDS-CART | 1.85 | 2.45 | 2.73 | 0.25 |
The fields in Fig. 6 show the error of the 48-h surface temperature forecasts initialized on 19 December 2011. Figure 6a shows the error of the raw forecast. The errors of the bias corrected forecasts (Figs. 6b–e) are noticeably reduced compared to the error of the raw forecasts (Fig. 6a). As seen, the absolute values of the raw forecast errors are more than 3℃ over most parts of the domain, but the absolute values of the bias corrected forecast errors using either of the four mentioned methods are mostly less than 1℃. Furthermore, Kriging-CLR method (Fig. 6c) has provided the most improvement than the other methods as expected.

|
| Figure 6 The spatial distributions of the 48-h surface temperature forecast error over Iran from (a) raw forecasts, and forecasts corrected by using (b) IDSW-CLR, (c) Kriging-CLR, (d) GIDS-LR, and (e) GIDS-CART. |
According to Murphy (1988), the total error can be decomposed to systematic and random components as:
|
$\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\begin{aligned} & \frac{1}{K}\mathop \sum \limits_{i = 1}^K {\left({{O_i} - {T_i}} \right)^2} = {\left({\frac{1}{K}\mathop \sum \limits_{i = 1}^K \left({{O_i} - {T_i}} \right)} \right)^2} \\ & \quad\;+ \frac{1}{K}\mathop \sum \limits_{i = 1}^K {\left({\left({{O_i} - {T_i}} \right) - \frac{1}{K}\mathop \sum \limits_{i = 1}^K \left({{O_i} - {T_i}} \right)} \right)^2}, \end{aligned}$
|
(9) |
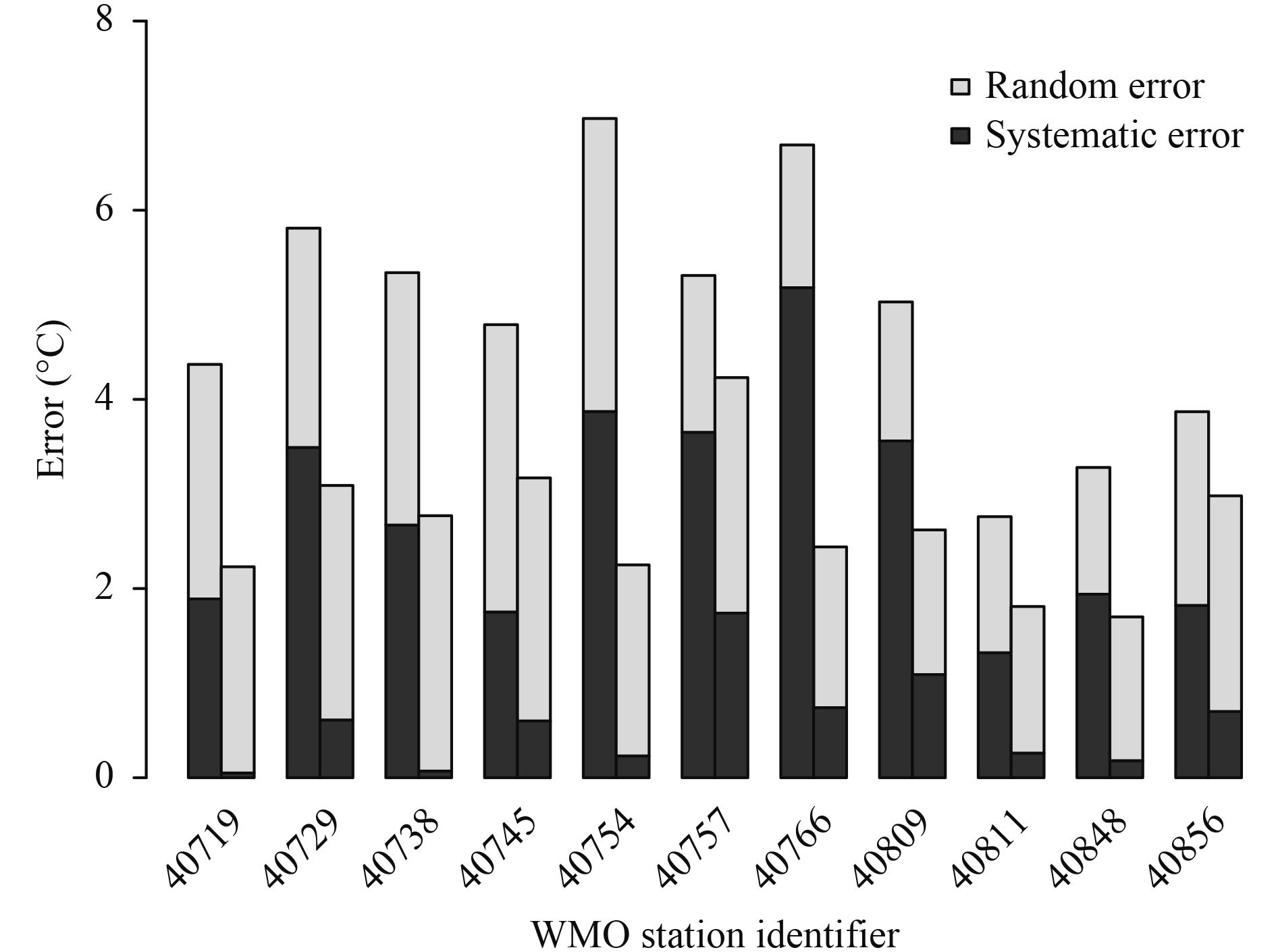
where T and O are temperature forecast and observation, respectively, and K is the number of cases used in the verification. Here, the absolute value of the mean error and the standard deviation of the error are the systematic and random error, respectively. Figure 7 shows the decomposed temperature errors of forecasts corrected by Kriging-CLR and raw forecasts at some stations that are considered as the prediction points where there is no historical observation data. As can be seen, the systematic errors dominate the surface temperature errors at many stations and thus, the total error is significantly reduced after bias correction. The stations in Fig. 7 are selected in such a way that they cover all parts of the country. As such, their altitude varied from –8.6 to 1659.4 m. The locations of the selected stations are indicated by stars in Fig. 1.
|
| Figure 7 Systematic and random erros of the surface temperature at some stations. For each station, left bar is errors of the raw forecast and right bar is errors of the forecasts corrected by the Kriging-CLR method. |
In this paper, four methods are proposed and applied for the gridded bias correction of 48-h surface temperature forecasts over Iran during 1 October and 31 December 2011. Since there is no historical bias data on the prediction grid points, the bias corrected forecasts at surrounding observation stations are interpolated to the desired grid points. Moreover, the temperature change with elevation (lapse rate) has been taken into account in the interpolation procedures. All the applied methods are based on weighed averaging, but differ from each other primarily in the way how the weight and lapse rate are calculated. The IDSW-CLR method uses the inverse distance squared weighting and a constant lapse rate; the Kriging-CLR method uses Kriging weighting and a constant lapse rate too; the GIDS-LR method uses the inverse distance squared weighting and a multiple regression with longitude, latitude, and altitude of points as its predictors to adjust for elevation; the GIDS-CART uses the inverse distance squared weighting and a random forest tree to calculate the lapse rate. The novelty of the last method (GIDS-CART) is that it incorporates nonlinear relationships between the predictand (temperature forecast) and predictors (longitude, latitude, and altitude) while they have a linear relationship in the GIDS-LR method.
A semivariogram is constructed to obtain a range value that is considered as the radius of the neighboring circle that is approximately 800 km. To calculate the constant lapse rate, a linear regression model is fitted between the observed temperature and elevation. The slope coefficient is considered as the lapse rate that is estimated 5.6 ℃ km–1 over the training period.
The results were verified by using the cross validation method. It is found that all applied bias correcting methods are successful in generating bias corrected forecasts on the grid points where there is no observation data, and have reduced the value of the bias to near zero. The verification measures including MAE, RMSE, RMSESS, and improvement ratio calculated for the interpolated bias corrected forecasts on grid points showed more or less similar results but the Kriging-CLR method is slightly better than the other methods.
The better performance of Kriging-CLR compared to other methods is probably due to the more sophisticated approach that is used in the weight calculations. The weights of Kriging-CLR are estimated by minimizing the error variance of the estimate in contrast to other methods whose weights depend simply on the inverse of squared distance. Fitting a mathematical function to the distribution of the points on a semivariogram is the important priority of the Kriging to the other methods.
Acknowledgments. We would like to show our gratitude to Islamic Republic of Iran Meteorological Organization (IRIMO) for providing access to the observation data.
| Acharya N., Chattopadhyay S., Mohanty U. C., et al., 2013: On the bias correction of general circulation model output for Indian summer monsoon. Meteor. Appl., 20, 349–356. DOI:10.1002/met.2013.20.issue-3 |
| Breiman L., 2001: Random forests. Machine Learning, 45, 5–32. DOI:10.1023/A:1010933404324 |
| Breiman, L. , J. Friedman, C. J. Stone, et al. , 1984: Classification and Regression Trees. Taylor and Francis, Oxford, 368 pp. |
| Courault Monestiez, 1999: Spatial interpolation of air temperature according to atmospheric circulation patterns in Southeast France. Int. J. Climatol., 19, 365–378. DOI:10.1002/(SICI)1097-0088(19990330)19:4 < 365::AID-JOC369 > 3.0.CO; 2-E |
| Cressie, N. A. C. , 2015: Statistics for Spatial Data. Wiley, New York, 928 pp. |
| Cressman G. P., 1959: An operational objective analysis system. Mon. Wea. Rev., 87, 367–374. DOI:10.1175/1520-0493(1959)087 < 0367:AOOAS > 2.0.CO; 2 |
| Dodson Marks, 1997: Daily air temperature interpolated at high spatial resolution over a large mountainous region. Climate Res., 8, 1–20. DOI:10.3354/cr008001 |
| Galanis Anadranistakis, 2002: A one-dimensional Kalman filter for the correction of near surface temperature forecasts. Meteor. Appl., 9, 437–441. DOI:10.1017/S1350482702004061 |
| Gel Y. R., 2007: Comparative analysis of the local observation-based (LOB) method and the nonparametric regression-based method for gridded bias correction in mesoscale weather forecasting. Wea. Forecasting, 22, 1243–1256. DOI:10.1175/2007WAF2006046.1 |
| Glahn B., Gilbert K., Cosgrove R., et al., 2009: The gridding of MOS. Wea. Forecasting, 24, 520–529. DOI:10.1175/2008WAF2007080.1 |
| Glahn R., H. A. Lowry, 1972: The use of model output statistics (MOS) in objective weather forecasting. J. Appl. Meteor., 11, 1203–1211. DOI:10.1175/1520-0450(1972)011 < 1203:TUOMOS > 2.0.CO; 2 |
| Hacker P., J. L. Rife, 2007: A practical approach to sequential estimation of systematic error on near-surface mesoscale grids. Wea. Forecasting, 22, 1257–1273. DOI:10.1175/2007WAF2006102.1 |
| Homleid M., 1995: Diurnal corrections of short-term surface temperature forecasts using the Kalman filter. Wea. Forecasting, 10, 689–707. DOI:10.1175/1520-0434(1995)010 < 0689:DCOSTS > 2.0.CO; 2 |
| Klein H., W. M. Lewis, B. Enger, 1959: Objective prediction of five-day mean temperatures during winter. J. Atmos. Sci., 16, 672–682. |
| Lam K.-Y. Shum, H. S.-Y. Tang, 2011: Regional temperature forecast for the next day in Hong Kong. Acta Meteor. Sinica, 25, 725–733. DOI:10.1007/s13351-011-0603-9 |
| Li C., Chen D. H., Li X. L., et al., 2015: Effects of terrain-following vertical coordinates on high-resolution NWP simulations. J. Meteor. Res., 29, 432–445. DOI:10.1007/s13351-015-4212-x |
| Li J., Wang P., Han H., et al., 2016: On the assimilation of satellite sounder data in cloudy skies in numerical weather prediction models. J. Meteor. Res., 30, 169–182. DOI:10.1007/s13351-016-5114-2 |
| Liston E., G. Elder, 2006: A meteorological distribution system for high-resolution terrestrial modeling (MicroMet). J. Hydrometeor., 7, 217–234. DOI:10.1175/JHM486.1 |
| Marzban C., 2003: Neural networks for postprocessing model output: ARPS. Mon. Wea. Rev., 131, 1103–1111. DOI:10.1175/1520-0493(2003)131 < 1103:NNFPMO > 2.0.CO; 2 |
| Mass C. F., Baars J., Wedam G., et al., 2008: Removal of systematic model bias on a model grid. Wea. Forecasting, 23, 438–459. DOI:10.1175/2007WAF2006117.1 |
| Murphy A. H., 1988: Skill scores based on the mean square error and their relationships to the correlation coefficient. Mon. Wea. Rev., 116, 2417–2424. DOI:10.1175/1520-0493(1988)116 < 2417:SSBOTM > 2.0.CO; 2 |
| Nalder A., I. W. Wein, 1998: Spatial interpolation of climatic normals: Test of a new method in the Canadian boreal forest. Agric. Forest Meteor., 92, 211–225. DOI:10.1016/S0168-1923(98)00102-6 |
| Roeger C., Stull R., McClung D., et al., 2003: Verification of mesoscale numerical weather forecasts in mountainous terrain for application to avalanche prediction. Wea. Forecasting, 18, 1140–1160. DOI:10.1175/1520-0434(2003)018 < 1140:VOMNWF > 2.0.CO; 2 |
| Skamarock, W. C. , J. B. Klemp, J. Dudhia, D. Gill, D. Barker, W. Wang, J. G. Powers, 2008: A description of the Advanced Research WRF Version 3, NCAR Tech. Note NCAR/TN-475+STR. |
| Stahl K., Moore R. D., Floyer J. A., et al., 2006: Comparison of approaches for spatial interpolation of daily air temperature in a large region with complex topography and highly variable station density. Agric. Forest Meteor., 139, 224–236. DOI:10.1016/j.agrformet.2006.07.004 |
| Stein, M. L. , 1999: Interpolation of Spatial Data: Some Theory for Kriging. Springer Series in Statistics, New York, USA, 249 pp. |
| Stensrud J., D. A. Skindlov, 1996: Gridpoint predictions of high temperature from a mesoscale model. Wea. Forecasting, 11, 103–110. DOI:10.1175/1520-0434(1996)011 < 0103:GPOHTF > 2.0.CO; 2 |
| Sweeney P., C. Lynch, P. Nolan, 2013: Reducing errors of wind speed forecasts by an optimal combination of post-processing methods. Meteor. Appl., 20, 32–40. DOI:10.1002/met.2013.20.issue-1 |
| Wang F. Miao, D. L. Zhang, 2015: Numerical simulations of local circulation and its response to land cover changes over the Yellow Mountains of China. J. Meteor. Res., 29, 667–681. DOI:10.1007/s13351-015-4070-6 |
| Warner, T. T. , 2011: Numerical Weather and Climate Prediction. Cambridge University Press, Cambridge, 550 pp. |
| Wilks S., D. M. Hamill, 2007: Comparison of ensemble-MOS methods using GFS reforecasts. Mon. Wea. Rev., 135, 2379–2390. DOI:10.1175/MWR3402.1 |
| Yussouf J. Stensrud, 2006: Prediction of near-surface variables at independent locations from a bias-corrected ensemble forecasting system. Mon. Wea. Rev., 134, 3415–3424. DOI:10.1175/MWR3258.1 |
| Yuval W. Hsieh, 2003: An adaptive nonlinear MOS scheme for precipitation forecasts using neural networks. Wea. Forecasting, 18, 303–310. DOI:10.1175/1520-0434(2003)018 < 0303:AANMSF > 2.0.CO; 2 |
 2017, Vol. 31
2017, Vol. 31


