The Chinese Meteorological Society
Article Information
- Nagaraja HEMA, Krishna KANT . 2017.
- Reconstructing Missing Hourly Real-Time Precipitation Data Using a Novel Intermittent Sliding Window Period Technique for Automatic Weather Station Data. 2017.
- J. Meteor. Res., 31(4): 774-790
- http://dx.doi.org/10.1007/s13351-017-6084-8
Article History
- Received June 17, 2016
- in final form February 15, 2017
Accurate rainfall data are essential for agricultural purposes, especially for timely irrigation. Rainfall/precipitation data are acquired by rain gauges, which are installed by individuals or government agencies. Rainfall is one of the most discontinuous atmospheric parameters because of its temporal and spatial variability, and estimating missing real-time rainfall data is challenging. The estimation of missing precipitation records is a mandatory aspect of hydrological studies, so as to obtain unbiased results from hydrological models. In the present study, automatic weather stations (AWSs) installed by government agencies are used for real-time rainfall measurements.
Daily AWS observations of various climatic parameters are recorded over a 24-h period, including air temperature, dew-point temperature, atmospheric pressure, rainfall, wind speed, wind direction, maximum temperature, minimum temperature, and sunshine hours in minutes.
AWSs are useful for remotely accessing real-time data throughout the network. The quality of data is such that they are available on an almost real-time basis, which can then be used for weather forecasting, disaster management, and agricultural purposes. The major components of AWSs are a data logger, a satellite link transmitter, a transmitting antenna, a battery, solar panels, sensors, a GPS antenna, and an earth station for satellite-based AWS & server for GPRS (General Packet Radio Service) based AWS. Details of these components are provided and described under the guidelines of the Department of Agriculture & Cooperation Ministry of Agriculture, Government of India (2012).
Real-time AWS measurements are used as weather-based products for irrigation scheduling. Weather-based products calculate or adjust irrigation schedules based on the climatic parameters reading from nearby AWSs. A technical report on irrigation scheduling (Technical Service Center, 2015) describes weather-based irrigation scheduling systems. The system comprises a microcontroller device that calculates and regulates irrigation schedules based on one or more of the following parameters: 1) climatic conditions, such as minimum and maximum temperatures, humidity, rainfall, wind speed, and solar radiation, which affect evapotranspiration; 2) crop types and root depths, which affect the level of agricultural water consumption; and 3) irrigation field conditions, such as latitude, soil type, ground slope, and the level of shade. Some systems are fully automatic, while others are semi-automatic. In fully automatic systems, the quality of products depends on the quality of the real-time weather data used. Missing precipitation data can lead to inappropriate calculations of irrigation demand.
Water resources are very scarce in arid and semi-arid regions. According to the Ministry of Environment & Forests, Government of India (2004), around 53.4% of continental India is comprised of arid and semi-arid land. Such arid and semi-arid regions record intermittent rainfall, and therefore, the observed distribution of daily precipitation has more zero than non-zero values. Due to this characteristic of precipitation, statistical models are used to assess the probability of non-zero precipitation, as well as provide a conditional estimation of precipitation amounts. Diverse criteria are applied to estimate a missing value or set of missing values in a series of precipitation data. Deterministic, probabilistic, random, or mixed methods are available for interpolation purposes. Some of the ongoing studies for estimating missing data are discussed below.
Various studies have been carried out for estimating climatic parameters, especially precipitation. In one such study, Ly et al. (2011) presented an estimation of daily rainfall using deterministic methods [Thiessen’s polygon method and the inverse distance weighted (IDW) method] and a geostatistical method (variogram model and kriging). They reported that the IDW method outperformed Thiessen’s polygon method and, to avoid negative interpolation of rainfall, seven variogram models (logarithmic, power, exponential, Gaussian, rational quadratic, spherical, and penta-spherical) were adopted. The Gaussian model was the best fit, and recommended for the spatial interpolation of daily rainfall if one simple model is to be chosen.
An approach called the “index station percentile” method was proposed by Tang et al. (2009) to estimate real-time precipitation. In this method, the precipitation at each nearby station is aggregated over a multi-day period, called the sliding window period, until the desired day, and the percentile of the collected precipitation at each station is calculated. In their study, the streamflow of Kalmath River was best estimated with results over a 10-day period.
Teegavarapu and Chandramouli (2005) suggested that conceptual revisions of weight assignment and surrogate measures for distances can achieve a better estimation of missing precipitation records that are used in the IDW method. The revisions deal with two issues: first, the description of the distance used in the calculations; and second, the selection process of the nearby rain gauges. Artificial neural networks and kriging can be used to exhibit the leverage of deterministic and stochastic data-driven approaches. Furthermore, interpolation methods can be correlated with traditional distance-based weighting techniques in estimating the missing values.
Kajornrit et al. (2012) estimated missing rainfall data using modular neural networks. In this technique, wet and dry period estimation is implemented by using two different neural networks. Monthly missing rainfall data were estimated by using a modular artificial neural network in the northeast region of Thailand. The real-time rainfall data from nearby control stations were used to estimate the missing real-time rainfall data at the desired station. Kajornrit et al. (2012) proposed a method that uses two variants of artificial neural networks to learn the association between rainfall recorded in non-monsoon and monsoon periods. The IDW method and improved weight of subspace reconstruction method were used to collect the final estimated value from both networks. The results showed that modular artificial neural networks provide higher precision in terms of mean absolute error (MAE) compared to single neural networks or conventional neural networks.
Lee and Kang (2015) estimated missing precipitation using kernel approaches, which provide more accurate interpolation compared with the Kth nearest neighborhood (KNN) regression method. In their study, daily precipitation data were interpolated by using five different kernel functions: Epanechnikov, quartic, triweight, tricube, and cosine. They correlated the estimation of missing precipitation data through KNN regression to the five different kernel estimations and showed that kernel methods provide high quality estimates of precipitation with respect to both statistical data assessment and hydrologic modeling performance. In addition, the performance of KNN regression in simulating streamflow using the Soil Water Assessment Tool hydrologic model was compared with that of the five kernel approaches. The result shows that kernel approach has better interpolation quality than KNN method.
Noori et al. (2014) proposed the integration of the IDW method with a geographic information system, and used the approach to estimate the rainfall distribution in Duhok Governorate. A total of 25 rainfall stations with 10-yr rainfall data were used, with 6 rainfall stations used for cross-validation. The correlation between the interpolation accuracy and two important parameters of the IDW method was also evaluated. In the IDW method, a power α value in the range of 1 to 5 and an influential radius of 15–60 km were used. The results showed that, using α = 1 and a search radius of 105 km for all 25 rainfall stations, the IDW method is a suitable method of spatial interpolation to predict the probable rainfall in Duhok Governorate.
Hasan and Croke (2013) explored the idea that Poisson-gamma distributions hold useful statistical properties to concurrently model both the continuous and discrete components of daily rainfall. The results were compared with the popularly used IDW interpolation technique. The means and percentages of days with no rainfall in the observed and simulated datasets were comparable. However, it failed to capture extremely heavy rainfall events. The study proved that the Poisson-gamma model performs better than the IDW interpolation method.
Simolo et al. (2010) proposed a modified multi-linear regression technique for the estimation of wet and dry days. The modification follows two steps: first, the correct location of precipitation (wet/dry days) is preserved; and second, the probability distribution function of daily precipitation is preserved. This method prohibits overestimation of the number of wet days and underestimation of concentrated precipitation events, which are typical shortcomings of common regression-based approaches. Hence, the overall bias in estimation can be reduced.
Radar data are popularly used as inputs for hydrological modeling because they carry the benefit of a high spatial resolution. Verworn and Haberlandt (2011) estimated hourly precipitation using a multivariate geostatistical method like kriging with external drift (KED). KED method uses supplementary information such as weather radar data, topography, and rainfall data from the denser daily networks to assess estimation of semivariograms for short time step rainfall. The hourly estimation was used to predict the occurrence of flood events.
Observed rainfall is temporally discontinuous, but patterns can sometimes emerge in continuous rainfall during specific time periods. Harada (2003) defined an efficient sliding window algorithm for the detection of sequential patterns of interest in sensor data, by sliding window from left to right for pattern matching. In the present paper, a sliding window period concept is used to cluster the observed pattern of rainfall for AWS with its corresponding nearby AWSs in particular time periods.
In the above-mentioned studies, the interpolation of missing precipitation data was conducted either on a monthly basis and daily basis, or based on precipitation forecast data. There is a dearth of literature on the interpolation of real-time hourly data using real-time nearby AWSs. Longer-duration precipitation estimation contains fewer errors compared with real-time hourly estimation. However, weather-based smart irrigation systems require real-time data, along with the last few hours of data, and they need to be accurate to achieve the right amount of irrigation at the right time.
To estimate real-time data, we need a dynamic technique that analyzes data at each AWS and neighboring AWS for patterns during the same time period. Precipitation is spatiotemporally variable and always related to neighboring precipitation. During a longer period of rainfall, two major types of observation can be made: first, the initial hours of precipitation produce incremental values for a particular time period; and second, during breaks in the rainfall, decreasing values of precipitation are observed. In this way, consistency is exhibited throughout the precipitation period. The above characteristic of precipitation is considered in the present study’s proposal of a new Intermittent Sliding Window Period (ISWP) algorithm to reconstruct the majority of missing precipitation data accurately. The ISWP technique uses both spatial and temporal variability to define the window period. Moreover, it categorizes precipitation into four different categories. These reconstructed data are further used by other interpolation techniques, which improves the estimated values and reduces the estimation error.
The remainder of this paper is organized as follows: Section 2 describes the chosen study area and the data for anlysis and discussion; Section 3 presents the approach to reconstructing the missing data; Section 4 discusses the methodology used in the interpolation techniques used for comparison purposes; Section 5 validates the results of the interpolation techniques with/without the ISWP technique; and Section 6 summarizes the findings.
2 Study area and dataEleven AWSs located in the National Capital Region (NCR), Delhi, are considered in this study. Specifically, Akshardham, Ayanagar, Delhi University, Jafarpur, Najafgarh, Narela, the National Centre for Medium Range Weather Forecasting (NCMRWF), Pitampura, Pusa, and Sports Complex Delhi, are the areas under the NCR, Delhi. Figure 1 shows the locations of the AWSs in the NCR locality. They all are located within a 41-km radius. Precipitation data are acquired at a temporal resolution of 1 h and are available via the Indian Meteorological Department (IMD) website (http://www.imdaws.com/ViewAwsData.aspx). Tipping-bucket rain gauges are used at IMD AWSs, as described by Anjan et al. (2010). The collector diameter is 20 cm and the resolution of the gauge is 0.5 mm. The accuracy of the rain gauge is within 2% at 240 mm h–1. For the desired location, from the drop down menu of IMD AWS website, appropriate state, district, and location need to be selected, and data should be available for the recent week. Giri et al. (2015) reported that 1350 AWSs were installed across India during 2008–10.
| Station | Missing data (h) | Percentage (%) |
| Akshardham (S-1) | 922 | 1.76 |
| Ayanagar (S-2) | 314 | 0.6 |
| Delhi University (S-3) | 556 | 1.06 |
| Jafarpur (S-4) | 398 | 0.76 |
| Najafgarh (S-5) | 328 | 0.63 |
| Narela (S-6) | 1497 | 2.86 |
| NCMRWF (S-7) | 395 | 0.76 |
| New Delhi (S-8) | 1841 | 3.52 |
| Pitampura (S-9) | 430 | 0.82 |
| Pusa (S-10) | 264 | 0.5 |
| Sports Complex Delhi (S-11) | 199 | 0.38 |
| Total | 7144 | 13.66 |

|
| Figure 1 Locations of the AWSs used in this study. |
We refer to Deshpande et al. (2012) to validate the data acquired from the IMD website. In their paper, the maximum hourly precipitation between 1969 and 2005 for the NCR region is around 112 mm. In our study, the maximum areal precipitation between January 2015 and January 2016 is 103 mm for Ayanagar, Delhi. Some data errors are apparent in the IMD website data, e.g., 513, 624, and 864 mm for different stations, which are made as blank entries and considered as missed data during the reconstruction.
For experimental purposes, the data from January 2015 to January 2016 are considered. The total length of the data during this period is 52316 h, of which approximately 7144 h of data are missing. That is, a total of 13.66% of the precipitation data are missing from the observed dataset. The study area falls within a semi-arid region; conditions are mostly dry apart from concentrated precipitation during the monsoon season. All weather stations record zero precipitation of roughly 35673 h, and the remaining hours are a mixture of both zero and non-zero precipitation. Table 1 shows the total missing hours of precipitation from each AWS considered for discussion.
| Date | Time (LT) | S-1 | S-2 | S-3 | S-4 | S-5 | S-6 | S-7 | S-8 | S-9 | S-10 | S-11 | ||||||||||||
| 11-Aug-15 | 0900 | 7 | 51 | 16 | 1 | 0 | 17 | 17 | 12 | 3 | 6 | |||||||||||||
| 11-Aug-15 | 1000 | 11 | 30 | 1 | 0 | 18 | 18 | 22 | 16 | 6 | ||||||||||||||
| 11-Aug-15 | 1100 | 19 | 51 | 31 | 0 | 21 | 21 | 25 | 16 | 6 | ||||||||||||||
| 11-Aug-15 | 1200 | 20 | 52 | 32 | 1 | 0 | 22 | 22 | 26 | 16 | 8 | |||||||||||||
| 11-Aug-15 | 1300 | 20 | 52 | 1 | 0 | 23 | 23 | 26 | 17 | 8 | ||||||||||||||
| 11-Aug-15 | 1400 | 20 | 52 | 32 | 1 | 0 | 23 | 23 | 26 | 17 | 8 | |||||||||||||
| 11-Aug-15 | 1500 | 20 | 52 | 32 | 1 | 0 | 23 | 23 | 26 | 17 | 8 | |||||||||||||
| 11-Aug-15 | 1600 | 20 | 52 | 32 | 1 | 0 | 23 | 23 | 26 | 17 | 8 | |||||||||||||
| 11-Aug-15 | 1700 | 20 | 52 | 32 | 1 | 0 | 23 | 23 | 26 | 17 | 8 | |||||||||||||
| 11-Aug-15 | 1800 | 20 | 52 | 32 | 1 | 0 | 23 | 23 | 26 | 17 | 9 | |||||||||||||
| 11-Aug-15 | 1900 | 52 | 32 | 1 | 0 | 23 | 23 | 26 | 17 | 9 | ||||||||||||||
| 11-Aug-15 | 2000 | 20 | 52 | 32 | 1 | 0 | 23 | 23 | 26 | 17 | 9 | |||||||||||||
| 11-Aug-15 | 2100 | 20 | 52 | 32 | 1 | 0 | 23 | 23 | 26 | 17 | 9 | |||||||||||||
| 11-Aug-15 | 2200 | 20 | 52 | 32 | 1 | 0 | 23 | 23 | 26 | 17 | 9 | |||||||||||||
| 11-Aug-15 | 2300 | 20 | 52 | 32 | 1 | 0 | 23 | 23 | 26 | 17 | 9 | |||||||||||||
| 12-Aug-15 | 0000 | 20 | 52 | 32 | 1 | 0 | 23 | 23 | 26 | 17 | 9 | |||||||||||||
| 12-Aug-15 | 0100 | 20 | 52 | 32 | 1 | 0 | 23 | 23 | 26 | 17 | 9 | |||||||||||||
| 12-Aug-15 | 0200 | 20 | 52 | 32 | 1 | 0 | 23 | 23 | 26 | 17 | 9 | |||||||||||||
| 12-Aug-15 | 0300 | 20 | 52 | 32 | 1 | 0 | 23 | 23 | 26 | 17 | 9 | |||||||||||||
| 12-Aug-15 | 0400 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||||||||||||
The proposed algorithm is more suitable for semi-arid or arid regions where zero precipitation occurrences are more frequent than non-zero precipitation occurrences. IMD precipitation data for every hour are available for all seasons. The total observed data length during this time series is considered to be N. The maximum number of AWSs is denoted by m. In our case study, m is equal to 11, that is, a total of 11 AWSs (denoted by Sj, where j is the station number varying from 0 to m–1) are considered.
There are two types of sliding window period defined: one for individual AWSs, and the other for all AWSs within a considered area. The local sliding window (LSW) is the sliding window period defined for individual stations, which has a set of data that exhibits the same pattern of precipitation for a particular time period and its length is greater than 2 h. The global sliding window (GSW) is a common sliding window period, defined for all AWSs in the area under consideration. The GSW is obtained by taking the majority (which is also the mode) of all AWSs’ LSW sizes.
The variable length global sliding window period defined for all AWSs is the set of similar precipitation data falling in the time period n, where n ≤ N. Individual AWSs may have more than one LSW defined in a GSW. The length of the LSW and GSW period is denoted by lSj and gn, respectively. The length of lSj varies from 3, 4, 5, …, N. The length of LSW is considered to be greater than 2 h, as this is the minimum duration of precipitation for estimating a missing value. The accuracy of missing data improves with the length of sliding window. RSj represents the precipitation/rainfall data for the jth AWS.
The filling in missing precipitation data is carried out only after defining the GSW period, and the following is a list of the advantages for doing so: 1) while defining the LSW, it is assumed that any missing hours belong to the current LSW. Therefore, by defining the GSW, we know precisely where the LSW boundary is changing; 2) if the size of an LSW is the same as that of a GSW, then any missing precipitation is filled with the same pattern (same as the average) as that of the LSW pattern; and 3) for a particular AWS, there can be more than one LSW defined in a GSW. In such a case, if missing values cannot be reconstructed by using the ISWP method, then an alternate method can be used for that particular GSW. In such a case, the moving average method or strong correlation coefficient can be used to fill the missing precipitation values.
The precipitation in our study area (semi-arid region) is categorized into four main groups, as follows: 1) Category A, in which all AWSs have zero precipitation; 2) Category B, in which a single AWS’ precipitation has non-zero precipitation and the remaining AWSs have zero precipitation; 3) Category C, in which there is a mixed pattern of precipitation in a particular GSW period; and 4) Category D, in which there is hourly random precipitation.
The dataset used in the experiment has columns with precipitation data for each AWS and rows with precipitation data for all AWSs. The missing precipitation data have the following patterns: 1) a missing row indicates that no data are acquired for all AWSs, for particular time period; 2) a missing column indicates that a particular AWS’ data are missing for a continuous time period; and 3) a random row and column missing indicates that a single AWS has hourly missing data.
Next, we present three algorithms used in the ISWP method: Algorithm-1 provides the steps involved in creating the LSW; Algorithm-2 provides the steps used to obtain the GSW based on the precipitation pattern; and Algorithm-3 presents a method to fill in the missing precipitation values. The following notation is used in all three algorithms:
1) The length of the LSW period is denoted by lSj, where 2 < lSj ≤ N;
2) The length of the GSW period is denoted by gn;
3) RSj represents the precipitation data of the jth AWS;
4) RSj[i] refers to the ith hour of precipitation data for the jth AWS, where i ≤ N;
5) The variable wt represents the total number of hours for which different sized GSWs are created and traversed, wherein wt is the sum of gn until i reaches N. Initially, wt = 0;
6) Initially, missing values in the array RSj[i] are blank.
For Algorithm-1, the following steps are used to obtain the LSW size lSj:
1) Loop j from 0 to m – 1. Initially, lSj for the jth AWS is zero;
2) Loop i for wt to N – 1; add RSj[i] to the LSW increment lSj by 1;
3) Loop i to read the next precipitation data. If |RSj[i + 1] – RSj[i] | = 0 or RSj[i + 1] = missing data, then add RSj[i + 1] into the current LSW and increase lSj by 1;
4) Keep repeating step 3) until |RSj[i + 1] – RSj[i]| ≠ 0. Non-zero values indicate a change in the LSW period;
5) If there is a change in the precipitation data, that is, RSj[i + 1] ≠ RSj[i] and ≠ blank, then stop iterating. Return the value of lSj if lSj > 2;
6) Otherwise, if lSj < 2, return NONE (i.e., the LSW size cannot be defined);
7) Increment the value of j and repeat the steps 1) to 6).
Example: Algorithm-1 is applied to the data shown in Table 2 obtained on 11 and 12 August 2015, and the thin-rectangular-box data show the corresponding LSW for each AWS.
| Station | Single AWS precipitation (mm) | Error influence (%) |
| Akshardham | 111 | 1.594 |
| Ayanagar | 31 | 0.445 |
| Delhi University | 65 | 0.934 |
| Jafarpur | 74 | 1.063 |
| Najafgarh | 10 | 0.144 |
| Narela | 234 | 3.361 |
| NCMRWF | 32 | 0.46 |
| New Delhi | 28 | 0.402 |
| Pitampura | 20 | 0.287 |
| Pusa | 38 | 0.546 |
| Sports Complex Delhi | 29 | 0.416 |
For Algorithm-2, the following steps are used to obtain the GSW size gn based on the pattern of the rainfall:
1) For all AWSs, if the sum of their LSW precipitation is zero, then such patterns are grouped into one GSW. The size of the GSW is the minimum of all AWSs’ LSW sizes;
2) A single AWS having the same pattern of precipitation and the remaining AWSs having zero precipitation are grouped into one GSW. The size of the non-zero precipitation of the AWS’ LSW size is the size of the GSW;
3) For mixed patterns of rainfall, at least two AWSs should have non-zero precipitation; the GSW is defined by the mode or majority of all LSW sizes. Thus, the maximum repeated occurrence of LSW size will be the GSW size;
4) All remaining precipitation, where no pattern is found and the LSW cannot be defined, is grouped together to form one GSW if the dataset is continuous. The random hourly precipitation GSW size may vary from 1 to n.
5) The variable wt = wt + gn, if the traversed index wt < N – 1, in which case repeats the steps in Algorithm-1 and Algorithm-2.
Example: Algorithm-2 is applied to the same data shown in Table 2. The horizontally gray-area data show the GSWs for all AWSs. To obtain the first GSW, the data have the following precipitation patterns: S-1, S-3, and S-9 have 3-h random precipitation; S-7 and S-8 have 4-h random precipitation; S-2 and S-11 have 3-h continuous precipitation; S-4 has 20-h continuous precipitation; S-5 has 20-h blank data; and S-10 has 1-h undefined window precipitation. By applying the mode on these AWS precipitation patterns, we obtain the first GSW size as equal to 3. Similarly, to obtain the second GSW, the next set of data have the following pattern: S-1, S-2, S-3, S-4, and S-9 have 15-h continuous precipitation; S-5 has 16-h zero precipitation; S-6 has 16-h blank precipitation; S-7, S-8, and S-10 have 1-h undefined window precipitation; and S-11 has 6-h continuous precipitation. By applying the mode on these AWS precipitation patterns, we obtain the second GSW size as equal to 15.
Algorithm-3 aims to fill in missing precipitation data. The following steps are used for filling in the missing precipitation data depending on the GSW category:
1) For all AWSs having a GSW with zero precipitation only, fill all missing precipitation data with zero precipitation. Completing AWS missing data may have an error associated with it; Table 3 shows each AWS’ associated error, in which the data are obtained based on a single AWS’ precipitation;
2) For a single AWS having precipitation, if missing values are from a non-zero precipitation station, then fill it with the same pattern as that of its LSW. Any missing values from remaining AWSs will be filled with zero precipitation;
3) For a mixed precipitation pattern, missing precipitation will be reconstructed by using its LSW’s pattern. If missing values are at the boundary of an LSW or a complete AWS is missing, then reconstruction will be carried out by using other interpolation techniques;
4) In random hourly precipitation pattern, if an LSW is defined for any AWS, then only that missing precipitation can be filled. Otherwise, some other interpolation techniques have to be used.
The ISWP algorithm can reconstruct around 6477-h data out of 7144-h missing precipitation data. That is, around 90.66% of missing data are filled by using the sliding window period. The remaining 667-h missing data have to be estimated/reconstructed by using other interpolation techniques.
By applying the ISWP method to the observed data, the following classifications are obtained for GSWs: (i) 35673-h AWS precipitation data fall into a category of having zero precipitation only, with 60 different sized GSWs; (ii) 6963-h AWS precipitation data fall into a category of having single non-zero precipitation, with 55 different sized GSWs; (iii) 473-h AWS precipitation data fall into a category of having total random precipitation, with 18 different sized GSWs; and (iv) 9207-h AWS precipitation data fall into a category of having mixed precipitation patterns, with 94 different sized GSWs.
Figure 2 summarizes the missing and filled data in hours under each category of GSW period after applying the ISWP technique. We can see from Fig. 2 that, for Categories A and B, all missing data are reconstructed. In Category C, most of the missing data are reconstructed successfully. Whereas in Category D, most of the missing data are still missing, due to random precipitation patterns, and also no correlation is observed among otherAWSs for the reconstruction.
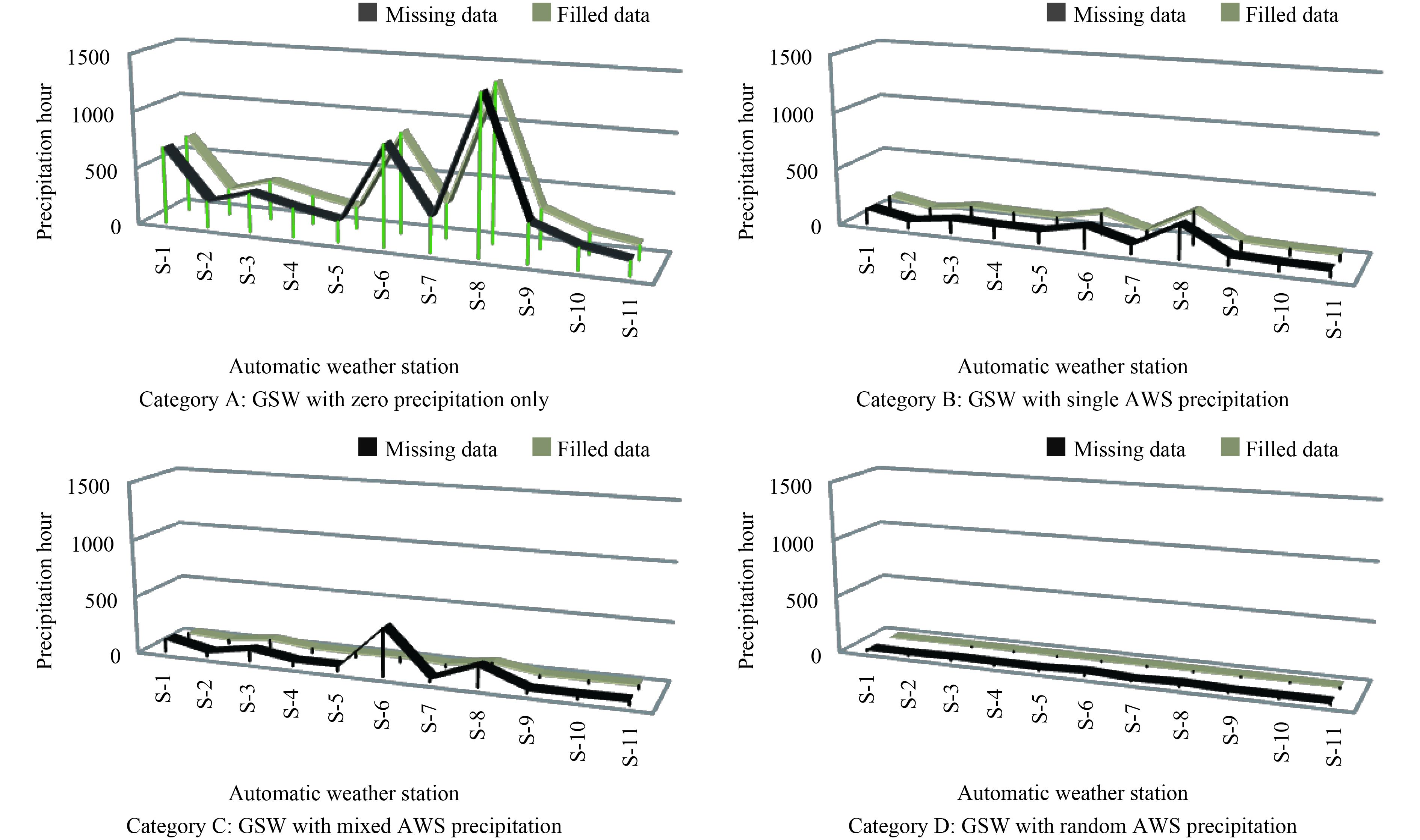
|
| Figure 2 Missing and reconstructed precipitation data for all GSW (global sliding window) categories. |
However, in Categories A and B, the reconstruction of continuous data may have some error. The error is due to filling of those missing data with zero precipitation. ISWP anticipates missing data as zero precipitation because of its neighbor’s zero precipitation data but in actual AWS may have some precipitation. For example, the 1-yr data acquired from the IMD have a single AWS with minimum precipitation (1–6 mm), while other AWSs have zero precipitation. The error also signifies that the AWS precipitation bears no correlation with the other AWSs. Table 4 shows the individual AWSs’ precipitation and their error influence. The error is computed by taking 6963 h of observation data under Category B of the GSW period.
| Date | Time (LT) | S-1 | S-2 | S-3 | S-4 | S-5 | S-6 | S-7 | S-8 | S-9 | S-10 | S-11 |
| 14-Jan-15 | 0000 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 14-Jan-15 | 0100 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 14-Jan-15 | 0200 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 14-Jan-15 | 0300 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 14-Jan-15 | 0400 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 14-Jan-15 | 0500 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 14-Jan-15 | 0600 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 14-Jan-15 | 0700 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 14-Jan-15 | 0800 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 14-Jan-15 | 0900 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |
| 14-Jan-15 | 1000 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 14-Jan-15 | 1100 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 14-Jan-15 | 1200 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 14-Jan-15 | 1300 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 14-Jan-15 | 1400 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |
| 14-Jan-15 | 1500 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | |
| 14-Jan-15 | 1600 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | |
| 14-Jan-15 | 1700 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 0 | 0 |
| 14-Jan-15 | 1800 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 0 | 0 | |
| 14-Jan-15 | 1900 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 0 | 0 |
| 14-Jan-15 | 2000 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 0 | 0 |
| 14-Jan-15 | 2100 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 0 | 0 |
| 14-Jan-15 | 2200 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 0 | 0 | |
| 14-Jan-15 | 2300 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 0 | 0 |
| 15-Jan-15 | 0000 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 0 | 0 |
| 15-Jan-15 | 0100 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 0 | 0 |
| 15-Jan-15 | 0200 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 0 | 0 |
| 15-Jan-15 | 0300 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 2 | 0 | 0 |
Table 4 shows the precipitation data acquired from 0000 local time (LT) 14 January 2015 to 0300 LT 15 January 2015, which are used to demonstrate the workflow of the ISWP algorithm.
| Date | Time (LT) | S-1 | S-2 | S-3 | S-4 | S-5 | S-6 | S-7 | S-8 | S-9 | S-10 | S-11 |
| 09-Aug-15 | 0100 | 0 | 5 | 0 | 1 | 0 | 0 | 0 | 1 | 2 | 0 | |
| 09-Aug-15 | 0200 | 18 | 25 | 23 | 4 | 1 | 0 | 0 | 2 | 4 | 6 | |
| 09-Aug-15 | 0300 | 48 | 36 | 25 | 10 | 14 | 26 | 26 | 3 | 21 | 16 | |
| 09-Aug-15 | 0400 | 17 | 39 | 24 | 6 | 25 | 20 | 20 | 22 | 16 | 17 | |
| 09-Aug-15 | 0500 | 25 | 47 | 28 | 17 | 35 | 22 | 22 | 40 | 21 | 18 | |
| 09-Aug-15 | 0600 | 28 | 58 | 42 | 24 | 47 | 23 | 23 | 54 | 34 | 20 |
In the first iteration for Table 4, the LSW period is calculated as lS0 = 2, lS1 = 2, lS2 = 9, lS3 = 4, lS4 = 4, lS5 = 9, lS6 = 9, lS7 = 5, lS8 = 4, lS9 = 3, and lS10 = 29. The mode is applied to the LSW size to obtain the GSW period size gn, which is 4 (n = 4). No missing values are to be filled in this iteration.
In the second iteration for Table 4, wt will start at 4. The LSW period is calculated as lS0 = 24, lS1 = 5, lS2 = 5, lS3 = 5, lS4 = 5, lS5 = 5, lS6 = 5, lS7 = 1, lS8 = 13, lS9 = 24, and lS10 = 24. The variable gn is defined by using the mode of the LSW period size, which is 5 (n = 5). No missing values are to be filled in this iteration. The traversed sliding window wt = 9.
In the third iteration for Table 4, wt will start at 9. The LSW period is calculated as lS0 = 19, lS1 = 19, lS2 = 19, lS3 = 19, lS4 = 19, lS5 = 18, lS6 = 19, lS7 = 19, lS8 = 8, lS9 = 19, and lS10 = 19. The variable gn is defined by using the mode of the LSW size, which is 19 (n = 19). Six missing values have to be filled in this iteration. The traversed sliding window wt = 28.
The filling of missing data is as follows:
1) One missing value on 0900 LT 14 January 2015 for AWS-10 exists. The LSW size lS10 = 19 and GSW period size gn = 19 are the same; therefore, the missing value is the same as that of the rest of the pattern. The missing value is 0 mm;
2) One missing value on 1400 LT 14 January 2015 for AWS-9 exists. The LSW size lS9 = 19 and global sliding window size gn = 19 are the same; therefore, the missing value is the same as that of the rest of the pattern. The missing value is 0 mm;
3) Two missing values at 1500 and 1600 LT 14 January 2015 for AWS-5 exist. The LSW size lS5 = 19 and GSW size gn = 19 are the same. For the two missing values at RS5 [16] and RS5 [15], they are filled with the same pattern as that of the LSW. Therefore, missing values are both filled with 1 mm;
4) One missing value at 1800 LT 14 January 2015 for AWS-4 exists. The LSW size lS9 = 19 and GSW size gn = 19 are the same; therefore, the missing value is the same as that of the rest of the pattern. The missing value is 1 mm;
5) One missing value at 2200 LT 14 January 2015 for AWS-2 exists. The LSW size lS9 = 19 and GSW size gn = 19 are the same; therefore, the missing value is the same as that of the rest of the pattern. The missing value is 1 mm.
Example: Table 5 shows the precipitation observed from 0100 to 0600 LT 9 August 2015. These are random precipitation patterns ranging from 0 to 58 mm for all AWSs. For this set of random precipitation, the LSW cannot be defined. However, they are grouped together to form one GSW. The estimation of Narela (S-6) in this random dataset is not possible using the ISWP algorithm, as all the precipitation data are blank in both the LSW and GSW.
| Distance matrix (km) | ||||||||||
| S1 | 20.72 | 9.5 | 36.00 | 26.00 | 32.00 | 9.00 | 10.00 | 15.00 | 12.00 | 6.00 |
| 0.06 | S2 | 23.00 | 25.00 | 20.96 | 39.00 | 28.00 | 16.00 | 25.00 | 17.00 | 27.00 |
| 0.59 | 0.34 | S3 | 31.00 | 20.00 | 22.00 | 17.00 | 7.30 | 5.36 | 7.40 | 11.00 |
| 0.12 | 0.15 | 0.42 | S4 | 11.00 | 30.00 | 45.00 | 27.00 | 28.00 | 25.00 | 41.00 |
| 0.36 | 0.29 | 0.53 | 0.71 | S5 | 21.00 | 35.00 | 16.63 | 16.58 | 15.00 | 30.00 |
| 0.02 | 0.02 | 0.06 | 0.42 | 0.09 | S6 | 38.00 | 26.00 | 17.00 | 24.00 | 32.00 |
| 0.74 | 0.14 | 0.59 | 0.07 | 0.18 | 0.02 | S7 | 19.00 | 22.00 | 20.00 | 6.00 |
| 0.40 | 0.47 | 0.82 | 0.38 | 0.66 | 0.05 | 0.45 | S8 | 9.00 | 2.00 | 14.00 |
| 0.11 | 0.02 | 0.12 | 0.06 | 0.04 | 0.03 | 0.10 | 0.08 | S9 | 8.00 | 16.00 |
| 0.41 | 0.40 | 0.70 | 0.11 | 0.42 | 0.08 | 0.62 | 0.85 | 0.06 | S10 | 16.00 |
| 0.83 | 0.17 | 0.75 | 0.23 | 0.28 | 0.02 | 0.84 | 0.52 | 0.14 | 0.53 | S11 |
| Correlation matrix | ||||||||||
Table 6 shows the distance matrix (upper diagonal half) and correlation matrix (lower diagonal half) for data obtained from the ISWP reconstruction. The reconstructed precipitation data obtained are around 45936 records of hourly data. These hourly data constitute a set of all records (at all AWSs) without fields missing. Table 6 shows that the shorter the distance from other AWSs, the better the correlation coefficient.
| Correlation for no missing data from all automatic weather stations | ||||||||||
| S1 | 0.24 | 0.64 | 0.25 | 0.43 | 0.02 | 0.57 | 0.45 | 0.18 | 0.43 | 0.74 |
| 0.06 | S2 | 0.50 | 0.27 | 0.43 | 0.03 | 0.30 | 0.60 | 0.15 | 0.49 | 0.32 |
| 0.59 | 0.342 | S3 | 0.44 | 0.73 | 0.07 | 0.55 | 0.73 | 0.27 | 0.79 | 0.68 |
| 0.12 | 0.151 | 0.422 | S4 | 0.64 | 0.41 | 0.20 | 0.41 | 0.16 | 0.43 | 0.30 |
| 0.36 | 0.294 | 0.527 | 0.708 | S5 | 0.10 | 0.36 | 0.62 | 0.24 | 0.70 | 0.49 |
| 0.02 | 0.023 | 0.065 | 0.423 | 0.094 | S6 | 0.02 | 0.05 | 0.03 | 0.07 | 0.02 |
| 0.74 | 0.138 | 0.593 | 0.074 | 0.179 | 0.019 | S7 | 0.57 | 0.19 | 0.55 | 0.73 |
| 0.40 | 0.474 | 0.817 | 0.383 | 0.664 | 0.054 | 0.452 | S8 | 0.21 | 0.78 | 0.57 |
| 0.11 | 0.022 | 0.116 | 0.062 | 0.042 | 0.030 | 0.100 | 0.075 | S9 | 0.23 | 0.24 |
| 0.41 | 0.402 | 0.699 | 0.113 | 0.415 | 0.078 | 0.624 | 0.845 | 0.063 | S10 | 0.56 |
| 0.83 | 0.166 | 0.752 | 0.232 | 0.278 | 0.022 | 0.844 | 0.521 | 0.136 | 0.533 | S11 |
For analysis of precipitation data, we need all fields (all AWS data) for each hour. Note that, even if single AWS’ data are missing in that hour, then the corresponding AWS’ data are discarded from the analysis. Table 7 shows the correlation coefficient matrix between the original precipitation data without missing field and the reconstructed precipitation data without missing field. The original precipitation data are represented in the upper diagonal half of the matrix. The reconstructed data using the ISWP method are represented in the lower diagonal half of the matrix. We can see that the original precipitation dataset without missing field has been reduced to 13838 h out of 52316 h acquired of data. These filtrations are due to numerous holes in the precipitation fields.
| Station | Missing hourly data (h) | Missing data before ISWP (%) | Reconstructed hourly data with ISWP (h) | Still missing(h) | Missing data after ISWP (%) |
| Akshardham | 922 | 19.4 | 853 | 69 | 1.5 |
| Ayanagar | 314 | 6.6 | 309 | 5 | 0.1 |
| Delhi University | 556 | 11.7 | 519 | 37 | 0.8 |
| Jafarpur | 398 | 8.4 | 384 | 14 | 0.3 |
| Najafgarh | 328 | 6.9 | 311 | 17 | 0.4 |
| Narela | 1497 | 31.5 | 1100 | 397 | 8.3 |
| NCMRWF | 395 | 8.3 | 393 | 2 | 0 |
| New Delhi | 1841 | 38.7 | 1730 | 111 | 2.3 |
| Pitampura | 430 | 9 | 424 | 6 | 0.1 |
| Pusa | 264 | 5.6 | 260 | 4 | 0.1 |
| Sports Complex Delhi | 199 | 4.2 | 194 | 5 | 0.1 |
| Total | 7144 | 13.65 | 6477 | 667 | 1.27 |
From Table 7, it can be concluded that, with the reconstructed dataset obtained via the ISWP method, there is a linear decrease in the correlation with the original data for the majority of cases. This is first due to the fact that a large number of hours are missing in the early months of the year 2015, where precipitation occurrence is much less frequent; second, the reconstructed data add more variation in the precipitation patterns.
In a few cases, like Akshardham and NCMRWF, Akshardham and Sports Complex Delhi, the correlation coefficient of the reconstructed data increases. This happens for two reasons: (i) when the reconstructed data between these two AWSs have almost similar patterns; and (ii) the distance between the two AWSs is also minimal.
4 Methodology used for comparisonsPrecipitation data from AWSs may have single or few continuous hours of missing records due to instrument failure, communication failure, or data logger failure. It is necessary to reconstruct these missing records for agricultural purposes. In this section, the ISWP method is compared with traditional interpolation techniques. The following methods are basic and popular methods for reconstructing data using nearby AWSs.
4.1 Arithmetic mean methodThe arithmetic mean method is one of the simplest methods for computing missing precipitation. In this method, missing precipitation data are estimated from simultaneous observations of precipitation at nearby stations that are evenly spaced (as much as possible) around the missing record station. A simple arithmetic average of the rainfall of three selected stations gives the estimation of the missing records. This method can be used to calculate hourly, monthly, and annually missing precipitation values. However, the approach is successful only when the usual annual precipitation amount at each of the selected stations is within 10% of the variation of the station for which records are missing. According to the arithmetic mean method, the missing precipitation RSx is obtained by
|
${R_{{s_x}}} = \frac{1}{m}\mathop \sum \limits_{j = 1}^{m} {R_{{s_j}}}, $
|
(1) |
where m is the number of nearby stations, RSj is the precipitation at the jth station, and RSx is the missing precipitation. De Silva et al. (2007) propose a new aerial precipitation method. Arithmetic mean, normal ration, and inverse distance weighted method are compared with aerial precipitation method using root mean square error, mean absolute error, and correlation coefficient. This paper uses the same methodology to compare proposed method with existing interpolation techniques for precipitation estimation. In our case study, for instance, if unknown precipitation at location NCMRWF is considered, then the three nearby AWSs are Sports Complex Delhi, Akshardham, and Delhi University. These nearby locations are located within a distance of 10 km.
4.2 Simple linear regressionThe simple linear regression (SLR) model provided by Pennsylvania State University (https://onlinecourses.science.psu.edu/stat501/node/253) predicts precipitation data of an unknown location, based on a nearby AWS. The precipitation predicted is called the estimation variable and is referred to as RSy, and the variable upon which the prediction is based is called the nearby variable, referred to as RSx. If the method uses only one nearby variable, the prediction method is called SLR. In SLR, the predictions of RSy, when plotted as a function of RSx, form a straight line. SLR consists of finding the best-fitting straight line through the points of the estimation variable. The best-fitting line is called a regression line. A popularly used criterion for the best-fitting line is the line that minimizes the root-mean-square error (RMSE) of the prediction. The formula for a regression line is defined as follows:
|
${R_{{s_y}}}' = b{R_{{s_x}}} + A.$
|
(2) |
MX is the mean of RSx, MY is the mean of RSy, SX is the standard deviation of RSx, SY is the standard deviation of RSy, and r is the correlation between RSx and RSy. The slope b can be calculated as follows:
|
$b = r\frac{{{S_Y}}}{{{S_X}}}, $
|
(3) |
and the intercept A can be calculated by using
|
$A = {M_Y} - b{M_X}.$
|
(4) |
In the present study, for example, if we have to compute missing precipitation at NCMRWF (RSy), RSx is taken as the nearest AWS, which is Sports Complex Delhi.
4.3 Multiple linear regressionIn contrast to the SLR model with one predictor, two or more predictors can be used in multiple linear regression (MLR) models. In SLR, the distribution of errors occurs at fixed values of the single predictor, whereas in MLR it occurs at a fixed set of values for all the predictors. In MLR, the relationship between multiple input variable (x1, x2, …., xk) and a dependent variable (Y) is derived. The model defined below is an MLR model with k regressor variables:
|
$Y = \alpha + {\beta _0} + {\beta _1}{x_1} + {\beta _2}{x_2} + \ldots + {\beta _k}{x_k} + {\cal ϵ}, $
|
(5) |
where parameters βj (j = 0, 1, …, k) are called the regression coefficients, α is called the intercept, and ϵ is an error with zero mean and constant variance. It is assumed that each independent variable has a linear relationship with the dependent variable.
This model describes a hyperplane in the k-dimensional space of the regressor variable {xj}. The parameter βj represents the expected change in response Y per unit change in xj when all the remaining regressors xi (i ≠ j) are held constant.
Equation (5) can also be written in matrix form:
|
$\left({\begin{array}{*{20}{c}}{y_1}\\{y_2}\\{{\begin{array}{*{20}{c}} \vdots \\ y_n \end{array}}}\end{array}} \right) = \left({\begin{array}{*{20}{c}}1\\ \vdots \\1\end{array}\begin{array}{*{20}{c}}{{x_{11}}}\\ \vdots \\{{x_{n1}}}\end{array}\begin{array}{*{20}{c}}{{x_{12}}}& \cdots &{{x_{1k}}}\\ \vdots & \ddots & \vdots \\{{x_{n2}}}& \cdots &{{x_{nk}}}\end{array}} \right)\left({\begin{array}{*{20}{c}}\alpha \\{{\beta _1}}\\{{{\begin{array}{*{20}{c}} \vdots \\\beta_k \end{array}}}}\end{array}} \right) + \left({\begin{array}{*{20}{c}}{{{\cal ϵ}_1}}\\{{{\cal ϵ}_2}}\\{{{\begin{array}{*{20}{c}} \vdots \\{\cal ϵ}_n\end{array}}}}\end{array}} \right).$
|
(6) |
In our study, yi represents the hourly precipitation observations of a particular AWS, and xij the hourly precipitation observations of the remaining AWSs under consideration. Therefore, in this case, n = k = 11 and βk are the coefficients realted to location k. To obtain the intercept and the coefficient, the least-squares approach with a confidence interval of 95% is considered. The correlation coefficient (r) is defined as
|
$r = \frac{{\sum\limits_{i = 1}^n {\left( {{R_{xi}} - {{\overline R }_{xl}}} \right)\left( {{R_{yi}} - {{\overline R }_{yl}}} \right)} }}{{\sqrt {\sum\limits_{i = 1}^n {{{\left( {{R_{xi}} - {{\overline R }_{xl}}} \right)}^2}\sum\limits_{i = 1}^n {{{\left( {{R_{xi}} - {{\overline R }_{xl}}} \right)}^2}} } } }}, $
|
(7) |
where Rxi and Ryi are the hourly readings of precipitation at station x and y, respectively, and
The inverse distance weighted (IDW) method is the simplest deterministic interpolation method. All neighborhoods about the interpolated point are identified, and a weighted average is taken from the observation values within this neighborhood. The weights are in decreasing function with respect to its corresponding distance d. The user has the option to use the weighting function, the size of the neighborhood for interpolation, in addition to other options. A general form for finding an interpolated value R at a given point x based on samples Ri = R(xi) for i=1, 2, 3, …, m using the IDW method is an interpolating function:
|
$R \!\! \left(x\right) = \left\{ {\begin{array}{*{20}{c}}{\frac{{\sum\limits_{i = 1}^N {{w_i}\left( x \right){R_i}} }}{{\sum\limits_{i = 1}^N {{w_i}\left( x \right)} }},\;{\rm{if}}\;d\left( {x,{x_i}} \right) \ne 0\;{\rm{for}}\;{\rm{all}}\;i},\\{{R_i},\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{if}}\;d\left( {x,{x_i}} \right) = 0\;{\rm{for}}\;{\rm{some}}\;i},\end{array}} \right. $
|
(8) |
where m is the total number of AWSs used for interpolation of unknown location. The simplest weighting function is the inverse power, defined as
|
${w_i}\left(x \right) = \frac{1}{{d{{\left({x, {x_i}} \right)}^2}}}.$
|
(9) |
The moving average method is useful for observed time series analysis and forecasting. This method uses the mean of time series data from the consecutive period of order m to obtain the next estimation value. Averaging is moving because, as it progresses, this method drops the earliest value and adds the latest value. A moving average of order m can be written as
|
${P_t} = \frac{1}{m}\mathop \sum \limits_{j = - k}^k {P_{t + j}}, $
|
(10) |
where m = 2k + 1. The estimation of precipitation at time t is obtained by taking average values of the time series of k earlier observations, k later observations, and the middle observation of the time period. Observations of precipitation that are nearby in time are closer to the values and averaging eliminates randomness in the estimated data.
4.6 Validation of the modelsThe RMSE has been used as a benchmark statistical metric to measure model performance in meteorology, air quality, and other climate research studies, as discussed by Chai and Draxler (2014). The MAE is another important and useful standard used in model evaluations. This validation procedure includes 10 of the 11 AWSs in the model to obtain the estimated value in the 11th AWS in order to calculate the RMSE and MAE for this station. The process is repetitive for all 11 AWSs individually.
The performance of the above discussed four methods is evaluated for estimating missing values using the RMSE and MAE both expressed in mm as in Eqs. (11) and (12), and in percentages of the measured mean values as in Eqs. (13) and (14):
|
${\rm{RMSE}} = \mathop \sum \limits_{i = 1}^{n} \sqrt {\frac{1}{n}{{\left( {{\overline R_l} - {R_i}} \right)}^2}} ,$
|
(11) |
|
$\!\!\!\!\!\!\!\!\!\!\!\!{\rm{MAE}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left| {\overline R{_l} - {R_i}} \right|,$
|
(12) |
|
${\rm{RMSE}}({\%}) = \frac{{{\rm{RMSE}}}}{{\displaystyle\frac{1}{n}\sum\limits_{i = 1}^{n} {{\overline R_i}} }}\times 100,$
|
(13) |
|
$\!\!\!{\rm{MAE}}({\%}) = \frac{{{\rm{MAE}}}}{{\displaystyle\frac{1}{n}\sum\limits_{i = 1}^{ n} {{\overline R_i}} }}\times 100,$
|
(14) |
where Ri and
In this section, we present the results of the different models with/without the ISWP method in order to compare their performances. For testing purposes, we consider 45936 h of precipitation data. The comparisons aid us in demonstrating that the reconstructed data using the ISWP method reduce the error in the above interpolation techniques. Table 8 summarizes all AWSs’ missing precipitation data in hours and the filled precipitation data via the ISWP method. The remaining 667-h data have to be reconstructed by using other interpolation techniques. These missing hours of data cannot be reconstructed due to the following reasons: 1) missing values are found at the boundary of the changing LSW period where precipitation values are changing. Moreover, conflict exists in deciding to which window it belongs; 2) the LSW cannot be defined for hourly changing precipitation data; and 3) all of an AWS’s precipitation data are missing in a defined GSW.
| Model parameter | Akshardham | Ayanagar | Delhi University | Jafarpur | Najafgarh | Narela | NCMRWF | New Delhi | Pitampura | Pusa | Sports Complex Delhi |
| Intercept (α) | 0.04 | 0.04 | 0.06 | 0.05 | –0.01 | 0.09 | 0.07 | –0.03 | –0.02 | 0.03 | –0.03 |
| Akshardham (β1) | – | –1.21 | 0.03 | –0.89 | 0.64 | 1.35 | 0.24 | 0.29 | 0.10 | –0.18 | 0.32 |
| Ayanagar (β2) | –0.34 | – | 0.01 | –0.26 | 0.16 | 0.56 | –0.15 | 0.29 | –0.08 | –0.01 | 0.17 |
| Delhi University (β3) | 0.06 | 0.08 | – | 0.12 | –0.03 | –0.91 | –0.13 | 0.23 | 0.50 | 0.15 | –0.04 |
| Jafarpur (β4) | –0.58 | –0.58 | 0.04 | – | 0.61 | 1.29 | 0.31 | 0.13 | 0.28 | –0.24 | 0.06 |
| Najafgarh (β5) | 0.84 | 0.74 | –0.02 | 1.23 | – | –1.36 | –0.41 | –0.03 | –0.40 | 0.13 | –0.10 |
| Narela (β6) | 0.16 | 0.23 | –0.05 | 0.23 | –0.12 | – | –0.01 | –0.07 | 0.08 | 0.11 | –0.11 |
| NCMRWF (β7) | 0.06 | –0.14 | –0.02 | 0.13 | –0.08 | –0.02 | – | –0.01 | –0.15 | 0.24 | 0.20 |
| New Delhi (β8) | 0.57 | 2.03 | 0.22 | 0.40 | –0.04 | –1.25 | –0.05 | – | 0.24 | 0.54 | –0.31 |
| Pitampura (β9) | 0.11 | –0.32 | 0.29 | 0.49 | –0.35 | 0.79 | –0.64 | 0.14 | – | –0.08 | 0.52 |
| Pusa (β10) | –0.21 | –0.06 | 0.09 | –0.45 | 0.12 | 1.14 | 1.09 | 0.33 | –0.08 | – | 0.01 |
| Sports Complex Delhi (β11) | 0.60 | 1.09 | –0.04 | 0.17 | –0.15 | –1.68 | 1.42 | –0.30 | 0.86 | 0.01 | – |
Figure 3 shows the MAE and RMSE for the arithmetic mean model with/without the ISWP technique. The three nearest AWSs are considered, taking their mean for the estimation, and these AWSs are located within 10 km, except for Ayanagar, Jafarpur, Najafgarh, and Narela. In real-time, in order to estimate unknown/missing location data, its corresponding period’s nearby AWS data are required. If captured data are missing, the arithmetic mean model assumes the data to be zero and computes the wrong estimation. At the place where these missing time series data are used, if the missing data are reconstructed with the ISWP method, the estimation of the arithmetic mean model can be improved. The results show an average RMSE reduction of 4.2% when using the arithmetic mean method with the ISWP technique. The difference in RMSE with values for all AWSs is shown in Fig. 3.

|
| Figure 3 Mean absolute error (MAE) and root mean squre error (RMSE) for the arithmetic mean model with/without the ISWP technique, and the RMSE difference. |
Figure 4 shows the MAE and RMSE for the SLR model with/without the ISWP technique. In this experiment, the actual precipitation and interpolated precipitation are taken as the input to the model. Interpolated values are taken by the mean of the three nearest AWSs. The SLR method shows significant improvements in error (RMSE) reductions, by 19.44%, using the ISWP technique. The difference in RMSE with values for all AWSs is shown in Fig. 4.

|
| Figure 4 As in Fig. 3, but for the SLR. |
In Table 9, the MLR models for all AWSs are presented. As anticipated, for each model, the maximum coefficient is related with the AWS that shows the maximum correlation (see correlation coefficients in Table 8) and in some cases, the stations with less correlation show negative values from the model. Moreover, it is clear that the nearest locations have the maximum weight within the total of AWSs’ locations.
| Station | MAE (mm) | RMSE (mm) |
| Akshardham | 1.28 | 5.01 |
| Ayanagar | 1.37 | 5.18 |
| Delhi University | 1.18 | 3.8 |
| Jafarpur | 1.11 | 4.57 |
| Najafgarh | 0.87 | 3.03 |
| Narela | 0.68 | 2.69 |
| NCMRWF | 1.51 | 6.23 |
| New Delhi | 1.13 | 3.99 |
| Pitampura | 1.42 | 5.55 |
| Pusa | 0.99 | 3.92 |
| Sports Complex Delhi | 1.47 | 5.79 |
Figure 5 shows the MAE and RMSE for the MLR model with/without the ISWP technique. In this experiment, the interpolation of precipitation is computed by using all other AWSs. The MLR method shows significant improvements in error reduction. MLR outperforms other interpolation techniques in terms of error reduction and its overall performance shows that on average, the RMSE is reduced by 55.47% when using the ISWP technique. The difference in RMSE with values for all AWSs is shown in Fig. 5.

|
| Figure 5 As in Fig. 3, but for the MLR. |
The observed precipitation data acquired for all AWSs amount to around 52316 h. From these observational data, all records with any individual missing precipitation values are removed, which results in 13838 h of precipitation data. Table 10 shows the MAE and RMSE for the IDW method without missing data. The results show that the average RMSE is around 4.53, which indicates highly biased interpolated data. For instance, from 2000 LT 23 to 0300 LT 24 August 2015, there is continuously observed rainfall of 3 mm at Akshardham station; whereas at its neighboring station, it is within 0–103-mm rainfall. This variation in the data from nearby stations estimates Akshardham station as 17 mm, which is a highly biased output. Accordingly, the reconstructed dataset contains increased errors with the IDW method.
| Date | Time | S-1 | S-2 | S-3 | S-4 | S-5 | S-6 | S-7 | S-8 | S-9 | S-10 | S-11 | Global sliding window |
| 22-Jan-15 | 1000 | 4 | 6 | 6 | 4 | 4 | 3 | 7 | 6 | 3 | 4 | 1 | Global window-1 |
| 22-Jan-15 | 1100 | 4 | 6 | 6 | 4 | 4 | 3 | 7 | 6 | 3 | 4 | 1 | |
| 22-Jan-15 | 1200 | 5 | 6 | 6 | 4 | 4 | 3 | 7 | 6 | 3 | 4 | 1 | |
| 22-Jan-15 | 1300 | 5 | 6 | 6 | 4 | 4 | 3 | 7 | 6 | 3 | 4 | 1 | |
| 22-Jan-15 | 1400 | 5 | 6 | 6 | 4 | 4 | 3 | 7 | 6 | 3 | 4 | 1 | |
| 22-Jan-15 | 1500 | 5 | 6 | 6 | 4 | 4 | 3 | 7 | 6 | 3 | 4 | 1 | |
| 22-Jan-15 | 1600 | 6 | 6 | 6 | 4 | 4 | 3 | 7 | 6 | 3 | 4 | 1 | |
| 22-Jan-15 | 1700 | 6 | 6 | 6 | 4 | 4 | 3 | 7 | 6 | 3 | 4 | 1 | |
| 22-Jan-15 | 1800 | 6 | 6 | 6 | 4 | 4 | 3 | 7 | 6 | 4 | 4 | 1 | |
| 22-Jan-15 | 1900 | 6 | 6 | 6 | 4 | 4 | 3 | 7 | 6 | 4 | 4 | 1 | |
| 22-Jan-15 | 2000 | 6 | 6 | 6 | 4 | 4 | 3 | 7 | 6 | 4 | 4 | 1 | |
| 22-Jan-15 | 2100 | 6 | 6 | 6 | 4 | 4 | 3 | 7 | 6 | 4 | 4 | 1 | |
| 22-Jan-15 | 2200 | 6 | 6 | 6 | 4 | 4 | 3 | 7 | 6 | 4 | 4 | 1 | |
| 22-Jan-15 | 2300 | 6 | 6 | 7 | 4 | 4 | 3 | 7 | 6 | 4 | 4 | 1 | |
| 23-Jan-15 | 0000 | 6 | 6 | 7 | 4 | 4 | 3 | 7 | 6 | 4 | 4 | 1 | |
| 23-Jan-15 | 0100 | 6 | 6 | 7 | 5 | 4 | 3 | 7 | 6 | 4 | 4 | 1 | |
| 23-Jan-15 | 0200 | 6 | 6 | 7 | 5 | 4 | 3 | 7 | 6 | 4 | 4 | 1 | |
| 23-Jan-15 | 0300 | 6 | 6 | 7 | 5 | 4 | 0 | 7 | 6 | 4 | 4 | 1 | |
| 09-Mar-15 | 0000 | 2 | 3 | 0 | 1 | 0 | 13 | 0 | 0 | 2 | 0 | 0 | Global window-2 |
| 09-Mar-15 | 0100 | 2 | 3 | 0 | 1 | 0 | 13 | 0 | 0 | 2 | 0 | 0 | |
| 09-Mar-15 | 0200 | 2 | 3 | 0 | 1 | 0 | 13 | 0 | 0 | 2 | 0 | 0 | |
| 09-Mar-15 | 0300 | 2 | 3 | 0 | 1 | 0 | 0 | 0 | 0 | 2 | 0 | 0 |
Figure 6 shows the MAE and RMSE for the IDW model with/without the ISWP technique. In spite of the short distance (< 40 km) between the AWSs, the IDW model offers the poorest results. The power parameter p in this experiment is 2. Seven AWSs show a decrease in RMSE, and the remaining four shows an increase. The difference in RMSE with values for all AWSs is shown in Fig. 6. The overall performance shows an average 0.07% increase in RMSE when using the ISWP technique. This increase in RMSE for the ISWP method is very likely due to the reconstruction of missing data having added more weight, leading to more biased results.

|
| Figure 6 As in Fig. 3, but for the IDW. |
The moving average method is the most suitable for time series data estimation. For experimental purposes, the moving averaging order is taken as two. The order two is the minimum order for the moving average method, as it gives nearer values for missing data. Figure 7 shows that the moving average method without the ISWP reconstructed data shows minimum interpolation error compared to all the above interpolation techniques. After applying the ISWP method to reconstruct the missing data, the moving average method further reduces the RMSE by 9.64%. The difference in RMSE with values for all AWSs is shown in Fig. 7. This shows that the ISWP method improves the estimation results.
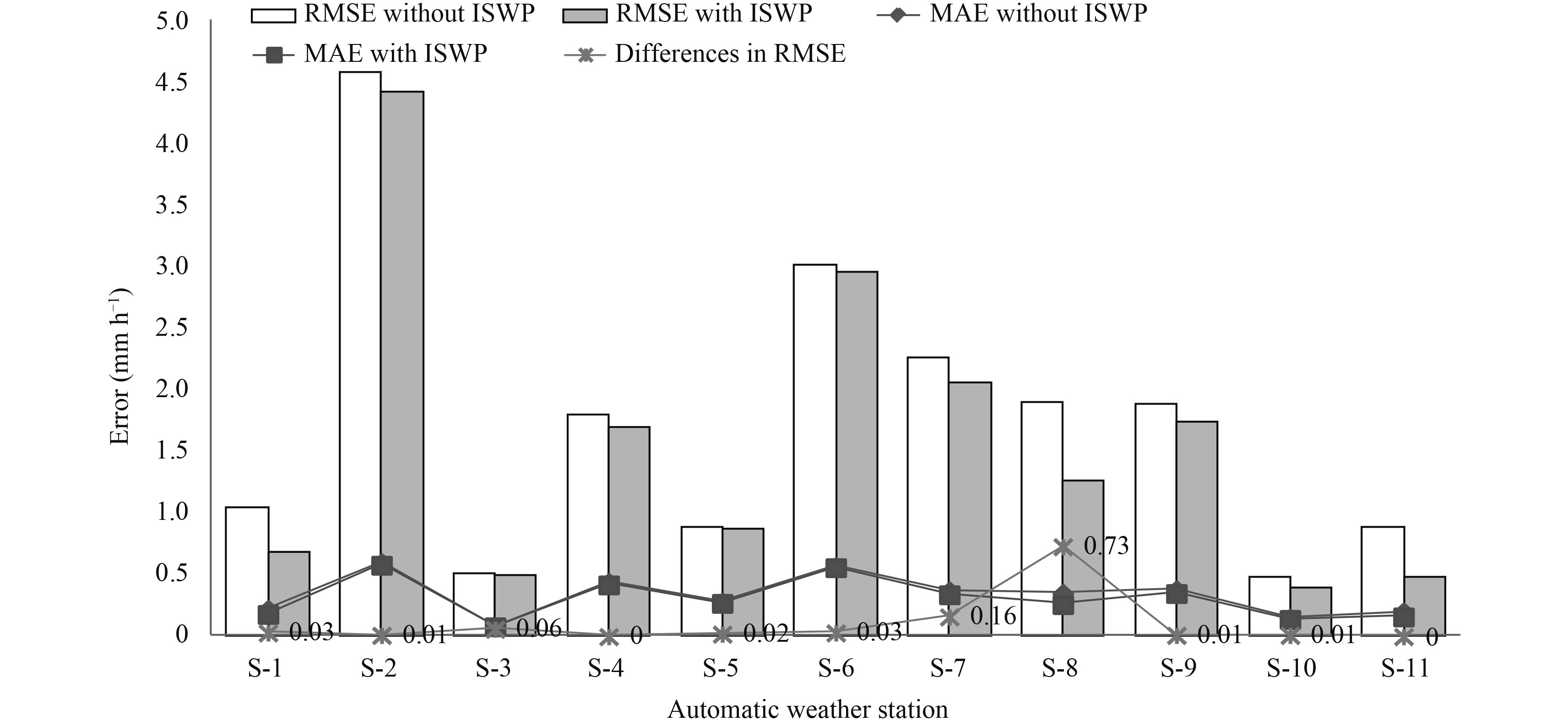
|
| Figure 7 As in Fig. 3, but for the moving average model. |
The ISWP reconstruction method is accurate if the missing values are not at the border of the LSW or GSW. It can be seen that, when missing values are at the border of the GSW and LSW, the reconstructed data are not accurate but are approximate values. In Table 11, missing values are represented by light and dark gray cells. More specifically, missing data filled in light gray cells are 100% accurate, due their previous and future precipitation falling in the same range. Missing data filled in dark gray cells, which are boundary cases, are not accurate; rather, they are approximate values.
If the data shown in the black cells are missing, the reconstructed data would then be approximate data. For example, if the S-1 AWS has missing data from 1000 to 1500 LT 22 January 2015, the ISWP method would reconstruct the data as 6-mm precipitation instead of 4- and 5-mm precipitation.
In the presented case study, by excluding the random precipitation class, we obtain around 209 GSWs for 51843-h precipitation data. It should be noted that, assuming that most of the LSW sizes are equal to that of the GSW, we can have 418 h as missing boundary cases in the worst case. For all 11 AWSs, we can have 4598 h as missing boundary cases in the worst case, and all these hours may not be accurately reconstructed.
6 SummaryThe estimation of missing data requires deterministic, random, or mixed methods of interpolation techniques. These techniques enable prediction models to be created and improved. Accurate real-time precipitation data are mandatory for smart irrigation products such as weather-based products for scheduling irrigation at the right times and in the right amounts.
Initial reconstruction (also called pre-processing) of some missing data helps in improving interpolation techniques. The ISWP method alone is unable to estimate all missing precipitation due to its limitations but, with other interpolation techniques, it can definitely reduce estimation errors significantly. The ISWP technique is very helpful in the simulation of missing precipitation, as hourly data exhibit continuous (rainfall depth) and discrete (rainfall occurrence) characteristics.
Precipitation observations show very high variability on an hourly basis, and apparently random behavior, in the NCR, Delhi. Hence, data reconstruction is difficult when a data point or a set of data is lost. The SLR and MLR methods perform very well in reducing the MAE and RMSE when adopting the ISWP method. The IDW method shows reduced RMSE for seven AWSs, but the overall performance shows an RMSE increase of 0.07%.
Since the area considered in this case study is a semi-arid region, the majority of data tend to have zero precipitation. Reconstruction of these data under zero precipitation GSW periods is easier. Moreover, for individual AWS precipitation data, reconstruction is easier and unbiased. However, in the case of random precipitation GSWs, any missing value reconstruction is very challenging. Estimation of missing values at the boundary of changing LSWs or GSWs is less accurate. The ISWP method performs well when the sizes of LSW and GSW are same. This indicates that precipitation patterns are the same and the reconstruction is unbiased. The present results prove that this novel ISWP approach can significantly reduce errors in the majority of interpolation techniques.
| Anjan, A., R. Pratap, U. K. Shende, R.D.Vashistha, 2010: Comparison of automatic raingauge station with observatory and its performance in Indian subcontinent. TECO-2010-WMO Technical Conference on Meteorological and Environmental Instruments and Methods of Observation, Helsinki, Finland, 1-10. |
| Chai R. Draxler, 2014: Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature.. Geoscientific Model Development, 7, 1247–1250. DOI:10.5194/gmd-7-1247-2014 |
| De Silva, R. P., N. D. K. Dayawansa, M. D. Ratnasiri, 2007: A comparison of methods used in estimating missing rainfall data. The Journal of Agricultural Sciences, 3, 101–108. |
| Department of Agriculture & Cooperation Ministry of Agriculture, Government of India, Krishi Bhavan, New Delhi, 2012: A Technical Note on Automatic Weather Station (AWS) and Automatic Rain Gauge (ARG), Draft Report/Guidelines for setting up Automatic Weather Stations (AWSs) and Automatic Rain Gauge (ARGs) & Their Accreditation, Standardization, Validation and Quality Management of Weather Data for Implementation of Weather Based Crop Insurance Scheme (WBCIS), 3-31. Available at http://agricoop.nic.in/sites/default/files/GuidlinesforAWSandWeather%20Data-15.04.pdf (accessed on April 9, 2017). |
| Deshpande R., N. Kulkarni, A. K. Kumar, 2012: Characteristic features of hourly rainfall in India. Int. J. Climatol., 32, 1730–1744. DOI:10.1002/joc.v32.11 |
| Giri K., R. Devendra, P. K. Sen, 2015: Rainfall comparison of automatic weather stations and manual observations over Bihar region. Int. J. Phys. Math. Sci., 5, 1–22. DOI:10.9734/PSIJ |
| Harada, L., 2003: An efficient sliding window algorithm for detection of sequential patterns. Proceedings of the Eighth International Conference on Database Systems for Advanced Applications, Kyoto, Japan, 26-28 March, IEEE Computer Society, 73-80. |
| Hasan, M. M., and B. F. W. Croke, 2013: Filling gaps in daily rainfall data: A statistical approach. 20th International Congress on Modeling and Simulation, Adelaide, Australia, 1-6 December, 380-386. |
| Kajornrit, J., K. W. Wong, and C. C. Fung, 2012: Estimation of missing precipitation records using modular artificial neural networks. Neural Information Processing: Lecture Notes in Computer Science. T. W. Huang, Z. G. Zeng, C. D. Li, et al., Eds. Springer, Berlin Heidelberg, 7666, 52-59, doi: 10.1007/978-3-642-34478-7_7. |
| Lee, H., and K. Kang, 2015: Interpolation of missing precipitation data using Kernel estimations for hydrologic modeling. Adv. Meteor., 2015, 935868, doi: 10.1155/2015/935868. |
| Ly Charles, S. Degré, 2011: Geostatistical interpolation of daily rainfall at catchment scale: The use of several variogram models in the Ourthe and Ambleve catchments, Belgium. Hydrol. Earth. Syst. Sci., 15, 2259–2274. DOI:10.5194/hess-15-2259-2011 |
| Ministry of Environment & Forests, Government of India, New Delhi, 2004: Executive Summary. India’s Initial First National Communication to The United Nations Framework Convention on Climate Change, 6-13. Available at http://unfccc.int/resource/docs/natc/indnc1.pdf (accessed on April 9, 2017). |
| Noori J., M. H. Hassan, H. T. Mustafa, 2014: Spatial estimation of rainfall distribution and its classification in Duhok Governorate using GIS. J. Water Resource Prot., 6, 75–82. DOI:10.4236/jwarp.2014.62012 |
| Simolo C., Brunetti M., Maugeri M., et al., 2010: Improving estimation of missing values in daily precipitation series by a probability density function-preserving approach. Int. J. Climatol., 30, 1564–1576. DOI:10.1002/joc.1992 |
| Tang H., Q. W. Wood, A. P. Lettenmaier, 2009: Real-time precipitation estimation based on index station percentiles. J. Hydrometeor., 10, 266–277. DOI:10.1175/2008JHM1017.1 |
| Technical Service Center, 2015: Weather- and Soil Moisture-Based Landscape Irrigation Scheduling Devices. Technical Review Report, 5th Edition, Denver, Colorado, 1-145. |
| Teegavarapu S. V., R. Chandramouli, 2005: Improved weighting methods, deterministic and stochastic data-driven models for estimation of missing precipitation records. J. Hydrol., 312, 191–206. DOI:10.1016/j.jhydrol.2005.02.015 |
| Verworn Haberlandt, 2011: Spatial interpolation of hourly rainfall-effect of additional information, variogram inference and storm properties. Hydrol. Earth Syst. Sci., 15, 569–584. DOI:10.5194/hess-15-569-2011 |
 2017, Vol. 31
2017, Vol. 31


