The Chinese Meteorological Society
Article Information
- Jiandong LI, Tianhe WANG, Ammara HABIB . 2017.
- Observational Characteristics of Cloud Radiative Effects over Three Arid Regions in the Northern Hemisphere. 2017.
- J. Meteor. Res., 31(4): 654-664
- http://dx.doi.org/10.1007/s13351-017-6166-7
Article History
- Received October 26, 2016
- in final form January 16, 2017
2. State Key Laboratory of Loess and Quaternary Geology, Institute of Earth Environment, Chinese Academy of Sciences, Xi'an 710054;
3. Key Laboratory for Semi-Arid Climate Change of the Ministry of Education, College of Atmospheric Sciences, Lanzhou University, Lanzhou 730000
Clouds play key roles in surface energy and hydrological cycles (Randall et al., 2007; Boucher et al., 2013). In the atmosphere–land surface system, clouds reflect shortwave (SW) and trap longwave (LW) radiation at the top of the atmosphere (TOA) and reduce incident SW and increase LW radiative fluxes at the surface. These cloud roles strongly alter the TOA and surface radiative flux, the regional energy budget, surface air temperature, and the resultant general circulation. Cloud radiative effects (CREs) are defined as the difference in radiative fluxes at the TOA or surface under clear-and all-sky conditions, to show the bulk cloud effects (Ramanathan et al., 1989; Liu et al., 2011). As a widely used and effective method for studying cloud–radiation interactions, CREs are used to quickly diagnose the cloud effects on regional climate, particularly the contribution of clouds to radiative heating or cooling (Cess et al., 2001; Mace et al., 2006; Loeb et al., 2009).
With the development of satellite datasets and climate models, increasingly abundant information on cloud properties and climate effects is being revealed on global scale (Trenberth et al., 2009; Stubenrauch et al., 2013; Wild et al., 2013). However, important questions on regional cloud effects and simulations remain unanswered (Lauer and Hamilton, 2012; Flato et al., 2013). The cloud processes and relevant climatic feedback remain one of the largest sources of uncertainty in simulating the present climate (Bony et al., 2006; Boucher et al., 2013). Regional cloud–radiation issues are therefore the subject of increasing attention.
Arid and semi-arid regions in midlatitudes of the Northern Hemisphere (NH), including North America (NA), central Asia (CA), and East Asia (EA) arid regions, are fragile climate zones, and their drought intensity and areas have increased in recent decades (Ma and Fu, 2007; Dai, 2013; Zhao et al., 2014, 2015). Meanwhile, the surface warming trend over these arid regions is much more significant in cold season (Huang et al., 2012). The studies summarized by IPCC reports (Meehl et al., 2007; Boucher et al., 2013) show that, due to large-scale responses and feedbacks in the context of global warming, middle-and low-cloud fractions (hereafter, MCF and LCF) are likely to decrease, and the likelihood of strong surface warming and drought over the midlatitudes of the NH has intensified. Hence, quantitative investigations of cloud–radiation processes through CREs are crucial for in-depth understanding of climatic states and relevant changes over arid regions.
Many observational studies associated with cloud–radiation issues have focused on cloud properties or the radiation budget at one or several sites over arid regions (e.g., Liu et al., 2011; Wang et al., 2013). Moreover, specific midlatitude arid regions, such as EA, have been examined in detail by some researchers (Chen et al., 2008; Min et al., 2010; Zhang and Zhou, 2015). There have been, however, few comparative studies conducted regarding the major characteristics of CREs over the three aforementioned arid regions of the NH. Therefore, the purpose of the present study is to investigate the sea-sonal features of CREs, and the corresponding inter-annual variation, over these three arid regions in the NH. Furthermore, the quantitative relationships between CREs and cloud fractions (CFs) are examined for these arid regions, to reveal their individual characteristics.
2 Datasets and methods 2.1 Observational datasetsThe radiative flux data are from the recent CERES-EBAF (Clouds and the Earth's Radiant Energy System-Energy Balance and Filled product) Ed2.8 dataset (Doelling et al., 2013), including SW and LW radiative fluxes at the TOA and surface under clear-sky and all-sky conditions. The CERES-EBAF dataset has been widely used in studying the role of clouds and the energy cycle in the earth–climate system (Loeb et al., 2009; Boucher et al., 2013). The column total CF (TCF) and high CF (HCF) data used in this study are from the NASA CERES-Moderate Resolution Imaging Spectroradiometer (hereafter, MODIS) (SYN1) dataset, edition 3. The uncertainty in the CERES-MODIS TCF is approximately 7% (Minnis et al., 2011). Both datasets have a spatial resolution of 1.0° latitude by 1.0° longitude and are available from March 2000 to the present. Moreover, another column of CFs (TCF, HCF, MCF, and LCF) and 3D cloud vertical distributions are from the general circulation model (GCM) Oriented CALIPSO Cloud Product (GOCCP). The GOCCP data are based on CALIPSO satellite datasets, which are designed to evaluate the vagueness simulated in climate models (Chepfer et al., 2010) and have shown their value in climate analysis (Cesana and Chepfer, 2012; Boucher et al., 2013). The GOCCP data have a horizontal resolution of 2.0° latitude by 2.0° longitude, with 40 vertical levels at 480-m intervals, and cover the period from June 2006 to the present.
The total precipitation observation data are from the Global Precipitation Climatology Project (GPCP) mon-thly products, with a global resolution of 2.5° latitude by 2.5° longitude from 1979 to the present (Adler et al., 2003). The meteorological data are from the ERA-Interim reanalysis (Dee et al., 2011), including horizontal wind, vertical velocity, and humidity, with a spatial resolution of 1.0° latitude by 1.0° longitude. The period of coverage for ERA-Interim is the same as that for GPCP. These datasets are used as reference standards to provide the observational state.
2.2 MethodsIn the present study, CREs at the TOA are defined as the differences in radiative fluxes between clear-sky and all-sky conditions, based on Ramanathan et al. (1989) and Boucher et al. (2013), as follows:
|
$\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{\rm{LWCR}}{{\rm{E}}_{{\rm{TOA}}}} = {\rm{OL}}{{\rm{R}}_{{\rm{clr}}}} - {\rm{OL}}{{\rm{R}}_{{\rm{all}}}},$
|
(1) |
|
$\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{\rm{SWCR}}{{\rm{E}}_{{\rm{TOA}}}} = {\rm{RSU}}{{\rm{T}}_{{\rm{clr}}}} - {\rm{RSU}}{{\rm{T}}_{{\rm{all}}}},$
|
(2) |
|
${\rm{NCR}}{{\rm{E}}_{{\rm{TOA}}}} = {\rm{LWCR}}{{\rm{E}}_{{\rm{TOA}}}} + {\rm{SWCR}}{{\rm{E}}_{{\rm{TOA}}}},$
|
(3) |
where OLRclr and OLRall are the outgoing LW radiative fluxes at the TOA; RSUTclr and RSUTall are the corresponding outgoing SW radiative fluxes, under the clear-sky and all-sky condition, respectively; and net CRE (NCRE) is the arithmetic sum of LWCRE and SWCRE. The definitions of surface CREs follow those of Liu et al. (2011) and are listed below:
|
$\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{\rm{LWCR}}{{\rm{E}}_{{\rm{SRF}}}} = {\rm{RLD}}{{\rm{S}}_{{\rm{all}}}} - {\rm{RLD}}{{\rm{S}}_{{\rm{clr}}}},$
|
(4) |
|
$\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{\rm{SWCR}}{{\rm{E}}_{{\rm{SRF}}}} = {\rm{RSD}}{{\rm{S}}_{{\rm{all}}}} - {\rm{RSD}}{{\rm{S}}_{{\rm{clr}}}},$
|
(5) |
|
${\rm{NCR}}{{\rm{E}}_{{\rm{SRF}}}} = {\rm{LWCR}}{{\rm{E}}_{{\rm{SRF}}}} + {\rm{SWCR}}{{\rm{E}}_{{\rm{SRF}}}},$
|
(6) |
where RLDS and RSDS are the downward LW and SW radiative fluxes at the surface, respectively.
We focus on semi-arid and arid regions over CA, EA, and NA. Following Huang et al. (2016), three arid regions over the NH are selected, and their longitudinal ranges are 40°–80°E, 80°–120°E, and 230°–270°E, respectively, with the same latitudinal range of 35°–55°N. Hereafter, these three arid regions are named CA, EA, and NA, and the latitudinal zone of 35°–55°N in the NH is designated as NH. The arid regions are located in the mid–high latitudes and have moderately cold months and warm months over the course of a year. Thus, the climatological states in the cold season (November to March) and warm season (May to September) are used to obtain the seasonal contrast. The yearly annual, cold-and warm-seasonal means of CREs during 2001–15 are calculated to reveal their seasonal and interannual variations. The MODIS CFs during 2001–15 are used for analysis of interannual variation, and the CALIPSO-GOCCP CFs during 2007–15 are used for the climatological mean state.
3 ResultsFigure 1 shows the spatial distribution of annual mean precipitation, TCF, and NCRE. Precipitation is sparse over the NH arid regions, especially over the deserts of North Africa and the Middle East (Fig. 1a). Due to low precipitation and moisture, the TCF is quite low over South and North African, Middle Eastern, and Australian arid regions, with values of 20%–30% (Fig. 1b). In contrast, the TCF is over 50% over midlatitude arid regions and even up to 60% over the arid regions of NA. Meanwhile, although the magnitude of the NCRE at the TOA over the aforementioned arid regions is lower than that over oceanic regions at the same latitude, the NCRE over the former remains at –15 to 0 W m–2 (Fig. 1c), exerting a certain radiative cooling effect on the regional atmosphere–land surface system. The results indicate that there exist certain intensities of the TCF and CREs over midlatitude arid regions in the NH.

|
| Figure 1 Annual mean (a) total precipitation (mm day–1) from GPCP (2001–15), (b) total cloud fraction (%) from GOCCP (GCM Oriented CALIPSO Cloud Product) (2007–15), and (c) net cloud radiative effect (W m–2) at the TOA derived from CERES-EBAF (2001–15). The black boxes represent the Northern Hemispheric arid regions in this study, including central Asia (40°–80°E), East Asia (80°–120°E), and North America (230°–270°E), with a latitudinal range of 35°–55°N. |
Figure 2 shows domain-averaged CREs at the TOA and surface over the three arid regions and the NH. For the global means, the magnitude of SWCRE is larger than that of LWCRE, and then the values of NCRE at the TOA and surface over the above regions are negative (Figs. 2a, d), indicating net radiative cooling in the regional atmosphere–land surface climate system. The annual mean CREs over CA and EA are very close and their TOA NCREs are –7.6 and –7.4 W m–2, respectively (Fig. 2a). NA is adjacent to the North Pacific and Atlantic oceans, where the SWCRE and NCRE are much higher (Fig. 1c), and its NCRE (–14.4 W m–2) is therefore larger than that over CA and EA (Fig. 2a). Compared to the TOA, the annual mean SWCRE and NCRE at the surface are enhanced, mainly because of scattering and absorption by whole atmospheric clouds. The surface NCRE over NA and NH are –23.0 and –30.0 W m–2, respectively, larger than those of CA (–13.6 W m–2) and EA (–17.0 W m–2) (Fig. 2d).
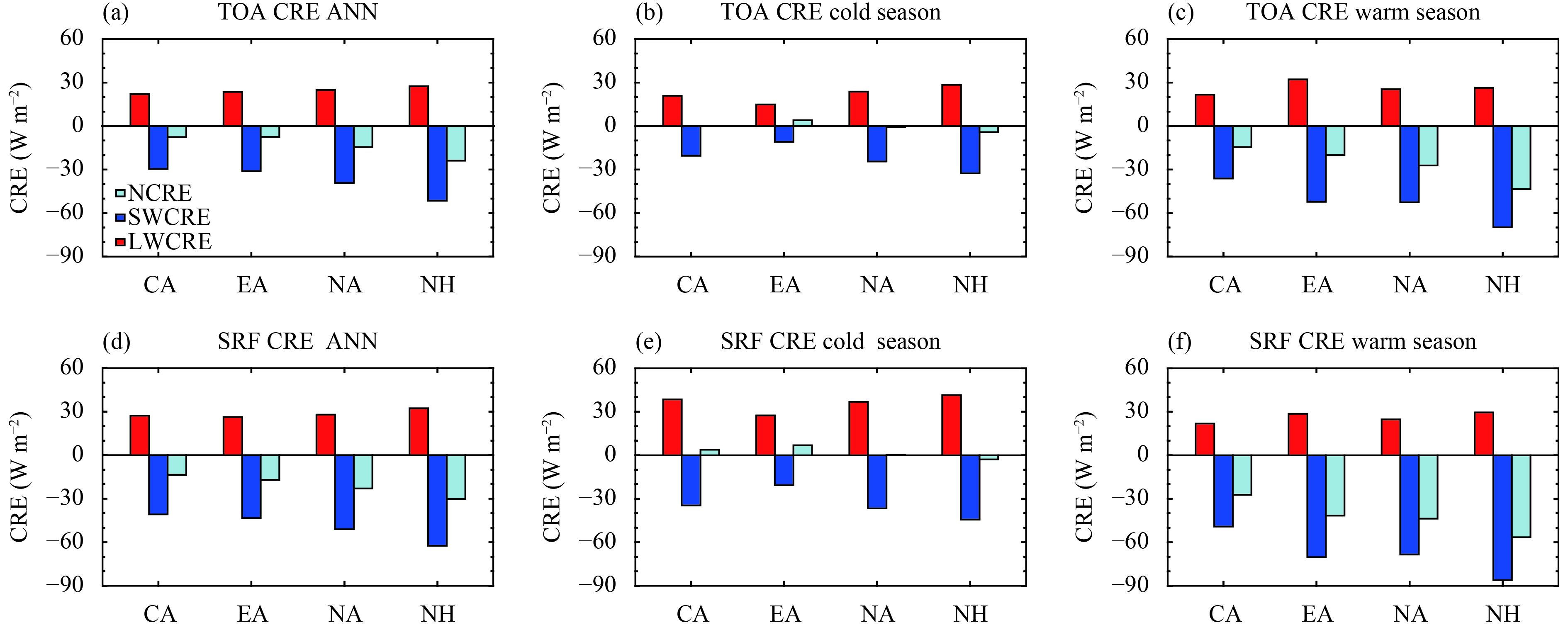
|
| Figure 2 Climatological mean TOA (top of atmosphere) CRE (cloud radiative effect) (W m–2) (2001–15) averaged over CA (central Asia), EA (East Asia), NA (North America), and the NH (Northern Hemisphere) (35°–55°N). Panels (a)–(c) show the annual, cold-season, and warm-season means, respectively, and (d)–(f) are the corresponding results at the surface (SRF). NCRE, SWCRE, and LWCRE are short for net CRE, shortwave CRE, and longwave CRE, respectively. |
In the cold season, the solar zenith angle and incident solar radiation are low over the arid latitudes of the NH, and the SWCRE at the TOA is weaker than the annual and warm-season mean SWCRE (Figs. 2b, c). Meanwhile, the magnitudes of LWCRE and SWCRE are very close, resulting in a weak NCRE (Fig. 2b). At the TOA, the cold-season NCRE over CA and NA is only 0.3 and –0.7 W m–2, respectively, but the NCRE over EA is 4.1 W m–2, showing a slight radiative warming effect (Fig. 2b). At the surface, the LWCRE and SWCRE are also stronger than the corresponding TOA values. The surface NCRE over CA and EA increases to 3.8 and 6.9 W m–2 (Fig. 2e), indicating a clear cloud warming effect on the surface. The surface NCRE over NA is only 0.17 W m–2, indicating a slight warming. The value of the surface NCRE over the NH is –2.9 W m–2 and implies a cooling effect of clouds (Fig. 2e).
In the warm season, the SWCRE evidently increases relative to that in the cold season. The strongest seasonal contrast of SWCRE occurs over EA, where the TOA SWCRE increases from –10.8 W m–2 in cold season to –52.2 W m–2 in warm season, and the surface SWCRE increases from –20.6 to –70.2 W m–2 (Figs. 2b, c, e, f). The SWCRE contrast over EA is the largest, probably because the arid region of EA is adjacent to the monsoon regions to its south and is easily influenced by the strong seasonal variation of the latter. In the warm season, the magnitude of SWCRE is much larger than that of LWCRE, and the arid regions of the NH are therefore dominated by the SWCRE, showing a cooling effect. Relatively speaking, the warm-season SWCRE and NCRE over CA are the weakest among the arid regions of the NH (Figs. 2c, f), primarily because of its weak CF during the warm season.
Figure 3 further shows the annual cycles of CREs over the three arid regions. The SWCRE and NCRE have clear in-phase variations, and the variations in their amplitude over EA are stronger than those over CA and NA. The amplitude of variation in LWCRE is much weaker than that of SWCRE, and the annual change in surface LWCRE is different to that of TOA LWCRE. Over EA, the annual variations of TOA CRE are consistent with its CF, with the maximum values showing up during June –July (Fig. 3b). However, the annual cycles of SWCRE over CA and NA are different to their TCF annual cycles. For the NCRE, the values are positive from November to January over CA and NA (Figs. 3a, c, d, f); the positive time duration over EA is longer, with the positive value from December to February at the surface and TOA (Figs. 3b, e). The surface NCRE reaches 10 W m–2 over EA during February (Fig. 3e). This further shows that the NCRE over EA is dominated by the warming role of the LWCRE during the cold season, and its duration is also longer than that of the arid regions of CA and NA.

|
| Figure 3 Annual cycles of TOA (top of atmosphere) CRE (cloud radiative effect) (W m–2) over the arid regions of (a) central Asia (CA), (b) East Asia (EA), and (c) North America (NA), during the period 2001–15. Panels (d–f) show the corresponding results at the surface (SRF). Red, blue, and black lines denote the longwave CRE (LWCRE), shortwave CRE (SWCRE), and net CRE (NCRE), respectively. |
CREs are closely related to cloud types and cloud distributions (Hartmann et al., 1992). Hence, Fig. 4 shows the annual cycles of the vertical distribution of CFs and different column CFs over the arid regions of the NH. Meanwhile, clouds highly depend on large-scale general circulation (Bony et al., 1997). Some general circulation fields, including vertical velocity and wind, are presented in Fig. 5 to explain the CF characteristics over the three arid regions. As can be seen in the vertical distribution, the highest altitude of CF is less than 12 km over the three regions (Figs. 4a–c). The largest CF over EA is located at approximately 10 km in height and occurs during late winter and early summer (Fig. 4b). The highest CF over CA is slightly lower than that over EA and occurs at 9 km during winter and spring (Fig. 4a). The highest altitude of CF over NA is lower than that over CA and EA, and a large amount of CFs occur at 8–9 km during spring; unlike in CA and EA, the largest CF over NA is located below 2 km during summer (Fig. 4c). Over CA, the largest TCF occurs in February, while the smallest CF (Fig. 4d) occurs in summer. CA is located on the west side of a high altitude area, including the Tibetan Plateau and Pamirs. The orographic uplift easily leads to ascending motion (Wu et al., 2009), especially on the windward slope in the west to the high altitude area over CA (Figs. 5c, d). Meanwhile, wintertime westerly wind prevails in CA and brings moisture from the Mediterranean and Persian Gulf (Figs. 5a, c), which was also pointed out by Yin et al. (2014). Due to the above effects of circulation and moisture, the largest precipitation and TCF over CA occur in winter. In summer, many areas of CA are controlled by the anticyclone in the Caspian Sea, meaning northerly wind prevail in those regions (Figs. 5b, d). Thus, CA suffers with an arid climate, and the amount of precipitation and clouds in summer is much less than in winter. Over EA, the HCF dominates the CF, and has a significant annual cycle, with the maximum in June (Fig. 4e). The annual cycles of TCF and HCF over the arid region of EA basically agree with those over the monsoon region of EA (figures omitted), further demonstrating that the arid region of EA is greatly affected by the monsoon region to its south. Over NA, the HCF is dominant in the cold season and peaks in March, but the LCF dominates the CF over CA, particularly in summer. Notably, the LCF over CA and NA is larger than that over EA in the cold months (December to March) (Figs. 4d, e, f). Moreover, the largest TCF and HCF over the three arid regions reach 60% and 40%, respectively, indicating that the intensity of CREs cannot be ignored.

|
| Figure 4 Annual cycles of the vertical cloud fraction (CF) (%) and column CF averaged over the three arid regions. Panels (a) and (d) present the vertical and column CF, respectively, over central Asia (CA); (b) and (e) show the corresponding results over East Asia (EA); and (c) and (f) are for North America (NA). The CF data are from GOCCP (GCM Oriented CALIPSO Cloud Product) during the period 2007–15. HCF, MCF, and LCF are short for high, middle, and low CF, respectively. |

|
| Figure 5 Cold-season mean (a) 500-hPa vertical velocity (hPa day–1) and horizontal wind (m s–1), and (c) 850-hPa specific humidity (103 kg kg–1) and horizontal wind, from ERA-Interim (2001–15). Panels (b) and (d) are the corresponding results in warm season. The three arid regions are delineated with black boxes. |
The CF characteristics over the arid regions of the NH presented above affect their individual CREs. Here, we further examine the relationships between the CF and CREs with scatter diagrams. As displayed in Figs. 6b, f, j, the linear correlation between the TOA LWCRE and HCF reaches 0.6 over the three arid regions. The correlation between the TOA LWCRE and TCF over EA is also high, with a value of 0.62 (Fig. 6e). Furthermore, the surface LWCRE is also closely related to the TCF, and the corresponding linear correlations between them are 0.71, 0.60, and 0.90, over CA, EA, and NA (Figs. 6c, g, k), respectively, implying that the HCF strongly affects the LWCRE over the arid regions of the NH. Note that the correlation between the LWCRE and HCF is only 0.37 over NA (Fig. 6l), possibly because the LCF weakens the effect of the HCF on the surface. In contrast, the correlation between the surface LWCRE and HCF is 0.8 and 0.6 over CA and EA (Figs. 6d, h), respectively, indicating strong effects of the HCF at the surface. In particular, the inland cirrus over CA strongly influences the surface LW radiation (Sassen and Campbell, 2001).
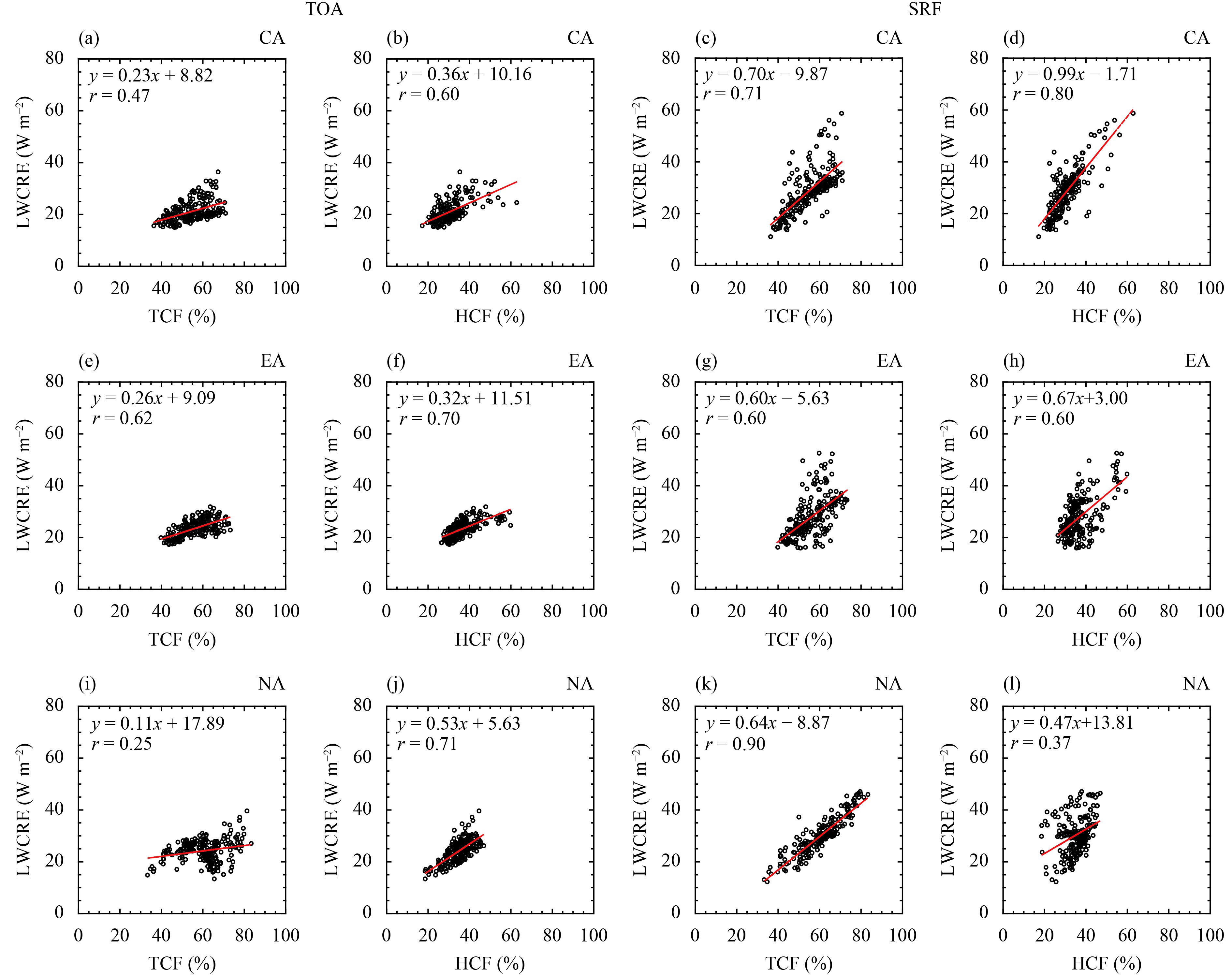
|
| Figure 6 Scatter plots of the climatological annual mean LWCRE (longwave cloud radiative effect) and column CF (cloud fraction) over the three arid regions: the TOA LWCRE versus (a) the TCF (total cloud fraction) and (b) the HCF (high-cloud fraction) over CA (central Asia); and the surface LWCRE versus (c) the TCF and (d) the HCF over CA. Panels (e–f) and (g–h) show the corresponding TOA and surface plots over EA (East Asia). Panels (i–j) and (k–l) are the corresponding plots over NA (North America). The period of coverage for CRE and CF is 2007–15. The linear regression equation, correlation coefficient, and regression line (red) are shown in each panel. |
As shown in Fig. 7, the correlation between the SWCRE and TCF at the TOA is –0.73, –0.67, and –0.94 over CA, EA, and NA (Figs. 7a, e, i), respectively; and the corresponding values are –0.74, –0.66, and –0.81 at the surface (Figs. 7c, g, k). Owing to the large LCF, the relationship between the SWCRE and LCF is very close over NA, with a correlation of –0.77 (Figs. 7j, l); however, the correlation between the SWCRE and LCF is low over CA and EA because of their relatively smaller LCF (Figs. 7b, d, f, h). In addition, the relationship between the SWCRE and TCF (LCF) is very close at the TOA and surface for the arid regions. This means that the effects of clouds on SW radiation differ little at the TOA and surface. Unlike the SWCRE, the relationships of the surface LWCRE with the above column CFs differ with that at the TOA.

|
| Figure 7 As in Fig. 6, but for the SWCRE (shortwave cloud radiative effect). |
In addition to the climatological mean states, we also investigate the interannual changes in CREs over the three arid regions during 2001–15. Here, each value represents the yearly area mean minus the corresponding multi-year mean. Three time series of the annual, cold-season, and warm-season means are derived. The standard deviation (STD) is used to describe the fluctuation in intensity of the interannual variation. As displayed in Fig. 8, a pronounced feature is that the interannual variation of most surface CREs is larger than the corresponding TOA CREs. For instance, the STDs of the TOA SWCRE are 1.84 and 2.38 W m–2 over EA and NA (Figs. 8h, n), respectively, but the corresponding surface STDs are 2.55 and 3.19 W m–2 (Figs. 8k, q). This indicates that the whole atmosphere–land surface system is relatively more stable, with a smaller interannual variation, but the interannual changes in surface CREs is larger. The differences in interannual CREs between the cold and warm seasons are small over CA and EA, but the SWCRE over NA has a larger interannual variation in the warm season than that in the cold season, because a large LCF occurs in summer and strongly affects the SWCRE over NA. In addition, there are no evident variation trends for TOA CREs. The annual mean interannual trends of surface LWCRE are –0.41 and –0.35 W m–2 yr–1 over CA and EA (Figs. 8d, j), respectively, showing a decreasing change; as a result, the annual mean trend of their NCRE also shows a decreasing change, with corresponding values of –0.18 and –0.42 W m–2 yr–1 (Figs. 8d, j). According to the above analysis, the surface LWCRE over CA and EA is closely related to the TCF. In fact, the annual mean TCF over CA and EA also shows a clearly decreasing trend of –0.29% and –0.23% yr–1 (Figs. 9a, b), respectively, while their HCFs do not present an evident trend (Figs. 9d, e). Both the LWCRE and HCF interannual changes are likely caused by large-scale circulation anomalies, the causes of which are complex and beyond the scope of this work. Moreover, Fig. 8 shows that the STDs of CREs during 2001–15 are much weaker than their climatological means. For example, as shown in Figs. 8h, k, the cold-season STDs of NCRE over EA are 0.69 and 1.18 W m–2 at the TOA and surface, respectively, only approximately 17% of the corresponding cold-season mean NCRE at the TOA (4.1 W m–2) and surface (6.9 W m–2). This further indicates that the radiative warming from the LWCRE is significant over EA during the cold season.

|
| Figure 8 Time series of area mean CRE (cloud radiative effect) anomalies (W m–2) over the three arid regions during the period 2001–15. Panels (a–c) show the LWCRE (longwave CRE), SWCRE (shortwave CRE), and NCRE (net CRE) at the TOA, respectively, over CA (central Asia); and (d–f) show the LWCRE, SWCRE, and NCRE at the surface, respectively, over CA. Panels (g–i) and (j–l) are the corresponding CREs over EA (East Asia). Panels (m–o) and (p–r) are the corresponding CREs over NA (North America). Blue, red, and black lines denote the cold-season, warm-season, and annual mean (ANN), respectively, and their standard deviation values (W m–2) are given to the left of each legend. |

|
| Figure 9 Time series of area mean total cloud fraction (TCF) anomalies (%) in the arid regions of (a) central Asia (CA), (b) East Asia (EA), and (c) North America (NA), during the period 2001–15. Panels (d–f) are the corresponding results for the high-cloud fraction (HCF). The TCF and HCF are from the CERES-MODIS satellite data. Blue, red, and black lines denote the cold-season, warm-season, and annual mean, respectively, and their standard deviation values (W m–2) are given to the left of each legend. |
This study investigates the characteristics of CREs among three arid regions in the NH using recent satellite datasets. The major conclusions are summarized below.
The annual mean CREs are dominated by the SWCRE over the three arid regions. EA has the strongest contrast in CREs between cold and warm seasons among the three arid regions. In the cold season, the LWCRE is stronger than the SWCRE over CA and EA, leading to a positive NCRE and a radiative warming; specifically, the NCRE over EA is 4.1 and 6.9 W m–2 at the TOA and surface, respectively. The sign of the cold-season mean NCRE over NA and the same latitudinal zone of the NH is still negative (radiative cooling). In the warm season, the SWCRE and NCRE are clearly negative over the above arid regions. A large TCF (HCF) is distributed over the above arid regions, with the highest TCF (HCF) of 60% (40%). The maximum TCF (HCF) occurs in the cold months (February to March) over CA and NA, but the corresponding peak is in summer over EA, where the pronounced annual cycles of TCF and HCF exist. The CREs over the arid regions of the NH are closely related to their CFs. Over CA and EA, the TOA LWCRE relates well to the HCF, with a linear correlation of over 0.6. However, the correlation between the HCF and surface LWCRE is only 0.37 over NA, showing a weak effect of the HCF at the surface. The correlation between the SWCRE and TCF is also high over the three arid regions, reaching –0.66. The correlation between the SWCRE and LCF reaches –0.77 over NA, because of the large LCF. The interannual change of CREs at the TOA is small, but their variations at the surface are larger. The LWCRE clearly shows a decreasing trend, with surface trends of –0.41 and –0.35 W m–2 yr–1 over CA and EA, respectively. This decreasing LWCRE trend agrees well with the decreasing TCF trend over these two regions.
This study emphasizes the relationship between CFs and CREs. Indeed, CREs also depend on cloud water content, particle sizes, and their distributions (Kiehl, 1994; Hartman et al., 2001). Satellite-retrieved CFs and other properties generally suffer from some uncertainty in measuring sensors and retrieval algorithms (Stubenrauch et al., 2013). For example, the definition of the column CF and its magnitude retrieved from MODIS and GOCCP satellites bear some differences. As a result, the conclusions in our work should be further verified with more cloud micro-and macro-physical observations. In addition, this study focuses on CREs at the surface and the TOA, and does not examine atmospheric CREs and their vertical distribution, which have recently received more attention (e.g., Li et al., 2015). Atmospheric CREs are another important aspect of concern. Moreover, the CF and its spatial distribution depend greatly on atmospheric general circulation, and the seasonal and interannual variations of the general circulation deeply influence CREs (Bony et al., 1997). On the other hand, surface states, such as albedo and air temperature, distinctly alter incident solar and upward LW radiation, which affect CREs. Thus, a further analysis on meteorological and surface characteristics is needed to achieve in-depth analysis of climatic feedback and long-term changes associated with CREs over arid regions in the NH. Given the complexity of cloud–radiation processes, it is also necessary to utilize climate model simulations. The aspects mentioned above should be addressed in further studies.
Acknowledgments. The authors would like to thank the reviewers for their valuable comments.
| Adler R. F., Huffman G. J., Chang A., et al., 2003: The version-2 global precipitation climatology project (GPCP) monthly precipitation analysis (1979–present). J. Hydrometeor., 4, 1147–1167. DOI:10.1175/1525-7541(2003)004 < 1147:TVGPCP > 2.0.CO; 2 |
| Bony M. Lau, S. C. Sud, 1997: Sea surface temperature and large-scale circulation influences on tropical greenhouse effect and cloud radiative forcing. J. Climate, 10, 2055–2077. DOI:10.1175/1520-0442(1997)010 < 2055:SSTALS > 2.0.CO; 2 |
| Bony S., Colman R., Kattsov V. M., et al., 2006: How well do we understand and evaluate climate change feedback processes. J. Climate, 19, 3445–3482. DOI:10.1175/JCLI3819.1 |
| Boucher, O. , D. Randall, P. Artaxo, et al. , 2013: Clouds and aerosols. Climate Change 2013: The Physical Science Basis. Contribution of Working Group Ⅰ to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. T. F. Stocker, D. Qin, G. -K. Plattner, et al. , Eds. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA. 总页码? |
| Cesana Chepfer, 2012: How well do climate models simulate cloud vertical structure? A comparison between CALIPSO-GOCCP satellite observations and CMIP5 models. Geophys. Res. Lett., 39, L20803. DOI:10.1029/2012GL053153 |
| Cess R. D., Zhang M. H., Wielicki B. A., et al., 2001: The influence of the 1998 El Niño upon cloud–radiative forcing over the Pacific warm pool. J. Climate, 14, 2129–2137. DOI:10.1175/1520-0442(2001)014 < 2129:TIOTEN > 2.0.CO; 2 |
| Chen Y. H., Bai H. T., Huang J. P., et al., 2008: Comparison of cloud radiative forcing on the atmosphere–earth system over northwestern China with respect to typical geo-topographic regions. China Environ. Sci., 28, 97–101. |
| Chepfer H., Bony S., Winker D., et al., 2010: The GCM-oriented CALIPSO cloud product (CALIPSO-GOCCP). J. Geophys. Res., 115, D00H16. DOI:10.1029/2009JD012251 |
| Dai A. G., 2013: Increasing drought under global warming in observations and models. Nature Climate Change, 3, 52–58. DOI:10.1038/nclimate1633 |
| Dee D. P., Uppala S. M., Simmons A. J., et al., 2011: The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Quart. J. Roy. Meteor. Soc., 137, 553–597. DOI:10.1002/qj.v137.656 |
| Doelling D. R., Loeb N. G., Keyes D. F., et al., 2013: Geostationary enhanced temporal interpolation for CERES flux products. J. Atmos. Oceanic Technol., 30, 1072–1090. DOI:10.1175/JTECH-D-12-00136.1 |
| Flato, G. , J. Marotzke, B. Abiodun, et al. , 2013: Evaluation of climate models. Climate Change 2013: The Physical Science Basis. Contribution of Working Group Ⅰ to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. T. F. Stocker, D. Qin, G. -K. Plattner, et al. , Eds. Cambridge University Press, Cambridge, United Kingdom and New York, 571-658. |
| Hartmann L., D. E. Ockert-Bell, M. L. Michelsen, 1992: The effect of cloud type on earth's energy balance: Global analysis. J. Climate, 5, 1281–1304. DOI:10.1175/1520-0442(1992)005 < 1281:TEOCTO > 2.0.CO; 2 |
| Hartman L., D. A. Moy, L. Fu, 2001: Tropical convection and the energy balance at the top of the atmosphere. J. Climate, 14, 4495–4511. DOI:10.1175/1520-0442(2001)014 < 4495:TCATEB > 2.0.CO; 2 |
| Huang P., J. D. Guan, X. Ji, 2012: Enhanced cold-season warming in semi-arid regions. Atmos. Chem. Phys., 12, 5391–5398. DOI:10.5194/acp-12-5391-2012 |
| Huang J. P., Ji M. X., Xie Y. K., et al., 2016: Global semi-arid climate change over last 60 years. Climate Dyn., 46, 1131–1150. DOI:10.1007/s00382-015-2636-8 |
| Kiehl J. T., 1994: On the observed near cancellation between longwave and shortwave cloud forcing in tropical regions. J. Climate, 7, 559–565. DOI:10.1175/1520-0442(1994)007 < 0559:OTONCB > 2.0.CO; 2 |
| Lauer Hamilton, 2012: Simulating clouds with global climate models: A comparison of CMIP5 results with CMIP3 and satellite data. J. Climate, 26, 3823–3845. DOI:10.1175/JCLI-D-12-00451.1 |
| Li W. J. Thompson, Y. Bony, 2015: The influence of atmospheric cloud radiative effects on the large-scale atmospheric circulation. J. Climate, 28, 7263–7278. DOI:10.1175/JCLI-D-14-00825.1 |
| Liu, R. J. , L. Zhang, H. B. Wang, et al. 2011: Cirrus cloud measurement using lidar over semi-arid areas. Chinese J. Atmos. Sci. , 35(5): 863-870. |
| Liu Y. G., Wu W., Jensen M. P., et al., 2011: Relationship between cloud radiative forcing, cloud fraction and cloud albedo, and new surface-based approach for determining cloud albedo. Atmos. Chem. Phys., 11, 7155–7170. DOI:10.5194/acp-11-7155-2011 |
| Loeb N. G., Wielicki B. A., Doelling D. R., et al., 2009: Toward optimal closure of the Earth's top-of-atmosphere radiation budget. J. Climate, 22, 748–766. DOI:10.1175/2008JCLI2637.1 |
| Ma G., Z. B. Fu, 2007: Evidence of the global drying trend during the latter half of the 20th century and its relationship with large-scale climate background. Sci. China Earth Sci., 50, 776–788. DOI:10.1007/s11430-007-0036-6 |
| Mace G. G., Benson S., Sonntag K. L., et al., 2006: Cloud radiative forcing at the atmospheric radiation measurement program climate research facility. 1: Technique, validation, and comparison to satellite-derived diagnostic quantities. J. Geophys. Res., 111, D11S90. DOI:10.1029/2005JD005921 |
| Meehl, G. A. , T. F. Stocker, W. D. Collins, et al. , 2007: Global Climate Projections. Climate Change 2007: The Physical Science Basis. Contribution of Working Group Ⅰ to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. S. Solomon, D. Qin, M. Manning, et al. , Eds. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA. 总页码? |
| Min M., Wang P. C., Campbell J. R., et al., 2010: Midlatitude cirrus cloud radiative forcing over China. J. Geophys. Res., 115, D20210. DOI:10.1029/2010JD014161 |
| Minnis P., Sun-Mack S., Chen Y., et al., 2011: CERES Edition-2 cloud property retrievals using TRMM VIRS and Terra and Aqua MODIS data. Part Ⅱ: Examples of average results and comparisons with other data. IEEE Trans. Geosci. Remote Sensing, 49, 4401–4430. DOI:10.1109/TGRS.2011.2144602 |
| Ramanathan V., Cess R. D., Harrison E. F., et al., 1989: Cloud-radiative forcing and climate: Results from the earth radiation budget experiment. Science, 243, 57–63. DOI:10.1126/science.243.4887.57 |
| Randall, D. A. , R. A. Wood, S. Bony, et al. , 2007: Climate models and their evaluation. Climate Change 2007: The Physical Science Basis. Contribution of Working Group Ⅰ to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. S. Solomon, D. Qin, M. Manning, et al. , Eds. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA. 总页码? |
| Sassen R. Campbell, 2001: A midlatitude cirrus cloud climatology from the facility for atmospheric remote sensing. Part Ⅰ: Macrophysical and synoptic properties. J. Atmos. Sci., 58, 481–496. DOI:10.1175/1520-0469(2001)058 < 0481:AMCCCF > 2.0.CO; 2 |
| Stubenrauch C. J., Rossow W. B., Kinne S., et al., 2013: Assessment of global cloud datasets from satellites: Project and data-base initiated by the GEWEX radiation panel. Bull. Amer. Me-teor. Soc., 94, 1031–1049. DOI:10.1175/BAMS-D-12-00117.1 |
| Trenberth E., K. T. Fasullo, J. Kiehl, 2009: Earth's global energy budget. Bull. Amer. Meteor. Soc., 90, 311–323. DOI:10.1175/2008BAMS2634.1 |
| Wang J., Zhang L., Huang J. P., et al., 2013: Macrophysical and optical properties of midlatitude cirrus clouds over a semi-aridarea observed by micro-pulse lidar. J. Quant. Spectros. Radiative Transfer, 122, 3–12. DOI:10.1016/j.jqsrt.2013.02.006 |
| Wild Folini, M. Schär, et al., 2013: The global energy balance from a surface perspective. Climate Dyn., 40, 3107–3134. DOI:10.1007/s00382-012-1569-8 |
| Wu G. X., Liu Y., Zhu X., et al., 2009: Multi-scale forcing and the formation of subtropical desert and monsoon. Annales Geophysicae, 27, 3631–3644. DOI:10.5194/angeo-27-3631-2009 |
| Yin Y., Z. L. Wang, H. D. Liu, 2014: A comparative study on precipitation climatology and interannual variability in the lower midlatitude East Asia and central Asia. J. Climate, 27, 7830–7848. DOI:10.1175/JCLI-D-14-00052.1 |
| Zhang X., L. J. Zhou, 2015: Drought over East Asia: A Review. J. Climate, 28, 3375–3399. DOI:10.1175/JCLI-D-14-00259.1 |
| Zhao S. Y., Zhang H., Feng S., et al., 2015: Simulating direct effects of dust aerosol in arid and semi-arid regions using an aerosol–climate coupled system. Int. J. Climatol., 35, 1858–1866. DOI:10.1002/joc.2015.35.issue-8 |
| Zhao B., T. Chen, L. G. Ma, 2014: Simulation of historical and projected climate change in arid and semi-arid areas by CMIP5 models. Chinese Sci. Bull., 59, 412–429. DOI:10.1007/s11434-013-0003-x |
 2017, Vol. 31
2017, Vol. 31


