The Chinese Meteorological Society
Article Information
- DUAN Wansuo, FENG Rong . 2017.
- Reducing the Prediction Uncertainties of High-Impact Weather and Climate Events: An Overview of Studies at LASG. 2017.
- J. Meteor. Res., 31(1): 224-235
- http://dx.doi.org/10.1007/s13351-016-6099-6
Article History
- Received June 13, 2016
- in final form September 9, 2016
2. University of Chinese Academy of Sciences, Beijing 100049
Weather or climate events often have substantial adverse impacts on societies and economies; therefore, predicting these events—especially with numerical models—has been an important focus of oceanic and atmospheric research in recent decades. The essence of numerical weather forecasting and climate prediction is to solve the initial-boundary problems of complicated partial differential equations. However, due to the limitations of observational methods and instruments, observational errors inevitably influence the accuracy of the initial conditions (Mu et al., 2002). Furthermore, numerical models cannot accurately describe the fluid flow, which ultimately causes model errors. Both initial errors and model errors yield the uncertainties of weather forecasts and climate predictions, which of course severely limits their predictability (Lorenz, 1963;Mu et al., 2002).
To reduce initial errors and provide proper initial conditions, sufficient quantities of observations are required. However, field observations, especially those over the oceans, are costly and sparse. They will never be dense enough to completely cover the vast areas associated with weather and climate events (McPhaden et al., 1998,2001,2010;International CLIVAR Project Office, 2006;Masumoto et al., 2009). Therefore, it is necessary to optimize the design of observing networks by developing an efficient and effective observation strategy in which additional observations with limited coverage can be implemented in such a way to have a considerable positive impact on the forecast skill (Mu et al., 2015). In fact, an observation strategy referred to as “targeted observation”, or “adaptive observation”, has been in development since the 1990s (Snyder, 1996;Palmer et al., 1998;Buizza and Montani, 1999). In short, this method seeks to skillfully predict an event at a future time,t1 (the verification time), in a focused area (the verification area), by utili-zing additional observations at a future time,t2 (the target time,t2 <t1), in a number of special areas (sensitive areas), where the additional observations are expected to contribute greatly to reducing the prediction errors in the verification area (Snyder, 1996;Mu, 2013). By assimila-ting the additional observations into the model's initial fields, a more skillful prediction will be achieved. That is, the sensitive areas represent the optimal observing locations for implementing target observations. Identifying the sensitive areas (i.e., the optimal observing locations) is the key aspect of targeted observations. Previous studies have shown that there are two main categories of methods to identify these sensitive areas. The first category is the optimal perturbation methods, such as singular vectors (SVs) (Palmer et al., 1998); and the second category is the ensemble methods, such as the ensemble transform Kalman filter (ETKF) (Bishop et al., 2001), the ensemble Kalman filter (Hamill and Snyder, 2002), and the ensemble transform technique (Bishop and Toth, 1999). However, these methods employ the linear approximation approach to estimate the prediction errors (or covariances) (e.g.,Palmer et al., 1998;Bishop et al., 2001), which is a limitation considering the nonlinear nature of atmospheric and oceanic motions.
A better data assimilation system is one that makes better use of observational data and supplies more realistic initial conditions for forecast models to improve the forecast skill. The four-dimensional variational (4DVar) method is one of the best choices for operational use. The 4DVar method uses a non-sequential approach that provides an analysis best fitted to observations in a time window (i.e., the assimilation window) through the trajectory of the model solution initiated at the analysis time (i.e., the beginning of the assimilation window). The analysis is dynamically consistent with the forecast model, and all model variables are balanced because of physical constraints. The covariance matrix of the background error (referred to simply as the “B matrix” hereinafter) in 4DVar has been proven to be implicitly developed within the window, although it is modeled and kept constant at the analysis time. Many applications or case studies have shown that the 4DVar method has the potential to be used in various observational data types, including radiosonde data (e.g.,Zhang and Ni, 2005), satellite remote sensing data (e.g.,Chevallier et al., 2004;Zhao et al., 2005), Doppler radar data (e.g.,Sun and Zhang, 2008), accumulated station rainfall data (e.g.,Zou and Kuo, 1996), surface observations (e.g.,Järvinen et al., 1999), and even tropical cyclone bogus data (e.g.,Xiao et al., 2000). These features have led to 4DVar becoming increasingly attractive in numerical weather prediction (NWP), especially following the rapid development of computer technology. Several NWP centers around the world have successfully applied 4DVar in their global and/or regional analyses (e.g.,Klinker et al., 2000;Gauthier and Thépaut, 2001;Honda et al., 2005;Gauthier et al., 2007;Rawlins et al., 2007). The application at these major NWP centers indicates that 4DVar is one of the best choices for operational use. However, three key problems in using 4DVar in an operational setting still exist. Specifically: its high computational cost, which limits its application in many countries; the lack of global flow-dependence in its B matrix from window to window, although the B matrix is implicitly evolved within the assimilation window; and the difficulty in using an imperfect model in strong-constraint 4DVar.
The existence of initial errors or model errors indicates that the weather and climate have a predictability limit beyond which forecasts will lose all skill. Based on the uncertainty of atmosphere and ocean predictions, any single forecast is simply an estimate of the future state of the atmosphere and ocean within a stochastic framework, but provides no information regarding its reliability. Since the early 1970s, ensemble prediction has been regarded as a practical approach to generate probabilistic forecasts of the future state of a system. In particular, the ensemble mean of forecast members is often thought as the result of a deterministic forecast, which may filter the unpredictable parts and leave the common parts of the forecast members, ultimately decreasing the uncertainties of single forecast results. Therefore, ensemble prediction systems based on different schemes to generate the initial perturbations have been developed and used operationally by many weather prediction centers (Toth and Kalnay, 1993;Molteni et al., 1996). For example, the bred vector (BV) was developed and used operationally at the National Centers for Environmental Prediction, and the SV at the European Center for Medium-Range Weather Forecasts (Molteni and Palmer, 1993;Toth and Kalnay, 1993,1997;Molteni et al., 1996;Buizza, 1997). However, these methods present ensemble initial perturbations of either linear approximation (e.g.,Molteni and Palmer, 1993;Molteni et al., 1996) or non-independence (e.g.,Toth and Kalnay, 1993), and have limitations in yielding proper and reasonable members for the ensemble forecast, which certainly limits the forecast skill of ensemble predictions.
The above introduction demonstrates that targeted observations, data assimilation, and ensemble prediction are three effective strategies in reducing the prediction uncertainties of weather and climate events and improving the forecast skill. However, these strategies have limitations that restrict their operational use in weather forecasts and climate prediction. In this context, the present paper reviews recent progress at the State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics (LASG), Institute of Atmospheric Physics, Chinese Academy of Sciences in overcoming the limitations related to these strategies, and so making them more favorable in reducing prediction uncertainties and improving the forecasting of weather and climate.
2 Targeted observationsFrom the discussion in the introduction, it is clear that targeted observations, by which additional observations are obtained, are urgently needed to optimize observing networks. By assimilating these additional observations in sensitive areas into a model's initial state, the forecasting skill for weather or climate events will be improved. The key to targeted observations is to identify these sensi-tive areas (i.e., the optimal observing locations). Following the general idea of targeted observations, to improve numerical prediction models in terms of physics, the key/optimal observing regions associated with model errors can also be identified, in which improvement to the model simulation through additional observations may greatly improve the forecast skill. Although several methods have been proposed in previous studies to identify such sensitive areas (Palmer et al., 1998;Bishop and Toth, 1999;Bishop et al., 2001;Hamill and Snyder, 2002), many of them employ linear approximation to estimate the prediction errors, which is a limitation considering the nonlinear nature of the atmosphere and ocean.
Towards initial errors,Mu et al. (2003) developed the conditional nonlinear optimal perturbation (CNOP) approach, which overcomes the linear limitations of the linear singular vector (LSV) method and represents the initial perturbation that exhibits the largest prediction growth at the end time of the forecast period. This approach has been used to identify the sensitive areas for targeted observations (Duan et al., 2009;Yu et al., 2009;Mu et al., 2014a). Regarding model errors,Duan and Zhou (2013) generalized the forcing SV (FSV) to the nonlinear regime and proposed the nonlinear FSV (NFSV). Since it describes the combined effect of different kinds of model errors, the NFSV can reveal the most disturbing tendency errors of predictions and provide guidance on targeted observations to improve the forecasting by optimizing the model performance. In this section, we review recent progress in determining the sensitive areas of targeted observations with these methods for the El Niño–Southern Oscillation (ENSO), Indian Ocean dipole (IOD), and tropical cyclones (TCs), and explore their role in optimizing observing networks and thus increasing prediction skill.
2.1 ENSOTo identify the sensitive areas for eastern Pacific (EP) El Niño events,Mu et al. (2007) and Yu et al. (2009) used the Zebiak–Cane model and revealed two types of CNOP initial errors (i.e., EP-type-1 and EP-type-2) that cause the largest prediction errors of EP-El Niño (Fig. 1). These two CNOP-type initial errors have almost oppo-site spatial patterns. It was found that the large values of the CNOP initial errors concentrate in the central–eastern equatorial Pacific, which indicates that the initial errors over this area make the largest contribution to the prediction errors of EP-El Niño. Therefore, these regions are considered to be the sensitive areas of targeted observations for EP-El Niño events.Yu et al. (2012) further demonstrated that when the CNOP initial errors in the central–eastern equatorial Pacific are eliminated, without changing the initial errors in other regions, the resultant prediction errors are significantly reduced. Furthermore,Mu et al. (2014b) demonstrated the similarities between the optimal precursor for EP-El Niño events and the CNOP initial errors. They indicated that additional observations in the sensitive areas determined by CNOP can not only reduce initial errors but also be used to detect precursory signals, thereby improve ENSO predictions.
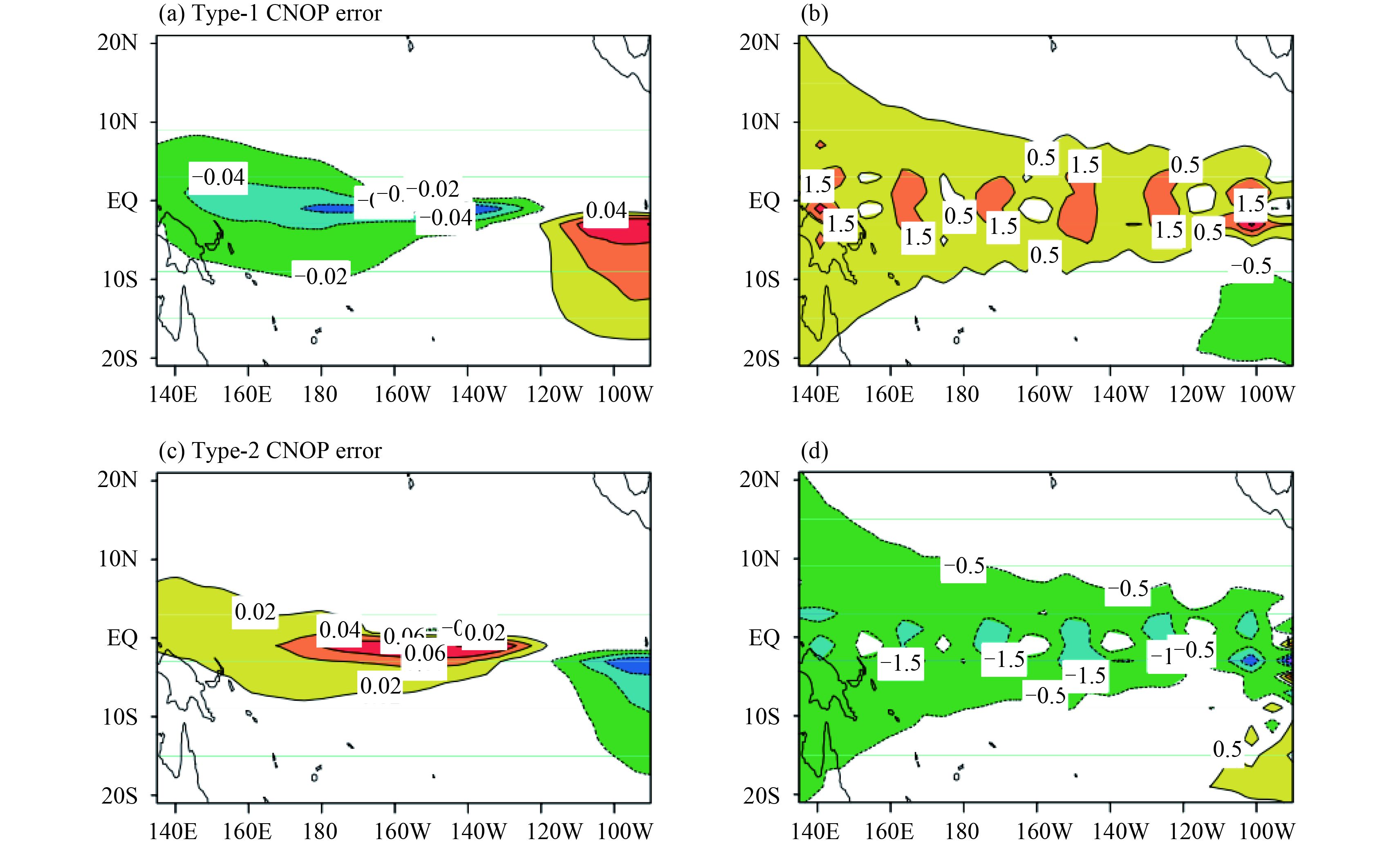
|
| Fig. 1 The (a, c) SST anomaly component (units: °C) and (b, d) thermocline depth anomaly (units: m) of the composite (a, b) type-1 and (c, d) type-2 conditional nonlinear optimal perturbation initial errors for eastern Pacific El Niño events in the Zebiak–Cane model. Adapted from Yu et al. (2009). |
Morss and Battisti (2004a, b) suggested that the eastern equatorial Pacific, south of the equator, is the most important area for observations for ENSO forecasting. These results were explored based on observation system simulation experiments (OSSEs) and were consis-tent with those explored by the Zebiak–Cane model and the CNOP method. Therefore, these results serve as a verification of those determined with the CNOP sensiti-vity in the Zebiak–Cane model. Besides, by applying the sequential importance sampling assimilation method,Kramer and Dijkstra (2013) suggested that the eastern tropical Pacific is the optimal observing location for sea surface temperature (SST) to reduce prediction uncertainties, which also offers strong support to the results with CNOP methods in the Zebiak–Cane model.
Limited by the simplicity of the Zebiak–Cane model, the results within this model mainly focused on the role of the SST anomaly (SSTA) component and did not consider subsurface anomalies in the equatorial Pacific, which actually play an important role in the evolution of EP-El Niño. Using the Community Earth System Model (CESM),Duan and Hu (2016) explored the three-dimensional structure of sea temperature initial errors by an ensemble approach based on the CNOP idea. They identified two types of optimally growing initial errors for EP-El Niño predictions, and suggested that the sensitive areas are the lower layers of the western equatorial Pacific and the upper layers of the eastern equatorial Pacific (regions A, B, and C in Fig. 2). Using Coupled Model Intercomparison Project Phase 5 model outputs,Zhang et al. (2015) confirmed that similar initial errors that cause the largest prediction errors for EP-El Niño also exist in other coupled climate models. Compared to the results in the Zebiak–Cane model, the results of complex coupled models further supplement and highlight the sensitive areas in the subsurface layers of the western equatorial Pacific.

|
| Fig. 2 Composite patterns of (a, c) type-1 and (b, d) type-2 initial errors in the Community Earth System Model: (a, b) the SST anomaly component (units: °C) and (c, d) the equatorial (5°S–5°N) subsurface temperature anomaly (units: °C). Regions A, B, and C are (5°S–5°N, 150°–85°W; 0–5 m), (5°S–5°N, 150°–85°W; 5–85 m), and (5°S–5°N, 150°E–135°W; 120–165 m), respectively. Dotted areas indicate that the composite errors exceed the 99% confidence level, as determined by a t-test. Adapted from Duan and Hu (2016). |
In addition to the conventional EP-El Niño, a new type of El Niño called the central Pacific (CP) El Niño has become increasingly frequent and common from the 1990s (Ashok et al., 2007;Kao and Yu, 2009;Kug et al., 2009). Current models show more uncertainties in simulating CP-El Niño events than EP-El Niño events, in terms of the SST anomaly pattern and intensity (Ham and Kug, 2012).Duan et al. (2014) proposed an optimal forcing vector approach to correct the Zebiak–Cane model simulation closest to observations. Based on the reproduced CP-El Niño events, they investigated the CNOP initial errors associated with CP-El Niño predictions and compared them to those of EP-El Niño (Tian and Duan, 2016). For the CP-El Niño events, two types of CNOP initial errors also existed, denoted as CP-type-1 and CP-type-2 CNOP errors, respectively. Both CP-type-1 and CP-type-2 grow in a manner similar to an EP-El Niño event and tend to predict the corresponding CP-El Niño events to spurious EP-El Niño, which has also been verified in the CESM model (Chen, 2015). It was noted that the CP-type-1 errors share a similar pattern to the EP-type-1 errors (Fig. 1a), while the SSTA of the CP-type-2 errors is confined to the eastern equatorial Pacific, different from the large-scale zonal dipole of the EP-type-2 errors. In any case, both of the CNOP initial errors of CP-El Niño mainly concentrate in the central–eastern equatorial Pacific, which probably represent the sensitive areas for targeted observations associated with CP-El Niño prediction. Combining EP-El Niño and CP-El Niño events, it was found that the central and eastern equatorial Pacific may represent the common sensitive areas of the two types of El Niño events because both predictions are sensitive to the initial errors in these regions. By implementing targeted observations in the sensitive areas to obtain additional observations and assimilate them into the initial fields, the forecasting skill for the two types of El Niño events can be greatly improved.
Besides initial errors, an increasing number of studies has shown that model errors also significantly influence the ability to forecast ENSO (Blanke et al., 1997;Latif et al., 1998;Mu et al., 2002;Zhang et al., 2003;Williams, 2005;Duan and Zhang, 2010;Yu et al., 2012;Duan et al., 2016). The effects of different kinds of model errors are mixed and it is very difficult to distinguish their respective roles in yielding prediction uncertainties. With the Zebiak–Cane model,Duan and Zhao (2015) identified the model errors characterized by NFSV-type tendency error for EP-El Niño events that yield the largest prediction errors in a perfect initial conditions scenario. The NFSVs often concentrate the large values of tendency errors in a few areas of the central and eastern equatorial Pacific, which make a large contribution to prediction uncertainties. Therefore, these few areas may represent key regions of model errors for EP-El Niño predictions. That is, if we can improve the model's simulation ability in these regions, the EP-El Niño forecasting skill will probably be greatly improved. In fact,Zhang (2015) indicated that reducing model errors in the central–eastern equatorial Pacific via multi-model ensemble forecasting can improve the EP-El Niño forecasting skill more significantly than by reducing them in other regions. Furthermore, the key regions associated with model errors are the same as the sensi-tive areas of targeted observations for EP-El Niño deter-mined by the CNOP initial errors. Therefore, improving the observing network in these sensitive areas, compared to in other areas, not only can provide a more accurate initial field, but also is more conducive to a better understanding of ENSO physics, thus allowing the optimization of ENSO models and so greatly improving ENSO forecasting skill. It is generally accepted that global warming and its recent hiatus have substantial effects on climate. Thus, many new questions arise for targeted observations. For instance, are existing observing systems adequate with respect to ENSO under the scenario of global warming and its hiatus? If not, how should they be updated? Do the sensitive areas of targeted observations change under global warming? Uncovering the answers to these questions will be of great help in designing better observing networks and improving the forecast skill for ENSO.
2.2 IODTo the best of the authors' knowledge, no attempts were made regarding targeted observations for the IOD until very recently.Feng and Duan (2014) explored the initial errors that cause a significant winter predictability barrier (WPB) (hereafter referred to as WPB-related optimal initial errors) using an ensemble approach with the Geophysical Fluid Dynamics Laboratory Climate Model, version 2p1. It was demonstrated that the WPB-related optimal initial errors present a west–east dipole pattern in sea temperature both at the sea surface and at a depth of 95 m.Feng et al. (2016) further compared the relative effects of spatially correlated noise and WPB-related optimal initial errors on IOD predictions, and demonstrated that the WPB-related optimal initial errors cause larger prediction errors in winter and are more likely to cause a significant WPB. The large values of WPB-related optimal initial errors are concentrated within a few areas (at the depth of the thermocline in the eastern tropical Indian Ocean), indicating that the initial errors in these areas may make the largest contribution to the prediction errors of IOD events and probably represent the sensitive areas for targeted observations of IOD events. Based on sensitivity experiments, these areas were proved to be the optimal observing locations (i.e., sensitive areas) of targeted observations for positive IOD events. Therefore, by carrying out intensive observations over these areas and assimilating the additional observations there into the initial state of IOD predictions, the forecast skill will probably be largely improved. This certainly needs to be further verified by using OSSEs and OSEs (observing system experiments). As these studies were only focused on the effects of sea temperature at the surface and at 95 m on the predictability of positive IOD events, several questions remain unanswered. For instance, what are the effects of sea temperature in the whole Indian Ocean on IOD prediction and what is the role of ENSO in the predictability of IOD events? It is expected that answering these questions will offer great help in optimizing the observation network in the Indian Ocean and greatly improve the IOD forecasting skill.
2.3 TCsTargeted observations associated with TCs refer to the augmentation of the regular observing network over the ocean with additional, specially chosen observations to be assimilated into operational numerical prediction models, in order to improve both the track and intensity forecasts of TCs. Naturally, the effects of targeted observations have a lot to do with the observation locations (i.e., sensitive areas). With the help of targeted observations, TC track forecasts have been statistically improved over the past decade (Aberson, 2010;Chou et al., 2011;Weissmann et al., 2011).
As one method to identify the sensitive areas, CNOP aims to locate the initial errors with special structure, which will nonlinearly develop to the largest forecast errors. Theoretically, it is expected that conducting targeted observations according to CNOP sensitivity, obtaining and assimilating additional observations, reducing initial errors, and improving initial condition qua-lity, within these areas, will benefit the TC forecasting skill. Generally, CNOP sensitivity captures the steering flow at the border between the subtropical high and storms themselves (Fig. 3;Chen et al., 2013) as the sen-sitive areas, which infers a significant role played by the subtropical high in TC movements over the western North Pacific. OSSEs based on CNOP (LSV) sensitivity show a 13%–46% (14%–25%) improvement in TC track forecasts (Fig. 4;Qin and Mu, 2012). Further results indicate that applying real dropwindsonde data within CNOP sensitivity results in improvements in forecasting the TC track, which is similar to, and occasionally better than, those gained by assimilating all the available data (fourth and third column in Table 1, respectively); and they both offer greater benefits than LSV and random method (fifth and sixth columns in Table 1, respectively;Chen et al., 2013). These results demonstrate the statis-tically positive effects of CNOP on TC track forecasts, but also shed light on future operational applications. However, these targeted observations show little impact on TC intensity forecasts. This is probably because almost all the existing targeted observations related to the TC forecast are focused on atmospheric aspects and ignore the effects of the ocean. As TCs generally originate and absorb energy from the ocean, and the ocean has a considerable effect on TC development and its prediction, it is therefore necessary to take ocean-TC interaction into account when exploring the sensitive areas of targeted observations. This will certainly lead to improvements in the forecasting skill of TCs, especially TC intensity.
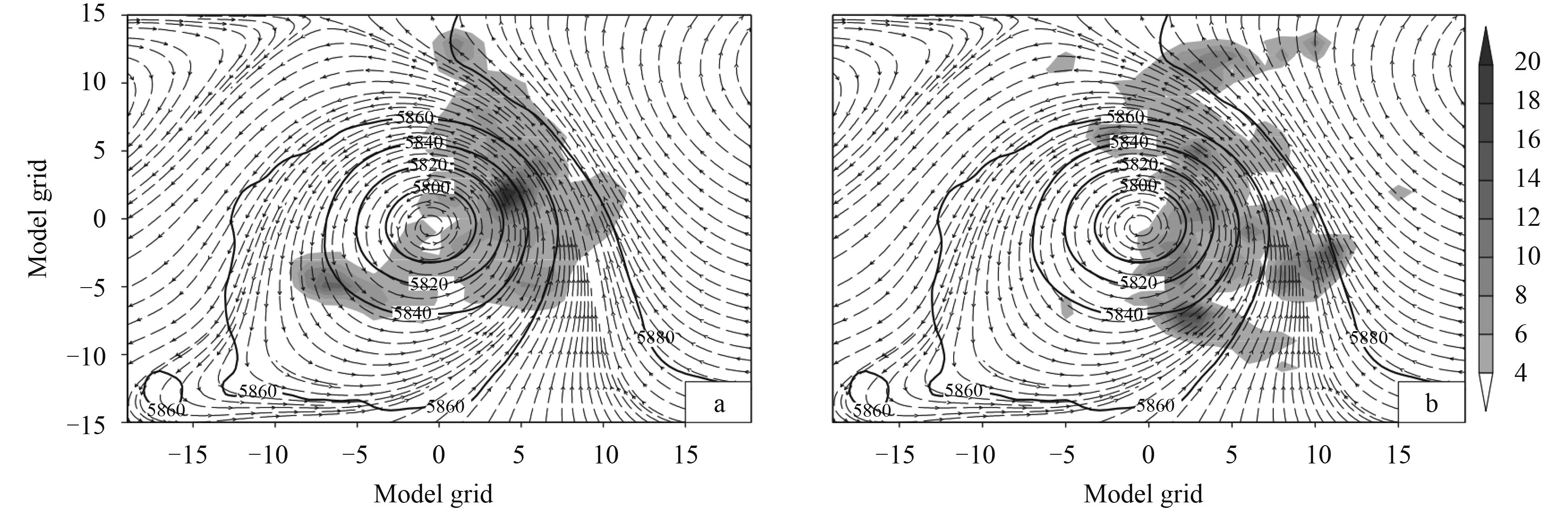
|
| Fig. 3 (a) Storm-centered (0, 0) composite conditional nonlinear optimal perturbation sensitivity (shaded; units: J kg–1), geopotential height at 500 hPa (contours; units: gpm), and deep layer mean wind (streamlines; units: m s–1) for 14 cases steered by the subtropical high. (b) As in (a), but for LSV sensitivity. The x- and y-axis represent the model grid with 60-km spacing. Adapted from Chen et al. (2013). |

|
| Fig. 4 (a) Scatter diagram of all track forecast errors for typhoon case Vamco. The y–axis represents the track forecast errors with dropsondes, and the x-axis represents those without dropsondes. Filled and empty diamonds denote the results of conditional nonlinear optimal perturbations and singular vectors, respectively. The colour of each diamond indicates the forecast time. (b) Histogram showing the relative differences corresponding to each case. Adapted from Qin and Mu (2012). |
| CTRL | ALL | CNOP | LSV | RAN | |
| Error (24 h-MM5) | 202.23 | 202.23 | 161.36 | 170.20 | 202.23 |
| Improvement | – | 0 | 20.2% | 15.8% | 0 |
| Error (36 h-MM5) | 298.55 | 267.04 | 260.30 | 314.62 | 279.59 |
| Improvement | – | 10.6% | 12.8% | –5.4% | 7.0% |
| Error (24 h-WRF) | 79.83 | 48.34 | 29.02 | 73.36 | 98.81 |
| Improvement | – | 39.4% | 63.6% | 8.1% | –23.8% |
| Error (36 h-WRF) | 176.57 | 126.33 | 114.73 | 163.32 | 181.85 |
| Improvement | – | 28.5% | 35.0% | 7.5% | –3.0% |
| Notes: CTRL, the control run that simulated the 36-h typhoon prediction using the National Centers for Environmental Prediction reanalysis data; ALL, experiments with all sonde data assimilated; CNOP (LSV), experiments with only the observational data from sensitive regions identified by conditional nonlinear optimal perturbation (linear singular vector) approach assimilated; RAN, experiments with randomly selected dropwindsondes assimilated. | |||||
As mentioned in the introduction, 4DVar is one of the best choices operationally to supply accurate initial conditions and improve the forecasting skill of weather and climate. However, three key challenges still exist in terms of using 4DVar in an operational setting. One of the strategies that can be used to improve the operational implementation of 4DVar involves the application of ensemble-based 4DVar (En4DVar), which uses an ensemble method—similar to that used in the ensemble Kalman filter (EnKF)—for a flow-dependent B matrix, and performs 4DVar minimization to obtain the optimal solution in a reduced space. En4DVar includes the advantages of both standard 4DVar and the EnKF.
There have been a number of efforts made in the development of the En4DVar family (e.g.,Qiu and Chou, 2006;Liu et al., 2008;Tian et al., 2008). One of the representative approaches in this family is dimension-reduced-projection-based 4DVar (DRP-4DVar), proposed by Wang et al. (2010). This approach minimizes the cost function of 4DVar in the low-dimension sample space and does not require implementation of the adjoint of the tangent linear approximation. It offers great timesaving compared to both standard 4DVar and the EnKF. The B matrix used in DRP-4DVar is not only locally evolved within the time window, but also globally developed from window to window.
In recent years, DRP-4DVar has been conducted with single-observation experiments, OSSEs, case studies, and batch experiments (e.g., 50-day continuous assimilation-hindcast experiments in 2007). The experiments have been carried out by using different models, such as the fifth-generation Pennsylvania State University-National Center for Atmospheric Research Mesoscale Model (MM5), the Weather Research and Forecasting model, and the Advanced Regional Eta Model. The results from these experiments show that DRP-4DVar is a promising approach and is suitable for operational use in the near future.
Figure 5 shows the results of a case study. It is indi-cated that DRP-4DVar performs comparably to MM5 adjoint-based 4DVar (MM5-4DVar) when assimilating 6-h accumulated rainfall observations. The incorporation of rainfall observations into the initial conditions by histo-rical-sample-projection 4DVar (HSP-4DVar) or MM5-4DVar can significantly reduce the errors of 24-h rainfall forecasts (Fig. 5). However, HSP-4DVar offers much greater timesaving than MM5-4DVar. To facilitate the operational implementation of DRP-4DVar, a dataset to collect historical forecast samples and corresponding simulated observation samples in the past should be established first, from which DRP-4DVar can automati-cally choose a high-quality sample (i.e., an analog forecast sample) for its analysis. In addition, because of significant impacts of the covariance matrix of the observation error (O matrix) on 4DVar and other assimilation approaches, studies on the inclusion of horizontal and vertical correlations between observation errors in the O matrix should be emphasized and strengthened in the near future.
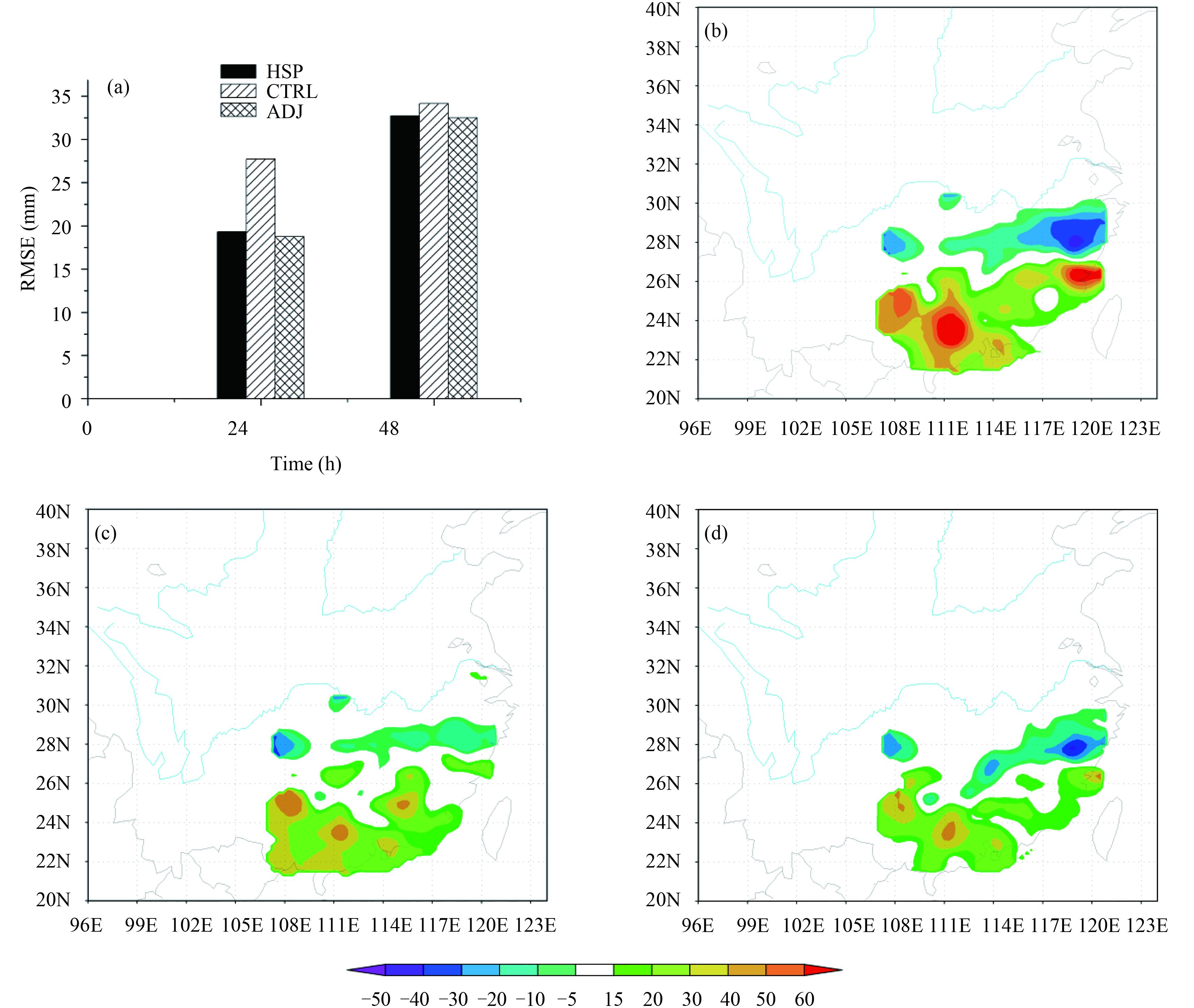
|
| Fig. 5 (a) Root-mean-square errors (RMSEs) of three experiments: A control (CTRL) experiment, in which precipitation is generated by a forecast model without assimilation, by using the initial fields produced at 0000 UTC 4 June 2006, with 1° × 1° National Centers for Environmental Prediction–National Center for Atmospheric Research reanalysis data; an experiment (HSP) that assimilates the 6-h accumulated rainfall observations of 1834 stations in China into the initial field with dimension-reduced-projection-based four-dimensional variational data assimilation, and an experiment (ADJ) that is the same as HSP except it uses MM5 adjoint-based four-dimensional variational data assimilation. (b) Horizontal distribution of forecast errors of 24-h accumulated rainfall from 0000 UTC 4 to 0000 UTC 5 June 2006 in CTRL. Panels (c) and (d) are the same as (b), but for the HSP and ADJ experiments, respectively. Both HSP and ADJ use a 6-h assimilation window from 0000 to 0006 UTC 4 June 2006, and a diagonal covariance matrix of observation error with a constant RMSE of 0.3 mm. The forecast model used in all experiments is MM5. Adapted from Liu (2009). |
As a single forecast is simply an estimate of the future state of the atmosphere and ocean within a stochastic framework, but provides no information regarding its reliability, ensemble prediction is needed and regarded as a practical approach to generate probabilistic forecasts of the future state of the system. In particular, the ensemble mean of forecast members may filter the unpredictable parts and leave the common parts of forecast members, ultimately reducing the prediction uncertainties of single forecasts. Different schemes are employed to generate the initial perturbations for ensemble prediction systems, such as BVs and SVs (Molteni and Palmer, 1993;Toth and Kalnay, 1993,1997;Molteni et al., 1996;Buizza, 1997). However, SVs are currently applied using a tangent linear system with limited physical parameterizations, and so they are unable to reflect the nonlinear cha-racteristics of weather or climate, meaning they possess a number of limitations. BVs are a nonlinear extension of the local Lyapunov vectors (LLVs) proposed by Toth and Kalnay (1993). However, BVs are not completely orthogonal; they may not span the fast-growing subspace efficiently and not fully reflect the uncertainty of the initial conditions. Recently, a number of methods based on ensemble assimilation have been developed to overcome the limitations of BVs and SVs. These methods include the EnKF and ETKF (Evensen, 1994;Houtekamer and Derome, 1995;Descamps and Talagrand, 2007). However, to date, there remain some real limitations and technical problems when using these methods in operational forecasting. These methods are still at their trial stages, and far from being widely applied operationally.
Based on nonlinear dynamical system theory,Feng et al. (2014) developed nonlinear local Lyapunov exponents (NLLEs) and vectors (NLLVs). NLLVs represent the vectors along the directions from the fastest-growing direction to the fastest-shrinking direction. The first few of these are utilized as ensemble initial perturbations. The NLLV method is quick in computational terms, and physically and dynamically effective for generating ensemble perturbations; plus, it also reduces the depen-dence among perturbations because of the global orthogonality. Therefore, NLLVs may be suited as the initial perturbations for ensemble prediction. The NLLV method performs better than the BV and SV methods in ensemble forecast experiments including a simple Lorenz model, barotropic model, and baroclinic model. The forecast skill of the NLLV method is close to that of the EnKF, but the computational cost is just 1/3 as much as the latter. Therefore, the NLLV method has a great advan-tage, and is expected to develop into an effective method for operational application. The NLLV approach mentioned here has only been applied in simple models and demonstrated to be effective for generating ensemble perturbations. It would be worthwhile investigating the performance of NLLVs in more complex models. Besides, the physical explanation of NLLVs is not clear, and further clarification is needed to explain why the application of NLLVs in generating ensemble perturbations can improve the forecast skill. These questions need to be explored to strengthen the understanding of the NLLV method.
5 Summary and outlookThis paper reviews recent progress made at LASG regarding targeted observations, data assimilation, and ensemble prediction, which are three effective strategies to reduce the prediction uncertainties and improve the forecast skill of weather and climate events.
Targeted observation, as a new observational strategy, is an efficient and effective method to optimize the design of observing networks. Identifying the sensitive areas (i.e., the optimal observing locations) is a key part of the targeted observation approach. Among the different methods available to identify the sensitive areas, CNOP overcomes the linear limitations of the LSV method and represents the initial perturbation that exhibits the largest prediction growth at the end time of the forecast period; and the NFSV method has been proposed to reveal the most disturbing tendency errors of predictions. These approaches have been used to identify the sensi-tive areas of targeted observations for ENSO, IOD, and TCs, and demonstrated to be effective. Therefore, target observations will provide guidance for ongoing and planned observational networks.
To assimilate these targeted observations into the initial state of numerical models, DRP-4DVar has been proposed to overcome the challenging problems of using 4DVar in an operational setting. This approach mini-mizes the cost function of 4DVar in the low-dimension sample space and does not require implementation of the adjoint of the tangent linear approximation. Indeed, a case study suggests that the performance of DRP-4DVar is good, and its computational cost is much lower than standard 4DVar.
Considering that a single forecast is simply an esti-mate of the future state of the atmosphere and ocean within a stochastic framework, ensemble prediction is often used to generate probabilistic forecasts of the future state of the system, and the ensemble mean usually reduces the prediction uncertainties of single forecasts. The NLLV method reviewed in the present paper is not only computationally quick and physically and dynamically effective for generating ensemble perturbations, but it also reduces the dependence among perturbations because of the global orthogonality. Therefore, NLLVs may be applicable in generating initial perturbations for ensemble prediction.
Although considerable progress has been made regarding these three strategies, much more work is needed to further improve the forecast skill of weather and climate events. Regarding targeted observations, for ENSO, we should further examine the effects of global warming and its recent hiatus on identifying the sensitive areas of targeted observations; for the IOD, although previous stu-dies have demonstrated encouraging results on the sensi-tive areas, further analysis with hindcast and forecast experiments is needed to verify the credibility; and for TCs, the effect of the ocean on TCs should be paid particular attention, to discuss the role played by oceanic targeted observations in TC predictions, especially in terms of TC intensity. For DRP-4DVar, an improvement of the B matrix can be achieved by including an analog prediction sample of which the corresponding simulated observation increment is highly correlated with the real observation increment. Besides, the NLLV approach mentioned here, whilst demonstrated as effective for generating ensemble perturbations, has only been applied in a low-order model. It would be worthwhile investigating the performance of NLLVs in more complex models. These problems are challenging, but are of great importance for increasing the prediction skill of weather and climate events.
Acknowledgments. We thank Drs. Ruiqiang Ding, Juanjuan Liu, Xiaohao Qin, and Junya Hu for providing material for, and assisting with the writing of, this paper.
| S. D. Aberson ,2010: 10 years of hurricane synoptic surveillance (1997–2006). Mon. Wea. Rev. , 138 , 1536–1549. |
| K. Ashok, S. K. Behera, S. A. Rao, et al ,2007: El Niño Modoki and its possible teleconnection. J. Geophys. Res. , 112 , C11007. |
| C. H. Bishop, Z. Toth ,1999: Ensemble transformation and adaptive observations. J. Atmos. Sci. , 56 , 1748–1765. |
| C. H. Bishop, B. J. Etherton, S. J. Majumdar ,2001: Adaptive sampling with the ensemble transform Kalman filter. Part I: Theoretical aspects. Mon. Wea. Rev. , 129 , 420–436. |
| B. Blanke, J. D. Neelin, D. Gutzler ,1997: Estimating the effect of stochastic wind stress forcing on ENSO irregularity. J. Climate , 10 , 1473–1486. |
| R. Buizza ,1997: Potential forecast skill of ensemble prediction and spread and skill distributions of the ECMWF Ensemble Prediction System. Mon. Wea. Rev. , 125 , 99–119. |
| R. Buizza, A. Montani ,1999: Targeting observations using singular vectors. J. Atmos. Sci. , 56 , 2965–2985. |
| Chen Lei, 2015: Similarity of optimally growing initial errors and optimal precursors for ENSO and its application for recognizing sensitive area. Ph. D. dissertation, University of Chinese Academy of Sciences, Beijing. (in Chinese). |
| B. Y. Chen, M. Mu, X. H. Qin ,2013: The impact of assimila-ting dropwindsonde data deployed at different sites on typhoon track forecasts. Mon. Wea. Rev. , 141 , 2669–2682. |
| F. Chevallier, P. Lopez, A. M. Tompkins, et al ,2004: The capa-bility of 4D-Var systems to assimilate cloud-affected satellite infrared radiances. Quart. J. Roy. Meteor. Soc. , 130 , 917–932. |
| K. H. Chou, C. C. Wu, P. H. Lin, et al ,2011: The impact of dropwindsonde observations on typhoon track forecasts in DOTSTAR and T-PARC. Mon. Wea. Rev. , 139 , 1728–1743. |
| L. Descamps, O. Talagr ,2007: On some aspects of the definition of initial conditions for ensemble prediction. Mon. Wea. Rev. , 135 , 3260–3272. |
| W. S. Duan, X. C. Liu, K. Y. Zhu, et al ,2009: Exploring the initial errors that cause a significant “spring predictability barrier” for El Niño events. J. Geophys. Res. , 114 , C04022. |
| W. S. Duan, R. Zhang ,2010: Is model parameter error related to a significant spring predictability barrier for El Niño events? Results from a theoretical model. Adv. Atmos. Sci. , 27 , 1003–1013. |
| W. S. Duan, F. F. Zhou ,2013: Non-linear forcing singular vector of a two-dimensional quasi-geostrophic model. Tellus A , 65 , 18452. |
| W. S. Duan, B. Tian, H. Xu ,2014: Simulations of two types of El Niño events by an optimal forcing vector approach. Climate Dyn. , 43 , 1677–1692. |
| W. S. Duan, P. Zhao ,2015: Revealing the most disturbing tendency error of Zebiak–Cane model associated with El Niño predictions by nonlinear forcing singular vector approach. Climate Dyn. , 44 , 2351–2367. |
| W. S. Duan, J. Y. Hu ,2016: The initial errors that induce a significant “spring predictability barrier” for El Niño events and their implications for target observation: Results from an earth system model. Climate Dyn. , 46 , 3599–3615. DOI:10.1007/s00382-015-2789-5 |
| G. Evensen ,1994: Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. , 99 , 10143–10162. |
| R. Feng, W. S. Duan ,2014: The spatial patterns of initial errors related to the “winter predictability barrier” of the Indian Ocean dipole. Atmos. Oceanic Sci. Lett. , 7 , 406–410. DOI:10.3878/jissn.1674-2834.14.0018 |
| J. Feng, R. Q. Ding, D. Q. Liu, et al ,2014: The application of nonlinear local Lyapunov vectors to ensemble predictions in Lorenz systems. J. Atmos. Sci. , 71 , 3554–3567. |
| R. Feng, W. S. Duan, M. Mu ,2016: Estimating observing locations for advancing beyond the winter predictability barrier of Indian Ocean dipole event predictions. Climate Dyn. . DOI:10.1007/s00382-016-3134-3 |
| J. N. Thépaut Gauthier ,2001: Impact of the digital filter as a weak constraint in the preoperational 4DVAR assimilation system of Météo-France. Mon. Wea. Rev. , 129 , 2089–2102. |
| P. Gauthier, M. Tanguay, S. Laroche, et al ,2007: Extension of 3DVAR to 4DVAR: Implementation of 4DVAR at the me-teorological service of Canada. Mon. Wea. Rev. , 135 , 2339–2353. |
| Y. G. Ham, J. S. Kug ,2012: How well do current climate models simulate two types of El Niño?. Climate Dyn. , 39 , 383–398. |
| T. M. Hamill, C. Snyder ,2002: Using improved background-error covariances from an ensemble Kalman filter for adap-tive observations. Mon. Wea. Rev. , 130 , 1552–1572. |
| Y. Honda, M. Nishijima, K. Koizumi, et al ,2005: A pre-operational variational data assimilation system for a non-hydrostatic model at the Japan Meteorological Agency: Formulation and preliminary results. Quart. J. Roy. Meteor. Soc. , 131 , 3465–3475. |
| P. L. Houtekamer, J. Derome ,1995: Methods for ensemble prediction. Mon. Wea. Rev. , 123 , 2181–2196. |
| International CLIVAR Project Office, 2006: Report of the Third Meeting of the CLIVAR-GOOS Indian Ocean Panel, Honolulu, USA. International CLIVAR Project Office, Southampton, UK, 32 pp. |
| Andersson Järvinen, F. Bouttier H. ,1999: Variational assimilation of time sequences of surface observations with serially correlated errors. Tellus A , 51 , 469–488. |
| H. Y. Kao, J. Y. Yu ,2009: Contrasting eastern-Pacific and central-Pacific types of ENSO. J. Climate , 22 , 615–632. |
| E. Klinker, F. Rabier, G. Kelly, et al ,2000: The ECMWF operational implementation of four-dimensional variational assimilation. III: Experimental results and diagnostics with operational configuration. Quart. J. Roy. Meteor. Soc. , 126 , 1191–1215. |
| K. Kramer, H. A. Dijkstra ,2013: Optimal localized observations for advancing beyond the ENSO predictability barrier. Nonlinear Processes in Geophysics , 20 , 221–230. |
| J. S. Kug, F. F. Jin, S. I. An ,2009: Two types of El Niño events: Cold tongue El Niño and warm pool El Niño. J. Climate , 22 , 1499–1515. |
| M. Latif, D. Anderson, T. Barnett, et al ,1998: A review of the predictability and prediction of ENSO. J. Geophys. Res. , 103 (C7) , 14375–14393. |
| C. S. Liu, Q. N. Xiao, B. Wang ,2008: An ensemble-based four-dimensional variational Data Assimilation Scheme. Part I: Technical formulation and preliminary test. Mon. Wea. Rev. , 136 , 3363–3373. |
| Liu Juanjuan, 2009: A timesaving approach to four-dimensional variational data assimilation and its application in the simulation of rainstorm. Ph. D. dissertation, Beijing, University of Chinese Academy of Sciences. |
| E. N. Lorenz ,1963: Deterministic nonperiodic flow. J. Atmos. Sci. , 20 , 130–141. |
| Masumoto, Y., W. Yu, G. Meyers, et al., 2009: Observing systems in the Indian Ocean.Proceedings of OceanObs'09: Sustained Ocean Observations and Information for Society, ESA Publication, Venice, Italy. |
| M. J. McPhaden, A. J. Busalacchi, R. Cheney, et al ,1998: The tropical ocean–global atmosphere observing system: A de-cade of progress. J. Geophys. Res. , 103 (C7) , 14169–14240. |
| McPhaden, M. J., T. Delcroix, K. Hanawa, et al., 2001: The El Niño/Southern Oscillation (ENSO) observing system.Observing the Ocean in the 21st Century, Koblinsky, C. J., and N. R. Smith, Eds., Australian Bureau of Meteorology, Melbourne, Australia, 231-246. |
| M. J. McPhaden, A. J. Busalacchi, D. L. T. Anderson ,2010: A TOGA retrospective. Oceanography , 23 , 86–103. |
| F. Molteni, T. N. Palmer ,1993: Predictability and finite-time instability of the northern winter circulation. Quart. J. Roy. Meteor. Soc. , 119 , 269–298. |
| F. Molteni, R. Buizza, T. N. Palmer, et al ,1996: The new ECMWF ensemble prediction system: Methodology and validation. Quart. J. Roy. Meteor. Soc. , 122 , 73–119. |
| R. E. Morss, D. S. Battisti ,2004a: Evaluating observing requirements for ENSO prediction: Experiments with an intermediate coupled model. J. Climate , 17 , 3057–3073. |
| R. E. Morss, D. S. Battisti ,2004b: Designing efficient observing networks for ENSO prediction. J. Climate , 17 , 3074–3089. |
| M. Mu, W. S. Duan, J. C. Wang ,2002: The predictability problems in numerical weather and climate prediction. Adv. Atmos. Sci. , 19 , 191–204. |
| M. Mu, W. S. Duan, B. Wang ,2003: Conditional nonlinear optimal perturbation and its applications. Nonlinear Process in Geophysics , 10 , 493–501. |
| M. Mu, W. S. Duan, B. Wang ,2007: Season-dependent dynamics of nonlinear optimal error growth and El Niño–Southern Oscillation predictability in a theoretical model. J. Geophys. Res. , 112 (D10) , D10113. |
| M. Mu ,2013: Methods, current status, and prospect of targeted observation. Sci. China (Ser. D) , 56 , 1997–2005. |
| M. Mu, Y. S. Yu, H. Xu, et al ,2014b: Similarities between optimal precursors for ENSO events and optimally growing initial errors in El Niño predictions. Theor. Appl. Climatol. , 115 , 461–469. DOI:10.1007/s00704-013-0909-x |
| M. Mu, W. S. Duan, D. K. Chen, et al ,2015: Target observations for improving initialization of high-impact ocean–atmospheric environmental events forecasting. National Science Review , 2 , 226–236. |
| T. N. Palmer, R. Gelaro, J. Barkmeijer, et al ,1998: Singular vectors, metrics, and adaptive observations. J. Atmos. Sci. , 55 , 633–653. |
| X. H. Qin, M. Mu ,2012: Influence of conditional nonlinear optimal perturbations sensitivity on typhoon track forecasts. Quart. J. Roy. Meteor. Soc. , 138 , 185–197. |
| C. Qiu, J. Chou ,2006: Four-dimensional data assimilation method based on SVD: Theoretical aspect. Theor. Appl. Climatol. , 83 , 51–57. |
| F. Rawlins, S. P. Ballard, K. J. Bovis, et al ,2007: The Met Office global four-dimensional variational data assimilation scheme. Quart. J. Roy. Meteor. Soc. , 133 , 347–362. |
| C. Snyder ,1996: Summary of an informal workshop on adaptive observations and FASTEX. Bull. Amer. Meteor. Soc. , 77 , 953–961. |
| J. Z. Sun, Y. Zhang ,2008: Analysis and prediction of a squall line observed during IHOP using multiple WSR-88D observations. Mon. Wea. Rev. , 136 , 2364–2388. |
| B. Tian, W. S. Duan ,2016: Comparison of the initial errors most likely to cause a spring predictability barrier for two types of El Niño events. Climate Dyn. , 47 , 779–792. DOI:10.1007/s00382-015-2870-0 |
| X. J. Tian, Z. H. Xie, A. G. Dai ,2008: An ensemble-based explicit four-dimensional variational assimilation method. J. Geophys. Res. , 113 (D21) . DOI:10.1029/2008JD010358 |
| Z. Toth, E. Kalnay ,1993: Ensemble forecasting at NMC: The generation of perturbations. Bull. Amer. Meteor. Soc. , 74 , 2317–2330. |
| Z. Toth, E. Kalnay ,1997: Ensemble forecasting at NCEP and the breeding method. Mon. Wea. Rev. , 125 , 3297–3319. |
| B. Wang, J. J. Liu, S. D. Wang, et al ,2010: An economical approach to four-dimensional variational data assimilation. Adv. Atmos. Sci. , 27 , 715–727. DOI:10.1007/s00376-009-9122-3 |
| M. Weissmann, F. Harnisch, C. C. Wu, et al ,2011: The influence of assimilating dropsonde data on typhoon track and midlatitude forecasts. Mon. Wea. Rev. , 139 , 908–920. |
| Williams, P. D., 2005: Modelling climate change: the role of unresolved processes.Philosophical Transactions of the Royal Society A:Mathematical,Physical and Engineering Sciences, 363, 2931-2946. |
| Q. N. Xiao, X. L. Zou, B. Wang ,2000: Initialization and simu-lation of a landfalling hurricane using a variational bogus data assimilation scheme. Mon. Wea. Rev. , 128 , 2252–2269. |
| Y. S. Yu, W. S. Duan, H. Xu, et al ,2009: Dynamics of nonlinear error growth and season-dependent predictability of El Niño events in the Zebiak–Cane model. Quart. J. Roy. Meteor. Soc. , 135 , 2146–2160. |
| Y. S. Yu, M. Mu, W. S. Duan ,2012: Does model parameter error cause a significant “Spring Predictability Barrier” for El Niño events in the Zebiak–Cane Model?. J. Climate , 25 , 1263–1277. |
| Zhang Jing, 2015: Sensitive areas for targeted observation associated with ENSO Predictions and its application in the predictions of the tropical pacific climate variability. Ph. D. dissertation, Nanjing University of Information and Science Technology, Nanjing. (in Chinese). |
| R. H. Zhang, S. E. Zebiak, R. Kleeman, et al ,2003: A new intermediate coupled model for El Niño simulation and prediction. Geophys. Res. Lett. , 30 . DOI:10.1029/2003GL018010 |
| L. Zhang, Y. Q. Ni ,2005: Four-dimensional variational data assimilation experiments for a heavy rain case during the 2002 IOP in China. Adv. Atmos. Sci. , 22 , 300–312. |
| J. Zhang, W. S. Duan, X. F. Zhi ,2015: Using CMIP5 model outputs to investigate the initial errors that cause the “spring predictability barrier” for El Niño events. Sci. China (Ser. D) , 58 , 686–696. |
| Y. Zhao, B. Wang, Z. Z. Ji, et al ,2005: Improved track forecasting of a typhoon reaching landfall from four-dimensional variational data assimilation of AMSU-A retrieved data. J. Geophys. Res. , 110 (D14) , D14101. DOI:10.1029/2004JD005267 |
| X. Zou, Y. H. Kuo ,1996: Rainfall assimilation through an optimal control of initial and boundary conditions in a limited-area mesoscale model. Mon. Wea. Rev. , 124 , 2859–2882. |
| W. S. Duan, P. Zhao, J. Y. Hu ,2016: The role of nonlinear forcing singular vector tendency error in causing the “Spring Predictability Barrier” for ENSO. J. Meteor. Res. , 30 , 853–866. DOI:10.1007/s13351-016-6011-4 |
| M. Mu, Q. Wang, W. S. Duan ,2014a: Application of conditional nonlinear optimal perturbation to targeted observation studies of the atmosphere and ocean. J. Meteor. Res. , 28 , 923–933. DOI:10.1007/s13351-014-4057-8 |
 2017, Vol. 31
2017, Vol. 31


