中国气象学会主办。
文章信息
- 冯业荣, 薛纪善, 李梦婕, 戴光丰. 2021.
- FENG Yerong, XUE Jishan, LI Mengjie, DAI Guangfeng. 2021.
- 基于扰动模式的四维变分资料同化系统框架的设计完善和数值试验
- The framework of the 4DVar data assimilation system based on perturbation forecast model:Development and numerical experiment
- 气象学报, 79(6): 902-920.
- Acta Meteorologica Sinica, 79(6): 902-920.
- http://dx.doi.org/10.11676/qxxb2021.061
文章历史
-
2021-02-10 收稿
2021-08-16 改回
初值是数值天气预报的关键科学技术问题。已有研究和业务实践表明,在变分资料同化方法中由于考虑不同时刻观测资料的影响并受预报模式的约束,四维变分资料同化(4DVar)相比于三维变分资料同化(3DVar)可为数值模式提供更好的初值,进而改善模式预报效果(Lorenc,et al,2005;Rawlins,et al,2007)。故此,欧洲中期天气预报中心(ECMWF)等国际上的先进数值预报中心从20世纪末开始相继采用4DVar作为基本的业务同化系统(Courtier,et al,1994;Gauthier,et al,2007;Rawlins,et al,2007)。尤其是ECMWF,1996年3DVar投入使用(Courtier,et al,1998),但很快便于1997年由4DVar取代(Rabier,et al,2000)。4DVar和卫星观测资料的结合,提高了其全球模式的预报质量(McNally,et al,2006;Bauer,et al,2010)。尤其对南半球,尽管直接观测资料不足,但ECMWF全球模式的可用预报时效在2000年前后有较大提高,4DVar与卫星观测资料同化应用功不可没(Bauer,et al,2015)。经过多年努力,中国气象局的全球四维变分同化系统(GRAPES-4DVar,现为CMA-GFS 4DVar)也于2018年7月投入业务运行(Zhang,et al,2019),使中国自主数值预报发展的步伐又迈出了关键的一步。
迄今为止,4DVar较多的是与全球模式结合。对于区域模式而言,初值或直接取自全球模式降尺度分析场,或通过混合使用区域3DVar与其他方法(Jones,et al,1997;Dixon,et al,2009;Bloom,et al,1996)得到,且同化所用的资料以单时刻观测为主。为了科学利用本地区多时刻稠密观测资料,改善区域模式的初值质量,提高模式预报准确度,建立区域4DVar同化系统是一个较好的选择。中国由于区域GRAPES模式已被广泛用于业务,开发与GRAPES模式相配套的区域4DVar系统更具有现实意义。
开发4DVar最复杂与最繁重的工作在于开发切线性模式及其伴随模式。切线性模式通常要求扰动趋于比较小时与非线性模式的偏差保持一致,它的程序可以根据非线性模式代码按一定规则直接编程,这种做法使切线性模式和伴随模式的建立成为近似机械的操作,尽管工作量大,难度一般不大,但后续系统维护和升级比较困难。而且由于非线性模式中存在各种复杂物理开关,连续的切线性模式其实并不存在,对物理过程处理不好会导致极小化迭代失败;另一种做法是不依赖非线性模式代码,而是直接建立扰动模式方程组并通过简化的线性物理过程使扰动模式保持较好的线性特征,以利于极小化计算平稳进行。这种所谓扰动模式并不追求在扰动为0的极限情况下无限逼近切线性模式,仅要求一定随机分布的扰动期望值的演变与扰动在切线性模式中的演变一致。为此需要从非线性模式控制方程组出发,推导一套线性扰动方程组(包括线性物理过程),进而开发扰动预报模式及其伴随模式,如英国气象局的4DVar系统便是基于扰动模式建立的(Rawlins,et al,2007)。
冯业荣等(2020)在GRAPES模式原始方程组基础上建立了线性扰动预报模式(GRAPES_PF),试验表明该扰动模式是GRAPES切线性模式的一个合理近似。本研究是上述工作的继续和深入,即通过GRAPES_PF搭建适应GRAPES区域模式的4DVar系统框架,为最终建立GRAPES区域四维变分同化业务系统奠定基础。
2 扰动4DVar框架设计 2.1 控制变量的设置完善四维变分同化问题最终归结为求以下目标函数的极小值
| $ J\left({\boldsymbol w}\right)=\frac{\,1\,}{\,2\,}{{\boldsymbol w}}^{\mathrm{T}}{\boldsymbol w}+\frac{\,1\,}{\,2\,}\sum _{i}{{{\boldsymbol R}}_i}^{\mathrm{T}}{{\boldsymbol O}}^{-1}{{\boldsymbol R}}_{i} $ | (1) |
式中,w为控制变量,定义在模式空间;
原GRAPES 3DVar的平衡方程是定义在气压坐标上的,先在等压面上求解平衡方程得到
| $ {c}_{p}\overline{\theta }{\nabla }^{2}{\varPi }^{*}=-\beta u+f\zeta $ | (2) |
式中,相当无量纲气压
| $ u=-\frac{\partial \psi }{a\partial \varphi }+\frac{\partial \chi }{a\mathrm{c}\mathrm{o}\mathrm{s}\varphi \partial \lambda } $ |
| $ v=\frac{\partial \psi }{a\mathrm{c}\mathrm{o}\mathrm{s}\varphi \partial \lambda }+\frac{\partial \chi }{a\partial \varphi } $ |
于是水平涡度
| $ \zeta ={\nabla }^{2}\psi $ |
其中拉普拉斯算子为
| $ {\nabla }^{2}=\frac{1}{{a}^{2}{\mathrm{c}\mathrm{o}\mathrm{s}}^{2}\varphi }\frac{{\partial }^{2}}{\partial {\lambda }^{2}}+\frac{1}{{a}^{2}\mathrm{c}\mathrm{o}\mathrm{s}\varphi }\frac{\partial }{\partial \varphi }\left(\mathrm{c}\mathrm{o}\mathrm{s}\varphi \frac{\partial }{\partial \varphi }\right) $ |
进一步假设平衡运动为水平无辐散的涡旋运动,于是式(2)可写成
| $ {c}_{p}{\overline\theta }{\nabla }^{2}{\varPi }^{*}=\beta \frac{\partial \psi }{a\partial \varphi }+f{\nabla }^{2}\psi $ | (3) |
式(3)已用无量纲气压Π代替原来使用的位势高度(
| $ {c}_{p}\overline{\theta }{\nabla }^{2}{\varPi {'}_{b}}=\beta \frac{\partial \psi {'}}{a\partial \varphi }+f{\nabla }^{2}\psi {'} $ | (4) |
式中,上标“
原GRAPES 3DVar只使用4个控制变量:流函数
切线性模式采用扰动预报模式GRAPES_PF(冯业荣等,2020)代替。扰动模式的积分过程可以表示为
| $ {{\boldsymbol M}}_{0\to i}{\boldsymbol P}{\boldsymbol U}{\boldsymbol w}={{\boldsymbol M}}_{i-1\to i}{{\boldsymbol M}}_{i-2\to i-1}\cdots {{\boldsymbol M}}_{1\to 2}{\boldsymbol {M}}_{0\to 1}{\boldsymbol P}{\boldsymbol U}{\boldsymbol w} $ |
式中,
目标函数极小化过程是一个迭代过程,采用L-BFGS拟牛顿法(Liu,et al,1989)求解。初始控制矢量一般取
| $ \nabla J={\boldsymbol w}+{{\boldsymbol U}}^{\mathrm{T}}{{\boldsymbol P}}^{\mathrm{T}}\sum _{i}{{\boldsymbol M}}_{0\to i}^{\mathrm{T}}{{\boldsymbol H}}^{\mathrm{T}}{{\boldsymbol O}}^{-1}{{\boldsymbol R}}_{i} $ | (5) |
式(5)中需要对扰动模式做转置运算(
| $ {{\boldsymbol M}}_{0\to i}^{\mathrm{T}}={{\boldsymbol M}}_{0\to 1}^{\mathrm{T}}{{\boldsymbol M}}_{1\to 2}^{\mathrm{T}}\cdots {{\boldsymbol M}}_{i-2\to i-1}^{\mathrm{T}}{{\boldsymbol M}}_{i-1\to i}^{\mathrm{T}} $ |
与多数4DVar相似,采用“增量分析”的策略,因此计算涉及两个循环(外循环和内循环)。外循环过程中高分辨非线性模式从分析时刻开始连续积分到同化窗的每一个观测时刻,所得到的预报量用于计算新息向量。内循环在极小化过程内部发生,在搜索目标函数的下降点过程中需要反复计算梯度
扰动模式的计算最终体现为通过广义共轭余差法(GCR)迭代求解扰动亥姆霍兹方程(冯业荣等,2020)。由于GCR迭代是否终止由收敛判据决定,事先并不能确定迭代次数,故无法根据一般伴随规则直接编写伴随程序。实际上扰动亥姆霍兹方程的伴随方程也是亥姆霍兹方程,其系数矩阵不过是原来扰动亥姆霍兹方程系数矩阵的转置。因此,文中仍利用GCR方法迭代求解亥姆霍兹伴随方程,只需将系数矩阵“行、列”位置互换即可,当然系数矩阵的“行、列”在亥姆霍兹求解程序中并不显现,编程者须将下标变量的对应关系弄清楚。
编写伴随模式需要开展伴随检验,若设扰动模式和伴随模式的初值分别为
| $ \Big\langle{\mathrm{d}{{\boldsymbol x}}_{0}\text{,}{{\boldsymbol M}}_{0\to i}^{\mathrm{T}}\mathrm{d}{{{\boldsymbol x}}_{i}}^{*}}\Big\rangle=\Big\langle{{{\boldsymbol M}}_{0\to i}\mathrm{d}{{\boldsymbol x}}_{0}\text{,}\mathrm{d}{{{\boldsymbol x}}_{i}}^{*}}\Big\rangle $ | (6) |
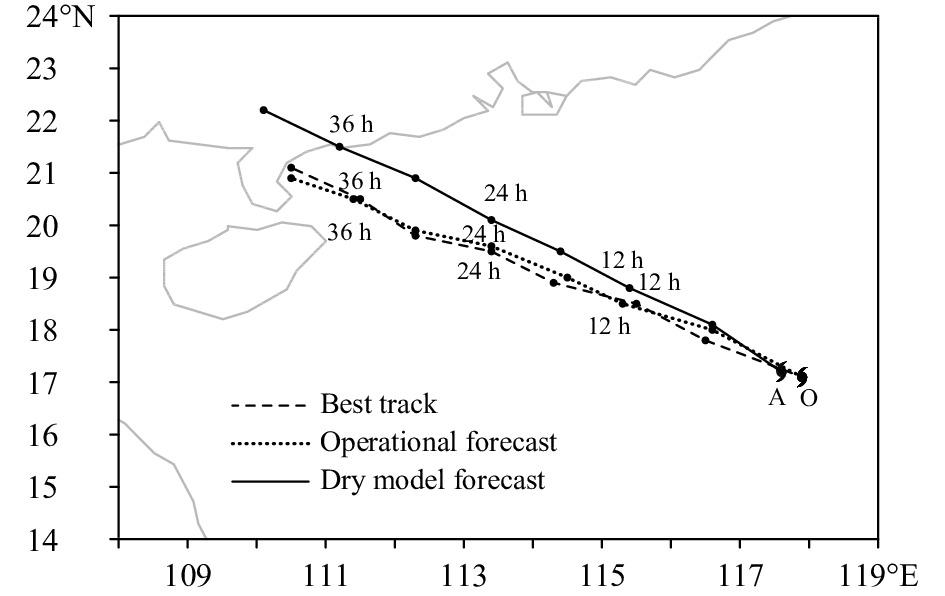
为了开展同化试验,利用GRAPES模式模拟天气“实况”,借此形成几组人造 “探空”观测数据。所选个例是2015年南海台风“彩虹”。“彩虹”起源于菲律宾吕宋岛东部,2015年10月2日移入中国南海,随后快速加强并向西北方向移动,4日06时10分(世界协调时,下同)以强台风级别在湛江市登陆。“彩虹”影响期间,华南区域气象中心的GRAPES台风业务模式(现为CMA-TRAMS)曾于2015年10月2日12时准确预报了“彩虹”的移动和登陆,预报路径几乎与实况重合(图1)。鉴于当前扰动4DVar动力框架尚未包括物理过程,因此,文中没有选择包含全套物理过程且预报效果较好的业务模式作为4DVar的非线性模式,仅对GRAPES非线性模式进行干模式积分,即关闭了所有物理选项(辐射、微物理、边界层和积云对流等)。模拟范围(12°—24°N,105°—123°E),水平分辨率0.12°,模式垂直67层,模式顶高30 km。取ECMWF全球预报模式IFS资料作初边值,以2日12时为模式初始时刻,积分42 h。图1可见,与湿模式(业务模式)相比,干模式预报的登陆位置偏东,登陆时间早6 h,但仍可报出“彩虹”向西北方向移动的趋势,因此将此干模式积分结果作为理想 “真实”大气,既可对应现有扰动模式框架,又不失去“彩虹”运动的基本特征。需要指出,图1中ECMWF分析场的台风中心位置(A)比实际位置(O)偏西32.6 km,文中做干模式积分时未对初始场台风中心进行重定位。
|
| 图 1 台风“彩虹”的观测和预报路径:实况 (虚线)、业务模式 (点线) 和干模式 (实线),干模式台风初始位置 (A)位于台风实际位置 (O) 偏西32.6 km Fig. 1 The observed and forecasted tracks of typhoon Mujigae:best track (dashed),simulations of operational model (dotted) and dry model (solid),symbol A indicates Mujigae's initial position in the dry model,which is 32.6 km west of the observed position (O) |
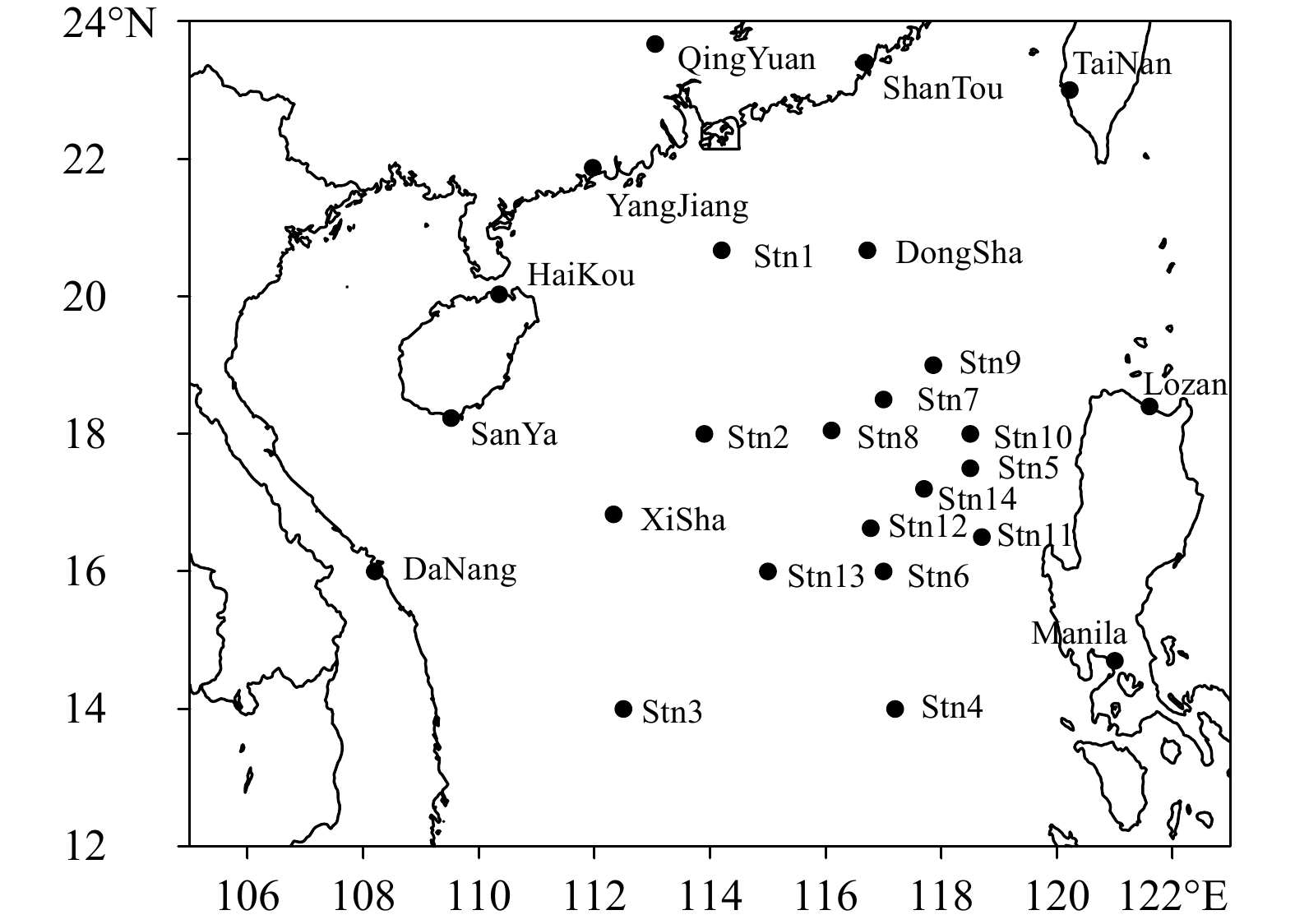
在中国南海及其周边放置25个人造“探空”观测站,间距100—300 km不等(图2)。为更好描述台风中心特征,有意在“彩虹”中心附近使探空站分布密一些(间距80—100 km)。人为构造了间隔3 h的3组“探空”观测数据,即将前面干模式的初始场(ECMWF的2日12时分析场)和预报场(15 和18时)插值到每个“探空”站的基本等压面上,形成人造“探空”观测数据。要素包括气压(p)、纬向风(u)、经向风(v)、位势高度(
|
| 图 2 25个人造“探空”站点分布 Fig. 2 The layout of the 25 pseudo radiosonde stations |
为评估4DVar效果,人为制造一个有误差的背景场。利用Kurihara等(1993)提出的方法将ECMWF的2日12时分析场(图3a)进行涡旋分离和重定位,即以不同波长在水平面上连续多次滤波,得到一个平滑场,然后通过柱状滤波器,从“真实”场分离出台风涡旋,将分离出来的台风涡旋向东北方向移位约230 km,同时将台风涡旋的

|
| 图 3 2015年10月2日12 (a、b) 和18 (c、d) 时850 hPa位势高度场 (黑色线条,单位:dagpm)、风矢量和风速 (色阶,单位:m/s)(a、c. “真实”大气,b、d. 人为改变的背景场) Fig. 3 Initial fields of 12:00 (a,b) and 18:00 (c,d) UTC 2 October 2015 at 850 hPa geopotential heights (black contour,unit:dagpm), wind vectors and wind speed (shaded,unit:m/s)(a,c. idealized "truth" fields;b,d. artificially changed fields) |
四维变分同化中目标函数
文中将三维变分同化与四维变分同化设计成一体化系统,因而可以很方便地进行3DVar或4DVar试验。利用这一系统做了4个同化试验:2个三维变分(3DVar_1和3DVar_2)、2个四维变分(4DVar_1和4DVar_2)。3DVar_1和3DVar_2 的分析时刻分别为10月2日12 时和18时。4DVar_1和4DVar_2的分析时刻均为10月2日12时,但4DVar_1使用2个时次(12和15时)的观测,4DVar_2使用3个时次(12、15和18时)的观测。尽管4DVar_2分析时刻是12时,但也用到了18时的观测,因此模式有效预报时效是18时以后,故增加分析时刻为10月2日18时的一次三维变分同化试验(3DVar_2),以便公平评估观测资料对于3DVar和4DVar效果的影响。
三维变分极小化迭代的初始值取
| 同化试验 | 目标函数J | 初始w | 资料组数 | 资料时刻 | 分析时刻 | ||
| 初始Js | 结束Je | 减少率%((Je |
|||||
| 3DVar_1 | 375.73 | 95.56 | −74.57 | 取0 | 1 | 12时 | 12时 |
| 3DVar_2 | 417.54 | 160.00 | −61.68 | 取0 | 1 | 18时 | 18时 |
| 4DVar_1 | 281.87 | 86.18 | −69.43 | 取3DVar_1分析值 | 2 | 12、15时 | 12时 |
| 4DVar_2 | 538.66 | 158.38 | −70.60 | 取3DVar_1分析值 | 3 | 12、15、18时 | 12时 |
作为合理选择,4DVar_1和4DVar_2控制变量初始值不取
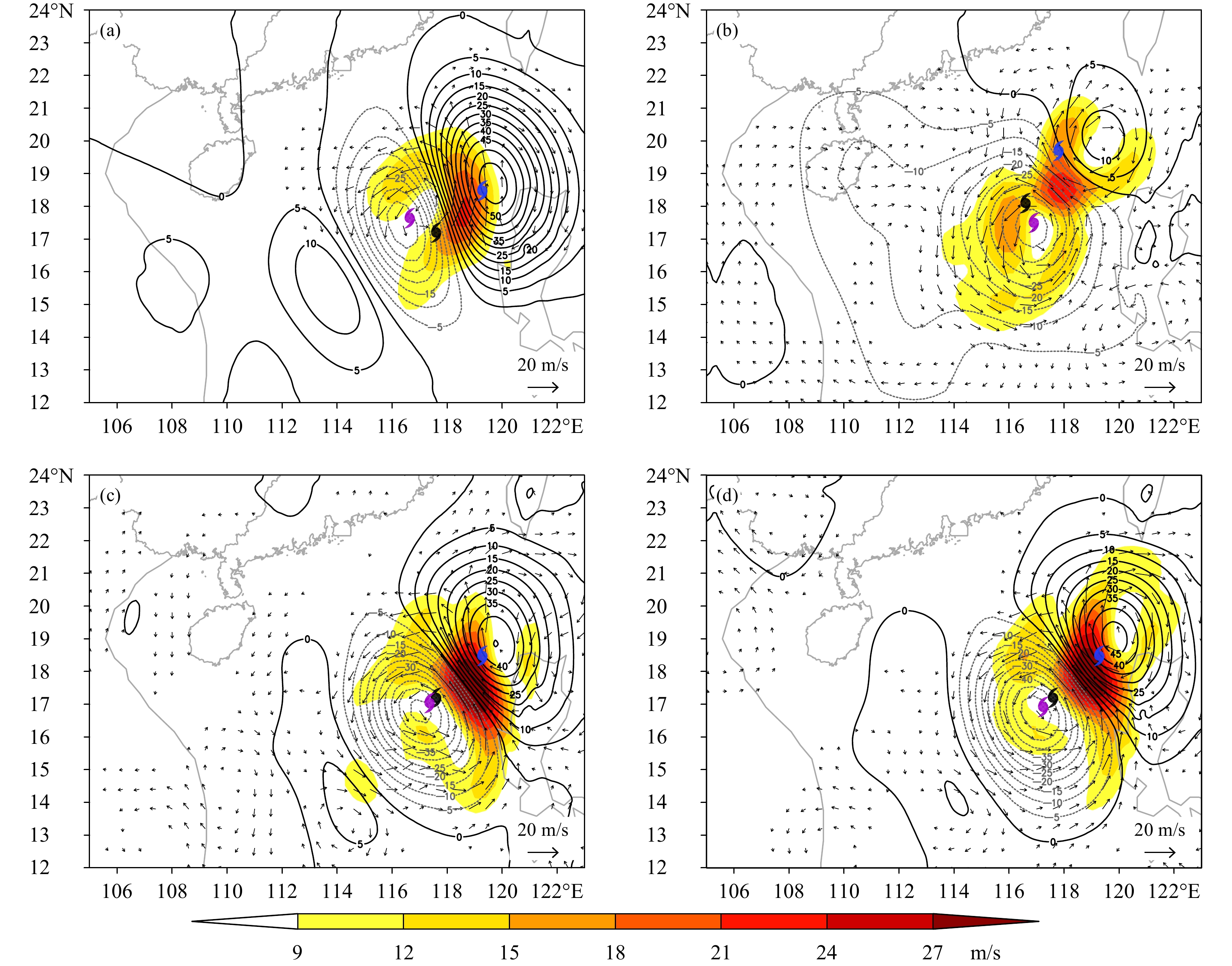
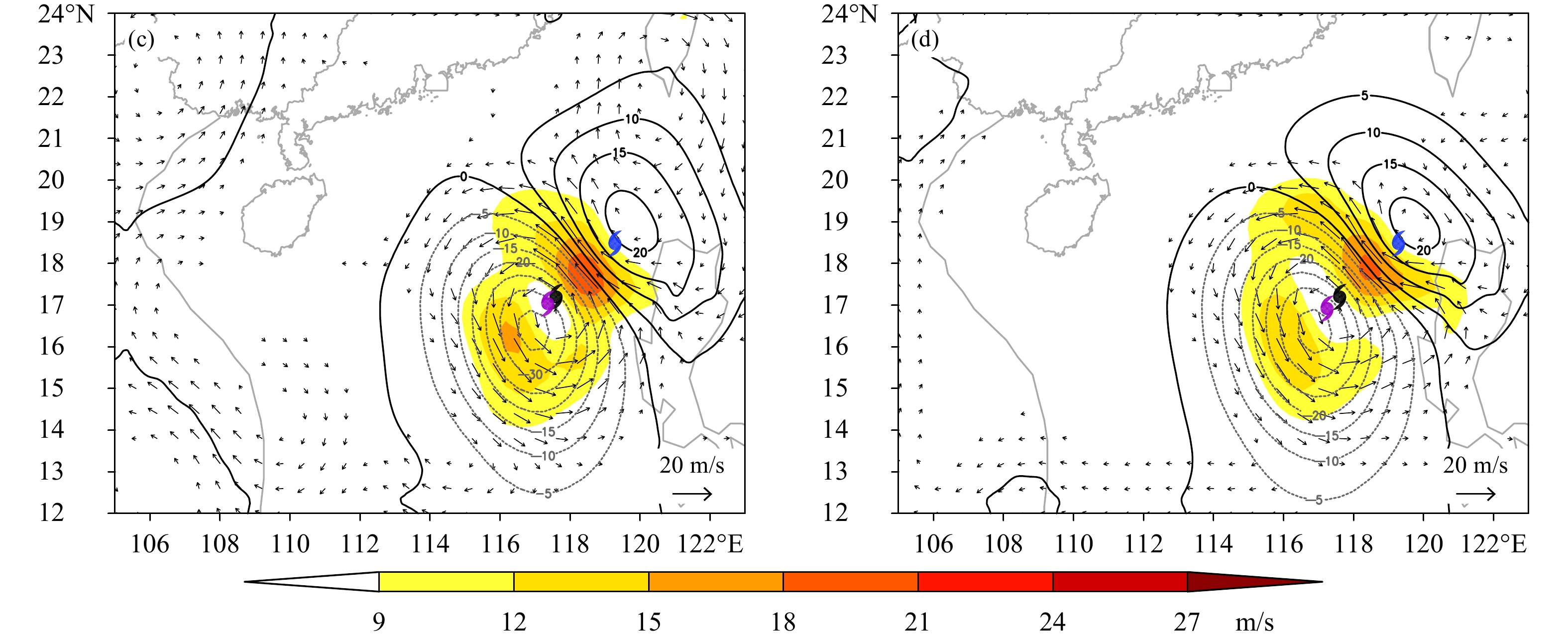
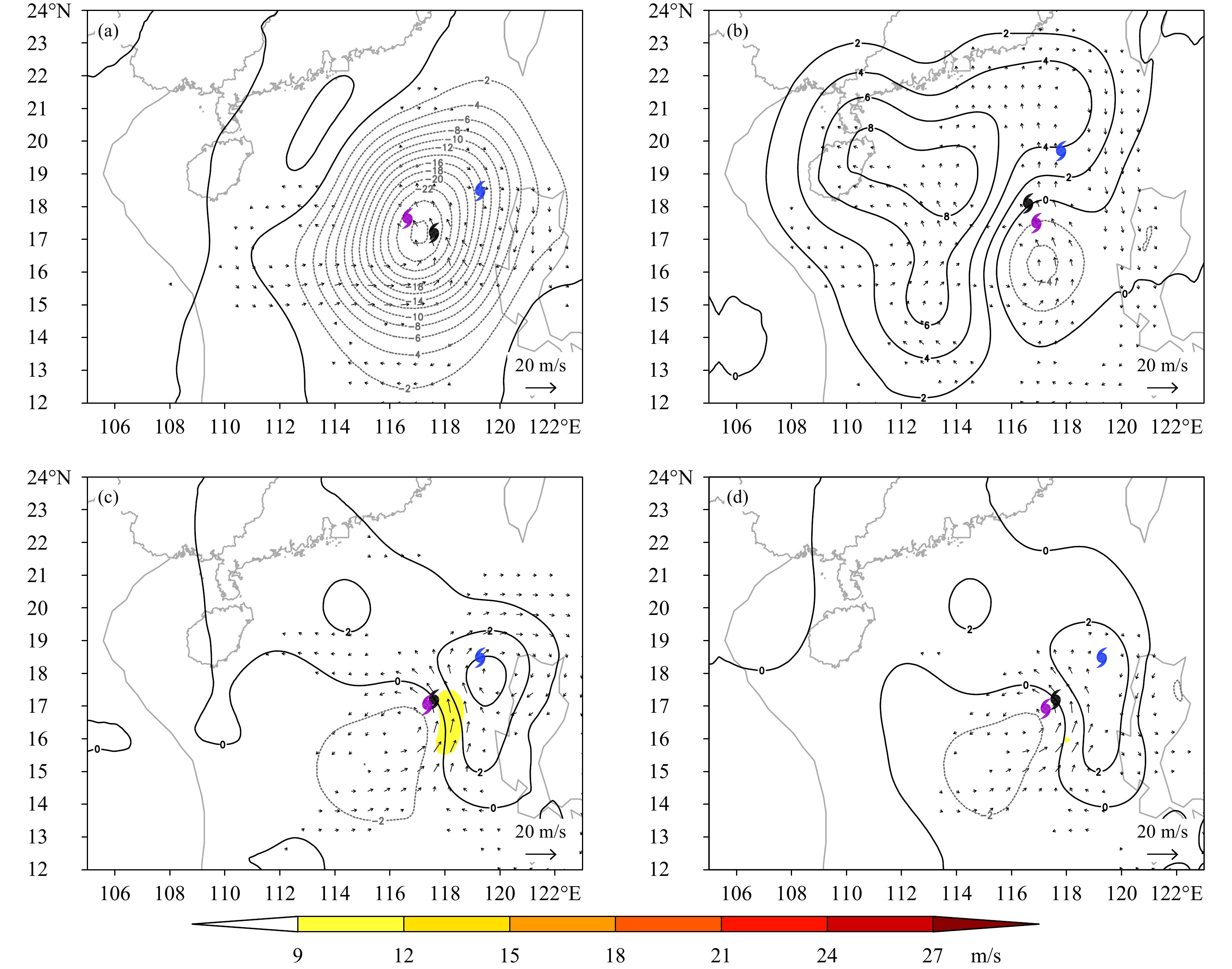
图4—6给出了4个同化试验在850、500和200 hPa的分析增量(风场和位势高度场)。在850 hPa(图4)和500 hPa(图5),4个试验均分析出偶极子型非对称增量场,即涡旋对。尽管背景场台风与“实况”的位置偏离均超过210 km,4个同化试验得到的台风分析位置明显靠近“实况”,其中2个4DVar台风分析位置几乎与“实况”重叠。偶极子型的分析增量恰好反映了同化观测资料之后对背景场的合理修正:背景场台风中心附近升压,升压区配以反气旋性环流增量,而分析场台风中心附近降压,降压区配以气旋性环流增量。500 hPa(图5)的结果与850 hPa大致相同。200 hPa(图6)上的风场和高度场增量很小,2个3DVar试验没有出现偶极子流型,风场和高度场不太配合,但2个4DVar试验仍给出有风压场配合的弱偶极子环流。由于200 hPa台风涡旋较弱,且个别时次部分“观测”资料未通过质量控制(最多时有约24%的气压观测列入黑名单),一定程度对3DVar有影响,故该层的分析有一定不确定性;而4DVar因使用了多时次观测,不同时次的有效观测可通过扰动模式以及伴随模式传播分配,对分析场有整体贡献。由于台风移动主要受大尺度环流引导,偶极子风压场增量不仅有助于对“差”的背景场进行修正,而且涡旋对之间强的通风气流(850 hPa可超过20 m/s)对调整台风引导气流有作用。通风气流的作用可参阅Fiorino等(1989)和Holland(1983)。Mathur(1991)曾将偶极子环流加到飓风涡旋区域,对改进飓风路径预报有帮助。
|
| 图 4 四个试验850 hPa分析增量:风矢量 (箭头)、风速 (色阶) 和位势高度 (等值线,单位:gpm)(a. 3DVar_1,b. 3DVar_2,c. 4DVar_1,d. 4DVar_2;台风记号黑色为“实况”位置,蓝色为背景场位置,紫色为分析场位置) Fig. 4 Analysis increments at 850 hPa of four experments:wind vectors (arrow),wind speed (shaded) and geopotential height (contour,unit:gpm)(a. 3DVar_1,b. 3DVar_2,c. 4DVar_1,d. 4DVar_2;the typhoon symbols in black,blue and purple mark the positions of typhoon center for the "truth",the background and the analysis,respectively) |
|
| 图 5 同图4,但为500 hPa Fig. 5 Same as Fig. 4 but for 500 hPa |
|
| 图 5 Fig. 5 Continued |
|
| 图 6 同图4,但为200 hPa Fig. 6 Same as Fig. 4 but for 200 hPa |
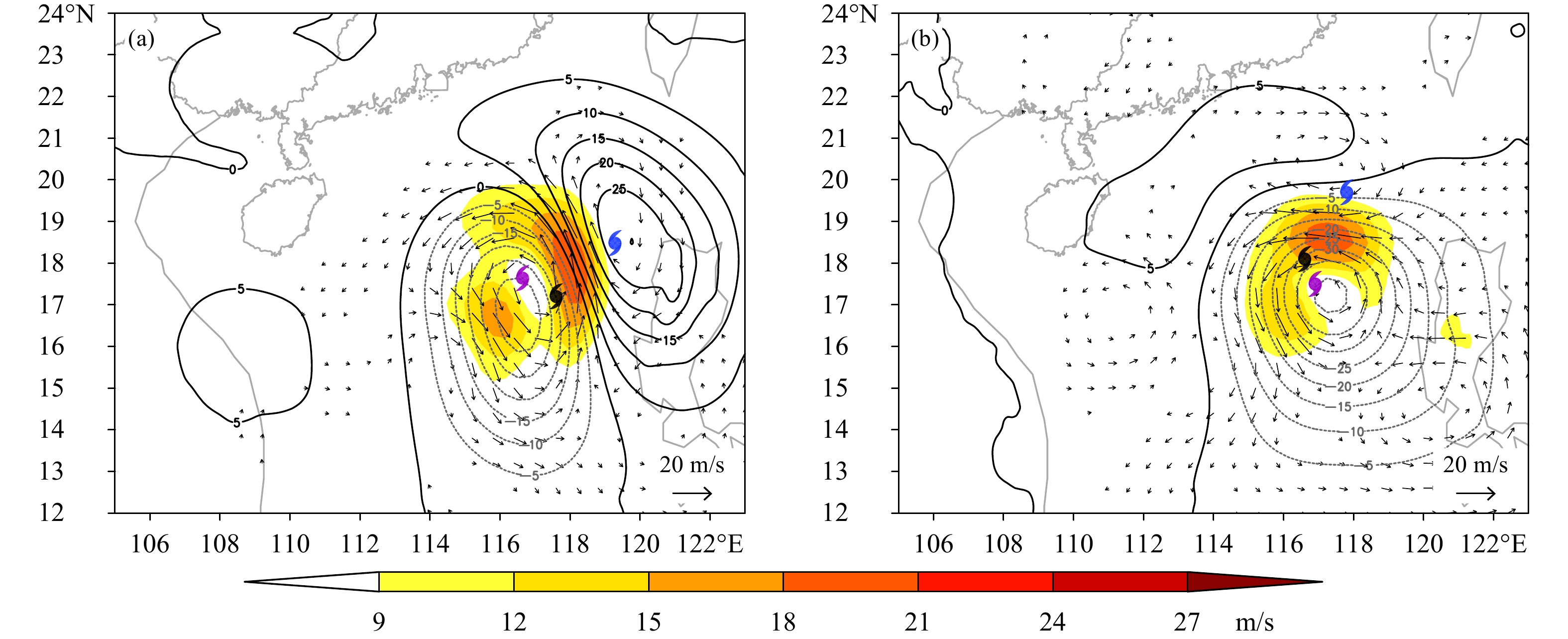
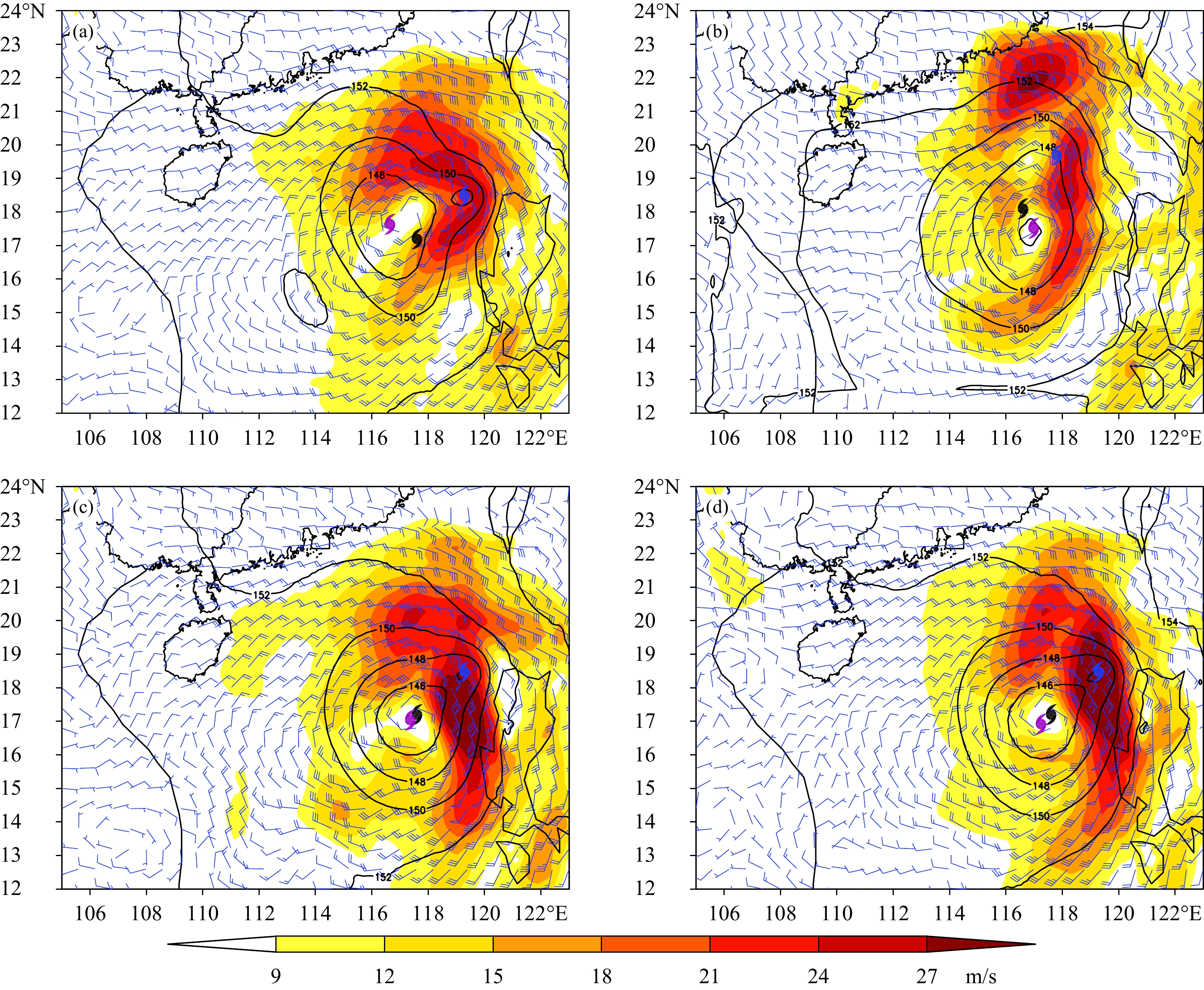
图7给出同化试验得到的850 hPa分析场(风和位势高度)。4个试验的分析场和背景场(图3b和d)相比均得到明显改善,更靠近“真值”(图3a和c),台风涡旋的风场和高度场配置合理,风速不对称分布也与“真值”比较符合。与3DVar相比,4DVar分析场的台风涡旋更对称,146 dagpm闭合线位置和范围更接近实况,台风中心的位置和强度更合理且更接近“实况”。4个试验均显示台风环流东偏北处存在曲率较大的倒槽,与背景场台风中心(蓝色台风记号)对应,反映了分析结果对背景场的敏感性,可通过多次外循环即利用分析场更新背景场积分非线性模式,做多次极小化加以改善。
|
| 图 7 850 hPa风矢、风速 (色阶,单位:m/s) 和位势高度 (等值线,单位:dagpm) 的分析结果 (a. 3DVar_1,b. 3DVar_2,c. 4DVar_1,d. 4DVar_2;台风记号同图4) Fig. 7 Analyses of wind voctor,wind speed (shaded,unit:m/s) and geopotential height (contour,unit:dagpm) at 850 hPa (a. 3DVar_1,b. 3DVar_2,c. 4DVar_1,d. 4DVar_2;the symbols of typhoon are the same as Fig. 4) |
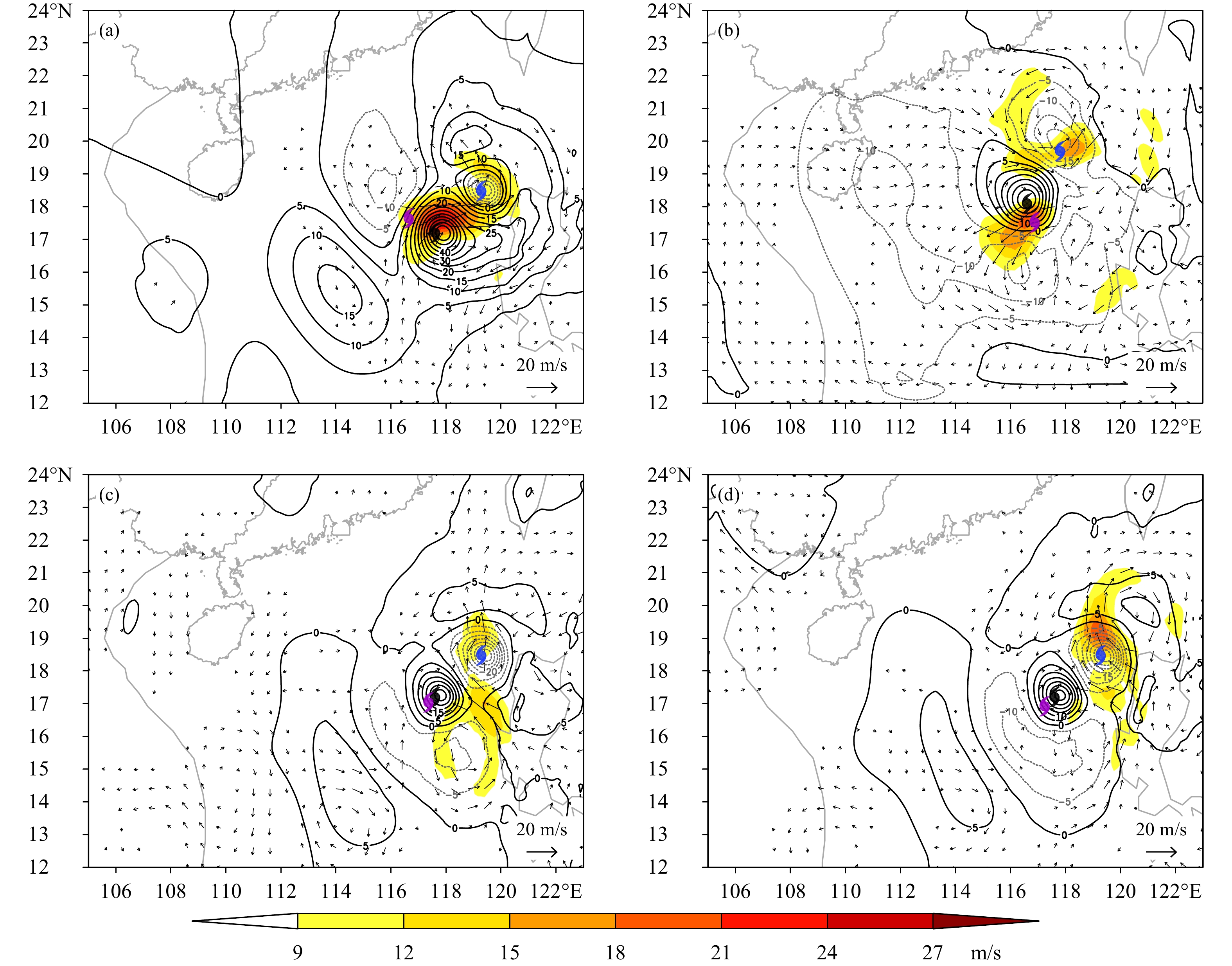
图8是850 hPa分析场与“真值”的差(简称“A−O”)。从位势高度来看,差值大的地方主要集中在背景场台风中心和台风“实况”的位置,背景场台风中心处为负偏差,而台风“实况”位置处为正偏差。由于分析场是背景场和观测的加权平均(权重分别与背景误差协方差和观测误差协方差有关),因而分析场既不完全靠近背景场也不完全靠近观测,而是取两者中间的最佳状态,所以图8出现这样的偏差结构是自然的(也是图7中倒槽出现的原因)。4DVar试验相对于3DVar试验,偏差更加集中于台风中心,反映台风中心气压的影响。3DVar偏差场较发散,从另一个角度反映了4DVar的风压场分析效果优于3DVar。
|
| 图 8 850 hPa 风矢 (箭头)、风速 (色阶) 和位势高度 (等值线,单位:gpm) 分析场与“真值”之差(分析−观测)(a. 3DVar_1,b. 3DVar_2,c. 4DVar_1,d. 4DVar_2;台风记号同图4) Fig. 8 Analysis minus "truth" (A−O) for wind vector (arrow),wind speed (shaded) and geopotential height (contour,unit:gpm) at 850 hPa (a. 3DVar_1,b. 3DVar_2,c. 4DVar_1,d. 4DVar_2;the symbols of typhoon are same as Fig. 4) |
针对2日12时的分析增量(简称“A−B”),在“实况”台风中心(17.2°N,117.6°E)附近分别沿17°N和沿117°E做纬向(图9)和经向(图10)高度剖面。为了和“真值”与背景场的差异(简称“O−B”)进行对比,图9和10中增加了“O−B”的剖面。如果分析合理,“A−B”的结构应与“O−B”相似。

|
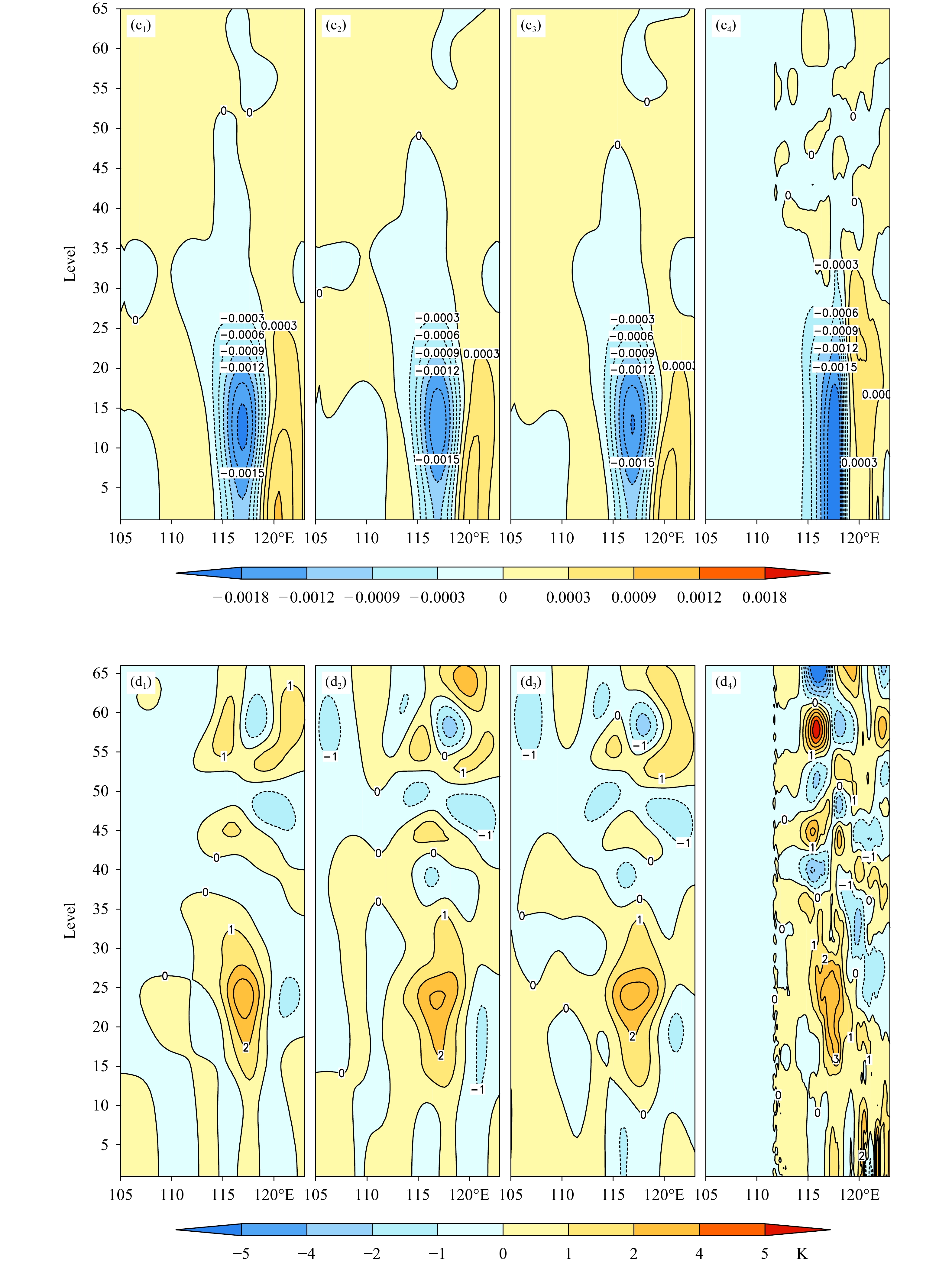
| 图 9 沿17°N穿过台风中心所做的分析增量纬向高度剖面 (a. u,b. v,c. Π,d. θ,e. q;a1—e1. 3DVar_1,a2—e2. 4DVar_1,a3—e3. 4DVar_2,a4—e4. 观测减背景场) Fig. 9 Latitude-height cross sections of analysis increments along 17°N (a. u,b. v,c. Π,d. θ,e. q;a1—e1. 3DVar_1,a2—e2. 4DVar_1,a3—e3. 4DVar_2,a4—e4. O−B) |
|
| 图 9 Fig. 9 Continued |

|
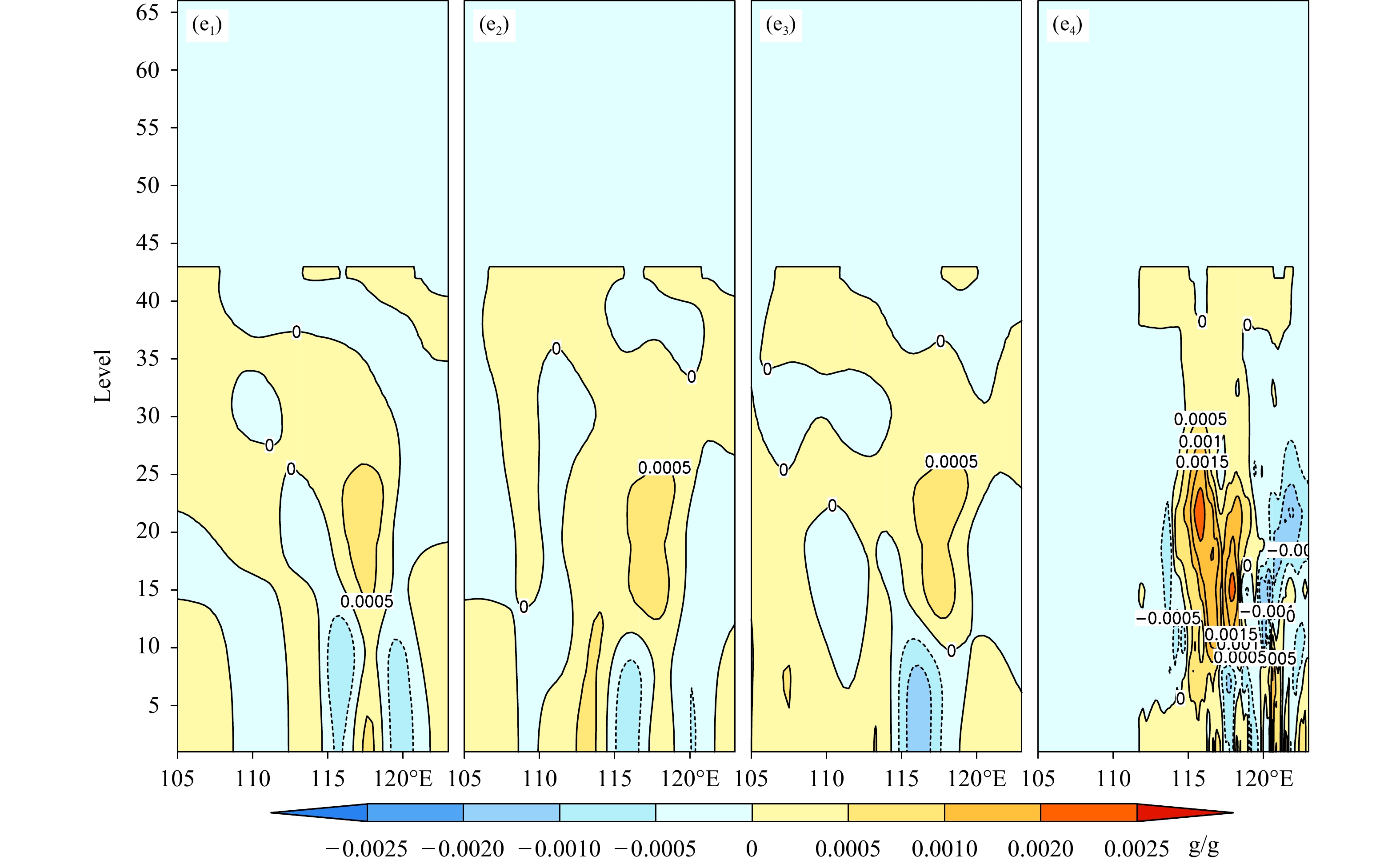
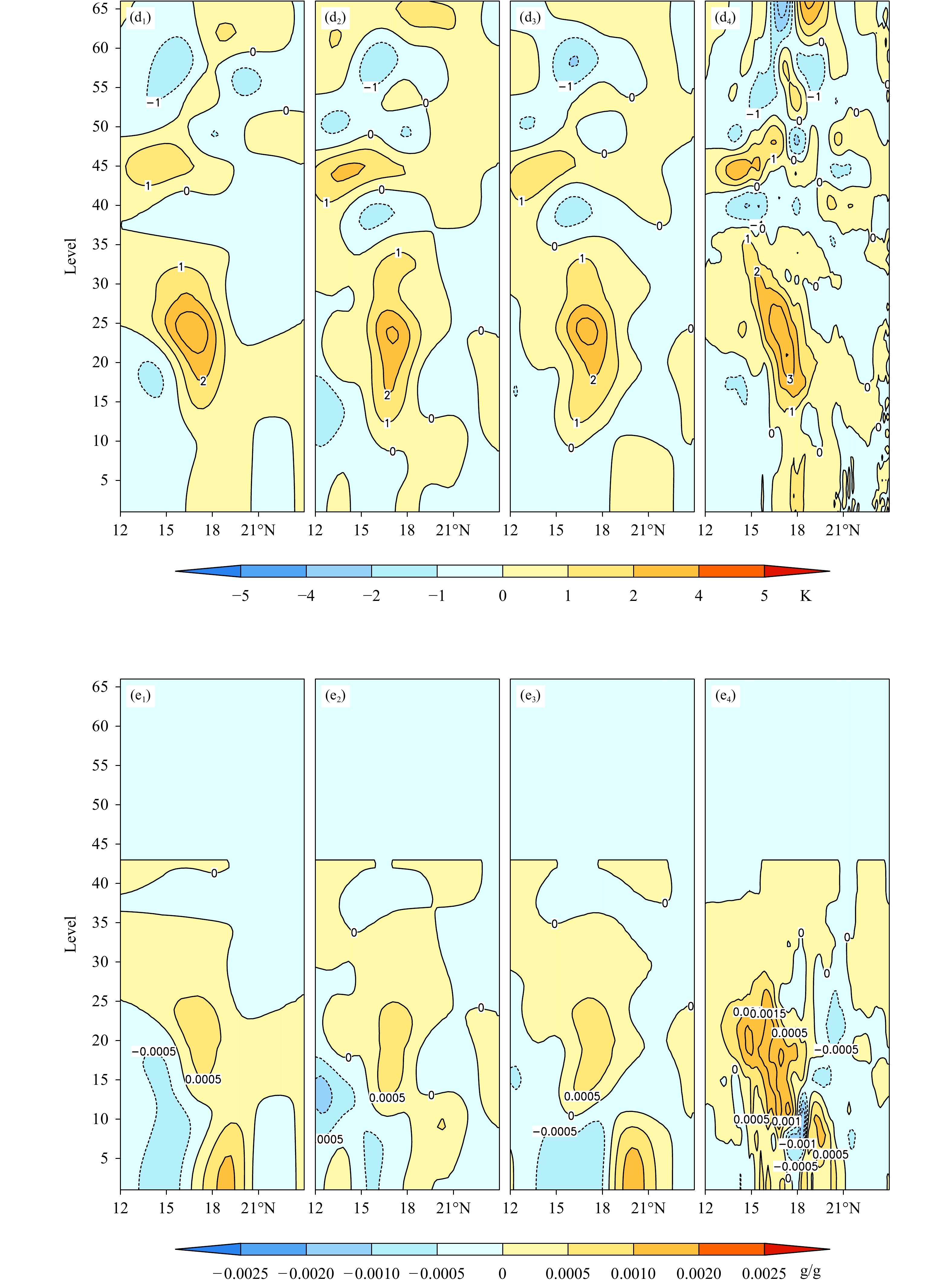
| 图 10 同图9,但沿117°E Fig. 10 Same as Fig. 9 but for along 117°E |
图9中,3DVar_1、4DVar_1和4DVar_2 各变量的分析增量“A−B”的主要分布特征是一致的,且与“O−B”相似。在台风东侧,u风有较强的东风增量,v风有较强的南风增量。在台风西侧,u风有较弱的西风增量,v风有弱的北风增量。对流层中下部,台风中心附近降压,东侧升压。东西向气压增量差与强南风增量相对应。位温(θ)增量在台风中心上空20—25层(约400—300 hPa)有暖心结构,比湿(q)在台风中心附近的15—25层存在弱的增湿。3个试验结果的垂直结构很相似,但也存在细节上的差异。
|
| 图 9 Fig. 9 Continued |
图10与图9的结论相同,3DVar 和4DVar的 “A−B”垂直结构十分接近,也与“O−B”相似。u风在台风北侧有较强的东风增量,南侧有较强的西风增量。v风在台风中心及北侧有北风增量,南侧低层有弱的南风增量。对流层中下部台风中心附近有较明显降压,强南北向气压增量差与强东风增量相对应。位温在台风中心上空20—25层有升高,比湿在中低层台风中心北侧有弱的增大。

|
| 图 10 Fig. 10 Continued |
|
| 图 10 Fig. 10 Continued |
将4个试验的分析结果作为初值进行干模式积分,并与对照试验(CTL)和“实况”(真值)进行对比。3DVar_2试验的起报时间为2日18时,其他3个同化试验(3DVar_1、4DVar_1和4DVar_2)的起报时间均为2日12时。表2是台风预报位置与“实况”位置的偏差,0 h代表分析时刻,其余为预报时刻。表中可以看到,3DVar和4DVar均明显改善了台风的分析位置。3DVar_1和3DVar_2分析场台风位置偏差分别为115.1和73.9 km,相比背景场的位置偏差(12时为230.8 km,18时为218.1 km),积分初始时刻的台风中心位置得到明显修正。4Dvar_1和4DVar_2分析位置偏差分别只有30.8和54.0 km,明显好于2个3DVar。从预报位置偏差来看,对照试验路径预报误差最大,3DVar比对照试验有较大改善,且3DVar_2优于3DVar_1,但2个4DVar试验则明显优于2个3DVar试验,可见初值质量对台风路径预报有明显影响。4DVar_2尽管在初始位置上不及4DVar_1,但多个预报位置比4DVar_1好,表明6 h同化时间窗比3 h同化时间窗对路径预报有一定改善。
| 预报时效(h) | 位置偏差(km) | ||||
| 3DVar_1 | 3DVar_2 | 4DVar_1 | 4DVar_2 | CTL | |
| 0 | 115.1 | 73.9 | 30.8 | 54.0 | 230.8 |
| 6 | 92.5 | 95.4 | 21.1 | 21.1 | 218.1 |
| 12 | 74.5 | 39.4 | 24.7 | 11.2 | 196.1 |
| 18 | 73.4 | 15.3 | 33.4 | 33.4 | 168.1 |
| 24 | 84.3 | 53.2 | 35.0 | 30.5 | 142.4 |
| 30 | 103.6 | 56.3 | 15.2 | 10.4 | 99.9 |
| 36 | 83.4 | 45.4 | 15.2 | 20.7 | 75.7 |
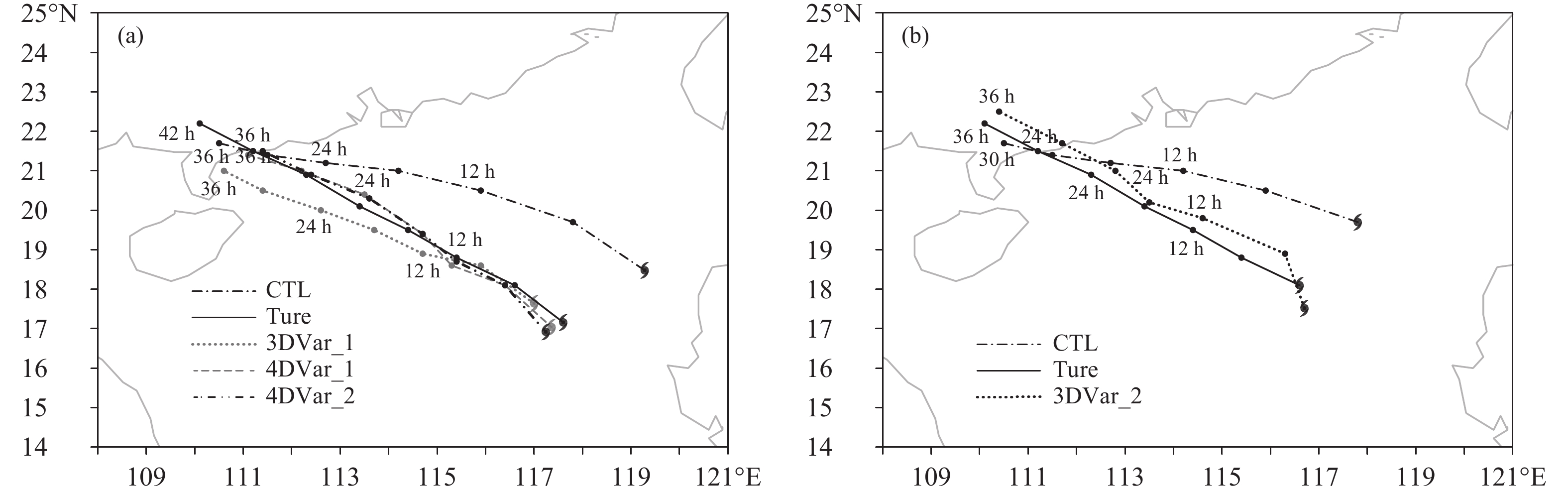
图11 是不同初值(对照试验和4次同化试验)预报的“彩虹”路径和“真实”路径。以同化分析场作为初值,“彩虹”的路径预报均比以背景场为初值有明显改善,其中2个4DVar试验的预报路径更接近“实况”(图11a),2个3DVar试验的预报路径与“实况”有一定偏离。分析时刻为18时的3DVar_2路径预报误差小于分析时刻为12时的3DVar_1,但仍明显不及分析时刻为12时的4DVar试验。
|
| 图 11 “彩虹”台风的路径预报 (a. 起报时间2015年10月2日12时,b. 起报时间2015年10月2日18时) Fig. 11 Track forecasts of typhoon Mujigae (a. initial time at 12:00 UTC 2 October 2015,b. initial time at 18:00 UTC 2 October 2015) |
图12是4个同化试验和对照试验给出的3日18时的预报。其中3DVar_1、4DVar_1和4DVar_2是30 h预报,3DVar_2是24 h预报。对照试验预报(图12e)台风强度与“真值”(图12f)相比明显弱很多,台风登陆时间明显偏早。4个同化试验均比对照试验有显著改善(图12a—d),台风强度和风速非对称分布更像“真值”(图12f)。3DVar_2(图12b)较3DVar_1(图12a)涡旋结构更接近实况,显示同是3DVar,基于最近时刻分析场的预报优于更早时刻分析场的预报。4DVar的预报比3DVar试验更好一些,风场分布细节上4DVar_2略优于4DVar_1。

|
| 图 12 基于不同初始场预报的2015年10月3日18时850 hPa“彩虹”台风的风场 (风矢和色阶) 和位势高度场 (等值线,单位:dagpm)(a. 3DVar_1,b. 3DVar_2,c. 4DVar_1,d. 4DVar_2,e. CTL,f. truth) Fig. 12 Model forecasts of wind (arrow and shaded) and geopotential height (contour,unit:dagpm) at 850 hPa at 18:00 UTC 3 October 2015 for typhoon Mujigae (a. 3DVar_1,b. 3DVar_2,c. 4DVar_1,d. 4DVar_2,e. CTL,f. truth) |
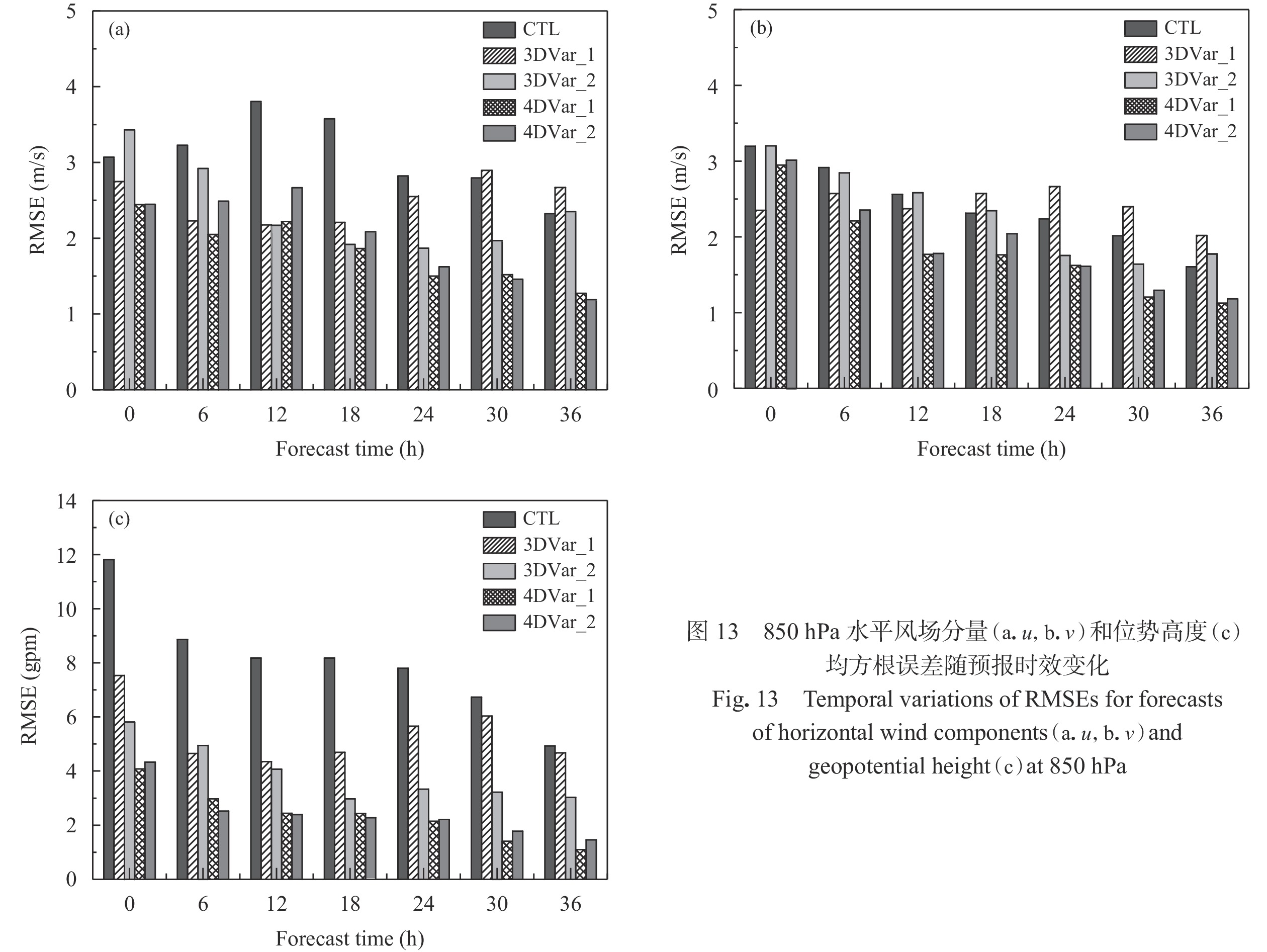
图13是不同初值得到的850 hPa风场和高度场的均方根误差随预报时间变化。可以看出以4DVar分析场为初值,预报场的均方根误差整体明显下降,预报效果明显比对照试验好很多,也优于3DVar。除了12 h前的预报,3DVar_2整体优于3DVar_1,尤其是在高度场的预报上。但是计算结果也显示,同化3个时次资料的4DVar_2并不比同化2个时次资料的4DVar_1均方根误差小,原因可能与短的同化时间带来模式积分的噪音有关,留待今后更加细致地分析。
|
| 图 13 |
在GRAPES区域扰动预报模式基础上开发了四维变分同化(4DVar)系统,该同化系统采用增量分析策略建立,是一个三维和四维一体化的区域同化系统框架。与原有GRAPES 3DVar相比,增加温度作为第5个控制变量,同时采用了地形追随坐标下的平衡方程,即建立气压(Π)和流函数
为评估所建立的四维变分同化系统,针对2015年10月2—3日台风“彩虹”进行了理想试验。利用在中国南海及周边区域人为设置的25个假想“探空”站,通过运行关掉物理过程选项的GRAPES非线性模式(干模式),产生测试需要的“真实”大气,并用于生成理想人造“探空”观测资料。共设计了4个同化试验,即2个三维变分同化试验及2个分别使用3和6 h时间窗的四维变分同化试验。利用涡旋分离和重定位技术产生一个明显变“差”的背景场。
试验表明,4个同化试验均在对流层中低层台风环流附近分析出偶极子型风压增量场,在背景场台风中心附近为反气旋高压增量,分析场台风中心附近为气旋性低压增量。偶极子增量对初始背景场产生了很好的修正作用,使得分析场的台风涡旋更接近观测。垂直剖面图显示分析增量符合台风环流物理量场基本分布特征。使用同化得到的分析场作为初值,不论是三维变分还是四维变分,GRAPES模式对台风“彩虹”的路径和强度预报都得到了明显改进。四维变分同化试验比三维变分同化试验有显著的分析和预报效果。试验也表明,6 h同化时间窗仅在台风路径预报上比3 h同化时间窗略优。测试表明,开发的四维变分同化框架得到了符合理论预期的分析结果,同化更多资料并反复受到模式约束的四维变分同化系统确实能有效改善初值质量,进而改善区域数值预报。本项工作为进一步发展有完整物理过程的区域四维变分同化系统打下科学基础。
由于缺乏实际观测资料,文中对于4DVar系统框架的测试仅基于“理想”大气进行,人为构造的观测资料也不能完全反映实际大气的状态。另外,系统框架也没有包含完整的物理过程,后续工作还要进一步开发各种主要的线性物理过程方案,并通过实际观测资料进一步检验。
冯业荣, 薛纪善, 陈德辉等. 2020. GRAPES区域扰动预报模式动力框架设计及检验. 气象学报, 78(5): 805-815. Feng Y R, Xue J S, Chen D H, et al. 2020. The dynamical core for GRAPES regional perturbation forecast model and verification. Acta Meteor Sinica, 78(5): 805-815. (in Chinese) |
薛纪善, 陈德辉. 2008. 数值预报系统GRAPES的科学设计与应用. 北京: 科学出版社: 65-136. Xue J S, Chen D H. 2008. Scientific Design of the GRAPES Numerical Weather Prediction Model and Its Application. Beijing: Science Press: 65-136. (in Chinese) |
Bauer P, Geer A J, Lopez P, et al. 2010. Direct 4D-Var assimilation of all-sky radiances. Part Ⅰ: Implementation. Quart J Roy Meteor Soc, 136(652): 1868-1885. DOI:10.1002/qj.659 |
Bauer P, Thorpe A, Brunet G. 2015. The quiet revolution of numerical weather prediction. Nature, 525(7567): 47-55. DOI:10.1038/nature14956 |
Bloom S C, Takacs L L, da Silva A M, et al. 1996. Data assimilation using incremental analysis updates. Mon Wea Rev, 124(6): 1256-1271. DOI:10.1175/1520-0493(1996)124<1256:DAUIAU>2.0.CO;2 |
Courtier P, Thépaut J N, Hollingsworth A. 1994. A strategy for operational implementation of 4D-Var, using an incremental approach. Quart J Roy Meteor Soc, 120(519): 1367-1387. DOI:10.1002/qj.49712051912 |
Courtier P, Andersson E, Heckley W, et al. 1998. The ECMWF implementation of three-dimensional variational assimilation (3D-Var). Ⅰ: Formulation. Quart J Roy Meteor Soc, 124(550): 1783-1807. |
Dixon M, Li Z H, Lean H, et al. 2009. Impact of data assimilation on forecasting convection over the United Kingdom using a high-resolution version of the Met Office unified model. Mon Wea Rev, 137(5): 1562-1584. DOI:10.1175/2008MWR2561.1 |
Fiorino M, Elsberry R L. 1989. Some aspects of vortex structure related to tropical cyclone motion. J Atmos Sci, 46(7): 975-990. DOI:10.1175/1520-0469(1989)046<0975:SAOVSR>2.0.CO;2 |
Gauthier P, Tanguay M, Laroche S, et al. 2007. Extension of 3DVAR to 4DVAR: Implementation of 4DVAR at the meteorological service of Canada. Mon Wea Rev, 135(6): 2339-2354. DOI:10.1175/MWR3394.1 |
Holland G J. 1983. Tropical cyclone motion: Environmental interaction plus a beta effect. J Atmos Sci, 40(2): 328-342. DOI:10.1175/1520-0469(1983)040<0328:TCMEIP>2.0.CO;2 |
Jones C D, Macpherson B. 1997. A latent heat nudging scheme for the assimilation of precipitation data into an operational mesoscale model. Meteor Appl, 4(3): 269-277. DOI:10.1017/S1350482797000522 |
Kurihara Y, Bender M A, Ross R J. 1993. An initialization scheme of hurricane models by vortex specification. Mon Wea Rev, 121(7): 2030-2045. DOI:10.1175/1520-0493(1993)121<2030:AISOHM>2.0.CO;2 |
Liu D C, Nocedal J. 1989. On the limited memory BFGS method for large scale optimization. Math Program, 45(1-3): 503-528. DOI:10.1007/BF01589116 |
Lorenc A C. 2003. Modelling of error covariances by 4D-Var data assimilation. Quart J Roy Meteor Soc, 129(595): 3167-3182. DOI:10.1256/qj.02.131 |
Lorenc A C, Rawlins F. 2005. Why does 4D-Var beat 3D-Var?. Quart J Roy Meteor Soc, 131(613): 3247-3257. DOI:10.1256/qj.05.85 |
Mathur M B. 1991. The national meteorological center's quasi-Lagrangian model for hurricane prediction. Mon Wea Rev, 119(6): 1419-1447. DOI:10.1175/1520-0493(1991)119<1419:TNMCQL>2.0.CO;2 |
McNally A P, Watts P D, Smith J A, et al. 2006. The assimilation of AIRS radiance data at ECMWF. Quart J Roy Meteor Soc, 132(616): 935-957. DOI:10.1256/qj.04.171 |
Rabier F, Järvinen H, Klinker E, et al. 2000. The ECMWF operational implementation of four-dimensional variational assimilation. Ⅰ: Experimental results with simplified physics. Quart J Roy Meteor Soc, 126(564): 1143-1170. DOI:10.1002/qj.49712656415 |
Rawlins F, Ballard S P, Bovis K J, et al. 2007. The Met Office global four-dimensional variational data assimilation scheme. Quart J Roy Meteor Soc, 133(623): 347-362. DOI:10.1002/qj.32 |
Zhang L, Liu Y Z, Liu Y, et al. 2019. The operational global four-dimensional variational data assimilation system at the China Meteorological Administration. Quart J Roy Meteor Soc, 145(722): 1882-1896. DOI:10.1002/qj.3533 |
 2021, Vol. 79
2021, Vol. 79

