中国气象学会主办。
文章信息
- 龚建东, 王瑞春. 2021.
- GONG Jiandong, WANG Ruichun. 2021.
- 集合预报误差在GRAPES全球四维变分同化中的应用研究Ⅰ:局地化方案设计与动力平衡特征分析
- The study of introducing ensemble forecast errors into the GRAPES global 4DVar Part Ⅰ:Localization scheme and dynamic balance analysis
- 气象学报, 79(1): 31-47.
- Acta Meteorologica Sinica, 79(1): 31-47.
- http://dx.doi.org/10.11676/qxxb2021.006
文章历史
-
2020-04-24 收稿
2020-10-13 改回
2. 中国气象局数值预报中心,北京,100081
2. Numerical Weather Prediction Center of CMA,Beijing 100081,China
背景误差协方差简称背景误差,它的准确估计直接影响资料同化的分析性能。背景误差一般使用气候历史样本进行统计,并考虑到误差协方差结构的复杂性,采用高度模型化的误差自相关、协相关等模型和各向同性均质误差假设来简化协方差结构,使得背景误差可以显式表达并用于资料同化系统中(Lorenc,1986;Bannister,2008)。这样处理的不足是在变分资料同化的每个分析循环中,虽然数值预报背景场在不断更新,误差特征也在不断变化,但同化框架中背景误差的特征却固定不变。导致背景误差在不同时刻不断变化的因素较多,但其明显受到所在地天气尺度系统的影响,天气系统的斜压不稳定成为背景误差增长的主导因素,呈现出随不同天气流型变化的“流依赖”特征(Kalnay,2003,第5.6节)。如果能在同化框架中引入具备流依赖特征的背景误差,将会帮助同化框架更加有效地确定背景场和观测的相对权重,也能更加合理地将观测信息在空间上传递出去,从而提高分析质量和预报技巧。
随着集合卡尔曼滤波(EnKF,ensemble Kalman filtering)等集合资料同化技术的快速发展与逐步成熟(Evensen,1994;Anderson,2001;Houtekamer,et al,2005),利用集合样本的短期预报来估计集合预报误差协方差(简称集合预报误差)作为背景误差更为合理。从使用集合预报误差角度分析,在现有资料同化方法中,三维变分资料同化(3DVar)使用气候背景误差协方差。4DVar在同化时间窗起始时刻使用气候背景误差协方差,并利用切线性和伴随模式在同化时间窗内实现背景误差的时间演变。基于4DVar,通过扰动观测资料和海温、叠加随机物理过程等来表示观测资料、海洋下边界条件及模式的不确定性,产生多组分析和预报的集合样本来估计集合预报误差,这种方法被称为集合方式的四维变分资料同化方法,简称集合资料同化(EDA,ensemble of data assimilations)方法。在4DVar同化时间窗的起始时刻,同时使用气候背景误差和EnKF或EDA方法生成集合样本估计的集合预报误差,使得在同化时间窗的起始时刻就具有随天气形势演变特征的流依赖动态背景误差,这种方法被称为集合四维变分同化(En4DVar,ensemble four dimensional variational data assimilation),其与4DVar的主要差别在于是否使用集合预报误差。而在同化时间窗内,使用集合预报在时间序列上的多组集合样本来直接估计整个同化时间窗内不同时刻的背景误差,这种方法被称为四维集合变分同化(4DEnVar,four dimensional ensemble variational data assimilation),其与4DVar和En4DVar的主要区别是不再引入切线性和伴随模式。熊春晖等(2013)、Fairbairn等(2014)对这些方法的差异做了详细介绍。
目前,国际上领先的业务变分资料同化系统大多已实现从静态的、表示气候特征的背景误差向基于集合样本估计的、能表示随天气形势演变特征的流依赖动态背景误差的升级(熊春晖等,2013)。英国气象局采用在目标函数中增加扩展控制变量的方式将集合转置卡尔曼滤波(ETKF)估计的集合预报误差与气候背景误差结合,发展了En4DVar系统(Clayton,et al,2013),加拿大气象局也发展了EnKF与4DVar结合的En4DVar同化系统(Buehner,et al,2010a,2010b)。业务数值预报中心的试验结果表明,考虑集合预报误差改善了4DVar的分析质量,特别是在南半球、热带地区,并对台风路径预报也有显著改进。欧洲中期天气预报中心与法国气象局使用基于4DVar的集合资料同化方法来生成集合样本,采用谱滤波来滤除噪声以保留有用的天气系统变化的集合预报误差并用于4DVar,显著地改善了分析和模式预报质量,且正贡献在全球范围10 d预报中都有效(Bonavita,et al,2012)。此外,英国气象局(Lorenc,et al,2015;Bowler,et al,2017)、美国环境预报中心(NCEP)还进一步采用扩展控制变量方式将集合预报误差用于全球4DEnVar(Wang,et al,2013;Kleist,et al,2015a,2015b),加拿大气象局也发展并业务应用了4DEnVar系统(Buehner,et al,2013)。
应用集合预报误差虽然可以通过不同方式实现,但事实证明这些方式之间是等价的(Buehner,2005;Wang,et al,2007)。可以看到,在上述业务实践中,Lorenc(2003a,2003b)提出的增加扩展控制变量方法是引入集合预报误差的常用方案。增加扩展控制变量可以使得分析增量有更大的空间自由度,从而帮助更好地引入观测信息。使用集合样本来估计集合预报误差有优势,但其不足也很明显。Lorenc(2003a)指出,当集合样本数较少时预报误差容易被低估,且存在虚假遥相关,需要进行误差协方差的局地化,而局地化容易破坏集合样本中所包含的动力平衡关系(Kepert,2009)。
GRAPES于2018年6月实现了全球4DVar业务运行(Zhang,et al,2019),中国成为世界上为数不多的采用四维变分同化的全球业务预报中心之一。4DVar方法的基本原理表明,虽然其能在同化时间窗内通过切线性与伴随模式积分来隐式计算流依赖背景误差,但其初始时刻的背景误差一直是气候态的。要克服这一缺陷,需要在4DVar中引入集合预报误差,发展GRAPES全球En4DVar技术,从而实现在同化时间窗起始时刻就应用流依赖背景误差。
在GRAPES全球4DVar基础上进行拓展,有效使用集合样本估计的集合预报误差来改进全球分析质量是本研究的重点。文中主要研究这几个方面的问题:首先,GRAPES全球4DVar采用增量分析方案(Courtier,et al,1994),在具体实施上有自己的特殊性(薛纪善等,2008),有必要研究在该系统框架中增加扩展控制变量的科学方案。虽然已有一些研究基于GRAPES区域3DVar开展了使用集合预报误差的工作(Chen,et al,2015),但全球4DVar中尚未开展相关研究。其次,通过增加集合样本数来降低抽样误差,并对集合预报误差给予较大权重是各业务中心同化技术发展的趋势。考虑到扩展控制变量的空间维数与集合样本数有关,集合样本数越大对应的扩展控制变量的空间维数越大。在大于100个集合样本数的条件下,如何在GRAPES全球4DVar中既能有效使用集合预报误差,又使得扩展控制变量的维数增加受到限制,以减少4DVar系统的计算与存储消耗。最后在GRAPES全球4DVar引入扩展控制变量并对其进行局地化时,需要研究局地化对分析场平衡造成的影响,并发展减缓局地化影响的办法。
2 GRAPES全球4DVar背景误差公式表达GRAPES全球模式为水平经纬度格点模式。GRAPES全球4DVar的气候背景误差矩阵(B)可以表示为
| $ {\rm{\delta}}{{X}}_{1}={{U}}{{v}}={{{U}}}_{\rm{P}}{{{U}}}_{\rm{K}}{{{\varepsilon }}_{\rm{b}}{{{U}}}_{\rm{h}}{{U}}}_{\rm{v}}{{v}} $ | (1) |
式中,
| $ {\rm{\delta}}{{X}}_{\rm{u}}={{{\varepsilon }}_{\rm{b}}{{{U}}}_{\rm{h}}{{U}}}_{\rm{v}}{{v}}={{{\varepsilon }}_{\rm{b}}{{G}}_{{\rm{s}}\to {\rm{d}}}^{1}{{S}}}^{-1}\sqrt{{{{B}}}_{{\rm{s}}}}{{{E}}{{\varLambda }}}^{\frac{\,1\,}{\,2\,}}{{S}}{{W}}_{\rm{g}}^{-\frac{\,1\,}{\,2\,}}{{v}} $ | (2) |
式中,
式(1)中
| $ {\rm{\delta}}\pi ={\rm{\delta}}{\pi }_{\rm{b}}+{\rm{\delta}}{\pi }_{\rm{u}}={{N}}{\rm{\delta}}\psi +{\rm{\delta}}{\pi }_{\rm{u}} $ | (3) |
| $ {\rm{\delta}}\chi ={\rm{\delta}}{\chi }_{\rm{b}}+{\rm{\delta}}{\chi }_{\rm{u}}={{M}}{\rm{\delta}}\psi +{\rm{\delta}}{\chi }_{\rm{u}} $ | (4) |
式中,
| $ {\rm{\delta}}{\theta }_{\rm{v}}=\frac{{{c}}_{p}{\theta }_{{\rm{v}}{\rm{b}}}^{2}}{{g}}\left(\frac{\partial \left({\rm{\delta}}\pi \right)}{\partial {{z}}}\right) $ | (5) |
式中,
式(2)中经验正交函数分解和水平谱滤波的参数由背景误差垂直相关模型和水平相关模型决定。误差垂直相关矩阵(
| $ {\rho }_{{{l}},{{k}}}=\frac{1}{1.0+{{K}}_{{{z}}}{\left({{{z}}}_{{{l}}}-{{{z}}}_{{{k}}}\right)}^{2}} $ | (6) |
| $ {{K}}_{{{z}}}={{{K}}\left(\frac{{{RT}}}{{g}}\right)}^{2} $ | (7) |
式中,zl、zk是任意模式层l、k的平均高度。K是经验系数,当K=0时,所有垂直层次间的相关均为1,当其数值增大时,垂直相关结构逐步变得更加局地。垂直相关结构也可以通过误差样本统计给出(王金成等,2014)。龚建东等(2020)在GRAPES全球4DVar基础上发展了EDA方法生成多组集合样本,也可以用于统计垂直相关结构。
定义新息向量
| $ J\left({{v}}\right)\!=\!\frac{\,1\,}{\,2\,}{{{v}}}^{{\rm{T}}}{{v}}\!+\!\frac{\,1\,}{\,2\,}\sum \limits_{{{n}}=0}^{{L}}{\left({{d}}_{{n}}\!-\!{{{H}}}_{{n}}{{M}}{{U}}{{v}}\right)}^{{\rm{T}}}{{R}}^{-1}\left({{d}}_{{n}}\!-\!{{{H}}}_{{n}}{{M}}{{U}}{{v}}\right)\!+\!{J}_{\rm{c}} $ | (8) |
式中,R是观测误差协方差。
由式(1)与(8)可知,在4DVar的
定义预报变量
| $ {\rm{\delta}}{{X}}_{2}=\frac{1}{\sqrt{{{N}}-1}}\sum \limits_{{{i}}=1}^{{{N}}}{{\rm{\delta}}{{X }}}_{{i}}^{\rm{f}}\circ {{{\alpha }}}_{{i}} $ | (9) |
这时
定义扩展控制变量
| $ {{{\alpha }}}_{{i}}={{C}}^{1/2}{{{v}}}_{{i}}^{\rm{\alpha }}={{{U}}}^{\rm{\alpha }}{{{v}}}_{{i}}^{\rm{\alpha }} $ | (10) |
式中,
| $ {\rm{\delta}}{{X}}_{2}=\frac{1}{\sqrt{{{N}}-1}}\sum\limits _{{{i}}=1}^{{{N}}}({\rm{\delta}}u,{\rm{\delta}}v,{\rm{\delta}}\pi,{\rm{\delta}}q{{)}_{{i}}^{{\rm{T}}}}^{\rm{f}}\circ {{{U}}}_{\rm{h}}^{\rm{\alpha }}{{{U}}}_{\rm{v}}^{\rm{\alpha }}{{{v}}}_{{i}}^{\rm{\alpha }} $ | (11) |
结合式(11),以
| $\begin{split} J\left({{{v}}}_{1}^{\rm{\alpha }}{,\cdots,{{v}}}_{{{N}}}^{\rm{\alpha }}\right)=&\frac{\,1\,}{\,2\,}{\sum\limits _{{{i}}=1}^{{{N}}}{({{v}}}_{{i}}^{\rm{\alpha }})^{{\rm{T}}}}{{{v}}}_{{i}}^{\rm{\alpha }}+\\&\frac{\,1\,}{\,2\,}\sum\limits _{{{n}}=0}^{{L}}{\left({{d}}_{{n}}-{{{H}}}_{{n}}{{M}}{\rm{\delta}}{{X}}_{2}\right)}^{{\rm{T}}}{{R}}^{-1}\left({{d}}_{{n}}-{{{H}}}_{{n}}{{M}}{\rm{\delta}}{{X}}_{2}\right)\end{split} $ | (12) |
式(12)相较于式(8)的定义表明,对以
| $ {{{{v}}}_{{i}}^{\rm{\alpha }}={{T}}^{\rm{\alpha }}{\bf{\alpha }}}_{{i}}{={{{T}}_{\rm{v}}^{\rm{\alpha }}{{T}}}_{\rm{h}}^{\rm{\alpha }}{{\alpha }}}_{{i}} $ | (13) |
由于水平与垂直的局地化的尺度都要明显大于气候背景误差相关的尺度,因而水平局地化可以只取前若干波数,垂直局地化只取主导特征向量,这样
在GRAPES全球4DVar中实现局地化分析变量有两种方式,一是只进行水平局地化而不进行垂直局地化。此时,扩展控制变量(
| $ {{{{\alpha }}}_{{i}}{={{G}}}_{{\rm{s}}\to {\rm{\alpha }}}^{1}{{S}}}^{-1}\sqrt{{{{B}}}_{{\rm{s}}{\rm{\alpha }}}}{{S}}{{W}}_{\rm{g}}^{-\frac{1}{2}}{{{v}}}_{{i}}^{\rm{\alpha }} $ | (14) |
式中,
另一种办法是进行三维局地化—同时考虑水平和垂直方向的局地化。此时,通过在式(13)的
| $ {{{\alpha }}}_{\rm{i}}={{{G}}_{{\rm{s}}\to {\rm{\alpha }}}^{2}{{{{S}}}_{\rm{\alpha }}^{-1}}}\sqrt{{{{B}}}_{{\rm{s}}{\rm{\alpha }}}}{{{{E}}}_{\rm{c}}{{{\varLambda }}}_{\rm{c}}^{\frac{1}{2}}}{{{S}}}_{\rm{\alpha }}{{W}}_{\rm{g}}^{-\frac{1}{2}}{{{v}}}_{\rm{i}}^{\rm{\alpha }} $ | (15) |
式中,
在实际应用时,当局地化所采用网格的水平分辨率与内循环的分辨率不一致时,需要重新定义一组网格用于局地化变量,这会使得GRAPES的网格定义更为复杂。一种替代的办法是在水平局地化网格分辨率不变的情况下,仅在垂直局地化时使用较少的主导特征向量。Clayton等(2013)的研究表明,当经验正交函数分解前若干个特征值对总误差的解释比例达到95%时可以获得满意的结果。目前的GRAPES全球4DVar中,水平局地化与内循环的网格一致,垂直方向按照解释比达到90%来截取主导特征向量。试验表明前8个特征值占比已经超过90%,后续试验中取前8个特征模态进行垂直局地化。
3.3 GRAPES全球En4DVar公式表达采用增加扩展控制变量,是在具有气候背景误差特征的分析增量上增加扩展控制变量给出的具备随流型演变的分析增量,最终获得的分析增量是这两部分增量的加权之和(Lorenc,2003b;Wang,et al,2007)
| $ {\rm{\delta}}{{X}}_{1}=\sqrt{{\rm{\beta }}_{\rm{c}}}{{U}}{{v}} $ | (16) |
| $ {\rm{\delta}}{{X}}_{2}=\sqrt{{\rm{\beta }}_{\rm{e}}}\frac{1}{\sqrt{{{N}}-1}}\sum\limits _{{{i}}=1}^{{{N}}}{{\rm{\delta}}{{X }}}_{{i}}^{\rm{f}}\circ {{{U}}}^{\rm{\alpha }}{{{v}}}_{{i}}^{\rm{\alpha }} $ | (17) |
其中,气候背景误差(
由新息向量定义,分析值在观测空间投影(
| $ {{y}}_{{n}}={\cal{H}}_{{n}}{\cal{M}}{({{X }}}^{\rm{b}}+{\rm{\delta}}{{X}}_{1}+{\rm{\delta}}{{X}}_{2}) $ | (18) |
于是
| $ {{y}}_{{n}}^{\rm{o}}-{{y}}_{{n}}={{d}}_{{n}}-{{{H}}}_{{n}}{{M}}({\rm{\delta}}{{X}}_{1}+{\rm{\delta}}{{X}}_{2}) $ | (19) |
考虑了扩展控制变量的目标函数表示为
| $\begin{split} J\left({{v}},{{{v}}}_{1}^{\rm{\alpha }}{,\cdots,{{v}}}_{{{N}}}^{\rm{\alpha }}\right)=&\frac{\,1\,}{\,2\,}{{{v}}}^{{\rm{T}}}{{v}}+\frac{1}{2}{\sum\limits _{{{i}}=1}^{{{N}}}{({{v}}}_{{i}}^{\rm{\alpha }})^{{\rm{T}}}}{{{v}}}_{{i}}^{\rm{\alpha }}+\\&\frac{\,1\,}{\,2\,}\sum\limits _{{{n}}=0}^{{L}}{\left({{y}}_{{n}}^{\rm{o}}-{{y}}_{{n}}\right)^{{\rm{T}}}}{{R}}^{-1}\left({{y}}_{{n}}^{\rm{o}}-{{y}}_{{n}}\right)\end{split} $ | (20) |
由式(20)及式(16)—(17),对控制变量(
| $ {\nabla }_{\bf{v}}J={{v}}+\sqrt{{\rm{\beta }}_{\rm{c}}}{{{U}}}^{{\rm{T}}}\sum\limits _{{{n}}=0}^{{L}}{{{M}}}^{{\rm{T}}}{{{H}}}_{{n}}^{{\rm{T}}}{{R}}^{-1}\left({{y}}_{{n}}^{\rm{o}}-{{y}}_{{n}}\right) $ | (21) |
| $ {\nabla }_{{{{v}}}_{{i}}^{\rm{\alpha }}}J={{{v}}}_{{i}}^{\rm{\alpha }}+\sqrt{{\rm{\beta }}_{\rm{e}}}{\frac{1}{\sqrt{{{N}}-1}}\left({{\rm{\delta}}{{X }}}_{{i}}^{\rm{f}}\circ {{{U}}}^{\rm{\alpha }}\right)}^{{\rm{T}}}\sum\limits _{{{n}}=0}^{{L}}{{{M}}}^{{\rm{T}}}{{{H}}}_{{n}}^{{\rm{T}}}{{R}}^{-1}\left({{y}}_{{n}}^{\rm{o}}-{{y}}_{{n}}\right) $ | (22) |
对式(21)和(22)再次求偏导数,计算目标泛函相对于控制变量的二阶偏导数(公式略),构成海森矩阵可以发现,将权重系数
最后,在GRAPES全球4DVar中具体实现的步骤是:首先由外循环计算新息向量
(1)给定
(2)由控制变量(
(3)由式(19)计算分析值在观测空间投影(
(4)由式(20)计算目标函数J(
(5)由式(21)计算
(6)利用目标函数(
(7)回到第(2)步,进入下一次循环。如精度满足需求,则退出循环。
由扩展控制变量(
| $ \sum {{\rm{\delta}}{{X}}_{2}^{i}}=\sum {{\rm{\delta}}{{X}}_{2}^{{i}-1}}+{{\rm{\delta}}{{X}}_{2}^{i}}\qquad{{i}}=1,{{N}} $ | (23) |
采用以上的计算策略时,通过循环集合样本,全部样本只需要存储一个
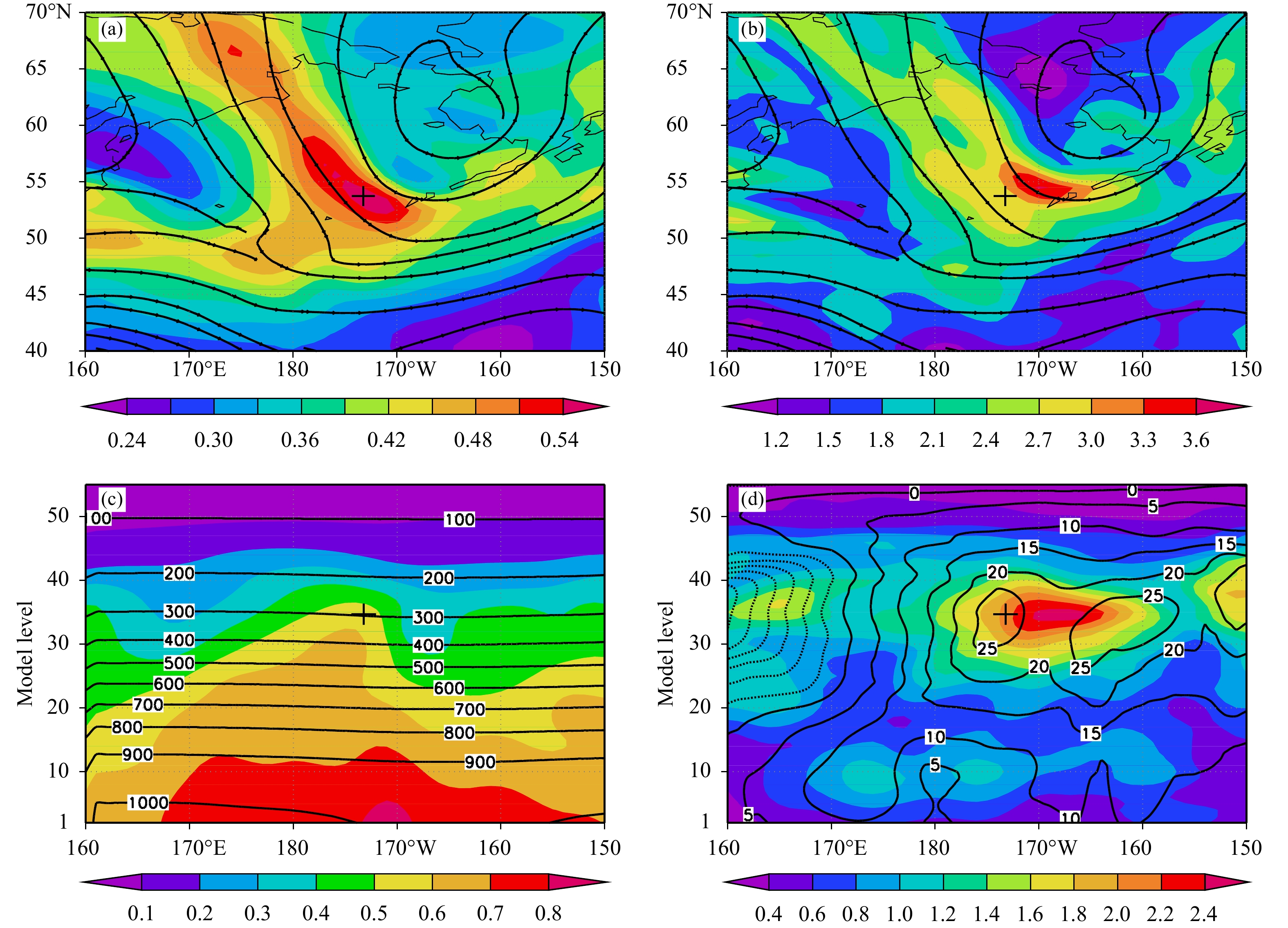
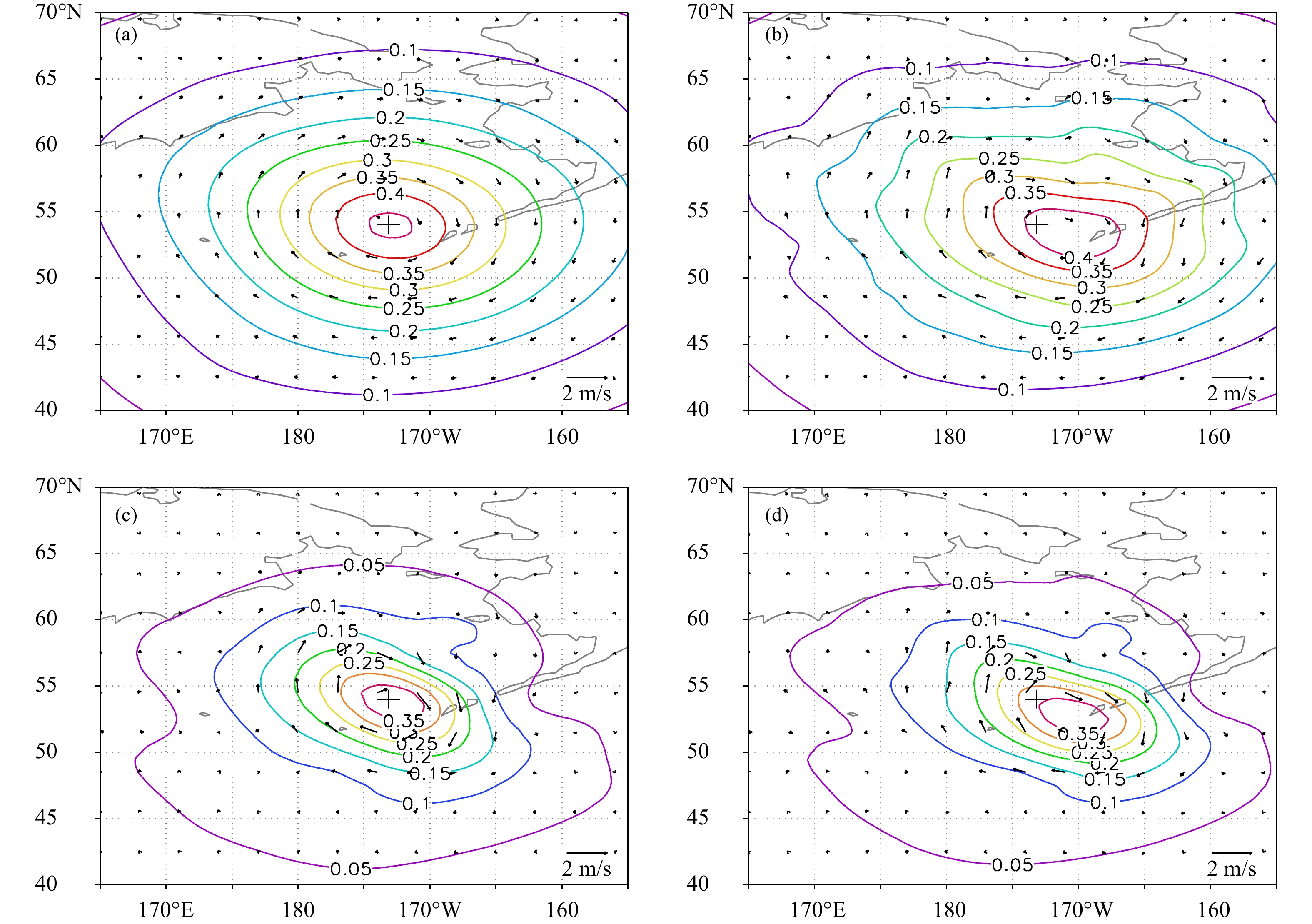
GRAPES全球4DVar的气候背景误差的水平相关模型采用融合水平相关模型(龚建东等,2020),水平局地化模型采用高斯型相关函数。借鉴Xu等(2008a,2008b)提出的在分析时刻前后利用集合样本在时间序列上的扩展来增加集合样本数的方法,试验利用20个NCEP全球集合预报的6与9 h预报的集合样本,并采用扣除对应时间集合平均的扰动样本来减缓因预报时长不一致带来的大尺度场存在的相位误差,总计40个样本。任选2018年7月9日太平洋北部地区一次锋面天气过程进行分析。由集合样本估计出来的集合预报误差如图1所示,在300 hPa高度水平面上(图1a、b,约为模式35层)集合样本估计的气压与风场误差最大的位置位于冷锋槽及槽后位置,在沿54°N的垂直剖面上(图1c、d),气压误差随高度升高而递减,槽后明显大于槽前,纬向风场的误差主要位于风速急流区附近。
|
|
图 1 40个集合样本估计的
|
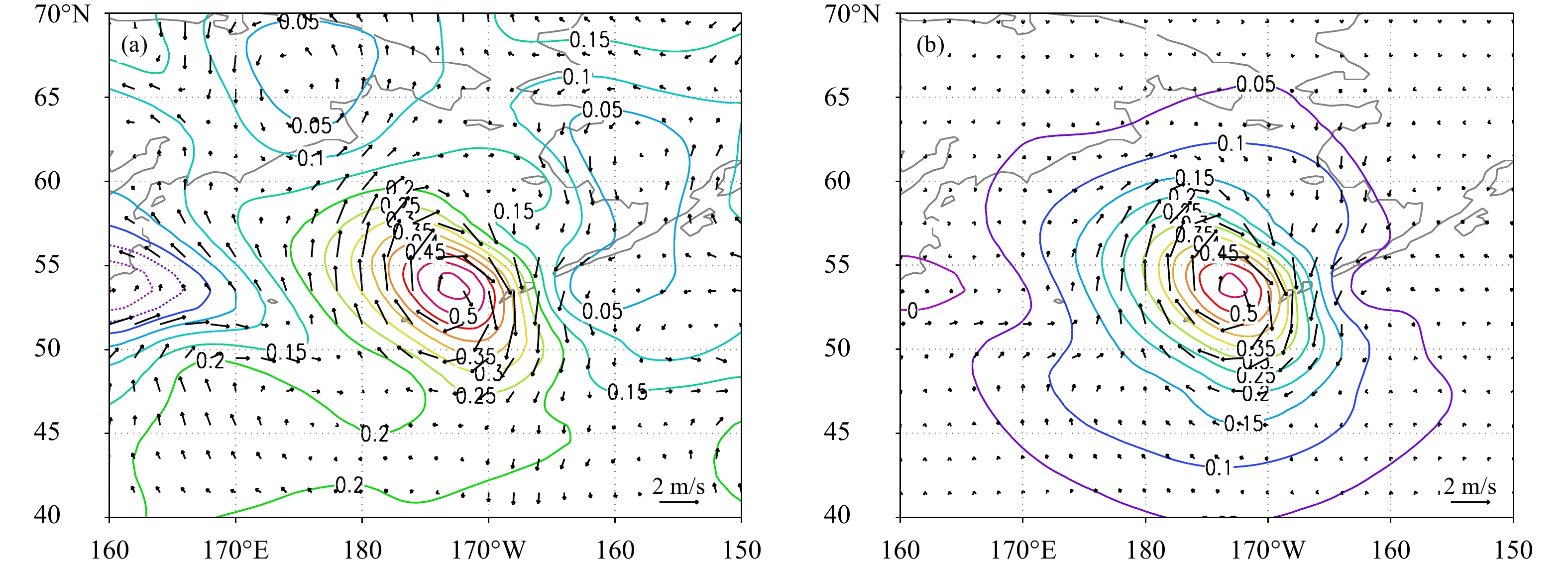
将单个观测资料放置在冷锋锋面后的西北平直气流上,位于(54°N,173°W)的模式35层(约250 hPa)位置(图1)。取气候背景误差与集合预报误差的权重分别为0.1与0.9,这时分析增量主要体现集合预报误差的作用,并考虑不同水平局地化尺度参数来研究其对分析增量的影响,试验结果如图2所示。水平局地化采用高斯相关分布特征,在水平局地化尺度的4倍距离的位置,水平相关系数基本降为0。当水平相关尺度参数取值较大时(如28000 km),地球上最远大圆距离(20000 km)处的分析增量受局地化作用将会衰减到原值的70%,水平局地化基本不起作用,可以作为不进行水平局地化的试验结果。由于集合样本数有限,直接由集合样本估计
|
|
图 2 局地化水平相关尺度(a. 28000 km,b. 850 km)对单点气压观测产生的分析增量的影响 (新息向量大小为1 hPa,观测时间位于
|
Mitchell等(2002)、Clayton等(2013)研究表明,直接对水平风场及气压进行局地化时,由于集合样本中的水平风与气压变量之间已经包含大尺度准地转平衡约束关系,进行水平局地化容易破坏这种关系。以纬向风(
| $ {\rm{\delta}}{u}_{\rm{g}}=-\frac{1}{{{f}}{\rm{\rho}}}\frac{\partial{\rm{\delta}} p}{\partial {\rm{y}}} $ | (24) |
式中,f为科里奥利参数,
| $ {{\rm{\delta}}{{X}}_{{u}}^{{i}}={({\rm{\delta}}\psi,{\rm{\delta}}{\chi }_{\rm{u}},{\rm{\delta}}{\pi }_{\rm{u}},{\rm{\delta}}q{)}_{{i}}^{{\rm{T}}}={{T}}}_{\rm{K}}{{T}}}_{\rm{P}}{{\rm{\delta}}{{X }}}_{{i}}^{\rm{f}} $ | (25) |
| $ {\rm{\delta}}{{X}}_{2}={{{U}}}_{\rm{P}}{{{U}}}_{\rm{K}}\left\{\frac{1}{\sqrt{{{N}}-1}}\sum\limits _{{{i}}=1}^{{{N}}}\left({{{{T}}_{\rm{K}}{{T}}}_{\rm{P}}{\rm{\delta}}{{X }}}_{{i}}^{\rm{f}}\right)\circ {{{U}}}_{\rm{h}}^{\rm{\alpha }}{{{U}}}_{\rm{v}}^{\rm{\alpha }}{{{v}}}_{{i}}^{\rm{\alpha }}\right\} $ | (26) |
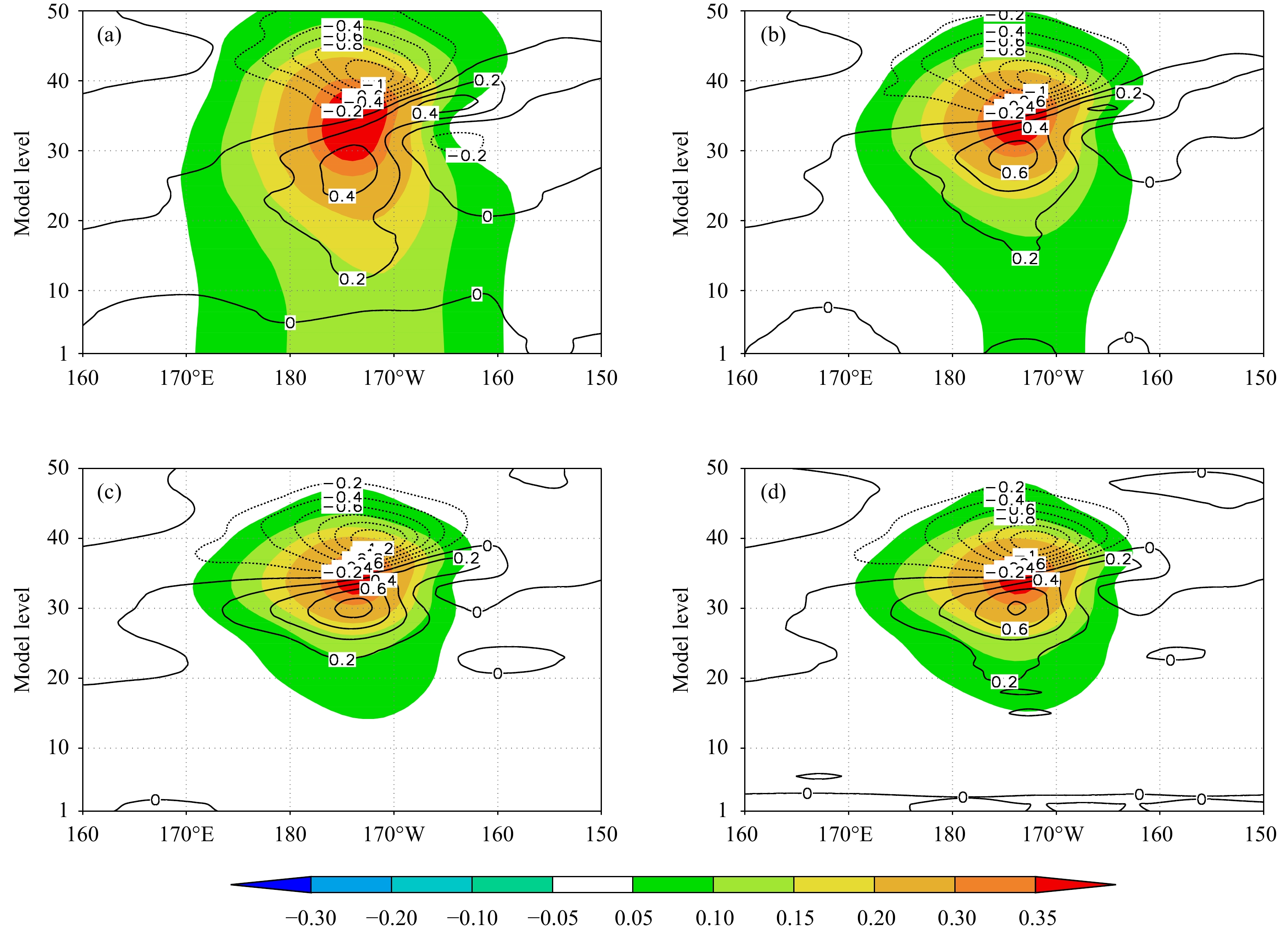
图3给出了分别在分析变量空间与非平衡分析变量空间进行局地化时,对分析平衡影响的差异。为方便比较起见,同时给出水平局地化相关尺度28000 km的结果,作为不进行水平局地化的对比试验。由图3c、f可见,当不进行局地化时,同化时间窗起始时刻(
|
|
图 3 水平局地化对分析增量准地转平衡的影响 (a、d. 分析变量空间分布;b、e. 非平衡分析变量空间分布,局地化水平尺度为850 km;c、f. 分析变量空间分布,水平局地化尺度为28000 km;a、b、c.
|
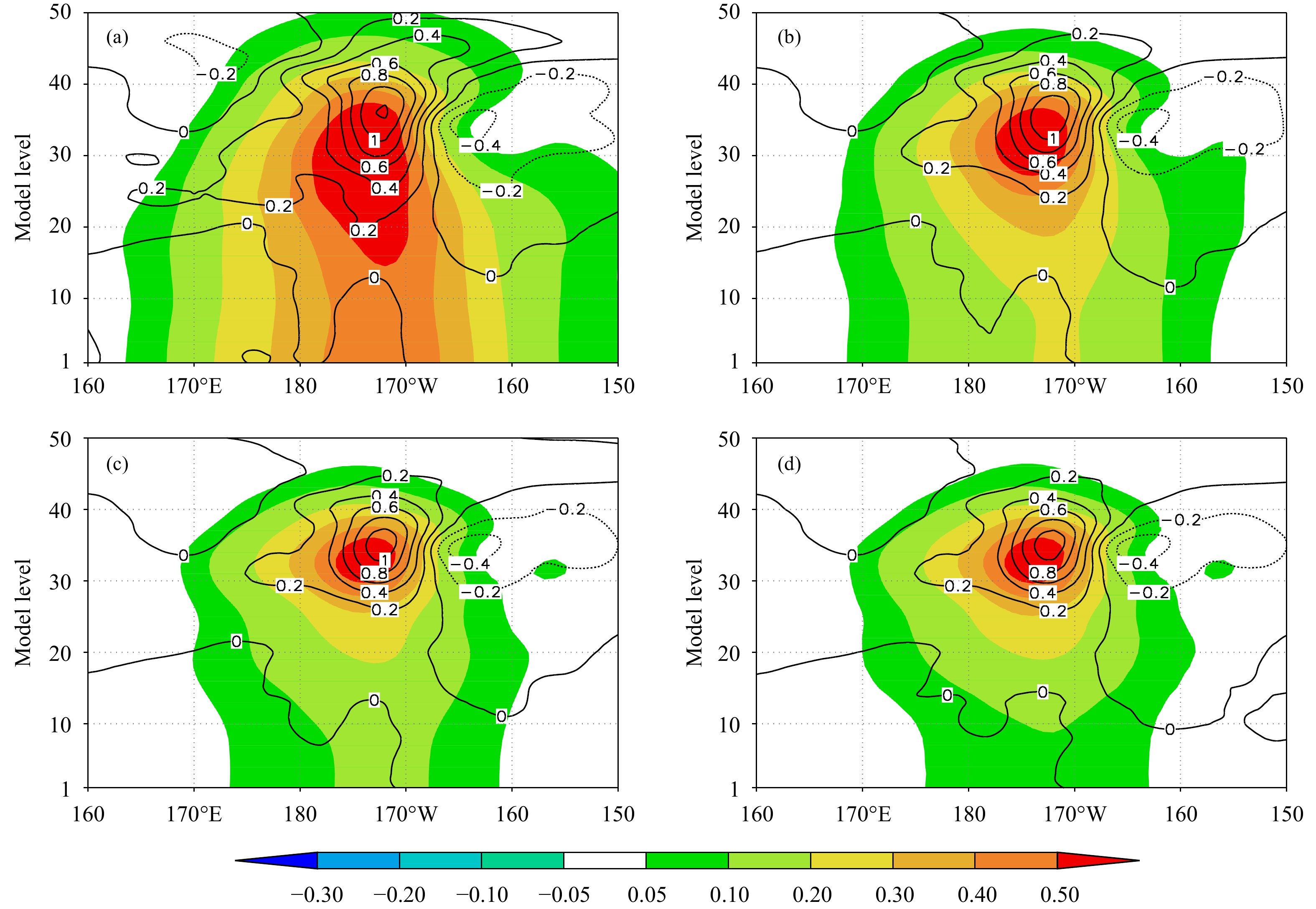
GRAPES全球4DVar采用静力平衡分析方案,根据静力平衡关系通过式(5)由无量纲气压增量计算虚位温增量。垂直局地化的相关结构可以采用式(6)和(7)所给出的垂直相关模型来实现,也可以直接利用模式预报的统计样本来估计。王金成等(2014)比较了垂直相关模型与同一检验时刻的不同预报时效统计样本估计出的垂直相关结构的差异,结果表明统计样本估计的垂直相关结构更加合理。文中采用EDA方法生成的集合样本来估计垂直相关结构(龚建东等,2020)。由集合样本估计的垂直相关结构(

|
| 图 4 |
进行垂直局地化时,要对无量纲气压增量(
|
| 图 5 垂直局地化相关尺度对单点气压观测分析增量的影响 (a. K=1,b. K=7,c.K=20,d. 集合样本估计的局地化尺度;等值线为纬向风分析增量,单位:m/s;色阶为气压分析增量,单位:hPa) Fig. 5 Impacts of correlation scale of vertical localization on analysis increment when assimilating single-point pressure observations (a. K=1,b. K=7,c.K=20,d. correlation scale of vertical localization estimated by ensemble samples;contours are for zonal wind analysis increment,unit:m/s;shaded are for pressure analysis increment,unit:hPa) |
进一步考察垂直局地化对位温分析增量的影响,结果如图6所示。由式(5)可知,位温分析增量一般位于无量纲气压增量(
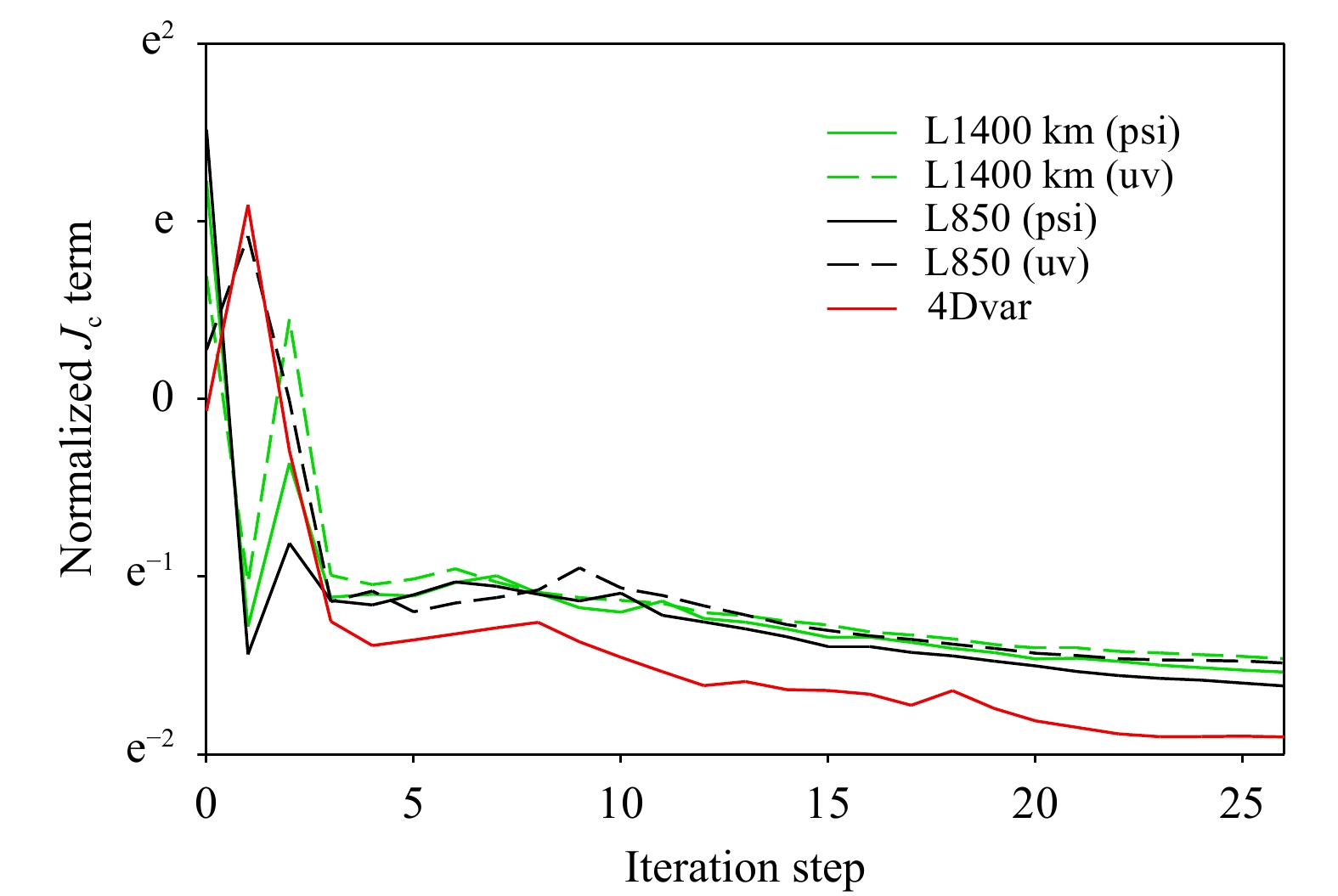
4DVar中低分辨率切线性模式积分时存在由诸多因素引起的高频重力振荡,当集合预报误差引入4DVar后,与之相随的水平与垂直局地化也是造成分析不平衡、激发高频重力振荡的原因之一。刘艳等(2019)研究表明,通过在4DVar中引入基于数字滤波方案的初始化过程,可以很好地抑制高频振荡过程,使得分析场在动力上更为平衡。由式(8),
|
|
图 7 集合预报误差引入4DVar对目标函数约束项
|
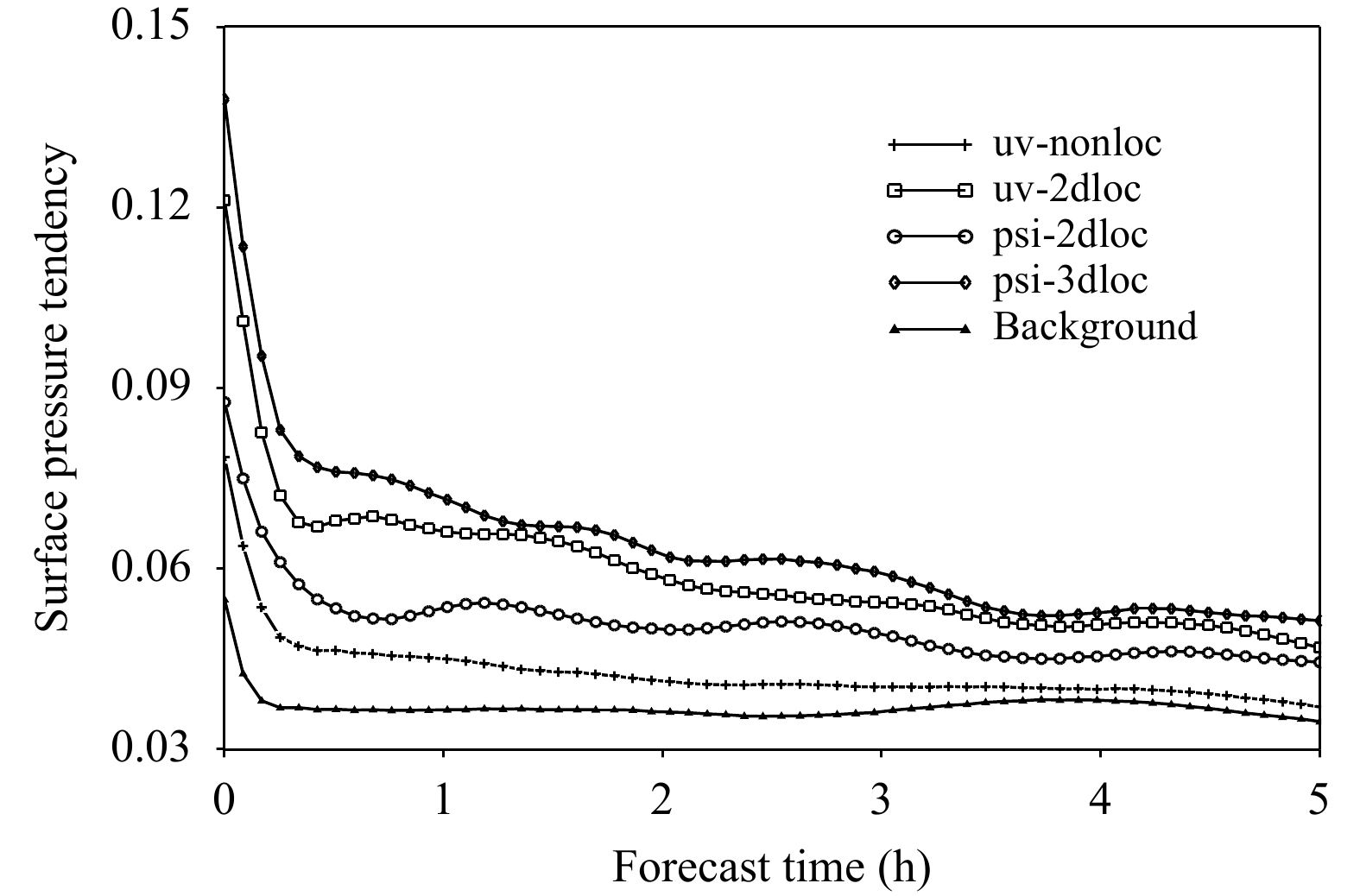
这里将4DVar退化为3DVar,不考虑切线性模式积分的影响,以进一步评估水平与垂直局地化对分析场平衡特征的影响。利用引入集合预报误差的3DVar同化实际常规资料与卫星资料,并用分析场驱动GRAPES全球模式,通过模式启动初期地面气压的时间倾向来分析局地化对分析场平衡特征的影响(图8)。由于背景场中未引入新的同化增量,由其驱动的模式轨迹平衡特征较好,这里作为对照试验。从图8中可以看到,当在分析变量空间进行水平局地化时,模式积分初始时刻的地面气压倾向明显大于背景场启动的结果,且在5 h积分后仍然高于背景场结果。而在非平衡分析变量空间进行水平局地化时,平衡特征明显改善。这进一步说明,在非平衡分析变量空间进行水平局地化更有优势。当在水平局地化基础上进一步考虑垂直局地化时,地面气压倾向增加十分显著。这表明相较于水平局地化,垂直局地化是造成分析不平衡的主要原因。对不同大小的垂直局地化相关尺度,随局地化特征尺度变宽,不平衡程度会略有所减缓,但改善不大。这表明垂直局地化造成的不平衡与垂直局地化的相关尺度有关,但其影响较小。此外,采用集合样本统计给出的垂直局地化结构对分析平衡的改善也有限(图略)。
|
| 图 8 背景与分析地面气压倾向随预报时间的演变 (水平局地化尺度为1500 km,background为背景,uv-nonloc为引入集合预报误差但不进行局地化,uv-2dloc为对分析变量进行二维局地化,psi-2dloc为对非平衡分析变量进行二维局地化,psi-3dloc为对非平衡分析变量进行三维局地化) Fig. 8 Temporal evolution of background and analysis surface pressure tendency (the correlation scale of horizontal localization is 1500 km;"background" indicates background field,"uv-nonloc" indicates the introduced ensemble forecast errors without non-localization,"uv-2dloc" indicates horizontal localization on analysis variables,"psi-2dloc" is for horizontal localization on unbalanced analysis variables,"psi-3dloc" is for three-dimensional localization on unbalanced analysis variables) |
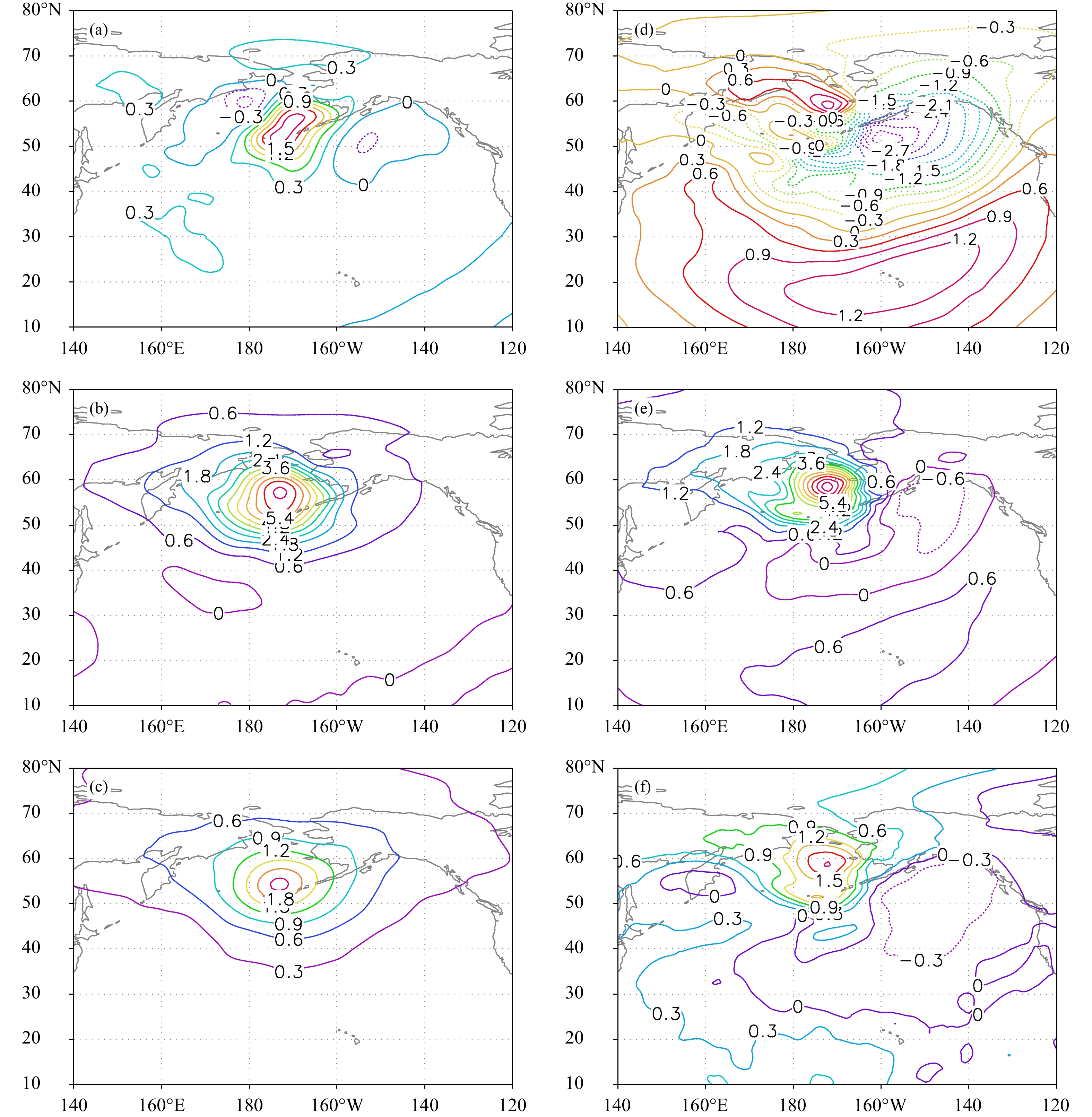
气候背景误差与集合预报误差所起的作用由其权重系数
|
|
图 9 4DVar同化时间窗内分析增量的变化 (a、b. 气候背景误差在
|
对N个集合样本的抽样统计,则对应的蒙特卡洛抽样误差是
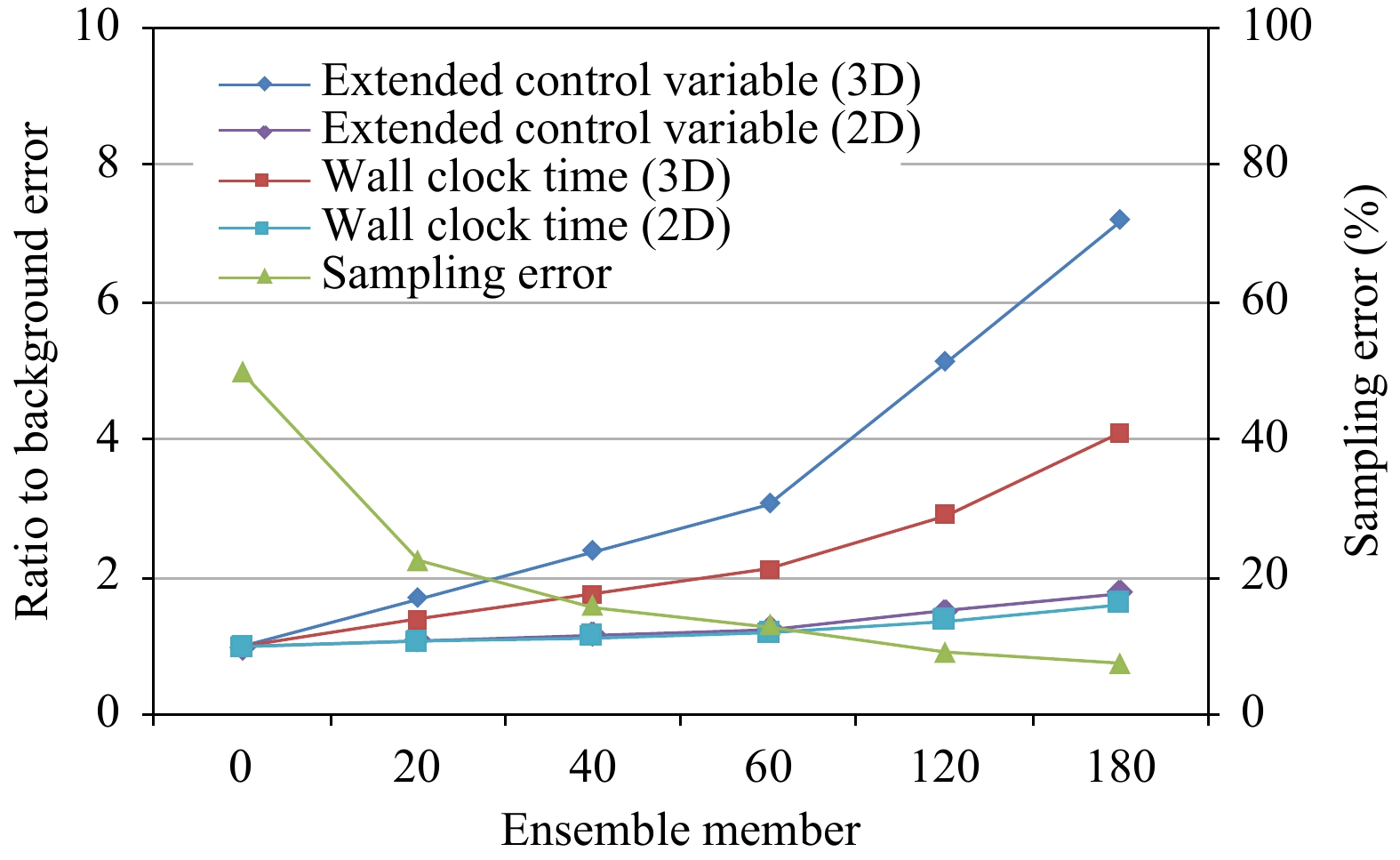
|
| 图 10 增加扩展控制变量与集合样本数对计算效率的影响 (采用GRAPES 3DVar参数配置的数值试验;右侧纵轴为集合样本数对应的抽样误差) Fig. 10 Impacts of adding extended control variables and the number of ensemble samples on computational efficiency (numerical experiment with GRAPES 3DVar configuration;the vertical axis on the right shows the sampling error corresponding to the number of ensemble samples) |
GRAPES模式是中国自主发展的非静力格点模式,全球模式采用三/四维变分资料同化作为分析方法。文中研究在现有四维变分资料同化的基础上,有效使用集合样本估计预报误差扩展变分资料同化的分析能力。围绕GRAPES全球4DVar在具体实施上的特殊性,探讨了在引入扩展控制变量过程中,如何在大于100个集合样本数条件下,增加扩展控制变量的同时能显著降低扩展控制变量的维数增加,并减少对计算机存储和计算的压力,提高算法的实用性。此外,重点研究了水平局地化与垂直局地化对分析场平衡性的影响,通过单点试验、常规与卫星观测资料试验,分析了局地化对地面气压倾向的影响。
研究表明,可以充分利用GRAPES全球4DVar气候背景误差结构模型在水平方向采用谱滤波和在垂直方向采用经验正交分解的特点,利用谱滤波实现水平局地化,利用经验正交分解实现垂直局地化。考虑到水平局地化所采用的相关模型更宽,对谱滤波可以采用更少的波数、更粗的高斯网格来降低扩展控制变量的空间维数。考虑到需要独立定义扩展控制变量所依托的网格,在实施上较为复杂,目前GRAPES变分同化系统只用了较宽的水平特征长度模型,没有再定义独立的高斯网格。对垂直局地化,可以通过仅采用前8个主导特征模态来降低空间的维数,此时主导特征模态方差解释占比超过90%。在引入20—180个集合样本的情形下,对二维局地化,控制变量增加至1.1—1.8倍,墙钟时间增加至1.1—1.6倍。对三维局地化,仅考虑垂直局地化降低空间维数,扩展控制变量增加至1.7—7.1倍,墙钟时间增加至1.4—4.1倍。对100—200个集合样本,引入扩展控制变量的计算机墙钟时间增加可控,文中所发展的引入扩展控制变量的方式具备实用性。
为了减少局地化操作对分析平衡的负面影响,发展水平局地化方案时,先将风压准地转平衡关系抽取出来,然后在非平衡分析变量上进行局地化操作,最后再将风压准地转平衡关系加回到非平衡分析变量上。试验结果表明,相比直接在分析变量空间进行水平局地化,本研究发展的在非平衡分析变量空间进行局地化的方案能更好保持分析场的平衡特征。研究还发现,引入垂直局地化会对分析场平衡特征产生较大影响,但依靠GRAPES全球4DVar目标函数中重力波弱约束控制,分析场仍能保证动力平衡约束关系。
气候背景误差与集合预报误差所起的作用由其权重系数
致 谢:感谢数值预报中心苏勇、孙健、王金成博士对本研究给予的支持。
龚建东, 张林, 王金成. 2020. 背景误差水平相关结构对四维变分资料同化的影响研究. 气象学报. 78(6): 988-1001. Gong J D, Zhang L, Wang J C. 2020. The impact study of background error horizontal correlation structure on 4DVar. Acta Meteor Sinica, 78(6): 988-1001 (in Chinese)
|
刘艳, 薛纪善. 2019. GRAPES的新初始化方案. 气象学报, 77(2): 165-179. Liu Y, Xue J S. 2019. The new initialization scheme of the GRAPES. Acta Meteor Sinica, 77(2): 165-179. (in Chinese) |
王金成, 庄照荣, 韩威等. 2014. GRAPES全球变分同化背景误差协方差的改进及对分析预报的影响: 背景误差协方差三维结构的估计. 气象学报, 72(1): 62-78. Wang J C, Zhuang Z R, Han W, et al. 2014. An improvement of background error covariance in the global GRAPES variational data assimilation and its impact on the analysis and prediction: Statistics of the three-dimensional structure of background error covariance. Acta Meteor Sinica, 72(1): 62-78. (in Chinese) |
王瑞春, 龚建东, 张林等. 2015. 热带风压场平衡特征及其对GRAPES系统中同化预报的影响研究Ⅱ: 动力与统计混合平衡约束方案的应用. 大气科学, 39(6): 1225-1236. Wang R C, Gong J D, Zhang L, et al. 2015. Tropical balance characteristics between mass and wind fields and their impact on analyses and forecasts in GRAPES system. Part Ⅱ: Application of linear balance equation-regression hybrid constraint scheme. Chinese J Atmos Sci, 39(6): 1225-1236. (in Chinese) |
熊春晖, 张立凤, 关吉平等. 2013. 集合-变分数据同化方法的发展与应用. 地球科学进展, 28(6): 648-656. Xiong C H, Zhang L F, Guan J P, et al. 2013. Development and application of ensemble-variational data assimilation methods. Adv Earth Sci, 28(6): 648-656. DOI:10.11867/j.issn.1001-8166.2013.06.0648 (in Chinese) |
薛纪善, 庄世宇, 朱国富等. 2008. GRAPES新一代全球/区域变分同化系统研究. 科学通报, 53(22): 3446-3457. Xue J S, Zhuang S Y, Zhu G F, et al. 2008. Scientific design and preliminary results of three-dimensional variational data assimilation system of GRAPES. Chinese Sci Bull, 53(22): 3446-3457. (in Chinese) |
Anderson J L. 2001. An ensemble adjustment Kalman Filter for data assimilation. Mon Wea Rev, 129(12): 2884-2903. DOI:10.1175/1520-0493(2001)129<2884:AEAKFF>2.0.CO;2 |
Bannister R N. 2008. A review of forecast error covariance statistics in atmospheric variational data assimilation.Ⅱ: Modelling the forecast error covariance statistics. Quart J Roy Meteor Soc, 134(637): 1971-1996. DOI:10.1002/qj.340 |
Bonavita M, Isaksen L, Hólm E. 2012. On the use of EDA background error variances in the ECMWF 4D-Var. Quart J Roy Meteor Soc, 138(667): 1540-1559. DOI:10.1002/qj.1899 |
Bowler N E, Clayton A M, Jardak M, et al. 2017. The effect of improved ensemble covariances on hybrid variational data assimilation. Quart J Roy Meteor Soc, 143(703): 785-797. DOI:10.1002/qj.2964 |
Buehner M. 2005. Ensemble-derived stationary and flow-dependent background-error covariances: Evaluation in a quasi-operational NWP setting. Quart J Roy Meteor Soc, 131(607): 1013-1043. DOI:10.1256/qj.04.15 |
Buehner M, Houtekamer P L, Charette C, et al. 2010a. Intercomparison of variational data assimilation and the ensemble Kalman filter for global deterministic NWP. PartⅠ: Description and single-observation experiments. Mon Wea Rev, 138(5): 1550-1566. DOI:10.1175/2009MWR3157.1 |
Buehner M, Houtekamer P L, Charette C, et al. 2010b. Intercomparison of variational data assimilation and the ensemble Kalman filter for global deterministic NWP. PartⅡ: One-month experiments with real observations. Mon Wea Rev, 138(5): 1567-1586. DOI:10.1175/2009MWR3158.1 |
Buehner M, Morneau J, Charette C. 2013. Four-dimensional ensemble-variational data assimilation for global deterministic weather prediction. Nonlin Processes Geophys, 20(5): 669-682. DOI:10.5194/npg-20-669-2013 |
Chen L L, Chen J, Xue J S, et al. 2015. Development and testing of the GRAPES regional ensemble-3DVar hybrid data assimilation system. J Meteor Res, 29(6): 981-996. DOI:10.1007/s13351-015-5021-y |
Clayton A M, Lorenc A C, Barker D M. 2013. Operational implementation of a hybrid ensemble/4D-Var global data assimilation system at the Met Office. Quart J Roy Meteor Soc, 139(675): 1445-1461. DOI:10.1002/qj.2054 |
Courtier P, Thépaut J N, Hollingsworth A. 1994. A strategy for operational implementation of 4D-Var: Using an incremental approach. Quart J Roy Meteor Soc, 120(519): 1367-1387. DOI:10.1002/qj.49712051912 |
Evensen G. 1994. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J Geophys Res, 99(C5): 10143-10162. DOI:10.1029/94JC00572 |
Fairbairn D, Pring S R, Lorenc A C, et al. 2014. A comparison of 4DVar with ensemble data assimilation methods. Quart J Roy Meteor Soc, 140(678): 281-294. DOI:10.1002/qj.2135 |
Houtekamer P L, Mitchell H L. 2005. Ensemble Kalman filtering. Quart J Roy Meteor Soc, 131(613): 3269-3289. DOI:10.1256/qj.05.135 |
Kalnay E. 2003. Atmospheric Modeling, Data Assimilation and Predictability. Cambridge: Cambridge University Press, 175-185
|
Kepert J D. 2009. Covariance localisation and balance in an Ensemble Kalman Filter. Quart J Roy Meteor Soc, 135(642): 1157-1176. DOI:10.1002/qj.443 |
Kleist D T, Ide K. 2015a. An OSSE-Based evaluation of hybrid variational-ensemble data assimilation for the NCEP GFS. PartⅠ: System description and 3D-hybrid results. Mon Wea Rev, 143(2): 433-451. DOI:10.1175/MWR-D-13-00351.1 |
Kleist D T, Ide K. 2015b. An OSSE-Based evaluation of hybrid variational-ensemble data assimilation for the NCEP GFS. Part Ⅱ: 4DEnVar and hybrid variants. Mon Wea Rev, 143(2): 452-470. DOI:10.1175/MWR-D-13-00350.1 |
Lorenc A C. 1986. Analysis methods for numerical weather prediction. Quart J Roy Meteor Soc, 112(474): 1177-1194. DOI:10.1002/qj.49711247414 |
Lorenc A C. 2003a. Modelling of error covariances by 4D-var data assimilation. Quart J Roy Meteor Soc, 129(595): 3167-3182. DOI:10.1256/qj.02.131 |
Lorenc A C. 2003b. The potential of the ensemble Kalman filter for NWP: A comparison with 4D-Var. Quart J Roy Meteor Soc, 129(595): 3183-3203. DOI:10.1256/qj.02.132 |
Lorenc A C, Bowler N E, Clayton A M, et al. 2015. Comparison of hybrid-4DEnVar and Hybrid-4DVar data assimilation methods for global NWP. Mon Wea Rev, 143(1): 212-229. DOI:10.1175/MWR-D-14-00195.1 |
Mitchell H L, Houtekamer P L, Pellerin G. 2002. Ensemble size, balance, and model-error representation in an Ensemble Kalman filter. Mon Wea Rev, 130(11): 2791-2808. DOI:10.1175/1520-0493(2002)130<2791:ESBAME>2.0.CO;2 |
Wang X G, Snyder C, Hamill T M. 2007. On the theoretical equivalence of differently proposed ensemble: 3DVAR hybrid analysis schemes. Mon Wea Rev, 135(1): 222-227. DOI:10.1175/MWR3282.1 |
Wang X G, Parrish D, Kleist D, et al. 2013. GSI 3DVar-based ensemble-variational hybrid data assimilation for NCEP global forecast system: Single-resolution experiments. Mon Wea Rev, 141(11): 4098-4117. DOI:10.1175/MWR-D-12-00141.1 |
Xu Q, Lu H J, Gao S T, et al. 2008a. Time-expanded sampling for ensemble Kalman filter: Assimilation experiments with simulated radar observations. Mon Wea Rev, 136(7): 2651-2667. DOI:10.1175/2007MWR2185.1 |
Xu Q, Wei L, Lu H J, et al. 2008b. Time-expanded sampling for ensemble-based filters: Assimilation experiments with a shallow-water equation model. J Geophys Res, 113(D2): D02114. |
Zhang L, Liu Y Z, Liu Y, et al. 2019. The operational global four-dimensional variational data assimilation system at the China Meteorological Administration. Quart J Roy Meteor Soc, 145(722): 1882-1896. DOI:10.1002/qj.3533 |
 2021, Vol. 79
2021, Vol. 79