中国气象学会主办。
文章信息
- 张华龙, 伍志方, 肖柳斯, 涂静. 2021.
- ZHANG Hualong, WU Zhifang, XIAO Liusi, TU Jing. 2021.
- 基于因子分析的广东省短时强降水预报模型及其业务试验
- A probabilistic forecast model of short-time heavy rainfall in Guangdong province based on factor analysis and its operational experiments
- 气象学报, 79(1): 15-30.
- Acta Meteorologica Sinica, 79(1): 15-30.
- http://dx.doi.org/10.11676/qxxb2020.076
文章历史
-
2020-06-23 收稿
2020-10-13 改回
2. 中国气象局广州热带海洋气象研究所/广东省区域数值天气预报重点实验室,广州,510640;
3. 广州市气象台,广州,511430
2. Institute of Tropical and Marine Meteorology/ Key Laboratory of Regional Numerical Weather Prediction,CMA,Guangzhou 510640,China;
3. Guangzhou Meteorological Observatory,Guangzhou 511430,China
广东省地处亚热带季风气候区,短时强降水频率和最大小时雨强在中国均位于最高水平(陈炯等,2013)。短时强降水多由中小尺度系统造成,具有尺度小、突发性强、生命期短、致灾严重的特点,已有一些研究总结了广东短时强降水出现的不同天气流型配置(伍志方等,2016;陈元昭等,2016)以及华南前、后汛期引发强降水的天气系统配置(王坚红等,2014;梁巧倩等,2019)。边界层急流(Du,et al,2018)、华南复杂地形特别是海陆对比(Chen,et al,2018)在华南强降雨演变过程中起重要作用,这些要素之间的特殊相互作用是复杂的,导致了华南强降水的独特特征,致使预报存在相当大的困难(Luo,et al,2020)。如2017年广州“5•7”特大暴雨过程,增城新塘镇记录雨强184.4 mm/h,各主流模式对该区域仅预报小雨或中雨级别降水(伍志方等,2018),造成业务预报的严重漏报。在目前数值模式对于华南降水预报评分仍较低的情况下(Zhang,et al,2016),利用天气过程的物理参数建立综合多方面要素的预报模型,是一个有益尝试。
短时强降水属于强对流天气现象之一,不同类别的强对流具有不一样的环境条件和物理量阈值特征,目前已有较多研究工作利用观测或再分析资料计算强对流发生的物理量,并使用统计后处理技术或机器学习方法构建预报模型,在雷电(Gijben,et al,2017;Bates,et al,2018)、强雷暴(Gallo,et al,2018)、强冰雹(Mohr,et al,2015)和龙卷(Simon,et al,2018)的预测上取得一定效果。这种基于构成要素预报强对流的方法称“配料法”(俞小鼎等,2020)。中国国家气象中心较早基于“配料法”思路开展强对流天气概率预报业务(张小玲等,2012),之后一些研究通过模式输出参数进行统计后处理,构建短时强降水预报模型。雷蕾等(2012)基于快速更新循环同化预报系统(BJ-RUC模式)计算了一系列物理量,探索对强对流天气分类预报的可行性。曾明剑等(2015)应用相对偏差模糊矩阵评价技术,对中尺度模式输出的对流参数进行逐次筛选和权重分配,构建分类强对流天气预报概率模型并业务应用。朱月佳等(2019)借鉴“配料法”的思路建立基于集合预报的对流联合概率预报方法,对区域性集中短时强降水取得较好的应用效果。洪伟等(2018)利用ECMWF全球模式细网格预报产品,通过物理量阈值判定和箱形图差异指数评估与短时强降水发生敏感度的方法建立短时强降水预报模型。
多数概率预报方法均直接以物理量作为模型预报因子。当物理量数增多时,某些无效物理量的引入会影响预测模型效果,因此需要构建合理的物理量筛选标准;另外,部分物理量之间的相关也会为模型带来冗余信息。为简化模型的输入变量,可对物理量进行二次处理,减少因子数量,提高因子的有效性。因子分析是一种构建少数几个因子描述多个指标联系的方法,能够从变量的方差/协方差结构入手,在尽可能多地保留原始变量信息的基础上,用少数新变量来解释原始变量。由于因子模型的特性,能够对包含复杂信息的对流性降水(Godart,et al,2010)和极端强降水(Felzer,et al,2020)的环境因子进行有效分析,并基于因子分析改进预报模型(熊开国等,2012;农孟松等,2011)。
为解决一般物理量预测短时强降水出现的命中率和虚警率同步上升而导致TS评分降低的问题,提高模型预测有效性,文中以显著性(物理量与多年平均态的差异)和敏感性(特征曲线面积)为标准,筛选在业务应用中具有较低虚警率和高预报技巧的物理量。广东省北依南岭,南邻南海,在华南前、后汛期,不同区域气候和降水特征差异大,导致短时强降水发生时各物理量与多年平均态偏差的差异显著,若采用所有数据样本直接进行因子建模,将导致因子预测能力减弱。为此文中按照前、后汛期以及不同区域的有效因子特征,建立分期、分区短时强降水概率预报模型。在实际业务应用中,将欧洲中期天气预报中心细网格数值模式(ECMWF-Fine)预报数据输入概率预报模型,形成短时强降水0—36 h逐6 h概率预报产品。除提供概率预报外,模型还可输出多个独立因子,分别反映短时强降水发生、发展的不同环境特征,可提供有利条件的定量指标,帮助识别不同类型的短时强降水,为主观预报短时强降水落区、强度提供参考。
2 数据处理与预报模型建立方法 2.1 数据处理建模实况数据为广东省区域地面气象站(包含基本站和自动站)的小时雨量数据。自动气象站雨量资料经过质量控制处理:若某一站点记录到20 mm/h以上降水量,但以该站为中心,50 km半径范围内的其余站点均无降水,则认为该短时强降水记录可疑;当1 a内某一站点缺测数据比例超过5%,则视为故障站点。故障站点当年的数据与可疑数据均不作为短时强降水事件记录。基于站点观测记录,构建与ERA-Interim具有相同空间分辨率(0.125°)的格点数据集并进行参数统计(曾明剑等,2015),方法如下:遍历所有格点,在再分析资料时次对应代表时段(前后3 h)内,若格点区域内有站点记录到≥20 mm/h降水,则认为该格点出现了短时强降水。
文中使用欧洲中期天气预报中心的再分析同化数据集(ERA-Interim)计算相关物理量。ERA-Interim作为目前广泛使用的再分析资料,使用四维变分同化技术同化了大量卫星观测资料,结合多种误差校正技术实现了资料质量的提升,对于形势场具有较好的反映能力(Dee,et al,2011;慕丹等,2018),在中国地形复杂、观测资料稀缺的地区具有较好的适用性(Bao,et al,2013)。建模数据样本训练期为2009—2018年的4—9月,测试期为2019年4—9月,模型效果验证和业务运行均使用ECMWF-Fine预报场。ECMWF-Fine提供1天2次起报(08时与20时,北京时,下同)、地面要素空间分辨率为0.125°、高空要素分辨率为0.25°的预报;为生成0.125°分辨率的模型输出产品,将高空预报要素进行双线性插值,形成与地面要素分辨率(0.125°)一致的格点场。将ECMWF-Fine预报场计算的物理量参数输入概率预报模型,生成0—36 h逐6 h短时强降水客观概率预报产品。
2.2 建模方法 2.2.1 物理量计算与遴选利用各层次ERA-Interim资料风、温度、湿度、气压等要素,计算49个反映大气动力、热力的物理量(见附录表1)。为减少气候背景差异对建模的影响,对物理量进行多年平均态扣除处理:对应某一天的某个时次,计算多年(2001—2018年)当天及前后各2 d(共5 d)同一时次的物理量平均值。
| 物理量排序 | 物理量名称 | 敏感性指数 | 显著性指数 | 综合评价得分 |
| 1 | 大气可降水量 | 9.13 | 880.0 | 2.25 |
| 2 | 大气垂直液态水积分 | 9.13 | 856.2 | 2.21 |
| 3 | 925 hPa 相对湿度 | 7.98 | 774.4 | 1.74 |
| 4 | K 指数 | 7.28 | 798.2 | 1.58 |
| 5 | 700 hPa 相对湿度 | 7.67 | 734.0 | 1.58 |
| 6 | 修正 K 指数 | 7.45 | 734.7 | 1.52 |
| 7 | 850 hPa 相对湿度 | 6.67 | 689.2 | 1.22 |
| 8 | 对流有效位能 | 7.83 | 358.1 | 0.98 |
| 9 | 850 hPa 假相当位温 | 6.48 | 544.7 | 0.91 |
| 10 | 中低层垂直速度积分 | 8.00 | 257.1 | 0.85 |
| 11 | 925 hPa 假相当位温 | 6.55 | 453.5 | 0.77 |
| 12 | 1000 hPa 假相当位温 | 6.50 | 409.2 | 0.68 |
| 13 | 700 hPa 垂直速度 | 7.42 | 209.3 | 0.60 |
| 14 | 500 hPa 垂直速度 | 7.33 | 215.7 | 0.59 |
| 15 | 850 hPa 垂直速度 | 7.06 | 174.5 | 0.44 |
| 16 | 850 hPa 涡度 | 6.83 | 144.6 | 0.32 |
| 17 | 总指数 | 5.37 | 331.0 | 0.23 |
| 18 | 500 hPa 涡度 | 6.55 | 122.2 | 0.20 |
| 19 | 925 hPa 水汽通量散度 | 6.42 | 141.8 | 0.20 |
| 20 | 925 hPa 散度 | 6.28 | 138.2 | 0.16 |
| 21 | 850 hPa 水汽通量 | 6.00 | 137.7 | 0.07 |
| 22 | 700 hPa 涡度 | 6.06 | 72.5 | −0.02 |
| 23 | 能量螺旋度指数 | 5.79 | 0.5 | −0.22 |
| 24 | 850 hPa 散度 | 5.17 | 98.7 | −0.23 |
| 25 | 850 hPa 水汽通量散度 | 5.09 | 92.0 | −0.26 |
| 26 | 200—850 hPa 散度差 | 4.99 | 87.4 | −0.30 |
| 27 | 925 hPa 水汽通量 | 5.17 | 34.0 | −0.34 |
| 28 | 风暴螺旋度 | 5.31 | −18.4 | −0.39 |
| 29 | 850 hPa 比湿 | 4.38 | 105.1 | −0.45 |
| 30 | 925—500 hPa 假相当位温差 | 4.27 | 117.9 | −0.46 |
| 31 | 2 km 以下风暴螺旋度 | 5.10 | −37.3 | −0.49 |
| 32 | 925 hPa 假相当位温平流 | 4.43 | 64.0 | −0.50 |
| 33 | 925—700 hPa 风切变 | 4.62 | −2.5 | −0.56 |
| 34 | 850—500 hPa 假相当位温差 | 3.79 | 117.9 | −0.59 |
| 35 | 850 hPa 假相当位温平流 | 4.18 | 43.4 | −0.61 |
| 36 | 粗理查德森数 | 4.45 | −5.3 | −0.62 |
| 37 | 925—700 hPa 假相当位温差 | 4.02 | 44.5 | −0.65 |
| 38 | 850—500 hPa 温度差 | 4.12 | 21.1 | −0.67 |
| 39 | 925—500 hPa 风切变 | 4.32 | −48.4 | −0.73 |
| 40 | 300 hPa 散度 | 3.96 | −11.1 | −0.77 |
| 41 | 925—700 hPa 温度差 | 3.98 | −27.7 | −0.79 |
| 42 | 700 hPa 散度 | 3.77 | −17.8 | −0.83 |
| 43 | 850—500 hPa 风切变 | 4.08 | −89.3 | −0.87 |
| 44 | 低层总比湿 | 3.47 | −15.0 | −0.91 |
| 45 | 925 hPa 比湿 | 3.19 | −83.8 | −1.11 |
| 46 | 700 hPa 比湿 | 2.98 | −62.8 | −1.14 |
| 47 | 925—500 hPa 温度差 | 3.11 | −123.1 | −1.20 |
| 48 | 200 hPa 散度 | 2.08 | −211.1 | −1.65 |
| 49 | 边界层高度 | 1.99 | −228.0 | −1.71 |
为遴选具有更好指示意义的物理量作为建模参数,以显著性指标和敏感性指标为标准。显著性即短时强降水发生时物理量与多年平均态差异的显著性。用T检验量作为评价指标,计算公式
| $ T=\frac{\overline {X}}{\dfrac{{\sigma }_{x}}{\sqrt{n-1}}} $ | (1) |
式中,
除考虑显著性以外,引入特征曲线面积(AROC,Area under Receiver Operating Characteristic Curve)(Richardson,2000)作为敏感性指标,该指标衡量物理量作为预报因子识别短时强降水发生的能力,值越大,预报技巧越高,对事件预报的敏感性越优。图1为49个物理量对应的受试者操作特征曲线(ROC,Receiver Operating Characteristic Curve)(Richardson,2000),其中红线为24个T检验量显著性较高的指标,可见,并非所有显著性高的因子均具有较优的敏感性,部分红线对应物理量的AROC处于较低分位水平,表明两个指标的优势参数并不具有一致性。

|
| 图 1 49个物理量受试者操作特征曲线 (AROC为受试者操作特征曲线与y=x函数线围成的面积;红、蓝色线分别代表在所有物理量的显著性检验中,显著度位于前50%分位、后50%分位的物理量) Fig. 1 ROC curves of 49 physical parameters (AROC represents the area surrounded by the ROC curve and the y=x line;Red lines and blue lines respectively represent physical parameters ranking the top 50% and the last 50% in the significance test of all physical parameters) |
对所有物理量的T和AROC两个指标进行标准化处理并相加,计算综合评价指标。综合评价指标较小的物理量,倾向于对应某一指标值较低,或两个指标优势均不明显(见附录表1)。文中挑选综合评价指标最大的18个物理量作为建模参数,对遴选的18个物理量利用因子分析方法,组合成6个表征热力、动力、水汽等不同物理特性的因子,并赋予不同权重。
2.2.2 因子分析基于2.2.1节选取的18个物理量进行因子分析,因子分析的算法核心是将p个物理量
| $ {{x}}={{Af}}+{{u}} $ | (2) |
式中,A为因子分析法的因子荷载矩阵,通过对原始变量(
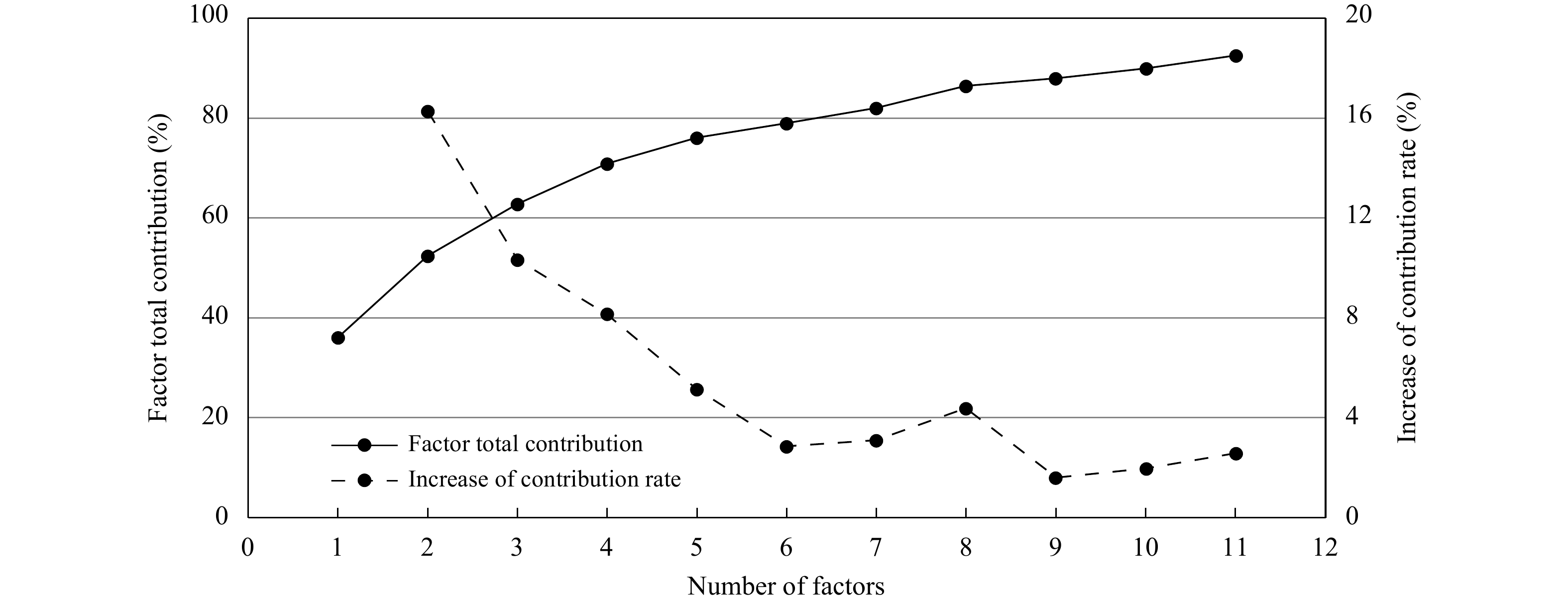
|
| 图 2 因子总贡献和贡献率增加值随因子数变化 Fig. 2 Total factor contribution and the variation of increase in the contribution rate with the number of factors |
图3为式(2)计算的载荷系数矩阵A。载荷系数反映了因子与物理量的相关性,同一因子对应的几个高载荷物理量所代表的共同物理意义反映了因子主要特征。如物理量组合因子1(简称组合因子1,其余因子同)系数较高的物理量分别为1000、925和850 hPa的假相当位温、总指数、修正K指数与K指数等,可知主要是反映大气的热力不稳定尤其是低层(850 hPa以下)能量增长的因子。组合因子2的高相关物理量为大气垂直液态水积分和大气可降水量,主要是反映大气水汽变化的因子;组合因子3的高相关物理量为500 hPa垂直速度、700 hPa垂直速度与中低层垂直速度积分,主要反映大气中层垂直运动条件;组合因子4的高相关物理量为修正K指数、K指数、700 hPa相对湿度和总指数;组合因子5的高相关物理量为850 hPa垂直速度和涡度、700 hPa垂直速度与中低层垂直速度积分;组合因子6的高相关物理量为850 hPa假相当位温和相对湿度、总指数、K指数。
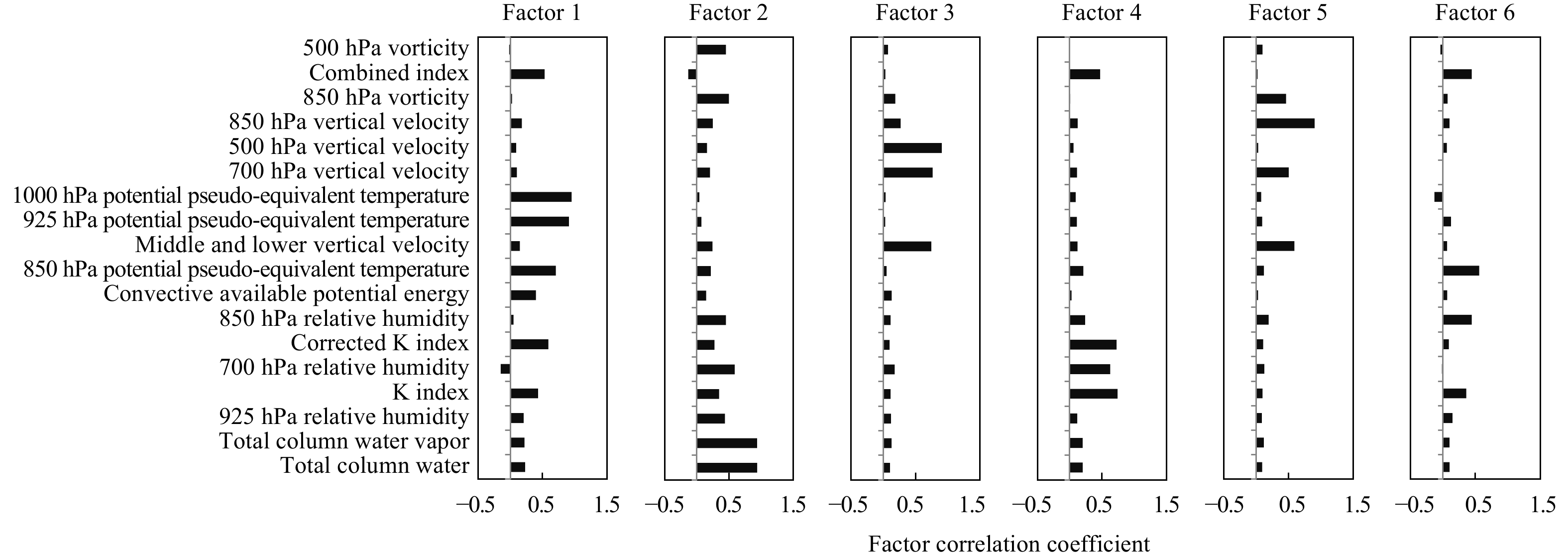
|
| 图 3 6个物理量组合因子对应遴选出的18个物理量的因子相关系数 Fig. 3 The load coefficients of 18 selected physical parameters corresponding to 6 factors |
因子概率通过对因子得分处理得到,因子得分通过Thompson方法(Devlieger,et al,2016)计算所得,即对2.2.2节计算的因子载荷矩阵A采用正交旋转变换,计算公式为
| $ \widehat{{{F}}}={{{A}}}^{{'}}{{{R}}}^{-1}{{X}} $ | (3) |
式中,
重组后的因子概率指示短时强降水的效果较单一物理量更好。以组合因子1为例,该因子的AROC显著大于6个高权重物理量(图4a);对比该因子与各物理量在30%预测阈值时的虚警率与命中率(图4b),可以发现该因子的虚警率(35%)低于所有单个物理量,而命中率(88.2%)与6个物理量相比接近(相差在1%范围内)。因此物理量组合后的因子模型在保证具有较高命中率的同时,显著降低了虚警率,体现了优化模型因子的效果。
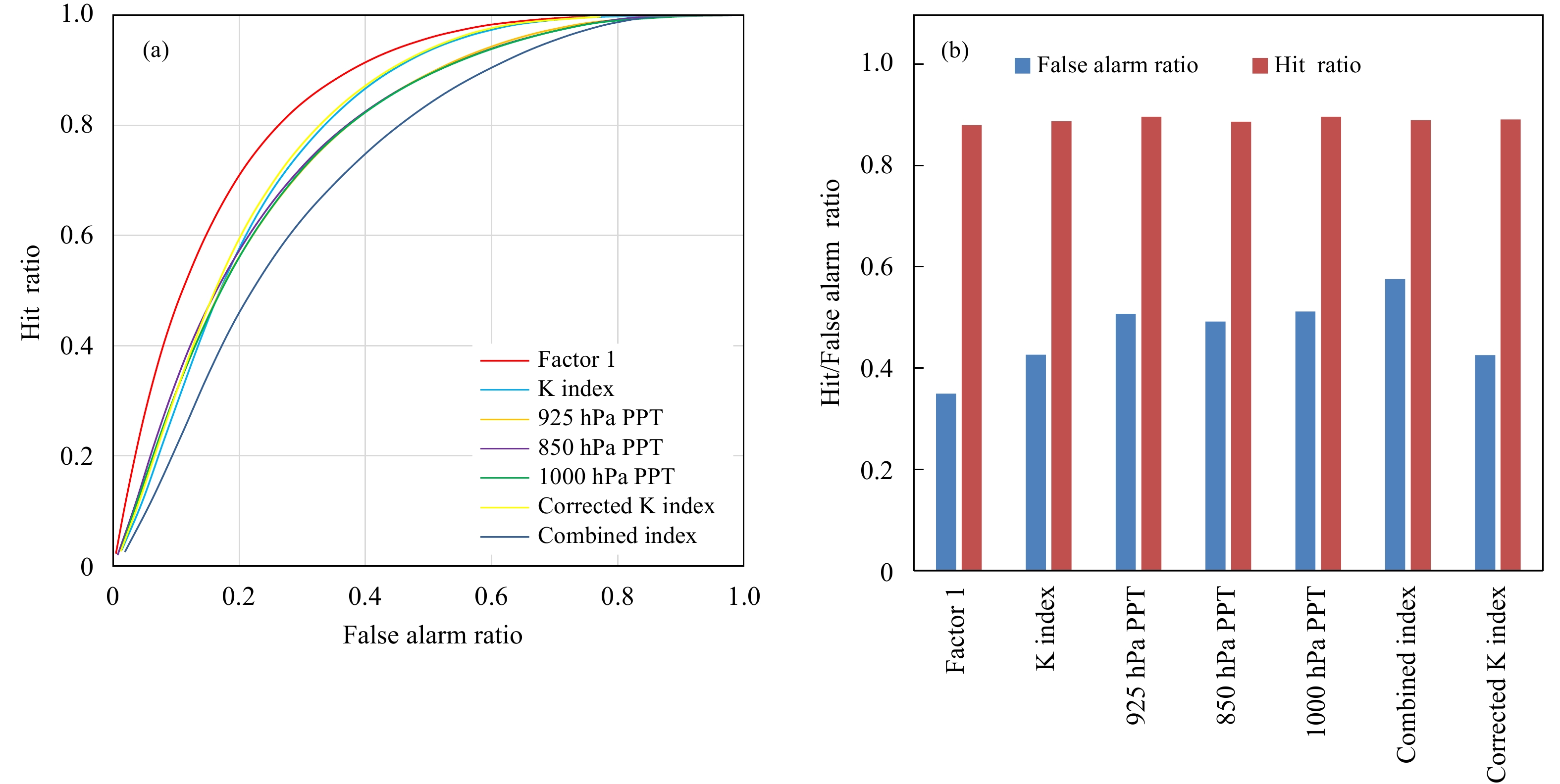
|
| 图 4 组合因子1与高相关物理量受试者操作特征曲线检验 (a)、虚警率与命中率 (b) (a选取物理量为构成组合因子1相关系数较高的物理量,b为各因子与物理量对应30%分位预测阈值时的虚警率与命中率,PPT为假相当位温缩写) Fig. 4 ROC tests (a),false alarm ratio and hit ratio (b) of Factor 1 and its highly correlated physical parameters (Physical parameters which are highly correlated with Factor 1 are selected. Fig. 4b presents the false alarm ratio and hit ratio of Factor 1 and each physical parameter corresponding to 30% fractional forecast threshold value. PPT is the abbreviation name of potential pseudo-equivalent temperature) |
在业务中为应用概率预报模型生成产品,利用ECMWF-Fine预报数据,通过2.2.3节的处理步骤计算各因子概率;进一步对6个因子概率进行加权组合,形成综合概率预报模型。各个因子概率的权重为因子贡献率占总贡献的比值(因子贡献率计算方法见2.2.2节),因子贡献率占比越大,则该因子对环境物理量变化的总方差贡献越大,可在预报结果中有效体现大气环境参数的主要变化特征。当因子数为6时,因子总贡献率为75.9%,单个因子的权重值是因子贡献率占6个因子总贡献率的比值。因此综合概率计算公式为
| $\begin{split} {F_{{\rm{all}}}} =& ( 19.1 {f_1}\! +\! 18.9 {f_2} \!+\! 12.2 {f_3} \!+\! 10.8 {f_4} \!+\! 9.8 {f_5} \!+\! 5.2 {f_6} )/75.9 \end{split}$ | (4) |
式中,
由于前、后汛期广东省短时强降水的气候背景与环流形势明显不同(梁巧倩等,2019),致使各物理量阈值分布也具有显著差别,因此首先对因子进行时、空统计,划分因子特征相似的时期与区域,进而建立独立模型,以提升模型有效性。为体现因子得分相对于多年平均态的偏离幅度,定义短时强降水对应的各因子偏离度(FB,Factor Bias)。
| $ {\rm{FB}}=\frac{{F}_{i}-{F}_{\rm{mean}}}{{F}_{\rm{mean}}} $ | (5) |
式中,
图5为广东省范围内所有格点的因子偏离度逐月变化,前汛期(4—6月)所有因子偏离度随月份增长均呈下降态势,但不同因子的偏离度差异较小,显著小于后汛期(7—9月);后汛期除组合因子1随月份增长而增大外,其余因子均维持相对稳定。与动力和水汽条件相关的因子(组合因子2、3、5)偏离度比较一致,但与热力条件相关的因子(组合因子1、4、6)偏离度均低于动力和水汽因子,且因子间偏离度有明显差异,上述特征表明,随着季节逐渐从前汛期过渡到后汛期,上、下气层间的热力差异逐渐减小,组合因子1的相对重要性也不断下降。值得注意的是,多数因子在6月出现谷值,可能与该月短时强降水发生频率较高有关,过多的样本量导致因子偏离度较低。上述因子偏离度差异特征可作为前、后汛期独立建模的依据。
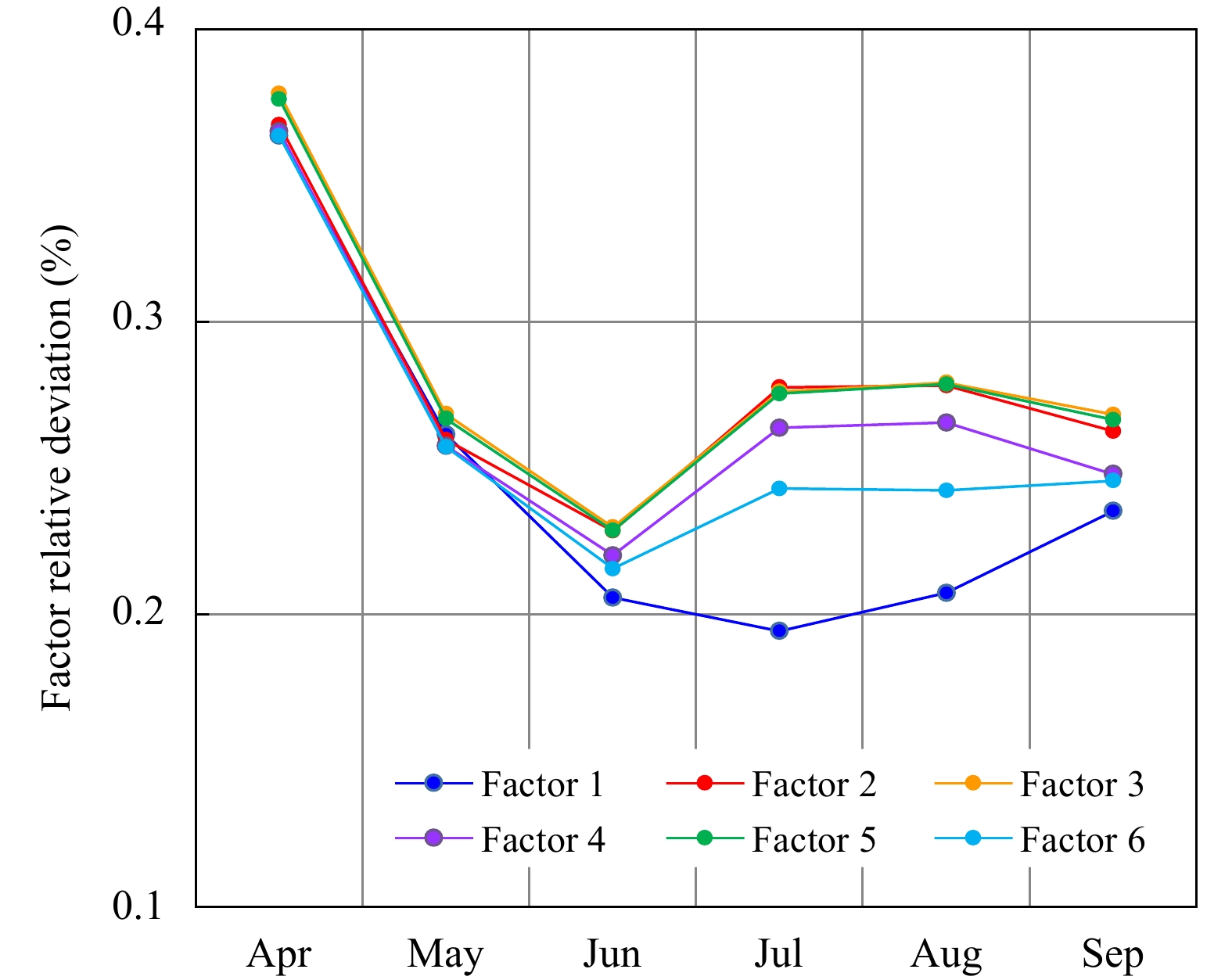
|
| 图 5 不同月份广东省短时强降水因子偏离度 Fig. 5 SHR deviation rates of individual factors in Guangdong in different months |
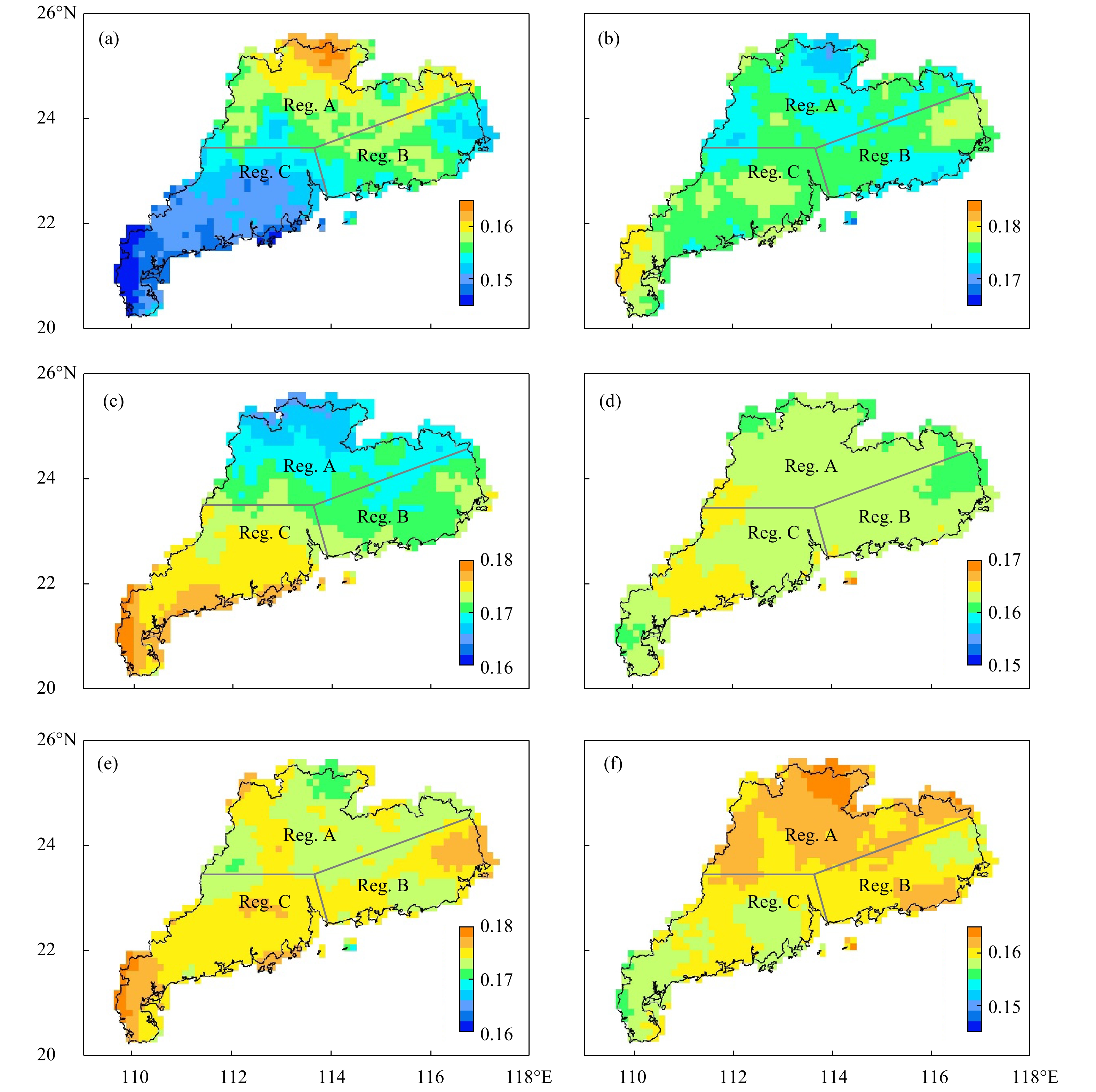
除季节差异外,不同地区的气候背景差异(孙喜艳等,2017)亦导致不同地域因子偏离度不同。为体现因子偏离的空间分布特征,计算广东省区域格点因子偏离度占所有格点总因子偏离度的比值,作为因子的相对偏离度,反映各因子对不同区域的相对重要性。由图6可见,除组合因子4外,其余因子在广东省北部和西南部均具有反向分布特征,组合因子1相对偏离度较高的区域(粤北),不稳定能量条件对于短时强降水重要性高于相对偏离度较小的区域(粤西南)(图6a);与之类似,组合因子3的南北差异(图6c)表明垂直运动条件对于粤西南的短时强降水发生具有更重要作用。组合因子2、5、6也有类似的南北差异特征,且高、低值分布区域相似。因此,在分区建模中,考虑到上述因子相对偏离度的空间分布特征,以及广东沿海两个降水中心与内陆降水中心性质的不同(王坚红等,2017;Li,et al,2008),将广东省划分为3个区域进行单独建模(图6a)。
|
| 图 6 汛期短时强降水的因子相对偏离度空间分布与区域划分 (色阶为各因子相对偏离度,Reg. A—C分别对应3个独立建模区域,a—f. 组合因子1—6) Fig. 6 Spatial distributions of factor relative deviation rate of SHR in flood season (Color shadings represent relative deviation rate of each factor,Reg. A—C represent three independent areas for model training,a—f. respectively indicate Factor 1—6) |
基于上述的分时期与分区域方法,可形成6个因子模型,在相同的因子数目下,不同模型选取的物理量、各因子贡献率、组成各因子的物理量的权重系数均有差别。进行时、空分区的独立建模后,其应用效果较未分区前模型有一定改善,尤其对于广东省西南部地区,短时强降水的命中率明显提升(图略)。
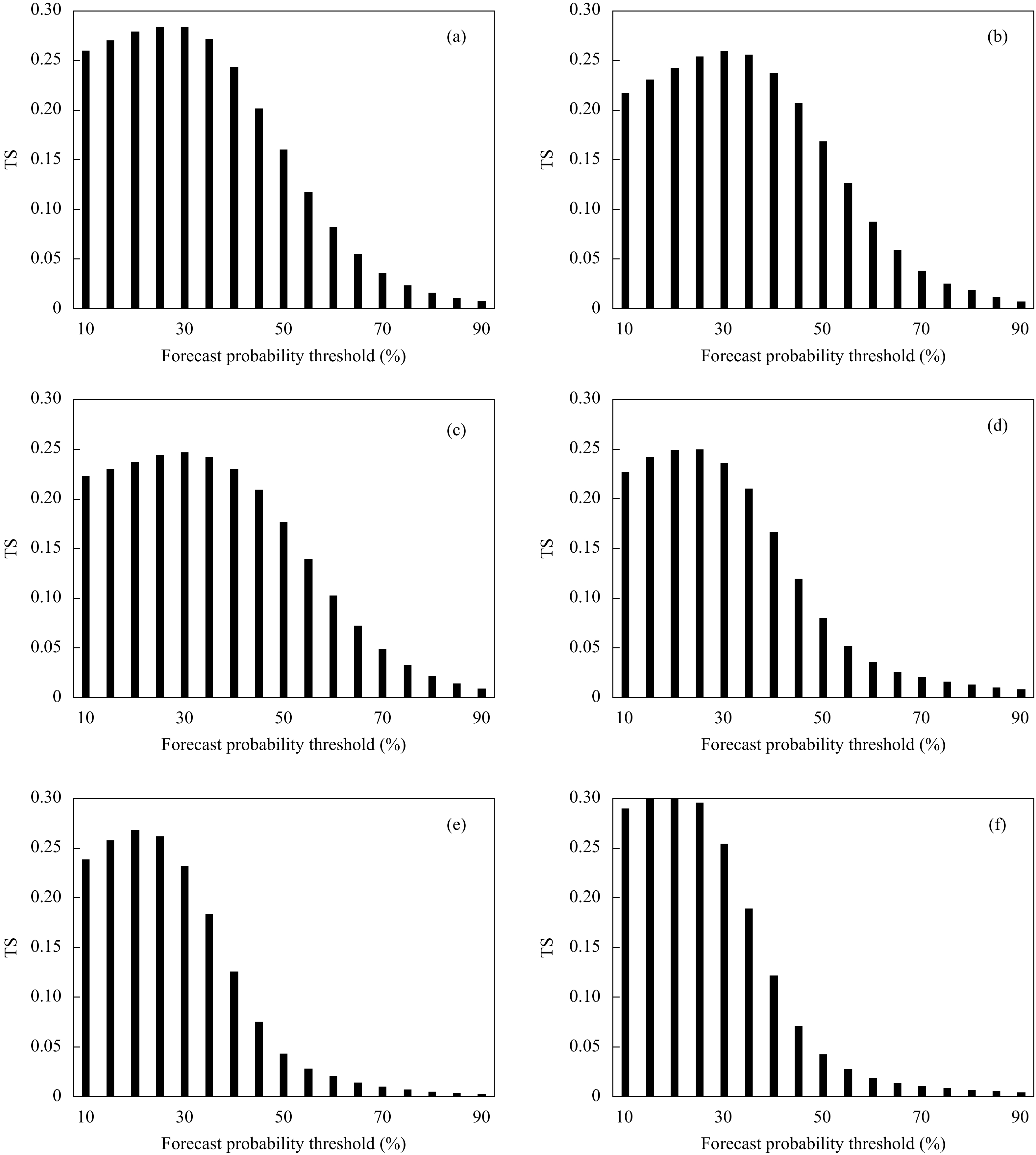
4 概率预报模型效果检验 4.1 TS评分检验为检验概率模型的业务应用效果,对测试期(2019年4—9月)模型输出结果进行检验。由于模型输出为概率值,为得到格点短时强降水预报产品,需要设定一个固定概率值作为预测概率阈值,阈值的选取方法为:对训练期间前、后汛期和不同区域设置不同的因子概率阈值,检验对应短时强降水TS评分,以最优TS评分对应概率值作为预报业务中的短时强降水的预测概率阈值。图7为不同区域和时期预测概率阈值对应的TS评分,可见,随着概率阈值增大,TS评分均为先增大、后减小的趋势,当概率阈值大于40%时,命中率迅速下降。以分区、分期的最优TS评分对应的概率阈值代入预测模型,并在测试期进行检验,具体概率阈值见表1。检验方案为:参考洪伟等(2018)区块TS检验方法,对广东省区域划分为空间分辨率更高的0.5°×0.5°网格,同时采用更精细的时间尺度,预报时段为每天两次起报(08、20时)12 h预报时效内的逐6 h产品,如08时起报,则检验14和20时的短时强降水,对应短时强降水实况时段分别为11—17时、17—23时。在判定区块的对应时段内,若有2个以上的测站记录到>20 mm/h降水,则认为实况出现短时强降水。
| 区域 | Reg. A | Reg. B | Reg. C |
| 前汛期 | 25% | 30% | 30% |
| 后汛期 | 25% | 20% | 20% |
|
| 图 7 训练期分期、分区模型不同预测概率阈值与对应TS评分 (a. 前汛期Reg. A,b. 前汛期Reg. B,c. 前汛期Reg. C,d. 后汛期Reg. A,e. 后汛期Reg. B,f. 后汛期Reg. C) Fig. 7 TS corresponding to different probability thresholds of the forecast model in different regions and periods during the training period (Results of Reg. A,Reg. B and Reg. C during pre-flood season are respectively shown in (a,b,c),and results of Reg. A,Reg. B and Reg. C during post-flood season are respectively shown in (d,e,f)) |
为体现上述方法相对确定性模式要素预报的优势,将模型结果与业务常用的ECMWF-Fine雨量预报产品进行对比。由于ECMWF-Fine预报产品时间分辨率为3 h,并且检验评估表明ECMWF-Fine对华南对流性降水经常低估(Huang,et al,2017),因此对确定性模式采取较宽松的标准:当检验时段对应格点内3 h累计雨量预报最大值超过20 mm,则判定预报为短时强降水。另外,为考察模型对短时强降水的预报偏差,计算逐个格点的偏差(Bias)(江崟等,2019),当偏差大于1时,表明模型虚警较多,值越大,虚警越严重;当偏差小于1时,模型漏报较多。图8为上述模型与ECMWF-Fine模式的检验结果对比,可见,无论前汛期或后汛期,概率模型在全省大部分地区TS评分均在0.25以上,前汛期TS评分高值(>0.30)区位于珠江三角洲及粤北地区(图8a),最大TS评分超过0.42;后汛期TS评分高值(>0.30)区则位于南部沿海区域(图8d),最大TS评分超过0.41。而ECMWF-Fine预报评分在前汛期较低,南部地区均在0.1以下,后汛期有所增大,但最大不超过0.15(图8b、e)。前、后汛期概率模型全场平均较ECMWF-Fine分别提升0.23与0.21,尤其对前汛期的广东省南部沿海,以及后汛期广东省西南部,模型TS评分提升显著。TS评分提高的主要贡献来源于漏报率的降低,在获得高命中率的同时,虚警率虽有一定程度增大,但与命中率之间有较好的平衡。从图8c可见,前汛期在TS评分较高的珠江三角洲地区,偏差整体为0.75—1.5,而粤东以及粤西的沿海地区则是虚警相对较多的区域(偏差>1.5);后汛期,除了在粤东的沿海地区偏差接近1以外,其余地区出现一定程度的虚警,以粤北地区虚警相对更多(图8f)。在天气尺度强迫较弱的情况下,应用概率模型有助于弥补数值模式漏报严重的缺陷,有效降低漏报率,并在短时强降水高频地区获得虚警率与命中率较好的平衡,但在部分地区会出现虚警增多的情况。

|
| 图 8 前汛期 (a、b、c)、后汛期 (d、e、f) 短时强降水概率预报模型TS评分 (a、d)、偏差 (c、f) 与ECMWF-Fine模式降水预报TS评分 (b、e) Fig. 8 TS scores of probabilistic model forecasts of SHR (a,d),TS scores of ECMWF-Fine model precipitation forecasts (b,e) and BIAS of SHR probabilistic model forecasts (c,f) during the pre-flood season (a,b,c) and the post-flood season (d,e,f) |
实际业务应用中,基于模型输出的各因子概率对比可为预报难度更大的暖区强降水提供更多预警信息。目前主流的数值模式对于暖湿平流驱动的局地对流性降水预报技巧较低(Huang,et al,2017),因此当反映热力条件增长的因子概率较高时,业务人员仍要密切关注短时强降水发生的可能性。
选择2019年2次暖区降水个例(个例1为2019年5月26日,个例2为2019年6月13日)进行对比分析。个例期间华南地区低层(700 hPa以下)均受西南或偏南气流控制,无明显温度锋区。图9分别为ECMWF-Fine预报的6 h累计降水、短时强降水实况及模型概率预报。两个个例短时强降水分别集中发生于珠江三角洲和粤西沿海(图9a、c矩形),最大小时雨量均超过50 mm。ECMWF-Fine显著低估了两个个例的雨量预报,尤其对个例2,在强降水发生区的6 h雨量预报<5 mm。而概率模型对于两个个例的预报效果均较好,个例1位于珠江三角洲及韶关、清远南部(图9a)的短时强降水落区与模型高概率区(>0.7)(图9b)一致,个例2预报的短时强降水概率在粤西南部(图9d)虽低于个例1,空间分布较不均匀,但仍出现>0.6的高概率中心。整体而言,两个个例模型的高概率区对于短时强降水均有较好的指示作用。

|
| 图 9 2019年5月25日23时—26日05时 (a、b)和6月13日11—18时 (c、d) 数值模式6 h降水量预报 (单位:mm)、短时强降水实况及模型概率预报 (a、c色阶为ECMWF细网格模式6 h累计降水量预报,散点为小时分级的短时强降水观测站点分布,b、d色阶为短时强降水概率预报模型预报场) Fig. 9 NWP precipitation forecasts (unit:mm),observations at weather sites and probabilistic model forecasts of SHR from 23:00 BT 25 May 2019 to 05:00 BT 26 May 2019 (a,b) and from 11:00 to 18:00 BT 13 June 2019 (c,d)(6 h cumulative precipitation forecast of ECMWF-Fine and the distribution of SHR graded by hourly precipitation at weather stations are respectively shown in (a,c),color shadings in (b,d) represent the SHR forecast by the probabilistic model) |
两个个例的主要驱动因子不同,个例1与沿海风速辐合的动力作用关系密切,个例2则是在弱动力强迫、强热力不稳定的环境下发生的,预报难度更大(Huang,et al,2017),对上游不稳定能量具有更显著的敏感性。图10给出了两个个例组合因子1、组合因子3的空间分布以及925 hPa风场、中低层垂直速度分布。个例1降水区的组合因子3概率(图10c)高于组合因子1(图10a),而个例2降水区组合因子1概率则更高(图10b、d)。个例1动力条件更好的原因为南海北部存在西南气流与东南气流的辐合区,因此在珠江口西侧具有大的垂直上升运动区(图10e箭头),但个例2动力条件相对较弱,南海北部受西南气流控制(图10f),风向与海岸线接近平行,因此粤西南部的垂直速度也较小。但对于热力条件,则是个例1显著弱于个例2,两个个例降水区的925 hPa假相当位温分别为354 K与362 K(图10e、f箭头),后者高假相当位温主要来源于季风气流导致强烈的增暖、增湿。在热力条件较好的背景下,个例2出现了超50 mm/h的短时强降水。而ECMWF-Fine降水量预报以及组合因子3概率对个例2的降水预报值均显著偏低,仅组合因子1(图10b)给出了较高概率,提示了降水系统将在不稳定区域内发展的可能性。

|
| 图 10 2019年5月26日02时 (a、c、e)、6月13日14时 (b、d、f) 组合因子1、组合因子3概率 (a—d,色阶) 与925 hPa风场 (矢量)、假相当位温 (色阶;单位:K) 和中低层垂直速度 (等值线分别对应ω=−0.5、−0.7、−1.3、−1.9、−2.5;单位:Pa/s)(e、f) 分布 Fig. 10 Probability of Factor 1 and Factor 3,925 hPa wind fields,potential pseudo-equivalent temperatures (unit:K),and middle- and low-level vertical velocitis (unit:Pa/s) at 02:00 BT 26 May 2019 (a,c,e) and 14:00 BT 13 June 2019 (b,d,f). (Color shadings in (a,b) represent the probability of Factor 1 and color shadings in (c,d) represent the Probability of Factor 3;Vectors in (e,f) represent 925 hPa wind fields,color shadings in (e,f) represent 925 hPa potential pseudo-equivalent temperature,contours in (e,f)correspond to ω=−0.5,−0.7,−1.3,−1.9 and −2.5 Pa/s on middle and low levels respectively) |
在华南汛期季风爆发后,暖湿平流增强,热力不稳定性导致与个例2类似的对流性降水增多,这一类强降水通常难以被业务模式的降水预报很好反映。而通过因子分析模型,预报员可进一步结合低空环流形势对不同地区的热力条件进行分析,有助于提升对暖区对流性降水事件预报的命中率。
5 结论和讨论利用2009—2018年汛期(4—9月)广东省地面气象观测站数据建立短时强降水数据集,采用ERA-Interim再分析资料计算数十个物理量与多年平均态的偏差值。在计算物理量参数及扣除多年平均态的基础上,提出了遴选物理量的指标AROC和分期、分区域建立因子分析模型方法,在业务应用中提升预报命中率的同时控制虚警率上升,为预报难度大的暖区短时强降水提供更多参考信息。
不同月份的因子偏离度具有明显差异:前汛期各因子偏离度随月份增长而不断下降,但各因子偏离度差异较小;后汛期与热力条件有关的因子偏离度差异较大,其相对重要性与前汛期相比也明显降低;各因子在不同区域的相对重要性也有差异,多数因子具有明显的南、北反向特征。根据因子偏离度的时、空分布,划分前、后汛期以及3个空间区域,构建6个因子模型。将各因子贡献率作为6个因子概率的权重,采用加权组合方法构建分期、分区的短时强降水概率预报模型,其预测效果较未分区前有明显改善。
以训练期间最优TS评分的概率阈值作为短时强降水预报阈值,在测试期对短时强降水概率预报模型进行TS评分检验,前、后汛期广东省大部分区域TS评分在0.25以上,最高达0.42,相对于ECMWF-Fine全场平均在前、后汛期分别提升0.23与0.21,南部沿海TS评分提升幅度最大。模型在获得高命中率的同时,虚警率与命中率取得较好的平衡,短时强降水高频地区偏差接近1,验证了模型业务应用的有效性。选择2019年2次ECMWF-Fine模式漏报的暖区强降水个例,概率模型对于两个个例的强降水均做出高概率预报;对于动力强迫较弱,但不稳定条件好的对流性强降水,确定性模式容易漏报,而通过分析各个因子,可知表征不稳定的组合因子1概率较高,为业务中预报难度较大的暖区强降水提供早期预警信号。
模型中输入因子与输出概率具有明确的映射关系,能清晰反映短时强降水发生、发展的环境条件。但模型的输入因子多,并且输入因子与短时强降水发生概率存在非线性关系,因此从模型优化角度而言,可引进机器学习算法,以应对具有复杂输入、输出因子关联特征的预报建模问题。将各建模因子作为输入量,针对华南区域进行机器学习训练以获得更优的预测效果,加强气象领域的人工智能技术专业性,将是未来的发展方向。
致 谢:感谢孙继松研究员和王秀明教授的指导。
陈炯, 郑永光, 张小玲等. 2013. 中国暖季短时强降水分布和日变化特征及其与中尺度对流系统日变化关系分析. 气象学报, 71(3): 367-382. Chen J, Zheng Y G, Zhang X L, et al. 2013. Analysis of the climatological distribution and diurnal variations of the short-duration heavy rain and its relation with diurnal variations of the MCSs over China during the warm season. Acta Meteor Sinica, 71(3): 367-382. (in Chinese) |
陈元昭, 俞小鼎, 陈训来. 2016. 珠江三角洲地区重大短时强降水的基本流型与环境参量特征. 气象, 42(2): 144-155. Chen Y Z, Yu X D, Chen X L. 2016. Characteristics of short-time severe rainfall events based on weather flow and key environmental parameters in Pearl River Delta. Meteor Mon, 42(2): 144-155. DOI:10.7519/j.issn.1000-0526.2016.02.002 (in Chinese) |
洪伟, 郑玉兰. 2018. 基于ECMWF产品福建省前汛期短时强降水预报方法. 应用气象学报, 29(5): 584-595. Hong W, Zheng Y L. 2018. A method of short-time strong rainfall forecasting during pre-rainy season in Fujian based on ECMWF productions. J Appl Meteor Sci, 29(5): 584-595. DOI:10.11898/1001-7313.20180507 (in Chinese) |
江崟, 陈训来, 朱江山等. 2019. 深圳对流尺度集合预报系统在华南暴雨中的应用研究. 气象科技进展, 9(3): 124-131. Jiang Y, Chen X L, Zhu J S, et al. 2019. Application of Shenzhen storm-scale ensemble forecast system in heavy rainfall of South China. Adv Meteor Sci Technol, 9(3): 124-131. (in Chinese) |
雷蕾, 孙继松, 王国荣等. 2012. 基于中尺度数值模式快速循环系统的强对流天气分类概率预报试验. 气象学报, 70(4): 752-764. Lei L, Sun J S, Wang G R, et al. 2012. An experimental study of the summer convective weather categorical probability forecast based on the rapid updated cycle system for the Beijing area (BJ-RUC). Acta Meteor Sinica, 70(4): 752-764. (in Chinese) |
梁巧倩, 蒙伟光, 孙喜艳等. 2019. 广东前汛期锋面强降水和后汛期季风强降水特征对比分析. 热带气象学报, 35(1): 51-62. Liang Q Q, Meng W G, Sun X Y, et al. 2019. Contrastive analysis of frontal rainstorm VS monsoon rainstorm processes during the April-May-June raining season VS July-August-September raining season. J Trop Meteor, 35(1): 51-62. (in Chinese) |
慕丹, 李跃清. 2018. 基于ERA-interim再分析资料的近30年九龙低涡气候特征. 气象学报, 76(1): 15-31. Mu D, Li Y Q. 2018. Climatic characteristics of the Jiulong low vortex in recent 30 years based on the ERA-interim reanalysis data. Acta Meteor Sinica, 76(1): 15-31. (in Chinese) |
农孟松, 黄海洪, 孙崇智等. 2011. 基于主分量神经网络的降水集成预报方法研究. 气象, 37(3): 352-355. Nong M S, Huang H H, Sun C Z, et al. 2011. A neural network model based on principal component analysis for ensemble precipitation prediction. Meteor Mon, 37(3): 352-355. DOI:10.3969/j.issn.1671-6345.2011.03.016 (in Chinese) |
孙喜艳, 伍志方, 梁巧倩等. 2017. 广东省不同等级小时强降水时空特征分析. 自然灾害学报, 26(5): 102-109. Sun X Y, Wu Z F, Liang Q Q, et al. 2017. Analysis of spatio temporal characteristics of hourly heavy precipitation in different grades in Guangdong. J Nat Disasters, 26(5): 102-109. (in Chinese) |
王坚红, 徐碧裕, 刘刚等. 2014. 华南前汛期广东暴雨分区动力特征及特大暴雨分析. 气象与环境学报, 30(6): 43-51. Wang J H, Xu B Y, Liu G, et al. 2014. Dynamics characteristics of rainstorm division in Guangdong province and analysis of a severe rainstorm process. J Meteor Environ, 30(6): 43-51. (in Chinese) |
王坚红, 杨艺亚, 苗春生等. 2017. 华南沿海暖区辐合线暴雨地形动力机制数值模拟研究. 大气科学, 41(4): 784-796. Wang J H, Yang Y Y, Miao C S, et al. 2017. The numerical study of terrain dynamic influence on warm area heavy rainfall of convergence lines in South China coast. Chinese J Atmos Sci, 41(4): 784-796. (in Chinese) |
伍志方, 庞古乾, 郭春迓等. 2016. 广东前汛期强对流天气分类流型及物理量阈值. 自然灾害学报, 25(3): 166-175. Wu Z F, Pang G Q, Guo C Y, et al. 2016. Classification pattern and physical threshold of severe convective weather during pre-flood period in Guangdong. J Nat Disasters, 25(3): 166-175. (in Chinese) |
伍志方, 蔡景就, 林良勋等. 2018. 2017年广州“5•7”暖区特大暴雨的中尺度系统和可预报性. 气象, 44(4): 485-499. Wu Z F, Cai J J, Lin L X, et al. 2018. Analysis of mesoscale systems and predictability of the torrential rain process in Guangzhou on 7 May 2017. Meteor Mon, 44(4): 485-499. DOI:10.7519/j.issn.10000526.2018.04.002 (in Chinese) |
熊开国, 赵俊虎, 封国林等. 2012. 汛期降水相似动力预报——模式误差主分量相似预报方法. 物理学报, 61(14): 149204. Xiong K G, Zhao J H, Feng G L, et al. 2012. A new method of analogue—Dynamical prediction of monsoon precipitation based on analogue prediction principal components of model errors. Acta Phys Sinica, 61(14): 149204. DOI:10.7498/aps.61.149204 (in Chinese) |
俞小鼎, 郑永光. 2020. 中国当代强对流天气研究与业务进展. 气象学报, 78(3): 391-418. Yu X D, Zheng Y G. 2020. Advances in severe convective weather research and operational service in China. Acta Meteor Sinica, 73(5): 391-418 (in Chinese)
|
曾明剑, 王桂臣, 吴海英等. 2015. 基于中尺度数值模式的分类强对流天气预报方法研究. 气象学报, 73(5): 868-882. Zeng M J, Wang G C, Wu H Y, et al. 2015. Study of the forecasting method for the classified severe convection weather based on a meso-scale numerical model. Acta Meteor Sinica, 73(5): 868-882. (in Chinese) |
张小玲, 谌芸, 张涛. 2012. 对流天气预报中的环境场条件分析. 气象学报, 70(4): 642-654. Zhang X L, Chen Y, Zhang T. 2012. Meso-scale convective weather analysis and severe convective weather forecasting. Acta Meteor Sinica, 70(4): 642-654. (in Chinese) |
朱月佳, 邢蕊, 朱明佳等. 2019. 联合概率方法在安徽强对流潜势预报中的应用和检验. 地球科学进展, 34(7): 731-746. Zhu Y J, Xing R, Zhu M J, et al. 2019. Application and verification of joint probability method in potential forecast for severe convective weather in Anhui Province. Adv Earth Sci, 34(7): 731-746. DOI:10.11867/j.issn.1001-8166.2019.07.0731 (in Chinese) |
Bao X H, Zhang F Q. 2013. Evaluation of NCEP-CFSR, NCEP-NCAR, ERA-interim, and ERA-40 reanalysis datasets against independent sounding observations over the Tibetan Plateau. J Climate, 26(1): 206-214. DOI:10.1175/JCLI-D-12-00056.1 |
Bates B C, Dowdy A J, Chandler R E, et al. 2018. Lightning prediction for australia using multivariate analyses of large-scale atmospheric variables. J Appl Meteor Climate, 57(3): 525-534. DOI:10.1175/JAMC-D-17-0214.1 |
Chen G X, Lan R Y, Zeng W X, et al. 2018. Diurnal variations of rainfall in surface and satellite observations at the monsoon coast (South China). J Climate, 31(5): 1703-1724. DOI:10.1175/JCLI-D-17-0373.1 |
Dee D P, Uppala S M, Simmons A J, et al. 2011. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Quart J Roy Meteor Soc, 137(656): 553-597. DOI:10.1002/qj.828 |
Devlieger I, Mayer A, Rosseel Y. 2016. Hypothesis testing using factor score regression: A comparison of four methods. Educ Psychol Meas, 76(5): 741-770. DOI:10.1177/0013164415607618 |
Du Y, Chen G X. 2018. Heavy rainfall associated with double low-level jets over Southern China. Part Ⅰ: Ensemble-based analysis. Mon Wea Rev, 146(11): 3827-3844. DOI:10.1175/MWR-D-18-0101.1 |
Felzer B S, Ember C R, Cheng R, et al. 2020. The relationships of extreme precipitation and temperature events with ethnographic reports of droughts and floods in nonindustrial societies. Wea Climate Soc, 12(1): 135-148. DOI:10.1175/WCAS-D-19-0045.1 |
Gallo B T, Clark A J, Smith B T, et al. 2018. Blended probabilistic tornado forecasts: Combining climatological frequencies with NSSL-WRF ensemble forecasts. Wea Forecasting, 33(2): 443-460. DOI:10.1175/WAF-D-17-0132.1 |
Gijben M, Dyson L L, Loots M T. 2017. A statistical scheme to forecast the daily lightning threat over southern Africa using the Unified Model. Atmos Res, 194: 78-88. DOI:10.1016/j.atmosres.2017.04.022 |
Godart A, Leblois E, Anquetin S, et al. 2010. Analysis of the relationship between banded orographic convection and atmospheric properties using factorial discriminant analysis and neural networks. J Appl Meteor Climate, 49(4): 646-663. DOI:10.1175/2009JAMC2217.1 |
Huang L, Luo Y L. 2017. Evaluation of quantitative precipitation forecasts by TIGGE ensembles for South China during the presummer rainy season. J Geophys Res Atmos, 122(16): 8494-8516. DOI:10.1002/2017JD026512 |
Li J, Yu R C, Zhou T J. 2008. Seasonal variation of the diurnal cycle of rainfall in southern contiguous China. J Climate, 21(22): 6036-6043. DOI:10.1175/2008JCLI2188.1 |
Luo Y L, Xia R D, Chan J C L. 2020. Characteristics, physical Mechanisms, and prediction of pre-summer rainfall over South China: Research progress during 2008–2019. J Meteor Soc Japan. Ser. II, 98(1): 19-42. DOI:10.2151/jmsj.2020-002 |
Mohr S, Kunz M, Keuler K. 2015. Development and application of a logistic model to estimate the past and future hail potential in Germany. J Geophys Res, 120(9): 3939-3956. DOI:10.1002/2014JD022959 |
Richardson D S. 2000. Skill and relative economic value of the ECMWF ensemble prediction system. Quart J Roy Meteor Soc, 126(563): 649-667. DOI:10.1002/qj.49712656313 |
Simon T, Fabsic P, Mayr G J, et al. 2018. Probabilistic forecasting of thunderstorms in the eastern Alps. Mon Wea Rev, 146(9): 2999-3009. DOI:10.1175/MWR-D-17-0366.1 |
Zhang X B, Luo Y L, Wan Q L, et al. 2016. Impact of assimilating wind profiling radar observations on convection-permitting quantitative precipitation forecasts during SCMREX. Wea Forecasting, 31(4): 1271-1292. DOI:10.1175/WAF-D-15-0156.1 |
 2021, Vol. 79
2021, Vol. 79


