1 引　言

增量形式的四维资料变分同化（4D-Var）系统是依据同化时间窗内的背景场（由非线性模式提供）和观测信息求代价函数的极小值，得到最优分析场。这个最优化过程需要反复积分切线性模式（TLM，Tangent Linear Model）及对应的伴随模式（ADM，Adjoint Model）。切线性模式是对非线性模式（NLM，Non-Linear Model）的线性化，国际上普遍采用代码对代码（Code to Code）的方式建立，即直接针对非线性模式代码进行线性化编程。这样产生的切线性模式与原来的非线性模式高度关联，在扰动很小的情形下具有很高的逼近精度。

另一种做法是构造扰动预报模式（PFM，Perturbation Forecast Model），该模式从组成非线性模式的原始微分方程组出发，通过小扰动线性化导出连续微分形式的扰动方程组，再采用一定的数学方案进行差分计算。研究（Lawless, et al, 2003）表明，尽管从扰动逼近无限小的角度来看，切线性模式比扰动模式具有更高的精度，但由于扰动量往往是有限大小的，故扰动模式能够代替切线性模式而得到较好的数学结果。Lawless等（2005）进一步试验表明，在增量4D-Var系统中使用扰动模式的收敛速率和分析结果与使用切线性模式几乎相同。

传统切线性模式对原来的非线性模式依赖性大，不具备相对独立性。非线性模式的更新或升级会导致切线性模式以及相应的伴随模式的重新编写，工作量巨大，维护成本较高。另外，切线性模式需要的内存空间也比较大，对于非线性模式中存在迭代计算的情形处理起来比较麻烦。而扰动模式独立性较好，不需要严格遵循复杂的非线性模式代码，直接基于非线性模式的基本物理原理和方案进行编写，能在代码层面保持清晰的物理意义，开发和维护成本较低。扰动模式另一个优点是可以避开非线性模式复杂计算方案带来的问题，例如针对非线性模式中半拉格朗日平流插值或某些迭代求解方案的切线性模式代码编写难度大，而扰动模式处理起来要容易得多。

扰动模式在研究和业务中已经得到较好的应用。英国气象局（UK Met Office）采用扰动模式建立了4D-Var系统（Lorenc, 1997；Lorenc, et al, 2005），并将该4D-Var系统与1.5 km水平分辨率的UKV模式结合，发展了一个主要用于预报对流降水的0—24 h短时临近预报系统，并应用于2012年伦敦奥运会，使得雷达、卫星、风廓线仪等高频次探测资料得到充分利用，降水预报效果明显优于基于3D-Var系统的区域模式和基于外推的临近预报系统（Ballard, et al，2016）。扰动模式还有其他的用途，例如通过扰动模式及其伴随模式评估模式预报对于观测资料的敏感性（Lorenc, et al，2014）。此外，还可用于分析模式误差的远距离传播特征等。

现阶段GRAPES区域模式的区域同化系统仍主要采用3D-Var，一个主要原因是还没有建立起GRAPES区域模式的较成熟的切线性模式以及相应的伴随模式。针对这一问题，不同于GRAPES全球模式的切线性模式编写方法，文中针对GRAPES区域模式采用小扰动方法开发线性模式动力框架，不仅为完整线性模式及其伴随模式的建立打下重要基础，而且由于该线性模式框架有很高的相对独立性，也可为进一步建立区域4D-Var系统提供便利。

文中从GRAPES模式的原始方程组（薛纪善等，2008）出发，推导线性扰动基本方程组，进而建立区域扰动预报模式— —GRAPES_PF。为评估GRAPES_PF对于GRAPES非线性模式的线性近似程度，设计了数值试验。通过同时在非线性模式和线性模式中施加一个中尺度初始扰动高压，分别模拟扰动的传播和演变。数值试验表明，GRAPES_PF较好地模拟了初始高压扰动所激发的惯性重力内波快速传播过程，且具有较高的计算精度，可作为GRAPES区域模式较好的线性模式。

2 扰动模式的设计 2.1 GRAPES非线性模式基本方程组

GRAPES非线性模式在地形追随垂直坐标下的球面基本方程组如下（薛纪善等，2008）：

运动方程

$ \begin{split} \frac{{\rm d}{{{V}}}}{{\rm d}t}=&-{c}_{p}\theta {\left({\nabla }_{{\rm{h}}}\varPi \right)}_{\hat {\textit z}}-{c}_{p}\theta \frac{\partial \varPi }{\partial \hat{{\textit z}}}\left({Z}_{{{s}}{{x}}}{{\bf{i}}}+{Z}_{{{s}}{{y}}}{{\bf{j}}}+{Z}_{{{s}}\hat{{{\textit z}}}}{{\bf{k}}}\right)+\\&\left\{fv+{\delta }_{{\rm{M}}}\left(\frac{vu\tan\varphi }{r}-\frac{uw}{r}\right)-{\delta }_{{\rm{\varphi}}}{f}_{{\rm{\varphi}}}w\right\}{{\bf{i}}}- \\ &\left\{fu+{\delta }_{{\rm{M}}}\left(\frac{{u}^{2}\tan\varphi }{r}+\frac{vw}{r}\right)\right\}{{\bf{j}}}-\\&\left\{g-{\delta }_{\rm M}\frac{{u}^{2}+{v}^{2}}{r}-{\delta }_{{\rm{\varphi}}}{f}_{{\rm{\varphi}}}u\right\}{{\bf{k}}}+{{{F}}}\\[-12pt] \end{split} $

(1)

式中， ${{ V}} = {{u}}{\bf{ i}} + {{v{\bf j}}} + {{w{\bf k}}}$ 为三维风矢量。 ${\left({{\nabla _{\rm{h}}}\varPi } \right)_{{\rm{\hat z}}}} = \dfrac{{\partial \varPi }}{{\partial x}}{\bf i} +$ $ \dfrac{{\partial \varPi }}{{\partial y}}{{\bf j}} $ 表示地形坐标面上的水平气压梯度， ${{\varPi }} = {\left({\dfrac{{{p}}}{{{{{p}}_0}}}} \right)^{\frac{{{{{R}}_{\rm{d}}}}}{{{{{c}}_{{p}}}}}}}$ 为Exner无量纲气压； ${{ F}}$ 为次网格尺度的物理过程参数化项和摩擦项的总和； ${\delta _{\rm{M}}}$ 和 ${\delta _{\rm{\varphi }}}$ 分别为曲率修正项开关和地转偏向力修正项开关； $\hat {\textit z}$ 为地形追随高度坐标，一般是纬度、经度和高度的函数（ $\hat {\textit z} = {{f}}\left({\lambda,\varphi,{\textit z}} \right)$ ）；特别地，文中取 $\hat {\textit z} = {Z_{\rm{T}}}\dfrac{{{\textit z} - {Z_{\rm{s}}}}}{{{{\rm{Z}}_{\rm{T}}} - {Z_{\rm{s}}}}}$ 。其中 ${Z_{\rm{T}}}$ 和 ${Z_{\rm{s}}}$ 分别为模式顶和地表面的高度；而 ${Z_{{{sx}}}} = \dfrac{{\partial \hat {\textit z}}}{{\partial x}}$ ， ${Z_{{{sy}}}} = \dfrac{{\partial \hat {\textit z}}}{{\partial y}}$ ， ${Z_{{{s\hat {\textit z}}}}} = \dfrac{{\partial \hat {\textit z}}}{{\partial {\textit z}}}$ 分别是模式面空间梯度的3个分量；其他符号与GRAPES模式相同，详细可参阅薛纪善等（2008）第二章。空气质点距地球中心的距离 $r = a + {\textit z}$ ，a为地球平均半径，z为距地面的高度。实际上，文中采用了浅层大气假设 $r \approx a$ ，并忽略地球曲率项和垂直科里奥利力项，即令开关参数 ${\delta _{\rm{M}}}$ 和 ${\delta _{\rm{\varphi }}}$ 为0。

连续方程

$ \frac{{{\rm{d}}\varPi }}{{{\rm{d}}t}} = - \hat \gamma \varPi {D_3} + \frac{{\hat \gamma }}{{{c_{{p}}}\theta }}\left({{Q_{\rm{R}}} + L{P_{\rm{w}}}} \right) $

(2)

式中， $\hat \gamma = \dfrac{{{R_{\rm{d}}}}}{{{c_p} - {R_{\rm{d}}}}}$ ，Q_R为辐射加热，P_w为降水率。

散度 ${D_3} = {\left({\dfrac{{\partial u}}{{\partial x}}} \right)_{{\rm{\hat z}}}} + {\left({\dfrac{{\partial v}}{{\partial y}}} \right)_{{\rm{\hat z}}}} + \dfrac{{\partial \hat w}}{{\partial \hat {\textit z}}} - \dfrac{{\partial {Z_{sx}}}}{{\partial \hat {\textit z}}}{{u}} - \dfrac{{\partial{Z_{sy}}}}{{\partial \hat {\textit z}}}{{v}} + \dfrac{{2w - v{\rm{tan}}\varphi }}{r}$ ，实际应用中忽略了地球曲率项，即 ${D_3} = {\left({\dfrac{{\partial u}}{{\partial x}}} \right)_{{\rm{\hat z}}}} + {\left({\dfrac{{\partial v}}{{\partial y}}} \right)_{{\rm{\hat z}}}} + \dfrac{{\partial \hat w}}{{\partial \hat {\textit z}}} - \dfrac{{\partial {Z_{sx}}}}{{\partial \hat {\textit z}}}u - \dfrac{{\partial {Z_{{sy}}}}}{{\partial \hat {\textit z}}}v$ 。而 $\hat {\textit z}$ 坐标的垂直速度 $\hat w = {Z_{sx}}u + {Z_{{sy}}}v + {Z_{{{s\hat {\textit z}}}}}w$ 。

热力学方程

$ \frac{{\rm{d}}\theta }{{\rm{d}}t}=\frac{{Q}_{{\rm{R}}}+L{P}_{{\rm{w}}}}{{c}_{{{p}}}\varPi } $

(3)

水汽方程

$ \frac{{\rm{d}}q}{{\rm{d}}t}=-{P}_{{\rm{w}}} $

(4)

2.2 扰动预报方程组推导

设预报变量 $A $ 分解为基本态与扰动量，即 $ {A=\bar{A}+A}' $ ，其中基本态从GRAPES非线性模式获得，即已假设基本态严格满足式（1）—（4）。采用小扰动法线性化后有

$\begin{split} {\left(\frac{{\rm{d}}A}{{\rm{d}}t}\right)}'&={\left(\frac{\partial A}{\partial t}+{{{V}}}{\text •} \nabla A\right)}'\approx \frac{\partial {A}'}{\partial t}+{{{V}}}{\text •} \nabla {A}'+{{{{V}}}}'{\text •} \nabla A\\&=\frac{{\rm{D}}{A}'}{{\rm{D}}t}+{{{{V}}}}'{\text •} \nabla A \end{split}$

(5)

上式表明，时间全导数的扰动等于扰动量的时间全导数加上扰动风场对基本态的平流。为简洁，推导过程已忽略基本态的标记“—”。其中全导数算子： $\dfrac{{\rm{D}}}{{{\rm{D}}t}} = \dfrac{\partial }{{\partial t}} + { V} {\text •} \nabla = \dfrac{\partial}{{\partial t}} + u\dfrac{\partial }{{\partial x}} + v\dfrac{\partial}{{\partial y}} + \hat w\dfrac{\partial }{{\partial \hat {\textit z}}}$ 。

将式（1）写成分量形式并线性化

$ \frac{{{\rm{D}}u}'}{{\rm{D}}t}=-{{{{V}}}'}{\text •} \nabla u+{c}_{{{p}}}{{L}_{{\text{π}}{{x}}}\theta }'+{L}_{{\rm{\theta}}}({\varPi }_{x}'+{Z}_{sx}{\varPi }_{\hat{{\textit z}}}')+fv' $

(6)

$ \frac{{{\rm{D}}v}'}{{\rm{D}}t}={-{{{{V}}}'}{\text •} \nabla v+c}_{{{p}}}{L}_{{\text{π}}{y}}{\theta }'+{L}_{{\rm{\theta}}}({\varPi }_{y}'+{Z}_{{sy}}{\varPi }_{\hat{{\textit z}}}')-fu' $

(7)

$ \frac{{\rm{D}}{w}'}{{\rm{D}}t}=-{{{{V}}}'}{\text •} \nabla w+{c}_{{{p}}}{L}_{{\text{π}}\hat{{{\textit z}}}}\theta '+{L}_{{\rm{\theta}}}{\textit Z}_{{{s}}\hat{{{\textit z}}}}{\varPi }_{\hat{{\textit z}}}' $

(8)

式中，算子 $-{{{{V}}}'}{\text •} \nabla \!=\!-\left(u'\dfrac{\partial }{\partial x}\!+\!v'\dfrac{\partial }{\partial y}\!+\!\hat{w}'\dfrac{\partial }{\partial \hat{{\textit z}}}\right)$ 。且 ${L}_{{\text{π}} x}\!=\!-({\varPi }_{x}\!+ {Z}_{s{{x}}}{\varPi }_{\hat{{\textit z}}})$ ， ${L}_{{\text{π}}y}={-(\varPi }_{y}+{Z}_{{sy}}{\varPi }_{\hat{{\textit z}}})$ ， ${L}_{{\text{π}}\hat{{{\textit z}}}}=-{Z}_{{{s}}\hat{{{\textit z}}}}{\varPi }_{\hat{{\textit z}}}$ ， ${L}_{{\rm{\theta}}}={-c}_{{{p}}}\theta$ 。

对式（2）进行线性化，得到扰动连续方程

$ \frac{{\rm{D}}{\varPi }'}{{\rm{D}}t}=-{{{{V}}}'}{\text •} \nabla \varPi -{\alpha }_{{\rm{D}}}{\varPi }'-{\alpha }_{\Pi}{D}_{3}'+{\gamma }_{{\rm{\theta}}}{P'_{{\rm{w}}}} $

(9)

此处做简化， $\dfrac{1}{{\theta + \theta '}} \approx \dfrac{\,1\,} {\,\theta \,}$ 。并且设 $ {\alpha _{\rm{D}}} = \hat \gamma {D_3},{\alpha _\Pi} =$ $ \hat \gamma \varPi,\;{\gamma _{\rm{\theta }}} = \dfrac{{L\hat \gamma }}{{{c_{{p}}}\theta }}$ 。

对式（3）和（4）做线性化，分别得到扰动热力学方程和扰动水汽方程

$ \frac{{\rm{D}}{\theta }'}{{\rm{D}}t}=-{{{{V}}}'}{\text •} \nabla \theta +{\gamma }_{\Pi}{P'_{{{{\rm{w}}}}}} $

(10)

此处做简化 $\dfrac{1}{\varPi +{\varPi }'}\approx \dfrac{\,1\,}{\,\varPi \,}$ ，并设 ${\gamma }_{\varPi }=\dfrac{L}{\varPi {c_p}}$ 。式（9）和（10）中已忽略辐射扰动项 $Q'_{{\rm{R}}}$ 。

$ \frac{{{\rm{D}}q}'}{{\rm{D}}t}=-{{{{V}}}'}{\text •} \nabla q-{P'_{{\rm{w}}}} $

(11)

最终得到包含6个扰动变量（u′、v′、 ${w}'{\text{、}}{\varPi }'{\text{、}}{q}'{\text{、}}{\theta }'$ ）的扰动预报方程组

$ \begin{split} \frac{{{\rm{D}}u}'}{{\rm{D}}t}=&-\left({u}'{u}_{x}+{v}'{u}_{y}+{\hat{w}}'{u}_{\hat{{\textit z}}}\right)+{c_p}{{L}_{{\text{π}}x}\theta }'+\\&{L}_{{\rm{\theta}}}({\varPi }_{x}'+{Z}_{sx}{\varPi }_{\hat{{\textit z}}}')+fv' \end{split}$

(12)

$\begin{split} \frac{{{\rm{D}}v}'}{{\rm{D}}t}=&{-\left({u}'{v}_{x}+{v}'{v}_{y}+{\hat{w}}'{v}_{\hat{{\textit z}}}\right)+c_p}{L}_{{\text{π}}{\rm{y}}}{\theta }'+\\&{L}_{{\rm{\theta}}}({\varPi }_{y}'+{Z}_{sy}{\varPi }_{\hat{{\textit z}}}')-fu' \end{split}$

(13)

$ \frac{{\rm{D}}{w}'}{{\rm{D}}t}=-\left({u}'{w}_{x}+{v}'{w}_{y}+{\hat{w}}'{w}_{\hat{{\textit z}}}\right)+{c_pL}_{{\text{π}}\hat{{{\textit z}}}}\theta '+{L}_{{{\theta}}}{Z}_{{{s}}\hat{{{\textit z}}}}{\varPi }_{\hat{{\textit z}}}' $

(14)

$\begin{split} \frac{{\rm{D}}{\varPi }'}{{\rm{D}}t}=&-\left({u}'{\varPi }_{x}+{v}'{\varPi }_{y}+{\hat{w}}'{\varPi }_{\hat{{\textit z}}}\right)-{\alpha }_{{\rm{D}}}{\varPi }'-\\&{\alpha }_{\Pi}{D}_{3}'+{\gamma }_{{\rm{\theta}}}{P}_{{\rm{w}}}'\end{split} $

(15)

$ \frac{{\rm{D}}{\theta }'}{{\rm{D}}t}=-\left({u}'{\theta }_{x}+{v}'{\theta }_{y}+{\hat{w}}'{\theta }_{\hat{{\textit z}}}\right)+{\gamma }_{\Pi}{P}_{{\rm{w}}}' $

(16)

$ \frac{{{\rm{D}}q}'}{{\rm{D}}t}=-\left({u}'{q}_{x}+{v}'{q}_{y}+{\hat{w}}'{q}_{\hat{{\textit z}}}\right)-{P}_{{\rm{w}}}' $

(17)

其中，　 $D{'_3} = u{'_x} + v{'_y} + \hat w{'_{\hat {\textit z}}} - \dfrac{{\partial {Z_{sx}}}}{{\partial \hat {\textit z}}}u' - \dfrac{{\partial {Z_{sy}}}}{{\partial \hat {\textit z}}}v'$

$ \hat w' = {Z_{sx}}u' + {Z_{sy}}v' + {Z_{{{s\hat {\textit z}}}}}w'\qquad\qquad\qquad $

2.3 半隐式半拉格朗日时间积分

与GRAPES非线性模式类似，采用两个时间层的半隐式半拉格朗日（Temperton, et al，1987)）时间积分方案。

假定扰动量 $ {A}' $ 的预报方程为 $\dfrac{{\rm{D}}{A}'}{{\rm{D}}t}={L}_{{\rm{A}}}$ ，则半隐式半拉格朗日方案可表示为

$ \frac{{\left({A}'\right)}_{{\rm{a}}}^{{{n+1}}}-{\left({A}'\right)}_{{\rm{d}}}^{n}}{\Delta t}=\alpha {\left({L}_{{\rm{A}}}\right)}_{{\rm{a}}}^{n+1}+(1-\alpha) {\left({L}_{{\rm{A}}}\right)}_{{\rm{d}}}^{n} $

或写成

$ {\left({A}'\right)}_{{\rm{a}}}^{n+1}-{\left({A}'\right)}_{{\rm{d}}}^{n}={\alpha }_{{\rm{\varepsilon}}}{\left({L}_{{\rm{A}}}\right)}_{{\rm{a}}}^{{n}+1}+ {\beta }_{{\rm{\varepsilon}}}{\left({L}_{{\rm{A}}}\right)}_{{\rm{d}}}^{{n}} $

(18)

这里 $ {\alpha }_{\varepsilon }=\alpha \Delta t $ ， $ {\beta }_{{\rm{\varepsilon}}}=\left(1-\alpha \right)\Delta t $ 。下标a和d分别表示到达点与出发点（或称上游点），前者定义在模式网格点上，后者则需依照空气质点的拉格朗日运动轨迹计算，且默认到达点在n+1时刻，上游点在n时刻。因此，式（18）右端第一项 ${\left({L}_{{\rm{A}}}\right)}_{{\rm{a}}}^{{{n}}+1}$ 在到达点隐式求解（对应未知的n+1时刻状态）；第二项 ${\left({L}_{{\rm{A}}}\right)}_{{\rm{d}}}^{{{n}}}$ 在出发点显式计算（对应已知的n时刻状态）。由于大气中包含各种尺度的波动，曾庆存（1979）指出，原始方程对误差很敏感，随着时间推移计算误差导致的虚假快波强度将会远远大于慢波强度。因此为保证计算稳定，与快波（重力波、声波）有关的气压梯度力、科里奥利力和散度项写成半隐式，与平流有关的慢过程写成全显式。隐式权重系数（ $ \alpha $ ）代表隐式积分的偏心状况（off-centered），取值范围为 $ \left[0.5,1\right] $ 。 $ \alpha $ 越接近1，计算越稳定，但计算精度是一阶的； $ \alpha $ 越接近0.5，时间积分精度越高，但不容易保持计算稳定。当取 $ \alpha =0.5 $ 即时间中央差时，时间差分方案是二阶精度的，因此应尽可能取 $ {\rm{\alpha}} $ 接近0.5，同时使模式积分稳定。文中取 $ \alpha =0.55 $ 时仍能保持扰动模式稳定积分。可以针对实际情况对不同的预报变量取不同的 $ {\rm{\alpha}} $ 值，文中暂时对所有扰动变量预报方程均取相同的 $ {\rm{\alpha}} $ 值。

因此，对扰动纬向速度方程（12），利用式（18）得到

$ {\left({u}'\right)}_{{\rm{a}}}^{{{n}}+1}-{\alpha }_{{\rm{\varepsilon}}}{\left[{L}_{{\rm{\theta}}}{(\varPi }_{x}'+{Z}_{{{sx}}}{\varPi }_{\hat{{\textit z}}}')+fv'\right]}_{{\rm{a}}}^{{{n}}+1}={X}_{u}' $

(19)

为书写简便，下面除必须外，下标a和时间上标n+1一概略去。于是上式变为

$ {u}'-{\alpha }_{{\rm{\varepsilon}}}f{v}'-{\alpha }_{{\rm{\varepsilon}}}{L}_{{\rm{\theta}}}{(\varPi }_{x}'+{Z}_{{{sx}}}{\varPi }_{\hat{{\textit z}}}')={X}_{{{u}}}' $

(20)

右端项 $ {X}_{{\rm{u}}}' $ 是n时刻已知项，一般在上游点取值，但为方便计算，且不失计算精度，当前把平流项和位温扰动项均写在n时刻网格点上。于是，

$\begin{split} {X}_{u}'=&({u}')_{{\rm{d}}}^{{{n}}}+{\beta }_{{\rm{\varepsilon}}}f{\left({v}'\right)}_{{\rm{d}}}^{{{n}}}+{\beta }_{{\rm{\varepsilon}}}{L}_{{\rm{\theta}}}{{(\varPi }_{x}'+{Z}_{{{s}}{{x}}}{\varPi }_{\hat{{\textit z}}}')}_{{\rm{d}}}^{{{n}}}+\\&\Delta t{c}_{{{p}}}{L}_{{\text{π}}{{x}}}{\theta }'^{{{n}}}-\Delta t{\left({{{V}}'}{\text •} \nabla u\right)}^{{{n}}}\end{split} $

类似地，扰动经向速度方程为

$ {v}'+{\alpha }_{{\rm{\varepsilon}}}f{u}'-{\alpha }_{{\rm{\varepsilon}}}{L}_{{\rm{\theta}}}{(\varPi }_{y}'+{Z}_{{\rm{s}}{\rm{y}}}{\varPi }_{\hat{{\textit z}}}')={X}_{v}' $

(21)

式中， ${X}_{v}'\!=\!({v}')_{{\rm{d}}}^{{{n}}}\!-\!{\beta }_{{\rm{\varepsilon}}}{f\left({u}'\right)}_{{\rm{d}}}^{{n}}\!+\!{\beta }_{{\rm{\varepsilon}}}{L}_{{\rm{\theta}}}{{(\varPi }_{y}'\!+\!{Z}_{{{sy}}}{\varPi }_{\hat{{\textit z}}}')}_{{\rm{d}}}^{{{n}}}\!+\!{\Delta tc}_{{{p}}}{L}_{{\text{π}}{{y}}}{{\theta }'}^{{n}}\!- \Delta t{\left({{{V}}'}{\text •} \nabla v\right)}^{{n}}$

扰动垂直速度方程

$ {w}'+{\alpha }_{{\rm{\varepsilon}}}{c}_{{{p}}}\theta {'Z}_{{{s}}\hat{{{\textit z}}}}{\varPi }_{\hat{{\textit z}}}+{\alpha }_{{\rm{\varepsilon}}}{c}_{{{p}}}\theta {Z}_{{s}\hat{{\textit z}}}{\varPi }_{\hat{{\textit z}}}'={X}_{{{w}}}' $

(22)

式中， ${X}_{{{w}}}'={\left({w}'\right)}_{{\rm{d}}}^{{n}}-{\beta }_{{{\varepsilon}}}{c}_{{{p}}}{\left(\theta {'Z}_{{s}\hat{{\textit z}}}{\varPi }_{\hat{{\textit z}}}\right)}_{{\rm{d}}}^{{{n}}}-{\beta }_{{\rm{\varepsilon}}}{c}_{{{p}}}{\left(\theta {Z}_{{s}\hat{{\textit z}}}{\varPi }_{\hat{{\textit z}}}'\right)}_{{\rm{d}}}^{{{n}}}-\Delta t({{{V}}'}{\text •} $ $ \nabla w)^{{n}}$

将地形追随坐标垂直速度 $\hat w' = {Z_{{{sx}}}}u' + {Z_{{{sy}}}}v' + {Z_{{{s\hat {\textit z}}}}}w'$ 代入式（22）得

$ \begin{split}&\hat w' - {Z_{{{sx}}}}u' - {Z_{{{sy}}}}v' + {\alpha _\varepsilon }{c_{{p}}}\theta {Z_{{{s\hat z}}}^2}\varPi {'_{\hat {\textit z}}} + {\alpha _\varepsilon }{c_{{p}}}{Z_{{{s\hat z}}}^2}{\varPi _{\hat {\textit z}}}\theta ' = X_{{{\hat w}}}' \end{split}$

(23)

式中， ${X}_{\hat{{w}}}'\!=\!{\left({\hat{w}}'\right)}_{{\rm{d}}}^{n}\!-\!{Z}_{{{s}}{{x}}}{\left(u'\right)}_{{\rm{d}}}^{{{n}}}\!-\!{Z}_{{{sy}}}{\left(v'\right)}_{{\rm{d}}}^{{n}}\!-\!{\beta }_{{\rm{\varepsilon}}}{{c}_{{{p}}}{{Z}_{{s}\hat{{\rm{z}}}}^{2}}(\theta \varPi '_{\hat{{\textit z}}}\!+\!} { {\varPi }_{\hat{{\textit z}}}\theta ')}_{{\rm{d}}}^{{{n}}}- \Delta t{Z}_{{{s}}\hat{{{\textit z}}}}{\left({{{V}}'}{\text •} \nabla w\right)}^{n}$

扰动连续方程

$ \begin{split}& {\varPi }'+{\alpha }_{{\rm{\varepsilon}}}\left({u}'{\varPi }_{x}+{v}'{\varPi }_{y}+{\hat{w}}'{\varPi }_{\hat{\textit z}}\right)+{\alpha }_{{\rm{\varepsilon}}}{\alpha }_{{\rm{D}}}{\varPi }'+{\alpha }_{{\rm{\varepsilon}}}{\alpha }_{\Pi}{D}_{3}'={X}_{\varPi }' \end{split}$

(24)

式中， ${X}_{\Pi}'={\left(\varPi '\right)}_{{\rm{d}}}^{{{n}}}-{\beta }_{{\rm{\varepsilon}}}{\left({\alpha }_{{\rm{D}}}\varPi '\right)}_{{\rm{d}}}^{{n}}-{\beta }_{{\rm{\varepsilon}}}{\left({{{{V}}}'}{\text •} \nabla \varPi \right)}_{{\rm{d}}}^{{n}}-{\beta }_{{\rm{\varepsilon}}}{\left({\alpha }_{\Pi}{D}_{3}'\right)}_{{\rm{d}}}^{{{n}}}+ \Delta t({\gamma }_{{\rm{\theta}}}{P'_{\rm{w}})}_{{\rm{d}}}^{{n}}$

潜热加热项 $P'_{\rm w}$ 只在n时刻的上游点上计算。

将 ${D'_{3}}={u'_{x}}+{v'_{y}}+{{\hat w}'}_{\hat{\textit z}}-\dfrac{{\partial Z}_{{sx}}}{\partial \hat{\textit z}}u'-\dfrac{{\partial Z}_{{sy}}}{\partial \hat{\textit z}}v'$ 代入式（24），整理得到

$\begin{split}& {\varPi }'={A}_{\varPi1}u'+{A}_{\varPi2}v'+{A}_{\varPi3}{\hat{w}}'+\\&{A}_{\varPi4}\left({u}'_{x}+{v}'_{y}+\hat{w}'_{\hat{{\textit z}}}\right)+{A}_{\varPi0} \end{split}$

(25)

其中系数

$\begin{split} &{A_{{{\varPi }}1}} = {\alpha _{\rm{\varepsilon }}}\dfrac{{{\alpha _{{\varPi }}}\dfrac{{\partial {Z_{sx}}}}{{\partial \hat {\textit z}}} - {\varPi _x}}}{{1 + {\alpha _{\rm{\varepsilon }}}{\alpha _{\rm{D}}}}},\quad{A_{{{\varPi }}2}} = {\alpha _\varepsilon }\dfrac{{{\alpha _{{\varPi }}}\dfrac{{\partial {Z_{sy}}}}{{\partial \hat {\textit z}}} - {\varPi _y}}}{{1 + {\alpha _{\rm{\varepsilon }}}{\alpha _{\rm{D}}}}},\\&{A_{{{\varPi }}3}} = - \frac{{{\alpha _\varepsilon }{\varPi _{\hat {\textit z}}}}}{{1 + {\alpha _{\rm{\varepsilon }}}{\alpha _{\rm{D}}}}},\quad{A_{{{\varPi }}4}} = - \frac{{{\alpha _{\rm{\varepsilon }}}{\alpha _{{\varPi }}}}}{{1 + {\alpha _{\rm{\varepsilon }}}{\alpha _{\rm{D}}}}},\quad{A_{{{\varPi }}0}} = \frac{{X_{{\varPi }}'}}{{1 + {\alpha _{\rm{\varepsilon }}}{\alpha _{\rm{D}}}}} \end{split}$

扰动水汽方程

$ {q}'=-{\alpha }_{{\rm{\varepsilon}}}{q}_{\hat{{\textit z}}}{\hat{w}}'+{X}_{{\rm{q}}}' $

(26)

式中， ${X}_{{\rm{q}}}'={\left({q}'\right)}_{{\rm{d}}}^{{n}}-\Delta t{\left({{u}'q}_{x}+{{v}'q}_{y}\right)}^{{n}}-{\beta }_{{\rm{\varepsilon}}}{\left({\hat{w}}'{q}_{\hat{{\textit z}}}\right)}_{{\rm{d}}}^{{n}}-\Delta t{\left({P}_{{\rm{w}}}'\right)}_{{\rm{d}}}^{{{n}}}$

这里扰动风对基态水汽的垂直平流用半隐式计算，水平平流用显式计算。

扰动位温方程形式与水汽方程完全类似，即

$ {\theta }'=-{\alpha }_{{\rm{\varepsilon}}}{\hat{w}}'{\theta }_{\hat{{\textit z}}}+{X}_{{\rm{\theta}}}' $

(27)

式中， ${X}_{{\rm{\theta}}}'={\left({\theta }'\right)}_{{\rm{d}}}^{{{n}}}-\Delta t{\left({u}'{\theta }_{x}+{v}'{\theta }_{y}\right)}^{{{n}}}-{\beta }_{{\rm{\varepsilon}}}{\left(\hat{w}'{\theta }_{\hat{{\textit z}}}\right)}_{{\rm{d}}}^{{{n}}}+\Delta t{\gamma }_{\Pi}{\left({P}_{{\rm{w}}}'\right)}_{{\rm{d}}}^{{{n}}}$

2.4 扰动变量亥姆霍兹方程推导

通过一系列代数消元后，扰动方程组最终化为只含变量 $ {\varPi }' $ 的亥姆霍兹方程。先将方程（20）和（21）联立求解得到 $ u'{\text{和}}v' $ 关于 $ \varPi ' $ 的方程

$ u'={A}_{{u}1}{\varPi }_{x}'+{A}_{{u}2}{\varPi }_{y}'+{A}_{{u}3}{\varPi }_{\hat{{\textit z}}}'+{A}_{{u}0} $

(28)

$ v'={A}_{{v}1}{\varPi }_{x}'+{A}_{{v}2}{\varPi }_{y}'+{A}_{{v}3}{\varPi }_{\hat{{\textit z}}}'+{A}_{{v}0} $

(29)

$\begin{split} \text{其中，} &{A_{{{u}}1}} = \frac{{{\alpha _{\rm{\varepsilon }}}{L_{\rm{\theta }}}}}{{1 + {{({\alpha _{\rm{\varepsilon }}}f)}^2}}},\quad{A_{{{u}}2}} = \frac{{{\alpha _{\rm{\varepsilon }}}^2f{L_{\rm{\theta }}}}}{{1 + {{({\alpha _{\rm{\varepsilon }}}f)}^2}}},\\&{A_{{{u}}3}} = \frac{{{\alpha _{\rm{\varepsilon }}}{L_{\rm{\theta }}}\left({{Z_{{sx}}} + {\alpha _{\rm{\varepsilon }}}f{Z_{sy}}} \right)}}{{1 + {{({\alpha _{\rm{\varepsilon }}}f)}^2}}},\quad{A_{{{u}}0}} = \frac{{{\alpha _\varepsilon }fX_{{v}}' + X_{{u}}'}}{{1 + {{({\alpha _{\rm{\varepsilon }}}f)}^2}}}\end{split} $

$\begin{split} &{A_{{{v}}1}} = - \frac{{{\alpha _{\rm{\varepsilon }}}^2f{L_{\rm{\theta }}}}}{{1 + {{({\alpha _{\rm{\varepsilon }}}f)}^2}}},\quad{A_{{{v}}2}} = \frac{{{\alpha _{\rm{\varepsilon }}}{L_{\rm{\theta }}}}}{{1 + {{({\alpha _{\rm{\varepsilon }}}f)}^2}}},\\ &{A_{{{v}}3}} = \frac{{{\alpha _{\rm{\varepsilon }}}{L_{\rm{\theta }}}\left({{Z_{{{sy}}}} - {Z_{{sx}}}{\alpha _{\rm{\varepsilon }}}f} \right)}}{{1 + {{({\alpha _{\rm{\varepsilon }}}f)}^2}}},\quad{A_{{{v}}0}} = \frac{{X_v' - {\alpha _\epsilon }fX_u'}}{{1 + {{({\alpha _{\rm{\varepsilon }}}f)}^2}}}\end{split} $

联立式（23）和（27），得 ${\hat{w}}'$ 预报方程

$ \begin{split} {\hat{w}}'=&\frac{{Z}_{{{sx}}}}{1-{\alpha }_{\varepsilon }^{2}{c}_{{{p}}}{Z}_{{{s}}\hat{{{\textit z}}}}^{2}{\varPi }_{\hat{{\textit z}}}{\theta }_{\hat{{\textit z}}}}{u}'+\frac{{Z}_{{{sy}}}}{1-{\alpha }_{\varepsilon }^{2}{c}_{{{p}}}{Z}_{{s}\hat{{{\textit z}}}}^{2}{\varPi }_{\hat{{\textit z}}}{\theta }_{\hat{{\textit z}}}}{v}'-\\ &\frac{{\alpha }_{\varepsilon }{c}_{{{p}}}\theta {Z}_{{s}\hat{{\textit z}}}^{2}}{1-{\alpha }_{\varepsilon }^{2}{c}_{{{p}}}{Z}_{{s}\hat{{\textit z}}}^{2}{\varPi }_{\hat{{\textit z}}}{\theta }_{\hat{{\textit z}}}}{{\varPi }}'_{\hat{{\textit z}}}+\frac{{X}_{\hat{{{w}}}}'-{\alpha }_{{\rm{\varepsilon}}}{c}_{{{p}}}{Z}_{{{s}}\hat{{{\textit z}}}}^{2}{\varPi }_{\hat{{\textit z}}}{X}_{\theta }'}{1-{\alpha }_{\varepsilon }^{2}{c}_{{{p}}}{Z}_{{{s}}\hat{{{\textit z}}}}^{2}{\varPi }_{\hat{{\textit z}}}{\theta }_{\hat{{\textit z}}}} \end{split}$

将式（28）和（29）代入上式，得到 $\hat w'$ 仅依赖于Π′的方程

$ {\hat{w}}'={A}_{\hat{{{w}}}1}{\varPi }_{x}'+{A}_{\hat{{{w}}}2}{\varPi }_{y}'+{A}_{\hat{{{w}}}3}{\varPi }_{\hat{{\textit z}}}'+{A}_{\hat{{{w}}}0} $

(30)

其中， ${A_{{{\hat w}}1}} = \dfrac{{{Z_{{{sx}}}}{A_{{{u}}1}} + {Z_{{{sy}}}}{A_{{{v}}1}}}}{{1 - \alpha _\varepsilon ^2{c_{{p}}}{Z_{{{s\hat {\textit z}}}}^2}{\varPi _{\hat {\textit z}}}{\theta _{\hat {\textit z}}}}},$

$ \begin{split} &\ {A_{{{\hat w}}2}} = \frac{{{Z_{{{sx}}}}{A_{{{u}}2}} + {Z_{{{sy}}}}{A_{{{v}}2}}}}{{1 - \alpha _\varepsilon ^2{c_{{p}}}Z_{{{s\hat {\textit z}}}}^2{\varPi _{\hat {\textit z}}}{\theta _{\hat {\textit z}}}}},\\ &\ {A_{{{\hat w}}3}} = \frac{{{Z_{{{sx}}}}{A_{{{u}}3}} + {Z_{{sy}}}{A_{{{v}}3}} - {\alpha _\varepsilon }{c_{{p}}}\theta {Z_{{{s\hat {\textit z}}}}^2}}}{{1 - \alpha _\varepsilon ^2{c_{{p}}}{Z_{{s\hat {\textit z}}}^2}{\varPi _{\hat {\textit z}}}{\theta _{\hat {\textit z}}}}},\\ &\ {A_{{{\hat w}}0}} = \frac{{{Z_{{{sx}}}}{A_{{{u}}0}} + {Z_{{{sy}}}}{A_{{{v}}0}} + X_{{{\hat w}}}' - {\alpha _{\rm{\varepsilon }}}{c_{{p}}}{Z_{{s\hat {\textit z}}}^2}{\varPi _{\hat {\textit z}}}X_\theta '}}{{1 - \alpha _\varepsilon ^2{c_{{p}}}{Z_{{{s\hat {\textit z}}}}^2}{\varPi _{\hat {\textit z}}}{\theta _{\hat {\textit z}}}}} \end{split} $

进一步将式（30）代入式（26）和（27）得到 $ \theta ' $ 和 $ {q}' $ 仅依赖 $ \varPi ' $ 的方程

$ {\theta }'={A}_{{{\theta}}1}{\varPi }_{x}'+{A}_{{{\theta}}2}{\varPi }_{y}'+{A}_{{{\theta}}3}{\varPi }_{\hat{{\textit z}}}'+{A}_{{{\theta}}0} $

(31)

$ \begin{split} \text{其中，}\qquad &{A_{{{\theta }}1}} = - {\alpha _{{\varepsilon }}}{\theta _{{{\hat {\textit z}}}}}{A_{{{\hat w}}1}},\quad{A_{{{\theta }}2}} = - {\alpha _{{\varepsilon }}}{\theta _{{{\hat {\textit z}}}}}{A_{{{\hat w}}2}},\qquad\qquad\\ &{A_{{{\theta }}3}} = - {\alpha _{{\varepsilon }}}{\theta _{{{\hat {\textit z}}}}}{A_{{{\hat w}}3}},\quad{A_{{\rm{\theta }}0}} = - {\alpha _{\rm{\varepsilon }}}{\theta _{{{\hat {\textit z}}}}}{A_{{{\hat w}}0}} + X_{{\theta }}'\\ &q' = {A_{{{q}}1}}\varPi _x' + {A_{{{q}}2}}\varPi _y' + {A_{{{q}}3}}\varPi _{\hat {\textit z}}' + {A_{{{q}}0}}\\[-10pt] \end{split} $

(32)

$ \begin{split} \text{其中，}\qquad &{A_{{{q}}1}} = - {\alpha _{{\varepsilon }}}{q_{{{\hat {\textit z}}}}}{A_{{{\hat w}}1}},\quad{A_{{{q}}2}} = - {\alpha _{{\varepsilon }}}{q_{{{\hat {\textit z}}}}}{A_{{{\hat w}}2}},\\ &{A_{{{q}}3}} = - {\alpha _{{\varepsilon }}}{q_{{{\hat {\textit z}}}}}{A_{{{\hat w}}3}},\quad{A_{q0}} = - {\alpha _\varepsilon }{q_{{{\hat {\textit z}}}}}{A_{{{\hat w}}0}} + X_{{q}}'\end{split} \hspace{27pt} $

方程（28）—（32）中，扰动变量（u'、v'、 $ {\hat{w}}'{\text{、}} {q}'{\text{、}} {\theta }' $ ）最终只与n时间层的已知状态（ ${A}_{{{u}}0}$ 、 ${A}_{{{v}}0}$ 、 ${A}_{\hat{{{w}}}0}$ 、 ${A}_{{{q}}0}$ 、 ${A}_{{{\theta}}0}$ ）及n+1时间层的 $ {\varPi }' $ 有关，且每个方程中与 $ {\varPi }' $ 有关各项的系数只与基本态有关，它们可以通过非线性模式计算。

沿用GRAPES非线性模式的空间离散差分方案，垂直方向采用Charney-Phillips跳点，水平方向采用Arakawa C网格。为提高精度，垂直差分使用非均匀分层的二阶精度差分方案。

空间离散化后的运动方程为

$ {u}'={A}_{{{u}}1}{\varPi }_{x}'+{A}_{{{u}}2}{\left({\overline{{\varPi }'}}^{yx}\right)}_{y}+{A}_{{{u}}3}{\left({\overline{{\varPi }'}}^{\hat{{\textit z}}x}\right)}_{\hat{{\textit z}}}+{A}_{{{u}}0} $

$ {v}'={A}_{{{v}}1}{\left({\overline{{\varPi }'}}^{xy}\right)}_{x}+{A}_{{{v}}2}{\varPi }_{y}'+{A}_{{{v}}3}{\left({\overline{{\varPi }'}}^{y\hat{{\textit z}}}\right)}_{\hat{{\textit z}}}+{A}_{{{v}}0} $

$ {\hat{w}}'={A}_{\hat{{{w}}}1}{\left({\overline{{\varPi }'}}^{x\hat{{\textit z}}}\right)}_{x}+{A}_{\hat{{{w}}}2}{\left({\overline{{\varPi }'}}^{y\hat{{\textit z}}}\right)}_{y}+{A}_{\hat{{{w}}}3}{\varPi }_{\hat{{\textit z}}}'+{A}_{\hat{{{w}}}0} $

变量上方的横线表示因为跳点的原因需要在相应的平面上取平均。将上面3个公式代入式（25）并离散化，得

$ \begin{split} {\varPi }'=&{A}_{{\varPi}1}{\overline{\left[{A}_{{{u}}1}{\varPi }_{x}'+{A}_{{{u}}2}{\left({\overline{{\varPi }'}}^{yx}\right)}_{y}+{A}_{{{u}}3}{\left({\overline{{\varPi }'}}^{\hat{{\textit z}}x}\right)}_{\hat{{\textit z}}}+{A}_{u0}\right]}}^{x}+\\ &{A}_{\varPi2}{\overline{\left[{A}_{{{v}}1}{\left({\overline{{\varPi }'}}^{xy}\right)}_{x}+{A}_{{{v}}2}{\varPi }_{y}'+{A}_{{{v}}3}{\left({\overline{{\varPi }'}}^{y\hat{{\textit z}}}\right)}_{\hat{{\textit z}}}+{A}_{{{v}}0}\right]}}^{y}+\\ &{A}_{\varPi3}{\overline{\left[{A}_{\hat{{{w}}}1}{\left({\overline{{\varPi }'}}^{x\hat{{\textit z}}}\right)}_{x}+{A}_{\hat{{{w}}}2}{\left({\overline{{\varPi }'}}^{y\hat{{\textit z}}}\right)}_{y}+{A}_{\hat{{{w}}}3}{\varPi }_{\hat{{\textit z}}}'+{A}_{\hat{w}0}\right]}}^{\hat{{\textit z}}}+ \\&{A}_{\varPi4}\left\{{\left[{A}_{{{u}}1}{\varPi }_{x}'+{A}_{{{u}}2}{\left({\overline{{\varPi }'}}^{yx}\right)}_{y}+{A}_{{{u}}3}{\left({\overline{{\varPi }'}}^{\hat{{\textit z}}x}\right)}_{\hat{{\textit z}}}+{A}_{u0}\right]}_{x}\right.+ \\&{\left[{A}_{{{v}}1}{\left({\overline{{\varPi }'}}^{xy}\right)}_{x}+{A}_{{{v}}2}{\varPi }_{y}'+{A}_{{{v}}3}{\left({\overline{{\varPi }'}}^{y\hat{{\textit z}}}\right)}_{\hat{{\textit z}}}+{A}_{{{v}}0}\right]}_{y}+ \\&\left.{\left[{A}_{\hat{w}1}{\left({\overline{{\varPi }'}}^{x\hat{{\textit z}}}\right)}_{x}+{A}_{\hat{{\rm{w}}}2}{\left({\overline{{\varPi }'}}^{y\hat{{\textit z}}}\right)}_{y}+ {A}_{\hat{w}3}{\varPi }_{\hat{{\textit z}}}'+{A}_{\hat{{{w}}}0}\right]}_{\hat{{\textit z}}}\right\}+{A}_{\varPi 0} \end{split}$

(33)

将式（33）在网格点上展开，得到如下形式的亥姆霍兹方程

$ \begin{split} & {B}_{1}{\varPi }_{{{i}},{{j}},{{k}}}+{B}_{2}{\varPi }_{{{i}}-1,{{j}},{{k}}}+{B}_{3}{\varPi }_{{{i}}+1,{{j}},{{k}}}+{B}_{4}{\varPi }_{{{i}},{{j}}-1,{{k}}}+{B}_{5}{\varPi }_{{{i}},{{j}}+1,{{k}}}+\\ &\quad{B}_{6}{\varPi }_{{{i}}+1,{{j}}+1,{{k}}}+{B}_{7}{\varPi }_{{{i}}+1,{{j}}-1,{{k}}}+{B}_{8}{\varPi }_{{{i}}-1,{{j}}-1,{{k}}}+{B}_{9}{\varPi }_{{{i}}-1,{{j}}+1,{{k}}}+\\ &\quad{B}_{10}{\varPi }_{{{i}},{{j}},{{k}}-1}+{B}_{11}{\varPi }_{{{i}}-1,{{j}},{{k}}-1}+{B}_{12}{\varPi }_{{{i}}+1,{{j}},{{k}}-1}+{B}_{13}{\varPi }_{{{i}},{{j}}-1,{{k}}-1}+\\ &\quad{B}_{14}{\varPi }_{{{i}},{{j}}+1,{{k}}-1} +{B}_{15}{\varPi }_{{{i}},{{j}},{{k}}+1}+{B}_{16}{\varPi }_{{{i}}-1,{{j}},{{k}}+1}+{B}_{17}{\varPi }_{{{i}}+1,{{j}},{{k}}+1}+\\&\quad{B}_{18}{\varPi }_{{{i}},{{j}}-1,{{k}}+1}+{B}_{19}{\varPi }_{{{i}},{{j}}+1,{{k}}+1}={B}_{0}\\[-10pt] \end{split} $

(34)

式中系数 $ {B}_{1} $ 到 $ {B}_{19} $ 只与基本态有关，而 $ {B}_{0} $ 则与n时刻扰动态在上游点的取值有关。

亥姆霍兹方程（34）的求解采用广义共轭余差法（GCR）迭代求解，关于该方法详见薛纪善等（2008）。当前求解过程取 $ {P}_{{\rm{w}}}' $ 始终为0，即暂时只考虑干模式。

为使方程（34）的求解闭合，使用了上下边界为刚体的边界条件，即 ${\left({\hat{w}}'\right)}_{\rm{T}}={\left({\hat{w}}'\right)}_{\rm{B}}=0$ 。由此推导出上、下边界的两个差分方程：

上边界

$ {\left({\hat{w}}'\right)}_{{\rm{T}}}={\left[{A}_{\hat{{{w}}}1}{\left({\overline{{\varPi }'}}^{x\hat{{\textit z}}}\right)}_{x}+{A}_{\hat{{{w}}}2}{\left({\overline{{\varPi }'}}^{y\hat{{\textit z}}}\right)}_{y}+{A}_{\hat{{{w}}}3}{\varPi }_{\hat{{\textit z}}}'+{A}_{\hat{{{w}}}0}\right]}_{{\rm{T}}}=0 $

(35)

下边界

$ {\left({\hat{w}}'\right)}_{{\rm{B}}}={\left[{A}_{\hat{{{w}}}1}{\left({\overline{{\varPi }'}}^{x\hat{{\textit z}}}\right)}_{x}+{A}_{\hat{{{w}}}2}{\left({\overline{{\varPi }'}}^{y\hat{{\textit z}}}\right)}_{y}+{A}_{\hat{{{w}}}3}{\varPi }_{\hat{{\textit z}}}'+{A}_{\hat{w}0}\right]}_{{\rm{B}}}=0 $

(36)

3 数值求解试验和分析

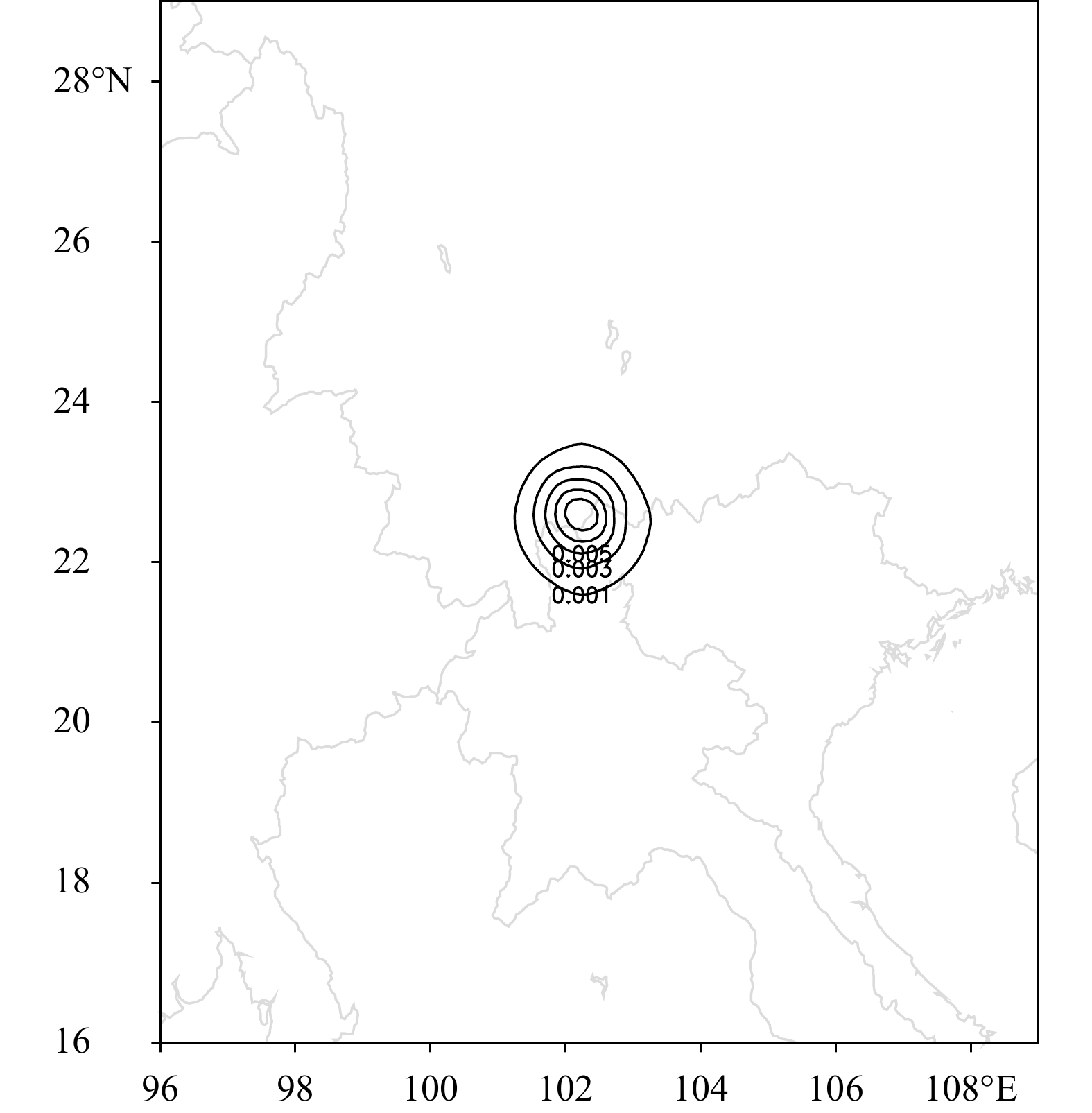
为了测试扰动模式动力框架的合理性，首先利用非线性模式产生检验所需要的扰动场。具体做法为，将非线性模式GRAPES的物理过程全部关闭（干模式），设计两组试验，分别以2015年5月16日00:00:00 UTC的ECMWF分析场作为初值进行积分。第一组试验（CTRL）直接以ECMWF分析场作为模式初始场进行时间积分；第二组试验（PERT）在ECMWF分析场上叠加一个中尺度小高压扰动后进行时间积分。试验PERT与试验CTRL的差值作为真值用于对扰动模式GRAPES_PF的积分结果进行检验。非线性模式GRAPES和扰动模式GRAPES_PF的水平分辨率均取0.12°（约12 km），垂直层为67层，模式顶高度为30 km，时间积分步长为60 s。模式范围为（16°—29.8ºN，96°—110.04ºE）（图1），侧边界采用Davies松弛边界处理方案（薛纪善等，2008），现阶段扰动模式在侧边界上简单取0，即令侧边界无扰动。

使用12 km分辨率的GRAPES-3DVar同化系统产生扰动高压。利用3D-Var中的单站探空分析功能，在模式面约6 km高度（约在模式25层）的（22.78°N，102.7°E）位置上进行气压要素的单点分析，得到水平方向尺度半径约120 km大致符合高斯分布的初始高压扰动（ ${\varPi }'$ ）。考虑到精度对扰动模式积分的影响，此处将3D-Var单点试验得到的扰动扩大了100倍，即用于扰动模式初始场的气压扰动量级为10⁻³（图1）。

扰动求解过程从n时刻初始扰动 ${x'}^{{{n}}}=(u',v',{\hat{w}}',{\theta }',$ ${{q}',{\varPi }')}^{n}$ 出发，求解扰动变量亥姆霍兹方程（式（34）），得到n+1时刻扰动气压 ${{\varPi }'}^{n+1}$ ，进而计算n+1时刻的其他5个扰动变量 ${(u',v',{\hat{w}}',{\theta }',{q}')}^{{{n}}+1}$ 。然后以n+1时刻的扰动量为初值，重复前面的过程，计算出n+2时刻的扰动量，依此类推，不断积分下去。特别要指出，文中每一时步亥姆霍兹方程广义共轭余差法迭代求解收敛精度均很高，余差均可收敛到10⁻²⁶。

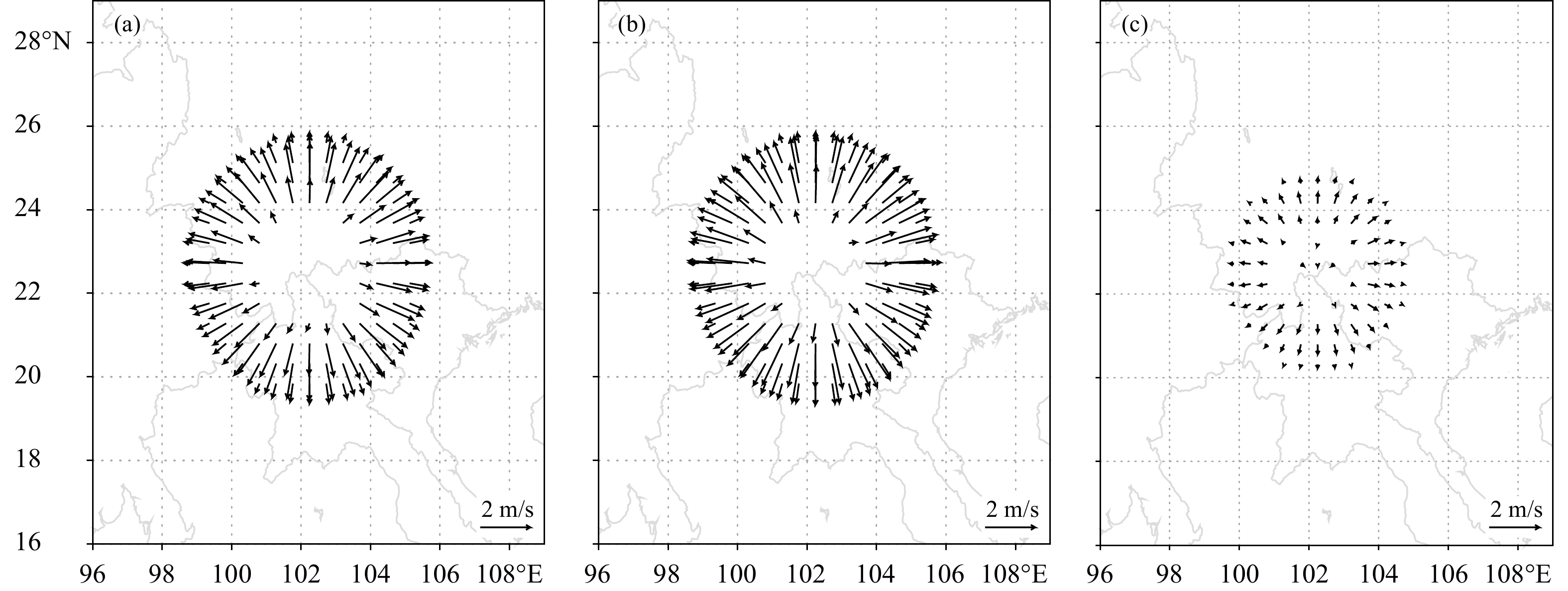
可以预计，如果扰动模式设计合理，扰动的传播图像应与非线性模式两次试验的差值场相似。图2是模式积分11步后第20层的水平扰动风场，其中图2a是积分两组非线性模式的差值场，代表扰动的实际演变（视为真值）；图2b是从扰动初值出发经过扰动模式积分11步后得到的结果，代表扰动模式的预报值。图2c是图2a与图2b的差值，代表扰动模式的预报与实际情况的差异。可以看到，扰动模式的预报与非线性模式的结果非常相似，差异较小，能够较好地模拟扰动风场的变化。

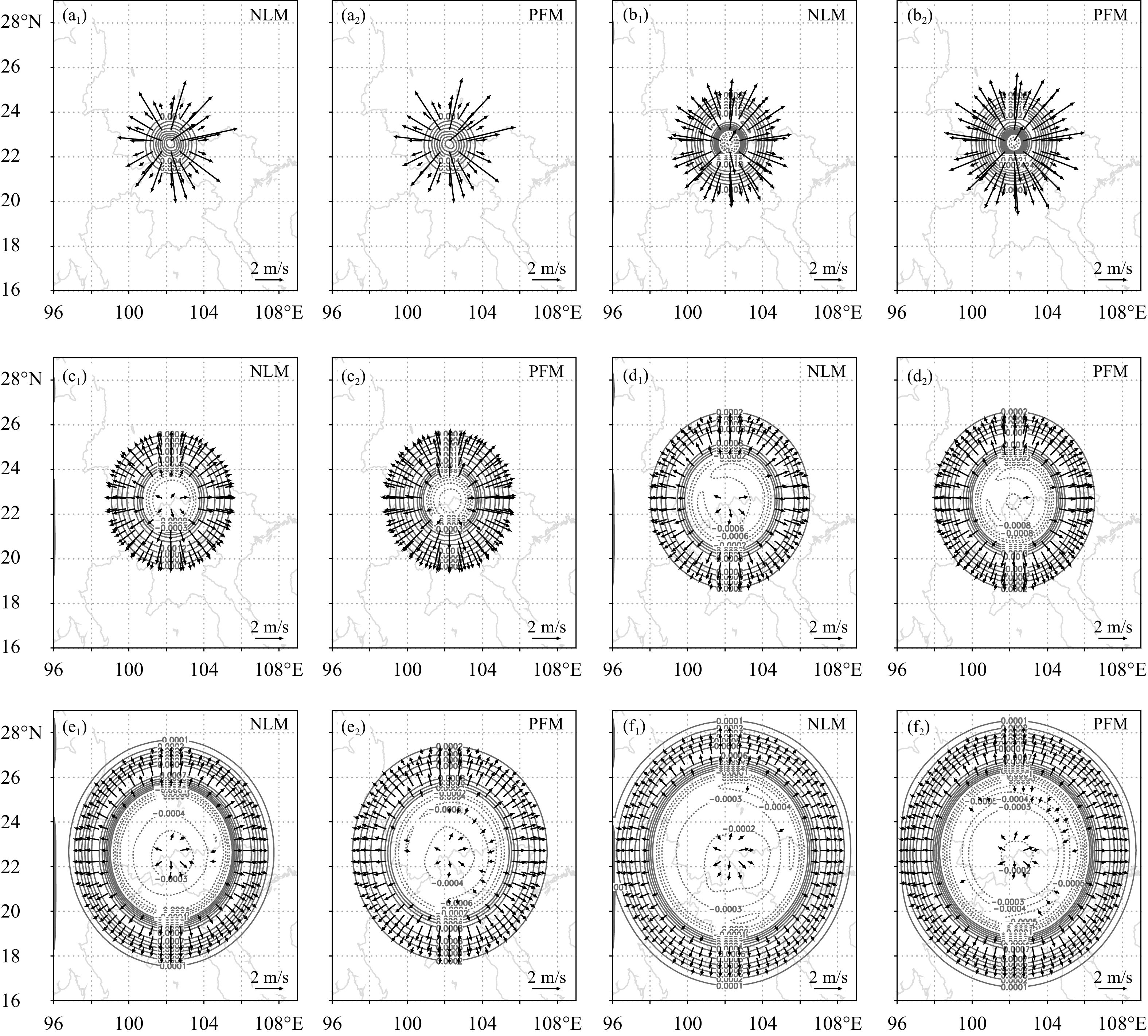
图3是非线性模式和扰动模式不同时刻在模式第25层的预报结果。可以看出，人为设置高压扰动后，大气运动的大尺度准平衡遭到破坏，初始没有风场支持的扰动高压迅速激发出了强的非地转风，以惯性重力内波的形式迅速向四周传播。这实际上是一个非常快的地转适应过程，叶笃正等（1965）以及曾庆存（1963）和曾庆存等（1980）从理论上对这一过程作了充分的研究。由图3可见，扰动模式非常逼真地模拟了这个气压场向风场适应的过程。伴随非地转扰动能量迅速向外弥散，扰动气压场迅速减弱，扰动风场也随之迅速趋于减弱，模式大气迅速恢复到原来的准平衡状态。

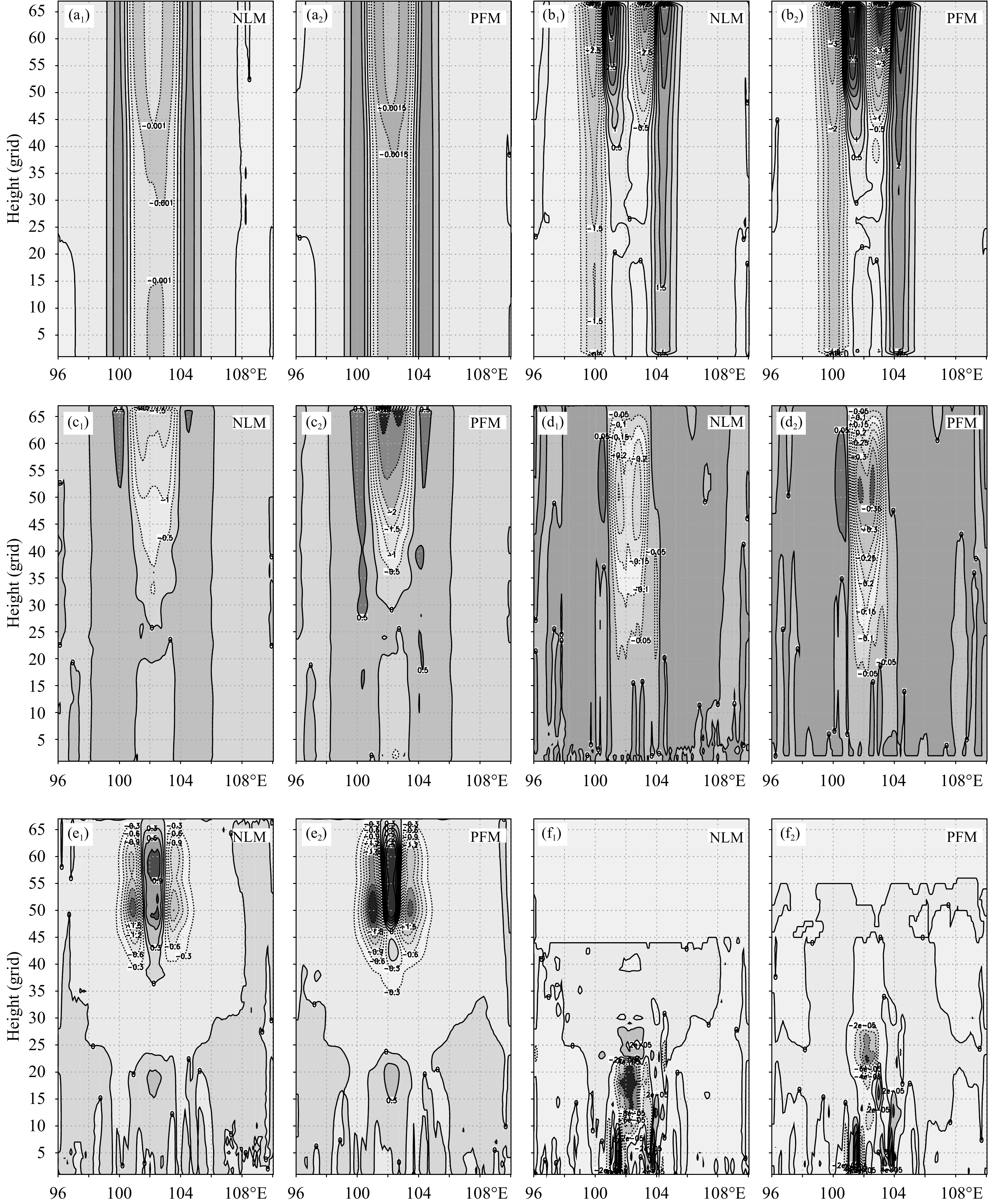
适应过程是准线性快过程，是以辐散辐合运动和垂直运动为特征的（曾庆存，1963），因此线性扰动模式必须能合理反映这个基本特征。从给出的积分第11步后6个扰动变量经过初始扰动高压中心所做的纬度高度剖面（图4）可见，初始高压扰动除了激发水平方向迅速传播的重力波涟漪，也引起了垂直方向的运动增量，并进而引起各变量在垂直方向上重新分配。与非线性模式相比，扰动模式能够较好地预报扰动随时间变化的空间分布，各个扰动变量的数量级和正负数值分布与非线性模式的结果相近。值得一提的是， $ \theta ' $ 和 $ q' $ 的扰动方程性质接近，两者采用相同的计算方案，但扰动位温（ $ \theta ' $ ）的计算差异性较小。只有比湿（ $ q' $ ）的预报，扰动模式的负值中心比非线性模式位置略高，数值上也有一定差异，这是计算精度引起的。由于比湿基本态本身数值就很小（10⁻³），远小于位温基本态（量级达10²），且数值试验初始时刻只有气压扰动，水汽相对于基本态无增量（ $ {q}'=0 $ ），后续的水汽增量完全是因模式自身激发出来的，量级极小（10⁻⁶），故此处 $ q' $ 计算有一定误差。

为了整体评估扰动模式相对于非线性模式的线性近似程度，利用Frobonius范数对扰动模式进行正确性检验。若将初始基本态（ $ {x}_{0} $ ）出发的非线性模式积分表示为 $ {\rm{NLM}}\left({x}_{0}\right) $ （试验1），将初始基本态（ $ {x}_{0} $ ）加小扰动量（ $\gamma {{\rm{\delta}}x}_{0}$ ），再次积分非线性模式，得到 ${\rm{NLM}}\left({x}_{0}+\gamma {{\rm{\delta}}x}_{0}\right)$ （试验2）。 $ \gamma $ 是一个小的正数，用于控制初始扰动的大小。如果设 ${R}_{0\to i}\gamma {{\rm{\delta}}x}_{0}$ 为非线性模式的切线性模式从初值（ $\gamma {{\rm{\delta}}x}_{0}$ ）出发的一次积分。i表示积分步数。于是应有：

$ {\rm{NLM}}\left({x}_{0}+\gamma {{\rm{\delta}}x}_{0}\right)={\rm{NLM}}\left({x}_{0}\right)+{R}_{0\to i}\gamma {{\rm{\delta}}x}_{0}+O\left({\gamma }^{2}\right) $

(37)

设 ${\rm{PFM}}\left(\gamma {{\rm{\delta}}x}_{0}\right)$ 为从初值（ $\gamma {{\rm{\delta}}x}_{0}$ ）出发的一次扰动模式积分。为清楚表示，扰动模式表示为 ${\rm{PFM}}\left(\gamma {{\rm{\delta}}x}_{0}\right)= {M}_{0\to i}\gamma {{\rm{\delta}}x}_{0}$ 。令测试指数为：

$ \begin{split} F\left(\gamma \right)&=\frac{\left\|{\rm{NLM}}\left({x}_{0}+\gamma {{\rm{\delta}}x}_{0}\right)-{\rm{NLM}}\left({x}_{0}\right)\right\|}{\left\|\rm{PFM}\left(\gamma {{\rm{\delta}}x}_{0}\right)\right\|} \\& = \frac{\left\|{R}_{0\to i}{{\rm{\delta}}x}_{0}\right\|}{\left\|{M}_{0\to i}{{\rm{\delta}}x}_{0}\right\|}+O\left(\gamma \right) \end{split} $

(38)

式中，‖•‖表示Frobonius范数。当 $ {\rm{\gamma}} $ 趋近0时，如果扰动模式的积分结果与非线性模式的余差（两次积分试验之差）接近，则 $F \left(\gamma \right)$ 应趋近1，进而说明扰动模式 ${M}_{0\to i}$ 与切线性模式 ${R}_{0\to i}$ 相当。

根据上、下边界条件公式（35）和（36），求解亥姆霍兹方程需要在模式顶和模式底计算扰动气压垂直导数 $ {\varPi }_{\hat{ {\textit z}}}' $ 。为此需要在模式顶以上和模式底以下（即地表以下）各设一层气压虚层。由于已假定模式顶和模式底是没有垂直运动的刚体边界，故可利用以下静力平衡关系计算 ${\varPi }_{\hat{{\textit z}}}'$

$ {\left({\varPi }_{\hat{{\textit z}}}'\right)}_{{\rm{bottom}}\;{\rm{or}}\;{\rm{top}}}=\frac{g{\theta }'}{{c}_{p}{Z}_{{{s}}\hat{{{ {\textit z}}}}}{\theta }^{2}} $

(39)

式中， ${\varPi }_{\hat{{\textit z}}}'$ 与 $ \theta $ 和 $ \theta ' $ 有关，根据Charney/Philips垂直跳层设置，式（39）中位温可在模式底和模式顶直接取值，因此可避免使用气压虚层进行计算。

表1给出不同 $ {\rm{\gamma}} $ 下的测试指数F(γ)。可以看出，当 $ {\rm{\gamma}} $ 取10⁻²－10⁻³时F(γ)接近1。而且对上下边界条件采用静力平衡处理后的扰动模式相比采用虚层计算效果更好，精度可达到10⁻³。

4 结论和讨论

为发展基于扰动预报模式的四维变分资料同化系统，从GRAPES数值预报模式的原始方程组出发，采用小扰动分离方法推导了连续微分形式的线性扰动预报方程组，开发了扰动预报模式GRAPES_PF动力框架。扰动模式中时间积分采用两个时间层的半隐式半拉格朗日方案，空间差分采用Arakawa C水平网格跳点和Charney/Phillips垂直跳层方案，利用代数消元法进一步推导，得到关于扰动无量纲气压（ $ \varPi ' $ ）的亥姆霍兹方程，并通过广义共轭余差法（GCR）进行求解。

为了测试所开发的扰动模式动力框架的合理性，在干模式（无物理过程）条件下开展了数值试验。首先在非线性模式中施加一个初始扰动，积分非线性模式得到扰动的时间演变场，然后将相同的初始扰动作为扰动模式的初值进行时间积分，最后比较扰动模式与非线性模式的预报结果。

试验在模式第25层（约6 km处）施加了一个水平半径约120 km的中尺度扰动高压，根据地转适应理论，在这样小的尺度下气压场将向风场适应，即小高压所激发的不稳定能量将迅速向四周频散，导致扰动趋于减弱。数值试验表明，初始的非地转平衡状态激发了一个快速向外传播的惯性重力内波，迅速引起了水平辐散风和铅直运动，进而引起位温和湿度扰动。随着时间的推移，适应过程使扰动气压场迅速频散消失，扰动风场也随之迅速减弱，大气运动重新恢复到原来的平衡状态。对比非线性模式和扰动模式，两者动力热力场分布特征相似，数值结果接近。地转适应过程是以水平辐散辐合运动和垂直运动为特征的准线性快过程，试验结果表明，扰动模式GRAPES_PF合理反映了这个运动的基本特性，可作为GRAPES非线性模式系统的近似线性模式，为下一步发展基于扰动模式的四维变分同化系统奠定了研究和开发基础。

文中仅设计开发了扰动模式的动力框架，完善该扰动模式还需要逐步完成各种线性物理过程方案的开发。

致　谢：袁丽君参与了扰动模式的检验以及部分代码编写和测试，吴亚丽进行了非线性模式的运算，在此一并感谢。