中国气象学会主办。
文章信息
- 舒谦, 唐杰, 陈春刚, 肖锋, 沈学顺, 周立隆, 李泽椿, 朱克云, 李兴良. 2020.
- SHU Qian, TANG Jie, CHEN Chungang, XIAO Feng, SHEN Xueshun, ZHOU Lilong, LI Zechun, ZHU Keyun, LI Xingliang. 2020.
- 高阶正定守恒的中心约束多矩有限体积平流模式
- A high order positive-definite conservative multi-moment center constrained finite volume transport model
- 气象学报, 78(4): 665-678.
- Acta Meteorologica Sinica, 78(4): 665-678.
- http://dx.doi.org/10.11676/qxxb2020.039
文章历史
-
2019-11-22 收稿
2020-03-12 改回
2. 中国气象局数值预报中心,北京,100081;
3. 国家气象中心,北京,100081;
4. 西安交通大学,西安,710049;
5. 日本东京工业大学机械工程系,东京,152-8850
2. Numerical Weather Prediction Center of CMA,Beijing 100081,China;
3. National Meteorological Center,Beijing 100081,China;
4. Xi'an Jiaotong University,Xi'an 710049,China;
5. Department of Mechanical engineering,Tokyo Institute of Technology,Tokyo 152-8850,Japan
大气中水物质(如水汽、云水等)分布复杂,具有梯度大、不连续、多相变等特点,使得数值模拟水汽等输送过程容易产生非物理的负值及数值振荡。因而,采用良好的数值方法精确地模拟水物质的分布与输送,对数值天气预报输送模式的改进,特别是准确模拟降水过程,具有重要意义。
低精度的一阶迎风格式不产生数值振荡,但是数值耗散大,满足不了实际高精度模式的需求。高阶(大于一阶)平流算法精度较高,但是会产生非物理数值振荡,导致水物质输送产生较大误差(沈学顺等,2011),例如基于欧拉方法的Lax-Friedrich方法、Lax-Wendroff方法、MacCormach方法等。为了抑制数值振荡,中外学者提出了一系列的方法,例如通量修正(Book,et al,1975)方案,基于Godunov方法的MUSCL (Monotone Upstream-centered Schemes for Conservation Laws;van Leer,1977)方案,以及基于分段抛物线函数的PPM(Piecewise Parabolic Method ;Colella,et al,1984)方案,两步保型平流方案(TSPAS)(Yu,1994)等。
与欧拉方法相比,半拉格朗日方案(Robert,1981)可取较大的时间步长,效率较高,数值耗散低,被广泛应用于大气数值平流模式。Bermejo等(1992)设计出一个混合算法使传统的半拉格朗日方法转化为准单调的半拉格朗日(QMSL)方法,该方法在强梯度、不连续区域低阶插值不能保证守恒。Zerroukat等(2002)提出的守恒高效型半拉格朗日方案( SLICE)和Lauritzen等(2009)提出的守恒型半拉格朗日多示踪物方案(CSLAM),Xiao等(2002)提出的分段有理数插值(PRM)方案和CSLR (Conservative Semi-Lagrangian with Rational function)方案,都能保证平流方案的守恒性。为了获得良好的计算精度,Guo等(2014)把半拉格朗日方法和不连续伽辽金算法结合,设计出了SLDG(Semi-Lagrangian Discontinuous Galerkin)方案,该方案能够保证守恒,精度大于二阶,并且能通过限制器去除数值振荡。
多矩有限体积方法(Multi-moment finite volume scheme)是近年提出来的一种新的有限体积方法(Yabe,et al,1991,2001;Xiao,et al,2001,2006,2013;Xiao,2004;Ii,et al,2007,2009;Chen,et al,2008),该方法引入多矩概念,如体积积分平均值和点值、导数值进行局地高阶重构,通过控制方程更新预报变量时间向前积分(Li,et al,2015;Chen,et al,2014);其积分平均值约束条件能严格保证数值守恒,是传统有限体积方法的拓展。文中采用的新三点中心约束多矩有限体积方法(3-point Multi-moment Constrained finite-Volume scheme for Uniform Points with Center Constraints,MCV3_UPCC;Xiao,2012)能够基于单个网格构造高阶插值多项式,获得高阶计算精度,并且该格式计算简洁、计算模板紧致。该方案与原三阶多矩有限体积方案(MCV3)(Ii,et al,2009)相比,具有网格边界不连续,计算精度高,不用求解边界导数黎曼问题,计算效率高等特点。和其他高阶方法一样,多矩约束有限体积方法在非光滑解附近仍会出现数值振荡,并可能导致负值。文中采用边界保型(BP)限制器对其进行修正,保持该方案的正定性,以期设计一种可以用于大气模式的高精度平流输送模式。
2 均匀三点中心约束多矩有限体积方法文中采用三点均匀中心约束多矩有限体积法,该方案在单个网格内进行局地高阶通量重构,约束条件施加在单元网格中心点值及其一阶和二阶导数上,保证单元边界处通量函数的连续性,通过控制方程得到点值矩的时间演变方程。该方法计算精度高,严格保证数值守恒。MCV3方案局地高阶通量重构约束限制发生在单元网格界面(Ii,et al,2009),与之相比,MCV3_UPCC方案约束主要体现在单元网格中心上,具有较高的精度和允许更大的CFL(Courant-Friedrich-Lewy)条件,并且计算模板紧致。针对格式产生的数值振荡,引入边界保型限制器,该限制器优势在于不影响试验误差和精度的同时,抑制间断处的数值振荡并保持正定。
2.1 均匀三点中心约束多矩有限体积方法数值离散考虑一维守恒平流方程
| $\frac{{{\text {∂}} q}}{{{\text {∂}} t}} + \frac{{{\text {∂}} f}}{{{\text {∂}} x}} = 0$ | (1) |
式中,
在单元

|
| 图 1 一维单元上的矩和节点值 Fig. 1 The locations of unknowns in one dimension |
| ${q_{i1}}(t) = q({x_{i1}},t),\;\;{q_{i2}}(t) = q({x_{i2}},t),\;\;{q_{i3}}(t) = q({x_{i3}},t)$ | (2) |
| ${x_{i1}} = {x_{i - {1 / 2}}},\;\;{x_{i2}} = {{({x_{i - {1 / 2}}} + {x_{i + {1 / 2}}})} / 2},\;\;{x_{i3}} = {x_{i + {1 / 2}}}$ | (3) |
引入局地坐标
| $ \begin{split} &\xi = {\rm{2}}\frac{{x - {x_{i - {1 / 2}}}}}{{\Delta x{}_i}} - 1\quad\quad x \in [{x_{i - {1 / 2}}},{x_{i + {1 / 2}}}],\\&\Delta {x_i} = {x_{i + {1 / 2}}} - {x_{i - {1 / 2}}}\quad\quad \xi \in [ - 1,1]\end{split}$ | (4) |
假定连续的通量函数
| $\frac{{{\rm d}{q_{il}}}}{{{\rm d}t}} = - {\left({\frac{{{\rm d}\xi }}{{{\rm d}x}}} \right)_i}{\left({\frac{{{\rm d}{{\tilde f}_i}(\xi)}}{{{\rm d}\xi }}} \right)_{il}} = - {\left({\frac{{{\rm d}\xi }}{{{\rm d}x}}} \right)_i}{\tilde f_{\xi il}}\quad\quad l = 1,2,3$ | (5) |
为了求解方程(5),需要寻找上述假定连续的修正通量函数
首先,通过单元内的3个点值,利用拉格朗日多项式构造出在单个网格内不连续的主重构函数
| ${f_i}(\xi) = \sum\limits_{l = 1}^3 {{f_{il}}{\phi _{il}}(\xi)} $ | (6) |
| ${\phi _{il}} = \prod\limits_{k = 1,k \ne l}^3 {\frac{{\xi - {\xi _{il}}}}{{{\xi _{ik}} - {\xi _{il}}}}} $ | (7) |
式中,
| $f_i^{\rm B}(1) = \frac{{\rm{\,1\,}}}{{\rm{\,2\,}}}[(f_i^ + + f_{i + {\rm{1}}}^ -) - \left| u \right|(q_i^ + - q_{i + {\rm{1}}}^ -)]$ | (8) |
式中,
利用单元边界连续的边界通量
| $\left\{ {\begin{array}{*{20}{l}} {{{\tilde f}_i}(- 1) = f_i^{\rm B}(- 1)} \\ {{{\tilde f}_i}(1) = f_i^{\rm B}(1)} \\ {{{\tilde f}_i}(0) = {f_i}(0)} \\ {\tilde f_{\xi i}^{\left[ 1 \right]}(0) = f_{\xi i}^{\left[ 1 \right]}(0)} \\ {\tilde f_{\xi i}^{\left[ 2 \right]}(0) = f_{\xi i}^{\left[ 2 \right]}(0)} \end{array}} \right.$ | (9) |
用构建埃尔米特(Hermite)四次多项式
| $ \begin{split} {{\tilde f}_i}(\xi) =& \frac{\,1\,}{\,2\,}(f_i^{\rm B}(- 1) + f_i^{\rm B}(1) - {f_{i1}} - {f_{i3}}){\xi ^4} +\\& \frac{\,1\,}{\,2\,}(f_i^{\rm B}(1) - f_i^{\rm B}(- 1) + {f_{i1}} - {f_{i3}}){\xi ^3}+ \\ & \frac{\,1\,}{\,2\,}({f_{i1}} - 2{f_{i2}} + {f_{i3}}){\xi ^2} + \frac{\,1\,}{\,2\,}({f_{i3}} - {f_{i1}})\xi + {f_{i2}} \end{split} $ | (10) |
对多项式求导得
| $ \begin{split} {{\tilde f}_{\xi i}}(\xi) =& 2(f_i^{\rm B}(- 1) + f_i^{\rm B}(1) - {f_{i1}} - {f_{i3}}){\xi ^3} +\\& \frac{\,3\,}{\,2\,}(f_i^{\rm B}(1) - f_i^{\rm B}(- 1) + {f_{i1}} - {f_{i3}}){\xi ^2} +\\ & ({f_{i1}} - 2{f_{i2}} + {f_{i3}})\xi + \frac{\,1\,}{\,2\,}({f_{i3}} - {f_{i1}}) \end{split} $ | (11) |
代入单元内3个点值,分别为局地坐标
| $\left\{ {\begin{split} & {{{\tilde f}_{\xi i1}} = {{\tilde f}_{\xi i}}({\xi _1}) = 2({f_{i1}} + {f_{i2}}) - \frac{\,1\,}{\,2\,}(7f_i^{\rm B}(- 1) + f_i^{\rm B}(1))} \\ & {{{\tilde f}_{\xi i2}} = {{\tilde f}_{\xi i}}({\xi _2}) = \frac{\,1\,}{\,2\,}({f_{i3}} - {f_{i1}})} \\ & {{{\tilde f}_{\xi i3}} = {{\tilde f}_{\xi i}}({\xi _3}) = - 2({f_{i2}} + {f_{i3}}) + \frac{\,1\,}{\,2\,}(f_i^{\rm B}(- 1) + 7f_i^{\rm B}(1))} \end{split}} \right.$ | (12) |
从而得到更新后的3个点值
| $\left\{ {\begin{split} &{\frac{{{\rm d}{q_{i1}}}}{{{\rm d}t}} = - {{\left({\frac{{{\rm d}\xi }}{{{\rm d}x}}} \right)}_i}{{\tilde f}_{\xi i1}}} \\ & {\frac{{{\rm d}{q_{i2}}}}{{{\rm d}t}} = - {{\left({\frac{{{\rm d}\xi }}{{{\rm d}x}}} \right)}_i}{{\tilde f}_{\xi i2}}} \\ &{\frac{{{\rm d}{q_{i3}}}}{{{\rm d}t}} = - {{\left({\frac{{{\rm d}\xi }}{{{\rm d}x}}} \right)}_i}{{\tilde f}_{\xi i3}}} \end{split}} \right.$ | (13) |
为了验证该方案的守恒性,积分守恒方程的平流项得到
| $ \begin{split} \sum\limits_{l = 1}^{\rm{3}} \left({{{\tilde f}_{\xi il}}\int_{ - 1}^1 {{\phi _{il}}(\xi){\rm d}\xi } } \right) =& \frac{\,1\,}{\,3\,} {\tilde f_{\xi i1}} + \frac{\,4\,}{\,3\,}{\tilde f_{\xi i2}} + \frac{\,1\,}{\,3\,}{\tilde f_{\xi i3}} \\=& f_i^{\rm B}(1) - f_i^{\rm B}(- 1)\end{split}$ | (14) |
由此可见,式(1)单元内守恒量的变化等于单元边界通量的净变化,亦即单元网格界面通量是连续的,因而均匀三点中心约束多矩有限体积方法能够保证数值严格守恒。
2.2 边界保型限制器边界保型限制器(Zhang,et al,2010)是通过重新构造局部插值函数来起到限定的效果,该限制器计算精简,应用方便,能够把数值解控制在初始物理场的极大、极小值范围内,并且不损失守恒性(Katta,et al,2015;Guo,et al,2016)。边界保型限制器是基于Liu等(1998)所设计的限制器,其构造原理如下
| $M = \mathop {{\rm{max}}}\limits_x {q_0}(x,0),\quad m = \mathop {\min }\limits_x {q_0}(x,0)$ | (15) |
| ${\tilde p_i}\left(x \right) = \theta \left({{p_i}\left(x \right) - {{\bar p}_i}} \right) + {\bar p_i}$ | (16) |
限制器通过重构一个新的插值函数
| ${\bar p_i}(t) = \frac{1}{{\Delta {x_i}}}\int_{{x_{i{\rm{ - }}{1 / 2}}}}^{{x_{i + {1 / 2}}}} {q(x,t){\rm d}x} $ | (17) |
在单元网格
| $\begin{split}\frac{1}{{\Delta {x_i}}}\int_{{x_{i - {1 / 2}}}}^{{x_{i + {1 / 2}}}} {{{\tilde p}_i}(x){\rm d}x} =& \frac{1}{{\Delta {x_i}}}\int_{{x_{i - {1 / 2}}}}^{{x_{i + {1 / 2}}}} {(\theta ({p_i}(x) - {{\bar p}_i}) + {{\bar p}_i}){\rm d}x}\\ =& {\bar p_i}\end{split}$ | (18) |
可以看到,新重构的插值函数
二维笛卡尔坐标下的通量形式平流方程为
| $\frac{{{\text {∂}} q}}{{{\text {∂}} t}} + \frac{{{\text {∂}} e}}{{{\text {∂}} x}} + \frac{{{\text {∂}} f}}{{{\text {∂}} y}} = 0$ | (19) |
式中,
在笛卡尔坐标结构网格下(图2),可以直接将一维数值离散推广到二维
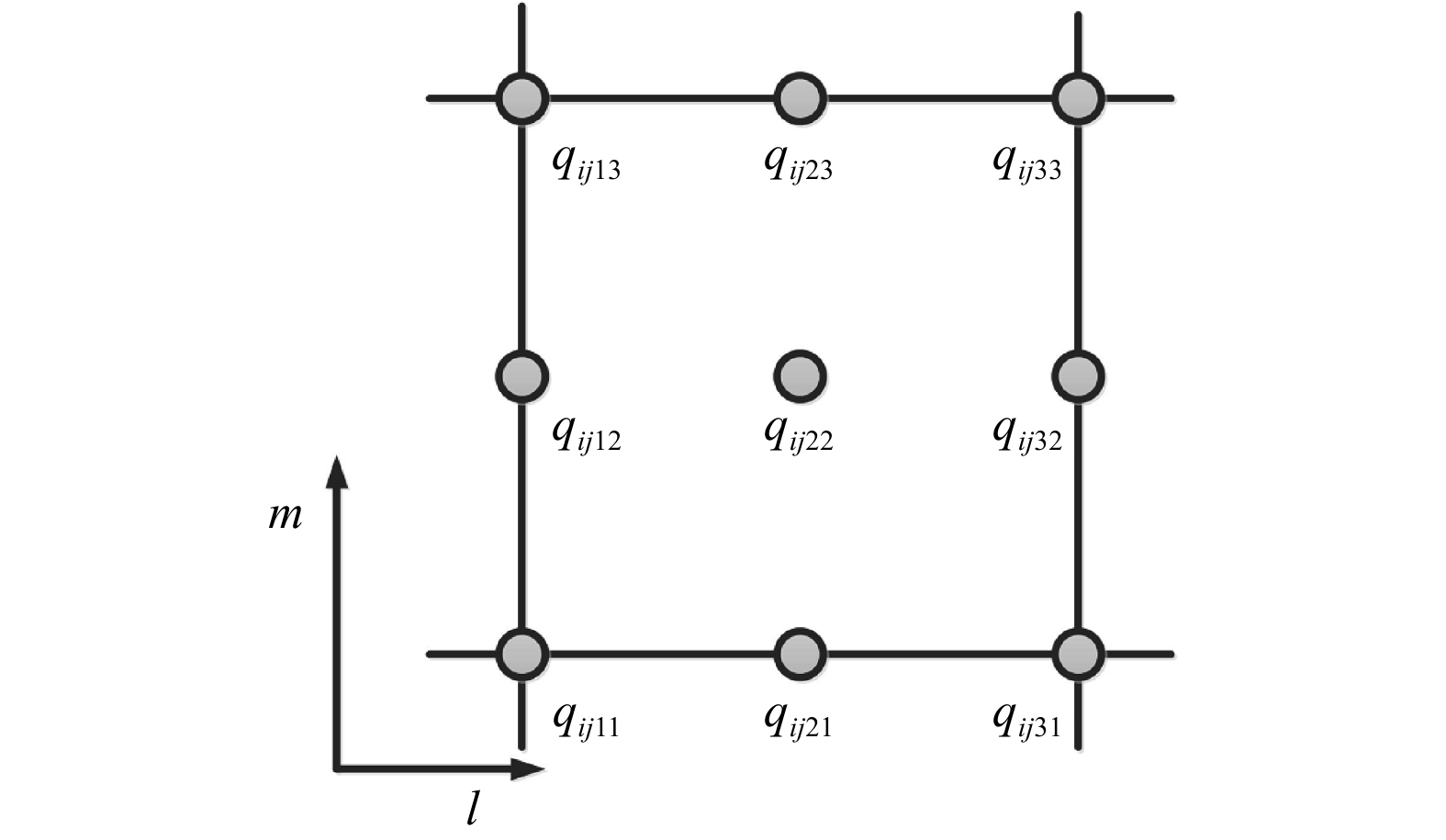
|
| 图 2 二维单元内点值 (求解点) 分布 Fig. 2 The locations of solution points (unknowns) in two dimensions |
| $\frac{{{\rm d}{q_{ijlm}}}}{{{\rm d}t}} = \frac{{{\rm d}q_{ijlm}^{(x)}}}{{{\rm d}t}} + \frac{{{\rm d}q_{ijlm}^{(y)}}}{{{\rm d}t}}$ | (20) |
式中,
| $\left\{\begin{split} &\frac{{{\rm d}q_{ijlm}^{(x)}}}{{{\rm d}t}} = - {\left({\frac{{{\rm d}\xi }}{{{\rm d}x}}} \right)_{ijlm}}\frac{{{\rm d}\tilde f_{ijlm}^{(x)}(\xi)}}{{{\rm d}\xi }} = - {\left({\frac{{{\rm d}\xi }}{{{\rm d}x}}} \right)_{ijlm}}\sum\limits_{m = 1}^3 {\sum\limits_{l = 1}^3 {\tilde f_{\xi ijlm}^{(x)}} } \\ &\frac{{{\rm d}q_{ijlm}^{(y)}}}{{{\rm d}t}} = - {\left({\frac{{{\rm d}\xi }}{{{\rm d}y}}} \right)_{ijlm}}\frac{{{\rm d}\tilde f_{ijlm}^{(y)}(\xi)}}{{{\rm d}\xi }} = - {\left({\frac{{{\rm d}\xi }}{{{\rm d}y}}} \right)_{ijlm}}\sum\limits_{m = 1}^3 {\sum\limits_{l = 1}^3 {\tilde f_{\xi ijlm}^{(y)}} } \end{split}\right. $ | (21) |
式中
| $\left\{ {\begin{split} &{\sum\limits_{m = 1}^3 {\tilde f_{\xi ij1m}^{(x)}} = \sum\limits_{m = 1}^3 {2({f_{ij1m}} + {f_{ij2m}}) - \frac{\,1\,}{\,2\,}(7f_{ij1m}^{\rm B}(- 1) + f_{ij3m}^{\rm B}(1))} } \\ & {\sum\limits_{m = 1}^3 {\tilde f_{\xi ij2m}^{(x)} = \sum\limits_{m = 1}^3 {\frac{\,1\,}{\,2\,}({f_{ij3m}} - {f_{ij1m}})} } } \\ & {\sum\limits_{m = 1}^3 {\tilde f_{\xi ij3m}^{(x)}} = \sum\limits_{m = 1}^3 { - 2({f_{ij2m}} + {f_{ij3m}}) + \frac{\,1\,}{\,2\,}(f_{ij1m}^{\rm B}(- 1) + 7f_{ij3m}^{\rm B}(1))} } \end{split}} \right.$ | (22) |
| $\left\{ {\begin{split} &{\sum\limits_{l = 1}^3 {\tilde f_{\xi ijl1}^{(y)}} = \sum\limits_{l = 1}^3 {2({f_{ijl1}} + {f_{ijl2}}) - \frac{\,1\,}{\,2\,}(7f_{ijl1}^{\rm B}(- 1) + f_{ijl3}^{\rm B}(1))} } \\ &{\sum\limits_{l = 1}^3 {\tilde f_{\xi ijl2}^{(y)} = \sum\limits_{l = 1}^3 {\frac{\,1\,}{\,2\,}({f_{ijl3}} - {f_{ijl1}})} } } \\ &{\sum\limits_{l = 1}^3 {\tilde f_{\xi ijl3}^{(y)}} = \sum\limits_{l = 1}^3 { - 2({f_{ijl2}} + {f_{ijl3}}) + \frac{\,1\,}{\,2\,}(f_{ijl1}^{\rm B}(- 1) + 7f_{ijl3}^{\rm B}(1))} } \end{split}} \right.$ | (23) |
经过上述数值离散,得到关于守恒量(
| $\frac{{{\rm d}{q_{ijlm}}}}{{{\rm d}t}} = R({q_{ijlm}})$ | (24) |
采用三阶TVD(Total Variation Diminishing)龙格库塔时间积分方法来求解该常微分方程(Shu,1988)
| $\left\{\begin{split} &q_{ijlm}^{(1)} = q_{ijlm}^n + \Delta tR(q_{ijlm}^n) \\ &q_{ijlm}^{(2)} = \frac{\,3\,}{\,4\,}q_{ijlm}^n + \frac{\,1\,}{\,4\,}q_{ijlm}^{(1)} + \frac{\,1\,}{\,4\,}\Delta tR(q_{ijlm}^{(1)}) \\ & q_{ijlm}^{n + 1} = \frac{\,1\,}{\,3\,}q_{ijlm}^n + \frac{\,2\,}{\,3\,}q_{ijlm}^{(2)} + \frac{\,2\,}{\,3\,}\Delta tR(q_{ijlm}^{(2)}) \end{split}\right. $ | (25) |
式中,
各类标准误差定义如下
| $\left\{ {\begin{split} & {{L_1} = \frac{{\int_\Omega {\left| {q - {q_t}} \right|{\rm d}\Omega } }}{{\int_\Omega {\left| {{q_t}} \right|{\rm d}\Omega } }}} \\ & {{L_2} = \frac{{{{\left[ {\int_\Omega {{{\left({q - {q_t}} \right)}^2}{\rm d}\Omega } } \right]}^{{{\rm{1}} / {\rm{2}}}}}}}{{{{\left[ {\int_\Omega {{{\left({{q_t}} \right)}^2}{\rm d}\Omega } } \right]}^{{1 / 2}}}}}} \\ &{{L_\infty } = \frac{{\max \left| {q - {q_t}} \right|}}{{\max \left| {{q_t}} \right|}}} \end{split}} \right.$ | (26) |
式中,
| $\left\{ {\begin{split} &{{E_2} = {{\left\{ {\sum\limits_{i = 1}^{i_{\max} } {\left[ {q_i^e - q_i^n} \right]/i_{\max} } } \right\}}^{{1 / 2}}}} \\ &{{E_\infty } = {{\max }_{1 \leqslant i \leqslant i_{\max} }}(q_i^e - q_i^n)} \end{split}} \right.$ | (27) |
式中,
一维收敛性试验初始场为
| $q(x,0) = \sin ({\text{π}} x)\; \quad\;- 1 \leqslant x \leqslant 1$ | (28) |
式(1)中的平流速度
从表1标准误差中可以看出,MCV3_UPCC方案具有三阶收敛。考虑到MCV3_UPCC方案单网格内自由度和高次多项式构建的优势,跟Ii等(2009)MCV3方案数值误差相比(文献中的
| 网格数 | L1误差 | L1阶数 | L2误差 | L2阶数 | L∞误差 | L∞阶数 |
| 10 | 1.099×10−2 | 1.100×10−2 | 1.099×10−2 | |||
| 20 | 1.368×10−3 | 3.00 | 1.368×10−3 | 3.00 | 1.371×10−3 | 3.00 |
| 40 | 1.703×10−4 | 3.00 | 1.703×10−4 | 3.00 | 1.704×10−4 | 3.00 |
| 80 | 2.124×10−5 | 3.00 | 2.124×10−5 | 3.00 | 2.125×10−5 | 3.00 |
| 160 | 2.653×10−6 | 3.00 | 2.653×10−6 | 3.00 | 2.653×10−6 | 3.00 |
| 网格数 | L1误差 | L1阶数 | L2误差 | L2阶数 | L∞误差 | L∞阶数 |
| 10 | 1.098×10−2 | 1.115×10−2 | 1.151×10−2 | |||
| 20 | 1.369×10−3 | 3.00 | 1.370×10−3 | 3.02 | 1.398×10−3 | 3.04 |
| 40 | 1.704×10−4 | 3.00 | 1.704×10−4 | 3.00 | 1.718×10−4 | 3.02 |
| 80 | 2.125×10−5 | 3.00 | 2.125×10−5 | 3.00 | 2.199×10−5 | 2.96 |
| 160 | 2.653×10−6 | 3.00 | 2.656×10−6 | 3.00 | 3.277×10−6 | 2.74 |
为了严格测试数值格式模拟强梯度和保持极值的能力,采用Blossey等(2008)的试验设置,初始场由两个等振幅正弦函数叠加
| $q(x,0) = \sin (6{\text{π}} x) + \sin (8{\text{π}} x)$ | (29) |
试验区域
| 数值格式 | E2误差 | E∞误差 | qmax | qmin |
| MCV3 | 0.06469 | 0.12300 | 0.9739 | −0.9747 |
| MCV3_UPCC | 0.03585 | 0.06502 | 0.9841 | −0.9821 |
| MCV3_UPCC_BP | 0.03608 | 0.06688 | 0.9727 | −0.9727 |
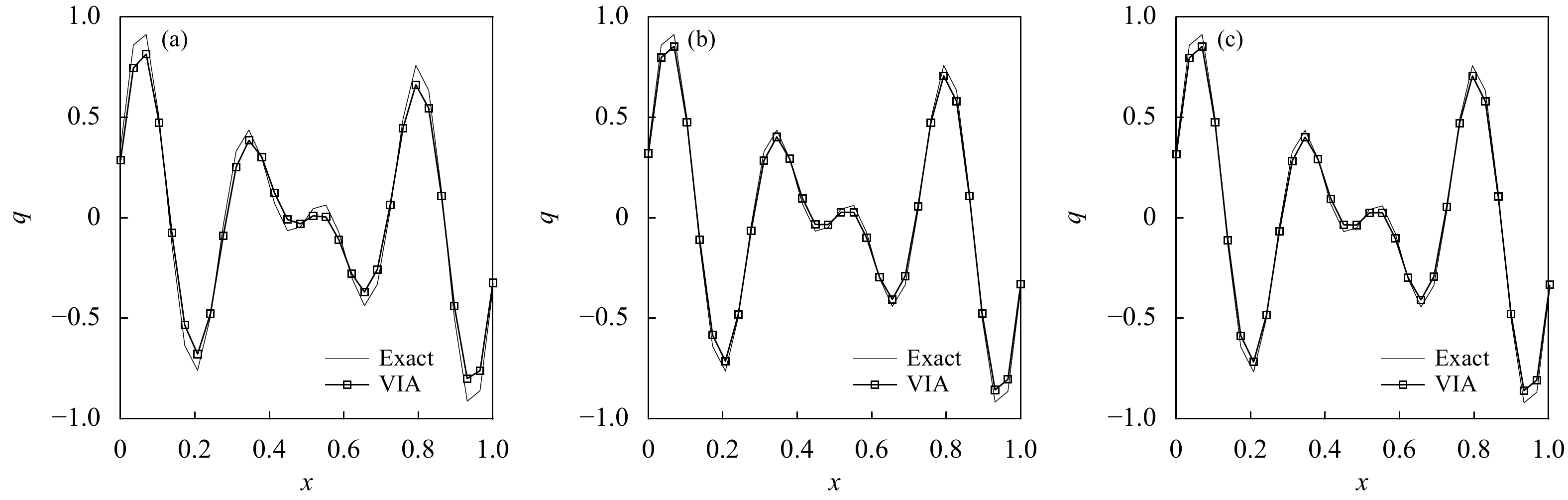
|
|
图 3 正弦叠加波试验 (a. MCV3,b. MCV3_UPCC,c. MCV3_UPCC_BP)
Fig. 3 Sum of 7.5 and 10
|
从表3中可以看出,MCV3_UPCC方法的
为了测试平流方案的保正定性,取式(29)中函数的正值部分,区间和网格同正弦叠加波试验,即
| $q(x,0) = \max \left[ {0,\sin (6{\text{π}} x) + \sin (8{\text{π}} x)} \right]$ | (30) |
图4为MCV3、MCV3_UPCC、MCV3_UPCC_BP 3种方案模拟正弦叠加波数值结果。可以看到,MCV3_UPCC方案对波峰的模拟极值高于MCV3,但它们在间断附近有明显的数值下冲,即存在非物理数值振荡,表4中两方案的极小值(
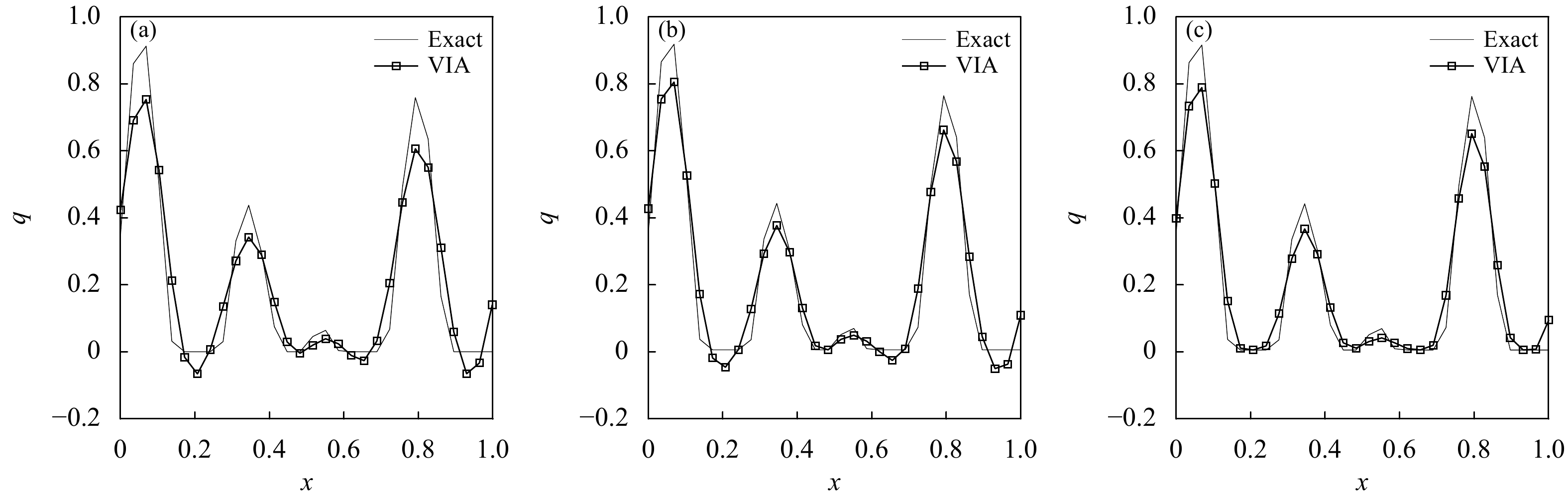
|
|
图 4 正值部分的正弦叠加波试验 (a. MCV3,b. MCV3_UPCC,c. MCV3_UPCC_BP)
Fig. 4 The positive parts of sum of 7.5 and 10
|
| 格式 | E2误差 | E∞误差 | qmax | qmin |
| MCV3 | 0.08759 | 0.1840 | 0.9781 | −7.8085×10−2 |
| MCV3_UPCC | 0.06496 | 0.1207 | 0.9907 | −7.4397×10−2 |
| MCV3_UPCC_BP | 0.06098 | 0.1391 | 0.9727 | −3.4694×10−18 |
同样,对比Blossey等(2008)的通量修正方案在间断处的模拟结果,文中MCV3、MCV3_UPCC和MCV3_UPCC_BP3种方案计算精度高,它们的数值模拟误差
为了验证数值格式在强间断的附近是否能够有效地抑制非物理数值振荡,设计的方波试验初值分布如下
| $q(x,0) = \left\{ {\begin{array}{*{20}{l}} {1\;\;\;\;\left| {{x}} \right| \leqslant 0.4}\\ {0\;\;\;\;{\text{其他}}} \end{array}} \right.\;\;\;\;\;(- 1 \leqslant x \leqslant 1)$ | (31) |
一维的计算区域为[−1,1],其内网格数为200,网格距0.01,水平速度场

|
| 图 5 方波试验结果 (a. MCV3,b. MCV3_UPCC,c. MCV3_UPCC_BP) Fig. 5 The square wave experiments (a. MCV3,b. MCV3_UPCC,c. MCV3_UPCC_BP) |
| 格式 | L1误差 | L2误差 | L∞误差 | qmax | qmin |
| MCV3 | 0.035425 | 0.085082 | 0.3664 | 1.1296 | −1.296×10−1 |
| MCV3_UPCC | 0.029940 | 0.077023 | 0.3382 | 1.2012 | −2.012×10−1 |
| MCV3_UPCC_BP | 0.024208 | 0.075610 | 0.3371 | 1.0000 | −6.938×10−18 |
二维收敛性试验初始场分布如下
| $q(x,y,0) = \sin ({\text{π}} (x + y))\;\;x \in \left[ { - 1,1} \right],y \in \left[ { - 1,1} \right]$ | (32) |
试验速度
数值试验结果如表6所示,从表中可知,MCV3_UPCC方案获得了三阶收敛阶数,并且比MCV3方案误差减小了一半。MCV3_UPCC方法引入边界保型限制器后,对试验误差几乎没有影响,
| 网格 | L1误差 | L1阶数 | L2误差 | L2阶数 | L∞误差 | L∞阶数 | |
| MCV3 | 10 | 4.3164×10−2 | 4.1639×10−2 | 4.3164×10−2 | |||
| 20 | 5.4950×10−3 | 2.97 | 5.4436×10−3 | 2.93 | 5.4263×10−3 | 2.99 | |
| 40 | 6.900×10−4 | 2.99 | 6.8840×10−4 | 2.98 | 6.8782×10−4 | 2.99 | |
| 80 | 8.6418×10−5 | 2.99 | 8.6366×10−5 | 2.99 | 8.6348×10−5 | 2.99 | |
| MCV3_UPCC | 10 | 2.3037×10−2 | 2.2830×10−2 | 2.3037×10−2 | |||
| 20 | 2.8627×10−3 | 3.00 | 2.8568×10−3 | 2.99 | 2.8566×10−3 | 3.01 | |
| 40 | 3.5608×10−4 | 3.00 | 3.5590×10−4 | 3.00 | 3.5590×10−4 | 3.00 | |
| 80 | 4.4403×10−5 | 3.00 | 4.4398×10−5 | 3.00 | 4.4397×10−5 | 3.00 | |
| MCV3_UPCC_BP | 10 | 2.727×10−2 | 2.635×10−2 | 2.743×10−2 | |||
| 20 | 2.835×10−3 | 3.26 | 2.928×10−3 | 3.17 | 3.323×10−3 | 3.04 | |
| 40 | 3.560×10−4 | 2.99 | 3.661×10−4 | 2.99 | 5.019×10−4 | 2.73 | |
| 80 | 4.440×10−5 | 3.00 | 4.893×10−5 | 2.90 | 1.037×10−4 | 2.28 | |
为了验证数值格式同时捕获光滑和间断处的解的能力,一维复杂波试验最早由Jiang等(1996)提出,Ii等(2009)将它推广至二维,该试验由高斯波、方波、尖三角波和半椭圆波组合而成,速度场分布为
| $q(x,y,0) = \left\{ {\begin{array}{*{20}{l}} {\dfrac{\,1\,}{\,6\,}(G({r_1} + \delta,\beta) + G({r_1} - \delta,\beta) + 4G({r_1},\beta))}&{\left| {{r_1}} \right| \leqslant 0.2}\\ 1&{\left| x \right| \leqslant 0.2, - 0.7 \leqslant y \leqslant - 0.3}\\ {1 - \left| {5{r_2}} \right|}&{\left| {{r_2}} \right| \leqslant 0.2}\\ {\dfrac{\,1\,}{\,6\,}(F({r_3} + \delta,\alpha) + F({r_3} - \delta,\alpha) + 4F({r_3},\alpha))}&{\left| {{r_3}} \right| \leqslant 0.2}\\ 0&{\text{其他}} \end{array}} \right.$ | (33) |
式中,
从图6中可以看出,MCV3_UPCC方法和MCV3方法一样,都在强间断处出现了数值振荡,并且两种方法对于波峰处的极值保持都不错,MCV3_UPCC方法引入边界保型限制器后没有影响到波峰处的极值。由表7可知,加上边界保型限制器后,整个波的点值在精确解的最大值和最小值之间,除去了数值振荡,而且得到的
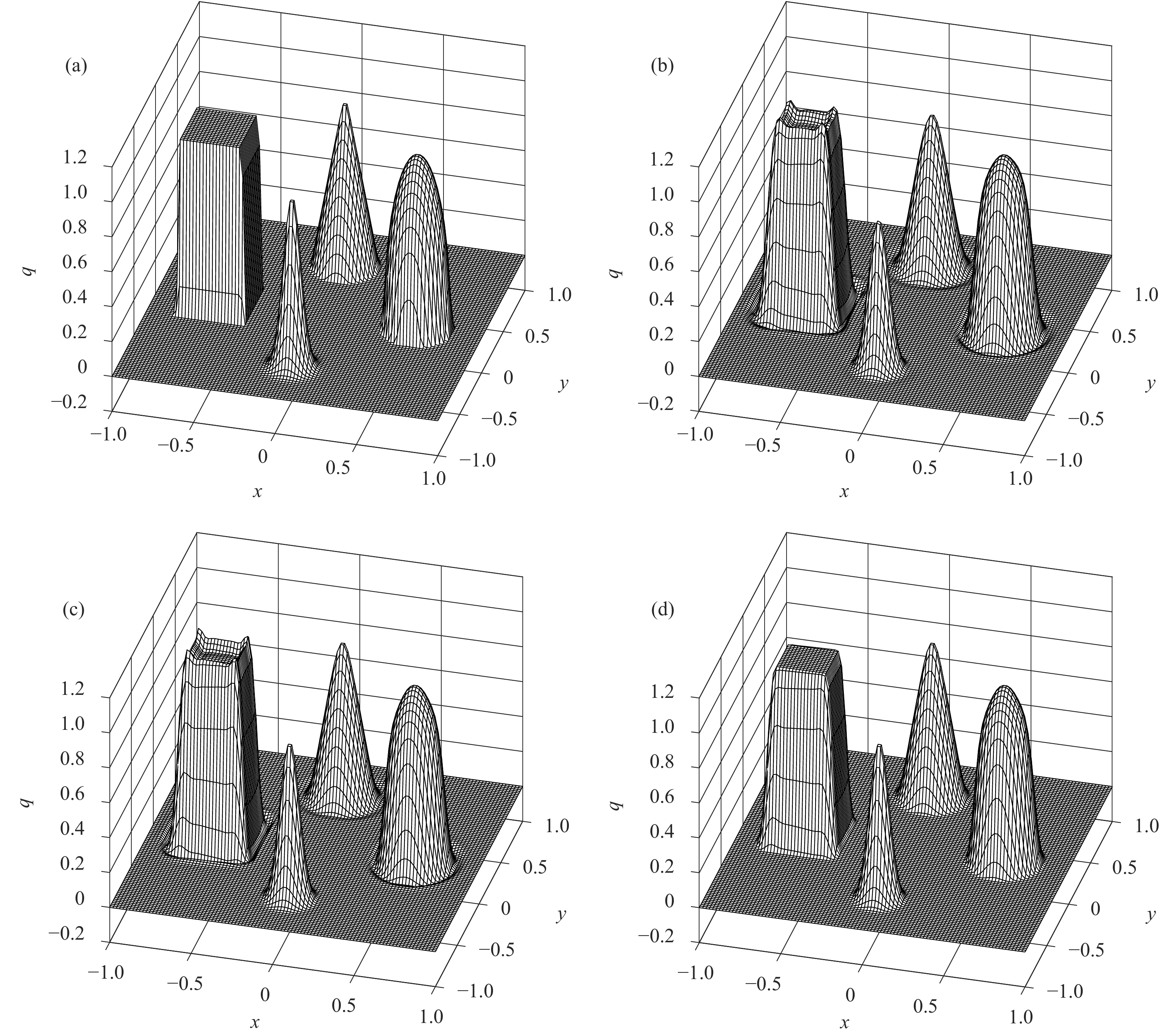
|
| 图 6 二维复杂波试验结果 (a. 初始场,b、c、d分别为MCV3、MCV3_UPCC和MCV3_UPCC_BP旋转一周后的结果) Fig. 6 The complex waves experiment (a. the initial field of complex waves,b. MCV3,c. MCV3_UPCC,d. MCV3_UPCC_BP) |
| 格式 | L1误差 | L2误差 | L∞误差 | qmax | qmin |
| MCV3 | 0.14920 | 0.16966 | 0.30347 | 1.1637 | −1.325×10−1 |
| MCV3_UPCC | 0.11888 | 0.14806 | 0.27518 | 1.5092 | −3.827×10−1 |
| MCV3_UPCC_BP | 0.099466 | 0.14813 | 0.27699 | 1.0000 | −1.839×10−16 |
该试验主要是验证平流的保型能力,在二维网格数为100×100,时间积分总步数为1500步,时间周期t=1的圆柱凹槽试验中,初始场半径为0.5,中心位于原点,高为1的凹槽圆柱,速度场为
| ${q_0}(x,y,t) = \left\{ {\begin{array}{*{20}{l}} {1\;\;\;\;\left| \xi \right| \geqslant {{{W_{\rm s}}} / 2}, r \leqslant \sigma }\\ {1\;\;\;\;\zeta \geqslant {{{L}}_{\rm{s}}} - \sigma, r \leqslant \sigma }\\ {0\;\;\;\;{\text{其他}}} \end{array}} \right.$ | (34) |
式中,
从图7b、c可知,MCV3_UPCC方案具有良好的保型能力,在旋转了10周后凹槽圆柱的形状保持较好,只是在强间断处会产生小的数值振荡。从表8可知,应用边界保型限制器后,在对凹槽圆柱有很好保型效果的同时,能有效去除数值振荡,并把最大、最小值严格控制在初始场的最大、最小值,即0到1之间。对比苏勇等(2013)的凹槽旋转试验,采用准单调半拉格朗日方案在旋转10周后极值被削弱到了0.953,而MCV3_UPCC方法引入边界保型限制器旋转10周后极值还能维持初始场的最大值1,说明MCV3_UPCC方案的计算精度高,保型能力强。
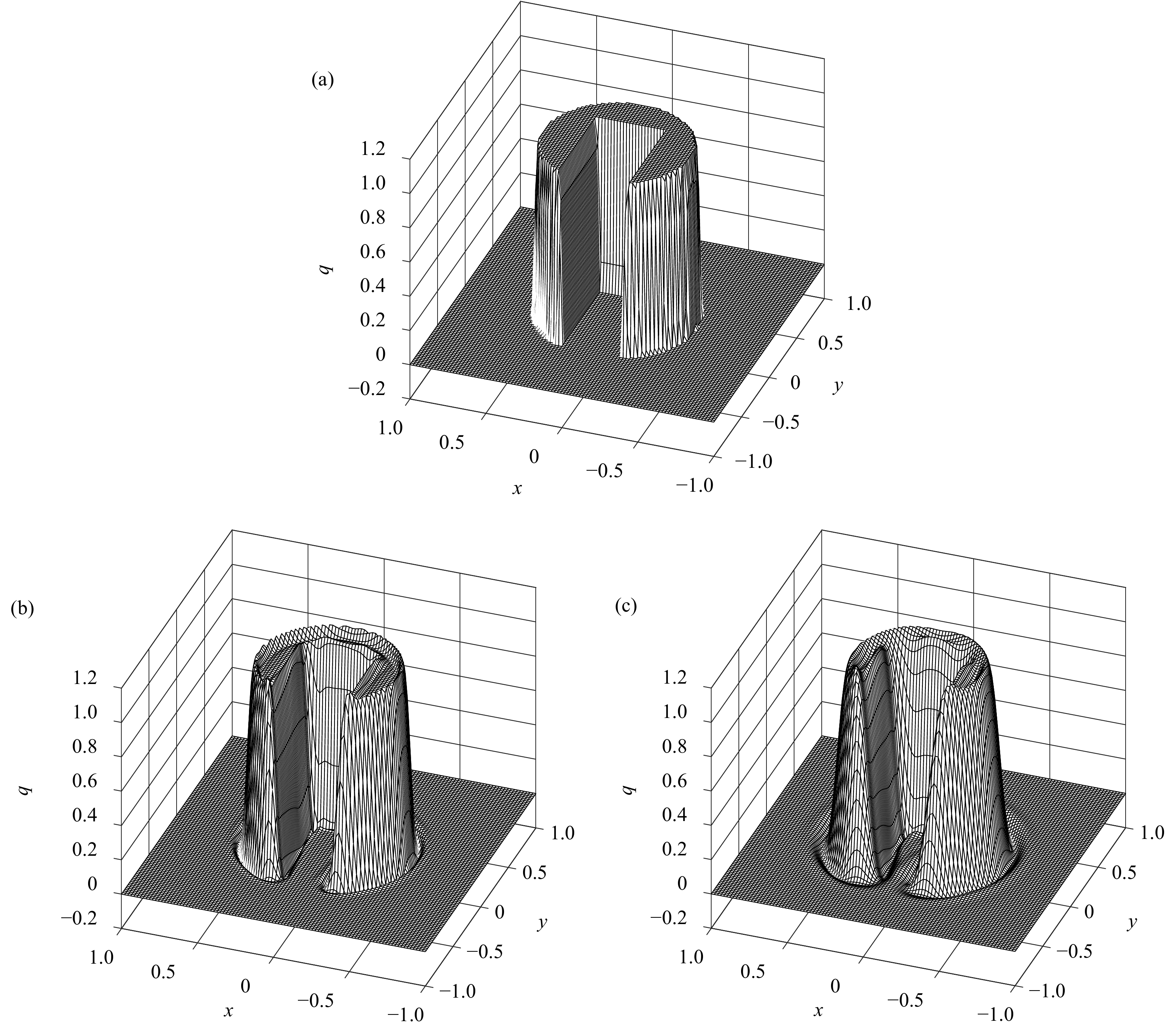
|
| 图 7 凹槽圆柱模拟试验结果 (a. 初始时刻,b和c分别为MCV3_UPCC旋转1周和10周后结果,d和e分别为MCV3_UPCC_BP旋转1周和10周后结果) Fig. 7 The cut-cylinder rotation experiment:(a) the initial distribution of cut-cylinder rotation;(b),(c) result of MCV3_UPCC scheme after 1 and 10 period,respectively;(d),(e) results of MCV3_UPCC scheme with BP filter after 1 and 10 period,respectively |

|
| 图 7 Fig. 7 Continued |
| 格式 | L1误差 | L2误差 | L∞误差 | qmax | qmin |
| MCV3_UPCC | 0.1209 | 0.1444 | 0.4068 | 1.5751 | −5.683×10−1 |
| MCV3_UPCC_BP | 0.07627 | 0.1244 | 0.3906 | 1.0000 | −5.551×10−17 |
数值试验采取Durran(1999)的试验,该试验是具有挑战性的复杂变形试验,其速度场随时间变化,该试验初始场为
| ${q_0}(x,y,t) = \frac{\,1\,}{\,2\,}\left[ {1 + \cos \left({{\text{π}} r} \right)} \right]$ | (35) |
式中
| $r(x,y) = \min \left\{ {1,4{{\left[ {{{\left({x - \frac{\,1\,}{\,4\,}} \right)}^2} + {{\left({y - \frac{\,1\,}{\,4\,}} \right)}^2}} \right]}^{{\frac{1}{2}}}}} \right\}$ | (36) |
速度场为
| $\left\{ {\begin{array}{*{20}{l}} {u\left({x,y,t} \right) = {{\sin }^2}({\text{π}} x)\sin (2{\text{π}} y)\cos \left({{\text{π}} t/5} \right)} \\ {v\left({x,y,t} \right) = - {{\sin }^2}({\text{π}} y)\sin (2{\text{π}} x)\cos \left({{\text{π}} t/5} \right)} \end{array}} \right.$ | (37) |
速度场的定义使得初始场从平滑的状态在

|
| 图 8 变形场试验结果 (a. 初始场,b和c分别为50×50和100×100网格的MCV3_UPCC方案运动1个周期的结果) Fig. 8 (a) The initial field,(b) the result of MCV3_UPCC scheme after 1 period in 50×50 mesh,(c) the result of MCV3_UPCC scheme after 1 period in 100×100 mesh |

|
| 图 9 二维变形流模拟试验结果 (a. MCV3_UPCC方案t/2时刻,b. MCV3_UPCC方案t时刻,c. MCV3_UPCC_BP方案t/2时刻,d. MCV3_UPCC_BP方案t时刻) Fig. 9 The deformational flow experiment:(a),(b) the result of MCV3_UPCC scheme after t/2 and t,respectively;(c),(d)the result of MCV3_UPCC scheme with BP filter after t/2 and t,respectively |
由图8可知,在网格数为50和100的数值试验中,MCV3_UPCC方案
| 格式 | E2误差 | E∞误差 | qmax | qmin |
| MCV3_UPCC | 0.04060 | 0.1955 | 1.0277 | −8.6954×10−2 |
| MCV3_UPCC_BP | 0.04128 | 0.1670 | 1.0000 | −3.4694×10−18 |
基于新的三点均匀中心约束多矩有限体积方法,发展了一个三阶正定守恒的平流模式。与传统有限体积方法相比,新发展的三点均匀中心约束多矩有限体积平流格式(MCV3_UPCC)能够在单个网格内进行局地高阶重构,计算模板紧致。由于采用积分平均值矩积分通量形式控制方程,并保持边界通量连续,因此能够保证数值解严格守恒。数值收敛试验表明,新发展的平流模式具有三阶计算精度。通过分析标准误差,发现MCV3_UPCC方案相比于MCV3方案,计算误差减小了约一半,模拟的不连续函数峰值也更接近数值真解,计算精度高。为了有效控制高阶格式产生的数值噪音(振荡),文中引入边界保型限制器,它能够有效抑制非物理数值振荡,具有良好的保型能力。数值试验表明采用边界保型限制器并不降低方案的计算精度,并且能够严格控制每一步的数值解在初始场的最大、最小值之间。综上所述,文中发展的二维平流模式具有良好的发展潜力,下一步计划将新发展的三点均匀中心约束多矩有限体积方案推广到二维球面。
沈学顺, 王明欢, 肖锋等. 2011. GRAPES模式中高精度正定保形物质平流方案的研究Ⅰ: 理论方案设计与理想试验. 气象学报, 39(1): 1-15. |
苏勇, 沈学顺, 彭新东等. 2013. PRM标量平流方案在GRAPES全球预报系统中的应用. 大气科学, 37(6): 1309-1325. DOI:10.3878/j.issn.1006-9895.2013.12164 |
Bermejo R, Staniforth A. 1992. The conversion of semi-Lagrangian advection schemes to quasi-monotone schemes. Mon Wea Rev, 120(11): 2622-2632. DOI:10.1175/1520-0493(1992)120<2622:TCOSLA>2.0.CO;2 |
Blossey P N, Durran D R. 2008. Selective monotonicity preservation in scalar advection. J Comput Phys, 227(10): 5160-5183. DOI:10.1016/j.jcp.2008.01.043 |
Book D L, Boris J P, Hain K. 1975. Flux-corrected transport Ⅱ: Generalizations of the method. J Comput Phys, 18(3): 248-283. DOI:10.1016/0021-9991(75)90002-9 |
Chen C G, Xiao F. 2008. Shallow water model on cubed-sphere by multi-moment finite volume method. J Comput Phys, 227(10): 5019-5044. DOI:10.1016/j.jcp.2008.01.033 |
Chen C G, Li X L, Shen X S, et al. 2014. Global shallow water models based on multi-moment constrained finite volume method and three quasi-uniform spherical grids. J Comput Phys, 271: 191-223. DOI:10.1016/j.jcp.2013.10.026 |
Colella P, Woodward P R. 1984. The piecewise parabolic method (PPM)for gas-dynamical simulations. J Comput Phys, 54(1): 174-201. DOI:10.1016/0021-9991(84)90143-8 |
Durran D R. 1999. Numerical Methods for Wave Equations in Geophysical Fluid Dynamics. New York: Springer-Verlag, 465
|
Guo W, Nair R D, Qiu J M. 2014. A conservative semi-Lagrangian discontinuous Galerkin scheme on the cubed sphere. Mon Wea Rev, 142(1): 457-475. DOI:10.1175/MWR-D-13-00048.1 |
Guo W, Nair R D, Zhong X H. 2016. An efficient WENO limiter for discontinuous Galerkin transport scheme on the cubed sphere. Int J Numer Methods Fluids, 81(1): 3-21. DOI:10.1002/fld.4171 |
Ii S, Xiao F. 2007. CIP/multi-moment finite volume method for Euler equations: A semi-Lagrangian characteristic formulation. J Comput Phys, 222(2): 849-871. DOI:10.1016/j.jcp.2006.08.015 |
Ii S, Xiao F. 2009. High order multi-moment constrained finite volume method. Part Ⅰ: Basic formulation. J Comput Phys, 228(10): 3669-3707. DOI:10.1016/j.jcp.2009.02.009 |
Jiang G S, Shu C W. 1996. Efficient implementation of weighted ENO schemes. J Comput Phys, 126(1): 202-228. DOI:10.1006/jcph.1996.0130 |
Katta K K, Nair R D, Kumar V. 2015. High-order finite-volume transport on the cubed sphere: Comparison between 1D and 2D reconstruction schemes. Mon Wea Rev, 143(7): 2937-2954. DOI:10.1175/MWR-D-13-00176.1 |
Lauritzen P H, Nair R D, Ullrich P A. 2009. A conservative semi-Lagrangian multi-tracer transport scheme (CSLAM)on the cubed-sphere grid. J Comput Phys, 229(5): 1401-1424. |
Li X L, Chen C G, Xiao F, et al. 2015. A high-order multi-moment constrained finite-volume global shallow-water model on the Yin-Yang grid. Quart J Roy Meteor Soc, 141(691): 2090-2102. DOI:10.1002/qj.2504 |
Liu X D, Tadmor E. 1998. Third order nonoscillatory central scheme for hyperbolic conservation laws. J Numer Math, 79(3): 397-425. DOI:10.1007/s002110050345 |
Robert A. 1981. A stable numerical integration scheme for the primitive meteorological equations. Atmos Ocean, 19(1): 35-46. DOI:10.1080/07055900.1981.9649098 |
Shu C W. 1988. Total-variation-diminishing time discretizations. SIAM J Sci Stat Comput, 9(6): 1073-1084. DOI:10.1137/0909073 |
Skamarock W C. 2006. Positive-definite and monotonic limiters for unrestricted-time-step transport schemes. J Mon Wea Rev, 134(8): 2241-2250. DOI:10.1175/MWR3170.1 |
Van Leer B. 1977. Towards the ultimate conservative difference scheme. J Comput Phys, 135(2): 229-248. |
Xiao F, Yabe T. 2001. Completely conservative and oscillationless semi-lagrangian schemes for advection transportation. J Comput Phys, 170(2): 498-522. DOI:10.1006/jcph.2001.6746 |
Xiao F, Yabe T, Peng X, et al. 2002. Conservative and oscillation-less atmospheric transport schemes based on rational functions. J Geophys Res Atmos, 107(D22): ACL 2-1-ACL 2-11. |
Xiao F. 2004. Unified formulation for compressible and incompressible flows by using multi-integrated moments Ⅰ: One-dimensional inviscid compre-ssible flow. J Comput Phys, 195(2): 629-654. DOI:10.1016/j.jcp.2003.10.014 |
Xiao F, Akoh R, Ii S. 2006. Unified formulation for compressible and incompressible flows by using multi-integrated moments Ⅱ: Multidimen-sional version for compressible and incompressible flows. J Comput Phys, 213(1): 31-56. DOI:10.1016/j.jcp.2005.08.002 |
Xiao F. 2012. Two variants of the MCV3 scheme. ArXiv: 1207.6844
|
Xiao F, Ii S, Chen C G, et al. 2013. A note on the general multi-moment constrained flux reconstruction formulation for high order schemes. Appl Math Model, 37(7): 5092-5108. DOI:10.1016/j.apm.2012.10.050 |
Yabe T, T Aoki. 1991. A universal solver for hyperbolic equations by cubic-polynomial interpolation Ⅰ: One-dimensional solver. Comput Phys Commun, 66(2-3): 219-232. DOI:10.1016/0010-4655(91)90071-R |
Yabe T, Tanaka R, Nakamura T, et al. 2001. An exactly conservative semi-Lagrangian scheme(CIP-CSL)in one dimension. Mon Wea Rev, 129(2): 332-344. DOI:10.1175/1520-0493(2001)129<0332:AECSLS>2.0.CO;2 |
Yu R C. 1994. A two-step shape-preserving advection scheme. Adv Atmos Sci, 11(4): 479-490. DOI:10.1007/BF02658169 |
Zerroukat M, Wood N, Staniforth A. 2002. SLICE: A semi-Lagrangian inherently conserving and efficient scheme for transport problems. Quart J Roy Meteor Soc, 128(586): 2801-2820. DOI:10.1256/qj.02.69 |
Zhang X X, Shu C W. 2010. On maximum-principle-satisfying high order schemes for scalar conservation laws. J Comput Phys, 229(9): 3091-3120. DOI:10.1016/j.jcp.2009.12.030 |
 2020, Vol. 78
2020, Vol. 78


