中国气象学会主办。
文章信息
- 沈学顺, 王建捷, 李泽椿, 陈德辉, 龚建东. 2020.
- SHEN Xueshun, WANG Jianjie, LI Zechun, CHEN Dehui, GONG Jiandong. 2020.
- 中国数值天气预报的自主创新发展
- China's independent and innovative development of numerical weather prediction
- 气象学报, 78(3): 451-476.
- Acta Meteorologica Sinica, 78(3): 451-476.
- http://dx.doi.org/10.11676/qxxb2020.030
文章历史
-
2019-09-02 收稿
2019-12-31 改回
2. 中国气象局数值预报中心,北京,100081;
3. 中国气象科学研究院灾害天气国家重点实验室,北京,100081
2. Numerical Weather Prediction Center of CMA,Beijing 100081,China;
3. State Key Laboratory for Severe Weather,Chinese Academy of Meteorological Sciences,Beijing 100081,China
数值天气预报是基于数学物理方法客观定量计算未来天气演变的科学。数值天气预报从20世纪50年代试验成功以来,经过70 a的发展,已经成为一个跨学科的复杂而严格的系统性工程,使得天气预报从传统的以统计和经验为主的天气图方法转变成为客观定量的科学(曾庆存,2013;Benjamin,et al,2019)。数值天气预报从100年前概念的提出到70 a的发展应用历史表明,数值天气预报的进步是建立在多年稳步持续的科学认知和技术进步的积累之上,被认为是物理学科各领域中最具影响的成就之一(Bauer,et al,2015;纪立人,2011)。可以说,数值天气预报是气象科技水平的综合体现,是保障国计民生和国防安全的核心科技的重要组成部分。
中国的数值天气预报研究始于1954年,是国际上较早开展数值天气预报的国家之一,20世纪50年代到60年代末是中国在该领域研究非常活跃的时期,并取得了在国际上有广泛影响的成果(顾震潮,1959;Blumen,et al,1973)。20世纪50年代的研究多集中于准地转正压模式。顾震潮(1959)做了系统性的总结,并指出数值天气预报中最根本的还是对大气过程本质的了解、物理因子的重要作用以及在模式的建立、选择和解的方法上必须做大量工作。早期的研究是用图解法求解两层准地转方程,并在寒潮爆发的短期预报、500 hPa高度场的48 h预报方面取得了较好的效果(顾震潮等,1957;廖洞贤,1956),值得指出的是,陈雄山等(1957)应用位温坐标系的两层模式研究了锋面的预报问题,这应该是国际上较早将位温用作垂直坐标的研究。1960年2月,中央气象局数值预报组与中国科学院地球物理研究所和计算技术研究所合作,用准地转正压模式制作亚欧范围内24和48 h 500 hPa形势预报(中央气象局数值预报组,1965)。中央气象局数值预报组在《我国的数值预报业务工作》一文中做了很好的总结,指出了差分格式的设计、初始风场和地形影响的重要性,并指出斜压模式是发展的方向(中央气象局数值预报组,1965)。沈如桂等(1965)对该正压模式1964—1965年500 hPa 48 h数值预报图在中央气象局的应用情况进行了系统的总结,指出认识数值天气预报误差和能力、充分利用正确的一面对有效应用数值天气预报的重要帮助作用,这些结论至今在应用数值天气预报结果时仍然具有指导意义。
在开展准地转正压模式研究及在天气预报业务中应用的同时,中国科学家也开展了在准地转模式中考虑斜压过程及原始方程模式的研究。朱永禔(1961,1962)在苏联科学院应用地球物理研究所访问期间(1959—1960年)发展了一个球坐标3层非线性模式(1000、500和300 hPa),研究了地形对24 h预报的影响。1961年,曾庆存首次用原始方程组做出了实际天气预报,并在莫斯科世界气象中心实现了业务应用,比美国1966年开始用原始方程做预报早了5 a(Zeng,1961;曾庆存,2013)。特别是在求解原始方程模式时,曾庆存以大气中运动的适应过程理论为基础,提出“半隐式(或称半显式)差分格式”,对影响时间步长和计算稳定性的快波取隐式格式,增加了计算稳定性且大幅度减少了计算量(Zeng,1961;曾庆存,1963a,1963c)。Robert(1969)和Robert等(1985)进一步丰富和发展了半隐式格式,并与半拉格朗日方法结合,形成了半隐式半拉格朗日方法,这是迄今仍为世界业务数值天气预报模式广泛采用的计算格式。针对数值模式中地形带来的计算复杂性问题,曾庆存(1963b)提出了静力扣除(或标准层结扣除)方法,使得在气压梯度力计算中不再出现基本量的计算误差,避免了大量小差问题。这种静力扣除法后来在谱模式以及半拉格朗日平流计算减缓地形影响中发挥了重要作用(Simmons,et al,1991;Temperton,et al,2001)。刘瑞芝等(1965)发展了一个北半球的正压原始方程,该模式采用时间空间中央差分和Lilly(1961)提出的跳点网格,空间网格距为600 km,对4个实例进行了模拟研究,并与地转正压模式的结果进行了对比,得到了比较好的结果。
20世纪50年代及60年代初期,以赵九章、顾震潮、叶笃正、谢义炳、朱抱真、黄仕松等为代表的老一辈科学家,关于动力气象、大气环流、青藏高原动力热力作用、大气运动的适应理论和大气频散理论、风压场的平衡关系等方面的研究成果(徐尔灏,1959;赵九章,1959;叶笃正,1963),直接或间接地指导并推动了中国数值天气预报的发展(纪立人等,2005)。以周秀骥、巢纪平、周晓平、苏从先、赵柏林等为代表的科学家,在云微物理、积云动力学、中小尺度动力学、边界层湍流等方面的研究成果不仅在理论上当时处于国际前列,而且对在数值天气预报中考虑非绝热过程、理解物理机理等方面起到了重要的理论支撑作用(苏从先,1958,1959;周秀骥,1963;巢纪平等,1964)。中国学者在这个时期提出了将初值问题的数值天气预报提升为基于近期历史演变资料的创新性思想(顾震潮,1958a,1958b)。之后,以丑纪范(1974)为代表对数值天气预报中使用历史资料的问题进一步深化,将数值天气预报这一微分方程的定解问题变成使用多时刻历史观测资料的泛函极值问题—变分问题。顾震潮的思想和丑纪范引入的泛函极值处理方法,正是今天四维变分同化的主体思想。
20世纪70年代是国际数值天气预报真正实现业务应用,并成为逐日天气预报不可或缺的科技支撑的重要时期(Kalnay,2003)。1975年成立的欧洲中期天气预报中心(ECMWF,European Centre for Medium range Weather Forecast)是这期间的标志性事件。在此期间,中国科学家虽然没有条件开展系统性的研究,但在数值天气预报基础理论研究方面做了大量的工作(陶诗言等,2003);而且,中国科学院大气物理研究所数值预报研究组及时跟踪国际进展,将国际上先进的数值天气预报成果介绍到国内(数值预报研究组,1975)。这期间具有代表性的工作是《数值天气预报的数学物理基础(第一卷)》的出版(曾庆存,1979)。在该著作中,曾庆存针对数值天气预报模式发展中的数学物理基础问题开展了系列阐述,将重点关注的大气流体力学的计算问题进一步升华为科学理论,形成了数值天气预报的数学物理基础。
改革开放之后,中国数值天气预报研究和业务应用迎来了新的契机。在20世纪70—80年代,中国科学家有关数值天气预报基础理论和方法的研究主要集中于与计算格式相关的领域,包括计算稳定性的理论问题和差分格式的构造等(曾庆存,1978;曾庆存等,1981;季仲贞等,1982)。20世纪90年代后,在可预报性、大气数值模式新算法、资料同化新方法等领域也涌现了在国际上有影响或领先的成果。同时,改革开放之后也是中国数值天气预报模式在自主研发方面活跃的时期,并在中国现代化数值天气预报业务建立的过程中发挥了重要作用(陶诗言等,2003)。
设计适当的计算格式使得离散化的模式方程组满足一定的物理属性或约束是发展数值天气预报模式的核心问题之一,如总能量守恒、总质量守恒和总拟能守恒等。这些约束一方面保证模式具有良好的长期积分性能,另一方面也有助于克服计算不稳定问题。Arakawa(1966,1972)提出的通过构造格点间合理相互作用的平流雅可比差分格式保持平均动能和涡度拟能的守恒,是研究计算格式的经典之作。中国学者研究指出了Arakawa提出的瞬时守恒格式存在的问题(季仲贞,1981;曾庆存等,1981)。曾庆存等(1981)提出了总能量守恒隐式平流项的差分格式,在时间离散和任何初值情况下均计算稳定,具有能量守恒、广义能量守恒和平均尺度守恒。尽管隐式完全能量守恒格式计算是稳定的,但实际求解困难,需费巨大的工作量。王斌等(1990)和季仲贞等(1991)在此基础上提出了显式完全平方守恒格式。钟青等(1992,1993)在显式完全平方守恒格式上进一步发展了完全平方和三阶守恒格式。也有学者探索了全隐式差分格式的可能应用(陈长胜等,2007)。这些与计算格式有关的研究显示了中国科学家对数值计算基本方法研究方面的一贯重视。
中国在可预报性研究方面也做出了国际上有影响的研究成果。Mu等(2003)将线性奇异向量(linear singular vector,LSV)推广到非线性领域,提出条件非线性最优扰动(Conditional Nonlinear Optimal Perturbation,CNOP)。线性奇异向量代表了切线性模式中具有最大增长率的一类初始扰动;条件非线性最优扰动代表了满足一定物理约束条件下,在预报时刻具有最大非线性发展的一类初始扰动。Mu等(2010)进一步将条件非线性最优扰动拓展到初始误差和模式参数误差同时存在的情形,将仅与初始扰动有关的条件非线性最优扰动称为CNOP-I;与模式参数扰动有关的条件非线性最优扰动称为CNOP-P。条件非线性最优扰动在各类时间尺度的可预报性研究、目标观测和集合预报中有广泛的应用前景。
现有世界主要数值天气预报业务中心的谱模式和格点模式均采用球面高斯或经纬度网格以及半隐式半拉格朗日时间积分方案。这些模式尤其是全球模式在应用众核高性能计算机实现千米尺度全球数值天气预报时,网格和时、空离散化算法存在可扩展性的计算瓶颈问题,不能满足高效及时、高可扩展性、高分辨率高精度的数值天气预报业务发展需求。因此,世界主要数值天气预报业务中心均将可扩展性作为发展下一代模式考虑的重要问题。研发高精度、守恒、适用百米到数十千米分辨率的数值天气预报模式动力框架和相应的尺度自适应物理过程是发展下一代数值天气预报模式的重点(Mengaldo,et al,2019)。沈学顺及其研究团队研究并发展了基于多矩约束的有限体积离散化算法求解全可压大气方程组的新方法,该方法严格保证数值守恒,与传统的有限体积法相比具有局地自由度高、各类网格适应性好、无全局通信、算法局地性强等特点,具有高的可扩展性(Li,et al,2013;Chen,et al,2014)。该方法得到了国际发展同类下一代模式同行专家的认可(Smolarkiewicz,et al,2016)。在尺度自适应物理过程这一前沿研究领域,Huang等(2018)基于Arakawa提出的积云对流尺度自适应概念发展了一个新的表征积云对流参数化尺度自适应的表述方法;Zhang X等(2018)发展了一个三维湍流尺度自适应参数化方案,在百米级分辨率和千米尺度数值模拟中取得了物理上更为合理的结果。
先进的资料同化技术被认为是数值天气预报系统业务应用效果大幅度提高的重要原因之一(Bannister,2017)。中国科学家有关资料同化的系统性研究相对于计算格式等的研究起始较晚,但发展很快。结合数值天气预报业务需求,在20世纪80年代至90年代初,曾经发展了采用最优插值客观分析与非线性正规模初始化相结合的初始化方案(屠伟铭等,1995;朱宗申等,1992;薛纪善等,1992)。特别是,进入21世纪以来,中国科学家研究发展的资料同化系统已经实现了先进资料同化系统的基本功能(Zhang L,et al,2019)。GRAPES变分同化系统是21世纪中国变分类同化方法研究的一个代表性综合成果(薛纪善等,2008)。
中国科学家也开展了资料同化新方法的研究。Wang B等(2010)提出的降维投影四维变分同化(DRP-4DVar,4DVar based on a Dimension-Reduced Projection)以及Tian等(2018)提出的集合四维变分同化方法(NLS-En4DVar,Non-linear Least Squares enhanced proper orthogonal decomposition based Ensemble 4DVar algorithm)是代表性的研究工作。DRP-4DVar方法的基本思路是利用集合方法替代伴随方法实现代价函数梯度的计算,将模式变量空间和观测变量空间降维投影到样本空间,并结合使用局地化相关函数的主模态对样本空间进行扩展,最终在扩展样本空间完成四维变分分析。DRP-4DVar在计算目标函数梯度中回避了切线性与伴随模式,计算量大幅度减少。NLS-En4DVar实现了4DVar (four-dimensional variational data assimilation)与EnKF (Ensemble Kalman Filter)的优势互补,该方法通过严格的理论推导将集合四维变分同化问题转换为非线性最小二乘最优化问题,实现非线性最小二乘最优化问题的理论体系与集合数据同化方法的融合。这两种四维变分同化新方法,显示出较强的业务应用潜力。
20世纪70年代后期开始,也是中国自主研制数值天气预报模式的热点时期。国家气象局与中国科学院大气物理研究所(以后简称大气所)合作研制的亚欧区域3层原始方程绝热模式(当时称为A模式,1980年开始发布48 h形势预报)、中国科学院大气物理研究所-北京大学-国家气象中心联合研制的北半球5层格点模式(当时称为B模式,1982年业务运行;陶诗言等,2003)和一个有限区域的5层格点模式(当时称为B小模式,1982年业务运行)、国家气象中心发展的LAFS(Limited Area Forecast System;后逐步发展为High-resolution LAFS—HLAFS;该模式是以北京大学张玉玲教授提出的基本模式架构建立起来的)有限区域模式(郭肖容等,1995),代表了20世纪80年代中后期中国业务数值天气预报模式的自主创新成就,并支撑了中国20世纪80年代到90年代初的逐日天气预报和防灾、减灾工作(陈德辉等,2004),其中,HLAFS一直业务运行至2006年才被GRAPES_Meso取代。同时,上海、广州、兰州等地都独立研制了各自的模式,如上海的台风模式(朱永禔等,1987)、广州的热带模式(Xue,et al,1988)、兰州的复杂地形模式(颜宏,1987)等,并且都曾经应用于预报业务。针对中国的复杂地形和暴雨预报问题,宇如聪参考Mesinger(1984)的工作于1986年开始发展一个通过引入η坐标考虑陡峭地形的预报模式(后称为REM,Regional Eta-coordinate Model;宇如聪等,1994)。经过多年对模式物理过程的更新、完善,REM进一步发展为AREM(Advanced Regional Eta-coordinate Model),在武汉暴雨研究所和军队等单位的科研和业务中曾得到应用(宇如聪,2004)。这时期,除了面向业务的数值天气预报模式自主创新研究外,中国科学家自主研制的模式在数值天气预报研究中也发挥了重要作用。郑庆林(1980,1989)基于完全形式的涡度方程和散度方程,采用球函数为基底,构造了7层半球谱模式,并成功给出了一批数小时的实例预报结果。他的工作大致和国际上谱模式的研究同步,其模式对非线性项的计算采用经典的“相互作用系数法”,而不是现在流行的“变换方法”。中国也比较早地开展了非静力平衡模式的研究,但多限于研究之用,如非静力平衡研究模式(王东海等,1996)、三维非静力平衡研究模式(胡志晋等,1991)等。
需要指出的是,文中重点关注对中国数值天气预报方面自主创新成果的综述,不包括长期积分的大气环流模式和气候模式。有关大气环流模式自主创新发展的成果可以参见曾庆存等(1985;IAP AGCM-I,Institute of Atmospheric Physics Atmospheric General Circulation Model-I)和Wang等(2004;GAMIL,Grid-point Atmospheric General Circulation Model of IAP/LASG)以及沈学顺等(2010)的综述。
1.2 中国现代数值天气预报业务体系的建立和创新发展如上所述,中国科学家虽然在20世纪50—60年代早期探讨性地开展了数值天气预报业务试验,但限于当时的条件很难形成业务能力。真正形成实际业务能力则始于1980年之后A模式、B模式的业务运行,建成了短期数值天气预报业务系统。中国全球中期数值天气预报业务系统的研发始于20世纪80年代中期,1985年被国家科学技术委员会批准为“七五”国家重点科技攻关项目(李泽椿,2010)。鉴于当时中国数值天气预报系统的研发能力和支撑条件与先进国家存在很大差距,确定了预报模式从先进国家整体引进的技术路线。“七五”期间,李泽椿主持了17个单位参加的近300人的跨部门联合攻关小组,以从ECMWF引进的全球谱模式为核心,在国产银河大型机上建立了T42L9全球预报系统,并于1991年投入业务运行。在20世纪90年代与21世纪初几经升级(T63L16、T106L19、T213L31、TL639L60;之后称为T系列),在中国的气象预报业务与服务中发挥了重要作用,为之后开展自主研发工作奠定了重要基础。20世纪90年代该系统的建立标志着中国具备了从全球中期到区域短期的现代化数值天气预报业务和服务能力。
20世纪末至21世纪初,中国气象局做出了未来数值天气预报业务发展技术路线由引进为主转为自主开发为主的重大决策,开启了中国新一代数值天气预报系统的自主开发工作。2001年开始,在科学技术部“十五”国家重点科技攻关项目“中国气象数值预报系统创新研究”支持下,中国气象局联合多家单位,自主研究并初步建立了新一代多尺度通用资料同化与数值天气预报系统—GRAPES(薛纪善等,2008)。之后,在科学技术部“十一五”“十二五”科技支撑计划项目以及中国气象局GRAPES专项的连续支持下,经过十几年持续不懈的努力,以自主技术研发建成了从区域3—10 km到全球25—50 km分辨率的确定性与集合预报的完整数值天气预报业务技术体系,并锻炼培养出一支数值天气预报业务全链条(即从观测资料前处理和质量控制、资料同化、模式动力物理、模式并行计算到模式系统集成、数值天气预报产品后处理等)研发队伍。通过GRAPES的研发,中国在非静力全可压格点动力框架、四维变分同化、云降水物理、高精度大气模式数值算法、卫星资料偏差订正和卫星资料同化技术等方面取得了创新性的成果,为今后中国数值预报的全面深入发展奠定了重要科研和技术积累以及人才储备。
伴随数值天气预报业务的发展,一些学者对不同阶段的数值天气预报业务研发进展也做了总结和综述(陈德辉等,2004;李泽椿,2010;沈学顺等,2010)。文中在回顾中国数值天气预报自主创新发展历史的基础上,重点总结近10年GRAPES的发展成果,包括GRAPES科学技术进展、业务系统研发和应用状况以及未来发展技术路线。
2 GRAPES研发历程和业务体系的形成GRAPES由区域和全球一体化模式及同化系统构成,其研发酝酿于2000年初。发展非静力格点大气模式以克服高分辨率谱模式在大规模并行计算时的瓶颈问题,是当时国际数值天气预报界的共识。应该说,在设计GRAPES系统时做出的格点模式技术方向选择是科学合理的。同时,发展同化系统的策略则采取先三维再逐步走向四维变分同化的路线,也是符合科学发展规律的。
2.1 研发和业务应用的重要节点至“十五”科技攻关项目结束(2001—2005年),完成了半隐式半拉格朗日非静力动力框架、适用于中尺度数值天气预报的物理过程、区域等压面三维变分同化及并行计算的研发。基于这些成果,形成了GRAPES中尺度数值天气预报系统(GRAPES_Meso 2.0),并于2006年7月实现业务应用(30 km水平分辨率),代替HLAFS成为中央气象台业务中尺度预报系统。
GRAPES_Meso 2.0是GRAPES的第一个业务应用成果。2007年,经过水平分辨率从30 km到15 km的升级,形成了GRAPES_Meso 2.5版。在业务应用中,发现预报雨带散乱、降水强度偏低等系统性问题。针对此状况,研发了基于分段有理函数的高精度守恒标量平流方案PRM (Piecewise Rational Method)、考虑陡峭地形的单调水平扩散等技术,并依据模式有效分辨率在模式中考虑了有效地形。这些改进大幅度提高了模式对水汽等水物质的模拟精度,显著改进了降水预报效果(沈学顺等,2011,2013)。高精度守恒标量平流PRM的应用也显著改进了GRAPES区域台风预报模式(GRAPES_TYM)对台风强度的预报效果。这些成果使得GRAPES中尺度数值天气预报系统有了第一次重要升级(2010年2月GRAPES_Meso 2.5版升级到3.0版)。
GRAPES_Meso业务应用中影响预报效果的另外一个关键问题是中尺度资料同化系统。之前,GRAPES_Meso所用三维变分同化是以等压面上的位势高度、风及水汽(比湿或相对湿度)作为基本大气状态变量,与GRAPES_Meso预报模式并不匹配。无论预报模式给同化系统提供背景场或同化系统向模式提供分析结果作为初始场都要经过附加的中间过程,不可避免会引入额外的误差(薛纪善等,2012)。这个问题在研发GRAPES全球中期预报系统的初期同样存在。此外,还缺乏能够为中尺度模式提供云水等云信息初始场的同化功能或者云分析系统。为此,研发了模式空间三维变分同化系统,形成了与GRAPES模式匹配的区域/全球一体化的三维变分同化系统(薛纪善等,2012),这也成为后续GRAPES全球四维变分同化系统顺利研发成功的重要一步。在区域模式空间三维变分同化系统的基础上,Wang R C等(2018)进一步将控制变量更新为纬向和经向风,且实现了温度和地表气压的直接同化,并通过背景误差协方差、平衡约束关系、水平相关模型等的优化与研发以及大尺度约束的引入,使之能够有效应用在千米尺度分辨率的GRAPES_Meso系统中。同时,以ARPS(Advanced Regional Prediction System)中的云分析方案为基础,通过优化改进,研发了有效应用分钟级探空、地面观测、风云二号静止气象卫星云产品及多普勒天气雷达三维组网拼图产品等资料的云分析系统,通过松弛逼近方法在GRAPES_Meso中实现了对云微物理初始信息的应用(朱立娟等,2017)。以上研发的这些核心技术成为继GRAPES_Meso 3.0之后的重要科学技术进步。当然,包括积云对流、云物理及动力物理耦合计算的优化工作也对GRAPES_Meso的不断进步起到了积极作用。
以上工作促进了GRAPES_Meso业务应用效果的不断提升,并使得GRAPES_Meso系统得到多样化应用。基于GRAPES_Meso的快速循环系统(GRAPES_RAFS)和区域台风预报系统(GRAPES_TYM)于2012年实现了业务应用。2014年,GRAPES_Meso分辨率从15 km升级为10 km(黄丽萍等,2017),并在垂直方向进行了加密(由原来的30层增加到50层)。2016年建立了中国东部区域3 km分辨率的GRAPES_Meso准业务系统,该系统在2019年进一步扩展为覆盖全中国的3 km分辨率预报系统,在逐日天气预报业务中发挥了重要作用。
2007年7月开始系统地研发GRAPES全球中期数值天气预报系统(GRAPES_GFS)。在半隐式半拉格朗日非静力动力框架和扩展至全球的等压面三维变分同化系统的基础上,研发了适用于全球预报的动力框架、物理过程以及全球卫星资料的系列同化应用技术。2009年3月完成了GRAPES_GFS的前期试验,并在业务环境中建立了运行试验平台,确定了GRAPES_GFS的准业务版本—GRAPES_GFS 1.0,实现准业务化运行(沈学顺等,2009)。这期间,不仅研发了GRAPES全球预报模式、全球同化和卫星资料应用等核心技术,而且建立了全球多卫星平台资料的业务接收和处理流程,数值天气预报自主创新发展过程也带动了气象业务全链条的进步发展。
但是,不可否认的是,GRAPES研发时采用了传统两时间层半隐式半拉格朗日算法(Temperton,et al,2001;Gospodinov,et al,2001),为保持积分稳定,模式中取较大的半隐式权重系数使得时间离散化精度仅为1阶,且计算上游点和方程右端非线性项时需要时间外插,造成模式计算噪音并导致个别情况下计算不稳定;同时,采用了非守恒方程组和半拉格朗日算法,模式的质量守恒问题在算法设计上没有很好考虑。另外一个严重影响全球预报效果的问题是资料同化,如前所述,GRAPES_GFS 1.0的同化系统是一个在标准等压面上的三维变分分析系统,分析变量为位势高度、风和相对湿度,在17层标准等压面和Arakawa-A网格上分析后,通过静力关系导出模式预报变量,再插值到模式格点上作为初值。由于插值误差,等压面3DVar存在精度上的局限,对预报初值的精度带来严重影响。这些影响预报效果的问题涉及到模式动力框架、同化框架和数值算法的根本问题,也是GRAPES在2005年初步研发成功之后走向业务应用所面临的重要挑战。
在GRAPES_GFS 1.0准业务化之后,开展了3个阶段的攻关。第一阶段以完善模式物理过程为代表,包括辐射引入RRTMG(The Rapid Radiative Transfer Model for GCMs)方案提高辐射计算精度、以中国自主研发的CoLM(Common Land Model)陆面模式代替简单的5层热扩散模型(SLAB)、引入次网格地形重力波参数化、对积云对流参数化进行优化,这些工作使得GRAPES全球模式具备了适用于全球预报的一套物理过程。第二阶段,重点攻克模式空间GRAPES三维变分同化系统以避免同化后插值到模式空间带来的误差,并在改进卫星资料同化应用效果的同时增加更多卫星资料的同化应用(薛纪善等,2012)。第三阶段以同化和模式协同攻关为代表,重点解决了动力框架中部分影响计算精度和稳定性的问题、以云-降水为重点的物理过程协调性改进和优化、同化系统中风压平衡问题、背景误差协方差随季节变化问题、同化系统中背景廓线的精确插值和求解、观测资料的质量控制和偏差订正以及更多卫星资料的同化应用等。这些成果不仅在GRAPES_GFS中取得很好的效果,同时也在GRAPES_Meso系统中得到了应用(具体的改进内容参见沈学顺等(2017))。
在上述研究成果的基础上,建立了水平0.25°×0.25°分辨率垂直方向60层的全球预报系统新版本—GRAPES_GFS 2.0,并于2015年年底通过业务化验收(沈学顺等,2015)。到目前为止的业务运行结果表明,GRAPES_GFS 2.0预报形势场统计检验指标虽与ECMWF、NCEP相比尚存在些许差距,但全面超越了国家气象中心引进的业务模式TL639,且雨带预报能力已经接近ECMWF的预报水平,不同阈值下的模式空报问题得到了抑制,中国区域的降水预报形势,特别是中国东南部的主降水区的形势与实况更为接近。
在GRAPES_GFS 2.0基础上,进一步解决了GRAPES-4DVar面向业务应用存在的问题。重点解决了计算效率、观测剖分、多次外循环更新等技术细节问题,并发展了包括垂直扩散、深积云对流、次网格地形阻塞流拖曳、大尺度凝结等线性化物理过程,研发了卫星资料动态偏差订正技术,引入数字滤波弱约束,并对同化框架中的风压平衡、背景误差协方差等进行了进一步优化。有关GRAPES-4DVar的具体科学技术细节可参考Zhang等(2019)。2018年7月带有GRAPES-4DVar的GRAPES_GFS 2.4实现业务运行。GRAPES-4DVar的业务运行标志着中国业务数值天气预报同化技术迈入国际前列,成为国际上少数具有自主研发和业务应用四维变分同化系统的国家级预报中心之一。
集合预报是业务数值天气预报系统的重要组成部分。2010年,中国气象局数值预报中心开始研发GRAPES中尺度集合预报(GRAPES_REPS,GRAPES Regional Ensemble Predication System)和全球集合预报系统(GRAPES_GEPS,GRAPES Global Ensemble Predication System)。对于中尺度集合预报系统,先后研发了考虑初值不确定性的ETKF(Ensemble Transform Kalman Filter)方法,以及考虑模式不确定性的随机物理过程倾向扰动SPPT(Stochastically Perturbed Parameterization Tendencies)和随机动能后向散射SKEB(Stochastic Kinetic-energy Backscatter)方案。GRAPES_REPS于2015年实现业务应用,分辨率为15 km×15 km,2019年GRAPES_REPS进一步升级为水平分辨率10 km×10 km和垂直50层。对于全球集合预报,基于GRAPES全球切线伴随模式,研发了基于奇异向量(SV)构造初值扰动的方法,并研发了随机物理过程倾向扰动(SPPT)和随机物理参数扰动(SPP)。全球集合预报系统GRAPES_GEPS于2018年实现业务应用,水平分辨率为50 km×50 km,垂直方向60层。
伴随GRAPES模式和同化技术的不断深化发展,至2018年实现了从区域3—10 km到全球25—50 km分辨率的确定性与集合预报的完整数值天气预报体系,并建立了观测资料前处理和质量控制、数值天气预报产品后处理、预报检验和产品解释应用、观测和预报数据库、试验分析平台、监控系统全链条支撑系统。回溯数值天气预报自主研发历程,可以看到,与GRAPES体系之前的T系列相比,中国业务数值天气预报系统又向前跨了一大步,实现了自主研发、应用、改进、发展的良性循环。尤为重要的是,在坚持不懈的自主发展过程中,培养了一支稳定、全技术链条的研发和业务应用队伍。
2.2 GRAPES业务体系概述及应用效果 2.2.1 主要科学技术特点引进的T系列自1991年开始服务中国气象预报和防灾、减灾逾20年,在国家、省、市、县各级预报员中有着深刻的影响。基于自主研发的GRAPES成果构建全新的业务体系满足预报业务的需要并不是一件简单的事。从上一节对GRAPES研发重要节点的叙述中可以看到,研究成果的叠加与反复迭代、在应用中研发业务系统并不断改进需要团队长期的研究和知识经验的积累。沿着既定的技术路线、注重研究成果的积累、在应用实践中解决科学技术难题谋发展,对于自主发展数值天气预报业务体系并扎实掌握气象预报核心科技而言至关重要。
自2005年GRAPES研发成功之后,历经13 a的深化改进,到2018年建成了完整数值天气预报体系。与早期相比,GRAPES的动力框架、模式物理过程、同化框架以及观测资料应用等诸方面有了长足的进步。有关GRAPES的科学技术设计和初期研发成果参见《数值预报系统GRAPES的科学设计与应用》(薛纪善等,2008)。
从表1可以看出,模式动力框架在科学技术方案上有了长足的进步,与目前英国气象局、加拿大气象局数值天气预报模式采用的预估修正半隐式半拉格朗日方案类似,与传统半隐式半拉格朗日相比时间离散化精度更高、稳定性更好,突破了传统半隐式半拉格朗日中非线性项和拉格朗日轨迹中间点风速的时间外推带来的计算噪音问题。GRAPES业务体系区域/全球预报系统采用一体化框架的非静力格点半隐式半拉格朗日模式,在当前国际业务数值天气预报单位中也只有英国气象局和加拿大气象局;另外,全球预报采用非静力模式的目前仅有英国(ENDGame/UKMO)、美国(FV3_GFS/NCEP)、德国(ICON/DWD)和中国(GRAPES/CMA)(Mengaldo,et al,2019)。模式物理过程的研发与应用也有了长足的进步,从早期借用WRF的物理过程,到自主研发双参数云物理过程,并在此基础上研发了云宏物理和预报云方案(Ma,et al,2018),同时研发了次网格地形重力波拖曳和小尺度地形湍流拖曳等过程,使得GRAPES模式的物理过程更加完备。GRAPES模式物理过程在应用中得到了不断的改进与发展,成为提高区域/全球预报技巧的重要因素之一。
| 动力框架 | 物理过程 | |||
| GRAPES 1.0 | GRAPES业务体系 | GRAPES 1.0 | GRAPES业务体系 | |
| 1. 非静力全可压方程组
(浅大气近似) 2. 等温参考大气 3. 传统两时间层半隐式半拉 格朗日(SISL)算法 4. 动量方程三维矢量离散化 5. 传统 SISL 求解位温预报 方程 6. 准单调正定标量平流 QMSL |
1. 非静力全可压方程组(浅 大气近似)
2. 三维参考大气 3. 预估修正半隐式半拉格朗 日算法 4. 动量方程三维矢量离散 化+ W damping 5. 垂直方向非插值 SISL 求 解位温预报方程 6. 高精度守恒标量平流 PRM |
1. NCEP-3/5 种水物质的微物
理方案 2. Betts-Miller 积云对流参数化 3. Dudhia 短波、RRTM 长波辐 射方案 4. MRF 边界层参数化 5. SLAB 陆面过程 6. 动力物理反馈:线性插值 |
1. 双参数云物理方案或 WSM-6
(中尺度模式) 2. 宏云物理与预报云方案(全球模式) 3. NSAS 积云对流参数化或 Meso-SAS (区域模式) 4. RRTMG 长短波辐射 5. CoLM (全球模式)或 Noah(中尺度模 式)陆面过程 6. NMRF 或 YSU (区域模式)边界层参数化 7. 次网格地形重力波拖曳 8. 小尺度地形湍流拖曳 9. 动力物理反馈:三次样条、准单调三次 样条插值 |
|
从表2可以看到,初期是与预报模式完全不匹配的等压面三维变分同化,历经10多年发展,开发了基于GRAPES非静力切线和伴随模式的全球四维变分同化、适用于千米尺度高分辨率数值天气预报的区域三维变分同化,与模式进步一样展现出了显著的进步,具体的技术进步在后文进一步阐述。全球GRAPES-4DVar的业务应用是中国自主发展数值天气预报的重要节点,中国成为继ECMWF、日本、法国、英国和加拿大之后业务运行四维变分同化的国家。
| GRAPES 1.0
区域等压面三维变分同化 |
业务体系区域
GRAPES-3DVar |
业务体系全球
GRAPES-4DVar |
|
| 基本公式 | 增量分析方案 | 增量分析方案 | 增量分析方案 |
| 网格 | 水平 A 网格、垂直标准等压面 | 水平 C 网格,垂直高度地形追随坐标 | 水平 C 网格,垂直高度地形追随坐标 |
| 分析变量 | φ、ψ、χ、RH/q | T、ps、u、v、q/RH/RH* | π、ψ、χ、q/RH/RH* |
| 背景误差协方差 | NMC 方法 | NMC 方法 | NMC 方法 |
| 平衡关系 | 线性平衡 | 线性平衡+统计 | 线性平衡+统计 |
| 最优化方法 | 有限记忆变尺度方法(LBFGS) | 有限记忆变尺度方法(LBFGS) | Lanczos-CG |
| 初始化 | 全量数字滤波 | 增量数字滤波 | 数字滤波弱约束 |
| 1. 非静力切线伴随模式 | |||
| 2. 切线性物理过程(垂直扩散、次网 格地形阻塞流拖曳、深积云对流、 云物理) |
观测资料的精细化处理与同化是影响数值天气预报效果的重要因素(Magnusson,et al,2013)。与早期GRAPES_Meso业务系统仅使用常规资料相比,目前的GRAPES系统具备了同化应用更多非常规资料的能力,包括全中国雷达反射率和径向风、地基GPS可降水量、中外静止与极轨卫星多平台多通道辐射率、GPS掩星资料等。各种类型观测资料处理和同化应用能力的提升是自主发展数值天气预报技术的重要成果之一。具体可参考有关文献(Han,et al,2010;Liu,et al,2014;Li,et al,2014;王金成等,2016;万晓敏等,2017)。表3、4分别给出了目前GRAPES全球和区域预报系统中的资料应用情况。
| 观测类型 | 仪器 | 平台 | 变量 | 占比(%) | 分类占比(%) |
| 常规资料 | TEMP | u、v、p、q | 3.4 | 30.1 | |
| SYNOP | p | 3.1 | |||
| SHIP | p | 0.2 | |||
| BUOY | u、v | 0.1 | |||
| AIREP | u、v、T | 23.3 | |||
| 卫星资料 | AMSUA | NOAA-15,-18,-19,Metop-A,-B | Radiance | 9.6 | 69.9 |
| MWHS-2 | FY-3C,-3D | Radiance | 0.2 | ||
| GIIRS | FY-4A | Radiance | 0.7 | ||
| ATMS | NPP | Radiance | 4.1 | ||
| IASI | Metop-A,-B | Radiance | 39.8 | ||
| AIRS | EOS-2 | Radiance | 2.3 | ||
| GNSSRO | COSMIC-1,Metop-A,B,FY-3C/D | Refractivity | 2.1 | ||
| AMVs-IR/VIS/WVs | FY-2E,GOES-13,GOES-15,MTSAT-2,METEOSAT_10 | u、v | 10.4 | ||
| ASCAT | Metop-A,-B | u、v | 0.7 |
| 观测类型 | 仪器 | 平台 | 变量 | 占比(%) | 分类占比(%) |
| 常规资料 | TEMP | u、v、T、RH | 4.22 | 6.24 | |
| SYNOP | p、RH | 0.74 | |||
| SHIP | p、RH | 0.04 | |||
| AIREP | u、v、T | 1.24 | |||
| 非常规资料 | Doppler radar | SA/SB/CB/SC/CD/CC | VAD wind
Radial wind Refractivity |
0.09
53.35 20.85 |
93.76 |
| WPR | Wind | 0.57 | |||
| GPSPW | Precipitable Water | 0.14 | |||
| GNSSRO | COSMIC-1,Metop-A,B,FY-3C/D | Refractivity | 0.11 | ||
| AMVs-IR/VIS/WVs | FY-2E,GOES-13,GOES-15,MTSAT-2,METEOSAT_10 | u、v | 0.36 | ||
| Rain | Rain(nudging) | 18.29 |
从表3中可以看到,全球预报系统中卫星资料应用取得了大幅度进步,这在后文中有进一步叙述。就表4中中尺度预报系统的资料应用情况而言,虽然雷达等高时、空分辨率资料的应用有了长足进步,但在卫星资料应用方面仍然需要加强。
2.2.2 业务体系概况和应用效果到2018年为止,基于GRAPES成果建成了高、低分辨率搭配适当、确定性和集合预报有机结合的完整数值天气预报体系。与基于引进技术的体系相比,自主业务体系的建立不仅需要模式和同化研发成果向业务转化的大量工作,而且涉及从观测资料检索、前处理和监控,直至预报数据的后处理、检验、可视化等各个环节的重构或者研发。在GRAPES业务体系建设过程中,除模式、同化和观测资料应用方面的显著进步外,在大数据库、试验平台、分析诊断工具和检验平台等支撑系统的研发和应用方面也取得了丰硕成果。
GRAPES业务体系由0.25°×0.25°水平分辨率垂直方向60层和0.5°×0.5°水平分辨率垂直方向60层的全球确定性和集合预报、亚太区域0.09°×0.09°垂直方向68层的中尺度确定性预报系统和覆盖中国区域0.03°×0.03°垂直方向50层的高分辨率数值天气预报系统以及覆盖中国区域0.1°×0.1°垂直方向50层的中尺度集合预报系统构成。同时,基于GRAPES驱动的全球/区域海浪预报系统、东亚沙尘暴预报系统和核污染应急预报系统作为专业数值天气预报系统也是GRAPES体系的重要组成部分。表5和6分别给出了GRAPES确定性预报系统和集合预报系统的配置情况。
| GRAPES_GFS
全球预报系统 |
亚太区域中尺度预报系统
GRAPES_TYM |
中国千米尺度高分辨率预报系统 GRAPES_Meso 3 km | |
| 分辨率 | 0.25°×0.25°L60 | 0.09°×0.09°L68 | 0.03°×0.03°L50 |
| 模式区域 | 全球,模式顶 3 hPa | ||
| 预报时次 | 00:00、06:00、12:00、18:00 UTC | 00:00、06:00、12:00、18:00 UTC | 00:00、06:00、12:00、18:00 UTC |
| 预报时长 | 240 h | 120 h | 36 h |
| 同化系统 | 4DVar | 全球分析降尺度+涡旋初始化 | 全球分析降尺度+云分析 |
| 物理过程 | 1. 双参数云物理方案
2. 云宏物理与预报云方案 3. NSAS 积云对流参数化 4. RRTMG 长短波辐射 5. CoLM 陆面过程 6. NMRF 边界层参数化 7. 次网格地形重力波拖曳 8. 小尺度地形湍流拖曳 |
1. Meso-SAS 积云对流参数化
2. WSM-6 云物理方案 3. RRTM 长波/Goddard 短辐射 4. NOAH 陆面过程 5. YSU 边界层参数化和垂直扩散 |
1. WSM-6 云物理方案
2. RRTMG 长短波辐射 3. NOAH 陆面过程 4. NMRF 边界层参数化和垂直扩散 |
| GRAPES_GEPS 全球集合预报系统 | 区域中尺度集合预报系统 GRAPES_REPS | |
| 模式区域 | 全球,模式顶3 hPa | 70°−145°E,10°−65°N,模式顶 10 hPa |
| 预报时次 | 00:00、06:00、12:00、18:00 UTC | 00:00、06:00、12:00、18:00 UTC |
| 预报时长 | 360 h | 84 h |
| 同化系统 | 全球 4DVar 升尺度 | 全球分析降尺度+云分析 |
| 初值扰动 | 奇异向量 | ETKF |
| 模式扰动 | SPPT、SKEB | SPPT |
| 侧边界条件 | GRAPES_GEPS | |
| 集合成员数 | 30 | 15 |
应该指出,过去的20 a是国际上数值天气预报持续高速发展,且各国纷纷加强数值天气预报投入的时期。中国气象局数值预报系统尽管取得了很大的成绩,但与国际先进业务系统相比,GRAPES业务体系仍存在一定的差距,包括GRAPES全球预报系统的分辨率较低、所用资料同化系统尚未考虑集合信息、缺乏云雨区卫星资料同化和卫星资料变分偏差订正等先进技术、尚未建立对流尺度集合预报系统、缺乏对流尺度同化系统和千米尺度分辨率快速循环系统以及集合预报的成员数较少且分辨率较低等。这些问题是一个全新的数值天气预报业务体系在形成之初不可避免但必须认真对待的问题,也是今后加快补缺的重点。
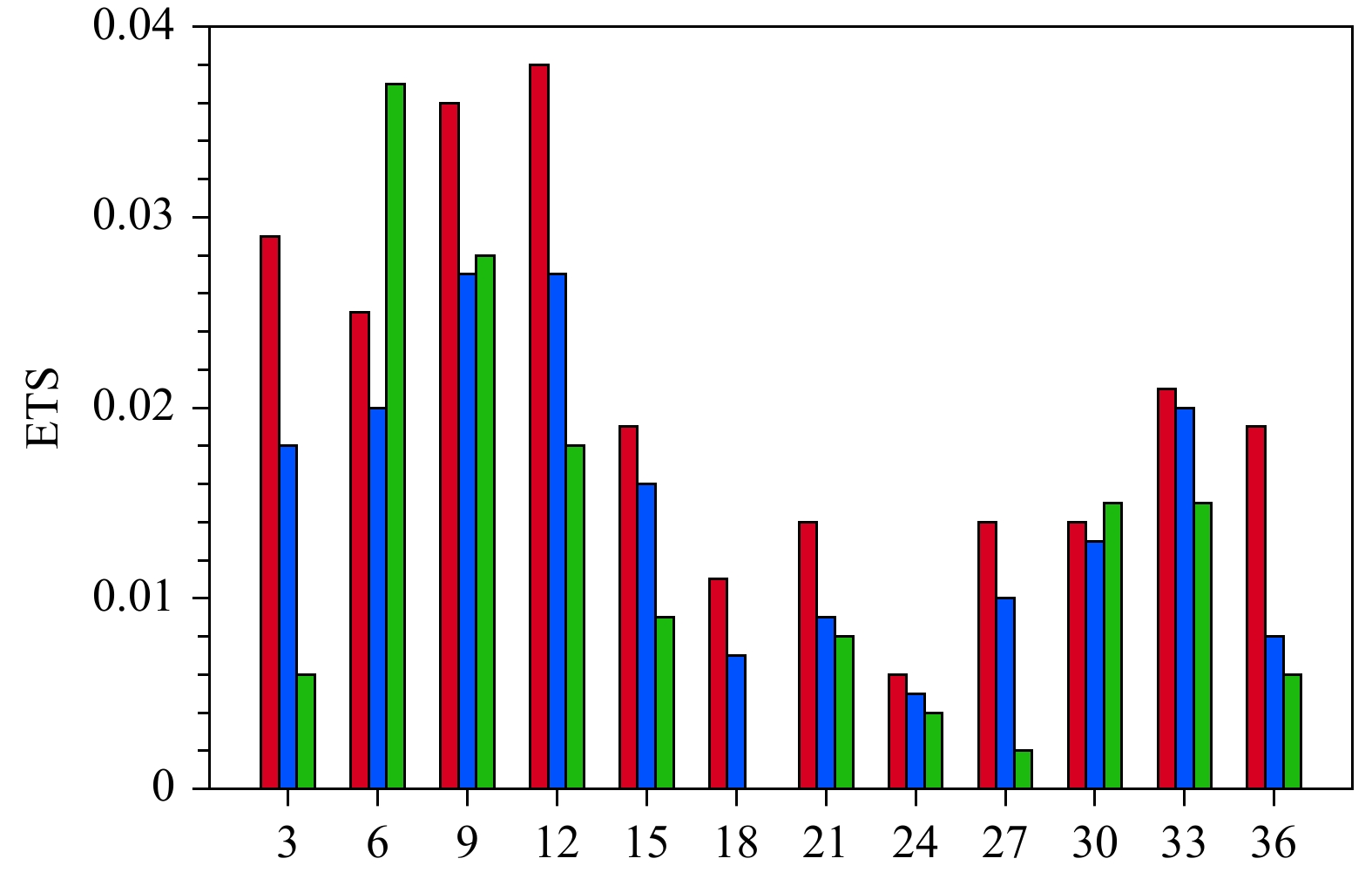
从业务GRAPES_Meso系统降水预报评分的逐年提高情况(图1)可以看出,GRAPES_Meso在各量级降水预报方面均有长足的进步,成为中央气象台逐日天气预报不可或缺的重要支撑。GRAPES_Meso的进步包含了分辨率的提高、模式动力框架和物理过程改进以及有效应用雷达资料的云分析系统的引入。2019年6月,水平分辨率3 km、覆盖全中国的GRAPES_Meso系统正式上线,该系统对强降水的预报能力将GRAPES业务应用水平推上了新的台阶。图2给出2019年6—8月平均的GRAPES_Meso 3 km预报的逐3 h暴雨预报的ETS评分,为了比较也给出了上海SMS-WARMS(9 km×9 km分辨率)以及ECMWF(水平分辨率9 km×9 km)的预报ETS评分。从图2可以看到,GRAPES_Meso 3 km在预报前20 h表现出了明显的优势。需要指出的是,不仅是前20 h的暴雨预报,对于其他时段降水的预报ETS评分也表现出明显的优势。

|
| 图 1 GRAPES_Meso从2006年7月业务化以来24 h降水预报逐月TS演变及变化趋势(TS评分是依据中国2510站的降水观测计算) Fig. 1 Monthly-averaged TS and its linear trend of GRAPES_Meso 24 h rainfall forecasts since its operational application in July 2006 (TS is calculated by using 2510 rain-gauge observations) |
|
| 图 2 GRAPES_Meso 3 km暴雨预报(≥50 mm) ETS评分 (2019年6月10日—8月18日的平均,红色柱:GRAPES_Meso 3 km,蓝色柱:上海9 km WRF模式,绿色柱:ECMWF的预报;数据来自中国气象局业务内网idata.cma/areaHighResolution;各模式预报均来自每日12时(世界时)起报结果;ETS评分依据中国11000自动气象站降水观测计算) Fig. 2 ETS skill scores of 3 h heavy rainfall forecast by GRAPES_Meso 3 km version (red color). Also shown are the forecasts from Shanghai WRF and ECMWF model. This figure is based on data from the CMA internal network: idata.cma/areaHighResolution. The forecast of each model started from 12:00 UTC. The ETS score is calculated based on 11000 AWS observations over China |
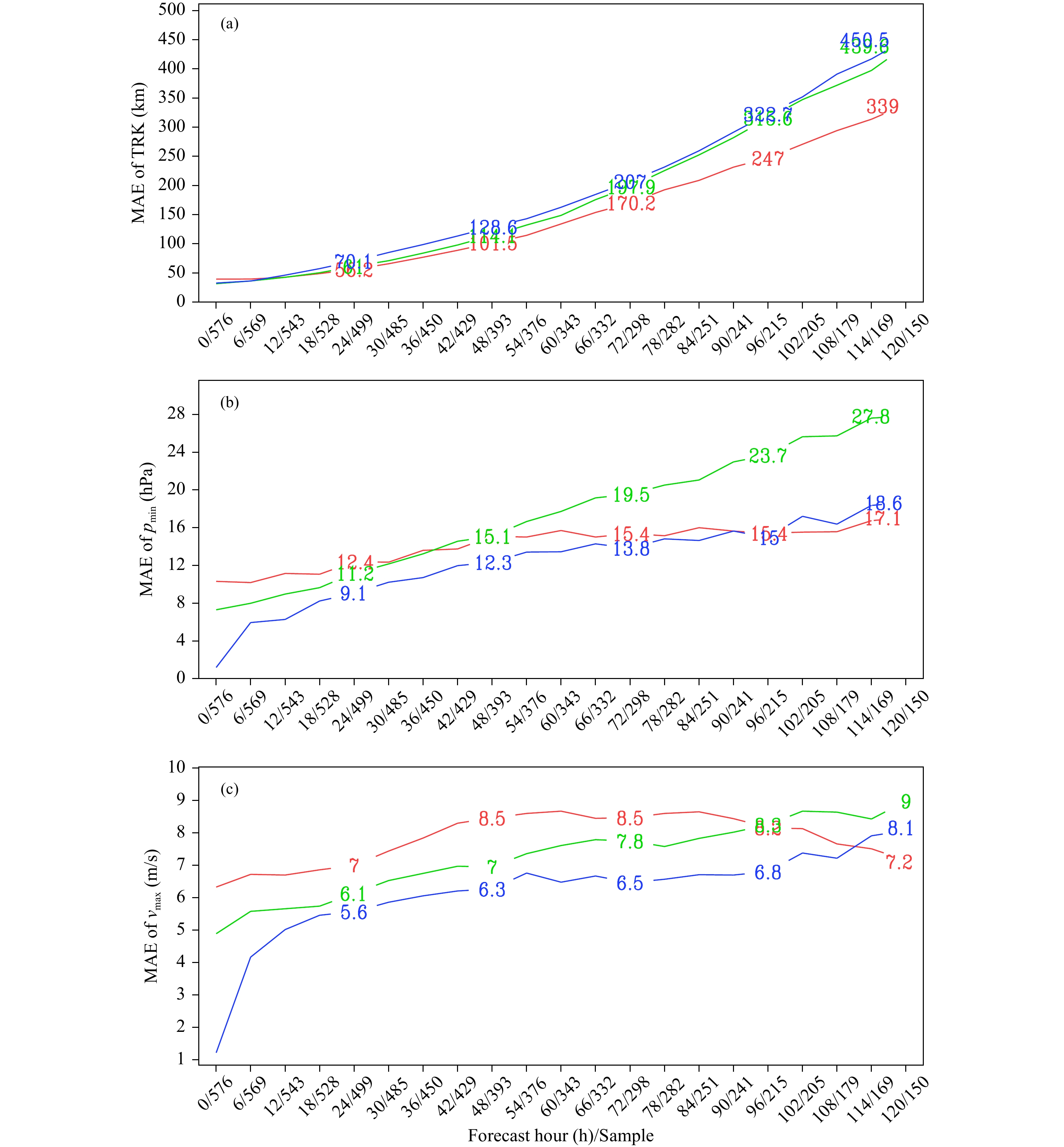
图3给出了区域模式GRAPES_TYM 2019年业务版本(V3.0)对台风路径和强度回报的误差随时间的演变。图3a、b、c分别为对2016—2018年所有西太平洋台风回报的平均路径误差、中心最低气压平均误差和最大风速平均误差5 d预报的演变情况。为了比较,在图中也给出了预报员常参考的ECMWF和NCEP全球模式的预报误差情况。从路径预报来看,目前仍是ECMWF全球预报占优,GRAPES_TYM与NCEP全球预报的结果相当。从强度预报来看,无论是中心最低气压平均预报误差或者是最大风速平均预报误差,GRAPES_TYM均表现出了比较明显的优势。
|
| 图 3 GRAPES_TYM 2019年业务版本(V3.0)对台风路径和强度回报的误差随时间的演变 (a、b、c分别为对2016—2018年所有西太平洋台风回报的平均路径误差、中心最低气压平均误差和最大风速平均误差5 d预报的演变情况;蓝线:GRAPES_TYM、绿线:NCEP、红线:ECMWF) Fig. 3 Time evolutions of forecast errors for TC track,center pressure and maximum wind by the 2019 operational version of GRAPES_TYM (a,b,c are for forecasts of all the typhoons over the western Pacific during 2016—2018;blue line: GRAPES_TYM,green line: NCEP,red line: ECMWF) |
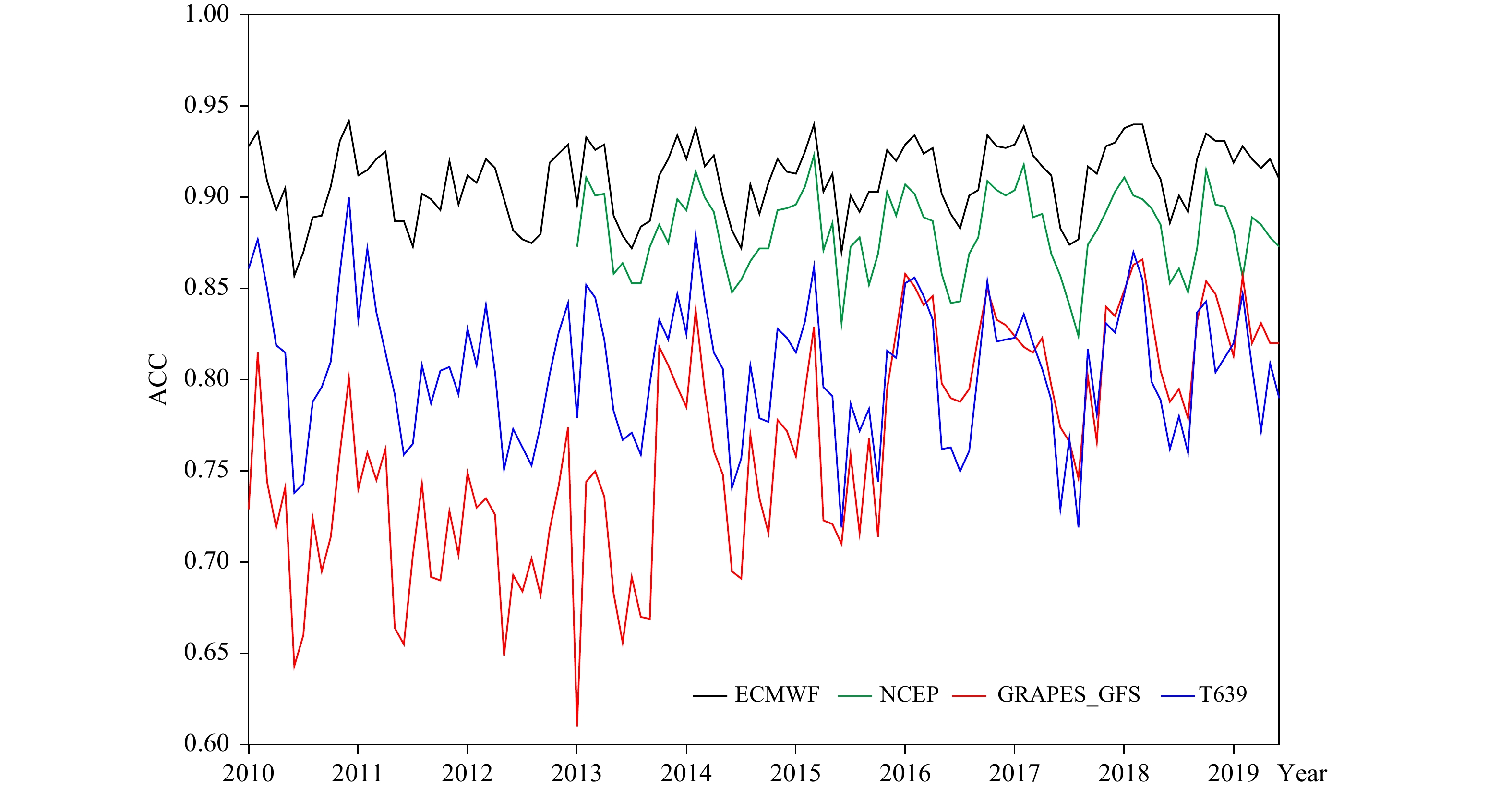
图4是2010年以来GRAPES_GFS预报第5天500 hPa高度场距平相关系数(Anomaly correlation coefficient,ACC)的时间序列,同时在图中也给出了ECMWF、NCEP的预报结果。可以看到,GRAPES_GFS对形势场的预报技巧10年来逐步提高,虽与ECMWF、NCEP还有差距,但逐年预报技巧的不断提高反映了GRAPES_GFS模式、同化以及观测资料应用等诸方面的巨大进步,这将在第4节中进一步说明。
|
| 图 4 2010年以来GRAPES_GFS预报第5天北半球500 hPa高度场距平相关系数时间序列 Fig. 4 Time series of ACC of 500 hPa height in the Northern Hemisphere on the 5th day forecast by GRAPES_GFS since 2010 |
特别是,2019年汛期以来,GRAPES_GFS对中国强降水的预报效果多次超过ECMWF,对江南、江淮、江汉大型暖切变等导致的系统性降水(2019年5月26日),GRAPES_GFS(TS评分0.29)性能明显优于ECMWF(TS评分0.16)。另外,在江淮、江南、江汉、华南冷切变强降水(2019年6月6—7日、12日)GRAPES_GFS的性能也明显优于ECMWF,为预报员提供了重要的参考。图5是2019年5月24日20时(北京时)起报的36 h预报降水与观测的散点分布。可以清楚地看出,此次强降水过程的预报GRAPES_GFS明显好于ECMWF。

|
| 图 5 GRAPES_GFS(a)与ECMWF(b)模式2019年5月24日20时(北京时)起报的12—36 h预报累计超过25 mm的降水与观测的散点分布 (单位:mm;降水观测来自中国2400站) Fig. 5 Scatter plots of 12-36 h accumulated precipitation (unit:mm) forecasts larger than 25 mm and observations (a. GRAPES_GFS,b. ECMWF;The model initial time is 20:00 BT 24 May 2019;The 2400 rain-gauge stations are adopted) |
目前,对于确定性预报而言,GRAPES_GFS与GRAPES_Meso的预报产品形成了很好的搭配,GRAPES_GFS把握形势场和雨带的中期变化,3 km分辨率的GRAPES_Meso则重点为预报员提供强降水雨量和落区的预报。这两个系统目前已经成为中央气象台逐日预报的核心支撑。
同样地,GRAPES全球和区域集合预报的业务应用为GRAPES“大家庭”增加了丰富的概率预报产品,在提前一周预报大范围强降水概率及局地强天气定量、定点概率预报中发挥了重要作用。
3 GRAPES主要科学技术进展在GRAPES模式和同化技术不断深化发展和业务应用过程中,取得了自主创新的成果。与GRAPES设计和研发之初相比(薛纪善等,2008),在模式动力框架的核心算法、变分同化框架、卫星资料同化技术、适合千米尺度分辨率的变分同化技术、集合预报初值和模式扰动方法等方面有了显著的进步。
3.1 GRAPES模式动力框架实现了从经典半隐式半拉格朗日算法到预估修正半隐式半拉格朗日算法的转变,模式计算精度和运算效率大幅度提高GRAPES模式动力框架在设计和研发之初,采用了当时国际业务数值天气预报模式主流采用的两时间层半隐式半拉格朗日算法解决离散化后平流和快波计算的稳定性问题。两时间层半隐式半拉格朗日算法虽然在节省计算内存提高计算效率方面有明显优势,但需要解决线性化时采用等温参考大气、半隐式处理时权重系数选取和非线性项时间外推及上游点计算时中间点风速外推带来的计算精度和稳定性问题(Simmons,et al,1997;Ritchie,et al,1996;Temperton,et al,2001)。这些方面在GRAPES模式开始研发时没有很好地考虑。为此,借鉴UKMO等的成功经验,进一步在GRAPES模式中发展了预估修正半隐式半拉格朗日算法,并在线性化时引入三维参考大气(Côté,et al,1998)。在动力框架中将三维参考大气与预估-修正算法结合,减小非线性项数量级的同时,通过迭代算法避免时间外推带来的影响,也可以使半隐式系数取值接近0.5,时间积分算法接近二阶精度(苏勇等,2018)。这些新的改进大幅度提高了模式的稳定性、计算效率和计算精度。
半拉格朗日模式均面临的另一个重要问题是对诸如水汽等标量平流计算的正定、守恒。半拉格朗日算法通过寻找上游点进而通过上游点处物理量的插值获得下一时间步的预报。插值过程必然带来不守恒和一定程度的耗散。Bermejo等(1992)提出了准单调半拉格朗日算法(QMSL,Quasi-Monotone Semi-Lagrangian),简捷且易于实现,但在水汽的强梯度、不连续区计算精度较低,且不能做到守恒。Bermejo等(2002)随后在准单调半拉格朗日算法基础上提出了订正的守恒算法。这些方法由于简捷和计算高效,在半拉格朗日模式中应用较多,ECMWF的半隐式半拉格朗日谱模式中至今仍在应用(Diamantakis,et al,2014)。不少研究者也发展了精度高且严格守恒的“体元映射”型半拉格朗日算法,如Cell-integrated semi-Lagrangian advection scheme(CSLAM,Lauritzen,et al,2010)、Semi-Lagrangian Inherently Conserving and Effi-cient scheme(SLICE,Zerroukat et al,2004,2009)等。但是,由于这些方法计算代价过高,在业务数值天气预报模式中较少采用。针对这种状况,研发了基于分段有理函数的标量平流方案(PRM,Piecewise Rational Method)。PRM方案通过将拉格朗日形式的标量预报方程重新写成易于构造守恒格式的通量形式,结合单元格界面通量更新的半拉格朗日算法,实现了高精度守恒且高效的水汽平流计算(苏勇等,2013)。
3.2 研发了GRAPES全球四维变分同化系统,实现业务应用自1997年ECMWF将四维变分同化成功业务应用并显示出在提高数值天气预报技巧方面的巨大潜力后,4DVar一直在研究和业务应用中被认为是先进的资料同化技术(Rabier,et al,2000;Bannister,2017;Bonavita,et al,2017;Kwon,et al,2018)。由于4DVar中所需切线伴随模式开发的巨大工作量和难度,研发4DVar是一项挑战性的工作。GRAPES全球4DVar系统的研发始于2008年,至2018年7月才实现业务应用,历经10 a。在全球非静力GRAPES模式基础上,发展了非静力的切线和伴随模式。为保持在同化时间窗内切线性模式与非线性模式在演变轨迹上较高的近似程度,研发了基于简化物理过程的切线性物理过程,包括积云对流、云物理、边界层垂直扩散、次网格地形阻塞流拖曳。这些研发工作成为GRAPES全球4DVar系统的重要基础。如前所述,GRAPES全球4DVar采用增量分析方案,在代价函数中引入数字滤波作为弱约束以抑制高频重力波,在系统中设计了多重外循环(目前在业务中采用单重外循环),极小化算法采用Lanczos-CG算法(Liu,et al,2018)。4DVar分析框架采用了水平和垂直不可分离的背景场误差协方差模型,水平相关模型采用二阶自回归模型,相关尺度随高度变化,垂直相关模型则直接由集合样本统计得到。平衡约束考虑了旋转风和散度风、旋转风和质量场、非平衡散度风和质量场的平衡,采用动力和统计结合方案来实现。
GRAPES全球4DVar系统每天进行4次6 h的分析,同化时间窗的起始时刻分别是03:00、09:00、15:00和21:00 UTC。全球4DVar分析结束后生成同化时间窗起始时刻的分析场,然后做6 h全球模式预报,为下个时次的全球4DVar分析提供背景场,同时输出3 h的模式预报结果,也就是06:00、12:00、18:00和00:00 UTC四个标准时刻的分析场,作为10 d全球预报的初值。GRAPES全球4DVar业务同化系统使用的观测资料包括探空报的温度、风场、相对湿度,地面报的气压,船舶报的气压,飞机报的风场,云导风,洋面散射风,GNSSRO掩星折射率和NOAA15 AMSUA、NOAA18 AMSUA、NOAA19 AMSUA、METOP-A AMSUA、METOP-B AMSUA、ATMS AMSUA、AIRS、FY4A GIIRS、FY-3C MWHS等卫星辐射率资料(表3)。相对于3DVar来说,GRAPES全球4DVar增加了近50%的观测资料使用量。
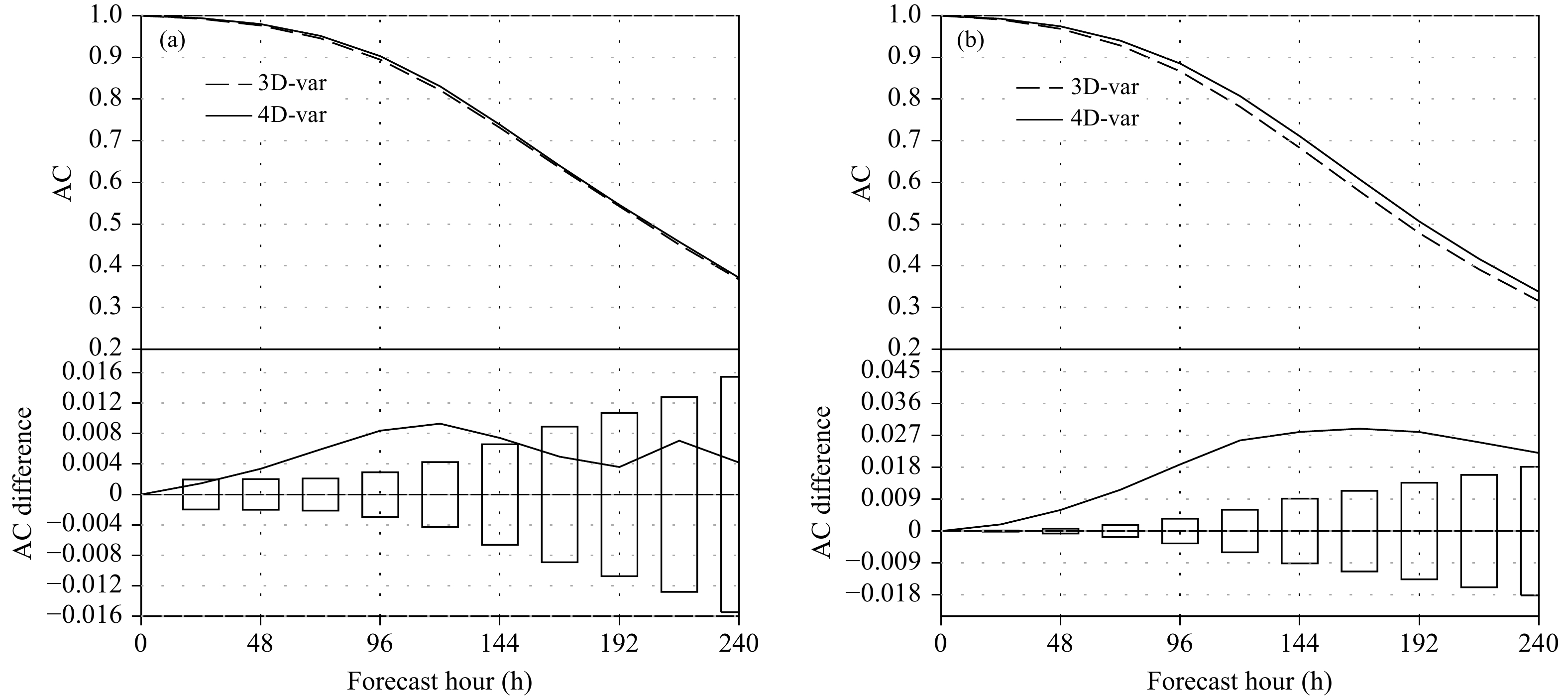
在分析质量方面,GRAPES全球4DVar全面超过3DVar的结果,尤其是质量场和风场。从均方根误差的角度来看,GRAPES全球4DVar背景场(6 h预报场)甚至优于同时刻的全球3DVar分析场。从分区域统计结果来看,南半球位势高度场和热带高层风场的改进更为明显。在不同时效和不同变量的预报方面,GRAPES全球4DVar都有改进。从图6 500 hPa位势高度的距平相关系数来看,平均预报时效有望提高5 h,其中南半球能够达到7—8 h。对于降水预报来说,GRAPES全球4DVar能够明显提高中雨以上量级的预报技巧。在台风预报方面,路径和强度预报均有明显改进,其中路径预报误差能够减小15%左右。
|
|
图 6 500 hPa位势高度场距平相关系数随预报时间的演变 (a. 北半球,b. 南半球;4D-Var与3D-Var的结果为2016年6月至2017年5月的平均; |
自从NCEP和ECMWF分别于1995和1996年在业务三维变分同化中实现卫星辐射率资料(TOVS,The Television and Infrared Observation Satellite(TIROS)Operational Vertical Sounder)的直接同化后,卫星资料作为全球数值天气预报的重要资料源及其在提高数值天气预报技巧方面的重要作用一直受到重视(Eyre,2007)。ECMWF在此领域处于领先地位,其同化系统中所用观测资料超过90%来自卫星探测。不同于引进和本地化国外系统,GRAPES卫星资料同化技术的系统性研发始于2004年,在早期的GRAPES等压面三维变分同化系统中加入了NOAA-16微波温度计AMSU-A辐射率资料的直接同化(Zhang,et al,2004)。包括NOAA系列(NOAA 15、16、17、18)ATOVS(Advanced TOVS)、GPS掩星资料、静止和极轨卫星云导风等批量卫星资料同化技术的系统研发和业务应用始于全球中期预报系统GRAPES_GFS的开发(沈学顺等,2009)。在GRAPES_GFS准业务化、业务化过程中,陆续开发了中国风云系列、欧洲Metop等微波温度计AMSU-A、微波湿度计MHS、高光谱大气红外等辐射率(IASI、AIRS)资料,多平台卫星资料的成功同化是GRAPES_GFS预报能力持续提高的重要因素(沈学顺等,2015)。
从图7给出的GRAPES系统中同化卫星资料的种类和平台数目逐年变化情况可以看到,近10年卫星资料的同化应用进展非常迅速,尤其是GRAPES_GFS 2.0版本2016年正式业务化之后(沈学顺等,2017)。目前GRAPES系统同化应用的卫星遥感资料占观测资料总量的约70%(表3),在提高GRAPES_GFS的预报能力方面显示出了重要作用。
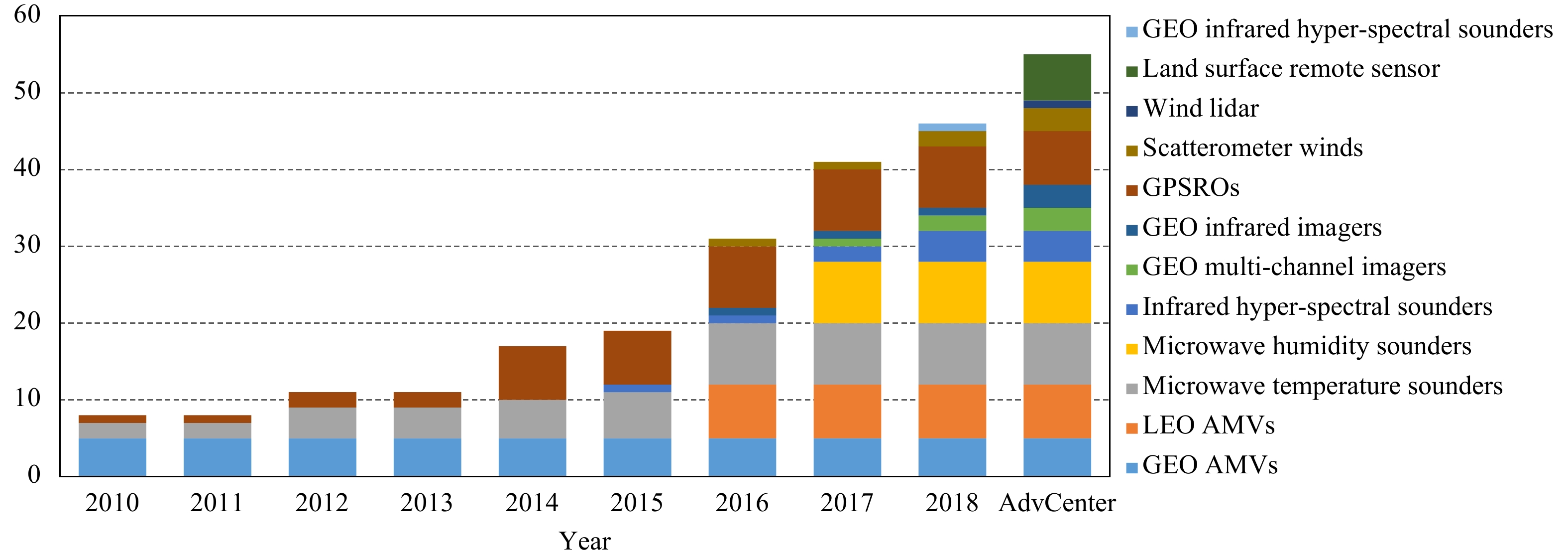
|
| 图 7 GRAPES全球模式可同化的卫星资料种类逐年演变 (图的最右侧给出的是先进数值天气预报中心的卫星资料应用情况) Fig. 7 Changes of satellite data types and number of platforms assimilated by GRAPES_GFS (The right side of the figure shows the status at advanced NWP center) |
上述卫星资料同化应用的进步得益于观测数据质量分析、偏差订正、云检测、通道选择、质量控制等关键技术的逐步掌握和成熟运用,当然,GRAPES同化框架本身的不断进步也至关重要。而且,根据GRAPES_GFS模式的特点,还发展了国际先进的有约束卫星资料偏差订正方案。传统的观测资料偏差订正主要依赖于观测和背景的差异(O−B),在业务应用中存在当模式有显著偏差时观测信息会被错误订正,以及当质量控制不完善时会造成不合理的观测偏差估计和订正等问题。这两个问题在GRAPES_GFS发展过程中表现得尤为凸出,主要表现在同化预报循环中,预报偏差与观测偏差订正会产生相互作用,从而导致观测偏差订正向模式偏差的漂移。借鉴数学物理反问题中正则化思想中的“极小模解”方法,把卫星辐射率资料定标和辐射传输模式不确定性估计通过正则化参数把不等式约束引入目标泛函,发展了有约束的卫星资料偏差订正技术—CBC(Constrained Bias Correction)(Han,2014;Han,et al,2016),减小了模式的背景偏差对卫星辐射率资料偏差订正的影响,较好地去除了资料本身的系统性偏差,更好地利用了观测信息。
有约束卫星资料偏差订正技术是在发展GRAPES数值天气预报系统中提出的原创技术,在2016年被引入到ECMWF的同化系统(Han,et al,2016),发展为有约束变分偏差订正(Constrained Variational Bias Correction,CVarBC),克服了卫星观测偏差订正向模式平流层偏差的漂移,提高了平流层初值分析精度,并改进了全球中期预报效果。CVarBC在ECMWF的2018年业务版本(IFS CY46R1)中开始业务化应用(ECMWF,2018a),此技术还将用于ECMWF第6代大气再分析(ECMWF,2018b)。
随着中国风云气象卫星的不断进步,风云卫星观测资料在GRAPES业务系统中同化应用的数量和效益不断提高。同时,通过在GRAPES中的定量评估和同化应用,也不断发现不足和问题并反馈,促使风云卫星观测资料质量和精度不断提升,中国气象局业务中逐步形成了卫星资料同化应用与改进的全链条业务协作。中国第一代静止气象卫星FY-2的卫星云导风产品十几年来精度持续提高,在GRAPES全球和区域同化预报中发挥了重要作用(Han,et al,2006;万晓敏等,2017,2018)。可见光和红外自旋辐射扫描仪(VISSR,Visible and Infrared Spin Scan Radiometer)是中国自主研发的第一代静止卫星FY-2上搭载的有效载荷,VISSR的晴空水汽通道辐射率资料实现了在GRAPES全球4DVar中的同化应用(王皓,2017),充分发挥了其高时间分辨率观测的优势。
为充分发挥中国第二代极轨气象卫星FY-3多平台多载荷观测的综合优势,弥补单一仪器通道信息不足的缺点,在定量应用中发展了综合云和降水检测算法,实现了FY-3卫星微波温度计(MWTS)、湿度计(MWHS)、成像仪(MWRI)和掩星观测(GNOS)在GRAPES业务系统中的同化应用(Li,et al,2016;Wang,et al,2019)。
2016年发射成功的中国新一代静止气象卫星FY-4A,搭载了地球静止轨道干涉式探测仪(GIIRS,Geosynchronous Interferometric Infrared Sounder),在国际上首次实现了静止轨道高光谱探测(Yang,et al,2017)。在GRAPES同化系统中发展了GIIRS观测算子(Di,et al,2018)、基于观测区域背景误差协方差的通道选择技术(尹若莹等,2019),以及适合大阵型探测器的偏差在线估计和订正算法等关键技术(Yin,et al,2020),2018年12月实现了GIIRS辐射率资料在业务GRAPES全球4DVar中的同化。同时,充分利用FY-4A探测仪机动灵活观测能力和数值天气预报系统的云预报和敏感区识别技术,在国际上首次实现了“智能快速晴空业务观测模式”和“高影响天气目标观测模式”。2018年在实时业务环境下,针对台风“玛丽亚”“安比”和“山竹”,应用GRAPES奇异矢量识别的敏感区,对卫星观测区域、观测频次等参数进行最优确定,通过观测和预报的协同互动,实现了面向预报对象的静止卫星探测模式,并同化到GRAPES全球4DVar,改进了对台风路径的预报。
3.4 研发了适合千米尺度分辨率数值天气预报的三维变分同化技术和云信息初始化技术发展千米尺度资料同化系统,改善模式初值中的中小尺度信息,对于提高极端天气和近地面气象要素的预报能力十分重要(Gustafsson,et al,2018)。GRAPES千米尺度资料同化系统基于GRAPES全球区域一体化变分同化框架(薛纪善等,2008)开发,采用三维变分同化(3DVar)选项(以下简称为km-scale 3DVar),框架主体、观测算子、资料流程等与区域3DVar系统保持一致。
在同化分析框架上,km-scale 3DVar面向千米尺度数值天气预报的需求做了针对性开发(Wang R C,et al,2018)。首先,km-scale 3DVar将极小化目标泛函中的动力学控制变量由流函数(ψ)、势函数(χ)、以及π转换为u风、v风以及温度(T)和地面气压(ps),并且不再考虑控制变量间的地转平衡关系。新控制变量对应的背景误差空间相关尺度更小,且为观测系统的直接测量要素。如图8所示,与业务10 km 3DVar相比,km-scale 3DVar(试验水平分辨率为3 km)的分析增量要更加局地,适合中小尺度系统的同化分析。其次,为了能在分析好中小尺度系统的同时兼顾天气尺度环境气流的正确描述,还研发了多尺度分析方案,包括采用多尺度水平相关模型(吴洋等,2018)、取千米尺度分析场中的中小尺度信息与全球分析场中的大尺度信息进行重组的直接混合,以及在km-scale 3DVar的目标泛函中引入大尺度信息作为弱约束的隐式混合(Yang M J,et al,2019)等。此外,为适应中小尺度信息发展迅速、生命史短的特征,也为弥补3DVar时间维的缺失,km-scale 3DVar采用快速同化预报循环更新的方式运行,同化分析间隔为1—3 h,采用数字滤波抑制快速循环过程中的噪音问题。

|
| 图 8 单点探空温度观测 (位置:31.93°N,118.9°E,850 hPa) 分别在GRAPES区域10 (a) 和3 (b) km变分同化系统中强迫出的温度分析增量 (沿32°N的垂直剖面,等值线单位:K) Fig. 8 Temperature analysis increments forced by single-point sounding temperature observations (location: 31.93°N,118.9°E,850 hPa) by 10 (a) and 3 (b) km variational assimilation systems in GRAPES_Meso (vertical profiles along 32°N,isoline unit: K) |
在观测资料应用方面,km-scale 3DVar除了同化现有业务系统所用观测资料,还积极发展时、空稠密资料的同化应用。首先,在雷达资料的应用上,径向风和风廓线雷达资料已在km-scale 3DVar中实现直接同化应用,改进了流场分析;反射率资料则在云分析系统中用于诊断水凝物和潜热倾向信息,并通过张驰逼近的形式引入到模式轨迹中。其次,对中国新一代地球静止卫星FY-4A提供的高时、空分辨率观测资料,km-scale 3DVar也已具备了同化应用能力。此外,面对越来越丰富的地面自动气象站观测资料,km-scale 3DVar也正在加强对其的同化应用研究,尤其是复杂地形下的资料应用。
与原有采用全球分析场降尺度结合云分析系统驱动GRAPES千米尺度模式的方案相比,引入km-scale 3DVar可以有效改善模式短时预报性能(前12小时),包括短时降水(图9)和近地面气象要素预报。在以上工作基础上,覆盖全国的包含km-scale 3DVar的GRAPES千米尺度快速循环数值天气预报系统将在2020年实现业务运行。
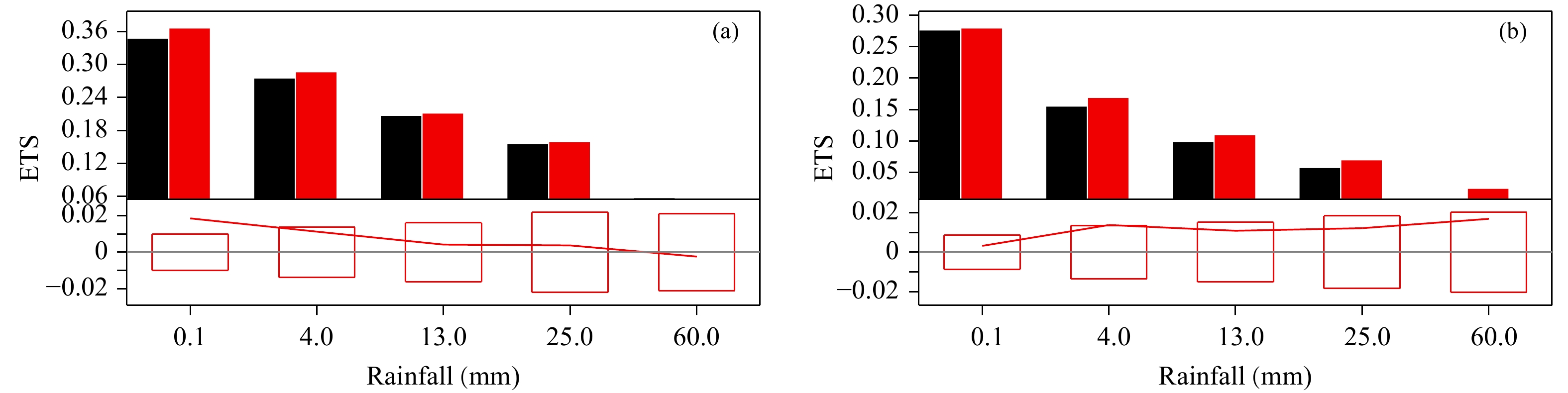
|
| 图 9 不同量级降水ETS评分 (a. 0—6 h累计降水,b. 6—12 h累计降水,两个方案分别为全球分析场降尺度(黑色)和3 km变分同化分析(红色)结合云分析系统驱动GRAPES 3 km预报系统;ETS为基于中国2400站的平均值;红色方框表示95%信度,红线超过方框范围为通过置信度检验) Fig. 9 ETS scores of precipitation with different intensity for 0—6 (a) and 6—12 (b) h forecasts (The black and red bars show ETS scores using initial values from downscaling of global analysis and from 3 km-scale 3DVar combined with cloud analysis,respectively;The ETS scores are averages based on 2400 rain-gauge observations over China;The red line box represents the 95% significance interval) |
集合数值天气预报是业务数值预报的重要组成部分,也是数值预报技术发展的趋势。研发GRAPES全球和区域集合预报系统是构建GRAPES业务体系的重要内容。
在GRAPES全球集合预报(GRAPES_GEPS)方面,构建了基于奇异向量(SV)初值扰动方法的全球集合预报系统。奇异向量是基于GRAPES切线和伴随模式通过定义特定权重模求得的在最优化时间间隔内增长最快的一组正交扰动。GRAPES全球奇异向量权重模定义为水平风分量(u, v)、扰动位温(θ′)、扰动无量纲气压(π′)的总能量模。通过考察GRAPES SV的总能量及其组成(动能和势能)的空间分布特征,验证了GRAPES全球奇异向量能够代表中高纬度对流层扰动的斜压不稳定增长特征(刘永柱等,2013),在求得的奇异向量基础上采用高斯取样构造全球集合预报初始扰动场(李晓莉等,2019a,2019b)。2018年基于奇异向量初值扰动方法的GRAPES全球集合预报实现了业务化(李晓莉等,2019b)。从2019年1—5月GRAPES_GEPS的预报表现(表7)可以看到,以500 hPa位势高度场距平相关系数0.6作为有效预报参考值,2019年1—5月,北半球集合平均预报有效预报8.62 d,而对照预报为7.56 d,提高1.06 d。南半球集合平均预报有效预报7.46 d,对照预报为6.94 d,提高0.52 d。这表明,通过集合预报,北半球和南半球500 hPa位势高度场的距平相关系数均有了明显提高。
| 北半球 | 南半球 | |||||
| 集合平均 | 对照预报 | 集合平均相对控制预报提高量 | 集合平均 | 对照预报 | 集合平均相对控制预报提高量 | |
| 8.620 | 7.557 | 1.062 | 7.459 | 6.936 | 0.523 | |
在GRAPES区域集合系统(GRAPES_REPS)方面,构建了基于集合变换卡尔曼滤波器(ETKF)初值扰动方法的区域集合预报系统(张涵斌等,2014)。ETKF由卡尔曼滤波同化技术发展而来,通过在观测空间计算变换矩阵,将预报扰动转换为分析扰动。在ETKF的基础上,进一步发展了多尺度混合初始扰动方法(MSB)(Zhang,et al,2015)。多尺度混合技术将区域集合预报系统中的中小尺度分量与全球集合预报系统中的大尺度分量相结合,产生多尺度混合初始扰动,可以明显改进区域集合预报的性能。为了减少集合预报平均误差,还开发了一种三维偏差校正方法(Wang J Z,et al,2018)。结果表明,集合预报的质量对模式系统性误差非常敏感。在积分过程中进行偏差订正可以有效地提高综合预测技术,减少集合预报误差。2019年建立了基于GRAPES_GEPS驱动的10 km区域集合预报业务流程,检验结果显示基于GRAPES_GEPS驱动的10 km区域集合预报效果优于T639集合预报驱动的15 km区域集合预报系统,2019年8月实现了业务应用。
针对集合预报中的模式不确定性,发展了多种随机物理扰动方法,如随机倾向项扰动(SPPT)、随机动能后向散射(SKEB)和随机参数扰动(SPP)方法来描述GRAPES全球和区域模式的物理过程不确定性。随机物理扰动方法的一个重点是如何构造随机场,GRAPES全球和区域集合预报的随机扰动方案随机场均基于具有时间相关特性和高斯分布的一阶马尔可夫过程(袁月等,2016)。SPPT方案在GRAPES区域集合预报的试验结果表明,该方案能显著提高暴雨预报效果。SPPT对GRAPES_REPS的影响也与随机扰动场的振幅和时间相关标度有关。在SKEB方案中,通过估计数值扩散引起的局部动能耗散率的不确定性,建立了随机流函数强迫来模拟局部动能耗散率。SKEB试验表明,大气动能谱的预测和GRAPES_GFS的误差扩散关系得到了改善,特别是在热带地区(彭飞等,2019)。降水预报具有很大的不确定性,为更好地描述与GRAPES模式降水预报密切相关的物理过程关键参数的不确定性,研究了随机参数扰动方案(徐致真等,2019),从对模式降水预报不确定性有较大影响的物理参数化方案中选取了18个关键参数,结果表明SPP方案能够有效地提高中尺度降水概率预报技巧,具有良好的业务应用与发展前景。
3.6 研发了全球云量预报方案Ma等(2018)基于Tiedtke云方案(Tiedtke,1993)的思想在GRAPES_GFS中建立了一个新的云量预报方案,该方案考虑了边界层湍流过程、积云对流卷出、大尺度层云凝结过程以及云与不饱和空气的水平湍流混合引起的蒸发过程等对云量生消的影响。利用物理基础更为扎实的云量预报方案在模式中合理地表述了全球不同区域云量产生的机制,对于中高纬度地区云量主要是由层云组成的,而低纬度地区的云量则是由积云和层云共同构成。同时,在将云量预报方案与GRAPES_GFS原有的将云量参数化为相对湿度和水凝物含量的诊断方案(Xu,et al,1996)对比中发现,云量预报方案能更好地模拟出海上层-积云的日变化特征、改正低云量和高云量显著偏小的问题。另外,其对总云量也有较明显的改进。云量的改进也间接提高了GRAPES_GFS模式的辐射计算精度,例如云量预报方案显著地减少了诊断方案由于模拟云量偏小引起的大气顶向外长波辐射偏大现象,其对模式的辐射加热率也有一定程度的改进。鉴于上述优点,新的云量预报方案已在GRAPES_GFS业务预报系统中应用。GRAPES_GFS中全球云量预报方案的具体内容可参考Ma等(2018)。
4 展 望到目前为止,建立了以GRAPES_GFS为核心的数值预报业务体系,实现了天气预报核心技术的全面自主研发。但必须清醒地认识到,与国际上主要数值天气预报业务中心相比,中国的全球预报能力尚有差距,而且在分辨率、卫星资料应用数量等业务配置指标上也同样存在差距。还缺乏陆面、积雪、海温、海冰等资料同化系统,尚不能实现完全的业务闭合。尤其是面向未来发展,还缺乏基于地球系统科学发展预报、预测技术和系统的研究基础与能力。因此,继续提高GRAPES的预报能力以满足中国精细化天气预报的需求是今后2—3年的首要任务,同时必须加快发展适应未来业务和数值预报技术发展需要的高精度可扩展数值预报技术和相应的全新支撑体系。需要在以下7个方面强化研发和组织工作,促进自主数值预报技术体系又好又快地发展。
(1)进一步发展GRAPES全球4DVar技术,实现集合预报信息在4DVar中的应用,提高同化分析的精度。
(2)发展先进的卫星资料同化技术。重点发展卫星变分质量控制、变分偏差订正技术,实现微波湿度计同化能力,并发展受地表影响的微波资料在GRAPES中的同化应用。
(3)发展陆面、积雪、海洋等资料分析同化技术,尽快实现自主业务体系的全链条闭合。
(4)继续改进GRAPES动力框架的计算精度、计算效率和可扩展性,并继续深入优化GRAPES模式物理过程,实现10—15 km分辨率全球预报和中国区域千米尺度快速循环系统的业务应用。
(5)为适应未来精细化和无缝隙天气预报、气候预测业务需求,以及未来异构众核高性能计算机发展的挑战,研发高精度可扩展守恒的大气模式新框架和尺度自适应物理过程,并逐步开展耦合数值预报技术的研究,迎接未来局地百米、全球千米级分辨率和耦合数值预报的发展挑战。
(6)加强部门内外的技术合作,共同突破技术瓶颈问题应对未来新科学技术的发展,实现气象预报、预测核心技术的自主可控和可持续发展。
(7)稳定、全技术链条的专业研发队伍来之不易,是中国未来天气预报核心科技自主可控和高水平发展的重要人才基础。强化对研发业务应用队伍建设的顶层设计、集中优势力量、稳定团队并提高研发和业务应用水平、持之以恒坚持既定技术路线和自主发展,对于保障气象事业高水平发展和提高国家气象基础科技实力至关重要,应该得到高度的重视。
致 谢:感谢韩威、苏勇、张林、李兴良、张华、孙健、陈静、刘永柱、朱立娟、王瑞春、王金成、黄丽萍、陈起英、马占山、麻素红、代刊、王雨等提供的素材和图表,其中陈静、韩威、马占山、王瑞春、张林、苏勇等撰写了部分材料,王金成、代刊、麻素红、王雨提供了部分图和表格。
巢纪平, 周晓平. 1964. 积云动力学. 北京: 科学出版社, 116pp. Chao J P, Zhou X P. 1964. Cumulus Dynamics. Beijing: Science Press, 116pp (in Chinese)
|
陈长胜, 纪立人, 陈嘉滨等. 2007. JFNK方法在求解全隐式一维非线性平流方程中的应用. 大气科学, 31(5): 963-972. DOI:10.3878/j.issn.1006-9895.2007.05.19 |
陈德辉, 薛纪善. 2004. 数值天气预报业务模式现状与展望. 气象学报, 62(5): 623-633. |
陈雄山, 刘瑞芝, 许有丰等. 1957. 强锋存在时天气发展两层模式预报的试验. 气象学报, 28(4): 275-281. |
丑纪范. 1974. 天气数值预报中使用过去资料的问题. 中国科学, 4(6): 635-644. Chou J F. 1974. A problem of using past data in numerical weather forecasting. Scintia Sinica, 17(6): 814-825
|
顾震潮, 巢纪平, 瞿章. 1957. 准地转两层模式天气数值预报方法的试验. 气象学报, 28(1): 41-62. |
顾震潮. 1958a. 作为初值问题的天气形势数值预报与由地面天气历史演变作预报的等值性. 气象学报, 29(2): 93-98. |
顾震潮. 1958b. 天气数值预报中过去资料的使用问题. 气象学报, 29(3): 176-184. |
顾震潮. 1959. 我国数值预报的成就. 气象学报, 30(3): 236-242. |
郭肖容, 张玉玲, 闫之辉等. 1995. 有限区分析预报系统及其业务应用. 气象学报, 53(3): 306-318. |
胡志晋, 邹光源. 1991. 大气非静力平衡模式和弹性适应. 中国科学: B辑, 21(5): 550-560. Hu Z J, Zou G Y. 1992. Atmospheric non-hydrostatic model and elastic adaptation. Sci China Ser B, 35(4): 463-475
|
黄丽萍, 陈德辉, 邓莲堂等. 2017. GRAPES_Meso V4. 0主要技术改进和预报效果检验. 应用气象学报, 28(1): 25-37. |
纪立人, 陈嘉滨, 张道民等. 2005. 数值预报模式动力框架发展的若干问题综述. 大气科学, 29(1): 120-130. DOI:10.3878/j.issn.1006-9895.2005.01.14 |
纪立人. 2011. 数值天气预报发展进程中若干亮点的回顾及其启迪. 气象科技进展, 1(1): 40-43. |
季仲贞. 1981. ARAKAWA格式非线性计算不稳定的例子. 气象学报, 39(2): 237-239. |
季仲贞, 曾庆存. 1982. 发展方程差分格式的构造和应用. 大气科学, 6(1): 88-94. DOI:10.3878/j.issn.1006-9895.1982.01.13 |
季仲贞, 王斌. 1991. 再论发展方程差分格式的构造和应用. 大气科学, 15(2): 1-10. DOI:10.3878/j.issn.1006-9895.1991.02.01 |
李晓莉, 陈静, 刘永柱等. 2019a. GRAPES全球集合预报初始条件及模式物理过程不确定性方法研究. 大气科学学报, 42(3): 348-359. |
李晓莉, 刘永柱. 2019b. GRAPES全球奇异向量方法改进及试验分析. 气象学报, 77(3): 552-562. |
李泽椿. 2010. 回顾数值预报业务的建立发展历程. 北京: 中国气象报社. Li Z C. 2010. Review of History of NWP Operation. Beijing: China Meteorological News (in Chinese)
|
廖洞贤. 1956. 简化的两个参变数模型的图解数值预报. 气象学报, 27(2): 153-166. |
刘瑞芝, 张济朋. 1965. 正压原始方程的一个数值试验. 气象学报, 37(1): 75-81. |
刘永柱, 沈学顺, 李晓莉. 2013. 基于总能量模的GRAPES全球模式奇异向量扰动研究. 气象学报, 71(3): 517-526. |
彭飞, 李晓莉, 陈静等. 2019. GRAPES全球集合预报系统模式扰动随机动能补偿方案初步探究. 气象学报, 77(2): 180-195. |
沈如桂, 牟惟丰. 1965. 中央气象局气象台48小时500毫巴数值预报图应用的初步经验. 气象学报, 37(4): 383-398. |
沈学顺, 韩威, 孙健等. 2009. GRAPES_GFS全球数值预报系统准业务化验收技术报告. 中国气象局数值模式创新基地, 150pp. Shen X S, Han W, Sun J, et al. 2009. Technical report for quasi-operation of GRAPES_GFS global numerical prediction system. Innovation base of Numerical Model of the China Meteorological Administration, 150pp (in Chinese)
|
沈学顺, 薛纪善, 纪立人等. 2010. 数值预报研究∥大气科学学科发展报告. 北京: 中国科学技术出版社, 149-160. Shen X S, Xue J S, Ji L R, et al. 2010. Numerical prediction research∥Report on Advances in Atmos-pheric Science. Beijing: China Science and Technology Press, 149-160 (in Chinese)
|
沈学顺, 王明欢, 肖锋. 2011. GRAPES模式中高精度正定保形物质平流方案的研究Ⅰ: 理论方案设计与理想试验. 气象学报, 69(1): 1-15. |
沈学顺, 周秀骥, 薛纪善等. 2013. GRAPES暴雨数值预报系统. 北京: 气象出版社, 186pp. Shen X S, Zhou X J, Xue J S, et al. 2013. GRAPES Numerical Prediction System for Heavy Rainfall. Beijing: China Meteorological Press, 186pp (in Chinese)
|
沈学顺, 王建捷. 2015. GRAPES_GFS技术报告. 中国气象局数值预报中心, 232pp. Shen X S, Wang J J. 2015. Technical Report of GRAPES_GFS. Center of Numerical Weather Prediction of CMA, 232pp (in Chinese)
|
沈学顺, 苏勇, 胡江林等. 2017. GRAPES_GFS全球中期预报系统的研发和业务化. 应用气象学报, 28(1): 1-10. DOI:10.11898/1001-7313.20170101 |
数值预报研究组. 1975. 近年来大气环流数值试验的进展∥中国科学院大气物理研究所. 近代气象学若干问题的进展. 北京: 科学出版社, 1-45. Numerical Prediction Research Team. 1975. Progress in atmospheric general circulation numerical experiment in recent years∥Institute of Atmospheric Physics, Chinese Academy of Sciences. Advances in Modern Meteorology. Beijing: Science Press, 1-45 (in Chinese)
|
苏从先. 1958. 层结大气中近地层湍流. 气象学报, 29(2): 73-82. |
苏从先. 1959. 关于总结大气中近地总湍流交换的基本规律性. 气象学报, 30(1): 114-118. |
苏勇, 沈学顺, 彭新东等. 2013. PRM标量平流方案在GRAPES全球预报系统中的应用. 大气科学, 37(6): 1309-1325. DOI:10.3878/j.issn.1006-9895.2013.12164 |
苏勇, 沈学顺, 陈子通等. 2018. GRAPES_GFS中三维参考大气的研究: 理论设计和理想试验. 气象学报, 76(2): 241-254. |
陶诗言, 赵思雄, 周晓平等. 2003. 天气学和天气预报的研究进展. 大气科学, 27(4): 451-467. DOI:10.3878/j.issn.1006-9895.2003.04.03 |
屠伟铭, 张跃堂. 1995. 全球最优插值客观分析. 气象学报, 53(2): 148-156. |
万晓敏, 田伟红, 韩威等. 2017. FY-2E云导风的算法改进及其在GRAPES中的同化应用研究. 气象, 43(1): 1-10. DOI:10.7519/j.issn.1000-0526.2017.01.001 |
万晓敏, 韩威, 田伟红等. 2018. 加密FY-2G云导风质量评估及其在GRAPES_RAFS系统中的应用分析. 高原气象, 37(4): 1083-1093. |
王斌, 季仲贞. 1990. 显式完全平方守恒差分格式的构造及其初步检验. 科学通报, (10): 766-768. Wang B, Ji Z Z. 1990. The construction and preliminary test of the explicit complete square conservative difference schemes. Chinese Sci Bull, 35(20): 1724-1728
|
王东海, 周晓平. 1996. 大气非静力数值模式中声波的阻尼和压缩. 热带气象学报, 12(3): 265-271. |
王皓. 2017. 静止卫星辐射率资料在GRAPES全球预报系统的同化应用研究. 成都: 成都信息工程大学. Wang H. 2017. Assimilation and application of geostationary satellite emissivity data in GRAPES global prediction system. Chengdu: Chengdu University of Information Engi-neering (in Chinese)
|
王金成, 龚建东, 王瑞春. 2016. GRAPES全球三维变分同化中卫星微波温度计亮温的背景误差及在质量控制中的应用. 气象学报, 74(3): 379-406. |
吴洋, 徐枝芳, 王瑞春等. 2018. 基于多尺度混合滤波的GRAPES_3Dvar及其在实际暴雨预报中的应用分析. 气象, 44(5): 621-633. DOI:10.7519/j.issn.1000-0526.2018.05.003 |
徐尔灏. 1959. 十年来我国对动力气象的研究. 气象学报, 30(3): 243-250. |
徐致真, 陈静, 王勇等. 2019. 中尺度降水集合预报随机参数扰动方法敏感性试验. 气象学报, 77(5): 849-868. |
薛纪善, 李璨玑, 王志明. 1992. 非线性正规模初值化原则在有限区模式的实现. 大气科学, 16(6): 686-697. DOI:10.3878/j.issn.1006-9895.1992.06.06 |
薛纪善, 陈德辉. 2008. 数值预报系统GRAPES的科学设计与应用. 北京: 科学出版社, 383pp. Xue J S, Chen D H. 2008. Scientific Design and Application of GRAPES Numerical Prediction System. Beijing: Science Press, 383pp (in Chinese)
|
薛纪善, 刘艳, 张林等. 2012. GRAPES全球三维变分同化系统模式变量分析版. 中国气象局数值预报中心技术文档. Xue J S, Liu Y, Zhang L, et al. 2012. Version of global 3DVar system at model space. Documentation of Numerical Weather Prediction Center of CMA (in Chinese)
|
颜宏. 1987. 复杂地形条件下嵌套细网格模式的设计: (一)数值模式的基本原理. 高原气象, 6(S1): 1-63. |
叶笃正. 1963. 动力气象学论文集(二). 北京: 科学出版社, 133-152. Ye D Z. 1963. Collected Papers of Dynamic Meteorology (2). Beijing: Science Press, 133-152 (in Chinese)
|
尹若莹, 韩威, 高志球等. 2019. 基于FY-4A卫星探测区域模式背景误差和观测误差估计的长波红外通道选择研究. 气象学报, 77(5): 898-910. |
宇如聪, 曾庆存, 彭贵康等. 1994. “雅安天漏”研究Ⅱ: 数值预报试验. 大气科学, 18(5): 535-551. DOI:10.3878/j.issn.1006-9895.1994.05.04 |
宇如聪, 薛纪善, 徐幼平等. 2004. AREMS中尺度暴雨数值预报模式系统. 北京: 气象出版社, 233pp. Yu R C, Xue J S, Xu Y P, et al. 2004. AREM Meso-Scale Numerical Prediction Modeling System for Heavy Rainfall. Beijing: China Meteorological Press, 233pp (in Chinese)
|
袁月, 李晓莉, 陈静等. 2016. GRAPES区域集合预报系统模式不确定性的随机扰动技术研究. 气象, 42(10): 1161-1175. DOI:10.7519/j.issn.1000-0526.2016.10.001 |
曾庆存. 1963a. 二层模式的完整流体力学热力学方程组在短期天气预报中的应用∥动力气象学论文集(二). 北京: 科学出版社, 133-152. Zeng Q C. 1963a. Application of a Two-Layer Model of Full Fluid Dynamic and Thermo-Dynamic Equations in the Short-Term Weather Prediction∥Collected Papers of Dynamic Meteorology (2). Beijing: Science Press, 133-152 (in Chinese)
|
曾庆存. 1963b. 大气运动的特征参数和动力学方程. 气象学报, 33(4): 472-483. |
曾庆存. 1963c. 大气中的适应过程和发展过程(一): 物理分析和线性理論. 气象学报, 33(2): 163-174. |
曾庆存. 1978. 计算稳定性的若干问题. 大气科学, 2(3): 181-191. DOI:10.3878/j.issn.1006-9895.1978.03.01 |
曾庆存. 1979. 数值天气预报的数学物理基础: 第一卷. 北京: 科学出版社, 543pp. Zeng Q C. 1979. Mathematical and Physical Basis of Numerical Weather Prediction(Vol. 1). Beijing: Science Press, 543pp (in Chinese)
|
曾庆存, 季仲贞. 1981. 发展方程的计算稳定性问题. 计算数学, (1): 79-86. |
曾庆存, 袁重光, 张学洪等. 1985. 一个大气环流模式差分格式的检验. 气象学报, 43(4): 441-449. |
曾庆存. 2013. 天气预报: 由经验到物理数学理论和超级计算. 物理, 42(5): 300-314. |
张涵斌, 陈静, 智协飞等. 2014. GRAPES区域集合预报系统应用研究. 气象, 40(9): 1076-1087. DOI:10.7519/j.issn.1000-0526.2014.09.005 |
赵九章. 1959. 十年来中国气象学研究的进展. 气象学报, 30(3): 206-211. |
郑庆林. 1980. 北半球七层初始方程波谱模式∥第二次全国数值天气预报会议论文集. 北京: 科学出版社, 13-24. Zheng Q L. 1980. A 7-level spectral model of primitive equations for the Northern Hemis-phere∥Proceedings of the 2nd Meeting of the All China Numerical Weather Prediction. Beijing: Science Press, 13-24 (in Chinese)
|
郑庆林. 1989. 北半球七层原始方程谱模式(三)及其五天中期数值预报试验. 气象科学研究院院刊, 4(1): 3-4. |
钟青. 1992. 论发展问题保真计算格式的一般构造原理和若干应用. 计算物理, 9(4): 758-764. |
钟青. 1993. 长效、经济的发展问题保真计算格式反演补偿. 科学通报, 38(12): 1101-1105. DOI:10.1360/csb1993-38-12-1101 |
中央气象局数值预报组. 1965. 我国的数值预报业务工作. 科学通报, 16(2): 131-133. DOI:10.1360/csb1965-10-2-131 |
周秀骥. 1963. 暖云降水微观物理机制的统计理论. 气象学报, 33(1): 97-107. |
朱立娟, 龚建东, 黄丽萍等. 2017. GRAPES三维云初始场形成及在短临预报中的应用. 应用气象学报, 28(1): 38-51. DOI:10.11898/1001-7313.20170104 |
朱永禔. 1961. 球坐标三层模式的一个非线性预报. 气象学报, 31(3): 216-233. |
朱永禔. 1962. 斜压大气中地形扰动过程的一个数值试验. 气象学报, 32(1): 37-43. |
朱永禔, 殷鹤宝. 1987. 五层原始方程模式套网格台风路径预报方案∥1985年台风会议文集. 北京: 气象出版社, 253-262. Zhu Y T, Yin H B. 1987. A scheme for predicting typhoon track by using 5-layer primitive equation model with nesting grids∥Proceeding of Typhoon Meeting in 1985. Beijing: China Meteorological Press, 253-262 (in Chinese)
|
朱宗申, 汪厚君, 张跃堂. 1992. 国家气象中心准业务有限区客观分析方案. 应用气象学报, 3(4): 459-467. |
Arakawa A. 1966. Computational design for long-term numerical integration of the equations of fluid motion: Two-dimensional incompressible flow. Part I. J Comput Phys, 1(1): 119-143. DOI:10.1016/0021-9991(66)90015-5 |
Arakawa A. 1972. Design of the UCLA General Circulation Model. Los Angeles: University of California
|
Bannister R N. 2017. A review of operational methods of variational and ensemble-variational data assimilation. Quart J Roy Meteor Soc, 143(703): 607-633. DOI:10.1002/qj.2982 |
Bauer P, Thorpe A, Brunet G. 2015. The quiet revolution of numerical weather prediction. Nature, 525(7567): 47-55. DOI:10.1038/nature14956 |
Benjamin S G, Brown J M, Brunet G, et al. 2019. 100 years of progress in forecasting and NWP applications. Meteor Monogr, 2.1-2.5
|
Bermejo R, Staniforth A. 1992. The conversion of semi-Lagrangian advection schemes to quasi-monotone schemes. Mon Wea Rev, 120(11): 2622-2632. DOI:10.1175/1520-0493(1992)120<2622:TCOSLA>2.0.CO;2 |
Bermejo R, Conde J. 2002. A conservative quasi-monotone semi-Lagrangian scheme. Mon Wea Rev, 130(2): 423-430. DOI:10.1175/1520-0493(2002)130<0423:ACQMSL>2.0.CO;2 |
Blumen W, Washington W M. 1973. Atmospheric dynamics and numerical weather prediction in the People's Republic of China 1949-1966. Bull Amer Meteor Soc, 54(6): 502-518. DOI:10.1175/1520-0477(1973)054<0502:ADANWP>2.0.CO;2 |
Bonavita M, Trémolet Y, Hólm E, et al. 2017. A strategy for data assimilation. ECMWF
|
Chen C G, Li X L, Shen X S, et al. 2014. Global shallow water models based on multi-moment constrained finite volume method and three quasi-uniform spherical grids. J Comput Phys, 271: 191-223. DOI:10.1016/j.jcp.2013.10.026 |
Côté J, Gravel S, Méthot A, et al. 1998. The operational CMC-MRB Global Environmental Multiscale (GEM) model. Part Ⅰ: Design considerations and formulation. Mon Wea Rev, 126(6): 1373-1395. DOI:10.1175/1520-0493(1998)126<1373:TOCMGE>2.0.CO;2 |
Di D, Li J, Han W, et al. 2018. Enhancing the fast radiative transfer model for FengYun-4 GIIRS by using local training profiles. J Geophys Res Atmos, 123(22): 12583-12596. DOI:10.1029/2018JD029089 |
Diamantakis M, Flemming J. 2014. Global mass fixer algorithms for conservative tracer transport in the ECMWF model. Geosci Model Dev, 7(3): 965-979. DOI:10.5194/gmd-7-965-2014 |
ECMWF. 2018a. Implementation of IFS cycle 45r1. https://confluence.ecmwf.int/display/FCST/Implementation+of+IFS+cycle+45r1
|
ECMWF. 2018b. C3S global reanalysis-variational bias correction for ERA6. https://climate.copernicus.eu/sites/default/files/2018-04/ECMWF_C3S_321a_Volume_II_final.pdf
|
Eyre J R. 2007. Progress achieved on assimilation of satellite data in numerical weather prediction over the last 30 years∥ECMWF Seminar on Recent Development in the Use of Satellite Observations in NWP. UK: ECMWF
|
Gospodinov I G, Spiridonov V G, Geleyn J F. 2001. Second-order accuracy of two-time-level semi-Lagrangian schemes. Quart J Roy Meteor Soc, 127(573): 1017-1033. DOI:10.1002/qj.49712757317 |
Gustafsson N, Janjić T, Schraff C, et al. 2018. Survey of data assimilation methods for convective-scale numerical weather prediction at operational centres. Quart J Roy Meteor Soc, 144(713): 1218-1256. DOI:10.1002/qj.3179 |
Han W, Xue J S, Xu J M, et al. 2006. Assimilation of FY-2C AMV in GRAPES∥The Eighth International Winds Workshop. Beijing, China
|
Han W, Shen X, Zhuang Z, et al. 2010. The use of satellite data in Chinese new GFS∥ITSC-XVII Conference. Monterey, CA, USA
|
Han W. 2014. Constrained variational bias correction for satellite radiance assimilation∥Proceedings of the 19th International TOVS Study Confe-rence. Jeju Island, South Korea
|
Han W, Bormann N. 2016. Constrained adaptive bias correction for satellite radiance assimilation in the ECMWF 4D-Var system. ECMWF Technical Memorandum, 783. ECMWF
|
Huang W, Bao J W, Zhang X, et al. 2018. Comparison of the vertical distributions of cloud properties from idealized extratropical deep convection simulations using various horizontal resolutions. Mon Wea Rev, 146(3): 833-851. DOI:10.1175/MWR-D-17-0162.1 |
Kalnay E. 2003. Atmospheric Modeling, Data Assimilation, and Predictability. Cambridge: Cambridge University Press, 341pp
|
Kwon I H, English S, Bell W, et al. 2018. Assessment of progress and status of data assimilation in numerical weather prediction. Bull Amer Meteor Soc, 99(5): ES75-ES79. DOI:10.1175/BAMS-D-17-0266.1 |
Lauritzen P H, Nair R D, Ullrich P A. 2010. A conservative semi-Lagrangian multi-tracer transport scheme (CSLAM)on the cubed-sphere grid. J Comput Phys, 229(5): 1401-1424. DOI:10.1016/j.jcp.2009.10.036 |
Li J, Zou X L. 2014. Impact of FY-3A MWTS radiances on prediction in GRAPES with comparison of two quality control schemes. Front Earth Sci, 8(2): 251-263. DOI:10.1007/s11707-014-0405-3 |
Li J, Liu G Q. 2016. Direct assimilation of Chinese FY-3C Microwave Temperature Sounder-2 radiances in the global GRAPES system. Atmos Meas Tech, 9(7): 3095-3113. DOI:10.5194/amt-9-3095-2016 |
Li X L, Chen C G, Shen X S, et al. 2013. A multimoment constrained finite-volume model for nonhydrostatic atmospheric dynamics. Mon Wea Rev, 141(4): 1216-1240. DOI:10.1175/MWR-D-12-00144.1 |
Lilly D K. 1961. A proposed staggered-grid system for numerical integration of dynamic equation. Mon Wea Rev, 89(3): 59-65. DOI:10.1175/1520-0493(1961)089<0059:APSSFN>2.0.CO;2 |
Liu Y, Xue J S. 2014. Assimilation of global navigation satellite radio occultation observations in GRAPES: Operational implementation. J Meteor Res, 28(6): 1061-1074. DOI:10.1007/s13351-014-4028-0 |
Liu Y Z, Zhang L, Lian Z H. 2018. Conjugate gradient algorithm in the four-dimensional variational data assimilation system in GRAPES. J Meteor Res, 32(6): 974-984. DOI:10.1007/s13351-018-8053-2 |
Ma Z S, Liu Q J, Zhao C F, et al. 2018. Application and evaluation of an explicit prognostic cloud-cover scheme in GRAPES global forecast system. J Adv Model Earth Syst, 10(3): 652-667. DOI:10.1002/2017MS001234 |
Magnusson L, Källen E. 2013. Factors influencing skill improvements in the ECMWF forecasting system. Mon Wea Rev, 141(9): 3142-3153. DOI:10.1175/MWR-D-12-00318.1 |
Mengaldo G, Wyszogrodzki A, Diamantakis M, et al. 2019. Current and emerging time-integration strategies in global numerical weather and climate prediction. Arch Comput Methods Eng, 26(3): 663-684. DOI:10.1007/s11831-018-9261-8 |
Mesinger F. 1984. A blocking technique for representation of mountains in atmospheric models. Riv Meteor Aeronaut, 44: 195-202. |
Mu M, Duan W S, Wang B. 2003. Conditional nonlinear optimal perturbation and its applications. Nonlin Processes Geophys, 10(6): 493-501. DOI:10.5194/npg-10-493-2003 |
Mu M, Duan W, Wang Q, et al. 2010. An extension of conditional nonlinear optimal perturbation approach and its applications. Nonlin Processes Geophys, 17(2): 211-220. DOI:10.5194/npg-17-211-2010 |
Rabier F, Järvinen H, Klinker E, et al. 2000. The ECMWF operational implementation of four dimensional variational assimilation. Ⅰ: Experi-mental results with simplified physics. Quart J Roy Meteor Soc, 126(564): 1143-1170. |
Ritchie H, Tanguay M. 1996. A comparison of spatially averaged eulerian and semi-Lagrangian treatments of mountains. Mon Wea Rev, 124(1): 167-181. DOI:10.1175/1520-0493(1996)124<0167:ACOSAE>2.0.CO;2 |
Robert A. 1969. The integration of a spectral model of the atmosphere by the implicit method∥Proceedings of WMO/IUGG Symposium on Numerical Weather Prediction. Ote-machi, Chiyoda-ku, Tokyo, Japan: Meteorolo-gical Agency
|
Robert A, Yee T L, Ritchie H. 1985. A semi-Lagrangian and semi-implicit numerical integration scheme for multilevel atmospheric models. Mon Wea Rev, 113(3): 388-394. DOI:10.1175/1520-0493(1985)113<0388:ASLASI>2.0.CO;2 |
Simmons A J, Chen J B. 1991. The calculation of geopotential and the pressure gradient in the ECMWF atmospheric model: Influence on the simulation of the polar atmosphere and on temperature analyses. Quart J Roy Meteor Soc, 117(497): 29-58. DOI:10.1002/qj.49711749703 |
Simmons A J, Temperton C. 1997. Stability of a two-time-level semi-implicit integration scheme for gravity wave motion. Mon Wea Rev, 125(4): 600-615. DOI:10.1175/1520-0493(1997)125<0600:SOATTL>2.0.CO;2 |
Smolarkiewicz P K, Szmelter J, Xiao F. 2016. Simulation of all-scale atmospheric dynamics on unstructured meshes. J Comput Phys, 322: 267-287. DOI:10.1016/j.jcp.2016.06.048 |
Temperton C, Hortal M, Simmons A. 2001. A two-time-level semi-Lagrangian global spectral model. Quart J Roy Meteor Soc, 127(571): 111-127. DOI:10.1002/qj.49712757107 |
Tian X J, Zhang H Q, Feng X B, et al. 2018. Nonlinear least squares En4DVar to 4DEnVar methods for data assimilation: Formulation, analysis, and preliminary evaluation. Mon Wea Rev, 146(1): 77-93. DOI:10.1175/MWR-D-17-0050.1 |
Tiedtke M. 1993. Representation of clouds in large-scale models. Mon Wea Rev, 121(11): 3040-3061. DOI:10.1175/1520-0493(1993)121<3040:ROCILS>2.0.CO;2 |
Wang B, Wan H, Ji Z Z, et al. 2004. Design of a new dynamical core for global atmospheric models based on some efficient numerical methods. Sci China Ser A Math, 47(7): 4-21. DOI:10.1360/04za0001 |
Wang B, Liu J J, Wang S D, et al. 2010. An economical approach to four-dimensional variational data assimilation. Adv Atmos Sci, 27(4): 715-727. DOI:10.1007/s00376-009-9122-3 |
Wang J, Gong J, Han W, et al. 2020. The assimilation of FY-3C GNOS GPS radio occultation observations within GRAPES 3D-Var: Assimilation experiments and forecast impact. (in press)
|
Wang J Z, Chen J, Du J, et al. 2018. Sensitivity of ensemble forecast verification to model bias. Mon Wea Rev, 146(3): 781-796. DOI:10.1175/MWR-D-17-0223.1 |
Wang R C, Zhuang Z, Xu Z, et al. 2018. Development of km-scale 3DVAR for GRAPES-Meso∥Technical Documentation for the 4th SSC Meeting, Numerical Weather Prediction Center of CMA(available from NWPC)
|
Xu K M, Randall D A. 1996. A semiempirical cloudiness parameterization for use in climate models. J Atmos Sci, 53(21): 3084-3102. DOI:10.1175/1520-0469(1996)053<3084:ASCPFU>2.0.CO;2 |
Xue J S, Wang K L, Wang Z M, et al. 1988. Test of a tropical limited area numerical prediction model including effect of real topography. Adv Atmos Sci, 5(1): 1-13. DOI:10.1007/BF02657341 |
Yang J, Zhang Z Q, Wei C Y, et al. 2017. Introducing the new generation of Chinese geostationary weather satellites, Fengyun-4. Bull Amer Meteor Soc, 98(8): 1637-1658. DOI:10.1175/BAMS-D-16-0065.1 |
Yang M J, Gong J D, Wang R C, et al. 2019. A comparison of the blending and constraining methods to introduce large-scale information into GRAPES mesoscale analysis. J Trop Meteor, 25(2): 227-244. |
Yin R Y, Han W, Gao Z Q. 2020. The evaluation of FY4A's Geostationary Interferometric Infrared Sounder (GIIRS)long-wave temperature sound-ing channels using the GRAPES global 4D-Var. Quart J Roy Meteor Soc.146:1459-1476.
|
Zeng Q T. 1961. The application of a complete system of thermo-hydro-dynamic equations to short-term weather forecast in a two-level model. Dokl Akad Nauk SSSR, 137(1): 76-78. |
Zerroukat M, Wood N, Staniforth A. 2004. SLICE-S: A semi-Lagrangian inherently conserving and efficient scheme for transport problems on the Sphere. Quart J Roy Meteor Soc, 130(602): 2649-2664. DOI:10.1256/qj.03.200 |
Zerroukat M, Wood N, Staniforth A, et al. 2009. An inherently mass-conserving semi-implicit semi-Lagrangian discretisation of the shallow-water equations on the sphere. Quart J Roy Meteor Soc, 135(642): 1104-1116. DOI:10.1002/qj.458 |
Zhang H, Xue J S, Zhu G F, et al. 2004. Application of direct assimilation of ATOVS microwave radiances to typhoon track prediction. Adv Atmos Sci, 21(2): 283-290. DOI:10.1007/BF02915715 |
Zhang H B, Chen J, Zhi X F, et al. 2015. Study on multi-scale blending initial condition perturbations for a regional ensemble prediction system. Adv Atmos Sci, 32(8): 1143-1155. DOI:10.1007/s00376-015-4232-6 |
Zhang L, Liu Y Z, Liu Y, et al. 2019. The operational global four-dimensional variational data assimilation system at the China Meteorological Admi-nistration. Quart J Roy Meteor Soc, 145(722): 1882-1896. DOI:10.1002/qj.3533 |
Zhang X, Bao J W, Chen B D, et al. 2018. A three-dimensional scale-adaptive turbulent kinetic energy scheme in the WRF-ARW model. Mon Wea Rev, 146(7): 2023-2045. DOI:10.1175/MWR-D-17-0356.1 |
 2020, Vol. 78
2020, Vol. 78


