中国气象学会主办。
文章信息
- 刘凑华, 曹勇, 符娇兰. 2013.
- LIU Couhua, CAO Yong, FU Jiaolan. 2013.
- 基于变分法的客观分析算法及应用
- An objective analysis algorithm based on the variational method
- 气象学报, 71(6): 1172-1182
- Acta Meteorologica Sinica, 71(6): 1172-1182.
- http://dx.doi.org/10.11676/qxxb2013.091
-
文章历史
- 收稿日期:2012-09-12
- 改回日期:2013-07-16
客观分析是将不规则分布的观测资料转换到规则网格上的过程,其最初目的是为数值模式提供初始场。因为起初的数值模式是有限差分模式,它的空间定义域是规则的网格区域(王跃山,2000)。经过几十年的发展,客观分析方法已由最初的基于多项式插值(Panofsky,1949; Gilchrist et al,1954;刘克武,1981,1982)、逐步订正法(Bergthorsson et al,1955;Cressman,1959)、统计插值(徐一鸣等,1989)和最优插值(屠伟铭,1994)等方法发展到今天数值模式初值构建时采用的3维同化(3DVAR)、4维同化(4DAVR)和集合卡尔曼滤波等方法(Kalnay,2003;Lorenc,1986;Zupanski,1993; Bouttier et al,1997),越来越多的信息正被考虑进来以提高分析结果的准确性。在对一些缺乏动力约束的物理量(如降水等)进行客观分析时,目前常用的方法还是多项式插值、反距离权重、克里金插值等方法(Karnieli,1990; 邬伦等,2010;高歌等,2007;靳国栋等,2003)。现有的客观分析方法大都只须考虑分析结果的准确性,因为其结果常用作其他计算的输入场,例如4DVAR的分析结果会被用作模式的初始场,降水量的客观分析结果被用作水文预报模型的输入场等。
客观分析的格点结果的另一个重要用途是以图形方式输出,供分析人员或决策者使用,还以降水为例,业务气象台站要将离散的降水观测分析成规则的格点场,以绘制二维的降水分布图。当客观分析用于图形显示时,应用者希望其结果能够既准确又平滑。之所以要求平滑,其本质上是追求信息量的最小化,以便应用者更容易把握物理量的主要分布特征。目前,针对图形显示用途,兼顾准确性和平滑性的客观分析方法很少见,实际业务中通常将反距离权重和Cressman插值等方法用作图形显示的客观分析方法(冯旭明,2001;于连庆等,2012),由于这些方法的分析结果通常很不平滑,一般会在插值后采用九点平滑等方法对格点场进行平滑,然而平滑操作又会让准确性降低。平滑性和准确性的矛盾常常使得分析者很难获得满意的结果。为此有必要发展一类直接针对图像显示的客观分析方法,此即本研究的方向。
在发展一种方法之前,人们首先要清楚它的目标是什么?本研究将要提出的客观分析方法目的是用于图形显示,其目标是给出既准确又平滑的分析场。此处“既准确又平滑”成为衡量分析场优劣的标准,它实际上是关于分析场的泛函数,而该泛函数的最小值函数必定最大程度地满足“既准确又平滑”。由此,本研究提出基于变分法的客观分析方法,其基本思路是将客观分析的目标表达成格点场的泛函数,然后利用数值方法求解泛函数最小值对应的格点场,从而得到最优的分析结果。2 算法原理
变分法是用于求解泛函数极值和极值函数的方法。在进行客观分析时,人们总是希望分析场最大程度地满足特定的要求,而这种要求实际上是关于分析场的一个泛函数,若能将其表达成具体的数学形式,即可借助变分法求解客观分析的问题。
本研究关注的客观分析的目标是求解准确度和平滑度最大化的格点场。为讨论方便,将与准确度相反的度量称为失真度,将与平滑度相反的度量称为粗糙度,客观分析的目标亦可表述为求解失真度和粗糙度最小化的格点场。所谓失真度和粗糙度也都是关于整个物理量场的泛函数,它们的总和可表示成
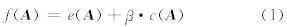
应用变分方法进行客观分析,首先要定义失真度和粗糙度。由于真实场是无法得知的(否则就不需要插值或客观分析),因此,失真度必须通过计算分析场A偏离已知物理量的程度来获得。已知物理量包括离散站点的观测记录和已知的定量物理规律。在只有观测记录的情况下,失真度可定义成分析场偏离所有观测记录的程度,此时失真度可表达成
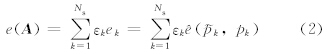
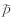 k分别为第k个站点位置的观测值和分析值。由于格点位置通常和站点位置不一致,因此,
k分别为第k个站点位置的观测值和分析值。由于格点位置通常和站点位置不一致,因此,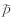 k需要由站点附近的格点值反插得到。格点向站点的反插可以采用线性插值或其他高次函数插值方法,在格点分布密度明显高于站点分布密度的情况下,反插方法的选择对反插结果影响甚微,为了计算方便,一般采用线性方法反插即可。ê(
k需要由站点附近的格点值反插得到。格点向站点的反插可以采用线性插值或其他高次函数插值方法,在格点分布密度明显高于站点分布密度的情况下,反插方法的选择对反插结果影响甚微,为了计算方便,一般采用线性方法反插即可。ê(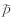 k,pk)是度量单个站点失真度的函数,其作用是将分析值
k,pk)是度量单个站点失真度的函数,其作用是将分析值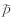 k约束在观测值pk附近,从而使站点附近的格点值和站点观测值接近。根据不同的应用要求,失真度ê(
k约束在观测值pk附近,从而使站点附近的格点值和站点观测值接近。根据不同的应用要求,失真度ê(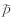 k,pk)可以有不同的形式,若分析目标是均方根误差最小,则ê(
k,pk)可以有不同的形式,若分析目标是均方根误差最小,则ê(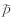 k,pk)=(
k,pk)=(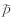 k-pk)2。而在有些问题中,物理量被分成不同等级,人们关心的是分析值
k-pk)2。而在有些问题中,物理量被分成不同等级,人们关心的是分析值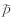 k和观测值pk的等级误差,则ê(
k和观测值pk的等级误差,则ê(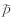 k,pk)应在这两者存在等级差别时取值较大,具体的函数形式参见第4节。总而言之,失真度并没有固定的形式,而是根据实际问题进行设定。2.2 粗糙度的定义
k,pk)应在这两者存在等级差别时取值较大,具体的函数形式参见第4节。总而言之,失真度并没有固定的形式,而是根据实际问题进行设定。2.2 粗糙度的定义当一维分析场的分布曲线完全呈直线或者二维分析场的分布曲面完全呈平面,可以认定此分析场是完全平滑的,此时粗糙度为0。若以此作为平滑的标准,将分析场中相邻格点取值分布偏离线性的程度作为不平滑的程度,则粗糙度可以由格点场的二阶差分来度量,对于一维情况粗糙度可表示为

二维情况下粗糙度可表示为
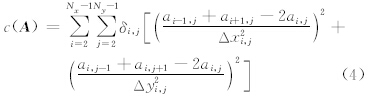
然而,在另一些问题中人们并不以分析场呈完全的线性分布作为绝对平滑的参考标准。例如,在地质物理量的客观分析问题中,分析区域内沿某一条曲线上可能存在断层,物理量分布在曲线的两侧可以存在不连续。虽然该曲线附近格点场的二阶差分非常大,但它不应该被考虑成不平滑的因素而进行惩罚,此时可以通过将这些格点的粗糙度权重δi,j设置为0来体现这种特殊的应用要求。再例如,在气压场的客观分析问题中,大尺度气旋和反气旋是平滑的成分,但这些系统的气压场分布曲面不是平面,若采用式(4)定义粗糙度,其约束作用会使气压场分布向平面靠近,从而损害了气旋和反气旋的中心强度。分析发现这些系统的分布曲面与抛物面较吻合,故可用抛物面作为其平滑的参考标准,定义其粗糙度为0,在这种标准下,粗糙度是以格点场的三阶差分来度量的。
综上所述,粗糙度也没有固定的表达形式,其函数形式和各项参数都可以根据实际问题进行设定。2.3 失真度和粗糙度的相对权重
式(1)中β是用来调节失真度和粗糙度的比重,β的大小决定了最终分析结果是偏向准确还是偏向平滑,β越大,分析结果越偏向平滑,可称之为平滑系数。具体应用时,可以通过调节平滑系数控制最终分析结果的平滑程度。2.4 变分法客观分析的最优性
要保证变分法求得的目标函数f(A)的极小值等于其最小值,需保证f(A)只有一个极小值,f(A)是严格的下凸函数时,这一点可以得到保证。为使f(A)是严格下凸函数,失真度e(A)和粗糙度c(A)也应该设计成下凸函数,且其中至少有一个是严格下凸函数。
在一个具体问题中,当网格、失真度、粗糙度和权重系数β确定下来之后,其对应的最优分析场Am也就确定了。若存在一个分析场A1≠Am,满足e(A1)=e(Am),则根据f(A1)>f(Am)和式(1)必然可得c(A1)>c(Am),即变分法的客观分析结果在相同准确度的条件下必定比其他方法的分析结果更平滑,而在平滑度相同时,它比其他结果更准确。因此,将应用中对平滑性和准确性的要求合理地表达成粗糙度和失真度函数,采用变分方法进行客观分析可以保证分析结果的最优性。
然而,上述最优性不是绝对的,因为如果不能保证粗糙度和失真度函数设计合理,也就无法保证其分析结果的最优性。而目标函数的合理性最终还是要通过判断Am是否让应用者满意来检验。Am是由目标函数唯一决定的,应用者对Am满意,就说明目标函数设计是合理的或者满足要求的。如果应用者对Am不满意,则说明应用者的要求并未完整地被考虑到目标函数的设计当中,此时可逐步改进目标函数的设计以更加完整的包含应用需求,最终使得客观分析的结果达到令人满意的程度。3 理想计算分析
本研究先以一维插值为例讨论变分方法的具体实现。设有一组离散的站点观测资料O={(xk,pk)|k=1,2,…,Ns,xk∈R,pk∈R},xk和pk分别代表第k个站点的位置和观测值,Ns是站点数。基于这个观测,插值计算一组等间距(格距记为d)分布的格点上的值A={(i,ai)|i=0,1,2,…,N,ai∈R},N+1为总格点数。采用分析值和观测值之差的平方和作为失真度,结合2.1节的讨论,给出失真度的具体形式为
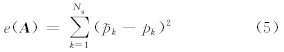
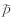 k是根据格点场线性插值到站点得到的估计值
k是根据格点场线性插值到站点得到的估计值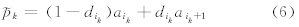
 是第k个站点的左侧最邻近的一个格点编号,dik=
是第k个站点的左侧最邻近的一个格点编号,dik=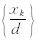 是第k个站点到第ik个格点的距离与格距之比。
是第k个站点到第ik个格点的距离与格距之比。采用格点场二阶差分的大小作为粗糙度,结合2.2节的讨论,给出粗糙度的形式为
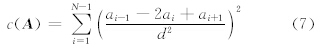

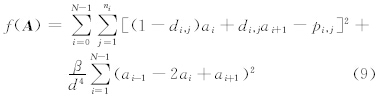
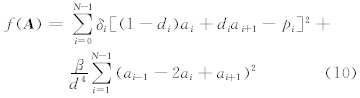

为说明数值解的结果同解析解的一致性,以一个具体的例子对比这两种结果。图 1给出了一个计算实例,图 1中点线是一个正弦函数,作为真实的分布曲线,圆圈为10个带有一定误差的站点观测值,站点的分布并不均匀。实际工作中能得到的只有观测值,而观测值背后对应的真实场是未知的,因此,图 1中显示的真实函数并不具有确切的代表意义,只是在本研究的实验中观测值是以它作为真实场来扰动的。根据10个观测值在区
域[0,100]内进行客观分析,格距取为4,β取为16。图 1表明,数值解和解析解基本一致,两者微小的差别主要是式(11)的计算误差导致的。为此,下文中的试验结果都采用共轭梯度法进行数值求解。
 |
| 图 1 一次试验中的一维变分法客观分析的解析解和数值解 (细实线:真实函数,圆圈:观测值序列,粗实线:变分法客观分析的解析解,×线:变分法客观分析的数值解,带点实线:两种解之差) Fig. 1 Analytical solution and numerical solution from the variational objective analysis in a test (thin line is true function,circles are observations,thick line is the analytical solution from the variational objective analysis,×-line is the numerical solution from the variational objective analysis and line with dot is their difference) |
根据第2节的讨论,基于变分法的客观分析结果最终决定于目标函数的设计。若客观分析结果对目标函数中具体的算子选择和函数参数过于敏感,则很难得到稳定的分析效果。以第3节的客观分析问题为例讨论分析结果对参数的敏感性,在这一类问题中影响目标函数的因素包括格点反插站点的算子、网格(主要是格距)选取和平滑系数β的取值。
目标函数失真度的计算过程中需将格点反插到站点,反插的方法既可以用线性插值,也可以用三次插值或其他插值方法,第2节的分析指出,在网格分布比站点密度大时,反插导致的误差很小,对最终结果影响不大。本研究将线性反插和三次多项式反插分别用于失真度函数的构造中,目标函数的其他部分设置相同,通过试验对比两者最终结果的差异(图 2)。图 2表明两种结果差别确实很小,由此说明变分法客观分析对失真度函数构建时的反插算法并不敏感。
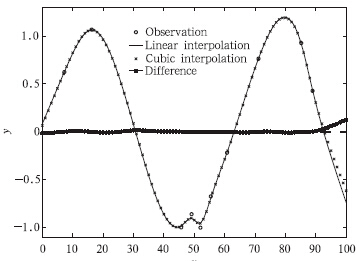 |
| 图 2 失真度函数中的反插算法采用线性插值(实线)和三次多项式插值(×线)时分别对应的客观分析结果以及两者之差(带点实线),圆圈为观测 Fig. 2 Corresponding objective analysis results of different distortion degrees with linear and cubic as reverse interpolation(solid line and ×-line,respectively) and their difference(line with dot),circles are observations |
变分法客观分析的结果不是分布在整个实数域,而是直接分析在网格上,从式(8)可以看出,网格的选择也可能会影响到最终的结果。若网格的格距大于站点间的距离,则必定会有些观测中包含的波动无法被描述,缩小格距则可描述更多的小尺度信息。那么在网格距已经小于站点之间距离时,进一步缩小网格距会不会导致分析结果的明显变化呢?为此设计一组对比试验:第1个试验中格距设置为2,总格点数为51,平滑系数β取为0.1;第2个试验在此基础上加密一倍,格距设为1,总格点数为101,由于网格数增加约一倍,为保证失真度和粗糙度两者的权重大致不变,平滑系数β取为0.05。两个试验的其他设置同第3节,计算结果如图 3所示,图 3中实线和×线分别是格距选为1和2的试验结果,带点实线是两种结果在相同格点位置上的偏差。图 3表明,网格密度加倍后分析结果略微有所调整,但是分析结果的整体并未有大的改变。
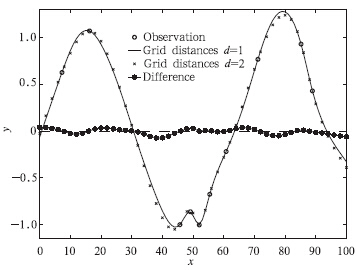 |
| 图 3 格距d=1(实线)和d=2(×线)分别对应的客观分析结果以及两者之差(带点实线),圆圈为观测 Fig. 3 Corresponding objective analysis results to the grid distances setting as d=1(solid line) and d=2(×-line),and their difference(line with dot),circles are observations |
平滑系数β用于调节失真度和粗糙度的比重,应用者通过它调节分析结果的平滑性,分析结果应该对β有明显的响应。应用者选定一个平滑系数后,往往需要将它用于大量同类型的客观分析问题中,为此,分析结果对β的响应应该是一个渐变的方式,否则可能由于平滑系数选在突变点附近而导致不同实例分析效果差别很大。依然采用第3节的实例进行试验,图 4显示了平滑系数取10和0.1对应的分析结果(实线和×线),对比两种结果可见,β=10对应分析结果同观测值的偏差更大,同时由于滤除了一些尺度较小的波动,整体显得更平滑。进一步将β设置成一系列不同的值,计算分析结果的失真度和粗糙度,绘制成失真度和粗糙度对平滑系数的响应曲线如图 5。图 5表明,分析场的失真度和粗糙度对平滑系数的响应是单调渐变的,不存在突变的情况。
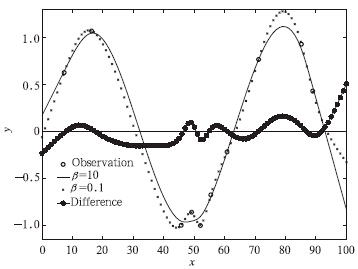 |
| 图 4 平滑系数β=10(实线)和β=0.1(×线)分别对应的客观分析结果以及两者之差(带点实线),圆圈为观测 Fig. 4 Corresponding objective analysis results to the smooth coefficients setting as 10 and 0.1(solid line and ×-line),and their difference(line with dot),circles are observations |
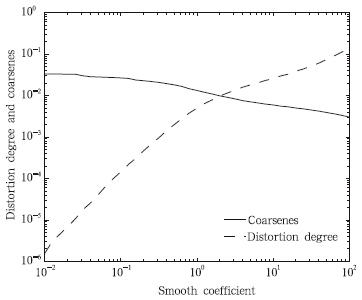 |
| 图 5 失真度和粗糙度对平滑系数的响应 Fig. 5 Response of the distortion degree and the coarseness to the smooth coefficient |
通过试验表明基于变分法的客观分析对失真度计算时的反插算法选择不敏感;当网格距已经小于站点密度时,进一步加密网格对分析结果影响不大;分析结果对平滑系数有渐变的响应关系。5 应用举例:降水量的客观分析
对观测的累积降水量的分析是各级气象台日常业务的基本内容,然而降水是空间分布非常不均匀的一种物理量,面对大量的降水量观测记录,若不借助客观分析将其绘制成二维的等值线或填色图,分析人员很难把握降水分布的主要特征。在对降水量进行分析时,常常将其分成几个等级进行讨论,这样实际上也是为了简化信息以便把握主要信息。以观测的24 h累积雨量为例,业务中通常将其分为小雨(小于10 mm)、中雨(10—24.9 mm)、大雨(25—49.9 mm)、暴雨(50—99.9 mm)、大暴雨(100—249 mm)和特大暴雨(不低于250 mm)等6个等级。客观分析的降水分布等值线(或填色)图也通常要求按此等级进行分级显示。
在绘制降水量等值线(或填色)图的客观分析问题中,应用者希望分析场能够尽量平滑,这实际上也是为了减少信息量,以免各等级的填色区域分布凌乱。应用者对分析场准确性的要求是每种等级的填色区域要覆盖所有同等级降水的站点,特别是对强降水中心,分析场中应该有相同等级的降水与之对应。以下根据上述要求对一个应用实例的目标函数设计进行论述。
图 6中显示了区域(36°—43°N,110°—120°E)内247个地面站观测的2012年9月2日08时24 h累积降水量,要求对区域内降水量进行客观分析,并根据分析场绘制降水分布。格点场设置为0.1°×0.1°经纬度网格,纬向和经向的网格数分别为101和71。
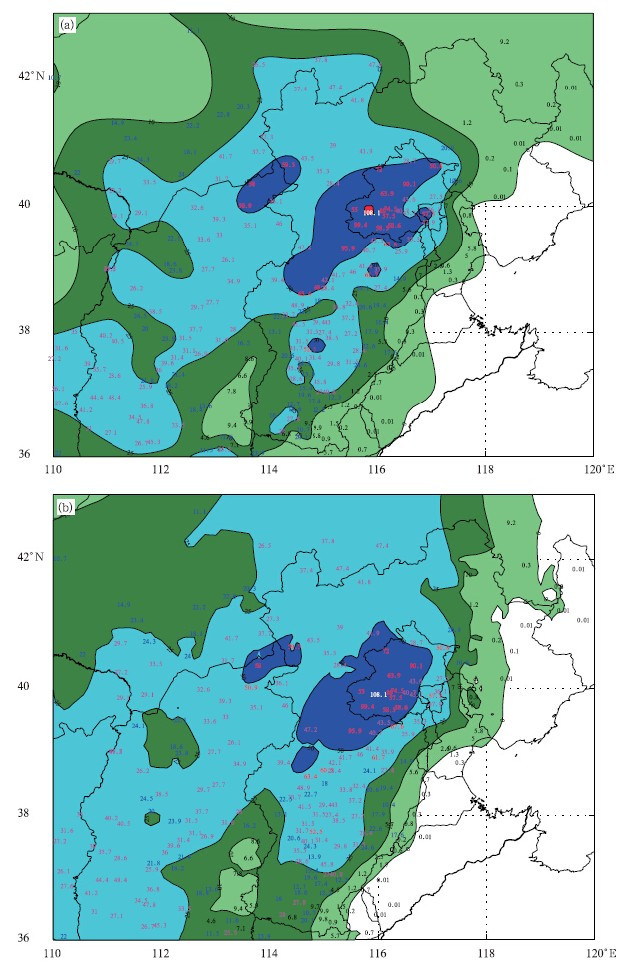 |
| 图 6 2012年9月2日08时24 h累积降水量的地面观测(数字)和客观分析的降水量分布(阴影区) (a. 变分法; b. Cressman方法) Fig. 6 Observation of 24 h cumulative rainfall(figure)at 08:00 BT 2 Sep 2012 and its objective analysis distribution(shaded) (a. Variational method,b. Cressman method) |
在此实例中,关于平滑性的要求并无特殊之处,根据2.2节的讨论,粗糙度可用二阶差分来度量,总粗糙度的表达式可以由式(4)简化成
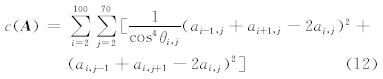
在准确性方面,应用者实际上关注的是站点位置的分析值和观测值的等级误差,若分析值和观测值等级相同,则站点位置的分析图填色就是正确的。为此失真度函数对分析值的约束作用主要表现在分析值和观测值存在等级差异的情况,而当两者无等级差异时,失真度表现出较小约束作用或不表现出约束作用。将各个降水量等级用区间分别表示为[0,0]、(0,10)、[10,25)、[25,50)、[50,100)、[100,250)和[250,1000)(单位省略表示,下文类同),这些区间的中点位置分别为0、5、17.5、37.5、75、175、625,区间的长度为0、10、15、25、50、150、750。按上面的讨论,单个站点上的失真度可以这样设计:当分析值离观测值所在区间中点的距离不超过γ(0<γ<0.5)倍的区间长度时失真度取值为0,当此距离超过γ倍区间长度时,即分析值接近或已经偏离观测值所在区间的两侧边缘时,失真度迅速增大。单点的失真度函数ê(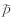 k,pk)可以表达成
k,pk)可以表达成

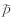 k为格点场通过双线性方式反插到第k个站点位置的分析值,γlk为
k为格点场通过双线性方式反插到第k个站点位置的分析值,γlk为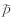 k偏离区间中心而不被约束的最大距离。γ的取值范围为(0,0.5),γ越大分析场整体受到失真度的约束越小,分析场会越平滑,但如果γ过分接近0.5,则容易出现失真度的约束作用不足导致分析结果出现等级误差的情况。将式(13)代入式(2)可得总失真度的函数,并将其中的权重系数都取为1。参考式(1)将总失真度和总粗糙度函数按权重求和即得总目标函数f(A),试验中β取为0.1,γ取为0.45。大量降水客观分析的试验表明,分析场对参数β和γ等的响应是稳定渐变的,不会出现参数的微小变化导致分析结果激烈震荡的情况。本研究β和γ的取值是根据同类客观分析试验中获得的较满意的参数,它并非针对特定个例挑选的最优参数。目标函数f(A)是关于各个格点值的多元函数,通过分析可知此处构建的e(A)是下凸函数,c(A)是严格下凸函数,因此,目标函数f(A)是严格下凸函数,其极小值就是最小值。
k偏离区间中心而不被约束的最大距离。γ的取值范围为(0,0.5),γ越大分析场整体受到失真度的约束越小,分析场会越平滑,但如果γ过分接近0.5,则容易出现失真度的约束作用不足导致分析结果出现等级误差的情况。将式(13)代入式(2)可得总失真度的函数,并将其中的权重系数都取为1。参考式(1)将总失真度和总粗糙度函数按权重求和即得总目标函数f(A),试验中β取为0.1,γ取为0.45。大量降水客观分析的试验表明,分析场对参数β和γ等的响应是稳定渐变的,不会出现参数的微小变化导致分析结果激烈震荡的情况。本研究β和γ的取值是根据同类客观分析试验中获得的较满意的参数,它并非针对特定个例挑选的最优参数。目标函数f(A)是关于各个格点值的多元函数,通过分析可知此处构建的e(A)是下凸函数,c(A)是严格下凸函数,因此,目标函数f(A)是严格下凸函数,其极小值就是最小值。在完成目标函数设计后,通过数值方法求解目标函数最小值对应的分析场,为此先给每个格点赋一个初始猜测值,在此实例中可以都赋为0,然后通过共轭梯度法进行迭代求解,其结果显示如图 6a。本研究另外采用了业务中常用的Cressman方法进行分析,其结果如图 6b。经计算可知,在此实例中Cressman方法的分析结果有61个站点的分析值和观测值的等级不一致,而变分法的客观分析结果中错误分析的站点数为0。Cressman方法和变分法的客观分析场的粗糙度分别为170698和13184,前者要比后者高出10倍。对比图 6a和b,也可以看出,基于变分法的客观分析所得到的(图 6a)等值线与观测站点对应的降水量等级一致,并且对强降水中心单个站点大于100 mm的等值线分析也与实况完全吻合,与此同时,等值线较Cressman方法所得到的(图 6b)更为平滑。可见,图 6a达到了应用要求的效果,由此也说明此实例中设计的目标函数是合理的。6 总 结
本研究提出将变分方法应用于客观分析问题,将分析要求设计成关于格点场的目标函数,通过数值方法求解目标函数的最小值对应的格点场来获得最优的分析结果。在用于图形显示的客观分析问题中,应用者要求客观分析的结果既准确又平滑,表达这种要求的目标函数相应地包含失真度和粗糙度两部分。在具体的各类问题中,虽然应用者对准确性和平滑性的要求可能各不相同,但每一类问题的失真度和粗糙度函数可以根据需求灵活设计,因此,变分法在此类客观分析问题中具有普遍适用性。
本研究将变分法应用于一维的客观分析问题中,针对一种具体的目标函数给出了分析场的理论求解过程和结果,并与采用共轭梯度法数值计算的结果进行了对比,结果表明两种基本一致。并进一步以一维客观分析为例,测试分析结果对目标函数中的算子和参数的响应情况。结果表明目标函数中格点反插站点的算法对最终结果影响很小,当网格距已经小于站点密度时,进一步加密网格对分析结果影响不大,此外,
分析结果对平滑系数有稳定渐变的响应关系。在一些更复杂的二维客观分析问题中,目标函数可能包含更多的参数,分析结果对函数中各个参数的响应情况还需要目标函数设计者进一步测试。
最后,本研究结合一个具体降水量客观分析的实例展示了将分析要求表达成目标函数的过程,并在此实例中获得了满意的分析结果。附录A
将式(10)对ai,i=0,1,…,N求偏导可得
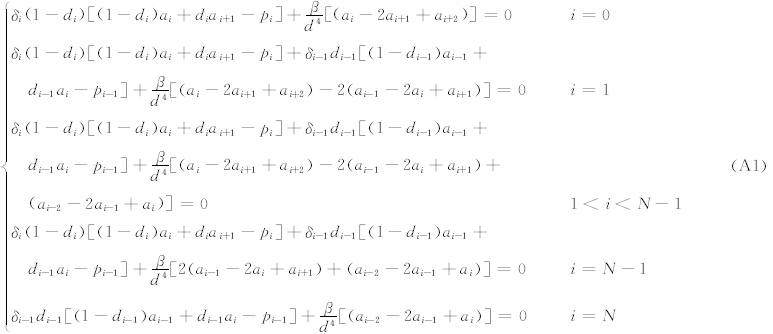
整理式(A1)得
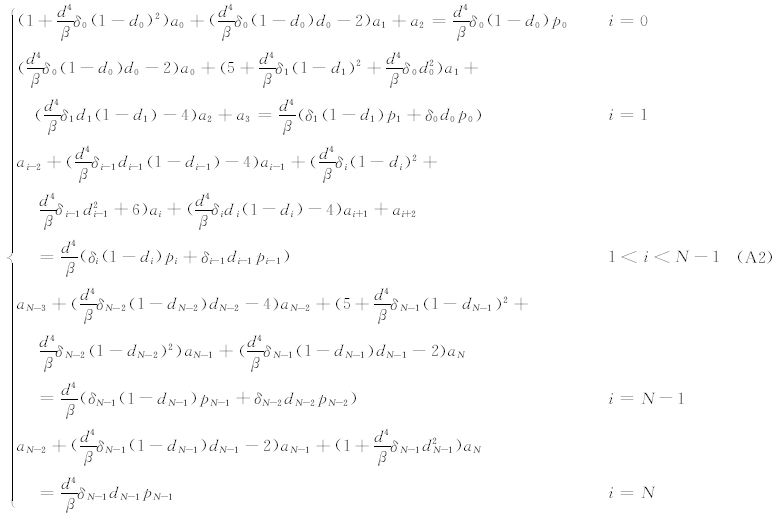
式(A2)可以简写成如下形式

并可以进一步以矩阵的形式表示为

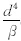 δi(1-di)2+
δi(1-di)2+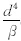 δi-1di-12,i=2,3,…,N-2; hi,i-1=hi-1,i=
δi-1di-12,i=2,3,…,N-2; hi,i-1=hi-1,i=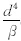 δi-1(1-di-1)di-1-4,i=2,3,…,N-1; hi,i-2=hi-2,i=1,i=2,3,…,N,左上角和右下角的元素为h0,0=1+
δi-1(1-di-1)di-1-4,i=2,3,…,N-1; hi,i-2=hi-2,i=1,i=2,3,…,N,左上角和右下角的元素为h0,0=1+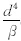 δ0(1-d0)2,h1,1=5+
δ0(1-d0)2,h1,1=5+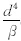 δ1(1-d1)2+
δ1(1-d1)2+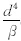 δ0d02,h0,1=h1,0=
δ0d02,h0,1=h1,0=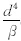 δ0(1-d0)d0-2,hN-1,N-1=5+
δ0(1-d0)d0-2,hN-1,N-1=5+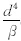 δN-1(1-dN-1)2+
δN-1(1-dN-1)2+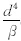 δN-2dN-22,hN,N=1+
δN-2dN-22,hN,N=1+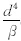 δN-1dN-12,hN-1,N=hN,N-1=
δN-1dN-12,hN-1,N=hN,N-1=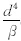 δN-1(1-dN-1)·dN-1-2。矢量Y的第一个和最后一个元素为y0=
δN-1(1-dN-1)·dN-1-2。矢量Y的第一个和最后一个元素为y0=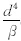 δ0(1-d0)p0和yN=
δ0(1-d0)p0和yN=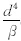 δN-1dN-1pN-1,中间部分的元素为yi=
δN-1dN-1pN-1,中间部分的元素为yi=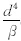 (δi(1-di)pi+δi-1di-1pi-1),i=1,2,…,N-1。
(δi(1-di)pi+δi-1di-1pi-1),i=1,2,…,N-1。
| 冯旭明. 2001. 气象探空资料的客观分析. 四川气象, 21(3): 36 |
| 高歌, 龚乐冰, 赵珊珊等. 2007. 日降水量空间插值方法研究. 应用气象学报, 18(5): 732-736 |
| 靳国栋, 刘衍聪, 牛文杰. 2003. 距离加权反比插值法和克里金插值法的比较. 长春工业大学学报(自然科学版), 24(3): 53-57 |
| 刘克武. 1981. 样条插值在客观分析中的应用. 气象学报, 39(2): 157-167 |
| 刘克武. 1982. 样条插值在客观分析中的应用:风场客观分析试验. 气象学报, 40(1): 123-128 |
| 屠伟铭. 1994. 近十年来国家气象中心业务客观分析技术介绍. 应用气象学报, 5(4): 477-482 |
| 王跃山. 2000. 客观分析和思维同化—站在新世纪的回望(I):客观分析概念辨析. 气象科技, 28(3): 1-8 |
| 邬伦, 吴小娟, 肖晨超等. 2010. 五种常用降水量插值方法误差时空分布特征研究:以深圳市为例. 地理与地理信息科学, 26(3): 19-24 |
| 徐士良. 1995. Fortran常用算法程序集(第二版). 北京: 清华大学出版社, 549pp |
| 徐一鸣, 丁荣富, 李佐凤. 1989. 统计插值客观分析方法的试验研究. 气象学报, 47(2): 237-243 |
| 于连庆, 李月安, 韩强. 2012. 中央气象台探空资料客观分析业务系统的研究与实现. 气象科技, 40(2): 153-159 |
| Bergthorsson P, Ds B, Frykland S, et al. 1955. Routine forecasting with the barotropic model. Tellus, 7(2): 329-340 |
| Bouttier F, Rabier F. 1997. The operational implementation of 4D-Var. ECMWF Newsletter, (78): 2-5 |
| Cressman G P. 1959. An operational objective analysis system. Mon Wea Rev, 87(10): 367-374 |
| Gilchrist B, Cressman G. 1954. An experiment in objective analysis. Tellus, 6(4): 309-318 |
| Kalnay E. 2003. Mospheric Modeling, Data Assimilation and Predictability. London: Cambridge University Press, 364pp |
| Karnieli A M. 1990. Application of Kriging Technique to Areal Precipitation Mapping in Arizona. Geo J, 22(4): 391-398 |
| Lorenc A. 1986. Analysis methods for numerical weather prediction. Quart J Roy Meteor Soc, 112(474): 1177-1194 |
| Panofsky H. 1949. Objective weather-map analysis. J Appl Meteor, 6: 386-392 |
| Zupanski M. 1993. Regional 4-dementtional variational data assimilation in a quasi-operational forecasting environment. Mon Wea Rev, 121: 2396-2408 |
 2013, Vol. 71
2013, Vol. 71

