中国气象学会主办。
文章信息
- 郝晓龙, 王咏薇, 胡凝, 陈卫东. 2020.
- HAO Xiaolong, WANG Yongwei, HU Ning, CHEN Weidong. 2020.
- 太阳能光伏屋顶对城市热环境及能源供需影响的模拟
- Simulation of the influence of solar photovoltaic roof on urban thermal environment and energy supply and demand
- 气象学报, 78(2): 301-316.
- Acta Meteorologica Sinica, 78(2): 301-316.
- http://dx.doi.org/10.11676/qxxb2020.015
文章历史
-
2019-07-13 收稿
2019-11-11 改回
2. 南京信息工程大学大气环境中心,南京,210044;
3. 国家电网电力科学研究院,南京,210003
2. Yale-NUIST Center on Atmospheric Environment,International Joint Laboratory on Climate and Environment Change (ILCEC),Nanjing University of Information Science and Technology,Nanjing 210044,China;
3. State Grid Electric Power Research Institute,Nanjing 210003,China
在全球气候变暖的背景下,以高温热浪为代表的极端天气更加频繁与剧烈,对自然环境和人类社会造成重大的影响(Hansen,et al,2006)。而在局地气候中,城市化进程的加快以及下垫面的改变可能是导致城市高温的重要原因之一(Liu,et al,2014;Chi,et al,2015;Oke,1987;张艳等,2012)。随着气候变暖,建筑制冷设备的保有量和使用量也在逐年攀升,室内的废热排放会对建筑周围大气产生加热作用(Hassid,et al,2000)。此外,化石能源的使用也会带来环境污染、温室效应加剧等一系列问题,因此中国正在大力推广利用太阳能等可再生清洁能源的发电技术(艾欣等,2013)。
太阳能屋顶是通过在房屋顶部安装太阳能发电装置,将部分太阳能转化为电能,减少直接通过屋顶进入建筑的热量,同时产生的电能可以减少化石能源的使用,减轻能源负担。对于城市气候而言,太阳能屋顶的大规模使用会改变反照率,影响冠层对能量的吸收、存储以及长短波辐射的释放,从而改变冠层辐射平衡。光伏屋顶影响城市气温受到很多因素的制约,如安装前后表面的反照率(Sailor,1995;Atkinson,2003),太阳能电池的光电转化效率,安装的太阳能板的厚度、比容、热传递系数等。构建的模型中是否考虑化石燃料的使用等都会影响最终的模拟结果。Salamanca等(2016)对太阳能板内部的传递过程进行简化,将其看作一个单层薄板,建立热平衡方程,并与WRF模式耦合,研究表明,亚利桑那州安装太阳能屋顶可以使夏季近地面气温降低0.8°C,降温能耗减少11%—4%。Golden(2006)的研究显示,光伏组件的使用可以减少城市的贮热量,从而对城市热岛有较好的减缓作用。此外,太阳能板的架设会改变原先建筑的热传递过程,影响空调的降温负荷,间接地影响城市环境。Dominguez等(2011)研究了光伏屋顶对建筑隔热的影响,4月白天光伏组件下屋顶内表面温度比普通屋顶低2.5°C,但晚上由于光伏板的隔热作用,屋顶内表面温度要高于普通屋顶。光伏屋顶对采暖负荷影响较小,全年减少5.9 kWh/m2的制冷负荷。Masson等(2014)通过巴黎光伏组件模型研究指出,夏季使用光伏屋顶能够减少12%的空调能耗。Yang等(2001)研究了带通风流道的光伏屋顶的传热性能和电性能,由于光伏组件的遮挡和通风流道的作用,与普通屋顶相比通过屋顶的冷负荷减少了65%。张艳晴等(2019)利用耦合单层冠层方案的WRF模式,研究了不同发电效率的太阳能屋顶对夏季高温的缓解作用。
目前对于将光伏建筑传热模型与气象模式结合的研究还比较少。Masson等(2014)通过离线模式TEB,研究了光伏组件对城市微气候的影响。张艳晴等(2019)通过削弱太阳短波辐射的方式模拟了光伏屋顶对气温的影响。而Salamanca等(2016)虽然将太阳能板参数化与WRF多层城市冠层方案相结合,但是简化了光伏板内部具体的热传递过程,多层的更合理的屋顶光伏板的方案仍然需要进一步发展。
江苏省近几年城市化发展迅速,地处温带和亚热带区,夏季受副热带高压控制,在大陆辐射升温和副热带高压脊线附近下沉升温的影响下,易受到高温热浪等极端天气影响。而且江苏省一次能源资源95%以上都是煤炭,但在已探明的煤炭储量中,可利用的工业储量仅为28.4×108 t,占全国的0.58%,能源资源的短缺造成了江苏省电力工业以资源输入为主的发展格局(赵媛等,2006;刘晓明,2017)。光伏屋顶的使用在一定程度上也能缓解能源输入的需求。
基于上述背景,选择江苏省作为研究对象,评估BEP/BEM方案对于江苏省气候的模拟效果,并研究城市地区太阳能屋顶的安装对于江苏省气候及能源方面的影响。
2 模式及相关数据 2.1 研究区域及天气背景2017年夏季,中国受到大范围持续高温天气影响,江苏地区电网用电负荷突破往年极值(王国复等,2018)。选取江苏省2017年7月21—27日一次持续的高温天气过程作为研究时段。从气温高于30°C及35°C的站点数占总站点数的比例(表1)可以看出,江苏省大部分区域受到高温控制。
| 21日 | 22日 | 23日 | 24日 | 25日 | 26日 | 27日 | |
| >35°C | 0.88 | 0.99 | 0.99 | 1 | 0.67 | 0.64 | 0.93 |
| >30°C | 1 | 1 | 1 | 1 | 0.96 | 0.98 | 1 |
文中采用WRF v3.9.1模式,模拟区域为三重嵌套,研究区域下垫面数据使用2016年500 m分辨率的MODIS静态数据,根据不透水率,将江苏省城市下垫面分成3类:低密度住宅区(30%—70%)、高密度住宅区(70%—90%)及工业区(>90%)。模拟区域及第三重嵌套内城市分布情况如图1所示,其中高密度住宅区主要集中于江苏省的东南部。

|
| 图 1 (a) 嵌套区域 (方框) 和地形高度 (色阶,单位:m) 及 (b) 最内层土地利用类型 (数字) 分布 Fig. 1 (a) Nested simulation areas (black rectangles indicate D01,D02,D03) and terrain height (shaded,unit:m);(b) land-use types (number) for the inner-most domain D03 |
模拟中三重嵌套网格分辨率分别为27、9和3 km,模式垂直分为43层,其中1 km以下有13层。背景场和边界条件选用美国环境预报中心(NCEP)的FNL资料,模式参数化方案主要为WSM6微物理方案(Hong,et al,2006)、RRTM长波辐射方案(Mlawer,et al,1997)、Duhia短波辐射方案(Dudhia,1989)、MYJ边界层方案(Janjić,1994)、Noah陆面方案(Tewari,et al,2004)以及BEP/BEM城市冠层方案(Salamanca,et al,2010)。BEP/BEM方案是在原来的多层城市冠层模型基础上考虑了室内、外热量的传递,主要考虑室内人体热排放、空调及室内电器等产生的热量对室内、室外温度产生的影响。模式中城市参数参考Xu等(2018)的设置,低密度住宅区、高密度住宅区、商业区建筑长度分别为15、20及25 m,建筑高度及不同建筑高度的占比如表2所示。
| 低密度住宅区 | 高密度住宅区 | 商业区 | |||||
| 高度(m) | 占比(%) | 高度(m) | 占比(%) | 高度(m) | 占比(%) | ||
| 6 | 63 | 6 | 28 | 6 | 13 | ||
| 9 | 17 | 9 | 15 | 9 | 10 | ||
| 12 | 1 | 12 | 5 | 12 | 6 | ||
| 15 | 6 | 15 | 25 | 15 | 24 | ||
| 18 | 12 | 18 | 20 | 18 | 24 | ||
| 21 | 1 | 21 | 3 | 21 | 8 | ||
| 24 | 3 | 24 | 4 | ||||
| 27 | 1 | 27 | 4 | ||||
| 30 | 3 | ||||||
| 33 | 2 | ||||||
| 36 | 1 | ||||||
| 39 | 1 | ||||||
文中共设计了3个算例:对照算例(没有太阳能板)、支架式安装算例(带有通风流道)、贴覆式安装算例(没有空气夹层)。为了便于分析,在下文分别用Ctr、Gap、Nogap表示,其中太阳能板屋顶的算例(Gap和Nogap)设置为100%的屋顶覆盖。工业晶体硅电池的光电转换效率为14%—16%(王进华,2007),本研究中光电转换效率取16%。此外,为了使结果更加贴近现实,参考Xu等(2018)的方法,将08—18时(北京时,下同)设置为商业区空调使用时间,其余时间设为住宅区空调启动时间。
2.3 WRF模式中太阳能屋顶热平衡方案的引入在化工机械、建筑等领域已有学者(任建波,2006;田玮,2006;Tian,et al,2007;Krauter,et al,1990)对架设光伏屋顶的离线过程做了大量的研究,文中参考这些已有的成果,并将这些过程的计算引入到WRF模式BEP/BEM方案中,增加新的太阳能屋顶的计算方案。WRF模式中BEP/BEM城市冠层参数化方案,显式计算了室内外热量的传递,同时还计算了室内安装空调时的能耗以及由于空调制冷对室外废热的排放(Salamanca,et al,2010)。在WRF/BEM/BEP方案中增加光伏屋顶热量平衡方程以及对空调能源供给的计算,该方案的引入除了能够计算对城市建筑物室内、外气温产生的影响,还能够计算光伏屋顶为室内建筑物提供的能源。
目前光伏板的安装方式主要有3种:带通风流道支架安装、贴覆式安装及封闭流道的支架安装(王玥,2017)。文中在WRF模式中引入了较为常见的带通风流道的支架安装以及贴覆式安装两种方式(图2)的计算过程。
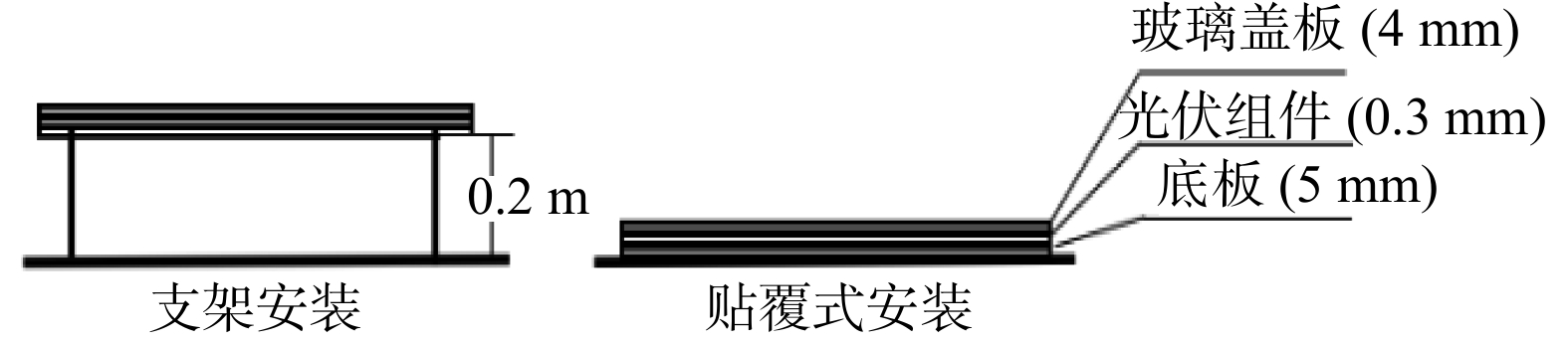
|
| 图 2 屋顶安装方式示意 Fig. 2 Roof installation methods |
参考Krauter 的分层理论模型(Krauter,et al,1990)将光伏板分为三层,从上至下分别为玻璃盖板、光伏组件及底板,相关参数详见表3。
| 导热系数(W/(m·K)) | 密度(kg/m3) | 比热容(J/(kg·K)) | 厚度(mm) | |
| 玻璃板 | 1.04 | 2500 | 835 | 4 |
| 光伏组件 | 150 | 2330 | 950 | 0.3 |
| 底板 | 0.14 | 1475 | 1130 | 5 |
该方案假设光伏板平行于屋顶表面,在光伏板的遮蔽下,能够减少到达屋顶的太阳辐射。底板与屋顶间的空气流通能够加快屋顶的热量扩散,从而达到降低屋顶温度的目的。通过有限差分方法,增加光伏板不同层的热平衡方程,具体方程参考任建波(2006)的研究结果
| $\begin{split}&{R_{\rm s}} \times {a_1}(1 - r) + \varepsilon \left[ {{R_{\rm l}} - \sigma {{(T_1^{{{n - 1}}})}^4}} \right] - {H_1} - {h_{12}} \times \\&\quad(T_1^{{n}} - T_2^n){\rm{ - }}\frac{{{\rho _1}{c_{{\rm p}1}}\Delta {x_1}}}{{{\rm d}t}}(T_1^{{n}} - T_1^{{{n - 1}}}) = 0\end{split}$ | (1) |
| $\begin{split}&{R_{\rm s}} \times {a_2}(1 - {a_1})(1 - r) - E + {h_{12}} \times (T_1^{{n}} - T_2^n) - {h_{23}} \times\\&\quad (T_2^{{n}} - T_3^n){\rm{ - }}\frac{{{\rho _2}{c_{{\rm p}2}}\Delta {x_2}}}{{{\rm d}t}}(T_2^{{n}} - T_2^{{{n - 1}}}) = 0\end{split}$ | (2) |
| $\begin{split}&{h_{23}} \times (T_2^{{n}} - T_3^n) + {h_{3{\rm a}}} \times (T_{\rm a}^{{n}} - T_3^n) + \varepsilon {}_1\sigma {(T_{\rm{r}}^{{{n - 1}}})^4} -\\&\quad {\varepsilon _2}\sigma {(T_3^{{{n - 1}}})^4}{\rm{ - }}\frac{{{\rho _3}{c_{{\rm p}3}}\Delta {x_3}}}{{{\rm d}t}}(T_3^{{n}} - T_3^{{{n - 1}}}) = 0\end{split}$ | (3) |
| $\begin{split}&{h_{3{\rm a}}} \times (T_3^{{n}} - T_{\rm a}^n) + {h_{\rm{ar}}} \times (T_{{\rm r}1}^{{n}} - T_{\rm a}^n) - \rho S{U'}{c_{\rm{pa}}} \times\\&\quad (T_{{\rm{out}}}^{{n}} - {T_{in}^n}) - \frac{{{\rho _{\rm a}}{c_{\rm{pa}}}\Delta {x_{\rm a}}}}{{{\rm d}t}}(T_{\rm a}^{{n}} - T_{\rm a}^{{{n - 1}}}) = 0\end{split}$ | (4) |
| $\begin{split}&{h_{\rm{ar}}} \times (T_{\rm a}^{{n}} - T_{{\rm r}1}^n) + {h_{{\rm r}12}} \times (T_{{\rm r}2}^{{n}} - T_{{\rm r}1}^n) + {\varepsilon _2}\sigma {(T_3^{{{n - 1}}})^4} -\\&\quad {\varepsilon _3}\sigma {(T_{{\rm r}1}^{{{n - 1}}})^4} - \frac{{{\rho _{{\rm r}1}}{c_{{\rm{pr}}1}}\Delta {x_{{\rm r}1}}}}{{{\rm d}t}}(T_{{\rm r}1}^{{n}} - T_{{\rm r}1}^{{{n - 1}}}) = 0\end{split}$ | (5) |
式(1)—(5)分别为玻璃板、光伏组件、底板、通风夹层空气及第1层屋顶的能量平衡方程,所用参数见表4。
| 参数 | 参数说明 | 参数 | 参数说明 | |
|
|
光伏板表面的感热通量(W/m2) |
|
玻璃板厚度(m) | |
|
|
向下的太阳短波辐射(W/m2) |
|
光伏组件厚度(m) | |
|
|
向下的大气长波辐射(W/m2) |
|
底板厚度(m) | |
|
|
玻璃板反射率 |
|
通风夹层空气层厚度(m) | |
|
|
玻璃板发射率 |
|
屋顶第一层厚度(m) | |
|
|
底板发射率 |
|
玻璃板与光伏组件传热系数(W/(m·K)) | |
|
|
屋顶发射率 |
|
光伏组件与底板传热系数(W/(m·K)) | |
|
|
发电量(W/m2) |
|
底板与空气对流交换系数(W/(m·K)) | |
|
|
玻璃板密度(kg/m3) |
|
屋顶与空气对流交换系数(W/(m·K)) | |
|
|
光伏组件密度(kg/m3) |
|
玻璃板温度(K) | |
|
|
底板密度 (kg/m3) |
|
光伏电池温度(K) | |
|
|
空气密度 (kg/m3) |
|
底板温度(K) | |
|
|
屋顶第一层密度(kg/m3) |
|
夹层气温(K) | |
|
|
玻璃板比热容(J/(kg·K)) |
|
进口气温(K) | |
|
|
光伏组件比热容(J/(kg·K)) |
|
出口气温(K) | |
|
|
底板比热容(J/(kg·K)) |
|
n时刻温度(K) | |
|
|
空气比热容(J/(kg·K)) |
|
屋顶第一层比热容(J/(kg·K)) | |
|
|
玻璃板吸收率 |
|
光伏组件吸收率 |
式(1)左边第1项为玻璃板吸收的太阳短波辐射,第2项为入射的净长波辐射,第3项为与空气的对流热交换(Louis,1979),第4项为玻璃板与光伏组件的热传递,最后一项为储热项。式(2)从左到右依次代表透过玻璃板被电池组件吸收的短波辐射、电池的发电量、与玻璃板及底板的热传递。此处忽略了辐射在光伏板内部的多次反射过程。考虑到电池温度超过25°C后,每升高1℃,输出功率下降0.5%。发电量计算公式参考Salamanca等(2016)的工作。
| $E = {\rm{\varepsilon }}R_{\rm s}{a_2}(1 - {a_1})(1 - r)\min [1;1 - 0.005({T_2} - 298.15)]{\rm{ }}$ | (6) |
式中,
式(3)从左到右依次代表光伏电池与底板的热传递、底板与空气的热交换、屋顶向上的及底板本身向下的长波辐射、热储存项。式(4)从左到右依次代表底板与空气的热交换、屋顶表层与空气的热交换、通风作用带来的热量损失、热储存项,假设流道中空气进口温度等于环境温度,流道内风速参考Afonso等(2000),与空气的对流交换系数参考Dominguez等(2011)提到的方法。式(5)从左到右依次代表空气与屋顶表层的热交换、第2层屋顶与表层屋顶的热交换、向下的来自底板的长波辐射、本身向上发射的长波辐射及储存项。
对于贴覆式安装,将对流交换和辐射换热过程用底板与屋顶的热传递过程替代即可。
2.3.2 光伏屋顶与WRF/BEP/BEM方案的耦合在BEM方案中,将上述方程和原模式中屋顶的热传递方程组成离散化的方程组,并整理成三对角矩阵的形式,求解出各层的温度。用光伏板的表面温度代替原先屋顶温度参与模式中表面通量的计算。此外,支架式安装要额外考虑由于空气流通产生的光伏板下表面与屋顶上表面向周围大气的热量传输过程。
3 结果分析 3.1 模拟效果检验为检验模拟结果,使用2017年7月江苏省70个气象站点的观测数据。根据下垫面类型将70个站点分为城区和郊区,分布在下垫面类型为31、32、33的站点划分为城市站点,分布在类型12,即农田区域的站点作为郊区站点。主要运用李耀孙等(2012)的检验方法,统计量主要有:模拟与观测值的吻合指数(IA),均方根误差(RSME),观测值的标准偏差(SD_O),模拟值的标准偏差(SD_P)。
| ${\rm{IA}}{\rm{ = }}1{\rm{ - }}\frac{{\displaystyle\sum\limits_{i = 1}^N {{{{\varphi _i}}^2}} }}{{\displaystyle\sum\limits_{i = 1}^N {(\left| {{p_i} - \bar o} \right| + } \left| {{o_i} - \bar o} \right|{)^2}}}{\rm{ }}$ | (7) |
| ${\rm{SD}}\_{\rm O} = {\left(\frac{1}{{N - 1}}\displaystyle\sum\limits_{i = 1}^N ({o_i} - \bar o)^2\right)}^{{1/2}}$ | (8) |
| ${\rm{SD}}\_{\rm P} = {\left(\frac{1}{{N - 1}}\displaystyle\sum\limits_{i = 1}^N ({p_i} - \bar p)^2\right)}^{{1/2}}$ | (9) |
| ${\rm{RMSE}} = {\left[\frac{1}{N}\displaystyle\sum\limits_{i = 1}^N {{{\varphi _i}}^2} \right]}^{1/2}$ | (10) |
式中,
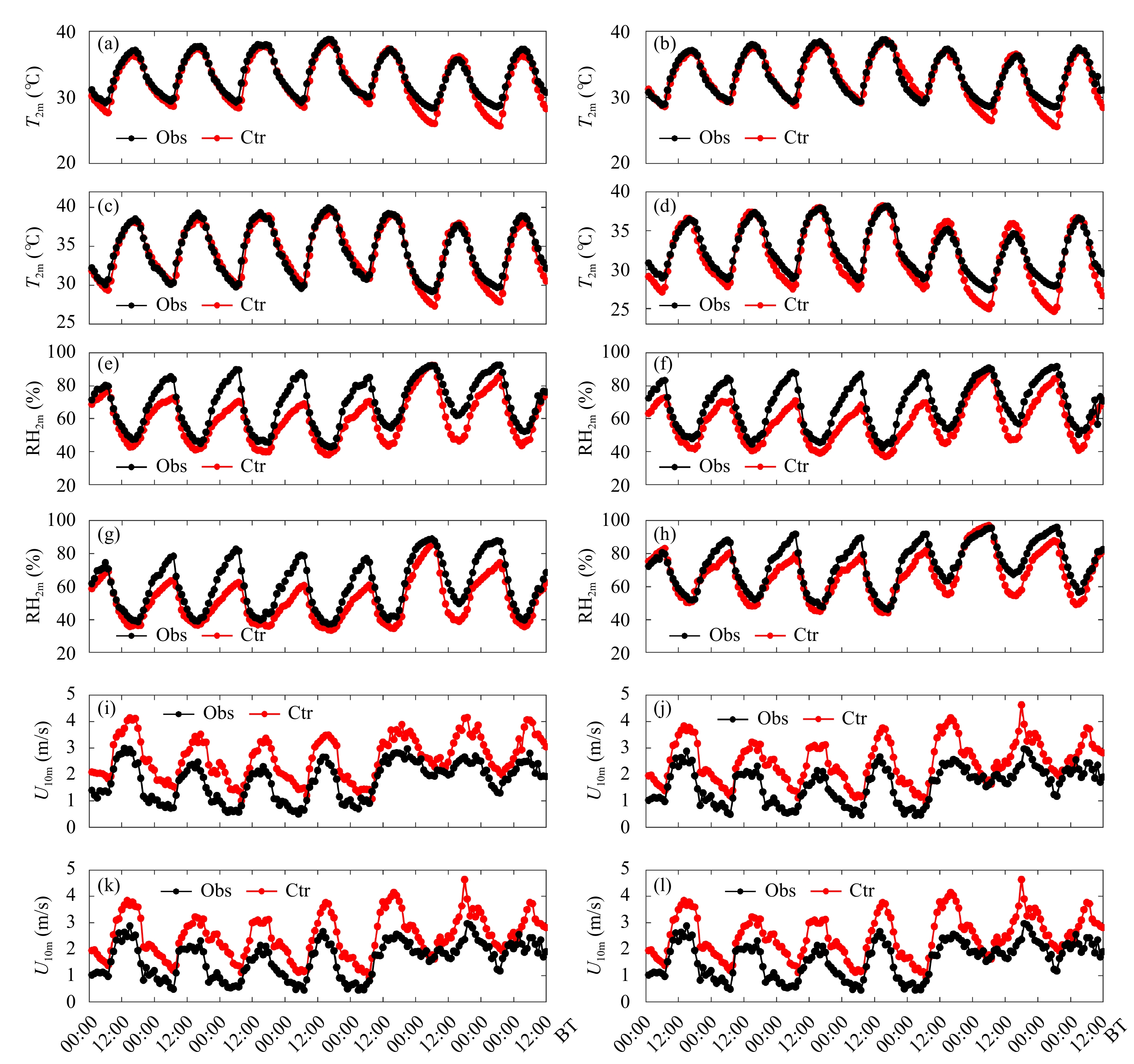
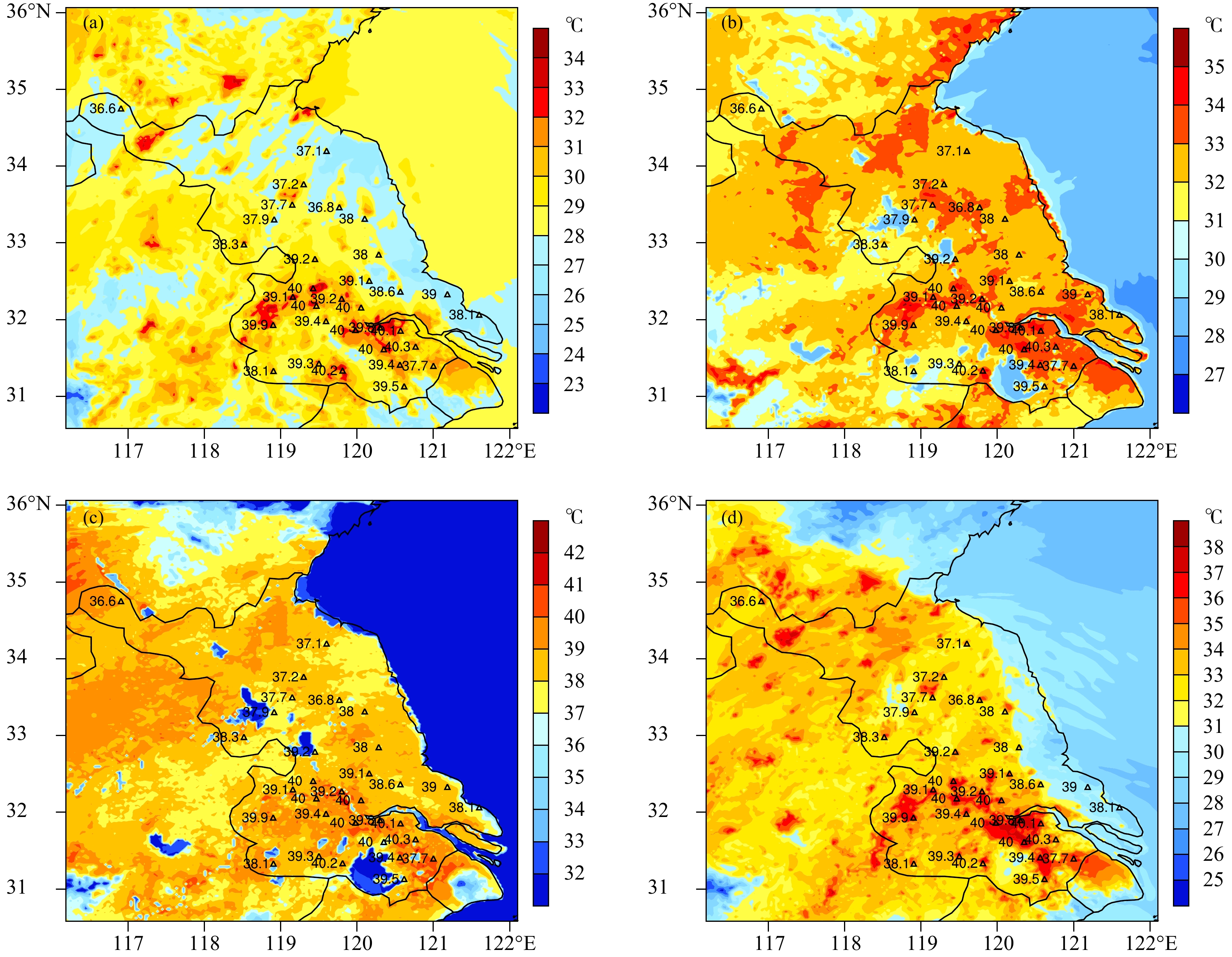
从图3a、b可以看出,城市高密度住宅区和低密度住宅区对于温度模拟较好,均方根误差分别为1.02、1.09°C。商业区吻合系数为0.98,均方根误差为0.83°C,整体模拟效果较好。从模拟的2 m气温的水平分布与观测的对比情况(图4)可以看出,本次模拟过程较好地呈现出江苏省南部城市密集区的高温分布特征,模拟值与观测值匹配程度较高,但夜间城市模拟温度偏低,分析其原因可能是冠层方案中建筑对长波辐射的储热效应考虑还不够充分。另外,城市形态参数的不精确,如楼层高度、建筑分布密度等对于最终的模拟结果也可能会造成影响。如表5所示,郊区吻合系数达到0.96,均方根误差为1.36°C,SD_O与SD_P的比值达到0.88。因此,基本可以认定本次过程对于温度模拟结果可信。
|
| 图 3 各气象要素 (2 m气温(a—d)、2 m相对湿度(e—h)、10 m风速(i—l)) 模拟与观测值时间序列 (a、e、i. 低密度住宅区,b、f、j. 高密度住宅区,c、g、k. 商业区,d、h、l. 郊区) Fig. 3 Comparisons of simulated and observed 2 m air temperature (a-d),2 m relative humidity (e-h),10 m wind speed (i-l) (a,e,i. low-density residential areas;b,f,j. high-density residential areas;c,g,k. business district;d,h,l. suburban areas) |
|
| 图 4 江苏省7月24日2 m气温模拟 (色阶) 与观测 (图中数字) 水平分布 (a. 02时,b. 08时,c. 14时,d. 20时) Fig. 4 Distributions of simulated (shaded) and observed (the numbers in the figures) 2 m temperature in Jiangsu Province on 24 July (a. 02:00 BT,b. 08:00 BT,c. 14:00 BT,d. 20:00 BT) |
| IA | RMSE | SD_O | SD_P | ||
| 低密度住宅区 | T2m(°C) | 0.97 | 1.09 | 3.03 | 3.52 |
| RH2m(%) | 0.88 | 10.24 | 14.55 | 13.67 | |
| W10m(m/s) | 0.71 | 0.95 | 0.70 | 0.80 | |
| 高密度住宅区 | T2m(°C) | 0.97 | 1.02 | 3.12 | 3.44 |
| RH2m(%) | 0.86 | 11.03 | 14.16 | 12.90 | |
| W10m(m/s) | 0.69 | 0.97 | 0.67 | 0.80 | |
| 商业区 | T2m(°C) | 0.98 | 0.83 | 3.26 | 3.43 |
| RH2m(%) | 0.87 | 10.56 | 15.38 | 12.75 | |
| W10m(m/s) | 0.90 | 0.49 | 0.72 | 0.90 | |
| 郊区 | T2m(°C) | 0.96 | 1.36 | 3.03 | 3.90 |
| RH2m(%) | 0.92 | 7.63 | 13.61 | 13.21 | |
| W10m(m/s) | 0.64 | 1.12 | 0.68 | 0.77 |
Zhang等(2017)模拟了2017年长三角地区的一次高温过程,其结果表明,对于湿度的模拟,城市和郊区站点的RSME分别为7.8%、5.5%。本次模拟结果显示,城市模拟结果偏差,其中高密度住宅区的RSME达到11.03%。但从吻合系数来看,各区都超过0.85,SD_O与SD_P的比值也较小。对风速的模拟存在高估现象,除了商业区的吻合系数达到0.9,其他区都低于0.75。低密度区、高密度区、郊区的均方根误差分别达到0.95、0.97、1.12 m/s,差别较大。WRF模式对于风速的模拟不够准确,主要原因是模式分辨率不够高,很难准确地描述出由于建筑物、植被以及地形起伏等原因对于局地流场的影响。
3.2 太阳能屋顶的设置对近地层2 m气温的影响根据地表入射短波辐射量为正的时段,将06—18时归为白天,其余时间为夜间。图5是光伏屋顶对2 m气温的影响,其中商业区的温度起伏最为明显。从图5可以看出,使用设置通风流道的光伏屋顶,白天商业区温度降低0.12—0.23°C,夜间降低0.21—0.60°C。贴覆式安装白天降温0.10—0.29°C,夜间温度几乎不变,小部分地区出现轻微升温现象。

|
| 图 5 2017年7月21—27日光伏屋顶 (a、b. 支架式,c、d. 贴覆式) 与对照算例中2 m气温 (单位:°C) 的差值 (a、c.06—18时平均降温幅度,b、d. 19—05时平均降温幅度) Fig. 5 Mean differences (unit:°C )in 2 m air temperature between results of photovoltaic roofs (a,b. the bracket roof,c,d. the attached roof) and control run during 21—27 July 2017 (a,c. average cooling rates during 06:00-18:00 BT,b,d. average cooling rates during 19:00-05:00 BT) |
光伏屋顶的大规模使用会改变城市的辐射能量平衡,进而影响城市气候。地表的感热加热是低层大气的重要能量来源,对于城市近地层气温的影响不容忽视。图6反映了光伏屋顶安装前、后地表感热通量的日变化特征。白天入射的短波辐射部分被转换为电能储存起来,故光伏板的存在可能会削弱城市表面向上的感热通量。12时,入射短波辐射达到峰值。对比对照案例,此时支架式安装的感热通量在低密度住宅区、高密度住宅区及商业区减少的峰值分别为20.93、42.39、59.99 W/m2。对于郊区的影响很小,可以忽略。贴覆式安装感热通量减少更加明显,分别减少39.03、83.65、109.66 W/m2。从能量平衡的角度看,通风流道中空气的流通,光伏板及屋顶的部分热量被输送到环境中去,建筑中的储热降低,图8中白天废热排放低于贴覆式安装也侧面反映了进入室内热量的减少。夜间带有通风流道的屋顶表面温度要低于贴覆式屋顶及普通屋顶,夜间室内空调的废热排放较低,故夜间室外环境降温明显。

|
| 图 6 对照算例及两种光伏屋顶感热通量的平均日变化特征 (a. 低密度住宅区,b. 高密度住宅区,c. 商业区,d. 郊区) Fig. 6 Diurnal variation characteristics of average sensible heat flux for the two types of photovoltaic roof (a. low-density residential areas,b. high-density residential areas,c. commercial areas,d. suburbs) |
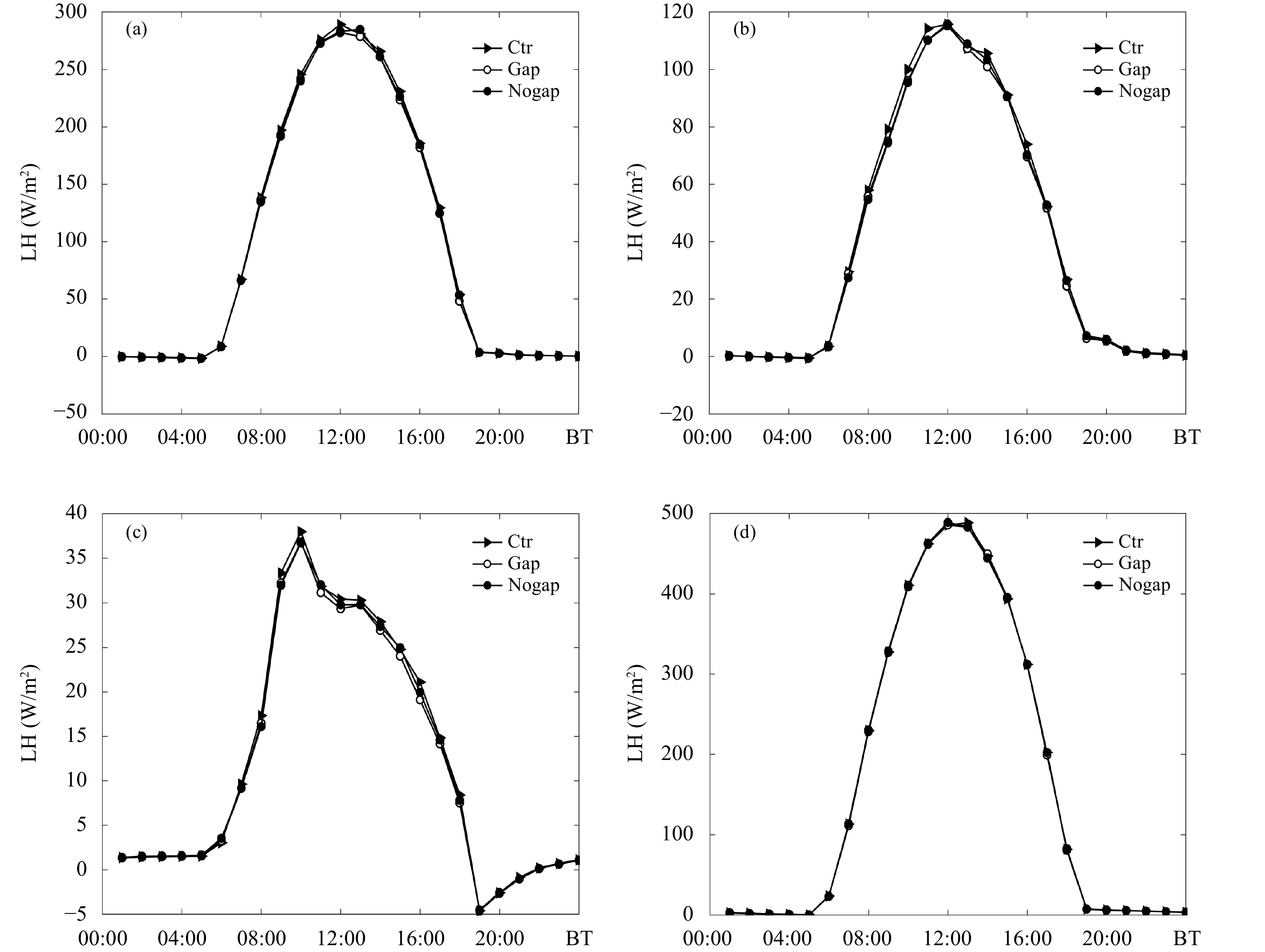
从图7可以看出,光伏屋顶对于潜热通量的影响很小,特别是商业区,其城市覆盖率高,大多为不透水面,普通屋顶的潜热通量峰值仅为37.98 W/m2。贴覆式安装和支架式安装分别减少了1.28和1.16 W/m2。
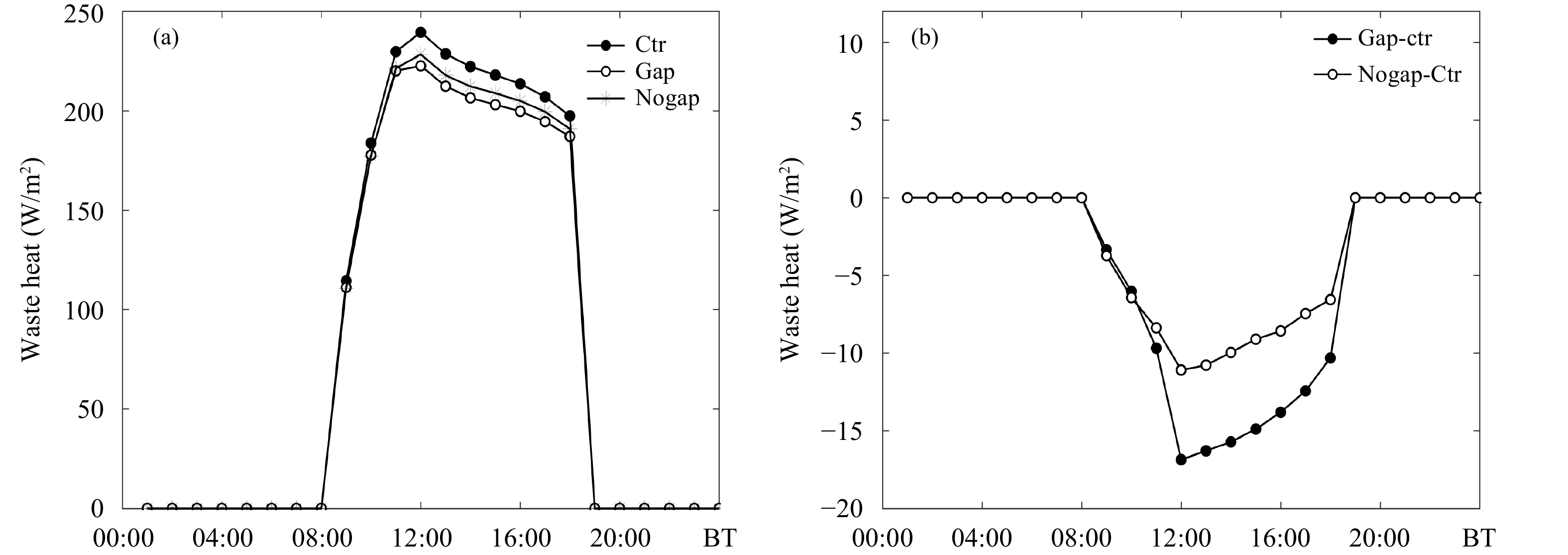
除了地表的热通量,建筑物的废热排放也可能对近地层气温产生影响。由于光伏板的遮蔽作用,白天较少的短波辐射入射到屋顶,抑制热量进入室内,从而降低空调的能耗。在BEP/BEM方案中,室内的热量主要有两个来源,一是人为排放,另外一个重要来源是从屋顶、墙壁及楼道渗透进来的辐射通量。白天太阳辐射越强,光伏屋顶对室内的降温效果越明显。从而间接地减少室内空调的工作能耗,与室外环境形成良性的双向反馈。图8是商业区使用光伏屋顶前、后建筑向外的废热排放量的差值随时间的变化。此处废热排放是根据空调能耗及空调实际能效比反算出来的向室外排放的废热,里面包含了室内人为热及墙壁屋顶等传导进来的热量。从图8可以看到,带有通风流道的屋顶,08—18时(即商业区空调使用期),废热排放均有所减小,最高可减少16.86 W/m2,占排放峰值的7%。
|
| 图 8 使用光伏屋顶前后建筑废热排放随时间的变化 (a. 各屋顶的废热排放,b. 光伏屋顶与普通屋顶差值) Fig. 8 Waste heat from construction (a. waste heat discharge from each type of roof,b. the difference between photovoltaic roof and ordinary roof) |
湍流动能作为湍流边界层中最重要的物理量之一,关系到边界层内动量、热量及水汽的垂直输送。光伏屋顶影响近地面气象要素的同时,对于湍流动能也可能产生影响。
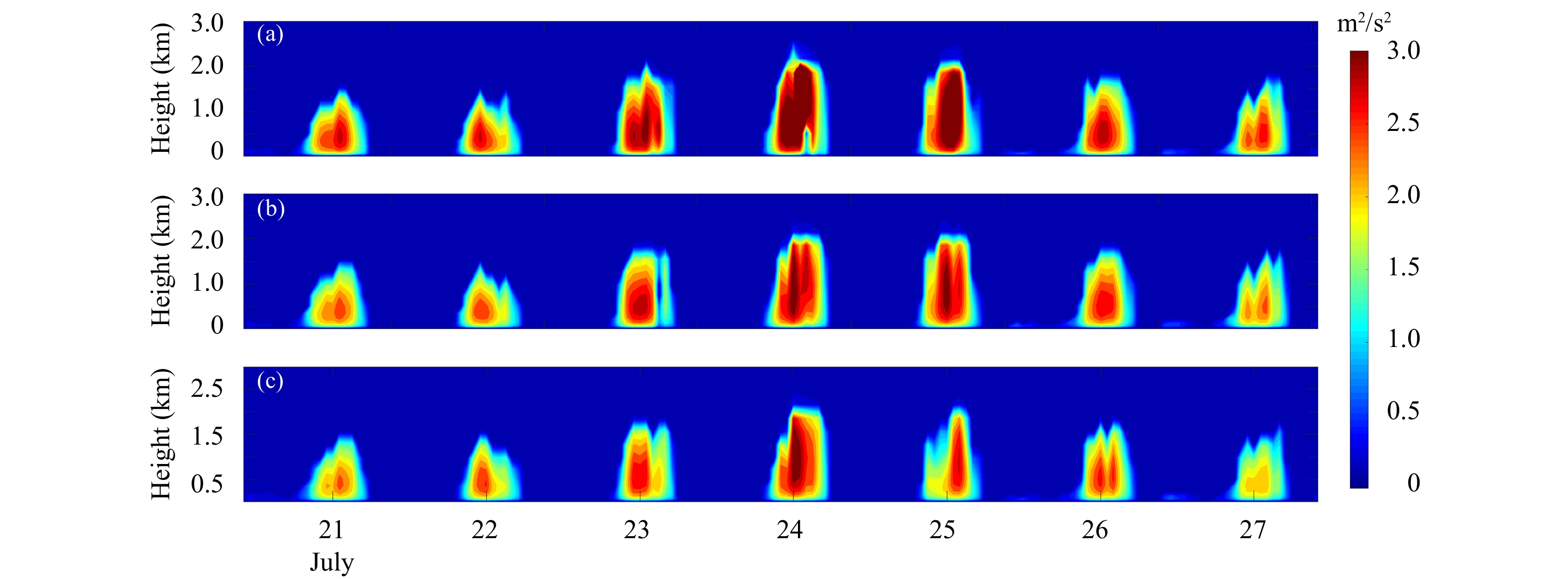
以南京站为例,图9给出南京站7月21—27日湍流动能的时、空分布特征。
|
| 图 9 南京站各屋顶湍流动能的垂直分布 (a. 普通屋顶,b. 支架式安装,c. 贴覆式安装) Fig. 9 Vertical distributions of turbulence energy for various types of roof in Nanjing Station (a. normal roof,b. scaffolding roof,c. attached roof) |
从图9可以看到,3种屋顶的湍流垂直分布结构相似,最大值出现在14时前后,夜间明显减弱。白天湍流发展较弱时(如7月27日),普通屋顶、支架式及贴覆式光伏屋顶的峰值分别为2.69、2.47、2.17 m2/s2。在湍流发展旺盛时(如7月24日),3种屋顶的动能峰值分别6.44、3.38、3.31 m2/s2。由此可见,光伏屋顶对于湍流动能起削弱作用,一定程度上抑制白天边界层的发展。在湍流发展旺盛的情形下,光伏屋顶的削弱作用更加明显。贴覆式光伏屋顶由于白天表面温度更低,对大气的加热作用弱于其他两种屋顶,湍流动能强度最弱。边界层高度影响污染物在垂直方向上的分布和扩散,对大气污染的形成、发展、维持与消散起重要作用。在不稳定大气层中,湍流尺度受上边界(边界层顶)和下边界(地面)限制,空间上的尺度大小可以侧面反映边界层高度的变化。在局地闭合方案中,以湍流动能的临界值为指标,一般认为小于0.1 m2/s2的最低高度为边界层高度。图10给出的是7月24日14、18及22时湍流动能随高度的变化,可以明显地看到,14时普通屋顶在2.63 km处(模式第12层)湍流动能已降至0.1 m2/s2。光伏屋顶湍流影响高度低于普通屋顶,支架式屋顶最高达到2.17 km(模式第11层),贴覆式屋顶影响高度为1.85 km(模式第10层)。18和22时,失去太阳短波辐射的加热,湍流动能逐渐减弱,湍流影响高度随之降低,屋顶之间的差异也随之变小。

|
| 图 10 7月24日不同时段湍流动能随高度变化 (a. 14时,b. 18时,c. 22时) Fig. 10 Variations of turbulent energy with altitude at different times on July 24 (a. 14:00 BT,b. 18:00 BT,c. 22:00 BT) |
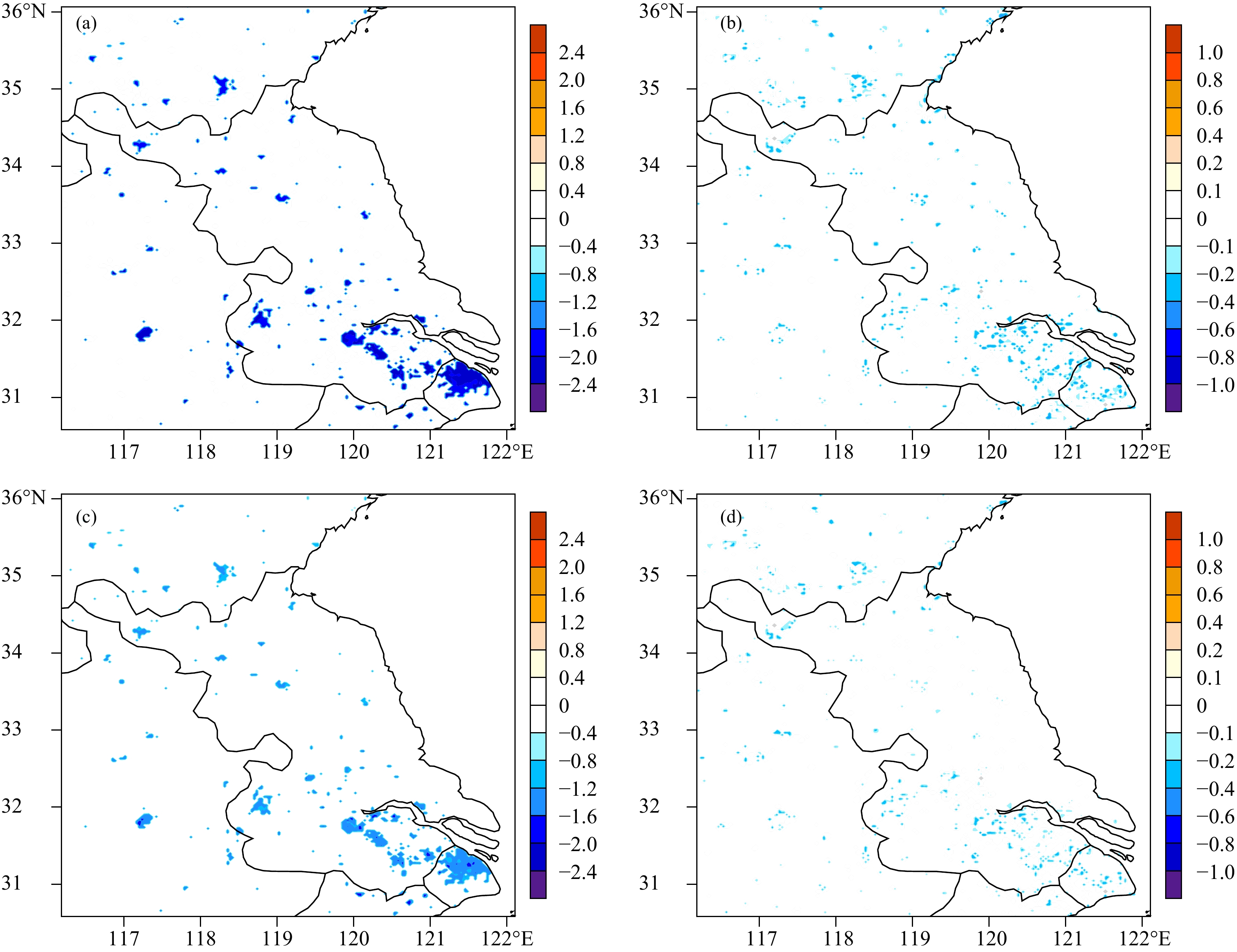
除了降低城市热岛强度外,减少室内电能消耗是安装太阳能屋顶的很重要的一个目标。光伏屋顶除了能减少能耗,最大的一个优势在于它能够将部分太阳能转化为电能,缓解当前的能源压力。从白天及夜间光伏屋顶与普通屋顶空调能耗差异的平均值(图11)可以看出,屋顶光伏板(图11a)在白天可以减少商业区空调用电量,其中支架式屋顶最多可减少2.35 W/m2的能耗。而贴覆式屋顶白天的节能效果弱于支架式屋顶,可以达到1.72 W/m2。夜间住宅区空调开启,支架式屋顶可减少0.43 W/m2,而贴覆式最多可以减少0.26 W/m2。
|
| 图 11 光伏屋顶 (a、b. 支架式,c、d. 贴覆式) 与普通屋顶空调能耗 (单位:W/m2) 的差值 (a、c. 06—18时平均,b、d.19—05时平均) Fig. 11 Spatial distributions of the influence of photovoltaic roof (a,b. the bracket roof,c,d. the attached roof) on air conditioning energy consumption (a,c. the average cooling rates during 06:00—18:00 BT; b,d. the average cooling rates during 19:00—05:00 BT) |
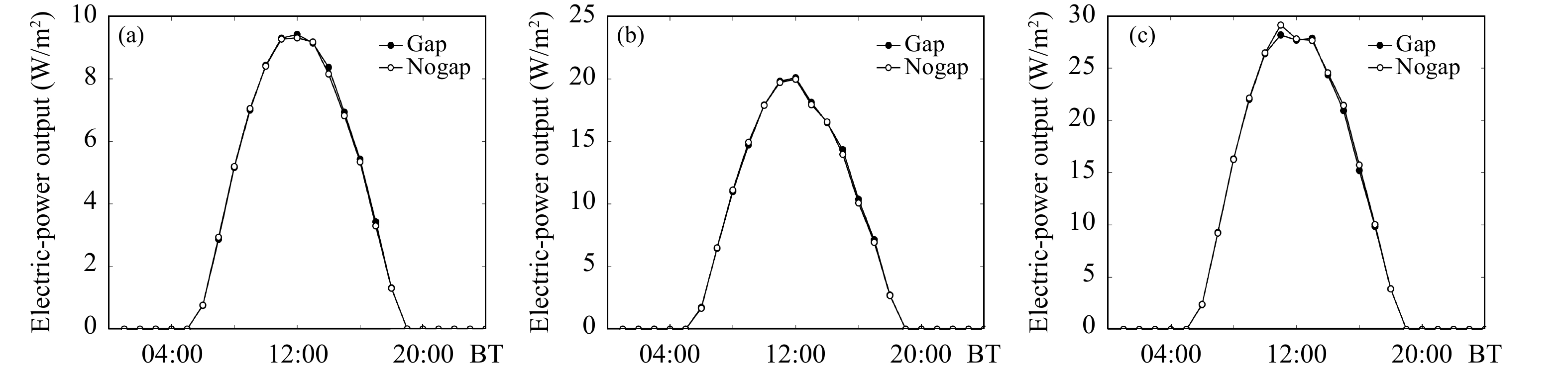
图12、13分别为高密度建筑物区域、低密度建筑区域以及金融区域3种不同城市类型下两种光伏屋顶的发电量和发电效率的平均日变化曲线。此处计算的发电量是参照BEP/BEM方案中空调能耗的处理在整个城市网格上作了加权平均得到的,加权系数
|
| 图 12 光伏屋顶发电量的日变化特征 (a. 低密度住宅区,b. 高密度住宅区,c. 商业区) Fig. 12 Diurnal variation characteristics of photovoltaic roof power generation (a. low-density residential area,b. high-density residential area,c. commercial area) |
|
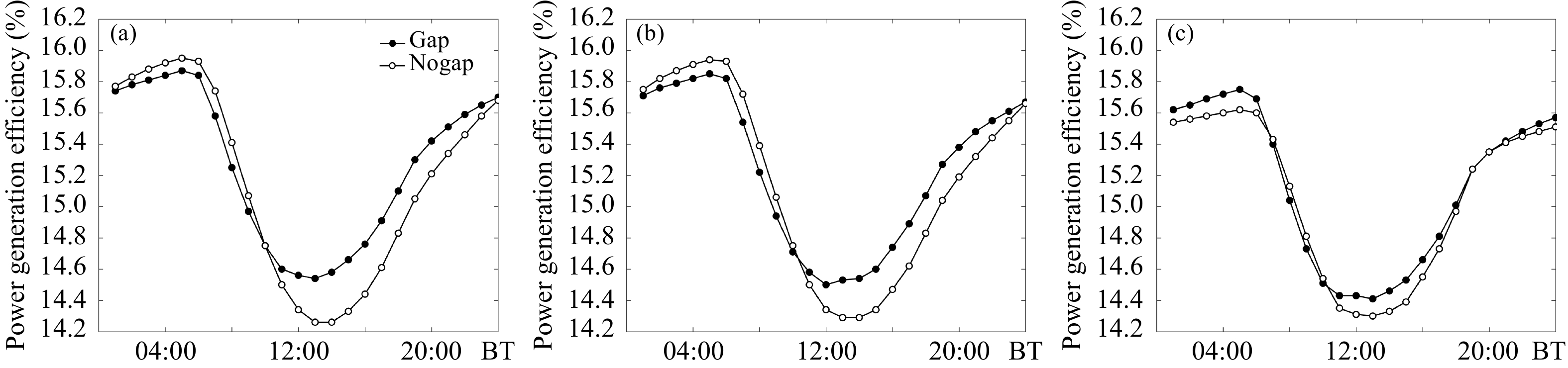
| 图 13 光伏屋顶发电效率的日变化特征 (a. 低密度住宅区,b. 高密度住宅区,c. 商业区) Fig. 13 Diurnal variation characteristics of photovoltaic roof power generation efficiency (a. low-density residential area,b. high-density residential area,c. commercial area) |
| $a = \frac{\,1\,}{\,4\,} \times P \times \left(\frac{{{B_{\rm w}} \times {B_{\rm l}}}}{{({S_{\rm w}} + {B_{\rm w}}) \times {B_{\rm l}}}}{\rm{ + }}\frac{{{B_{\rm w}} \times {B_{\rm l}}}}{{({S_{\rm l}} + {B_{\rm l}}) \times {B_{\rm w}}}}\right)$ |
式中,
不同城市类型下,由于建筑类型、密度不同,区域平均发电量的峰值也各有不同。发电效率为不同高度建筑上计算的发电效率的均值。由图12可以看出,当有阳光照射到光伏组件上时,光伏电池开始工作,随着太阳短波辐射的增强,瞬时发电量也逐渐增大。但与此同时,光伏电池的温度迅速升高,光伏电池的温度成为影响电池发电效率的主要因素,从而降低了光伏组件的发电效率。从图13可以看出,12时前后,光电转换效率降到最低,以商业区为例,支架式及贴覆式屋顶的转换效率分别降至14.4%和14.3%。但此时发电量依旧达到峰值,两种屋顶瞬时发电量均接近30 W/m2。理论上通风流道的设置带走了多余的热量,降低了光伏组件的温度,从而可以提高光伏组件的发电效率和瞬时发电量。但是文中构建的模型是在整个屋顶上铺设光伏板,并未考虑板间的间隔在实际计算过程中的影响,因此流道中空气体积远大于以往试验,模拟时段的空气流速很难对底板温度起到足够的影响。从图12、13中无法特别清晰地看出两种形式光伏屋顶上光伏组件的发电效率和瞬时发电量的差异。
以带通风流道的光伏屋顶为例,其中低密度住宅区、高密度住宅区、商业区发电量峰值分别为9.42、20.09、28.17 W/m2,而空调能耗的峰值分别为4.52、15.59、49.46 W/m2,由此可见光伏板的瞬时发电量是十分可观的。另外,由于模式中设定空调分区域周期工作,而光伏板是在白天有太阳辐射时工作,为了评估光伏板的总体性能,对研究时段作日平均处理,如表6所示,3种城市类型日平均发电率为3.23、6.70、9.76 W/m2,空调总能耗日均值为1.68、5.64、17.91 W/m2,从模拟结果上看,住宅区光伏发电量能够满足同期空调的用电消耗,商业区能够负担同期空调能耗的54.5%。城市类型间比值的差异主要是由于不同城市型的楼层高度不同,楼层越高,住户越多,空调能耗也就越高,商业区仅靠光伏屋顶无法达到低矮住宅区的效果。
| 低密度住宅区 | 高密度住宅区 | 商业区 | |
| 发电量(W/m2) | 3.23 | 6.70 | 9.76 |
| 空调能耗(W/m2) | 1.68 | 5.64 | 17.91 |
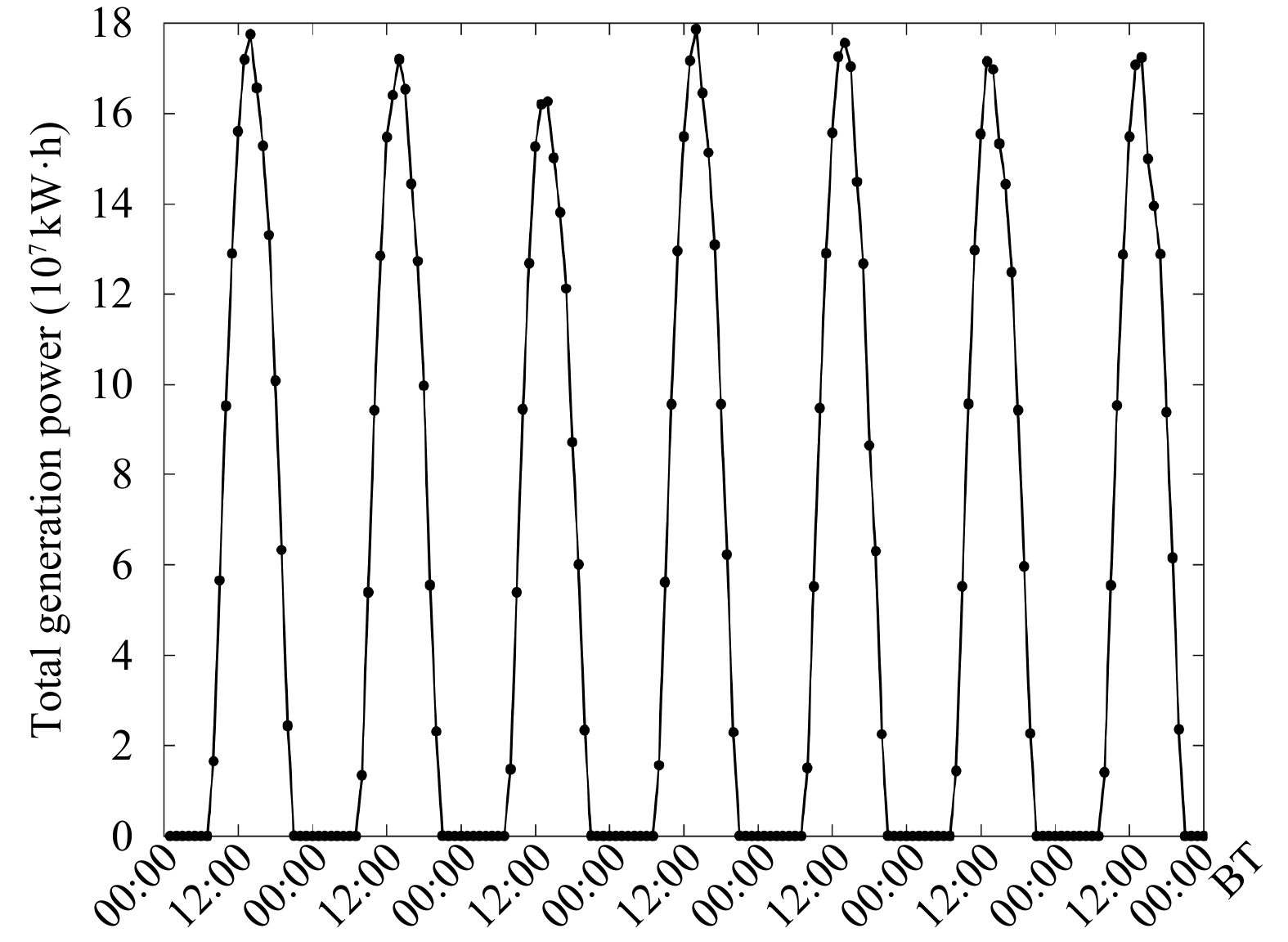
为了能够更加直观地体现光伏屋顶发电量对于全省能源的贡献,文中估算了模式计算所得江苏省光伏屋顶的总发电量。根据模式中城市下垫面分布,估算出低密度住宅区约占城市格点的63%(最内层格点数838),高密度住宅区约占25.3%(格点数337),商业区占11.7%(格点数155)。图14是江苏省总发电量的逐时变化情况(各点数值代表每个时刻之后1小时内的累计发电量)。通过对逐时发电量累计,最终估算得出模拟期间(7月21—27日)使用太阳能屋顶时江苏省发电量约为0.98×1010 kW·h。根据江苏省统计局发布的2017年7月的全社会用电量6.09×1010 kW·h,假设每天用电量相同,则7 d累计用电量为1.38×1010 kW·h,由此可见基本上可以满足城市同期的用电需求。
|
| 图 14 全省光伏屋顶发电量逐时变化 Fig. 14 Hourly change of photovoltaic roof power generation in Jiangsu |
将太阳能光伏板的热传递模型引入到WRF/BEP/BEM多层城市冠层方案中,模拟了贴覆式和支架式两种安装形式的光伏屋顶对于城市热环境及能源的影响。研究结果表明:
(1)2017年7月21—27日江苏省高温热浪期间,安装贴覆式光伏屋顶可以使城市2 m气温白天平均降低0.29°C,降温效果优于支架式屋顶,但夜间降温效果不明显。支架式屋顶白天降温0.23°C,夜间降温效果明显,最高降温0.60°C。
(2)光伏屋顶白天对城市确实可以起到降温作用,但同时也会削弱湍流动能,一定程度上抑制白天边界层的发展。在湍流发展旺盛的情形下,光伏屋顶的削弱作用更加明显。贴覆式屋顶由于白天表面温度更低,对大气的加热作用弱于其他两种屋顶,湍流动能强度最弱。
(3)光伏屋顶除了影响城市气象条件,最重要的还是对能源的贡献。文中将城市分作高密度、低密度居民区以及商业区3类进行讨论,从结果上看,当城市屋顶100%铺设太阳能光伏电池板时,住宅区光伏发电量基本能够满足同期用电需求,商业区发电量能够负担同期空调54.5%的能耗。商业区由于建筑分布密集,它的区域发电量高于其他两种城市类型,但是商业区高层建筑物比例较大,空调的能耗要远高于其他两种城市类型,承载能力弱。结合两种屋顶的模拟结果,贴覆式屋顶对城市热环境的降温效果更好,但对于室内空调能耗的节能效果弱于支架式屋顶。从城市节能角度看,使用支架式屋顶效果更加明显,但支架式屋顶的架设成本高于贴覆式屋顶,因此在城市建筑设计时,应综合考虑收益及成本,选取最适合的架设方式。
文中为了更好地模拟出光伏屋顶对于城市环境的影响,将光伏板的热传递模型引入城市冠层方案,但仍存在一些不足,在实际城市中,建筑物屋顶并非全部水平,而文中构建的光伏屋顶的模型中,并未考虑屋顶存在倾角时的影响,与实际情况仍有出入。文中假设城市100%使用太阳能光伏屋顶,这在未来的规划设计方案中不可能一次性实现。随着材料科学的发展,光伏材料的发电效率会进一步提高,因此在今后的研究中,进一步考虑光伏屋顶按照比例增加以及光伏材料发电效率的提高对于气温变化和能耗的影响状况。此外,当一次能源消耗降低,将会有效地降低二氧化碳的排放量,并进一步对温室效应和城市的气温产生影响,对于中国大城市气候可持续发展的影响也需进一步研究。
致 谢:感谢南京信息工程大学大气环境中心各位老师在写作期间提供的帮助,感谢电力科学研究院的专家在技术方面的指导。
艾欣, 韩晓男, 孙英云. 2013. 大型光伏电站并网特性及其低碳运行与控制技术. 电网技术, 37(1): 15-23. DOI:10.3969/j.issn.1674-0629.2013.01.004 |
李耀孙, 石春娥, 杨军等. 2012. 我国东部地区冬季模式边界层探空效果评估. 高原气象, 31(6): 1690-1703. |
刘晓明. 2017. 基于能源结构视角下的江苏风电发展对策探究. 智库时代, (15): 210,213. |
任建波. 2006. 光伏屋顶形式优化的实验和理论研究[D]. 天津: 天津大学. Ren J B. 2006. Experimental and theoretical study on photovoltaic roofs[D]. Tianjin: Tianjin University (in Chinese)
|
田玮. 2006. 光伏建筑的性能优化及其与城市微气候的相互影响[D]. 天津: 天津大学. Tian W. 2006. Performance optimization of building integrated photovoltaics and its interaction with urban microclimate[D]. Tianjin: Tianjin University (in Chinese)
|
王国复, 叶殿秀, 张颖娴等. 2018. 2017年我国区域性高温过程特征及异常大气环流成因分析. 气候变化研究进展, 14(4): 341-349. DOI:10.12006/j.issn.1673-1719.2018.008 |
王进华. 2007. 激光加工技术使太阳能电池的效率提高到22%. 光机电信息, 24(7): 23-24. DOI:10.3969/j.issn.1007-1180.2007.07.001 |
王玥. 2017. 光伏屋顶遮阳与供电综合节能研究[D]. 西安: 西安建筑科技大学. Wang Y. 2017. Study on comprehensive energy-saving of shading and photovoltaics of roof added PV module[D]. Xi'an: Xi'an University of Architecture and Technology (in Chinese)
|
张艳晴, 刘寿东, 王咏薇等. 2019. 南京地区太阳能屋顶缓解夏季高温的模拟研究. 气象学报, 77(2): 358-370. |
张艳, 鲍文杰, 余琦等. 2012. 超大城市热岛效应的季节变化特征及其年际差异. 地球物理学报, 55(4): 1121-1128. DOI:10.6038/j.issn.0001-5733.2012.04.007 |
赵媛, 郝丽莎. 2006. 江苏省电力工业空间结构优化研究. 长江流域资源与环境, 15(3): 292-297. DOI:10.3969/j.issn.1004-8227.2006.03.005 |
Afonso C, Oliveira A. 2000. Solar chimneys: Simulation and experiment. Energy Build, 32(1): 71-79. DOI:10.1016/S0378-7788(99)00038-9 |
Atkinson B W. 2003. Numerical modelling of urban heat-island intensity. Bound Layer Meteor, 109(3): 285-310. DOI:10.1023/A:1025820326672 |
Chi W F, Shi W J, Kuang W H. 2015. Spatio-temporal characteristics of intra-urban land cover in the cities of China and USA from 1978 to 2010. J Geogr Sci, 25(1): 3-18. DOI:10.1007/s11442-015-1149-z |
Dominguez A, Kleissl J, Luvall J C. 2011. Effects of solar photovoltaic panels on roof heat transfer. Solar Energy, 85(9): 2244-2255. DOI:10.1016/j.solener.2011.06.010 |
Dudhia J. 1989. Numerical study of convection observed during the Winter Monsoon Experiment using a mesoscale two-dimensional model. J Atmos Sci, 46(20): 3077-3107. DOI:10.1175/1520-0469(1989)046<3077:NSOCOD>2.0.CO;2 |
Golden J S. 2006. Photovoltaic canopies: thermodynamics to achieve a sustainable systems approach to mitigate the urban heat island hysteresis lag effect. Int J Sustain Energy, 25(1): 1-21. DOI:10.1080/14786450600593139 |
Hansen J, Sato M, Ruedy R, et al. 2006. Global temperature change. Proc Natl Acad Sci USA, 103(39): 14288-14293. DOI:10.1073/pnas.0606291103 |
Hassid S, Santamouris M, Papanikolaou N, et al. 2000. The effect of the Athens heat island on air conditioning load. Energy Build, 32(2): 131-141. DOI:10.1016/S0378-7788(99)00045-6 |
Hong S Y, Lim J O J. 2006. The WRF single-moment 6-class microphysics scheme (WSM6). J Korean Meteor Soc, 42(2): 129-151. |
Janjić Z I. 1994. The step-mountain eta coordinate model: Further developments of the convection, viscous sublayer, and turbulence closure schemes. Mon Wea Rev, 122(5): 927-945. DOI:10.1175/1520-0493(1994)122<0927:TSMECM>2.0.CO;2 |
Krauter S, Hanitsch R. 1990. The influence of the capsulation on the efficiency of PV-modules//Sayigh A A M. Energy and the Environment. Amsterdam: Elsevier, 371-375
|
Liu J Y, Kuang W H, Zhang Z X, et al. 2014. Spatiotemporal characteristics, patterns, and causes of land-use changes in China since the late 1980s. J Geogr Sci, 24(2): 195-210. DOI:10.1007/s11442-014-1082-6 |
Louis J F. 1979. A parametric model of vertical eddy fluxes in the atmosphere. Bound-Layer Meteor, 17(2): 187-202. DOI:10.1007/BF00117978 |
Masson V, Bonhomme M, Salagnac J L, et al. 2014. Solar panels reduce both global warming and urban heat island. Front Environ Sci, 2: 14. |
Mlawer E J, Taubman S J, Brown P D, et al. 1997. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J Geophys Res Atmos, 102(D14): 16663-16682. DOI:10.1029/97JD00237 |
Oke T R. 1987. Boundary Layer Climate. Cambridge: Great Britain at the University Press, 471-508
|
Sailor D J. 1995. Simulated urban climate response to modifications in surface albedo and vegetative cover. J Appl Meteor, 34(7): 1694-1704. DOI:10.1175/1520-0450-34.7.1694 |
Salamanca F, Martilli A. 2010. A new building energy model coupled with an urban canopy parameterization for urban climate simulations--part II. Validation with one dimension off-line simulations. Theor Appl Climatol, 99(3-4): 345-356. |
Salamanca F, Georgescu M, Mahalov A, et al. 2016. Citywide impacts of cool roof and rooftop solar photovoltaic deployment on near-surface air temperature and cooling energy demand. Bound Layer Meteor, 161(1): 203-221. DOI:10.1007/s10546-016-0160-y |
Tewari M, Chen F, Wang W, et al. 2004. Implementation and verification of the unified NOAH land surface model in the WRF model//Proceedings of the 20th Conference on Weather Analysis and Forecasting/16th Conference on Numerical Weather Prediction. Seattle: Amer Meteor Soc, 11-15
|
Tian W, Wang Y P, Xie Y Y, et al. 2007. Effect of building integrated photovoltaics on microclimate of urban canopy layer. Build Environ, 42(5): 1891-1901. DOI:10.1016/j.buildenv.2006.02.022 |
Xu X Y, Chen F, Shen S H, et al. 2018. Using WRF-urban to assess summertime air conditioning electric loads and their impacts on urban weather in Beijing. J Geophys Res Atmos, 123(5): 2475-2490. DOI:10.1002/2017JD028168 |
Yang H X, Zhu Z J, Burnett J, et al. 2001. A simulation study on the energy performance of photovoltaic roofs. ASHRAE Trans, 107(2): 129-135. |
Zhang N, Chen Y, Luo L, et al. 2017. Effectiveness of different urban heat island mitigation methods and their regional impacts. J Hydrometeorol, 18(11): 2991-3012. DOI:10.1175/JHM-D-17-0049.1 |
 2020, Vol. 78
2020, Vol. 78