中国气象学会主办。
文章信息
- 江志红, 常奋华, 丁裕国 . 2013.
- JIANG Zhihong, CHANG Fenhua, DING Yuguo . 2013.
- 基于马尔科夫链转移概率极限分布的降水过程持续性研究
- An investingation into continuous precipitation based on the Markov transition probability limit distribution
- 气象学报, (2): 286-294
- Acta Meteorologica Sinica, (2): 286-294.
- http://dx.doi.org/10.11676/qxxb2013.028
-
文章历史
- 收稿日期:2011-07-12
- 改回日期:2012-12-10
逐日天气变化是气候变化的基础,气候特征又是逐日天气演变的背景。转折性天气往往是日常业务预报的难点,尤其是极端天气气候事件的出现,往往因强烈的天气状态转折而产生,某种天气状态的持续与转折总是有一定规律可寻的。根据马尔科夫链理论,若一种天气状态转移为其他天气状态的转移概率很小,则意味着这种状态的持续性很强。各地不同气候条件所具有的天气状态转移概率的极限分布实际上代表了各地天气气候的持续性和转折性特征。从理论上说,在大量同类自然现象中,往往会表现出相对于某种标准值的偏差状态(例如:对于逐日天气状态为有雨),这种偏差状态随着时间的推移维持不变时,就形成了持续性。例如对于逐日天气状态为连续有雨或无雨,对于逐月(或旬)持续旱涝,连续暴雨,连续高温(或低温)等。这些现象的发生,对人们日常生活和生产影响很大,也是灾害性天气气候的持续性特征,更是各种时间尺度预报的重要基础之一。
马尔科夫链方法很早就成为统计气象学研究和应用的主要模型之一,并已取得很多成果。例如,Brooks等(1953)曾在他们的著作中首次应用马尔科夫链分析逐日晴雨变化。其后,Gabriel 等(1962)又用一阶两状态简单马尔科夫链模拟研究了以色列首都特拉维夫逐日降水纪录。Katz(1974)提出一个计算湿日出现概率的改进方法。Gates等(1976)再次计算了特拉维夫站的逐日降水记录,认为二阶马尔科夫链对降水拟合很好。
马尔科夫链模式模拟气候序列的工作中国做得不多,最早由么枕生(1966)提出改进的马尔科夫链,在划分状态时将以往记录的影响考虑在内,用各个状态的历史演变来定义新的状态,取得较好效果。王宗皓等(1974)曾用马尔科夫链研究天气变化持续性指标及其预报问题。周家斌等(1997)用马尔科夫链预报浙北汛期逐日晴雨变化。张耀存等(1990a)从逐日降水过程干、湿日演变的一阶马尔科夫链及日降水量的伽马分布模式出发,从理论上求得任意给定的N日总雨量及最大日雨量的理论分布函数,同时得到N日总雨量和最大日雨量的数学期望及方差,初步证实所得模式的普适性。由此可利用该模式估计任意给定时期内N日降水总量和最大日降水量的概率。丁裕国等(1992)利用马尔科夫链研究中国各大气候区若干代表测站干、湿月游程的统计特征,得到许多有实际应用意义的统计气候信息。但是,以往应用马尔科夫链大多是以长期天气预报的研究为目标,并未联系到气候变化和全球气候问题。自20世纪90年代以来,全球气候变暖及人类活动对气候影响的问题日益突出,利用基于马尔科夫链理论所构建的随机天气发生器进行统计随机模拟使得降尺度方法可直接模拟极端天气气候事件。张耀存等(1990b)曾用多状态的马尔科夫链,采用蒙特卡罗方法建立了一种可以产生单站逐日降水量记录的随机模式。通过检验发现,模式模拟的气候统计参数同实测结果十分吻合。廖要明等(2004)曾建立以两状态一阶马尔科夫和两参数伽马分布为基础的适用于中国广大地区的随机天气发生器,根据中国720个气象站点30 a的逐日降水资料计算了降水转移及分布参数并分析了伽马分布参数在中国各地的空间分布特征与不同地区各参数的季节分布特征,最后根据各地不同月份计算结果进行了统计检验,效果较好。董婕等(1997)用这一方法对陕西省6个代表站(30 a资料)的逐日降水资料模拟结果也较好。由此可见,利用马尔科夫链模型作为描述逐日气象要素演变过程的统计模型是相当可行的。然而,基于马尔科夫链模型的随机天气发生器尚有许多值得深入探讨的问题,而马尔科夫链模型本身的一些理论问题尚未深入探讨,例如,状态的划分究竟以多少为宜;对于逐日晴雨状态明显不对称的各站或地区,如何划分状态更为合理;转移概率矩阵的极限分布有何物理意义等,都有必要深入探讨(丁裕国等,1989;张耀存等,1990b)。特别是么枕生(1984)虽提到正则马尔科夫链的应用,但并未能作深入探讨。本研究的目的在于,从马尔科夫链理论出发,根据逐日降水状态的转移矩阵,初步研究逐日降水天气状态演变过程的极限分布。由此若能算得各地逐日降水天气状态演变过程的极限分布,则各地的天气气候状态的自然持续性(如自然天气周期)(章基嘉等,1994)的气候状况,就可一目了然。2 马尔科夫链状态转移规律
据马尔科夫链理论(丁裕国等,2009a),随机变量的状态空间具有不同的类型,而马尔科夫链也有不同的类别。首先,根据实测天气气候记录,总可以找到符合实际的马尔科夫链类型作为模拟模式。根据一般的分类方法,按照状态空间的性质(集合属性),马尔科夫链大致可分为:(1)非瞬时集的马尔科夫链,包括正则马尔科夫链(仅含有一个各态遍历集)和循环马尔科夫链(含有周期状态)。(2)瞬时集的马尔科夫链。
本文主要涉及到(1)中的正则马尔科夫链。所谓正则马尔科夫链,简单地说就是其转移概率矩阵是没有0值分量的矩阵,不论从任何状态出发,在n步以后都能达到其状态集中的任何一种状态(么枕生,1984;么枕生等,1990)。由于正则马尔科夫链较易数学处理,而且,天气气候的随机变化一般都符合正则马尔科夫链。即从任一状态i出发,经过若干步转移都可到达任何一种状态(含自身),这也就是正则马尔科夫链的主要性质特点。特别是,正则马尔科夫链的转移概率具有极限: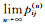 =ak,下标j,k分别代表任一状态,而且,它们彼此无关。其右端的元素ak正是极限转移矩阵A=
=ak,下标j,k分别代表任一状态,而且,它们彼此无关。其右端的元素ak正是极限转移矩阵A= 的元素,其中,向量ak即为极限向量。这就是正则马尔科夫链的转移概率矩阵的极限分布。3 数值试验及其结果分析3.1 资料与状态划分
的元素,其中,向量ak即为极限向量。这就是正则马尔科夫链的转移概率矩阵的极限分布。3 数值试验及其结果分析3.1 资料与状态划分
本文选用全中国160个站(图 1)1960—2009年共有50 a逐日降水资料。
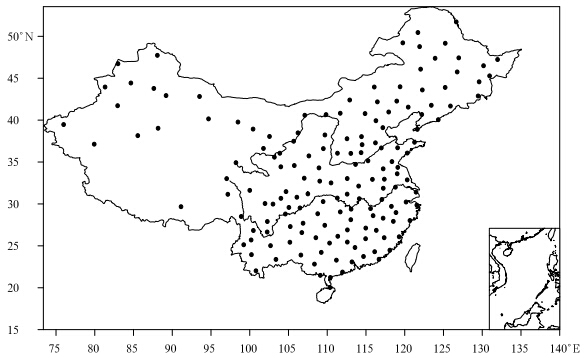 |
| 图 1 站点分布 Fig. 1 Distribution of the stations used in this article |
根据马尔科夫链理论,系统的某一状态在转移过程中,其第n次结果只受第n-1次结果的影响,即系统只与当前所处状态有关,而与过去状态无关。在状态转移过程中,系统由一种状态到另一种状态的概率可作为考察系统变化过程的重要指标。
参考丁裕国等(2009b)和Ding等(2010)对各站逐日降水变化过程的状态划分标准,对上述160个测站都采用下列经验公式划分为8种状态,并按四季分别进行统计。
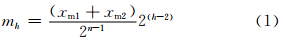
| 状态 | S0 | S1 | S2 | S3 | S4 | S5 | S6 | S7 |
| 齐齐哈尔 | (0.0,0.1] | (0.1,1.6] | (1.6,3.2] | (3.2,6.4] | (6.4,12.9] | (12.9,25.7] | (25.7,51.5] | (51.5,∞) |
| 北京 | (0.0,0.1] | (0.1,2.9] | (2.9,5.8] | (5.8,11.5] | (11.5,23.0] | (23.0,46.1] | (46.1,92.1] | (92.1,∞) |
| 郑州 | (0.0,0.1] | (0.1,2.8] | (2.8,5.7] | (5.7,11.3] | (11.3,22.7] | (22.7,45.3] | (45.3,90.7] | (90.7,∞) |
| 成都 | (0.0,0.1] | (0.1,3.1] | (3.1,6.2] | (6.2,12.3] | (12.3,24.7] | (24.7,49.3] | (49.3,98.6] | (98.6,∞) |
| 南京 | (0.0,0.1] | (0.1,3.0] | (3.0,6.0] | (6.0,12.1] | (12.1,24.2] | (24.2,48.3] | (48.3,96.6] | (96.6,∞) |
| 上海 | (0.0,0.1] | (0.1,2.9] | (2.9,5.8] | (5.8,11.5] | (11.5,23.1] | (23.1,46.1] | (46.1,92.2] | (92.2,∞) |
| 广州 | (0.0,0.1] | (0.1,3.9] | (3.9,7.7] | (7.7,15.4] | (15.4,30.8] | (30.8,61.6] | (61.6,123.2] | (123.2,∞) |
众所周知,运用马尔科夫链分析方法,最关键的是如何估计系统的转移概率矩阵,因为齐次马尔科夫链仅与初始分布和一步转移概率矩阵有关,故本文利用统计估算法,设(s1,s2,…,sv)代表变量的v种状态序列,假定用fj(n)表示样本序列从状态si经n步转移到达状态sj的频数,由pij(n)组成的矩阵为转移频率矩阵,其中,转移频率的计算公式为
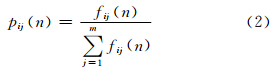
从理论上说,当n充分大时,转移频率近似等于转移概率,其中,一步转移概率矩阵为P1=Pij,转移概率矩阵P1的估计为

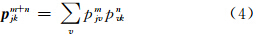
(1)一步转移概率矩阵
在用59 a(1951—2009年)160站逐日降水资料计算出的各个(一步)转移矩阵中,以夏季(6—8月)喀什、南京、海口3个站的结果为例,说明其逐日转移规律。由3个站的一阶转移概率矩阵可见:喀什站从任何状态经一步(天)转为晴日的概率均在0.65以上,而海口站从状态S7至状态S1的概率(0.31)大于状态S7至S0的概率(0.25),即大雨经过1 d后转为小雨的概率比转晴的概率大。这几个站的转移概率矩阵数值为
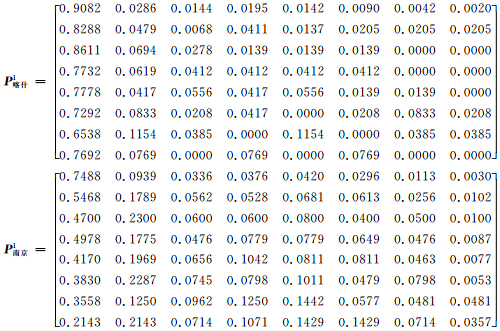
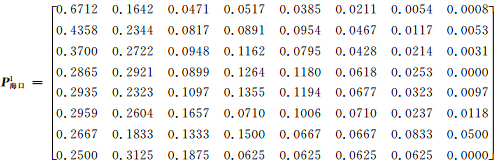
(2)多步转移概率矩阵
由马尔科夫链的遍历性可见,转移矩阵的极限正是指:当转移步数n→∞时,状态的转移概率是否收敛于极限概率P*,而P*与初始状态无关。本文对所选测站求得的极限分布,完全符合正则马尔科夫链的各态遍历性。例如,从后面所列出的南京站夏季多步转移概率矩阵结果可见,从1步转移概率矩阵到4步转移概率矩阵,其各列并无0值分量(表明它符合正则马尔科夫链),而且各列已将近相等,说明经过4步(天)的平稳转移后,趋于一个稳定的状态,通常将这个稳定的状态称为极限状态。比较全国各站四季的极限矩阵的分布特征可以看到(表略):春季,长江以北大部分地区的首列数值均超过0.60。秋季,西南地区首列数值均在0.60以下。冬季,江南南部和华南北部地区一步转移概率矩阵首列数值均在0.60以下。其中夏季数值最小,冬季数值最大的区域位于北部和中西部;而一年四季无明显差别的是贵州和新疆地区,秋季最大,春季最小值则位于江南地区(湖南、江西、福建、浙江),且春夏一致,秋冬一致的地区为广东和上海。经过多步转移后,天气状态的概率就收敛于某一极限P*,而与初始状态无关。根据柯尔莫哥洛夫方程,可求得各步转移矩阵,依此类推,可求得全中国160站的逐日天气气候状态转移概率极限矩阵,为节省篇幅,引入矩阵的F范数加以表述(丁裕国等,1993)。因为范数乃是长度概念的推广,它既节省篇幅,又可以标志转移概率极限矩阵的主要特征(向量或矩阵的数字特征)。所谓矩阵A的F范数,定义为
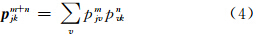
例如,在表 2—7中,列出了北京、南京、广州等7个代表测站不同年限的夏季各步转移矩阵的F范数,由表可见,其收敛的稳定性不论对于哪一个年份段,都基本符合上述规律。
| 站点 | 1步 | 2步 | 3步 | 4步 | 5步 | 6步 | 7步 |
| 齐齐哈尔 | 1.622639 | 1.783703 | 1.820839 | 1.828580 | 1.830254 | 1.830743 | 1.830968 |
| 北京 | 1.630113 | 1.821459 | 1.870340 | 1.879929 | 1.881744 | 1.882127 | 1.882203 |
| 成都 | 1.450076 | 1.561722 | 1.593520 | 1.599587 | 1.600775 | 1.601010 | 1.601042 |
| 郑州 | 1.686708 | 1.896850 | 1.986136 | 2.011880 | 2.019093 | 2.021134 | 2.021780 |
| 南京 | 1.522967 | 1.750887 | 1.850577 | 1.883947 | 1.894500 | 1.897751 | 1.898760 |
| 上海 | 1.523723 | 1.706741 | 1.804449 | 1.838302 | 1.849577 | 1.853231 | 1.854429 |
| 广州 | 1.370592 | 1.419357 | 1.485333 | 1.514792 | 1.525913 | 1.529973 | 1.531454 |
| 站点 | 1步 | 2步 | 3步 | 4步 | 5步 | 6步 | 7步 |
| 齐齐哈尔 | 1.634495 | 1.791264 | 1.830098 | 1.838497 | 1.840291 | 1.840792 | 1.840923 |
| 北京 | 1.614473 | 1.813403 | 1.864442 | 1.874862 | 1.876861 | 1.877143 | 1.877074 |
| 成都 | 1.450375 | 1.556128 | 1.585414 | 1.592127 | 1.593062 | 1.593172 | 1.593238 |
| 郑州 | 1.680179 | 1.883778 | 1.985764 | 2.016782 | 2.025915 | 2.028634 | 2.029428 |
| 南京 | 1.526709 | 1.745660 | 1.841672 | 1.872832 | 1.882391 | 1.885411 | 1.886429 |
| 上海 | 1.486291 | 1.703475 | 1.800716 | 1.836099 | 1.848531 | 1.852764 | 1.854269 |
| 广州 | 1.329925 | 1.386514 | 1.453344 | 1.484310 | 1.496893 | 1.501867 | 1.503875 |
| 站点 | 1步 | 2步 | 3步 | 4步 | 5步 | 6步 | 7步 |
| 齐齐哈尔 | 1.612365 | 1.781335 | 1.826298 | 1.836178 | 1.838359 | 1.838858 | 1.839022 |
| 北京 | 1.672209 | 1.861316 | 1.903536 | 1.911580 | 1.913064 | 1.913342 | 1.913324 |
| 成都 | 1.454375 | 1.557128 | 1.586414 | 1.592027 | 1.592962 | 1.593072 | 1.592938 |
| 郑州 | 1.620982 | 1.868994 | 1.965125 | 1.995525 | 2.004828 | 2.007622 | 2.008437 |
| 南京 | 1.532913 | 1.760435 | 1.849490 | 1.876173 | 1.883647 | 1.885767 | 1.886284 |
| 上海 | 1.495137 | 1.676095 | 1.781660 | 1.823883 | 1.839834 | 1.845780 | 1.847894 |
| 广州 | 1.330779 | 1.385473 | 1.444945 | 1.473849 | 1.486270 | 1.491447 | 1.493609 |
| 站点 | 1步 | 2步 | 3步 | 4步 | 5步 | 6步 | 7步 |
| 齐齐哈尔 | 1.540433 | 1.684659 | 1.735176 | 1.747548 | 1.750376 | 1.750955 | 1.751019 |
| 北京 | 1.727264 | 1.865315 | 1.894034 | 1.898132 | 1.898861 | 1.899024 | 1.899097 |
| 成都 | 1.450736 | 1.558867 | 1.586761 | 1.591799 | 1.592666 | 1.592785 | 1.592793 |
| 郑州 | 1.707621 | 1.932279 | 2.011730 | 2.032524 | 2.037655 | 2.039047 | 2.039569 |
| 南京 | 1.547005 | 1.765452 | 1.876561 | 1.917336 | 1.931643 | 1.936630 | 1.938381 |
| 上海 | 1.582679 | 1.743348 | 1.878341 | 1.934004 | 1.955715 | 1.963955 | 1.967087 |
| 广州 | 1.445974 | 1.395641 | 1.461653 | 1.494652 | 1.508076 | 1.513294 | 1.515301 |
| 站点 | 1步 | 2步 | 3步 | 4步 | 5步 | 6步 | 7步 |
| 齐齐哈尔 | 1.616368 | 1.782812 | 1.822367 | 1.829894 | 1.831216 | 1.831367 | 1.831346 |
| 北京 | 1.638597 | 1.821456 | 1.870389 | 1.880914 | 1.883002 | 1.883315 | 1.883329 |
| 成都 | 1.449104 | 1.562837 | 1.595722 | 1.602089 | 1.603299 | 1.603450 | 1.603482 |
| 郑州 | 1.682404 | 1.919716 | 2.002970 | 2.024101 | 2.029163 | 2.030261 | 2.030491 |
| 南京 | 1.543347 | 1.772490 | 1.880170 | 1.918440 | 1.931400 | 1.935663 | 1.937020 |
| 上海 | 1.543496 | 1.758369 | 1.864479 | 1.901805 | 1.914350 | 1.918609 | 1.920074 |
| 广州 | 1.364248 | 1.391599 | 1.452048 | 1.478905 | 1.488930 | 1.492485 | 1.493701 |
| 站点 | 1步 | 2步 | 3步 | 4步 | 5步 | 6步 | 7步 |
| 齐齐哈尔 | 1.578011 | 1.770151 | 1.821074 | 1.832298 | 1.834736 | 1.835317 | 1.835508 |
| 北京 | 1.642873 | 1.845475 | 1.892400 | 1.901472 | 1.903227 | 1.903471 | 1.903490 |
| 成都 | 1.445916 | 1.568441 | 1.602466 | 1.609320 | 1.610617 | 1.610923 | 1.610987 |
| 郑州 | 1.651586 | 1.892188 | 1.982048 | 2.007934 | 2.015261 | 2.017373 | 2.018058 |
| 南京 | 1.528817 | 1.763466 | 1.858561 | 1.888088 | 1.896668 | 1.898946 | 1.899406 |
| 上海 | 1.552948 | 1.715596 | 1.795549 | 1.824190 | 1.833883 | 1.837040 | 1.837977 |
| 广州 | 1.330262 | 1.391460 | 1.455035 | 1.485053 | 1.497388 | 1.502225 | 1.504083 |
若各站转移概率矩阵随样本容量增大而达到稳定状态,则计算结果较为可靠,否则,因转移概率抽样波动太大会造成计算结果出现较大波动。为了论证状态转移矩阵的最小样本容量,以南京逐日降水资料为例,计算了样本为10 a(1960—1969年)、20 a(1960—1979年)、30 a(1960—1989年)夏季的转移概率矩阵,结果如表 2—7。
当样本容量为30 a(P30)时,转移矩阵已基本稳定(非常接近于样本容量为50 a(P50)的数值),换言之,30 a的数据已经趋于稳定状态了。即使样本数量再增加,最后也是趋于这个稳定状态。
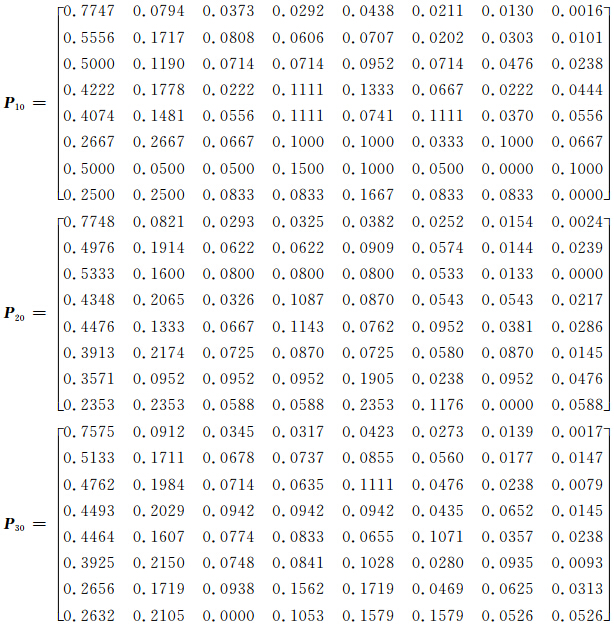
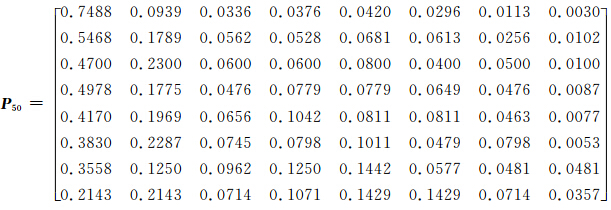
此外,为了更好地说明上述规律,对全部站点做了相应的试验,结果表明,基本上都有上述规律。表 4—7列出了北京等7个代表站的各步转移矩阵的F范数。由表可见,30 a的数据已经趋于稳定状态了。它与50 a的数据非常相似相近。尤其是第6至第7步转移矩阵范数几乎完全相同。4 转移概率极限分布特征
根据一阶转移概率矩阵求极限转移概率矩阵,可以估计各地降水持续期的极限天数长短,例如在图 2中,运用50 a(1960—2009年)降水资料估计得到中国除西藏地区以外的所有地区各季降水持续期极限天数。
 |
| 图 2 各地四季降水持续期的极限天数(a.春季,b.夏季,c.秋季,d.冬季) Fig. 2 Limit number of days of seasonal precipitation duration in the various areas(a.spring,b.summer,c.autumn,and d.winter) |
由图 2可见,春季,在华南中东部和西南地区南部的持续时间在6 d以上,夏季江南和华南地区的持续期在6 d以上,内蒙古和东北地区一年四季的持续期都相对较短,华南和江南地区一年四季的持续期都相对较长。综合4幅图可看到夏季持续期最短,持续期由北向南、由西向东呈增加趋势。
就全中国平均而言,春季平均降水持续期为5.1 d,夏季平均为5.0 d,秋季平均为6.5 d,冬季平均为6.2 d(表 8)。一般夏季要比其他季节的降水持续期短,这可能是因为夏季的天气系统比较复杂,而且中小尺度天气系统较多的缘故。
| 可预报长度 | 春季 (3—5月) | 夏季 (6—8月) | 秋季 (9—11月) | 冬季 (12—2月) |
| 平均值 | 5.1 | 5.0 | 6.5 | 6.2 |
| 众数值 | 5 | 4 | 8 | 5 |
利用正则马尔科夫链理论中的一阶转移概率矩阵的极限分布性质,估算了全中国(主要是东部地区)各地一阶转移概率的极限分布,经统计分析各站多步转移概率的分布规律发现,就全中国平均而言,如图 2所示,夏季持续期最短,持续期由北向南、由西向东呈增加趋势,而且,春季平均降水持续期为5.1 d,夏季平均为5.0 d,秋季平均为6.5 d,冬季平均为6.2 d。可见夏半年比冬半年的降水持续期短,这可能是因为春夏季的天气系统比较复杂且中小尺度天气系统较多的缘故。这就从另一侧面再次证明,各地逐日降水天气状态演变过程具有一定的天气气候状态自然转折的持续性即自然天气周期的气候状况,从而为短期天气预报提供了气候背景。总而言之:
(1)从马尔科夫链理论出发,研究中国各站逐日天气状态演变过程的极限分布,所得结果可以描述降水过程的持续性。
(2)分析和计算结果表明,多状态马尔科夫链的状态转移概率极限矩阵估算降水持续期的极限天数,有的地区仅有3 d持续期,有的可达4—6 d或更长,充分反映出不同地区因其影响天气系统的差异而造成的逐日天气气候的持续性和转折性特征所固有的差异,为天气气候分型区划提供了一种理论依据。
| 丁裕国, 张耀存. 1989. 降水气候特征的随机模拟试验. 南京气象学院学报, 12(2): 146-154 |
| 丁裕国, 牛涛. 1992. 干、湿月游程的Markov链模拟. 南京气象学院学报, 13(3): 286-297 |
| 丁裕国, 江志红. 1993. 气象场相关结构对EOF展开稳定性的影响. 气象学报, 51(3): 448-456 |
| 丁裕国, 江志红. 2009a. 极端气候研究方法导论. 北京: 气象出版社, 235pp |
| 丁裕国, 张金铃, 江志红. 2009b. 基于多状态Markov链模式的极端降水模拟试验. 气象学报, 67(1): 20-27 |
| 董婕, 周小刚. 1997. 西安气象要素变化的马尔科夫链概型预报. 陕西师范大学学报(自然科学版), 25(3): 104-106 |
| 廖要明, 张强, 陈德亮. 2004. 中国天气发生器的降水模拟. 地理学报, 59(5): 689-698 |
| 王宗皓, 李麦村. 1974. 天气预报中的概率统计方法. 北京: 科学出版社, 116-128 |
| 么枕生. 1966. 湿日与干日随机变化的概率. 气象学报, 36(2): 249-256 |
| 么枕生. 1984. 气候统计学基础. 北京: 科学出版社, 594pp |
| 么枕生, 丁裕国. 1990. 气候统计. 北京: 气象出版社, 594pp |
| 章基嘉, 葛林, 孙照勃. 1994. 中长期天气预报基础. 北京: 气象出版社, 364pp |
| 张耀存, 丁裕国. 1990a. N日降水量的随机分布模式. 南京气象学院学报, 13(1): 23-30 |
| 张耀存, 丁裕国. 1990b. 我国东部地区几个代表测站逐日降水序列统计分布特征. 南京气象学院学报, 13(2): 194-203 |
| 周家斌, 黄嘉佑. 1997. 近年来中国统计气象学的新进展. 气象学报, 55(3): 297-305 |
| Brooks C E P, Carruthers N C. 1953. Handbook of Statistical Methods in Meteorology. London: Her Majesty's Stationery Office, 413pp |
| Ding Y G, Zhang J L, Jiang Z H. 2010. Experimental simulations of extreme precipitation based on the multi-status Markov chain model. Acta Meteor Sinica, 24(4): 484-491 |
| Gabriel K R, Neurpann J. 1962. A Markov chain model for daily rainfall occurrence at Telaviv. Quart J Roy Meteor Soc, 88(375): 90-95 |
| Gates P, Tong H. 1976. On Markov chain modeling to some weather data. J Appl Meteor, 15(11): 1145-1151 |
| Katz R W. 1974. Computing probabilities associated with Markov chain model for precipitation. J Appl Meteor, 13(8): 953-954 |
 2013, Vol.
2013, Vol. 

