中国气象学会主办。
文章信息
- 李江浩, 彭新东. 2013.
- LI Jianghao, PENG Xindong. 2013.
- 守恒型有理函数插值半拉格朗日平流方案及性能分析
- Analysis of computational performance of the conservative Semi-Lagrangian with rational function advection scheme
- 气象学报, 71(4): 709-718
- Acta Meteorologica Sinica, 71(4): 709-718.
- http://dx.doi.org/10.11676/qxxb2013.062
-
文章历史
- 收稿日期:2012-12-31
- 改回日期:2013-04-12
在气象数值模式中,平流作为一种最基本的动力过程对大气环境场和中小尺度运动场的演变都起着关键作用,因此,高精度物质平流方案在数值模式中的有效应用对提高数值预报质量至关重要。对于大气示踪物(如水汽)平流,平流计算算法的正定性更为重要,而在气候数值模式中,计算守恒性也是对水汽平流计算的重要要求。半拉格朗日平流方案由于具有良好的计算稳定性和高效的特点,在计算流体力学和大气数值模式中得到广泛应用(沈学顺等,2011)。在三次约束曲线插值法(Constrained Interpolation Profile,简称CIP)原理的基础上,Xiao等(2002)提出了一种基于有理函数插值的CIP-CSLR(守恒型有理函数插值半拉格朗日法,Conservative Semi-Lagrangian with Rational function,简称CSLR)物质平流方案,利用单元格上的积分平均值和界面值,通过半拉格朗日后向追踪方法和分段有理插值函数计算上游点值,进而计算单元格积分值,有理函数的正定性保证了物质平流计算的非负要求,消除了高阶多项式插值在不连续界面处带来的虚假数值振荡。同时采用通量形式平流方程,利用单元网格界面的通量收支平衡计算单元格内积分平均值,保证了平流计算的守恒性。Xiao等(2002)、Peng等(2005)、常燕等(2008)曾对CSLR物质平流方案在一些理想试验和气象数值模式实际应用中进行了检验,并与其他同类算法(如CIP,PPM(Piecewise Parabolic Method))进行了比较,发现CSLR物质平流方案在保证守恒型的同时,获得了正定的结果,取得了较理想的预报和模拟效果,但是,都没有明确指出该方法的计算精度和收敛速度阶数,而收敛速度是平流数值算法应用于高分辨率数值模式时所要考虑的。另外,由于多维有理函数构建时面临困难,CSLR物质平流方案向多维空间扩展时采用简单的分维计算技术,这种分维算法易于实现,容易编程,但是,当流场在x方向或y方向存在辐合、辐散时,就会产生虚假的梯度,那么这种分维算法多大程度上影响多维CSLR物质平流方案的计算精度呢?为了加深对CSLR物质平流方案计算性能的进一步了解,本研究着重分析讨论CSLR物质平流方案在平面直角坐标和球面坐标中的计算性能,并评估分维技术的计算精度和数值收敛问题,为其在复杂数值模式中的实际应用提供理想试验资料和参考。2 CSLR物质平流方案及其误差评估
一维无辐散平流问题的通量型平流方程可写为
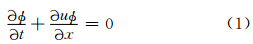

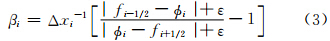
关于数值计算收敛速度的评估方法较多(马利斌等,2010; Lauritzen et al,2012),本研究采用分辨率倍增后误差减小倍数的对数和分辨率提高倍数的对数之比作为收敛阶数,即在柯朗数(Courant-Friedrichs-Lewy,CFL)(nCFL=|u|Δt/Δx)一定情况下,空间网格距为Δx时的计算误差为E1,当分辨率提高1倍(格距为Δx/2,时间步长为Δt/2)后,积分计算相同时间后的计算误差为E2,则定义其收敛阶数

高维计算类似,这种收敛率计算方式同时考虑了空间分辨率和时间积分步长的影响。同时为了更加直观地表示收敛速度,还采用了Lauritzen等(2012)的方法,即利用最小二乘法计算误差收敛阶数


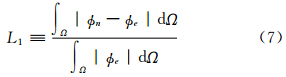
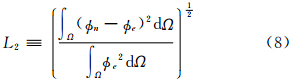

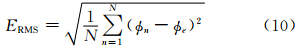
为全面考察CSLR物质平流方案的数值收敛性,评估引入空间分维算法及其在曲线坐标系中的计算效果,本研究按照平面二维和球面坐标的顺序给出数值试验结果。在理想试验的选取和设计上,参考了Williamson等(1992)、 Xiao等(2002)、沈学顺等(2011)、Zhang等(2012)常用的理想试验设定,研究平流函数连续性、尺度大小和水平风场辐散、辐合等对模拟结果的影响,试验设计由简单到复杂,以求全面了解CSLR物质平流方案的数值计算特点。
首先在平面直角坐标系下检验了一维CSLR物质平流方案的计算性能(图略)。对于光滑平缓的物理量分布(如正弦波),CSLR物质平流方案获得了二阶收敛速度和严格的正定单调数值解,CSL2方案(β=0)则获得三阶收敛精度,但数值解有微小数值振荡;对不连续分布(如方波)的平流计算,CSLR物质平流方案仍然给出了很好的保形和单调无振荡特性数值结果,而CSL2方案在间断处给出明显的振荡数值解,表现为“上冲”和“下冲”。此外,两者均能准确获得数值解相位,体现了半拉格朗日方法具有很强的位相描述能力。
3.1 平面直角坐标系下二维理想试验在实际应用中,面临二维、三维平流计算,现行方法主要通过分维技术来实现(Xiao et al,2002; Peng et al,2005),即将多维问题进行空间和时间的分离,分解成几个连续的一维问题来求解。分维技术简单方便,计算量小,所以被广泛应用,但是分维技术将多维平流过程人为划分成多个一维平流过程,造成平流过程在时间和空间上的分离,势必引入一定的计算误差,并且,当流场在x方向或y方向存在辐合、辐散时,也会产生虚假的梯度,针对分维技术的误差订正方法已有研究(Clappier,1998),本研究主要就二维问题中应用简单分维技术后分析CSLR物质平流方案的收敛速度和计算效果。对于二维通量型平流方程
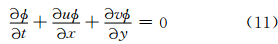
首先针对平缓光滑的二维正弦波平流进行分析,平流物理量场的初始条件为二维正弦波动


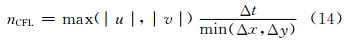
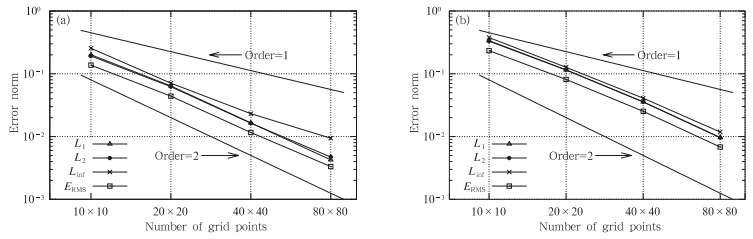 |
| 图 1 在CSLR物质平流方案(a)和CSL2方案(b)下各种计算误差的收敛率 Fig. 1 Convergence plots for L1,L2,Linf and ERMS,computed with the schemes of CSLR(a) and CSL2(b),respectively(the solid lines without mark show reference convergence rates of different orders) |
在二维计算中选用凹槽圆柱平流试验(Zhang et al,2012)来考察CSLR物质平流方案对于不连续分布的模拟能力,同时检验分维技术对有理函数保证计算结果正定性的影响。凹槽圆柱体在角速度为ω的旋转风场中运动,初始场为
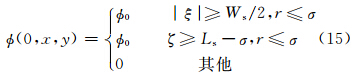
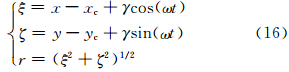
选择角速度ω=1.0的逆时针旋转速度场,圆柱高度φ0=1,圆柱最大半径σ=20,Ws=10,Ls=25,γ=25,风场中心为(50,50),nCFL最大值为1。图 2给出旋转风场示意图、初始场以及用CSLR物质平流方案和CSL2方案计算凹槽圆柱旋转5圈(时间步长是0.02 s,积分步数为1571)后回到出发点的模拟结果,CSLR物质平流方案能够保证不连续处的正定分布,不会产生新的极值,而CSL2方案由于采用二次插值函数则在不连续处产生明显的数值振荡,即带来了虚假上冲和负值,产生了较大的频散误差,破坏了标量场固有的空间分布特点和守恒特性。由此,本试验说明CSLR物质平流方案在向二维问题扩展中,针对这种空间变化幅度大、存在大梯度和强间断的标量场分布,通过分维技术,CSLR物质平流方案仍能够保持一维有理函数的基本特性,可以保证计算的正定和守恒性,这一点对流体物质平流输送是非常重要的特性。
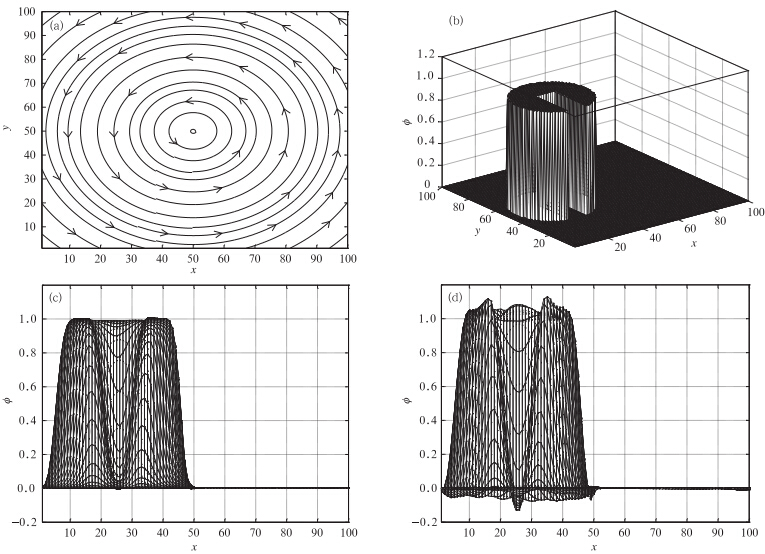 |
| 图 2 在旋转风场(a)、初始场(b)、CSLR物质平流方案(c)和CSL2方案(d)下计算旋转5圈后的凹槽-圆柱 Fig. 2 Rotational wind field(a),initial field(b) and slotted-cylinders after 5 loops with the schemes of CSLR(c) and CSL2(d) |
采用孤立的二维平缓余弦钟形物做进一步的平流试验,相对凹槽圆柱的不连续分布,这种连续平缓余弦钟平流试验更适合对数值算法的收敛速度评价。初始场为
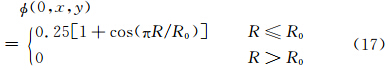
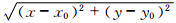 ,首先选择均匀定常速度场
,首先选择均匀定常速度场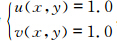 ,这里R0=0.2,x0=0,y0=0,nCFL=0.5,给定周期性边界条件,计算区域为[-0.2,0.2]×[-0.2,0.2],积分时间为余弦钟运动一个周期T=0.4 s。图 3给出不同分辨率下CSLR物质平流方案和CSL2方案的计算误差及网格收敛率,可以看出,在这个试验中CSLR物质平流方案的计算误差要比CSL2方案略大,其收敛阶数不到2阶,而CSL2方案的收敛阶数平均能达到2阶;从实际模拟结果上来看(图略),在同等分辨率下CSL2方案的模拟效果优于CSLR物质平流方案,两种算法数值解的位相和精确解保持一致,说明分维算法保持了半拉格朗日方法精确位相求解的特点。
,这里R0=0.2,x0=0,y0=0,nCFL=0.5,给定周期性边界条件,计算区域为[-0.2,0.2]×[-0.2,0.2],积分时间为余弦钟运动一个周期T=0.4 s。图 3给出不同分辨率下CSLR物质平流方案和CSL2方案的计算误差及网格收敛率,可以看出,在这个试验中CSLR物质平流方案的计算误差要比CSL2方案略大,其收敛阶数不到2阶,而CSL2方案的收敛阶数平均能达到2阶;从实际模拟结果上来看(图略),在同等分辨率下CSL2方案的模拟效果优于CSLR物质平流方案,两种算法数值解的位相和精确解保持一致,说明分维算法保持了半拉格朗日方法精确位相求解的特点。  |
| 图 3 CSLR物质平流方案(a)和CSL2方案(b)各种计算误差的收敛率 Fig. 3 Convergence plots for L1,L2,Linf and ERMS,computed with the schemes of CSLR(a) and CSL2(b),respectively(The solid lines without mark denote reference convergence rates of different orders) |
在相同初始分布条件下,还进行了无辐散旋转风场下余弦钟平流试验,即将二维风场改为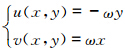 ,其中,角速度ω=1,nCFL=0.5。图 4给出余弦钟旋转一个周期T=2π s后的计算误差和对应的网格收敛速度,可以看出,在这种旋转风场下,CSLR物质平流方案和CSL2方案的计算误差基本达到相当水平,而两者的收敛阶数相对于均匀风场下也都有下降,且随分辨率提高收敛阶数都有所降低,这与在分维计算中二维风场存在切变梯度(如u在y方向的梯度)造成上游点后向追踪计算误差增大有关。
,其中,角速度ω=1,nCFL=0.5。图 4给出余弦钟旋转一个周期T=2π s后的计算误差和对应的网格收敛速度,可以看出,在这种旋转风场下,CSLR物质平流方案和CSL2方案的计算误差基本达到相当水平,而两者的收敛阶数相对于均匀风场下也都有下降,且随分辨率提高收敛阶数都有所降低,这与在分维计算中二维风场存在切变梯度(如u在y方向的梯度)造成上游点后向追踪计算误差增大有关。
 |
| 图 4 CSLR物质平流方案(a)和CSL2方案(b)各种计算误差的收敛率 Fig. 4 Convergence plots for L1,L2,Linf and ERMS,computed with the schemes of CSLR(a) and CSL2(b),respectively(The solid lines without any mark denote reference convergence rates of different orders) |
上述二维试验所用的二维均匀风场无论一维还是二维方向都是无散度流场,平流过程中没有形变,其中,一维问题的半拉格朗日后向追踪计算都可以精确得到上游点位置,而在旋转凹槽圆柱试验和余弦钟旋转平流试验中,虽然二维散度为0,但风场存在切变梯度,在利用分维技术计算二维平流问题时就会带来一定的计算误差。本试验条件更为苛刻,进一步考察CSLR物质平流方案在单一方向风场散度不为0的变形流场中的模拟情况(Zhang et al,2012),评估CSLR物质平流方案在这种相当于有源汇项存在的流场中的计算性能。数值模拟计算区域为[1,100]×[1,100],同样设置周期边界条件,初始场计算格点均匀为1,速度场是一种二维方向无辐散而一维方向存在风速梯度的强变形流场

解析解(真值)在这种无辐散流场下应该是均匀、定常初始值,不随时间和空间变化。图 5给出CSLR物质平流方案和CSL2方案获得平流100步后的模拟结果,可以看出,对于这种强烈的变形流场,两者利用半拉格朗日方法计算上游点均可取得较理想的模拟效果,整体计算误差和单个网格点的绝对误差都比较小,对于这种均匀连续分布的物理场模拟,分维技术和有理(二次)插值函数都没有产生严重的计算误差。进一步对比两个算法的计算结果,可以看出CSL2方案的绝对误差要比CSLR物质平流方案大,CSLR物质平流方案的计算结果中格点最大值为1.10852,最小值为0.89195,而CSL2方案计算结果中的格点最大值为1.11088,最小值为0.75698,说明在本试验中CSL2方案计算能力稍逊于CSLR物质平流方案,在平流计算中产生了较大的极值,而CSLR物质平流方案借助有理插值函数能够更好地处理这种变形流场中的平流模拟。
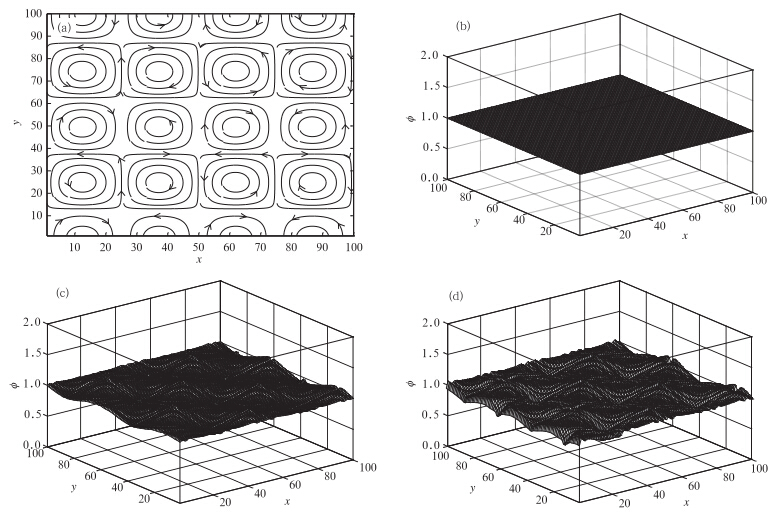 |
| 图 5 变形流场试验的风场(a)、初始场(b)、CSLR物质平流方案(c)和CSL2方案(d)平流100步的模拟结果(时间步长为1 s) Fig. 5 Deformational flow test: wind field(a),initial field(b),and the numerical results after the 100-step run with the schemes of CSLR(c) and CSL2(d),respectively(time step is 1 s) |
平面锋生试验(Zhang et al,2012)包含一个二维定常切线速度为

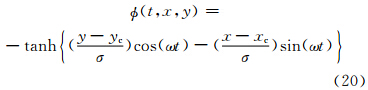
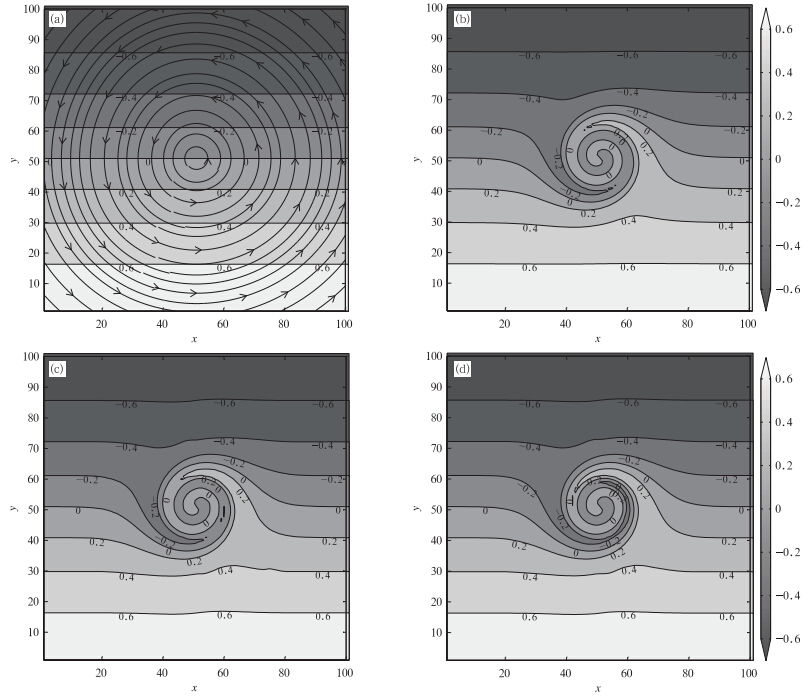 |
| 图 6 理想锋生试验的初始场和风场(a)、平流3 s后的解析解(b)以及CSLR物质平流方案(c)和CSL2方案(d)下的数值平流结果 Fig. 6 Idealized cyclogenesis tests: the initial field and wind field(a),the analytical solution(b) and the numerical solution with the schemes of CSLR(c) and CSL2(d)for the 3 s integration |
前面在平面直角坐标上进行了一维和二维理想试验,可以看出在不同维数计算和针对不同平流问题时,CSLR物质平流方案和CSL2方案的计算性能及收敛速度均有不同表现。最后利用球面准均匀网格——阴阳网格(Kageyama et al,2004; Peng et al,2006; 李江浩等,2013)分析球面坐标系下CSLR物质平流方案的计算性能和收敛性,采用球面阴阳网格是因为其避免了传统经纬度网格所具有的“极点问题”,选择初始物理场为光滑平缓的高度场(Li et al,2012)
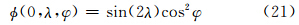
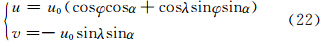
选择α=0,采用3种网格分辨率,它们相应的时间步长分别是360、180、90 s,平流积分12 d回到初始位置。图 7给出在本试验中CSLR物质平流方案和CSL2方案的计算误差与网格收敛率,可以看出,CSLR物质平流方案的网格收敛率大概在1—2阶,范数误差ERMS相对另外3种误差的收敛率较高,而CSL2方案的网格收敛率相比前者要略小,因此,两者在相对复杂的球面阴阳网格上的平流计算中,网格收敛速度都维持在1—2阶;进一步比较两者的计算误差,在同等空间分辨率和积分时间步长下,经过相同时间积分后CSL2方案的计算误差略小于CSLR物质平流方案的计算误差,从两者的实际模拟结果(图 8)上也可看出,CSL2的模拟效果要优于CSLR物质平流方案,这与一维波动试验得出的结论一致;另外,与直角平面平流试验相比,可以发现球面曲率的存在影响了算法的计算精度和收敛速度,这可能与球面上半拉格朗日出发点的计算有关。
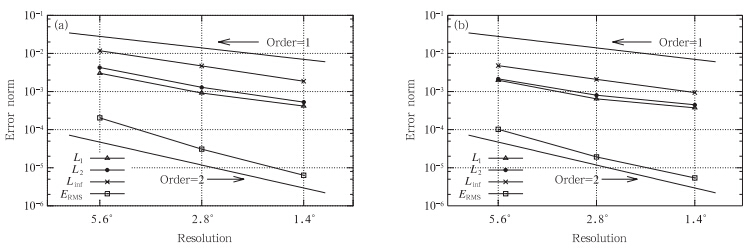 |
| 图 7 CSLR物质平流方案(a)和CSL2方案(b)各种计算误差的收敛率(上下两根黑斜线分别表示1阶和2阶收敛速度) Fig. 7 Convergence plots for L1,L2,Linf and ERMS,computed with the schemes of CSLR(a) and CSL2(b),respectively(The upper and lower heavy lines on each plot correspond to the slopes of the first- and second- order convergence rates,respectively) |
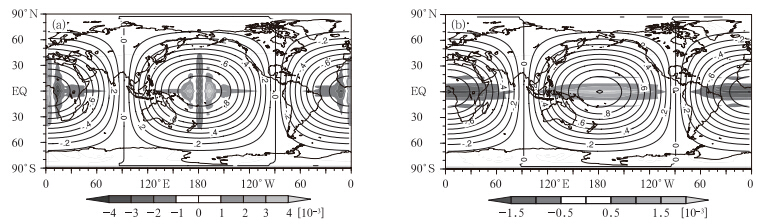 |
| 图 8 阴阳网格上正弦波试验的CSLR物质平流方案(a)和CSL2方案(b)积分12 d后的数值解(等值线)以及绝对误差(阴影) Fig. 8 Sine wave tests on the Yin-Yang grid: the numerical solution(contour) and the absolute error(shaded)with the schemes of CSLR(a) and CSL2(b)after the 12 day’s integration |
本文讨论和分析了平面直角坐标系和阴阳网格球面坐标系下CSLR物质平流方案的计算性能,与CSL2方案对比给出了不同理想数值试验下的网格收敛速度和计算精度,得到以下结论:
(1)采用一维有理函数插值的CSLR物质平流方案在一维计算中,能够保持正定和单调,并且在采用分维技术的多维计算中仍能够保持一维有理函数的性质,对物质平流计算具有较好的刻画。
(2)CSLR物质平流方案在一维光滑平缓的物理场计算中可以获得约二阶的网格收敛速度,而CSL2方案能够严格取得三阶收敛速度,有理函数的正定单调性一定程度上降低了CSLR物质平流方案本身的计算精度;但在有不连续物理场情况下,CSLR物质平流方案具有正定性,可以更好地计算物质平流,得到更好的计算质量。在多维计算中采用了简单的分维技术,而这种空间/时间平流分离计算降低了平流方案的计算精度和数值收敛速度,但两者仍能取得1—2阶的网格收敛速度。
(3)对于均匀无辐散流场中平缓波动和余弦钟等光滑连续函数平流计算时,CSL2方案的网格收敛速度和模拟效果要优于CSLR物质平流方案,而对于理想锋生试验和有源汇项存在的变形流场等存在不连续分布的平流试验,CSLR物质平流方案表现要优于CSL2方案,因此CSLR物质平流方案在增强不连续分布平流计算能力的同时,对平滑函数的计算略有负面影响。
(4)球面曲率影响半拉格朗日出发点的计算,CSLR物质平流方案和CSL2方案在球坐标中的网格收敛速度相对平面直角坐标下都有所降低。
| 常燕,王文,刘丽薇.2008.平流计算算法对一次江淮梅雨暴雨模拟的影响.高原气象,27(4):814-821 |
| 李江浩,彭新东.2013.阴阳网格上质量守恒计算性能分析.大气科学,37(4):852-862 |
| 马利斌,胡晓燕,莫则尧.2010.二维保单调保守恒插值算子.计算物理,27(5):633-640 |
| 沈学顺,王明欢,肖锋.2011.GRAPES模式中高精度正定保形物质平流方案的研究Ⅰ:理论方案设计与理想试验.气象学报,69(1):1-15 |
| Clappier A. 1998. A correction method for use in multidimensional time-splitting advection algorithms: Application to two-and three-dimensional transport. Mon Wea Rev, 126(1):232-242 |
| Kageyama A, Sato T. 2004. The Yin-Yang grid: An overset grid in spherical geometry. Ueochem Ueophys Ueosyst, 5,Q09005 |
| Lauritzen P H, Skamarock W C,Prather M I,et al. 2012. A stand ard test case suite for two-dimensional linear transport sphere. Ueosci Model Dev, 5(3):887-901 |
| LX L, Shen X S,Peng X D, et al. 2012. Fourth order transport model on Yin-Yang grid by multi-moment constrained Iinite volume scheme Procedia Computer Sci, 9:1004-1013 |
| Peng X D, Xiao F, Takahashi K. 2006. Conservative constraint for a quasi-unilorm overset grid on the sphere. Quart J Roy Meteor Soc, 132(616):979-996 |
| Peng X D, Xiao F, Ohluchi W, et al. 2005. Conservative Semi-Lagrangian transport on a sphere and the impact on vapor advection in an atmospheric general circulation model. Mon Wea Rev, 133(3):504-520 |
| Williamson D I,Drake J B, Hack J J,et al. 1992. A standard test set for numerical approximations to the shallow water equations in spherical geometry. J Computer Phys, 102(1):211-224 |
| Xiao F, Yabe T, Peng X, et al. 2002. Conservative and oscillation-less atmospheric transport schemes based on rational Iunctions.J Ueophys Res, 107(D22): ACL2-1-ACL2-11 |
| Zhang Y F, Juang H M H. 2012. A mass-conserving non-iteration-dimensional-split semi-Lagrangian advection scheme for limited-area modelling. Quart J Roy Meteor Soc, 138(669):2118-2125 |
 2013, Vol. 71
2013, Vol. 71


