中国气象学会主办。
文章信息
- 史加荣, 杨柳. 2020.
- SHI Jiarong, YANG Liu. 2020.
- 基于奇异值分解的气象数据推测
- Meteorological data estimation based on singular value decomposition
- 气象学报, 78(1): 128-142.
- Acta Meteorologica Sinica, 78(1): 128-142.
- http://dx.doi.org/10.11676/qxxb2020.005
文章历史
-
2018-10-22 收稿
2019-09-09 改回
2. 西安建筑科技大学建筑学院,西安,710055;
3. 西安建筑科技大学理学院,西安,710055
2. School of Architecture,Xi'an University of Architecture and Technology,Xi'an 710055,China;
3. School of Science,Xi'an University of Architecture and Technology,Xi'an 710055,China
在建筑物的设计与运行过程中,能源消耗与当地主要气候条件密切相关。若在建筑物方案设计中充分考虑气候因素对各个环节的影响,将会大幅度提高建筑物的节能效率。建筑气候学是将气候学引入到建筑设计中的一门新兴学科,也是低能耗建筑设计的科学基础(杨柳,2010)。在建筑气候分析与能耗模拟中,需要收集当地的气温、相对湿度、太阳辐射、降水和风速等多个气象参数。在建筑节能领域中,基本气象数据由平均气温、相对湿度、日照时数、日最高气温、日最低气温、降水量、风速、风向、平均气压、总云量和太阳总辐射等20余个气象参数组成。目前,中国拥有地面气象观测站约2500个,其中太阳辐射观测台(站)约100个。虽然中国的台站网能基本满足实时气象业务的需要,但气象历史资料仍存在如下缺陷:部分气象观测站点建立时间较短,观测数据不足;设备故障或站点迁移造成观测数据缺失或异常;太阳辐射观测站点太少,日总辐射观测数据连续记录超过30年的台站仅有50余个;缺少大量逐时、定时的气象数据。
中国的气象台站有基准气候站、基本气象站和一般气象站等不同类别,但许多气象台站不具有暖通空调设计、热工设计和建筑能耗模拟等需要的完备参数测试值。此外,气象数据存在缺、漏、错测现象,有些观测数据不能满足时间跨度要求。如:在热工及暖通空调设计室外计算参数中,采暖度日数和空调度日数一般要求10年以上的日平均气温数据(ANSI/ASHRAE Standard 169-2013,2013),采暖室外计算温度至少需要连续20年的测量数据(BS EN ISO 15927,2004);在建筑能耗模拟中,典型气象年主要涉及气温、露点温度、风速和太阳总辐射等气象参数,且一般需要能代表一个地区气候特征的30年以上的连续气象数据(李红莲,2016)。在建筑节能模拟等实际应用中,人们希望获取到长期的、连续的实测气象数据(张晴原等,2012)。鉴于中国气象数据资料的不足,故可以采用少量的、不连续的观测数据来推测缺失数据。因此,对缺、漏测数据进行推测是建筑节能基础数据研究中一个非常重要的科学问题。
在建筑节能研究中,人们期望获得气象数据长期的、稳定的变化趋势,即推测气象要素的平均变化特征。空间插值法是一类数据推测方法,这类方法通常将某地的气象数据表示成其若干邻近站点的观测数据的凸组合,主要包括反距离权重法和普通克里金插值法(Hofstra,et al,2008;Sluiter,2009;Chen,et al,2017;封志明等,2004;夏智武等,2016;Berndt,et al,2018;Xu,et al,2018;李金洁等,2019)。当某地不存在邻近观测数据时,样条插值、薄板样条函数、线性回归和自回归滑动平均(ARMA)等数据拟合方法通过寻找最优的趋势函数来推测缺失值(Hofstra,et al,2008;Sluiter,et al,2009;Lee,et al,2007;Arowolo,et al,2017;Sharifi,et al,2019),而调和分析是推测周期数据常使用的一种方法(魏凤英,1999;Zhang,2018)。前述推测方法在实际应用时主要存在2个缺陷:没有充分利用数据的全局信息,无法处理大量缺测数据情形。史加荣等(2019)将矩阵补全应用到气象数据推测中,该方法虽然用到了全局信息,但不能得到数据集的基向量。为此,提出一种新的气象数据推测方法,该方法使用奇异值分解(SVD)来获得全局的基向量。
奇异值分解经常被应用在气象数据预测中(魏凤英,1999),但文中使用奇异值分解的方法与以往不同,主要表现在2个方面:(1)气象数据的使用方式不同,已有的研究工作(Cherry,1996;谢炯光等,1997;Thompson,et al,2001;张万诚等,2002;张永领等,2006;周后福等,2010;苏海晶等,2013)考虑了2个气象要素场,并对它们的交叉协方差矩阵进行奇异值分解,文中仅针对一个气象场;(2)对奇异向量的使用不同,其他学者使用奇异向量的时间系数,并基于其间的相关系数来研究2个变量场的相关,文中仅把左奇异向量作为基向量。此外,经验正交函数分解(EOF)也使用奇异值分解来获得空间特征向量,是分离变量场主要空间分布结构的一种有效方法(周家斌等,1997;Hannachi,et al,2007;洪梅等,2010;秦正坤等,2011;韩荣青等,2014;赵虹等,2015;Schmidt,et al,2019)。文中提出的方法与经验正交函数分解在选用奇异向量的方式上不同。
《民用建筑热工设计规范》(GB50176−2016)把中国按气候划分成5个一级区、11个二级区,同一个二级区域内的气候一般差异较小。此外,待推测站点与其邻近站点的气候特征也往往相似。因此,根据中国部分观测站点的资料来推测待研究站点的气象数据是完全可行的。文中先研究气象要素资料的近似低秩结构。鉴于此结构,使用矩阵奇异值分解来得到若干主要的基向量,并依据这些基向量进行气象数据的推测。
2 基于奇异值分解的推测方法与性能评价 2.1 奇异值分解用
| ${{F}} = {{{U}}_R}{{SV}}_R^{\rm{T}} = \sum\limits_{i = 1}^R {{\sigma _i}{{{u}}_i}} {{v}}_i^{\rm{T}}$ | (1) |
式中,
已知F的最佳秩r
| ${{{F}}_r} = {{{U}}_r}{{{S}}_r}{{V}}_r^{\rm{T}}$ | (2) |
式中,
记
| ${a_{ij}} = {{{{{{\bar f}}}_i}^{\rm T}{{{{\bar f}}}_j}} \Big/ {\left({{{\left\| {{{{{\bar f}}}_i}} \right\|}_F}{{\left\| {{{{{\bar f}}}_j}} \right\|}_F}} \right)}}$ | (3) |
式中,
记相似度矩阵
在进行数据推测之前,需要根据奇异值分解来求解若干个基向量。对于某个气象要素,先将所有观测站点完整的气象数据表示成矩阵F,称这些数据集为训练集;再对所构造的矩阵进行奇异值分解;最后取前r个最大的奇异值对应的左奇异向量作为基向量组,从而得到基矩阵(
对于一个新给定的d维观测向量
| ${{R_{\rm e}}}({{{{\overset{\frown} { f}} }}_{\rm{new}}}) = {{{{\bigg\| {{{{f}}_{\rm{new}}} - {{{{{\overset{\frown} { f}} }}}_{\rm{new}}}} \bigg\|}_F}} \bigg/ {{{\bigg\| {{{{f}}_{\rm{new}}}} \bigg\|}_F}}}$ | (4) |
在很多实际推测问题中,往往只知道
假设
由于受到大噪声的腐蚀,气象数据往往具有较大的振荡幅度,这不便于掌握数据的真实趋势。在统计模型中,通常将气象数据分解为趋势成分与噪声成分之和,并假设趋势成分为时间的连续且光滑的函数,噪声成分为高斯白噪声。在进行统计推测时,可以有效地估计趋势成分,但无法推测高斯白噪声,只能估计其方差。此外,气象数据的趋势成分已基本满足建筑节能基础数据的要求。因此,在现实推测过程中,期望推测数据具有较小的振荡幅度或更高的光滑性。若对数据进行降噪处理,则处理后的数据将在一定程度上降低振荡幅度,从而变得更加光滑。常用的降噪方法包括小波分析(Lyu,et al,2014;Zhang,2018)和搜索平均法(侯威等,2007)等,而奇异值分解本质上也是一种非常有效且简单的降噪方法。
在现有的文献中,尚未见到测量气象数据光滑性或振荡幅度的指标。为此,使用全变差来度量向量的光滑性。对于d维列向量f,对应的全变差(Chambolle,2004)为
| ${{T_{\rm V}}}({{f}}) = \sum\limits_{i = 1}^{d - 1} {\big| {{f_{i + 1}} - {f_i}} \big|} $ | (5) |
当
所用气象资料来源于中国国家气候中心,选取中国662个气象台站的日值资料,且仅考虑其中的4个气象要素:平均气温、平均相对湿度、日照时数和气温日较差,其中前3个是太阳辐射预测中应用最广泛的气象要素(Aybar-Ruiz A,et al,2016)。气象资料的起止时间为2004年1月1日至2013年12月31日,总计10年。对于闰年,不考虑2月29日。图1给出了662个气象台站的地理分布,每个台站用实心圆点表示。渤海A平台站缺少日照时数数据,研究日照时数气象要素时,只考虑661个台站。平均气温、平均日照时数和气温日较差的单位分别为0.1℃、0.1 h和0.1℃。

|
| 图 1 662个气象台站分布 Fig. 1 Spatial distribution of 662 meteorological stations |
某些气象台站存在少量的缺测数据,此处将异常值(超出正常取值范围的值)视作缺测值。依据所搜集的气象资料,设定平均气温、平均相对湿度、日照时数和气温日较差的取值分别为[−450,400]、[2,100]、[0,150]、[3,350]。在以上4个气象要素中,缺测数据占比分别为0.53‱、3.71‱、3.67‱和0.15‱,使用邻近插值和线性插值方法对其进行补充。为了减轻随机性对试验结果的影响,对每个气象台站的某种气象要素,取10年的日平均值作为研究对象,即日平均值组成365维列向量。由于只考虑一年的气象要素值,故
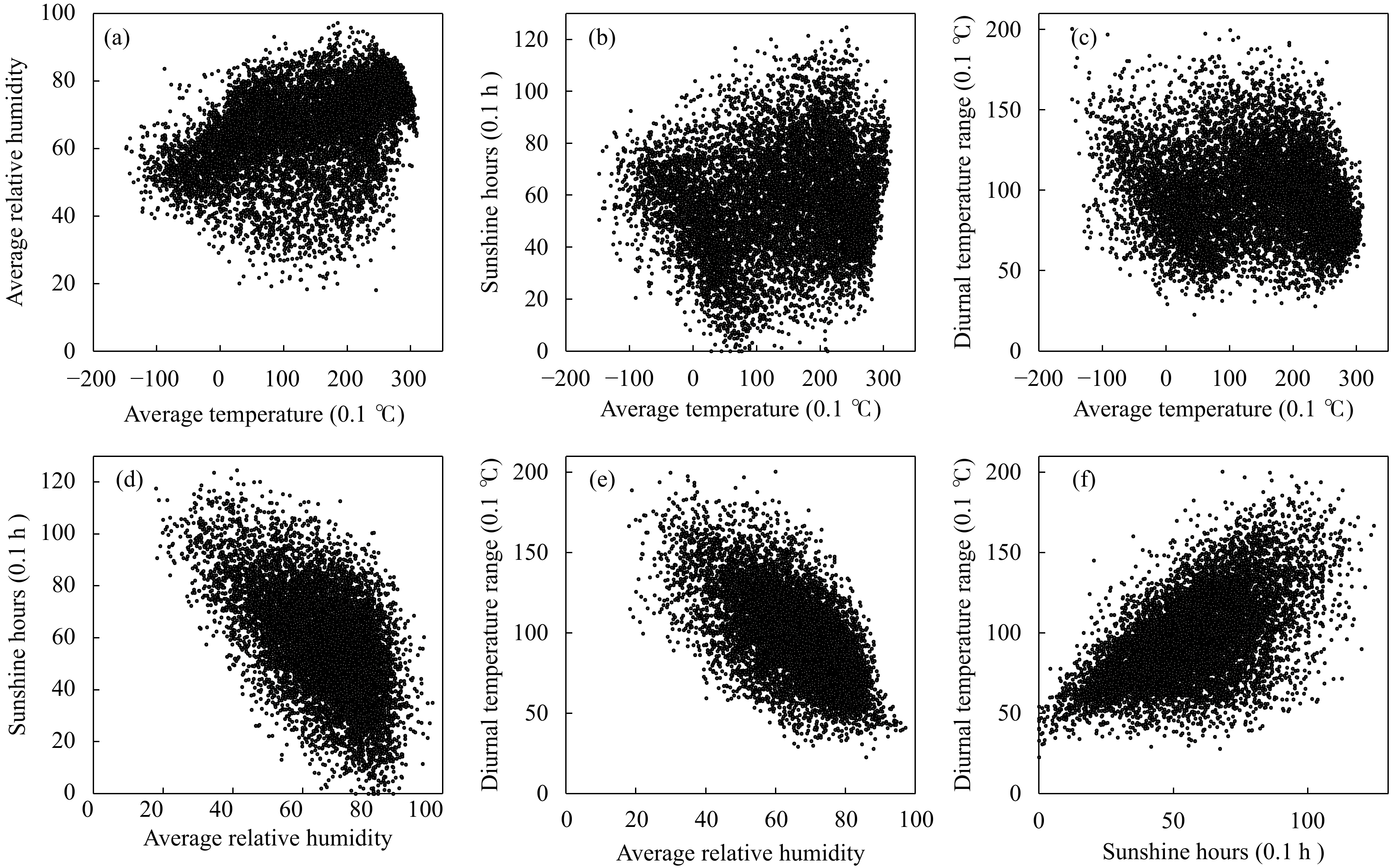
各个气象要素不是独立存在的,它们之间存在某种相关,下面讨论选取的4个气象要素之间的相关。不同地域,气象要素之间的相关一般存在显著差异。此处仅以中国某个10°×10°的网格为例(30°—40°N,105°—115°E),共167个气象台站,主要包括寒冷地区和夏热冬冷地区。对于平均气温、平均相对湿度和气温日较差3个气象要素,数据量为365×167=60955,日照时数的数据量为365×166=60590。在4个气象要素中任选2个,通过绘制散点图(图2)来寻求它们之间的相关。
|
| 图 2 4个气象要素之间的相关 Fig. 2 Correlations between four meteorological elements |
图2a、b、c的线性相关非常弱,相应的决定系数(R2)分别为0.1693、0.0208和0.0136,这意味着日照时数与平均温度、气温日较差与平均温度这2对气象要素几乎线性不相关。与日照时数相关的白天时长主要与赤纬角和纬度有关,这在理论上解释了日照时数与平均温度几乎线性不相关。图2d、e、f相应的决定系数分别为0.2760、0.3798和0.2991,说明日照时数与平均相对湿度、气温日较差与平均相对湿度和气温日较差与日照时数这3对气象要素有一定的线性相关性,前两对呈负相关,第三对呈正相关。
进一步考虑某个气象要素与其他气象要素的线性相关性。平均温度与其他3个要素的决定系数为0.3506。类似地,平均相对湿度、日照时数和气温日较差对应的决定系数分别为0.5815、0.4874、0.4269。可见,尽管某些气象要素对之间几乎线性不相关,但所研究的4个气象要素存在着比较强的耦合关系。理论上证明:当2组气象要素的决定系数为1且其中一组要素具有低秩性时,另一组气象要素也是低秩的。该结论为数据集的低秩性研究提供了一定的理论基础。若2组气象要素的决定系数较大且一组是近似低秩的,则认为另一组气象要素也具有低秩性。此处仅定性地说明2组气象要素可能有相同的近似低秩性。在实际应用中,可以用矩阵奇异值来定量地度量数据的低秩性。
3.3 低秩性检验由于所研究的台站数量较多,某些气象台站的气象要素存在很强的关联性,因此气象数据集所构成的矩阵F是近似低秩的。在组成矩阵F时,将气象台站号从小到大进行排列。由前述分析可知矩阵F与相似度矩阵A具有相同的秩,图3给出了可视化的相似度矩阵。

|
| 图 3 不同气象要素的气象台站相似度 (a. 平均气温,b. 平均相对湿度,c. 日照时数,d. 气温日较差) Fig. 3 Similarity of meteorological stations under different meteorological elements (a. average temperature, b. average relative humidity, c. sunshine hours, d. diurmal temperature range) |
矩阵F的秩为1的充要条件是相似度矩阵A的元素全为1或−1。若某些邻近的气象台站数据比较接近,则它们在矩阵A中呈现比较明显的块效应。从图3a可以看出,各个气象台站的平均气温有非常高的相似度,均大于0.75且相似度矩阵中有93.80%的元素在 [0.95,1]内,意味着平均气温矩阵具有非常高的近似低秩性。图3b—d展示的相似度取值比平均气温要分散,但也有较显著的块效应或条纹,说明这些相似度矩阵也具有一定的低秩性,即平均相对湿度、日照时数和气温日较差对应的矩阵也是近似低秩的。
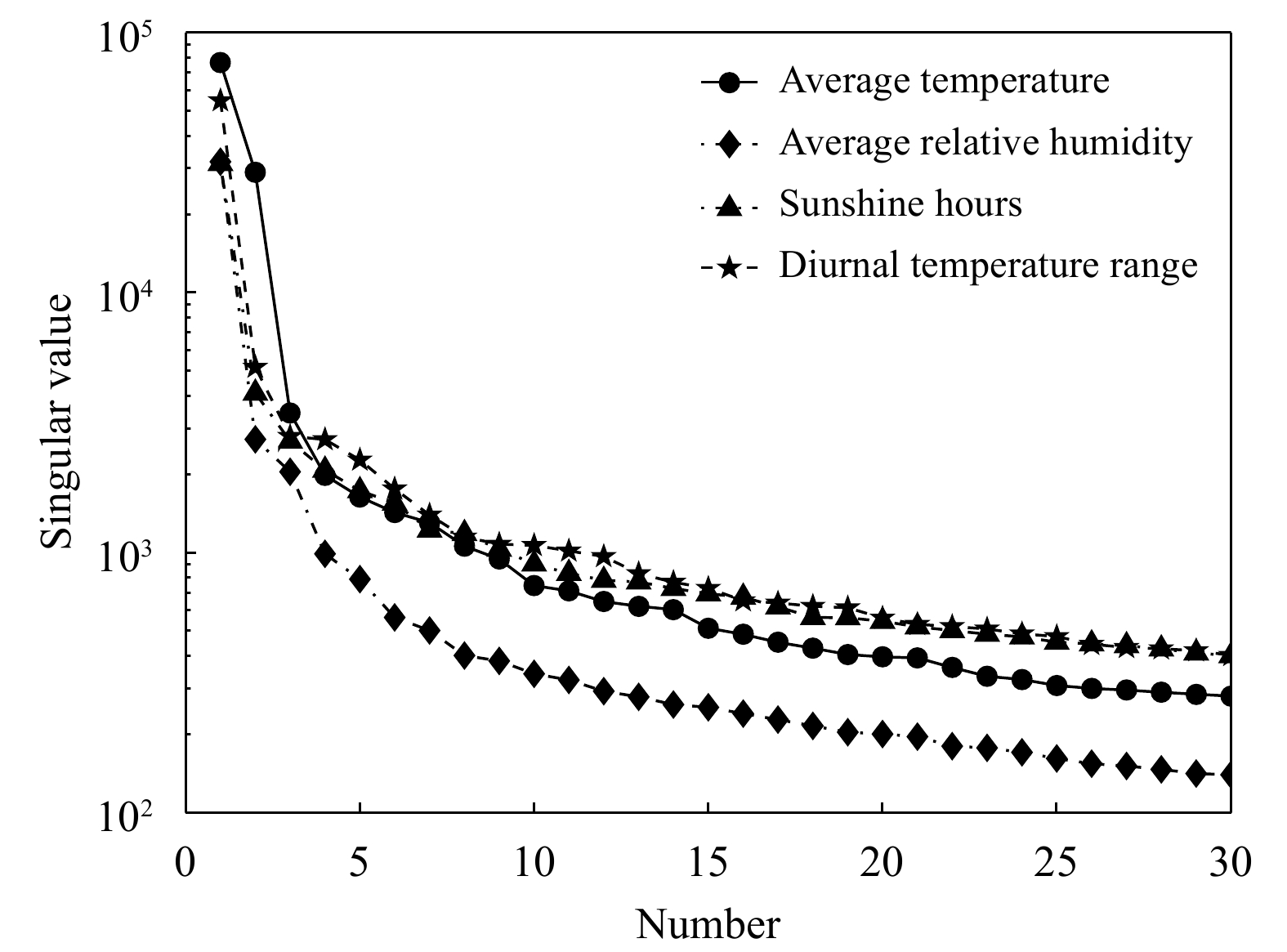
对F进行奇异值分解,F的奇异值一共有365个,4个气象要素对应的前30个最大奇异值如图4所示。可以看出,矩阵奇异值一开始剧烈下降,之后趋于平缓;前几个奇异值特别大,后边的相对小,4个气象要素的最大奇异值分别是第5大奇异值的46、40、18、24倍。相比而言,第30大奇异值比最大奇异值小两个数量级,且前30个奇异值的累积贡献率
|
| 图 4 前30个最大的奇异值 Fig. 4 Top 30 largest singular values |
从秩逼近的相对误差来评价数据矩阵的近似低秩性。选择最优的秩r逼近等价于选择r个最佳的基向量,不同秩下的相对误差见图5。在此实验中,基向量的个数r从1递增变化到30,相对误差先迅速下降,再趋于平缓。若取秩为5,则平均温度和平均相对湿度的逼近误差大约为5%,气温日较差的逼近误差大约为8%,日照时数的逼近误差最大,约为14%。若取秩为20,则平均温度和平均相对湿度的逼近误差大约为3%,气温日较差的逼近误差大约为6%,日照时数的逼近误差大约为9%。当r不小于5时,最佳的低秩逼近达到了比较好的性能,这也从另一方面验证了气象观测数据的近似低秩性。

|
| 图 5 不同秩下的相对误差 Fig. 5 Relative errors under different ranks |
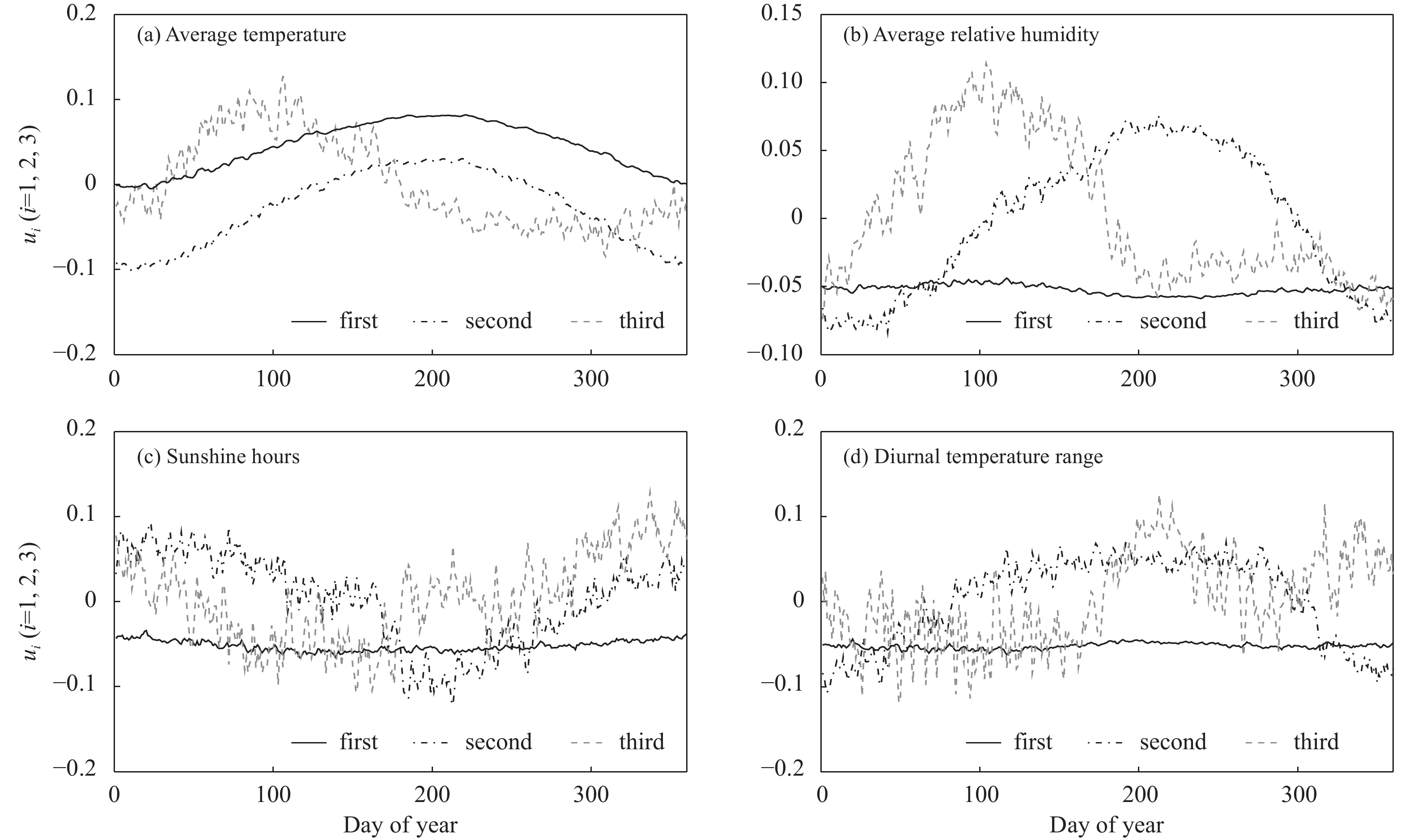
用所有气象台站的数据资料可以大致获得中国每个气象要素的前r个最优的基向量,即奇异值分解中的前r个最大的奇异值对应的左奇异向量。当r=3时,4个气象要素的相对误差均低于16%,故此处只分析前3个最主要的基向量(图6)。从图6a可见,第一基向量和第二基向量是单峰的,在7至8月(年积日180—225)达到峰值;第三基向量也近似单峰,峰值大概出现在4月(年积日100—110),这或许与中国春季末期气温迅速回升有关。图6b—d,第一基向量大致是恒定的,这说明平均相对湿度、日照时数和气温日较差等气象要素不存在明显的单调性,它们的取值主要与各个气象台站的地理位置有关。对于平均相对湿度,其第二、三基向量存在显著的单峰,出现峰值的时间分别是8月(年积日210—220)和4月(年积日90—110),这可能受雨季影响较大。对于日照时数,第二基向量呈现单峰,峰值点出现在7至8月(年积日180—215),可能与夏天白昼时间长有关;在第三基向量中,10月中旬至次年的2月中旬与2月下旬至6月的日照时数有相反的变化趋势,7月至10月上旬变化趋势不明显。图6d中,气温日较差的第二基向量大致存在单峰,峰值出现在夏季和秋季;第三基向量表明1至6月与7至12月气温日较差变化趋势相反。
|
| 图 6 前3个基向量 (a. 平均气温,b. 平均相对湿度,c. 日照时数,d. 气温日较差) Fig. 6 The first three main base vectors (a. averge temperature, b. averge relative humidity, c. sunshine hours, d. diurnal temperature range) |
在气象数据推测试验中,随机选取6个气象台站的数据用于推测,其余气象台站数据作为训练集,以获得最优的基向量组。为试验设计方便,对于各个气象要素,均取r=5,即选取5个最主要的基向量。对于待推测的气象台站,依均匀分布随机选取1年内p天的气象观测数据,根据选定的基向量组和p个观测数据来推测1年内其余365−p天的气象要素值,此处取p=12。全年的推测向量记为
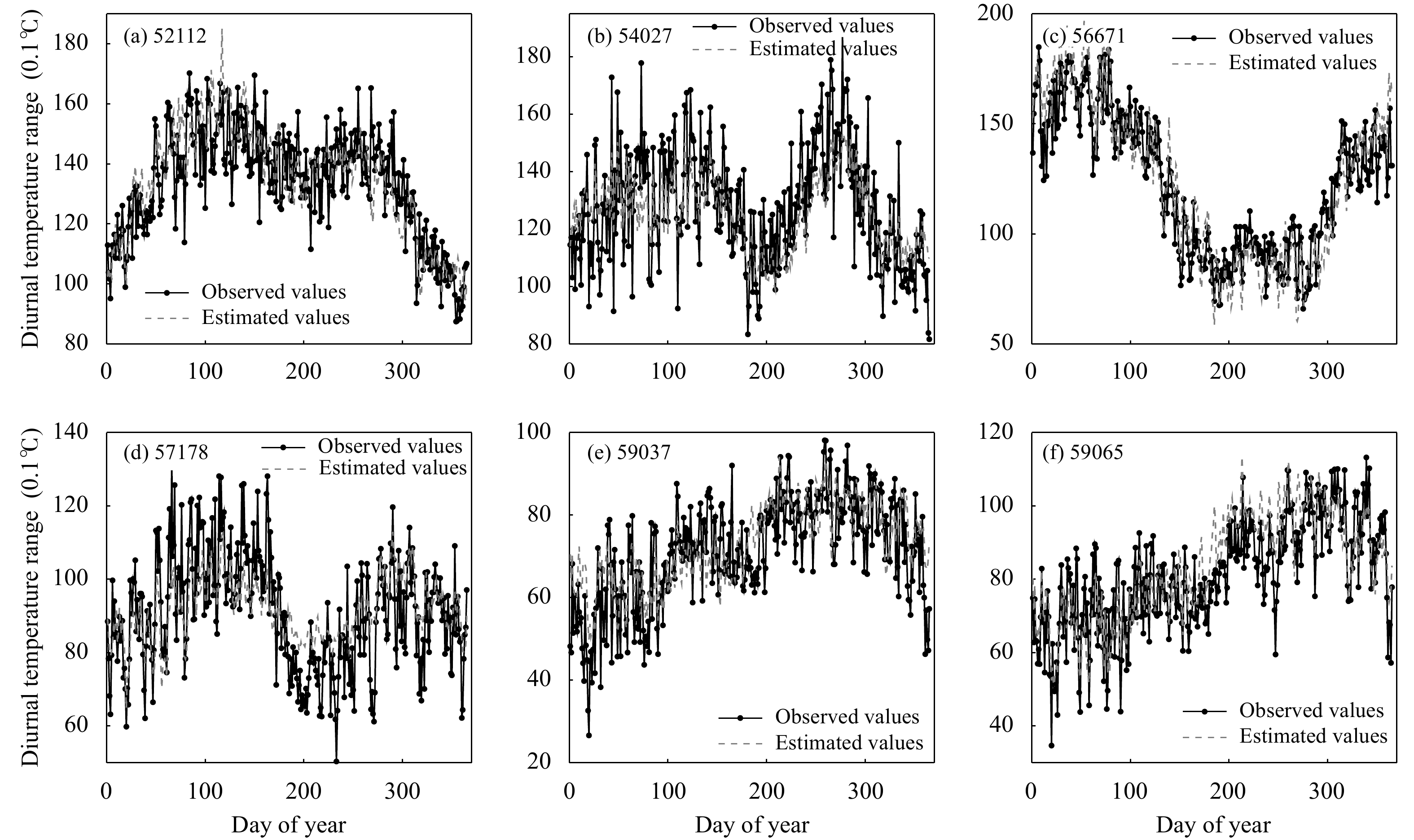
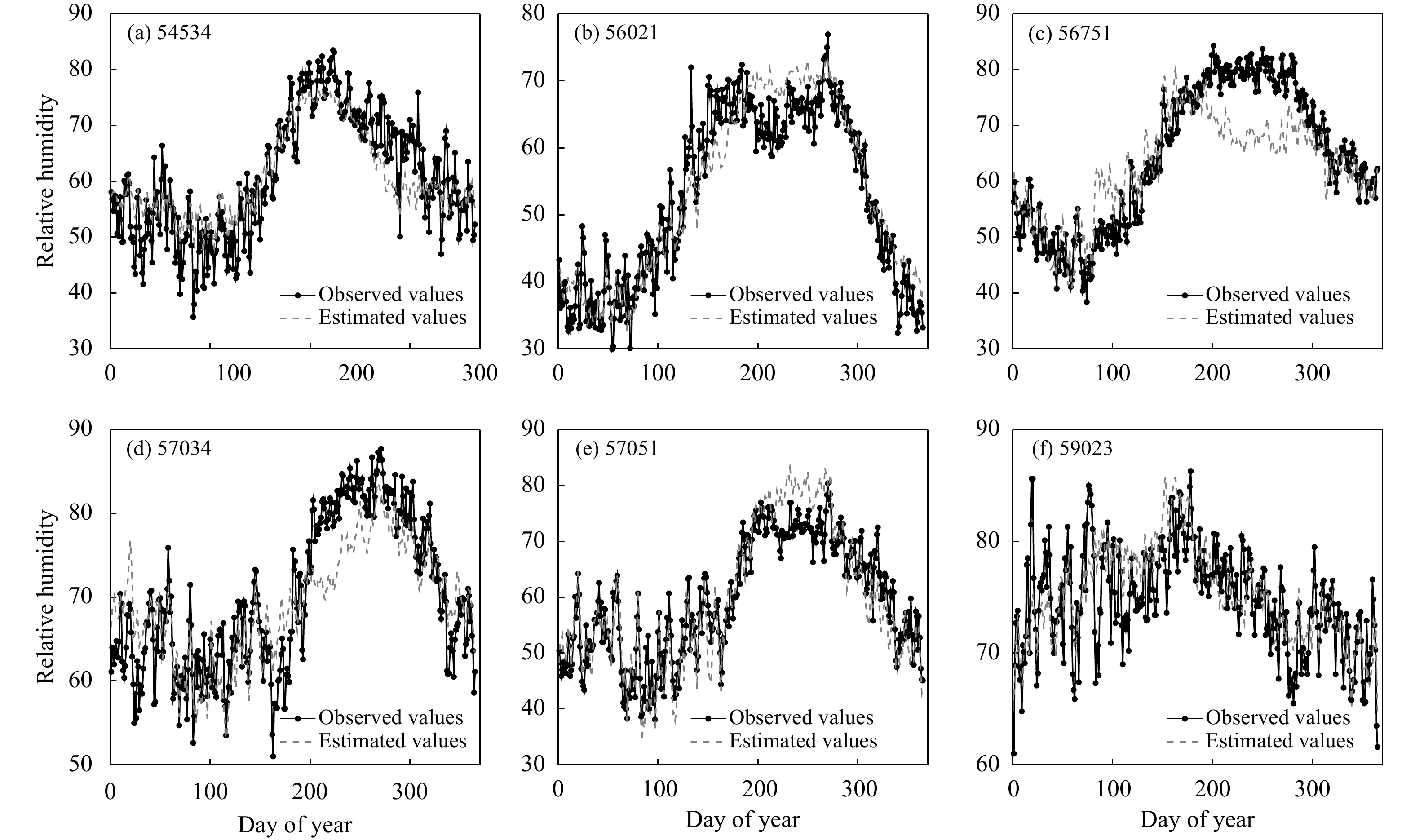
图7—10分别比较了6个气象台站的各个气象要素的观测数据与推测结果,可以看出,多数情形下推测方法达到了较好的性能,同时也有效地降低了数据的振荡幅度。表1给出了4个气象要素下6个气象台站的推测误差。就相对误差而言,平均相对湿度的推测性能最好,平均推测误差为7.83%;平均气温和气温日较差的推测性能比平均相对湿度稍差,平均推测误差分别为8.00%和10.82%;日照时数的推测误差最大,为13.49%—28.82%。对于推测方法的稳定性而言,4个气象要素推测误差的极差分别为8.93%、6.13%、15.33%和3.6%,说明气温日较差的推测结果最稳定,而日照时数最不稳定。
| 气象要素 | 平均气温 | 平均相对湿度 | 日照时数 | 气温日较差 |
| 台站1 | 12.16 | 8.63 | 16.20 | 9.05 |
| 台站2 | 5.46 | 8.65 | 15.04 | 9.91 |
| 台站3 | 6.26 | 10.76 | 14.88 | 10.71 |
| 台站4 | 5.33 | 6.77 | 14.57 | 12.06 |
| 台站5 | 13.85 | 7.55 | 13.49 | 12.65 |
| 台站6 | 4.92 | 4.63 | 28.82 | 10.54 |
| 平均值 | 8.00 | 7.83 | 17.17 | 10.82 |

|
| 图 7 平均温度观测值与推测值 Fig. 7 Comparison of average temperature between observations and estimations |
|
| 图 10 气温日较差观测值与推测值 Fig. 10 Comparison of diurnal temperature range between observations and estimations |
|
| 图 8 平均相对湿度观测值与推测值 Fig. 8 Comparison of average relative humidity between observations and estimations |

|
| 图 9 日照时数观测值与推测值 Fig. 9 Comparison of sunshine hours between observations and estimations |
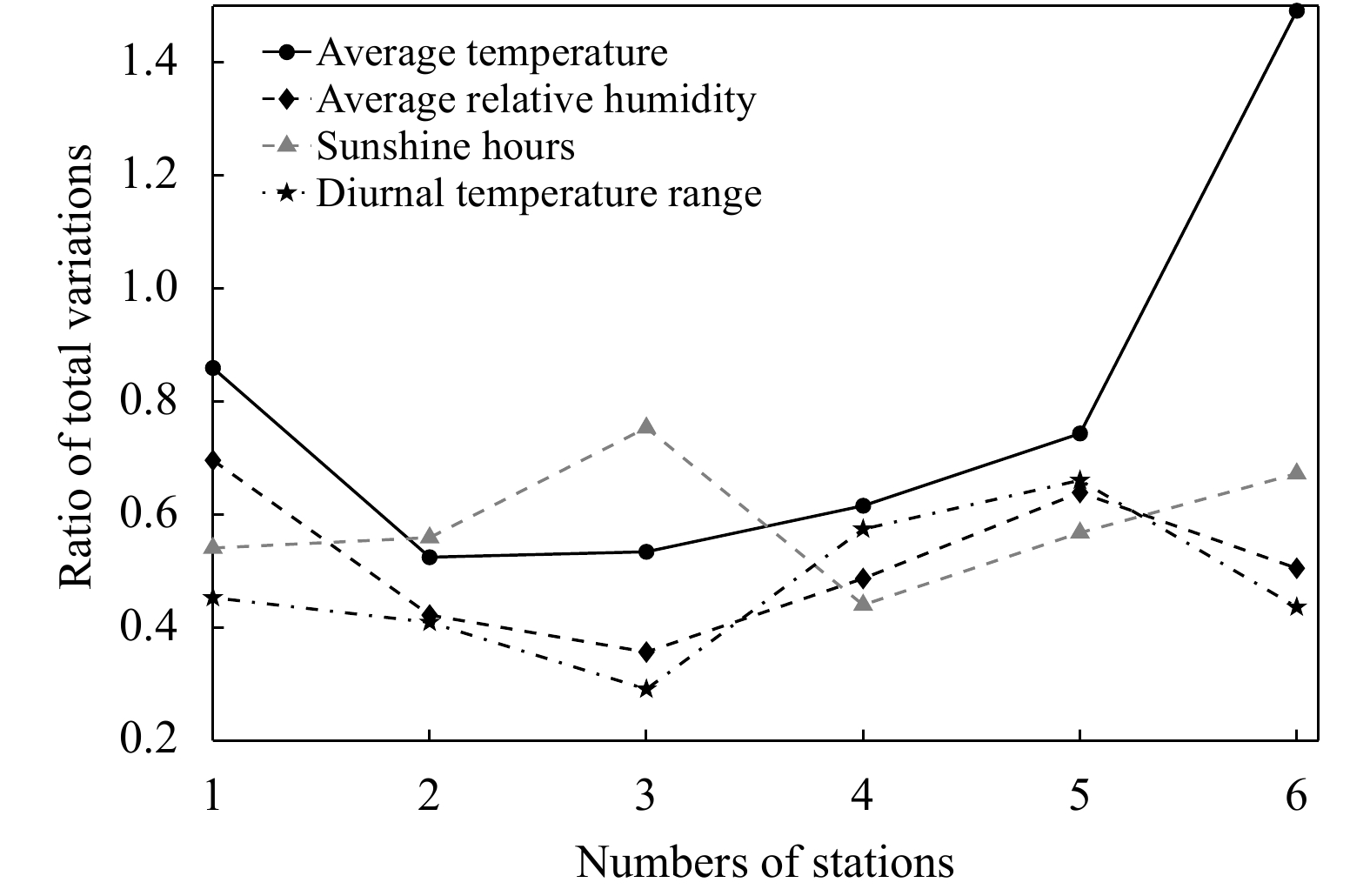
在上述试验中,多数推测数据的振幅比实际观测数据的振幅小,这在一定程度上达到了移除噪声的目的。使用全变差来定量地衡量推测结果是否具有更好的光滑性。对于某个待推测的气象台站,用推测结果的全变差与实际观测的全变差之比来评价光滑性的改善程度。当全变差比值小于1时,推测结果具有更好的光滑性,比值越小,光滑性越好(图11)。在24组试验结果中,仅有1个台站平均温度的全变差比值大于1,其余结果均小于0.86。4个气象要素在6个气象台站的全变差比值的平均结果分别为0.79、0.52、0.59和0.47。可见,提出的推测方法可以有效地降低数据的振荡幅度,从而增加光滑性、去除噪声。
|
| 图 11 推测结果与实际值的全变差比值 Fig. 11 Ratio of total variations of estimations to that of observations |
在第1组试验中,用固定基的数量和待推测气象台站的观测数据数量,同时仅选6个气象台站用于推测。这种试验方法受推测台站数量少、参数固定和随机性强等因素的影响较大。为此,设计了第2组试验。
将所有气象台站分成训练集和测试集两部分,使用训练集来训练基向量组,测试集来验证推测性能。随机选取70%的气象台站(463个)作为训练集,剩余30%的气象台站作为测试集。对于每个测试台站的气象数据,随机选取p个日值数据作为已知数据,其余的365−p个数据作为待推测数据。由训练集得到某气象要素的r个主要基向量,据此来求解待推测气象台站其余的未知数据。使用相对误差的平均值来评价推测性能,其定义为
| ${\overline R}_{\rm e} = \frac{1}{M}\sum\limits_{i = 1}^M {{\overline R}_{\rm e}({{{\hat{ f}}}_i})} $ | (6) |
式中,M为待推测气象台站的数量,
为了检验所提方法的性能,在实验设计中考虑r的不同取值,r从1到20;对于给定的r,随机选取某气象台站的p个日值数据,此处考虑p=1.5r和p=2r两种情形,在实际计算中1.5r按四舍五入取整。对于每种组合(r,p),将实验重复20次,得到20个平均相对误差(
|
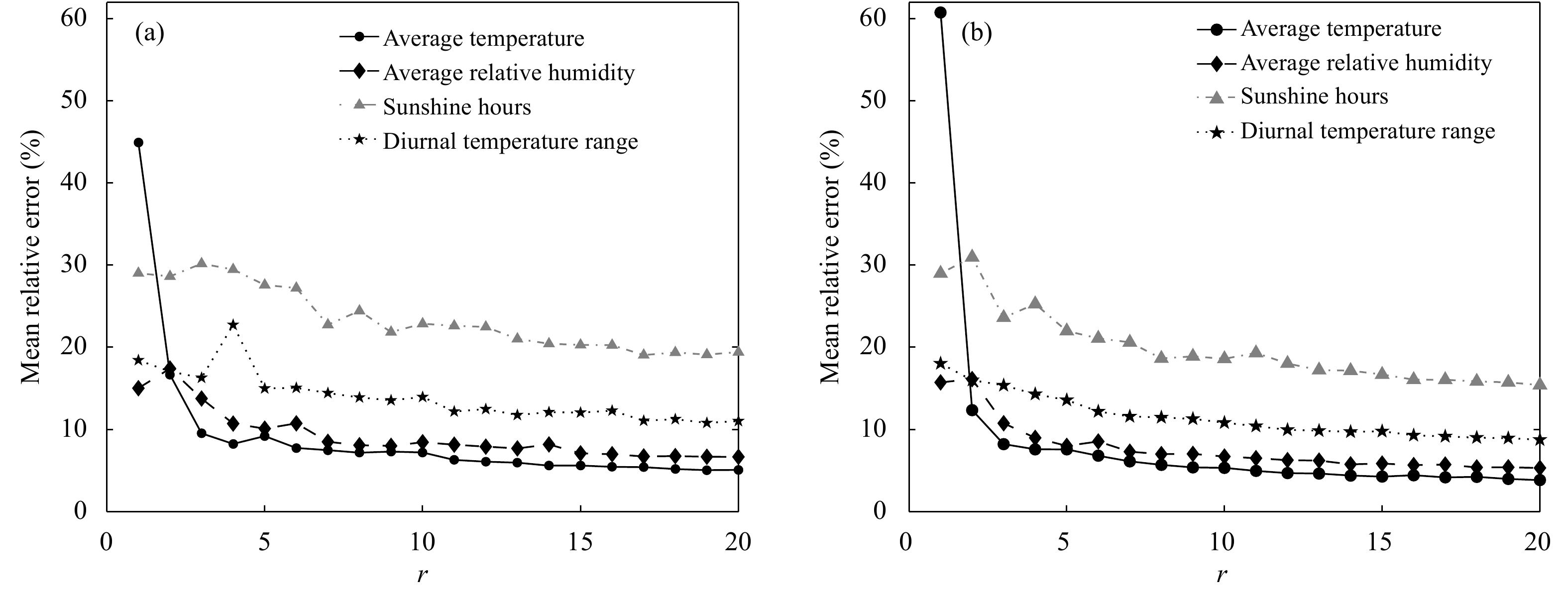
| 图 12 p=1.5r (a) 与p=2r (b) 时的推测误差 Fig. 12 Estimation errors for p=1.5r (a) and p=2r (b) |
从图12可以看出,平均相对误差随r增大有明显的下降趋势,r>10时,平均相对误差变化非常平缓;r>1时,观测数据量的值越大,平均相对误差越小。r=10时,4个气象要素在p=1.5r和p=2r两种情形下的平均相对误差分别改善了1.43%、2.00%、4.92%和2.82%。此外,平均温度和平均相对湿度的推测误差比较小,气温日较差的推测性能稍差,日照时数的推测结果最差,当(r,p)=(15,30)时,这4种气象要素的平均相对误差分别为4.24%、5.65%、16.74%和9.67%。总的来说,当
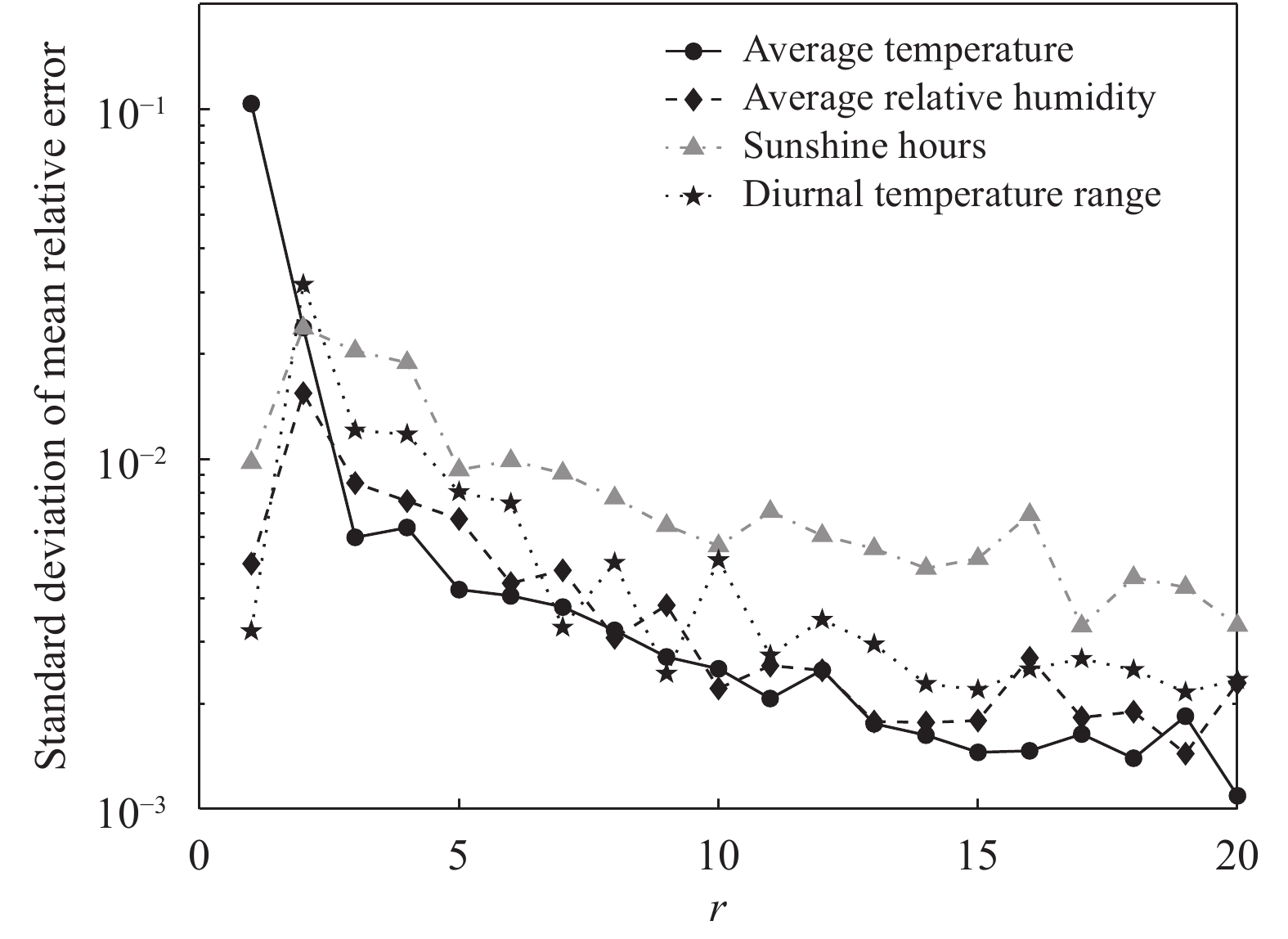
关于推测方法的稳定性,在给定r和p的条件下,将实验重复20次,计算平均相对误差的标准差(图13、14)。可以看出,平均相对误差的标准差随r的增加有单调递减的趋势,意味着r值越大,算法越稳定。当r>5时,标准差均小于1%,说明算法比较稳定。在理论上,r值越大(但要小于p值),推测误差就越小。但不能选取太大的r,因为大的r值无法有效地去除噪声,还可能导致过拟合。通过前面的实验分析,当r从5增加到15时,推测误差下降幅度比较小,且推测方法也比较稳定。因此,在实际应用中建议r的取值介于5到15之间。
|
| 图 13 p=1.5r时推测误差的标准差 Fig. 13 Standard deviations of estimation errors for p=1.5r |

|
| 图 14 p=2r时的推测误差的标准差 Fig. 14 Standard deviations of estimation errors for p=2r |
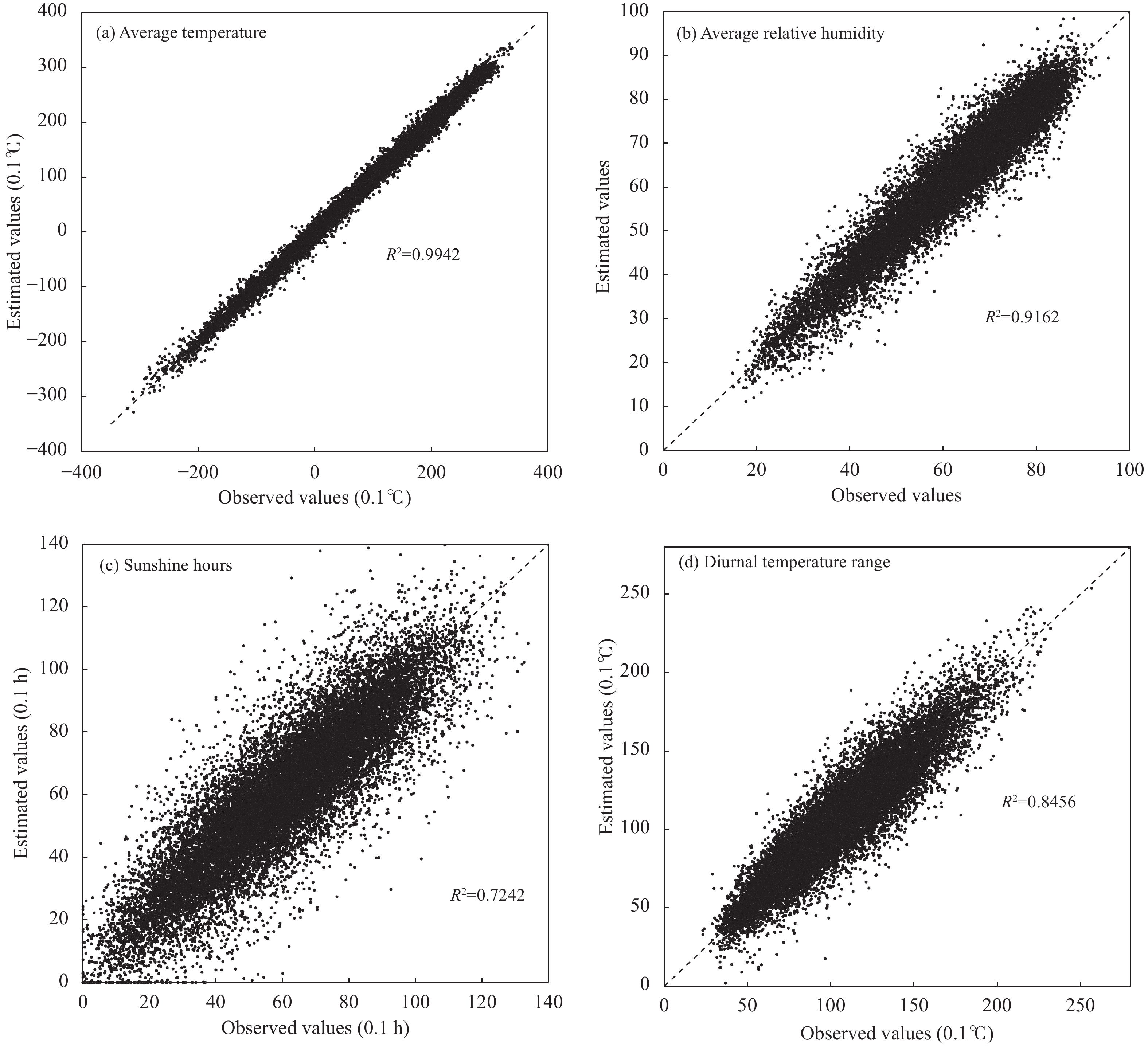
使用观测值和推测值的决定系数(R2)来度量推测方法的性能。仅考虑r=10、p=15的情形,观测值与推测值的散点分布如图15。4种气象要素的推测性能按优劣顺序为:平均气温、平均相对湿度、气温日较差、日照时数。图15a平均气温的决定系数为0.9942,意味着提出的方法在推测平均气温时具有良好性能;图15b的决定系数为0.9162,说明可以较好地推测平均相对湿度;图15c日照时数的决定系数为0.7242,推测性能较差,这可能是日照时数受云量的影响较大,难以较好地推测;图15d的决定系数为0.8456,比日照时数的决定系数大0.1214,但比平均相对湿度小0.076,即气温日较差的推测性能介于日照时数和平均相对湿度之间。
|
| 图 15 4个气象要素的观测值与推测值散点分布 Fig. 15 Scatter plots of observations versus estimations among four meteorological elements |
20世纪50年代,中国部署的气象台站数量较少,且存在大量的缺测现象。下面选取10个台站为研究对象(自1952年7月开始有气象记录),根据1952年7—12月的气象数据来推测1952年1—6月的缺测值。多数气象台站缺少日照时数数据,故在试验中未考虑此气象要素。
根据2004—2013年的气象数据,计算各气象要素的前r个主要左奇异向量;由得到的奇异向量和1952年7—12月的观测值,推测该年所有数据。试验中r=10,使用7—12月的观测值与推测值的相对误差来度量推测性能(表2)。可以看出,在10个台站中,气温日较差的推测相对误差最大,其次是平均气温,平均相对湿度的相对误差最小,分别为31.62%、18.14%和12.07%。
| 台站 | 平均温度 | 平均相对湿度 | 气温日较差 |
| 54236 | 20.09 | 12.34 | 27.80 |
| 50756 | 22.72 | 9.56 | 28.01 |
| 57598 | 12.49 | 7.21 | 38.00 |
| 57067 | 16.93 | 10.39 | 37.79 |
| 57355 | 10.49 | 11.89 | 33.41 |
| 57584 | 13.34 | 7.88 | 38.77 |
| 59072 | 10.61 | 7.34 | 31.64 |
| 56265 | 29.01 | 8.03 | 22.83 |
| 52436 | 24.48 | 25.90 | 26.70 |
| 51495 | 21.25 | 20.13 | 31.26 |
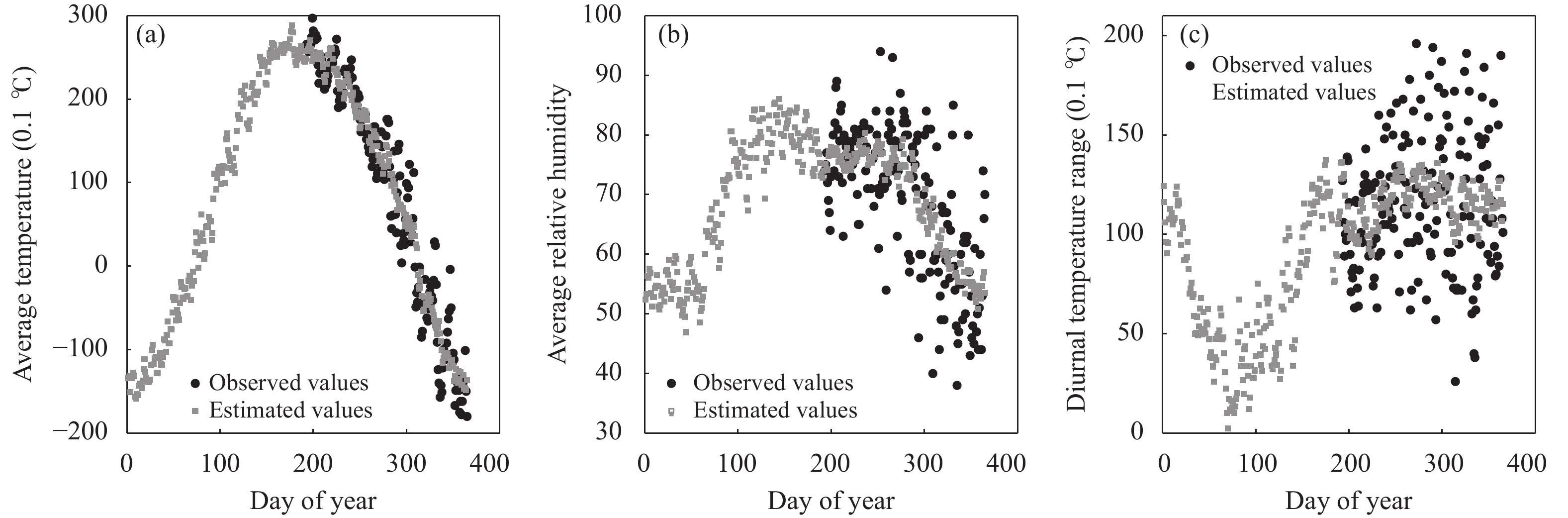
以台站54236为例,图16对比了3个气象要素在1952年的观测值与推测值。平均温度在一年内大致是近似对称且单峰的,7月到达峰值,与实际情形比较吻合(图16a);相对湿度(图16b)和气温日较差(图16c)的观测值比较发散,而推测值相对集中于一条连续曲线附近,说明推测值在一定程度上能有效地抑制噪声。与实验1和2相比,实验3推测值的相对误差偏大,可能是实验1和2的数据采用10年平均值,受随机性影响较小。
|
| 图 16 54236台站3个气象要素(a—c)的观测值与推测值 Fig. 16 Comparison between observations and estimations for three meteorological elements (a−c) at Station 54236 |
根据1952年1—6月的推测值,进一步推测1951年7—12月的数据。先将2004—2013年的数据重新组织,即每年的7月至次年的6月作为一个完整年度数据。再对这些年度数据取平均值,并进行奇异值分解,得到若干主要的左奇异向量。最后,根据得到的奇异向量和1952年1—6月的推测值来估计1951年7—12月的数据。重复上述过程,可以继续向前推测。当然,随着推测时间的不断推移,推测结果的可靠性可能会变差。
4 结 论研究气象数据的推测问题,提出基于矩阵奇异值分解的推测方法。选取中国662个气象台站10年的4个气象要素观测数据,探讨气象要素之间的相关和各个气象要素数据集的低秩性,分析各个气象要素的主要基向量。推测实验结果表明:平均气温和平均相对湿度的推测误差比较小,而日照时数和气温日较差的推测误差稍大,这可能与后2个气象要素的噪声较大有关。同时,推测方法也具有较好的稳定性。这些结果证实所提出的方法在实际推测中是有效的、可行的。提出的气象数据推测方法可进一步补充和完善中国地面观测气象数据与太阳辐射数据,从而为建筑热工设计、暖通空调设计和建筑节能设计等室外基础参数的提出提供数据支持。在今后的研究工作中,下面的几个研究方向值得关注:一是推测更多的气象要素,如太阳总辐射、风速、云量和降水量等;二是把推测方法应用到4次定时或逐时气象数据中;三是增加中国气象台站的数量,以覆盖更多的县级行政单位。
封志明, 杨艳昭, 丁晓强等. 2004. 气象要素空间插值方法优化. 地理研究, 23(3): 357-364. Feng Z M, Yang Y Z, Ding X Q, et al. 2004. Optimization of the spatial interpolation methods for climate resources. Geogr Res, 23(3): 357-364. DOI:10.3321/j.issn:1000-0585.2004.03.009 (in Chinese) |
Golub G H, Van Loan C F. 袁亚湘, 译. 2011. 矩阵计算. 北京: 人民邮电出版社, 60. Golub G H, Van Loan. 2011. Matrix Computations. Yuan Y X, trans. Beijing: Posts & Telecom Press, 60 (in Chinese)
|
韩荣青, 高辉, 李维京. 2014. 旋转经验正交函数分解回归方法在东北夏季气温季节预测和成因诊断中的应用. 气象学报, 72(2): 291-305. Han R Q, Gao H, Li W J. 2014. An application of the REOF and stepwise regression to seasonal forecast and cause diagnosis for summer temperature anomaly in northeast China. Acta Meteor Sinica, 72(2): 291-305. (in Chinese) |
洪梅, 张韧, 万齐林等. 2010. EOF分解与GA优化的热带太平洋海温场动力预报模型反演. 气象学报, 68(5): 731-739. Hong M, Zhang R, Wan Q L, et al. 2010. Retrieving the parameters of the dynamic forecast model of tropical Pacific ocean SST field based on the EOF technique and GA optimization. Acta Meteor Sinica, 68(5): 731-739. (in Chinese) |
侯威, 廉毅, 封国林. 2007. 基于搜索平均法的气象观测数据的非线性去噪. 物理学报, 56(1): 589-596. Hou W, Lian Y, Feng G L. 2007. Nonlinear noise reduction for the observation data of climatology based on the searching average method. Acta Phys Sinica, 56(1): 589-596. DOI:10.3321/j.issn:1000-3290.2007.01.096 (in Chinese) |
李红莲. 2016. 建筑能耗模拟用典型气象年研究[D]. 西安: 西安建筑科技大学. Li H. 2016. Research on the typical meteorological year for building energy consumption simulation [D]. Xi'an: Xi'an University of Architecture and Technology (in Chinese)
|
李金洁, 王爱慧. 2019. 基于西南地区台站降雨资料空间插值方法的比较. 气候与环境研究, 24(1): 50-60. Li J J, Wang A H. 2019. Comparison of spatial interpolation methods based on monthly precipitation obsevation data of station in southwest China. Climatic Environ Res, 24(1): 50-60. (in Chinese) |
秦正坤, 林朝晖, 陈红等. 2011. 基于EOF/SVD的短期气候预测误差订正方法及其应用. 气象学报, 69(2): 289-296. Qin Z K, Lin Z H, Chen H, et al. 2011. The bias correction methods based on the EOF/SVD for short-term climate prediction and their applications. Acta Meteor Sinica, 69(2): 289-296. (in Chinese) |
史加荣, 李雪霞. 2019. 基于矩阵补全的气象数据推测. 气象科技, 47(3): 420-425. Shi J R, Li X X. 2019. Meteorological data estimation based on matrix completion. Meteor Sci Technol, 47(3): 420-425. (in Chinese) |
苏海晶, 王启光, 杨杰等. 2013. 基于奇异值分解对中国夏季降水模式误差订正的研究. 物理学报, 62(10): 109202. Su H J, Wang Q G, Yang J, et al. 2013. Error correction on summer model precipitation of China based on the singular value decomposition. Acta Phys Sinica, 62(10): 109202. DOI:10.7498/aps.62.109202 (in Chinese) |
魏凤英. 1999. 现代气候统计诊断与预测技术. 北京: 气象出版社, 156-156. Wei F Y. 1999. Modern Climate Statistics Diagnosis and Prediction Technology. Beijing: China Meteorological Press, 156 (in Chinese)
|
夏智武, 刘鹏举, 陈增威等. 2016. 山地环境日气温PRISM空间插值研究. 北京林业大学学报, 38(1): 83-90. Xia Z W, Liu P J, Chen Z W, et al. 2016. Spatial interpolation of daily air temperature in mountain area based on PRISM. J Beijing Forestry Univ, 38(1): 83-90. (in Chinese) |
谢炯光, 秦冰冰, 王静渊. 1997. 奇异值分解方法在季降水预测中的应用. 气象学报, 55(1): 117-123. Xie J G, Qin B B, Wang J Y. 1997. The application of singular value decomposition analysis in the prediction of seasonal rainfall. Acta Meteor Sinica, 55(1): 117-123. (in Chinese) |
杨柳. 2010. 建筑气候学. 北京: 中国建筑工业出版社, 4pp. Yang L. 2010. Bioclimatic Architecture. Beijing: China Architecture & Building Press, 4pp (in Chinese)
|
张晴原, 杨洪兴. 2012. 建筑用标准气象数据手册. 北京: 中国建筑工业出版社, 1pp. Zhang Q Y, Yang H X. 2012. Typical Meteorological Database Handbook for Buildings. Beijing: China Architecture & Building Press, 1pp (in Chinese)
|
张万诚, 解明恩. 2002. 奇异值分解方法对降水的预测试验. 高原气象, 21(1): 102-107. Zhang W C, Xie M E. 2002. The singular value decomposition method to prediction experiment of rainfall. Plateau Meteor, 21(1): 102-107. DOI:10.3321/j.issn:1000-0534.2002.01.017 (in Chinese) |
张永领, 丁裕国, 高全洲等. 2006. 一种基于SVD的迭代方法及其用于气候资料场的插补试验. 大气科学, 30(3): 526-532. Zhang Y L, Ding Y G, Gao Q Z, et al. 2006. The method based on SVD iteration and its application to interpolation of climate data. Chinese J Atmos Sci, 30(3): 526-532. DOI:10.3878/j.issn.1006-9895.2006.03.15 (in Chinese) |
赵虹, 秦正坤, 王金成等. 2015. 经验正交函数分解质量控制法在地面观测资料变分同化中的个例研究与应用. 气象学报, 73(4): 749-765. Zhao H, Qin Z K, Wang J C, et al. 2015. Case studies and applications of the Empirical Orthogonal Function quality control in variational data assimilation systems for surface observation data. Acta Meteor Sinica, 73(4): 749-765. (in Chinese) |
周后福, 方茸, 张建军等. 2010. 基于SVD和修正Z指数的汛期旱涝预测及其应用. 气候与环境研究, 15(1): 64-72. Zhou H F, Fang R, Zhang J J, et al. 2010. Prediction for drought/flood during the flood season based on SVD method and modified Z-index and its application. Climatic Environ Res, 15(1): 64-72. DOI:10.3878/j.issn.1006-9585.2010.01.07 (in Chinese) |
周家斌, 黄嘉佑. 1997. 近年来中国统计气象学的新进展. 气象学报, 55(3): 297-305. Zhou J B, Huang J Y. 1997. Advances in statistical meteorology in China in recent years. Acta Meteor Sinica, 55(3): 297-305. (in Chinese) |
Arowolo A O, Bhowmik A K, Qi W, et al. 2017. Comparison of spatial interpolation techniques to generate high-resolution climate surfaces for Nigeria. Int J Climatol, 37: 179-192. DOI:10.1002/joc.4990 |
ANSI/ASHRAE Standard 169-2013. 2013. Climatic data for building design standards. American Society of Heating, Refrigerating and Air-Conditioning Engineers, 1791 Tullie Circle, NE, Atlanta, GA, USA
|
Aybar-Ruiz A, Jiménez-Fernández S, Cornejo-Bueno L, et al. 2016. A novel grouping genetic algorithm: Extreme learning machine approach for global solar radiation prediction from numerical weather models inputs. Solar Energy, 132: 129-142. DOI:10.1016/j.solener.2016.03.015 |
Berndt C, Haberlandt U. 2018. Spatial interpolation of climate variables in Northern Germany: Influence of temporal resolution and network density. J Hydrol Reg Stud, 15: 184-202. DOI:10.1016/j.ejrh.2018.02.002 |
BS EN ISO 15927. 2004. Hygrothermal performance of buildings: Calculation and presentation of climatic data, Part 5: Data for design heat load for space heating. London: British Standards Institution.
|
Chambolle A. 2004. An algorithm for total variation minimization and applications. J Math Imaging Vis, 20(1-2): 89-97. |
Chen S N, Guo J. 2017. Spatial interpolation techniques: Their applications in regionalizing climate-change series and associated accuracy evaluation in Northeast China. Geomat, Geomat Nat Haz Risk, 8(2): 698-705. |
Cherry S. 1996. Singular value decomposition analysis and canonical correlation analysis. J Climate, 9(9): 2003-2009. DOI:10.1175/1520-0442(1996)009<2003:SVDAAC>2.0.CO;2 |
Hannachi A, Jolliffe I T, Stephenson D B. 2007. Empirical orthogonal functions and related techniques in atmospheric science: A review. Int J Climatol, 27(9): 1119-1152. DOI:10.1002/joc.1499 |
Hofstra N, Haylock M, New M, et al. 2008. Comparison of six methods for the interpolation of daily European climate data. J Geophys Res: Atmos, 113(D21): D21110. DOI:10.1029/2008JD010100 |
Lee J H, Sohn K T. 2007. Prediction of monthly mean surface air temperature in a region of China. Adv Atmos Sci, 24(3): 503-508. DOI:10.1007/s00376-007-0503-1 |
Lyu L, Kantardzic M, Arabmakki E. 2014. Solar irradiance forecasting by using wavelet based denoising∥Proceedings of 2014 IEEE Symposium on Computational Intelligence for Engineering Solutions. Orlando, FL, USA: IEEE, 110-116
|
Schmidt O T, Mengaldo G, Balsamo G, et al. 2019. Spectral empirical orthogonal function analysis of weather and climate data. Mon Wea Rev, 147(8): 2979-2995. DOI:10.1175/MWR-D-18-0337.1 |
Sharifi E, Saghafian B, Steinacker R. 2019. Downscaling satellite precipitation estimates with multiple linear regression, artificial neural networks, and spline interpolation techniques. J Geophys Res Atmos, 124(2): 789-805. DOI:10.1029/2018JD028795 |
Sluiter R. 2009. Interpolation methods for climate data: Literature review. Netherlands: De Bilt, Royal Netherlands Meteorological Institute (KNMI)
|
Thompson M L, Reynolds J, Cox L H, et al. 2001. A review of statistical methods for the meteorological adjustment of tropospheric ozone. Atmos Environ, 35(3): 617-630. DOI:10.1016/S1352-2310(00)00261-2 |
von Luxburg U. 2007. A tutorial on spectral clustering. Stat Comput, 17(4): 395-416. DOI:10.1007/s11222-007-9033-z |
Xu C D, Wang J F, Li Q X. 2018. A new method for temperature spatial interpolation based on sparse historical stations. J Climate, 31(5): 1757-1770. DOI:10.1175/JCLI-D-17-0150.1 |
Zhang Z H. 2018. Multivariate Time Series Analysis in Climate and Environmental Research. Cham: Springer International Publishing, 37-96
|
 2020, Vol. 78
2020, Vol. 78


