中国气象学会主办。
文章信息
- 黄超, 彭新东, 李晓涵. 2019.
- HUANG Chao, PENG Xindong, LI Xiaohan. 2019.
- 阴阳网格上通量型非静力模式动力框架的理想试验
- Idealized experiments of a flux-form non-hydrostatic dynamic core on the Yin-Yang grid
- 气象学报, 77(1): 154-164.
- Acta Meteorologica Sinica, 77(1): 154-164.
- http://dx.doi.org/10.11676/qxxb2018.047
-
文章历史
- 2018-02-26 收稿
- 2018-06-12 改回
近年来, 中国超级计算机发展迅速, 成就世界瞩目, 其中位于无锡超算中心的“太湖之光”计算机已连续4次夺得世界计算机TOP500的第1位, 为中国开展全球高分辨率数值预报和多尺度模拟提供了计算条件。目前, 全球高分辨数值天气预报和长期气候预测依赖于建立在准均匀网格上的守恒大气动力学模式的应用。球面经纬网格由于其正交性和简单的特点, 在大气动力模式中得到普遍应用, 但在高纬度地区由于经线的收缩和极点奇异性问题, 在高分辨率计算应用时遇到计算代价过大的麻烦。极点奇异性问题可用洛必达法则有效绕开(Kageyama, et al, 1995), 常用的谱方法离散也可以缓解高纬度地区经线收缩计算时间步长减小的严格限制, 但高低纬度间存在的最大稳定积分时间步长的差异问题仍然存在, 导致模式积分计算的时间浪费, 也为模式物理过程参数化制造了困难, 而球面准均匀网格则可有效缓解这两方面的问题。目前国际上通用的准均匀网格主要包括结构网格和非结构网格两种。非结构网格包括Sadourny等(1968)和Williamson(1968)提出的正二十面体网格(分为三角形网格和六边形网格)。结构网格包括Sadourny(1972)提出的立方体球面网格和由Kageyama等(2004)提出的阴阳网格等。
阴阳网格是Kageyama等(2004)提出的一种准均匀交叉重叠网格, 具有网格准均匀、无奇异点的特点。阴阳网格保留了球面经纬网格的正交性, 同时采用两个经纬网格的低纬度部分组合而成, 较好地解决了传统球面经纬网格存在的计算问题, 但也引入了重叠区域和内部边界。目前, 建立在阴阳网格上的数值预报模式包括加拿大国家气象局的GEM(Global Environmental Multiscale atmospheric model)全球静力模式(Girard, et al, 2014)、日本气象厅的ASUCA非静力模式和中国气象局开发的GRAPES_YY模式(Li, et al, 2015; 2018)。
GRAPES_YY模式采用半隐式半拉格朗日方法对平流型的纳维-斯托克斯方程和连续方程求解, 因此模式计算不具守恒性。对中期数值天气预报而言, 这种质量不守恒并不会产生很严重的影响, 但对气候模拟的长期积分而言, 则会造成气候态漂移和模拟结果的严重失真。为建立阴阳网格上的多尺度大气动力框架, 本研究将以有限体积法为基础建立通量型的非静力全球大气动力框架, 以满足未来高分辨率全球中期数值预报和气候预测发展的需求。在球面阴阳网格上有限体积法的约束下构建局地守恒的计算方案, 同时可以采用Peng等(2006)开发的阴阳网格边界通量守恒强迫计算方案, 来保证全球质量守恒计算。
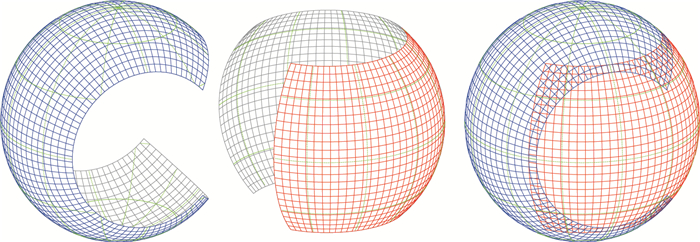
2 模式动力框架和基本算法 2.1 阴阳网格简介阴阳网格是由两块相同的传统经纬度网格的低纬度区域组成的正交重叠的球面网格系统。该网格系统由于与中国阴阳图相似而得名, 其平面最大与最小网格之比约为1:0.707。图 1给出了阴阳网格的基本构成, 其中阴网格和阳网格都是普通经纬度坐标球面上的低纬度部分, 其经纬度范围为
|
| 图 1 阴阳网格示意 Figure 1 Schematic diagram of the Yin-Yang grid |
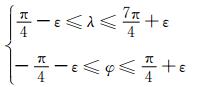
|
(1) |
式中, λ为经度, φ为纬度, ε为网格的扩展区域, 扩展域的大小与计算方法相关。因此, 阴阳网格的两个物理分区是大小相同、网格结构完全一致的, 且由于各自采用经纬度坐标度量, 具有正交性和准均匀性。为了阴、阳网格间信息的正常传递, ε≥1个网格。
阴阳网格的主要缺点是网格重叠和内部边界问题。与传统经纬度网格和其他准均匀网格相比, 阴阳网格具有以下优点:
(1) 阴阳网格是结构网格, 并行处理简单。
(2) 阴阳网格中的两个网格区域是对称的。可以根据业务或研究的需要, 将整个网格围绕着球面任意旋转。阴阳网格的这种旋转对称性并不会随着旋转角度的改变而改变。
(3) 阴阳网格是正交的。这对于结构化网格上很多复杂的数值计算更为方便, 如高阶插值等。同时, 阴阳网格采用了低纬度网格, 比较利于传统球面网格上的一些算法和物理过程移植到基于阴阳网格的模式中。
阴阳网格完全对称, 构造一样, 两个计算区域可公用一个源代码, 较为方便。最近主要有李江浩等(2013)和刘洁等(2017)对阴阳网格守恒性能进行了研究。本研究基于阴阳网格, 构建通量型非静力大气动力模式框架, 以解决模式平流型方程和半拉格朗日型算法带来的物理量计算不守恒问题(陈嘉滨等, 2004)。
2.2 模式动力框架和基本算法 2.2.1 非静力大气动力框架为满足非静力大气动力框架的计算守恒性, 考虑采用具有更好守恒性的预报量构建通量型的预报方程组。考虑动量、质量的良好物理守恒性, 选定通量型变量ρu、ρv、ρw和ρ为预报变量, 来描述单位体积内的动量和质量的时间变化。同时, 在动力方程的构建过程中, 采用通量型动力方程, 采用有限体积概念离散化计算, 可以保证预报量的平流计算守恒, 从而保证模式较好的守恒性能。为方便动量方程中气压梯度力的离散化求解和避免采用位温预报方程面临非线性项离散化问题, 对热力方程选取了气压p的预报方程构建模式。由纳维-斯托克斯方程、连续方程和能量方程组成的非静力大气通量型动力方程组为

|
(2) |
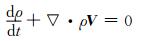
|
(3) |
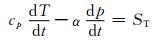
|
(4) |
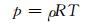
|
(5) |
式中, V为大气运动三维风速, ρ为大气密度, p为气压, T为气温。α=1/ρ, 为密度的倒数, Ω为地球自转角速度。DρV表示湍流扩散, cp为定压比热, ST为源汇项。在动量方程中, 采用p来计算气压梯度力。考虑地形的存在, 为了简化模式下边界条件的处理, 在垂直方向上采用了垂直高度地形追随坐标
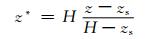
|
(6) |
式中, H为模式层顶高度, zs为地形高度, z为海拔高度。为了减小计算误差, 对模式预报量中随高度变化明显的物理量(p, ρ, T)采用扰动量表达的方式进行离散化, 以气压(p)为例

|
(7) |
式中, 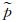
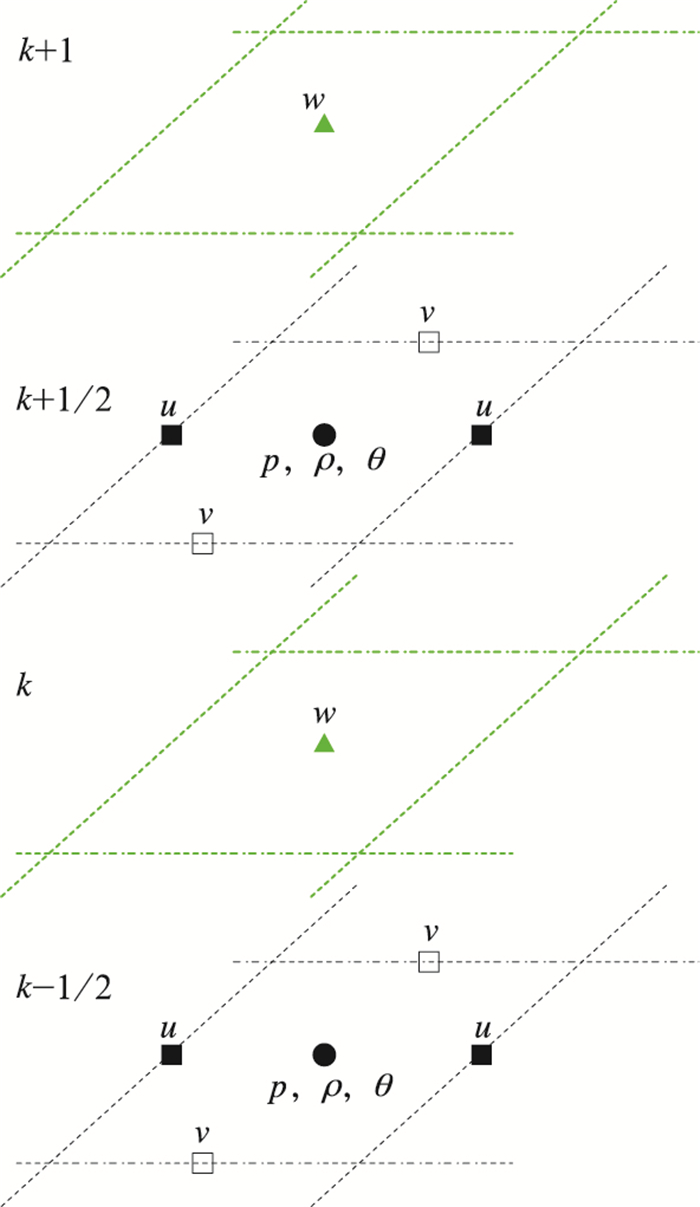
对动力框架中的预报变量离散, 水平方向上采用荒川(Arakawa)-C网格, 垂直方向上采用洛伦兹跳层分布。如图 2所示, 在水平方向上标量位于整数层的网格中央, 而速度矢量分别位于网格边界上, 其中纬向风在x方向界面, 而经向风在y方向界面。
|
| 图 2 模式分层和水平网格示意 Figure 2 The schema of vertical coordinate and horizontal grid of the model |
垂直方向, w在半数层, 水平位置与标量一致。模式整数层和半数层各有一层位于地面下, 地表为半数层2-1/2(记为第k=2层)。整数层的边界设在k=2, 是整数层边界。对于上边界, 第km+1/2半数层位于模式顶(z=H, z*=H)整数层的上边界位于km。
2.2.3 时间积分方案考虑到模式水平网格相对于垂直分层要大得多, 积分时间步长主要受垂直方向的限制, 而完全隐式计算需要求解三维亥姆霍兹方程则有非常高的计算成本问题。这里时间离散采用水平显式、垂直隐式(HEVI)时间积分方案。该方案对垂直方向声波、重力波快波项采用半隐式算法。对于水平方向声波、重力波采用小时间步长显式求解, 慢波项采用大步长显式求解。该方案在水平方向为显式积分, 计算简单、速度快。由于水平网格较大, 受计算稳定性条件的约束并不苛刻。在垂直方向, 分层较密, 网格距小, 非静力模式中的声波计算使得计算步长受到严格的限制, 在垂直方向采用隐式计算可以放大垂直方向积分时间步长, 而且相应的k层大气的亥姆霍兹方程求解也仅涉及小矩阵运算, 计算简单轻便。
时间积分方案采用显式3阶龙格-库塔(Runge-Kutta)方案。龙格-库塔多步时间积分是高精度的显式积分方案, 现有版本较多, 如Gottlieb等(1998)和Wicker等(2002)。在计算力学领域Gottlieb等(1998)的方法应用较多, 考虑快慢波分离算法, 文中选用Wickerdeng(2002)的3阶龙格-库塔法作为平流慢波的时间积分方案, 水平方向快波采用向前-向后方法进行小时间步长积分。为改善计算精度, 将快波计算分散在慢波的龙格-库塔多步计算中, 即在进行龙格-库塔计算时首先进行大时间步长运算, 再将大时间步长的变量时间倾向分段加入小步长积分过程, 将快慢过程统一分步计算。所以, 这里的小步长时间积分采用时间向前格式
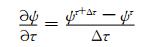
|
(8) |
式中, τ为时间, Δτ为时间步长, ψ为任意变量。
2.2.4 空间积分方案采用Wicker等(2002)的5阶迎风有限差分格式对平流过程离散化
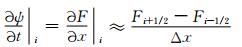
|
(9) |
式中, Δx为空间网格距。其中F=uψ为变量ψ的x方向通量
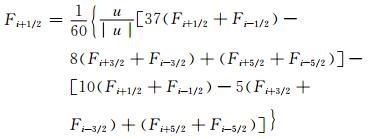
|
(10) |
采用5阶迎风格式计算有限体积界面上的水平通量, 并按照上式有限差分获得平流计算, 实现有限体积上的通量收支和质量时间变化计算。在垂直方向由于层数较少, 高阶离散方法受到限制, 模式中利用2阶通量型有限差分方法离散。
需要指出, 模式采用有限体积法和通量型平流计算保证了模式局地守恒性, 但由于阴阳网格边界的存在, 并且Peng等(2006)的守恒强迫方案还没有在本模式中安装, 现阶段还无法保证模式的全球质量守恒。
2.2.5 边界处理由于阴阳网格存在内部边界, 模式积分过程中需要进行边界更新, 文中采用3次拉格朗日差值方案(Peng, et al, 2006; Li, et al, 2006)进行更新。对于阴阳网格重叠区的内部网格, 这里没有进行额外处理。
3 三维理想试验及结果为检验模式框架动力性能及动力过程离散计算的效果, Jablonowski等(2008)在Williamson等(1992)二维浅水波理想试验的基础上发展了一套三维空间大气动力理想试验, 分别模拟地转平衡流、地形强迫罗斯贝波和罗斯贝-豪威茨波发展等动力过程。参照阴阳网格上GRAPES_YY非静力动力框架的检验方法(Li, et al, 2015), 定义阴阳网格中任意一个标量q在整个球面上的积分量M(q)为

|
(11) |
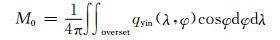
|
(12) |
式中, qyin和qyang分别为阴网格和阳网格上的标量, M0为阴阳网格重叠部分的积分量。定义标准误差为
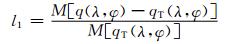
|
(13) |

|
(14) |
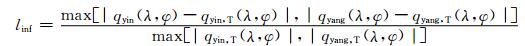
|
(15) |
式中l1、l2分别为绝对值平均误差和均方根平均误差, linf为极值误差, q(λ, φ)为模式变量数值解, qT(λ, φ)代表变量的解析解。
鉴于目前该模式动力框架的开发基于Linux平台个人计算机, 计算机内存的限制使得高分辨率计算非常困难, 而且为了使试验结果便于和Li等(2015)半拉格朗日方案的一些理想试验结果进行比较, 文中模式水平分辨率取2.5°×2.5°, 模式层顶为30 km, 垂直方向分17层, z*的值分别为0、144、557.35、1221.35、2136、3301.35、4717.35、6384、8301.35、10469.35、12668、15557.35、18477.35、21666.65、25000、28333.35和31666.65 m。
3.1 三维平衡流试验平衡流试验是假设垂直方向上静力平衡、水平方向上地转平衡的一个三维理想试验。对于保持平衡流动, 理论上流动的形态永远保持不变, 因此模式的数值积分结果也应该保持与初始场一致。在离散化模式中, 计算误差越小, 积分结果相对初始场的偏离就越小。平衡流试验具体设计为
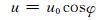
|
(16) |
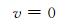
|
(17) |
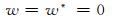
|
(18) |
式中, u、v、w分别为纬向、经向、垂直风速, w*为模式z*坐标系中的垂直速度, u0=20 m/s。此外, 假设在垂直方向上满足静力平衡关系
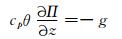
|
(19) |
位温θ满足
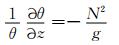
|
(20) |
初始水平中纬向风u满足地转平衡关系
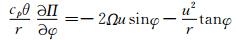
|
(21) |
式中, g为重力加速度, Ω=7.29212×10-5s-1为地球自转角速度, N表示布伦特-维赛拉(Brunt-Vaisalla, B-V)频率, Π为气压埃克斯纳(Exner)函数, 解得
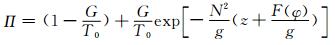
|
(22) |
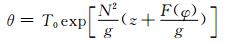
|
(23) |

|
(24) |
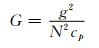
|
(25) |
式中, G为万有引力常数, T0为参考温度, F(φ)为设定函数。然后算出气压p=p0Πcp/R, 密度ρ=P/(θΠR)。
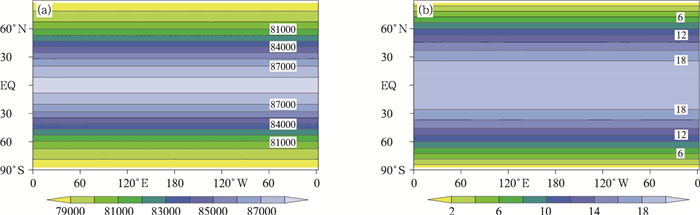
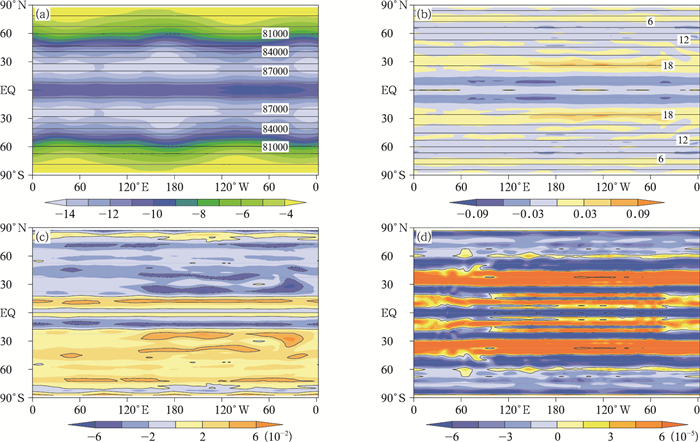
根据平衡流试验的初始场设定, 给出了模式第5层的初始气压和纬向风的水平分布(图 3), 经向风和垂直速度均为0。利用上述初值, 对新开发动力框架进行12 d积分试验。由于受计算机内存限制, 模式水平分辨率取2.5°×2.5°, 垂直方向上将模式顶30 km以下分为17个非均匀层, 越靠近地面分层越密, 远离地面则间隔变大。模式模拟气压p、三维风速u、v、w场(图 4), 模式积分时间步长为1800 s。整体来看, 积分12 d后, 气压场呈现纬向等值线分布, 与初始场保持一致, 在中纬度地区气压的南北梯度最大; 纬向风流型保持平直, 呈平行等纬度线分布, 梯度也基本保持了原有的分布态势。同时, 模拟结果仍然保持了南北半球对称或反对称的变量分布, 不仅反映了三维科里奥利力在平衡流中南北半球的对称作用, 也证实了模式有限体积上通量计算的正确性。此外, 虽然变量误差呈现纬向带状分布, 但无论气压还是风场均表现出绝对误差的纬向非均匀性, 这显然与阴阳网格边界的插值计算有关。气压的绝对误差从赤道向极区逐渐减小, 在低纬度地区纬向存在小的波动, 低纬度地区误差最大, 约为-14 Pa, 中纬度地区约-5 Pa, 极地地区误差约为-3 Pa。纬向风u在中低纬度地区偏差较大, 约为-0.06 m/s, 纬向风误差明显与网格边界和纬向风本身大小相关, 最大约为0.08 m/s, 出现在阳网格下游边界处, 纬向风偏差在南北两半球呈对称分布。经向风v误差的分布也是呈现南北对称的结构, 赤道地区误差最小, 约为-1×10-2 m/s, 误差随着纬度的升高有小幅增长, 在阴阳网格边界处的误差最大, 达到了±4×10-2 m/s。垂直速度的误差在10-5 m/s的数量级, 误差最大值出现在中低纬度地区, 网格边界附近的误差较大。从经向风速和垂直速度绝对误差可以发现, 本框架的计算误差较半隐式半拉格朗日模式(Li, et al, 2015)中对应变量绝对误差大。误差分布反映出阴阳网格边界的插值对计算结果的影响, 特别是变量纬向波动的存在与阴阳边界插值误差的传播直接相关。
|
| 图 3 模式第5层初始气压p(单位:Pa)(a)和纬向风u(单位:m/s)(b)的分布 Figure 3 Initial fields of (a) p (unit: Pa) and (b) u (unit: m/s) at the 5th model level |
|
| 图 4 积分12 d后, 模式第5层的数值解及其绝对误差 (a.气压(单位:Pa), b.纬向风(单位:m/s), c.经向风(单位:m/s), d.垂直速度(单位:m/s); 等值线为试验结果, 色阶为绝对误差) Figure 4 Numerical results at the 5th model level after 12 d of integration for the balanced flow test (a. p (Pa), b. u (m/s), c. v (m/s), d. w (m/s); shadings show absolute errors of corresponding variables) |
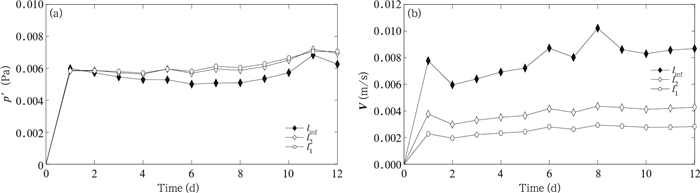
采用模式平衡流试验初值作为解析解, 图 5给出了基于阴阳网格的平衡流试验中气压扰动量p′和风场的数值解标准误差12 d的时间序列。可以看出, 由于模式分辨率较低, 初始时刻非静力平衡和初始场静力平衡关系存在偏差, 气压和风场的标准化误差都随时间缓慢增长, 在第12天气压扰动量的l1和l2误差都在0.007 Pa附近, 扰动量极值误差linf约为0.006 Pa, 风速V的标准化误差l1和l2约为0.003和0.005 m/s, 风速极值误差linf约为0.009 m/s。从误差的时间序列可以看出, 模式误差在第1天增长很快, 可能与静力平衡的初始场的调整有关, 随后误差平稳缓慢增长, 而半隐式半拉格朗日模式(Li, et al, 2015)的预报量误差呈线性增长, 这与半拉格朗日追踪方向上流场均匀分布也有很大关系, 对于均匀流场, 半拉格朗日计算误差较小。
|
| 图 5 模式积分12 d的标准误差时间序列 (a.气压扰动量(单位: Pa), b.三维速度矢量(单位: m/s)) Figure 5 Temporal variations of the error norms of (a) p′ (unit: Pa) and (b) V (unit: m/s) during the 12 d integration |
简单的三维平衡流试验的积分结果表明, 该动力框架性能稳定, 积分结果正确, 但计算结果误差仍然偏大, 阴阳网格边界插值造成的误差传播在模式中表现突出。
3.2 罗斯贝-豪威茨试验罗斯贝-豪威茨波是正压涡度方程的解析解, 可以用来检验二维浅水模式的动力性能。对于三维罗斯贝-豪威茨波理想试验, 水平方向与二维问题一致, 但垂直方向上假定温压场满足静力平衡。由于该试验中存在大小相当的水平二维风场和长波传播, 模式积分过程中对波形的保持和波传播速度的刻画要求较高, 因此模式的积分时间步长比地转平衡流试验要求更加苛刻, 计算误差也更明显。
在罗斯贝-豪威茨波试验中, 垂直速度准确解为0, 水平风速周期性波动变化, 且在南北两个球呈对称分布, 初始时刻风场设置为
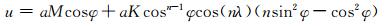
|
(27) |
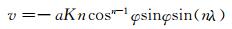
|
(28) |
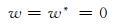
|
(29) |
初始气压满足静力平衡
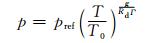
|
(30) |
温度随高度递减且满足线性递减关系
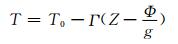
|
(31) |
式中, a=6371.23 km为地球半径, pref=955 hPa为参考气压, T0=288 K, Γ=0.0065 km-1, Φ表示地面投影到参考等压面上的位势高度
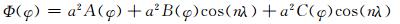
|
(32) |
式中, A、B、C均为系数, 波数n=4, M=K≈1.962×10-6s-1,
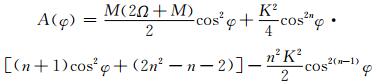
|
(33) |
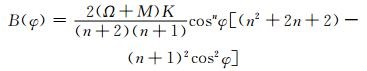
|
(34) |
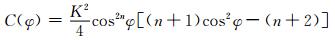
|
(35) |
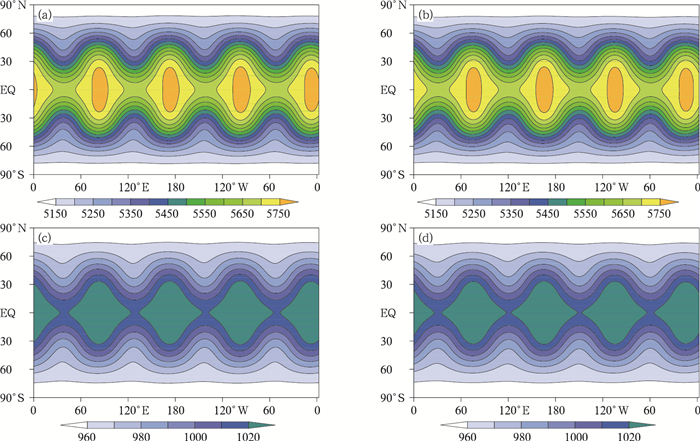
在罗斯贝-豪威茨波试验中, 积分时间步长取为600 s。从模式积分到第7天和第14天500 hPa的位势高度和地面气压(图 6)可以发现, 无论地面气压还是高空位势高度, 均能保持均匀整齐的波动, 波谷和波峰高度或气压都与初始场相同。积分第7天和第14天的豪威茨波也非常相似, 除了由于波的传播而造成两个时刻的位相差异外。在相同模式水平分辨率下, 位势高度的波峰相对半拉格朗日计算结果(Li, et al, 2015)稍显平滑, 从地面气压的分布也能看出相同结果。可见, 高阶离散有限体积法对平流场的平滑效应较明显, 但这种高阶离散的波动传播整体效果令人印象深刻, 变形很小。
|
| 图 6 罗斯贝-豪威茨波第7天(a、c)与第14天(b、d)的500 hPa位势高度(a、b, gpm)和地表气压(c、d, hPa) Figure 6 Numerical results of simulated geopotential height (a, b; gpm) and surface pressure (c, d; hPa) at the 7th day (a, c) and 14th day (b, d) of integration in the Rossby-Haurwitz wave test |
从模式第7天和第14天850 hPa的水平风场分布(图 7)可以看出, 风场在模式积分过程中同样有序而规整传播, 尽管模式分辨率较低, 但波形保持了原有特征, 形变微小。纬向和经向风保持了初始场的纬向周期性分布和南北对称。在与相同分辨率的半隐式半拉格朗日计算结果(Li, et al, 2015)比较中, 同样发现本框架计算的纬向和经向风极大值较2.5°分辨率的半拉格朗日计算稍微偏小, 主要归因于5阶迎风格式相对于3阶拉格朗日多项式更平滑。虽然罗斯贝-豪威茨波要求的稳定积分时间步长较小, 但采用600 s时间步长的稳定积分结果仍可以很好反映豪威茨波的对称性和传播特征, 在通过阴阳网格边界时所有预报量没有表现出明显的边界插值痕迹。

|
| 图 7 罗斯贝-豪威茨波第7天(a、c)与第14天(b、d)的850 hPa纬向风(a、b)和经向风(c, d)(单位:m/s) Figure 7 Numerical results of simulated zonal wind u (a, b) and meridional wind v (c, d) (unit: m/s) at the 7th day (a, c) and 14th day (b, d) of integration for the Rossby-Haurwitz wave test |
在检验了无地形条件下模式动力框架的动力性能后, 进一步考察了模式对地形的处理和数值表达能力。地形罗斯贝波试验就是模拟有地形情况下大气中地形罗斯贝的产生和发展, 从而检测模式的动力性能。该试验同样利用浅水波模式的地形重力波风压场配置, 在垂直方向考虑满足静力平衡条件而得到, 初始时刻T(λ, φ, r)=T0=288 K, 为等温大气, 初始风场与三维平衡流试验相同, 以(λc, φc)为中心设置一个钟形山体, 山体半径d=1500 km, 中心高度h0=2000 m, 地形高度中心位于阴阳网格的重叠区域
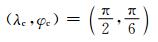
|
(36) |
地形高度为
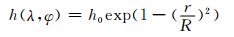
|
(37) |
该位置刚好位于两个网格的重叠区域, 式中, r为山脉表面到中心位置的水平距离
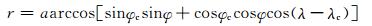
|
(38) |
地表气压满足
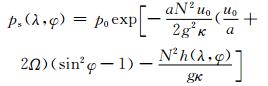
|
(39) |
式中, κ=2/7, α=6371.23 km, p0=930 hPa为两极地面气压。在气流经过孤立的山体时, 就会激发出地形罗斯贝波, 并不断发展向下游传播, 波及全球。
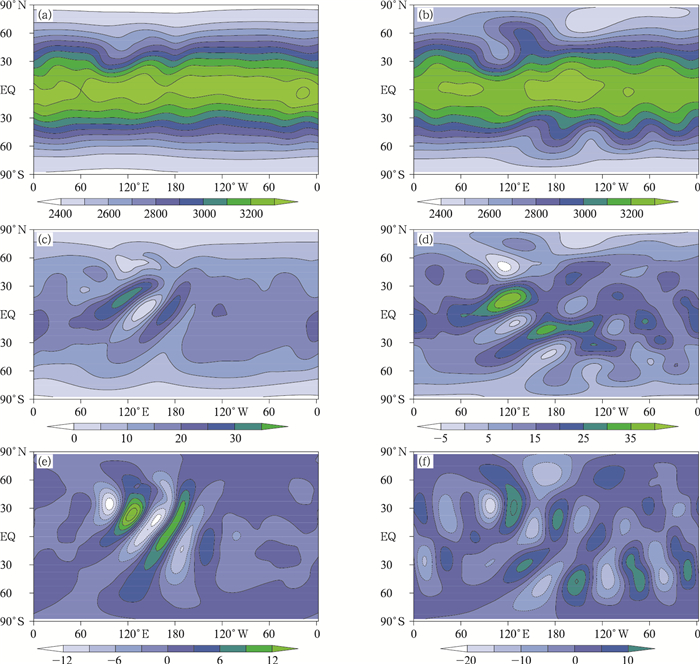
地形强迫罗斯贝波试验积分15 d的结果在图 8中给出, 包括了模拟700 hPa位势高度和水平风场。从位势高度可以看出, 气流过山后形成了明显的地形强迫罗斯贝波, 并随着时间不断发展增长, 在向下游传播的过程中南北半球的罗斯贝波槽脊不断加深, 尤其是在山脉地形附近, 形成最大槽脊系统。结果与其他模式(Li, et al, 2015; 陈德辉等, 2008; 牛嫣静等, 2018)模拟相似, 但是可以看出背风槽相对稍深。从水平风场看, 气流在遇到山脉地形以后, 大部分向南绕流, 山脉下游则向北回流, 山脉下游南侧形成强西风中心, 北侧有弱西风中心, 强弱西风中心向南半球传播。
|
| 图 8 地形强迫罗斯贝波试验中模式第5天(a、c、e)和第15天(b、d、f)的700 hPa位势高度(a、b, gpm)、纬向风u(c、d, m/s)和经向风v(e、f, m/s) Figure 8 Simulated geopotential height (a, b; gpm), zonal wind u (c, d; m/s) and meridional wind v (e, f; m/s) at the 5th day (a, c, e) and 15th day (b, d, f) of simulation |
比较Li等(2015)的山脉罗斯贝波试验, 在波动基本分布相似的同时, 背风槽发展的深浅、赤道高压的分布和南半球波动的发展等都有明显差异。
4 结论和讨论从水平方向上采用荒川(Arakawa)-C网格, 垂直方向上采用洛伦兹跳层变量分布在球面阴阳网格上初步构建了以高度地形追随坐标为垂直坐标的通量型非静力大气动力框架, 该动力框架利用有限体积法离散化来保证模式的局地守恒性, 对快波采用水平显式、垂直隐式(HEVI)计算不仅可以缓解快波对积分时间步长的限制, 还可避免在完全隐式计算中大型矩阵求解。对慢波的时间积分选用3阶龙格-库塔显式方案, 在保证较高计算精度的同时又节省计算时间, 空间差分方案选择了精度较高的5阶迎风有限差分格式来计算平流项。通量型的预报方程和具有守恒属性的预报变量选取有利于保证模式守恒性能的塑造。
构建的通量型非静力动力框架在3个三维大气理想试验中进行了积分检验, 由于模式框架是在基于Linux系统的微机上构建, 且尚未在大型计算机上移植, 并受到微机计算能力和内存的限制以及为了方便比较, 文中的所有理想试验为低分辨率(2.5°×2.5°)运行结果。三维平衡流试验、罗斯贝-豪威茨波试验和山脉罗斯贝波试验都证实了新开发通量型模式动力框架的初步成功和较好的数值计算效果。三维平衡流试验中获得了12 d积分保持平直的纬向风和平行纬圈的等压线分布, 充分体现了模式平流、气压梯度力计算和科里奥利力计算较好的计算精度和很好的计算稳定性, 气压扰动量的标准误差和风速的标准误差都反映出缓慢的时间增长特点, 阴阳边界插值处理没有给模式积分带来不可接受的误差和不可克服的困难。虽然罗斯贝-豪威茨波理想试验采用较小的时间步长, 该框架仍然很好地模拟了罗斯贝-豪威茨波的传播和波形分布, 规整的波形关于赤道对称, 且在纬向具有均匀的周期分布特征, 计算方案基本可以正确描述大尺度波动的传播。孤立山体强迫的罗斯贝波在该通量型非静力框架中可在正确的位置生成并发展, 逐步向下游传播, 并扩展到全球。地形罗斯贝波的生成和传播证实了该动力框架在描述地形强迫和地形处理上的成功, 基本验证了垂直坐标选取和相应动力过程处理的合理性。
本研究是阴阳网格上通量型非静力模式建立的基础工作, 目前仅完成了微机版的动力框架的构建, 有很多后续工作尚待进行, 包括阴阳网格边界守恒强迫方案的安装、代码的普适化、并行计算、物理过程安装等。
| 陈嘉滨, 季仲贞. 2004. 半隐式半拉格朗日平方守恒计算格式的构造. 大气科学, 28(4): 527–535. Chen J B, Ji Z Z. 2004. A study of complete square-conserving semi-implicit semi-Lagrangian scheme. Chinese J Atmos Sci, 28(4): 527–535. (in Chinese) |
| 陈德辉, 薛纪善, 杨学胜, 等. 2008. GRAPES新一代全球/区域多尺度统一数值预报模式总体设计研究. 科学通报, 53(22): 3433–3445. Chen D H, Xue J S, Yang X S, et al. 2008. New generation of multi-scale NWP system (GRAPES):General scientific design. Chinese Sci Bull, 53(22): 3433–3445. (in Chinese) |
| 李江浩, 彭新东. 2013. 守恒型有理函数插值半拉格朗日平流方案及性能分析. 气象学报, 74(4): 709–718. Li J H, Peng X D. 2013. Analysis of computational performance of the conservative Semi-Lagrangian with rational function advection scheme. Acta Meteor Sinica, 74(4): 709–718. (in Chinese) |
| 刘洁, 彭新东. 2017. 阴阳网格守恒算法的设计和改进. 大气科学, 41(5): 1076–1086. Liu J, Peng X D. 2017. Design and improvement of the conservative constraint algorithm on the Yin-Yang grid. Chinese J Atmos Sci, 41(5): 1076–1086. (in Chinese) |
| 牛嫣静, 彭新东. 2018. GRAPES模式中三维科氏力计算及其效果评估.气象学报, 76(3): 473-484. Niu Y J, Peng X D, Fan G Z. 2018. Impact of the three-dimensional Coriolis force in the GRAPES model. Acta Meteor Sinica, 76(3): 473-484 (in Chinese) http://www.cmsjournal.net/qxxb_cn/ch/reader/view_abstract.aspx?file_no=2018003&flag=1 |
| Girard C, Plante A, Desgagné M, et al. 2014. Staggered vertical discretization of the Canadian environmental Multiscale (GEM) model using a coordinate of the log-hydrostatic-pressure type. Mon Wea Rev, 142(3): 1183–1196. DOI:10.1175/MWR-D-13-00255.1 |
| Gottlieb S, Shu C W. 1998. Total variation diminishing Runge-Kutta schemes. Math Comp, 67(221): 73–85. DOI:10.1090/mcom/1998-67-221 |
| Jablonowski C, Lauritzen P H, Nair R D, et al. 2008. Idealized test cases for the dynamical cores of Atmospheric General Circulation Models. A proposal for the NCAR ASP 2008 summer colloquium. http://esse.engin.umich.edu/admg/publications.php. |
| Li X H, Peng X D, Li X L. 2015. An improved dynamic core for a non-hydrostatic model system on the Yin-Yang grid. Adv Atmos Sci, 32(5): 648–658. DOI:10.1007/s00376-014-4120-5 |
| Li X H, Peng X D. 2018. Long-term integration of a global non-hydrostatic atmospheric model on an aqua planet. J Meteor Res, doi: 10.1007/s13351-018-8016-7(Submitted) |
| Li X L, Chen D H, Peng X D, et al. 2006. Implementation of the semi-Lagrangian advection scheme on a quasi-uniform overset grid on sphere. Adv Atmos Sci, 23(5): 792–801. DOI:10.1007/s00376-006-0792-9 |
| Kageyama A, Sato T. 1995. Computer simulation of a magnetohydrodynamic dynamo. Ⅱ. Phys Plasmas, 2(5): 1421–1431. DOI:10.1063/1.871485 |
| Kageyama A, Sato T. 2004. "Yin-Yang grid":An overset grid in spherical geometry. Geochemistry, Geophysics, Geosystems, 5(9): Q09005. |
| Peng X D, Xiao F, Takahashi K. 2006. Conservative constraint for a quasi-uniform overset grid on the sphere. Quart J Roy Meteor Soc, 132(616): 979–996. DOI:10.1256/qj.05.18 |
| Sadourny R. 1972. Conservative finite-difference approximations of the primitive equations on quasi-uniform spherical grids. Mon Wea Rev, 100(2): 136–144. DOI:10.1175/1520-0493(1972)100<0136:CFAOTP>2.3.CO;2 |
| Sadourny R, Arakawa A, Mintz Y. 1968. Integration of the nondivergent barotropic vorticity equation with an icosahedral-hexagonal grid for the sphere. Mon Wea Rev, 96(6): 351–356. DOI:10.1175/1520-0493(1968)096<0351:IOTNBV>2.0.CO;2 |
| Wicker L J, Skamarock W C. 2002. Time-splitting methods for elastic models using forward time schemes. Mon Wea Rev, 130(8): 2088–2097. DOI:10.1175/1520-0493(2002)130<2088:TSMFEM>2.0.CO;2 |
| Williamson D L. 1968. Integration of the barotropic vorticity equation on a spherical geodesic grid. Tellus, 20(4): 642–653. DOI:10.3402/tellusa.v20i4.10044 |
| Williamson D L, Drake J B, Hack J J, et al. 1992. A standard test set for numerical approximations to the shallow water equations in spherical geometry. J Comput Phys, 102(1): 211–224. DOI:10.1016/S0021-9991(05)80016-6 |
 2019, Vol. 77
2019, Vol. 77


