中国气象学会主办。
文章信息
- 代刊, 朱跃建, 毕宝贵. 2018.
- DAI Kan, ZHU Yuejian, BI Baogui. 2018.
- 集合模式定量降水预报的统计后处理技术研究综述
- The review of statistical post-process technologies for quantitative precipitation forecast of ensemble prediction system
- 气象学报, 76(4): 493-510.
- Acta Meteorologica Sinica, 76(4): 493-510.
- http://dx.doi.org/10.11676/qxxb2018.015
-
文章历史
- 2017-11-10 收稿
- 2018-02-07 改回
2. 美国国家环境预报中心/环境模式中心, 马里兰, 20740
2. NOAA/NWS/NCEP/Environmental Modeling Center, Maryland 20740, USA
集合数值模式已在全球多个国家的天气业务预报中心实现常规运行(Molteni,et al,1996;Toth,et al,1993)。2005年,中国全球T213集合预报系统投入实时运行(田华等,2005),并在2014年进一步升级为T639集合模式系统。集合预报的目标是提供关于天气预报的不确定性信息,即在不同环流条件下给出未来大气可能状态的概率分布样本集。在理想情况下,未来天气事件的出现概率可以通过估计该样本集中事件相对频率获得。发布概率预报,有利于用户基于自身花费/损失比来进行更科学的决策(Zhu,et al,2002)。此外,概率预报结果连续和稳定性更高(Buizza,2008),且能提供灾害性天气的早期预警(Legg,et al,2004)。但在实际应用中,基于集合模式得到的预报结果常表现出系统性偏差以及欠离散或过离散的情况(Hamill,et al,1998;李俊等,2015)。其出现原因包括模式系统误差,成员样本少及分辨率不足(Mullen,et al,2002; Ma,et al,2012);生成初始条件的同化及扰动方法不完善,不能完整描述大气所有不确定性(Hamill,et al, 2000, 2003)等。
为校正集合模式结果表现出的偏差,需要进行统计后处理以便改善其可靠性和预报技巧(Wilks,et al,2007; 熊敏诠,2017)。目前,统计后处理已经成为集合预报系统的重要组成部分。传统的模式输出统计预报(Glahn,et al,1972)已广泛应用。模式输出统计预报主要是寻找观测数据与某一数值模式输出结果的回归模型,并在实际预报中利用该统计关系将一个单值的模式预报转变为另一个单值预报以获得更准确的预报。在考虑集合模式时,若将传统模式输出统计预报用于各个成员只能调整中心倾向的预报误差,不能提供完整的集合校正(Cui,et al,2012)。尤其对具有偏态分布的降水变量,Flowerdew(2012)指出,其统计特征使得应用常规的偏差订正困难,若使用加减项会影响所有的0值成员,而使用乘项则不利于校正有无降水的频率偏差。为此,对集合模式更适用的方法是通过统计后处理生成未来天气变量或事件的全概率预报。集合概率预报有可靠性和解析度两个关键特征(Toth,et al,2006),其中,可靠性为模式预报概率与实际观测频率的一致程度(若相等则可靠性最佳);解析度为概率预报对天气事件出现与否可能性的区分程度(若给出可能出现或不出现的区分越明确,则解析度越高)。Toth等(2006)指出,由于统计校正不能引入因模式能力有限而出现的个例误差信息,因此解析度很难改善;但通过训练样本能提供预报和观测的统计特征关系,可在尽量保持解析度的情况下,提高预报的可靠性。除生成概率预报外,为了支持传统的确定性预报并发布最有可能的预报结果,还存在多种后处理技术将集合模式的有效信息集成起来获得精准度更高的单值预报(Ebert,2001),在业务中也得到使用(Novak, et al,2014;毕宝贵等,2016)。综上所述,文中将集合预报统计后处理技术定义为:针对集合模式,采用统计关系或模型来获得概率预报或校正后的集合预报,以及集成多个成员信息获得最有可能结论的技术方法。
在所有气象要素中,降水在众多应用领域备受关注,其预报可用于发布灾害天气预警(Messner,et al,2014a)、预报洪水(Kim, et al,2001)等。相对于气温、风速等,降水量的统计后处理具有更高难度(Scheuerer, et al,2015),表现在具有离散/连续混合的统计模型特性、预报不确定性随着雨量的增大而增大,而且强降水的发生频率也较低。
近年来,基于集合数值模式的定量降水预报(Quantitative Precipitation Forecast,简称QPF)技术发展快速,如杜钧等(2014)从模式构建、预报方法及后处理等方面探讨了集合预报方法在暴雨研究和预报中的应用;Gneiting等(2014)从统计学的角度描述了适合不同变量的概率分布模型,以及普遍的集合统计后处理和检验方法;毕宝贵等(2016)从数值模式发展、模式后处理、检验评估等方面总结了定量降水预报业务进展;Li等(2017)重点回顾了水文集合预报中的降水后处理技术。上述回顾从不同角度对集合模式定量降水预报统计后处理进行总结,但未完整包括目前业务应用研究中的技术方法。文中将系统地归纳集合模式定量降水预报统计后处理方法的研究进展,以及各种方法的优缺点及适用范围,最后进行总结和讨论。这里依据技术方法的途径和成熟度进行了分类,主要考虑单变量的非参数化和参数化两类后处理方法;而基于变量结构的后处理方法在近年来得到快速发展,将作为第三类进行介绍。
2 非参数化后处理方法非参数化的集合模式定量降水预报后处理不用预先设定降水的统计分布模型,避免了与模型构建相关的难点;具有灵活多样的形式,可用于系统误差订正或者多个成员或模式的有效信息集成。与参数化后处理方法相比,非参数化后处理一般缺乏推演能力;若用于订正一般需要大量的训练样本,尤其对于低频率的强降水事件。非参数化后处理方法归纳为3类:集合定量降水预报订正方法,通过匹配模式预报和观测之间的统计特征,或寻找历史相似样本,订正模式降水预报的系统性误差,可以获得订正后的成员预报或者概率预报;集合定量降水预报集成方法,通过集合预报有效信息提取或权重叠加,获得最有可能的单值预报;此外,随着云分辨率集合模式的出现(Gebhardt,et al,2008),常用的全球模式集合处理方法变得不再适用,基于空间分析的后处理方法得到快速发展。
2.1 集合定量降水预报订正法 2.1.1 统计特征匹配法统计特征匹配法首先获取模式预报与相应观测数据的统计特征,然后利用两者的映射关系将预报量匹配到观测量上,得到订正结果。该类方法数学意义明确,发展时间较长且在天气、气候研究中均有应用。表 1给出5种统计特征匹配法及其特点。下面重点介绍应用较为广泛的频率匹配法和分位值映射法的计算、改进以及业务应用。
| 名称 | 匹配统计量 | 参考文献 | 特点 |
| Rank histogram recalibration | 排序直方图 | Hamill, et al, 1998; Eckel, et al, 1998 |
改善预报技巧,但当成员值相近时概率值可能异常,对直方图的形状很敏感 |
| Frequency-Matching Method | 不同阈值的频率分布 | Zhu, et al, 1996; Zhu,et al, 2015 |
改善降水量级系统偏差,对极端降水和干偏差的订正能力有限 |
| Quantile mapping | 不同分位值的频率分布 | Hopson, et al, 2010 | 使预报和观测不同分位值的频率一致,保留时、空结构,但不能保证预报技巧提高 |
| Simple binning technique | 频率分布直方图 | Stensrud, 2007 | 改进预报技巧和可靠性,但不保证空间分布的连续性 |
| Reliability calibration | 可靠性曲线 | Flowerdew, 2014 | 提高预报可靠性,保留空间结构,但对样本数量敏感 |
(1) 频率匹配法:Zhu等(1996和2015)详细介绍了频率匹配法并对其进行了改进。该方法分为两个步骤。第1步需要通过构建样本降水预报量级以及相应观测量的累积分布函数获得降水频率分布。这里累积分布函数通过计算指定空间范围内超过一系列降水阈值(升序排列)的预报或观测的格点数量而获得。在实际应用中,预报和观测的累积分布函数采用卡尔曼滤波方法实时更新

|
(1) |
式中,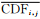

|
| 图 1 频率匹配方法示意(Zhu, et al,2015) Figure 1 Schematic of the frequency-matching algorithm demonstrated as precipitation distributions normalized by observation frequency varying with threshold (Zhu, et al, 2015) |
(2) 分位值映射法:是另一种较为常用的降水量级订正方法,不仅用于天气模式(Bremnes,2007),也多用于气候模式(Maraun,2013)。分位值映射具有与频率匹配法相同的两个步骤,主要不同点在于其采用降水样本的分位值分布曲线。Maraun(2013)指出当观测数据的分辨率远高于预报数据时,分位值映射还起到将低分辨预报转换为高分辨率的功能,但该降尺度作用会使得校正后降水序列的时、空结构歪曲(如区域平均的极端值被过高估计,降水变化趋势受到影响等);为避免这些问题,需要加入随机偏差订正。Cannon等(2015)进一步引入分位差值映射来确保订正后降水时间序列的变化趋势不变,并将单变量的分位值映射拓展到多变量(降水和温度)协同订正。Hamill等(2017)以分位值映射法为基础,发展了多中心集合模式的降水概率预报后处理技术,得到的结果表现出更高的预报技巧和可靠性,同时保留了解析度和空间分布细节。
2.1.2 相似分析方法上述统计特征匹配方法,对与影响天气系统密切相关的降水分布误差订正作用有限。为此,通过搜索与预报相似的历史个例,分析与不同影响系统有关的预报误差,进而构建确定性或概率预报的相似分析方法再次受到关注。与早期如Van den Dool(1989)等查找与当前预报相似的分析场不同,新方法基于对回报样本进行搜索,考虑了模式预报误差的影响。相似分析理论的前提假设是要在气候稳定情况下提供无限数量的回报训练样本。这在应用中无法实现,只能提供数量更多的训练样本使订正结果向实际观测靠拢。为获得大量的训练样本,再预报资料的研究得到推进(Hamill,et al, 2004, 2006b)。这里再预报为采用与业务运行相同的模式,进行长时间的历史回报。Hamill等(2006b)基于25 a的再预报资料,引入了两步相似统计订正技术用于制作概率预报:第1步将当前预报场与再预报资料中同区域、同时期、同时效的预报场进行比较,比较方法可用均方差或相关系数;第2步,确定最相似的数个样本日期,用对应日期的高分辨率观测分析场构成集合场,并用于计算事件频率得到概率预报。Hamill等(2006a)推导了相似分析方法的理论基础,具体为:设Xt|r=[xt|r(1), …, xt|r(s)]为再预报中排名前s个相似的预报所对应的观测量,这里,t表示实况,r表示再预报;对于指定位置的天气事件概率为

|
(2) |
式中,T表示事件发生的阈值,当xt|r(k)>T时,I[xt|r(k), T]=1,否则I[xt|r(k), T]=0。此式表示天气事件概率,即为相似样本对应的观测集中超过阈值的频率;此外,若观测数据具有更高的分辨率,该方法还起到了降尺度的作用(Keller,et al,2017)。在实际应用中,Hamill等(2006a)还给出以下几点条件:(1)只考虑预报点及其周围局地的相似;(2)只需要集合平均或集合平均及离散度相似;(3)只考虑单个预报量或密切相关变量的相似;(4)再预报的回报时段需要考虑气候态和分析场的稳定。之后,Hamill等(2015)对相似分析方法进一步改进,包括引入高分辨率的降水分析场,采用补充相似点,随时效变化选择相似样本数量,以及进行空间平滑等,进一步提升了预报技巧和可靠性。对相似方法的检验表明,能够提供更好的降水空间分布特征(Voisin,et al,2010)以及在长时效预报表现出更好的订正能力(Messner,et al,2011)。
2.2 集合定量降水预报集成方法在业务应用中,常需要将集合成员或多个模式预报集成起来形成单值预报。通常认为集合平均值具有更高的预报技巧,但对偏态分布的降水,集合平均会使得小量级降水范围扩大,大量级降水受到平滑而减弱。为此,需要发展针对降水的集成方法,从众多的成员或模式预报中提取出有效信息,得到比单个成员预报技巧更高的单值预报。目前,业务中常用集合定量降水预报集成方法如表 2所列4种。此外,需要注意的是,与上节订正方法不同,集成方法更侧重于提取有效预报信息,并滤除可预报性低的信息。
| 名称 | 参考文献 | 特点 |
| 概率匹配平均法 | Ebert, 2001 | 将具有较好空间分布的集合平均和更高量级准确度的成员预报结合,不需要历史样本;对小尺度信息有平滑作用;离散度小时,预报能力接近成员预报。 |
| 多模式相似集成法 | 陈力强等, 2005; 林建等, 2013 |
依据成员之间分布和量级相似性,相似度越高(低)权重越大(小),进行集成,不需要历史样本;存在小雨的预报面积偏大,强降水极值偏低的情况。 |
| 最优百分位法 | 代刊等, 2016 | 针对不同等级降水,利用历史样本确定最优百分位值进行集成,有效提高各等级降水预报评分;预报不确定性增大会使得空报率上升。 |
| 伪偏差校正法 | Novak, et al, 2014 | 不确定性越大越平滑以滤除小尺度系统,反之则引入确定性模式更多的细节;通过经验确定订正参数。 |
(1) 概率匹配平均法:由Ebert(2001)提出并用于“穷人”集合预报。在其工作中,提出了权重平均(权重依据前期检验确定)、中位值预报、偏差校正(依据面积偏差比值线性变换集合平均场)和概率匹配平均来代替集合平均,检验结果表明多模式集成的结果的位移误差减少了30%;4种集成方法中,概率匹配平均法结果最优。概率匹配平均法用于融合不同时、空分布的数据源:通常一种数据源具有较好的空间分布,而另一种数据具有更高的量级准确度。在集合预报中,采用该方法结合具有较好空间分布的集合平均场和更高量级准确度的集合成员预报。具体步骤如图 2:选定某一矩形格点区域(区域纬向w个格点,经向h个格点),计算该区域的集合平均场,并将w×h个格点集合平均值从大到小排列得到序列A;每个格点上有m个成员,将区域内的w×h×m个集合成员预报值从大到小排列得到序列C;将序列C顺序划分为w×h个长度为m的序列段,从每个序列段抽取中值出来从大到小排列形成序列B;用序列B的值替换A相同位置的平均值;将序列A恢复到集合平均场的原位置,即得到概率匹配平均场。概率匹配平均作为替代降水集合平均的方法得到广泛应用(Clark,et al,2012)。Fang等(2013)进一步将概率匹配平均法应用于台风暴雨集合预报,主要思路是利用成员数量多的低分辨率集合预报来确定台风路径及调整降水空间分布,成员数量少的高分辨率集合预报来确定降水频率分布,结果明显地降低了模式固有误差,为台湾地区由台风和地形增强引发的强降水提供有用的指导预报。最后需要注意,Surcel等(2014)指出概率匹配平均法的空间结构来自于集合平均场,过滤掉了可预报性较低的小尺度信息而变得更平滑。

|
| 图 2 概率匹配平均法示意 Figure 2 Schematic of probability matching mean method |
(2) 多模式相似集成法和最优百分位法是目前在中国国家气象中心运行的两种集成方法(代刊等, 2016)。多模式相似集成法(陈力强等,2005;林建等,2013)遵循预报员思路,采用相似离度指数反映模式成员两两之间的雨带形状和降水强度的相似,之后利用逐级归并法确定各个成员的总体相似度,进而确定各成员预报场的延伸半径对其进行修正(相似度越低,预报的不确定性越高,需扩大预报区的范围指示最有可能发生暴雨的区域),最后依据每个成员与其余成员的相似度确定权重系数并进行叠加。多模式相似集成法与集合平均法相比提高了对强降水的预报能力,但由于是权重平均,仍存在小雨的预报面积偏大,降水极值偏低的情况。最优百分位法(代刊等,2016)基于预报经验,通过长时间检验发现不同的集合预报百分位值对不同降水等级的降水具有预报优势。例如,对于24 h时效暴雨(≥50 mm)通常90%分位值具有很好的指导意义。为将不同百分位值的有效预报信息集成起来,发展最优百分位值方法。其公式为
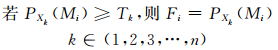
|
(3) |
式中,Fi为格点位置i的最优百分位预报值,Mi为位置i的所有成员预报,PXk()表示百分位Xk的计算函数,Tk为预先设定的降水阈值,Xk则为Tk对应的最优百分位。具体做法为:(1)预先设定从大到小排列n个降水阈值Tk(如100,50,25,10,0.1 mm);(2)选取预报区域内的历史同期预报及相应观测样本(如过去5 a同期前后15 d);(3)针对每个Tk,计算历史样本中不同集合百分位(如0%, 2%, 4%, …, 98%, 100%)的预报评分,选出预报评分最高的百分位作为最优百分位Xk;(4)按照Tk的从大到小排列顺序,依次判别PXk(Mi)≥Tk,若满足条件则停止判别,该位置的预报值Fi为PXk(Mi),若都不满足则Fi为0。与中国国家气象中心运行的其余客观方法相比(包括“配料法”等级、多模式相似集成和频率匹配法),最优百分位法对暴雨的预报技巧表现最好,已经接近或略超过预报员水平(代刊等,2016)。陈博宇等(2016)将该方法与台风路径优选法结合起来,提高了台风暴雨的预报能力。需要注意的是,该方法若降水阈值Tk取得稀疏则会造成频率分布的不连续;且对于3 d以上时效,由于预报不确定性增大会使得空报率上升,需进一步改进。
(3) 集合伪偏差校正(ENSemble pseudo-Bias-Corrected QPF,ENSBC)法:由美国天气预报中心(WPC, Weather Prediction Center)发展并运行(Novak,et al,2014)。集合伪偏差校正由两个步骤构成。第1步,主要考虑预报的不确定性信息,即预报不确定性越大预报场应越平滑以滤除小尺度可预报性低的系统,反之不确定性越小应该引入高分辨率模式更多的细节,用公式表示为
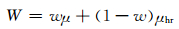
|
(4) |
式中,μhr为高分辨率集合平均(由分辨率相对高的确定性模式组成),μ为全集合平均(由高分辨率确定性模式和集合预报系统共同组成),权重系数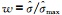
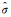
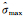
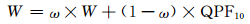
|
(5) |
式中,QPF10为全集合预报10%的分位值,权重系数ω随W在0至6—9 mm范围内变化而线性增大至1(预报时效越长,W上限越高)。对于10 mm以上的预报,则循环一系列降水阈值,将超过阈值的W与高分辨率集合平均值进行对比得到定量降水预报总量比值,然后使用订正因子将总量比值校正为1(订正因子为0.5—2.0)。此外,为避免集合平均值强降水偏小的情况,随降水阈值的增大,高分辨率集合平均值逐步向全集合预报90%的分位值靠拢。通过上述订正方案得到结果,同样表现出优于同期预报员的预报能力(Novak,et al,2014)。
2.3 云分辨率集合模式后处理方法随着计算能力的不断提高,云分辨率模式发展起来用于显式地模拟降水“真实”的精细结构(Lean,et al,2008)。由于在对流尺度上误差增长非常迅速(数小时内)(Hohenegger,et al,2007),其强降水位置并不能被准确地预报出来,需要构建云分辨率的集合模式系统提供预报的不确定性信息(Roebber, et al, 2004)。由于云分辨模式小的系统位置偏差会使格点上的降水产生很大差异,因此,常用的基于“点对点”的计算方式并不适用。为解决此问题,基于“面对面”的后处理方法得到发展,典型的有考虑周围格点的邻域法(Theis,et al,2005)、将雨区作为整体的对象法(Johnson,et al,2012)。
(1) 邻域法(Neighborhood approaches):最初用于确定性预报(Theis,et al,2005),Schwartz等(2010)扩展到集合预报。由于该方法直观、高效,已被作为生成云分辨率模式概率预报的常规方法(Sobash,et al,2016)。Schwartz等(2017)区分了邻域法的两种类型,并指出其表面相似,但实际上定义了不同尺度上的天气事件概率,即一种在格点尺度上,而另一种在更粗的尺度上。对于定义格点尺度上概率的邻域法(NEP,Neighborhood Ensemble Probability),其计算式为

|
(6) |
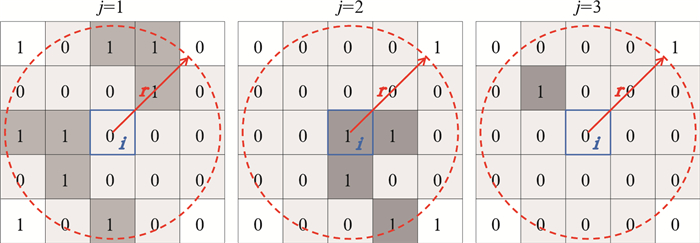
式中,q为事件阈值,i为格点位置,N为集合成员数量,Nb为邻域内格点数量,Si为格点i的Nb个邻域格点集合,BP(q)kj为事件发生的二元概率函数,若格点k上成员j的预报值fkj≥q则BP(q)kj=1,否则BP(q)kj=0。邻域Si的尺度r可以通过格点数或实际距离来定义,形状可以使用矩形(Roberts, et al,2008)或圆形(Schwartz,et al,2009)。图 3为邻域法的计算示意,对于格点i,计算3个成员的邻域范围内格点上事件出现概率分别为33%、19%和5%,成员平均即为i的NEP值19%。可以看到,对Si范围内格点计算平均等同于平滑,因此格点尺度的邻域概率是格点i在平滑尺度r下的集合平均概率。
对于定义在更粗尺度上的邻域法,需要确定搜索尺度为r的邻域范围,并判断搜索范围内事件是否发生,即判断搜索范围内格点最大预报值是否超过阈值,然后对集合成员计算平均,得到邻域最大值集合概率(NMEP,Neighborhood Maximum Ensemble Probability)
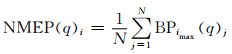
|
(7) |
式中,若集合成员j在格点i搜索范围内的最大值≥q,则BPimax(q)j为1,否则为0。可见邻域最大值集合概率与式(6)的邻域概率不同,并不包括空间平滑作用。同样以图 3为例,3个集合成员的邻域范围内都出现了天气事件(即最大值概率都为100%),因此邻域最大值集合概率值为100%。邻域最大值集合概率可以采用两种格点计算方式:一种是将原始网格划分成格点尺度为r的粗网格,然后在每个粗网格内计算邻域最大值集合概率(Sobash,et al,2016);另一种是直接计算原始网格内每个格点的邻域最大值集合概率。无论哪种格点计算方式都起到了“升尺度”的作用,即邻域最大值集合概率表示的是格点i的r范围内事件发生的概率。此外,值得注意的是,由于邻域概率和邻域最大值集合概率尺度不同,检验方式也不一样:邻域概率定义在格点尺度上,可以直接用相同网格的观测资料进行检验;NMEP则需要对观测资料进行同样的升尺度计算,才能用于检验。
|
| 图 3 邻域法示意 (中心蓝色方框为计算概率的格点i,r为搜索尺度,红色虚线内为邻域范围,阴影为邻域格点;值1表示事件发生,0则表示未发生;j表示集合成员序号) Figure 3 Schematic illustration of neighborhood approach (the grid point i of interest is denoted by the blue square, r is the searching length scale, the circular neighborhoods (shadow grids) about selected points are shown by red dashed lines; the value 1 denotes that the event has occurred, and 0 is for event no occurred; the ensemble member number is j) |
(2) 基于对象的概率预报法:将降水系统当作对象整体,然后计算每个对象的出现概率。Johnson等(2012)采用基于对象诊断的评估方法(MODE,Method for Object-based Diagnostic Evaluation)(Davis,et al,2009)进行对象识别和配对。该方法首先定义高于某一阈值的连通区域为识别对象;然后计算每一个对象的面积、中心位置、形状比例等,并综合成“Total interest”指数,对比不同成员之间各对象指数的差别,小于某一预设值的对象可认为同一组;最后计算有多少个集合成员预报了该组的对象,得到对象的概率。基于对象的概率预报法接近预报员的主观判断,物理意义清楚,但需要主观设置方法参数。
上述邻域法和对象法都用于计算云分辨率模式的降水事件概率,可进一步引入订正方法进行偏差校正。如Schaffer等(2011)在邻域法的基础上,采用历史样本构建QPF-POP(Probability of Precipitation),并按照预报的成员最大降水量(或平均降水),以及超过阈值的成员数量查询该表,得到历史正确预报率作为预报值。Johnson等(2012)对比了逻辑回归法、QPF-POP法和分位值映射法对基于邻域法和对象法得到的概率预报进行订正,表明各种方法都能改善预报技巧,并且订正能力相近。
3 参数化后处理方法参数化后处理方法将离散的成员预报转变为连续的概率分布。与非参数化后处理相比,该方法能利用概率分布模型进行外插,因此减轻了对训练数据量的要求。方法的预报质量依赖于参数模型假设的准确性。目前有两类代表性的参数化后处理方法,包括集合模式输出统计(EMOS,Ensemble Output Statistics)法(Gneiting,et al,2005)、贝叶斯模型平均(BMA,Bayesian Model Averaging)法(Raftery,et al,2005)。集合模式输出统计主要预报单个概率分布模型,其一般形式为
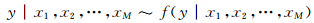
|
(8) |
公式左侧表示给定集合成员预报x1,x2,…,xM条件下预报量y的条件分布;右侧f表示概率分布模型,其参数由训练样本确定。贝叶斯模型平均法则集成多个分布模型

|
(9) |
式中,g(y|xm)表示依赖于集合成员xm的核密度分布,权重系数w1, w2, …, wM为非负数且总和为1,反映训练期间各个成员对预报技巧的贡献。一般情况下,集合模式输出统计法较为简洁且易于实现,而贝叶斯模型平均法复杂但更灵活。例如,若f和g均为高斯分布,集合模式输出统计预报结果为单峰对称分布,而贝叶斯模型平均法通过多高斯分布的叠加可以实现多峰和非对称分布。除上述一般形式外,其他一些用于预报概率分布的方法也可归类到上述两种框架,如延伸逻辑回归(Wilks,2009)、分位数回归(Bremnes,2004)等都预报单个统计模型,属于集合模式输出统计法;而集合敷料法(Roulston, et al,2003)、集合核密度模式输出统计法(Glahn,et al, 2009)、集合回归法(Unger,et al, 2009)等都集成多个模型,类似于贝叶斯模型平均法框架。
3.1 集合模式输出统计法(1) 非均匀回归(NHR, Non-homogeneous Regression)法是对传统线性回归的拓展。Gneiting等(2005)最初发展非均匀回归法应用于高斯分布的变量(如温度),使用两个线性回归模型来确定高斯分布的均值和方差两个参数。非均匀回归法的非均匀性表现在分布的方差不固定,依赖于预报量。用公式表示为
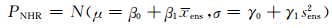
|
(10) |
式中,N(μ, σ)表示均值为μ和方差为σ的高斯分布函数,μ和σ由系数(β0, β1, γ0, γ1)确定,xens表示集合平均值,sens2表示集合离散度。若γ1=0,则退化为不考虑离散度和预报误差的关系,预报分布有固定的方差。分布模型系数通过最小化连续排名概率技巧评分(CRPSS,Continuous Ranked Probability Skill Score)估计。对于降水事件,其非负值以及偏态的分布特征,使得高斯分布的假设不适用。通常采用混合分布模型(Bentzien,et al,2012),即降水的概率分布由两部分组成:第1部分表示有无降水的概率π0=Pr(y>0|x1, …, xM),可以通过逻辑回归(见式(13))来估计;第2部分用合适的概率分布模型F*来表示降水量的概率。其公式表示为
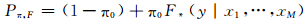
|
(11) |
式中,F*可采用不同的分布模型,如高斯分布(Scheuerer, et al,2015)、广义极值分布(Scheuerer,2014)、双正态分布(Sharma,et al,2017)、对数正态分布和反高斯分布(Bentzien,et al,2012)等。此外,为了更准确拟合极端降水分布,对于高于某一极端阈值uτ的降水概率,还可采用更恰当的分布模型,如Bentzien等(2012)使用广义帕雷托分布(GPD,Generalized Pareto Distribution)
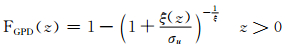
|
(12) |
式中,σu为尺度参数,ξ为形状参数。
(2) 逻辑回归法是一种应用广泛的非线性回归模型,尤其适合二分事件(如有无降水或超过某一阈值的降水)的概率预报。逻辑回归法是较早用于集合模式后处理的统计方法(Hamill,et al,2004),该方法基于样本数据拟合“S形状”的逻辑分布函数
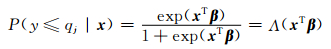
|
(13) |
式中,x为集合预报向量(1,x1,x2,…)T,P(y≤qj|x)为给定x条件下预报量≤阈值qj的概率,β为系数向量(1,β1,β2,…)T,Λ(·)=exp(·)/[1+exp(·)]表示逻辑分布的累积分布函数。其中,β采用最大似然函数进行估计。逻辑回归法具有良好的订正性能(Wilks, et al,2007),不足之处包括只能得到一系列阈值qj的回归模型,不能得到全概率预报模型;不同qj得到的回归曲线可能相交,如对于降水阈值qa < qb可能会出现P(y≤qa|x)>P(y≤qb|x)不合理的结果。为避免上述缺点,Wilks(2009)提出将阈值作为预报因子加入到逻辑回归法,得到扩展逻辑回归法(Extended logistic regression):
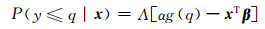
|
(14) |
式中,α为附加系数,g(·)为单调变换函数。此式定义了Log-odds空间内具有相同斜率和不同截距的平行曲线,避免了回归曲线相交的问题,且能对任意阈值q计算概率。在Wilks(2009)提出的扩展逻辑回归法中,阈值q相关的系数为常数,因此,只有截距随q线性变化,且曲线陡度固定。为避免该问题,Ben Bouallègue(2013)在αg(q)的定义中引入交互项。此外,Messner等(2014b)为了在模型中有效利用不确定性信息,引入了额外的预报因子z=(1, z1, z2, …)T(如集合离散度)来直接控制预报模型的发散度,即
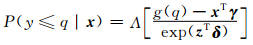
|
(15) |
式中,γ=(γ0, γ1, γ2, …)T和δ=(δ0, δ1, δ2, …)T为系数矢量,采用最大似然法估计。除逻辑回归法和扩展逻辑回归法外,类似方法还有序逻辑回归、审查逻辑回归等。Messner等(2014a)比较研究表明,对于等级降水概率有序逻辑回归法与扩展逻辑回归法预报能力相似;而对于全概率预报,审查逻辑回归有优势。
(3) 分位数回归法:由Bremnes(2004)引入到集合模式的降水预报后处理中,用于直接预报降水的分位值,避免了对降水分布的假设。该方法分为两步,第1步采用概率回归判断有无降水的概率,第2步采用分位数回归来预报在有降水概率的条件下选定分位值的降水

|
(16) |
式中,Q(p)(·)为分位为p的值,系数(a0,a1,…,aI)通过最小化最低绝对偏差函数估计。由于分位数回归法可能会出现回归线交叉的现象(即估计出的低分位值大于高分位值),Bremnes(2004)建议采用局部分位数回归来缓解,但也指出该限定可能并不符合实际情况;同时,分位数回归法不能给出全概率的分布。为此,Corinna(2012)为分位数回归模型引入一个半参数贝叶斯框架来解决这些问题。
3.2 贝叶斯模型平均法框架(1) 集合敷料法属于核密度估计问题,类似于贝叶斯模型平均法框架,但更早应用于集合预报后处理。集合敷料法首先为每个成员定义核密度分布(即“dressing”),然后平均所有成员分布得到整体的概率密度分布。集合敷料法的关键是找到合适、能够反映不确定信息特征的dressing核。Roulston等(2003)发展了最佳成员敷料(Best member dressing)法,即采用“最佳成员”来估计误差的集合模式误差分布,这里“最佳成员”定义为所有成员中与实际观测偏差最小的成员。具体设yt为对于时间t的实际观测,xt={xt,k,k=1,2,…,K}为相应的集合成员预报(成员数量为K),其中的最佳成员xt*定义为与yt之间的模最小,即xt*=argxt, kmin‖yt-xt, k‖;对于给定训练样本集,可以估计最佳成员误差ε*=yt-xt*的概率分布pε*;最后在预报时,将误差概率分布围绕每个成员定义,然后叠加得到概率预报上
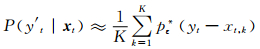
|
(17) |
在实际计算中采用简单方式来模拟P(y′t|xt),即针对每个集合成员,从训练样本误差集中抽样N个误差加到每个成员上,最终得到由(N×K)个成员构成的新集合用于概率预报。可见,上述最佳成员敷料法可以方便地增加集合成员的数量,敷料的过程反映误差分布特征,并且保留了不同流型的不确定信息。最佳成员敷料法不能保证预报的概率分布与观测频率一致(即可靠性),为此Wang等(2005)发展了二阶矩约束的敷料方法。该方法不采取抽样,而使用高斯分布作为核函数来“Dressing”每个成员,并且推导核函数方差的分析表达式,来约束预报概率分布的方差等于训练集中成员预报与观测之间平方距离的期望值,从而改进预报的可靠性。Wang等(2005)的方法只能订正集合预报欠离散的情况。Fortin等(2006)对此做出了进一步改进,即使用不同集合排列的误差分布,对不同的成员采用不同的辅料和权重,可以订正欠离散和过离散的情况,且更加可靠。Fortin等(2006)方法已与贝叶斯模型平均非常接近。
(2) 集合核密度模式输出统计法:将传统模式输出统计预报法与核密度估计结合起来,订正集合预报的系统性和离散度误差。该方法由Glahn等(2009)提出,具体步骤为:首先筛选美国和加拿大业务集合系统的集合平均量作为预报因子,分别建立模式输出统计预报模型;将该模型应用于每个集合成员,得到订正后的预报量;基于新的成员预报,采用核密度拟合(Wilks,2011)法构建概率密度函数(PDF),如针对温度变量使用高斯核函数,其标准差等于模式输出统计方程的标准误差估计;最后,需要对概率密度函数的离散度进行校正,Glahn等(2009)采用一个经验的离散度调整因子来修正,即调整后的离散度较原概率密度函数的离散度小(1-x),其中
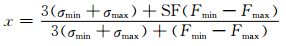
|
(18) |
式中,Fmin和Fmax为最小和最大的模式输出统计预报成员,σmin和σmax相应的模型标准误差,SF为一个经验调节系数。Veenhuis(2013)引入离散度-预报技巧关系来替代最后一步经验调整公式,即采用一个单项线性回归方程来预测给定集合离散条件下集合平均的预报精度,检验表明预报结果可靠性更高,并显示更好的离散度-误差关系。
(3) 贝叶斯模型平均法用于集成来自不同统计模型的预测结果,以便考虑模型选择的不确定性(Hoeting,et al,1999)。Raftery等(2005)将贝叶斯模型平均法引入到集合预报后处理,成为针对集合降水预报应用较广的方法(梁莉等,2013;Liu,et al,2014)。与集合敷料法查找“最佳成员”的思路不同,贝叶斯模型平均法每个成员的权重由该成员成为最好预报的先验概率决定。通常分为两步,第1步使用如回归方法以消除系统性偏差;第2步对每个权重成员使用核密度分布,其一般形式见式(9),核密度分布g(y|xm)针对不同的预报量采用不同的形式,如温度、气压和风速分量等用正态分布(Raftery,et al,2005),风速用高斯分布(Sloughter,et al,2010),风向用冯-米塞斯分布(Bao,et al,2010),能见度用β分布(Chmielecki,et al,2011)。针对降水,Sloughter等(2007)采用伯努利-高斯混合分布,不连续部分通过逻辑回归提供降水为0处的点值,表示为
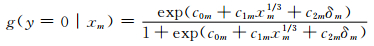
|
(19) |
式中,c0m、c1m、c2m为回归模型系数。在c1m≤0,c1m≥0的约束条件下,若xm=0则δm为1,否则为0;连续部分先对降水量进行立方根变换y1/3,然后采用高斯分布,其平均μm=a0m+a1mxm1/3和方差σm2=b0m+b1mxm。式(9)中权重表示每个成员在训练期间的预报能力,因此贝叶斯模型平均法适合集成多模式系统,若存在可互换成员(如同一集合模式成员)和缺失成员,可采用Fraley等(2010)给出的处理方法。权重和分布系数采用期望最大化算法估计(Dempster,et al,1977),也可采用马尔可夫链-蒙特卡罗方法估计(Vrugt,et al,2008)。由于贝叶斯模型平均方法需要估计比集合模式输出统计法更多的参数,其训练样本量要足够大以避免过度拟合。为此,可使用再预报资料(Hamill,2007),或者加入补充站点(Hamill,et al,2017)。在Raftery等(2005)工作的基础上,贝叶斯模型平均法得到持续完善,如Bishop等(2008)指出,贝叶斯模型平均法对集合欠离散订正过度,使得预报极端事件能力降低,并提出加入范式转移处理来解决该问题;Schmeits等(2010)指出贝叶斯模型平均法中若对每个成员进行偏差订正会使得集合发散度减小,从而订正效果降低,为此提出使用附加偏差订正来改进;Kleiber等(2011)将贝叶斯模型平均法和地学统计法结合起来发展出地学统计模型平均法,能在预报的同时进行空间插值;Marty等(2015)将贝叶斯模型平均法和输出贝叶斯处理器结合起来形成集合成员贝叶斯处理器,能进一步改进预报技巧。
4 考虑变量结构的后处理方法前述统计后处理方法通常应用于某一预报时效、某一位置的单个变量,然而很多应用情景需要考虑预报量的时间、空间或时、空变化特征,以及不同预报量之间的关系,如冬季道路维护气象保障需要同时考虑降水和温度(Berrocal,et al,2010);水文预报的输入量需要考虑时、空演变的连续性以及变量之间的统计依赖关系(Li,et al,2017)。以时间演变为例,为了保证订正后的预报量有真实物理意义,需要解决两个方面的问题:(1)经过统计后处理的预报变量需避免无意义的、突然的变化;(2)需保留具有真实物理意义的时效变化特征。为解决前一个问题,可以给参数模型系数加上约束条件,使其随时效平滑变化;而解决后一个问题,需要用到连接方法。连接方法依据连接途径可分为参数化和经验两种类型。
4.1 参数化连接方法参数化连接方法将单变量的集合模式输出统计、贝叶斯模型平均等方法延伸到多变量,并考虑时空或变量间结构。设yl=1,2,…,L为不同变量、位置和时效的预报量,相应的Fl=1,2,…,L为经过后处理的累积分布函数预报,F为具有真实物理意义的多元联合累积分布函数。根据Sklar(1959)的定理,多元联合累积分布函数具有特征
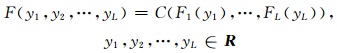
|
(20) |
式中,C:[0,1]L→[0,1]为连接函数,是一个具有标准均匀边际分布的多元累积分布函数。式(20)在给定合适的连接函数情况下,可作为考虑变量结构的标准后处理过程。当连接函数为参数化函数时,计算量很大,因此适合较小维度L,或只考虑时间或空间的结构的情况。Schölzel等(2008)对参数化连接函数簇进行了总结,包括椭圆型/高斯连接、t-连接等。
在实际应用中,参数化连接方法被显式或隐式地使用。以保留预报量空间结构为例,可将地学统计输出扰动与前述单变量后处理方法结合起来。如Gel等(2004)将基于地学统计输出扰动的高斯误差场加到确定性预报场上,以引入不同站点的空间依赖关系;Berrocal等(2007)将地学统计输出扰动和贝叶斯模型平均结合起来发展空间贝叶斯模型平均方法;之后Scheuerer等(2014)和Feldmann等(2015)将地学统计输出扰动法和集合模式输出统计法结合起来形成空间集合模式输出统计模型。对于保留预报量的时间结构,可参考Engeland等(2014)采用基于高斯连接的回归模型,保持不同预报时效的相关关系。对于保留预报变量之间的依赖关系,Möller等(2013)和Baran等(2017)利用高斯联合分布或高斯连接函数将经过集合模式输出统计或贝叶斯模型平均处理后的不同变量结合起来。
4.2 经验连接方法经验连接方法典型的有Schaake shuffle(SS)(Clark,et al,2004)法和集合连接耦合(Ensemble copula coupling,ECC)法(Schefzik,2011)。SS和集合连接耦合法都通过对集合成员进行重新排序,从而保留空间、时间或变量之间的依赖结构。两者的主要不同之处在于对排序模板的选择:SS法假设变量结构不随时间变化,可以从历史观测数据中得到;集合连接耦合法则认为集合模式的原始预报已经表现出真实的物理结构,因此以集合模式直接输出为模板。下面以集合连接耦合法为主介绍经验连接法思路。集合连接耦合通过多级后处理过程(Schefzik,et al,2013),生成与原始集合同样数量的成员预报,并保持原始集合成员的秩序。步骤为:(1)使用前述的单变量统计后处理技术,分别订正每个位置、时效和变量的集合预报量Yl,得到其预报概率分布Fl;(2)从Fl中抽取与原始成员相同数量的M个预报值,这可通过计算Fl的M个等距分位值实现,即:

|
(21) |
式中,m=1,2,…,M和l=1,2,…,L,分别对每个Yl进行计算。(3)将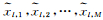
统计后处理技术已经成为集合预报系统的重要组成部分。近年来各种集合预报统计后处理方法得到快速发展,文中针对定量降水预报分3个类别总结了相关进展。
(1) 非参数化后处理,包括集合定量降水预报偏差订正、多成员或模式信息集成以及基于空间分析的云分辨率模式后处理。
(2) 基于统计模型的参数化后处理技术,包括集合模式输出统计和贝叶斯模型平均两种方法框架。
(3) 考虑预报量的时间、空间和多变量间依赖关系或结构的处理方法,包括参数化和经验连接法。表 3列出本文总结的技术类别、参考工作和典型发展应用。
下面讨论使用统计后处理技术需要注意的问题。
(1) 后处理技术很难订正数值模式的固有缺陷。例如,采用静力平衡和参数化物理过程的全球模式系统,对于中小尺度对流系统不能很好表现,因此期望通过后处理技术提升对流性降水的预报能力很困难。要缓解该问题,需要进一步改进和完善数值模式系统,并发展云分辨率集合预报系统(Roebber,et al,2004)。此外,需要在处理过程中集成不同来源、不同尺度的模式预报信息,从而减小单一模式的固有误差。如前述的Fang等(2013)将高、低分辨率模式降水结合进行台风降水预报,以及近年来研究比较多的TIGGE(THORPEX Interactive Grand Global Ensemble)集合预报(Park,et al, 2008)。
(2) 若要通过后处理得到精细化的网格预报,需要高质量、高分辨率的降水分析资料。如Hou等(2014)将具有良好质量控制的气候预报中心分析资料,和具有更高的时空分辨率的阶段4估测资料,通过线性回归模型协调,得到高质量及高分辨率的CCPA(Climatology Calibrated Precipitation Analysis)分析资料。前述的Zhu等(2015)、Hamill等(2017)都在订正过程中采用CCPA降水分析资料,得到高分辨率的格点预报。
(3) 需要充足的训练样本来提供误差订正经验或统计模型参数评估。如果集合系统的误差恒定,那么少量的训练集就能满足订正需求。但实际情况是,不同天气特征或环流形势下,模式会表现出不同的系统误差,尤其是对于降水预报。研究表明扩大训练样本有助于提高订正能力,如Wilks等(2007)研究显示训练期长度对预报技巧的影响比选择订正方法更显著;Scheuerer等(2015)也指出即使对于参数化的后处理方法,足够大的训练数据也是至关重要的。为保证训练样本的误差与预报误差的一致,一般采用近年同期或近期滚动的历史预报,或通过分区域(Zhu, et al,2015)或增加补充站点来扩大样本量(Hamill,et al,2017)。此外,Hamill等(2004, 2006b)发展的再预报技术值得关注。该技术采用1998年版NCEP全球模式GFS进行1979—2001年的回报,极大地扩充了训练样本量。将再预报资料用于温度和降水预报的逻辑回归订正,能显著地提高预报技巧和可靠性。Hamill等(2008)比较了基于再预报资料和滑动30 d训练期的降水预报订正结果,显示前者在所有预报时效表现更有优势,尤其对中等量级以上的降水预报,将预报时效提前1.5 d。至今,再预报资料被广泛应用于各种后处理中,如再预报资料使得相似分析方法成为可能(Hamill, et al, 2006a);将再预报资料用于改善2周的延伸期预报(Ou,et al,2016);Guan等(2015)基于2012年版GFS的再预报资料,后处理结果显示对于转换季节的预报效果提升幅度更明显;ECMWF(European Centre for Medium-Range Weather Forecasts)开展实时的再预报业务用于集合预报订正(Hagedorn,2008);Fundel等(2010)使用30 a再预报资料订正,表明有助于捕捉极端降水事件的时、空变化特征。Hagedorn等(2012)和Hamill(2012)还对基于TIGGE多模式和再预报资料的后处理进行了对比,结果表明两种方式提升原始预报技巧的水平相当,并指出将两者结合对降水预报来说是最佳途径。
(4) 不同后处理方法有不同优势,需要依据不同订正目的、应用场景来选择。如相似分析方法适用于大样本的条件,逻辑回归等模型有利于推演训练集中没有的事件预报,非均匀回归法在离散度-预报技巧关系强时更有效。有研究采用相同的区域、数据和训练期来对比不同统计后处理技术(Wilks,2006;Sloughter,et al,2007;Schmeits,et al,2010;Mendoza,et al,2015;Messner,et al,2014b),结果表明后处理效果依赖于气候条件、训练策略(Zhu,et al,2015)、检验方式(Mendoza,et al,2015)、预报时长(Schmeits,et al,2010)和偏差类型(Erickson,et al,2012)等因素。
(5) 对于集合定量降水预报统计后处理技术的未来发展,需要关注:进一步发展强(极端)降水的后处理技术,由于发生频率低,且一般如Γ分布模型不能有效反映大量级降水特征,使其订正能力不高(Williams,et al,2014; 刘琳等,2018);对于水文、交通、能源等应用场景,需要考虑预报量的时间、空间和变量间的依赖关系,因此考虑变量结构的后处理方法将得到快速发展(Schefzik,2011);在多模式和再预报条件下,训练和预报数据量快速增长,将神经网络方法应用于海量数据的后处理将得到深入研究(Yuan,et al,2007;Vladimir,et al,2012)。
| 毕宝贵, 代刊, 王毅, 等. 2016. 定量降水预报技术进展. 应用气象学报, 27(5): 534–549. Bi B G, Dai K, Wang Y, et al. 2016. Advances in techniques of quantitative precipitation forecast. J Appl Meteor Sci, 27(5): 534–549. DOI:10.11898/1001-7313.20160503 (in Chinese) |
| 陈博宇, 郭云谦, 代刊, 等. 2016. 面向台风暴雨的集合预报成员优选订正技术研究及应用试验. 气象, 42(12): 1465–1475. Chen B Y, Guo Y Q, Dai K, et al. 2016. Research for the ensemble member optimization correction technique on typhoon rainstorm forecast and its application experiment. Meteor Mon, 42(12): 1465–1475. DOI:10.7519/j.issn.1000-0526.2016.12.004 (in Chinese) |
| 陈力强, 周小珊, 杨森. 2005. 短期集合预报中定量降水预报集合方法初探. 南京气象学院学报, 28(4): 543–548. Chen L Q, Zhou X S, Yang S. 2005. A quantitative precipitation forecasts method for short-range ensemble forecasting. J Nanjing Inst Meteor, 28(4): 543–548. (in Chinese) |
| 代刊, 曹勇, 钱奇峰, 等. 2016. 中短期数字化天气预报技术现状及趋势. 气象, 42(12): 1445–1455. Dai K, Cao Y, Qian Q F, et al. 2016. Situation and tendency of operational technologies in short and medium range weather forecast. Meteor Mon, 42(12): 1445–1455. DOI:10.7519/j.issn.1000-0526.2016.12.002 (in Chinese) |
| 杜钧, 李俊. 2014. 集合预报方法在暴雨研究和预报中的应用. 气象科技进展, 4(5): 6–20. Du J, Li J. 2014. Application of ensemble methodology to heavy-rain research and prediction. Adv Meteor Sci Technol, 4(5): 6–20. (in Chinese) |
| 李俊, 杜钧, 陈超君. 2014. 降水偏差订正的频率(或面积)匹配方法介绍和分析. 气象, 40(5): 580–588. Li J, Du J, Chen C J. 2014. Introduction and analysis to frequency or area matching method applied to precipitation forecast bias correction. Meteor Mon, 40(5): 580–588. DOI:10.7519/j.issn.1000-0526.2014.05.008 (in Chinese) |
| 李俊, 杜钧, 刘羽. 2015. 北京"7.21"特大暴雨不同集合预报方案的对比试验. 气象学报, 73(1): 50–71. Li J, Du J, Liu Y. 2015. A comparison of initial condition-, multi-physics-and stochastic physics-based ensembles in predicting Beijing "7.21" excessive storm rain event. Acta Meteor Sinica, 73(1): 50–71. DOI:10.11676/qxxb2015.008 (in Chinese) |
| 梁莉, 赵琳娜, 齐丹, 等. 2013. 基于贝叶斯原理降水订正的水文概率预报试验. 应用气象学报, 24(4): 416–424. Liang L, Zhao L N, Qi D, et al. 2013. The experiment of hydrologic probabilistic forecast based on the precipitation forecast calibrated by Bayesian model averaging. J Appl Meteor Sci, 24(4): 416–424. DOI:10.11898/1001-7313.20130404 (in Chinese) |
| 林建, 宗志平, 蒋星. 2013. 2010-2011年多模式集成定量降水预报产品检验报告. 天气预报, 5(1): 67–74. Lin J, Zong Z P, Jiang X. 2013. The verification report of multi-model integrated QPF products from 2010-2011. Wea Forecast Rev, 5(1): 67–74. (in Chinese) |
| 刘琳, 陈静, 汪娇阳. 2018. 基于T639集合预报的持续性强降水中期客观预报技术研究. 气象学报, 76(2): 228–240. Liu L, Chen J, Wang J Y. 2018. A study on medium-range objective weather forecast technology for persistent heavy rainfall events based on T639 ensemble forecast. Acta Meteor Sinica, 76(2): 228–240. DOI:10.11676/qxxb2018.002 (in Chinese) |
| 田华, 邓国, 姚明明等. 2005. T213全球集合预报的研究进展//中国气象学会2005年年会论文集. 苏州: 中国气象学会, 5580-5585. Tian H, Deng G, Yao M M, et al. 2005. The research progress of T213 global ensemble forecast system//Chinese Meteorological Society 2005 Annual Conference Proceedings. Suzhou: China Meteorological Society, 5580-5585 (in Chinese) |
| 熊敏诠. 2017. 基于集合预报系统的日最高和最低气温预报. 气象学报, 75(2): 211–222. DOI:10.11676/qxxb2017.023 |
| Xiong B Q. 2016. Calibrating daily 2 m maximum and minimum air temperature forecasts in the ensemble prediction system. Acta Meteor Sinica, 75(2): 211–222. |
| 周迪, 陈静, 陈朝平, 等. 2015. 暴雨集合预报-观测概率匹配订正法在四川盆地的应用研究. 暴雨灾害, 34(2): 97–104. Zhou D, Chen J, Chen C P, et al. 2015. Application research on heavy rainfall calibration based on ensemble forecast vs observed precipitation probability matching method in the Sichuan basin. Torrent Rain Disast, 34(2): 97–104. (in Chinese) |
| Bao L, Gneiting T, Grimit E P, et al. 2010. Bias correction and Bayesian model averaging for ensemble forecasts of surface wind direction. Mon Wea Rev, 138(5): 1811–1821. DOI:10.1175/2009MWR3138.1 |
| Baran S, Möller A. 2017. Bivariate ensemble model output statistics approach for joint forecasting of wind speed and temperature. Meteor Atmos Phys, 129(1): 99–112. DOI:10.1007/s00703-016-0467-8 |
| Ben Bouallègue Z. 2013. Calibrated short-range ensemble precipitation forecasts using extended logistic regression with interaction terms. Wea Forecasting, 28(2): 515–524. DOI:10.1175/WAF-D-12-00062.1 |
| Bentzien S, Friederichs P. 2012. Generating and calibrating probabilistic quantitative precipitation forecasts from the high-resolution NWP model COSMO-DE. Wea Forecasting, 27(4): 988–1002. DOI:10.1175/WAF-D-11-00101.1 |
| Berrocal V J, Raftery A E, Gneiting T. 2007. Combining spatial statistical and ensemble information in probabilistic weather forecasts. Mon Wea Rev, 135(4): 1386–1402. DOI:10.1175/MWR3341.1 |
| Berrocal V J, Raftery A E, Gneiting T, et al. 2010. Probabilistic weather forecasting for winter road maintenance. J Amer Stat Assoc, 105(490): 522–537. DOI:10.1198/jasa.2009.ap07184 |
| Bishop C H, Shanley K T. 2008. Bayesian model averaging's problematic treatment of extreme weather and a paradigm shift that fixes it. Mon Wea Rev, 136(12): 4641–4652. DOI:10.1175/2008MWR2565.1 |
| Bremnes J B. 2004. Probabilistic forecasts of precipitation in terms of quantiles using NWP model output. Mon Wea Rev, 132(1): 338–347. DOI:10.1175/1520-0493(2004)132<0338:PFOPIT>2.0.CO;2 |
| Bremnes J B. 2007. Improved calibration of precipitation forecasts using ensemble techniques. Part 2: Statistical calibration methods. Oslo, Norway: Norwegian Meteorological Institute, 38pp |
| Buizza R. 2008. The value of probabilistic prediction. Atmos Sci Lett, 9(2): 36–42. DOI:10.1002/(ISSN)1530-261X |
| Cannon A J, Sobie S R, Murdock T Q. 2015. Bias correction of GCM precipitation by quantile mapping:How well do methods preserve changes in quantiles and extremes?. J Climate, 28(17): 6938–6959. DOI:10.1175/JCLI-D-14-00754.1 |
| Chmielecki R M, Raftery A E. 2011. Probabilistic visibility forecasting using Bayesian model averaging. Mon Wea Rev, 139(5): 1626–1636. DOI:10.1175/2010MWR3516.1 |
| Clark A J, Weiss S J, Kain J S, et al. 2012. An overview of the 2010 hazardous weather testbed experimental forecast program spring experiment. Bull Amer Meteor Soc, 93(1): 55–74. DOI:10.1175/BAMS-D-11-00040.1 |
| Clark M, Gangopadhyay S, Hay L, et al. 2004. The schaake shuffle:A method for reconstructing space-time variability in forecasted precipitation and temperature fields. J Hydrometeorol, 5(1): 243–262. DOI:10.1175/1525-7541(2004)005<0243:TSSAMF>2.0.CO;2 |
| Corinna M F. 2012. Probabilistic forecasts of precipitation using quantiles[D]. Heidelberg: Ruprecht-Karls-Universität, 29-34 |
| Cui B, Toth Z, Zhu Y J, et al. 2012. Bias correction for global ensemble forecast. Wea Forecasting, 27(2): 396–410. DOI:10.1175/WAF-D-11-00011.1 |
| Davis C A, Brown B G, Bullock R, et al. 2009. The method for object-based diagnostic evaluation (MODE) applied to numerical forecasts from the 2005 NSSL/SPC spring program. Wea Forecasting, 24(5): 1252–1267. DOI:10.1175/2009WAF2222241.1 |
| Dempster A P, Laird N M, Rubin D B. 1977. Maximum likelihood from incomplete data via the EM algorithm. J Roy Stat Soc Series B, 39(1): 1–38. |
| Ebert E E. 2001. Ability of a poor man's ensemble to predict the probability and distribution of precipitation. Mon Wea Rev, 129(10): 2461–2480. DOI:10.1175/1520-0493(2001)129<2461:AOAPMS>2.0.CO;2 |
| Eckel F A, Walters M K. 1998. Calibrated probabilistic quantitative precipitation forecasts based on the MRF ensemble. Wea Forecasting, 13(4): 1132–1147. DOI:10.1175/1520-0434(1998)013<1132:CPQPFB>2.0.CO;2 |
| Engeland K, Steinsland I. 2014. Probabilistic postprocessing models for flow forecasts for a system of catchments and several lead times. Water Resour Res, 50(1): 182–197. DOI:10.1002/wrcr.v50.1 |
| Erickson M J, Colle B A, Charney J J. 2012. Impact of bias-correction type and conditional training on Bayesian model averaging over the northeast United States. Wea Forecasting, 27(6): 1449–1469. DOI:10.1175/WAF-D-11-00149.1 |
| Fang X Q, Kuo Y H. 2013. Improving ensemble-based quantitative precipitation forecasts for topography-enhanced typhoon heavy rainfall over Taiwan with a modified probability-matching technique. Mon Wea Rev, 141(11): 3908–3932. DOI:10.1175/MWR-D-13-00012.1 |
| Feldmann K, Scheuerer M, Thorarinsdottir T L. 2015. Spatial postprocessing of ensemble forecasts for temperature using nonhomogeneous Gaussian regression. Mon Wea Rev, 143(3): 955–971. DOI:10.1175/MWR-D-14-00210.1 |
| Flowerdew J. 2012. Calibration and combination of medium-range ensemble precipitation forecasts. UK Met Office, 24pp |
| Flowerdew J. 2014. Calibrating ensemble reliability whilst preserving spatial structure. Tellus A:Dyn Meteor Oceanogr, 66(1): 22662. DOI:10.3402/tellusa.v66.22662 |
| Fortin V, Favre A C, Saïd M. 2006. Probabilistic forecasting from ensemble prediction systems:Improving upon the best-member method by using a different weight and dressing kernel for each member. Quart J Roy Meteor Soc, 132(617): 1349–1369. DOI:10.1256/qj.05.167 |
| Fraley C, Raftery A E, Gneiting T. 2010. Calibrating multimodel forecast ensembles with exchangeable and missing members using Bayesian model averaging. Mon Wea Rev, 138(1): 190–202. DOI:10.1175/2009MWR3046.1 |
| Fundel F, Walser A, Liniger M A, et al. 2010. Calibrated precipitation forecasts for a limited-area ensemble forecast system using reforecasts. Mon Wea Rev, 138(1): 176–189. DOI:10.1175/2009MWR2977.1 |
| Gebhardt C, Theis S, Krahe P, et al. 2008. Experimental ensemble forecasts of precipitation based on a convection-resolving model. Atmos Sci Lett, 9(2): 67–72. DOI:10.1002/(ISSN)1530-261X |
| Gel Y, Raftery A E, Gneiting T. 2004. Calibrated probabilistic mesoscale weather field forecasting:The geostatistical output perturbation (GOP) method. J Amer Stat Assoc, 99(467): 575–583. DOI:10.1198/016214504000000872 |
| Glahn B, Peroutka M, Wiedenfeld J, et al. 2009. MOS uncertainty estimates in an ensemble framework. Mon Wea Rev, 137(1): 246–268. DOI:10.1175/2008MWR2569.1 |
| Glahn H R, Lowry D A. 1972. The use of model output statistics (MOS) in objective weather forecasting. J Appl Meteor, 11(8): 1203–1211. DOI:10.1175/1520-0450(1972)011<1203:TUOMOS>2.0.CO;2 |
| Gneiting T, Raftery A E, Westveld Ⅲ A H, et al. 2005. Calibrated probabilistic forecasting using ensemble model output statistics and minimum CRPS estimation. Mon Wea Rev, 133(5): 1098–1118. DOI:10.1175/MWR2904.1 |
| Gneiting T, Katzfuss M. 2014. Probabilistic forecasting. Annu Rev Stat Appl, 1: 125–151. DOI:10.1146/annurev-statistics-062713-085831 |
| Guan H, Cui B, Zhu Y J. 2015. Improvement of statistical postprocessing using GEFS reforecast information. Wea Forecasting, 30(4): 841–854. DOI:10.1175/WAF-D-14-00126.1 |
| Hagedorn R. 2008. Using the ECMWF reforecast dataset to calibrate EPS forecasts. ECMWF Newsl, 117: 8–13. |
| Hagedorn R, Buizza R, Hamill T M, et al. 2012. Comparing TIGGE multimodel forecasts with reforecast-calibrated ECMWF ensemble forecasts. Quart J Roy Meteor Soc, 138(668): 1814–1827. DOI:10.1002/qj.v138.668 |
| Hamill T M, Colucci S J. 1998. Evaluation of Eta-RSM ensemble probabilistic precipitation forecasts. Mon Wea Rev, 126(3): 711–724. DOI:10.1175/1520-0493(1998)126<0711:EOEREP>2.0.CO;2 |
| Hamill T M, Snyder C, Morss R E. 2000. A comparison of probabilistic forecasts from bred, singular-vector, and perturbed observation ensembles. Mon Wea Rev, 128(6): 1835–1851. DOI:10.1175/1520-0493(2000)128<1835:ACOPFF>2.0.CO;2 |
| Hamill T M, Snyder C, Whitaker J S. 2003. Ensemble forecasts and the properties of flow-dependent analysis-error covariance singular vectors. Mon Wea Rev, 131(8): 1741–1758. DOI:10.1175//2559.1 |
| Hamill T M, Whitaker J S, Wei X. 2004. Ensemble reforecasting:Improving medium-range forecast skill using retrospective forecasts. Mon Wea Rev, 132(6): 1434–1447. DOI:10.1175/1520-0493(2004)132<1434:ERIMFS>2.0.CO;2 |
| Hamill T M, Whitaker J S. 2006a. Probabilistic quantitative precipitation forecasts based on reforecast analogs:Theory and application. Mon Wea Rev, 134(11): 3209–3229. DOI:10.1175/MWR3237.1 |
| Hamill T M, Whitaker J S, Mullen S L. 2006b. Reforecasts:An important dataset for improving weather predictions. Bull Amer Meteor Soc, 87(1): 33–46. DOI:10.1175/BAMS-87-1-33 |
| Hamill T M. 2007. Comments on "Calibrated surface temperature forecasts from the Canadian ensemble prediction system using Bayesian model averaging". Mon Wea Rev, 135(12): 4226–4230. DOI:10.1175/2007MWR1963.1 |
| Hamill T M, Hagedorn R, Whitaker J S. 2008. Probabilistic forecast calibration using ECMWF and GFS ensemble reforecasts. Part Ⅱ:Precipitation. Mon Wea Rev, 136(7): 2620–2632. DOI:10.1175/2007MWR2411.1 |
| Hamill T M. 2012. Verification of TIGGE multimodel and ECMWF reforecast-calibrated probabilistic precipitation forecasts over the contiguous United States. Mon Wea Rev, 140(7): 2232–2252. DOI:10.1175/MWR-D-11-00220.1 |
| Hamill T M, Scheuerer M, Bates G T. 2015. Analog probabilistic precipitation forecasts using GEFS reforecasts and climatology-calibrated precipitation analyses. Mon Wea Rev, 143(8): 3300–3309. DOI:10.1175/MWR-D-15-0004.1 |
| Hamill T M, Engle E, Myrick D, et al. 2017. The U.S. national blend of models for statistical postprocessing of probability of precipitation and deterministic precipitation amount. Mon Wea Rev, 145(9): 3441–3463. DOI:10.1175/MWR-D-16-0331.1 |
| Hoeting J A, Madigan D, Raftery A E, et al. 1999. Bayesian model averaging:A tutorial (with comments by M Clyde, David Draper and E I George, and a rejoinder by the authors. Stat Sci, 14(4): 382–417. DOI:10.1214/ss/1009212519 |
| Hohenegger C, Schär C. 2007. Atmospheric predictability at synoptic versus cloud-resolving scales. Bull Amer Meteor Soc, 88(11): 1783–1793. DOI:10.1175/BAMS-88-11-1783 |
| Hopson T M, Webster P J. 2010. A 1-10-day ensemble forecasting scheme for the major river basins of Bangladesh:Forecasting severe floods of 2003-07. J Hydrometeorol, 11(3): 618–641. DOI:10.1175/2009JHM1006.1 |
| Hou D C, Charles M, Luo Y, et al. 2014. Climatology-calibrated precipitation analysis at fine scales:Statistical adjustment of stage Ⅳ toward CPC gauge-based analysis. J Hydrometeorol, 15(6): 2542–2557. DOI:10.1175/JHM-D-11-0140.1 |
| Johnson A, Wang X G. 2012. Verification and calibration of neighborhood and object-based probabilistic precipitation forecasts from a multimodel convection-allowing ensemble. Mon Wea Rev, 140(9): 3054–3077. DOI:10.1175/MWR-D-11-00356.1 |
| Keller J D, Monache D L, Alessandrini S. 2017. Statistical downscaling of a high-resolution precipitation reanalysis using the analog ensemble method. J Appl Meteor Climatol, 56(7): 2081–2095. DOI:10.1175/JAMC-D-16-0380.1 |
| Kim G, Barros A P. 2001. Quantitative flood forecasting using multisensor data and neural networks. J Hydrol, 246(1-4): 45–62. DOI:10.1016/S0022-1694(01)00353-5 |
| Kleiber W, Raftery A E, Gneiting T. 2011. Geostatistical model averaging for locally calibrated probabilistic quantitative precipitation forecasting. J Amer Stat Assoc, 106(496): 1291–1303. DOI:10.1198/jasa.2011.ap10433 |
| Krasnopolsky V M, Lin Y. 2012. A neural network nonlinear multimodel ensemble to improve precipitation forecasts over continental US. Adv Meteor, 2012: 649450. DOI:10.1155/2012/649450 |
| Lean H W, Clark P A, Dixon M, et al. 2008. Characteristics of high-resolution versions of the met office unified model for forecasting convection over the United Kingdom. Mon Wea Rev, 136(9): 3408–3424. DOI:10.1175/2008MWR2332.1 |
| Legg T P, Mylne K R. 2004. Early Warnings of severe weather from ensemble forecast information. Wea Forecasting, 19(5): 891–906. DOI:10.1175/1520-0434(2004)019<0891:EWOSWF>2.0.CO;2 |
| Li W T, Duan Q G, Miao C Y, et al. 2017. A review on statistical postprocessing methods for hydrometeorological ensemble forecasting. WIREs Water, 4: e1246. DOI:10.1002/wat2.1246 |
| Liu J G, Xie Z H. 2014. BMA probabilistic quantitative precipitation forecasting over the Huaihe basin using TIGGE multimodel ensemble forecasts. Mon Wea Rev, 142(4): 1542–1555. DOI:10.1175/MWR-D-13-00031.1 |
| Ma J H, Zhu Y J, Wobus R, et al. 2012. An effective configuration of ensemble size and horizontal resolution for the NCEP GEFS. Adv Atmos Sci, 29(4): 782–794. DOI:10.1007/s00376-012-1249-y |
| Maraun D. 2013. Bias correction, quantile mapping, and downscaling:Revisiting the inflation issue. J Climate, 26(6): 2137–2143. DOI:10.1175/JCLI-D-12-00821.1 |
| Marty R, Fortin V, Kuswanto H, et al. 2015. Combining the Bayesian processor of output with Bayesian model averaging for reliable ensemble forecasting. J Roy Stat Soc, 64(1): 75–92. DOI:10.1111/rssc.2014.64.issue-1 |
| Mendoza P A, Rajagopalan B, Clark M P, et al. 2015. Statistical postprocessing of high-resolution regional climate model output. Mon Wea Rev, 143(5): 1533–1553. DOI:10.1175/MWR-D-14-00159.1 |
| Messner J W, Mayr G J. 2011. Probabilistic forecasts using analogs in the idealized Lorenz96 setting. Mon Wea Rev, 139(6): 1960–1971. DOI:10.1175/2010MWR3542.1 |
| Messner J W, Mayr G J, Wilks D S, et al. 2014a. Extending extended logistic regression:Extended versus separate versus ordered versus censored. Mon Wea Rev, 142(8): 3003–3014. DOI:10.1175/MWR-D-13-00355.1 |
| Messner J W, Mayr G J, Zeileis A, et al. 2014b. Heteroscedastic extended logistic regression for postprocessing of ensemble guidance. Mon Wea Rev, 142(1): 448–456. DOI:10.1175/MWR-D-13-00271.1 |
| Möller A, Lenkoski A, Thorarinsdottir T L. 2013. Multivariate probabilistic forecasting using ensemble Bayesian model averaging and copulas. Quart J Roy Meteor Soc, 139(673): 982–991. DOI:10.1002/qj.2009 |
| Molteni F, Buizza R, Palmer T N, et al. 1996. The ECMWF ensemble prediction system:Methodology and validation. Quart J Roy Meteor Soc, 122(529): 73–119. DOI:10.1002/(ISSN)1477-870X |
| Mullen S L, Buizza R. 2002. The impact of horizontal resolution and ensemble size on probabilistic forecasts of precipitation by the ECMWF ensemble prediction system. Wea Forecasting, 17(2): 173–191. DOI:10.1175/1520-0434(2002)017<0173:TIOHRA>2.0.CO;2 |
| Novak D R, Bailey C, Brill K F, et al. 2014. Precipitation and temperature forecast performance at the weather prediction center. Wea Forecasting, 29(3): 489–504. DOI:10.1175/WAF-D-13-00066.1 |
| Ou M H, Charles M, Collins D C. 2016. Sensitivity of calibrated week-2 probabilistic forecast skill to reforecast sampling of the NCEP global ensemble forecast system. Wea Forecasting, 31(4): 1093–1107. DOI:10.1175/WAF-D-15-0166.1 |
| Park Y Y, Buizza R, Leutbecher M. 2008. TIGGE:Preliminary results on comparing and combining ensembles. Quart J Roy Meteor Soc, 134(637): 2029–2050. DOI:10.1002/qj.v134:637 |
| Raftery A E, Gneiting T, Balabdaoui F, et al. 2005. Using Bayesian model averaging to calibrate forecast ensembles. Mon Wea Rev, 133(5): 1155–1174. DOI:10.1175/MWR2906.1 |
| Roberts N M, Lean H W. 2008. Scale-selective verification of rainfall accumulations from high-resolution forecasts of convective events. Mon Wea Rev, 136(1): 78–97. DOI:10.1175/2007MWR2123.1 |
| Roebber P J, Schultz D M, Colle B A, et al. 2004. Toward improved prediction:High-resolution and ensemble modeling systems in operations. Wea Forecasting, 19: 936–949. DOI:10.1175/1520-0434(2004)019<0936:TIPHAE>2.0.CO;2 |
| Roulston M S, Smith L A. 2003. Combining dynamical and statistical ensembles. Tellus A:Dyn Meteor Oceanogr, 55(1): 16–30. DOI:10.1034/j.1600-0870.2003.201378.x |
| Schaffer C J, Gallus Jr W A, Segal M. 2011. Improving probabilistic ensemble forecasts of convection through the application of QPF-POP relationships. Wea Forecasting, 26(3): 319–336. DOI:10.1175/2010WAF2222447.1 |
| Schefzik R. 2011. Ensemble copula coupling[D]. Heidelberg: Ruprecht-Karls-Universität |
| Schefzik R, Thorarinsdottir T L, Gneiting T. 2013. Uncertainty quantification in complex simulation models using ensemble copula coupling. Stat Sci, 28(4): 616–640. DOI:10.1214/13-STS443 |
| Scheuerer M. 2014. Probabilistic quantitative precipitation forecasting using ensemble model output statistics. Quart J Roy Meteor Soc, 140(680): 1086–1096. DOI:10.1002/qj.2183 |
| Scheuerer M, Büermann L. 2014. Spatially adaptive post-processing of ensemble forecasts for temperature. J Roy Stat Soc, 63(3): 405–422. DOI:10.1111/rssc.2014.63.issue-3 |
| Scheuerer M, Hamill T M. 2015. Statistical postprocessing of ensemble precipitation forecasts by fitting censored, shifted Gamma distributions. Mon Wea Rev, 143(11): 4578–4596. DOI:10.1175/MWR-D-15-0061.1 |
| Schmeits M J, Kok K J. 2010. A comparison between raw ensemble output, (modified) Bayesian model averaging, and extended logistic regression using ECMWF ensemble precipitation reforecasts. Mon Wea Rev, 138(11): 4199–4211. DOI:10.1175/2010MWR3285.1 |
| Schölzel C, Friederichs P. 2008. Multivariate non-normally distributed random variables in climate research-introduction to the copula approach. Nonl Proc Geophys, 15(5): 761–772. DOI:10.5194/npg-15-761-2008 |
| Schuhen N, Thorarinsdottir T L, Gneiting T. 2012. Ensemble model output statistics for wind vectors. Mon Wea Rev, 140(10): 3204–3219. DOI:10.1175/MWR-D-12-00028.1 |
| Schwartz C S, Kain J S, Weiss S J, et al. 2009. Next-day convection-allowing WRF model guidance:A second look at 2-km versus 4-km grid spacing. Mon Wea Rev, 137(10): 3351–3372. DOI:10.1175/2009MWR2924.1 |
| Schwartz C S, Kain J S, Weiss S J, et al. 2010. Toward improved convection-allowing ensembles:Model physics sensitivities and optimizing probabilistic guidance with small ensemble membership. Wea Forecasting, 25(1): 263–280. DOI:10.1175/2009WAF2222267.1 |
| Schwartz C S, Sobash R A. 2017. Generating probabilistic forecasts from convection-allowing ensembles using neighborhood approaches:A review and recommendations. Mon Wea Rev, 145(9): 3397–3418. DOI:10.1175/MWR-D-16-0400.1 |
| Sharma S, Siddique R, Balderas N, et al. 2017. Eastern U.S. verification of ensemble precipitation forecasts. Wea Forecasting, 32(1): 117–139. DOI:10.1175/WAF-D-16-0094.1 |
| Sklar A. 1959. Fonctions de répartition àn dimensions et leurs marges. Publications de l'Institut de Statistique de L'Universitéde Paris, 8: 229–231. |
| Sloughter J M, Raftery A E, Gneiting T, et al. 2007. Probabilistic quantitative precipitation forecasting using Bayesian model averaging. Mon Wea Rev, 135(9): 3209–3220. DOI:10.1175/MWR3441.1 |
| Sloughter J M, Gneiting T, Raftery A E. 2010. Probabilistic wind speed forecasting using ensembles and Bayesian model averaging. J Amer Stat Assoc, 105(489): 25–35. DOI:10.1198/jasa.2009.ap08615 |
| Sobash R A, Schwartz C S, Romine G S, et al. 2016. Severe weather prediction using storm surrogates from an ensemble forecasting system. Wea Forecasting, 31(1): 255–271. DOI:10.1175/WAF-D-15-0138.1 |
| Stensrud D J, Yussouf N. 2007. Reliable probabilistic quantitative precipitation forecasts from a short-range ensemble forecasting system. Wea Forecasting, 22(1): 3–17. DOI:10.1175/WAF968.1 |
| Surcel M, Zawadzki I, Yau M K. 2014. On the filtering properties of ensemble averaging for storm-scale precipitation forecasts. Mon Wea Rev, 142(3): 1093–1105. DOI:10.1175/MWR-D-13-00134.1 |
| Theis S E, Hense A, Damrath U. 2005. Probabilistic precipitation forecasts from a deterministic model:A pragmatic approach. Meteor Appl, 12(3): 257–268. DOI:10.1017/S1350482705001763 |
| Toth Z, Kalnay E. 1993. Ensemble forecasting at NMC:The generation of perturbations. Bull Amer Meteor Soc, 74(12): 2317–2330. DOI:10.1175/1520-0477(1993)074<2317:EFANTG>2.0.CO;2 |
| Toth Z, Talagrand O, Zhu Y J. 2005. The attributes of forecast systems: A general framework for the evaluation and calibration of weather forecasts//Palmer T, Hagedorn R. Predictability of Weather and Climate. New York: Cambridge University Press, 584-595 |
| Unger D A, Van Den Dool H, O'Lenic E, et al. 2009. Ensemble regression. Mon Wea Rev, 137(7): 2365–2379. DOI:10.1175/2008MWR2605.1 |
| Van Den Dool H M. 1989. A new look at weather forecasting through analogues. Mon Wea Rev, 117(10): 2230–2247. DOI:10.1175/1520-0493(1989)117<2230:ANLAWF>2.0.CO;2 |
| Veenhuis B A. 2013. Spread calibration of ensemble MOS forecasts. Mon Wea Rev, 141(7): 2467–2482. DOI:10.1175/MWR-D-12-00191.1 |
| Voisin N, Schaake J C, Lettenmaier D P. 2010. Calibration and downscaling methods for quantitative ensemble precipitation forecasts. Wea Forecasting, 25(6): 1603–1627. DOI:10.1175/2010WAF2222367.1 |
| Vrugt J A, Diks C J H, Clark M P. 2008. Ensemble Bayesian model averaging using Markov chain Monte Carlo sampling. Environ Fluid Mech, 8(5-6): 579–595. DOI:10.1007/s10652-008-9106-3 |
| Wang X G, Bishop C H. 2005. Improvement of ensemble reliability with a new dressing kernel. Quart J Roy Meteor Soc, 131(607): 965–986. DOI:10.1256/qj.04.120 |
| Wilks D S. 2006. Comparison of ensemble-MOS methods in the Lorenz'96 setting. Meteor Appl, 13(3): 243–256. DOI:10.1017/S1350482706002192 |
| Wilks D S, Hamill T M. 2007. Comparison of ensemble-MOS methods using GFS reforecasts. Mon Wea Rev, 135(6): 2379–2390. DOI:10.1175/MWR3402.1 |
| Wilks D S. 2009. Extending logistic regression to provide full-probability-distribution MOS forecasts. Meteor Appl, 16(3): 361–368. DOI:10.1002/met.v16:3 |
| Wilks D S. 2011. Statistical Methods in the Atmospheric Sciences. 3rd ed. San Diego: Academic Press: 704pp. |
| Williams R M, Ferro C A T, Kwasniok F. 2014. A comparison of ensemble post-processing methods for extreme events. Quart J Roy Meteor Soc, 140(680): 1112–1120. DOI:10.1002/qj.2198 |
| Yuan H L, Gao X G, Mullen S L, et al. 2007. Calibration of probabilistic quantitative precipitation forecasts with an artificial neural network. Wea Forecasting, 22(6): 1287–1303. DOI:10.1175/2007WAF2006114.1 |
| Yussouf N, Stensrud D J. 2008. Reliable probabilistic quantitative precipitation forecasts from a short-range ensemble forecasting system during the 2005/06 cool season. Mon Wea Rev, 136(6): 2157–2172. DOI:10.1175/2007MWR2314.1 |
| Zhu Y, Iyengar G, Toth Z, et al. 1996. Objective evaluation of the NCEP global ensemble forecasting system//Preprints, 15th Conf on Weather Analysis and Forecasting. Norfolk, VA: Amer Meteor Soc, 79-82 |
| Zhu Y J, Toth Z, Wobus R, et al. 2002. The economic value of ensemble-based weather forecasts. Bull Amer Meteor Soc, 83(1): 73–83. DOI:10.1175/1520-0477(2002)083<0073:TEVOEB>2.3.CO;2 |
| Zhu Y J, Luo Y. 2015. Precipitation calibration based on the frequency-matching method. Wea Forecasting, 30(5): 1109–1124. DOI:10.1175/WAF-D-13-00049.1 |
 2018, Vol. 76
2018, Vol. 76

