中国气象学会主办。
文章信息
- 牛嫣静, 彭新东, 范广洲. 2018.
- NIU Yanjing, PENG Xindong, FAN Guangzhou. 2018.
- GRAPES模式中三维科氏力计算及其效果评估
- Impact of the three-dimensional Coriolis force in GRAPES model
- 气象学报, 76(3): 473-484.
- Acta Meteorologica Sinica, 76(3): 473-484.
- http://dx.doi.org/10.11676/qxxb2018.003
-
文章历史
- 2017-05-02 收稿
- 2017-11-15 改回
2. 中国气象科学研究院, 灾害天气国家重点实验室, 北京, 100081
2. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081, China
作为一种连续可压缩流体,大气具有分层流体特性,其状态变化可由牛顿第二定律、热力学第一定律、连续方程和理想大气状态方程组成的偏微分方程组描述。由于对该偏微分方程组的数值求解方法不同和需要保持的模式守恒特性不同,对模式方程组会有不同程度的简化。中国气象局研发的GRAPES模式(陈德辉等,2008),由于在浅薄大气假定下考虑模式动力框架角动量守恒和半隐式半拉格朗日积分求解的简化,考虑垂直运动速度的量级相对较小,在水平动量方程中忽略了地球自转角速度水平分量(即下文中的fφ)形成的科氏力分量(fφw)。另外,随着全球大气环流模式分辨率的不断提高,数十千米至数千米水平分辨率模式则可以很好地描述β中尺度、甚至γ中尺度系统,垂直速度可以达到水平速度量级;并且在非静力模式的垂直运动方程中fφu项并不能作为小项忽略,武断地省略该项可能在非静力模式中造成明显的误差。
模式改进包括算法改进(李江浩等, 2013a, 2013b;Li, et al,2013; 苏勇等, 2013)、动力性能改进(刘洁, 2017)和物理过程改进(黄翊等, 2017;Huang, et al, 2017)等,还可以从模式误差订正(Peng, et al, 2013; Che, et al, 2016; 常俊等, 2015; 佟铃等,2017)入手提高模式预报质量。在动力过程方面,有不少非静力模式(如MM5、WRF、GRAPES-TYM等)均已考虑了三维科氏力的计算,但在全球大气环流模式中基本只保留地球自转垂直分量的科氏力成分,这与目前大气环流模式基本仍为静力平衡模式有关。在非静力模式GRAPES中,出于三方面的考虑忽略fφ的作用,其一是在浅大气近似中保证模式的角动量守恒,其二通常大尺度系统的垂直运动较弱,第三是在半隐式半拉格朗日积分方案中,其近似使三维动量方程间保持“单线联系”,大幅度简化了相应亥姆霍兹方程以方便计算。以牺牲模式的计算精度为代价来保证模式的角动量守恒对中期预报系统而言是否必要,或者在一个积分时间为两周的非静力数值模式中如何简化动力过程,是开发全球高分辨率模式时需要关心的问题。可喜的是,Li等(2015)在阴阳网格GRAPES_YY模式的构建过程中,给出了半隐式半拉格朗日求解非静力模式的亥姆霍兹方程系数矩阵和相应的系数表达式,并与原模式具有相似的求解过程,这为重新构建GRAPES模式包含三维科氏力的亥姆霍兹方程求解提供了数学解决方案。
本研究将通过完善三维科氏力的计算尝试对GRAPES-GFS模式的动力框架进一步优化,然后通过三维大气理想试验检验和讨论完整科氏力对大气环流模拟的影响,评估惯性力过程对数值模式计算稳定性和计算精度的影响。
2 GRAPES动力框架改进GRAPES-GFS模式(薛纪善等,2008)是一个完全可压缩的非静力大气动力模式,水平方向上采用经、纬度网格,垂直方向上使用高度地形追随坐标(Gal-Chen,et al,1975),时间积分方案为两时间层的半隐式半拉格朗日方案(Ritchie,et al,1994),变量在水平方向为Arakawa-C网格分布(Arakawa,et al,1977),垂直方向为Charney-Philips跳层(Charney,et al,1953)分布。
2.1 基本方程组球坐标系下,在动量方程中考虑三维科氏力的模式方程组可表示为
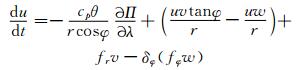
|
(1) |
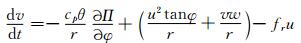
|
(2) |
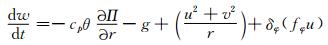
|
(3) |
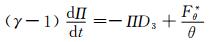
|
(4) |
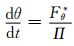
|
(5) |
式中,u为经向风速,v纬向风速,w为垂直风速,θ为位温,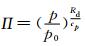
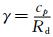
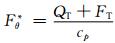
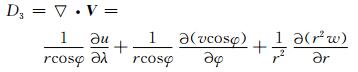
|
对式(1)—(5)应用半隐式-半拉格朗日方法求解,并将其中的线性项和非线性项分离,时间离散化预报方程组可写为
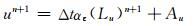
|
(6) |
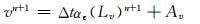
|
(7) |
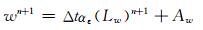
|
(8) |
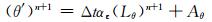
|
(9) |

|
(10) |
式中,Δt表示积分时间步长,αε为非中央差分权重系数,θ′、Π′分别为相对于参考态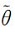
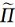
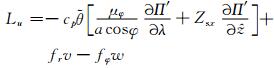
|
(11) |
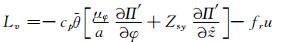
|
(12) |

|
(13) |
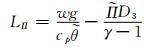
|
(14) |
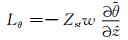
|
(15) |
式中,地形参数

|
非线性项和半拉格朗日出发点的计算包含在Aχ项中,其表达保持与原模式相同(薛纪善等,2008),此处不再赘述。
把式(11)—(15)代入(6)—(10),并为方便表达,直接采用Π代表Π′,可得离散化求解形式
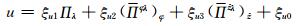
|
(16) |
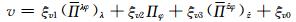
|
(17) |
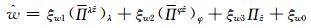
|
(18) |

|
(19) |
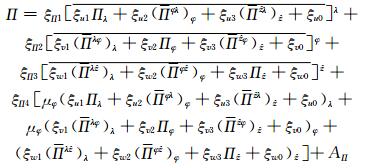
|
(20) |
其中,式(20)为关于埃克斯纳函数Π的典型亥姆霍兹方程,其系数表示式分别为
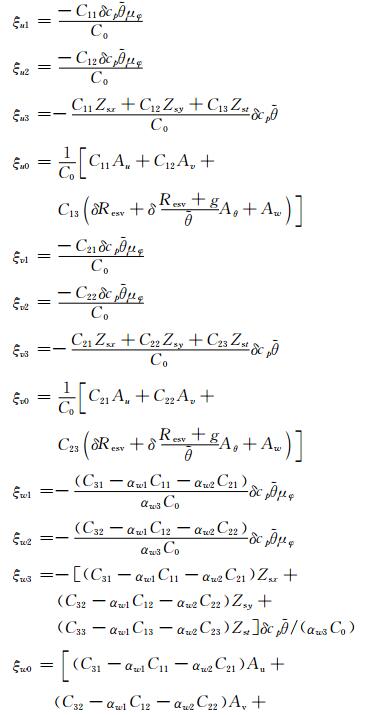
|
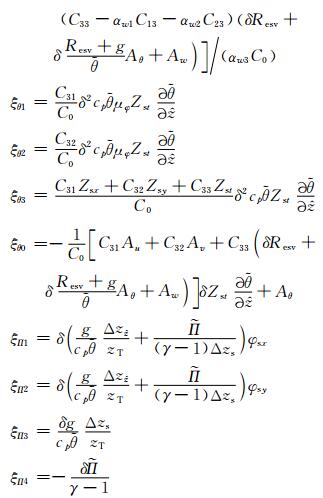
|
其中,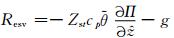
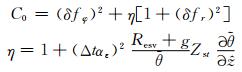
|
其中,C11、C12、C13、C21、C22、C23、C31、C32、C33为矩阵C的元素
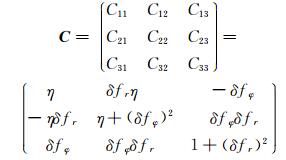
|
其中,ξw0、ξw1、ξw2、ξw3式中的
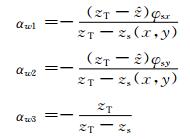
|
可见,在考虑三维科氏力的情况下,亥姆霍兹方程的表现形式与原模式(薛纪善等,2008)保持一致,但各项系数的表达有所不同。这里,仍然采用广义共轭余差(GCR)法对该亥姆霍兹方程进行求解。
3 理想试验及结果为了检验在考虑三维科氏力分量后,GRAPES模式动力过程计算的正确性、准确性和稳定性,采用常用的三维大气理想试验(Lauritzen,et al, 2013)对非静力模式的动力框架进行检验,这些理想试验包括平衡流试验、罗斯贝-豪威兹波试验、山脉激发罗斯贝波试验和斜压波试验等。
3.1 平衡流试验平衡流试验(Williamson,et al, 1992)是为检验浅水波模式中计算方法的精度和模式的稳定性而设计的,假设了气压梯度力和科氏力的平衡运动。为了能在三维模式的开发中发挥作用,Jablonowski等(2008)将该试验扩展到三维流体,除假定大气在水平方向上满足地转平衡外,在垂直方向上还满足静力平衡。在给定的气压和风场初始状态在垂直和水平方向分别满足静力平衡和地转平衡关系,即使对非静力模式而言,这种平衡关系应该在模式积分过程中得以维持。
平衡流的初始场满足地转平衡关系
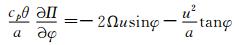
|
(21) |
和静力平衡关系
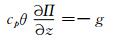
|
(22) |
位温满足
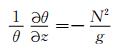
|
(23) |
式中,N为Brunt-Vaisalla频率,这里给定为N2=1.44×10-4。选定水平风场为
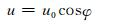
|
(24) |
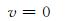
|
(25) |
而垂直速度
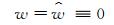
|
(26) |
由式(21)—(26)可得
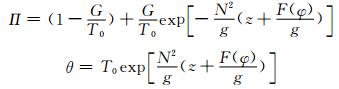
|
其中
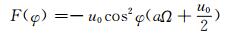
|
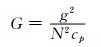
|
式中,a=6371 km,为地球半径,u0=10 m/s,Ω=7.292×10-5s-1为地球自转角速度,T0=290 K。可见,初始时刻等高面上的气压仅随纬度变化,也只有纬向风,等压线和等风速线都与纬圈平行,在没有地形和物理过程的情况下,这种平衡关系得以维持,与纬圈平行的等压线和等风速线也不随模式的积分发生变化。
为了便于对计算方法和模式计算精度进行评估,采用Williamson等(1992)对标量和矢量的定义来计算数值模拟结果的误差。定义某一标量q的全球积分为
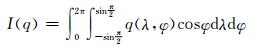
|
(27) |
则对标量q和矢量场V(u,v,w)的误差分别定义为
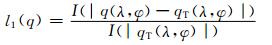
|
(28) |
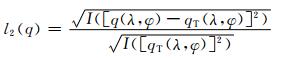
|
(29) |

|
(30) |
和
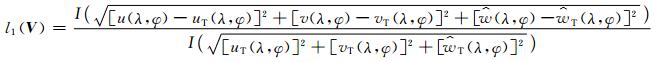
|
(31) |

|
(32) |
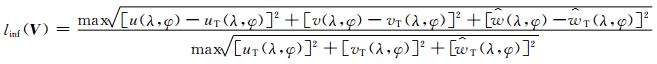
|
(33) |
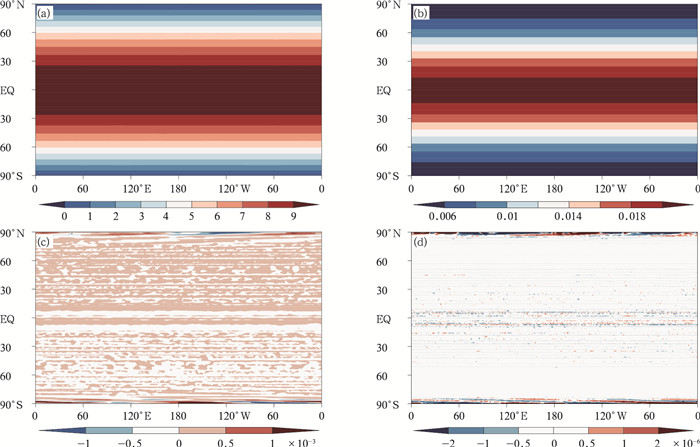
在包含三维科氏力与否的两个动力框架中,采用水平分辨率为1°×1°,垂直均匀36层的网格进行试验,时间积分步长取1200 s。图 1给出了在平衡流试验中考虑三维科氏力的新动力框架经过15 d积分后第5层气压场、纬向风、经向风和垂直风速的结果。可见模式积分15 d后,纬向风场和气压场均保持其纬向均匀分布,保持了与初始场相同的分布特征,而经向风和垂直风速分别为10-3和10-6 m/s量级,接近于0。可见模式中地转平衡关系得以很好的维持,并且垂直运动表现的误差极值出现在极地附近,这主要是由于“极地混合”和极点附近纬向网格距缩小导致误差增长。
|
| 图 1 在考虑三维科氏力情况下模式积分15 d后第5层Π′(a)、纬向风u(m/s)(b)、经向风v (m/s)(c)、垂直风速w (m/s)(d)的平衡流试验结果 Figure 1 Numerical results of Π′ (a), u (m/s) (b), v (m/s) (c) and w (m/s) (d) at the 5th model level in a 15 d integration of the balanced flow experiment, in which the full three-dimensional Coriolis force is considered |
为定量描述考虑三维科氏力给模式动力过程计算带来的影响,通过计算水平面上的变量误差来评估。图 2给出了新旧两个动力框架在平衡流试验中积分15 d的模式第5层的标量Π′和矢量V的标准误差时间演变。可以看出,在考虑三维科氏力分量情况下,模式计算Π′和V的标准化误差均比原模式大幅度减小,其中l1和l2约为原模式的1/10。标准化误差随积分时间呈线性增长,积分15 d后,原模式Π′的l1和l2误差分别为0.0028和0.0033,linf为0.0065,而考虑三维科氏力作用的新模式框架的模拟结果中,Π′的l1和l2则分别为0.00023和0.0004,总体平均误差比原模式小一个量级,而linf则为0.004左右,说明linf反映的单点极大误差与原模式在同一水平。对于矢量V,同样可见在考虑三维科氏力的模式中,l1和l2分别为0.002和0.003,linf约为0.016,而原模式的l1和l2分别为0.013和0.018,linf为0.042。三维科氏力动力框架可使模式的l1和l2减小一个量级。

|
| 图 2 平衡流试验中标量Π′和矢量V的标准化误差随时间变化 (a.原GRAPES模式的Π′,b.考虑三维科氏力后新框架的Π′,c.原模式V矢量,d.新框架V矢量) Figure 2 Temporal evolution of the error norms l1, l2 and linf (a. Π′ of the original GRAPES model, b. Π′ of the new model core with the 3D Coriolis force considered, c. vector V of the original model, d. vector V of the new frame in the balanced flow experiment during the 15 d integration) |
从简单平衡流试验的结果可以看出,在GRA- PES模式的动力框架中引入三维科氏力可以提高模式动力过程的计算精度,减小模式误差,增强模式对惯性坐标系中大气动力过程的描述能力。尽管这里忽略了其对角动量守恒的影响,在中短期数值预报中,三维科氏力的考虑对GRAPES模式的动力过程有明显的改进效果。
3.2 罗斯贝-豪威兹波传播试验罗斯贝-豪威兹波是正压涡度方程的解析解(Thuburn,et al,2000)。由于罗斯贝-豪威兹波试验中水平风速方向呈周期变化、南北半球对称,该试验较平衡流试验更为苛刻,可用以检验模式对波的保形性和守恒特征,对模式的计算性能要求较高。由于动力框架中插值误差存在,在计算过程中,波动可能随着时间的积分变平,而波形的保持是衡量模式动力框架优越性的指标之一。
该试验中,水平风场设为
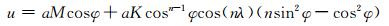
|
(34) |
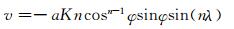
|
(35) |
位势高度为
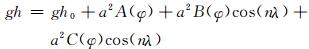
|
(36) |
其中
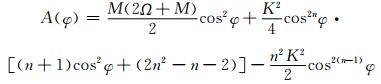
|
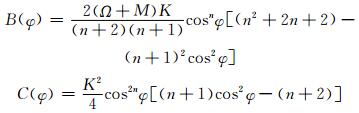
|
式中,地球半径a=6371 km,地球自转速度Ω=7.292×10-5s-1, 波数n取为4,M=K≈1.962×10-5s-1。
温压场定义为
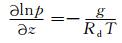
|
(37) |

|
(38) |
或采用其垂直积分形式
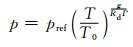
|
(39) |
其中
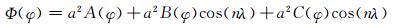
|
(40) |
式中,Γ为温度递减率,T0=288 K, pref=955 hPa为南、北极的地表气压,设为参考气压。
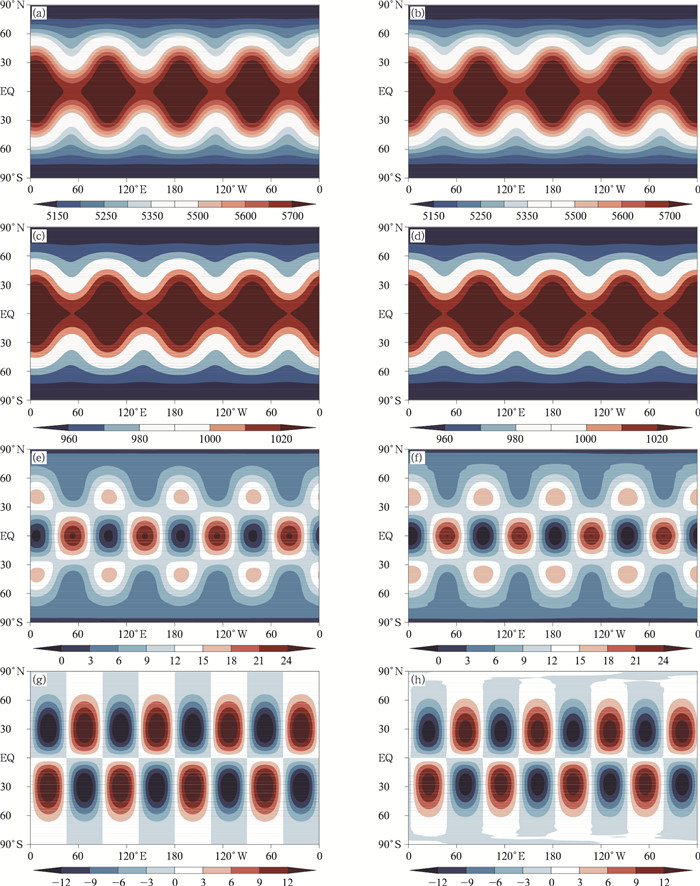
在罗斯贝-豪威兹波试验中,模式积分时间步长取300 s,水平分辨率为1°×1°,垂直分为非均匀的36层。图 3为考虑三维科氏力的罗斯贝-豪威兹波试验结果,给出了500 hPa位势高度、地面气压、850 hPa纬向风和经向风的初始场(图 3a、c、e、g)及对应的15 d后的预报结果(图 3b、d、f、h),模式积分15 d后各变量对应的波数为4的波形与初始场保持一致,南、北半球关于赤道对称,很难看出积分结果变形,模式对罗斯贝-豪威兹波具有较高的保形性能,也说明三维科氏力的计算对GRAPES动力框架处理大尺度波动问题仍能保持较高的计算性能。
|
| 图 3 考虑三维科氏力情况下罗斯贝-豪威兹波试验的结果 (a、b.500 hPa位势高度(gpm),c、d.地面气压(hPa),e、f.850 hPa纬向风(m/s),g、h.850 hPa经向风(m/s);a、c、e、g.初始场,b、d、f、h.15 d的积分结果) Figure 3 Numerical results of the Rossby-Haurwitz wave experiment with 3D Coriolis force (a, b. geopotential height (gpm) at 500 hPa, c, d. surface pressure (hPa), e, f. zonal wind u (m/s), g, h. meridional wind v (m/s) at 850 hPa, a, c, e, g. initial data; numerical results of the day 15) |
由于没有解析解参考,这里无法给出标准误差统计,仅就有无三维科氏力的新旧动力框架模拟结果做对比讨论。
3.3 地形罗斯贝波试验地形罗斯贝波试验(Tomita, et al, 2004)是在一个中纬度平直西风气流中放入一个钟形的山脉,在地形强迫下,激发罗斯贝波并发展。该试验用以检验模式地形处理和过山气流中的波动发展,以及模式对波动结构的描述。其初始风场设定和平衡流相同,而增加的模式地形为
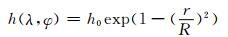
|
(41) |
式中,山脉的中心高度h0=2000 m,山脉的半径R=1500 km, 山脉的中心位置(λc, φc)取为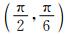
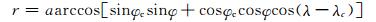
|
地表气压ps为
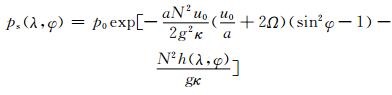
|
(42) |
式中,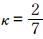
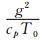
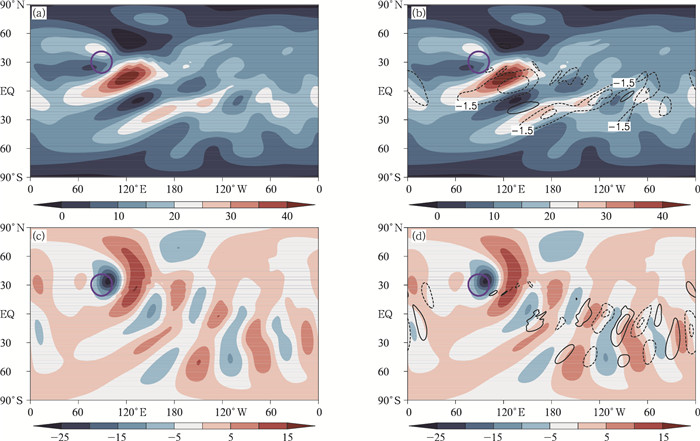
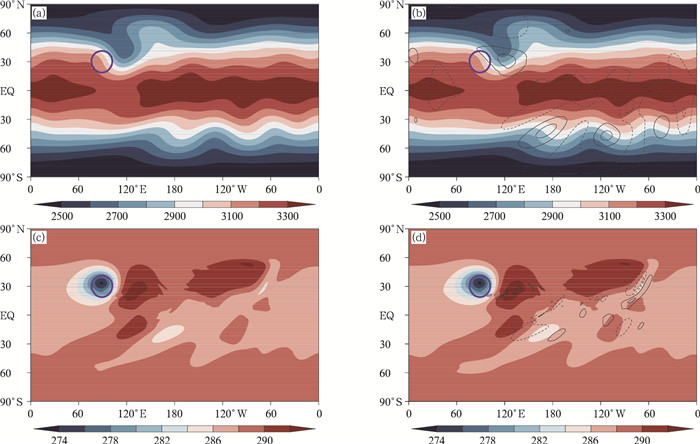
试验中水平分辨率为1°×1°,垂直方向非均匀分为36层,积分时间步长取600 s,本试验仍积分15 d。图 4给出了两个模式动力框架计算的第15天预报700 hPa位势高度场和温度场对比。在考虑三维科氏力作用的700 hPa位势高度场中,山地背风坡罗斯贝波大槽的发展与原模式中大槽发展类似,从等高线看不出明显差异,但赤道高压带则明显较原模式弱,控制范围减小,与南、北半球的波动振幅略有加强有关。为了更清楚地显示考虑三维科氏力对地形罗斯贝波发展的影响,在图中给出了新框架相对于原模式的预报增量,罗斯贝大槽的顶端为正增量,表明大槽略变浅,但大槽根部的高纬度地区和高压脊上负增量显示出降压特征,可见三维科氏力的考虑使背风坡罗斯贝槽、脊发展略有减弱。赤道地区负变高为主,高压系统确有减弱。在南半球,脊前正变高,而槽前负变高说明三维科氏力使南半球的槽、脊发展加强。温度场显示出在山顶形成的低温中心,并向上游地区扩展,而暖中心形成于山体背风坡,向下游高纬度地区扩展,而考虑三维科氏力时对温度预报的影响主要集中在冷、暖交界288 K线附近,总体上使高温区升温减缓。
|
| 图 4 地形罗斯贝波试验第15天700 hPa位势高度(a、b,单位:gpm)和温度场(c、d,单位:K) (a、c.原模式,b、d.新模式;等值线表示新框架较原模式的预报量增量,粗实线圆圈表示山体位置) Figure 4 Simulated geopotential height (a, b. unit: gpm) and temperature (c, d. unit: K) on 700 hPa in a 15 d integration of the mountain-Rossby wave experiment (a, c.original model. b, d.new model. The contours show the differences between the two models. The thick solid ring shows the mountain location) |
图 5中也给出了两个框架模拟的15天后700 hPa的纬向风场和经向风场的对比。两个框架仍然给出了相似的水平风场,背风槽区为弱纬向风区,而槽区南部则为强纬向风区,强经向风位于槽前。考虑三维科氏力时,强纬向风区减弱,弱纬向风区加强;而经向风的增强中心位于弱风速中心前和强风速中心后。
斜压波试验(Jablonowski, et al, 2006; Lauritzen, et al, 2008)是在一个平直的西风气流上叠加一个扰动的纬向风场。对于垂直坐标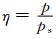
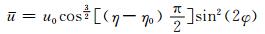
|
(43) |
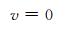
|
(44) |
式中,η0=0.252,u0=35 m/s, φ为纬度。
纬向风场扰动为
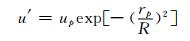
|
(45) |
式中,rp=aarccos[sinφcsinφ+cosφccosφcos(λ-λc)],a=6371 km为地球半径,扰动中心设为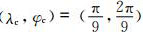
本试验中初始纬向风为
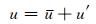
|
(46) |
而初始温度场为
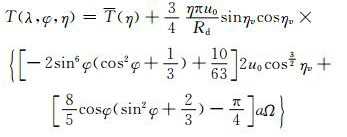
|
(47) |
式中,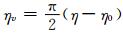
平均温度场则给定为
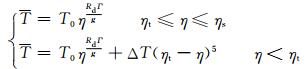
|
(48) |
式中,地表平均温度T0=288 K,最低层ηs=1,对流层顶ηt=0.2,温度递减率Γ取为0.005 K/m。
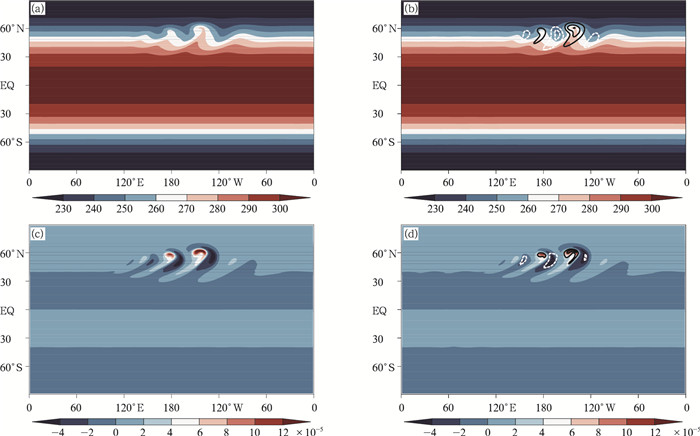
本试验的空间分辨率和时间积分步长与地形罗斯贝波试验相同,从两个模式积分10 d后850 hPa的温度场和涡度场水平分布(图 6)可以看出,考虑三维科氏力与否模拟的斜压波发展非常相像,无论从温度分布和垂直涡度的水平结构看都没有表现出明显差别。但为了比较,图 6也给出了三维科氏力作用下模拟温度和涡度与原模式预报结果的差(图 6b、d的等值线),可见斜压波发展的暖温度脊处呈现正温度差,而冷温度槽处则为负温度偏差,即三维科氏力的作用加强了温度槽脊的发展。垂直涡度的发展也表现出相同的特征,在负涡度区有负偏差,正涡度区有正偏差,从水平环流角度来看同样反映了气旋性环流和反气旋性环流在三维科氏力作用下可进一步发展,而单纯垂直方向科氏力参数削弱了波动的发展强度。斜压波的模拟同样说明三维科氏力可以显著影响波动发展的模拟结果,且呈现系统性强度差异,但没有表现出位相差。
|
| 图 6 原模式(a、c)和考虑三维科氏力的新模式(b、d)在斜压波试验中积分10 d后850 hPa的温度场(a、b,K)和涡度场(c、d,s-1)(等值线表示新框架与原模式的预报量增量) Figure 6 Simulated temperature (a, b, unit: K) and vorticity (b, d, unit: s-1) at 850 hPa at 10 d integration with the original GRAPES model (a, c) and the new frame with the 3D Coriolis force considered (b, d) (the contours show the difference between the two models) |
在GRAPES-GFS模式中完善三维科氏力的处理,并对模式动力框架中的离散化和数值求解方法进行了重新整理,在不改变原有基本算法的基础上实现了对模式三维动力过程的精细化计算。通过理想试验,检验了动力过程升级前后模式计算结果的一致性、模式稳定性和对模式计算误差的改善。在三维平衡流试验中,模拟标量误差和矢量误差随时间都呈线性增长,但考虑三维科氏力后误差增长速率变慢,l1和l2误差约为原模式对应误差的1/10,而新框架的标量linf为0.004,也较原模式0.0065的误差有所减小,矢量场linf也从0.042减小为0.016,大大减小了模式动力过程的计算误差。在罗斯贝-豪威兹波、地形罗斯贝波和斜压波试验中,三维科氏力计算都显示了模式很好的稳定性和波形结构,与原模式结果的对比也表明三维科氏力计算对波动强度和环流特征都有显著影响。
虽然罗斯贝-豪威兹波、地形罗斯贝波和斜压波试验没有标准解作为参考,无法获得考虑三维科氏力的动力框架对波动解影响的定量评估,但对波动扰动、特别是槽脊模拟的影响明显,从而影响数值模式在大尺度过程预报中的计算效果。综上所述,在GRAPES-GFS模式中考虑三维科氏力,仍能保持模式计算的稳定性,结果合理,并有明显改进,对提高GRAPES-GFS的动力过程描述和预报精度具有科学和应用价值。
| 常俊, 彭新东, 范广洲, 等. 2015. 结合历史资料的数值天气预报误差订正. 气象学报, 73(2): 341–354. Chang J, Peng X D, Fan G Z, et al. 2015. Error correction of numerical weather prediction with historical data. Acta Meteor Sinica, 73(2): 341–354. DOI:10.11676/qxxb2015.021 (in Chinese) |
| 陈德辉, 薛纪善, 杨学胜, 等. 2008. GRAPES新一代全球/区域多尺度统一数值预报模式总体设计研究. 科学通报, 53(22): 3433–3445. Chen D H, Xue J S, Yang X S, et al. 2008. New generation of multi-scale NWP system (GRAPES):General scientific design. Chinese Sci Bull, 53(22): 3433–3445. (in Chinese) |
| 黄翊, 彭新东. 2017. 边界层湍流参数化改进对雾的模拟影响. 大气科学, 41(3): 533–543. Huang Y, Peng X D. 2017. The impact of an improved planetary boundary layer parameterization scheme on the simulation of fog. Chinese J Atmos Sci, 41(3): 533–543. (in Chinese) |
| 李江浩, 彭新东. 2013a. 阴阳网格上质量守恒计算性能分析. 大气科学, 37(4): 852–862. Li J H, Peng X D. 2013a. Analysis of computational performance of conservative constraint on the Yin-Yang grid. Chinese J Atmos Sci, 37(4): 852–862. (in Chinese) |
| 李江浩, 彭新东. 2013b. 守恒型有理函数插值半拉格朗日平流方案及性能分析. 气象学报, 71(4): 709–718. Li J H, Peng X D. 2013b. Analysis of computational performance of the conservative semi-Lagrangian with rational function advection scheme. Acta Meteor Sinica, 71(4): 709–718. (in Chinese) |
| 刘洁, 彭新东. 2017. 阴阳网格守恒算法的设计和改进. 大气科学, 41(5): 1076–1086. Liu J, Peng X D. 2017. Design and improvement of the conservative constraint algorithm on the Yin-Yang grid. Chinese J Atmos Sci, 41(5): 1076–1086. (in Chinese) |
| 苏勇, 沈学顺, 彭新东, 等. 2013. PRM标量平流方案在GRAPES全球预报系统中的应用. 大气科学, 37(6): 1309–1325. Su Y, Shen X S, Peng X D, et al. 2013. Application of PRM scalar advection scheme in GRAPES global forecast system. Chinese J Atmos Sci, 37(6): 1309–1325. DOI:10.3878/j.issn.1006-9895.2013.12164 (in Chinese) |
| 薛纪善, 陈德辉. 2008. 数值预报系统GRAPES的科学设计与应用. 北京: 科学出版社: 65-132. Xue J S, Chen D H. 2008. Scientific Design and Application of Numerical Forecast System GRAPES. Beijing: Science Press: 65-132. |
| 佟铃, 彭新东, 范广洲, 等. 2017. GRAPES全球模式的误差评估和订正. 大气科学, 41(2): 333–344. Tong L, Peng X D, Fan G Z, et al. 2017. Error evaluation and correction for GRAPES global forecasts. Chinese J Atmos Sci, 41(2): 333–344. (in Chinese) |
| Arakawa A, Lamb V R. 1977. Computational design of the basic dynamical processes of the UCLA general circulation model. Methods Comput Phys:Adv Res Appl, 17: 173–265. DOI:10.1016/B978-0-12-460817-7.50009-4 |
| Charney J G, Phillips N A. 1953. Numerical integration of the quasi-geostrophic equations for barotropic and simple baroclinic flows. J Atmos Sci, 10(2): 71–99. |
| Che Y Z, Peng X D, Monache L D, et al. 2016. A wind power forecasting system based on the weather research and forecasting model and Kalman filtering over a wind-farm in Japan. J Renew Sustain Energy, 8: 013302. DOI:10.1063/1.4940208 |
| Gal-Chen T, Somerville R C J. 1975. On the use of a coordinate transformation for the solution of the Navier-Stokes equations. J Comput Phys, 17(2): 209–228. |
| Huang Y, Peng X D. 2017. Improvement of the Mellor-Yamada-Nakanishi-Niino planetary boundary layer scheme based on observational data in China. Bound-Layer Meteor, 162(1): 171–188. DOI:10.1007/s10546-016-0187-0 |
| Jablonowski C, Williamson D L. 2006. A baroclinic instability test case for atmospheric model dynamical cores. Quart J Roy Meteor Soc, 132(621C): 2943–2975. DOI:10.1256/qj.06.12 |
| Jablonowski C, Lauritzen P H, Nair R D, et al. 2008. Idealized test cases for the dynamical cores of Atmospheric General Circulation Models. A proposal for the NCAR ASP 2008 summer colloquium. http://esse.engin.umich.edu/admg/publications.php |
| Lauritzen P H, Jablonowski C. 2008. A rotated version of the Jablonowski-Williamson baroclinic wave test case//AGU Fall Meeting Abstracts. Washington, DC: American Geophysical Union |
| Lauritzen P H, Ullrich P A, Jablonowski C, et al. 2013. A standard test case suite for two-dimensional linear transport on the sphere:Results from a collection of state-of-the-art schemes. Geosci Model Dev Dis, 6(3): 4983–5076. DOI:10.5194/gmdd-6-4983-2013 |
| Li X H, Peng X D, Li X L. 2015. An improved dynamic core for a non-hydrostatic model system on the Yin-Yang grid. Adv Atmos Sci, 32(5): 648–658. DOI:10.1007/s00376-014-4120-5 |
| Li X L, Shen X S, Peng X D, et al. 2013. An accurate multimoment constrained finite volume transport model on Yin-Yang grids. Adv Atmos Sci, 30(5): 1320–1330. DOI:10.1007/s00376-013-2217-x |
| Peng X D, Che Y Z, Chang J. 2013. A novel approach to improve numerical weather prediction skills by using anomaly integration and historical data. J Geophy Res:Atmos, 118(16): 8814–8826. DOI:10.1002/jgrd.50682 |
| Ritchie H, Beaudoin C. 1994. Approximations and sensitivity experiments with a baroclinic semi-lagrangian spectral model. Mon Wea Rev, 122(10): 2391–2399. DOI:10.1175/1520-0493(1994)122<2391:AASEWA>2.0.CO;2 |
| Thuburn J, Li Y. 2000. Numerical simulations of Rossby-Haurwitz waves. Tellus A:Dyn Meteor Oceanogr, 52(2): 181–189. DOI:10.3402/tellusa.v52i2.12258 |
| Tomita H, Satoh M. 2004. A new dynamical framework of nonhydrostatic global model using the icosahedral grid. Fluid Dynamics Res, 34(6): 357–400. DOI:10.1016/j.fluiddyn.2004.03.003 |
| Williamson D L, Drake J B, Hack J J, et al. 1992. A standard test set for numerical approximations to the shallow water equations in spherical geometry. J Comput Phys, 102(1): 227–228. |
 2018, Vol. 76
2018, Vol. 76