中国气象学会主办。
文章信息
- 苏勇, 沈学顺, 陈子通, 张红亮. 2018.
- SU Yong, SHEN Xueshun, CHEN Zitong, ZHANG Hongliang. 2018.
- GRAPES_GFS中三维参考大气的研究:理论设计和理想试验
- A study on the three-dimensional reference atmosphere in GRAPES_GFS: Theoretical design and ideal test
- 气象学报, 76(2): 241-254.
- Acta Meteorologica Sinica, 76(2): 241-254.
- http://dx.doi.org/10.11676/qxxb2017.097
-
文章历史
- 2017-04-25 收稿
- 2017-08-17 改回
2. 中国气象科学研究院, 北京, 100081;
3. 国家气象中心, 北京, 100081;
4. 中国气象科学研究院灾害天气国家重点实验室, 北京, 100081;
5. 中国气象局广州热带海洋气象研究所, 广州, 510080
2. Chinese Academy of Meteorological Sciences, Beijing 100081, China;
3. National Meteorological Center, Beijing 100081, China;
4. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081, China;
5. Guangzhou Institute of Tropical and Marine Meteorology, China Meteorological Administration, Guangzhou 510080, China
早期数值天气预报模式的发展过程中, 积分时间步长主要受制于积分的稳定性而不是精度, 特别是对于采用经、纬度网格的全球模式, 极区的格点辐合问题严重限制了时间步长。半隐式半拉格朗日(SISL)算法(Staniforth, et al, 1991; Robert, et al, 1985)的引入在很大程度上解决了这一问题, 相对于欧拉算法, 半拉格朗日算法使得平流计算不再受制于柯朗-弗里德里希斯-列维(Coutant-Friendrichs-Lewy, CFL)条件的限制, 再加上对重力波等过程采用半隐式的处理方法, 使得时间步长可以取得较大。因此, 半隐式半拉格朗日算法被广泛应用于业务数值预报模式的框架构建中, 如英国气象局(Staniforth, et al, 2006; Wood, et al, 2014b)、欧洲中期数值预报中心(Diamantakis, 2013)、加拿大气象局(Côté, et al, 1998)等都基于该方法求解其动力框架, 进一步考虑到计算效率以及内存空间的问题, 大部分业务中心都采用两个时间层的半隐式半拉格朗日算法。但直到今日, 基于该方法构建的模式框架仍然有一些问题需要进一步的优化和解决, 如下面提到的这几个方面:
(1) 设计半隐式计算方案时, 需要引入参考大气对预报方程进行线性化的处理(Chen, et al, 1990), 将其分解为线性项和非线性项, 其中线性项主要包含快速变化的重力波、声波等, 通过隐式积分求解; 非线性项为扰动量, 也就是残差项, 主要包含方程中缓慢变化以及定常的部分, 应远小于线性项, 通过显式积分求解
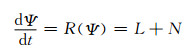
|
(1) |
式中, Ψ为预报变量, R(Ψ)为预报方程右端表达式, L为线性项, N为非线性项。因此, 参考大气需要尽量靠近模式大气, 以减小扰动量的数量级, 进而提高计算精度。各个业务中心参考大气的选法也不尽相同, 有基于等温大气构造的一维参考大气(薛纪善等, 2008), 有基于随高度变化的定常廓线构造的参考大气(王斌等, 2006; Wu, et al, 2008), 有基于初始时刻的水平平均廓线构造的参考大气(Lafore, et al, 1997), 也有基于上一时刻变量场构造的随时间变化的三维参考大气(Wood, et al, 2014a)。大多数模式为了避免求解过程过于复杂, 都选取不随时间变化的一维参考大气, 该类方法易于实现, 但无法使参考大气在所有计算区域都靠近模式大气, 一般情况下在高层和高纬度区域扰动量的数量级较大; 同时也有为了追求计算精度, 采用随时间变化的三维参考大气的, 如英国气象局的ENDGame(Wood, et al, 2014a), 但其求解过程较为复杂, 不易实现, 且计算代价较大。陈子通曾基于GRAPES_MESO模式实现了不随时间变化的满足静力平衡关系的三维参考大气, 但在公式推导过程中将参考大气的水平变化项纳入非线性项中, 这样求解过程较为简单, 但非线性项量级大于线性项, 会降低时间离散过程的计算精度, 同时模式也容易积分溢出。
(2) 对半隐式半拉格朗日模式来说, 虚假的地形响应(Ritchie, et al, 1996)也是一个需要处理的问题。理论分析和数值试验都证明, 其不是半隐式半拉格朗日算法设计思路的问题, 而是由于在CFL条件大于1的情况下, 半隐式半拉格朗日算法在地形复杂的区域会产生计算噪声, 特别是在分辨率较高的情况下, 这些噪声会很快地影响到模式的预报结果, 这就使得模式的积分时间步长不能选取得太大, 限制了半隐式半拉格朗日算法在计算效率方面发挥其优势。Rivest等(1994)做了很多相关的研究, 基于3个时间层的半隐式半拉格格朗日方法可以在不损失计算精度的情况下缓解这一问题。Ritchie等(1996)的研究中提到, 地形的作用是不随时间发生变化的, 可以把其看成一种能量的强迫, 通过参考大气将其扣除, 这样就可以提高扰动量的计算精度。ECMWF(European Centre for Medium range Weather Forecast)的业务模式利用和地形相关的地面气压场构建其参考大气(Temperton, et al, 2001), 再通过线性化的处理, 扣除了地形对半隐式半拉格朗日计算的影响, 有效地提高了气压梯度力以及半拉格朗日平流的计算精度。Wu等(2008)基于NCAR(National Center for Atmospheric Research)的CAM3(Community Atmosphere Model version 3), 引入利用地面气压和随高度变化的温度廓线构造的参考大气, 有效地抑制了虚假的地形响应, 提高了复杂地形处气压梯度力和半拉格朗日平流的计算精度。
(3) 两个时间层的半拉格朗日算法需要用拉格朗日轨迹中间点在中间时刻的速度近似整个轨迹的平均速度, 该速度既不在模式网格点上, 也不在时间层上, 需要通过时间外插得到, 当物理量随时间非线性变化时计算误差比较大, 会带来计算噪声, 引起模式积分不稳定。基于半隐式算法计算非线性项时, 也需要时间外插, 同样会带来类似的问题。如将式(1)按照半拉格朗日思路展开
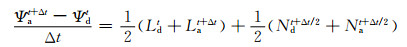
|
(2) |
式中, 下标a、d分别代表到达点和上游点, L项部分参与方程推导隐式求解, N项部分需要利用时间外插显式求解, 即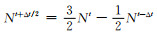
(4) 在半隐式半拉格朗日的时间积分方案中半隐式权重系数的选取非常重要。一般对模式方程组按照参考大气进行分离, 得到线性项和非线性项, 对线性项进行非中央权重的时间平均, 可以有效地抑制半拉格朗日算法带来的计算噪声, 但时间计算精度也由二阶降为一阶。如在式(2)右端取非中央权重
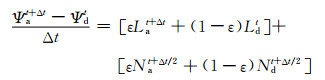
|
(3) |
式中, ε为半隐式的权重系数。部分业务模式为了保证积分的稳定性, 半隐式权重系数取得较大, 这样会造成短波系统的较强衰减, 降低模式的计算精度。Simmons(1997)提出一种针对线性项处理的二阶精度非中央权重的计算方法, 配合温度较高的等温参考大气, 在保证模式计算稳定性的情况下, 使线性项的计算可以达到二阶精度。另外, 英国气象局的ENDGame(Wood, et al, 2014a)在动力框架中将三维参考大气与预估-修正算法结合, 减小非线性项数量级的同时, 通过迭代算法减弱时间外插带来的影响, 也可以使半隐式系数取得较小, 时间积分算法接近二阶精度。
GRAPES_GFS(陈德辉等, 2006; 沈学顺等, 2011; 张华等, 2004; 张旭等, 2015)也是基于两个时间层的半隐式半拉格朗日算法构建的, 在上面几个技术环节的处理上也存在一些问题, 造成了模式速度场中有计算噪声, 框架计算的时间和空间精度都不高, 模拟的天气系统偏弱等。具体分析原因主要来自以下两个方面:
(1) GRAPES_GFS根据等温大气构造了一维的静力平衡参考大气, 且等温大气温度取得较低, 这样就造成了扰动量在高纬度地区以及模式高层量级较大, 如位势温度的扰动量在高纬度大约为40 K, 在模式面的高层可以达到200 K, 在这些区域模式的计算误差会比较大。地形的强迫作用没有通过参考大气扣除, 而是参与每一步扰动量的计算, 这样会影响气压梯度力以及半拉格朗日平流的计算精度; 过大的扰动量会导致非线性项较大, 进而增大时间外插的计算偏差, 给模式的计算精度以及稳定性带来影响。
(2) GRAPES_GFS在拉格朗日轨迹中间时刻、中间点速度计算, 以及中间时刻非线性项计算的问题上, 采用时间外插, 当质点做加速运动时计算偏差比较大, 且容易带来计算噪声。另外, 在半隐式时间离散的过程中, 线性项和非线性项的半隐式系数都取为0.72, 虽然可以保证计算的稳定性, 但是过大的中央权重系数降低了时间积分的精度, 给短波系统带来了较强的衰减, 也就造成了模式预报的天气系统偏弱。
基于GRAPES_GFS的现状以及存在的以上基本问题, 借鉴陈子通研究员在GRAPES_MESO上的工作, 在GRAPES_GFS的动力框架中引入不随时间变化的满足静力平衡的三维参考大气, 在公式推导过程中将参考大气的水平变化项放入线性项, 使线性项远大于非线性项, 保证时间积分的计算精度, 重新推导预报方程的求解过程, 使理论上更加完善和合理。后续工作将通过一定的初值构造方法使其在整个计算区域都能靠近模式大气, 并将地形的强迫作用包含在参考大气的计算部分, 提高气压梯度力和半拉格朗日平流的计算精度。但新的三维参考大气对模式初值的构造提出了更高的要求, 特别是参考大气水平平流项的计算精度以及地形强迫作用的处理面临很大的挑战。未来还将进一步结合预估-修正算法, 期待能够减小半隐式系数, 使时间积分接近二阶精度, 减小计算噪声, 提升模式的整体性能。
2 理论设计在GRAPES_GFS中引入三维参考大气之后, 需要对原GRAPES_GFS动力框架的求解过程重新进行设计, 从湿空气球坐标系下完全形式的控制方程组出发
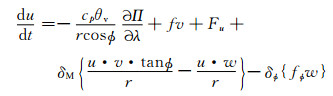
|
(4) |
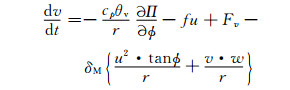
|
(5) |
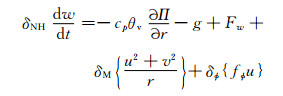
|
(6) |
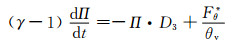
|
(7) |
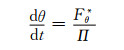
|
(8) |
式中, u、v、w为纬向、经向、垂直方向的速度矢量, Π为无量纲气压, θ为位势温度, θv为虚位势温度, λ、φ为经、纬度坐标, r为质点与地心的距离, f为科里奥利力参数, g为重力加速度, cp为定压比热容, δM为曲率修正项开关, δφ为地转偏向力开关, δNH静力平衡开关, Fu、Fv、Fw为纬向、经向、垂直方向的摩擦力, 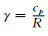
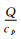
引入三维参考大气之后需要重新对控制方程进行线性化推导。因为线性化之后将方程整理为与原来类似的形式, 所以随后的时间离散化过程不需要重新推导。但由于线性项的具体表达式发生了变化, 所以需要重新推导模式预报方程组的求解过程。下面分别介绍线性化方程组的推导以及预报方程组的推导这两个部分。
2.1 线性化方程组的推导按照三维参考大气的设计思路, 在自然高度坐标系下有如下关系式
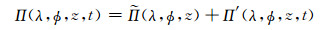
|
(9) |
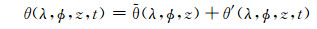
|
(10) |
式中, z为自然高度, 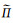
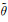
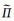
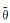
u方程, 将式(9)代入式(4)右端气压梯度力项进行线性展开, 然后将其转换到地形追随坐标下, 再令Lu、Nu分别代表u方程的线性项和非线性项, 可以将式(4)整理为
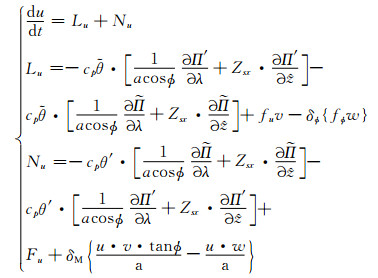
|
(11) |
式中, a为地球半径, 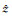
v方程的线性化过程与u方程类似
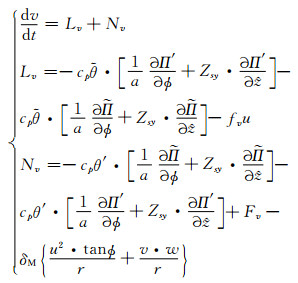
|
(12) |
式中, Lv、Nv分别代表v方程的线性项和非线性项, Zsy为坐标转换相关项(表达式略)。
w方程, 将式(9)代入式(6)右端气压梯度力项进行线性展开, 然后利用参考大气满足静力平衡抵消相关项, 再令Lw、Nw分别代表w方程的线性项和非线性项, 可以将式(6)整理为
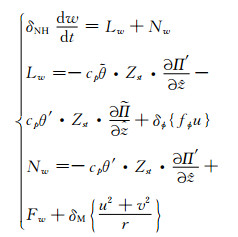
|
(13) |
式中, Zst为坐标转换相关项(表达式略)。
Π方程, 将式(7)左端Π的个别变化项在自然高度坐标系下展开
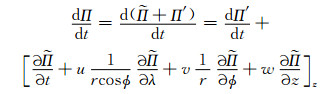
|
(14) |
考虑到参考大气不随时间发生变化, 并将式(14)右端参考大气沿x、y、z方向的平流项转换到地形追随坐标, 然后进行整理, 抵消相应的坐标转换项之后, 得到Π在地形追随坐标下的个别变化形式
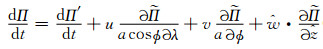
|
(15) |
式中, 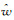
将式(7)右端散度项转换到地形追随坐标, 并代入式(9)进行线性展开
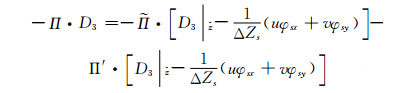
|
(16) |
式中, ΔZs为坐标转换相关项(表达式略), φsx、φsy为地形沿x、y方向的坡度。
将式(15)、(16)代入式(7), 令LΠ、NΠ分别代表Π方程线性项和非线性项, 然后进行整理可得
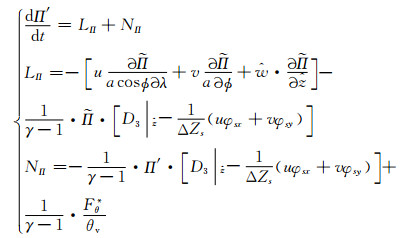
|
(17) |
θ方程的线性化过程与Π方程类似
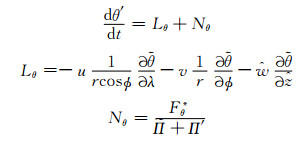
|
(18) |
式中, Lθ、Nθ分别代表θ方程线性项和非线性项。
在式(17)、(18)中都将参考大气的水平平流项放入线性项部分, 虽然这样会导致后续求解过程较为复杂, 但可以保证线性项远大于非线性项, 确保了线性化过程的合理; 反之, 若将其放入非线性项, 虽然后续求解过程大为简化, 但非线性项将大于线性项, 时间离散过程的计算精度将大幅度降低, 同时模式也容易不稳定, 背离了利用参考大气对方程组进行线性分离的初衷。
2.2 预报方程组的推导对线性化之后的方程(11)、(12)、(13)、(17)、(18)做半隐式半拉格朗日时间离散化的处理, 并在动量方程中考虑三维矢量离散化, 可以得到如下的时间离散化之后的方程组
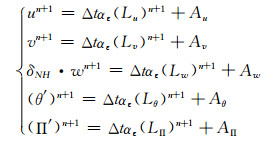
|
(19) |
式中, αε为半隐式系数, Au、Av、Aw、Aθ、AΠ为各预报方程时间离散化之后的相关项(表达式略)。
下面进一步推导模式的预报方程组。
将式(11)中Lu代入式(19)中的u方程, 整理可得
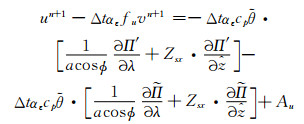
|
(20) |
将式(12)中Lv代入式(19)中的v方程, 整理可得
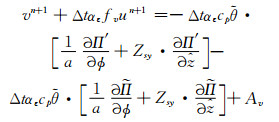
|
(21) |
做数学变换式(20)乘以Δtαεfu+式(21), 再进行整理可得
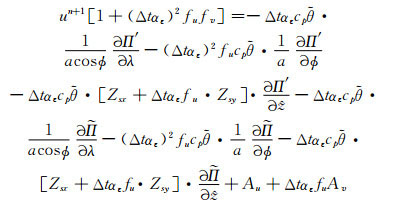
|
(22) |
将式(22)整理为u的预报方程
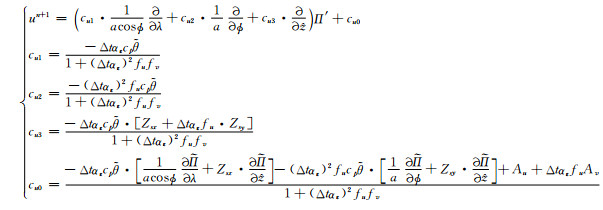
|
(23) |
式中, cu1、cu2、cu3、cu0为u预报方程的各个系数。
同理可得v的预报方程, 具体表达式略。
将式(13)中Lw代入式(19)中的w方程, 再代入自然坐标和地形追随坐标中垂直速度的关系式w= 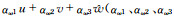
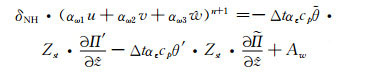
|
(24) |
将式(18)中Lθ代入式(19)中的θ方程, 可得
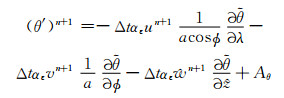
|
(25) |
将式(25)代入式(24), 整理可得
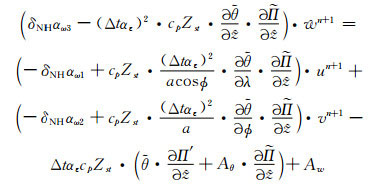
|
(26) |
再将式(23)以及v的预报方程代入式(26), 整理可得w的预报方程, 具体表达式略。
将式(23)以及v的预报方程、w的预报方程代入式(25), 整理可得θ的预报方程, 具体表达式略。
将式(17)中的LΠ代入式(19)中的Π方程, 整理可得Π的预报方程。
综合上面几个公式, 即得出模式最后的预报方程组
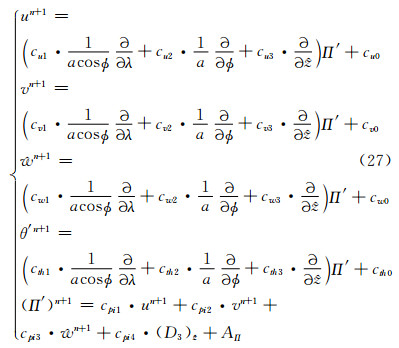
|
(27) |
式中, cv1、cv2、cv3、cv0为v预报方程的各个系数, cw1、cw2、cw3、cw0为w预报方程的各个系数, cth1、cth2、cth3、cth0为θ预报方程的各个系数, cpi1、cpi2、cpi3、cpi0为Π预报方程的各个系数。上式与原来一维参考大气情况下的模式预报方程组类似, 从形式上看区别在于θ的预报方程中出现了水平变化项, 且大部分系数的表达式都发生了变化。原来的一维参考大气情况下, cu1、cu2、cu3等不随积分时间发生变化的项中只包含参考大气的垂直变化; 现在三维参考大气中, cu1、cu2、cu3等则同时包含了参考大气的水平变化和垂直变化, cu0等每步发生变化的系数只包含量级很小的扰动量, 以此来提高框架的计算精度, 但同时也对参考大气部分的计算精度提出了很高的要求。另外, 上式可以直接套用模式中现有的赫姆霍兹方程求解器(张理论等, 2011)进行求解, 不用对繁杂的赫姆霍兹方程离散化过程做调整。求解赫姆霍兹方程得到n+1时刻的Π′之后, 代入式(24)即可得到n+1时刻的其他预报变量。
3 理想试验在GRAPES_GFS2.0版本中按照上一部分的推导引入三维参考大气之后, 通过一系列的理想试验检验该方案在模式中实现的正确性, 以及与原来基于等温大气构造的一维参考大气在计算精度等方面的差异。
3.1 平衡流试验平衡流试验中初始纬向风场与气压场之间满足地转平衡关系, 理想情况下流场不随时间发生变化, 该试验主要检验拉格朗日轨迹的计算精度, 同时兼顾气压梯度力的计算偏差等。三维参考大气的引入并不涉及拉格朗日轨迹的计算, 此处主要利用平衡流试验初步检验代码实现的正确性以及气压梯度力的计算精度。试验采用0.5°×0.5°水平分辨率, 垂直方向36层均匀分层, 层高400 m, 时间步长600 s, 积分30 d。其他具体的初值设置方法参考薛纪善等(2008)。
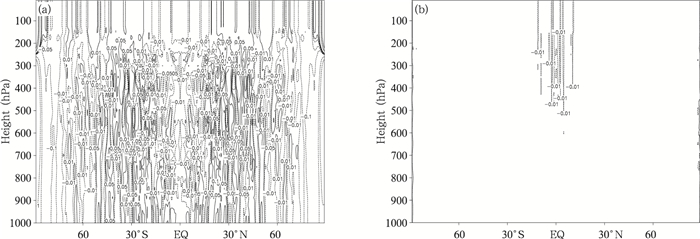
GRAPES_GFS采用一维参考大气的情况下, 在平衡流理想试验中基本可以保持住初始场的流型不发生变化, 积分30 d, 地面气压的变化大概在0.1 hPa以内(图 1a), u风场的变化大概在0.1 m/s之内, 但大部分计算区域都有这种量级的计算偏差(图 2a)。采用三维参考大气之后, 极大地减小了平衡流理想试验的计算偏差, 地面气压只在赤道和极区附近有约0.005 hPa的偏差(图 1b), u风场的偏差只存在于低纬度地区的高层和极区(图 2b), 明显优于一维参考大气。另外, 在30 d积分的过程中, 一维参考大气和三维参考大气的两组试验都可以保证质量场的严格守恒。

|
| 图 1 平衡流试验积分30 d ps的偏差 (a.一维参考大气, b.三维参考大气; 单位:hPa) Figure 1 Biases of ps in the balance flow experiment after 30 d of integration (a.1D reference profile, b.3D reference profile; unit:hPa) |
|
| 图 2 平衡流试验积分30 d u偏差的纬向平均垂直剖面 (a.一维参考大气, b.三维参考大气; 单位:m/s) Figure 2 Zonal mean vertical sections of bias of u in the balance flow experiment after 30 d integration (a.1D reference profile, b.3D reference profile; unit:m/s) |
DCMIP(Dynamical Core Model Intercomparison Project)的一个主要目的是通过一系列的理想试验对比各国模式动力框架的性能差异, 本研究工作选取其中的第20号试验, 即气压梯度力的计算精度测试, 主要考察静止大气中陡峭地形处的气压梯度力计算偏差。具体的初值设计参考Ullrich等(2012), 这里选择的试验参数为1.0°×1.0°水平分辨率, 30层均匀垂直分层, 层高400 m, 时间步长600 s, 积分6 d。
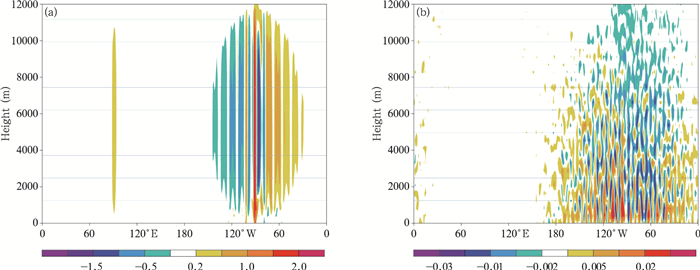
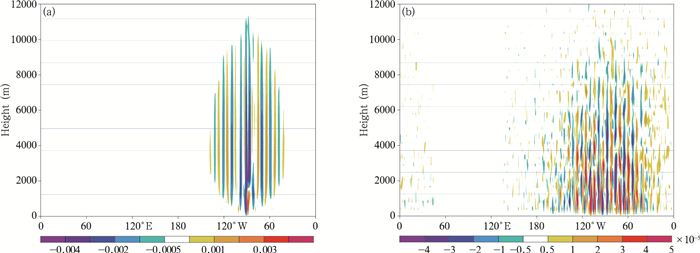
理想情况下, 模式大气应该始终保持初值的静止状态, 但是对于一个离散化的数值模型来说, 做到这一点非常困难, 陡峭地形处坐标转换以及数值离散的偏差会使气压梯度力发生变化, 进而激发出一定的大气运动, 这种运动越小, 代表模式的计算误差越小。DCMIP的试验结果在该网址均有展示(https://www.earthsystemcog.org/projects/dcmip-2012/), 约7家模式提供了该20号试验的模拟结果, 对比可以看出, 各国模式的表现差异较大, 德国气象局的ICON(ICOsahedral Non-hydrostatic)模式、法国气象局的DYNAMICO(Dynamic Adaptive, Monitoring and Control Objectives model)模式表现较好, 计算误差激发的水平风速非常小, 量级约在0.001 m/s之内; 英国气象局的ENDGAME(Even Newer Dynamics for General atmospheric modelling environment)模式和美国的FV3(Finite Volume model on the cubed-sphere grid)模式结果类似, 激发出的水平风速和地形有很高的相关, 且呈连续规则的分布, 量级约在0.1 m/s; 美国MPAS(Model for Prediciton Across Scales)模式的结果中有比较明显的计算噪声, 美国CAM(Community Atmosphere Model)的谱模式计算误差较大, 且传播到了整个计算区域。将本研究中的两组试验结果与上面各家结果进行对比可以看出, GRAPES_GFS采用一维参考大气时气压梯度力的计算误差较大, 激发出的水平风速(图 3a)达到了2 m/s, 略大于前面提到的CAM, 但u场和w场(图 4a)都与地形呈现较强的相关; 采用三维参考大气时可以很好地控制气压梯度力的计算误差, 水平风速(图 3b)控制在0.02 m/s之内, 仅次于ICON的试验结果, u场和w场(图 4b)的结构与地形都呈现出一定的相关, 但其分布都不连续, 类似于MPAS的试验结果。
|
| 图 3 DCMIP_20试验积分6 d后模式面u沿赤道的垂直剖面 (a.一维参考大气, b.三维参考大气; 单位:m/s) Figure 3 Vertical sections of u along the equator in the DCMIP_20 experiment after 6 d of integration (a.1D reference profile, b.3D reference profile; unit:m/s) |
|
| 图 4 DCMIP_20试验积分6 d后模式面w沿赤道的垂直剖面 (a.一维参考大气, b.三维参考大气; 单位:m/s) Figure 4 Vertical sections of w along the equator in the DCMIP_20 experiment after 6 days of integration (a.1D reference profile, b.3D reference profile; unit:m/s) |
该试验主要模拟天气尺度波动的传播和演变过程, 是检验数值模式动力框架的常用标准算例, 可以显示出框架在积分过程的耗散、质量守恒、相速度误差等性质。具体的试验设置请参考Jablonowski(2008)中的第4个标准算例, 这里采用1.0°×1.0°水平分辨率, 26层垂直分层, 时间步长1200 s, 积分30 d。
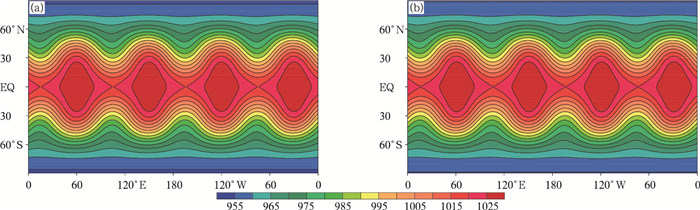
理想情况下, 初值中的4个波形在自西向东传播的过程中应该不发生衰减, 这里以Wan(2009)中提供的谱模式ECHAM(ECmwf, HAMburg)的计算结果做为参照, 该文档中同时提供了ICON的结果做为对比。另外, Jablonowski(2008)也提供了美国FV3模式的计算结果。将图 5和6中的模拟结果与初值中的波形分布以及ECHAM的计算结果进行对比, 可以看到采用一维和三维参考大气的GRAPES_GFS都可以较好地模拟罗斯贝波的传播过程, 但是计算结果中波形的衰减较强, 积分15 d之后罗斯贝波的强度以及u风场的强度都有所衰减, 一维和三维参考大气的模拟结果在波形强度上基本没有差异。此外, 在本试验30 d积分过程中质量场的守恒方面, 两者表现基本相当, 全球平均的地面气压都在约0.1 hPa的范围内波动(图略)。
|
| 图 5 罗斯贝-豪威兹波试验积分15 d后的地面气压 (a.一维参考大气, b.三维参考大气; 单位:hPa) Figure 5 ps in Rossby-Haurwitz wave experiment after 15 d of integration (a.1D reference profile, b.3D reference profile; unit:hPa) |

|
| 图 6 罗斯贝-豪威兹波试验积分15 d后850 hPa的u风场 (a.一维参考大气, b.三维参考大气; 单位:m/s) Figure 6 850 hPa u in the Rossby-Haurwitz wave experiment after 15 d of integration (a.1D reference profile, b.3D reference profile; unit:m/s) |
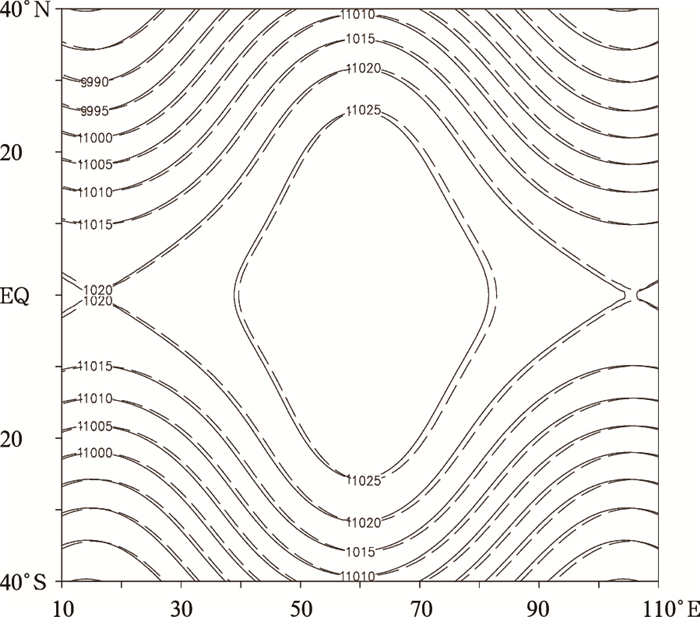
进一步考察GRAPES_GFS对波形移动速度的模拟精度, 由Jablonowski(2008)中相速度的计算公式可以得出该试验中波形每天移动约15.2°。选择子区域(40°S—40°N, 10°—110°E)进行观察, 如图 7所示, 并对比ECHAM5的计算结果, 可以看出采用一维参考大气的情况下, 模式存在一定的相速度误差, 积分15 d波形位置落后真解约1°; 采用三维参考大气的情况下, 与ECHAM5对比虽然中心强度上有一定的差异, 但移动位相一致, 没有相速度的计算误差。
|
| 图 7 罗斯贝-豪威兹波试验积分15 d后(40°S—40°N, 10°—110°E)的地面气压 (实线:一维参考大气, 虚线:三维参考大气; 单位:hPa) Figure 7 ps in Rossby-Haurwitz wave experiment after 15 d of integration (40°S-40°N, 10°-110°E) (Solid line:1D reference profile, dotted line:3D reference profile; unit:hPa) |
该试验主要模拟在大尺度地形的强迫作用下, 天气尺度波动是如何产生、演变和消亡的, 具体的试验设置参考Jablonowski(2008)中的第5个标准算例, 这里采用0.5°×0.5°水平分辨率, 60层均匀垂直分层, 层高400 m, 时间步长600 s, 积分15 d。
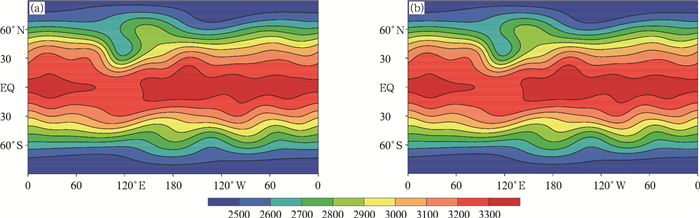
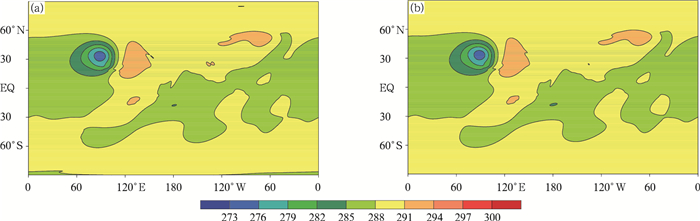
初值中的山脉在纬向的水平风场中激发出一定的涡旋运动, 逐渐演变为向山脉下游传播的波列。这里同样以Wan(2009)中提供的谱模式ECHAM的计算结果做为参照, 该文档中同时提供了ICON的结果做为对比, 并参考Jablonowski(2008)中NCAR FV3模式的计算结果。将图 8和9的计算结果与上述模式进行对比, 可以看出GRAPES_GFS在采用一维参考大气或者三维参考大气的情况下, 都可以模拟出山脉激发的罗斯贝波的产生、传播和消亡过程, 积分15 d之后700 hPa的高度场(图 8)、温度场(图 9)的分布形式、波列位置等与ECHAM保持一致, 但两组试验在山脉下游模拟出的天气尺度槽和脊的强度弱于ECHAM等模式。
|
| 图 8 山脉激发罗斯贝波试验积分15 d后700 hPa高度场(a.一维参考大气, b.三维参考大气; 单位:gpm) Figure 8 700 hPa height in Mountain-induced Rossby wave experiment after 15 d of integration (a.1D reference profile, b.3D reference profile; unit:gpm) |
|
| 图 9 山脉激发罗斯贝波试验积分15 d后700 hPa温度场(a.一维参考大气, b.三维参考大气; 单位:K) Figure 9 700 hPa temperature in Mountain-induced Rossby wave experiment after 15 d of integration (a.1D reference profile, b.3D reference profile; unit:K) |
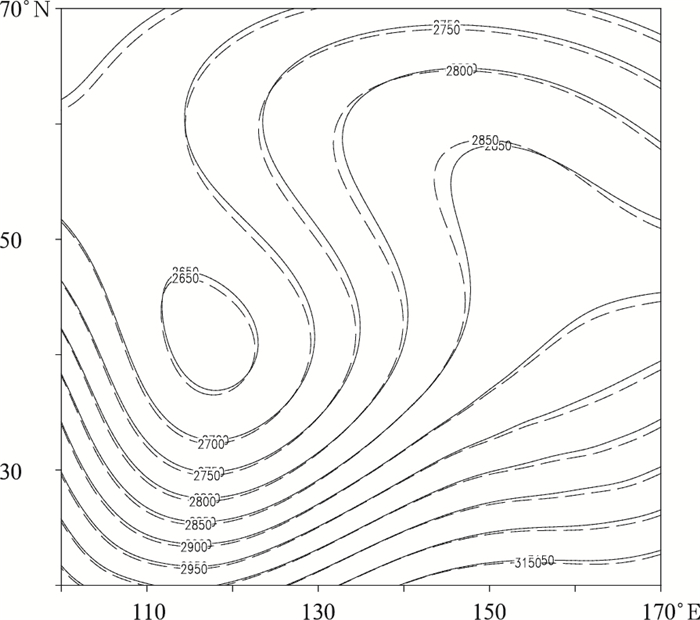
鉴于本研究中的两组试验模拟的700 hPa高度场中山脉下游区域的槽和脊相对于ECHAM5都偏弱, 选取该区域进一步仔细对比两组试验的差异, 如图 10所示, 三维参考大气模拟的槽和脊相对于一维参考大气较强, 在一定程度上缓解了系统偏弱的问题。
|
| 图 10 山脉激发罗斯贝波试验积分15 d后(20°—70°N, 100°—170°E)的700 hPa高度场 (实线:一维参考大气, 虚线:三维参考大气; 单位:gpm) Figure 10 700 hPa height in Mountain-induced Rossby wave experiment after 15 d of integration (20°-70°N, 100°-170°E) (Solid line:1D reference profile, dotted line:3D reference profile; unit:gpm) |
本研究针对GRAPES_GFS中基于等温大气构造的一维参考大气计算精度较低、扰动量过大进而影响计算稳定性等问题, 引入基于初值构造的满足静力平衡且不随时间发生变化的三维参考大气, 重新推导了动力框架中线性化分离以及预报方程组的求解过程, 通过若干个理想试验验证了理论方法以及代码编程的正确性, 并可以直观地说明新的三维参考大气相对于原来的一维参考大气, 在空间计算精度上有明显优势, 特别是复杂地形处气压梯度力的计算偏差更小, 同时在系统移动速度的计算上更加准确, 另外还可以缓解原来系统预报偏弱的问题。
对采用三维参考大气之后的动力框架进行更进一步的分析:
(1) 动力学方程组离散过程中的线性化处理要求线性项远大于非线性项, 若非线性项过大, 会放大半隐式处理中时间外插的偏差, 导致时间积分算法精度降低的同时带来计算噪声, 容易引起模式积分不稳定。采用基于等温大气构造的一维参考大气的情况, 为了保证中低纬度地区低层的计算精度, 一般使θ′或者Π′在这些区域较小, 也就无法兼顾高纬度和高层区域, 如模式面高层的θ′会高达200 K左右, 进而造成非线性项在高层或者高纬度区域非常大, 前面提到的问题非常明显。采用三维参考大气之后, 基于一定的初值构造方法, 可以保证θ′和Π′在所有的计算区域都非常小, 进而确保非线性项在所有的计算区域都远小于线性项, 提高空间计算精度的同时也能提供时间积分的计算精度, 减小非线性项外插的偏差。如果将三维参考大气与预估修正算法结合, 通过减小非线性项的数量级, 可以提高预估修正算法的精度, 进一步发挥其优势。
(2) 模式采用一维参考大气的情况下, 只需考虑参考大气在垂直方向的变化, 再考虑到参考大气满足静力平衡, 很容易做到参考大气部分的高精度计算, 模式计算的关键点和困难点在扰动量的精确计算上。采用三维参考大气之后, 扰动量的数量级大幅度减小, 其在整个积分过程中的重要性也明显降低, 反之参考大气部分出现了水平变化项, 在动力学方程组的求解过程中占据重要部分, 其精确计算对整个积分过程至关重要。因此, 采用三维参考大气的情况下, 如何科学合理地构造初值中参考大气的分布, 以及高精度的计算参考大气的水平变化等相关过程变得非常重要。
(3) 半拉格朗日模式中地形强迫作用的处理一直是一个关键点, 模式采用三维参考大气的情况下, 地形的强迫作用被包含在参考大气部分进行计算。实际个例预报的情况下, 如果大地形处参考大气相关的坐标转换、气压梯度力等计算精度不高, 就会产生一个持续的、不随时间变化的误差源, 导致这些区域的模拟效果逐渐地变差, 最终影响整个模式的预报性能。所以三维参考大气初值构造的关键点就在于地形强迫作用的精确计算。本研究工作主要基于理想试验, 后续工作中会对此问题进行深入的研究。
(4) 构造参考大气的基本考虑是使参考大气尽量地靠近模式大气, 减小扰动量的数量级, 提高空间、时间计算精度。本研究工作采用不随时间发生变化的三维参考大气, 虽然可以保证初始时刻参考大气靠近模式大气, 但是在长时间积分的情况下, 模式大气势必逐渐远离参考大气。所以可以基于现有的方法, 进一步考虑随时间发生变化的参考大气, 在动力学方程组求解的过程中, 加入参考大气随时间的变化项, 重新推导方程的求解过程。该方法需要在每步积分开始时刻都重新构造三维参考大气的分布, 并计算相关的水平变化等过程, 会增加模式的整体计算量, 但在一定程度上可以进一步的提高模式的计算精度。
本研究工作主要介绍了在GRAPES_GFS中引入三维参考大气相关的理论设计和实现方法, 通过若干个理想试验验证了方法实现的正确性, 并显示出其相对于一维参考大气的优越性。后续工作将主要着眼于采用三维参考大气情况下模式初值的构造方法, 特别是地形强迫作用的处理, 并通过连续的循环预报试验, 深入地分析三维参考大气对模式整体预报性能带来的影响。
| 陈德辉, 沈学顺. 2006. 新一代数值预报系统GRAPES研究进展. 应用气象学报, 17(6): 773–777. Chen D H, Shen X S. 2006. Recent progress on GRAPES research and application. J Appl Meteor Sci, 17(6): 773–777. DOI:10.11898/1001-7313.20060614 (in Chinese) |
| 沈学顺, 王明欢, 肖锋. 2011. GRAPES模式中高精度正定保形物质平流方案的研究Ⅰ:理论方案设计与理想试验. 气象学报, 69(1): 1–15. Shen X S, Wang M H, Xiao F. 2011. A study of the high-order accuracy and positive-definite conformal advection scheme in the GRAPES model Ⅰ:Scientific design and idealized tests. Acta Meteor Sinica, 69(1): 1–15. (in Chinese) |
| 王斌, 季仲贞. 2006. 大气科学中的数值新方法及其应用. 北京: 科学出版社: 171-177. Wang B, Ji Z Z. 2006. The New Numerical Method and Its Application in Atmospheric Science. Beijing: Science Press: 171-177. |
| 薛纪善, 陈德辉, 沈学顺, 等. 2008. 数值预报系统GRAPES的科学设计与应用. 北京: 科学出版社: 65-119. Xue J S, Chen D H, Shen X S, et al. 2008. The Scientific Design and Application of Numerical Forecast System GRAPES. Beijing: Science Press: 65-119. |
| 张华, 薛纪善, 庄世宇, 等. 2004. GRAPES三维变分同化系统的理想试验. 气象学报, 62(1): 31–41. Zhang H, Xue J S, Zhuang S Y, et al. 2004. Idea experiments of GRAPES three-dimensional variational data assimilation system. Acta Meteor Sinica, 62(1): 31–41. DOI:10.11676/qxxb2004.004 (in Chinese) |
| 张理论, 宋君强, 赵文涛, 等. 2011. 基于并行可扩展科学计算工具集求解GRAPES全球非静力模式亥姆霍兹问题. 气象学报, 69(3): 432–439. Zhang L L, Song J Q, Zhao W T, et al. 2011. Solving Helmholtz equations of the GRAPES global nonhydrostatic model based on the PETSc. Acta Meteor Sinica, 69(3): 432–439. DOI:10.11676/qxxb2011.037 (in Chinese) |
| 张旭, 黄伟, 陈葆德. 2015. 二阶精度半隐式半拉格朗日轨迹计算和时间积分方案在GRAPES区域模式中的应用. 气象学报, 73(3): 557–565. Zhang X, Huang W, Chen B D. 2015. Implementation of a 2nd order semi-implicit semi-Lagrangian trajectory algorithm and time integration scheme in the GRAPES regional model. Acta Meteor Sinica, 73(3): 557–565. DOI:10.11676/qxxb2015.023 (in Chinese) |
| Bénard P. 2003. Stability of semi-implicit and iterative centered-implicit time discretizations for various equation systems used in NWP. Mon Wea Rev, 131(10): 2479–2491. DOI:10.1175/1520-0493(2003)131<2479:SOSAIC>2.0.CO;2 |
| Chen J B, Simmons A J. 1990. Sensitivity of medium-range weather forecasts to the use of reference atmosphere. Adv Atmos Sci, 7(3): 275–293. DOI:10.1007/BF03179761 |
| Côté J, Gravel S, Méthot A, et al. 1998. The operational CMC-MRB Global Environmental Multiscale (GEM) model. Part Ⅰ:design considerations and formulation. Mon Wea Rev, 126(6): 1373–1395. |
| Diamantakis M. 2013. The semi-Lagrangian technique in atmospheric modelling:Current status and future challenges//ECMWF Seminar in Numerical Methods for Atmosphere and Ocean Modelling. ECMWF: 4–9. |
| Durran D R, Bretherton C. 2004. Comments on "the roles of the horizontal component of the earth's angular velocity in nonhydrostatic linear models". J Atmos Sci, 61(15): 1982–1986. DOI:10.1175/1520-0469(2004)061<1982:COTROT>2.0.CO;2 |
| Hortal M. 2002. The development and testing of a new two-time-level semi-Lagrangian scheme (SETTLS) in the ECMWF forecast model. Quart J Roy Meteor Soc, 128(583): 1671–1687. DOI:10.1002/(ISSN)1477-870X |
| Jablonowski C, Lauritzen P, Nair R, et al. 2008. Idealized test cases for the dynamical cores of Atmospheric General Circulation Models:A proposal for the NCAR ASP 2008 summer colloquium. NCAR ASP Summer Colloquium: 28–34. |
| Lafore J P, Stein J, Asencio N, et al. 1997. The Meso-NH atmospheric simulation system. Part Ⅰ:Adiabatic formulation and control simulations. Ann Geophys, 16(1): 90–109. |
| Ritchie H, Tanguay M. 1996. A comparison of spatially averaged Eulerian and semi-Lagrangian treatments of mountains. Mon Wea Rev, 124(1): 167–181. DOI:10.1175/1520-0493(1996)124<0167:ACOSAE>2.0.CO;2 |
| Rivest C, Staniforth A, Robert A. 1994. Spurious resonant response of semi-Lagrangian discretization to orographic forcing:Diagnosis and solution. Mon Wea Rev, 122(2): 366–376. DOI:10.1175/1520-0493(1994)122<0366:SRROSL>2.0.CO;2 |
| Robert A, Yee T L, Ritchie H. 1985. A semi-Lagrangian and semi-implicit numerical integration scheme for multilevel atmospheric models. Mon Wea Rev, 113(3): 388–394. DOI:10.1175/1520-0493(1985)113<0388:ASLASI>2.0.CO;2 |
| Simmons A J, Temperton C. 1997. Stability of a two-time-level semi-implicit integration scheme for gravity wave motion. Mon Wea Rev, 125(4): 600–615. DOI:10.1175/1520-0493(1997)125<0600:SOATTL>2.0.CO;2 |
| Staniforth A, Côté J. 1991. Semi-Lagrangian integration schemes for atmospheric models:A review. Mon Wea Rev, 119(9): 2206–2223. DOI:10.1175/1520-0493(1991)119<2206:SLISFA>2.0.CO;2 |
| Staniforth A, White A, Wood N, et al. 2006. Unified Model Documentation Paper No.15. Exeter, Devon, United Kingdom: Met Office: 135-198. |
| Temperton C, Hortal M, Simmons A. 2001. A two-time-level semi-Lagrangian global spectral model. Quart J Roy Meteor Soc, 127(571): 111–127. DOI:10.1002/(ISSN)1477-870X |
| Ullrich P A, Jablonowski C, Kent J, et al. 2012. Dynamical Core Model Intercomparison Project (DCMIP) test case document. DCMIP Summer School: 26–29. |
| Wan H. 2009. Developing and testing a hydrostatic atmospheric dynamical core on triangular grids[D]. Hamburg: University of Hamburg, 57-72 |
| Wood N, Staniforth A, White A, et al. 2014a. END Game formulation V4.01. Met Office: 18–59. |
| Wood N, Staniforth A, White A, et al. 2014b. An inherently mass-conserving semi-implicit semi-Lagrangian discretization of the deep-atmosphere global non-hydrostatic equations. Quart J Roy Meteor Soc, 140(682): 1505–1520. DOI:10.1002/qj.2014.140.issue-682 |
| Wu T W, Yu R C, Zhang F. 2008. A modified dynamic framework for the atmospheric spectral model and its application. J Atmos Sci, 65(7): 2235–2253. DOI:10.1175/2007JAS2514.1 |
 2018, Vol. 76
2018, Vol. 76


