中国气象学会主办。
文章信息
- 巩贺, 朱琳, 黄玫. 2017.
- GONG He, ZHU Lin, HUANG Mei. 2017.
- 基于多套再分析数据的全球山脉力矩计算及比较分析
- Calculation and comparison of global mountain torque:A study based on three reanalysis data
- 气象学报, 75(3): 471-480.
- Acta Meteorologica Sinica, 75(3): 471-480.
- http://dx.doi.org/10.11676/qxxb2017.025
-
文章历史
- 2016-10-01 收稿
- 2016-12-26 改回
2. 国家卫星气象中心, 北京, 100081;
3. 中国科学院地理科学与资源研究所, 北京, 100101
2. National Satellite Meteorological Center, China Meteorological Administration, Beijing 100081, China;
3. Institute of Geographical Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, China
山脉力矩是大气与固体地球角动量交换的途径之一。当山脉西侧存在高压,东侧气压较低时,整个气压系统会对山脉产生一个向东的力矩(负山脉力矩),并通过山脉作用于固体地球上,将角动量从大气传输到固体地球上使地球自转速率增大,大气角动量减少。反之,如果起伏地形的西侧地表面气压低于东侧,则会产生一个正的山脉力矩,从而使得大气获得轴向角动量(Weickmann, et al, 1994;Driscoll, 2010)。
Swinbank(1985)很早就证实了在短时间尺度上山脉力矩变化对大气角动量平衡影响的重要性。Madden等(1995)利用1987—1988年13个月的ECMWF(European Centre for Medium-Range Weather Forecasts)数据计算表明,山脉力矩和摩擦力矩共同作用导致了大气角动量在50 d尺度上的振荡现象,这一现象与热带季节内气候振荡密切相关,但在这一过程中,山脉力矩的贡献比摩擦力矩大3倍左右。多项研究表明,山脉力矩和摩擦力矩之和能够在很大程度上解释大气角动量的轴向变化,在季节尺度上山脉力矩更加重要(Oort, 1989; Egger, et al, 2007)。因此,山脉力矩对于分析观测和模拟的大气角动量平衡具有重要作用(Cess, et al, 1990;Huang et al, 1999, 2000; Egger, et al, 2003)。
由于大气角动量的变化与ENSO(El Nio-Southern Oscillation),MJO(Madden Julian Oscillation)等气候事件具有紧密的联系(Anderson, et al, 1983; Madden, 1987, 1988; Gutzler, et al, 1993; Lau, et al, 1989; Weickmann, et al, 1992), 因此,力矩分析方法已成为气候监测和模式偏差诊断的常用手段(Madden, et al, 1995; Weickmann, et al, 1997; Huang, et al, 1999)。例如Ponte等(1999)计算了北美和欧洲的山脉力矩变化,发现持续的正山脉力矩作用使得大气角动量在1982—1983年厄尔尼诺事件时达到正的极端峰值。作为大气轴向角动量变化的主要贡献因子,山脉力矩在空间和时间上也有其独特的变化规律。在全球气候变化的背景下,深入分析与比较全球山脉力矩时空分布及变化特征,有助于从机理上分析大气角动量变化,从而更好地了解极端气候事件的发生和气候变化。
Weickmann等(1994)、Huang等(1999, 2008)对山脉力矩进行了详细的推算,并给出了标准的计算公式。但由于以往观测技术及观测设备精度的原因,计算数值误差较大,长度较短,不能完全反映大气的动力学特征和物理意义。自从科学家们提出利用数值天气预报中的资料同化技术来恢复历史气候记录数据方法以来(Bengtsson, et al, 1988; Trenberth, et al, 1988),美国、欧盟和日本等就组织和实施了一系列研究计划,利用完善的数据同化系统将各种类型来源的观测资料与短期数值天气预报产品进行融合和最优集成,形成长时间尺度的具有高分辨率的全球大气再分析数据,以弥补高质量的全球观测资料的匮乏。但是再分析数据必然也包含有不同模式、不同同化方案和观测设备所引入的误差(苏涛等,2015)。因此,本研究将比较NCEP(National Centers for Environmental Prediction)、ECMWF和MERRA(The Modem Era Retrospective-analysis for Research and Applications)三套再分析数据计算的全球山脉力矩的时空分布特征,通过精确计算的山脉力矩,将有助于了解山脉力矩在角动量循环以及大气环流中所起的作用,对进一步分析地球与大气在不同时间尺度的相互作用机理有重要作用。
2 数据与方法 2.1 数据文中采用目前较为广泛使用的NCEP、ECMWF和MERRA三套再分析数据,具体来源如下:
(1) NCEP再分析数据
NCEP再分析数据是美国国家环境预测中心和大气研究中心(NCEP/NCAR)开发的第一套再分析资料(Kalnay, et al, 1996),这是最早发展的全球再分析资料,其利用全球谱模式(GSM)和三维变分同化技术对观测资料进行同化,以T62格式输出,时间分辨率为6 h。文中将其地表面气压自然对数的第一光谱系数和地形高度数据转化成高斯格点数据来计算全球山脉力矩。计算出的全球山脉力矩时间分辨率为1 d,空间分辨率为192×94高斯格点。
(2) ECMWF再分析数据
ECMWF再分析数据是由欧洲中期天气预报中心(ECMWF)提供的ERA-Interim再分析资料(Dee, et al,2011)。利用其地表位势数据和逐6 h的地表面气压数据计算山脉力矩。计算出的全球山脉力矩时间分辨率为1 d,空间分辨率为0.75°×0.75°。
(3) MERRA再分析数据
MERRA再分析数据是由NASA (National Aeronautics and Space Administration)戈达德地球科学数据和信息服务中心(Goddard Earth Sciences Data and Information Services Center, GESDISC)提供。MERRA数据使用GEOS-5大气模式和资料同化系统,以卫星观测数据为气候背景,改善了前几代再分析资料中的水文循环(Reinecker, et al, 2007)。利用其中的MAI6NPANA数据集(MERRA Data Assimilation System 3-Dimensional analyzed state on pressure)计算全球山脉力矩,全球为540×361个格点,空间分辨率为2/3°经度×1/2°纬度,地表面气压的时间分辨率为6 h。
所使用的环流指数数据来自中国国家气候中心气候系统诊断预测室,时段为1951—2012年。
2.2 山脉力矩计算方法全球积分形式的山脉力矩可用以下形式计算(Weickmann, et al, 1994; Huang, et al, 1999)
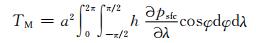
|
(1) |
为了优化计算机运算过程,山脉力矩计算公式亦可写为
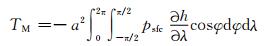
|
(2) |
式中,a为地球半径(单位为m),psfc为地表面气压(单位为Pa),h为地形高度(单位为m),λ为经度,φ为纬度。为了优化图形显示,文中山脉力矩以Hadley为单位,1 Hadley=1.0×1018 kg·m2/s2。
利用NCEP数据计算了总的轴向大气角动量(Madden, et al, 1995;Egger, et al, 2007)
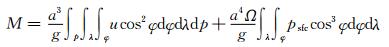
|
(3) |
式中,u为纬向风速(单位m/s),g为重力加速度(取9.8 m/s2),Ω为地球自转角速度,式中第1项为由风速变化引起的大气角动量变化,第2项为大气质量重分配导致的大气角动量变化。
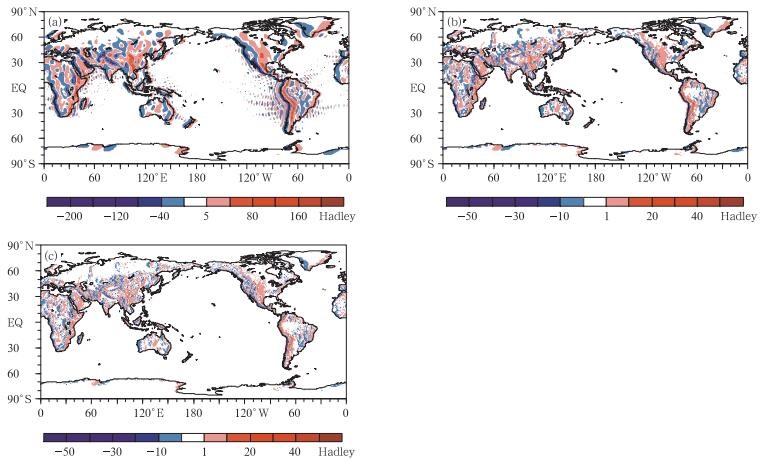
3 结果与讨论 3.1 全球山脉力矩空间分布比较图 1为基于三套数据计算的1979—2012年平均全球山脉力矩空间分布。三套数据的空间分布基本一致,山脉力矩主要分布在亚洲中部、北美洲、南美洲、非洲和大洋洲等中高纬度地区。山脉力矩的最大值出现在南美洲安第斯山脉东侧(21.9°S,63.75°W),最小值出现在南美洲安第斯山脉西侧(20°S,67.5°W),这一结果与以往研究结果一致(Iskenderian, et al, 1998;Weickmann, 2003;Egger, et al, 2007)。非洲地区和大洋洲地区山脉力矩对全球力矩的贡献较弱,北半球的青藏高原、落基山脉以及南半球的安第斯山脉是对全球山脉力矩贡献最大的三个地区。
|
| (a.NCEP再分析数据,b.ECMWF再分析数据,c.MERRA再分析数据) 图 1 基于不同数据计算的1979—2012年平均全球山脉力矩空间分布 (a. NCEP Reanalysis, b. ECMWF Reanalysis, c. MERRA Reanalysis) Figure 1 Spatial distribution of the mountain torque in 1979-2012 |
不同再分析资料计算的山脉力矩的数值空间差别较大。NCEP数据计算出的山脉力矩的空间差别最大,为-243—207 Hadley,其次是ECMWF数据计算出的山脉力矩,其空间数值差别为-88.62—67.86 Hadley。MERRA数据计算结果的空间差别最小,为-69.30—54.85 Hadley。
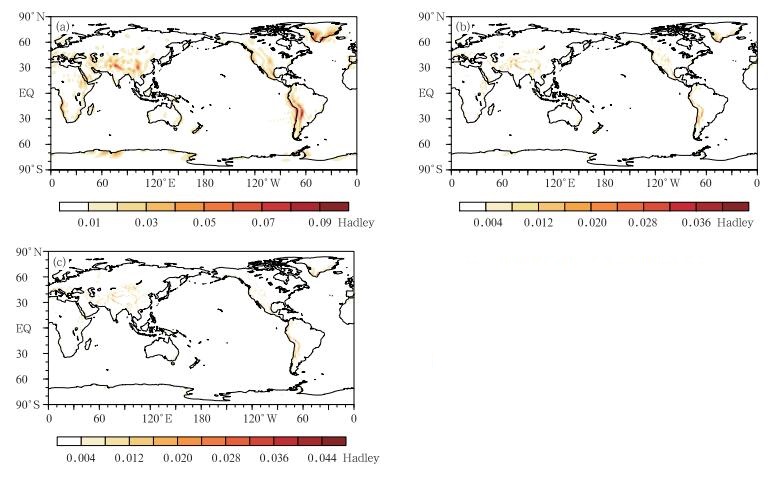
3.2 山脉力矩标准差的空间分布比较为了进一步研究各套资料计算的山脉力矩空间分布上的差异以及数据精度,对1979—2012年各套资料计算的山脉力矩空间上各点进行了标准差计算(图 2)。空间上任意一点(i,j)位置上的山脉力矩标准差为
|
| (a.NCEP再分析数据,b.ECMWF再分析数据,c.MERRA再分析数据) 图 2 1979—2012年各套数据计算的山脉力矩标准差的空间分布 (a. NCEP Reanalysis, b. ECMWF Reanalysis, c. MERRA Reanalysis) Figure 2 Spatial distributions of mountain torque standard deviation based on three datasets in 1979-2012 |
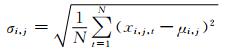
|
(4) |
式中,N为总的年数,文中为34年,μi, j为(i,j)位置上的所有年份山脉力矩的平均值,xi, j, t为此位置上第t年的山脉力矩数据(Bland, et al, 1996)。
三套数据计算的山脉力矩标准差在空间分布上基本一致,即山脉力矩标准差大的地方主要位于亚洲的青藏高原、南美洲的安第斯山脉、北美洲的落基山脉和格陵兰岛附近。NCEP数据计算的山脉力矩标准差数值最大,表明其计算的山脉力矩年际间波动较大。ECMWF数据和MERRA数据计算的山脉力矩标准差数值比较接近,皆小于NCEP数据计算的标准差。
在处理地形数据时,ECMWF和MERRA数据计算的山脉力矩均采用了地表位势高度除以重力加速度(g)来得到近似的地形高度数据,而NCEP数据则采用了实际的地形数据。因此NCEP数据计算的山脉力矩标准差不受地形影响,其力矩计算误差主要来源于地表面气压数据。因此NCEP数据的地表面气压的波动较大。
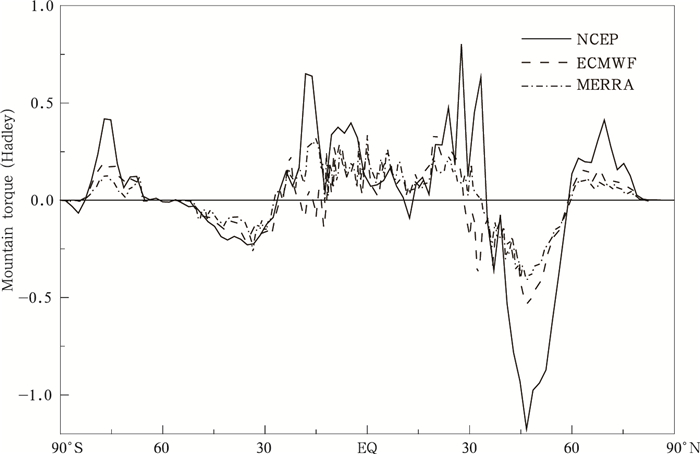
3.3 山脉力矩纬向分布特征比较从不同再分析资料计算的34年平均全球山脉力矩纬向分布(图 3)可以看出,NCEP、ECMWF和MERRA数据计算的山脉力矩表现出较为一致的纬向积分特征,即在赤道附近(30°N—20°S)存在明显的正的山脉力矩,其中30°N附近主要是青藏高原和落基山脉的贡献;而赤道以南至20°S的正的山脉力矩主要是安第斯山脉贡献。在北半球30°—60°N和南半球30°—60°S,存在明显的负山脉力矩。这与以往的研究结果一致,即在热带低纬度地区大气通过正的山脉力矩得到角动量,中高纬度地区,大气通过负的山脉力矩失去角动量(叶笃正等, 1955, 1958)。
|
| 图 3 纬向积分的全球山脉力矩(1979—2012年平均) Figure 3 Meridional profiles of zonally integrated mountain torque(1979-2012 average) |
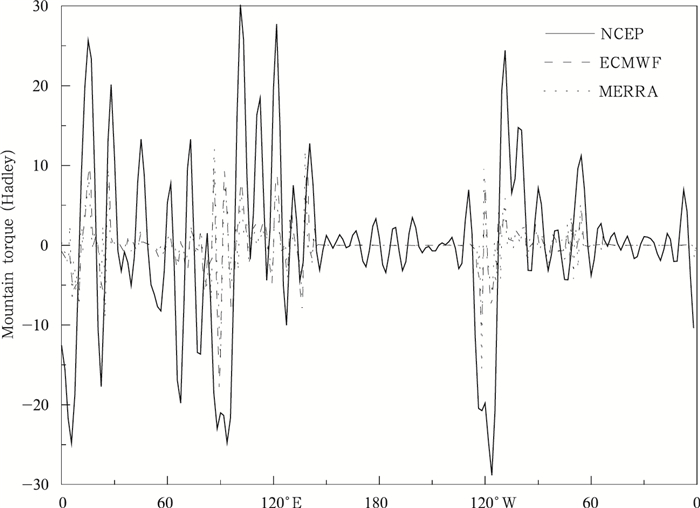
ECMWF与MERRA再分析数据计算的山脉力矩纬向积分结果差别较小,两者曲线波动基本一致。而NCEP再分析数据计算的结果与这两套数据相比,在大的形式相同的情况下,数值上下波动较大。差异较大的区域主要集中在20°—60°N和EQ—20°S。在20°—40°N、60°—80°N、EQ—20°S和70°—80°N,NCEP再分析数据计算的山脉力矩明显大于另外两套数据结果,而在40°—60°N,NCEP计算的结果明显小于另外两套数据结果,特别在47°N左右,其数值远远低于其他两种数据计算结果。为了寻找差异存在的位置,沿47°N纬线计算了三套数据的山脉力矩多年平均(图 4)。可以看出,ECMWF和MERRA数据结果基本一致。而NCEP数据在这一纬线上的5°E附近、60°—90°E和120°W附近,山脉力矩计算结果偏小,在25°E附近、90°—120°E和110°—100°W的山脉力矩计算结果偏大。从三套数据对比来看,NCEP数据在描述山脉力矩沿经线分布状态时,存在一定的误差,不利于研究小尺度小范围内山脉力矩变化。在图 4中也可看出,沿此纬线上山脉力矩波动较大的位置有3处,在其附近分别对应着欧亚浅槽、东亚大槽和北美大槽这3个北半球水平环流中的低压槽。由此可见,山脉力矩的变化与大气环流密切相关。
|
| 图 4 沿47°N纬线上的山脉力矩分布(1979—2012年平均) Figure 4 Profiles of mountain torque along 47°N(1979-2012 average) |
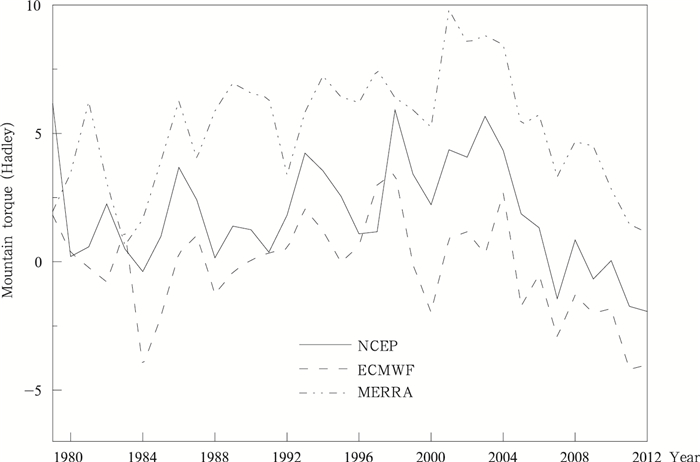
图 5比较了三套数据计算的山脉力矩的全球积分值年际变化。1979—2012年,NCEP、ECMWF和MERRA数据计算的山脉力矩时间序列的平均值分别为1.83、-0.25和5.17 Hadley,标准差分别为2.1、1.9和2.3 Hadley。期间三者力矩均呈下降趋势,下降速率分别为-0.039、-0.059和-0.03 Hadley/a。NCEP数据与ECMWF和MERRA数据计算出来的山脉力矩时间序列的相关系数分别为0.731和0.553,而ECMWF和MERRA数据计算出的山脉力矩时间序列的相关系数为0.541。
|
| 图 5 全球积分的山脉力矩年际变化 Figure 5 Annual changes in mountain torque |
由此看到,NCEP数据计算的山脉力矩虽然从空间格点上看与其他两套数据计算结果差异较大,但是经过全球积分以后,其年际变化与其他两套数据的差异并不大。因此全球积分的NCEP数据仍然具有一定的准确度,可以用来做山脉力矩的进一步分析。特别是NCEP再分析数据具有另外两套数据不一样的时间跨度,其数据可以从1948年开始,因此NCEP数据仍然是研究山脉力矩的重要数据。
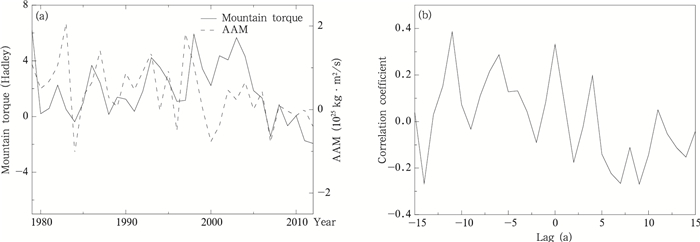
过去研究发现,在年以下时间尺度上,山脉力矩的变化导致大气角动量发生变化(Iskenderian, et al, 1998; Weickmann, et al, 2000; Weickmann, 2003; Egger, et al, 2007)。但是在年及以上时间尺度上,对二者关系研究较少。从图 6a中可以看出,全球山脉力矩与大气角动量总体变化趋势基本一致,但是不完全重合,这是因为摩擦力矩在大气角动量中具有不可忽视的作用。通过山脉力矩与大气角动量的滞后相关分析发现,两者在滞后时间为0时相关性最好(图 6b),相关系数为0.33,并且通过了显著性检验。这说明在年尺度上山脉力矩与大气角动量是同步变化的,与季节内变化特征不同。
|
| 图 6 (a)基于NCEP数据的全球山脉力矩与全球大气角动量(AAM)时间序列比较和(b)二者的滞后相关系数 Figure 6 (a) Time series of mountain torque and atmospheric angular momentum (AAM) and (b) their cross correlation coefficient |
Iskenderian等(1998)研究发现,欧亚地区和北美洲山脉力矩对北半球山脉力矩的贡献基本相同,南半球山脉力矩主要的贡献源为南美洲的安第斯山脉。文中计算的山脉力矩的空间分布也表明,青藏高原、落基山脉以及南半球的安第斯山脉的山脉力矩对全球总山脉力矩贡献较大。为了研究这三个区域内山脉力矩的年际变化,对上述山脉所处的欧亚大陆(1.5°—77°N,26°E—169.5°W)、北美洲(7.5°—71.5°N,56°—168°W)、南美洲区域(12°N—53.5°S,35°—81.5°W)的山脉力矩进行积分,然后计算其在研究时段内的距平,进一步分析三套数据的计算结果。
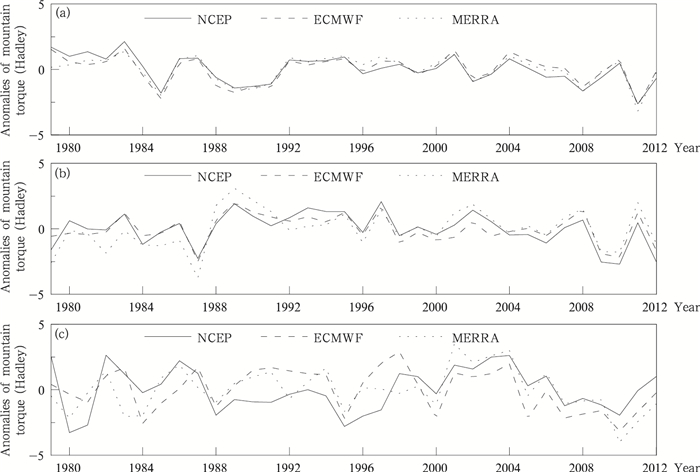
比较来看,三套再分析数据计算的北美的山脉力矩多年变化的一致性最高,变化波动基本一致(图 7a),可能是因为美国和欧洲在此区域设置的气象监测站点较密集所致。北美山脉力矩变化主要受落基山脉影响,在研究时段内呈下降趋势(-0.05 Hadley/a,P < 0.01),整体来看趋势变化不明显。1983年是北美山脉力矩的距平最高值年,该年是强厄尔尼诺年的末期。而2011年是其距平最低值年,在2011年的前一年,即2010年7月爆发了最近十几年内最强烈的拉尼娜事件。由此可见,北美地区山脉力矩的变化与厄尔尼诺和拉尼娜事件的发生有关。
|
| (a.北美,b.欧亚,c.南美) 图 7 三种再分析数据所得山脉力矩在不同区域的积分距平的多年变化 (a. North America, b. Eurasia, c. South America) Figure 7 Anomalies of mountain torque in different regions from three reanalysis datasets |
以青藏高原为主体的欧亚大陆山脉力矩年际变化在7 Hadley之间,1997年前后出现极大值,2010年出现极小值。变化范围比北美洲区域大,比南美洲小,整体变化趋势不明显。ECMWF和MERRA再分析数据计算的结果与NCEP结果差别不大。三套数据计算的山脉力矩在2005年以后一致性更好。
以安第斯山脉为主的南美洲山脉力矩变化波动在8 Hadley之间。但是相较于另外两个区域而言,三套数据在这一区域的计算一致性较差,差别较大的时段约在2000年之前,而2004年以后三者的波动基本一致。
欧亚、北美和南美地区山脉力矩的年变化与全球山脉力矩的相关系数分别为0.53、0.37和0.52。由此可知,青藏高原对全球山脉力矩变化影响最大,其次是南美洲的安第斯山脉,最后才是落基山脉。Oort等(1974)、Weickmann等(2007)、Lott等(2001)、王亚非等(2011)基于较小范围内计算也表明,北半球的青藏高原和喜马拉雅山脉是全球山脉力矩变化最为活跃的地区。三种不同再分析数据计算产生的误差大小,也进一步体现了不同区域气象观测的差别。美国和欧洲对于北美和欧洲地区气象监测最严密,仪器站点较密集,南美气象数据监测能力较弱,数据误差较明显。
3.6 山脉力矩与大气环流的关系山脉力矩作为地-气角动量交换的重要途径之一,与大气环流变化紧密相关。相关分析发现,基于NCEP数据的欧亚山脉力矩与大西洋—欧洲E型(东方型)环流相关系数为-0.684,并通过了0.01显著水平检验。当大西洋—欧洲大气环流型为E型时,欧洲由高压控制。由于欧洲地区的高压处在青藏高原西部,因而气压越强,青藏高原地区山脉力矩越低,这时大气通过山脉力矩将角动量传输给固体地球。
通过计算发现,北美地区山脉力矩还与太平洋区极涡面积有很强的相关(相关系数0.488,通过了0.01显著检验)。太平洋区极涡面积指数表征在北半球150°E—180°—120°W范围内极涡所占面积大小,当这一区域极涡面积增大时,地表极地高压范围向南扩展,同时挤压北太平洋的阿留申低压,使得落基山脉西侧气压下降,北美地区山脉力矩数值变大,大气获得角动量。利用其他两种数据也得出了相同的结论。
4 结论山脉力矩是地球和大气角动量交换的途径之一,本研究比较了NCEP/NCAR、ECMWF、MERRA三套再分析数据计算的1979—2012年全球山脉力矩数据。三套再分析数据计算的山脉力矩在不同的时空尺度上有不同的差别。由于本研究对三套再分析数据采用的数值计算方法都一样,因此计算结果差别主要由再分析数据本身的差别引起。对于再分析数据的误差评估,中外学者在不同的区域对不同的再分析数据进行了分析比较(Rusticucci, et al, 2002; Mooney, et al, 2011; Newman, et al, 2000; 赵天保等, 2004, 2010; 徐影等,2001),并按照可信度对再分析资料变量进行了分类(Kistler, et al, 2001)。再分析数据的差别主要是由采用的数值模型、同化方法以及观测仪器(观测仪器的更换或故障、观测系统的变更和观测位置改变)的差别引起的(Bengtsson, et al, 2004)。此外,不同地形数据以及不同的空间分辨率也会造成再分析数据的差别(赵天保等,2006)。本研究利用三套再分析数据进行对比分析,希望能发现和避免因再分析数据误差而可能产生的错误,体现山脉力矩真实的变化状况,通过比较得到如下研究结论:
(1) 三套再分析数据计算的山脉力矩空间分布基本一致,山脉力矩主要集中在中、低纬度地区,两极地区分布较少。这与过去的研究结果一致,即全球山脉力矩贡献最大的地方为北半球的青藏高原、落基山脉以及南半球的安第斯山脉。
(2) ECMWF和MERRA再分析数据计算的山脉力矩的纬向积分差别较小,但是与NCEP再分析数据相比则差别较大,NCEP再分析数据与这两套数据差异较大的区域主要集中在20°—60°N和EQ—20°S。
(3) NCEP再分析数据计算的山脉力矩的空间差异和年际变化明显高于其他两套数据,但从全球积分和大区域平均来看,三者的平均值和标准差基本一致,说明NCEP再分析数据在区域和全球尺度上的计算结果仍然具有一定的准确度。
(4) 从计算的欧亚、北美和南美三个大区域的山脉力矩来看,三套再分析数据计算的北美山脉力矩一致性最高,其次是欧亚和南美区域,表明北美的气象数据质量高于欧亚和南美。与大气环流关系的研究发现,欧亚地区山脉力矩与大西洋—欧洲环流关系密切,北美地区山脉力矩和太平洋区极涡面积有很好的相关。
| 苏涛, 封国林. 2015. 基于不同再分析资料的全球蒸发量时空变化特征分析. 中国科学:地球科学, 58(2): 255–269. Su T, Feng G L. 2015. Spatial-temporal variation characteristics of global evaporation revealed by eight reanalyses. Sci China:Earth Sci, 58(2): 255–269. (in Chinese) |
| 王亚非, 魏东, 李琰. 2011. 1998年5-6月区域大气角动量收支与东亚天气尺度系统变化. 高原气象, 30(5): 1189–1194. Wang Y F, Wei D, Li Y. 2011. Relationship between variability of the regional AAM torque and synoptic scale system over East Asia in May and June 1998. Plateau Meteor, 30(5): 1189–1194. (in Chinese) |
| 徐影, 丁一汇, 赵宗慈. 2001. 美国NCEP/NCAR近50年全球再分析资料在我国气候变化研究中可信度的初步分析. 应用气象学报, 12(3): 337–347. Xu Y, Ding Y H, Zhao Z C. 2001. Confidence analysis of NCEP/NCAR 50 year global reanalyzed data in climate change research in China. Quart J Appl Meteor, 12(3): 337–347. (in Chinese) |
| 叶笃正, 杨大升. 1955. 北半球大气中角动量的年变化和它的输送机构. 气象学报, 26(4): 281–294. Yeh T C, Yang T C. 1955. The annual variation of the atmospheric angular momentum of Northern Hemisphere and the mechanism of its transfer. Acta Meteor Sinica, 26(4): 281–294. DOI:10.11676/qxxb1955.010 (in Chinese) |
| 叶笃正, 朱抱真. 1958. 大气环流的若干基本问题. 北京: 科学出版社: 89-104. Yeh T C, Zhu B Z. 1958. Some Basic Problems of Atmospheric Circulation. Beijing: Science Press: 89-104. |
| 赵天保, 艾丽坤, 冯锦明. 2004. NCEP再分析资料和中国站点观测资料的分析与比较. 气候与环境研究, 9(2): 278–294. Zhao T B, Ai L K, Feng J M. 2004. An intercomparison between NCEP reanalysis and observed data over China. Climatic Environ Res, 9(2): 278–294. (in Chinese) |
| 赵天保, 符淙斌. 2006. 中国区域ERA-40、NCEP-2再分析资料与观测资料的初步比较与分析. 气候与环境研究, 11(1): 14–32. Zhao T B, Fu C B. 2006. Preliminary comparison and analysis between ERA-40, NCEP-2 reanalysis and observations over China. Climatic Environ Res, 11(1): 14–32. (in Chinese) |
| 赵天保, 符淙斌, 柯宗建, 等. 2010. 全球大气再分析资料的研究现状与进展. 地球科学进展, 25(3): 242–254. Zhao T B, Fu C B, Ke Z J, et al. 2010. Global atmosphere reanalysis datasets:Current status and recent advances. Adv Earth Sci, 25(3): 242–254. (in Chinese) |
| Anderson J R, Rosen R D. 1983. The latitude-height structure of 40-50 day variations in atmospheric angular momentum. J Atmos Sci, 40(6): 1584–1591. DOI:10.1175/1520-0469(1983)040<1584:TLHSOD>2.0.CO;2 |
| Bengtsson L, Shukla J. 1988. Integration of space and in situ observations to study global climate change. Bull Amer Meteor Soc, 69(10): 1130–1143. DOI:10.1175/1520-0477(1988)069<1130:IOSAIS>2.0.CO;2 |
| Bengtsson L, Hagemann S, Hodges K I. 2004. Can climate trends be calculated from reanalysis data. J Geophys Res, 109(D11): D11111. DOI:10.1029/2004JD004536 |
| Bland J M, Altman D G. 1996. Statistics notes:Measurement error. BMJ, 313(7059): 744. |
| Cess R D, Potter G L, Blanchet J P, et al. 1990. Intercomparison and interpretation of climate feedback processes in 19 atmospheric general circulation models. J Geophys Res, 95(D10): 16601–16615. DOI:10.1029/JD095iD10p16601 |
| Dee D, Uppala S M, Simmons A J, et al. 2011. The ERA-Interim reanalysis:Configuration and performance of the data assimilation system. Quart J Roy Meteor Soc, 137(656): 553–597. DOI:10.1002/qj.v137.656 |
| Driscoll S. 2010. The earth's atmospheric angular momentum budget and its representation in reanalysis observation datasets and climate models[D]. Reading:University of Reading |
| Egger J, Hoinka K P, Weickmann K, et al. 2003. Angular momentum budgets based on NCEP and ECMWF reanalysis data:An intercomparison. Mon Wea Rev, 131(11): 2577–2585. DOI:10.1175/1520-0493(2003)131<2577:AMBBON>2.0.CO;2 |
| Egger J, Weickmann K, Hoinka K P. 2007. Angular momentum in the global atmospheric circulation. Rev Geophys, 45(4): RG4007. |
| Gutzler D S, Madden R A. 1993. Seasonal variations of the 40-50-day oscillation in atmospheric angular momentum. J Atmos Sci, 50(6): 850–860. DOI:10.1175/1520-0469(1993)050<0850:SVOTDO>2.0.CO;2 |
| Huang H P, Sardeshmukh P D, Weickmann K M. 1999. The balance of global angular momentum in a long-term atmospheric data set. J Geophys Res, 104(D2): 2031–2040. DOI:10.1029/1998JD200068 |
| Huang H P, Sardeshmukh P D. 2000. Another look at the annual and semiannual cycles of atmospheric angular momentum. J Climate, 13(18): 3221–3238. DOI:10.1175/1520-0442(2000)013<3221:ALATAA>2.0.CO;2 |
| Huang H P, Weickmann K M. 2008. On the Computation of the mountain torque from gridded global datasets. Mon Wea Rev, 136(10): 4005–4009. DOI:10.1175/2008MWR2359.1 |
| Iskenderian H, Salstein D A. 1998. Regional sources of mountain torque variability and high-frequency fluctuations in atmospheric angular momentum. Mon Wea Rev, 126(6): 1681–1694. DOI:10.1175/1520-0493(1998)126<1681:RSOMTV>2.0.CO;2 |
| Kalnay E, Kanamitsu M, Kistler R, et al. 1996. The NCEP/NCAR 40-year reanalysis project. Bull Amer Meteor Soc, 77(3): 437–471. DOI:10.1175/1520-0477(1996)077<0437:TNYRP>2.0.CO;2 |
| Kistler R, Collins W, Saha S, et al. 2001. The NCEP-NCAR 50-year reanalysis:Monthly means CD-ROM and documentation. Bull Amer Meteor Soc, 82(2): 247–268. DOI:10.1175/1520-0477(2001)082<0247:TNNYRM>2.3.CO;2 |
| Lau K M, Kang I S, Sheu P J. 1989. Principal modes of intraseasonal variations in atmospheric angular momentum and tropical convection. J Geophys Res, 94(D5): 6319–6332. DOI:10.1029/JD094iD05p06319 |
| Lott F, Robertson A W, Ghil M. 2001. Mountain torques and atmospheric oscillations. Geophys Res Lett, 28(7): 1207–1210. DOI:10.1029/2000GL011829 |
| Madden R A. 1987. Relationships between changes in the length of day and the 40-to 50-day oscillation in the tropics. J Geophys Res, 92(D7): 8391–8399. DOI:10.1029/JD092iD07p08391 |
| Madden R A. 1988. Large intraseasonal variations in wind stress over the tropical Pacific. J Geophys Res, 93(D5): 5333–5340. DOI:10.1029/JD093iD05p05333 |
| Madden R A, Speth P. 1995. Estimates of atmospheric angular momentum, friction, and mountain torques during 1987-1988. J Atmos Sci, 52(21): 3681–3694. DOI:10.1175/1520-0469(1995)052<3681:EOAAMF>2.0.CO;2 |
| Mooney P A, Mulligan F J, Fealy R. 2011. Comparison of ERA-40, ERA-Interim and NCEP/NCAR reanalysis data with observed surface air temperatures over Ireland. Int J Climatol, 31(4): 545–557. DOI:10.1002/joc.v31.4 |
| Newman M, Sardeshmukh P D, Bergman J W. 2000. An assessment of the NCEP, NASA, and ECMWF reanalyses over the tropical west pacific warm pool. Bull Amer Meteor Soc, 81(1): 41–48. DOI:10.1175/1520-0477(2000)081<0041:AAOTNN>2.3.CO;2 |
| Oort A H, Bowman H D. 1974. A study of the mountain torque and its interannual variations in the Northern Hemisphere. J Atmos Sci, 31(8): 1974–1982. DOI:10.1175/1520-0469(1974)031<1974:ASOTMT>2.0.CO;2 |
| Oort A H. 1989. Angular momentum cycle in the atmosphere-ocean-solid earth system. Bull Amer Meteor Soc, 70(10): 1231–1242. DOI:10.1175/1520-0477(1989)070<1231:AMCITA>2.0.CO;2 |
| Ponte R M, Rosen R D. 1999. Torques responsible for evolution of atmospheric angular momentum during the 1982-83 El Niño. J Atmos Sci, 56(19): 3457–3462. DOI:10.1175/1520-0469(1999)056<3457:TRFEOA>2.0.CO;2 |
| Reinecker M, Suarez M, Todling R, et al. 2007. The GEOS-5 data assimilation system:A documentation of GEOS-5.0. NASA Technical Report 104606, Vol. 27 |
| Rusticucci M M, Kousky V E. 2002. A comparative study of maximum and minimum temperatures over Argentina:NCEP-NCAR reanalysis versus station data. J Climate, 15(15): 2089–2101. DOI:10.1175/1520-0442(2002)015<2089:ACSOMA>2.0.CO;2 |
| Swinbank B R. 1985. The global atmospheric angular momentum balance inferred from analyses made during the FGGE. Quart J Roy Meteor Soc, 111(470): 977–992. DOI:10.1002/qj.49711147004 |
| Trenberth K E, Olson J G. 1988. An evaluation and intercomparison of global analyses from the National Meteorological Center and the European Centre for Medium Range Weather Forecasts. Bull Amer Meteor Soc, 69(9): 1047–1057. DOI:10.1175/1520-0477(1988)069<1047:AEAIOG>2.0.CO;2 |
| Weickmann K, Khalsa S J S, Eischeid J. 1992. The atmospheric angular-momentum cycle during the tropical Madden-Julian Oscillation. Mon Wea Rev, 120(10): 2252–2263. DOI:10.1175/1520-0493(1992)120<2252:TAAMCD>2.0.CO;2 |
| Weickmann K. 2003. Mountains, the global frictional torque, and the circulation over the Pacific-North american region. Mon Wea Rev, 131(11): 2608–2622. DOI:10.1175/1520-0493(2003)131<2608:MTGFTA>2.0.CO;2 |
| Weickmann K, Berry E. 2007. A synoptic-dynamic model of subseasonal atmospheric variability. Mon Wea Rev, 135(2): 449–474. DOI:10.1175/MWR3293.1 |
| Weickmann K M, Sardeshmukh P D. 1994. The atmospheric angular momentum cycle associated with a Madden-Julian oscillation. J Atmos Sci, 51(21): 3194–3208. DOI:10.1175/1520-0469(1994)051<3194:TAAMCA>2.0.CO;2 |
| Weickmann K M, Kiladis G N, Sardeshmukh P D. 1997. The dynamics of intraseasonal atmospheric angular momentum oscillations. J Atmos Sci, 54(11): 1445–1461. DOI:10.1175/1520-0469(1997)054<1445:TDOIAA>2.0.CO;2 |
| Weickmann K M, Robinson W A, Penland C. 2000. Stochastic and oscillatory forcing of global atmospheric angular momentum. J Geophys Res, 105(D12): 15543–15557. DOI:10.1029/2000JD900198 |
 2017, Vol. 75
2017, Vol. 75


