中国气象学会主办。
文章信息
- 李磊, 张立杰, 陈柏纬 . 2016.
- LI Lei, ZHANG Lijie, CHAN Pakwai . 2016.
- 基于CFD技术的陡峭山体风场模拟方法研究
- The application of CFD techniques on the wind field simulation over steep mountains: A method study
- 气象学报, 74(4): 613-622.
- Acta Meteorologica Sinica, 74(4): 613-622.
- http://dx.doi.org/10.11676/qxxb2016.041
-
文章历史
- 2016-02-29 收稿
- 2016-04-19 改回
2. 深圳南方强天气研究重点实验室, 深圳, 518040;
3. 香港天文台, 香港, 999077
2. Shenzhen Key Laboratory of Severe Weather in South China, Shenzhen 518040, China;
3. Hong Kong Observatory, Hong Kong 999077, China
充分认识山地风场结构特征对于解决天气气候、能源利用、环境保护乃至军事指挥等多方面的理论和应用问题至关重要。中国从20世纪60年代即开始组织开展对山地问题的观测研究并持续至今, 对于理解地形对近地层风场结构的影响获得了大量认识(傅抱璞, 1963;陈长和等, 1993;郝为锋等, 2001;宋丽莉等, 2009)。与观测研究相比, 数值模拟的方法可以获得更高分辨率的风场数据, 对于分析山地风场的精细结构以及热-动力学机制有重要意义, 近20余年来随着计算机技术的普及, 出现了大量基于数值模拟方法的研究成果(齐瑛等, 1994;Uchida et al, 1999;吴涧等, 2000;黄倩等, 2007), 其中多数是基于中尺度模式展开的。然而, 中尺度模式往往存在其局限性, 多数中尺度模式对于陡峭地形都难以处理, 若不采取强制平滑, 当地形坡度大于45°时, 多数中尺度模式都会积分溢出, 这与中尺度模式在数值求解过程中主要采用结构化网格和有限差分方法有关。以区域大气模式(RAMS)为例, 为应对陡峭地形特别提出了多种平滑方法供选择, 以保证模式积分的稳定性(Walko et al, 2006), 因此对于陡峭地形即使中尺度模式能稳定积分并给出模拟结果, 也会因为模式地形与真实地形存在差异而不够准确。
近年来, 为应对陡峭地形的问题, 许多学者提出利用计算流体力学(Computational Fluid Dynamics, CFD)类模式研究山地风场问题, 并取得了不少成功的案例(程雪玲等, 2006;李磊等, 2010;Zajaczkowski et al, 2011)。由于在数值求解中采用了非结构化网格技术和有限体积法, CFD可以模拟任何复杂几何形体之上的流场结构, 在分辨率足够精细的情况下可以几乎真实地再现地形。但早期使用CFD模拟风场存在一个问题, 即通常以理想的幂指数风廓线为初始条件和边界条件, 使得来流信息不够准确。为解决这一问题, Li等(2007)提出将中尺度模式与CFD进行离线耦合, 将中尺度模式的输出结果用于驱动CFD运行, 以保障边界条件能包含更真实的上游来流信息。为解决初始场问题, Li等(2013)提出在CFD模拟中采用“二步法”:先用基于雷诺平均的稳态模拟得到初始场, 再利用基于大涡模拟的非稳态模拟研究风场的时空演变, 这一方法在以香港大屿山为对象的研究中取得了初步成功。
然而, 从实际应用情况来看, “中尺度模式/CFD”耦合的模拟方法仍有提升空间, 一些关键技术问题仍需明晰, 以便进一步建立对于“中尺度模式/CFD”耦合模拟方法的信心并将该方法推广应用, 这其中最重要的两个技术问题包括CFD模拟区域顶高设置和边界条件设置。本研究以强风背景下的香港大屿山为对象, 对上述两个问题进行了研究, 以期对“中尺度模式/CFD”耦合方法做进一步改进和提升, 从而使其能更好地用于陡峭地形风场结构和物理机制的研究。
2 研究问题 2.1 CFD解域顶高问题利用CFD模拟风场, 一般环境流体力学或建筑风工程领域的学者认为模拟区域的顶高越高越好, 例如5倍于地面障碍物的垂直高度(Cheng et al, 2011)。这主要是为了获得地面障碍物周边的整个流场结构, 避免顶边界过低影响障碍物顶部流场的准确性。然而对于真实的陡峭地形而言, 山体高度通常高达千米量级, 若CFD解域顶高设置过高, 例如达到5000 m, 会显著增加计算量而降低模拟效率。事实上, 对于真实地形, 解域顶高到底设置为多高比较合理;若只关心近地层的风场结构, 是否有必要将模式顶高设置为山体的5倍以上, 这些问题需要明确回答, 以便为将来陡峭地形风场问题的深入研究提供参考。
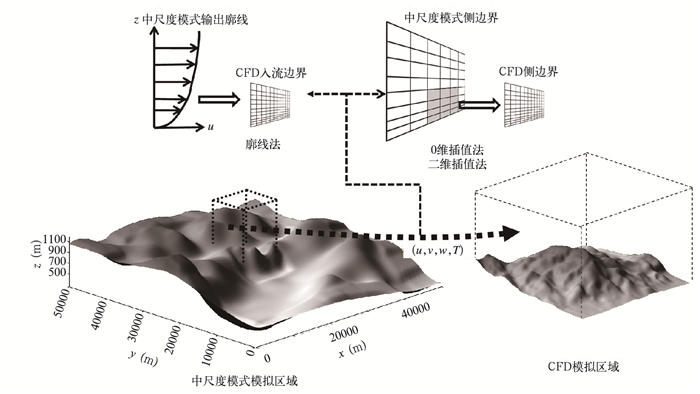
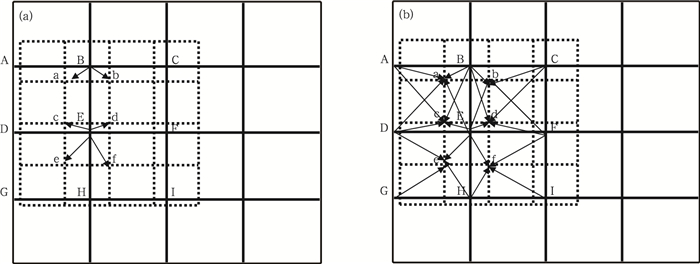
2.2 边界条件问题在“中尺度模式/CFD”耦合模拟方法中, CFD模拟区域的入流边界采用中尺度模式提供的数据, 其概念图如图 1所示。在数据从中尺度模式传递到CFD的过程中有3种可能的方法:一是“廓线法”, 即从模式中提取垂直风廓线, 并赋值给整个入流边界, 入流边界上气象要素在水平方向上大致是均匀的, 但有垂直梯度变化;二是“0维插值法”, 即将中尺度模式输出的三维场中离CFD入流边界最近的剖面上各个格点的气象要素提取出来, 再直接赋值到CFD入流边界上对应最近的格点;三是“二维插值法”, 即将前述方法二中所述的中尺度模式模拟剖面上各个格点的值通过二维插值赋值到CFD入流边界的各个格点上, 而非直接“点对点”赋值。在上述3种方法中, 第一种方法容易理解, 后两种方法可通过图 2更为直观地了解。这3种方法从难度和算法的耗时程度来讲是依次递增的, 其效果是否存在显著差别, 有待进一步探讨。需要特别说明的是, 二维插值法有多种, 本研究采用的是在地学研究中比较有代表性的克里格插值法。
|
| 图 1 “中尺度模式/CFD”耦合模拟中边界数据传递方法示意 Figure 1 The sketch map on data delivering process in Mesoscale-Model/CFD coupling simulation |
|
| 图 2 0维插值法和二维插值法示意(实线为中尺度模式网格,虚线为CFD网格;a.0维插值法,CFD每个格点上的值由最近的中尺度模式格点的值直接赋值;b.二维插值法,CFD每个格点上的值由相邻的多个中尺度模式格点的值插值得到) Figure 2 The sketch maps on zero dimensional interpolation (ZDI) method and two dimensional interpolation (TDI) method (Solid lines indicate mesoscale-model grid, and dotted lines indicate CFD grid; a. ZDI method, the data of each CFD grid point is directly fed by the most adjacent mesoscale-model grid point; b. TDI method, the data of each CFD grid point is interpolated from values at several mesoscale-model grid points) |
模拟选取时段为2011年9月29日19时(北京时, 下同)前后, 在该时段内, 台风“纳莎”过境香港, 给边界层带来了均匀而强劲的东南风, 比较适合进行边界层风场的模拟试验。
数值模拟试验选用RAMS作为中尺度模式的代表, 选用FLUENT作为CFD的代表。RAMS的模拟采用4层网格嵌套, 网格格距分别为4000、800、200和50 m, 本研究选取800 m网格距的数据驱动FLUENT进行计算。关于RAMS模拟更详细的描述可参见Chan(2014), 在此不再赘述。
对于FLUENT模拟, 鉴于边界层风速远小于声速, 故采用不可压近似的控制方程组, 如式(1)和(2)
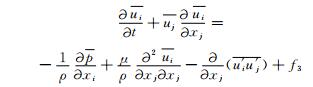
|
(1) |
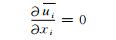
|
(2) |
式中, ui表示速度分量的平均值, u′i表示速度扰动量, i=1, 2, 3分别表示东西、南北和垂直3个方向上的分量;ρ为大气密度;f3为热力作用产生的浮力, 在本研究中考虑的背景风场为台风过境期间的强风个例, 按照Pasquill稳定度分类方法, 为大风中性层结, 故不考虑热力作用, f3取为0, 需要指出的是, 不考虑浮力是本研究的局限性所在。
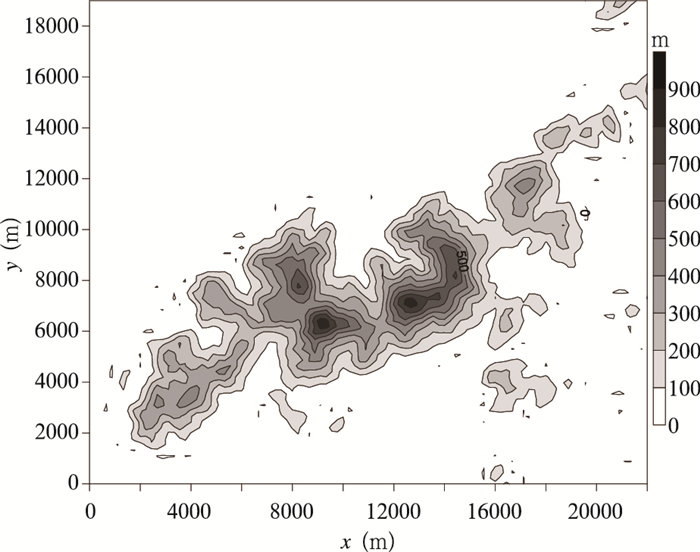
FLUENT解域东西长22 km, 南北宽19 km, 解域内的地形如图 3所示。解域两个水平方向上的网格数分别设置为140和120, 这意味着网格距大约在158 m, 以往的研究表明, 这个网格距的CFD模拟足够分辨出地形激发的波动, 且同时能有效控制解域内网格总数, 能保障在一台4 G内存和双核CPU的普通工作站上正常运算。在边界条件方面, 将东、南、西以及顶部边界都设为固定边界, 用中尺度模式输出结果赋予的值, 北侧采用出流边界条件, 假设物理量的出流梯度为0。FLUENT模拟沿用李磊等(2010)提出的两步法, 先在RANS框架下完成一个稳态的模拟, 将稳态模拟得到的结果作为初始场驱动LES框架下的非稳态模拟, 研究流场的动态变化特征。RANS框架下的湍流闭合方案采用realizable k-ε方案(Shih et al, 1995), 而LES框架下的湍流闭合方案采用Smagrinsky-Lilly方案(Smagorinsky, 1963;Lilly, 1966)。
|
| 图 3 FLUENT模拟区域地形 Figure 3 Terrain of the FLUENT simulation domain |
为研究CFD解域顶高问题, 设置了两组对比试验, 一组顶高设为3000 m, 垂直方向上分为22层, 另一组设为6000 m, 垂直方向上分为42层, 垂直格距从地面往上均按11.06的比例递增。为研究边界条件设置方法问题, 分别通过编程实现了3种从RAMS到FLUENT的数据传递方法:对廓线法生成一个FLUENT可识别的自定义函数文件, 包含了不同层高的入流风数据;对0维和二维插值则是分别给出包含了入流边界各个格点数据的ASCII码文件, 利用FLUENT的边界层廓线模块直接读入。
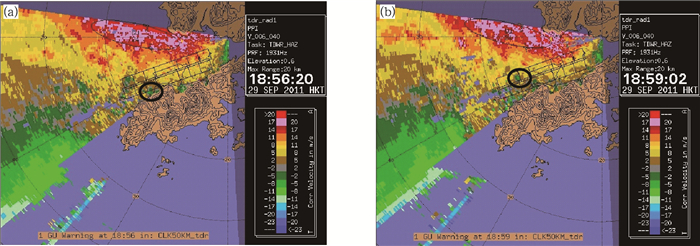
为了对香港新机场上空的风切变进行观测, 香港天文台在大屿山东北方向设置了一台多普勒雷达, 本研究使用了该雷达的径向风观测资料, 用于与模拟结果做对比分析。限于篇幅, 这里只给出了2011年9月29日19时前2个时刻的径向速度(图 4), 关于这个过程观测结果更详细的分析, 请参见Chan(2014), 在此只做简要介绍。从径向速度图可知在山体下风侧大片暖色区中出现了小范围的绿色斑块(图中黑色椭圆框内), 并且这些绿色斑块会随着时间往下游移动并慢慢消失——这标志着在大片平顺均匀的流场中出现了与背景流场不一致的扰动(波动或涡旋), 并且这种扰动会向下游移动消逝, 然后按一定周期重新生成, Chan认为这是一种典型的波动/涡旋脱体运动(Wave/Vortex Shedding), 会引起机场上空的风切变, 因而值得关注和研究。
|
| 图 4 大屿山东北侧多普勒雷达观测到的风场径向速度(单位:m/s; a.18时56分20秒;b.18时59分02秒) Figure 4 Radial velocity observed by the radar deployed to the north-east of Lantau Island(unit:m/s; a.18:56:20 BT, b.18:59:02 BT) |
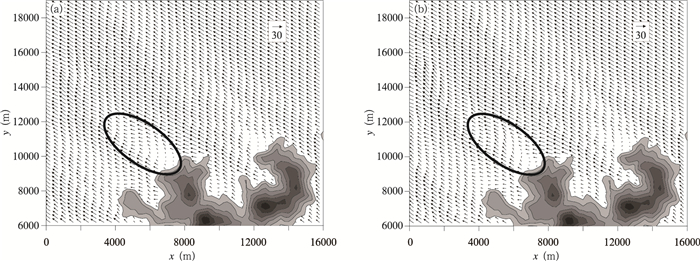
为便于与雷达观测结果进行对比, FLUENT以60 s时间间隔输出模拟结果。图 5给出了t=1800 s(t为积分时间)时两种解域顶高试验模拟得到的距地面220 m处的风矢量场, 由图 5可知, 两组试验均可很好地模拟出山体下风侧的波动结构(图 5椭圆圈标注处)。进一步对间隔为1 min的模拟结果进行分析, 可知两组试验均可描述波动结构从山体脱落后向下风向移动并最终慢慢消失的整个过程(图略), 二者模拟结果的差别主要在于波动结构生成的起始时间有所不同, 所以在同一时步的模拟结果波动结构所处的位置有一定差距。
|
| 图 5 FLUENT模拟得到的220 m高度处的风矢量(单位:m/s;a.顶高3000 m, b.顶高6000 m) Figure 5 FLUENT simulated wind vectors at the height of 220 m(unit:m/s; a.Top height 3000 m, b.Top height 6000 m) |
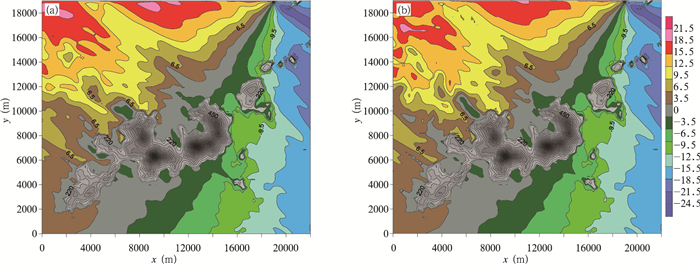
从模拟得到的径向速度(图 6)来看, 背景气流及扰动气流中的径向速度量级均与雷达观测数据吻合得较好, 表明二者模拟得到的风速大小与实测结果较为一致。进一步比较了220 m以上直至1000 m不同高度的模拟结果(图略), 发现在600 m及以下, 两组模拟试验得到的结果均较一致, 均能描述山体引起的波动脱体现象;在600 m以上, 两组试验模拟得到的风场差距才开始逐渐增大。这表明, 如果关心的只是边界层中下部(600 m及以下)风场结构, 按照文中给出的模拟方法, FLUENT的解域顶高设置为3000 m即已足够。相较于顶高为6000 m的设置, 解域顶高为3000 m的模拟设置计算量减少了近50%, 而模拟结果却仍足够准确。
|
| 图 6 FLUENT模拟的220 m高度处的风场径向速度(单位:m/s; a.顶高3000 m, b.顶高6000 m) Figure 6 FLUENT simulated radial velocity at the height of 220 m (unit:m/s; a.Top height 3000 m, b.Top height 6000 m) |
Chan(2014)利用RAMS对本研究的案例进行过模拟研究, 发现网格距为50m的第4层嵌套网格可以捕捉到波动结构, 但其得到的波动较弱(图略)。而本试验表明, 即使是网格距为158 m左右, FLUENT仍然可以捕捉到山体激发的波动, 并且波动相当强, 与观测结果较吻合。这凸显了CFD相对于中尺度模式的优势——由于不必对地形进行强制平滑, 模式地形与真实地形更为接近, 因此能够更准确地描述地形激发的波动。
4.2 不同边界条件设置为对比不同边界条件的区别, 图 7给出了不同边界条件设置方法得到的FLUENT解域中南侧入流边界上的风速u分量(东西方向上的分量)。从图 7可知廓线法边界条件上风速u分量分布较为简单, 水平方向上大致是均匀的。0维插值法和二维插值法得到的结果大体接近, 但二维插值法得到的变量分布细节特征被描述得更细致, 例如在垂直方向1000 m高度以下, x方向上4000—6000 m, 二维插值法得到的入流边界上的风速u分量表现出了更明显的非均匀性。

|
| 图 7 3种不同边界条件设置方法得到的FLUENT解域南侧边界风速u分量(单位:m/s; a.廓线法,b.0维插值法,c.二维插值法) Figure 7 u-components of the wind velocity at the southern inlet lateral boundary provided by three boundary condition setting methods (unit: m/s; a. Single profile (SP) method; b. ZDI method; c. TDI method) |
认为t=1200 s之前为FLUENT数值积分的调整阶段, 从t=1200 s开始分析模拟结果, 图 8给出了3种不同边界条件处理方法模拟得到的距地面220 m高度的风矢量模拟结果, 为了更清晰地展示波动结构的细节, 图 8只给出了大屿山西北侧局部的模拟结果。

|
| 图 8 3种不同边界条件设置方法得到的山体下风侧风矢量(单位:m/s; a.廓线法,b.0维插值法,c.二维插值法;a1、b1、c1.t=1200 s; a2、b2、c2.t=1260 s; a3、b3、c3.t=1320 s; a4、b4、c4.t=1380 s) Figure 8 The simulated wind vectors on the downwind side of the mountain with three boundary condition setting methods (unit:m/s; a. SP method, b. ZDI method, c. TDI method; a1、b1、c1.t=1200 s; a2、b2、c2.t=1260 s; a3、b3、c3.t=1320 s; a4、b4、c4.t=1380 s) |
从图 8可见, 3组试验都能得到山体下风侧的波动结构, 生成的波动都有随背景气流往下游移动的现象, 并且3组试验模拟得到的风速大小都较为接近。然而仔细对比可发现3组试验得到的结果还是有一定差别:廓线法得到的风场总体上更为平顺, 气流虽然有波动但振幅不大;而0维插值法和二维插值法得到的波动形流场振幅更大, 表明山体造成的扰动更强, 但单纯从流场图来看, 无法判断哪种方法更接近实测结果。
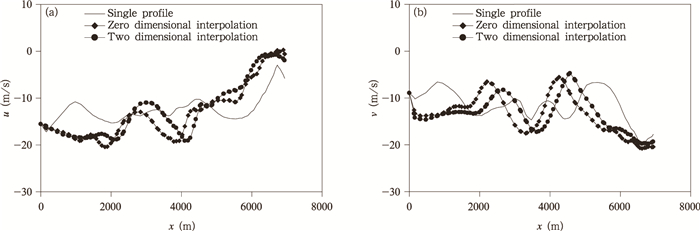
为定量对比3种方法模拟得到的波动强弱, 选取经过A(x=0 m, y=15000 m, z=220 m)、B(x=16900 m, y=0 m, z=220 m)两个控制点的直线(图 8a1), 分析t=1380 s时该直线上风速u和v分量的变化情况, 由于该条直线大致接近波动气流的轴线, 所以通过风速分量的变化起伏可以判断波动幅度。图 9给出了直线上位于山体下风向的风速分量变化情况, 山体大致位于直线上x=7000 m附近。由图 9不难看出, 0维插值法和二维插值法模拟得到的结果相对更接近, 而且模拟出的风速分量的起伏更大, 表明这两种方法模拟得到的波动更强、振幅更大。廓线法虽然也能模拟出风速分量的波动起伏, 但波动强度明显小于另外两种方法。
|
| 图 9 3种不同边界条件设置方法得到的波动轴线上的风速分量(a.u, b.v) Figure 9 The simulated wind components on the axis of the wave with three boundary condition setting methods (a.u, b.v) |
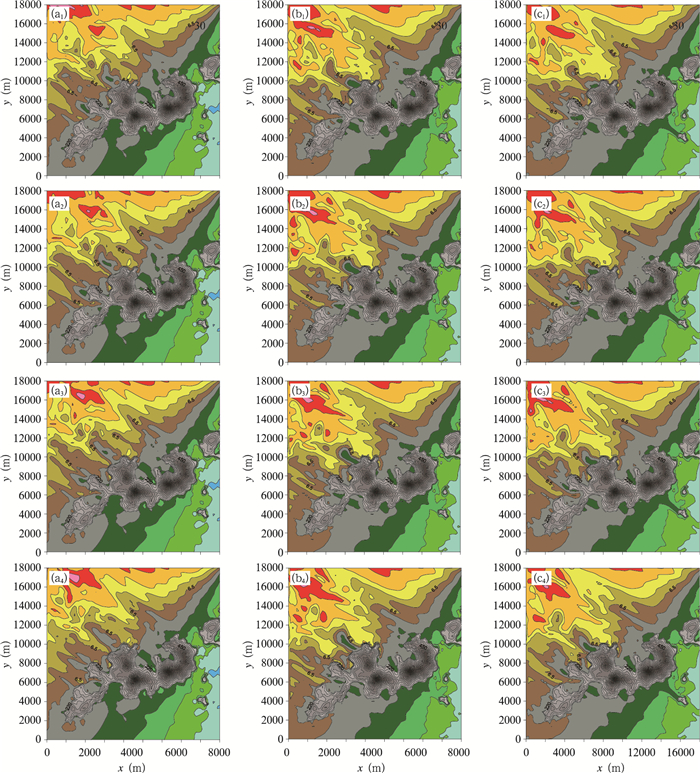
图 10径向速度的对比可以帮助更清晰地分析3种方法的效果, 虽然3者模拟结果都与雷达观测的径向速度空间分布大体一致, 但相较之下廓线法模拟得到的扰动比另两种方法得到的结果要弱, 主要体现在山体下风侧绿色斑块的面积更小, 且在t=1380 s时就完全消失了, 只留下浅灰色的条带。而0维插值法和二维插值法模拟得到的气流扰动则要强得多, 模拟得到的绿色斑块面积较大且在180 s内都持续存在, 这与雷达图的观测结果较为一致。对比0维插值法和二维插值法得到的结果, 0维插值法能更好地模拟出扰动气流生成后向下风向移动的过程, 体现在绿色斑块在生成后有明显拉伸和位移, 这与雷达观测结果比较接近;而利用二维插值法得到的模拟结果尽管得到了较强的扰动气流, 但从径向速度的模拟结果来看, 扰动区似乎移动缓慢, 粘滞在山体上, 尽管在之后的模拟结果中扰动区缓慢脱离山体向下游移动, 但总体上不如0维插值方法得到的结果更接近观测实况。
|
| 图 10 三种不同边界条件设置方法得到的径向风速(m/s; a.廓线法,b.0维插值法,c.二维插值法; a1、b1、c1.t=1200 s; a2、b2、c2.t=1260 s; a3、b3、c3.t=1320 s; a4、b4、c4.t=1380 s) Figure 10 The simulated radial velocities with three boundary condition setting methods (unit: m/s; a.SP method, b. ZDI method, c.TDI method; a1、b1、c1.t=1200 s; a2、b2、c2.t=1260 s; a3、b3、c3.t=1320 s; a4、b4、c4.t=1380 s) |
如前所述, 二维插值法得到的入流边界上的物理量的空间分辨率要高于0维插值, 理论上利用二维插值法得到的模拟结果应该更准确, 然而本研究结果却并非如此。仔细分析, 这样的结果也并不令人意外, 0维插值法和二维插值法所用的原始数据均是来自于RAMS输出的同一套数据, 二维插值法所谓的更高分辨率其实是采用了多点数据插值到某个点上, 其本质是一种数学处理, 得到的更高分辨率的边界数据是否在物理上真实还值得推敲。由此可知, 0维插值法生成的边界条件虽然简单, 但已“足够用”, 至少在本研究中相较二维插值法并未体现出任何劣势。
5 总结与展望对CFD技术用于陡峭山体风场模拟的两个关键问题进行了研究, 一是对于陡峭山体模拟所适宜的CFD解域顶高问题, 二是入流边界条件设置方法问题。
对于解域顶高, 一般环境流体力学或建筑风工程领域认为越高越好, 究其原因, 主要是为了获得地面障碍物周边的整个流场结构, 避免顶边界过低影响障碍物顶部流场的准确性。而本次数值试验表明, 若模拟关心的区域为较低海拔高度时, 不必完全拘泥于该惯例, 在本研究中设置了解域顶高为3000和6000 m两组试验, 对应地面障碍物垂直尺度的3和6倍, 而结果表明对于600 m及以下的边界层中下部, 两者模拟结果相差无几, 而3000 m顶高的设置可以节省约一半的计算量。
对于入流边界条件设置方法的问题, 进行了3组对比试验, 结果表明单纯采用廓线法不足以充分地描述来流信息, 得到的模拟结果与实际观测情况有明显差别;而二维插值法尽管提供了更高分辨率的边界数据, 也的确能模拟出与观测值强度接近的波动结构, 但其结果总体上逊于0维插值法。综合考虑模拟效果和算法难度, 0维插值法“性价比”最高。
本研究结果表明, 采用两步法及合理的解域顶高、边界条件设置, “中尺度模式/CFD”耦合使用可以很好地描述山地激发的涡旋/波动脱体运动, 比单纯采用中尺度模式效果要好得多。在利用CFD工具研究复杂山地风场时, 应本着“实用主义”的精神具体问题具体分析, 设置物理模型、参数和选取适当的方法、边界条件, 以达到模拟精度和计算量之间的优化平衡。
| 陈长和, 黄建国, 程麟生, 等. 1993. 复杂地形上大气边界层和大气扩散的研究. 北京: 气象出版社 . Chen C H, Huang J G, Cheng L S, et al. 1993. A Study on the Atmospheric Boundary Layer and the Atmospheric Dispersion in Complex Terrain. Beijing: China Meteorological Press . |
| 程雪玲, 胡非. 2006. 复杂地形网格生成研究. 计算力学学报 , 23 (3) : 313–316. Cheng X L, Hu F. 2006. A study of grid formation in complex terrain. Chinese J Comput Mech , 23 (3) : 313–316. (in Chinese) |
| 傅抱璞. 1963. 起伏地形中的小气候特点. 地理学报 , 29 (3) : 175–187. Fuh B P. 1963. The feature of microclimate in undulating country. Acta Geogr Sinica , 29 (3) : 175–187. (in Chinese) |
| 郝为锋, 苏晓冰, 王庆安, 等. 2001. 山地边界层急流的观测特性及其成因分析. 气象学报 , 59 (1) : 120–128. Hao W F, Su X B, Wang Q A, et al. 2001. The observational features and the cause analysis of hilly boundary-layer-jet. Acta Meteor Sinica , 59 (1) : 120–128. (in Chinese) |
| 黄倩, 田文寿, 王文, 等. 2007. 复杂山区上空垂直速度场和热力对流活动的理想数值模拟. 气象学报 , 65 (3) : 341–352. Huang Q, Tian W S, Wang W, et al. 2007. Idealized simulations of vertical velocity fields and thermal convection over a complex hilly terrain. Acta Meteor Sinica , 65 (3) : 341–352. (in Chinese) |
| 李磊, 张立杰, 张宁, 等. 2010. FLUENT在复杂地形风场精细模拟中的应用研究. 高原气象 , 29 (3) : 621–628. Li L, Zhang L J, Zhang N, et al. 2010. The Application of FLUENT on the fine-scale simulation of the wind field over complex terrain. Plateau Meteor , 29 (3) : 621–628. (in Chinese) |
| 齐瑛, 傅抱璞. 1994. 一个含地形的二阶矩湍流闭合的大气中尺度数值模式. 南京大学学报(自然科学版) , 30 (4) : 715–725. Qi Y, Fu B P. 1994. An atmospheric mesoscale numerical model with second-order moment turbulent closure over complex terrains. J Nanjing Univ (Nat Sci Ed) , 30 (4) : 715–725. (in Chinese) |
| 宋丽莉, 吴战平, 秦鹏, 等. 2009. 复杂山地近地层强风特性分析. 气象学报 , 67 (3) : 452–460. Song L L, Wu Z P, Qin P, et al. 2009. An analysis of the characteristics of strong winds in the surface layer over a complex terrain. Acta Meteor Sinica , 67 (3) : 452–460. (in Chinese) |
| 吴涧, 蒋维楣, 王卫国. 2000. 山区盆地大气湍流特征与污染扩散的数值试验. 环境科学学报 , 20 (5) : 554–557. Wu J, Jiang W M, Wang W G. 2000. A numerical simulation of atmospheric turbulence and diffusion over mountain areas. Acta Scien Circum , 20 (5) : 554–557. (in Chinese) |
| Chan P W. 2014. Observation and numerical simulation of vortex/wave shedding for terrain-disrupted airflow at Hong Kong International Airport during Typhoon Nesat in 2011. Meteorol Appl , 21 (3) : 512–520. DOI:10.1002/met.2014.21.issue-3 |
| Cheng W C, Liu C H. 2011. Large-eddy simulation of turbulent transports in urban street canyons in different thermal stabilities. J Wind Eng Ind Aerodyn , 99 (4) : 434–442. DOI:10.1016/j.jweia.2010.12.009 |
| Li L, Chan P W, Zhang L J, et al. 2013. Numerical simulation of terrain-induced vortex/wave shedding at the Hong Kong International Airport. Meteor Z , 22 (3) : 317–327. DOI:10.1127/0941-2948/2013/0439 |
| Li L, Hu F, Jiang J H, et al. 2007. An application of the RAMS/FLUENT system on the multi-scale numerical simulation of the urban surface layer-A preliminary study. Adv Atmos Sci , 24 (2) : 271–280. DOI:10.1007/s00376-007-0271-y |
| Lilly D K. 1966. The representation of small-scale turbulence in numerical simulation experiments//Proceedings, IBM Scientific Computing Symposium on Environmental Sciences. Boulder, Colorado http://link.springer.com/10.1007%2F978-3-540-89956-3_7 |
| Shih T H, Liou W W, Shabbir A, et al. 1995. A new k-ε eddy viscosity model for high Reynolds number turbulent flows. Comput Fluids , 24 (3) : 227–238. DOI:10.1016/0045-7930(94)00032-T |
| Smagorinsky J. 1963. General circulation experiments with the primitive equations Ⅰ: The basic experiment. Mon Wea Rev , 91 (3) : 99–164. DOI:10.1175/1520-0493(1963)091<0099:GCEWTP>2.3.CO;2 |
| Uchida T, Ohya Y. 1999. Numerical simulation of atmospheric flow over complex terrain. J Wind Eng Ind Aerodyn , 81 (1-3) : 283–293. DOI:10.1016/S0167-6105(99)00024-0 |
| Walko R L, Tremback C J. 2006. RAMS Regional Atmospheric Modeling System (Version 6. 0), Model input namelist parameters. ATMET. Boulder, 62pp |
| Zajaczkowski F J, Haupt S E, Schmehl K J. 2011. A preliminary study of assimilating numerical weather prediction data into computational fluid dynamics models for wind prediction. J Wind Eng Ind Aerodyn , 99 (4) : 320–329. DOI:10.1016/j.jweia.2011.01.023 |
 2016, Vol. 74
2016, Vol. 74

