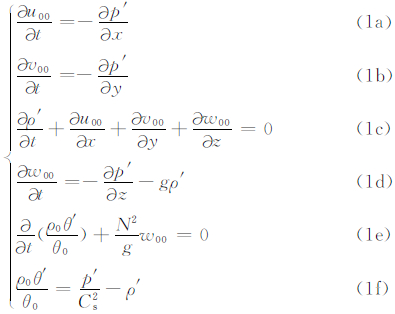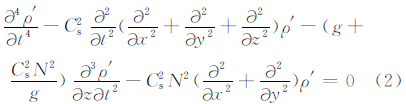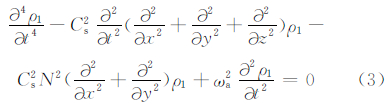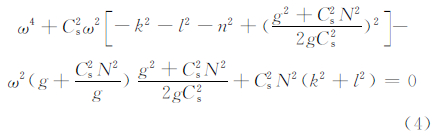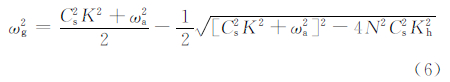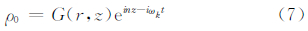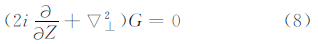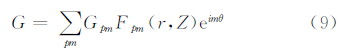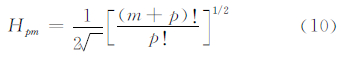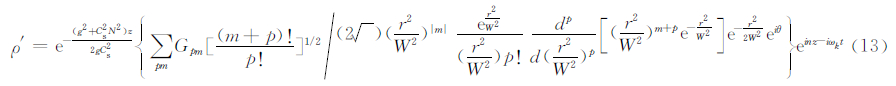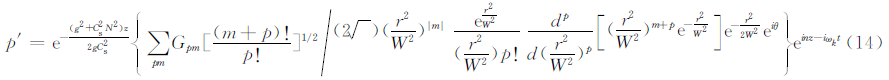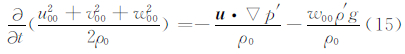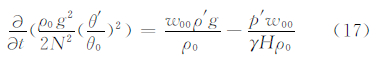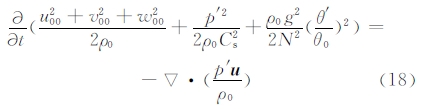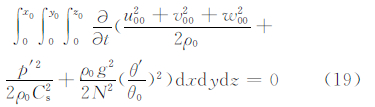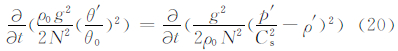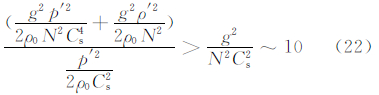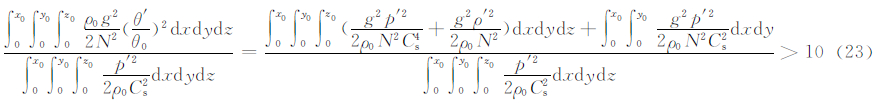中国气象学会主办。
文章信息
- 崔新东, 刘宇迪, 赵增亮, 李明华, 宋学儒, 胥永文. 2016.
- CUI Xindong, LIU Yudi, ZHAO Zengliang, LI Minghua, SONG Xueru, XU Yongwen. 2016.
- 三维静力适应过程中声重力波的特性和能量转换研究
- Study of characteristics of the acoustic gravity wave and energy conversion in the three-dimensional hydrostatic adjustment process
- 气象学报, 74(1): 127-132
- Acta Meteorologica Sinica, 74(1): 127-132.
- http://dx.doi.org/10.11676/qxxb2016.012
-
文章历史
- 2015-10-08 收稿
- 2015-12-29 改回
2. 解放军理工大学气象海洋学院, 南京, 211101;
3. 解放军 61828部队, 喀什, 844200
2. Institute of Meteorology and Ocean, PLA University of Science and Technology, Nanjing 211101, China;
3. Uint 61828, PLA, Kashi 844200, China
电离层、热层与中、低层大气的耦合主要通过三个过程:静电和光化学过程、电磁学过程和动力学过程。声重力波是动力学过程的主要控制波动,也是能量输送的载体,在中、低层大气与高层大气的耦合中起着十分重要的作用(肖赛冠等,2007)。
声重力波在对流层是静力适应过程的控制机制,最早由Lamb(1932)开始在由理想气体组成的稳定层结等温大气中,研究有外强迫作用时垂直方向静力适应过程。叶笃正等(1965)提出描述静力适应过程的方程组,并对这个方程组声波解和重力波解进行了研究。在等温、可压缩非旋转大气中,Bannon(1995,1996)研究在有限范围瞬时加热时线性和非线性垂直方向静力适应过程。分别在线性情况下用欧拉变量,在非线性情况下用拉格朗日变量研究了垂直方向静力适应过程终态和能量的转换,得出静力适应过程的守恒量和能量方程。应用该守恒量来研究静力衰减和适应终态。能量方程中包括3部分能量,分别是动能、有效弹性势能及有效势能。Duffy(2003)通过对不同垂直结构的基本大气进行分析,发现在线性静力适应过程中动能、有效弹性势能、有效势能在整个静力适应过程中一直相互转换。在非线性情况下,有效势能随时间保持不变,而能量在有效弹性势能和动能之间相互转换。Phillips(1990)研究静力平衡近似,得出静力平衡近似适用于低频浅扰动的流体中。Sotack等(1999)对于不同的加热函数进行分析,发现在加热量相同的情况下,静力适应的终态是相同的。用拉格朗日方法分析得出,静力适应终态中有效势能存在于加热层里,而有效弹性势能转换为声波能量。已有研究主要考虑温度直减率变化时对流层与平流层的声重力波传输,文中将对三维静力适应过程及其解析解以及能量转换过程进行研究,其中包括对描述三维静力适应过程的声重力波方程组进行波动特征分析,推导分析三维静力适应过程的解析解,并讨论三维静力适应过程中的能量转换机制和位涡。
2 波动特征采用叶笃正等(1965)提出的描述三维静力适应过程的声重力波方程组
式中,设ρ0=ρe-z/H,p0=pe-z/H,T0=T,θ0=Tez(1-γ)/Hγ,ρ 、p 、T 、θ 为对应变量的均值。u00=ρ0u′,v00=ρ0v′,w00=ρ0w′。 u =(u00 i,v00 j,w00 k),H=RT/g,R为干空气气体常数,H为大气标高,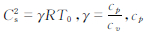 为干空气比定压热容,cv为干空气比定容热容,Cs为绝热声速,N为浮力振荡频率,
为干空气比定压热容,cv为干空气比定容热容,Cs为绝热声速,N为浮力振荡频率,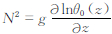 。g为重力加速度。
。g为重力加速度。
将式(1)消去其余变量得密度为
设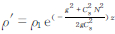 式(2)则变为
式中,
式(2)则变为
式中, 。
。
设波解ρ1=ρei(kx+ly+nz-ωt),其中,k,l,n分别为x,y,z方向上的波数,ω为圆频率。代入式(3),可得频率方程为
式中,K2=k2+l2+n2,Kh2=k2+l2。以上两组波解分别是声重力波和重力内波。由于浮力振荡频率很小,式(5)趋向于标准声波解,但是频率要小于标准声波解,式(6)趋向于标准重力内波解,但是频率要大于标准重力内波解,因此,静力适应过程中声重力波和重力内波的频率范围介于标准声波和标准重力内波之间。
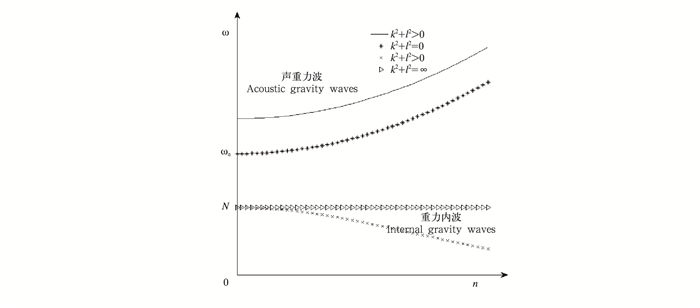
由式(5)、(6)可以看出,ωs、ωg在水平方向上具有各向同性的性质,为了简化,设k=l,这样的假设不影响后续问题的分析。下面分别给出ω随水平波数k和垂直波数n转换的结果(图 1、2)。
|
| 图 1 水平波数k取不同值时ω随垂直波数n的转换 Fig. 1 Changes in ω with the vertical wavenumber(n)for the different horizontal wavenumbers |
|
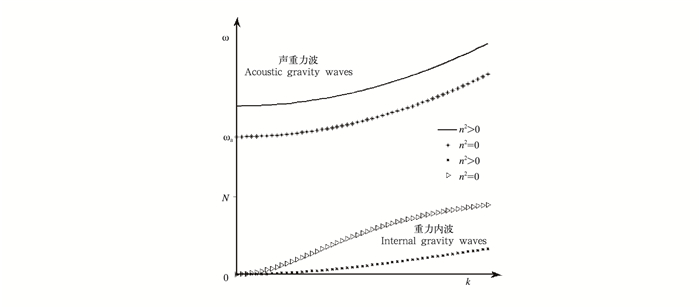
| 图 2 垂直波数n取不同值时ω随水平波数k的转换 Fig. 2 Changes in ω with the horizontal wavenumber(k)for the different vertical wavenumbers |
由图 1、2可以看出,声重力波频率随水平波数或垂直波数的增大而增大。而重力内波频率随水平 波数增大而增大,并趋于浮力振荡频率N;但随着垂直波数的增大而减少,并趋于0。在声重力波和重力内波之间存在着一段在静力适应过程中不存在的波动频率,这说明在静力适应过程中存在着两个可以区分开来的不同特征时间尺度,一个是由声重力波产生的快时间尺度,一个是由重力内波产生的慢时间尺度。同时由图 1、图 2可得,声重力波的频率要大于ωa,而重力内波的频率要小于浮力振荡频率N。
3 解析解按照Shukla等(2012)给出的采用近轴近似化简方程得出其解析解的方法,式(3)解析解的形式为
式中,G(r,z)为z的缓变函数,r2=x2+y2,n为z轴方向的波数。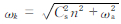 为声重力波的频率。利用式(7)在近轴近似
为声重力波的频率。利用式(7)在近轴近似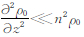 下,式(3)可写为
式中,
下,式(3)可写为
式中,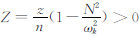 ,引进算子
,引进算子
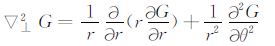
并采用柱坐标 r=(r,θ,z)。式(8)的解析解 可以写为Laguerre-Gaussian模态的叠加,每一个都表示角动量的状态,以量子数m为特征,则有
式中,模态结构函数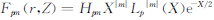 ,X=r2/W2,W为三维声重力涡旋柱的归一化宽度,Gpm为展开系数。归一化因子Hpm和连带Laguerre多项式Lp|m|(X)分别为
式中,m和p分别为声重力波角动量状态的角度方向和径向方向上的模态数。
,X=r2/W2,W为三维声重力涡旋柱的归一化宽度,Gpm为展开系数。归一化因子Hpm和连带Laguerre多项式Lp|m|(X)分别为
式中,m和p分别为声重力波角动量状态的角度方向和径向方向上的模态数。
这样,式(3)的解析解为
相应的式(2)的解析解为
式(13)对应的图形如图 3(Padgett et al,2000)所示。
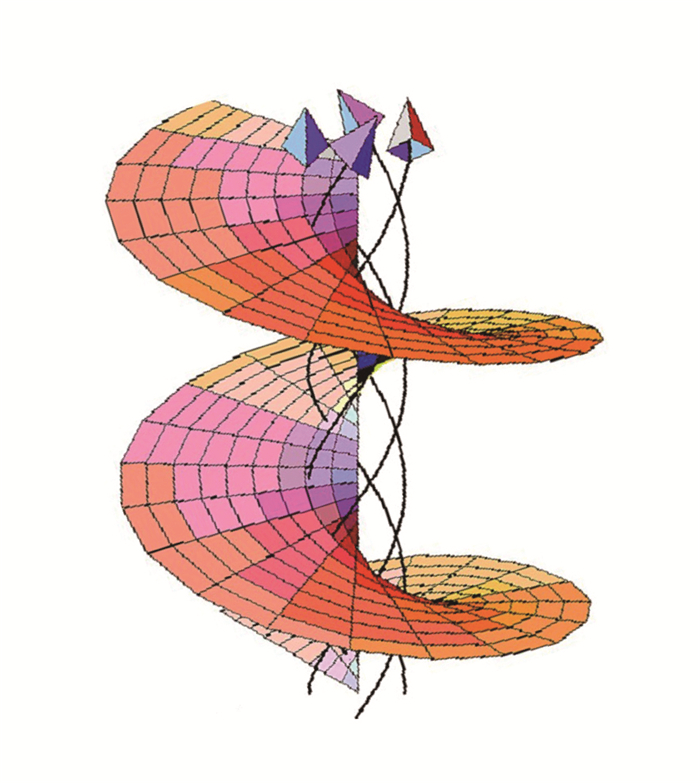
|
| 图 3 密度扰动解析解示意(螺旋曲面为波振面,带箭头的螺旋曲线为波动传播曲线) Fig. 3 Schematic illustration of the density perturbation solution(Helicoid is wavefronts and curve with arrowhead is transmissible curve) |
假定密度扰动满足近轴近似,即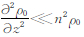 ,则静力适应密度解析解为三维涡旋波动。由于三维涡旋声重力波中存在涡旋角动量,因此,适应过程任 意气块密度的调整既包含垂直方向上的调整分量又包含着水平方向上的调整分量,两种分量同时存在,又相互影响。当空间上某一部分存在非静力扰动时,在三维涡旋波动的作用下,会绕着涡旋轴将扰动值传到环绕轴的涡旋面上,从而使得扰动能量能迅速的频散开来。当三维涡旋波柱的涡旋半径增大时,会使得扰动能量在更广的范围内传播,从而对于相同大小的初始扰动,扰动能量能传播到更广的空间内,静力适应过程将更快的完成。在静力适应过程中相对于平面传播的波动,三维涡旋波动的存在实际上使得扰动能量能传播到更广的空间内,有利于静力适应过程的迅速完成。为大气中热通量和动量从一个区域向另一个区域的输送提供了一种机制,从而为研究大气提供了新的视角。
,则静力适应密度解析解为三维涡旋波动。由于三维涡旋声重力波中存在涡旋角动量,因此,适应过程任 意气块密度的调整既包含垂直方向上的调整分量又包含着水平方向上的调整分量,两种分量同时存在,又相互影响。当空间上某一部分存在非静力扰动时,在三维涡旋波动的作用下,会绕着涡旋轴将扰动值传到环绕轴的涡旋面上,从而使得扰动能量能迅速的频散开来。当三维涡旋波柱的涡旋半径增大时,会使得扰动能量在更广的范围内传播,从而对于相同大小的初始扰动,扰动能量能传播到更广的空间内,静力适应过程将更快的完成。在静力适应过程中相对于平面传播的波动,三维涡旋波动的存在实际上使得扰动能量能传播到更广的空间内,有利于静力适应过程的迅速完成。为大气中热通量和动量从一个区域向另一个区域的输送提供了一种机制,从而为研究大气提供了新的视角。
由于解析解中存在指数项,从而使得解析解会随着高度成负指数衰减。三维涡旋波动的振幅在高层比在底层的小,因此,底层的涡旋角动量更大更有利于底层扰动的传播,而高层的扰动频散速度要小于底层。从密度角度来看,在适应过程中底层密度要大于高层密度扰动,这与一维静力适应过程所得的结论相吻合(崔新东等,2015)。
当假定气压扰动也满足近轴近似时,静力适应过程的气压解为
虽然密度和气压解的公式形式相同,密度和气压在空间上的传播都是涡旋波动,但是气压解与密度解的不同之处在于展开系数Gpm和θ等各系数的不同,不同的初值决定着不同的展开系数和角坐标值,从而从数学上将密度和气压解区分开来。从物理意义上说,在满足近轴近似时,静力适应过程中声重力波和重力内波在传播过程中形成了以涡旋运动传播的波动,而密度和气压在静力适应过程中的调整是以声重力波和重力内波的传播来实现的,因此在密度和气压解中都是以涡旋波动为形式的解。
4 能量转换和位涡守恒由式(1a)、(1b)、(1d)各自乘以其速度,可得动能为
由式(1c)和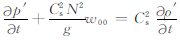 ,所得的有效弹性势能为
,所得的有效弹性势能为
由式(1e)以及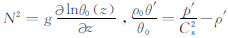 ,可得有效势能为
,可得有效势能为
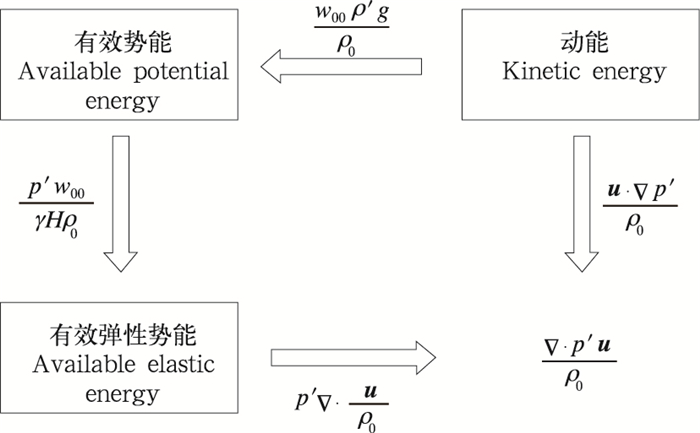
由式(15)、(16)、(17)和图 4可以看出,动能与有效势能的转换、有效势能与有效弹性势能的转换,垂直速度都发挥着重要的作用,它的存在使得上述能量的转换得以实现,并且动能与有效势能、有效势能与有效弹性势能之间的转换能量只发生在垂直方向上。当静力适应过程中存在水平气压的净流出量时,有效弹性势能与动能将进行扰动能量的相互转换。
|
| 图 4 能量转换示意 Fig. 4 Schematic illustration of the energy conversions |
将式(15)、(16)、(17)合并得
对式(18)进行空间积分,并且在边界上速度为0,得由式(19)可以看出,静力适应过程中总能量守恒。
由于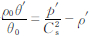 ,因此有效势能可以表示成
,因此有效势能可以表示成
由于各变量的量纲为N2~10-4,Cs2~105,gs2~102(各变量均为标准单位时的量纲),则
考虑到能量都为正值,积分区域也都为正值,终态有效势能和有效弹性势能的比值为
由式(23)可以看出,静力适应终态有效势能比有效弹性势能大一个量级。这说明在静力适应终态中,除动能外,有效势能占剩余能量的90%以上,而有效弹性势能只占不足10%。由式(1a)、(1b)、(1d)改写成为矢量形式后取旋度,然后与式(1c)、(1e)组合即可得到,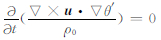 ,即位涡守恒,在静力适应过程中位涡守恒。
,即位涡守恒,在静力适应过程中位涡守恒。
为了研究三维静力适应过程的机理,从描述三维静力适应过程的声重力波方程组出发,讨论了声重力波的波动特征、解析解、能量转换和位涡方程,得到以下结论:
(1)描述静力适应过程的波动为声重力波和重力内波。声重力波的频率随着水平波数和垂直波数的增大而增大。而重力内波的频率随着水平波数增大而增加,并趋于浮力振荡频N;但随着垂直波数的增大而减少,并趋于0。声重力波和重力内波的频率在水平方向上可以区分开来。
(2)在密度扰动满足近轴近似时,静力适应过程的密度扰动会在空间中以螺旋型传播,这种螺旋型传播可以形成可观测的声重力波龙卷风(Shukla et al,2012)。这是以前的研究中没有发现的。由于解析解中存在指数项,从而使得解析解会随着高度成负指数衰减,三维涡旋波动的振幅在高层比在底层的小,因此底层的涡旋角动量更大更有利于在底层的扰动能量频散,而高层的扰动能量频散速度要慢于底层。
(3)在静力适应过程中,动能向有效势能转换、有效势能向有效弹性势能的转换,垂直速度都发挥着重要的作用。并且动能与有效势能、有效势能与有效弹性势能之间的转换能量只发生在垂直方向上。有效弹性势能与动能之间的相互转换是通过气压通量进行转换。在静力适应过程中位涡和总能量是守恒的。静力适应终态的有效势能比有效弹性势能大一个数量级。
| 崔新东, 刘宇迪, 艾细根等. 2015. 垂直方向静力适应过程的机理研究. 气象科学, 35(4):462-467. Cui X D, Liu Y D, Ai X G, et al. 2015. Mechanism study on vertical hydrostatic adjustment procedure. J Meteor Sci, 35(4):462-467 (in Chinese) |
| 肖赛冠, 张东和, 肖佐. 2007. 台风激发的声重力波的可探测性研究. 空间科学学报, 27(1):35-40. Xiao S G, Zhang D H, Xiao Z. 2007. Study on the detectability of Typhoon-generated acoustic-gravity waves. Chin J Space Sci, 27(1):35-40 (in Chinese) |
| 叶笃正, 李麦村. 1965. 大气运动中的适应问题. 北京:科学出版社, 93-106. Ye D Z, Li M C. 1965. The Atmosphere in Motion the Process of Adjustment. Beijing:Science Press, 93-106 (in Chinese) |
| Bannon P R. 1995. Hydrostatic adjustment:Lamb's problem. J Atmos Sci, 52(10):1743-1752 |
| Bannon P R. 1996. Nonlinear hydrostatic adjustment. J Atmos Sci, 53(23):3606-3617 |
| Duffy D G. 2003. Hydrostatic adjustment in nonisothermal atmospheres. J Atmos Sci, 60(2):339-353 |
| Lamb S H. 1932. Hydrodynamics. New York:Dover Publications, 738 |
| Padgett M, Allen L. 2000. Light with a twist in its tail. Contemp Phys, 41(5):275-285 |
| Phillips N A. 1990. Dispersion Processes in Large-Scale Weather Prediction. Vienna:World Meteorological Organization, 126 |
| Shukla P K, Stenflo L. 2012. Acoustic gravity tornadoes in the atmosphere. Phys Scr, 86(6):903-916 |
| Sotack T, Bannon P R. 1999. Lamb's hydrostatic adjustment for heating of finite duration. J Atmos Sci, 56(1):71-81 |
 2016, Vol. 74
2016, Vol. 74