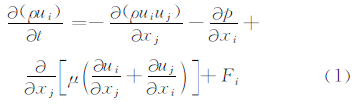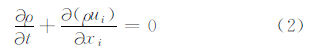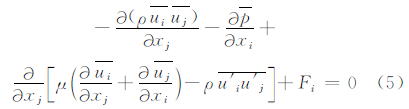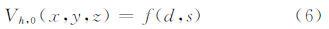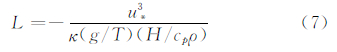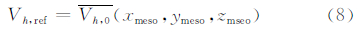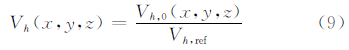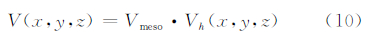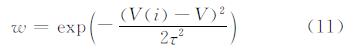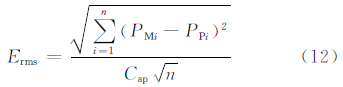2016, Vol. 74
中国气象学会主办。
文章信息
- 马文通, 朱蓉, 李泽椿, 龚玺. 2016.
- MA Wentong, ZHU Rong, LI Zechun, GONG Xi. 2016.
- 基于CFD动力降尺度的复杂地形风电场风电功率短期预测方法研究
- Study of the short-term wind power forecasting method for complex terrain wind farm based on the CFD dynamical downscalling
- 气象学报, 74(1): 89-102
- Acta Meteorologica Sinica, 74(1): 89-102.
- http://dx.doi.org/10.11676/qxxb2016.002
-
文章历史
- 2015-05-08 收稿
- 2015-10-23 改回
2. 国家气候中心, 北京, 100081;
3. 南京信息工程大学, 南京, 210044
2. National Climate Center, Beijing 100081, China;
3. Nanjing University of Information Science and Technology, Nanjing 210044, China
风电功率预测技术是缓解电网调峰压力、降低系统备用容量、提高电网风电接纳能力的有效手段之一。
同时，风电功率预测技术可以指导风电场的检修计划，提高风能利用率，改善风电场的经济效益。
目前，丹麦、德国、西班牙、美国等风电发达国家已建立完善的风电功率预测管理机制，并在风电场端和电网调度端进行风电功率预测。西班牙、爱尔兰、美国新墨西哥电力公司(PNM)和美国德克萨斯州电力可靠度委员会(ERCOT)等国家(地区)电网公司对风电场功率预测提出强制性要求；美国加利福尼亚州电网公司(CAISO)则规定在加利福尼亚州电网公司辖区内的风电场可以自由选择风电功率预测系统提供商，而不是必须选择由加利福尼亚州电网公司指定的风电功率预测提供商。丹麦、德国、西班牙等国的可再生能源法赋予风电场优先上网权，但风电必须参与电力市场交易，功率预测作为风电参加电力市场的支撑手段，受到广泛重视。Costa等(2008)和Giebel等(2006)根据对天气预报结果的解释方式将风功率预测业务分为统计模型和物理模型两类，基于统计模型的业务系统如Riahy等(2008)先对观测风速进行有效的过滤，再用最小二乘回归法预测风速，并与实测风速进行对比验证该线性预测方法的可行性。Barbounis等(2006)利用人工神经网络方法对风速进行预测，将预测的时间长度延长到72 h以上。Kariniotakis等(1996)、Barbounis等(2006)和Cadenas等(2009)使用了一个机遇高阶动态神经网络的先进模型预测了风电场风电功率输出曲线；Du等(2008)用基于小波分析的支持向量机法，先将风速分解为低频波段和高频波段，然后用支持向量机分别预测，最后将其组合；Alexiadis等(1998)和Li等(2010)基于灰色模型，根据实际风电功率和对应时间序列风速的关系建模，得到风电功率随风速变化的各类模型下的拟合参数，对超短时平稳风速进行了一步至四步的预测。
基于物理模型的业务系统则尽可能通过机理性的分析来刻画本地风速特性，最后再通过模型输出统计或各种相对简单的统计技巧降低系统残留误差。在风电功率预报中主要使用的物理模型是数值天气预报模式，而全球尺度的数值天气模式的水平尺度相对于风电场来说太大了，所以通常采用中尺度数值天气模式。如Landberg(1994)开发了以数值天气预报和WAsP(Wind Atlas Analysis and Application Program)为基础的Prediktor风电功率预测系统，并用不同模式或方法的组合与Prediktor风电功率预测系统的预测效果进行了对比，验证了该预测系统的优越性。Nielsen等(2001)开发了Prediktor与WPPT(Wind Power Prediction Tool)相结合的Zephyr风电功率预测系统，提高了风电功率预报能力，在丹麦全国范围内得到应用，并推广到西班牙、爱尔兰、美国、日本等国家和地区。西班牙电网公司的Sipre lico 风电功率预测系统采用西班牙气象局数值预报产品和欧洲中期天气预报中心数值天气预报产品，通过8个风电功率预测模型，进行风电功率预报，再结合荷兰AEOLIS预测服务公司、西班牙工程技术研究所(IIC)和西班牙气象专业风能预报和风电功率预测公司的风电功率预测产品，最终得到未来48 h和10 d的风电功率预测(González et al，2004)。Lange等(2006)使用数值天气预报的产品作为输入数据结合计算流体力学(CFD)模型建立稳定流场条件下的数据库，从而预测风电功率，该方法能较好地预测实际风电场的风电功率，但未考虑大气稳定度对CFD模型的影响。Liu等(2011)介绍了一种先进的多尺度天气模式，它将天气尺度(约2000 km)和微尺度(约100 m)嵌套来模拟天气过程。这种建模系统，简称为WRF-RTFDDA-LES，是美国国家大气研究中心(NCAR)在天气研究与预报模型(WRF)的基础上建成的，加强了NCAR实时四维数据的同化(RTFDDA)能力。这个多尺度嵌套模型，以模拟小型和微型规模的真实天气环流作为重点地区，如风力发电场，大涡模拟(LES)模型的网格是FDDA根据现实的大尺度天气而确定的。Myers等(2011)在已有的NCAR数值预报模式系统的基础上，运用其先进的资料同化技术和集合预报技术，将风电场气象塔测风和风机测风数据同化到数值预报模式中，建立了风电场风能短期数值预报系统。
中国的风电功率预测工作起步较晚，以往短期风功率预测采用统计模型根据观测记录直接推算未来的风功率。如张华等(2010)利用支持向量机(Support Vector Machine，SVM)模型进行了短时风速预测。陈德生等(2012)用小波分析对原始风速序列进行多分辨率分析，再对不同频段上的风速序列建立时间序列主模型，用自回归条件异方差模型(ARCH)和广义自回归条件异方差模型(GARCH)进行改进风速预测。李慧杰等(2013)建立了基于相关向量机的短期风速预测模型。李元诚等(2012)利用核心向量回归(Core Vector Regression，CVR)模型进行风速预测。栗然等(2009)采用经验模式分解(Empirical Model Decomposition，EMD)方法将风速序列分解，再用自回归滑动平均时间序列的建模方法对分量进行分别预测。Feng等(2010)在数值天气预报的基础上，采用解析原理分析风电场局地效应与风电机组尾流影响的预测方法对风电功率进行预测。另外，孟天星等(2013)、刘永前等(2007)、潘迪夫等(2008)、刘兴杰等(2010)、马应魁(2010)、孙翰墨(2011)、孙斌等(2012)和许杨等(2013))均采用了一些现代的人工智能算法，但直接采用统计方法无法反映短期天气系统的随机性变化，预测效果具有较大的改进空间。
中国风电功率预测系统虽然已得到普及，但技术开发工作主要集中于电网调度方面的气象信息预测，目前主流的短期风功率预测系统普遍采用数值天气预报与微尺度模型嵌套的方案。如白龙等(2013)采用逐步回归的统计方法，将MM5数值预报产品与福建沿海地区测风塔实测气象资料要素指标值共同引入回归方程，拟合两座测风塔特定高度的逐时风速预报方程。李艳等(2009)利用区域气候模式MM5V3进行动力降尺度，以水平分辨率5 km分析了江苏省风能的分布特征。陈玲等(2012)用WRF模式对风电场风速进行预测，发现在提高水平分辨率的情况下，预测结果略有提升，但相差不大。汪君等(2013)利用WRF模式较好地预报了如东和南通及其附近地区10 m高度的风速，但在不同季节，不同地区的模拟效果有差异。徐永清等(2013)使用WRF模式对黑龙江省东部地区风速进行预报研究，并与测风塔70 m实测风速比较。分析表明，WRF模式能够很好地预报出风速的变化趋势和主导风向。张宇等(2013)用WRF模式预报了内蒙古风电场的短时风速，研究表明：不同数值模式参数化方案的预报能力没有实质性的区别。严晓瑜等(2014)用WRF模式预报了宁夏风电场的短时风速。孙川永等(2009)将美国科罗拉多大学发展的三维非静力区域大气模式(RAMS)应用于短时风速预报，水平分辨率达到1 km，与70 m高度的铁塔资料对比发现该模式对短时风速、风向模拟较好。李得勤等(2012)应用小尺度模式(CALMET模式)和双线性插值(BLI)方法对WRF模式9和3 km分辨率的预报风速进行降尺度处理，并对比预报风速和风塔观测资料。结果表明：WRF模式9 km分辨率的模式输出经过CALMET模式降尺度以后得到的风速预报效果比3 km分辨率的模式输出略好，CALMET模式和BLI方法对10 m/s以上的风速预报效果相对较差。这些试验均是在没有考虑下垫面的复杂性和小尺度天气系统的影响以及阵风、湍流等现象本身的复杂性的情况下，在微尺度模型中仍然采用统计模型对数值天气预报结果进行降尺度计算，无法显式地刻画地表高程和粗糙度对风流场的影响，同时也难以考虑限电和运维因素对预测结果的影响，而且在实际应用中，风电场的尺度比模拟区域小，对模式分辨率的要求更高，预报风速的高度应该是实际风电机所在的高度，故短期甚至临近预报只有中尺度气象模式也是不能胜任的。Zhu等(2012)也提出虽然基于物理模型的风功率预测系统能够更显式地刻画风电场的实际情况，但受到计算机硬件条件的限制，物理模型仅被应用在中尺度区域天气预报环节，而难以精细化地将物理模型应用到微尺度的风功率预测环节。
中国超过2/3的土地属于山地，地形和地表特征复杂，基于大气原始运动方程组求解的中尺度数值预报模式不能满足复杂地形近地层风场的预报需求，因此山地风电场的风电功率预测有必要通过大气湍流运动方程求解得到复杂地形风场的运动规律。采用中尺度数值预报模式输出结果驱动计算流体力学模式运算的动力降尺度方法，可以得到精细化的复杂地形风电场风速预报和发电功率预报，提高风电功率预测业务水平。本研究以复杂地形的风场精细化预报作为切入点，将中尺度数值模式与计算流体力学技术结合，通过离线制作能够描述风电场动力特性的基础特性库，实现在线快速的风功率动力降尺度计算，以满足风电场风电功率预测的时效要求。此外，在风电场运行期间，实际发电功率受到电网限电、风机维护检修等人工干预的影响较大，每天都不固定地会有一些风电机组停机。如果能够给出每台风电机组的功率预测，则可以根据风电场实际发电计划，上报整场发电量预测，以减少人工干预的影响。本研究的关键问题是解决中尺度模式预报结果如何驱动CFD模式的计算；为满足风电场短期风电功率预测的需求，如何在保证预报时效的前提下，作出复杂地形风电场风场的精细化预报。
2 预测系统设计目前，CFD数值模拟技术在风电场微观选址中得到了广泛的应用，实践证明，CFD软件对复杂地形风场的模拟精度较高。中尺度数值模式与CFD技术结合的方法也越来越多地应用于风电场前期选址工作中，在没有开展测风之前，进行初步选址。事实上，同样的方法是可以用于风电场的短期风电功率预测。中尺度数值天气预报模式可以给出1—5 km水平分辨率的近地层风场预测，CFD模式在此基础上通过动力降尺度给出每台风电机组轮毂高度的风速预测，进而得到发电量预测。但是，这是一个庞大的计算过程，一般从基础气象数据收集完毕到发电量预测送出，只有5—8 h的时间。在这段时间内。中尺度数值预报可以完成，但CFD计算的时间远远不够。
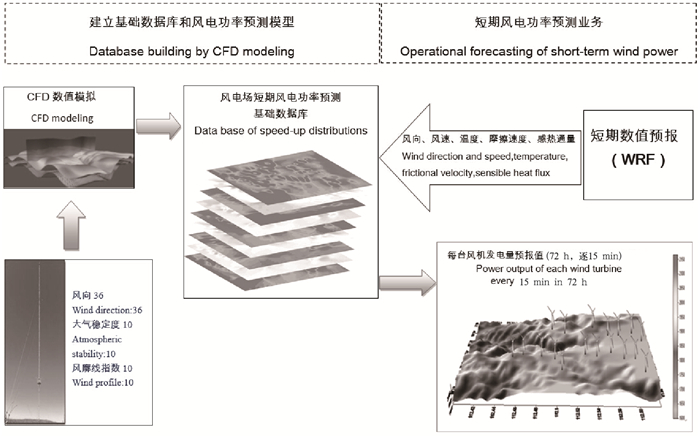
考虑到风电场区的风场分布是天气系统的运动在局地地形驱动下的结果，天气系统的运动可采用中尺度数值模式进行预报，由于局地地形是稳定不动的，可以采用CFD技术事先模拟出各种天气背景条件下的风场分布，建立微尺度风场基础数据库，然后直接根据中尺度数值天气预报，通过选择对应的风电场的风场分布，给出每台风电机组的风电功率预测。如图 1所示，风电场短期风电功率动力降尺度预测系统由中尺度短期数值天气预报模式、微尺度风场基础数据库和风电场端的风电功率预测集成系统组成，其中还包括两个统计订正模块：中尺度风速预报订正和风电机组模拟发电功率订正。
|
| 图 1 短期风电功率动力降尺度预测系统 Fig. 1 A schematic map for the short-term wind power dynamical downscaling forecast system |
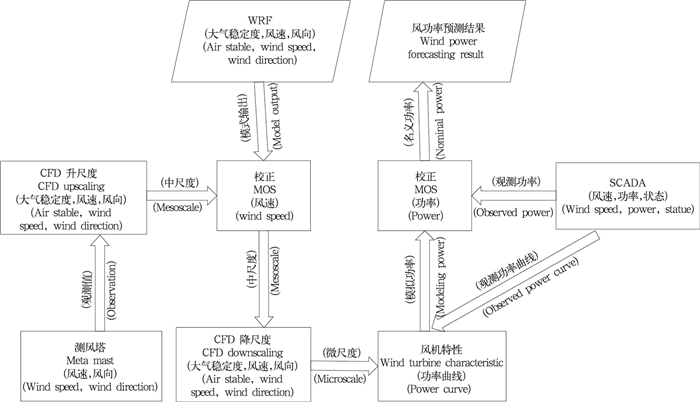
所示，首先采用基于风电场测风塔历史测风数据的中尺度风速预报订正模块对短期中尺度数值天气预报结果进行订正；然后根据订正后的中尺度数值天气预报结果，在微尺度风场基础数据库中选出对应的风电场微尺度风场分布，分析计算出各台风电机组的自由来流风速；再根据SCADA系统和测风塔观测风速统计得到的功率曲线，计算得到各台风电机组的模拟发电功率；之后采用风电机组模拟发电功率订正模块得到修正后的每台风电机组模拟发电功率；最后根据风电场运行维护计划，去除不运行的机组和机组不运行的时段，上报风电场全场发电功率预测。
|
| 图 2 短期风电功率预测业务流程 Fig. 2 Flow chart for the short-term wind power forecasting process |
对于近地层风场，空气密度变化幅度相对较小，因此采用不可压缩流体条件对下垫面流体进行简化，则近地层风场内部流场满足三维不可压缩瞬时纳维叶-斯托克斯方程的基本形式为
式中，ρ为空气密度，u为流速，p为气压，μ为粘度，F为重力、惯性、电场等体积力。
连续方程为
模拟流体最准确的方法是直接数值模拟(DNS)求解式(1)和(2)，但是要在远小于科尔莫哥罗夫长度尺度的网格中求解方程(针对自然风，湍流中最小涡旋尺寸从0.1 mm到1 mm)，由于式(1)的高度非线性特征，针对实际的工程流体直接数值模拟方法将远超出现有计算机的能力，因此，为了降低计算量，需要对式(1)进行简化。假设在给定空间与时间的任意一点处的风速是由平均风速(随时间变化很慢)与随机分量(随时间变化很快)叠加而成。因此，瞬时风速分量可以表示为
式中， u为平均风速，u′为脉动分量。
将式(3)代入式(1)与式(2)进行积分，对于定常流动可得如式(4)与式(5)中所示的定常不可压缩质量守恒和平均雷诺纳维叶-斯托克斯方程(RANS)。
式中，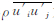
为针对扰动分量乘积所产生的高阶雷诺应力项，它表示由于湍流扰动而产生的动量附加传输，采用K-L湍流模型来预测雷诺应力对平均流的影响(Hurley，1997)。
与大气模式常用的基于控制方程在网格点泰勒展开的有限差分法不同，基于计算流体力学技术的微尺度建模采用有限体积法进行控制方程的离散化。在有限体积法中将所计算的区域划分成一系列控制体积，每个控制体积都有一个节点作代表，通过将守恒型的控制方程对控制体积作积分来导出离散方程。在导出过程中，需要对界面上的被求函数本身及其一阶导数的构成做出假定，这种构成的方式就是有限体积法中的离散格式。用有限体积法导出的离散方程可以保证具有守恒特性，而且离散方程系数的物理意义明确。采用有限体积法可以建立非正交甚至非结构化网格，能够更好地适应复杂地形网格划分和求解中对不规则区域刻画的需求，从而为精细化数值提供技术上的可能。
微尺度风场基础数据库描述在各种大气稳定度和风向的情况下风电场微尺度风速和风向偏差分布的相对关系。对于复杂地形风电场，风速分布与来流风向和大气稳定度密切相关，在指定大气稳定度和风向条件下，建立风电场区域的计算流体力学模型。如图 3所示，顶面和出口采用自由压力出流边界条件；地表采用固定壁面边界条件，通过地表粗糙度反映地表拖曳作用；侧面采用对称边界条件；入口采用风速廓线边界条件。
|
| 图 3 CFD模型边界条件 Fig. 3 CFD model boundary conditions |
对风电场CFD模型划分空间网格并求解后，获取风电场内各点相对于CFD模型入口处风速的加速因子。风电场区域内风加速因子Vh，0(x，y，z)是风向(d)和大气稳定度(s)的函数。
对于复杂地形风电场，不同海拔高度风速分布规律受大气稳定度的影响很大，应针对不同大气稳定度进行相应的湍流参数化计算，以增强微尺度风场基础数据库的可靠性。采用莫宁-奥布霍夫长度(L)来描述大气稳定度，L给出近地面层中机械湍流与因热效应而生成或抑制的湍流的相对比重。
其中，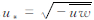
为摩擦风速，κ=0.35为冯卡门常数，g为重力加速度，T为空气温度，H为热通量，cp为空气比热，ρ为空气密度。莫宁-奥布霍夫长度可根据中尺度数值预报结果计算得到。各类大气稳定度所对应的风速垂直廓线，可根据测风塔历史观测资料分析得到，也可以采用CFD软件的预设值。
基于WT软件建立微尺度风场基础数据库，CFD模型定向计算扇区间隔为10°，水平网格分辨率为50 m，将大气稳定度划分为10个等级分别建立定向CFD模型。气象模式采用ARW内核的WRF模式，初值场为NCEP的00时再分析场资料逐日预报，水平分辨率为9 km×9 km，东西方向和南北方向网格数量分别为87和81，垂直分为49层，近地层加密。
| 莫宁-奥布霍夫长度 (L) | 稳定度等级 | 描述 |
| -140<L≤0 | 0 | 非常不稳定 |
| -1000<L≤-140 | 1 | 不稳定 |
| L≤-1000或L>2500 | 2 | 中性 |
| 1000<L≤2500 | 3 | 弱稳定 |
| 600<L≤1000 | 4 | 弱稳定 |
| 380<L≤600 | 5 | 稳定 |
| 240<L≤380 | 6 | 稳定 |
| 160<L≤240 | 7 | 稳定 |
| 80<L≤160 | 8 | 非常稳定 |
| L≤80 | 9 | 非常稳定 |
微尺度风场基础数据库描述了风电场风加速因子和风向偏差与中尺度风向、大气稳定度和CFD模型入口廓线的对应函数关系。在统一大气稳定度和CFD模型入口廓线的对应关系后，可由中尺度风向和大气稳定度驱动微尺度风场基础数据库，降尺度后获取风电场全场的风加速和风向偏差分布。中尺度风速代表大气模式水平分辨率尺度范围内的平均风速，如式(8)所示，以中尺度数据代表范围的风加速因子平均值作为参考风加速因子，并由式(9)获得相对于中尺度数据代表范围的风电场全场风加速因子Vh(x，y，z)。根据式(10)，利用大气模式输出的中尺度风速预报值Vmeso驱动微尺度风场基础数据库获得风电场全场风速预测值V(x，y，z)。
考虑到气象模式分辨率相对于CFD模型分辨率较低，气象模式对复杂地形风电场地形细节刻画不够细致，从而低估了地形起伏对中尺度风切变的影响。根据气象模式给出的行星边界层高度，划分气象模式与CFD模型各自的适用范围。采用气象模式进行行星边界层高度以上大气的中尺度模拟，采用风电场CFD模型描述行星边界层高度以下的风资源特性；选取常年平均行星边界层高度作为中尺度大气模式与微尺度风场基础数据库嵌套高度。
2.4 风机功率曲线辨识风电功率预测系统中风机特性描述的是轮毂高度处自由来流风速与风机发电功率的函数关系，通常用风机的功率曲线表达风机特性。风电机组SCADA(Supervisory Control And Data Acquisition)记录的风速是旋转风轮背后的风速，风轮前方自由来流风速可由风电场中的测风塔观测风速进行推算。为保证短期风电功率预测的准确率，有必要对采用SCADA记录风速还是采用推算自由来流风速获得风机功率曲线进行挑选。
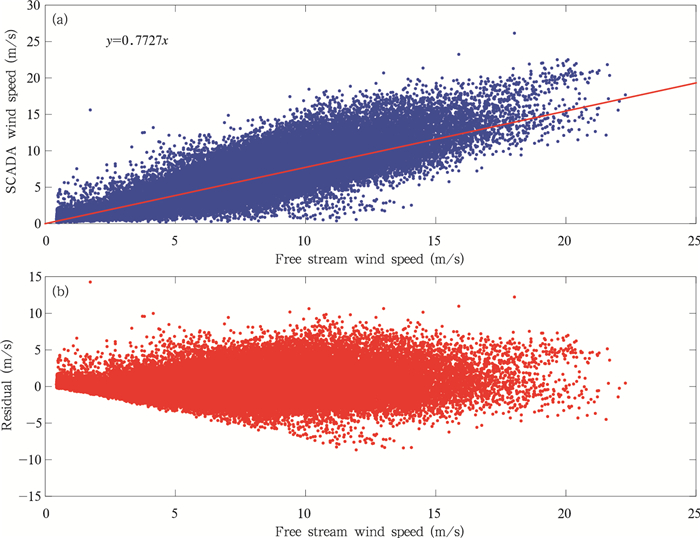
图 4为采用CFD微尺度模型由测风塔实测风速推算得到的辽宁某风电场1号机位自由来流风速与该风机SCADA记录风速的关联分析，图 4a为自由来流风速与SCADA记录风速时间序列散点分布和线性拟合曲线，图 4b为线性拟合的残差。可以看出，该风机SCADA记录风速为自由来流风速的0.7727倍，受到风轮遮挡的影响，SCADA记录的机舱顶部风速相对于自由来流风速具有明显的衰减，应采取自由来流风速代替SCADA记录风速进行风机的功率曲线分析。
|
| 图 4 辽宁某风电场1号机位自由来流风速与SCADA记录风速的关联 Fig. 4 Wind speed association between the free stream and SCADA recordings of No.1 windturbine in a Liaoning wind farm |
因此，本研究利用微尺度风场基础数据库中各类风向和稳定度条件下的微尺度风场分布关系，根据测风塔历史观测风速推算得到各风机机位自由来流风速，并与SCADA系统同期发电功率记录进行关联，拟合得到各台风机的功率曲线。在实际功率预测中，采用中尺度模式WRF和计算流体力学技术降尺度得到各风机自由来流风速后，再根据风机功率曲线插值获取风机发电功率预测结果。
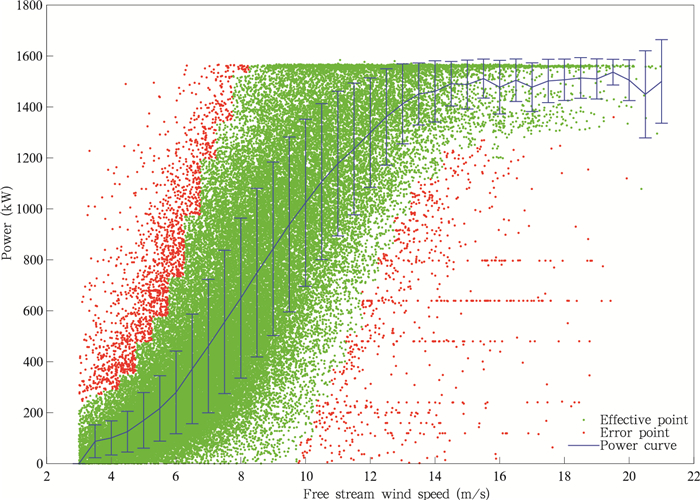
结合测风塔观测风速推算得到的各机位自由来流风速和各台风机SCADA系统观测的同期发电功率历史数据，拟合出各风机的功率曲线。考虑到风机故障点对SCADA记录的干扰，将风速分成若干个连续的统计区间，假设各风速区间内SCADA观测记录服从正态分布，采用拉依达准则(即3σ法则)对SCADA观测数据分区间处理，将发电功率超过统计区间内3倍功率方差的记录点作为坏点剔除。重新计算剔除坏值后测量序列的算术平均值和功率方差，再行判断，直至余下测量值中无坏点存在。2011年度辽宁某风电场1号风机对应自由来流风速的拟合功率曲线如图 5，剔除掉自由来流风速和发电功率记录坏点后，采用局部加权最小二乘回归法拟合功率曲线，指数衰减函数作为加权函数w，样本点距离预测点越远其权重越小:
式中，V为预测点风速，V(i)为统计区间内第i个样本点风速；τ为波长参数，它控制了权值随距离下降的速率。
|
| 图 5 辽宁某风电场1号风机功率曲线 Fig. 5 Power vs. free stream wind speed curve of No.1 windturbine in a Liaoning wind farm |
考虑到空气密度随着季节的变化，在实际风电功率预测业务中，采用最近3个月的SCADA数据记录滚动辨识功率曲线。
2.5 校正模块受到大气模式系统偏差的影响，需要采用风场实际观测数据对中尺度天气预报结果进行滚动校正。利用微尺度风场基础数据库，输入校正期间测风塔观测风速，计算出对应的中尺度风速并与模式输出风速进行相关分析，获得校正关系。考虑到风电功率预测业务的时效性，文中采用线性最小二乘法进行相关和校正。
受到季节变化引起空气密度变化的影响，不同季节的风机功率曲线有差异，因此需要对发电功率进行滚动校正。在实际业务中，筛选出校正期间发电计划不受人工干预的发电功率时间序列，采用线性最小二乘法进行相关预测功率与SCADA记录功率进行相关分析并确定校正系数。
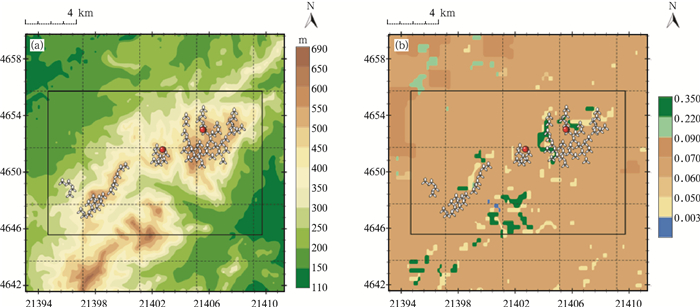
3 业务预报试验 3.1 项目概况本研究建立的风电场短期风电功率动力降尺度预测系统于2014年7月1日—2015年1月31日在辽宁省某风电场项目进行了业务预报试验。试验风电场地形地貌如图 6。该风电场配备67台风轮直径77 m的1500 kW双馈风力发电机组，轮毂高度为70 m。风场内部设有两座测风塔(图 6中的红点所示)，测风高度为70 m，综合考虑两座测风塔观测数据后，得到风电场范围内年平均风速分布(图 7)。采用2011年1月—2012年8月各风机的SCADA数据和同期的测风塔观测资料进行气象模式的校正和功率曲线的统计。
|
| 图 6 试验风电场地形地貌(a.地形，b.粗糙度) Fig. 6 Topography and l and forms of the experiment wind farm(a.topograqphy，b.roughness) |
|
| 图 7 试验风电场年平均风速分布 Fig. 7 Distribution of the annual average wind speed of the experiment wind farm |
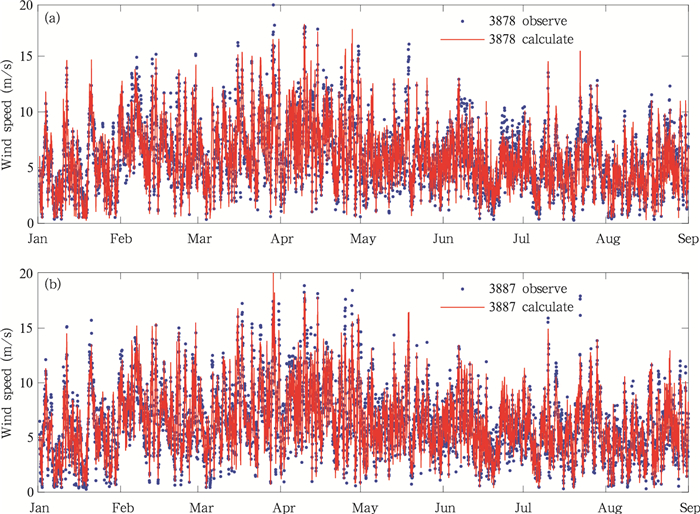
基于WT软件建立的微尺度风场基础数据库，水平网格分辨率为50 m，CFD定向计算扇区间隔为10°，将大气稳定度划分为10个等级分别建立定向CFD模型。风场内部两座测风塔编号分别为3887和3878，两塔相距3.16 km，采用测风塔观测数据互相推算彼此位置的风速(图 8)，验证微尺度风场基础数据库的准确度。
|
| 图 8 双塔互推验证 Fig. 8 Two tower mutual examination verification |
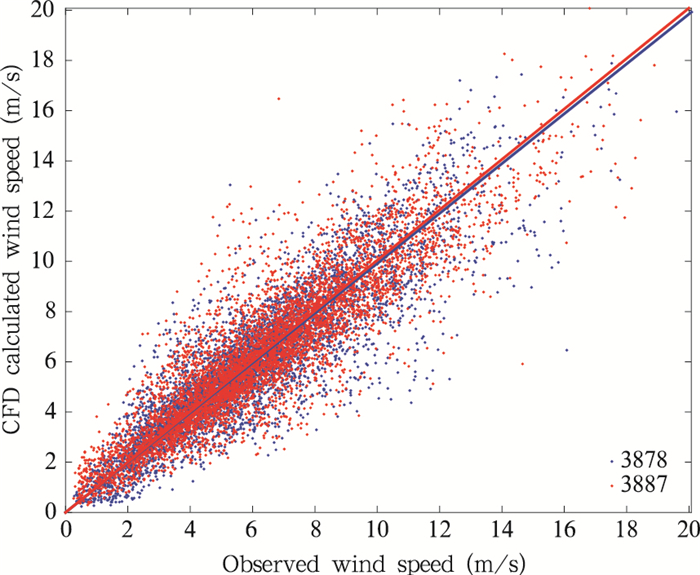
两测风塔观测数据的相关系数为0.8868(图 9)，3878号测风塔观测 值与计算值的相关系数为0.8895，平均风速相对误差为0.7616%；3887号测风塔观测值与计算值的相关系数为0.8938，平均风速相对误差为0.43%。由于在风电场基础数据库中融合了计算流体力学技术的动力模型，能够显式地描述地形和地貌对风流场的影响，相对于两测风塔观测数据的相关系数，微尺度风场基础数据库推算得到的计算值与观测值的相关系数有所提高，基于动力降尺度技术的风场基础数据库在微尺度精细化预报业务上相对于传统的统计模型具有技术上的优越性。
|
| 图 9 相关性分析 Fig. 9 Two tower correlation analysis |
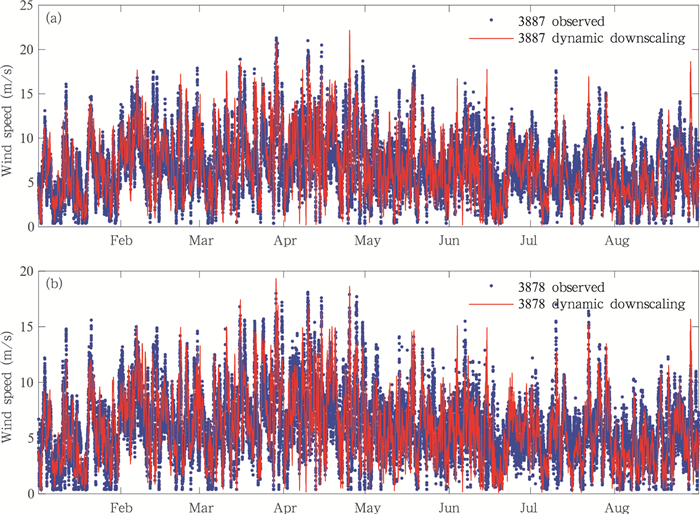
采用FNL再分析数据和WRF进行区域模式计算，获取与测风塔历史观测数据同期的9 km分辨率中尺度回报数据(图 10)，利用中尺度回报数据驱动微尺度风场基础数据库进行降尺度，获得测风塔位置的风速回报结果并与测风塔观测数据进行对比，验证降尺度模型的准确度。
|
| 图 10 动力降尺度回报验证 Fig. 10 Dynamic downscale correlation analysis |
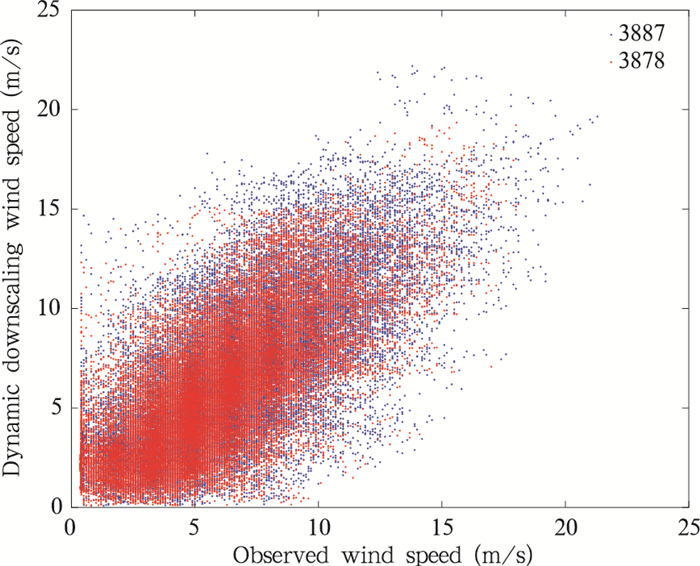
如图 11所示，3878号测风塔观测值与动力降尺度计算值的相关系数为0.688，3887号测风塔观测值与动力降尺度计算值的相关系数为0.693。相对于微尺度风场基础数据库采用测风塔观测值双塔互推的计算值与观测值的相关系数，采用中尺度回报值推算的计算值与观测值的相关系数明显下降，表明动力降尺度模型的主要误差来源于中尺度模式，动力降尺度技术本身已经能够较好地解决微尺度地形、地貌对近地层流场的影响问题。
|
| 图 11 动力降尺度相关性分析 Fig. 11 Dynamic downscale correlation analysis |
基于中尺度数值模式WRF与CFD结合的短期风电功率动力降尺度预测系统的优势在于具有复杂地形风场的风电功率预测能力，能够给出每台风电机组的功率预测，风电场可以将因限电和运维因素的影响而停运的风电机组的功率扣除，再上报整场发电量，从而提高预报准确率。
为检验短期风电功率动力降尺度预测系统的实际预测效果，对比分析了3种预测方法的误差：(1)直接采用中尺度模式WRF预测风速，借助微尺度风场基础数据库中各风向和稳定度条件下的微尺度流场分布关系，分析得到每台风机轮毂高度处风速，结合风机辨识曲线得到发电量预测；(2)采用短期风电功率动力降尺度预测系统，但不考虑风电场限电和运维因素的影响，默认每台风电机组都正常运行；(3)采用短期风电功率动力降尺度预测系统，考虑风电场限电和运维因素的影响，扣除停运风电机组的发电量。根据式(12)统计风电功率预测结果的误差。
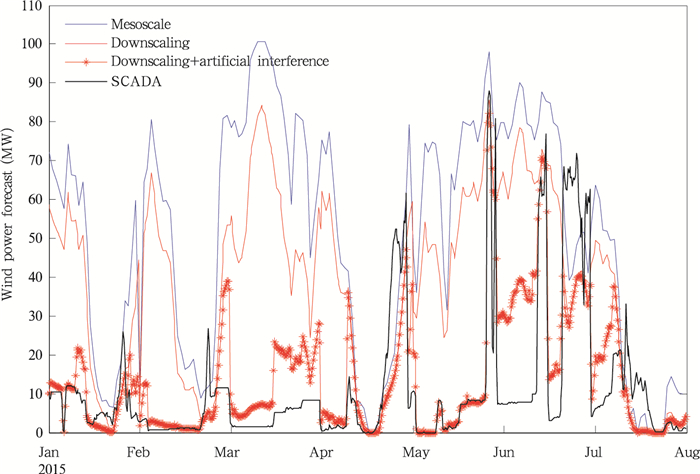
其中，PMi为i时刻的实际功率；PPi为i时刻的预测功率；Cap为风电场的开机总容量； n为所有的样本个数。 3.4.1 个例分析
随机选择2015年第1周发电功率预测结果(图 12)，分别对比中尺度模式预报直接预测与短期风电功率动力降尺度预测系统的预测效果和是否考虑风电场限电和运维因素的预测效果。
|
| 图 12 2015年第1周风电功率预测结果 Fig. 12 Wind power forcastiing results for the first week of 2015 |
从图 12可以看出，短期风电功率动力降尺度预测系统的预测误差明显低于中尺度模式直接预测的误差。中尺度模式的预测量代表网格平均值，模式中将地形也处理成网格平均，即在本研究的中尺度数值预测中，每个9 km×9 km网格中的地形为相同高度，风速代表中尺度网格区域的平均风速。由于中尺度网格分辨率较低，模式无法刻画9 km范围内地形起伏对近地层风流场的拖曳作用，导致近地层中尺度预测的风切变偏小，近地层预测的风速更接近高空的高风速，中尺度模式直接预测的发电功率偏大，预测相对误差为0.5182。而CFD动力降尺度模式的水平分辨率为50 m×50 m，明显较中尺度模式更接近真实地形，能够刻画50 m以上区域内地形起伏对风流的拖曳作用，因此预测风速更准确，风电功率预测准确率也更高，短期风电功率动力降尺度预测系统的预测相对误差为0.4685。
2015年第1周的短期风电功率动力降尺度预测系统预测结果表明，不考虑风电场限电和运维因素影响的预测相对误差为0.4685，考虑风电场限电和运维因素影响后，预测相对误差下降到0.1491。1月5日风电 场开机率为21.83%，不考虑风电场限电和运维因素影响的预测相对误差为0.5595，考虑风电场限电和运维因素影响后，预测相对误差下降到0.1399；1月6日的开机率为64.68%，不考虑风电场限电和运维因素影响的预测相对误差为0.5607，考虑风电场限电和运维因素影响后，预测相对误差0.2614。可以看出，开机率越低，考虑限电和运维因素影响对发电功率预测误差的改善越明显。
此外，短期风电功率预测效果受到中尺度模式预报系统误差的影响，例如1月2日夜间和1月5日凌晨在不限电的情况下，发电功率预测波形存在一定的滞后。可见，在不限电的情况下，天气预报的误差是导致发电功率预测误差的主要原因。
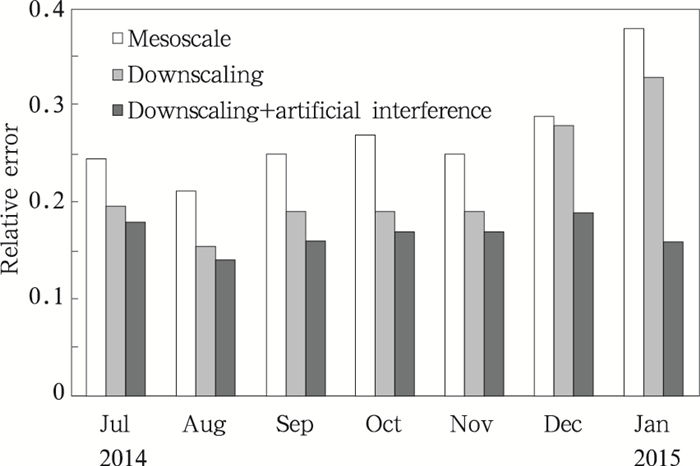
3.4.2 总体预测效果分析从2014年7月—2015年1月的逐月风电功率预测误差(图 13)可知，中尺度模式直接预测风电功率的预测平均相对误差为0.2759，考虑限电和运维因素影响后的中尺度模式直接预测风电功率预测平均相对误差为0.2058，7个月均不满足国家电网对风电功率预测月均误差低于0.2的要求。采用动力降尺度技术后，预测结果能够更好地刻画风电场复杂地形对近地层风流分布的影响，短期风电功率动力降尺度预测系统的风电功率预测平均相对误差为0.2269，2014年12月和2015年1月均不满足国家电网要求；考虑限电和运维因素影响后平均相对误差为0.1677，7个月均满足电网要求。
|
| 图 13 风电功率预测相对误差 Fig. 13 Wind power forecasting averaged relative errors(from Jul 2014 to Jan 2015) |
应用中尺度气象模式与微尺度的CFD模型相结合的动力降尺度技术，建立了适用于复杂地形的短期风电功率动力降尺度预测系统，业务预报试验验证表明：
(1)短期风电功率动力降尺度预测系统可预测不同大气稳定度条件下的复杂地形风场，可给出风电场中每台风电机组的功率预测，提高了复杂地形风场精细化预报能力，同时使风电场有条件在上报发电量时扣除因限电和运维因素等人工干预的影响。
(2)离线建立风电场微尺度风场基础数据库，解决了计算流体力学无法满足短期风电功率预测的时效问题。短期风电功率动力降尺度预测系统的应用不受具体项目地形复杂程度和历史观测数据样本量的限制，可以在新建风电场中推广应用，具备实际的可操作性。
(3)业务试验效果检验结果表明，考虑风电场限电和运维因素影响后，短期风电功率动力降尺度预测系统的预测误差可降低26%，能够满足国家电网对风电功率预测误差的业务要求。
(4)采用短期风电功率动力降尺度预测方法，在不限电的情况下，发电功率预测误差主要来自中尺度天气预报的误差；在限电的情况下，开机率越低，考虑风电场限电和运维因素影响对发电功率预测误差的改善越明显。
| 白龙, 吴息, 丁宇宇等. 2013. 用于风电场功率预测的逐时风速预报. 气象科技,41(4):777-783. Bai L, Wu X, Ding Y Y, et al. 2013. Hourly wind speed forecasting for wind farm power prediction. Meteor Sci Technol, 41(4):777-783 (in Chinese) |
| 陈德生, 李培强, 李欣然等. 2012. 基于小波变换的短期风速预测综合模型. 电工电能新技术,31(3):73-76. Chen D S, Li P Q, Li X R, et al. 2012. Integrated models of short-term wind speed forecasting based on wavelet transform. Adv Technol Elect Eng Energy, 31(3):73-76 (in Chinese) |
| 陈玲, 赖旭, 刘霄等. 2012. WRF模式在风电场风速预测中的应用. 武汉大学学报(工学版),45(1):103-106. Chen L, Lai X, Liu X, et al. 2012. Application of WRF model to wind speed forecasting in wind power farms. Eng J Wuhan Univ, 45(1):103-106 (in Chinese) |
| 李得勤, 陈力强, 周晓珊等. 2012. 风电场风速降尺度预报方法对比分析. 气象与环境学报,28(6):25-31. Li D Q, Chen L Q, Zhou X S, et al. 2012. Comparison analysis of downscaling forecast methods on wind speed in wind power field. J Meteor Environ, 28(6):25-31 (in Chinese) |
| 李慧杰, 刘亚南, 卫志农等. 2013. 基于相关向量机的短期风速预测模型. 电力自动化设备,33(10):28-32. Li H J, Liu Y N, Wei Z N, et al. 2013. Short-term wind speed forecasting model based on relevance vector machine. Elect Power Automat Equip, 33(10):28-32 (in Chinese) |
| 李艳, 汤剑平, 王元等. 2009. 区域风能资源评价分析的动力降尺度研究. 气候与环境研究,14(2):192-200. Li Y, Tang J P, Wang Y, et al. 2009. Application of dynamical downscaling method for assessment of wind energy resources. Climatic Environ Res, 14(2):192-200 (in Chinese) |
| 李元诚, 杨瑞仙. 2012. 用于短期风速预测的优化核心向量回归模型. 中国电力, 45(3):68-71. Li Y C, Yang R X. 2012. An optimized CVR model for short-term wind speed forecasting. Elect Power, 45(3):68-71 (in Chinese) |
| 栗然, 王粤, 肖进永. 2009. 基于经验模式分解的风电场短期风速预测模型. 中国电力, 42(9):77-81. Li R, Wang Y, Xiao J Y. 2009. Short-term wind speed forecasting for wind farms based on empirical mode decomposition model. Elect Power, 42(9):77-81 (in Chinese) |
| 刘兴杰, 米增强, 杨奇逊等. 2010. 基于经验模式分解和时间序列分析的风电场风速预测. 太阳能学报, 31(8):1037-1041. Liu X J, Mi Z Q, Yang Q X, et al. 2010. Wind speed forecasting based on EMD and time-series analysis. Acta Energ Solaris Sin, 31(8):1037-1041 (in Chinese) |
| 刘永前, 韩爽, 胡永生. 2007. 风电场出力短期预报研究综述. 现代电力, 24(5):6-11. Liu Y Q, Han S, Hu Y S. 2007. Review on short-term wind power prediction. Mod Elect Power, 24(5):6-11 (in Chinese) |
| 马应魁. 2010. 短期风速多步预测的研究. 工矿自动化, 36(9):54-58. Ma Y K. 2010. Research of multi-step forecasting for short-term wind speed. Indust Mine Automat, 36(9):54-58 (in Chinese) |
| 孟天星, 张厚升. 2013. 基于ARIMA模型的风电场短期风速预测. 科学技术与工程, 13(33):27-32. Meng T X, Zhang H S. 2013. Wind speed short-term forecast for wind farms based on ARIMA model. Sci Technol Eng, 13(33):27-32 (in Chinese) |
| 潘迪夫, 刘辉, 李燕飞. 2008. 风电场风速短期多步预测改进算法. 中国电机工程学报, 28(26):87-91. Pan D F, Liu H, Li Y F. 2008. Optimization algorithm of short-term multi-step wind speed forecast. Proc CSEE, 28(26):87-91 (in Chinese) |
| 孙斌, 姚海涛, 刘婷. 2012. 基于高斯过程回归的短期风速预测. 中国电机工程学报, 32(29):104-109. Sun B, Yao H T, Liu T, et al. 2012. Short-term wind speed forecasting based on Gaussian process regression model. Proc CSEE, 32(29):104-109 (in Chinese) |
| 孙川永, 陶树旺, 罗勇等. 2009. 高分辨率中尺度数值模式在风电场风速预报中的应用. 太阳能学报, 30(8):1097-1099. Sun C Y, Tao S W, Luo Y, et al. 2009. The application of high resolution mesoscale model in wind speed forecasting in wind farm. Acta Energ Solaris Sin, 30(8):1097-1099 (in Chinese) |
| 孙翰墨. 2011. 基于ARMA模型的风电机组风速预测研究[D].北京:华北电力大学. Sun H M. 2011. The research on wind speed prediction for WTG based on ARMA model[D]. Beijing:North China Electric Power University (in Chinese) |
| 汪君, 王会军. 2013. WRF模式对江苏如东地区风速预报的检验分析. 气候与环境研究, 18(2):145-155. Wang J, Wang H J. 2013. Forecasting of wind speed in Rudong, Jiangsu province, by the WRF model. Climatic Environ Res, 18(2):145-155 (in Chinese) |
| 徐永清, 刘春生, 张弛等. 2013. 基于WRF模式的短期风速预报研究. 安徽农业科学, 41(8):3539-3541, 3615. Xu Y Q, Liu C S, Zhang C, et al. 2013. Study of short-term wind speed forecast based on WRF. J Anhui Agri Sci, 41(8):3539-3541, 3615 (in Chinese) |
| 许杨, 陈正洪, 杨宏青等. 2013. 风电场风电功率短期预报方法比较. 应用气象学报, 24(5):625-630. Xu Y, Chen Z H, Yang H Q, et al. 2013. Comparison of short-term forecast method of wind power in wind farm. J Appl Meteorol Sci, 24(5):625-630 (in Chinese) |
| 严晓瑜, 李剑萍, 杨侃等. 2014. 两种模式在风电场风速预测应用中的对比. 干旱气象, 32(6):1015-1024. Yan X Y, Li J P, Yang K, et al. 2014. Application and comparison of WRF and BJ-RUC models on wind speed forecast in wind power field. J Arid Meteor, 32(6):1015-1024 (in Chinese) |
| 张华, 曾杰. 2010. 基于支持向量机的风速预测模型研究. 太阳能学报, 31(7):928-932. Zhang H, Zeng J. 2010. Wind speed forecasting model study based on support vector machine. Acta Energ Solaris Sin, 31(7):928-932 (in Chinese) |
| 张宇, 郭振海, 林一骅等. 2013. 中尺度模式风电场风速短期预报能力研究. 大气科学, 37(4):955-962. Zhang Y, Guo Z H, Lin Y H, et al. 2013. Predictive capacity of mesoscale model for short-range wind speed forecasting at wind power farm. Chinese J Atmos Sci, 37(4):955-962 (in Chinese) |
| Alexiadis M C, Dokopoulos P S, Sahsamanoglou H S, et al. 1998. Short-term forecasting of wind speed and related electrical power. Solar Energy, 63(1):61-68 |
| Barbounis T G, Theocharis J B, Alexiadis M C, et al. 2006. Long-term wind speed and power forecasting using local recurrent neural network models. IEEE Trans Energy Conv, 21(1):273-284 |
| Cadenas E, Rivera W. 2009. Short term wind speed forecasting in la venta, Oaxaca, México, using artificial neural networks. Renew Energy, 34(1):274-278 |
| Costa A, Crespo A, Navarro J, et al. 2008. A review on the young history of the wind power short-term prediction. Renew Sustain Energy Rev, 12(6):1725-1744 |
| Du Y, Lu J P, Li Q, et al. 2008. Short-term wind speed forecasting of wind farm based on least square-support vector machine. Power Syst Technol, 32(15):62-66 |
| Feng S L, Wang W S, Liu C, et al. 2010. Study on the physical approach to wind power prediction. Proc CSEE, 30(2):1-6 |
| Giebel G, Badger J, PerezI M, et al. 2006. Short-term forecasting using advanced physical modelling:The results of the anemos project//Proceedings of the European Wind Energy Conference. Athens |
| González G, Diaz-Guerra B, Soto F, et al. 2004. Sipreólico:Wind power prediction tool for the Spanish peninsular power system//Proceedings of the CIGRÉ 40th general session and exhibition. Paris, France |
| Hurley P J. 1997. An evaluation of several turbulence schemes for the prediction of mean and turbulent fields in complex terrain. Bound-Layer Meteor, 83(1):43-73 |
| Kariniotakis G N, Stavrakakis G S, Nogaret E F. 1996. Wind power forecasting using advanced neural networks models. IEEE Trans Energy Convers, 11(4):762-767 |
| Landberg L, Watson S J. 1994. Short-term prediction of local wind conditions. Bound-Layer Meteor, 70(1):171-195 |
| Lange M, Focken U. 2006. Physical Approach to Short-Term Wind Power Prediction. Beilin:Springer |
| Li J F, Zhang B H, Xie G L, et al. 2010. Grey predictor models for wind speed-wind power prediction. Power Syst Protect Control, 38(19):151-159 |
| Liu Y B, Warnera T, Liu Y W, et al. 2011. Simultaneous nested modeling from the synoptic scale to the les scale for wind energy applications. J Wind Eng Indust Aerodyn, 99(4):308-319 |
| Myers W, Linden S. 2011.A turbine hub height wind speed consensus forecasting system// 91st American Meteorological Society Annual Meeting, Seattle (US). |
| Nielsen T S, Madsen H, Nielsen H A, et al. 2001. Zephyr-the prediction models//European Wind Energy Conference, 868-871 |
| Riahy G H, Abedi M. 2008. Short term wind speed forecasting for wind turbine applications using linear prediction method. Renew Energy, 33(1):35-41 |
| Zhu X X, Genton M G. 2012. Short-term wind speed forecasting for power system operations. Int Statist Rev, 80(1):2-23 |