中国气象学会主办。
文章信息
- 熊敏诠. 2012.
- XIONG Minquan. 2012.
- Delaunay三角剖分法在降水量插值中的应用
- Delaunay triangulated method with an application to the precipitation interpolation
- 气象学报, 70(6): 1390-1400
- Acta Meteorologica Sinica, 70(6): 1390-1400.
- http://dx.doi.org/10.11676/qxxb2012.117
-
文章历史
- 收稿日期:2011-10-06
- 改回日期:2012-03-03
2. 中国科学院大学,北京,100049;
3. 国家气象中心,北京,100081
2. University of China Academy of Sciences, Beijing 100049, China;
3. National Meteorological Center, Beijing 100081, China
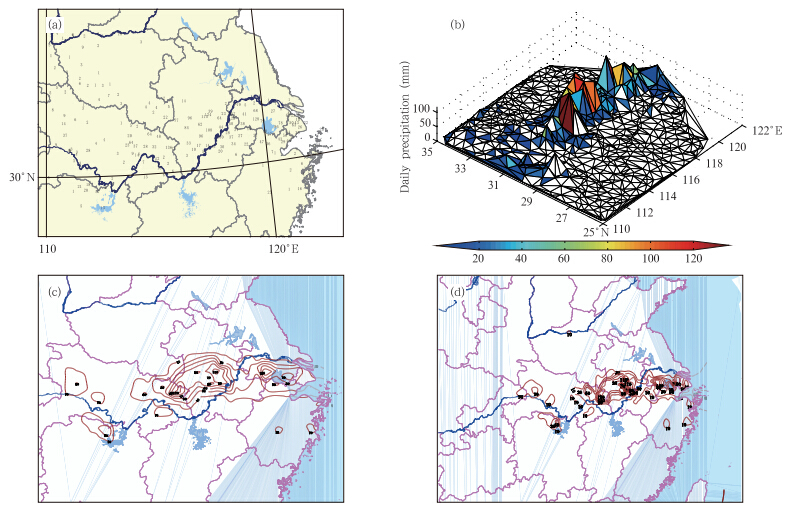
气象观测数据相对于广阔地域来说是十分有限的,而且呈离散分布。当需要更为精细的气象要素值时,将采取性能各异的数学方法和定性分析手段,把站点观测插值到相应空间上;同时,在较多研究和应用中,不仅需要空间某点的要素值,更需要了解气象要素在空间上的分布状况,或者能通过较直观的图形来描述,因此,在点上的插值算法难以满足要求。不规则三角网是基于平面提出的几何模型,其无缝隙、不重叠、完整地覆盖整个空间,主要是根据观测点状况将平面划分成许多较小的三角形,气象要素的空间关系可以通过这些紧密相连的面元表达。
例如:在分析某个区域的降水量空间分布时,往往是以观测点为基点进行泰森多边形划分,测点上的降水量就代表其所在的多边形面元上所有点的降水量,根据降水量大小,把各个多边形面元提升到相应高度,可以在空间上直观地描述降水量的面分布(图 1a);从图 1a中可以看出存在以下问题:首先难以得到多边形的各边上准确的降水量值;其次是由于断点的存在,边界附近的降水量呈现跳跃式、非连续性特点;另外,在多边形内部降水量是常数,这和降水量变化特性是不相符的。Delaunay三角剖分法能有效解决上述问题,使用观测点的位置作为三角形的顶点,构建Delaunay三角网,同样,以降水量为第三维,在空间中就生成了降水量分布的立体图(图 1b),构成了覆盖研究区域上的、由许多紧密相邻三角片自然拼成的大曲面,区域面上任意点的降水量和所在的三角形倾斜度、标高和位置相关,三角片上每个点的降水量并不是常数,同泰森多边形划分法相比,Delaunay三角剖分法对雨量空间描述更精确、更自然(de Berg et al,2000)。
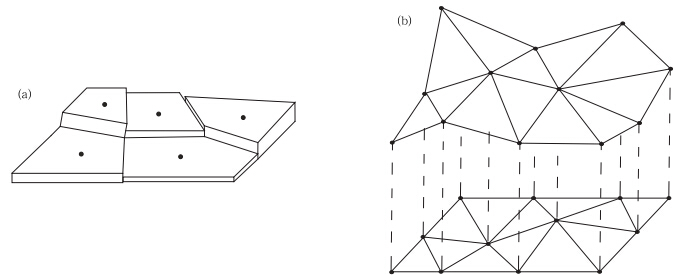 |
| 图 1 降水量三维图(a.泰森多边形,b.Delaunay三角形) Fig. 1 Three-dimensional illustrations of precipitation(a. Thiessen polygon,b.Delaung triangulation) |
科研机构十分重视气象站点资料的格点化,并有大量的研究,如美国国家海洋大气局(NOAA)的全球综合分析降水量数据集(CMAP),英国East Anglia大学的高分辨率地表气候变量数据集(CRU TS),美国的全球海洋大气综合数据集(COADS),Hulme(1992)的降水量数据集,李庆祥(2007)的中国区域气温格点数据集。插值方法是站点数据网格化的基础,往往需要对各种算法误差进行比较,再确定适用的插值法;但是,无论何种插值算法都要首先面对一个共同的问题——邻近点的选择。邻近点的选择是空间数据分析的重要研究方向,尽可能使所选择的邻近点均匀地分布在待估点周围;在站点较密集的区域,就显得尤为重要。这是因为:(1)使用适量的已知点对于插值的精度很重要,当已知点过多时,会使插值准确率下降,因为过多的信息量会掩盖有用的信息,这和降水量空间相关性有密切关系;(2)被选择的邻近点构成的点分布不均匀,若某个方位上的数据点过多,或点集的某些数据点位置较集中,或者数据点过远,都会带来较大的插值误差;(3)过多的数据点将导致较大的计算负担,例如:降水量插值中经常使用的克立格方法(Ling et al,2010; Schuurmans et al,2007),其计算复杂度是0(n3),当所选数据点n超过一定数值时,对于覆盖范围广和数据量大的气象领域的插值问题,普通计算环境无法承担如此量级的存储开销和计算耗时。显然,寻找一种恰当的空间拓扑结构是解决邻近点选择的有效途径之一,这方面有待深入研究。
Delaunay三角剖分法是根据一定规则,建立空间离散点的联系,构建正三角形,解决空间插值的难题。由于Delaunay三角网的良好特性,在地学、测绘、水利、城市规划、交通等多领域被普遍接受并广泛应用(Chris et al,2007;Hassan et al,2011; Sergio et al,2009;赵博等,2007)。Delaunay三角剖分法建立的观测站点间的几何拓扑结构则可以较好地解决邻近点选择问题,以此为基础进行的插值将能提高计算效率和获得更佳的插值精度;随着气象站点资料的网格化发展,Delaunay三角剖分法能发挥其应有的价值。
在气象领域的其他方面,Delaunay三角剖分法也有其可能的应用,例如:气象站网的设计;因为经常要使用观测站的资料插值到没有观测的空间任意点上,那么何种气象站空间分布能有较高插值精度,这就是气象站网设计的目标;结构函数(Drozdov et al,1946)是气象站网合理分布研究的主要手段。分析表明,台站的正三角形分布有利于提高插值精度(杨贤为等,1987;赵瑞霞等,2007),也就是说,在一定条件下,可以使用Delaunay三角剖分法获得合理的气象观测站布局。这也说明了性能良好的空间拓扑结构能够降低插值误差。另外,在雷达联合雨量计估测降水量时,雨量计的分布特点将影响到降水量估值精度(田付友等,2010; Till et al,2010)。2 Delaunay三角剖分法 2.1 Delaunay三角剖分法介绍
Delaunay三角剖分法具有严格的数学定义和完备的理论基础。它起源于Voronoi图(简称V图),1850年Dirichlet讨论了V图概念; Voronoi于1908年在数学上定义了V图,V图主要用于分析空间点集或者其他几何对象和距离有关的问题;1911年,Thiessen在计算面雨量时,根据观测站点的降水量分布,讨论了V图构造及其计算方法;1934年,Delaunay在分析V图的基点间直线嵌入时,首次提出了Delaunay三角网络概念;1975年,Shamos和Hey讨论了使用计算机有效地构建V图,标志着计算几何的诞生,V图和Delaunay三角网是计算几何的重要基石。
Delaunay三角网是V图的对偶图,具有两个重要特性:(1)空外接圆性质:在点集P构建的Delaunay三角网中,每个三角形的外接圆中均不包含点集P中其他任意点,即任意4点不共圆。(2)最大化最小角性质:三角网中每个三角形的角度尽可能最大,即在两个相邻三角形构成的四边行中,当变换四边形的对角线时,6个内角的最小角不再增大,并且使三角形各边尽量接近等边。
根据上述性质,Delaunay三角剖分是最优的三角剖分,具有广泛的应用价值,也常用来作为其他三角剖分算法的初始剖分;Miles(1969)证明Delaunay三角网是性能优秀的三角网;Sibson(1978)认为在一个有限点集中,只存在一个局部等角的三角网,也就是Delaunay三角网;Lingas(1986)证明了Delaunay三角网是最优的;Tsai(1993)认为,在不多于3个相邻点共圆的欧几里德平面中,Delaunay三角网是唯一的。 2.2 Delaunay三角网生成算法
经过多年的发展,Delaunay三角网生成算法已经趋于成熟,大致可以分成3类:分治算法(Shamos et al,1975; Lewis et al,1978)、三角网生长法(Green et al,1978; Mccullgh et al,1980)和随机增长法(Bowyer,1981; Watson,1981)。
分治算法:基本思路是首先对原始数据点集进行递归分割成更容易实现三角化的子集,对每个子集进行三角剖分,并用局部优化(LOP,Local Optimization Procedure)算法进行优化,保证三角剖分为Delaunay三角网,然后,寻找每个子集凸壳的底线和顶线,由底线到顶线自下而上的合并,最终完成整个数据点集的三角形网络。
三角网生长法:从一个起始点开始,逐步形成覆盖整个点集的三角网,有两种趋势相反的生长过程,划分为扩张生长法和收缩生长法;扩张生长法是首先以点集中任一点为源,寻找和起始点距离最短的另一点,并连接两点产生初始三角片的一条边,然后使用判别准则搜索包含此边的另一个顶点,以此类推,向外层层推展,最后形成覆盖整个区域的三角网;收缩生长法,正好相反,先在数据点集的最外边界生成凸壳,以此为源,向内扫描逐步缩小并形成整个三角网。
随机增长法基本步骤如下:
步骤1:由观测站构成点集P;额外再设置3点,令其连线形成的三角形能覆盖整个点集P,同时确保这3点不在点集P中任意3点的外接圆之中。
步骤2:从P中随机抽取任意点Pr,分析其和当前的三角形位置关系(如图 2);若Pr位于ΔPiPjPk中,那么将Pr和ΔPiPjPk的3个顶点建立连线,就形成新的边及其三角形;若Pr恰好落在ΔPiPjPk的某条边上,那么将该边对应两个三角形顶点和Pr及该边的两端点连接,形成新的三角形。
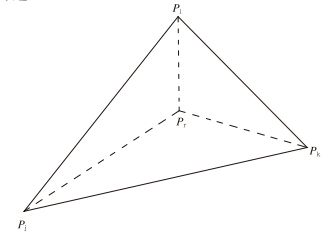 |
| 图 2 新增点Pr位于ΔPiPjPk内部 Fig. 2 Newly created point Pr within the triangulated slice ΔPiPjPk |
步骤3:得到新的三角剖分后,对非法边不断翻转,直到其满足Delaunay三角条件,成为合法边;因此,需要不断地递归调用判据,实现当前Delaunay三角网的更新和维护。
步骤4:重复步骤2、步骤3,直到完成对所有点的Delaunay三角剖分。
步骤5:删除步骤1中初始添加的3点及其关联的边。
上述5个步骤中有2个重要判别式需要列出。图 2显示了在步骤2中需要判断点Pr在ΔPiPjPk中的位置,使用矢量叉积法分析,其表达式为
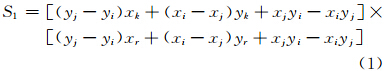
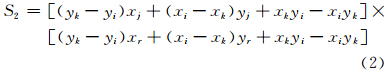
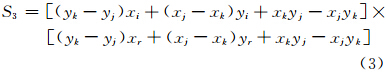
当S1、S2、S3的计算结果均大于0,表示点Pr位于ΔPiPjPk中;若S1、S2、S3至少有一个负数,那么Pr在ΔPiPjPk之外;若S1、S2、S3有零值,那么Pr在ΔPiPjPk某条边或顶点上。
步骤3必须判断每条边是否符合Delaunay三角条件,其判据式为(Leonidas,1985)
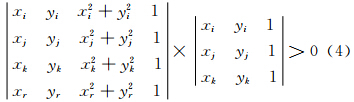
若满足式(4),则Pr在ΔPiPjPk外接圆内,需要通过对非法边的翻转直到符合Delaunay三角条件。
3种生成算法各有优缺点,随机增长法较容易实现,占用内存小。本文将采用随机增长法进行Delaunay三角剖分(实现的代码见附录1)。3 Delaunay三角分片线性插值
气象站点观测资料属于多元散乱数据;一方面,气象要素随时空变化,为多变量的函数;另一方面,站点呈高度离散分布。不同于单变量数据,多元散乱数据并没有满足符合harr条件的基函数(吴宗敏,2008),那么如何解决多元散乱数据插值问题,数学上通行的方法是把大而复杂的问题分解成一些小而简单的问题,然后再逐步解决。Delaunay三角分片线性插值也是遵循这一思路,为气象数据格点化分析提供了可靠的技术手段。 3.1 Delaunay三角分片线性插值原理
当完成三角剖分后,根据每个三角片顶点的观测数值,就可以对区域内任意点进行分片线性插值。假设三角片的3个顶点是A、B、C,其观测值分别为f(A)、f(B)、f(C),任何点相对于这个三角形有唯一的重心坐标表示
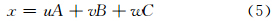
线性插值可写成

由式(5)和(6),点(x,f(x))可以表示为{(A,f(A));(B,f(B));(C,f(C))}的线性凸组合,也就是说这是一张平面;当0<u,v,w<1时,x位于三角形内部,(x,f(x))形成一个三角片(吴宗敏,2008)。
从以上原理出发,需要求得系数u、v、w,本文将使用三角形的3个顶点信息分别获得系数值,具体思路如下:3个顶点A、B、C分别用数字1、2、3表示,顶点位置的经度mi(i=1,2,3)和纬度ni(i=1,2,3),Ri(i=1,2,3)表示降水量,那么可以建立三元一次方程组
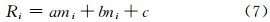
由式(7)求解得到方程系数a、b、c
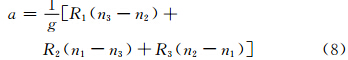

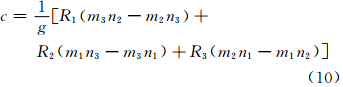
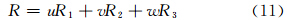
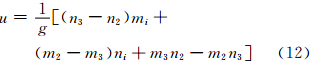
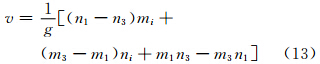
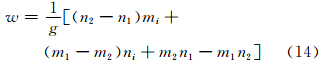
将空间散乱站点数据分析到规则分布的网格点上,生成格点数据场是插值技术在气象中的主要应用之一。为了定量分析三角分片线性插值格点化分析的精度,将使用反距离权重法与之进行对比分析;需要指出的是:在插值方法比较中,首先要考虑到参与估值的样本点数目,只有在采样点数目相近的情况下,不同插值方法的比较结果才具有合理性。
反距离权重法在收集样本点时,往往是以待估点为中心,在一定的影响半径(或最大搜索半径)范围内的观测点都将参与插值;显然,在站点较密集的地区,采样点数较大,而在观测稀疏地区,采样点数就很少;当对每个待估格点使用反距离权重法时,本文提出以其周围的4个站点参与插值的选择站点策略;具体过程如下:以格点为中心的360°的方位上,平均划分成4个象限,在每个象限区都选择距离格点最近的站点作为样本点,如此,每个格点都将有4个站点数据参与插值,也就是说,在选择站点时,尽量使已选的站点平均分布于格点周围;反距离权重法: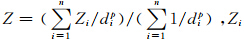 为观测点的降水量,Z是格点估计的降水量,di是格点到观测点的距离,n是观测站数,p是距离幂指数,将p从2到10分别试验,通过交叉检验比较插值误差的大小,在本文的数据条件下,取p为6时,插值误差略小,试验中的p值也就设为6。3.2.2 资料及检验方法
为观测点的降水量,Z是格点估计的降水量,di是格点到观测点的距离,n是观测站数,p是距离幂指数,将p从2到10分别试验,通过交叉检验比较插值误差的大小,在本文的数据条件下,取p为6时,插值误差略小,试验中的p值也就设为6。3.2.2 资料及检验方法
使用2008年1月1日—12月31日的中国2200个观测站08时(北京时,下同)24 h实况降水量资料。插值格点格距为0.28125°×0.28125°。把全中国划分为8个区(图 3):一区:东北,二区:新 疆,三区:西北,四区:华北,五区:西藏,六区:西南,七区:长江中下游,八区:华南。
 |
| 图 3 中国区域划分 Fig. 3 Division of China into the regions |
全中国8个分区中分别采取交叉检验方法,共10次不重复随机地抽取观测值不参与插值,也就是说,每次有10%的站不参与插值,只使用90%的站进行格点插值。获得格点值后,通过双线性方法再插回到没有参与插值的站点上,然后算出其实际观测值和估算值的差,以此评估插值方案的优劣。采用均方根误差、平均绝对误差、平均误差作为评估插值效果的标准。3.2.3 结果分析
图 4a、b、c分别表示三角分片线性插值法和反距离权重法全中国范围交叉检验的均方根误差、平均绝对误差和平均误差比较。从图中看到,三角分片线性插值的均方根误差要小于反距离权重法,两种插值方法的平均绝对误差近似,而两者平均误差的差异较大,从平均误差的全中国年平均对比来看:三角分片线性插值和反距离权重法分别对应是0.005和-0.107 mm,数值上的差异,显示三角分片线性插值法在平均误差的比较中优势突出。以上是全中国范围的插值误差比较,同时也对全中国8个区域分别进行了分区比较:在各分区的均方根误差和平均误差比较中,三角分片线性插值法对应的误差值都要小于反距离权重法,其中,平均误差的差异也都比较大;两种插值方法的平均绝对误差在各区域表现各异;总体上来看,8个分区中,三角分片线性插值法和反距离权重法的误差比较和图 4a、b、c的变化趋势一致。在分区比较中,也分析得到三角分片线性插值法在站点密集的地区有较好的表现,3项误差都较小,由于篇幅所限,文中只列出了长江中下游地区的比较分析(图 4d、e、f),长江中下游地区的三角分片线性插值在三项误差检验中都具有优势;不同于全中国范围的误差检验比较结果,三角分片线性插值法的平均绝对误差也较小。
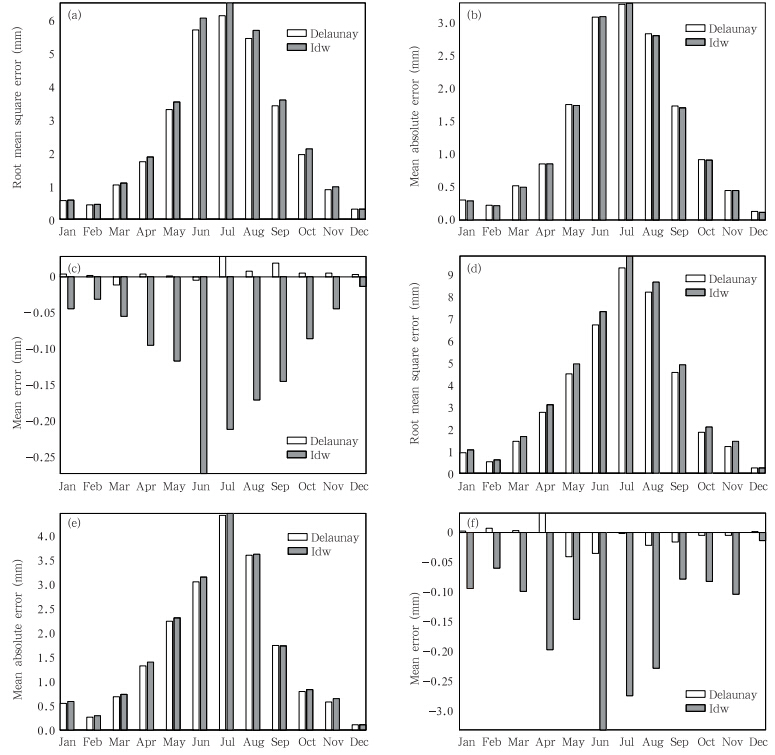 |
| 图 4 三角分片线性插值法和反距离权重法交叉检验结果(a. 全中国均方根误差对比,b. 全中国平均绝对误差对比,c. 全中国平均误差对比,d. 长江中下游地区均方根误差对比,e. 长江中下游地区平均绝对误差对比,f. 长江中下游地区平均误差对比) Fig. 4 Cross validations between the triangulated slice linear interpolation algorithm and the inverse distance weighting method(a. root mean square error for the whole nation,b. mean absolute error for the whole nation,c. mean error for the whole nation,d. root mean square error for the middle and lower reaches of the Yangtze River,e. mean absolute error for the middle and lower reaches of the Yangtze River,and f. mean error for the middle and lower reaches of the Yangtze River) |
反距离权重法的平均误差较大的可能原因分析:反距离权重法是以待估点为中心的4个象限分别选择1个距离最近的样本点;由于散乱分布的观测点,在某个象限站点密集,而在另一个象限站点稀疏、离待估点远,这是比较普遍的情况;那么选择距离待估点较远的观测站作为样本的可能性就很大。对于全中国2200个观测站,在同一时刻,出现降水的站点毕竟只有一小部分,而且,较大的降水又往往是分片密集分布,只有少数邻近的站点能够观测到;因此,反距离权重法的4点采样中收集到的零降水或降水量偏小的样本点可能性就增大了,使得最终的估值偏小,根据平均误差公式: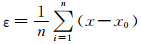 ,其中,x和x0分别表示交叉检验的插值估计降水和实况值,因此,反距离权重法的平均误差会呈现较大的负值。
,其中,x和x0分别表示交叉检验的插值估计降水和实况值,因此,反距离权重法的平均误差会呈现较大的负值。
两个插值方法比较也验证了Delaunay三角剖分的合理性:一是在采样点的数量上,三角分片线性插值选用的是3个样本点,反距离权重法使用了4个样本点参与估值,4个样本点的信息量要多于3个样本,通常也能得到更高的插值精度,但是,检验结果却是三角分片线性插值法更有优势。二是在权重系数的计算上,三角分片线性插值是线性估值方法,反距离权重法以距离幂次方的反比作为权重系数,距离幂次方的反比显然更能反映出降水相关性的特点,降水量的分布罕有呈线性变化的,但是,检验结果并非如此。造成上述问题的关键是站点选择策略的不同,由于Delaunay三角剖分的合理性,从而表现出较反距离权重法有更高的插值精度。Delaunay三角剖分的两个重要性质:一是任意4点不能共圆,该特征保证了最邻近的点构成三角形,使得三角形的三边长度之和达到最小;二是最大最小角原则,三角形的最小角不再增大,使三角形接近等边;Delaunay三角剖分的结果是尽可能地接近正三角形,而扁的形状则被认为是不好的,因为这表明要用到较远的样本点进行估值,会产生较大的误差。
本文使用的三角分片线性插值是无参数插值,其他众多的插值方法大都需要进行参数的设置,例如:反距离权重法、克立格方法、多元回归法、径向基函数法等都是带参数的算法,其中,反距离权重法简单易行并有较高的精度,但其存在着明显的缺点:权重幂数和搜索半径将影响到插值精度,对相关参数的估计过分依赖于经验,缺乏理论支持;对未知点的数据估计的好坏依赖于样本点的布局,这些问题在其他的有参数插值算法上同样存在,客观上增大了插值精度的不确定性。另外,由于原始数据点被定义为各个三角形的顶点,那么任意待估点都要受到该三角形表面的限制,三角形的倾斜和标高都由3个数据点决定,所以,三角分片线性插值法是一种精确的插值算法。最后,三角分片线性插值误差是确定的,因为Delaunay三角剖分的结果是唯一的,那么在三角分片线性插值情况下,未知点的估计值也就确定了。 3.3 降水量插值个例
图 5a为2008年6月22日08时长江中下游的24 h降水量实况和站点分布,共计647个观测站,主要降水区位于河南省东北部、安徽省中部偏南地区和江苏省南部,较强的降水出现在湖北罗田137 mm、安徽合肥125 mm、安徽肥西115 mm、江苏溧阳129 mm。图 5b是以Delaunay三角网表达的降水量三维分布,首先对观测站点进行Delaunay三角剖分,产生覆盖整个区域的三角网,每个三角片自然、无缝隙地连接成连续的平面,然后,将每个观测点提升到降水量数值对应的高度,三角形顶点的降水量值决定了三角片的标高和倾斜,原来平面上的三角片就转化为三维空间上的三角形;图形显示在三角网中有一东西走向的降雨“脊”,个别三角片的高度超过了100 mm,三角网描述的降水量立体图和实况保持一致,由于是立体图,在实践中可以旋转图形从不同侧面观察降水结构,有更为丰富的视觉效果。
 |
| 图 5 2008年6月22日08时长江中下游地区24 h降水量(mm)图形显示(a. 降水量实况和观测站点分布,b. 降水量Delaunay三角网的三维结构,c. 三角分片线性插值后的降水量格点场,d. 反距离权重法插值后的降水量格点场;等值线起始10 mm,间隔20 mm) Fig. 5 24 h accumulative precipitation graphic display for the middle and lower reaches of the Yangtze River at 08:00 BT 22 June 2008(a. the precipitation observation and the station distribution,b. the three-dimensional precipitation field based on Delaunay triangulated networks,c. the grid field from the triangulated slice linear interpolation algorithm,and d. the grid field from the inverse distance weighting algorithm) |
使用三角分片线性插值方法,将站点观测资料分析到0.28125°×0.28125°网格上,得到图 5c降水量格点场,图中以10 mm为起始,间隔20 mm绘出等值线;对比图 5a和c,格点场中雨带分布和降水中心位置以及强度是符合实况的,降水量格点场能准确描述实况特点。
对比图 5c和d,有3个较突出的差异:一是反距离权重法的固有缺陷——“牛眼”现象;即降水量大的观测站对周边格点值影响被放大,围绕湖北罗田137 mm、安徽合肥125 mm、安徽肥西115 mm、江苏溧阳129 mm就相应形成数个等值线密集分布的强中心(图 5c和d对应的初始等值线是10 mm,等值线间隔是20 mm);从图 5c的等值线光滑度和疏密度来看,有较好的视觉效果,并基本消除了“牛眼”现象。二是图 5d出现虚假降水现象,例如:在湖北中部附近有数个孤立的10 mm闭合等值线,通过细致的观测点数据分析,其中,有两个与闭合线相邻近的站点降水量并没有超过10 mm,也就意味着是虚假的,其产生的原因就是由于受到来自较远的东北部较大的降水量影响,其实也是“牛眼”现象的表现形式之一;从图 5c中没有看到这类由于插值方法原因产生的虚假降水。三是图 5c降水中心值普遍小于图 5d,对于反距离权重法,由于大降水量对其周围格点估值影响大,插值的结果是邻近格点值就接近观测值;在三角分片线性插值方法中,有较大降水量的观测点只会影响到以其为顶点的某个三角片中,它不会影响到周边的三角片;若格点并不位于其所在的三角片中,那么就不会出现较大的格点值;即便格点正好位于其所在三角片中,还要根据三角片中其他两个顶点的观测值大小确定格点的估值;例如在湖北省东部,图 5c中心最大值是110 mm,图 5d为130 mm,实况是湖北罗田137 mm,出现这种情况可以从上述分析中得到解释,图 5c和d反映的都是0.28125°×0.28125°格点估值场,若没有格点和湖北罗田站近似重合或十分靠近,那么在三角分片插值中,该地区周围的格点降水值出现大于130 mm的可能性就小,也只有在网格距离减小,更为精细的网格,格点数足够多,该区域的格点出现大于130 mm的可能性就变大,那么图 5c在湖北罗田地区才会出现130 mm闭合的等值线;由此,三角分片线性插值方法中,较大的降水值影响范围受到严格限制,是一种局地性的体现;这是符合降水特点的,降水量分布通常有地域性特点,降水强度愈强,其局地性特点也愈明显。相对于反距离权重法,三角分片线性插值方法获得的降水量格点化数据更精确、更客观。4 结论和讨论
通过上述原理介绍和实验分析,可以得出以下若干有益的结论和值得深入探讨的问题。
(1)三角分片线性插值是精确的估值方法,根据观测点进行三角剖分,再对待估格点进行三角分片线性插值,使用交叉检验方法分析插值精度,相对于反距离权重法的插值误差,三角分片线性插值的均方根误差有一定的优势;尤其在平均误差比较中,三角分片线性插值优势突出;相对于全中国范围,在站点密集地区(例如长江中下游地区),三角分片线性插值法优势有增大的趋势;在降水量格点场图形个例对比中,三角分片线性插值方法消除了反距离权重法的“牛眼”现象,在格点场上更为精确地描述了降水量分布。
(2)Delaunay三角剖分能构建多面连续的降水面,可以立体地展现降水空间变化趋势,达到较好的视觉效果;由于是以观测点为三角形顶点,三角形的倾斜和标高都由3个数据点决定,任意点的估值都要受到该三角形表面的限制,因此,多面连续的Delaunay三角面是精确的插值面,能准确描述降水的三维结构。
(3)Delaunay三角剖分法为估值中样本点采集提供了有效、可靠的几何拓扑结构,也可作为各类气象要素插值的重要工具之一。气象数据有范围广、随时空变化强的特点,是多元散乱数据,当需要获得有序的格点数据时,插值结果的好坏依赖于观测点的分布。因此,合理的样本点采集方法是保证插值算法效率和精度的首要条件。根据Delaunay三角剖分的两个重要性质,剖分的结果是尽可能地接近正三角形。在和反距离权重法的比较分析中,验证了Delaunay三角剖分法在站点选择上的合理性。
(4)气象数据格点化应用中还存在估值精度和计算效率的平衡问题。一般认为,随着采样点数量的增大,估值准确率也会增大;但是样本点数量在增加的过程中,会出现两种情况,一是计算耗时,需要处理的数据量越多,计算量也必然会上升,在一些较复杂的插值算法中,其对计算机的存储空间、计算速度都会有更高的要求;二是样本点超过一定的数量,插值误差可能会增大。Delaunay三角剖分为解决此类问题提供了有价值的实验分析手段,即可以使用Delaunay三角剖分法进行邻近点搜索。
(5)面雨量的计算是Delaunay三角剖分的主要应用之一。目前,中国面雨量的计算缺乏客观、合理的技术方法,Delaunay三角剖分是具有严格的数学定义,完备的理论基础和成熟的算法。构建Delaunay三角网是自动完成的,无需人工干预或其他主观分析,并能充分利用已知站点数据,在客观分析基础上得到的面雨量将更具说服力。
(6)三角分片线性插值是无参数插值方法,由于Delaunay三角网具有唯一性,三角分片线性插值结果也是确定的。无需通过大量的试验获得合理的参数,三角分片线性插值是客观、高效的算法。
计算几何起始于20世纪70年代,Delaunay三角网和V图是计算几何的重要基石。在计算几何产生之前,V图已经在气象中得到应用,气象实践中使用了基于不同判据的三角划分方法,但是,没有成熟、客观的理论体系支持,计算几何提供了坚实的理论基础和有力的技术手段,随着气象相关邻域研究的深入,Delaunay三角剖分法将会有更为广泛的应用前景。附录1
输入:由平面上n个散乱点组成的点集P。
输出:平面点集P上的Delaunay三角剖分。
1. 在所有点的坐标中,寻找x和y坐标绝对值的最大值,M=Max({|x1|,|x2|…|xn|}∪{|y1|,|y2|…|yn|}),确定P-1、P-2、P-3,建立ΔP-1P-2P-3,P-1=(0,3×M),P-2=(3×M,0),P-3=(-3×M,-3×M);ΔP-1P-2P-3将包含P中所有点。
2. 将点集P初始化为一个单独的三角形ΔP-1P-2P-3,初始网络用D表示。
3. 在点集P中随机排列,并对每个点分别赋予序号:P1、P2、P3…Pn。
4. for i=1 to n
5. do(将点Pr插入到D中)
6. 在D中找到与Pr落点相对应的ΔPiPjPk。
7. if(Pr位于ΔPiPjPk内部)
8. then 将ΔPiPjPk的3个顶点Pi、Pj、Pk都和Pr相连,生成新的3条边,ΔPiPjPk将划分成3个子三角形:ΔPiPjPr、ΔPrPjPk、ΔPiPrPk。
9. 删除ΔPiPjPk的3条边,并将新生成的3个子三角形并入到D中。
10. EDGE(Pr,Pi,Pj,D)
11. EDGE(Pr,Pk,Pj,D)
12. EDGE(Pr,pi,Pk,D)
13. else(Pr恰好落在ΔPiPjPk的某一条边上,假设:Pr落在PiPj上)
14.连接Pr和Pk,将PiPj对应的另一个三角形ΔPiPjPm上的点Pm和Pr相连。ΔPiPjPk、ΔPiPjPm将被划分成4个三角形:ΔPrPjPk、ΔPrPjPi、ΔPrPjPm、ΔPiPrPm
15. 删除ΔPiPjPk、ΔPiPjPm,将ΔPrPjPk、ΔPrPjPi、ΔPrPjPm、ΔPiPrPm并入到D中
16. EDGE(Pr,Pi,Pk,D)
17. EDGE(Pr,Pk,Pj,D)
18. EDGE(Pr,Pi,Pm,D)
19. EDGE(Pr,Pj,Pm,D)
20. 删除点P-1、P-2、P-3和与之相关联的边。
第9行和第15行中,得到一个新的三角剖分后,只有其所有边都是合法的(即满足Delaunay条件),才是Delaunay三角剖分。这部分算法在子程序EDGE中完成,算法通过对非法边不断翻转,直到所有边都满足Delaunay要求,成为合法边,因此,EDGE要不断递归调用自己,完成核对,以实现Delaunay三角网的维护和更新。EDGE(Pr,Pi,Pj,D)具体实现步骤如下:
1. 搜索与Pr位置相对应的ΔPiPjPk
2. if(Pr在圆PiPjPk中)
3. then删除PiPj,连接PrPk、PiPr、PrPj,得到新的三角形ΔPiPrPk、ΔPjPrPk,并将新的三角形并入到D中。
4. EDGE(Pr,Pi,Pk,D)
5. EDGE(Pj,Pr,Pk,D)
| 李庆祥,李伟. 2007. 近半个世纪中国区域历史气温网格数据集的建立. 气象学报,65(2):293-300 |
| 田付友,程明虎,张亚萍等. 2010. 校准雨量计密度对雷达联合雨量计估测流域平均面雨量的影响. 气象学报,68(5):717-730 |
| 吴宗敏. 2008. 散乱数据拟合的模型、方法和理论. 北京:科学出版社,1-40 |
| 杨贤为,何素兰. 1987. 江淮平原二类气象站网的设计. 气象学报, 45(1):104-110 |
| 赵博,孟小红,侯建全. 2007. 三维地震建模与可视化. 地球科学, 32(4):549-533 |
| 赵瑞霞,李伟,王玉彬等. 2007. 空间结构函数在北京地区气象观测站网设计中的应用. 应用气象学报,18(1):94-101 |
| Bowyer A. 1981. Computing dirichlet tessellations. Computer J,24:162-166 |
| Chris G, Maciej D. 2007. Dynamic cartography using Voronoi/delaunay methods. ISPRS workshop on updating geo-spatial database with imagery & the 5th ISPRS workshop on DMGISs, 41-47 |
| de Berg M, van Kreveld M, Overmars M, et al. 2000. Computational Geometry Algorithms and Applications (Second Edition). Springer, 340pp |
| Drozdov O A, Shepelevskij A A. 1946. The interpolation in a stochastic field of meteorological elements and its application to meteorological map and network rationalisation problem. Trudy Niu Gugms Series,1:13 |
| Green P J,Sibson R. 1978 .Computing dirichlet tesselations in the Plane. Computer J, 21(2): 168-173 |
| Hassan C, Majid H, Timothy P, et al. 2011. Delaunay triangulation as a new coverage measurement method in wireless sensor network. Sensors, 11(3):3162-3176 |
| Hulme M. 1992. A 1951-80 global land precipitation climatology for the evaluation of general circulation models. Climate Dyn,7(1):57-72 |
| Leonidas G, Jorge S. 1985. Primitives for the manipulation of general subdivisions and the computation of Voronoi diagrams. ACM Transactions on Graphics,4(2):74-123 |
| Lewis B A, Robinson J S. 1978. Triangulation of planar regions with applications. Computer J, 21(4): 324-332 |
| Ling T, Faisal H, George J H. 2010. Transfer of satellite rainfall uncertainty from gauged to ungauged regional and seasonal time scales. J Hydrometeor, 11(6):1263-1274 |
| Lingas A. 1986. The greedy and delaunay triangulations are not bad in the average case. Information Processing Letters, 22(1): 25-31 |
| Mccullagh M J, Ross C G T. 1980. Delaunay triangulation of a random data set for is arithmic mapping. Cartographic J, 17: 93-99 |
| Miles R E. 1969. Solution to problem (probability distribution of a network of triangles). SIAM, 11:399-402 |
| Schuurmans J M, Bierkens M F P, Pebesma E J R, et al. 2007. Automatic prediction of high-resolution daily rainfall fields for multiple extents: the potential of operational radar. J Hydrometeor,8:1204-1224 |
| Shamos M I, Hoey D. 1975. Closest-point problems//Proceedings of the 16th annual symposium on the foundations of computer science,151-162 |
| Sibson R. 1978. Locally equiangular triangulations. Computer J, 21 (3):243-245 |
| Sergio O, Damon S, Laura R, et al. 2009. Three-dimensional ray tracing on delaunay-based reconstructed surface. Applied Optics, 48(20):3886-3893 |
| Till H M V, Steve W L, Hoshin V G, et al. 2010. Multicriteria design of rain gauge networks for flash flood prediction in semiarid catchments with complex terrain. Water Resources Res, 46(11):554-670 |
| Tsai V J D. 1993. Delaunay triangulations in TIN creation: an overview and a linear-time algorithm. Int J GIS, 7(6):501-524 |
| Watson D F. 1981. Computing the n-dimension delaunay tessellation with application to Voronoi polytopes. Computer J,24:167-172 |
 2012, Vol. 70
2012, Vol. 70

