中国气象学会主办。
文章信息
- 江志红, 丁裕国, 马婷婷, 刘 冬. 2012.
- JIANG Zhihong, DING Yuguo, MA Tingting, LIU Dong. 2012.
- 气候极值推断的不确定性及其置信区间初步探讨
- The uncertainties of inference for extreme climate and countermove
- 气象学报, 70(6): 1327-1333
- Acta Meteorologica Sinica, 70(6): 1327-1333.
- http://dx.doi.org/10.11676/qxxb2012.111
-
文章历史
- 收稿日期:2012-03-17
- 改回日期:2012-08-12
2. 中国民用航空华东地区空中交通管理局气象中心,上海,200000
2. Meteorological Center, Air Traffic Management Bureau, Civil Aviation Administration of China, Shanghai 200000, China
当前,极端气候事件持续增多,天气气候灾害频繁出现的态势正愈演愈烈(Zhai et al,1999; Easterlling et al,2000; Zhai et al,2005)。众所周知,“极端气候”是相当复杂的科学问题,自20世纪80年代以来,国际科学界一直关注着平均气候的变化可能引发极端气候的各种非线性变化问题,且不少研究已经取得了共识(Greedwood et al,1979; Mearns et al,1984; Katz et al,1992; Guttman et al,1993; IPCC,2001,2007; 丁裕国等,2002)。例如,目前全球海、陆、气耦合模式所模拟的各种排放方案下的未来气候情景虽已具有时间上的高分辨率,但其空间尺度分辨率仍有细化的必要,在全球不同地区采用嵌套区域模式或采用各种降尺度方法已经成为研究区域尺度气候状况的有力工具。但其模式输出信息也仅对平均气候变化有较高的置信度,而面对极端气候变化的复杂性,迄今尚不能完全由动力气候数值模拟直接寻求极端气候变化规律,必须借助于动力气候数值模拟与统计极值分布模式或随机模拟等各种理论和方法相互结合加以研究。当然,根据历史气候记录提取气候极值信息并诊断其变化规律则更离不开各种统计手段。目前极端气候异常事件的许多统计特征量(如频率,强度等)与平均气温及其变率的线性或非线性关系已经有了一定的理论基础和研究成果,而各种气候数值模式模拟的最新结果也表明,模拟的平均气温场及其变率已有相当的可靠性,在给定的初边值条件下作第2类气候预报与观测结果已相当一致。因而,借助优良的气候数值模式输出结果,预测各种条件期望气候情景下,出现气候极端值引发自然灾害的风险也已取得一些新的进展(翟盘茂等,1999; Zhao et al,2004; Osborn,2001; Katz et al,2005; 江志红等,2007)。但是,正如人们所知,研究气候系统(或其任何一个子系统)都不能回避气候具有概率性即不确定性的一面。而研究极端气候更需要考虑不确定性因素。从统计学观点出发,一般可将气候变量视为随机变量,而气候极值就是这种气候随机变量的复杂函数,它更加需要采用各种统计学方法和理论。气候观测记录所记载的过去气候变化中某些极端气候指标虽然早已存在,它们不但具有比平均气候变化更强的长期变率特征,更受到各种偶然性因素影响。如何从大量的偶然性因素中提取必然性因素,一直是许多学者长期深入研究的课题。概括地说,气候极值推断中的不确定性主要有下列3方面:(1)来自全球气候模式模拟结果的不确定性;(2)来自各种降尺度技术方法所得结果的不确定性;(3)推断极值的统计理论本身所造成的不确定性。由上述3方面不确定性相互叠加必然形成相当大的误差或不确定性。而最引人关注的直接因素主要是后者。所以,本文着重探讨推断极值的统计理论本身所造成的不确定性。关于其他因素的不确定性问题将另文探讨。本文的研究意义在于:(1)为保证工程建设设计安全,必须计算重现期极值在一定信度下的置信区间,选取极值置信上限为设计参考基准。(2)重现期极值是原分布的样本统计量,它是总体分位数的一个抽样,因而具有抽样分布,重现期极值具有抽样误差。因而,探讨极值推断的统计理论本身所造成的不确定性,必然要求估计重现期极值的抽样误差。 2 极值分位数的抽样误差
极值统计的根本目的在于准确地推断极值序列的重现期,其理论实质就是概率分布的右侧(或左侧)小概率问题。愈是稀有的天气或气候事件,例如,通常的百年一遇(或百年不遇),即指按年为单位统计,具有至少百分之一的小概率。以此类推,通常所说的20 a一遇,即指按年为单位统计,具有至少百分之五的小概率。因此,极端值在短于T时间内也可能出现不止一次,也可能在T时间内一次也未出现,都属于正常情况。根据概率论,假定X为连续型随机变量,对于任意实数x来说,X取值小于x的概率为

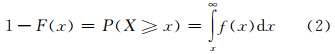
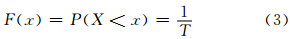

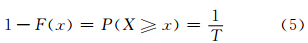
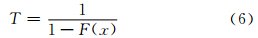
 )所超过的年气候最大值(或最小值),就称为“百年一遇”的极值。
)所超过的年气候最大值(或最小值),就称为“百年一遇”的极值。
任何一个统计总体,其概率分布的样本分位数都只不过是原分布的样本统计量,它也是一种随机变量,即总体分位数的一次抽样值,因而它具有抽样分布(么枕生等,1990;Lu et al,1992)。理论上早已证明在样本较大时,这种抽样分布具有渐近正态的极限分布。可用数学语言表述如下:
设有总体概率为p的分位数Zp,则有
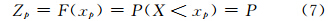

 p渐近地服从正态分布(么枕生等,1990);
p渐近地服从正态分布(么枕生等,1990);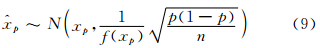
 p的标准误差为
p的标准误差为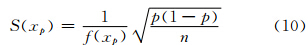
 p的取值。而参数n、p分别为样本量和相应的概率。研究表明,已经证明多种分布的样本分位数渐近标准误差或方差(Chowdhury et al,1991)。例如,正态分布分位数的标准误差为
p的取值。而参数n、p分别为样本量和相应的概率。研究表明,已经证明多种分布的样本分位数渐近标准误差或方差(Chowdhury et al,1991)。例如,正态分布分位数的标准误差为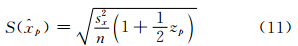
 p=x+zpsx为正态分布分位数估计值,zp为标准正态分布分位数估计值。
p=x+zpsx为正态分布分位数估计值,zp为标准正态分布分位数估计值。
对数正态分布分位数的标准误差为

 p=exp(y+zpsy)为对数的正态分布分位数估计值。
p=exp(y+zpsy)为对数的正态分布分位数估计值。
同理,对于耿贝尔分布的分位数,用矩法估计可得
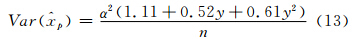
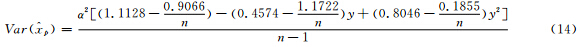
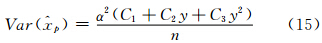
C1=1.1128-0.2384k+0.0908k2
对k>0有C2=0.458-3.0561k+1.1104k2
C3=0.8046-2.889k+8.7874k2-10.375k3对k<0有
C2=0.458-7.5124k+5.0832k2-11.623k3+2.250ln(1+2k)
C3=0.8046-2.6215k+6.8989k2+0.003k3-0.1ln(1+3k)
显然,对k=0,应有式(14)。值得指出的是,在一般情况下,3参数广义极值(形状参数k,尺度参数α和位置参数β)可用L矩估计(Hosking et al,1985)。而常用3参数广义极值分位数估计的渐近方差公式,只对较大样本适合(小样本误差较大):例如当-0.33<k<0.3时,其p阶分位数的方差估计公式为
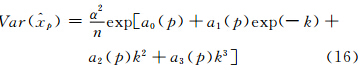
| 累积概率 | a0 | a1 | a2 | a3 |
| 0.80 | -1.813 | 3.017 | -1.401 | 0.854 |
| 0.90 | -2.667 | 4.491 | -2.207 | 1.802 |
| 0.95 | -3.222 | 5.732 | -2.367 | 2.512 |
| 0.98 | -3.756 | 7.185 | -2.314 | 4.075 |
| 0.99 | -4.147 | 8.216 | -0.203 | 4.780 |
| 0.998 | -5.336 | 10.711 | -1.193 | 5.300 |
| 0.999 | -5.943 | 11.815 | -0.630 | 6.262 |
现以中国160个代表性测站逐日降水量资料为例,考察逐日降水量的极值。首先,对其做广义极值分布模型拟合,结果表明,除了4站不能通过显著性检验外,绝大多数(156站,图 1)都符合广义极值分布。广义极值分布的分布函数(Coles,2001; Jenkinson,1955; 蔡敏等,2007)为

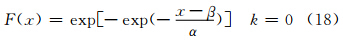
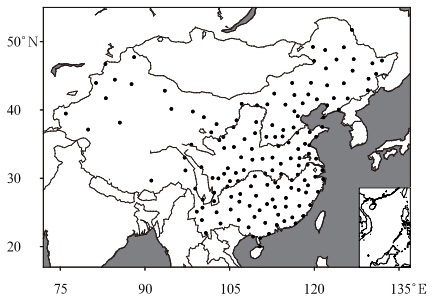 |
| 图 1 日降水量符合广义极值分布的站点分布 Fig. 1 Distribution of the stations fitting to the GEV distribution of the daily precipitation |
| 统计参数 | 北京站 | 南京站 | 广州站 |
| α | 23.9264 | 30.0134 | 34.9059 |
| β | 61.1325 | 78.9694 | 99.5079 |
| k | 0.186 | 0.0047 | 0.1339 |
| 分位数标准差 | 52.4304 | 32.6395 | 65.4651 |
| 百年一遇分位数 | 235.1526 | 218.5262 | 321.4693 |
| 50 a重现期极值 | 置信区间 | 100 a重现期极值 | 置信区间 | |
| 北京 | 198.29 | [189.71,206.87] | 235.15 | [221.57,248.74] |
| 南京 | 197.15 | [191.61,202.69] | 218.53 | [210.88,226.17] |
| 广州 | 278.39 | [268.06,288.72] | 321.47 | [305.88,337.06] |
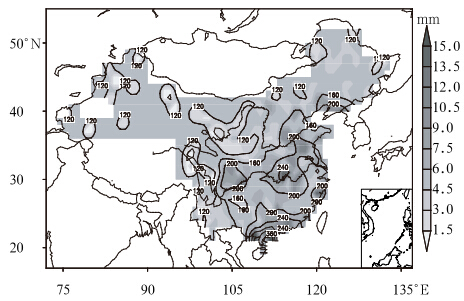 |
| 图 2 重现期为50 a的逐日降水量最大值(等值线)及95%置信水平下的置信区间(阴影) Fig. 2 Daily precipitation extremes(contours) and the confidence intervals at the 95% confidence level(shaded)for the 50-year return period |
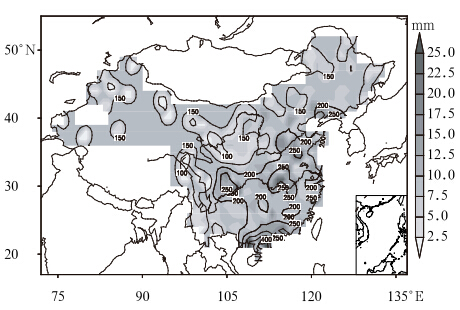 |
| 图 3 重现期为100 a的逐日降水量最大值(等值线)及95%置信水平下的置信区间(阴影) Fig. 3 As in Fig. 2 but for the 100-year return period |
从式(1)—(16)可见,要降低给定的第p阶分位数的抽样误差即分位数的抽样标准差,主要在于加大样本容量n和加强其他统计参数的稳定性。若以指数分布为例,由式(15)可见,在给定阈值β的条件下,要降低抽样标准差,只有加大样本容量n,以广义极值为例,在给定的形状参数k下,也主要取决于样本容量n和尺度参数α,而后者直接与变量本身的方差有关。由此可见,无论是何种分布型所拟合极值分布的分位数,其估计值的标准误差大小均取决于该变量本身的方差和取样多少。要想使得分位数估计误差减小,只能是加大样本量并使得其抽样方差减小。但这里还涉及到另一问题,那就是所拟合的分布模式是否符合实际且不随时间推移而变化,这必然在本质上涉及拟合模式的统计参数稳定性问题。5 关于广义极值模式的数值试验
以上述156站逐日降水量的广义极值拟合为例,研究了广义极值模式的p阶分位数抽样标准差与参数的关系。根据广义极值标准差公式,只改变其中一个参数,固定其他参数不变,来观察其标准差的变化情况。形状参数(k)只是由于计算误差,有小幅变动(幅度控制在-0.1—0.1,变动幅度为0.02);样本容量的变化范围为10—57;概率(即重现期)的变动范围为0.001—0.2(即千年一遇到5 a一遇)。表 4为3站的分位数标准差随形状参数(k)的变化,根据实测资料所估计的广义极值模式原始参数见表 2和3。
从表 4中可以看出,k值的变化对3站标准差的影响不大,随着k值增大,标准误差也变大,所以参数k对分位数的影响较小,参数相对比较稳定。再从图 4和5可以看出,随着样本容量的增大,3站的分位数标准差均有所减少;而随着重现期增大(即概率变小),其广义极值相应分位数标准差也会增大。由此而来的是,相应的置信区间也将发生变化,样本愈大,分位数标准差均趋于缩小,所以,小样本求得的分位数可信度不高,只有大样本求得的分位数其可信度才能增高。而分位数标准差随着重现期的增大而增大,这就意味着,愈是小概率事件其发生的可能性愈小,而由此所估计的分位数,它的不确定性也会相应地增大,因而其置信区间也要增大,这都是由于分位数的抽样标准误差加大的缘故。
| 相对变化 | 北京站 | 南京站 | 广州站 | |||
| k | 对应标准差 | k | 对应标准差 | k | 对应标准差 | |
| -0.1 | 0.1453 | 48.685 | 0.0139 | 32.4308 | 0.1313 | 61.2587 |
| -0.08 | 0.1486 | 49.410 | 0.0142 | 32.4724 | 0.1342 | 62.0751 |
| -0.06 | 0.1518 | 50.146 | 0.0145 | 32.5141 | 0.1371 | 62.9037 |
| -0.04 | 0.1550 | 50.895 | 0.0148 | 32.5558 | 0.1400 | 63.7448 |
| -0.02 | 0.1583 | 51.657 | 0.0151 | 32.5976 | 0.1430 | 64.5985 |
| 0 | 0.1615 | 52.4304 | 0.0154 | 32.6395 | 0.1459 | 65.4651 |
| 0.02 | 0.1647 | 53.217 | 0.0157 | 32.6814 | 0.1488 | 66.3446 |
| 0.04 | 0.1679 | 54.017 | 0.0160 | 32.7234 | 0.1517 | 67.2374 |
| 0.06 | 0.1712 | 54.830 | 0.0163 | 32.7655 | 0.1546 | 68.1436 |
| 0.08 | 0.1744 | 55.657 | 0.0166 | 32.8076 | 0.1575 | 69.0633 |
| 0.1 | 0.1776 | 56.497 | 0.0169 | 32.8498 | 0.1605 | 69.9969 |
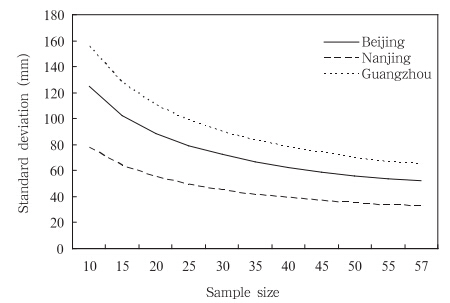 |
| 图 4 广义极值的分位数标准差随样本容量的变化 Fig. 4 Changes in the st and ard deviation of quartile with the sample size |
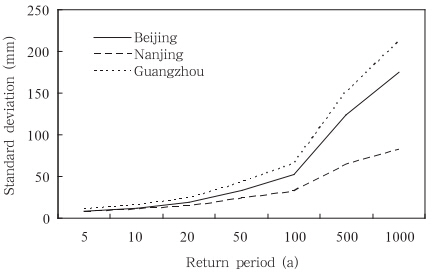 |
| 图 5 广义极值的分位数标准差随重现期的变化 Fig. 5 Changes in the st and ard deviation of quartile with the return period |
预估极值所产生的不确定性,其最直接的原因就是推断极值的统计理论本身所造成的不确定性。迄今为止,尚无法避免由此而造成的不确定性。这是因为自然界所产生的极端值(或极端事件)都是一种不可预测的复杂随机变量。即使原变量可以预报,在一定的条件下,其不确定性也不能完全消除,更何况是其极端值,因为其本身又是原变量的某种函数,所以更不能预测。理论和实践都已证明,目前之所以能预估出未来气候情景下的气候极值,也只是在一定的可信度条件下所作出的一种带有置信区间的估计。这一问题的理论意义必须搞清楚,否则会导致误解。本文只是为了重申这一观点而从理论上举出例证并借助于数值试验加以实证。所得到的结果表明:
(1)多年一遇的稀有气候事件,即统计学上的稀有气候极值——分位数,其本身因抽样分布而具有的抽样标准差是随其统计分布参数而变化的。无论气候变量符合何种分布型,其分位数的抽样分布都随样本容量n而变,抽样标准差随着样本容量n增大而减小。
(2)几乎所有的分布,其极值分位数的标准差或方差都是原变量方差s2x的函数,而且,原变量方差大,其极值分位数的标准差S(p)(或方差)也偏大。
(3)以广义极值分布为例,其分位数的标准差还与极值分布的形状参数(k)和尺度参数(α)有关。只改变其中一个参数,其他参数固定不变,观察标准差的变化情况。例如,形状参数(k)只是由于计算误差,有小幅变动(变化幅度控制在-0.1—0.1,变动幅度为0.02),其分位数的变化较小;而从样本容量(10—57)的变化可见,其分位数随着样本容量增大而变小很明显;另一方面,随着重现期加大即概率变小(如从千年一遇到5 a一遇),则各站的分位数标准差逐渐增大。
| 蔡敏, 丁裕国, 江志红. 2007. L-矩估计方法在极端降水研究中的应用. 气象科学, 27(6): 597-603 |
| 丁裕国, 金莲姬, 刘晶淼. 2002. 诊断天气气候时间序列极值特征的一种新方法. 大气科学, 26(3): 343-351 |
| 江志红, 丁裕国, 陈威霖. 2007. 21世纪中国极端降水事件预估. 气候变化研究进展, 3(4): 202-207 |
| 么枕生, 丁裕国. 1990. 气候统计. 北京: 气象出版社, 922pp |
| 翟盘茂, 任福民, 张强. 1999. 中国降水极值变化趋势检测. 气象学报, 57(2): 208-216 |
| Chowdhury J U, Stadinger J R. 1991. Confidence interval for design floods with estimated skew coefficient. J Hydraul Eng ASCL, 117(7): 811-831 |
| Coles S. 2001. An Introduction to Statistical Modeling of Extreme Values. London, UK: Springer Verlag |
| Easterlling D R, Evens L, Ya P, et al. 2000. Observed variability and trends in extreme climate events: A brief review. Bull Amer Meteor Soc, 81(3): 417-426 |
| Greedwood J A, Landwehr J M, Matalas N C, et al. 1979. Probability weighted moments: Definition and relation to parameters of several distributions expressable in inverse form. Water Resour Res, 15(5): 1049-1054 |
| Guttman N B, Hosking J R M, Wallis R. 1993. Regional precipitation quantile values for the continental United States computed from L moments. J Climate, 6(12): 2326-2340 |
| Hosking J R M, Wallis J R, Wood E F. 1985. Estimation of the GEV distribution by the method of PWM. Technomatrics, 27(3): 251-261 |
| IPCC. 2001. Climate Change, the Scientific Basis. Cambridge: Cambridge University Press, 881pp |
| IPCC. 2007. Climate Change 2007: The Physical Scientific Basis, Contribution of Working Group 1 to the AR4. Cambridge, UK, New York, USA: Cambridge University Press |
| Jenkinson A F. 1955. The frequency distribution of the annual maximum (or minimum) values of meteorological elements. Quart J Roy Meteor Soc, 81(348): 158-171 |
| Katz R W, Browns B G. 1992. Extreme events in a changing climate: Variability is more important than averages. Climatic Change, 21(3): 289-302 |
| Katz R W, Brush G S, Parlange M B. 2005. Statistics of extremes: Modeling ecological disturbances. Ecology, 86(5): 1124-1134 |
| Lu L H, Stadinger J R. 1992. Variance 2-and 3-parameter GEV/PWM quantile, confidence intervals and a comparison. J Hydrol, 138(1-2): 247-268 |
| Mearns L O, Katz R W, Schneider S H. 1984. Extreme high-temperature events: Changes in their probabilities with changes in mean temperature. Climate Appl Meteor, 23(2): 1601-1613 |
| Osborn T J, Hnhne M, Jones P D, et al. 2001. Observed trends in the daily intensity of United Kingdom precipitation. Int J Climatol, 20(4): 347-364 |
| Zhai P M, Sun A J, Ren F M, et al. 1999. Changes of climate extremes in China. Climatic Change, 42(1): 203-218 |
| Zhai P M, Zhang X B, Wan H, et al. 2005. Trends in total precipitation and frequency of daily precipitation extremes over China. J Climate, 18(7): 1096-1108 |
| Zhao Z C, Akimasa S, Chikako H, et al. 2004. Detection and projections of floods/droughts over east Asia for the 20th and 21st centuries due to human emissions. World Resour Rev, 16(3): 312-329 |
 2012, Vol. 70
2012, Vol. 70

