中国气象学会主办。
文章信息
- 韩慎友, 钟 青. 2012.
- HAN Shengyou, ZHONG Qing. 2012.
- 三阶龙格-库塔时间分裂显式算法的误差分析
- The error analysis of the third-order Runge-Kutta time split-explicit scheme
- 气象学报, 70(1): 119-127
- Acta Meteorologica Sinica, 70(1): 119-127.
- http://dx.doi.org/10.11676/qxxb2012.011
-
文章历史
- 收稿日期:2010-01-22
- 改回日期:2010-06-21
2. 中国科学院研究生院, 北京, 100049
2. Graduate University of Chinese Academy of Sciences, Beijing100049, China
大气模式中气象上重要的物理模态的频率通常比方程容许的高频模更低。静力系统的高频模为外波模(兰姆(Lamb)波),而非静力可压缩系统的高频模是声波。在数值模式中,稳定地积分高频模需要的时间步长常常比稳定且准确地积分低频模需要的时间步长短,可能只是其一半到十分之一。通常认为,高频的声波模在气象上是不重要的,并且,严重地限制了非静力模式积分方案的时间步长。一个提高计算效率的常用方法是,用显式数值方案以较小的时间步长积分高频模;而用更长的因而也更经济的时间步长积分低频模。这些方法常被称为分裂方法(Marchuk,1974)。
气象上,对可压缩的非静力方程组一个常用的时间分裂法是由Klemp等(1978)提出的(简称KW方案),这一时间分裂技术包括用比积分气象上重要的低频模更短的时间步长来积分与声波模有关的项。在短时间步长积分过程中,与水平传播模有关的项显式积分,而与垂直传播模有关的项隐式积分。隐式积分部分地减轻了当水平网格距与垂直格距比较大时由于垂直传播的声波模造成的严重柯朗(Courant)数限制,代价只是求解简单的三对角矩阵。KW方案对与低频模有关的项用蛙跳时间差分,对与高频声波模传播有关的项用Mesinger(1977)的前后差方案。
Skamarock等(1992,简称SK92)分析了KW方案的稳定性以及其他可能的分裂显式方案,发现在其所考虑的方案中,KW方案具有稳定性、简单性和最小滤波的最好综合效果。SK92又分析了基于KW方法的显式时间分裂方案,对慢模用向前时间方案,而对快模仍然用前后差方案。并发现对这样的方案即使加滤波也非常不稳定,这些方法不适合显式时间分裂模式。然而,如果能够找到合适的时间分裂方法,对于动量方程的平流项采用向前时间方法,例如Smolarkiewicz(1984)和Tremback等(1987)均表明这是可行的方法。这些时间向前方案通常用迎风和/或单调技术减小位相误差和减小或消除由于不可分辨的梯度造成的虚假振荡。前差方案使高频模积分的短时间步数可以潜在地比用前后差方案的KW方案减少一半,因为快模式计算是从t到t+Δt,而非t-Δt到t+Δt。因而,平流项前差与高频模前后差方案相结合是KW方案之外的一个选择。
龙格-库塔(Runge-Kutta)时间积分有许多优秀的数值计算特性,在计算流体力学中得到广泛应用,并逐渐在非静力模式中也得到广泛使用。Wicker等(1998,简称WS98)提出了结合二阶龙格-库塔(RK2)时间差分的时间分裂方法。龙格-库塔时间差分具有与许多前差方案相关的优点,例如,Hundsdorfer等(1995)指出其空间差分可以用迎风离散且能构造单调格式,尽管它需要的短的时间步数为KW方案的四分之三。WS98证明,平流项计算用RK2可以与KW分裂技术结合以积分弹性方程。WS98方案是稳定而且计算高效,并且,至少和蛙跳格式的KW方案一样精确。WS98说明迎风偏斜三阶空间差分与RK2结合是一个好的空间离散。然而Hundsdorfer等(1995)进一步说明中央差空间离散对于RK2是不稳定的,三阶迎风离散产生四阶的计算阻尼。而且,高阶的空间离散,如五阶或六阶差分,对于稳定性必须使用更短的平流时间。例如,RK2与五阶空间差分需要的时间步长约为RK2三阶空间方案的最大稳定时间步长的三分之一。RK2方案的这些局限性,使寻求允许高阶中央和迎风偏斜的空间离散以及对平流项具有更长稳定时间步长的时间分裂算法。
Wicker等(2002)发展了基于三阶龙格-库塔时间积分(称为RK3)的时间分裂显式算法(称为WS02)。RK3可以结合偶数和奇数阶的空间差分方案,并且允许更长的时间步长,即使对于高阶的空间差分柯朗数也可以等于或大于1。因此,RK3方案具有简单性、精确性和稳定性较好的综合效果。RK3方案解决了蛙跳方案本身存在的3个问题,(1)蛙跳方案是二阶精度,该方案需要时间滤波来防止其精度降低到一阶的时间步解耦;RK3方案不需要时间滤波。(2)蛙跳方案的位相误差比RK3方案大。(3)RK3方案容许对平流过程采用中性和耗散(迎风-偏斜)空间离散,而蛙跳方案仅对中央差(中性)算子才稳定。Purser(2007)指出,WS02方案的RK3就其本身而言不是标准的龙格-库塔方法。因为对线性方程,它是三阶精度的,对非线性方程它仅是二阶精度的。然而Skamarock等(2008)指出,这一方案比其他RK形式更容易使分裂显式方案达到稳定。
多数时间分裂非静力数值天气预报模式(如ARPS、COAMPS、MM5、LM)对慢模用蛙跳时间离散,耗散项用向前时间积分。许多半隐式模式对显式项(慢模)也用蛙跳时间积分,不过其中许多已经转向向前时间积分方案。由于RK3方案的许多优点,国际上新一代大气数值模式,如WRF_ARW(Klemp et al,2007)采用了该方案,另外,有些模式在改进其时间积分方案时也选用了它,如德国的局地模式等。
Gassmann(2005)详细分析了纯向前时间积分方案和二阶RK迎风格式(WS98)的时间分裂显式算法的稳定性质,并提出了新的改进方案。一些研究者最近发展了其他类型的分裂显式算法,如显式两步Peer法(Jebens et al,2009)和Adams-Bashforth-Moulton分裂显式法(Wicker,2009)(称为ABM方法)。
高阶时间格式的分裂显式算法稳定性分析涉及到高阶、高次幂振幅矩阵的特征值分析,对其特征值的公式推导以及最终得到的特征值的数学表达式极为复杂,需要借助数学软件的符号计算功能进行公式推导。
本文在Gassmann(2005)对二阶RK迎风型分裂显式格式的分裂误差分析基础上,通过符号计算推导出RK3分裂显式格式的振幅矩阵特征值的数学表达式,进一步讨论了该方案的稳定性和误差性质。并比较了迎风偏斜和空间中央差格式下的误差状况以及时间分裂显式算法对各种波长的稳定性。同时用空间中央差格式的RK3方案对一维线性声波-平流方程组进行了数值实验,检验了空间中央差格式RK3方案的模拟效果。最后分析ABM方法振幅矩阵的特征值性质,采用该方案对一维波动平流方程进行数值实验,比较ABM方案和RK3方案用于时间分裂算法的模拟效果。 2 一维线性声波-平流方程组的稳定性
一维线性声波-平流方程组经常用来检验时间分裂显式算法的稳定性,例如Gassmann(2005)将其表示为
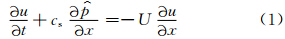
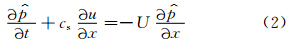
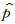 为除以平均密度和cs的扰动气压。存在两种不同的运动:声波和平流,各自具有不同的特征速度,其分裂算法为
为除以平均密度和cs的扰动气压。存在两种不同的运动:声波和平流,各自具有不同的特征速度,其分裂算法为
RK3方案表示为
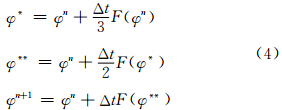
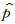 ),F为因变量的一个强迫矢量,上标表示时间层,Δt为时间步长,强迫可以是所有相关因变量的函数。该方案是WRF_ARW模式(Klemp et al,2007)选用的 RK3形式。所谓时间分裂算法,是对与快波(如声波)有关的项采用短时间步长,对慢波项采用长的时间步长。RK3方法是对长时间步长采用的方法,短步长采用直接向前积分,WRF_ARW模式采用的该RK3方法的三步中,每一步的短时间步长积分步数分别采用了1、2和4步。
),F为因变量的一个强迫矢量,上标表示时间层,Δt为时间步长,强迫可以是所有相关因变量的函数。该方案是WRF_ARW模式(Klemp et al,2007)选用的 RK3形式。所谓时间分裂算法,是对与快波(如声波)有关的项采用短时间步长,对慢波项采用长的时间步长。RK3方法是对长时间步长采用的方法,短步长采用直接向前积分,WRF_ARW模式采用的该RK3方法的三步中,每一步的短时间步长积分步数分别采用了1、2和4步。
对于三阶RK方法,分析稳定性可以用算子




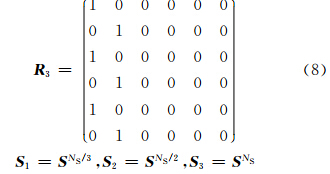
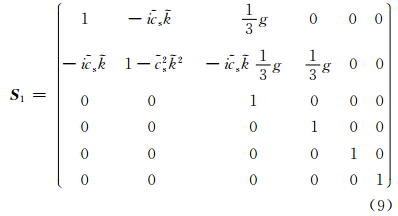
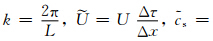
 . 其中,k为波数,L为波长,g为平流倾向G在傅里叶空间的表示。
. 其中,k为波数,L为波长,g为平流倾向G在傅里叶空间的表示。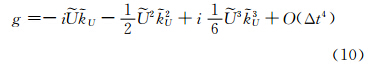
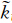 U为离散平流算子的无量纲波数,设其复数形式为
U为离散平流算子的无量纲波数,设其复数形式为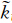 U=R+iM,这里R和M分别表示
U=R+iM,这里R和M分别表示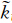 U的实部和虚部。
U的实部和虚部。
由式(5)—(10)可以看出,振幅矩阵 A 是一个非常复杂的高阶矩阵。它有以下特点:高阶(六阶);高次幂(NS≥4)的复数矩阵,且NS为变量;6个高阶、高次幂复数矩阵的乘积;矩阵的元素也是复杂的多项式,例如式(10)完全展开后有9项。因此,求矩阵 A 的特征值及其模的具体数学表达式是极为困难的。但是,可以运用数学软件的符号计算功能,进行公式推导。三大数学软件Matlab、Mathematica(Wolfram,1999)和Maple,都有符号计算、数值计算和图形功能,其中,Mathematica具有特别强大的符号计算功能,采用此软件使振幅矩阵 A 的特征值表达式的求解成为可能。
用Mathematica软件推导得出振幅矩阵 A 的表达式输出结果有数十页之多,这里略去具体形式,A 的特征值推导要耗费大量的CPU时间,用Intel的2.66 GHz处理器,优化后的算法用时也超过10 min。计算过程主要包括:矩阵的幂计算、矩阵乘积、求特征值、特征值泰勒级数展开和略去高阶项,复数的展开、复数求模、模的简化等步骤。
可以得到振幅矩阵 A 有两个特征值λ1和λ2,对它们的模进行级数展开,略去高阶项得到

从式(11)可以看出,右端第5项(公式的第2行)称为分裂误差项,因为该项只是由于采用了分裂机制才产生的。此项可以是正值也可以是负值,因此,可能导致数值计算不稳定的产生。与Gassmann(2005)不同的是,这里保留了更高阶误差项,这样可以分析空间差分为中央差时产生的分裂误差项。该项分3个部分,前两部分与离散平流算子的无量纲波数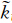 U的虚部有关,第3部分与其虚部无关。对于迎风偏斜格式
U的虚部有关,第3部分与其虚部无关。对于迎风偏斜格式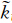 U为复数,而对中央差格式
U为复数,而对中央差格式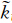 U为实数,不存在虚部。因此,中央差格式的时间分裂方案具有更小的、更高阶的误差。例如:
U为实数,不存在虚部。因此,中央差格式的时间分裂方案具有更小的、更高阶的误差。例如:
平流项的三阶迎风差分为

其平流无量纲波数为
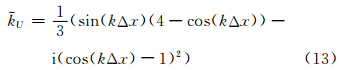
另外,RK2迎风方案的分裂误差为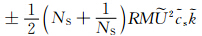 (Gassmann(2005)中式(30))。从主要时间分裂误差项(式(11)右端第5项的第1部分)可以看出,RK3时间方案的分裂误差不足RK2迎风方案的误差三分之一。
(Gassmann(2005)中式(30))。从主要时间分裂误差项(式(11)右端第5项的第1部分)可以看出,RK3时间方案的分裂误差不足RK2迎风方案的误差三分之一。
二阶中央差分平流项为
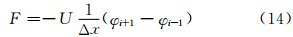
则其无量纲波数为
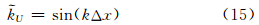

误差项的正、负分别对应着向前和向后传播的声波振幅的增长或衰减。
中央差分方案的时间分裂误差更小,因此,模拟得到的向前和向后的声波振幅差别更小。 2.2 Adams-Bashforth-Moulton时间分裂算法的稳定性及分裂误差分析
Wicker(2009)提出了基于Adams-Bashforth-Moulton时间积分方法的分裂显式算法。该方法需要用到3个时间层,其振幅矩阵为8阶(见Wicker(2009)的式6a—6e)。采用与上述对RK3方法类似的分析方法可以得到ABM时间分裂算法的4个非零特征值,其中,2个最大特征值的模的平方为
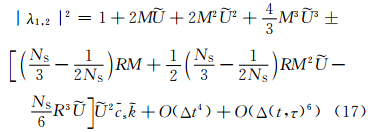
与式(11)比较可知,由于误差项中3个小项的系数ABM方案均大于RK3方案,所以无论对于迎风还是中央差格式(平流无量纲波数的虚部M=0),RK3的分裂误差都小于ABM的误差。 3 不同波数的特征值分析
由于分裂误差的存在,当误差项为正时,振幅矩阵特征值大于1,积分可能变得不稳定。为了增强稳定性,速度方程增加耗散项

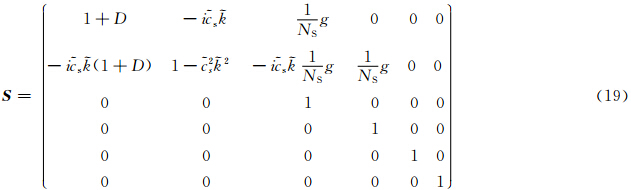
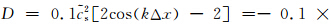
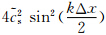 ,为傅里叶空间中的耗散项。
,为傅里叶空间中的耗散项。
图 1为三阶迎风格式的RK3时间分裂显式方案的稳定性。与Gassmann(2005)中图 4的RK2方案的稳定性对比,可以看出对于各种波长,RK3方案的不稳定区更小,不同方向
传播的声波振幅差别更小,这就说明RK3方案比RK2方案的模拟效果更加理想。
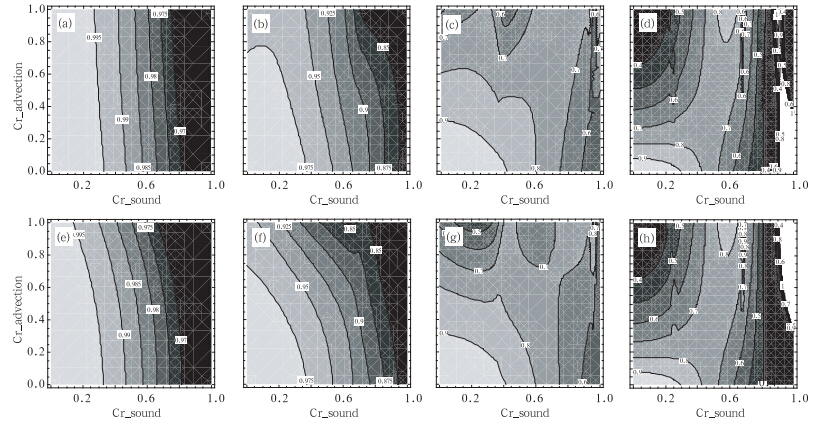 |
| 图 1 短时间步长为6时,三阶迎风差分格式RK3时间方案的稳定性(a—d. 向后传播的声波,e—h. 向前传播的声波;白色区域为特征值大于1而不稳定的区域;从左向右4个不同波长分别为16倍、8倍、4倍、2倍格距;等值线间隔分别为0.005、0.025、0.1、0.1)Fig. 1 Stability diagrams of the RK3 split-explicit time integration scheme with the third order upstream spatial difference scheme and 6 small time steps(a-b. the backward moving sound wave,e-h. the forward moving sound wave. White regions show eigenvalues larger than 1 and thus regions of instability. The four figures on each row present four different wavelengths of 16Δx,8Δx,4Δx and 2Δx from left to right,the contour intervals are 0.005,0.025,0.1 and 0.1,respectively) |
图 2说明了空间二阶中央差RK3时间分裂显式方案加耗散项时的稳定性,可以看出仅对于相对于风速向后移动的2倍格距声波,在 s大于0.88时,才产生不稳定,其他波长的特征值皆小于1,并且向前和向后传播的声波特征值差别较小。因此,时间分裂显式算法具有很好的稳定性,分裂误差也较小。空间二阶中央差的RK3时间分裂显式方案与迎风差分时(图 1)相比,可以看出,中央差的对称性更好一些,而且对于越短的波长,中央差的特征值对称性越好,2倍格距波的不稳定区也更小。
s大于0.88时,才产生不稳定,其他波长的特征值皆小于1,并且向前和向后传播的声波特征值差别较小。因此,时间分裂显式算法具有很好的稳定性,分裂误差也较小。空间二阶中央差的RK3时间分裂显式方案与迎风差分时(图 1)相比,可以看出,中央差的对称性更好一些,而且对于越短的波长,中央差的特征值对称性越好,2倍格距波的不稳定区也更小。
 |
| 图 2 小时间步数为6时,二阶空间中央差RK3分裂显式时间积分方案的稳定性(说明同图 1)Fig. 2 As in Fig. 1 but for the second order centered spatial difference scheme |
从ABM方案4个非零特征值(这里用5—8表示)的稳定性(图 3)分析可以看出,特征值5与7、6与8在形态上分别有互补的特点(黑色区域与灰色区域互补),分别与向左和向右传播的声波有关。从量值上看,其不对称性也大于RK3方案。
 |
| 图 3 短时间步数为8时,二阶中央差分格式ABM分裂显式时间积分方案的稳定性(从左到右4个非零特征值分别为5、6、7、8,白色区域为特征值大于1而不稳定的区域;从上到下4个不同波长分别为16倍、8倍、4倍、2倍格距;等值线间隔0.1)Fig. 3 Stability diagrams of the ABM split-explicit time integration scheme with the second order centered spatial difference scheme and 8 small time steps(The 4 panels on each row are for the 4 non-zero eigenvalues of 5,6,7 and 8 from left to right. White regions show eigenvalues larger than 1 and thus regions of instability. The four panels on each column present four different wavelengths of 16Δx,8Δx,4Δx and 2Δx,being larger on the upper panels and the smallest at the lowest panel. The contour intervals are 0.1) |
对于2倍格距波,当声速柯朗数(Cr)小于0.87时,ABM方案是稳定的。对于4倍格距波,主要的不稳定区域大约位于平流柯朗数大于1,而声波柯朗数小于0.2的区域。对于更长的波ABM方案是稳定的。四阶中央差分的稳定性质与二阶类似(图略),因此,Wicker(2009)文中提到的稳定性限制与2倍和4倍格距的短波有关。 4 一维线性声波-平流方程组的数值实验
为了验证二阶中央差RK3以及ABM时间分裂显式方案的实际应用效果,进行了一维线性声波-平流方程组的数值实验。实验条件同Gassmann(2005),无量纲化后的初始扰动气压p 〈 Δt/Δx=0.1位于模拟区域中间,区域的边界条件为周期的边界条件,短时间步数为4, s和 都等于0.75。加气压扰动产生的两个声波分别相对于平均风速向前和向后传播。图 4为前8个时间步的声波传播。实验结果表明,二阶中央差RK3时间分裂显式方案模拟的不同方向传播的声波的振幅基本相同,与特征值分析得出的结论一致。
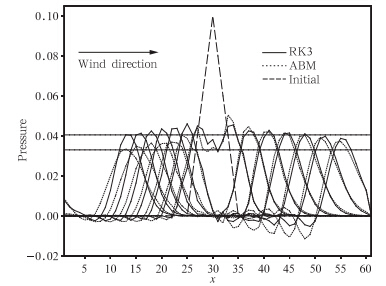 |
| 图 4 对二阶中央差RK3和ABM时间分裂显式算法的声波平流实验的初始扰动气压和前8个时间步Fig. 4 Initial perturbation and the first 8 time steps of the sound wave advection experiment for the second-order centered spatial difference with the RK3 and ABM split-explicit scheme |
ABM时间分裂算法所模拟出的不同方向传播的声波其振幅差别略大于RK3方案的模拟结果,这也与分裂误差公式所揭示的性质一致。
从波动振幅上看,不加耗散或耗散较小时,声波波峰ABM更对称一些; 波谷则是RK3更对称,但总体上RK3更对称些。当采用更大的Wicker(2009)所用的耗散系数时(是Gassmann(2005)所用耗散系数的1.78倍),波峰波谷都是RK3方案更对称。这与公式推导的结果是一致的。
对于一维声波平流实验,声波能量的衰减主要是为了计算而对运动方程加耗散项造成的,可以从声波振幅与耗散系数的密切相关这一点看出。如果不加耗散项,声波振幅衰减缓慢。不加耗散项时,RK3具有更好的稳定性。对于空间二阶中央差,当Δt=10时,RK3方案可以一直稳定积分。ABM方案只能积分几百步。因此,RK3格式具有内在的耗散性质,对速度方程只需要较小的显式耗散项,甚至可以不需要加显式的耗散项。 5 结论和讨论
(1)时间分裂显式算法是非静力中尺度模式提高计算效率的一种常用方法,几十年来不断得到发展和改进。本文通过特征值分析方法,讨论了以WRF(ARW)模式为代表的采用三阶龙格-库塔时间格式的时间分裂显式算法(WS02)的稳定性以及其误差性质。与Gassmann(2005)中对二阶龙格-库塔时间分裂显式算法(WS98)的分析结果对比,可以通过数学公式定量地比较RK3格式和RK2格式的分裂误差大小以及误差与短时间步数的关系,发现RK3的误差明显小于RK2的误差,对于三阶迎风格式,三阶RK时间方案的分裂误差在RK2的误差三分之一以下。
(2)对三阶RK时间方案的算子振幅矩阵特征值所作的级数展开给出了比Gassmann(2005)更高阶的展开项,可以同时分析迎风偏斜和中央差格式的分裂误差性质。傅里叶分析的离散平流算子的无量纲波数对于中央差格式为实数,迎风格式为复数,因此,对中央差格式,振幅矩阵特征值可以从式(11)简化为式(16),因而中央差格式的误差阶数更高,具有更小的时间分裂误差。
(3)分析了不同波长的振幅矩阵特征值所代表的分裂显式算法的稳定性质。迎风格式的RK3方案比RK2具有更好的稳定性和更小的分裂误差。特别是分析了采用中央差格式时RK3方案对于不同传播方向和不同波长声波的传播更具有对称性,分裂误差也更小。数值实验结果进一步证实空间差分采用中央差时,RK3时间分裂显式算法不同方向传播的声波振幅几乎没有差别。
(4)ABM时间分裂算法有4个特征值,所以,更为复杂(因为涉及3个时间层,矩阵为8阶),分析前两个主要特征值的公式可知,其分裂误差略大于RK3方案。一维声波平流方程数值模拟得到的向前、向后两个方向传播的声波振幅的差别也验证了这一结论,但是,两种方案的总体差别不大。这一结论是基于简单的一维声波平流方程的分析,对于更复杂的二维和三维模拟,仍需要更深入的分析。
高阶、高次幂矩阵的特征值数学表达式极其复杂,不可能人工完成公式的推导,需要借助数学软件的符号计算功能。Mathematica在符号计算方面性能优越,可以完成复杂的公式推导和计算,是进行高阶、高次幂矩阵特征值分析的强有力工具。
中央差的RK3时间分裂显式算法的分裂误差比较小,因此也适用于非静力中尺度模式,这一方案已应用到作者的非静力中尺度数值模式中。
| Gassmann A. 2005. An improved two-time-level split-explicit integration scheme for non-hydrostatic compressible models. Meteor Atmos Phys, 88: 23-38 |
| Hundsdorfer W B, Koren B, van Loon M, et al. 1995. A positive finite difference advection scheme. J Comput Phys, 117: 35-46 |
| Jebens S, Knoth O, Weiner R. 2009. Explicit two-step Peer methods for the compressible Euler equations. Mon Wea Rev, 137: 2380-2392 |
| Klemp J B, Wilhelmson R B. 1978. The simulation of three-dimensional convective storm dynamics. J Atmos Sci, 35: 1070-1096 |
| Klemp J B, Skamarock W C, Dudhia J. 2007. Conservative split-explicit time integration methods for the compressible nonhydrostatic equations. Mon Wea Rev, 135: 2897-2913 |
| Marchuk G I. 1974. Numerical Methods in Weather Prediction. Academic Press, 227 pp |
| Mesinger F M. 1977. Forward-backward scheme, and its use in a limited area model. Contrib Atmos Phys, 50: 200-210 |
| Purser R J. 2007. Accuracy considerations of time-splitting methods for models using two-time-level schemes. Mon Wea Rev, 135: 1158-1164 |
| Skamarock W C, Klemp J B.1992. The stability of time-split numerical methods for the hydrostatic and the nonhydrostatic elastic equations. Mon Wea Rev, 120: 2109-2127 |
| Skamarock W C, Klemp J B. 2008. A time-split nonhydrostatic atmospheric model for weather research and forecasting applications. J Comput Phys 227: 3465-3485 |
| Smolarkiewicz P K. 1984. A fully multidimensional positive definite advection transport algorithm with small implicit diffusion. J Comput Phys, 54: 325-362 |
| Tremback C J, Powell J J, Cotton W R, et al. 1987. The forward-in-time upstream advection scheme: Extension to higher orders. Mon Wea Rev, 115: 540-555 |
| Wicker L J, Skamarock W C. 1998. A time-splitting scheme for the elastic equations incorporating second-order Runge-Kutta time differencing. Mon Wea Rev, 126: 1992-1999 |
| Wicker L J, Skamarock W C. 2002. Time-splitting methods for elastic models using forward time schemes. Mon Wea Rev, 130: 2088-2097 |
| Wicker L J. 2009. A two-step Adams-Bashforth-Moulton split-explicit integrator for compressible atmospheric models. Mon Wea Rev, 137: 3588-3595 |
| Wolfram S.1999. The Mathematica Book. Cambridge Univ Press, 1470pp |
 2012, Vol. 70
2012, Vol. 70

