2.重庆大学机械传动国家重点实验室, 重庆400044;
3.中国人民解放军后勤工程学院, 重庆401331;
4.厦门大学航空航天学院, 厦门361005
2.The State Key Laboratory of Mechanical Transmissions, Chongqing University, Chongqing 400044, China;
3.Logistics Engineering University of PLA, Chongqing 401331, China;
4.School of Aerospace Engineering, Xiamen University, Xiamen 361005, China
板壳结构在各类装备中被广泛使用,比如飞机的机身、机翼和螺旋浆叶片运载火箭的燃料贮箱,核电站反应堆的压力容器等. 这些板壳构件在正常使用过程中由于受外部环境载荷作用、疲劳效应、腐蚀效应以及材料老化等各种不利因素的影响结构的力学性能逐渐退化. 虽然在现有标准下对这些结构都会进行监测和定期维护以保证其安全使用但是一些灾难性事故总是不可避免地发生,比如2009年2月12日美国一架客机由于服役时间偏长而积累下来的机翼局部损伤导致的故障问题而坠毁.这些事故说明虽然通过传统无损检测手段得到的检测报告都符合安全标准但是结构性能的退化过程并没有被有效评估和检测出来.随着航空航天、核电、机械和化工等领域对安全性和耐久性要求的日益严苛对各类装备中被广泛使用的板壳结构的评估和检测手段也提出了更高的要求.
相对于传统线性超声检测技术非线性超声检测技术对空间尺寸远小于超声波波长的材料微观结构特征有较高的灵敏度它对材料早期性能退化和结构内部早期损伤的评估和检测具有特殊优势因而受到广泛关注(Cantrell & Yost 2001, Donskoy 2006, Van Den Abeele et al. 2001, Aleshin & Van Den Abeele 2007, Solodov 1998).超声波的非线性是指超声波在材料中传播时发生波形畸变、谐波滋生、边频带形成等非线性现象并且非线性现象会随着材料性质的变化而变化.目前被广泛研究和应用的非线性超声检测技术包括高阶谐波技术(Shui et al. 2008)、次谐波和DC(直流direct current)响应技术、非线性超声共振谱技术和混频响应技术.由于非线性现象的复杂性至今人们对于非线性谐波产生机理的认识相当有限主要包括材料本构关系非线性的弹性动力学理论和接触声非线性理论两个方面.前者属于经典非线性理论,超声波在材料中传播时当在小振幅声波激励下,材料中的应力和应变都非常小超声波的传播遵循线性规律; 当在有限振幅声波激励下虽然材料的变形还在弹性范围内但是此时需要用非线性应力-应变关系来表征材料的力学性能并且在材料中传播的超声波将发生非线性响应表现为在波的能谱中有基频的高阶谐波或分阶谐波信号出现.对于完好的材料,这种非线性响应较小,但是当材料性能发生退化如疲劳、蠕变、应力残余等,这种非线性响应将显著增强高阶谐波或分阶谐波的能量会明显增大这一现象为材料早期性能退化的评估奠定了基础.当材料中出现闭合裂纹等接触类损伤后出现了和上述现象不一样的超声响应(Ostrocsky & Johnson 2001),主要表现为:(1)在小振幅声波激励下就出现谐波滋生现象而在有限振幅声波激励下,会出现明显的三阶或三阶以上的高次谐波其谐波幅值比经典非线性理论值要高几个数量级;(2)谐波幅值与基波幅值之比不再与经典非线性理论相符;(3)应力-应变关系的滞回效应导致高阶谐波随基波幅值的二次变化;(4)混频声波激励下的声场调制现象等. 经典非线性理论无法解释上述现象于是研究者转向接触声非线性理论提出了多种不同的理论和模型进行研究. 这类研究可以分为两类一类是从材料的微观物理机制出发,考虑裂纹界面微观特征建立有效物理模型,研究损伤对超声响应的影响;另一类从非线性声学现象出发,建立损伤及其演化过程的等效模型并结合超声波动方程分析超声波的非线性响应与损伤之间的关系.这类研究为利用非线性超声方法检测和评估结构损伤奠定了基础.
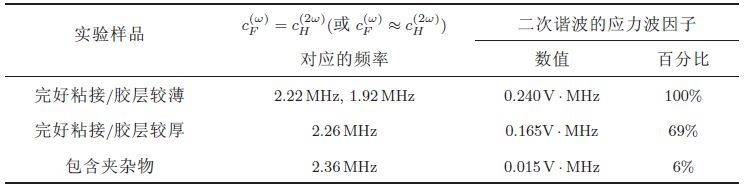
超声波在板壳结构中传播时,由于上下边界面的影响,超声波在两表面之间来回反射在满足相位匹配的条件下,入射波和反射波就会形成贯穿层厚的驻波从而波只能沿层的延伸方向传播,板壳结构成为波导,波导中的波被称为超声导波.对于板类结构,在其内部传播的超声导波根据质点的振动情况可分为两类:水平剪切波(shear horizontal wave,SH wave)和兰姆波(Lamb wave).由于SH波引起的质点振动(位移和速度)都位于平行于层面的平面中(图 1(a))因此可以认为SH波是沿平行于层面方向偏振的体剪切波上下反射叠加的结果(图 1(b)). 在不同的激励频率下板内会出现不同模态的SH波根据质点的位移场表达式可分为对称模式和反对称模式,图 2为铝板中的SH模态的相速度频散曲线,其中零阶模式(SH0波)是非频散波.相比垂直偏振横波(shear vertical wave,SV波)和纵波(longitudinal wave,L波)当SH波从平行于偏振方向的表面反射时,SH波不会转为其他类型的波且杂乱回波较少. 其次,SH波比体波散射少,衰减小在相同的频率下比体波传播得更远.因此在超声无损检测领域SH波具有极大的应用潜力. 但是,产生纯SH波比较难以前实验时多使用电磁超声换能器(EMAT)来激励和接收SH波但是电磁超声换能器只能适用于导电材料,极大地限制了SH波的实际应用.最近北京大学李法新课题组采用面内剪切(d24)型压电陶瓷换能器在平板中激励出单模态的零阶水平剪切波(SH0波)同时还可以有选择性地接收SH0波该工作在基于SH波的损伤检测应用方面实现了突破性的进展(Miao et al. 2016).但是目前研发出的面内剪切(d24)型压电陶瓷换能器只能在较低频率范围内激发纯SH0波和选择性接收SH0波.

|
| 图 1 水平剪切波的传播,其中传播方向为x1,质点位移方向为x3 |
|
| 图 2 铝板中的SH模态的相速度频散曲线(cT=3 100 m/s)其中实线代表对称模态虚线代表反对称模态 |
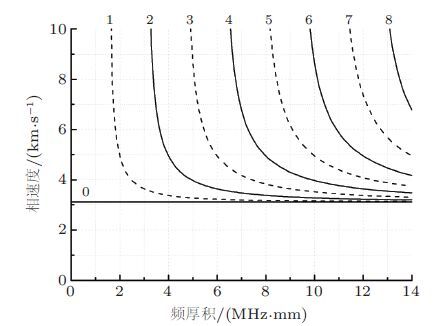
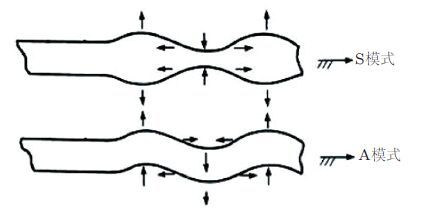
与SH波引起的平行于层面的质点运动不同兰姆波引起的质点振动在垂直于层面的平面内作椭圆轨迹运动.英国科学家Lamb(1917)在平板自由边界条件下求解波动方程时得到了一种特殊波动解后人把这种波动命名为兰姆波以纪念它的发现者.兰姆波是一种在厚度与激励声波波长为相同数量级的声导波(如金属薄板)中由纵波与横波耦合而成的特殊形式的应力波它在不同厚度及不同激发频率下会产生不同的传播模式(Viktorvo 1965).根据质点振动位移的分布形态不同兰姆波被分为对称型兰姆波(S模式)和反对称型兰姆波(A模式),如图 3所示. 同时对于不同模式的兰姆波,还有不同的阶次,通常用S0S1,S2... 表示不同的对称型兰姆波,用A0,A1A2... 表示不同的反对称型兰姆波. 此外兰姆波的另外一个基本特征是频散性,即传播速度随着频率的变化而变化图 4是兰姆波在铝板中传播的频散曲线,可以发现,与SH波不同兰姆波的零阶模式也是频散的. 与SH波相比兰姆波用常规压电换能器很容易被激励和接收. Giurgiutiu(2003,2005)研究了在单个压电晶片驱动器激励下的板中兰姆波模式及其特征.Sonti等(1995)分析了在条形、圆形、椭圆形、三角形等不同形状的压电晶片激励下板结构中产生的兰姆波模式.Su和Ye(2009)对压电晶片作为作动器和传感器的理论建模进行了综述.所以,虽然波动形式上SH波比兰姆波要简单但大量的研究迄今仍选择利用兰姆波对板壳结构进行损伤检测和评估.
|
| 图 3 对称型兰姆波(S模式)和反对称型兰姆波(A模式) |
|
| 图 4 兰姆波在铝板中传播的频散曲线.(a)相速度,(b)群速度 |
作为板壳结构中传播的一种典型声导波模式兰姆波可以实现对固体板的快速大范围损伤检测但兰姆波复杂的传播特性极大地限制了其实际应用. 直到20世纪60年代初美国工程师Worltony(1961)首次提出铝和锆的频散曲线的模式特征可应用于材料的无损检测之后人们才逐步开始研究基于兰姆波的结构损伤识别方法(Demer & Fentnor 1969). 自20世纪以来随着计算机和数值仿真技术的飞速发展和测试手段的不断改进基于线性超声理论的兰姆波损伤识别方法已获得长足的进步其中常用方法包括直接法、可能性评估法、层析成像法、相控阵法、人工智能法等.的参照结构对比产生的到达时间差来判断是否存在损伤以及确定损伤大小(Diamanti et al. 2007; Qiu et al. 2011,2013).可能性评估法根据由于损伤引起的波包到达时间来确定损伤可能存在的椭圆轨迹并且根据距该椭圆距离大小构造一个损伤概率密度函数来评估检测区域各点的损伤概率;为提高可靠性,通过布置传感器网络获取多条传感器路径的损伤概率信息从而实现检测区域的损伤分布评估(Wang et al. 2010,Lu et al. 2011).层析成像法同样通过布置传感器网络利用不同传感器路径在检测区域内重构一个反应损伤位置、大小、形状的图像(Wright et al. 1997,Sicard et al. 2002,Liu et al. 2014).与可能性评估法相比,层析成像法需要对整个检测区域进行扫描因而所需的传感器数目较多. 相控阵法也是基于布置一个传感器网络通过精确控制每个传感器的激励和接收时间以及相位延迟实现对结构的全面扫描从而获取结构中损伤的类型、位置以及形状等信息(Luo & Rose 2007,Purekar & Pines 2010). 同样相控阵法的传感器网络也是比较复杂的.人工智能法利用先前大量数据对人工神经网络算法或遗传算法进行训练再用训练好的算法来检测结构,实现结构的损伤评估甚至损伤图像重构(Su & Ye 2005,Vishnuvardhan et al. 2007). 可是这些基于线性超声理论的兰姆波损伤识别方法能检测出损伤的尺寸都受限于检测导波的波长对于材料早期性能退化和结构内部早期微损伤几乎不敏感.
鉴于非线性超声具有检测灵敏度高的优点和超声兰姆波具有检测速度快的特点若将两者加以结合则可望发展出一种既有高检测灵敏度又有快检测速度的非线性兰姆波检测技术. 但是关于非线性兰姆波的研究成果仍然非常有限,原因主要有两个方面:一是由于板上下边界反射、模式转换等因素的影响,兰姆波传播过程异常复杂理论上分析十分困难; 二是兰姆波具有频散特性一般情况下难以产生较明显的非线性效应因此通过实验测量兰姆波的非线性效应也十分困难.非线性超声在检测材料早期性能退化和结构早期损伤方面的潜力给无损探伤领域注入了新的活力然而非线性兰姆波的相关理论和实验研究的缓慢发展阻碍了其实际应用.本文从理论和实验两个方面总结了近二十年来关于非线性兰姆波的研究进展第2节介绍基于经典非线性理论的非线性兰姆波的相关工作;第3节介绍基于接触声非线性理论的非线性兰姆波的相关工作;最后展望了非线性兰姆波的未来研究重点和发展趋势.
2 基于经典非线性理论的非线性兰姆波本节主要介绍源于材料的固有物理非线性诱发的非线性兰姆波的相关研究进展.一般认为,材料的固有物理非线性产生的原因有两个:(1)由原子间的相互作用力或点阵的非简谐性引起的非线性;(2)由内部微观缺陷如位错、滑移带等引起的非线性.其中由位错等微观缺陷引起的非线性占主导地位.
2.1 理论和数值分析基于经典弹性非线性理论的声波动理论主要研究固体介质的固有物理非线性对声波传播特性的影响在理论分析中固有物理非线性主要通过应力-应变关系中的非线性系数予以描述(Auld 1973,Cantrell 2003,税国双等2005). 数学上应力-应变之间的非线性关系可以用非线性系数表示,对于一维情况,有
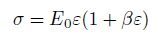
|
(1) |
式中σ为应力,ε为应变,E0 为材料的线弹性模量β 为二阶经典非线性系数. 由于在固体介质中声波传播非常复杂基于经典弹性非线性理论的声波动理论的研究之前主要针对声纵波和声表面波(Zabolotskaya 1992,Gusev et al. 1998,Kumon & Hamilton 2002). Breazeale等从连续介质模型出发将方程(1)和声波动方程结合,从数学上推导出一维纵波非线性波动方程求解该方程可得到非线性响应(即谐波幅值)与非线性系数之间的关系.若输入为连续正弦波,波动方程的近似解为
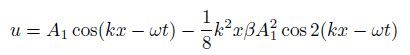
|
(2) |
式中ω 为激励波的角频率x为波的传播距离,k为波数,t为时间,A1为基波幅值. 从式中可以看出二次谐波幅值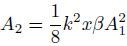

|
(3) |
由此可知β正比于二次谐波幅值与基波幅值的平方的比值,换而言之材料的非线性系数可以通过二次谐波幅值与基波幅值的平方的比值随传播距离增大的变化关系来衡量. 但是,与声纵波和声表面波相比,兰姆波的非线性理论研究进展缓慢.
直到20世纪90年代,邓明晰(1996,1997,1999)最先采用界面非线性声反射技术将兰姆波视为由满足边界条件的横、纵波在固体板的上、下界面反射重构而成假设了兰姆波的横、纵波的形式解将其代入非线性波动方程并采用逐级近似方法进行求解得到了共振条件下满足边界条件和初始条件的具有累积增长效应的兰姆波二次谐波的解析解;结果表明在共振条件下固体板中传播的兰姆波可激发出两种类型的二次谐波一种是自由二次谐波,其值非常微弱且难以对其进行实际测量另一种是累积二次谐波,它随传播距离的增大而累积增长是实验测量信号中二次谐波的主要成分.为克服共振条件下不能严格给出兰姆波自由二次谐波的解析解的不足,Deng(2003)、Lima和Hamilton(2003)先后各自分别采用导波激发的模式展开方法在二阶微扰近似条件下推导出了更具一般性的兰姆波二次谐波声场的解析解.据其研究结果可知,伴随基频兰姆波传播所产生的二次谐波声场可视为由一系列二倍频兰姆波模式叠加而成;只有与基频兰姆波相速度相等(相速度匹配)的二倍频兰姆波模式才表现出随传播距离累积增长的性质;其他与基频兰姆波相速度不等(相速度失配)的二倍频兰姆波模式其振幅随传播距离表现出拍效应可不考虑它们对基频兰姆波二次谐波声场的贡献;基频兰姆波的二次谐波声场主要取决于满足相速度匹配条件的二倍频兰姆波模式.邓明晰和Lima等研究均表明,累积二次谐波的产生需要两个条件:基频兰姆波有非零能量流馈入二次谐波、基频兰姆波模式的相速度须与二倍频兰姆波模式的相速度相同.Muller等(2010)考虑在实际的非线性实验中一般采用有限周波数的正弦或余弦信号激发兰姆波的情形补充了第三个条件:基波兰姆波模式的群速度须与二倍频兰姆波模式的群速度相等(群速度匹配);提出该条件主要是基于这样一种考虑采用有限长时域信号激励的兰姆波在结构中以波包的群速度向前传播基频兰姆波和二倍频兰姆波模式的群速度相匹配时才能同步传播如此由基频兰姆波传播至二次谐波的能量才能发生累积.若以上三个条件需同时满足则兰姆波累积二次谐波的产生条件就显得过于苛刻.在对兰姆波二次谐波发生效应的物理实质进行深入分析的基础上邓明晰等(2011,2012)从理论和实验上证明,即使群速度匹配条件不满足伴随有限长兰姆波时域信号传播所产生的二次谐波信号仍可随传播距离累积增长. 此外,Zhu等(2016)还从数值仿真的角度出发进一步证明了兰姆波累积二次谐波的产生并不受限于基频和二倍频兰姆波模式的群速度匹配条件.
目前,非线性兰姆波的理论研究还不能认为完全成熟因为从理论上既得不到封闭解的β系数而且在关于兰姆波高次谐波的对称性问题上结论还不统一. 邓明晰(1996,1999,2003)推导出的二次谐波位移场具有对称性质并由此得出结论不论基波是对称模式还是反对称模式被产生的二次谐波只能是对称模式的,即S模式. Srivastava和Scalea(2009)得到的结论是,反对称模式不会出现在偶数阶谐波它可以出现在奇数阶谐波; 而对称模式可以出现在所有高阶谐波即包括偶数阶谐波和奇数阶谐波. 这个结论在一定程度上和邓明晰的一致即二阶谐波(偶数阶谐波)只能是对称模式的.Muller等(2010)得到二次谐波可以交差产生的结论即一个反对称波的基波可以产生对称的二次谐波. 可以发现前面的结论在一定程度上都有相同的地方,而Lima和Hamilton(2003)从理论上得到的结论是: 一个基波只能产生与其同类的二次谐波如A波只能产生A波的二次谐波; S波只能产生S波的二次谐波. 因此在今后的研究中,不管是从理论还是实验都有必要对兰姆波高次谐波尤其是二次谐波的对称性问题进行深入研究以便在将来的非线性兰姆波的损伤检测应用中对合适模式的选取进行指导.
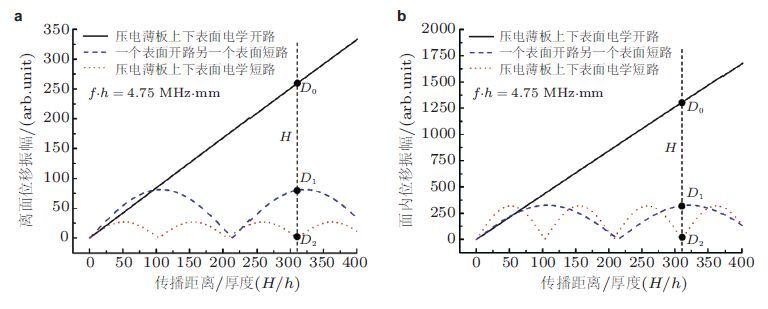
前面的研究都是针对普通的各向同性固体板的,邓明晰等(2005,2007)采用二阶微扰近似和导波的模式展开方法从理论上还研究了各向异性固体板和分层结构中的兰姆波的二次谐波发生效应并给出了二次谐波声场的一般形式解.板的各向异性会引起导波模式相速度的改变从而显著影响到导波二次谐波.分层结构中的二次谐波声场可视为各层结构中各自产生的一系列二倍频兰姆波的叠加如果某一二倍频兰姆波的相速度与基频兰姆波的相速度相等则该二倍频兰姆波在传播方向上将随传播距离呈线性积累增长趋势如果它们的相速度不相等则二倍频兰姆波的振幅将随传播距离呈正弦形式振荡变化并且速度相差越大二倍频兰姆波的振幅随传播距离的振荡越剧烈. 此外Deng和Xiang(2015)在考虑压电材料的弹性、压电及介电非线性之后首先从理论上研究了压电薄板中超声导波的二次谐波发生效应发现通过改变压电薄板表面的电边界条件可显著地调节或控制超声导波的二次谐波发生效应; 如图 5所示在一特定的传播距离H不同电边界条件所对应的二次谐波振幅(点D0D1和D2)差异甚大.
|
| 图 5 在厚度为h的YZ-LiNbO3压电薄板中伴随基频导波模式传播所发生的二倍频导波模式在薄板表面的振幅随传播距离的关系曲线.(a)离面位移,(b)面内位移(Deng & Xiang 2015) |
目前存在两种分析非线性兰姆波的理论方法. 邓明晰(1998, 1999)基于界面非线性声反射理论分析了单层各向同性固体板中的兰姆波二次谐波声场.采用该方法可得到满足二阶波动方程、边界条件和初始条件的具有累积效应的二次谐波的解析解在二阶微扰近似条件下该解为准确解,其物理意义直观,逻辑清晰易于理解. 但对于多层、各向异性或几何形状复杂的波导结构采用该方法的分析过程较为繁琐另外也难以分析在不满足相速度匹配条件下的二次谐波声场.为克服上述不足,邓明晰(2003)、Lima和Hamilton(2003)各自独立提出采用导波激发的模式展开分析方法以更全面地分析兰姆波的二次谐波发生效应. 其基本要点是在二阶微扰近似条件下伴随基频兰姆波传播所产生的二倍频彻体力和面驱动应力张量其作用是在板中激发出一系列的二倍频兰姆波模式它们叠加起来即构成基频兰姆波的二次谐波声场;当基频兰姆波的相速度与某一二倍频兰姆波模式的相速度相等时该二倍频兰姆波模式随传播距离累积增长此时其等同于之前基于界面非线性声反射理论所得的具有累积效应的二次谐波.关于发生累积效应兰姆波二次谐波的条件两种分析方法所得结论是相一致的. 众所周知模式展开分析方法是基于互易原理而理论上互易原理并不适于分析非线性问题,但在二阶微扰近似条件下非线性效应可视为是线性波动响应的一个二阶微扰兰姆波的二次谐波发生问题即成为一个已知二倍频激发源(源于基频兰姆波的传播)的线性激发问题.综合以上两种方法开展比较研究更加有利于理解非线性兰姆波传播问题的物理本质.
针对非线性兰姆波传播理论的研究,有争议的观点主要包括:(1)产生具有累积效应的二次谐波在满足初始的基频兰姆模式和二倍频兰姆波模式相速度匹配的同时是否还需要同时满足两者之间的群速度匹配条件?Deng等(2011,2016)不仅在理论上解释了相速度匹配就可产生具有累积效应的二倍频兰姆波信号同时还从实验上给予了证实. 在满足相速度匹配条件下无论基频与二倍频兰姆波模式是否满足群速度匹配都可产生具有累积效应的二次谐波故群速度匹配不是产生具有累积效应二次谐波的必要条件.(2)二倍频兰姆波是否存在反对称模式? 一般认为兰姆波的传播存在对称和反对称两种形式通过分析二倍频兰姆波声场(Deng 1999,2003)可发现无论初始激励的基频兰姆波模式是对称或非对称的所产生的二倍频兰姆波都应是对称的.
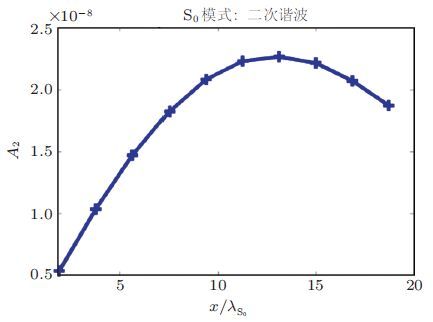
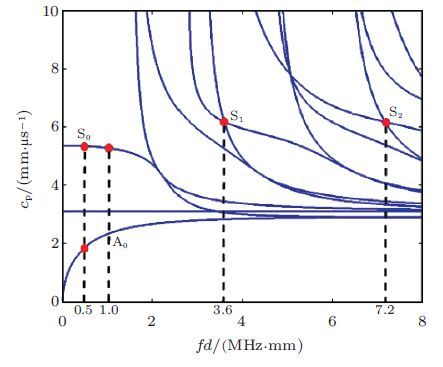
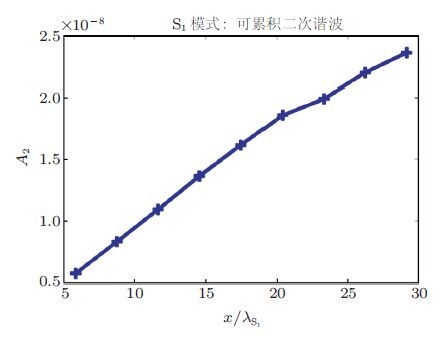
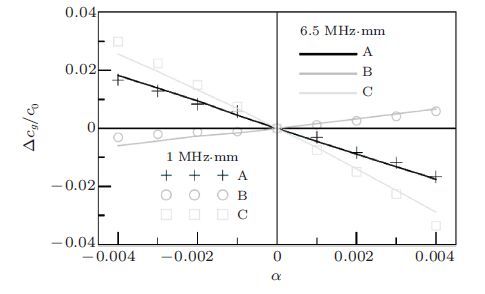
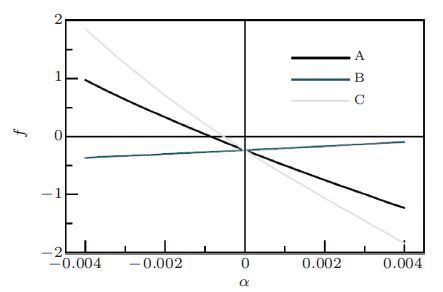
在数值分析中固有物理非线性主要通过固体介质的高阶弹性常数予以描述.目前大部分研究工作都是把材料的三阶弹性常数引入本构关系中构造超弹性本构模型并将其代入运动方程,从而获得非线性响应.常用的超弹性本构模型有Landau-Lifshitz模型和Murnaghan模型.Chillara和Lissenden(2014,2016)比较了线弹性本构模型超弹性Murnaghan本构模型和几何非线性三种情况下不同模式和频率的兰姆波在铝板中传播一定距离后的非线性响应结果显示线弹性本构模型基本不会引起兰姆波的非线性响应而几何非线性引起的非线性响应要远小于超弹性Murnaghan本构模型引起的非线性响应这说明材料本身的非线性是诱发超声非线性响应的主要因素. 另外Chillara和Lissenden(2014,2016)分析还发现当基波为0.5 MHz的S0波时获得的二次谐波主要为1 MHz的S0波;尽管0.5 MHz的S0波和其倍频的1 MHz的S0波的相速度并不严格匹配(两者近似相等)这种情况下诱发的二次谐波在一定传播距离范围内仍是具有累积效应的.图 6显示了在传播距离x/λS0 >10之后累积二次谐波的幅值呈下降趋势. 图 6所示结果说明了兰姆波累积二次谐波的产生并不需要严格满足相速度和群速度匹配条件这与邓明晰之前分析所得的当基频和二倍频兰姆波相速度近似相等也可产生累积二次谐波(邓明晰2003)、以及兰姆波累积二次谐波的产生并不受限于群速度匹配条件(邓明晰 2011,2012)是相一致的. 当基波为3.6 MHz的S1波时获得的二次谐波主要为7.2 MHz的S2波由于3.6 MHz的S1波与7.2 MHz的S2波的相速度严格相等(图 7),所以这种情形下诱发的二次谐波具有积累效应(图 8)二次谐波的幅值随着传播距离的增大呈线性增长趋势. Pau和Scalea(2015)提出一个模型来研究兰姆波在含预应力板内的传播规律该模型综合考虑了有限应变和包含三阶弹性常数的应变能表达式两个因素分两步求解含预应力板内的非线性兰姆波.第一步求解出以初始应力为变量的群速度和相速度的函数论文中讨论了沿波传播方向一致的单向拉压状态(A)、垂直于波传播方向的单向拉压状态(B)、平面内各向同性应力状态(C)这三种应力状态下板内兰姆波的群速度和相速度的变化并且比较了在这三种应力状态下兰姆波的群速度随板内应力变化的相对改变(如图 9); 第二步采用摄动法求解在给定波速下二次谐波的位移分量,图 10显示了三种应力状态下不同应力大小时二次谐波位移分量的变化曲线从图中可以看到,在平面内各向同性应力状态下受应力影响最大其次是沿波传播方向一致的单向拉压状态垂直于波传播方向的单向拉压状态受应力影响最小.
|
| 图 6 基波为S0波(0.5 MHz)时二次谐波幅值和传播距离之间的关系(Chillara & Lissenden 2016) |
|
| 图 7 在铝板的相速度频散曲线中显示基波和二次谐波之间相速度的关系(Chillara & Lissenden 2016) |
|
| 图 8 基波为S1波(3.6 MHz)时二次谐波幅值和传播距离之间的关系(Chillara & Lissenden 2016) |
|
| 图 9 三种应力状态下兰姆波的群速度随板内应力变化的相对改变(Pau & Scalea 2015) |
|
| 图 10 三种应力状态下二次谐波位移分量的变化曲线(Pau & Scalea 2015) |
利用数值分析方法研究非线性兰姆波的传播特性以进一步揭示非线性兰姆波的传播机理,近年来越来越受到重视.但目前的数值分析方法主要是基于将三阶弹性常数引入到应力-应变的非线性本构关系之中这种经典的非线性本构关系并不适用于在含有微损伤、微缺陷的材料结构中分析非线性兰姆波的传播特性.微损伤、微缺陷引发兰姆波非线性响应的机理目前还不清晰,特别是不同的损伤类型还可引发不同的非线性响应特征.因此利用数值分析方法研究非线性兰姆波尚需在非线性声学响应机理上作进一步探索以开发可被广泛应用的数值分析模型.
2.2 实验研究由于兰姆波的频散特性,一般情况下产生的二次谐波不具备积累效应因此通过实验获取兰姆波的非线性响应是一件非常困难的事情.目前绝大多数实验研究都使用Ritec公司开发的RAM-5000-SNAP测量系统开展进行RAM-5000-SNAP测量系统主要包括两个宽带射频脉冲放大器、独特的信号追踪接收器、90°相移敏感检测器、门积分器和多个频率合成器.实验时通过门控放大器放大发射信号在接收端运用超外差技术和向敏检波积分技术充分提取不同频率的信号(基频非线性效应产生的二次谐波、三次谐波及和频差频等).非线性超声实验测量系统如图 11所示RAM-5000-SNAP测量系统发出的信号经过衰减器后由超声换能器入射到试件中激发兰姆波在试件中传播一段距离后再由超声换能器接收波信号.将采集到的信号进行傅里叶变换或者短时傅里叶变换求出基频幅值和倍频幅值,进而计算材料的非线性系数.从图 11可知,非线性超声实验并不复杂难点在于兰姆波模式的选择.

|
| 图 11 非线性超声实验测量系统 |

|
| 图 12 基频与二倍频兰姆波的频散曲线(P点: c(ω) =c(2ω))(Deng et al. 2005) |
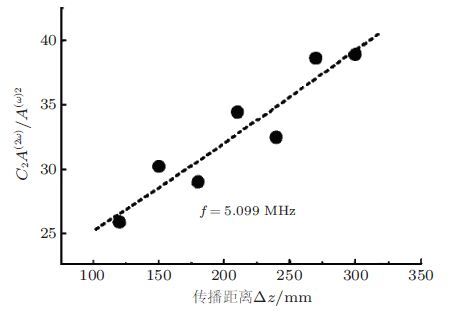
邓明晰等(2005,2006)最早通过实验验证了兰姆波在一定条件下其二次谐波随传播距离累积增长这一现象他们在2 mm厚的单层铝板中用斜劈换能器激发和接收兰姆波调整斜劈角度可选择被激发的兰姆波模式,通过相速度频散曲线(图 12)确定激发基频兰姆波模式(A4和S4模式)使其相速度与某一二倍频兰姆波模式的相速度相等或近似相等(P点).实验中以扫频方式依次产生从4.8 MHz到5.5 MHz的射频脉冲同时在不同传播距离处测量基频和二倍频兰姆波信号在铝板表面的振幅其中基频兰姆波信号通过对超声信号进行低通滤波而获得二倍频兰姆波信号通过对超声信号进行高通滤波而获得它们的振幅是通过匹配的门积分器进行积分运算而获得. 实验结果得到在f=5.10 MHz附近二次谐波振幅与基频波振幅的平方之比随传播距离增大呈线性增长趋势(图 13).
|
| 图 13 频率为5.099 MHz时二次谐波幅值与基频兰姆波振幅平方比值与传播距离的关系曲线(Deng et al. 2005) |
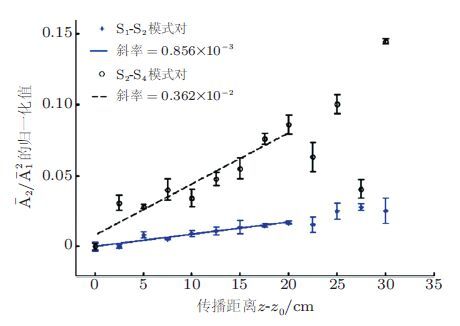
Liu等(2012)采用可变角度超声探头进行非线性超声实验研究非线性兰姆波二次谐波的对称性.实验研究了对称的S1-S2模式对与反对称A1-A2模式对、A2-A4模式对的非线性系数随传播距离的关系.结果表明三组模式对的非线性系数均随传播距离呈现线性增长趋势但对称的S1-S2模式对的斜率远大于反对称A1-A2模式对和A2-A4模式对(如图 14).为了进一步研究反对称模式对的非线性系数随传播距离的增长是否由累积效应产生他们还研究了反对称A1-A2模式对和A2-A4模式对在两种不同型号(代表不同损伤程度)的铝板中的非线性系数随传播距离的变化结果发现其拟合曲线的斜率基本不变这说明反对称兰姆波模式对的非线性系数随传播距离的增长与材料的非线性无关.因此得出结论,非对称二次谐波不具备积累效应只有对称的二次谐波才能随传播距离发生累积效应.

|
| 图 14 铝板(6061-T6型号)中三组模式对的归一化非线性系数cβ2 A2 /A12 ω 2 与传播距离的关系(Liu et al. 2012) |
Matlack等(2011)通过实验研究了对称的S1-S2模式对、S2-S4模式对的有效二次谐波的产生发现虽然两组模式对的非线性系数均随传播距离的增大而增大但是S2-S4模式对的增长斜率是S1-S2模式对的4.23倍(图 15),这说明高阶谐波对材料的非线性更加敏感. 但是,从实际的实验状况考虑采用S1-S2模式对所产生的其他模式杂波较少且基波和二次谐波的波速最快,在信号处理方面优于S2-S4模式对因此S1-S2模式对还是一种比较好的选择.
|
图 15 S1-S2模式对、S2-S4模式对的非线性系数 |
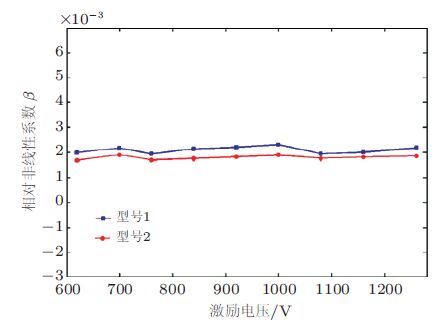
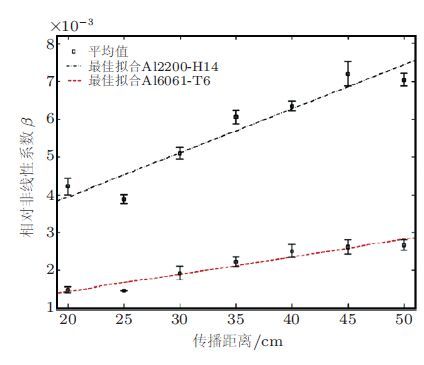
Bermes等(2008)采用斜劈式超声换能器和激光干涉仪(用于接收信号)研究了在两种型号不同的铝板中S1-S2模式对的非线性系数随激励电压、传播距离变化的关系.结果显示,非线性系数随激励电压的增大基本保持不变(图 16)说明非线性系数基本不受激励信号大小的影响;而非线性系数随传播距离的增大呈线性增长趋势但对于不同型号的铝板S1-S2模式对的非线性系数随传播距离的增长速率不同(图 17),说明S1-S2模式对可用于衡量材料的弹性非线性.目前大部分的实验结果只能定性地衡量材料的非线性程度如果能建立材料力学性能参数与兰姆波的非线性特征之间的定量关系则可实现对材料早期性能退化的定量评价.
|
| 图 16 一定传播距离处相对非线性系数β' = A2A12与激励电压的关系(Bermes et al. 2008) |
|
| 图 17 在不同型号铝板中S1-S2模式对的相对非线性系数β' = A2A12与传播距离的关系(Bermes et al. 2008) |
实验研究中目前广泛采用的方法是根据可产生具有累积效应兰姆波二次谐波的相速度匹配条件激励特定的基频兰姆波模式并验证二次谐波随传播距离的累积效应.研究分析满足相速度匹配条件的兰姆波各个模式的波结构发现这些模式都存在一个共同的特点: 板材表面上的法向位移分量为零而切向位移分量为最大值. 在实际的测量中,法向位移分量更容易被检测.邓明晰(2003)研究了基频与二倍频兰姆波信号在相速度近似匹配情况下二次谐波法向位移分量显著增大并通过实验证实了基频与二倍频兰姆波信号在相速度近似匹配的情况下也可以产生具有累积效应的二次谐波因此提出适度的相速度不匹配会更有利于实验测量兰姆波的二次谐波信号.
2.3 材料损伤评价方面的应用大量的试验研究证明材料的早期疲劳损伤,蠕变界面粘接强度的退化可用超声非线性系数进行表征,因为相对于基频波高次谐波对材料性能的微小变化更为敏感但是大部分研究都是针对非线性超声纵波和声表面波的在非线性兰姆波方面目前的研究工作还比较少.
2.3.1 材料疲劳损伤评价邓明晰和项延训等(2007,2008,2011)通过测量兰姆波的基波和二次谐波的幅-频曲线研究了采用非线性超声兰姆波方法评价铝板的拉-拉疲劳损伤、镍合金钢板的热降解的可行性.实验结果发现,铝板在疲劳加载过程中在其中传播的兰姆波的基波应力波因子随循环次数的改变并不明显且与循环次数的对应关系也不确定(图 18(a)和(图 18(c));而兰姆波二次谐波的应力波因子随循环次数的变化表现出非常敏感的性质尤其是在周期性载荷作用的最初阶段二次谐波的应力波因子随循环次数的变化非常显著并表现出明显的单调对应关系(图 18(b)和(图 18(d));将镍合金钢板放置高温环境中不同时长则相当于镍合金钢板经历不同的热降解时间发现兰姆波随着热降解时间表现出三个阶段不同的变化趋势在热降解时间较短的早期阶段,非线性系数呈单调上升趋势在中间相当长的热降解时间段,非线性系数表现出相对平稳的变化趋势当热降解时间进入第三阶段,非线性系数呈逐渐下降趋势(图 19)原因是长时间的高温环境引起位错变化和微孔萌生导致相速度不匹配.

|
| 图 18 超声兰姆波的归一化应力波因子与循环次数的关系(邓明晰 & 裴俊峰,2008).(a)基波,试件#A,(b)二次谐波试件#A,(c)基波试件#B,(d)二次谐波,试件#B |

|
| 图 19 频率为2.45 MHz时兰姆波声非线性系数与热退化时间的关系(Xiang et al. 2011) |
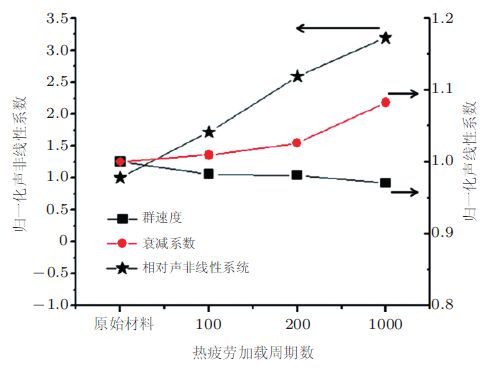
针对航空复合材料热疲劳问题,Li等(2012)通过实验比较了线性参数(群速度、衰减系数)和非线性系数(S1-S2模式对)对热疲劳加载周期数的敏感度从图 20可以看出,群速度几乎不受热疲劳加载周期数的影响而非线性系数的敏感度明显大于衰减系数并且非线性系数随周期数的增长呈明显的线性增长趋势这非常有利于对材料早期疲劳损伤进行评价.
|
| 图 20 比较兰姆波的群速度、衰减系数和相对声非线性系数对热疲劳加载周期数的敏感度(Li et al. 2012) |
Pruell等(2007)考察了材料的累积塑性对兰姆波的非线性响应的影响.实验中使用了1个未变形试件作为参考和5个塑性变形程度不同的试件其中最大程度的塑性变形都远低于试件发生紧缩所达到的塑性变形因此塑性变形被认为均匀分布于整个试件结果显示逐渐积累变大的塑性变形导致兰姆波的非线性逐渐增大(图 21)这说明非线性兰姆波可用于检测由塑性驱动的材料微观损伤.

|
| 图 21 兰姆波的非线性与塑性变形的关系(Pruell et al. 2007) |
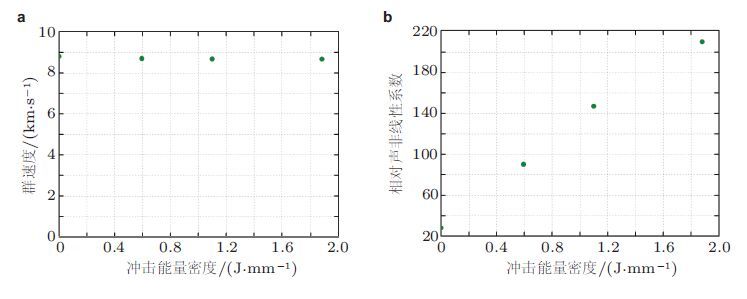
Rauter和Lammering(2015)比较了复合材料的冲击损伤对兰姆波的群速度和非线性响应的影响.实验时用4种不同的冲击能量冲撞试件的3个位置(图 22)然后激发S1-S2模式对在试件中传播采用Morlet小波变换处理接收到的信号比较兰姆波波包群速度和S1-S2模式对的非线性系数随冲击能量的变化.结果显示兰姆波波包群速度几乎不受冲击的影响(图 23(a))而S1-S2模式对的非线性系数随冲击能量的增大而明显增大(图 23(b)),这说明兰姆波的速度几乎不受复合材料中微结构损伤的影响所以不能期待通过测量兰姆波速度的变化来检测复合材料中微结构损伤;而兰姆波的非线性响应对冲击非常敏感如果能将非线性系数与冲击能量建立对应关系则可预测复合材料被冲击严重程度.

|
| 图 22 实验方案示意图(Rauter & Lammering 2015) |
|
| 图 23 实验结果:(a)群速度与冲击能量的关系(b)相对超声非线性系数与冲击能量的关系(Rauter & Lammering 2015) |
复合板材粘接层的质量优劣对复合板材结构性能影响很大,然而粘接层力学性能的微小变化,比如刚度系数的微小改变不足以引起兰姆波频散特性发生较显著的变化. 邓明晰(2005)将兰姆波检测技术与非线性超声测量方法结合起来在兰姆波具有强烈非线性效应的条件下对三种不同粘接情况的复合板材中传播的兰姆波的基波及二次谐波幅频特性进行了实验研究.实验结果如表 1所示三种粘接情况对应的二次谐波的应力波因子显示出良好的区分特性并且不同粘接状态导致的兰姆波频散特性的变化可通过二次谐波幅频曲线峰值(cF(ω) = cH(2ω) 或 cF(ω)≈cH(2ω))所对应频率值的差异得以体现.此结果也显示了非线性超声兰姆波测量技术对复合板材的粘接状况进行有效表征的巨大潜力.
以上的实验研究表明非线性超声兰姆波技术有望成为准确评估材料性能退化的有效方法.尽管利用非线性兰姆波评估和检测材料损伤已经受到广泛的关注但在实际评估和测试过程中,需要注意的是:由于损伤引发非线性响应的机理还不是很清晰而兰姆波非线性响应的形式也有不同的类型,针对不同类型的损伤作者认为需要开发特定的非线性兰姆波检测与评估技术. 同时如部分研究者发现,兰姆波的非线性响应(非线性声学参数β)也不一定是随着损伤程度的增大呈递增关系;针对不同程度的损伤演化阶段,仍需深入分析非线性兰姆波的响应特征.
3 基于接触声非线性理论的非线性兰姆波对于体积型缺陷(如空洞)及开口裂纹等结构损伤超声波在这类损伤处主要发生的反射、透射以及衰减现象使用线性超声理论便可阐释清楚但对于闭合微裂纹、分层等接触类结构损伤超声波遇到这类损伤会发生一些非线性现象比如高阶谐波滋生、次谐波滋生、声共振频率漂移和混频声场调制这些现象用传统的线性超声理论无法解释于是基于接触非线性的超声理论就逐渐发展起来了.国内外研究者为了解释上述非线性现象,提出了多种不同的理论和模型比如基于双线性刚度模型的呼吸裂纹模型(Solodov et al. 2002,Worden & Tomlinson 2001,Friswell & Penny 2002)修正应力-应变公式添加描述高阶非线性和滞回效应的系数(Ostrocsky & Johnson 2001,Guyer & Johnson 1999,Van Den Abeele & De Visscher 2000)考虑裂纹界面微观特征引入界面接触对呼吸裂纹模型进行修正(Baltazar et al. 2002,Pecorari 2003,Belyaeva et al. 1993). 但是目前这方面大多数的研究都是关于超声波的在少量的关于兰姆波的研究中都使用基于双线性刚度模型的呼吸裂纹模型来解释高阶谐波滋生现象.
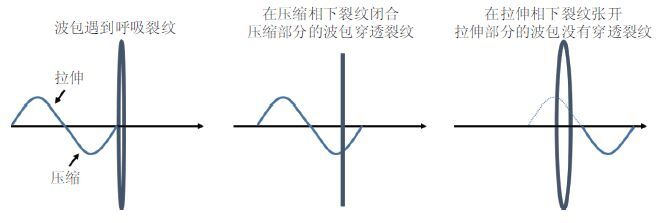
基于双线性刚度模型的呼吸裂纹模型(图 24)(Shen & Giurgiutiu 2012)假设裂纹在超声波传播通过时存在两种状态:闭合和张开. 因此,将裂纹等效为两个刚性接触的光滑并定义了接触刚度来表示裂纹的力学性能通过设置裂纹开口和闭合时所需要的力不同也就是两种状态对应的刚度不同,来模拟裂纹的开闭效应.当超声波传播至裂纹处压缩相的情况下会使得裂纹闭合从而超声波穿透裂纹拉伸相的情况下会使得裂纹开口导致超声波无法穿透裂纹因而只有在拉伸相时才能得到类似于半波整流状态的反射波因而该模型用于解释高次谐波滋生现象.
|
| 图 24 超声波传播通过呼吸裂纹示意图(Shen & Giurgiutiu 2012) |
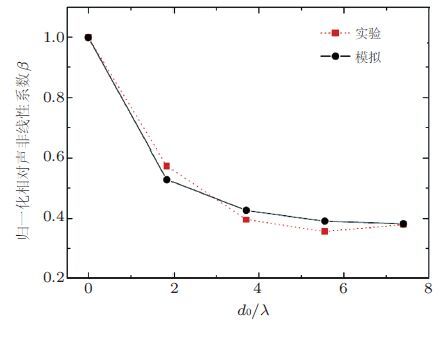
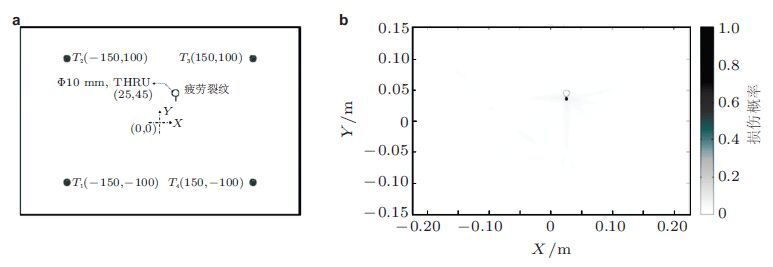
Wan等(2014)将呼吸裂纹模型引入数值计算模型研究了埋藏于薄板内的微裂纹诱发的S0波的非线性响应结果发现S0波的非线性响应随微裂纹的长度增大而增强随微裂纹的宽度增大而减弱. Hong等(2014)通过数值计算和实验研究考察了不同的传播路径S1-S2模式对的非线性系数与疲劳微裂纹位置的关系,发现当S1-S2模式对的传播路径经过裂纹或者极度靠近裂纹区域时非线性系数很大然而一旦传播路径不靠近裂纹区域非线性系数则急剧下降(图 25)这说明利用非线性系数可以对裂纹进行定位. 因而他们将稀疏传感器网络技术与非线性兰姆波方法结合起来(图 26(a))通过实验和数值模拟成功检测并定位出铆钉圆孔边的疲劳初始裂纹(图 26(b))(Hong et al. 2014). 总的来说,目前对于兰姆波的非线性现象,除了高阶谐波滋生尤其是二次谐波的产生现象被广泛研究和应用其他的非线性现象还没有受到广泛关注.
|
| 图 25 S1-S2模式对的非线性系数与传播路径到裂纹的距离的关系(Hong et al. 2014) |
|
| 图 26 (a)铆钉圆孔边疲劳初期裂纹的检测方案示意图(单位mm,疲劳微裂纹被放大示意),(b)检测结果图(Hong et al. 2014) |
非线性兰姆波具有兰姆波检测速度快等诸多优点及非线性超声测量方法检测灵敏度高的特点近年来引起了研究者的广泛关注和研究兴趣,迄今为止已就非线性兰姆波的理论、实验及应用研究开展了大量的工作在其二次谐波发生效应的物理机制、实验测量技术及材料/结构早期损伤评价方面均取得了较为丰硕的成果为发展板壳材料/结构早期损伤的准确无损评价技术奠定了理论和实验基础.从实际应用及理论研究的完备性方面考虑,仍有以下问题需作进一步研究具体包括:(1)兰姆波的非线性累积效应条件问题.对于兰姆波的非线性累积条件,之前主要的争议在于是否需要群速度匹配;近年来开展的理论和实验工作已经证明了群速度匹配条件并不是必需的;为更好地选择适于板壳材料/结构损伤评价的兰姆波模式仍需从理论上深入分析并计算在群速度匹配及失配的条件下兰姆波的二次谐波发生效率.(2)兰姆波二次谐波的对称性问题.关于各向同性固体板中兰姆波二次谐波的对称性已有明确的阐述即二次谐波声场只能呈对称分布但就各向异性或复杂结构中兰姆波的对称性问题,仍需开展进一步研究以确定二次谐波是否可呈反对称性质,若存在是否仍具有累积效应等.(3)建立物理或数学模型寻找非线性兰姆波特征系数与驱动材料损伤演化的因素之间的准确定量关系发展基于非线性兰姆波的材料损伤评估技术.(4)建立模型或寻找合适模型解释关于兰姆波的次谐波滋生、声共振频率漂移和混频声场调制现象从理论上指导基于非线性兰姆波的接触类损伤检测技术的发展.在实验方面,比如: 信号处理问题. 由于兰姆波的多模式特性不管用何种方法激励目标兰姆波模式,不可避免会产生其他兰姆波模式这导致接收信号的时域波形非常复杂,模式识别非常困难增大信号处理的难度. 现在常用的信号处理方法有快速傅里叶变换(FFT)短时傅里叶变换(STFT),时频分析(spectrogram)和小波变换.而目前降低该问题的影响的方法是尽量选择低阶模式减少其他模式的影响. 如能发展有效的可识别各种模式的信号处理方法则可有效推动非线性兰姆波研究的进展.鉴于兰姆波的信号处理复杂的情况未来值得开展的重点研究方向包括以下两个方面:
(1)研究基波为兰姆波的基频模式(S0和A0波)的非线性兰姆波损伤检测技术.由于受限于相速度匹配的条件目前绝大部分的研究都集中在基波为S1和A1模式或者更高阶的兰姆波.近来有研究者从数值模拟和实验两方面验证了不用严格满足相速度匹配条件S0波在铝板中传播也产生了明显的二次谐波. 显而易见采用能量更高、频率更低、传播距离更远的基频波作为基波可以提高信噪比,降低信号处理难度对未来的工程实际应用产生积极的影响.
(2)研究兰姆波的混频问题.揭示多个不同频率的兰姆波模式在板壳结构中传播时产生强烈混频效应的物理机制研究兰姆波混频效应的测量方法及在材料/结构早期损伤评价中的应用.
| 邓明晰, PriceD C, ScottD A. 2005. 兰姆波非线性效应的实验观察. 声学学报 , 30 :37–46. ( Deng M X, Price D C, Scott D A. 2005. Experimental observations of nonlinear effects of Lamb waves. Acta Acustica , 30 :37–46. ) |
| 邓明晰, 裴俊峰. 2008. 无损评价固体板材疲劳损伤的非线性超声兰姆波方法. 声学学报, 33: 360-369 (Deng M X, Pei J F. 2008. Nondestructive evaluation of fatigue damage in solid plates using nonlinear ultrasonic Lamb wave method. Acta Acustica, 33: 360-369). http://www.cnki.com.cn/Article/CJFDTOTAL-XIBA200804013.htm |
| 邓明晰, 项延训, 裴俊峰, 刘良兵. 2012. 基于群速度失配的超声兰姆波二次谐波的时域测量方法. 声学学报, 37: 621-628 (Deng M X, Xiang Y X, Pei J F, Liu L B. 2012. Time-domain measurement technique of second harmonic of ultrasonic Lamb waves using mismatch of group velocities. Acta Acustica, 37: 621-628). http://www.cnki.com.cn/Article/CJFDTOTAL-XIBA201206010.htm |
| 邓明晰. 1996. 兰姆波的非线性研究. 声学学报, 21: 429-436 (Deng M X. 1996. Research on nonlinearity of Lamb waves. Acta Acustica, 21: 429-436). http://www.cnki.com.cn/Article/CJFDTOTAL-XIBA6S1.006.htm |
| 邓明晰. 1997. 兰姆波的非线性研究(II). 声学学报, 22: 182-187 (Deng M X. 1997. Research on nonlinearity of Lamb waves (II). Acta Acustica, 22: 182-187). |
| 邓明晰. 2005. 分层结构中兰姆波二次谐波发生的模式展开分析. 声学学报, 30: 132-142 (Deng M X. 2005. Modal expansion analyses of second-harmonic generation of the Lamb waves in layered structures. Acta Acustica, 30: 132-142). http://www.cnki.com.cn/Article/CJFDTOTAL-XIBA200502007.htm |
| 邓明晰. 2005. 一种定征复合板材粘接层性质的非线性超声兰姆波方法. 声学学报, 30: 542-551 (Deng M X. 2005. Characterization of adhesive joints of composite solid layers using a nonlinear Lamb wave approach. Acta Acustica, 30: 542-551). http://www.cnki.com.cn/Article/CJFDTOTAL-XIBA200506010.htm |
| 邓明晰. 2006. 兰姆波非线性效应的实验观察(II). 声学学报, 31: 1-7 (Deng M X. 2006. Experimental observations of nonlinear effects of Lamb waves (II). Acta Acustica, 31: 1-7). http://www.cnki.com.cn/Article/CJFDTOTAL-XIBA200601001.htm |
| 税国双, 汪越胜, 曲建民. 2005. 材料力学性能退化的超声无损检测与评价. 力学进展, 35: 52-65. (Shui G S, Wang Y S, Qu J M. 2005. Advances in nondestructive test and evaluation of material degradation using nonlinear ultrasound. Advances in Mechanics, 35: 52-65). http://lxjz.cstam.org.cn/CN/abstract/abstract132738.shtml |
| Aleshin V, Van Den Abeele KEA. 2007. Micro contact-based theory for acoustics in micro damage materials. J. Mech. Phys. Solids , 55 :366–390. doi:10.1016/j.jmps.2006.07.002 |
| Auld B A. 1973. Acoustic Fields and Waves in Solids. New York: John Wiley. |
| Baltazar A, Rokhlin S I, Pecorari C. 2002. On the relationship between ultrasonic and micromechanical properties of contacting rough surfaces. J. Mech. Phys. Solids , 50 :1397–1416. doi:10.1016/S0022-5096(01)00119-3 |
| Belyaeva I Y, Zaitsev V Y, Ostrovsky L A. 1993. Nonlinear acousto-elastic properties of granular media. Acoust. Phys. , 39 :11–15. |
| Bermes C, Kim J Y, Qu J M, Jacobs L J. 2008. Nonlinear Lamb waves for the detection of material nonlinearity. Mech. Syst. Signal PR. , 22 :638–646. doi:10.1016/j.ymssp.2007.09.006 |
| Cantrell J H, Yost W T. 2001. Nonlinear ultrasonic characterization of fatigue microstructures. Int. J. Fatigue , 23 :487–490. doi:10.1016/S0142-1123(01)00162-1 |
| Cantrell J H. 2003. Fundamentals and Application of Nonlinear Ultrasonic Nondestructive Evaluation. Florida: CRC Press LLC. |
| Chillara V K, Lissenden C J. 2014. Nonlinear guided waves in plates: a numerical perspective. Ultrasonics , 54 :1553–1558. doi:10.1016/j.ultras.2014.04.009 |
| Chillara V K, Lissenden C J. 2016. Review of nonlinear ultrasonic guided wave nondestructive evaluaton: theory, numerics, and experiments. Opt. Eng. , 55 :011002. |
| Demer L J, Fentnor L H. 1969. Lamb wave techniques in nondestructive testing. International Journal of Nondestructive Testing , 1 :251–283. |
| Deng M X, Pei J F. 2007. Assessment of accumulated fatigue damage in solid plates using nonlinear Lamb wave approach. Appl. Phys. Lett., 90: Art. No. 121902. |
| Deng M X, Xiang Y X, Liu L B. 2011. Time-domain analysis and experimental examination of cumulative second-harmonic generation by primary Lamb wave propagation. J. Appl. Phys. , 109 :113525. doi:10.1063/1.3592672 |
| Deng M X, Xiang Y X. 2015. Analysis of second-harmonic generation by primary ultrasonic guided wave propagation in a piezoelectric plate. Ultrasonics , 61 :121–125. doi:10.1016/j.ultras.2015.04.005 |
| Deng M X, Wng P, Lv X F. 2005. Experimental observation of cumulative secondharmonic generation of Lamb-wave propagation in an elastic plate. J. Phys. D -Appl. Phys. , 38 :344–353. doi:10.1088/0022-3727/38/2/020 |
| Deng M X. 1999. Cumulative second-harmonic generation of Lamb mode propagation in a solid plate. J. Appl. Phys. , 85 :3051–3058. doi:10.1063/1.369642 |
| Deng M X. 2003. Analysis of second-harmonic generation of Lamb modes using a modal analysis approach. J. Appl. Phys. , 94 :4153–4159. |
| Deng M X, Yang J. 2007. Characterization of elastic anisotropy of a solid plate using nonlinear Lamb wave approach. J. Sound Vib. , 308 :201–211. doi:10.1016/j.jsv.2007.07.029 |
| Diamanti K, Soutis C, Hodgkinson J M. 2007. Piezoelectric transducer arrangement for the inspection of large composite structures. Composites Part A , 38 :1121–1130. doi:10.1016/j.compositesa.2006.06.011 |
| Donskoy D. 2006. Assessment of initial material damage and remaining life prediction with nonlinear acoustics. J. Acoust. Soc. Am. , 119 :3293. |
| Friswell M I, Penny J E T. 2002. Crack modeling for structural health monitoring. Struct. Health. Monit. , 1 :139–148. doi:10.1177/1475921702001002002 |
| Giurgiutiu V. 2003. Lamb wave generation with piezoelectric wafer active sensors for structural health monitoring// Smart Structures and Materials 2003: Smart structures and Integrated systems, 111-122. |
| Giurgiutiu V. 2005. Tuned Lamb wave excitation and detection with piezoelectric wafer active sensors for structural health monitoring. J Intell. Mater. Syst. Struct. , 16 :291–305. doi:10.1177/1045389X05050106 |
| Gusev V E, Lauriks W, Thoen J. 1998. New evolution equations for the nonlinear surface acoustic waves on an elastic solid of general anisotropy. J. Acoust. Soc. Am. , 103 :3203–3215. doi:10.1121/1.423036 |
| Guyer R A, Johnson P A. 1999. Nonlinear mesoscopic elasticity: evidence for a new class of materials. Phys. Today , 52 :30–36. |
| Hong M, Su Z, Lu Ye, Cheng L. 2014. Temporal information of linear and nonlinear Lamb waves for fatigue damage localization: analysis and synthesis//7th European workshop on Structural Health Monitoring, July 8-11, 2014, La Cite, Nantes, France. |
| Hong M, Su Z, Wang Q, Cheng L, Qing X. 2014. Modeling nonlinearities of ultrasonic waves for fatigue damage characterization: theory, simulation, and experimental validation. Ultrasonics , 54 :770–778. doi:10.1016/j.ultras.2013.09.023 |
| Kumon R E, Hamilton M F. 2002. Directional dependence of nonlinear surface acoustic waves in the (001) plane of cubic crystals. J. Acoust. Soc. Am. , 115 :2060–2069. |
| Lamb H. 1917. On the waves in an elastic plate. Proceedings of the Royal Society A , 293 . |
| Li W, Cho Y, Achenbach J D. 2012. Detection of thermal fatigue in composites by second harmonic Lamb waves. Smart Mater. Struct. , 21 :085019. doi:10.1088/0964-1726/21/8/085019 |
| Lima W J de, Hamilton M F. 2003. Finite-amplitude waves in isotropic elastic plates. J. Sound Vib. , 265 :819–839. doi:10.1016/S0022-460X(02)01260-9 |
| Liu Y L, Hu N, Xu H, Yuan W F, Yan C, Li Y, Goda R, Alamusi, Qiu J H, Ning H M, Wu L K. 2014. Damage evaluation based on a wave energy flow map using multiple PZT sensors. Sensors , 14 :1902–1917. doi:10.3390/s140201902 |
| Liu Y, Kim J Y, Jacobs L J, Qu J M, Li Z. 2012. Experimental investigation of symmetry properties of second harmonic Lamb waves. J. Appl. Phys. , 111 :053511. doi:10.1063/1.3691225 |
| Lu X, Lu M, Zhou L M, Su Z, Cheng L, Ye L, Meng G. 2011. Evaluation of welding damage in welded tubular steel structures using guided waves and a probability-based imaging approach. Smart Mater. Struct. , 20 :015018. doi:10.1088/0964-1726/20/1/015018 |
| Luo W, Rose J L. 2007. Phased array focusing with guided waves in a viscoelastic coated hollow cylinder. J. Acoust. Soc. Am. , 121 :1945–1955. doi:10.1121/1.2711145 |
| Matlack K H, Kim J Y, Jacobs L J, Qu J M. 2011. Experimental characterization of efficient second harmonic generation of Lamb wave modes in a nonlinear elastic isotropic plate. J. Appl. Phys. , 109 :014905. doi:10.1063/1.3527959 |
| Miao H, Huan Q, Li F. 2016. Excitation and reception of pure shear horizontal waves by using face-shear d24 mode piezoelectric wafers. Smart Mater. Struct. , 25 :11LT01. doi:10.1088/0964-1726/25/11/11LT01 |
| Muller M F, Kim J Y, Qu J, Jacobs L J. 2010. Characteristics of second harmonic generation of Lamb waves in nonlinear elastic plates. J. Acoust. Soc. Am. , 174 :2141–2152. |
| Ostrocsky L A, Johnson P A. 2001. Dynamic nonlinear elasticity in geomaterials. Riv. Nuovo Cimento , 24 :1–46. |
| Ostrocsky L A, Johnson P A. 2001. Dynamic nonlinear elasticity in geomaterials. Riv. Nuovo Cimento, 24: 1-46. |
| Pau A, Scalea F L di. 2015. Nonlinear guided wave propagation in prestressed plates. J. Acoust. Soc. Am. , 137 :1529–1540. doi:10.1121/1.4908237 |
| Pecorari C. 2003. Nonlinear interaction of plane ultrasonic waves with an interface between rough surfaces in contact. J. Acoust. Soc. Am. , 113 :3065–3072. doi:10.1121/1.1570437 |
| Pruell C, Kim J-Y, Qu J, Jacobs L J. 2007. Evaluation of plasticity driven material damage using Lamb waves. Appl. Phys. Lett. , 91 :231911. doi:10.1063/1.2811954 |
| Purekar A S, Pines D J. 2010. Damage detection in thin composite laminates using piezoelectric phased sensor arrays and guided Lamb wave interrogation. J. Intel. Mat. Syst. Str. , 21 :955–1010. doi:10.1177/1045389X10374163 |
| Qian Z W. 1995. Second order harmonics of surface-waves in isotropic solids. J. Sound Vib. , 187 :369–379. doi:10.1006/jsvi.1995.0530 |
| Qiu L, Yuan S F, Zhang X Y, Wang Y. 2011. A time reversal focusing based impact imaging method and its evaluation on complex composite structures. Smart Mater. Struct. , 20 :105014. doi:10.1088/0964-1726/20/10/105014 |
| Q iu, L ., L iu, M. L., Qi ng, X. L., Yu an, S .F. 2013. A quantitative multidamage monitoring method for large-scale complex composite. Struct. Health. Monit. , 12 :183–196. doi:10.1177/1475921713479643 |
| Rauter N, Lammering R. 2015. Impact damage detection in composite structures considering Nonlinear Lamb wave propagation. Mech. Adv. Mater. Struc. , 22 :44–51. doi:10.1080/15376494.2014.907950 |
| Shen Y, Giurgiutiu V. 2012. Simulation of interaction between Lamb waves and cracks for structural health monitoring with piezoelectric wafer active sensors//ASME 2012 Conference on Smart Materials, Adaptive Structures and Intelligent Systems. Stone Moutain, Georgia, USA. |
| Shui G S, Kim J Y, Qu J M, Jacobs L J. 2008. Nonlinear Lamb waves for the detection of material nonlinearity. Mech. Syst Signal Pr. , 22 :638–646. doi:10.1016/j.ymssp.2007.09.006 |
| Sicard R, Goyette J, Zellouf D E. 2002. A SAFT algorithm for lamb wave imaging of isotropic plate-like structures. Ultrasonics , 39 :487–494. doi:10.1016/S0041-624X(01)00087-7 |
| Solodov I Y, Krohn N, Busse G. 2002. CAN: an example of nonclassical acoustic nonlinearity in solids. Ultrasonics , 40 :621–625. doi:10.1016/S0041-624X(02)00186-5 |
| Solodov I Y. 1998. Ultrasonic of nonlinear contacts: propagation, reflection and NDE application. Ultrasonics , 36 :383–390. doi:10.1016/S0041-624X(97)00041-3 |
| Sonti V R, Kim S J, Jones J D. 1995. Equivalent forces and wavenumber spectra of shaped piezoelectric actuators. J. Sound Vib. , 187 :111–131. doi:10.1006/jsvi.1995.0505 |
| Srivastava A, Scalea F L di. 2009. On the existence of antisymmetric or symmetric Lamb waves at nonlinear higher harmonics. J. Sound Vib. , 323 :932–943. doi:10.1016/j.jsv.2009.01.027 |
| Su Z, Ye L. 2005. Lamb wave propagation-based damage identification for quasi-isotropic cf/ep composite laminates using aritificial neural algorithm: part i-methodology and database development. J. Intel. Mat. Syst. Str. , 16 :97–111. doi:10.1177/1045389X05047599 |
| Su Z, Ye L. 2009. Identification of damage using Lamb waves: from fundamentals to applications. Springer, 2009. |
| Van Den Abeele K, De Visscher J. 2000. Damage assessment in reinforced concrete using spectral and temporal nonlinear vibration techniques. Cement Concrete Res. , 30 :1453–1464. doi:10.1016/S0008-8846(00)00329-X |
| Van Den Abeele KEA., Sutin A, Carmeliet J, Johnson P A. 2001. Micro-damage diagnostics using nonlinear elastic wave spectroscopy (NEWS). NDT & E Int. , 34 :239–248. |
| Viktorov I A. 1965. Ultrasonic Lamb wave (Review). Ultrasonics , 11 :1. |
| Vishnuvardhan J, Krishnamurthy C V, Balasubramaniam K, 2007. Genetic algorithm based reconstruction of the elastic moduli of orthotropic plates using an ultrasonic guided wave single-transmitter-multiple-receiver SHM array. Smart Mater. Struct., 16: 1639-1650. |
| Wan X, Zhang Q, Xu G, Tse P W. 2014. Numerical simulation of nonlinear Lamb waves used in a thin plate for detecting buried micro-cracks. Sensors , 14 :8528–8546. doi:10.3390/s140508528 |
| Wang D, Ye L, Su Z, Lu Y, Li F, Meng G. 2010. Probabilistic damage identification based on correlation analysis using guided wave signals in aluminum plates. Struct. Health. Monit. , 9 :133–144. doi:10.1177/1475921709352145 |
| Worden K, Tomlinson G R. 2001. Nonlinearity in structural dynamics: Detection, Identification and Modelling. Bristol: IOP Publishing Ltd. |
| Worlton D C. 1961. Experimental confirmation of Lamb waves at Megacycle Frequencies. J. Appl. Phys. , 32 :967–971. doi:10.1063/1.1736196 |
| Wright W, Hutchins D, Jansen D, Schindel D. 1997. Air-coupled lamb wave tomography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control , 44 :53–59. doi:10.1109/58.585190 |
| Xiang Y, Deng M, Xuan F-Z, Liu C-J. 2011. Experimental study of thermal degradation in ferritic Cr-Ni alloy steel plates using nonlinear Lamb waves. NDT & E Int. , 44 :768–774. |
| Zabolotskaya E A. 1992. Nonlinear propagation of plane and circular Rayleigh waves in isotropic solids. J. Acoust. Soc. Am. , 91 :2569–2575. doi:10.1121/1.402993 |
| Zhu W J, Deng M X, Xiang Y X, Xuan F Z, Liu C J. 2016. Second harmonic generation of Lamb wave in numerical perspective. Chin. Phys. Lett. , 33 :104301. doi:10.1088/0256-307X/33/10/104301 |