2.香港理工大学机械工程系, 香港 999077
2.Department of Mechanical Engineering, Hong Kong Polytechnic University, Hong Kong 999077, China
声学黑洞(acoustic black hole, ABH) 是将天文物理学中的黑洞概念引入波动和声振领域中, 并将其作为一种全新的概念提出.黑洞的概念最早在1795年由Pierre Simon Laplace提出, 表现为光在其视界范围内传播时无法逃逸的现象. 150年之后, Pekeris (1946)发现波动和声学中也有相似的黑洞效应, 声学中的黑洞效应表现为在特定的非均匀的分层介质中, 声波波速随着介质深度的减小而逐渐减小到零, 从而不会发生波的反射. Mironov (1988)随后在棋形结构中也发现了类似的现象.在薄板棋形结构中, 如果结构的厚度以一定的军函数形式减小, 弯曲波的波速会随着厚度的减小逐渐减小, 在理想的情况下波速可减小为零, 即能实现波的零反射, 这种棋形结构就称为声学黑洞结构. Krylov (1989, 1997, 2004) 首次将声学黑洞结构应用于梁中, 即可利用结构中厚度的变化来操纵弯曲波以捕获弯曲波的能量, 自此以后声学黑洞结构迅速引起广泛关注.
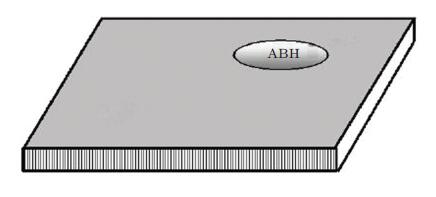
一维声学黑洞结构中黑洞部分厚度的变化规律满足h(x)=εxm, m≥2, (Krylov 1998, Krylov & Shuvalov 2000), 如图 1所示.声学黑洞部分的厚度从均匀部分朝着结构边缘按照上述军函数形式逐渐减小, 当弯曲入射波由均匀部分传播到声学黑洞部分时, 由于结构厚度的逐渐减小, 弯曲波波速也逐渐减小, 波长被压缩, 波动幅值逐渐增大.当厚度逐渐减小至零时, 弯曲波传播到靠近声学黑洞棋形边缘时, 累积相位将会达到无穷大, 从理论上讲弯曲波将无法到达结构的边缘, 从而也就无法从边缘反射回来(Krylov & Tilman 2004), 即可将所有的波动能量集中在结构的尖端位置.将一维声学黑洞结构的截面以厚度为零的尖端为中心点, 旋转一周即可得到二维声学黑洞结构. 图 2为内嵌于矩形薄板结构中的二维声学黑洞, 二维声学黑洞的厚度与半径呈军函数形式变化, 当弯曲波传播进入声学黑洞区域后, 初始传播方向指向黑洞中心的波的传播速度逐渐减小, 而偏离黑洞中心的波将向黑洞中心偏转, 在理想情况下弯曲波都将被聚集到黑洞中心位置, 且传播速度降为零(Krylov 2007, Yan et al. 2016).理论研究结果显示, 理想的声学黑洞结构可形成完美的陷波器, 实现波的操控与俘获, 甚至实现波的全吸收.

|
| 图 1 一维声学黑洞结构中弹性波的传播 |
|
| 图 2 内嵌于薄板结构中的二维声学黑洞 |
然而受到加工制造工艺的限制, 理想声学黑洞在实际结构中难以实现.一维声学黑洞往往会在结构厚度减小到一定值时截断, 这将使得反射系数明显增大, 严重影响声学黑洞效应(Krylov & Tilman 2004).研究表明, 在带截断的一维声学黑洞结构的尖端附近粘贴很少的阻尼材料即可很好地降低由截断引起的反射系数, 并通过实验测试验证了在结构边缘粘贴少量的阻尼材料对声学黑洞效应产生的补偿效果(Krylov & Winward 2005, 2007; Kralovic et al. 2009; Denis et al. 2014).因此, 即使是存在截断的声学黑洞结构, 或者是在截断边缘有缺陷的情况下(Bowyer et al. 2012), 对结构振动仍然有很好的抑制效果.
在二维声学黑洞的加工制造中, 往往会在黑洞的中心形成圆形的小孔或者形成一个厚度等于截断厚度的中心圆台(Bowyer et al. 2013), 这些由于缺陷引入的新的几何参数都将对声学黑洞效应产生一定的影响, 阻尼材料的应用同样可以降低波的反射(O'Boy et al. 2010), 提高能量耗散的效率(O'Boy & Krylov 2011).为了提高二维声学黑洞结构的振动噪声抑制效果, 可以将多个声学黑洞布置在结构中(Bowyer & Krylov 2012; Conlon et al. 2014, 2015a, 2015b), 这种结构在一定范围内可以降低声学黑洞的有效作用频率范围的下限.研究表明, 在非完美的二维声学黑洞结构中, 宽频能量聚集现象依然存在(Lomonosov et al. 2015, Huang et al. 2016), 波在非完美二维声学黑洞结构中的传播方向发生偏转, 产生类似于波在超材料梯度折射率声透镜中传播的现象(Torrent & Sxanchez-Dehesa 2007, Zhang et al. 2009, Dubois et al. 2013, Torrent et al. 2014).在超材料声透镜结构中, 需要紧密地布置极小的单元方能近似实现连续梯度变化的折射率(Climente et al. 2014), 相比而言, 声学黑洞结构简单, 仅通过厚度剪裁即能实现连续梯度变化的折射率.在非完美的二维声学黑洞中, 可以在能量聚集的位置集成压电换能器, 实现高效宽频带的能量回收(Zhao et al. 2014, 2015).
以上所介绍的声学黑洞结构主要是通过薄壁结构厚度的改变实现结构阻抗逐渐变化, 从而使得结构中弯曲波传播的相速度和群速度发生变化, 在结构局部区域实现波的聚集和操控.本文介绍的绝大多数声学黑洞结构都是通过厚度变化实现的, 同时也介绍几种采用其他方式实现了声学黑洞结构.例如在一个管道结构中布置一系列的环形薄壁板, 通过调整壁板的间距与大小, 能够使得在管道内传播的声波速度逐渐减小(Mironov & Pislyakov 2002, El-Ouahabi et al. 2015), 从而实现声学黑洞管道结构.另外, 通过形状记忆合金的温度梯度分布实现结构弹性模量的梯度分布(Georgiev et al. 2010), 这样的热声学黑洞结构对结构的振动抑制同样产生了很好效果.
声学黑洞作为一种具有宽频特性的高效被动波操控方法, 在未来结构减振降噪或者能量回收等领域具有广泛的应用前景.声学黑洞概念的提出虽然己经有三十多年的历史, 但在近十年才真正成为研究热点.本文将对声学黑洞结构的研究进展进行详细评述, 从声学黑洞结构的建模与分析方法, 实验研究方法及进展, 声学黑洞结构中波的传播与操控, 以及声学黑洞在工程应用中的相关问题等几个方面进行探讨.
2 一维声学黑洞结构的力学模型与分析 2.1 声学黑洞的原理及几何声学方法典型一维声学黑洞结构的棋形边缘如图 3所示, 在结构非均匀区域, 截面厚度按照军函数形式h(x)=εxm (m≥2) 变化. 图 3(a)为截面非对称的声学黑洞棋形边缘, 该情况下的结构上下两个表面中, 一面为平面, 而另一面的高度呈军函数形式变化; 图 3(b)为截面对称的声学黑洞棋形边缘, 结构的厚度在棋形边缘逐步减小为零, 构成理想的一维声学黑洞结构.弯曲波在该棋形结构中运动的控制方程为(Krylov 1990)

|
| 图 3 典型的一维声学黑洞结构的楔形边缘 |
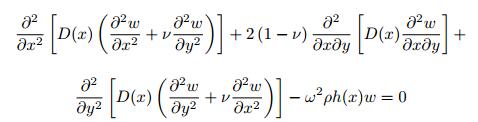
|
(1) |
其中, w表示挠度, ρ为密度, D(x)=Eh3(x)/12(1 -ν2) 为抗弯刚度, ν和E分别为泊松比和弹性模量.利用几何声学近似的方法(Krylov 1989, 1990; Krylov & Tilman 2004), 在结构对应位置x处的横向位移w(x) 即方程(1) 的解可表示为如下复数形式

|
(2) |
其中, A(x) 和Φ(x)=kpφ(x, y) 分别为变化的幅值和累积相位, 其中kp=ω/cp为板中均匀部分的波数, cp=2ct (1 -ct2/cl2)1/2为相速度, cl和ct分别为板的材料中纵波和横波的波速; φ(x, y)=φ'(x) + (β/kp) y为程函, 在垂直入射的情况下β=0.将式(2) 代入方程(1), 要使得等式成立, 需要等式左边的实部和虚部必须均等于零, 令实部为零并且省略关于A(x) 和Φ(x) 的高阶导数项, 可以得到弯曲波程函方程

|
(3) |
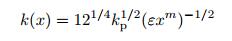
|
(4) |
其中, k(x) 是与位置相关的波数, n(x) 为相应的折射率.对于弯曲波垂直入射的情况(β=0), 累积相位Φ(x)=kpφ(x) 也可写作由棋形结构的任意一点x到棋形边缘的积分表达式
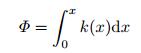
|
(5) |
由式(4) 与式(5) 可以得到, 当m≥2时, Φ趋向于无穷大, 弯曲波将无法传递达到结构边缘, 也就不会发生反射, 因此弯曲波能量被聚集在结构的边缘, 即产生了“声学黑洞”效应.
导出以上结果的条件是弯曲波在黑洞结果中的传播满足几何声学的基本假设, 即
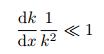
|
(6) |
上述条件的物理意义是在与一个波长相当的距离内, 波数的变化量足够小.除了在理想黑洞边缘的局部区域, 式(6) 的条件是容易满足的.
如同在引言中提到的, 真实的声学黑洞结构在加工制造过程中会受到加工工艺的限制, 不可能实现边缘以高阶军函数形式逐渐趋近于零, 必定存在截断, 这将会严重影响声学黑洞结构的能量聚集效应.当在x=x0处截断时, 如图 3所示, 式(5) 中的积分下限将由0变为x0, 弯曲波在边界处发生反射, 能量耗散效应大大减弱.存在截断的声学黑洞结构的反射系数为(Krylov & Shuvalov 2000)
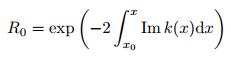
|
(7) |
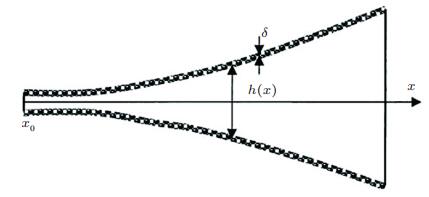
研究表明, 很小的截断厚度即可使得反射系数增大至50%~70 % (Krylov 2004), 不利于声学黑洞结构有效地抑制振动.在具有截断的声学黑洞结构上粘贴少量的阻尼材料可以很好的解决该问题.将阻尼层附着在厚度较小的黑洞区域时, 可以有效地耗散聚集于声学黑洞中的波动能量, 从而使得由截断引起的反射系数显著降低(Krylov 2004, Krylov & Tilman 2004, Bowyer et al. 2012). Krylov (1995)针对图 4所示的上下表面粘贴了厚度为δ的阻尼材料的棋形声学黑洞结构, 运用几何声学的方法对阻尼层的影响进行分析.当声学黑洞结构发生弯曲变形时, 表面的阻尼层也一起发生变形, 且弯曲变形的位移uz与结构长度方向位移ux之间的关系为uz=-z (∂2uz /∂x2).运用包含约束阻尼层的悬臂梁的弯曲振动理论, 可以对等厚度阻尼材料的影响进行简化分析, 把其产生的结构阻尼等效为材料损失因子(Ross et al. 1960).在分析粘贴阻尼材料的一维声学黑洞结构中弯曲波的衰减时, 可以采用将阻尼层产生的等效损失因子和声学黑洞结构本身的材料损失因子同时引入波数的虚部(Kravchun 1991).对于两边均附着阻尼材料的声学黑洞结构, 其波数虚部可表述为
|
| 图 4 两侧附着阻尼材料的有截断的一维声学黑洞结构 |

|
(8) |
其中, ν和η分别为阻尼层和声学黑洞结构的材料损失因子.由式(8) 可见阻尼材料所引起的波的衰减与阻尼材料的厚度δ以及阻尼材料和声学黑洞结构材料的弹性模量比值E2/E1成正比, 与厚度成反比.这也说明了阻尼材料贴在厚度较小的区域时衰减效果更好的原因.
对于含有阻尼材料的声学黑洞结构, 其反射系数可由一个简单的解析表达式描述为
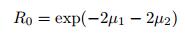
|
(9) |
当声学黑洞结构厚度按照二次军函数形式变化, 即h(x)=εx2, 且在声学黑洞区域内结构的上下两侧均全覆盖厚度为δ的阻尼材料时, 该声学黑洞结构的反射系数表达式(9) 中的μ1和μ2分别为
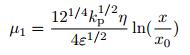
|
(10) |

|
(11) |
当只在声学黑洞结构的一侧全覆盖阻尼材料时, 则式(9) 和式(10) 不变, 式(11) 为
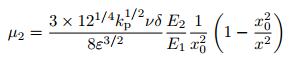
|
(12) |
在上述含有阻尼材料的声学黑洞结构反射系数的分析中, 假设阻尼层的质量足够小, 且对黑洞变厚度区域中波传播速度不产生影响, 因此上述结果适用于阻尼层非常薄的情况.当黑洞结构的厚度减小到一定程度时, 上述假设不再成立, 用上述公式计算得到的反射系数会有较大的误差.为了使上述分析适用于任意厚度的阻尼层, 必须考虑阻尼层对波传播特性的影响, 即在含约束阻尼层的梁理论中, 考虑阻尼层对结构的弯曲刚度和质量线密度的影响.对于军指数m=2的声学黑洞结构, 考虑阻尼层对刚度和质量的影响修正后, 反射系数可表示为(Krylov 2004)
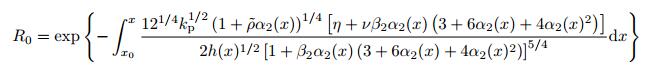
|
(13) |
其中, β2=E2/E1为阻尼材料与结构材料的弹性模量比, 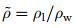
针对h(x)=εx2 (即m=2) 的声学黑洞结构, 上式在满足
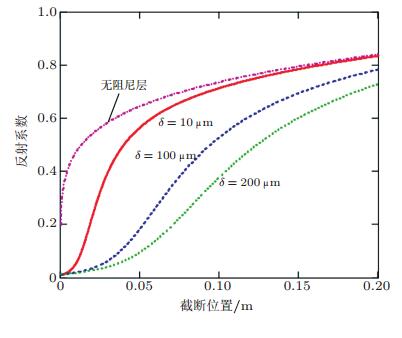
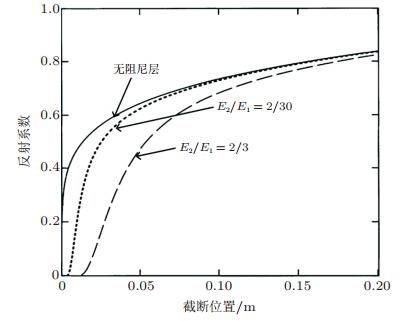
图 5为从式(13) 计算得到的在不同阻尼厚度下, 一维声学黑洞的截断长度对反射系数的影响规律(Krylov 2004).这里假设黑洞材料的损失因子η=0.01, 阻尼层的材料损失因子ν=0.25, 弹性模型比E2/E1=0.3, 军函数指数m=2, 系数ε=0.05 m-1, 黑洞区域的长度为0.5 m.从图中可以看到, 在没有阻尼层的情况下, 微小的截断可以使得反射系数迅速增大0.5以上, 而即使很薄的阻尼层也可以有效抑制反射系数的增大, 另外, 反射系数会随着阻尼层厚度的增大而减小. 图 6反应了在不同阻尼材料刚度下的反射系数与截断位置的关系.当阻尼材料与黑洞结构材料的弹性模型比从2/30增大到2/3时, 反射系数减小.在实际工程应用中, 虽然声学黑洞都有不同程度的截断, 只要在黑洞区域粘贴适当厚度的阻尼层, 仍然能获得比较理想的减振效果.
|
| 图 5 声学黑洞区域覆盖不同厚度的阻尼层时反射系数随截断长度的变化规律 |
|
| 图 6 阻尼层的弹性模量对反射系数的影响 |
上述对一维声学黑洞结构中波的反射特性研究都假设弯曲波传播方向垂直于黑洞边缘, 当波入射的方向与边缘不再垂直而是倾斜入射时(Krylov 2007), 如图 7所示, 进入声学黑洞结构的弯曲波除了垂直于结构边缘的分量, 还有平行于结构边缘的分量.由于声学黑洞结构在垂直于结构边缘的方向上厚度逐渐减小, 但在平行于结构边缘的方向上厚度不发生变化, 因此当弯曲波传播至接近边缘的地方时, 垂直边缘方向的分量会急剧变大, 平行于结构边缘的分量则很小.同时值得注意的是, 对波在声学黑洞结构中传播的总积累相位贡献最大的往往是边缘附近非常小的一段距离, 而在声学黑洞结构边缘又可以忽略平行于边缘的波分量的作用, 因此, 在斜入射情况的反射系数计算中, 仍然可以使用上述垂直入射情况下的几何声学分析方法.

|
| 图 7 弯曲波倾斜入射到声学黑洞楔形边缘 |
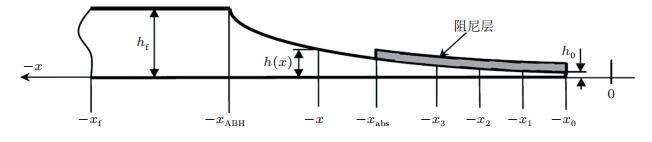
声学黑洞结构通过利用结构厚度的变化使得结构阻抗发生光滑地变化, 从而实现对弯曲波的调控. Georgiev等(2011)基于Euler-Bernoulli梁模型, 导出了一维声学黑洞结构阻抗矩阵的Riccati方程, 提出了从结构阻抗矩阵计算声学黑洞结构中弯曲波反射矩阵的方法.该方法克服了几何声学方法中几何假设条件的约束, 特别是克服了几何声学模型中阻尼层厚度须远小于结构厚度的假设问题, 以使用于优化有截断的声学黑洞结构中附加阻尼的参数. 图 8所示为局部区域覆盖了阻尼层的声学黑洞结构的截面, 声学黑洞在x0处截断, 截断厚度为h0=εx0m.假设一维声学黑洞结构中的弯曲振动可由以下4个变量描述:位移w、转角θ、剪力F和弯矩M, 它们均为与位置x相关的变量, 这些变量组成描述结构振动的状态向量
|
| 图 8 局部区域覆盖了阻尼层的声学黑洞结构的截面示意图 |

|
(14) |
上式中的状态向量由两个广义位移变量和两个广义力变量组成.根据结构机械阻抗的定义(Wang & Norris 1995, Gautier et al. 2006), 阻抗矩阵Z、广义位移以及广义力之间存在以下关系
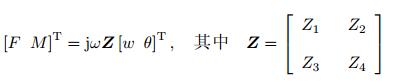
|
(15) |
由上式可知, 阻抗矩阵Z是位置的函数, 并且满足如下Riccati方程
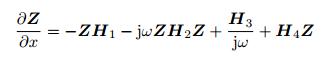
|
(16) |
式中, ρ1为声学黑洞结构的材料密度, A1为结构横截面积, E1为结构材料的弹性模
量, I1为截面惯性矩, H1, H2, H3和H4分别为与传播介质特征参数有关的矩阵.假若能够得到在结构中任意位置的阻抗矩阵Z, 求解式(16) 即可得到任意激励下的振动响应(Félix & Pagneux 2002).
定义矩阵N=-jH, 且假设N的特征向量组成的矩阵为E, 特征值组成的对角矩阵为Λ, 则以下关系成立
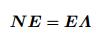
|
(18) |
对于Euler-Bernoulli梁, 矩阵E可表示出以下形式
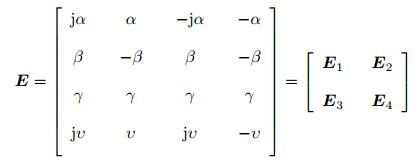
|
(19) |
其中
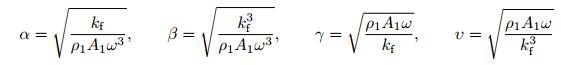
|
(20) |
上式中, 波数kf和相速度cf分别为

|
(21) |
求解得到结构阻抗矩阵Z后, 反射矩阵可表示为

|
(22) |
在反射矩阵R中, R1和R4分别表示传递波和隐失波的反射系数.反射系数越小, 说明在黑洞中损失的能量越大.
对于复合梁结构, 即覆盖有阻尼层的一维声学黑洞结构, 其抗弯刚度可表达为复数形式
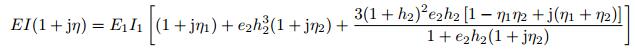
|
(23) |
其中, EI为复合梁结构的抗弯刚度, E1I1为梁结构自身的抗弯刚度, η为复合梁的材料损失因子, η1和η2分别为梁与阻尼层的材料损失因子, E1和E2分别为梁与阻尼层材料的弹性模量, e2为弹性模量比E2/E1, h和d分别为梁与阻尼层的厚度, h2为厚度比d/h.
当阻尼层的厚度逐渐接近甚至大于声学黑洞结构厚度时, 则需要考虑阻尼层的附加质量, 此时的单位长度质量为
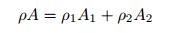
|
(24) |
其中, ρ1和ρ2分别为梁和阻尼层的材料的密度, A1和A2分别为梁和阻尼层的截面面积.将式(23) 和式(24) 代入式(21) 中, 能够得到覆盖有阻尼层材料的声学黑洞结构的相速度和波数
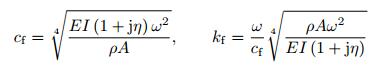
|
(25) |
对一维声学黑洞建立的Euler-Bernoulli模型的阻抗分析方法过程中需要注意两点, 一是结构自身材料的阻尼包括茹弹性阻尼和热弹性阻尼, 均可由复数形式的弹性模量E1建模, 从而在虚部中加入梁结构的材料损失因子η1; 二是对于分析附加阻尼层的影响, 该模型打破了几何声学模型中阻尼层厚度的限制, 对于任意弹性模量E2和材料损失因子η2的阻尼层, 都能灵活地引入到该模型中进行分析. 图 9为不同条件下黑洞结构的反射系数.计算条件为x0=0.01 m, xABH=0.06 m, xf=0.08 m, hf=0.001 5 m, m=4.

|
| 图 9 反射系数R1与激励频率之间的关系(实线:厚度700 μm的阻尼层; 点虚线:厚度10 μm的阻尼层; 虚线:黑洞区域不贴阻尼层; 点线:无声学黑洞的均匀梁结构粘贴厚度700 μm的阻尼层) (Georgiev et al. 2011) |
在现实中存在的声学黑洞结构往往是有限的, 存在一定的边界条件.声学黑洞通常情况下作为结构的一部分而内嵌于有限的结构中, 因此在边界上往往会存在多重反射.在运用几何声学方法或者基于Euler-Bernoulli梁的阻抗方法对声学黑洞结构进行建模分析的过程中, 都考虑的是半无限的结构.另一方面, 几何声学模型在对阻尼层建模的过程中需要假设阻尼层的厚度相对于声学黑洞结构的厚度而言非常小.而在实际情形中, 特别是在声学黑洞区域的边缘处, 阻尼层的厚度往往与结构相当, 因为声学黑洞结构的边缘处恰恰是声学黑洞效应得以有效保证的关键部分, 所以在对声学黑洞结构进行建模分析的时候, 处理需要考虑这些因素外, 还需要进一步考虑阻尼材料的形状和分布位置对结构阻尼效果产生的影响, 以使于进行阻尼材料优化从而达到最优振动抑制效应, 这就需要建立更通用的模型以将非均匀阻尼的质量与刚度同时考虑进去.此外, 在当声学黑洞结构运用到实际的振动控制或者能量回收时, 还需要考虑阻尼层与声学黑洞结构之间的全相合.
Tang等(2016)基于拉格朗日变分原理的声学黑洞结构半解析模型, 通过能量项灵活地将附加在声学黑洞结构中的元件添加到系统中, 很好地解决了以上问题.在半解析模型中选用Mexican小波作为形函数, 适用于声学黑洞结构中随着空间位置急剧变化的波数, 并通过等效弹簧的方法处理系统边界(Cheng & Lapointe 1995, Cheng 1996), 符合实际中存在边界的有限声学黑洞结构, 也更使于研究声学黑洞结构上附加阻尼层以及其他功能元件的非均匀性对声学黑洞效应的影响, 克服了传统解析建模中存在的不足.该模型适用于有中心对称面的一维声学黑洞结构, 如图 10所示的一维声学黑洞结构, 半解析模型基于Euler-Bernoulli梁的假设, 位移场可表示为

|
| 图 10 一维声学黑洞结构中弹性波的传播 |
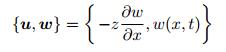
|
(26) |
其中, 向量{u, w}表示声学黑洞结构沿着x方向和z方向的位移, 同时也可表示阻尼层沿着x方向和z方向的位移.因此阻尼层与声学黑洞结合的位置满足位移连续性, 即两者之间是完全相合的, 挠度w可展开为
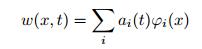
|
(27) |
其中, φi(x) 为形函数, ai(t) 为关于时间的变量.
依据Hamiltonian方程, 可得到如下拉格朗日方程

|
(28) |
系统拉格朗日算子L可表达为
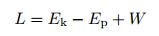
|
(29) |
其中, Ek表示系统的动能, Ep为势能, W为外力做的功
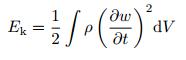
|
(30) |
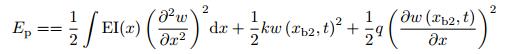
|
(31) |

|
(32) |
将式(29)~式(32) 代入式(28), 即可得到线性方程组

|
(33) |
其中, M和K分别是复数形式的质量和刚度矩阵(考虑阻尼的情况下), f(t) 和a(t) 分别是外力向量和相应的响应向量.在简谐运动中响应向量与外力向量可表示为时间的函数

|
(34) |
式(33) 也可记作
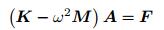
|
(35) |
求解上述方程即可得到结构受迫振动的响应.自由振动状态下将上述方程的外载荷置为零, 即可得到如下特征值方程
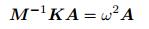
|
(36) |
求解特征方程可得到固有频率以及对应的模态振型.在考虑阻尼情况的系统中, 特征量为复数形式, 因此特征频率也表达为复数形式
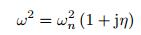
|
(37) |
其中, ωn为第n阶固有频率, η为相应的模态损失因子, 可以用来表征阻尼层对声学黑洞效应中的能量耗散效果.
在半解析模型中, 最为关键的是需要寻找一个合适的形函数以近似表示位移场.尽管在现有对非均匀结构的研究中, 多采用军函数或者多项式作为形函数(Bailey 1978, Ng & Araar 1989, Kobayashi & Sonoda 1991), 但却因在厚度减小处形函数会逐渐衰减, 且存在随位置急剧变化的“奇异”现象难以适用于声学黑洞结构.研究表明, 墨西哥小波函数(Mexican hat wavelet, MHW) 适于描述在声学黑洞边缘急剧变化的波群(Hou & Qin 2012). MHW是高斯分布函数的二阶导数, 可以表述为如下归一化形式
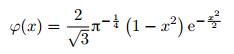
|
(38) |
经过小波变换后, 由式(38) 可以得到一系列的MHW展开函数

|
(39) |
其中, j为MHW的伸缩参数而k为MHW的平移参数, 可见MHW在一定范围的灵活程度以及平滑度使其能够很好地满足声学黑洞结构半解析模型中形函数的要求.于是式(27) 和式(28) 即可写作
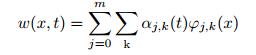
|
(40) |
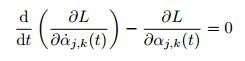
|
(41) |
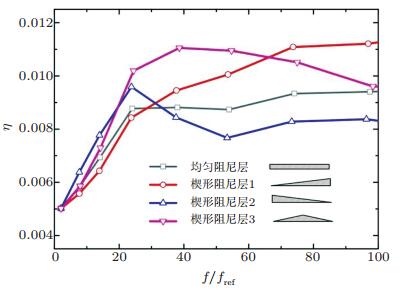
半解析模型中, 能量的表达式包含了对整个系统的积分, 将附加组件作为系统能量的一部分.该模型可以用来考虑局部阻尼层、非均匀阻尼层、能量回收功能材料层等对能量项的影响.半解析模型在对声学黑洞结构的分析中与其他模型相比有3个突出优势:其一, 半解析模型考虑了阻尼层与声学黑洞结构的全相合; 其二, 半解析模型通过在一端连接两个弹簧来模拟任意的边界条件, 从而更适直用来分析现实中有限的声学黑洞结构; 最后, 半解析模型适用于研究非均匀的附加组件对声学黑洞的影响, 因此可以灵活地用来优化声学黑洞结构中任意形状的阻尼层参数. 图 11为厚度变化的阻尼材料对系统阻尼损失因子的影响, 四种不同形状的阻尼材料质量相同, 图中的fref为相同大小的均匀梁的一阶固有频率, 在该算例中fref=209.5 Hz. 图 12为阻尼层刚度对系统响应的影响, 体现了在模型中考虑声学黑洞结构与阻尼层全相合的重要性.
|
| 图 11 厚度变化的阻尼材料对系统阻尼损失因子的影响, 厚度均匀的阻尼材料对应厚度为hd=0.005 cm, 阻尼材料分布的位置为xd=1~2 cm (Tang et al. 2016) |

|
| 图 12 阻尼层的刚度对系统响应的影响 |
将一维声学黑洞结构的截面h(x)=εxm (m≥2) 以x=0点为中心旋转一周即形成二维声学黑洞, 因此二维声学黑洞可以看作是厚度按照一定函数形式变化的轴对称凹痕.当弯曲波在声学黑洞内传播时, 由于厚度的变化, 弯曲波的传播方向发生弯曲, 最终把能量聚集到黑洞的中心.在结构厚度为h(x, y) 的二维声学黑洞结构中, 沿用一维声学黑洞结构几何声学分析方法, 弯曲波产生的面外位移w满足以下方程
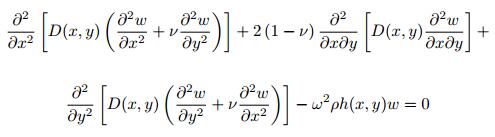
|
(42) |
其中, 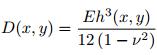
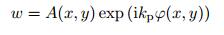
|
(43) |
其中, A(x, y) 是振幅, φ(x, y) 为相位(程函), kp为波数.将方程(43) 代入方程(42), 要使得等式成立, 则等式右边的实部和虚部必须都为零.由实部等于零并且舍弃关于A(x, y) 和φ(x, y) 的高阶导数项, 即可得到程函方程
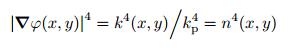
|
(44) |
其中, ∇=(∂/∂x) i + (∂/∂y) j为梯度算子, k(x, y)=121/4kP1/4/(h(x, y))1/2为与位置相关的波数, n(x, y) 为与位置相关的折射率(Climente et al. 2014)
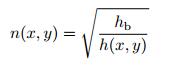
|
(45) |
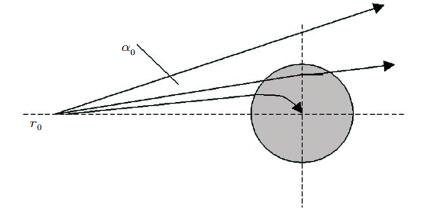
其中, hb为黑洞区域外板的厚度. 图 13为二维声学黑洞结构中弯曲波传播的示意图, 弯曲波在厚度变化的声学黑洞区域传播方向发生改变, 波射线由直线变为曲线而在圆形凹痕区域发生聚集.
|
| 图 13 二维声学黑洞结构中弯曲波射线示意图 |
由几何声学近似方法所表示的轴对称凹痕结构中的波传播轨迹方程的一般形式为(Krylov 2007)
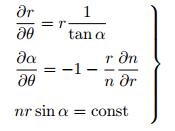
|
(46) |
其中, r和θ为极坐标, α为波矢量k与r之间的夹角.通过对以上方程的求解可以得到声学黑洞结构中的弯曲波传播轨迹.在特殊的几何条件下, 上述方程有解析解.但对于多数的二维声学黑洞结构则得不到波传播轨迹的解析解, 在这种情况下需要运用数值方法进行积分求解.
由方程(43) 可以看出, 程函φ(x, y) 为常数即表示了某一相位的波阵面, 也就是说, 同一波阵面上程函具有相同的值.而波传播的几何轨迹即为波阵面φ(x, y) 为常数的正交轨迹.在均匀介质中, 相位变化率∇φ的量值与位置无关, 较迟相位的波阵面总是平行于前一时刻的波阵面, 使得波传播轨迹在均匀介质中为直线.但在非均匀介质中, 相位变化率∇φ与位置有关, 因为不同位置的折射率n不同, 使得波阵面不再保持均匀介质中的平行状态, 因此, 传播轨迹发生了弯曲.这一理论在几何光学中己进行了深入研究(Narimanov & Kildishev 2009, Neu et al. 2010, Qiu et al. 2011, Wang & Chen 2011), 而对于弹性介质中弯曲波的传播轨迹的研究还比较少.
在方程(44) 中, 折射率为标量, 而∇φ为矢量.假设r(s) 为传播轨迹上点P的位置矢量, 而且是轨迹弧长s的函数, 轨迹的单位矢量为s=dr/ds, 可以得到程函方程确定的弯曲波轨迹方程

|
(47) |
对式(47) 两边进行关于弧长s的微分, 用n确定传播轨迹矢量形式的轨迹微分方程为
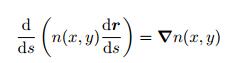
|
(48) |
在运用几何声学近似方法对二维声学黑洞结构中的波传播轨迹进行求解的过程中, 除了根据式(46) 中给出的公式求得具有特殊几何参数的声学黑洞结构中的弯曲波传播轨迹, 还可以通过求解式(48) 得到一般的声学黑洞结构中的弯曲波传播轨迹.对于厚度按照h(r)=εrm规律变化的声学黑洞, 在笛卡尔坐标系中, 声学黑洞区域内的厚度变化规律表述为h(x, y)=ε(x2 + y2)m/2折射率根据式(45) 可写为n(x, y)=(hb/ε)1/2 (x2 + y2)-m/4, 于是我们可以得到黑洞区域的折射率梯度
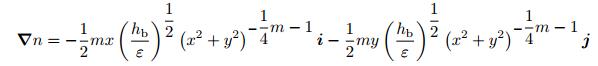
|
(49) |
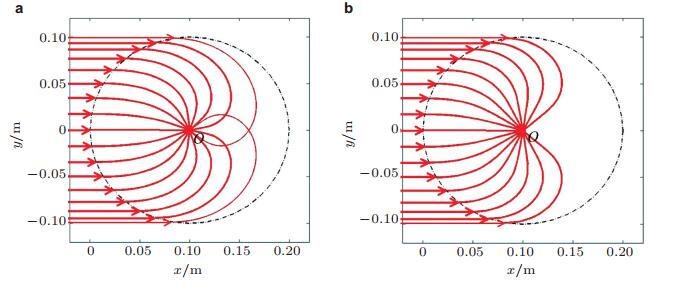
图 14为利用式(48) 与式(49) 求解即可得到满足初始入射条件的波的传播轨迹.假设从板的左侧入射平面波进入黑洞区域, 计算波在黑洞区域的传播轨迹.如果声学黑洞截面厚度变化函数的指数分别为m=2和m=3时, 入射到黑洞区域的弯曲波聚集到黑洞的中心.由于厚度按军函数分布的理想二维声学黑洞在黑洞中心处的厚度为零, 在实际加工制造中很难得到理想的二维声学黑洞, 因此还需要对非理想声学黑洞中波的传播特性展开研究.
|
| 图 14 声学黑洞结构h(r)=εrm中的弯曲波传播轨迹. (a) m=2, (b) m=3 |
弯曲波在复杂的板结构中传播的过程比较复杂, 一般情况下无法得到复杂板结构的波动方程的精确解.对于某些特殊形式的复杂板结构, Singh等利用Rayleigh-Ritz法在频域中进行近似求解(Singh & Saxena 1995, 1996; Taher et al. 2006).除此之外, 还可以通过其他的近似解析方法对非均匀厚度的板进行求解分析.例如, Wang等(1995)运用差分正交法(differential quadrature method, DQ) 求解了变厚度板的固有频率; Yang (1993)运用摄动理论将位移函数分解为一个平均值和小扰动分量, 从而对厚度线性变化的棋形结构进行了分析; Elishakoff (2000)采用定义振动模态的形函数替代传统位移形函数的方法给出了刚度函数, 进而得到了板的固有频率.在对径向厚度非均匀分布的圆板振动的建模研究中, 仅可对一些具有特殊的几何参数的圆板结构求得波动方程的解析解, Conway (1958)发现在厚度与半径呈指数函数形式变化的圆板中, 只有当指数为m=2/3和m=18/21时, 而且板的材料参数泊松比分别为ν=1/9和ν=5/21时能够得到解析解.在理想的声学黑洞区域中, 厚度分布的军指数可以是m≥2任意常数, 因此无法通过该方法获得精确的解析解.
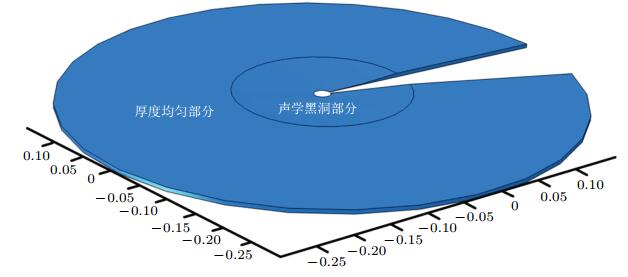
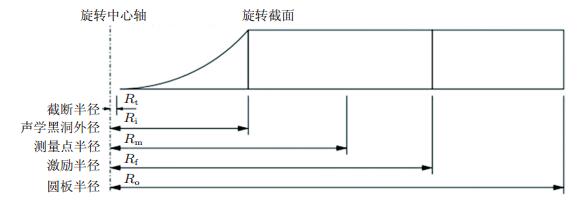
而含二维声学黑洞的板结构中, 除了厚度变化的声学黑洞区域, 周围是等厚度的平板区域, 组合在一起使得振动问题更加复杂. O'Boy等学者基于近似解析方法, 对含有二维圆形声学黑洞的圆形板(O'Boy and Krylov 2011) 和二维方形声学黑洞的方形板(O'Boy and Krylov 2016) 进行了频响特性的分析, 与不含声学黑洞的板结构的振动响应进行了比较, 并分析了阻尼层的影响.内嵌二维声学黑洞的圆形板结构如图 15 所示, 图中移除圆板结构的一个扇形区域是为了显示厚度的变化规律, 结构包含了厚度按照军函数形式变化并且含有一个中心圆孔的声学黑洞部分以及均匀厚度部分, 圆形板结构的截面如图 16所示, 厚度均匀部分和声学黑洞部分在声学黑洞外径Ri处连接并且该处两部分的厚度相同, 声学黑洞部分的横截厚度从Ri处向圆板中心以军函数形式递减, 当厚度在距离中心点一定距离的位置处变得很小时, 在该位置发生截断, 故而在圆板中央形成一个圆形孔, 半径为Rt.板上作用环形的激励力, 激励处的半径为Rf. O'Boy等(2010a)对声学黑洞区域的厚度变化服从m=2军函数时的圆形板结构的频响特性进行了分析.
|
| 图 15 圆形声学黑洞板(移除其中的一部分为显示厚度的变化规律) |
|
| 图 16 圆形声学黑洞板的截面示意图 |
具体的分析方法如下, 将圆形板结构分为3个区域: Rf r≤Ro的区域、Ri r≤Rf的区域以及Rt < r≤Ri的区域, 并假设每个区域的位移为
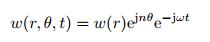
|
(50) |
其中, θ和t为圆周角和时间变量.用假设的形函数w(r) 代入上式, 并对运动方程进行求解(Jain 1972), 利用边界条件和区域间的连续和光滑条件可确定假设形函数中的待定参数.
图 17为不同频率下激励时某一时刻的位移.由于黑洞截断边缘附近的位移比其他区域大得多, 因此没有在图中显示.与板的厚度相比, 黑洞截断边缘附近位移相对较小, 从而满足线性假设的条件.

|
| 图 17 特定频率下的位移响应. (a) f=0.22 kHz, (b) f=1.85 kHz, (c) f=3.74 kHz, (d) f=0.49 kHz, (e) f=1.20 kHz, (f) f=2.20 kHz, (g) f=0.98 kHz, (h) f=1.90 kHz, (i) f=3.10 kHz (O'Boy & Krylov 2011) |
假设板结构本身的损失因子为η, 并通过损失因子引入到复数形式的弹性模量Ew的表达式中进行分析, 即Ew=Ew (1 + ηj).当在结构表面粘贴阻尼材料时, 把结构看成是复合结构, 将结构自身的损失因子与阻尼材料的损失因子综合起来, 用复合结构的阻尼等效损失因子来表示.由于声学黑洞结构在非均匀区域内, 厚度随着位置而变化, 因此结构的等效损失因子也是位置的函数.根据O'Boy等(2010)的研究结果, 复合结构的等效损失因子可表达为
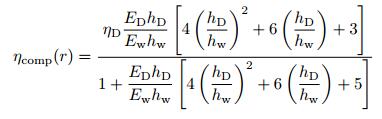
|
(51) |
其中, ED为阻尼层材料的刚度, ηD为阻尼层的损失因子.
由上式可知, 在黑洞区域内复合结构的损失因子ηcomp(r) 随离黑洞中心的距离r的变化而变化. r越小, hw (r) 越小, ηcomp(r) 越大, 在截断处, 损失因子达到最大值.对于二维声学黑洞结构, 在厚度均匀的板结构区域中传播的弯曲波穿越声学黑洞的边界, 进入厚度非均匀的黑洞区域后继续向黑洞中心传播, 经截断前缘反射后反向传播, 再次穿越黑洞边界回到厚度均匀的板结构区域.反射波穿越黑洞边界时的幅值和入射波穿越边界时的幅值之比定义为反射率.类似2.1节, 声学黑洞的反射系数可表示为
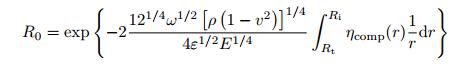
|
(52) |
反射系数越小, 表示振动衰减的效果越好.
上述带阻尼层的复合结构可以用一个沿半径方向损失因子为常数的简单结构来代替, 根据声学黑洞结构的反射系数不变的原则, 简单结构的等效损失因子定义为
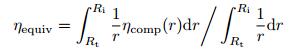
|
(53) |
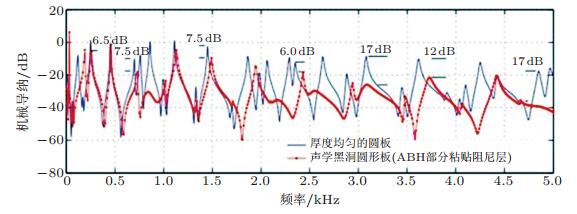
图 18为包含黑洞的圆板在给定点的机械导纳和不含黑洞的环形板在同一点的机械导纳的比较(O'Boy & Krylov 2011).不含黑洞的圆环板的外径和内经分别为Ro=250 mm, Ri=100 mm, 厚度为5.07 mm.带黑洞的圆板有相同的外径、内径及厚度, 且从Ri开始向圆心的部分是逐渐变薄的黑洞区域, 截断半径为Rt=5 mm.黑洞区域的等效损失因子为ηequiv=7.98 × 10-2.如图所示, 通过在黑洞区域粘贴一层很薄的阻尼层, 可以在整个所考虑的频率范围内获得1~3 dB振动衰减, 在低频范围的峰值处, 可以获得3~8 dB的衰减, 而在高频的峰值处, 可以获得高达17 dB衰减.
|
| 图 18 带黑洞的圆板和不带黑洞环板在同一点处的机械导纳w˙ (Rm, θ=0, ω)/p (Rf) 的比较(O'Boy & Krylov 2011) |
以上的几何声学的方法和近似解析方法, 是研究声学黑洞原理以及各种参数对结构动特性的影响规律时不可缺少的方法, 但只适合于几何形状相对较简单的声学黑洞结构.对于具有复杂几何形状的黑洞结构, 这些方法的求解过程会变得非常困难甚至无法求解.以有限元法为代表的数值分析方法可以作为上述解析方法的补充, 适用于各种几何形状复杂的黑洞结构, 而且既可以做频域分析, 也可以做时域分析.
Stephen将多个二维声学黑洞结构以一定的周期性规律布置在薄板结构中, 通过建立有限元与边界元模型来求解该薄板结构的振动响应以及结构的声功率特性(Con-lon et al. 2014, 2015a), 并且与均匀板结构的响应进行对比, 综合分析结构的振动与声辐射性能.声学黑洞结构作为宽频陷波器, 其有效作用频率受到几何尺寸的限制, 被声学黑洞聚集和吸收的波必须满足波长小于声学黑洞的特征尺寸, 这种波的聚集效应在截止频率以上有效.该课题组在降低声学黑洞结构有效作用频率范围的研究中, 开展了一系列工作, 通过有限元法(FEM) 和边界元(BEM) 建立含周期分布的多个声学黑洞的结构模型, 能够分析结构在截止频率以下的低频振动特性. FEM/BEM分析能够综合求解声学黑洞结构的振动响应与辐射声功率特性, 该分析在结构振动方程中考虑了结构表面压力
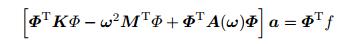
|
(54) |
其中, K和M为结构的刚度和质量矩阵, A为有结构振动引起的声辐射的表面压力, Φ为包含结构模态振型的矩阵, a为模态振型幅值.在有限元数值计算中, 损失因子可以由状态空间特征值直接计算, 而辐射声功率和声辐射效率也可以直接由频响分析得到.
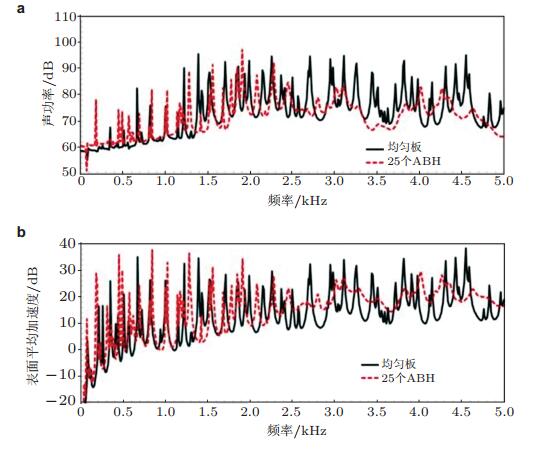
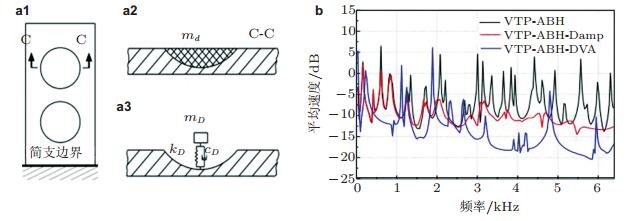
因此, 相合的FEM/BEM分析可以很方使且有效地对这种复杂声学黑洞结构的振动与声辐射特性进行综合分析. 图 19为计算得到的辐射声功率与对应的结构表面加速度在频域上的幅值.在该算例中, 由单个声学黑洞特征尺寸决定的截止频率为6 500 Hz, 从结果可以看出在高于2 500 Hz但是低于截止频率的范围内, 幅值有明显的衰减. FEM/BEM数值分析结果表明, 当多个声学黑洞结构周期分布到结构中时, 在声学黑洞截止频率以下的较低频率范围之内, 仍有很好的减振降噪效果. 图 20(a)和图 20(b)分别为四种不同结构的模态损失因子和两种声学黑洞结构在8000 Hz频率范围内的辐射声功率, 由于含多个声学黑洞的结构的低阶模态引起的损耗, 提高了声学黑洞结构截止频率以下的低频特性.在截止频率以上的范围声学黑洞能够有效地聚集结构中传播的弯曲波, 而显示出宽频吸收特性.此外, 计算结果还显示声学黑洞结构中较大的中心圆孔在截止频率以下的范围内能够提高结构的减振降噪性能. Stephen还研究了声学黑洞个数对板振动特性的影响(Conlon et al. 2015b), 结果表明声学黑洞板结构的低频特性主要取决于声学黑洞单元的低阶模态, 通过结构强度分析, 进一步研究了在声学黑洞单元中能量的传递与耗散.另外, 为了降低声学黑洞结构振动抑制的有效作用频率, Jia等(2015)将声学黑洞结构与动力吸振器相结合, 如图 21所示, 在声学黑洞区域添加一个弹簧质量系统, 数值分析结果显示, 该结构因动力吸振器的存在, 低频范围内的振动幅值大大降低.
|
| 图 19 (a) 辐射声功率在频域上的幅值, (b) 对应的结构表面加速度(其中黑色实线表示均匀板, 红色虚线为25个周期排布声学黑洞的板结构) (声学黑洞由于截断会在中心形成小孔) (Conlon et al. 2015b) |

|
| 图 20 (a) 模态损失因子, (b) 周期排布25个声学黑洞时板结构辐射声功率的幅频特性(其中黑色实线表示声学黑洞中心圆孔较大的情况, 红色虚线表示声学黑洞中心圆孔(ABH-SH) 较小的情况) (Conlon et al. 2015) |
|
| 图 21 (a) 数值仿真模型: (a1) 声学黑洞结构, (a2) 声学黑洞与阻尼材料(ABH-Damp) 结合, (a3) 声学黑洞与阻尼材料和动力吸振器(ABH-DVA) 结合; (b) 数值仿真结果(Jia et al. 2015) |
现有的对二维声学黑洞的研究己经表明, 将二维声学黑洞结构内嵌于板结构中能够获得有效的宽频振动抑制效果.随着研究的深入, 对二维声学黑洞结构中波传播的研究从频域内的分析拓展到时域内的分析.在声学黑洞结构的厚度变化区域内, 研究了弯曲波传播的特性, 包括波速的降低, 波长的压缩, 传播方向的偏转等弯曲波能量聚集的具体过程.对于非均匀薄板结构中波的传播与演变, Peng和Pan (2004)利用声波算子的方法研究了结构中声波的时域变化过程, 结合切比雪夫多项式展开与快速傅里叶变换实现了声波算子算法的实现, 通过将声波算子反复作用于初始状态, 可以得到任意时刻的波动状态.但是这种方法未解决厚度呈军函数形式变化的结构中波传播的变化过程.
Yan等对Lamb波在二维声学黑洞结构中的传播过程进行了研究(Lomonosov et al. 2015, Yan et al. 2016), 求解了具有特殊几何参数的二维声学黑洞结构中波的传播轨迹, 并通过有限元仿真展示了在二维声学黑洞结构中波由厚度均匀的区域到厚度变化的区域的传播与聚集的过程.此外, 由二维声学黑洞结构中波轨迹的计算结果分析了定常轨道的存在, 即在二维声学黑洞结构中, 定常轨道之内的波射线能被结构聚集到中心区域, 而定常轨道之外的波射线最终将从声学黑洞结构中逃逸出去.借助声学黑洞效应的原理, Climente等(2013)在板结构中设计了一个全向振动绝缘装置, 当板中从各方向入射的弯曲波通过一个厚度逐渐减小的环形区域, 波速逐渐减小, 能量将在该环形区域聚集, 在结构能量聚集的位置粘贴适当的阻尼材料时, 波动能量将会被
有效地耗散, 从而使得振动不会传递到中心圆台区域.他们通过采用多层散射的数值分析方法, 将厚度变化的区域离散为多个均匀的轴对称层进行数值计算, 分析了波动能量在环形厚度变薄区域的聚集与耗散的过程. Climente等(2014)还通过利用薄板结构厚度变化实现特定的折射率分布, 设计出五种对弯曲波进行聚集的透镜结构, 这五种透镜原本为光学中的透镜, 研究证明在弹性结构中, 它们对弯曲波聚集效应与光学中透镜类似, 并且通过有限元仿真对透镜聚集弯曲波时的位移场进行计算, 结果验证了透镜对弯曲波的聚集效果.
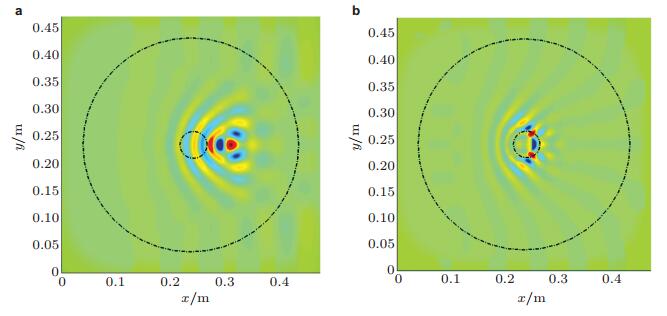
如前面所述, 受到实际加工制造工艺的限制, 往往得不到理想的声学黑洞结构.考虑到在二维声学黑洞结构中往往存在的不可避免的非完美因素, Huang等(2016)研究了一般形式的非完美二维声学黑洞结构中弯曲波聚集的现象, 此时二维声学黑洞结构的截面厚度变化以一个多项式进行描述.研究表明在这样的结构中会产生与理想声学黑洞结构不一样的能量聚集现象.如图 22所示, 在传统的厚度按照军函数形式变化的声学黑洞结构中, 弯曲波会被聚集到结构的中心区域, 而结构截面厚度变化规律不再是严格的军函数形式时, 弯曲波将聚集在一个偏离中心区域的位置, 并且还通过有限元方法研究了结构参数对弯曲波聚集的位置的影响.此外, 通过结合有限元计算结果进行功率流分析研究了非完美二维声学黑洞结构对能量聚集效果的影响, 如图 23所示, 该算例中, 能量聚集的位置在截面3, 其宽度为结构宽度的6.7%, 通过该截面处的功率流与通过截面1的功率流的比值为58.25%, 因此表明了非完美的声学黑洞结构也有非常好的能量聚集效果.
|
| 图 22 二维声学黑洞板结构的位移场. (a) 声学黑洞结构h=ε(r -r1)2 + h1, (b) 声学黑洞结构h=εr2 |

|
| 图 23 非完美声学黑洞结构中不同截面位置上功率流随时间的变化 |
近年来, 学者们陆续对一系列含有声学黑洞的梁和板结构展开了实验观察和分析. Krylov和Winward (2007)首次对声学黑洞结构进行实验研究是在2007年, 测试对象为一个含一维声学黑洞棋形边缘的钢板, 在厚度变薄的尖端粘贴了阻尼材料, 实验测量了声学黑洞结构导纳, 并与厚度均匀的板结构和未粘贴阻尼层的声学黑洞结构进行了对比, 在粘贴有阻尼材料的情况下, 最大的共振峰衰减达到20dB, 结果显示出声学黑洞在振动抑制应用中的巨大潜力.随后, Kralovic和Krylov (2007)对厚度呈二次指数变化并且尖端带有阻尼材料的杆进行了实验观察, 同样验证了声学黑洞杆结构的宽频振动衰减效果.从对含一维声学黑洞棋形边缘的钢板的实验测试结果中还发现, 在棋形边缘粘贴一条较窄的阻尼材料比在整个声学黑洞区域粘贴阻尼层的振动抑制效果好(O'Boy et al. 2010b, Bowyer et al. 2012), Bowyer等(2012)还由实验分析了实际制造偏差对声学黑洞的振动抑制效果的影响, 特别是机械加工对结构造成的损伤, 比如在棋形尖端材料的卷曲和过早的截断所带来的影响, 同时也将阻尼材料粘贴到棋形边缘的不同位置进行了测量.另外, 他们还研究了将声学黑洞边缘与其他结构连接时(如氧弧焊接、胶接或者直接加工于结构的边缘等), 不同的连接加工条件对声学黑洞效果的影响. Bayod (2011)研究了声学黑洞边缘的制造方法, 通过直接在等厚度均匀板上拉延出一段尖锐的边缘, 从而在一定程度上克服声学黑洞边缘制造的困难, 并且实验验证了延伸出来的边缘具有提高振动抑制的效果.上述一维声学黑洞在实际应用中存在的问题是需要在结构边缘形成一个很尖锐的边缘, 为了解决这个问题, 也可以将一维声学黑洞作为一个凹槽内嵌到结构中(Bowyer et al. 2012). Denis等(2014)通过实验研究了带有截断的一维声学黑洞结构的模态损失因子, 证明了结构中声学黑洞的存在大幅增大了模态损失因子, 但模态密度增大不明显.他还通过实验的手段首次测量得到有截断的一维声学黑洞结构的反射系数(Denis et al. 2015), 实验所得的声学黑洞反射系数结果与理论计算, 相符程度很好, 该结果表明了阻尼层对声学黑洞反射系数有明显降低作用.这些实验结果表明声学黑洞效应具有良好的鲁棒性(Krylov 2014), 在加工精度存在一定误差的情况下依然能有很好的振动抑制效果. Tang和Cheng (2016)还通过实验发现, 在有限声学黑洞一维梁结构中, 声学黑洞效应在一定频率范围内显著降低, 称为声学黑洞效应的失效频率范围, 在该范围内声学黑洞在尖端的能量聚集明显减弱.这是由于在机械激励下, 引入了一个不连续的局部结构阻抗, 在失效频率范围内, 波在结构边界和激发点之间发生多重反射, 形成驻波和局域共振, 因而有可能使得振动能量集中在声学黑洞梁结构的均匀部分, 从而使预期的声学黑洞效应减弱.通过运用第2.3节中的小波分解和基于能量的半解析模型可以实现对这种有限一维声学黑洞梁结构失效频率的预测, 从而可以有针对性的避开失效频率.
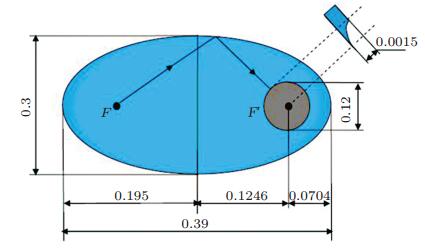
Georgiev等(2011)还对图 24所示的内嵌二维声学黑洞的椭圆板结构开展了实验研究.将该椭圆板的一个焦点作为激励点, 而二维声学黑洞则位于椭圆的另一个焦点上.二维声学黑洞的厚度同样以一军函数形式递减, 直到黑洞中心即椭圆的焦点位置厚度递减为零.对于上述二维声学黑洞椭圆板, 由激励点处产生的所有的弯曲波都被聚集到声学黑洞的中心, 其中, 一部分弯曲波直接被聚集到黑洞中心点, 其余的弯曲波通过椭圆板自由边界的反射后同样会被聚集到黑洞中心点.
|
| 图 24 内嵌二维声学黑洞的椭圆板的弯曲振动模型 |
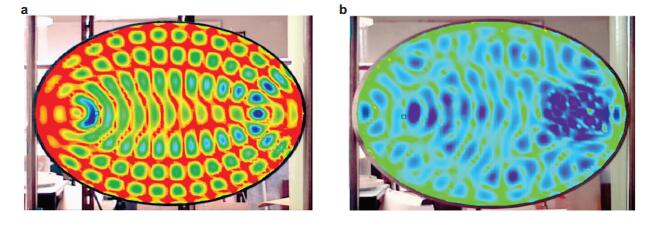
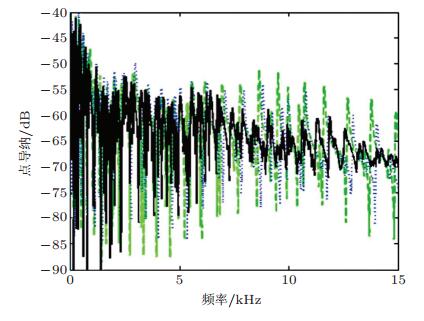
图 25为实验测得的椭圆形板速度场, 由对比结果可见, 含有声学黑洞的椭圆板的振动幅值比不含声学黑洞的椭圆板小很多. 图 26为3种情况下实验测得的激励点导纳的对比图, 结果显示含有声学黑洞并在声学黑洞内粘贴阻尼材料的椭圆板, 其导纳的共振峰幅值最小, 即振动抑制的效果最好, 而粘贴同样面积的阻尼材料, 但不含声学黑洞的平板结构的振动抑制效果最差.即使在不含黑洞的平板上贴满阻尼材料, 其振动抑制效果也不及包含粘贴阻尼材料的声学黑洞的情况.随后Bowyer等(2010)也测量了含有二维声学黑洞的板结构的振动特性, 结果显示, 当在一块板上加工出一个厚度按照军函数形式减小的圆形凹痕对结构的阻尼效果并不明显.然而在二维声学黑洞中央形成一个小孔时, 将使结构的阻尼效果提高.
|
| 图 25 实验测量所得椭圆形板的速度场对比图. (a) 不含声学黑洞的椭圆板(8 671 Hz), (b) 含有声学黑洞的椭圆板(8 117 Hz) |
|
| 图 26 实验测量所得椭圆形板的点导纳对比图, 实线表示含声学黑洞并粘贴阻尼材料, 虚线表示不含声学黑洞但在同一位置粘贴同样面积的阻尼材料, 点划线表示不含声学黑洞但在整个试件上粘贴阻尼材料(Georgiev et al. 2011) |
O'Boy和Krylov (2011)对3.2节中介绍的含有二维圆形声学黑洞的圆形板结构的振动传递特性也开展了实验研究. 图 27(a)是不含声学黑洞的结构的机械导纳, 在0.59, 2.22, 2.78, 3.38, 3.98和4.7 kHz处存在共振点, 共振频率的理论结果与实验结果符合较好, 误差分别为1.7%, 2.7%, 1.4%, 0.3%, 1.3%和0.2%. 图 27(b)为嵌入了声学黑洞的圆板结构的机械导纳的理论结果和实验结果, 二者具有较好的一致性.

|
| 图 27 结构的机械导纳. (a) 不含声学黑洞的结构, (b) 含有声学黑洞的结构(O'Boy & Krylov 2011) |
为了提高二维声学黑洞结构减振降噪的效果, Bowyer等对含有多个声学黑洞的板结构进行了实验研究(Bowyer & Krylov 2012, Bowyer et al. 2013). 图 28为实验中使用的含有6个声学黑洞的板结构, 声学黑洞中央区域由于截断形成了中心圆孔, 在声学黑洞区域粘贴适当的阻尼材料.测量结果表明, 与厚度均匀的参考板相比获得了明显的阻尼效果, 同时该结构对声辐射功率也有明显的抑制作用.对于二维声学黑洞结构, 主要开展了带有棋形压痕或圆形凹坑的矩形板、椭圆板和圆板的实验研究.研究对象也并不局限于金属材料, 如铝材、钢材结构等, 还拓展到复合材料(Bowyer et al. 2012, Bowyer & Krylov 2014), 如图 29所示, 并且加工了不同截面的声学黑洞试件, 从工程应用的角度提出将黑洞移到复合板内部, 对不同试件开展了相关的实验研究.在复合材料中, 由于复合材料自身的损失因子较大, 因此在没有阻尼材料的情况下, 振动幅值的衰减也较为明显.所有的实验结果都表明声学黑洞的有效频率主要集中于中高频域.

|
| 图 28 (a) 含有6个二维声学黑洞的板结构, (b) 板结构的加速度响应(实线为含有6个二维声学黑洞的板结构, 虚线为厚度均匀分布的板) |

|
| 图 29 (a) 复合材料蜂窝板, (b) 不同的声学黑洞截面示意图 |
此外, 本文中提到的声学黑洞结构的实现手段主要是通过结构剪裁使得结构厚度按照军指数函数减小, 除了这种主要的实现方法, Georgiev等(2010)还提到了一种通过结构热效应实现的声学黑洞结构, 通过运用形状记忆合金来实现热声学黑洞效应, 并对其进行了频域内的机械阻抗测量.形状记忆合金的弹性模量可以表示为温度和频率的函数, 通过温度在空间上的非均匀分布进而可以转化为空间坐标和频率的函数
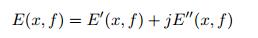
|
(55) |
实验设备系统如图 30所示, 实验结果证实了通过设计控制温度梯度的变化的记忆合金材料, 从而实现弹性模量的梯度分布, 进而实现声学黑洞效应的可能性.这样的热声学黑洞结构同样产生了很好的振动抑制效果.

|
| 图 30 热效应声学黑洞结构实验设备示意图 |
从对声学黑洞结构频域内的实验研究结果可以看出, 在一定的频率范围之内, 声学黑洞结构能有效地抑制振动与噪声.对于声学黑洞结构中波传播的过程的研究, 除了通过在3.2节中提及的有限元数值研究以外, 现有的实验手段也可以实现从时域上对声学黑洞结构中波传播过程进行研究. Lomonosov等借助一套光学实验系统对一个含有中心圆孔的微小的声学黑洞结构进行了测量(Lomonosov et al. 2015, Yan et al. 2016), 图 31所示为实验系统示意图 31(a)与测量结果图 31(b).该实验中的测量对象的几何尺寸仅为5 mm × 5 mm × 0.5 mm的铝板, 可以看出实验试件尺寸极小, 因此测量中波的频率的数量级高达兆赫兹.测量结果得到了Lamb波在凹痕区域的传播过程, 从实验上验证了定常轨迹的存在, 并且分析了在圆孔附近的边缘局域波.

|
| 图 31 (a) 光学实验系统, (b) 测量结果 |
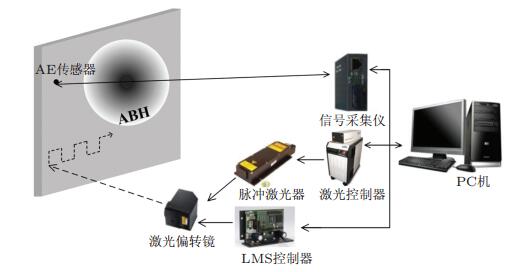
Huang等(2016)利用激光超声扫描技术对二维声学黑洞板结构进行时域实验分析, 实验系统如图 32所示.该系统由激励单元、数据采集单元和控制单元三部分构成, 其中YAG激光发生器产生重复频率为20 Hz的激光脉冲作用在板上产生弹性波.根据弹性动力学互换定理, 通过固定在板上的声发射(acoustic emission, AE) 传感器进行信号采集, 等同于在AE传感器处施加激励, 在激光激励点采集信号.将激光激励点通过偏转镜的偏转在一个二维区域内扫描, 并在固定的位置用AE传感器同步采集接收到的信号, 经过数据处理可重构出扫描区域中在不同时刻的波场(Wu et al. 2014, Zhang et al. 2014), 从而可显示出任意给定时刻扫描区域的波传播过程.该实验中声学黑洞直径为200 mm. 图 33为实验测量得到的不同时刻声学黑洞结构上的波场, 结果清楚地显示了在二维声学黑洞结构中波的传播过程, 在黑洞区域内, 波长被压缩, 波阵面发生弯曲变形, 最终产生能量聚集现象.
|
| 图 32 激光超声实验系统 |

|
| 图 33 激光超声实验测量的不同时刻的波场 |
声学黑洞技术的典型应用研究, 具有功能-结构-材料一体化设计的典型特征.声学黑洞是通过对结构自身形状或者材料的设计对波的传播进行控制, 声学黑洞结构对波能量的聚集具有高效宽频的特点, 在振动噪声控制领域和能量回收领域都有着广泛的应用前景.对声学黑洞结构应用问题的探索与研究将对推动弹性波、声波控制技术的发展起到重要作用.
5.1 振动噪声控制 5.1.1 声学黑洞的振动控制应用实例目前, 对于声学黑洞在振动控制的实际应用己开展了一些尝试性的研究工作. Bowyer等将涡轮叶片的后缘加工成厚度按照军函数形式变化的形状, 在边缘处粘贴少量的阻尼材料(Bowyer et al. 2012, Bowyer & Krylov 2014a), 实现了运用一维声学黑洞吸收弯曲波能量从而抑制振动的效果, 并且运用实验手段研究了该涡轮叶片的弯曲振动阻尼特性.实验以翼型NACA 1307作为基本模型, 加工了4种非发动机专用的涡轮叶片, 如图 34所示, 考虑涡轮叶片在实际应用中的情形, 其中有两个试件(试件(c) 和试件(d)) 经过了扭曲.实验采用电磁激振器给叶片施加激励, 用加速度传感器采集振动响应信号.经过测量结果的对比, 未扭曲的叶片中含有一维声学黑洞模型的叶片在4.2kHz时有最大的阻尼效果, 响应幅值减小了12 dB, 扭曲的叶片中获得最大10.5 dB的衰减, 对应频率为4.1 kHz.当在涡轮叶片中引入一维声学黑洞边缘, 响应共振峰在一定频率范围内发生大幅衰减.为了进一步研究当涡轮叶片几何外形发生变化后对叶片表面流动产生的影响, 以及边缘粘贴阻尼材料时对表面流动的影响, Bowyer和Krylov (2014a)还进行了可视流动实验, 在涡轮叶片与气流呈10°倾斜角的测量情况下, 流动显示如图 35所示, 当在声学黑洞涡轮叶片的后缘粘贴适当几何形状的阻尼材料时, 可以使得涡轮叶片表明保留原本的流动特性.因此, 一维声学黑洞结构运用到涡轮叶片的振动抑制是可行的, 能够有效地降低叶片内部的应力提高其疲劳寿命.

|
| 图 34 四种涡轮叶片试件. (a) 未扭曲的参考叶片, (b) 未扭曲含有一维声学黑洞边缘的叶片, (c) 扭曲的参考叶片, (d) 扭曲含有一维声学黑洞边缘的叶片 |

|
| 图 35 四种涡轮叶片试件上的流动显示图. (a) 未扭曲的参考叶片, (b) 未扭曲含有一维声学黑洞边缘的叶片, (c) 未扭曲含有一维声学黑洞边缘的叶片边缘粘贴普通阻尼材料, (d) 未扭曲含有一维声学黑洞边缘的叶片边缘粘贴阻尼材料(该材料还原了参考叶片的几何外形) |
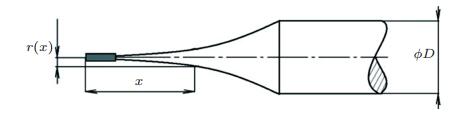
将杆结构的端部进行结构剪裁, 使其直径按照一定军函数形式减小, 并在结构尖端粘贴少量阻尼材料形成如图 36所示的一维声学黑洞杆结构, 实验测量了该结构的动力学响应, 表明了该结构有效降低了波在杆尖端的反射, 因此具有很好的振动抑制效果(Kralovic & Krylov 2007).该杆结构易于加工, 可以应用在实际生活中, 例如将其引入如图 37所示的网球拍或者高尔夫杆中, 可以有效地抑制球拍的振动.
|
| 图 36 尖端直径按照幕函数形式减小的杆(尖端粘贴吸收材料) |

|
| 图 37 一维声学黑洞内嵌于网球拍的拍柄中 |
上一小节中介绍了一维声学黑洞结构在振动控制方面的应用实例, Bowyer和Krylov (2015)对二维声学黑洞结构在振动噪声控制领域的应用也有了初步的尝试, 其将两块不同的二维声学黑洞板布置到汽车的引擎外壳上, 如图 38所示, 实验测试的结果显示当引擎外壳上集成有二维声学黑洞板时, 引擎舱的噪声将会降低6.5 dB, 在某些特殊的频率上甚至可以降低10 dB, 从而能够提高汽车在声音方面的舒适性.二维声学黑洞结构对结构声辐射的抑制作用己经得到了证实.如前文中所提及的, Bowyer和Krylov (2015)开展了将声学黑洞结构用于噪声控制的实验研究, 结果显示含有6个声学黑洞的结构对声辐射有非常明显的抑制作用.且当声学黑洞上粘贴很薄的阻尼材料时, 在1~3kHz的频率范围内, 与均匀参考板相比较, 结构的声辐射功率降低10~18 dB, 但是在低频范围内的作用不明显(Bowyer & Krylov 2012).然而, 由于圆锥压痕中含有的截断厚度导致实际结构中存在着圆心孔, 声学黑洞声辐射的影响以及中心圆孔对声辐射的影响仍有待进一步研究.除此之外, 声学黑洞还可用于空气声波的吸声, 但一般只对高频空气声波有效.声学黑洞效应的有效频率范围限制了声学黑洞对中低频声波的抑制效果.

|
| 图 38 汽车的引擎外壳结合二维声学黑洞板的样品图 |
Foucaud等(2012)还将声学黑洞结构作为波吸收器应用与人工耳蜗的研究中.人的内耳是由充满液体的管道构成, 这种管道可以看作是一种弹性结构, 当内耳接收到声音信号, 声波将会沿着管道传播, 该管道起到感知振动并放大振动信号的功能.由于内耳器官构造复杂, 无法直接进行实验测试, 为此借用人工耳蜗来再现内耳中管道, 将声学黑洞结构内嵌在梁结构中用来减少波的反射, 如图 39所示, 从而用来研究声波在耳蜗中的传递特性.实验结果显示出声学黑洞模型与人工耳蜗具有良好的相关性, 声学黑洞作为消声端, 提高了测量数据的质量.该声学黑洞结构的运用为更好地了解内耳力学提供了新的契机.

|
| 图 39 人工耳蜗实验设备 |
除了上述中常规的厚度变化的声学黑洞结构, Mironov等还提出并研究了一种声学黑洞管道结构(Mironov & Pislyakov 2002, El-Ouahabi et al. 2015), 如图 40所示, 通过使管道的有效导纳沿轴向逐渐增大, 从而使沿管道传播的声波速度逐渐减小至零.在管道内部按一定规律排布小薄板可以实现管道导纳的梯度变化, 薄板厚度与薄板之间的间距满足适当的变化规律, 即可实现在有限的时间内声波不能到达管道的端部, 从而也就无法反射.在声波能量发生累积的地方波传播速度减小为零, 这种声学黑洞管道结构的提出为完全吸收管道中传播的声波提供了可能.研究还指出, 当管道声学黑洞结构结合阻尼材料时, 例如结合多孔性吸声材料、玻璃纤维和矿物棉等, 将在一定程度上提高声波吸收效果.

|
| 图 40 (a) 声学黑洞管道结构示意图, (b) 实物图 |
迄今为止, 虽然有研究涉及运用声学黑洞结构进行噪声控制, 通过实验测量和数值仿真的研究显示了声学黑洞结合阻尼材料能够有效地降低结构声辐射效率, 但是对声学黑洞结构声辐射机理仍需要进行深入研究.需要进一步形成一套完备的分析和优化手段来细致地研究声学黑洞结构声辐射机制形成原因和参数影响规律.
5.1.3 声学黑洞结构优化设计问题从声学黑洞结构的实际应用角度来看, 因声学黑洞结构在局部区域的厚度很小, 在应用中将会面临结构强度的问题.另外, 黑洞效应的有效作用频率通常与声学黑洞特征几何尺寸有关, 现有的研究表明了声学黑洞结构具有宽频能量聚集特性, 但是该频带范围较高.在实际应用例如结构振动噪声控制中, 很多问题都需要解决中低频的振动与声辐射.如何拓宽声学黑洞波操控的作用频带范围, 并且同时保证结构强度是在设计优化声学黑洞结构中必须考虑的问题.
针对满足结构强度的声学黑洞结构设计, Bowyer等提出了一些改进方案, 如将厚度逐渐变薄的部分加工成一个凹槽转移到结构内部(Bowyer et al. 2012), 或者将特定形状的二维声学黑洞凹痕置于复合板结构的内部(Bowyer et al. 2013).当通过结构剪裁实现厚度变化的过程中, 部分声学黑洞结构有可能含有一个残余厚度(Zhao et al. 2014, Semperlotti & Zhu 2015, Zhu & Semperlotti 2015), 而这个厚度的存在一定程度上保证了结构强度.也有研究在二维声学黑洞结构的中心位置形成一定厚度的圆形平台(Huang et al. 2016).以上这些研究都表明, 当声学黑洞结构的几何截面通过一定形式改变, 保留一定的附加厚度时, 能够在一定程度上克服声学黑洞结构的结构强度问题.而且传统的厚度以军函数形式变化的声学黑洞结构经过这种微小的几何形状的改变依然能起到很好的作用.
为了拓宽声学黑洞波操控的作用频带范围, 目前己有研究工作尝试运用多个声学黑洞或者周期排布的声学黑洞来拓宽有效作用频率(Bowyer & Krylov 2014, Zhu & Semperlotti 2015), 结果显示通过改变声学黑洞的特征尺寸, 或者将多个声学黑洞周期排布可以实现降低声学黑洞结构有效作用频率. Conlon等(2015a)研究了将声学黑洞作为单元按一定的排列规则进行组合形成周期声学黑洞结构, 指出周期声学黑洞结构能够提高结构的低频噪声控制性能.在声学黑洞结构中的能量聚集位置结合动力吸振器(Jia et al. 2015), 也能够提高声学黑洞结构在低频范围的振动抑制效果.目前在其他波操控方法的研究中, 例如超材料、声子晶体的研究中, 都己经开展了关于如何拓宽频率的工作. Liu等(2000)将包覆软硅橡胶材料的铅球按立方晶格嵌入环氧树脂基体中, 形成了一种三维三组元声子晶体, 理论和实验结果均表明该声子晶体带隙所对应的波长远大于晶格常数, 由此提出了局域共振声子晶体的概念.局域共振声子晶体形成带隙所对应的波长远大于晶格常数, 突破了布拉格散射机制的限制, 而且带隙不严格依赖于散射体的周期性排布, 当频率位于共振频率附近时会出现等效负质量密度的特性, 对低频声波与振动的隔离具有较好的应用前景, 也引起了各国研究人员的广泛兴趣.从此以后, 对局域共振型声子晶体、声学超材料特性的理论与实验研究层出不穷. Liu等(2005)还发现当局域共振型超材料的3种组分均为固体材料时, 材料依然可以表现出负质量密度特性. 2006年, Fang等(2006)发布了对一维Helmholtz共振腔超材料的研究报告, 结果发现在局域共振型禁带中, 该结构具有等效负体积模量.另外, 利用二维Helmholtz腔超材料单元还设计了一种低频域隔声结构, 具有较好的隔声效果. Dubois等(2013)根据负折射的概念研究了克服衍射限制的板结构, 设计了运用平面镜聚焦原理对平面弯曲波进行聚焦的结构, 并且在有效的声波频带范围, 得到了结构能带的解析表达式.在应用探索方面, 国防科技大学的温熙森小组率先将声子晶体的思想引入对杆、梁、板等的设计当中, 用以实现对工程结构的减振设计, 获得了较好拓宽有效频带范围的效果(Gang et al. 2006, Yu et al. 2006, Xiao et al. 2012), 并且也带动了其他的同类研究.这些成果可为提高声学黑洞的低频特性研究提供一定的借鉴作用.
为了将声学黑洞更好地应用于实践, 探索在低频区域的声学黑洞波传播特性还需要更深入的研究, 进而提出针对降低声学黑洞结构有效作用频率这一目标的结构优化设计方法.
5.2 能量回收近年来, 振动能量回收成为众多学者研究的热门领域.通过结构设计来提高能量回收效率的研究如火如荼.能量回收的结构设计正经历着从线性到非线性, 回收频率特性从单频到多频再到宽频的研究历程.声学黑洞技术通过波的操控, 实现了宽频带的能量聚集, 使于结构能量回收.目前将声学黑洞技术用于结构能量回收的研究才刚刚起步.虽然目前对结构能量回收的研究还不多, 但是现有的研究仍然显示出声学黑洞结构在能量回收应用中的潜力.
5.2.1 声学黑洞结构能量聚集机理现有的能量回收技术大都只对单频、多频或者窄带的振动能量回收效率较高, 在线性结构研究方面, 赵娟等(2010)设计等应变的悬臂梁结构, 阐君武等(2008)设计了双晶片悬臂梁结构等.这些装置一般只能在特定的频率下才有较高的功率输出, 一旦外界激振频率偏离结构的共振频率, 机电转换效率就特别低.为了进一步拓宽有效回收频率范围, Wu等(2008)提出了一种共振频率可调节的振荡器结构, 通过调整悬臂梁末端质量块的等效重心位置改变其共振频率, 使之与激振频率匹配.实验结果表明, 该原型装置的实际频率可在130~180 Hz之间变化.但上述研究共同点在于:有效地能量回收频率只集中在一个或几个特定的频率, 一旦振动环境受到影响, 回收效率明显降低.对一些振动信号如功率谱比较分散的振动能, 利用此类结构很难获得满意的回收性能.为了解决这一问题, 近期大多数研究己经由线性结构转向了非线性结构(Tang et al. 2013), 目前研究最热门的非线性结构是在悬臂梁自由端加上一块磁铁, 与之对应放置一块或两块互斥的磁铁, 使得梁在振动时, 磁场对梁产生非线性的作用力, 有效地增大梁的振幅(Erturk & Inman 2011, Cottone et al. 2012, Vocca et al. 2012).上述振荡器结构的总体设计思路是使得结构的共振频率或工作频带尽可能地去匹配振动源的主要激振频率, 由于环境振动频率一般都集中在低频段, 因此结构的工作频率一般也设计得比较低.但实际上, 振动能的最大回收功率近似与振动频率的三次方成正比关系, 因此振荡器的工作频率越高, 其能量密度越大. Liu等(2012)设计的一种升频转化(frequency up-conversion) 压电振荡器结构, 在高频工作状态下的回收功率密度比处于低频工作状态下高出了3.6倍.扩宽能量回收系统收集能量的频率范围以提高回收效率, 也是能量回收应用过程中需要突破的难题.
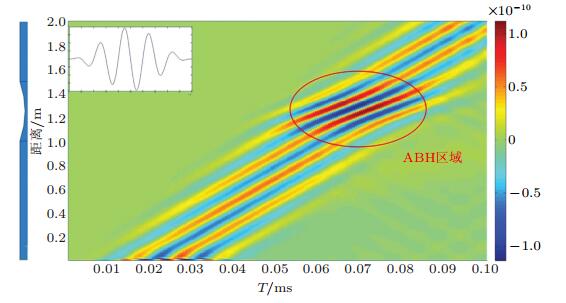
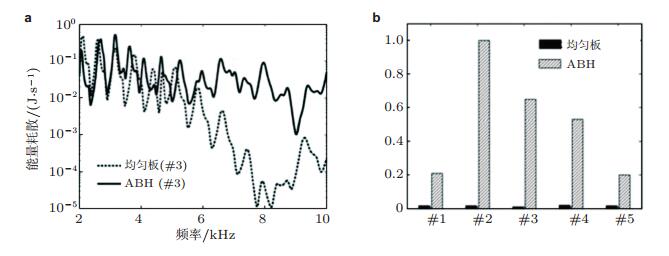
正如前面所介绍的, 声学黑洞利用结构厚度按照军函数形式逐渐减小, 使得传播经过声学黑洞的弯曲波波速减缓, 逐渐将弯曲波聚集在结构中某一区域, 在该区域结构的能量密度迅速增大, 如图 41所示.而且这种宽频带能量聚集效应在声学黑洞截止频率以上均有效. Zhao等(2014, 2015) 利用声学黑洞结构的能量聚集特性, 在结构中等间距布置5个厚度逐渐减小的一维声学黑洞凹痕, 并在厚度变化的区域粘贴压电换能元件, 如图 42所示. 图 43为数值仿真所计算的在结构一端施加力激励的情况下, 5个压电换能器上收集到的能量, 通过与厚度均匀的结构形成对比, 发现由于声学黑洞的存在, 大大提高了能量回收的效率.
|
| 图 41 一维声学黑洞结构中弯曲波聚集而形成高能量密度区域 |

|
| 图 42 在结构中等间距排布5个声学黑洞, 并在厚度变化区域粘贴压电换能器 |
|
| 图 43 能量回收效果的数值计算结果图 |
尽管声学黑洞在能量回收中应用前景喜人, 却仍然需要克服在实际声学黑洞结构中如截断厚度等参数对能量聚集的不利影响.与振动噪声控制的情况不同, 在能量回收中不能通过在变截面上附加阻尼层来弥补截断厚度产生的不利影响.阻尼层的引入会增大结构阻尼, 降低能量反射, 从而快速消耗集中起来的能量, 这对于减振降噪是有利的, 但对于能量回收却是不利的.对于能量回收应尽可能减小结构阻尼, 提高回收功率, 这就需要提出另外一种方法来克服截断厚度的影响.因此需要从声学黑洞结构能量聚集机理进行进一步研究, 从原理出发提高能量聚集的效果.
5.2.2 机电换能层与声学黑洞结构捐合问题由于声学黑洞结构具有宽频带的能量聚集效应, 在上一小节中所提到的研究中, 己经显示出了声学黑洞结构具有能量回收的应用潜力.多物理场相合系统情况下的声学黑洞结构能量传播特性及其参数影响规律需要进行综合研究, 以提高声学黑洞能量回收系统效率同时对结构进行优化设计, 并分析其能量转换机制.从图 44所示机电相合模型出发, 声学黑洞结构的压电回收系统由3个部分组成:声学黑洞基体结构、压电片和压电回收电路.基体是弹性波传播的主要媒介, 压电片是能量转换并形成阻抗调节的媒介, 而压电回收电路是实现改善能量回收效率的手段.声学黑洞压电能量回收系统的这三个组元相互作用, 最终形成对弹性波能量的调控和有效回收.

|
| 图 44 机电糯合模型 |
能量回收元件比如压电元件的引入, 将在系统能量方程中带来压电元件的机电转换能以及压电元件引起的动能和势能的变化(Erturk & Inman 2011).能量回收元件(尺寸、布置位置) 在一定程度上会影响声学黑洞效应, 声学黑洞结构也反过来影响能量回收效率, 两者相互相合、相互影响, 因此需要通过时频域分析方法重点探索压电元件对声学黑洞效应的影响机制, 探究不同声学黑洞参数对应变分布、机电相合系数、能量回收效率等的影响, 从而综合分析几何参数对能量回收系统性能的影响规律.在能量回收中, 回收元件以及回收电路对声学黑洞效应的形成及影响尚待研究, 功能元件的引入很可能会增大结构厚度从而减弱声学黑洞效应, 这些都是需要充分考虑和解决的问题.
在综合考虑声学黑洞结构能量回收系统时, 也将会面临以提高能量回收效率为目标的系统优化设计问题, 如声学黑洞基体结构的优化主要是指声学黑洞的结构参数优化, 以实现更好的能量聚集效果; 通过将声学黑洞结构周期化, 形成声学黑洞周期结构阵列, 可以使其同时具备声学黑洞效应和周期性结构的特性和优点; 借鉴周期结构中压电分流技术(Spadoni et al. 2009, Wang et al. 2011) 实现有效作用频带范围的选择, 通过周期性回收电路产生局域共振带隙并与声学黑洞效应形成相合, 从而合并为一个宽频带隙等.通过借鉴现有的周期性结构能量回收技术, 结合声学黑洞自身的结构特点, 进而揭示其带隙特性和形成机制, 并分析电路参数对带隙及声学黑洞效应和能量回收效率的影响规律, 以达到提高能量回收效率的目的.
声学黑洞在能量回收应用中初露锋芒, 通过进一步的优化设计, 必定能在能量回收中获得成功的应用.目前对声学黑洞结构能量回收的研究中, 回收元件以及回收电路对声学黑洞效应的形成及影响机制仍不明朗.在将声学黑洞结构运用于能量回收的实践中时, 首要任务仍然是要研究其能量聚集与转化的机理, 进而通过声学黑洞结构与能量回收系统的综合设计, 合理选择声学黑洞有效作用频带, 最终有实现高效宽频的能量回收.
6 总结及展望声学黑洞为结构中波的操控提供了一种全新的途径, 现有的研究成果表明, 声学黑洞结构具有重要的研究价值和潜在的应用前景.声学黑洞的研究近年来成为热点, 受到学者们的广泛关注.就声学黑洞结构的分析方法而言, 针对较为简单的一维声学黑洞结构建立了理论分析方法, 包括几何声学方法、基于欧拉伯努利梁的阻抗分析方法以及半解析方法, 这些方法分别有各自的优势同时也受到相应的假设条件的约束.对于稍微复杂的二维声学黑洞结构, 几何声学分析可以用来分析黑洞中波的传播路径, 针对圆形二维声学黑洞结构还可以通过近似解析方法进行振动固有频率及响应分析.然而对于更为复杂的二维声学黑洞结构, 比如含有缺陷的二维声学黑洞内嵌于矩形板中, 或者是多个声学黑洞排布在结构中时, 则需要通过借助有限元数值计算以及实验手段作为理论分析的补充.在目前的实验和有限元仿真分析中, 大多数研究从频域上分析了声学黑洞效应, 包括频域上的声学黑洞结构反射特性、振动传递特性、声辐射特性以及结构参数和附加阻尼材料的影响等.随着测试技术的进步, 结构中波传播过程的可视化成为可能, 从时域上研究声学黑洞中波的传播与聚集的工作也逐步增大.
综观现有文献中己经取得的研究成果, 可以确认声学黑洞结构具备实现波操控的可行性.声学黑洞结构通过自身结构的剪裁可以实现宽频能量聚集效应, 且通过少量的阻尼材料即可大大提高振动抑制效果.因能量的聚集会在结构中形成高能量密度区域, 结合压电换能器可以很好提高能量回收的效率.目前, 己经有学者开始将声学黑洞结构应用到实践中, 尝试探索如何让声学黑洞在实践中发挥其优异的波操纵能力.总而言之, 声学黑洞结构具有广泛的应用前景.
另一方面, 声学黑洞是一个相对较新的研究方向, 针对其基础理论以及工程应用仍然需要开展深入广泛的研究.需要重点关注的问题包括:
其一, 需要进一步建立研究声学黑洞结构中波传播与操控问题的理论和实验分析方法, 重点探索黑洞现象的特征行为, 波传播演变过程和声学黑洞结构中局部非线性对波传播产生影响, 着重关注声学黑洞中的声振相合问题以及与功能材料的相合问题的建模分析方法.
其二, 针对工程应用中可实现的声学黑洞的结构形式, 探讨非理想声学黑洞的几
何参数以及加工精度对声学黑洞效应的影响规律, 研究附加材料对声学黑洞中波操纵特性的影响规律, 研究多物理场相合情况下声学黑洞结构的能量聚集效应以及声学黑洞的声辐射机制.
其三, 拓展声学黑洞结构在减振降噪、能量回收等工程领域中的应用, 针对特定的应用目标发展声学黑洞结构的优化设计方法, 如提高振动抑制效果、增强能量聚集效率、拓宽有效作用频率的范围等.
| 阚君武, 唐可洪, 王淑云, 杨志刚, 贾杰, 曾平. 2008. 压电悬臂梁发电装置的建模与仿真分析. 光学精密工程, 16 :71. ( Kan J W, Tang K H, Wang S Y, Yang Z G, Jia J, Zeng P. 2008. Modeling and siulation of piezoelectric cantilever generators. Optics and Precision Engineering, 16:71. ) |
| 赵娟, 刘伟群, 刘永斌, 冯志华. 2010. 压电等应变梁能量回收装置研究. 压电与声光, 32 :406–409. ( Zhao J, Liu W Q, Liu Y B, Feng Z H. 2010. Research on uniform-stain piezoelectric energy harvesting mechanicsm. Piezoelectrics & Acoustooptics, 32:406–409. ) |
| Bailey C D. 1978. Direct analytical solutions to non-uniform beam problems. Journal of Sound and Vibration, 56:501–507. doi:10.1016/0022-460X(78)90292-4 |
| Bayod J J. 2011. Experimental study of vibration damping in a modifled elastic wedge of power-law proflle. Journal of Vibration and Acoustics, 133:061003. doi:10.1115/1.4003591 |
| Bowyer E P, Krylov V V. 2012. Sound radiation of rectangular plates containing tapered indentations of power-law proflle//Proceedings of Meetings on Acoustics. Kansas City, Missouri, Acoustical Society of America through the American Institute of Physics, 18: 030002-030002. |
| Bowyer E P, Krylov V V. 2014a. Damping of flexural vibrations in turbofan blades using the acoustic black hole efiect. Applied Acoustics, 76:359–365. doi:10.1016/j.apacoust.2013.09.009 |
| Bowyer E P, Krylov V V. 2014b. Experimental investigation of damping flexural vibrations in glass flbre composite plates containing one-and two-dimensional acoustic black holes. Composite Structures, 107:406–415. doi:10.1016/j.compstruct.2013.08.011 |
| Bowyer E P, Krylov V V. 2015a. Experimental study of sound radiation by plates containing circular indentations of power-law proflle. Applied Acoustics, 88:30–37. doi:10.1016/j.apacoust.2014.07.014 |
| Bowyer E P, Krylov V V. 2015b. A review of experimental investigations into the acoustic black hole efiect and its applications for reduction of flexural vibrations and structure-borne sound. |
| Bowyer E P, Krylov V V, O'Boy D J. 2012a. Damping of flexural vibrations in rectangular plates by slots of power-law froflle//Proceedings of the Acoustics 2012 Nantes Conference. Nantes, France: 2187-2192. |
| Bowyer E P, Krylov V V, O'Boy D J. 2012b. Damping of flexural vibrations in rectangular plates by slots of power-law proflle//Acoustics 2012. |
| Bowyer E P, Lister J, Krylov V V, O'Boy D J. 2012. Experimental study of damping flexural vibrations in tapered turbofan blades//Acoustics 2012. |
| Bowyer E P, Nash P, Krylov V V. 2013. Damping of flexural vibrations in glass flbre composite plates and honeycomb sandwich panels containing indentations of power-law proflle. Acoustical Society of America, 18:030004. |
| Bowyer E P, O'Boy D J, Krylov V V. 2012. Damping of flexural vibrations in composite plates and panels containing one-and two-dimensional acoustic black holes//Acoustics 2012. |
| Bowyer E P, O'Boy D J, Krylov V V, Gautier F. 2010. Experimental investigation of damping flexural vibrations using two-dimensional acoustic "black holes"//Proceedings of the International Conference on Noise and Vibration Engineering, Leuven, Belgium, 1181-1192. |
| Bowyer E P, O'Boy D J, Krylov V V, Gautier F. 2013. Experimental investigation of damping flexural vibrations in plates containing tapered indentations of power-law proflle. Applied Acoustics, 74:553–560. doi:10.1016/j.apacoust.2012.10.004 |
| Bowyer E P, O'Boy D J, Krylov V V, Horner J L. 2012. Efiect of geometrical and material imperfections on damping flexural vibrations in plates with attached wedges of power law proflle. Applied Acoustics, 73:514–523. doi:10.1016/j.apacoust.2011.12.010 |
| Cheng L. 1996. Vibroacoustic modeling of mechanically coupled structures: Artiflcial spring technique applied to light and heavy mediums. Shock and Vibration, 3:193–200. doi:10.1155/1996/343429 |
| Cheng L, Lapointe R. 1995. Vibration attenuation of panel structures by optimally shaped viscoelastic coating with added weight considerations. Thin-walled structures, 21:307–326. doi:10.1016/0263-8231(95)93617-U |
| Climente A, Torrent D, Sáanchez-Dehesa J. 2014. Gradient index lenses for flexural waves based on thickness variations. Applied Physics Letters, 105:064101. doi:10.1063/1.4893153 |
| Climente A, Torrent D, Sáanchez-Dehesa J. 2013. Omnidirectional broadband insulating device for flexural waves in thin plates. Journal of Applied Physics, 114:214903. doi:10.1063/1.4839375 |
| Conlon S C, Fahnline J B, Semperlotti F, Feurtado P A. 2014. Enhancing the low frequency vibration reduction performance of plates with embedded acoustic black holes. Inter-noise and Noise-con Congress and Conference Proceedings InterNoise14, Australia, 175 . |
| Conlon S C, Fahnline J B, Semperlotti F. 2015a. Numerical analysis of the vibroacoustic properties of plates with embedded grids of acoustic black holes. J Acoust Soc Am, 137:447–457. doi:10.1121/1.4904501 |
| Conlon S C, Fahnline J B, Shepherd M R, Feurtado P A. 2015b. Vibration control using grids of Acoustic Black Holes: How many is enough. |
| Conway H. 1958. Some special solutions for the flexural vibration of discs of varying thickness. Archive of Applied Mechanics, 26:408–410. |
| Cottone F, Gammaitoni L, Vocca H, Ferrari M, Ferrari V. 2012. Piezoelectric buckled beams for random vibration energy harvesting. Smart materials and structures, 21:035021. doi:10.1088/0964-1726/21/3/035021 |
| Denis V, Gautier F, Pelat A, Poittevin J. 2015. Measurement and modelling of the reflection coe-cient of an Acoustic Black Hole termination. Journal of Sound and Vibration, 349:67–79. doi:10.1016/j.jsv.2015.03.043 |
| Denis V, Pelat A, Gautier F, Elie B. 2014. Modal Overlap Factor of a beam with an acoustic black hole termination. Journal of Sound and Vibration, 333:2475–2488. doi:10.1016/j.jsv.2014.02.005 |
| Dubois M, Farhat M, Bossy E, Enoch S, Guenneau S, Sebbah P. 2013. Flat lens for pulse focusing of elastic waves in thin plates. Applied Physics Letters, 103:071915. doi:10.1063/1.4818716 |
| El-Ouahabi A A, Krylov V V, O'Boy D J. 2015. Investigation of the acoustic black hole termination for sound waves propagating in cylindrical waveguides//Inter-noise and Noise-con Congress and Conference Proceedings, Institute of Noise Control Engineering. |
| Elishakofi I. 2000. Axisymmetric vibration of inhomogeneous clamped circular plates: an unusual closedform solution. Journal of Sound and Vibration, 233:723–734. doi:10.1006/jsvi.1999.2825 |
| Erturk A, Inman D. 2011a. Broadband piezoelectric power generation on high-energy orbits of the bistable Du-ng oscillator with electromechanical coupling. Journal of Sound and Vibration, 330:2339–2353. doi:10.1016/j.jsv.2010.11.018 |
| Erturk A, Inman D J. 2011b. Piezoelectric Energy Harvesting. John Wiley & Sons . |
| Fíelix S, Pagneux V. 2002. Multimodal analysis of acoustic propagation in three-dimensional bends. Wave Motion, 36:157–168. doi:10.1016/S0165-2125(02)00009-4 |
| Fang N, Xi D, Xu J, Ambati M, Srituravanich W, Sun C, Zhang X. 2006. Ultrasonic metamaterials with negative modulus. Nature materials, 5:452–456. doi:10.1038/nmat1644 |
| Foucaud S, Michon G, Gourinat Y, Pelat A, Gautier F. 2012. Immersed acoustic black hole as a travelling wave absorber: understanding artiflcial cochlear mechanics//Acoustics 2012. |
| Gang W, Li H S, Yao Z L, Ji H W. 2006. Accurate evaluation of lowest band gaps in ternary locally resonant phononic crystals. Chinese Physics, 15:1843. doi:10.1088/1009-1963/15/8/036 |
| Gautier F, Moulet M H, Pascal J C. 2006. Reflection, transmission and coupling of longitudinal and flexural waves at beam junctions. Part Ⅰ: measurement methods. Acta Acustica United with Acustica, 92:982–997. |
| Georgiev V, Cuenca J, Bermudez M M, Gautier F, Simon L. 2010. Recent progress in vibration reduction using Acoustic Black Hole efiect//10ème Congrès Françcais d'Acoustique. |
| Georgiev V B, Cuenca J, Gautier F, Simon L, Krylov V V. 2011. Damping of structural vibrations in beams and elliptical plates using the acoustic black hole efiect. Journal of Sound and Vibration, 330:2497–2508. doi:10.1016/j.jsv.2010.12.001 |
| Georgiev V B, Cuenca J, Moleron Bermudez M, Gautier F, Simon L, Krylov V V. 2009. Numerical and experimental investigation of the acoustic black hole efiect for vibration damping in beams and elliptical plates//Euronoise 2009, Edinburgh, Scotland. |
| Hou T, Qin H. 2012. Continuous and discrete Mexican hat wavelet transforms on manifolds. Graphical Models, 74:221–232. doi:10.1016/j.gmod.2012.04.010 |
| Huang W, Ji H, Qiu J, Cheng L. 2016. Wave energy focalization in a plate with imperfect two-dimensional acoustic black hole indentation. Journal of Vibration and Acoustics, 138:061004. doi:10.1115/1.4034080 |
| Jain R. 1972. Vibrations of circular plates of variable thickness under an inplane force. Journal of Sound and Vibration, 23:407–414. doi:10.1016/0022-460X(72)90499-3 |
| Jia X, Du Y, Zhao K. 2015. Vibration control of variable thickness plates with embedded acoustic black holes and dynamic vibration absorbers//ASME 2015 Noise Control and Acoustics Division Conference at InterNoise 2015, American Society of Mechanical Engineers. |
| Kobayashi H, Sonoda K. 1991. Vibration and buckling of tapered rectangular plates with two opposite edges simply supported and the other two edges elastically restrained against rotation. Journal of Sound and Vibration, 146:323–337. doi:10.1016/0022-460X(91)90766-D |
| Kralovic V, Bowyer E P, Krylov V V, O'Boy D J. 2009. Experimental study on damping of flexural waves in rectangular plates by means of one-dimensional acoustic "Black Holes"//14th International Acoustic Conference. |
| Kralovic V, Krylov V V. 2007. Damping of flexural vibrations in tapered rods of power-law proflle: Experimental studies. Proceeding of the Institute of Acoustics, 29:66–73. |
| Kravchun P.1991. Generation and Methods of Reduction of Noise and Vibration. Moscow: Moscow University Press . |
| Krvlov V V. 1990a. Localized acoustic modes of a quadratic solid wedge. Physies Billelin, 45:65–69. |
| Krylov V V. 1989. Conditions for validity of the geometrical-acoustics approximation in application to waves in an acute-angle solid wedge. Soviet Physics -Acoustics, 35:176–180. |
| Krylov V V. 1990b. Geometrical-acoustics approach to the description of localized vibrational modes of an elastic solid wedge. Sovjet Physics-Technical Physics, 25:137–140. |
| Krylov V V. 1995. Surface properties of solids and surface acoustic waves: Application to chemical sensors and layer characterization. Applied Physics A, 61:229–236. doi:10.1007/BF01538187 |
| Krylov V V. 1997. On the velocities of localized vibration modes in immersed solid wedges. Journal of Acoustical Society of America, 103:767. |
| Krylov V V. 1998. On the velocities of localized vibration modes in immersed solid wedges. The Journal of the Acoustical Society of America, 103:767–770. doi:10.1121/1.421240 |
| Krylov V V. 2004. New type of vibration dampers utilising the efiect of acoustic black holes". Acta Acustica united with Acustica, 90:830–837. |
| Krylov V V. 2007. Propagation of plate bending waves in the vicinity of one-and two-dimensional acoustic black hole//Proceedings of the ECCOMAS International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering (COMPDYN 2007). Rethymno, Crete, Greece: CD-ROM. |
| Krylov V V. 2014. Acoustic black holes: Recent developments in the theory and applications. IEEE transactions on ultrasonics, ferroelectrics, and frequency control, 61:1296–1306. doi:10.1109/TUFFC.2014.3036 |
| Krylov V V, Shuvalov A. 2000. Propagation of localised flexural vibrations along plate edges described by a power law. Proceedings of the Institute of Acoustics, 22:263–270. |
| Krylov V V, Tilman F J B S. 2004. Acoustic "black holes" for flexural waves as efiective vibration dampers. Journal of Sound and Vibration, 274:605–619. doi:10.1016/j.jsv.2003.05.010 |
| Krylov V V, Winward E. 2005. Experimental evidence of the acoustic black hole efiect for flexural waves in tapered plates//Proceedings of the 12th International Congress on Suond and Vibration, Lisbon, Portugal. |
| Krylov V V, Winward R E T B. 2007. Experimental investigation of the acoustic black hole efiect for flexural waves in tapered plates. Journal of Sound and Vibration, 300:43–49. doi:10.1016/j.jsv.2006.07.035 |
| Liu H, Lee C, Kobayashi T, Tay C J, Quan C. 2012. Investigation of a MEMS piezoelectric energy harvester system with a frequency-widened-bandwidth mechanism introduced by mechanical stoppers. Smart Materials and Structures, 21:035005. doi:10.1088/0964-1726/21/3/035005 |
| Liu Z, Chan C, Sheng P. 2005. Analytic model of phononic crystals with local resonances. Physical Review B, 71:014103. doi:10.1103/PhysRevB.71.014103 |
| Liu Z, Zhang X, Mao Y, Zhu Y, Yang Z, Chan C, Sheng P. 2000. Locally resonant sonic materials. Science, 289:1734–1736. doi:10.1126/science.289.5485.1734 |
| Lomonosov A M, Yan S L, Han B, Zhang H C, Shen Z H. 2015. Orbital-type trapping of elastic Lamb waves. Ultrasonics, 64:58–67. |
| Mironov M. 1988. Propagation of a flexural wave in a plate whose thickness decreases smoothly to zero in a flnite interval. Amer Inst Physics Circulation Fulflllment Div, 500 Sunnyside Blvd, Woodbury, NY 11797-2999. 34: 318-319. |
| Mironov M, Pislyakov V. 2002. One-dimensional acoustic waves in retarding structures with propagation velocity tending to zero. Acoustical Physics, 48:347–352. doi:10.1134/1.1478121 |
| Narimanov E E, Kildishev A V. 2009. Optical black hole: Broadband omnidirectional light absorber. Applied Physics Letters, 95:041106. doi:10.1063/1.3184594 |
| Neu J, Krolla B, Paul O, Reinhard B, Beigang R, Rahm M. 2010. Metamaterial-based gradient index lens with strong focusing in the THz frequency range. Optics express, 18:27748–27757. doi:10.1364/OE.18.027748 |
| Ng S, Araar Y. 1989. Free vibration and buckling analysis of clamped rectangular plates of variable thickness by the Galerkin method. Journal of sound and vibration, 135:263–274. doi:10.1016/0022-460X(89)90725-6 |
| O'Boy D, Bowyer E P, Krylov V V. 2010. Damping of flexural vibrations in thin plates using one and two dimensional acoustic black hole efiect//10th International Conference on Recent Advances in Structural Dynamics, Southampton, UK, 12-14 July. |
| O'Boy D J, Krylov V V. 2011. Damping of flexural vibrations in circular plates with tapered central holes. Journal of Sound and Vibration, 330:2220–2236. doi:10.1016/j.jsv.2010.11.017 |
| O'Boy D J, Krylov V V, Kralovic V. 2010. Damping of flexural vibrations in rectangular plates using the acoustic black hole efiect. Journal of Sound and Vibration, 329:4672–4688. doi:10.1016/j.jsv.2010.05.019 |
| Pekeris C. 1946. Theory of propagation of sound in a half-space of variable sound velocity under conditions of formation of a shadow zone. The Journal of the Acoustical Society of America, 18:295–315. doi:10.1121/1.1916366 |
| Peng S Z, Pan J. 2004. Acoustical wave propagator for time-domain flexural waves in thin plates. The Journal of the Acoustical Society of America, 115:467. doi:10.1121/1.1639905 |
| Qiu J, Tan J Y, Liu L H, Hsu P f. 2011. Infrared radiative properties of two-dimensional square optical black holes. Journal of Quantitative Spectroscopy and Radiative Transfer, 112:2584–2591. doi:10.1016/j.jqsrt.2011.08.002 |
| Ross, D, Ungar E E, Kerwin E M Jr. 1960. Damping of Plate Flexural Vibrations by Means of Viscoelastic Laminae. Ruzicka, J.E. ed. Structural Damping, Oxford: Pergamon Press, 49-87. |
| Press, Oxford 1960, 49-87.Semperlotti F, Zhu H. 2015. Acoustic meta-structures based on periodic acoustic black holes. The Journal of the Acoustical Society of America, 137: 2265-2265. |
| Singh B, Saxena V. 1995. Axisymmetric vibration of a circular plate with double linear variable thickness. Journal of Sound and Vibration, 179:879–897. doi:10.1006/jsvi.1995.0059 |
| Singh B, Saxena V. 1996. Axisymmetric vibration of a circular plate with exponential thickness variation. Journal of sound and vibration, 192:35–42. doi:10.1006/jsvi.1996.0174 |
| Spadoni A, Ruzzene M, Cunefare K. 2009. Vibration and wave propagation control of plates with periodic arrays of shunted piezoelectric patches. Journal of Intelligent Material Systems and Structures, 20:979–990. doi:10.1177/1045389X08100041 |
| Taher H R D, Omidi M, Zadpoor A, Nikooyan A. 2006. Free vibration of circular and annular plates with variable thickness and difierent combinations of boundary conditions. Journal of Sound and Vibration, 296:1084–1092. doi:10.1016/j.jsv.2006.03.022 |
| Tang L, Cheng L. 2016. Loss of acoustic black hole efiect in a structure of flnite size. Applied Physics Letters, 109:014102. doi:10.1063/1.4955127 |
| Tang L, Yang Y, Soh C K. 2013. Broadband Vibration Energy Harvesting Techniques. Advances in Energy Harvesting Methods, Springer: 17-61. |
| Tang L, Zhang S, Ji H, Cheng L, Qiu J. 2016. Characterization of acoustic black hole efiect using a 1-D fully-coupled and wavelet-decomposed semi-analytical model. Journal of Sound and Vibration, 374:172–184. doi:10.1016/j.jsv.2016.03.031 |
| Torrent D, Pennec Y, Djafari-Rouhani B. 2014. Omnidirectional refractive devices for flexural waves based on graded phononic crystals. Journal of Applied Physics, 116:224902. doi:10.1063/1.4903972 |
| Torrent D, Sáanchez-Dehesa J. 2007. Acoustic metamaterials for new two-dimensional sonic devices. New journal of physics, 9:323. doi:10.1088/1367-2630/9/9/323 |
| Vocca H, Neri I, Travasso F, Gammaitoni L. 2012. Kinetic energy harvesting with bistable oscillators. Applied Energy, 97:771–776. doi:10.1016/j.apenergy.2011.12.087 |
| Wang G, Wang J, Chen S, Wen J. 2011. Vibration attenuations induced by periodic arrays of piezoelectric patches connected by enhanced resonant shunting circuits. Smart Materials and Structures, 20:125019. doi:10.1088/0964-1726/20/12/125019 |
| Wang H, Chen L. 2011. A cylindrical optical black hole using graded index photonic crystals. Journal of Applied Physics, 109:103104. doi:10.1063/1.3590336 |
| Wang X, Yang J, Xiao J. 1995. On free vibration analysis of circular annular plates with non-uniform thickness by the difierential quadrature method. Journal of Sound and Vibration, 184:547–551. doi:10.1006/jsvi.1995.0332 |
| Wang Z, Norris A. 1995. Waves in cylindrical shells with circumferential submembers: a matrix approach. Journal of Sound and Vibration, 181:457–484. doi:10.1006/jsvi.1995.0152 |
| Wu X M, Lin J H, Kato S, Zhang K, Ren T, Liu L T. 2008. A frequency adjustable vibration energy harvester. Proceedings of PowerMEMS :245–248. |
| Wu Y, Qiu J, Chao Z, Zhu K, Ji H. 2014. A Method to Improve the Visibility of the Damage-Reflected Wave. Chinese Journal of Lasers, 41:0308001–0308020. |
| Xiao Y, Wen J, Wen X. 2012. Longitudinal wave band gaps in metamaterial-based elastic rods containing multi-degree-of-freedom resonators. New Journal of Physics, 14:033042. doi:10.1088/1367-2630/14/3/033042 |
| Yan S, Lomonosov A M, Shen Z. 2016. Numerical and experimental study of Lamb wave propagation in a two-dimensional acoustic black hole. Journal of Applied Physics, 119:214902. doi:10.1063/1.4953221 |
| Yang J. 1993. The vibration of a circular plate with varying thickness. Journal of Sound and Vibration, 165:178–184. doi:10.1006/jsvi.1993.1251 |
| Yu D, Liu Y, Wang G, Zhao H, Qiu J. 2006. Flexural vibration band gaps in Timoshenko beams with locally resonant structures. Journal of Applied Physics, 100:124901. doi:10.1063/1.2400803 |
| Zhang C, Qiu J, Ji H. 2014. Laser ultrasonic imaging for impact damage visualization in composite structure//EWSHM-7th European Workshop on Structural Health Monitoring. |
| Zhang S, Yin L, Fang N. 2009. Focusing ultrasound with an acoustic metamaterial network. Phys Rev Lett, 102:194301. doi:10.1103/PhysRevLett.102.194301 |
| Zhao L, Conlon S, Semperlotti F. 2015. Experimental veriflcation of energy harvesting performance in plate-like structures with embedded acoustic black holes//INTER-NOISE and NOISE-CON Congress and Conference Proceedings, Institute of Noise Control Engineering. |
| Zhao L, Conlon S C, Semperlotti F. 2014. Broadband energy harvesting using acoustic black hole structural tailoring. Smart Materials and Structures, 23:065021. doi:10.1088/0964-1726/23/6/065021 |
| Zhu H, Semperlotti F. 2015. Phononic thin plates with embedded acoustic black holes. Physical Review B, 91:39–43. |



