微纳米量级的液滴、颗粒和胶囊在科学研究和工程实践中具有重要的应用价值, 特别是在医学、药学、材料科学、化学、食品、农业等诸多领域中, 往往需要将一种或多种物质包裹在另一种物质内, 形成具有壳核结构的微纳胶囊.内核材料可以是气体、液体或固体, 被外壳材料覆盖之后, 既能改变内核材料的结构特征, 又能提供更多的功能特征.例如, 在医学和药学中, 将药物或造影剂封装到不同囊材的微纳胶囊中能够满足各种临床需求, 包括提高药物的利用度(Zhang et al. 2015, Zhu et al. 2015, Wang et al. 2015)、控制药物的缓慢释放(Freiberg & Zhu 2004, Yuan et al. 2015)、靶向输运药物(Kumar 2000, Zhao 2013)、可控激发和释放药物与造影剂(Agnihotri et al. 2004, Xu et al. 2010, Sheeran & Dayton 2012)、固化和储存液体药物(Yow & Routh 2006, Xiao et al. 2011)、防止药物在胃内反应和失活(Graham et al. 1990)等.在食品工业中, 微纳胶囊亦被广泛使用以达到保护敏感原辅料、掩盖不良味道、将液体食品固化等目的(Gaonkar et al. 2014).在农业中, 将农药溶液雾化成微液滴能够节省农药用量并使农药覆盖更为均匀(Law 2001, Laryea & No 2003), 而将农药包裹在微纳胶囊中则可以减缓农药的氧化与光解, 提高农药的缓释效果, 并降低环境污染(Kong et al. 2009, Gu et al. 2010).此外, 微纳米量级的液滴、颗粒和胶囊对增材制造、组织工程、再生医学等国际重大需求及其涉及的新兴交叉学科领域也是至关重要的.
在实际应用中, 各种材料拥有不同的物理和化学性质, 难点在于将不同尺度的物质变成微纳米量级的形态, 并且可以控制和调节其形貌、尺寸、结构、分散性甚至功能.这是一个复杂的系统性工程, 涉及了材料学、化学、生物学、医学、力学等多种学科.目前的制备技术可以分为自下而上(bottom-up)和自上而下(top-down)两类.利用原子或分子自组装原理提出的化学或物理化学方法属于自下而上的制备技术, 主要是通过原子力、范德华力或者毛细力使微观尺度的物质形成具有一定功能形状或结构的产物.相对应地, 自上而下的制备技术主要涉及物理方法, 也就是将一个宏观尺度的物质材料离散成微纳米量级的细小产物(Gañán-Calvo et al. 2013).在这一过程中, 材料的初始状态一般是液体, 其表面张力扮演了重要的角色, 强烈抵抗物质比表面积的增大, 往往使制备的产物具有球形形状(Barrero & Loscertales 2007).这样带来的好处是, 制备的产物不仅在固定体积下拥有最小比表面积, 而且具有绝对的可重复性.为了制备出小尺度的液滴、颗粒或胶囊, 必须通过一定的外力作用将能量合理地提供给液体界面以克服表面张力.
乳化法是目前最常用的自上而下的方法, 它通过外力场做功(机械、超声或高压搅拌)破坏两种互不相溶液体之间的界面, 形成微纳米量级的产物(Xu et al. 2009, Chang et al. 2016).此类方法工艺简单, 生产率高, 但是由于外力场的不均匀性, 其制备的液滴一般是多分散性的, 而且乳化参数与物质的物理化学性质密切相关.另一类新型的自上而下的方法是基于纯粹的物理机制, 外力场平稳地拉伸液体界面到一定微小尺度, 界面由于毛细不稳定性自发地破碎成需要的产物, 因此这类流动也被称为毛细流动.这种方法涉及到微尺度孔隙出流、流体动力聚焦驱动的微流动以及电场力驱动的微纳流动等, 相关的研究进展已经刊登在Annual Reviews of Fluid Mechanics上(Barrero & Loscertales 2007).在这类方法中, 表面张力和其他作用力几乎在同一个量级, 制备的微纳液滴、颗粒和胶囊通常具有很好的单分散性, 而且其结构和尺寸可以精确控制和调节.
值得一提的是, 在制备单一结构的液滴或颗粒时, 毛细流动方法只需要提供一个界面来分开两种流体, 而为了制备复合结构的微纳胶囊, 就需要提供两个或多个界面来分开三层或更多层的流体.形成的流体界面一般呈圆柱形, 与球形类似, 也属于非常基础且绝对可重复的形态.然而, 这种形态只能维持在流体的上游, 随着流体向下游运动, 界面上的扰动将不断增长并最终截断流体界面, 形成离散化的小尺度产物.这种圆柱形的流体界面就是所谓的“射流”, 在自然界和工程实际中十分常见.这里我们所关注的研究对象是微小尺度的细射流, 不考虑大尺度的水力湍动射流和气体紊动射流问题.一层界面的单轴射流问题已经有许多年的研究历史, 产生了不同的制备技术和方法, 得到了学术界的广泛重视.国际著名期刊Reports on Progress in Physics上以“液体射流物理” (physics of liquid jets)为题的重要综述论文细致分析了不同尺度下单轴射流的物理现象和规律, 深刻揭示了射流形成和破碎的内在机制(Eggers & Villermaux 2008).为了得到壳核结构的微胶囊, 最简单的液体射流形态是两层界面分开三层流体, 两个界面的同轴拉伸使外层流体包裹内层流体同向运动形成同轴射流.当射流表面扰动增长并最终促使射流破碎时, 理论上具有100%的包裹效率.
同轴射流的产生方法一般是从相应的单轴方法中延伸而来的, 但是同轴射流多了一层界面, 问题更加复杂. 图 1显示了几种常见的同轴射流生成方法, 包括液体射流流出液面(Hertz & Hermanrud 1983)、同轴电雾化(Loscertales et al. 2002)、同轴流动聚焦(Gañán-Calvo et al. 2007)以及毛细管微流控器件(Utada et al. 2005)等, 其中同轴电雾化和同轴流动聚焦具有类似的流动现象和物理机理.电雾化技术的原理是:将具有一定电导率的液体通入金属毛细管, 同时在毛细管和电极板间施加直流电压, 毛细管出口处的流体在一定流量和电压下形成稳定的Taylor锥, 锥的顶端发出细射流并破碎成细小的带电雾滴(陈效鹏2003, 李芳2007).流动聚焦是一种新型的微细射流产生技术, 其原理为:从毛细管流出的流体由另一种高速运动的流体驱动, 经小孔聚焦后形成稳定的锥形, 在锥的顶端产生一股微射流穿过小孔, 射流因不稳定性破碎成单分散的液滴(司廷2009).该技术稳定、易操作、没有苛刻的环境条件的要求, 形成的液体射流直径要远小于毛细管和小孔的直径.流动聚焦技术的主要驱动力是流体惯性力, 制备的产物尺寸一般局限于微米量级; 而在电雾化中电场力是主要驱动力, 得到的射流直径可以达到纳米量级.如果用同轴毛细管代替单个毛细管, 将两种液体分别通入内管和两管间的间隙, 可产生同轴射流, 这就形成了同轴电雾化和同轴流动聚焦技术.

|
| 图 1 同轴射流生成方法的例子. (a)液体射流流出液面(Hertz & Hermanrud 1983), (b)同轴电雾化(Loscertales et al. 2002), (c)同轴流动聚焦(Gañán-Calvo et al. 2007), (d)毛细管微流控流动(Utada et al. 2005) |
电雾化现象最早在1745年被Bose发现, Rayleigh (1882)首先开展了与静电喷雾过程有关的理论研究, 之后出现了锥-射流模式的实验研究(Zeleny 1914, 1915).由于电雾化技术在质谱仪、薄膜、纳米材料、喷墨打印、燃料雾化、医药等领域的广泛应用, 人们逐渐关注Taylor锥、锥-射流转变、尺度律、射流的破碎机理、带电液滴的尺度分布、喷洒模式等基础科学问题, 相关的综述论文也层出不穷(Bailey 1988, Michelson 1990, 陈效鹏等2003, Fernández de la Mora 2007, 尹协振和李芳2009).同轴电雾化技术最早在Science上被报道(Loscertales et al. 2002), 之后的十余年得到了广泛的关注, 相关的基础研究进展和应用前景参见综述论文(Zhang et al. 2012).流动聚焦技术是在1998年第一次被提出, 目前人们基于流动聚焦原理陆续发展了气体驱动液体(Gañán-Calvo 1998, Gañán-Calvo et al. 2013)、液体驱动气体(Gañán-Calvo & Gordillo 2001)以及液体驱动液体(Gañán-Calvo & Riesco-Chueca 2006)的单轴流动聚焦、复合毛细管构成的复合流动聚焦(Martín-Banderas et al. 2005; Si et al. 2015, 2016a, 2016b)、电流动聚焦(Gañán-Calvo & Riesco-Chueca 2006, Li et al. 2014)以及微流控流动聚焦(Anna et al. 2003, Utada et al. 2005, Vladisavljevi et al. 2013)等技术.电流动聚焦结合了流动聚焦和电雾化两者的优势, 能够使雾化更稳定, 可应用的参数范围更广, 制备的产物直径更小.将流动聚焦原理应用于二维微管道或玻璃毛细管拉丝技术中形成的微流控流动聚焦, 已经成为微流控技术及微流控器件的一个重要研究方向, 在多学科交叉研究领域发挥了重要作用.
在流动聚焦中, 各种过程参数影响液体射流上的界面扰动, 而扰动发展最终使射流破碎成微纳液滴.同轴射流比单轴射流多一种流体, 也多一层界面, 从而增大了一定的过程参数(Gañán-Calvo et al. 2007, 2013; Zhu et al. 2015); 随着研究的深入, 多轴流动聚焦逐渐被提出, 形成的复合射流受到更多过程参数的影响(Si et al. 2015, 2016a, 2016b).而在电流动聚焦中, 要兼顾电场力和惯性力的耦合以及电场作用与射流表面自由电荷之间的关联(Gañán-Calvo & Riesco-Chueca 2006, Li et al. 2014).这些过程参数改变复合射流的破碎模态, 构成了一个复杂的多介质界面演化问题.从不稳定性角度考虑, 各种流动现象是界面扰动传播的结果.在一定条件下不稳定模态之间相互竞争, 促使扰动的增长率发生变化, 最终增长率最大的扰动控制流场, 确定了不同流动现象的出现.
不稳定性理论主要通过数学上的扰动分析方法考察小振幅扰动在无扰动基本流上的响应(尹协远和孙德军2003).在流体力学中, 一般基于Navier-Stokes方程组并引入扰动分析方法对不稳定性问题进行描述.如果小扰动不断增长使得流场发展成另外一种状态, 流场就是不稳定的; 反之流场能够恢复到原始状态就是稳定的.不稳定性理论主要包括了时间、时空和空间三种模式:时间模式反映的是扰动幅值随时间的演化, 在空间上是周期性的; 时空模式下扰动幅值同时随时间和空间变化; 而空间模式反映的是扰动幅值随空间的演化.时间域内的不稳定性研究方法相对简单, 能够预测增长率最大的扰动的动力学行为; 而时空和空间域的理论模型更接近实际情况, 能够预测不稳定模态之间的转换.在时空模式下又存在两种性质不同的不稳定性:当扰动仅向下游或上游一个方向传播时, 使得充分长时间后扰动“逸”出了流动区域, 则称流动是对流不稳定的; 如果增长的扰动既向下游传播又向上游传播, 在充分长的时间后扰动“污染”了整个流场, 则称流动是绝对不稳定的.
自从Rayleigh (1878)开展真空中无黏液体射流破碎问题的理论研究以来, 经过一百多年的发展, 不稳定性理论已经成为研究射流破碎机理的最有利工具(Huerre & Monkewitz 1990, Yarin 1993, Lin & Reitz 1998, Lasheras & Hopfinger 2000, Lin 2003), 也已经在电雾化、流动聚焦、电流动聚焦等领域取得了一定的研究进展(李芳2007, 司廷2009, 李广滨2016).但是, 随着对实际问题研究的深入, 射流不稳定性正面临一些挑战, 其难点在于:需要采用合理的近似和假设建立物理模型, 正确处理动力学、运动学等边界条件, 以及开展复杂条件下的射流不稳定性分析.所关心的研究内容从时间域推广到了时空和空间域, 从近似的速度型发展到接近实际情况的速度型, 从均匀的轴向电场或径向电场推广到交变电场, 从牛顿流体推广到非牛顿流体等.比如在电流动聚焦中(Gañán-Calvo & Riesco-Chueca 2006, Li et al. 2014), 带电复合射流的物理模型包含了流场和电场的耦合, 涉及了流体的电学模型及表面电荷分布, 求解时需要引入简化的物理模型, 包括完全导体或绝缘体模型、Taylor-Melcher漏电介质模型等(Melcher 1963, Taylor 1964, Saville 1997, Lpez-Herrera et al. 2005).此外, 需要针对高分子材料的非牛顿流体流变性质, 引入复杂的黏弹性模型(Reneker & Yarin 2008).总之, 在实验条件下开展射流不稳定性分析, 不仅能够获得过程参数对射流界面最不稳定扰动的影响规律, 而且能够揭示不同流动模态的动力学特征及其内在机制, 为实际应用提供可靠的理论指导.
本文将对流动聚焦的研究现状进行总结, 并重点回顾流动聚焦技术涉及的关键力学问题以及射流不稳定性的研究进展.本文的结构如下:第2节介绍不同流动结构的流动聚焦技术, 包括单轴流动聚焦、电流动聚焦、复合流动聚焦和微流控流动聚焦; 第3节总结流动聚焦涉及的关键力学问题, 可概括为过程控制、流动模式、尺度律理论和不稳定性分析; 第4节回顾射流不稳定性的研究方法和已取得研究成果.最后总结本文的工作并展望流动聚焦的研究方向和应用前景.
2 流动聚焦的类别根据核心装置结构以及提供驱动力的方式不同, 流动聚焦技术主要分为以下几类.
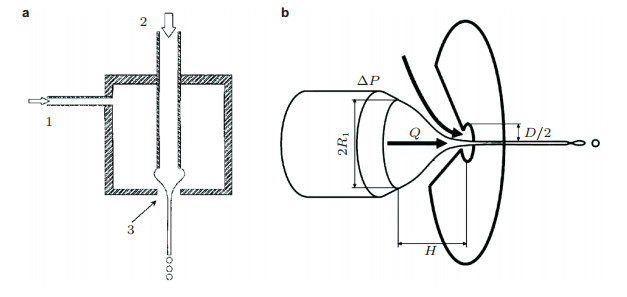
2.1 单轴流动聚焦单轴流动聚焦的核心装置如图 2(a)所示, 主要包括毛细管、腔体和小孔.小孔位于腔体的底面上, 毛细管正对小孔伸入腔体.主要几何参数包括毛细管内外径、小孔直径和毛细管出口与小孔之间的距离, 尺寸都在毫米到百微米范围(图 2(b)).根据内外流体的性质不同, 单轴流动聚焦主要涉及液-气、液-液、气-液三种界面结构, 锥形和射流的形态也最为简单, 相关的研究也最为深入.
|
| 图 2 单轴流动聚焦. (a)核心装置示意图(Martín-Banderas et al. 2005), 1-腔体(提供外部流体), 2-毛细管(输运内部流体), 3-小孔(聚焦流体), (b)流动原理示意图(Gañán-Calvo et al. 2013) |
国外Gañán-Calvo (1998)最早报道了液-气界面结构的单轴流动聚焦, 之后又进行了一系列实验、理论和数值模拟研究(Gañán-Calvo et al. 2013), 国内司廷等也开展了大量的实验和理论研究工作(司廷2009, 司廷和尹协振2011, 李广滨2016).在这种气驱流动聚焦中, 伸入到腔体内的毛细管正对腔体下壁面上的小孔, 液体从毛细管流入, 腔体内外的压力差源于气体, 于是高速流动的气流聚焦液体在毛细管口形成锥形, 锥形顶端发出微细射流并穿过小孔. 图 3(a)给出了气驱单轴流动聚焦中典型的锥-射流结构.可以看出, 锥形从宏观尺度(毫米量级, 与毛细管直径相当)减小到微观尺度(微米量级, 与液滴直径相当), 形成的液体射流直径远远小于聚焦小孔的直径.在周围高速气流作用下, 液体射流与小孔的固壁不会接触, 因此避免了装置本身对内部液体流动的干扰, 这与微流控芯片中的流体流动(李战华等2012, 林秉承2013, 陈晓东和胡国庆2015)完全不同.液体射流在周围气流的作用下破碎成液滴的频率能够达到兆赫兹(MHz)的量级(Gañán-Calvo & Barrero 1999), 表明流动聚焦技术具有很高的生产效率.已有研究表明, 在稳定的锥-射流模式下, 聚焦小孔出口处的射流直径与装置的几何参数无关, 只与液体流量、气体压力差以及流体本身的物理属性有关(Gañán-Calvo 1998, Si et al. 2009).此外, 驱动气体和被驱动液体的动能近似相等, 即ρgUg2/2=ρlUl2/2, 其中ρg, ρl分别为气体和液体的密度, Ug, Ul分别为周围气流和液体射流的平均速度.在驱动气体动能较低时, 射流直径较大, 扰动沿射流表面呈现轴对称发展, 此时获得的液滴是单分散的; 随着气体动能的增大, 液滴直径逐渐减小, 但由于非轴对称扰动的出现, 射流破碎后获得的液滴逐渐呈现出多分散性(Gañán-Calvo & Barrero 1999). 图 3(b)给出了该技术制备不同种类的均匀颗粒的微观形貌, 证明了流动聚焦技术的有效性和极强的可控性(Martín-Banderas et al. 2005, 2006).此外, Holgado等(2008)比较了流动聚焦与传统的溶剂蒸发方法在合成麻醉剂微颗粒方面的应用.在流动聚焦实验中, 药物溶解在高分子材料的溶液里, 当有机溶剂在射流破碎过程中挥发, 可以直接接收到固化的微颗粒.进一步的实验结果表明:流动聚焦制备的微颗粒有较窄的粒径分布, 而且具有较高的药物装载量和较慢的药物失效速率, 因此流动聚焦比传统的溶剂蒸发方法在制备麻醉剂微颗粒方面更有优势.

|
| 图 3 液-气界面结构的单轴流动聚焦实验结果. (a)稳定的锥-射流结构(Gañán-Calvo 1998), (b)冷冻干燥后直径约为5 μm的颗粒扫描电子显微镜图片(Martín-Banderas et al. 2005) |
在液-液界面结构的单轴流动聚焦中, 内外层流体均为液体, 一般要求两种液体不互溶, 因此能够形成清晰的流体界面.这种液驱单轴流动聚焦的实验条件相对温和, 内外层液体的流动速度在同一个量级.在最早的实验研究中, Gañán-Calvo和Riesco-Chueca (2006)采用蒸馏水为外部相, 硅油为内部相, 发现当其他条件不变时, 将内部液体较大的流量逐渐减小到能够观察射流模式向滴模式的转换, 而反过来也能够观察到滴模式向射流模式的转换, 只是存在明显的滞后效应, 也就是后者转换的临界流量值要大于前者.滞后效应与锥形的大小有关, 也就是与毛细管的直径和小孔的直径有关; 另外, 液体黏性越大, 相应的滞后效应越强, 此时细长的脉动射流容易填充成大液滴, 也有一些液滴因周围液体的阻力作用而回缩.此外, Gañán-Calvo和Riesco-Chueca (2006)根据实验建立了用于射流稳定性分析的理论模型, 假定内外流体速度相同推导出了均匀流场中解析形式的色散关系, 并采用时空稳定性分析方法获得了主要参数平面上的“绝对-对流”不稳定性转换曲线, 与实验结果吻合, 证明了实验中滴模式对应绝对不稳定性, 射流模式对应对流不稳定性. Montanero和Gañán-Calvo (2008)进一步采用非牛顿流体进行液驱流动聚焦实验, 发现液体的黏弹性性质对射流的不稳定性产生重要影响.笔者基于自行搭建的实验平台, 分别采用频闪图像采集系统和高速摄影显微系统得到了液驱流动聚焦的锥-射流结构, 并且结合数值模拟手段对实验现象进行了定量分析, 相关工作仍在开展中.数值模拟方法采用扩散界面模型跟踪界面变化, 直接数值求解流体力学控制方程, 不仅对比研究了实验中的射流模式和滴模式, 并进一步分析了滴模式中的亚模式和液滴生成的复杂动力学问题. Gañán-Calvo等(2006c)开展了流动聚焦在生物分子探测方面的应用研究, 利用流动聚焦结合溶剂蒸发和萃取过程一次到位的制备球形的缩氨酸、低聚核苷酸、蛋白质等的微颗粒, 还可以将配合基结合到微颗粒的表面上.在制备过程中, 有机溶剂溶解的油溶性试剂为内层流体, 水溶性液体为外层驱动流体, 能够形成稳定的锥-射流结构.射流破碎的液滴直接接收在装有水的烧杯中并不断搅拌, 一定时间后有机溶剂全部析出.通过改变驱动和被驱动流体的流量速度, 该方法可以制备平均直径在5~15 μm的均匀微颗粒.
2.1.3 气-液界面结构当内部流体为气体、外部流体为液体时, 能够形成气-液界面结构, 与图 3的液-气界面结构刚好反相.如图 4所示, 在一定的液体流量和气体流量下, 从毛细管流出的气体能够形成一个稳定的锥形气泡, 在毛细管口呈现圆球形, 而在小孔处快速缩小.从小孔流出的内部气流快速转化为小气泡, 在外部液体的作用下向下游运动(Gañán-Calvo 2001).小气泡直径在数十微米量级, 大小非常均匀. Gordillo等(2001a)利用绝对-对流不稳定性理论对实验中小气泡的产生进行分析, 发现绝对不稳定性控制了整个流场, 而且不稳定性源于气体与液体界面的剪切力以及表面张力的作用.由于绝对不稳定性下只能形成滴模式, 因此在这种气-液界面的流动聚焦中不存在射流模式, 也就是不能形成稳定的气柱状射流. Gañán-Calvo等(2004)利用水、甘油和添加的表面活性剂制备了直径在50~80 μm的均匀微气泡, 并收集成一定厚度的湿泡沫.由于得到的泡沫中的气泡均匀稳定, 因此在制备新轻质材料、新质地和低密度的食品等方面具有潜在应用价值.

|
| 图 4 “气-液”界面结构实验结果. (a)稳定的锥形以及小孔外液体裹挟气泡向下游运动(Gordillo et al. 2001a), (b)收集的大量气泡(Gañán-Calvo & Gordillo 2001) |
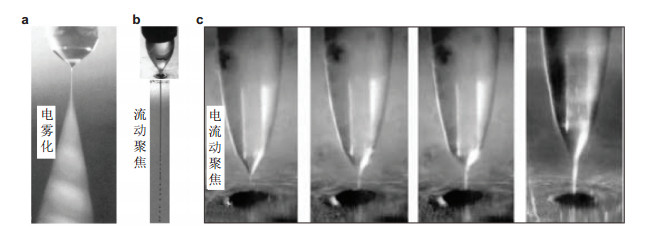
流动聚焦和电雾化都是通过外力场将液体界面拉伸成微细射流, 射流最后失稳而发生破碎.可见, 尽管提供外力场(能量)的方式有区别, 流动聚焦与电雾化的物理机理是一致的, 所形成的锥-射流结构也类似(图 5(a)和图 5(b)), 因此将电雾化和流动聚焦相结合成为了一种可行的方法(Gañán-Calvo et al. 2006b, Li et al. 2014).一种方式是以金属毛细管为正极、聚焦小孔所在的金属板为负极施加电压, 使液体表面产生电荷的同时也提供电场力作用于锥形和射流(Gañán-Calvo et al. 2006b).实验结果显示在小孔附近的锥形发生显著缩小, 锥形顶端发出的射流变细(图 5(c)), 获得的液滴直径变小.另一种方式是将电场作用到流动聚焦的同轴液-气射流区域, 司廷等(2011)在这种情况下系统研究了液体流量、气流压降和电压等主要控制参数对锥形和射流的流动模式的影响, 获得了锥振动模式和锥稳定模式的转换曲线以及射流的滴模式、轴对称模式、共存模式和非轴对称模式之间的转换曲线, 并测量了射流直径、扰动波长与破碎长度等射流尺寸参数随电压的变化趋势.实验发现:相比于单纯的流动聚焦, 电流动聚焦得到稳定锥-射流的参数范围更广, 射流雾化更为剧烈, 同时获得的液滴尺度也更小. Gañán-Calvo (2007a)通过理论分析得到了小孔出口射流直径的表达式, 与无电场作用下的流动聚焦尺度律有很大差别, 并利用时空稳定性理论推导了解析的色散关系, 得到了绝对和对流不稳定性的转换曲线, 和实验中的滴-射流模式的转换比较吻合.李广滨(2016)进一步基于电流动聚焦实验建立了简化的理论模型, 开展了带电液-气射流的无黏和黏性时间不稳定性分析, 主要研究了扰动在时间域的发展和演化情况(李广滨等2012, Li et al. 2014).必须指出, 流动聚焦中施加电场作用要考虑电场力和惯性力的耦合作用, 还要兼顾内外层流体的黏性以及非均匀流场结构的影响.理论研究的难点在于:与不带电场的同轴射流相比, 控制方程增大了一组电学方程; 与单一流体的带电射流相比, 边界条件更加复杂.由于流动聚焦的流动结构较多, 电场的施加方式也多样, 因此涉及的技术也不同, 目前这方面的研究还比较有限.电场力的作用以及表面电荷的分布给整个问题带来一定难度, 因此实验和理论研究都具有很强的挑战性.
|
| 图 5 流动聚焦和电雾化相结合形成电流动聚焦(Gañán-Calvo et al. 2006b). (a)电雾化的锥-射流结构, (b)流动聚焦的锥-射流结构, (c)不同条件下电流动聚焦的锥形 |
将单轴流动聚焦核心装置(图 2(a))中的单个毛细管替换成两个或多个毛细管的复合结构, 便形成复合流动聚焦.从核心装置的结构角度分析, 复合流动聚焦可以有多种形式:一种是不同直径的毛细管嵌套在一起, 能够直接实现外层流体包裹内层流体; 一种是相同直径的毛细管并排在一起, 实现多组分流体并列流动; 还有一种是将前两者的毛细管组合在一起, 形成复杂的多界面流动.目前复合流动聚焦的研究才刚起步, 由于其涉及了多种流体的耦合, 实验和理论研究都存在一定的难度.将两个毛细管嵌套形成的同轴流动聚焦相对简单, 在制备壳核结构的微胶囊方面已经展现出突出的优势, 包括低成本、易集成化以及较高的生产率和包裹效率等.而多轴流动聚焦利用不同结构的复合毛细管, 在制备微胶囊方面有更多选择, 具有潜在的应用价值.
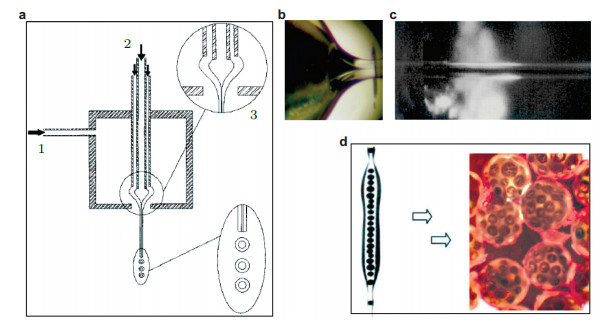
图 6(a)给出了同轴流动聚焦的核心装置(Martín-Banderas et al. 2005).通入同轴针头的外层流体一般为液体, 内层可以是气体或液体(也可以是固体颗粒的悬浮液), 驱动流体可以为气体或液体.在一定的内外层液体流量下, 从同轴针头流出的两层流体在外部驱动流体的拉伸以及小孔的聚焦作用下会在毛细管口形成稳定的同轴锥形图 6(b)), 同轴锥形顶端发出一股同轴微射流(图 6(c)), 射流破碎后可以得到具有壳-核结构的微胶囊(图 6(d)). Martín-Banderas等(2005)系统介绍了流动聚焦在制备微颗粒和微胶囊方面的应用.比较具有吸引力的方面是生物医学中的药物胶囊化, 传统的喷雾干燥方法或者乳剂挥发方法都不能轻易地控制药物颗粒和胶囊的均匀性, 往往需要进一步过滤才能实现, 而且每个微胶囊内药物颗粒的分布和形态都保持相同是很难实现的.但是利用同轴流动聚焦技术可以一步到位地制备分布均匀、形态相同的微颗粒和微胶囊.另一方面是制备荧光粒子, 因为在科研和诊断等方面, 当改变荧光素的成分、类型和大小时, 能够得到不同的荧光粒子以满足不同的需要.此外, 当外部液体流量足够大以保证外部锥形稳定, 相当于为内部流体提供了均匀的环境流场, 于是逐渐降低内部液体的流量速度, 内部液体仍能够形成细射流, 其破碎后得到的液滴能够减小到几百微米甚至更小.所以, 利用同轴流动聚焦可以实现亚微米量级液滴的制备, 能够突破单轴流动聚焦技术的最小流量速度极限(Gañán-Calvo et al. 2007). Gañán-Calvo等(2015)认为同轴流动聚焦可以用于细胞和药物的微包裹, 并开展了PLGA (聚乳酸-羟基乙酸共聚物, 是一种常用的可降解的功能高分子聚合物材料)包裹药物的实验研究. Zhu等(2015)利用液驱同轴流动聚焦制备了包裹高浓度荧光造影剂ICG (吲哚菁绿)的脂质体, 有机相逐渐挥发形成稳定磷脂双分子层, 获得了微液滴与小孔直径、内外层流量以及驱动流量之间的关系.对于包裹ICG的脂质体, 研究发现, 脂质体破碎前后的荧光差别明显, 破碎后的荧光强度与微液滴内部包裹的造影剂的浓度相关, 在靶向药物释放和医疗影像等方面具有重要的应用前景. Si等(2016a)利用气驱同轴流动聚焦技术制备了以磷脂分子为外壳、以溶有纳米银颗粒的十氟戊烷为核的可激发微胶囊, 具有较好的形貌以及单分散性.制备过程中拍摄到了边界明显的同轴锥-射流结构, 同时推导了微胶囊粒径的尺度律.此外还搭建了激光激发的实验平台, 拍摄到了微胶囊激发和破碎的典型图片, 建立了微胶囊可控激发的理论模型, 分析了主要控制参数的影响规律, 理论预测和实验结果一致, 初步证明这种微胶囊良好的定点可控激发潜力.
|
| 图 6 同轴流动聚焦. (a)同轴流动聚焦核心装置示意图(Martín-Banderas et al. 2005), 1-外层驱动流体, 2-被驱动流体, 3-同轴锥形, (b)稳定的同轴锥形(Gañán-Calvo et al. 2007), (c)同轴液体射流(Gañán-Calvo 1998), (d)同轴射流破碎图像及制备的多核胶囊微观形貌(Martín-Banderas et al. 2005) |
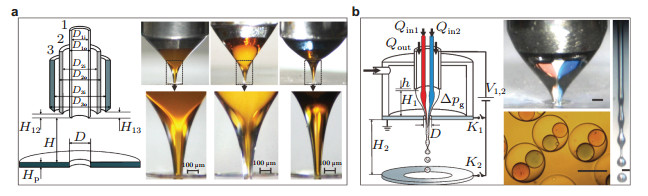
多轴流动聚焦是毛细管结构更为复杂的复合流动聚焦, 实验中通常涉及到三层或三层以上的流体界面, 实验难度较高, 目前的报道还很少. 图 7给出了两种多轴流动聚焦的例子(Si et al. 2015, 2016b).利用3个毛细管嵌套组合成三轴针头, 可以开展三轴流动聚焦实验(Si et al. 2015).为便于流场观测, 实验中使用的试剂从内到外依次为牛奶、食用油以及甘油和水的混合液, 驱动流体为空气, 得到了稳定的三轴锥形和三层结构的微胶囊, 从图 7(a)中可以清晰地分辨锥形内部两层液-液界面的微观形状.此外, 还实验研究了几何参数和外部控制参数对锥形的影响规律, 推导了内、中、外三层液体射流的直径尺度律. Si等(2016b)使用“一包二”结构的复合针头开展了复合流动聚焦实验, 并施加额外电场来提高锥形的稳定性. 图 7(b)中内层液体为不同染料染色后的石蜡油, 外层液体为海藻酸钠溶液, 得到了稳定的锥形、射流以及微胶囊, 并进一步给出了微泡直径的尺度律.所得到的多核微胶囊能够保存很长时间, 还可以通过机械振动、超声激发等外部能量来控制两个内层液滴的主动融合, 证明了该方法在药物制剂、药物输运和可控激发、微反应器等领域的重要价值.
|
| 图 7 多轴流动聚焦. (a)三轴流动聚焦的核心装置示意图及稳定的锥-射流结构(Si et al. 2015), (b) “一包二”复合电流动聚焦核心装置示意图、稳定的锥-射流结构及制备的多核胶囊微观形貌(Si et al. 2016b) |
将流动聚焦原理运用到微流控技术中已成为一个热门方向, 称之为微流控流动聚焦.微流控技术是一种在微观尺度下控制、操作和检测流体流动的技术, 是在微电子、微机械、生物工程和纳米技术等基础上发展起来的, 涉及了全新的交叉学科领域(陈晓东和胡国庆2015).微流控技术着重于构建微流体通道系统来实现各种复杂的微流体操纵功能.目前, 基于微流控技术产生的微流控器件层出不穷, 在医学、材料、药学、能源、环境等不同领域展现出广阔的应用前景, 具有低成本、低能耗、便携、快速灵活等优势(林秉承2013).根据结构的不同, 目前的微流控器件主要分两类:一类是二维微管道(microchannels), 也就是微流控芯片, 可以通过微机械加工、光刻、模具复制等方法在金属、玻璃、硅片或高聚物上进行加工得到; 另一类是玻璃微毛细管(glass microcapillaries), 可以通过对玻璃拉制成的微毛细管进行简单组装来完成.
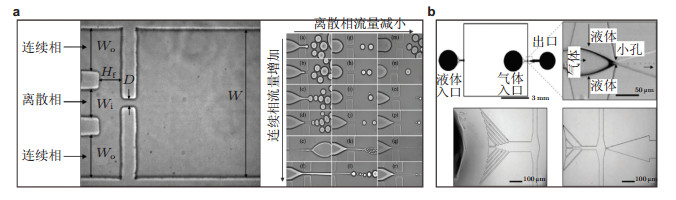
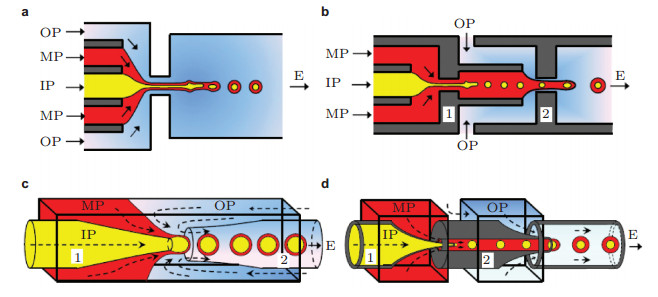
Anna等(2003)最早基于流动聚焦原理加工了二甲基硅氧烷(PDMS)微流控芯片, 如图 8(a)所示, 使用的内部流体(离散相)为水, 外部流体(连续相)为油, 主要研究了两种液体的流量与生成液滴的粒径间的关系.当射流在小孔内部破碎时(滴模式)可获得与小孔尺度相当的液滴; 当射流在小孔下游处破碎时(射流模式)可获得远小于小孔尺度的液滴.之后的几年内, 为了增强微流控技术的应用领域, 加工尺寸更小、流动更多样化的芯片成为学术界的热点. Hettiarachchi等(2007)利用PDMS微流控芯片制作出单分散率较好的超声造影剂脂质微泡, 外壳为脂质体, 内层为四氟化碳, 芯片最小尺寸为7 μm, 如图 8(b)所示, 通过优化微管道几何尺寸、液体流速和气体压强可以得到平均直径小于5 μm的微泡, 能够直接应用于超声成像. Zhu等(2016)制备了可激发脂质微泡, 实验证明了微液滴在超声和激光激发后具有超声影像增强效应.近年来, 为了得到包含两种或多种不相溶流体的乳化液, 复杂结构的微流控器件也逐渐被提出并得到迅速发展. 图 9(a)和图 9(b)给出了三相流体的流动聚焦结构, 可以是一级多组的微管道流经同一个小孔一次性包裹(Nie et al. 2005), 也可以是多级的微管道实现逐层包裹(Seo et al. 2007), 取决于芯片制作和流动控制.随着微纳加工技术的飞速发展, 越来越多的微纳尺度流动研究与生物、材料、医学、药学、工程等应用领域结合起来, 取得了突出进展.
|
| 图 8 两相流体的微流控流动聚焦. (a)油-水两相流动的二维微管道结构和不同油-水流量比下的流动模式(Anna et al. 2003), (b)气-液两相流体的二维微管道结构(Hettiarachchi et al. 2007) |
|
| 图 9 三相流体的微流控流动聚焦(Vladisavljevi et al. 2013). (a)二维微管道中的三相流动聚焦结构(Nie et al. 2005), (b)二维微管道中的两级流动聚焦结构(Seo et al. 2007), (c)玻璃微毛细管中的三相流动聚焦结构(Utada et al. 2005), (d)玻璃微毛细管中的两级流动聚焦结构(Chu et al. 2007) |
玻璃微毛细管技术是近年来发展的一种新技术, 目前已广泛用于制备各种各样的多功能微载体, 如脂质体、高聚物囊泡、光固化微球等, 在药物输送、油污去除、液体渗透压测量以及超疏水性微球制作等方面得到应用. Utada等(2005)最早利用嵌套的玻璃微毛细管制备出了壳核结构的微胶囊, 核心实验装置由两根圆管和一根方管组成, 圆管的外径与方管的内径相当, 以使圆管能固定在方管中(图 9(c)).一根圆管的端部经过拉丝处理成收缩状, 作为注入管, 另一根圆管端部有流线型的缩口, 作为收集管.当向三根玻璃微毛细管中注入不同的液体后, 三种液体将会在收集管管口处聚焦成复合锥形, 并于锥形顶端发出同轴微射流, 射流最终在下游一定距离处破碎成微胶囊.值得一提的是, 该技术常见的流动模式是滴模式, 因此制备的微液滴非常均匀, 但是也存在微液滴尺寸较大、产率低等缺陷. Chu等(2007)将玻璃微毛细管改装成两级结构, 也能够制备壳核结构的微胶囊(图 9(d)). Kim和Weitz (2011)将毛细管结构进行改进, 制备出具有不同形貌和结构的多核微液滴.与微管道中的二维流动不同, 微毛细管中的流动为轴对称的三维流动, 相对复杂一些, 但是由于玻璃耐腐蚀, 成本低廉, 与传统的微流控芯片相比, 微毛细管方法可以适用于更多的材料, 应用范围也更广.
自从20世纪90年代以来, 微流控技术得到了快速的发展, 相关的流体力学研究也逐渐深入.近年来, 国际力学界对微纳尺度流动的现象和机理极大关注, 国内外学术期刊已有系列专题评论文章和综述论文介绍微流控技术和微流控器件.其中, 陈晓东和胡国庆(2015)在《力学进展》上详细回顾了微流控器件中的多相流动现象和流体力学机理, 也总结了微流控流动聚焦的相关力学问题.下文中我们将不再关注微流控流动聚焦技术.
3 流动聚焦涉及的关键力学问题流动聚焦过程大致分为3个阶段:锥形的形成、射流的破碎以及液滴的收集.在第一阶段, 液体从毛细管中流出, 在周围流体剪切作用下加速运动, 尺度逐渐变小.锥形的失稳是一个全局不稳定性问题, 与诸多过程参数都有关联.界面能够维持稳定, 主要在于压力、表/界面张力、黏性力、惯性力、重力等在界面上达到了平衡.在第二阶段, 从锥形顶端发出的射流存在不同的流动模态, 受到过程参数的影响, 界面上扰动的发展演化也完全不同.在第三阶段, 液滴在流场中运动存在旋转、合并和碰撞等现象, 液滴下落将会与液面或固壁接触, 产生复杂的流动现象.
经过近二十年的发展, 流动聚焦的实验、理论和数值研究都取得了一定的进展.从流体力学的基础研究角度出发, 可将流动聚焦涉及的关键力学问题归纳为四个方面:过程控制、流动模式、尺度律理论、不稳定性分析.但是必须指出, 流动聚焦相关的研究仍处于初步阶段, 很多工作都有待进一步开展.此外, 现阶段的研究主要围绕牛顿流体开展, 而在各种实际应用中, 制备微纳液滴、颗粒和胶囊必须考虑高分子材料、有机试剂等特定材料的本构特性.这种情况下, 就需要考察材料特性、溶剂挥发、非线性扰动等带来的一系列新问题.
3.1 过程控制流动聚焦的实验现象与过程参数密切相关, 对制备产物的形貌、尺寸和分散性等特征也有突出影响.对于不同类型的流动聚焦, 实验涉及的过程参数一般可以总结为三类: (1)装置的几何参数, 包括毛细管的内外径、小孔的直径、毛细管口到小孔的距离、毛细管与小孔的同轴度、腔体的壁厚等; (2)外部控制参数, 比如液体流量速度、腔体内外的压力差和施加额外电场的强度等; (3)实验试剂的物理属性, 比如液体或气体的密度、黏性、电导率以及表/界面张力等.在不同参数组合下, 锥形和射流的动力学特征有很大差别, 因此, 流动聚焦的过程控制是非常关键的.
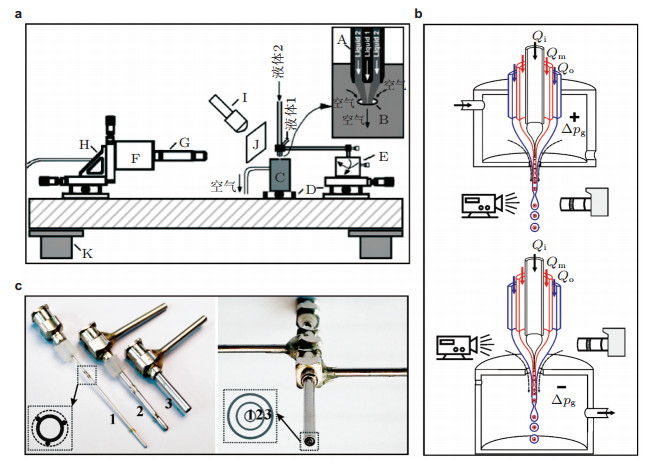
3.1.1 实验方法在流动聚焦实验中, 为了能够产生稳定的锥形和射流并对流场进行有效显示和测试, 需要搭建完善的实验系统.如图 10(a)所示, 实验平台主要包括流动生成系统和流场观测系统, 位于一个光学平台上.流动生成系统包括流动聚焦核心装置(毛细管、腔体、小孔等)、液体输送设备(微量注射泵、高压注射泵等)、气体输送设备(高压气瓶、真空泵等)、电压施加设备(高压直流电源、金属电极等)和相应的辅助设备(输液管道、鲁尔接头、精密位移台等); 流场观测系统包括显微镜头、光源(连续光源、频闪灯等)、拍摄设备(CCD、数码相机、高速摄影机等)和可能的辅助设备(精密位移台、菲涅尔透镜、毛玻璃片等).
|
| 图 10 流动聚焦的实验系统. (a)实验平台(Gañán-Calvo et al. 2011), (b)吹气式和吸气式的实验装置(Si et al. 2015), (c)复合针头的设计(Si et al. 2015) |
由于锥形和射流位于小孔所在平板两侧, 而且流动形态也有很大差别, 一般是将锥形和射流分开进行研究.为了得到清晰的流动图像, 气驱流动聚焦有两种运行方式可以采用(图 10(b)):一种是吹气式, 外部气体通过高压气瓶输送进腔体, 只能从腔体底部的小孔流出, 故在腔体内可以形成一定的正压; 另一种是吸气式, 腔体内的气体不断由真空泵抽出, 外部气体只能从腔体顶端的小孔流入内部, 可以在腔体内形成一定的负压(Vega et al. 2010, Gañán-Calvo et al. 2011, Si et al. 2015).比较而言, 在吸气式的装置中毛细管与腔体相对分离, 易于观察毛细管口形成的锥形; 而在吹气式的装置中毛细管与压力容器结为一体, 锥形位于腔体内部, 微射流位于其外部, 对于观察射流非常方便.总之, 吹气式和吸气式的装置相辅相成, 给流动聚焦实验研究提供了便利的操控条件.
单轴流动聚焦只需要采用单轴毛细管即可实现, 结构简单易加工; 复合流动聚焦需要使用多层毛细管结构, 还要使其保持较好的同轴度, 加工存在一定的困难. Si等(2015, 2016b)提供了一种简单但有效的复合针头组装技术.以三轴针头为例, 采用3个不同规格的金属针头分别作为内层、中间层和外层流体的输运管道, 针头的端部打磨平整并进行光滑处理, 避免毛刺、污染等对流场产生不必要的扰动.外针头和中间针头的侧部焊接细金属管, 用于连接流体输送设备.根据嵌套之后外针头与中间针头、中间针头与内针头的间距, 分别选取两种不锈钢丝, 使其直径分别与两种间距相等.之后利用激光焊接技术将不锈钢丝分别点焊在最内层和中间层的针头表面上.为了使3个针头同轴, 在针头的上下两处位置上分别点焊3段不锈钢丝, 且使其沿针头外表面的每一处位置均匀分布, 如图 10(c)所示.利用硅胶塞将3个针头组合在一起, 使上部密封, 于是形成简易的易于拆卸和易于调节的三轴针头, 这种结构的复合毛细管对流动聚焦实验现象没有影响, 实验效果比较理想.
第二部分是流场观测系统.由于锥形和射流尺寸较小, 常常伴随着非定常的高速运动, 比较有效的方法是在连续光源照明下用显微镜头结合高速摄影机拍摄, 能够得到一段时间序列里每一时刻的流动图像. 司廷等(2009)主要采用了一种更为简便且廉价的方法获得流场图像:用频闪灯照明, 在频闪灯和核心装置之间放置一块菲涅尔透镜, 并通过CCD结合显微镜将图像采集到计算机中. CCD的感光是对光能的积分过程, 当用连续光源照明时, 采集到的图像往往是不同时刻图像的叠加, 会产生一定的流动模糊, 而频闪灯光脉冲很窄, 因此能够有助于捕捉流场的瞬间图像.菲涅尔透镜具有凸透镜的聚光效果, 可以将频闪灯发出的光聚焦到CCD所拍摄的视场范围内.这种方法具有较高的空间分辨率, 更有利于捕获流动聚焦的界面结构. 图 11显示了单轴、同轴和三轴流动聚焦中稳定锥形的界面形态(Si et al. 2015), 可以清晰地分辨不同流体的边界面.

|
| 图 11 气驱流动聚焦中稳定锥形的界面形态(Si et al. 2015). (a)单轴流动聚焦的液-气界面, (b)同轴流动聚焦的液-液和液-气界面, (c)三轴流动聚焦的液-液(内)、液-液(外)和液-气界面 |
流动聚焦装置的几何参数主要对锥形的不稳定性和形貌影响较大.当毛细管未能对准小孔时, 锥形发生偏移.随着偏移量增大, 射流向小孔的固壁逐渐靠近, 但是仍然能够一直保持稳定(图 12(a)).当继续增大偏移量时, 锥形顶端发出的射流会与小孔处的固壁发生接触.因此, 只要保证毛细管和小孔存在较好的同轴度, 流动聚焦技术就能够确保从毛细管流出的流体不与周围固壁接触.此外, 当锥形顶端发出的射流通过小孔后, 将直接进入开放的空间, 没有固壁约束, 这些特点与微流控芯片内的流体流动情况不同.毛细管与小孔的间距直接影响锥形的不稳定性和微观形貌.在一定的参数范围内, 随着毛细管与小孔的间距增大, 处于稳定状态的锥形由“凹”向“凸”逐渐膨胀, 在锥形的顶端能够一直形成稳定的液体射流.但是当间距太大时, 锥形就变得不稳定, 一直处于振动状态, 这种工况就不能形成单分散性好的液滴.对于不同类型的流动聚焦(单轴、同轴、三轴等), 都存在类似的规律(如图 12(b)~图 12(d)所示), 但是随着流体界面的增大, 就要考虑每一层界面的失稳情况.在流动聚焦实验中, 一般选取合适的装置几何参数, 包括毛细管的内外径、小孔的直径、毛细管口到小孔的距离以及腔体的壁厚等, 通常在百微米到两毫米之间进行调节, 以便于形成稳定的锥形.研究表明, 一旦形成稳定的锥形, 射流的直径、形态及稳定性就几乎与几何参数无关, 主要取决于外部控制参数和流体的物理属性, 这是流动聚焦很重要的一个特征.

|
| 图 12 流动聚焦装置几何参数的影响. (a)单轴流动聚焦中毛细管与小孔不同轴(司廷等2008), (b)单轴流动聚焦中毛细管与小孔间距增大(司廷2009), (c)同轴流动聚焦中毛细管与小孔间距增大(李广滨2016), (d)三轴流动聚焦中毛细管与小孔间距增大(Si et al. 2015) |
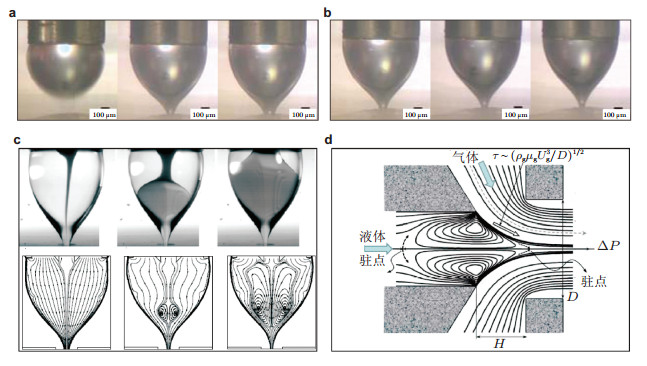
外部控制参数对锥形和射流流动模态的影响是相互关联的, 可以通过给出流动模式的相图来考察外部控制参数的影响, 这将在下一节进行详细介绍.定性来说, 增大被驱动流体的流量速度能够增强锥形的稳定性, 同时也会增大射流的直径和制备液滴的尺寸; 而改变驱动流体的流速, 将会改变锥形和射流的流动模态, 也会改变制备产物的尺寸和粒径分布. 图 13定性给出了气驱流动聚焦中液体流量速度Ql和气体压力差△pg对锥形微观形貌的影响.在一定的△pg下, 当Ql小于某个临界值时, 锥形处于振动状态; 一旦Ql大于该临界值, 锥形就一直处于稳定状态, 并且随着Ql的增大锥形整体形状不发生明显变化, 只是锥顶端的射流直径增大(图 13(a)); 当Ql不变时, 随着△pg的增大锥形顶端的射流直径会减小(图 13(b)).锥形的失稳涉及了全局不稳定性问题, 目前研究比较有限, 主要通过实验中的流场显示和定性的受力分析考察锥形的不稳定性.实验中在毛细管中心流场添加染料, 可以发现, 在一定条件下锥形内部出现一个回流环(recirculation cell), 改变过程参数能够改变回流环的大小和位置, 从而影响锥形内部的速度分布(图 13(c)).一般来说, 高速气流对界面的剪切作用使液体加速形成边界层, 远离边界层的液体速度开始衰减, 因此回流环能够使锥形的表面处于稳定状态, 就可以平稳地产生细射流, 此时回流环大小不变, 在锥形内部回流环的前后端是驻点(图 13(d)); 反之, 一旦破坏了回流环的稳定性, 不再存在驻点, 锥形将出现失稳(Gañán-Calvo & Montanero 2009, Herrada et al. 2008b).
|
| 图 13 气驱流动聚焦中外部控制参数的影响. (a)液体流量速度Ql增大(司廷2009); (b)气体压力差△pg增大(司廷2009); (c)内部添加染色剂观察回流环的产生, 并与数值模拟结果对比(Gañán-Calvo et al. 2011); (d)稳定锥形的流体边界层及回流环示意图(Gañán-Calvo & Montanero 2009) |
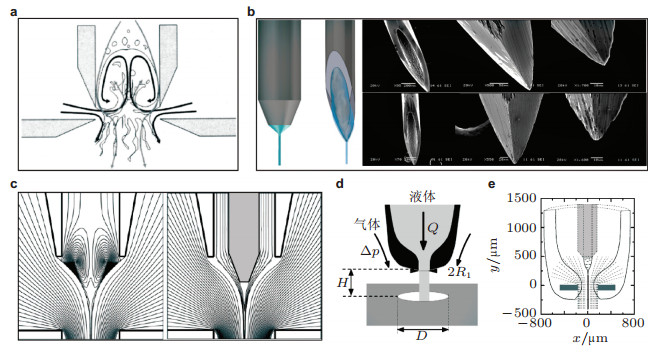
值得一提的是, 在流动聚焦的研究过程中, 特别是涉及到制备粒径更小的液滴、颗粒或胶囊时, 除了考虑施加额外电场或改变过程参数外, 研究者们还提出了一些改进实验系统的方法. Gañán-Calvo (2005)利用气驱流动聚焦的几何结构, 将毛细管口改成与中心轴呈角度θ的尖角, 毛细管的内径和小孔直径都为D, 通过减小毛细管口与小孔之间的距离H, 能够得到与液-气流动聚焦完全不同的实验现象, 如图 14(a)所示, 称之为“流动模糊” (flow blurring)或者“回流混合” (backflow mixing).当θ不大于60°时, 实验结果几乎不受到θ的影响.当H/D > 0.25时, 流动结构与气驱流动聚焦一样, 能够形成稳定的锥形和液体射流.一旦H/D < 0.25, 气流几乎变成径向流动, 与液体的流动方向垂直, 于是在毛细管口和小孔之间一部分气体流向毛细管内, 与流动的液体剧烈混合, 导致毛细管口的液体分叉, 形成模糊的羽毛状液体细丝.在这种流动结构中, 气体压力差△pg可高达500 kPa, 而制备的液滴直径可到1 μm或更小, 其雾化效率要比流动聚焦高好几倍(Rosell-Llompart & Gañán-Calvo 2008).另一种方法是将毛细管端口削成尖锐的斜角(图 14(b)), 当通入微量液体时, 液体沿斜角流动并聚集, 在较小流速下有效形成稳定的锥形(Acero et al. 2013).还有一种方法是在毛细管中心插入细导流棒, 将导流棒的端部削尖并伸出毛细管口一段距离, 如图 14(c)所示.当液体从毛细管流出时, 导流棒能够抑制回流环的产生, 可以有效增强边界层的形成, 大大降低最小液体流量速度的阈值, 从而达到减小液滴直径的目的(Acero et al. 2012b).其他方法还包括将毛细管加工成喷管形状(图 14(d)), 从而减小毛细管口直径, 可用于金属液体的聚焦(Vega et al. 2013); 或者将小孔所在平板改成喷管形状(图 14(e)), 有利于在毛细管口形成稳定的流场, 从而降低形成稳定锥形的最小液体流量速度以达到减小液滴尺寸的目的(Acero et al. 2012a).
|
| 图 14 核心装置的改进. (a)将毛细管和小孔之间的距离减小形成流动模糊(Gañán-Calvo 2005); (b)将毛细管端口削成尖锐的斜角有利于微量液体聚集(Acero et al. 2013); (c)在毛细管中心插入导流棒抑制回流环的产生(Acero et al. 2012b); (d)将毛细管加工成喷管形状大大减小毛细管口直径, 可用于金属液体聚焦(Vega et al. 2013); (e)将小孔所在平板改成喷管形状有利于形成稳定的流场(Acero et al. 2012a) |
在流动聚焦实验中, 当采用不同的牛顿流体试剂时, 尽管其密度、黏性、表面张力等物理属性不同, 实验现象仍具有类似的规律.但是当采用高分子聚合物材料的溶液时, 实验现象将发生改变, 与聚合物溶液浓度、黏性、表面张力以及非牛顿流体特性等密切相关.低浓度的高分子材料溶液黏性低, 能够形成稳定的锥射流结构.当浓度增大, 稳定锥形一般只能在一个比较小的参数范围内存在, 而形成的射流不再像牛顿流体那样快速破碎, 而是发生缠绕, 并且拉长(可达几厘米), 通常细丝上还会有一串珠状“鼓包”, 伴随细丝向下游运动(陈晓慧等2014, Ponce-Torres et al. 2016).当施加电场在流动聚焦的锥形和射流区域时, 随着电压增大, “鼓包”之间的距离缩短, 细丝也变得甩动起来, 从轴对称运动变为非轴对称运动(图 15).对于牛顿流体, 流体流动时其切应力与剪切应变速率成正比, 而对于非牛顿流体, 切应力与剪切应变速率之间不再有简单的线性关系.开展非牛顿流体的流动聚焦研究存在很多困难, 目前相关的工作才刚起步.

|
| 图 15 电流动聚焦中高分子溶液的射流形态随电场增大的变化情况(陈晓慧等2014) |
单轴流动聚焦涉及的流体结构相对简单, 其流动模式及形成条件已经得到深入的研究.复合流动聚焦涉及多层流体界面, 流动模式相对复杂, 目前的研究还比较有限.而电流动聚焦多了电场条件, 问题更加复杂.相关的研究内容正得到国内外学者的关注, 也为实际应用提供了理论和经验指导.
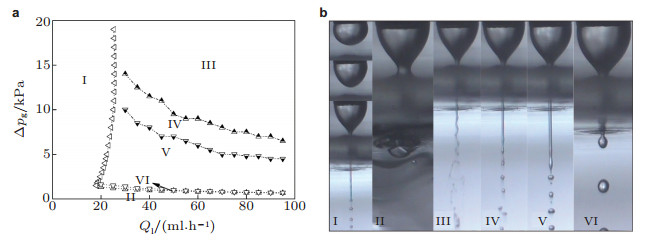
气驱单轴流动聚焦主要的外部控制参数是液体流量速度Ql和气体压力差△pg, 在这两个参数组成的Ql-△pg平面内, 可以得到流动聚焦的六种流动模式及其工作区域, 如图 16所示.六种模式分别是:锥振动模式(Ⅰ)、锥黏连模式(Ⅱ)、螺旋射流模式(Ⅲ)、共存射流模式(Ⅳ)、轴对称射流模式(Ⅴ)和滴模式(Ⅵ).锥振动模式对应低值的Ql, 而锥黏连模式对应低值的△pg, 都与锥形的不稳定性有关.其他四种模式都是在稳定锥形条件下得到的, 对应较大的参数范围.从机理上分析, 滴模式与绝对不稳定性有关; 射流模式与对流不稳定性有关:轴对称射流模式和螺旋射流模式分别是由轴对称扰动和非轴对称扰动引起的, 而共存射流模式是轴对称和非轴对称扰动共同作用的结果.不稳定性理论的研究进展将在下一节介绍.
|
| 图 16 “液-气”单轴流动聚焦的流动模式及其参数域(Si et al. 2009). (a)流动模式的参数域, (b)六种流动模式的锥-射流图像: (Ⅰ)锥振动模式; (Ⅱ)锥粘连模式; (Ⅲ)螺旋射流模式; (Ⅳ)共存射流模式; (Ⅴ)轴对称射流模式; (Ⅵ)滴模式 |
在锥振动模式中, 从毛细管口流出的液体先是在管口形成一个小液滴并不断向小孔扩张, 小液滴的顶端在高速气流剪切和表面张力作用下收缩并在小孔处发出微射流, 发出射流后锥形又快速缩回(Si et al. 2009).锥形的往复振动的原因在于:在较小的液体流量下, 毛细管口内的液体存在一个回流环, 若以流动方向为正方向, 则回流环在中心轴上的速度为负值, 从而会向流动反方向运动(Gañán-Calvo & Montanero 2009, Herrada et al. 2008b).只有当中心轴上的速度不为负时锥形才能保持稳定状态, 此时对应着一个最小的液体流量.在锥黏连模式中, 毛细管口形成的锥形顶端与小孔入口接触, 液体顺着小孔壁面流出小孔, 因此形成不了射流.在图 16(a)中, II区的边界值是在给定液体流量Ql下, 逐渐减小△pg观察锥形是否黏连小孔而测定的.当改变Ql的值时, 临界的气体压力差的大小也发生变化.锥黏连模式的产生与流动聚焦装置的几何参数以及气体和液体的相互作用有关.如果不存在气流和小孔的会聚作用, 从毛细管流出的液体会因表面张力作用在毛细管口有较小的收缩, 然后形成与毛细管尺寸可比的液滴或圆柱射流(Clanet & Lasheras 1999).对于流动聚焦装置, 在较小气体压力差△pg时, 气流对液体的作用不足以使液体在小孔入口产生较大的收缩, 液体在气流的引流作用下与小孔黏连在一起(司廷2009).
当Ql和△pg都大于一定的临界值时, 锥形将一直处于稳定状态, 此时产生的几种流动模式与射流的形态密切相关, 而且流动模式主要取决于气体压力差△pg的大小.当△pg值较大时, 小孔出口外的射流直径较小, 缠绕着向下游运动, 运动过程中高速流动的气流剪切作用使射流拉伸、直径变小直到破碎成细小的液滴, 该模式称为螺旋射流模式或非轴对称射流模式(图 16(a)中区域Ⅲ).该模式下气流的剪切起很重要的作用, 得到的液滴呈多分散性, 直径较小.当气体压力差△pg不太大时, 在小孔出口外射流的直径保持几乎不变, 射流沿直线向下游运动, 一定距离后轴对称的扰动变得明显, 直到破碎成液滴, 该模式称为轴对称射流模式(图 16(a)中区域Ⅴ).轴对称射流模式主要是轴对称扰动引起的, 得到的液滴单分散性好, 粒径与射流直径可比.在一定条件下, 由于非线性作用会伴随产生直径非常小的卫星液滴.在图 16(a)的区域Ⅲ和Ⅴ之间有一个转换模式Ⅳ, 在小孔出口外射流沿直线向下游运动, 但是一定距离后扰动变得明显并呈现非轴对称特征, 产生的液滴摆动着向下游运动, 称之为共存射流模式.该模式下轴对称和非轴对称的扰动共同作用, 是轴对称射流模式的结束, 也是非轴对称扰动起主导作用的开始.当气体压力差△pg较小时, 液滴在小孔出口处即可形成, 称之为滴模式, 此时液滴非常规则, 但直径较大.
可以看出, 对应不同的参数域, 存在不同的工作模式, 锥形和射流的形态也不同, 如图 16(b)所示.一般情况下, 稳定的锥-射流模式有利于制备单分散性好的产物, 对实际应用非常重要, 因此研究流动模式及其参数域是一项十分重要的工作.除了上述分类, Vega等(2010)详细分析了流动聚焦的流动模式, 从不稳定性角度将流动模式分为稳定射流模式、局部不稳定模式和全局不稳定模式. Rosell-Llompart和Gañán-Calvo (2008)根据气体和液体的相互作用将流动聚焦分为两类:一类是毛细流动聚焦, 液体射流主要是轴对称的毛细扰动引起的破碎(Rayleigh不稳定性); 另一类是湍动流动聚焦, 非轴对称扰动的增长率将超过轴对称的毛细扰动, 此时形成的射流缠绕着向下游运动.在两者的转换区域, 能够观察到非轴对称的缠绕射流, 液体射流偏离中心轴的距离越大, 射流与气流的相互作用越强, 射流能够拉伸成细长的丝并破碎成液滴.
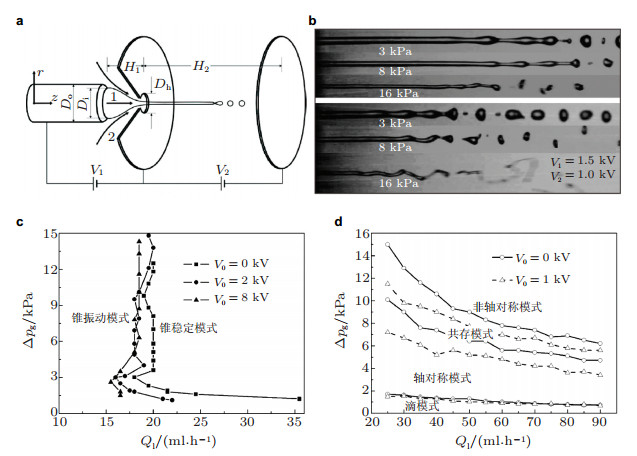
复合流动聚焦的流动模式比较复杂, 要考虑多层界面的失稳和相互作用, 目前尚缺少系统的实验研究(李广滨2016);关于电流动聚焦的流动模式及其参数域, 司廷等(2011)和Li等(2014)开展了初步的实验研究.电流动聚焦装置可以简化成图 17(a)所示的结构, 其中电压施加于锥形和射流区域, 能够得到单轴的带电液体射流. 图 17(b)给出了在不施加和施加电场两种情况下气体压力差△pg对射流的影响.随着△pg的增大, 射流逐渐由轴对称模式转换为非轴对称模式; 而且在施加电压后, 转换所需要的临界气体压力差明显减小, 同时射流的破碎变得更为剧烈, 破碎形成的颗粒也更小. 图 17(c)给出了电流动聚焦中Ql-△pg平面上锥形的稳定模式和不稳定模式之间的转换曲线.可以看出, 当施加电场作用后, 随着电压的增大维持稳定锥形的临界液体流量呈减小的趋势.因此, 电场的作用增强了锥形的稳定性, 有利于减小维持锥形稳定的最小液体流量速度. 图 17(d)给出了有、无电压作用下Ql-△pg平面上不同流动模式的转换曲线.滴模式受电压影响较小, 轴对称模式与共存模式、共存模式与非轴对称模式之间的模式转换受电场影响很大, 整体上增大电压使轴对称模式区域减小, 非轴对称模式区域增大.该现象产生的原因主要在于两个方面:一是射流表面带有电荷, 在电场力作用下流体产生较大的加速作用, 使非轴对称性扰动的增长速度加快, 更容易表现出来; 二是△pg稍大时, 射流表面一旦出现微小的非轴对称性扰动, 这种空间的不对称性便会因射流表面电荷分布的不均匀而被瞬间放大.当非轴对称射流产生后, 射流因表面带有相同的电荷而被拉伸扭曲, 径向位移变大, 破碎的液滴在电场作用下发生变形、剧烈扭曲并再破碎成更小的液滴.由于在非轴对称模式下射流运动速度快, 液滴直径小, 制备颗粒的生产率高, 因此电流动聚焦具有重要的实用价值.
|
| 图 17 电流动聚焦的流动模式及其参数域. (a)电场施加在锥形和射流所在区域(Li et al. 2014), (b)电压和气体压力差变化引起射流的模式转换(Li et al. 2014), (c)锥形稳定和不稳定的转换边界受电压影响(司廷等2011), (d)不同流动模式参数域受电压影响(司廷等2011) |
根据流动聚焦的物理机制, 射流直径以及液滴尺寸与过程参数之间存在明确的尺度律关系, 这是流动聚焦非常显著的特征之一.在气驱单轴流动聚焦中, 气体的动量和液体的动量之比非常接近于1, 也就是ρgUg2/2=ρlUl2/2, 其中ρg和Ug分别为气体的密度与速度, ρl和Ul分别为液体的密度和速度.在稳定锥形条件下, 一旦腔体内外的气体压力差△pg和从毛细管提供的液体流量速度Ql确定, 一个直径为dj的液体细射流便可从锥形的顶端平稳地产生.小孔出口处的射流直径dj在一阶近似条件下可以表达成(Gañán-Calvo 1998)
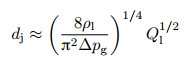
|
(1) |
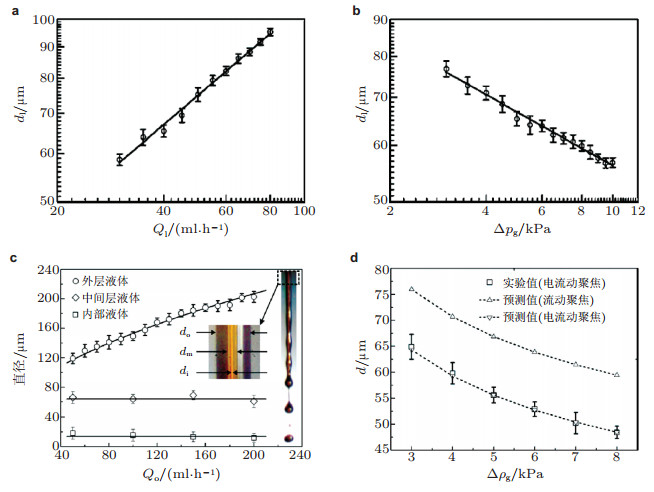
上式表明小孔出口处的射流直径dj只与气体压力差△pg、液体流量速度Ql以及液体的密度ρl有关, 而与结构参数、液体和气体的黏性以及液-气之间的表面张力系数无关.如图 18(a)和图 18(b)所示, 实验结果也验证了这一结论(Si et al. 2009).
|
| 图 18 气驱流动聚焦中射流直径的尺度律及实验验证. (a)单轴流动聚焦中射流直径随液体流量速度的变化(Si et al. 2009), (b)单轴流动聚焦中射流直径随气体压力差的变化(Si et al. 2009), (c)三轴流动聚焦中三层液体射流直径随最外层液体流量速度的变化(Si et al. 2015), (d)电流动聚焦中射流直径随气体压力差的变化以及与无电场作用下流动聚焦的尺度律进行对比(Li et al. 2014) |
当液体射流和周围高速流动的气流穿过小孔后, 气流和周围静止空气之间因Kelvin-Helmholtz不稳定性形成混合层, 混合层厚度的增长和涡的形成依赖于流动速度.在气体边界上脱落涡的波长的量级为小孔的直径Dh, 因此涡脱落的频率量级为Ug /Dh; 在液体表面上的扰动波长的量级为射流的直径dj, 射流破碎的频率量级为Ul/dj.因此, 射流破碎的频率可达到兆赫兹(MHz)量级, 这已经得到实验验证(Gañán Calvo & Barrero 1999, 司廷2009), 表明流动聚焦生产效率很高.此后, 当考虑表面张力的作用时, 液体射流的直径表达式可以修正为(Rosell-Llompart & Gañán-Calvo 2008)
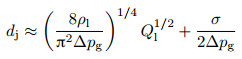
|
(2) |
当全面考虑表面张力、液体黏性和小孔直径的影响时, 可以给出相应的二阶修正, 与一阶结果没有明显偏离, 特别是在较大气体压力差△pg时, 一阶近似的结果能够很好地与实验数据吻合.
类似地, 复合流动聚焦的尺度律也可以推导出来.以气体驱动的三轴流动聚焦为例, 外层、中间层和内层射流的直径do, dm, di可以表示为(Si et al. 2015)

|
(3) |
其中, ρo是外层液体的密度, Qm和Qi分别是中间层液体和内部液体的流量速度, ΣQ是指三种液体的流量速度之和. 图 18(c)给出了一组实验测量和理论预测之间的对比图, 最外层液体的流量速度Qo是主要控制变量.可以看出, 只改变Qo时最内层和中间层的液体射流直径几乎不发生变化, 外层液体射流的直径符合尺度律关系.主要原因在于整个系统的驱动气流速度并没有发生明显变化, 因此改变最外层液体的流量速度并不能改变每一层流体的运动速度, 主要是对最外层流体的直径有影响.
当液体和气体反相时, 得到的尺度律关系将发生变化. Gañán-Calvo & Gordillo (2001)分析了气-液结构的单轴流动聚焦中小孔处气流尺寸以及形成的小气泡的直径db与过程参数的关系, 并得到了隐式的解析表达式, 之后Gañán-Calvo (2004)给出了简化的经验公式

|
(4) |
其中Qg是内部气体的流量速度.可以看出, 气泡的尺寸不仅与内外层液体的流量速度有关, 还与小孔的尺寸有关, 这是因为小孔的尺寸和液体流量速度决定了驱动流体的运动速度.
当分析电流动聚焦问题时, 除了要考虑惯性力的作用, 还要增大电场力的作用, 内部液体的运动将发生变化.引入单位体积的总能量△Θ, 其表达式为
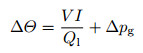
|
(5) |
其中, I为液体射流运动产生的总电流, VI/Ql为单位体积的电能(Gañán-Calvo et al. 2006b), 在射流运动过程中产生的能量耗散可以忽略不计.如果电压V很小, 总电流I也很小, 那么VI/Ql远小于△pg, 此时流动模式几乎不受影响, 产生的液滴大小也不会发生明显变化; 但是当电压V增大到一定程度, 总电流I也会增大, 当VI/Ql与△pg可比或更大, 射流就会受到明显影响(司廷等2011).电流动聚焦中液滴直径dr的尺度律关系为(Gañán-Calvo et al. 2006b)

|
(6) |
其中α表示为电能和气流动能之比, 下标FF, ES和EFF分别对应单一的流动聚焦、电雾化和电流动聚焦的技术.可见, 当流动聚焦中施加电场之后液滴尺寸会减小.
Li等(2014)根据单轴电流动聚焦的实验结果, 提出了液体射流直径的经验公式
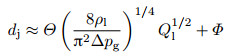
|
(7) |
其中Θ和Φ为两个拟合系数.当没有电场作用时Θ=1和Φ=0, 与式(1)相同; 当施加电场之后, Θ < 1, 而Φ取决于相应的实验条件, 说明射流直径将会减小(图 18(d)). Si等(2016b)进一步将这个经验公式应用到多轴电流动聚焦中, 也得到了与实验比较一致的结果.
3.4 不稳定性分析在流动聚焦中, 锥形和射流在尺度上存在数量级的差异, 而且锥形和射流的流动模态也存在显著差别, 因此在不稳定性分析中需要将两者分开研究.本节简要回顾锥形不稳定性的研究进展, 由于射流不稳定性的研究自成体系, 我们将在下文中深入讨论.
稳定的锥形是形成稳定射流的先决条件, 因此锥形的稳定性控制至关重要.当存在多相界面时, 复合锥形的稳定性与气体压力、内外层液体流量速度以及流量比、表面张力系数、电场强度、电导率、核心装置的几何参数等密切相关.特别地, 在复合流动聚焦中只有当内外层液体的流量达到一定阈值时才能获得稳定的锥形, 否则锥形将一直处于振动状态; 而施加额外的电场可以提高复合锥形的稳定性, 此时需要考虑内外层流体的导电能力以及诱导电荷的影响.在稳定锥形条件下, 复合射流的破碎模态也与上述参数相关, 直接影响微纳米颗粒与胶囊的形貌和实用性.可以看出, 锥形不稳定性涉及了多层界面、振荡界面以及从锥形到射流的多尺度效应, 处理这类全局不稳定性问题具有很大的挑战性.
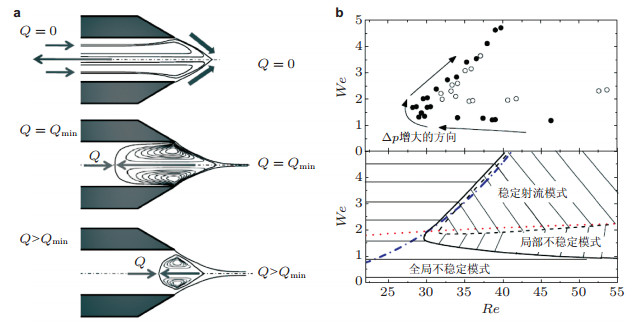
目前锥形不稳定性方面的研究工作主要集中在单轴流动聚焦的实验和数值方面, 一般采用定性分析的方法探索锥形的失稳机制, 定量的研究尚未开展.在图 19中显示了锥形不稳定性的机制和参数域.当锥形一直稳定且射流处于对流不稳定性状态时, 认为是稳定射流模式; 当锥形稳定且射流处于绝对不稳定性状态时, 称为局部不稳定模式; 当锥形失稳时, 就进入全局不稳定模式(Vega et al. 2010). 图 19(a)显示了气驱单轴流动聚焦中锥形稳定对应的最小流量速度Qmin以及相应的回流环结构(Gañán-Calvo & Montanero 2009).当Ql < Qmin时, 锥形处于全局不稳定性模式, 锥形表面的切向黏性应力拉伸界面, 而锥形内部流体为维持液体流量守恒将向毛细管内流动, 因此形成回流环, 随着流体在锥形内积聚, 回流环没有稳定的驻点, 锥形将逐渐伸出毛细管口, 直到一股流体从小孔射出, 锥形迅速弹回, 如此反复, 从而不断振动.而一旦Ql=Qmin, 切向黏性应力使液体界面拉伸成稳定的形状, 锥形内部的回流环稳定存在, 因此界面也处于平衡状态, 形状不再变化.随着液体流量速度Ql的增大, 回流环的尺寸将逐渐减小, 形成液体射流的直径将逐渐增大. Vega等(2010)在无量纲参数Re-We空间里得到全局不稳定、局部不稳定和稳定射流三种模式的参数域及其转换曲线, 可以有效区分不同模式的形成条件(图 19(b)).其中Re为雷诺(Reynolds)数, 是惯性力和黏性力之比, We为韦伯(Weber)数, 是惯性力和表面张力之比, 其定义可以表述为
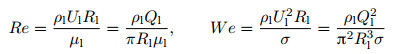
|
(8) |
|
| 图 19 气驱单轴流动聚焦的锥形不稳定性. (a)锥形稳定对应的最小流量速度(Gañán-Calvo & Montanero 2009), (b)在无量纲参数We-Re空间里全局不稳定、局部不稳定和稳定射流三种模式的参数域(Vega et al. 2010) |
其中μl为液体黏性系数, σ为表面张力, Rl为射流半径.
4 射流不稳定性在流动聚焦中, 当锥形处于稳定状态时, 从锥形顶端生成的射流仍然会有不同的流动模式.射流在每一种模式下的形态和界面扰动的发展, 以及不同模式之间的转换, 可以通过经典的不稳定性理论进行分析, 能够得到与实验吻合的结果.近年来, 不稳定性理论逐步被扩展到带电射流、同轴射流以及同轴带电射流等复杂问题的研究中, 取得一定研究成果.本文将对射流不稳定性的理论研究进展进行回顾, 并对流动聚焦中射流不稳定性的研究现状进行总结.
对液体射流破碎成液滴现象的不稳定性理论研究已经有一个多世纪的历史. Rayleigh (1878, 1879)最早利用线性不稳定性理论研究了真空中无黏液体射流的破碎问题, 认为表面张力引起的水动力学不稳定性是使射流失稳的主要原因, 发现随着时间增长的扰动对应的波长不小于射流的周长, 并且最不稳定扰动的波长λmax为射流周长的1.437倍. Rayleigh (1892)进一步考虑了液体的黏性后, 发现λmax可以为无穷大.对于低速射流, Rayleigh的结果与实验吻合很好, 而对于高速射流结果就偏离了实验. Weber (1931)在Rayleigh的研究基础上进一步考虑了周围气体密度的影响, 发现随着流体黏性的增大, λmax变大, 但黏性不会改变不稳定的临界波数αcut; 而且当射流速度较小时, 周围空气的影响很小, 可以忽略. Sterling和Sleicher (1975)对Weber的理论进行了改进, 在环境气体的控制方程中引入一个经验系数用来代替黏性的作用后, 得到的结果与实验能够吻合.在此期间, Tomotika (1935)指出通过调节液体射流与周围气体的黏性比, 可以使某一有限波长的扰动增长最快. Taylor (1940)考虑了周围气体的密度, 发现在气体惯性力相比表面张力足够大的情况下, 射流破碎后获得的液滴直径要远小于射流直径.区别于液滴与射流尺寸相当的Rayleigh模式, 该模式后来被称为Taylor模式. Chandrasekhar (1961)系统地开展了黏性射流的不稳定性研究, 发现黏性会抑制扰动的增长, 并使射流破碎后获得液滴的粒径增大, 同时指出Rayleigh模式下射流的破碎是由毛细收缩导致的.之后Donnelly和Glaberson (1966)与Goedde和Yuen (1970)的实验结果验证了Rayleigh和Chandrasekhar的理论. Re-itz和Bracco (1982, 1986)发现随着表面张力、射流惯性以及气动力大小的变化, 射流会有四种破碎模式, 即Rayleigh模式、第一风诱导模式、第二风诱导模式以及雾化模式. Lin和Ibrahim (1990)分析了竖直圆管中液体射流的不稳定性, 考虑了环境气体和液体射流的黏性并通过流体力学方程求解扰动前的基本流场, 得到了全部参数的影响规律.此外, 针对电雾化中的带电射流不稳定性问题, 已经有大量的理论分析工作(Rayleigh 1882, Melcher 1963, Taylor 1964, Saville 1997, Gañán-Calvo 1997, Artana et al. 1998, Lpez-Herrera et al. 2005).
上述的不稳定性分析都在时间域内开展, 但实际上射流的失稳以及破碎是扰动在时间域和空间域上共同发展演化的结果. Keller等(1973)对半无限长射流进行了空间和时空不稳定性分析, 同时理论预测了射流的破碎长度. Huerre和Monkewitz (1985)在实验中发现各向同性的射流在空间演化的混合层具有对流不稳定性的特征. Leib和Goldstein (1986a, 1986b)考虑了流体的黏性, 研究了不同表面张力和速度剖面下绝对不稳定性与对流不稳定性之间的转换情况, 并发现当忽略黏性的影响后, 绝对/对流不稳定性转换的临界韦伯数Wecrit的值恒为π. Lin和Lian (1989)与Monkewitz (1990)将滴模式和绝对不稳定性联系起来开展了研究. Kang和Lin (1989)分析了环境气体密度对旋拧射流中非轴对称扰动的影响. Eroglu等(1991)和Wu等(1992)研究了管口处的射流速度分布、气体和液体的热力学状态、管口速度的湍动等对射流的破碎的影响. Lin和Lian (1993)研究了处于竖直圆管中心的液体射流的绝对-对流不稳定性, 其中环境气体和液体射流均为黏性流体. Lin和Chen (1998)分析了界面上的剪切对射流不稳定性的影响, 并采用能量积分法分析了射流的破碎机理, 发现对流不稳定性状态下有两种模式, 即Rayleigh模式和Taylor模式. Rayleigh模式下射流的破碎由毛细收缩导致, 而Taylor模式下射流破碎的能量由气体压力和剪切的波动提供.界面剪切力在Rayleigh模式会抑制射流的失稳, 在Taylor模式则会促进射流的失稳.此外, 他们还发现绝对不稳定性也是毛细收缩导致的. Artana等(1997)对同轴电极作用下的无黏液体带电射流作了绝对/对流不稳定性分析, 计算结果显示当电场达到一定程度时, 射流由对流不稳定状态进入绝对不稳定状态.
需要指出, 在使用不稳定性理论时, 必须要给出流场在未扰动时的基本速度型.在界面上存在阶跃、在流体内均匀的速度型, 因其十分简单而被广泛使用, 特别用于无黏模型中.分段光滑的均匀速度型(Yecko et al. 2002)与真实的流动更接近, 比存在阶跃的均匀速度型有所改进.在有黏模型中, 满足流体力学方程和边界条件的基本速度型是最合理的情况(Lin 2003).另外, 在复杂问题中, 一些近似的函数被用于构造流动的基本速度型, 取得了一定的成功, 比如误差函数(Yecko et al. 2002, Boeck & Zaleski 2005)和双曲正切函数(Sevilla et al. 2002, Si et al. 2009)等.
经过一百多年的积淀, 射流不稳定性研究已形成一套较为成熟的理论, 也就是采用线性不稳定性理论来研究射流的失稳和破碎, 具体方法可以参考相关的综述和专著(Huerre & Monkewitz 1990, Yarin 1993, Lin & Reitz 1998, Lasheras & Hopfinger 2000, Lin 2003).此外, 随着对实际问题研究的深入, 一些复杂的实验现象被发现, 包括高速射流、非牛顿射流、非线性效应、非模态稳定性等方面的研究也引起了广泛关注(Eggers 1997; Lpez-Herrera et al. 1999; Zakaria 2000; Elhefnawy et al. 2001, 2004). Lin和Reitz (1998)回顾了射流在各种状态下的破碎机理, 认为射流在失稳的起始阶段的行为将决定最终的破碎状态, 而随后的非线性演化主要是对各物理量进行量化修正.因此, 线性不稳定性理论在射流的破碎机理研究以及定量预测射流和液滴尺度方面至关重要.
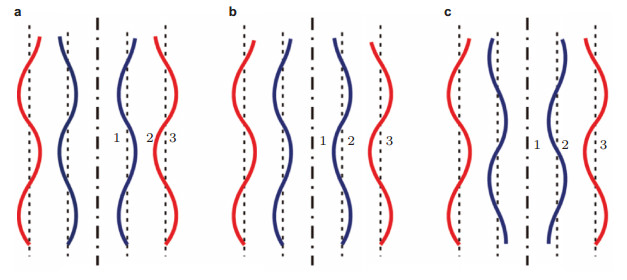
与单轴射流相比, 同轴射流的行为更复杂, 因为它涉及到两层界面:射流内外层流体之间的内界面与射流外流体和环境流体之间的外界面. Radev和Shkadov (1985), Sanz和Masseguer (1985)研究了同轴无黏射流的时间不稳定性, 在假定压力和速度只有轴向分量后, 发现主要存在两个不稳定模态:一个源于外界面上的毛细收缩, 只有波长大于外射流周长的扰动是增长的, 相应的内外界面上的扰动波相位相反, 两层界面在互相挤压的同时轴向振动, 称为squeezing模态.另一个源于内界面上的毛细收缩, 只有波长大于内射流周长的扰动是增长的, 相应内外界面上的扰动波相位相同, 两层界面在同时伸缩和轴向振动, 称为stretching模态.他们还发现, 在考虑的参数范围内, stretching模态都对应着更大的扰动增长率, 主导射流的失稳. Radev和Tchavdarov (1988), Shkadov和Sisoev (1996)进一步考虑了内外层流体的黏性并采用轴对称模型, 发现两个不稳定模仍然存在. Chauhan等(1996)研究了无黏同轴射流的时空稳定性, 发现存在一个临界韦伯数Wecrit, 当We < Wecrit时, 同轴射流是绝对不稳定的. Chauhan等(2000)详细分析了内外层液体的黏性、密度以及表面张力对最大扰动增长率、最不稳定波数以及内外界面振幅比的影响, 并发现当内外界面非常接近时射流的扰动增长与对应的单轴射流(射流的界面张力系数为同轴射流中两个界面张力系数之和)一致. Herrada等(2010)研究了有黏同轴射流的时空稳定性, 并将绝对-对流不稳定性的转换边界与实验中的“滴-射流”模式转换边界进行了比较.值得注意的是, 上面的研究都是基于均匀的速度剖面.另外Li等(2005, 2006, 2008, 2009)较为系统地研究了同轴带电射流的不稳定性, Si等(2014)也开展了同轴电雾化中射流不稳定性的理论研究, 发现除了squeezing模态和stretching模态, 还存在第三种transitional模态存在于Rayleigh模式下, 如图 20所示, 此时内外界面上扰动波的相位差随着周向波数的不同在0°~180°之间变化.文中squeezing也称为paravaricose (反相, 相位差约为180°), stretching也称为parasinuous (同相, 相位差约为0°).
|
| 图 20 同轴射流在Rayleigh模式下存在的可能模态(1-内流体, 2-外流体, 3-环境流体). (a) squeezing模态或paravaricose模态, (b) stretching模态或parasinuous模态, (c) transitional模态 |
随着微纳米量级的液滴、颗粒和胶囊在不同领域的广泛应用, 射流不稳定性理论研究逐渐与具体技术密切相结合, 比如电雾化(Saville 1997)、电纺丝(Reneker et al. 2000, Yarin et al. 2001)、选择性抽吸分离(Cohen & Nagel 2002)等, 当然也包括流动聚焦.线性不稳定性理论用于研究射流的破碎机理, 能够得到与实验吻合的结果一般需要具备以下条件:一个是射流的物理模型要与实际问题一致, 不能忽略重要的过程参数; 另一个是基本流动与真实的流动相同或相近.在实际的研究中, 当某些因素的重要性相比于其他因素比较小时, 可以将这些因素省略从而简化模型, 仍然能够取得与实验一致的结果, 而当这些因素对射流的不稳定性有重要影响时, 在理论分析时就必须考虑.下面介绍流动聚焦方面的射流不稳定性研究进展.
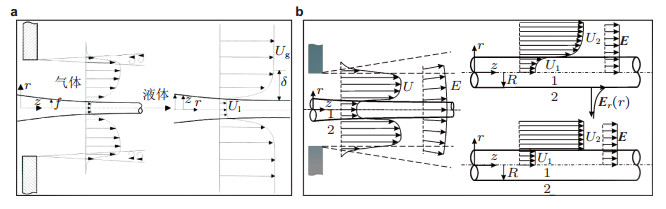
在气驱单轴流动聚焦中, 从毛细管流出的液体由高速流动的气体驱动, 经小孔聚焦后在毛细管口形成锥形, 并在锥形的顶端发出微射流.液体射流在同轴流动的气流中心与气流一起穿过小孔, 液体射流经一定距离后破碎成细小液滴, 气流穿过小孔后则由于和周围静止的空气相互作用在气流边界形成剪切层.在流动聚焦的理论研究中, 完全按照实验情况建立物理模型进行计算是十分繁琐且很难实现的.因此, 需要进一步简化物理模型. 图 21(a)绘出了液体和气体在小孔出口处的流动情况, 在液-气界面上由于黏性的作用产生了液体和气体的边界层, 而在气体的外边界由于剪切层的存在气流速度迅速衰减.由于在流动聚焦实验中小孔的直径(数百微米)远大于射流直径(数十微米或更小), 因此可以忽略气体外剪切层的影响, 认为在无穷远处气体的速度趋于一个固定的值.此外, 物理模型存在如下合理的假设: (1)液体和气体均为黏性、不可压缩的牛顿流体, 物理属性保持不变, (2)流体界面是物质面, 即分界面两边的物质在界面上不发生蒸发、凝结、渗透和互相溶解等现象, (3)忽略重力的影响.前两个假设对于通常的实验条件是容易理解的.与重力有关的无量纲参数为Froude数和Bond数, Froude数(Fr=Ul2/gRl)定义为惯性力与重力的比值, Bond数(Bo=ρlRl2g/σ)定义为重力与表面张力的比值.在实验中特征速度为1 m/s, 特征长度为10 μm, 密度取103 kg/m3, 重力加速度取9.8 m/s2, 表面张力系数取0.073 N/m (空气-水), 于是Fr~104, Bo~10-5, 可见重力相对于惯性力和表面张力是可以忽略的小量, 因此忽略重力的影响是合理的.在电流动聚焦中, 物理模型的建立遵循类似的假设, 但是需要对流体的导电性和自由电荷的分布进行约束(司廷等2011, 李芳2007, Li et al. 2014).因此, 气驱单轴流动聚焦或电流动聚焦中的射流模型一般认为是圆柱形液体射流和环形气体射流组成的同向流动的液-气射流(Gordillo et al. 2001b, Si et al. 2009, Li et al. 2014), 如图 21所示.而对于复合流动聚焦中复合射流的物理模型建立, 尽管流体界面增大了, 基本假设也需要类似考虑(Herrada et al. 2010, 李广滨2016).
|
| 图 21 液-气射流的简化物理模型. (a)气驱单轴流动聚焦的射流模型(Gordillo et al. 2001b), (b)气驱单轴电流动聚焦的射流模型, 包括有黏和无黏模型(Li et al. 2014) |
基于简化的物理模型, 相应的流体力学方程包括质量守恒方程和动量守恒方程
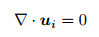
|
(9) |
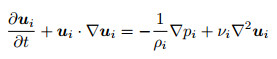
|
(10) |
其中, u为射流的速度矢量, p为压力, t为时间, ν为运动黏性系数(ν=μ/ρ), 下标i代表不同的流体.当施加额外电场时, 电场的控制方程需要考虑, 通常为电磁场的Maxwell方程组, 在不考虑磁场情况下表示为
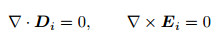
|
(11) |
其中E为电场强度, D为电位移矢量.电场的处理方法比流体要复杂很多, 不仅要考虑流体的电导率和介电系数, 还要考虑界面上自由电荷密度分布等因素, 一直是电流体力学中重要的研究内容之一(李芳2007).相应的边界条件包括对称轴上的速度和压力有限性条件, 流体界面上的速度连续条件、运动学边界条件、动力学边界条件以及电场边界条件, 还包括无穷远处的速度和压力有限性条件等.
对于流动聚焦中射流不稳定性的理论研究尚处于起步阶段, 目前主要围绕一种流体驱动另一种流体的射流模型开展工作. Gordillo等(2001a)首先研究了气驱单轴流动聚焦中液-气射流的时间不稳定性, 通过边界层方程数值求解了流动聚焦中的基本速度型, 重点讨论了不同速度剖面下液-气射流的不稳定性.在初始位置处, 液体的速度剖面为抛物线型, 控制参数为液体边界层的厚度△, 而气体的速度剖面为满足边界层方程的Blasius型, 控制参数为气体边界层的厚度δ, 于是在给定△和δ的情况下能够计算出液体和气体的基本速度型在空间上的演化.他们的不稳定性分析包括3个模型: (1)半径不变的液体射流的速度型为均匀的, 只考虑气体的非均匀速度型的影响.在这个模型中, 通过改变唯一的自由参数δ, Rayleigh模式和Taylor模式被区分出来.在Rayleigh模式下破碎波长和射流的半径是可比的, 表面张力对不稳定性起促进作用, 而在Taylor模式下扰动波长远小于射流半径, 当不考虑黏性时不稳定性主要是作用在界面上的气压扰动引起(Lin & Chen 1998).另外, 稳定性分析还得到了缠绕模式(也就是第一非轴对称模式或者正弦模式). (2)同时考虑液体和气体的非均匀速度型的影响, 只引入液体射流扰动, 同轴的外部气体无扰动.这种模型下非均匀的液体速度型修正了Rayleigh (1879b)的无黏均匀速度型的结果, 产生的轴对称模式下的毛细和运动不稳定模式以及非轴对称模式下的缠绕模式都是由液体表面上存在边界层引起. (3)同时考虑液体和气体的非均匀速度型的影响, 并在液体和气体中都引入扰动.在这种情况下, 能够得到与前两种模式相对应的模式, 同时可以考虑各参数的影响.结果表明随着We的增大, 不同模式之间存在着转换, 当We较大时, 缠绕模式的最大增长率要大于毛细的轴对称模式.得到的理论结果与实验中的射流破碎模式定性的一致. Gordillo等(2001b)开展了气-液流动聚焦的时空不稳定性分析, 采用的速度剖面能满足Blasius边界层方程, 分析发现微气流一直处于绝对不稳定状态. Gañán-Calvo等(2006a)将气-液流动聚焦中对流/绝对不稳定性转换边界与实验中的气泡-射流模式转换边界进行了比较. Gañán-Calvo (2007b)开展了空心射流的绝对不稳定性研究. Gañán-Calvo和Riesco-Chueca (2006)研究了液-液流动聚焦中的时空不稳定性.在利用Funada和Joseph (2002)的理论推导出相应的解析形式的色散关系后, 将对流/绝对不稳定性转换边界与实验中的滴-射流模式转换边界进行了比较, 两者符合很好. Montanero和Gañán-Calvo (2008)采用Oldroyd-B黏弹性模型和线性不稳定性理论来研究液-液流动聚焦中黏弹性对射流不稳定性的影响, 结果发现液体的弹性会促进轴对称扰动的增长, 抑制非轴对称扰动的衰减, 同时还会加速轴对称时空模式下对流/绝对不稳定性的转换. Montanero和Gañán-Calvo (2008)分析了同轴流动聚焦中非轴对称扰动的时间和时空不稳定性. Herrada等(2008a)采用时空不稳定性分析方法研究了微管道中滴-射流模式的转换. Si等(2009, 2010)系统的研究了气驱单轴流动聚焦中的时间、空间以及时空不稳定性, 详细分析了各个参数的影响.在时间不稳定性分析中获得了最大增长率对应的波数, 从而计算了最不稳定扰动的波长, 与实验结果一致(图 22(a)和图 22(b)); 在时空不稳定性分析中通过对不同参数下鞍点属性的判断, 得到了Re-We平面上绝对/对流不稳定性的转换曲线, 与实验中的滴-射流模式的转换曲线吻合(图 22(c)); 而在空间不稳定性分析中, 同时考虑了轴对称(n=0)和第一类非轴对称(n=1)模型, 验证了实验中轴对称射流模式向非轴对称射流模式的转换(图 22(d)).通过对时间、空间和时空不稳定性分析中基本速度型的选取进行讨论, 发现在实际问题中各个参数的影响要同时考虑, 因为各个参数之间也是相互影响的.此外, 针对实验中得到的高We下轴对称(n=0)向非轴对称(n=1)模式的转换, 对比了时间和空间不稳定性分析的结果, 发现只有空间不稳定性分析得到的结果能够和实验结果吻合, 这在一定程度上说明了在高We下空间不稳定性分析比时间不稳定性分析更可靠.

|
| 图 22 对单轴流动聚焦的理论预测和实验结果吻合. (a)射流形貌随液体流量速度呈现规律性变化(Si et al. 2009), (b)时间不稳定性理论对界面扰动波长的预测(Si et al. 2009), (c)时空不稳定性理论对滴和射流模式转换的预测(Si et al. 2009), (d)空间不稳定性理论对轴对称和非轴对称射流模式转换的预测(Si et al. 2010) |
此外, 电流动聚焦、复合流动聚焦等技术中射流不稳定性的理论研究也有少量工作已经开展(Li et al. 2014, Herrada et al. 2010, 李广滨2016). Li等(2014)基于电流动聚焦实验建立了用于带电射流不稳定性分析的物理模型, 分别开展了无黏和有黏线性稳定性分析.认为自由电荷只分布在液-气交界面上, 外部电场为轴向的均匀电场.在无黏模型中, 采用Kelvin-Helmholtz速度型, 得到了解析形式的色散关系; 在黏性模型中, 液体射流和驱动气体的基本速度型分别基于管流和误差函数构造.结果表明: (1)射流的不稳定性主要与轴对称(n=0)扰动和第一类非轴对称(n=1)扰动有关, 与其他扰动无关(n > 1时流动是稳定的); (2)界面处较强的黏性剪切以及驱动气体的惯性均能促进射流的失稳; (3)电场力与界面上的初始自由电荷密度Q0对射流不稳定性的影响是相互耦合的, 当Q0较小时轴向电场有抑制射流失稳的作用, 而当Q0较大时, 增大轴向电场强度将极大地促进射流的失稳; 同时还发现, 当Q0足够大时, 随着轴向电场强度的增大, 射流将从轴对称破碎模式转换到非轴对称破碎模式; (4)当内层液体的黏性较小时, 增大液体的黏性会促进射流的失稳, 驱动气体的黏性则会抑制射流的失稳; (5)表面张力对轴对称扰动有着双重影响而对非轴对称扰动起抑制作用. Herrada等(2010)开展了气驱同轴流动聚焦中同轴射流的不稳定性研究, 揭示了滴模式和射流模式的转换机理.李广滨(2016)进一步开展了液驱同轴流动聚焦的时间和时空不稳定性研究, 建立了三相“水-油-水”型复合射流模型, 并分析了过程参数对扰动增长率的影响, 揭示了实验中观察到的复杂现象的内在机理.
流动聚焦中不同的流动现象和流动模式是扰动在流体界面上发展和演化的结果.目前流动聚焦问题的不稳定性研究仍在开展当中, 复合射流以及带电射流问题的研究仍存在一定难度, 实验中涉及的很多物理问题尚未解决, 包括流场速度分布、射流表面自由电荷分布、流动模式及其转换、界面耦合、卫星液滴的产生、非牛顿流体射流的缠绕等.开展射流不稳定性分析将有助于理解流动聚焦的物理过程和流动规律以及揭示其内在力学机理, 对加强实验控制和改进制作工艺也都有重要的意义.
5 结束语流动聚焦是一种毛细流动现象, 是流体力学与材料学、化学、生物学、医学等多学科交叉的重要研究方向, 深入开展与流体力学相关的前沿基础科学问题研究对揭示其奥妙、总结其规律具有重大的科学价值.此外, 随着21世纪生命科学、生物医药技术、纳米技术等的迅猛发展, 该技术在科技领域和工程实践中显示了巨大的应用价值.本文回顾了流动聚焦的研究进展, 并进一步评述了流动聚焦涉及的关键力学问题.研究表明流动聚焦在制备微纳米量级的液滴、颗粒和胶囊方面具有一定的优势, 比如适用的材料范围广, 水溶性和油溶性材料均可; 过程可量化控制, 制备产物的尺寸存在尺度律; 材料利用度高, 理论上能够达到100%的包裹效率.此外, 该技术设备简单、稳定、易操作, 不存在流道浸湿特性控制等问题, 在相同的外部参数下能够保证每个设备的重复性, 因此比微流控芯片更适合工业集成化生产.目前不同流动结构的流动聚焦技术已经得到了一定的关注, 相应的物理现象和规律也在逐步地揭示出来.
在第2节中, 根据核心装置结构以及提供驱动力的方式不同, 将流动聚焦技术进行了分类介绍.单轴流动聚焦的结构最为简单, 主要涉及了液-气、液-液、气-液三种界面结构, 相关的实验、理论和数值研究都得到了广泛开展.在液-气流动聚焦中, 从毛细管流出的液体在周围高速流动气体驱动下穿过小孔, 可以形成稳定的锥-射流结构.液体射流不与小孔固壁接触, 离开小孔后在敞开式的环境中破碎成均匀的微液滴, 破碎频率可达到兆赫兹(MHz)的量级, 体现了该技术有别于微流控芯片的特点.如果将单轴流动聚焦核心装置中的单个毛细管替换成两个或多个毛细管的复合结构, 便形成复合流动聚焦.如果将流动聚焦和电雾化相结合, 使液体表面产生电荷的同时也提供电场力作用于被驱动流体, 能够显著降低所制备产物的尺寸, 称之为电流动聚焦.相比于单纯的流动聚焦, 电流动聚焦得到稳定锥-射流的参数范围更广, 射流雾化也更为剧烈.此外, 流动聚焦原理也已经被应用于微流控器件中, 包括二维微管道和玻璃微毛细管等, 形成了微流控流动聚焦技术, 近年来得到了快速的发展.
流动聚焦中流体的运动是一个复杂的多尺度、多界面物理过程, 涉及的关键力学问题包括过程控制、流动模式、尺度律和不稳定性分析等.在第3节中, 系统总结了流动聚焦基础研究的进展, 阐述了流动聚焦的实验和理论方法、定性和定量演化规律以及内在物理机制.在现阶段, 单轴流动聚焦的研究最为突出, 复合流动聚焦的研究还处于起步阶段.在实验方面, 已经建成了完善的实验平台, 包括流动生成系统和流场观测系统, 能够捕捉到清晰的流动图像, 可用于观测锥形和射流的微观形貌、分析过程参数的影响规律并区分不同的流动模式及其参数域.由于流动聚焦过程的多界面和多尺度效应, 目前数值模拟方面的进展十分有限, 主要利用商业软件对单轴流动聚焦开展了初步研究.在理论方面, 已经开展了复合射流的线性时间、时空和空间不稳定性分析, 推导了射流和液滴的尺寸同过程参数之间的尺度律关系.特别地, 在第4节中系统回顾了射流不稳定性的研究历史、方法以及进展, 并对流动聚焦中射流不稳定性的简化物理模型、控制方程和边界条件、主要研究成果等进行了总结.
通过改变流动聚焦的核心结构, 可以一步到位制备复杂结构的微胶囊, 因此这项技术在医学、药学、材料科学、化学等诸多领域都有潜在的应用价值.但是, 由于流动聚焦种类较多、起步较晚, 目前仍存在许多基础科学问题需要解决, 仍有许多物理规律和机理需要揭示.未来的问题可以概括为两个主要方面:一个是着眼于流动聚焦的研究方向, 解决前沿的基础科学问题; 另一个是着眼于流动聚焦的应用前景, 满足社会的重大实际需求.
复合流动聚焦能够实现微胶囊的结构和功能, 其制备过程具有多介质、多尺度、强非线性等复杂流动特征; 电流动聚焦能够大大降低微胶囊的尺寸, 其制备过程涉及了多场耦合条件下的多介质界面演化.在实际应用中, 当采用高分子材料溶液作为试剂时, 将会带来材料本构特性、溶剂挥发等对流场界面的影响; 当包裹纳米颗粒、细胞、蛋白质等时, 微流动中复合液滴或胶囊的行为特征和形态响应将与过程参数密切相关; 当收集制备的产物时, 将存在复合液滴或胶囊与流体界面或固壁之间的多相界面相互作用.此外, 复合射流中多介质流体界面之间的相互耦合将影响界面的扰动发展, 对制备的产物形貌也会带来变化.为了解决这些基础科学问题, 需要实验、理论和数值模拟相结合.在实验方面, 复合流动聚焦及电流动聚焦的流动模式及参数域需要完善, 非牛顿流体试剂有关的观测和分析有待开展, 产物的收集和表征需要进一步的研究.在理论方面, 线性不稳定性理论在多界面、多场耦合等复杂条件下的适用性尚需开展, 非线性和非模态不稳定性理论分析有待完成, 全局不稳定性理论也是具有挑战性的研究工作.此外, 还有待开展的工作包括多相、多尺度、高速条件下的数值方法研究和数值模拟研究, 以期为实验和理论提供准确的定量数据对比, 共同解决实际应用中包含的关键科学问题.总之, 流动聚焦只需一个步骤便可获得复杂结构的微胶囊, 能够实现制备过程的量化控制, 开展相关的基础科学问题研究对实际应用具有重要的指导意义, 也将促进流动聚焦的实用化进程, 推动科技和社会的进步.
| 陈晓东, 胡国庆. 2015. 微流控器件中的多相流动. 力学进展, 45 :201503. ( Chen X D, Hu G Q. 2015. Multiphase flow in microfluidic devices. Advances in Mechanics, 45:201503. ) |
| 陈晓慧, 张君鹏, 李广滨, 司廷, 尹协振. 2013. 电流动聚焦中非牛顿流体射流影响因素的实验研究. 实验力学, 28 :284–289. ( Chen X H, Zhang J P, Li G B, Si T, Yin X Z. 2013. Experimental study on the influencing factors of non-Newtonian fluid jets in electro-flow focusing. J. Exp. Mech., 28:284–289. ) |
| 陈效鹏. 2003.静电雾化电流体力学研究.[博士论文].合肥:中国科学技术大学. |
| 陈效鹏, 程久生, 尹协振. 2003. 电流体动力学研究进展及应用. 科学通报, 48 :637–646. doi:10.1360/03tb9136 ( Chen X P, Cheng J S, Yin X Z. 2003. Progress and application of electrohydrodynamics. Chinese Science Bulletin, 48:637–646. doi:10.1360/03tb9136 ) |
| 李芳. 2007.同轴带电射流的稳定性研究.[博士论文].合肥:中国科学技术大学. http://cdmd.cnki.com.cn/Article/CDMD-10358-2008039430.htm |
| 李广滨. 2016.复合流动聚焦的实验和理论研究.[博士论文].合肥:中国科学技术大学 Li G B. 2016.Experimental and theoretical investigation on compound flow focusing.[PhD Thesis]. Hefei:University of Science and Technology of China. http://cdmd.cnki.com.cn/Article/CDMD-10358-1016103170.htm |
| 李广滨, 司廷, 尹协振. 2012. 电场作用下无黏聚焦射流的时间不稳定性研究. 力学学报, 44 :876–883. ( Li G B, Si T, Yin X Z. 2012. Temporal instability study of an inviscid focusing jet under an electric field. Chinese J. Theo. Appl. Mech., 44:876–883. ) |
| 李战华, 吴健康, 胡国庆, 胡国辉.2012. 微流控芯片中的流体流动. 北京: 科学出版社 . ( Li Z H, Wu J K, Hu G Q, Hu G H.2012. Fluid Flow in Microfluidic Chips. Beijing: Science Press ). |
| 林炳承.2013. 微纳流控芯片实验室. 北京: 科学出版社 . |
| 司廷. 2009.流动聚焦的实验和理论研究.[博士论文]合肥:中国科学技术大学 Si T. Experimental and theoretical investigation on flow focusing.[PhD Thesis]. Hefei:University of Science and Technology of China. |
| 司廷, 李广滨, 田瑞军, 尹协振. 2011. 电场作用下流动聚焦的实验研究. 力学学报, 43 :1030–1036. ( Si T, Li G B, Tian R J, Yin X Z. 2011. Experimental study of the flow focusing under an electric field. Chinese J. Theor. Appl. Mech., 43:1030–1036. ) |
| 司廷, 刘志勇, 尹协振. 2008. 流动聚焦中锥形和射流直径影响因素的实验研究. 实验流体力学, 22 :21–26. ( Si T, Liu Z Y, Yin X Z. 2008. Experimental study of influencing parameters on the cone and the jet diameter in flow focusing. J. Exp. Fluid Mech., 22:21–26. ) |
| 司廷, 尹协振. 2011. 流动聚焦研究进展及其应用. 科学通报, 56 :537–546. doi:10.1360/972010-1639 ( Si T, Yin X Z. 2011. Progress and application of flow focusing. Chinese Science Bulletin, 56:537–546. doi:10.1360/972010-1639 ) |
| 尹协远, 孙德军. 2003.旋涡流动的稳定性.第1版.北京:国防工业出版社 Yin X Y, Sun D J. 2003.Vortex Stability. Beijing:National Defense Industry Press. |
| 尹协振, 李芳. 2009. 电雾化、电纺丝和带电射流稳定性研究. 力学与实践, 31 :1–7. ( Yin X Z, Li F. 2009. Electrospraying, electrospinning and instability of electrified jets. Mechanics in Engineering, 31:1–7. ) |
| Acero A J, Ferrera C, Montanero J M, Gañán-Calvo A M. 2012a. Focusing liquid microjets with nozzles. J. Micromech. Microeng., 22:065011. doi:10.1088/0960-1317/22/6/065011 |
| Acero A J, Montanero J M, Ferrera C, Herrada M A, Gañán-Calvo A M. 2012b. Enhancement of the stability of the flow focusing technique for low-viscosity liquids. J. Micromech. Microeng., 22:115039. doi:10.1088/0960-1317/22/11/115039 |
| Acero A J, Rebollo-Muñoz N, Montanero J M, Gañán-Calvo A M, Vega E J. 2013. A new flow focusing technique to produce very thin jets. J. Micromech. Microeng., 23:065009. doi:10.1088/0960-1317/23/6/065009 |
| Agnihotri S A, Mallikarjuna N N, Aminabhavi T M. 2004. Recent advances on chitosan-based micro-and nanoparticles in drug delivery. J. Control. Release, 100:5–28. doi:10.1016/j.jconrel.2004.08.010 |
| Anna S L, Bontoux N, Stone H A. 2003. Formation of dispersions using 'flow focusing' in microchannels. Appl. Phys. Lett., 82:364–67. doi:10.1063/1.1537519 |
| Artana G, Romat H, Touchard G. 1998. Theoretical analysis of linear stability of electrified jets flowing at high velocity inside a coaxial electrode. J. Electrost., 43:83–100. doi:10.1016/S0304-3886(97)00163-0 |
| Artana G, Touchard G, Romat H. 1997. Absolute and convective instabilities in an electrified jet. J.Electrost., 40:33–38. |
| Bailey A G.1988. Electrostatic Spraying of Liquids. UK: Research Studies Press Ltd . |
| Barrero A, Loscertales I G. 2007. Micro-and nanoparticles via capillary flows. Annu. Rev. Fluid Mech., 39:89–106. doi:10.1146/annurev.fluid.39.050905.110245 |
| Boeck T, Zaleski S. 2005. Viscous versus inviscid instability of two-phase mixing layers with continuous velocity profile. Phys. Fluids, 17:032106. doi:10.1063/1.1862234 |
| Chandrasekhar S. 1961. The capillary instability of a liquid jet. In Hydrodynamic and Hydromagnetic Stability. Oxford:Oxford University Press, 537-542 . |
| Chang S F, Si T, Zhang S W, Merrick M A, Cohn D E, Xu R X. 2016. Ultrasound mediated destruction of multifunctional microbubbles for image guided delivery of oxygen and drugs. Ultrason. Sonochem., 28:31–38. doi:10.1016/j.ultsonch.2015.06.024 |
| Chauhan A, Maldarelli C, Papageorgiou D T, Rumschitzki D S. 2000. Temporal instability of compound threads and jets. J. Fluid Mech., 420:1–25. doi:10.1017/S0022112000001282 |
| Chauhan A, Maldarelli C, Rumschitzki D S, and Papageorgiou D T. 1996. Temporal and spatial instability of an inviscid compound jet. Rheol. Acta, 35:567–583. doi:10.1007/BF00396508 |
| Chu L Y, Utada A S, Shah R K, Kim J W, Weitz D A. 2007. Controllable monodisperse multiple emulsions. Angew. Chem., 119:9128–9132. doi:10.1002/(ISSN)1521-3757 |
| Clanet C, Lasheras J C. 1999. Transition from dripping to jetting. J. Fluid Mech., 383:307–326. doi:10.1017/S0022112098004066 |
| Cohen I, Nagel S R. 2002. Scaling at the selective withdrawal transition through a tube suspended above the fluid surface. Phys. Rev. Lett., 88:074501. doi:10.1103/PhysRevLett.88.074501 |
| Donnelly R J, Glaberson W. 1966. Experimnets on the capillary instability of a liquid jet. Proc. R. Soc.London Ser. A., 290:547–556. doi:10.1098/rspa.1966.0069 |
| Eggers J. 1997. Nonlinear dynamics and breakup of free-surface flows. Rev. Mod. Phys., 69:865–929. doi:10.1103/RevModPhys.69.865 |
| Eggers J, Villermaux E. 2008. Physics of liquid jets. Rep. Prog. Phys., 71:036601. doi:10.1088/0034-4885/71/3/036601 |
| Elhefnawy A F F, Agoor B M H, Elcoot A E K. 2001. Nonlinear electrohydrodynamic stability of a finitely conducting jet under an axial electric field. Physica A, 297:368–388. doi:10.1016/S0378-4371(01)00173-X |
| Elhefnawy A F F, Moatimid G M, Elcoot A E K. 2004. Nonlinear electrohydrodynamic instability of a finitely conducting cylinder:Effect of interfacial surface charges. Z. angew. Math. Phys., 55:63–91. doi:10.1007/s00033-003-1115-y |
| Eroglu H, Chigier N, Farago Z. 1991. Coaxial atomizer liquid intact lengths. Phys. Fluids A, 3:303–308. doi:10.1063/1.858139 |
| Fernández de la Mora J. 2007. The fluid dynamics of Taylor cones. Annu. Rev. Fluid Mech., 39:217–243. doi:10.1146/annurev.fluid.39.050905.110159 |
| Freiberg S, Zhu X X. 2004. Polymer microspheres for controlled drug release. Int. J. Pharm., 282:1–18. doi:10.1016/j.ijpharm.2004.04.013 |
| Funada T, Joseph D D. 2002. Viscous potential flow analysis of capillary instability. Intl J. Multiphase Flow, 28:1459–1478. doi:10.1016/S0301-9322(02)00035-6 |
| Gaonkar A G, Vasisht N, Khare A R, Sobel R.2014. Microencapsulation in the Food Industry:A Practical Implementation Guide. Amsterdam: Elsevier . |
| Graham D Y, Lacey Smith J, Bouvet A A. 1990. What happens to tablets and capsules in the stomach:endoscopic comparison of disintegration and dispersion characteristics of two microencapsulated potassium formulations. J. Pharm. Sci., 79:420–424. doi:10.1002/jps.2600790512 |
| Gañán-Calvo A M. 1997. Cone-jet analytical extension of Taylor's electrostatic solution and the asymptotic universal scaling laws in electrospraying. Phys. Rev. Lett., 79:217–220. doi:10.1103/PhysRevLett.79.217 |
| Gañán-Calvo A M. 1998. Generation of steady liquid microthreads and micron-sized monodisperse sprays in gas streams. Phys. Rev. Lett., 80:285–288. doi:10.1103/PhysRevLett.80.285 |
| Gañán-Calvo A M. 2004. Perfectly monodisperse microbubbling by capillary flow focusing:an alternate physical description and universal scaling. Phys. Rev. E, 69:027301. doi:10.1103/PhysRevE.69.027301 |
| Gañán-Calvo A M. 2005. Enhanced liquid atomization:from flow-focusing to flow-blurring. Appl. Phys.Lett., 86:214101. doi:10.1063/1.1931057 |
| Gañán-Calvo A M. 2007a. Electro-flow focusing:the high-conductivity low-viscosity limit. Phys. Rev.Lett., 98:134503. doi:10.1103/PhysRevLett.98.134503 |
| Gañán-Calvo A M. 2007b. Absolute instability of a viscous hollow jet. Phys. Rev. E, 75:027301. doi:10.1103/PhysRevE.75.027301 |
| Gañán-Calvo A M, Barrero A. 1999. A novel pneumatic technique to generate steady capillary microjets. J. Aerosol Sci., 30:117–125. doi:10.1016/S0021-8502(98)00029-9 |
| Gañán-Calvo A M, Fernández J M, Oliver A M, Marquez M. 2004. Coarsening of monodisperse wet micro-foams. Appl. Phys. Lett., 84:4989–4991. doi:10.1063/1.1762992 |
| Gañán-Calvo A M, Ferrera C, Torregrosa M, Herrada M A, Marchand M. 2011. Experimental and numerical study of the recirculation flow inside a liquid meniscus focused by air. Microfluid. Nanofluid., 11:65–74. doi:10.1007/s10404-011-0774-9 |
| Gañán-Calvo A M, González-Prieto R, Riesco-Chueca P, Herrada M A, Flores-Mosquera M. 2007. Focusing capillary jets close to the continuum limit. Nat. Phys., 3:737–742. doi:10.1038/nphys710 |
| Gañán-Calvo A M, Gordillo J M. 2001. Perfectly monodisperse mircobubbling by capillary flow focusing. Phys. Rev. Lett., 87:274501. doi:10.1103/PhysRevLett.87.274501 |
| Gañán-Calvo A M, Herrada M A, Garstecki P. 2006a. Bubbling in unbounded coflowing liquids. Phys. Rev.Lett., 96:124504. doi:10.1103/PhysRevLett.96.124504 |
| Gañán-Calvo A M, López-Herrera J M, Riesco-Chueca P. 2006b. The combination of electrospray and flow focusing. J. Fluid Mech., 566:421–445. doi:10.1017/S0022112006002102 |
| Gañán-Calvo A M, Martín-Banderas L, González-Prieto R, Rodríguez-Gil A, Berdún-Alvarez T, Cebolla Á, Chávez S, Flores-Mosquera M. 2006c. Straightforward production of encoded microbeads by flow focusing:potential applications for biomolecule detection. Int. J. Pharm., 324:19–26. doi:10.1016/j.ijpharm.2006.05.032 |
| Gañán-Calvo A M., Montanero J M. 2009. Revision of capillary cone-jet physics:Electrospray and flow focusing. Phys. Rev. E, 79:066305. doi:10.1103/PhysRevE.79.066305 |
| Gañán-Calvo A M, Castro-Hernández E, Flores-Mosquera M, Martín-Banderas L. 2015. Massive, generic, and controlled microencapsulation by flow focusing:some physicochemical aspects and new applications. J.Flow Chem., 5 . doi:10.1556/JFC-D-14-00022 |
| Gañán-Calvo A M, Montanero J M, Martín-Banderas L, Flores-Mosquera M. 2013. Building functional materials for health care and pharmacy from microfluidic principles and flow focusing. Adv. Drug Deliv.Rev., 65:1447–1469. doi:10.1016/j.addr.2013.08.003 |
| Gañán-Calvo A M, Riesco-Chueca P. 2006. Jetting-dripping transition of a liquid jet in a lower viscosity co-flowing immiscible liquid:the minimum flow rate in flow focusing. J. Fluid Mech., 553:75–84. doi:10.1017/S0022112006009013 |
| Goedde E F, Yuen M C. 1970. Experiments on liquid jet instability. J. Fluid Mech., 40:495–512. doi:10.1017/S0022112070000289 |
| Gordillo J M, Gañán-Calvo A M, Pérez-Saborid M. 2001a. Monodisperse microbubbling:absolute instabil-ities in coflowing gas-liquid jets. Phys. Fluids, 13:3839–3842. doi:10.1063/1.1416188 |
| Gordillo J M, Pérez-Saborid M, Gañán-Calvo A M. 2001b. Linear stability of co-flowing liquid-gas jets. J.Fluid Mech., 448:23–51. |
| Gu X L, Zhu X, Kong X Z, Tan Y. 2010. Comparisons of simple and complex coacervations for preparation of sprayable insect sex pheromone microcapsules and release control of the encapsulated pheromone molecule. J. Microencapsul., 27:355–364. doi:10.3109/02652040903221532 |
| Herrada M A, Gañán-Calvo A M, Guillot P. 2008a. Spatiotemporal instability of a confined capillary jet. Phys. Rev. E, 78:046312. doi:10.1103/PhysRevE.78.046312 |
| Herrada M A, Gañán-Calvo A M, Ojeda-Monge A, Bluth B, Riesco-Chueca P. 2008b. Liquid flow focused by a gas:Jetting, dripping, and recirculation. Phys. Rev. E, 78:036323. doi:10.1103/PhysRevE.78.036323 |
| Herrada M A, Montanero J M, Ferrera C, Gañán-Calvo A M. 2010. Analysis of the dripping-jetting transition in compound capillary jets. J. Fluid Mech., 649:523–536. doi:10.1017/S0022112010000443 |
| Hertz C H, Hermanrud B. 1983. A liquid compound jet. J. Fluid Mech., 131:271–287. doi:10.1017/S0022112083001329 |
| Hettiarachchi K, Talu E, Longo M L, Dayton P A, Lee A P. 2007. On-chip generation of microbubbles as a practical technology for manufacturing contrast agents for ultrasonic imaging. Lab Chip, 7:463–468. doi:10.1039/b701481n |
| Holgado M A, Arias J L, Cózar M J, Alvarez-Fuentes J, Gañán-Calvo A M, Fernández-Arévalo M. 2008. Synthesis of lidocaine-loaded PLGA microparticales by flow focusing effects on drug loading and release properties. Int. J. Pharm., 358:27–35. doi:10.1016/j.ijpharm.2008.02.012 |
| Huerre P, Monkewitz P A. 1985. Absolute and convective instabilities in free shear flows. J. Fluid Mech., 159:151–168. doi:10.1017/S0022112085003147 |
| Huerre P, Monkewitz P A. 1990. Local and global instabilities in spatially developing flows. Annu. Rev.Fluid Mech., 22:473–537. doi:10.1146/annurev.fl.22.010190.002353 |
| Kang D J, Lin S P. 1989. Breakup of swirling liquid jets. Int. J. Eng. Fluid Mech., 2:47–62. |
| Keller J B, Rubinow S I, Tu Y O. 1973. Spatial instability of a jet. Phys. Fluids, 16:2052–2055. doi:10.1063/1.1694264 |
| Kim S H, Weitz D A. 2011. One-step emulsification of multiple concentric shells with capillary microfluidic devices. Angew. Chem. Int. Ed. Engl., 50:8731–8734. doi:10.1002/anie.201102946 |
| Kong X Z, Gu X, Zhu X, Zhang Z. 2009. Spreadable dispersion of insect sex pheromone capsules, preparation via complex coacervation and release control of the encapsulated pheromone component molecule. Biomed.Microdevices, 11:275–285. doi:10.1007/s10544-008-9234-z |
| Kumar M. 2000. Nano and microparticles as controlled drug delivery devices. J. Pharm. Pharm. Sci., 3:234–258. |
| Laryea G N, No S Y. 2003. Development of electrostatic pressure-swirl nozzle for agricultural applications. J. Electrostat., 57:129–142. doi:10.1016/S0304-3886(02)00122-5 |
| Lasheras J C, Hopfinger E J. 2000. Liquid jet instability and atomization in a coaxial gas stream. Annu.Rev. Fluid Mech., 32:275–308. doi:10.1146/annurev.fluid.32.1.275 |
| Law S E. 2001. Agricultural electrostatic spray application:a review of significant research and development during the 20th century. J. Electrostat., 51:25–42. |
| Leib S J, Goldstein M E. 1986a. Convective and absolute instability of a viscous liquid jet. Phys. Fluids, 29:952–954. doi:10.1063/1.866000 |
| Leib S J, Goldstein M E. 1986b. The generation of capillary instabilities on a liquid jet. J. Fluid Mech., 168:479–500. doi:10.1017/S0022112086000472 |
| Li F, Yin X Y, Yin X Z. 2005. Linear instability analysis of an electrified coaxial jet. Phys. Fluids, 17:077104. doi:10.1063/1.1996571 |
| Li F, Yin X Y, Yin X Z. 2006. Linear instability of a coflowing jet under an axial electric field. Phys. Rev.E, 74:036304. doi:10.1103/PhysRevE.74.036304 |
| Li F, Yin X Y, Yin X Z. 2008. Instability of a viscous coflowing jet in a radial electric field. J. Fluid Mech., 596:285–311. |
| Li F, Yin X Y, Yin X Z. 2009. Axisymmetric and non-axisymmetric instability of an electrified viscous coaxial jet. J. Fluid Mech., 632:199–225. doi:10.1017/S0022112009006429 |
| Li G B, Luo X S, Si T, Xu RX. 2014. Temporal instability of coflowing liquid-gas jets under an electric field. Phys. Fluids, 26:054101. doi:10.1063/1.4875109 |
| Lin S P.2003. Breakup of Liquid Sheets and Jets. Cambridge: Cambridge University Press . |
| Lin S P., Ch en, J. N. 1998. Role played by the interfacial shear in the instability mechanism of a viscous liquid jet surrounded by a viscous gas in a pipe. J. Fluid Mech., 376:37–51. doi:10.1017/S0022112098002894 |
| Lin S P, Ibrahim E A. 1990. Instability of a viscous liquid jet surrounded by a viscous gas in a pipe. J.Fluid Mech., 218:641–658. doi:10.1017/S002211209000115X |
| Lin S P, Lian Z W. 1989. Absolute instability in a gas. Phys. Fluids A, 1:490–493. |
| Lin S P, Lian Z W. 1993. Absolute and convective instability of a viscous liquid jet surrounded by a viscous gas in a vertical pipe. Phys. Fluids A, 5:771–773. doi:10.1063/1.858662 |
| Lin S P, Reitz R D. 1998. Drop and spray formation from a liquid jet. Annu. Rev. Fluid Mech., 30:85–105. doi:10.1146/annurev.fluid.30.1.85 |
| López-Herrera J M, Gañán-Calvo A M, Perez-Saborid M. 1999. One-dimensional simulation of the breakup of capillary jets of conducting liquids. Application to EHD spraying. J. Aerosol Sci., 30:895–912. |
| López-Herrera J M, Riesco-Chueca P, Gañán-Calvo A M. 2005. Linear stability analysis of axisymmetric perturbations in imperfectly conducting liquid jets. Phys. Fluids, 17:034106. doi:10.1063/1.1863285 |
| Loscertales I G, Barrero A, Guerrero I, Cortijo R, Marquez M, Ganan-Calvo A M. 2002. Micro/nano encapsulation via electrified coaxial liquid jets. Science, 295:1695–1698. doi:10.1126/science.1067595 |
| Martín-Banderas L, Flores-Mosquera M, Riesco-Chueca P, Rodríguez-Gil A, Cebolla A, Chávez S, Gañán-Ćalvo A M. 2005. Flow Focusing:A Versatile Technology to Produce Size-Controlled and Specific Mor-phology Microparticles. Small, 7:688–692. |
| Martín-Banderas L, Rodríguez-Gil A, Cebolla A, Chávez S, Berdún-Alvarez T, Fernendez-Garcia J M, Flores-Mosquera M, Gañán-Calvo A M. 2006. Towards High-Throughput Production of Uniformly En-coded Microparticles. Adv. Mater., 18:559–564. doi:10.1002/(ISSN)1521-4095 |
| Melcher J R.1963. Field-coupled surface waves. Cambridge MA: MIT . |
| Michelson D.1990. Electrostatic atomization. New York: American Institute of Physics . |
| Monkewitz P A. 1990. The role of absolute and convective instability in predicting the behavior of fluid systems. Eur. J. Mech. B/Fluids, 9:395–413. |
| Montanero J M, Gañán-Calvo A M. 2008a. Stability of coflowing capillary jets under nonaxisymmetric perturbations. Phys. Rev. E, 77:046301. |
| Montanero J M, Gañán-Calvo A M. 2008b. Viscoelastic effects on the jetting-dripping transition in co-flowing capillary jets. J. Fluid Mech., 610:249–260. |
| Nie Z, Xu S, Seo M, Lewis P C, Kumacheva E. 2005. Polymer particles with various shapes and morphologies produced in continuous microfluidic reactors, J. Am. Chem. Soc., 127:8058–8063. doi:10.1021/ja042494w |
| Ponce-Torres A, Montanero J M, Vega E J, Gañán-Calvo A M. 2016. The production of viscoelastic capillary jets with gaseous flow focusing. J. Non-Newton. Fluid Mech., 229:8–15. doi:10.1016/j.jnnfm.2016.01.004 |
| Radev S, Shkadov V. 1985. On a stability of two-layer capillary jet. Theor. Appl. Mech., 16:68–75. |
| Radev S, Tchavdarov B. 1988. Linear capillary instability of compound jets. Intl J. Multiphase Flow, 14:67–79. doi:10.1016/0301-9322(88)90034-1 |
| Rayleigh L. 1878. On the instability of jets. Proc. London Math. Soc., 10:4–13. |
| Rayleigh L. 1879. On the capillary phenomenon of jets. Proc. R. Soc. London, 29:71–97. doi:10.1098/rspl.1879.0015 |
| Rayleigh L. 1882. On the equilibrium of liquid conducting masses charged with electricity. Philos. Mag., 14:184–186. doi:10.1080/14786448208628425 |
| Rayleigh L. 1892. On the instability of a cylinder of viscous liquid under capillary force. Phil. Mag., 34:145–154. doi:10.1080/14786449208620301 |
| Reitz R D, Bracco F V. 1982. Mechanism of atomization of a liquid jet. Phys. Fluids, 25:1730–1742. doi:10.1063/1.863650 |
| Reitz R D, Bracco F V. 1986. Mechanisms of breakup of round liquid jets.//Cheremisnoff N ed. The Encyclopedia of Fluid Mechanics, Houston:Gulf. 233-249. |
| Reneker D H, Yarin A L. 2008. Electrospinning jets and polymer nanofibers. Polymer, 49:2387–2425. doi:10.1016/j.polymer.2008.02.002 |
| Reneker D H, Yarin A L, Fong H. 2000. Bending instability of electrically charged liquid jets of polymer solutions in electrospinning. J. Appl. Phys., 87:4531–4547. doi:10.1063/1.373532 |
| Rosell-Llompart J, Gañán-Calvo A M. 2008. Turbulence in pneumatic flow focusing and flow blurring regimes. Phys. Rev. E, 77:036321. doi:10.1103/PhysRevE.77.036321 |
| Sanz A, Meseguer J. 1985. One-dimensional linear analysis of the compound jet. J. Fluid Mech., 159:55–68. doi:10.1017/S0022112085003093 |
| Saville D A. 1997. Electrohydrodynamics:the Taylor-Melcher leaky dielectric model. Annu. Rev. Fluid Mech., 29:27–64. doi:10.1146/annurev.fluid.29.1.27 |
| Sevilla A, Gordillo J M, Martínez-Bazán C. 2002. The effect of the diameter ratio on the absolute and convective instability of free coflowing jets. Phys. Fluids, 14:3028–3038. doi:10.1063/1.1496511 |
| Seo M, Paquet C, Nie Z, Xu S, Kumacheva E. 2007. Microfluidic consecutive flowfocusing droplet generators. Soft Matter, 3:986–992. doi:10.1039/b700687j |
| Sheeran P S, Dayton P A. 2012. Phase-Change Contrast Agents for Imaging and Therapy. Current Phar-maceutical Design, 18:2152–2165. doi:10.2174/138161212800099883 |
| Shkadov V Y, Sisoev G M. 1996. Instability of a two-layer capillary jet. Intl J. Multiphase Flow, 22:363–377. doi:10.1016/0301-9322(95)00073-9 |
| Si T, Feng H X, Luo X S, Xu R X. 2015. Formation of steady compound cone-jet modes and multilayered droplets in a tri-axial capillary flow focusing device. Microfluid. Nanofluid., 18:967–977. doi:10.1007/s10404-014-1486-8 |
| Si T, Li F, Yin X Y, Yin X Z. 2009. Modes in flow focusing and instability of coaxial liquid-gas jets. J.Fluid Mech., 629:1–23. doi:10.1017/S0022112009006211 |
| Si T, Li F, Yin X Y, Yin X Z. 2010. Spatial instability of co-flowing liquid-gas jets in capillary flow focusing. Phys. Fluids, 22:112105. doi:10.1063/1.3490066 |
| Si T, Li G B, Wu Q, Zhu Z Q, Luo X S, Xu R X. 2016a. Optical droplet vaporization of nanoparticle-loaded stimuli-responsive microbubbles. Appl. Phys. Lett., 108:111109. doi:10.1063/1.4944539 |
| Si T, Yin C S, Gao P, Li G B, Ding H, He X M, Xie B, Xu R X. 2016b. Steady cone-jet mode in compound-fluidic electro-flow focusing for fabricating multicompartment microcapsules. Appl. Phys. Lett., 108:021601. doi:10.1063/1.4939632 |
| Si T, Zhang L L, Li G B, Roberts C J, Yin X Z, Xu R X. 2013. Experimental design and instability analysis of coaxial electrospray process for microencapsulation of drugs and imaging agents. J. Biomed. Opt., 18:075003. doi:10.1117/1.JBO.18.7.075003 |
| Sterling A M, Sleicher C A. 1975. The instability of capillary jets. J. Fluid Mech., 68:477–495. doi:10.1017/S0022112075001772 |
| Taylor G I. 1940. Generation of ripples by wind blowing over viscous fluids//Batchelor G K ed. The Scientific Papers of G.I. Taylor. Cambridge:Cambridge University Press. 244-254. |
| Taylor G I. 1964. Disintegration of water drops in an electric field. Proc. R. Soc. Lond. A, 280:383–397. doi:10.1098/rspa.1964.0151 |
| Tomotika S. 1935. On the instability of a cylindrical thread of a viscous liquid surrounded by another viscous fluid. Proc. R. Soc. London Ser. A, 150:322–337. doi:10.1098/rspa.1935.0104 |
| Utada A S, Lorenceau E, Link D R, Kaplan P D, Stone H A, Weitz D A. 2005. Monodisperse double emulsions generated from a microcapillary device. Science, 308:537–541. doi:10.1126/science.1109164 |
| Vega E J, Gañán-Calvo A M, Montanero J M, Cabezas M G, Herrada M A. 2013. A novel technique for producing metallic microjets and microdrops. Microfluid. Nanofluid., 14:101–111. doi:10.1007/s10404-012-1027-2 |
| Vega E J, Montanero J M, Herrada M A, Gañán-Calvo A M. 2010. Global and local instability of flow focusing:The influence of the geometry. Phys. Fluids, 22:064105. doi:10.1063/1.3450321 |
| Vladisavljevi G T, Khalid N, Neves M A., Kuroiwa T, Nakajima M, Uemura K, Ichikawa S, Kobayashi I. 2013. Industrial lab-on-a-chip:Design, applications and scale-up for drug discovery and delivery. Adv.Drug Deliv. Rev., 65:1626–1663. doi:10.1016/j.addr.2013.07.017 |
| Wang H, Agarwal P, Zhao S, Yu J, Lu X, He X. 2015. A biomimetic hybrid nanoplatform for encapsulation and precisely controlled delivery of theranostic agents. Nature Comm., 6:10081. doi:10.1038/ncomms10081 |
| Weber C Z. 1931. Zum Zerfall eines Flussigkeitsstrahles. Math. Mech., 11:136–154. |
| Wu P K, Tseng L K, Faeth G M. 1992. Primary breakup in gas/liquid mixing layers for turbulent liquids. At. Sprays, 2:295–318. doi:10.1615/AtomizSpr.v2.i3 |
| Xiao J, Yu H, Yang J. 2011. Microencapsulation of sweet orange oil by complex coacervation with soybean protein isolate/gum Arabic. Food Chem., 125:1267–1272. doi:10.1016/j.foodchem.2010.10.063 |
| Xu J S, Huang J, Qin R, Hinkle G H, Povoski S P, Martin E W, Xu R X. 2010. Synthesizing and binding dual-mode poly (lactic-co-glycolic acid)(plga) nanobubbles for cancer targeting and imaging. Biomaterials, 31:1716–1722. doi:10.1016/j.biomaterials.2009.11.052 |
| Xu R X, Huang J, Xu J S, Sun D, Hinkle G H, Martin E W, Povoski S P. 2009. Fabrication of indocya-nine green encapsulated biodegradable microbubbles for structural and functional imaging of cancer. J.Biomed. Opt., 14:034020. doi:10.1117/1.3147424 |
| Yarin A L.1993. Free Liquid Jets and Films:Hydrodynamic and Rheology. Essex: Longman Science and Technology . |
| Yarin A L, Koombhongse, Reneker D H. 2001. Bending instability in electrospinning of nanofibers. J. Appl.Phys., 89:3018–3026. doi:10.1063/1.1333035 |
| Yecko P, Zaleski S, Fullana J M. 2002. Viscous modes in two-phase mixing layers. Phys. Fluids, 14:4115–4122. doi:10.1063/1.1513987 |
| Yow H N, Routh A F. 2006. Formation of liquid core-polymer shell microcapsules. Soft Matter, 2:940–949. doi:10.1039/B606965G |
| Yuan S, Lei F, Liu Z F, Tong Q P, Si T, Xu R X. 2015. Coaxial electrospray of curcumin-loaded microparticles for sustained drug release. Plos One, 10:e0132609. doi:10.1371/journal.pone.0132609 |
| Zakaria K. 2000. Nonlinear instability of a liquid jet in the presence of a uniform electric field. Fluid Dyn.Res., 26:405–420. doi:10.1016/S0169-5983(99)00021-0 |
| Zeleny J. 1914. The electrical discharge from liquid points and a hydrostatic method of measuring the electric intensity at their surface. Phys. Rev., 3:69–91. doi:10.1103/PhysRev.3.69 |
| Zeleny J. 1915. On the conditions of instability of electrified drops, with applications to the electric discharge from liquid points. Proc. Camb. Phil. Soc., 18:71–83. |
| Zhang L L, Huang J W, Si T, Xu R X. 2012. Coaxial electrospray of microparticles and nanoparticles for biomedical applications. Expert Rev. Med. Devices, 9:595–612. doi:10.1586/erd.12.58 |
| Zhang L L, Si T, Fischer A, Letson A, Yuan S, Roberts C J, Xu R X. 2015. Coaxial electrospray of ranibizumab-loaded microparticles for sustained release of anti-VEGF therapies. PloS One, 10:e0135608. doi:10.1371/journal.pone.0135608 |
| Zhao C. 2013. Multiphase flow microfluidics for the production of single or multiple emulsions for drug delivery. Adv. Drug Deliv. Rev., 65:1420–1446. doi:10.1016/j.addr.2013.05.009 |
| Zhu Z Q, Si T, Xu R X. 2015. Microencapsulation of Indocyanine Green for potential applications in image-guided drug delivery. Lab Chip, 15:646–649. doi:10.1039/C4LC01032A |
| Zhu Z Q, Wu Q, Li G B, Han S Y, Si T, Xu R X. 2016. Microfluidic fabrication of stimuli-responsive microdroplets for acoustic and optical droplet vaporizations. J. Mater. Chem. B, 4:2723–2730. doi:10.1039/C5TB02402A |



