Sloshing must be considered for almost any moving vehicle or structure containing a liquid with a free surface and can be the result of resonant excitation of the tank liquid. Excitation with frequencies near the lowest natural frequency of the liquid motion is of primary practical interest. Sloshing can also be the result of transient motion, for instance, when we spill coffee from our coffee cup. Since foam dampens sloshing, it is easier to carry a glass of beer(Sauret et al. 2015). The fact that sloshing may strongly interact with the dynamics of the carrying "body" is evident when we carry a bucket of water. If sloshing starts in the bucket, it is difficult to stop it.
The hydrodynamics of sloshing can be complicated. Its understanding requires a combination of theory, computational fluid dynamics(CFD), and experiments. We start out with exemplifying resonant liquid motions in various engineering fields. Ship tank applications require that nonlinear free-surface effects are accounted for. Then an analytically based description of global sloshing flow follows. Finally, we consider sloshing-induced slamming where the effect on tank design is often based on model tests. However, scaling of impact slosh pressures from model to full scale in prismatic liquefied natural gas(LNG)ship tanks and its effect on structural stresses is not completely understood. When not explicitly mentioned, the textbook by Faltinsen and Timokha(2009)provides further details as well as many references on the presented subjects.
2 Resonant liquid motion in various engineering fieldsThe majority of resonant motions of an incompressible liquid with practical importance is associated with free-surface gravity waves. However, if a fabric structure is completely filled with an incompressible liquid, the structural elasticity causes resonances inside the container. The word fabric means a sandwich structure coated with a polymer on both sides. It is a very flexible structure with negligible bending stiffness. The consequence is small storage place when empty. A container as that has been proposed for water transportation. In order to find the natural frequencies we must analyze the coupling of the internal and external flow with the elastic behavior of the fabric structure. An example on resonant motions of a compressible gas is what happen in the supporting air cushion of a surface effect ship(SES)with uniform pressure and acoustic wave resonances(Faltinsen 2005). The resulting "cobblestone" oscillations occurring in small sea states represent a comfort problem in passenger transportation.
Resonant free surface flows in tanks in aircraft, missiles, and rockets have been the focus of extensive research. For these vehicles, sloshing will have a strong influence on their dynamic stability. The sloshing technology developed for space applications is not directly applicable to ship cargo tanks because emphasis was placed on frequencies and total forces as they related to control system requirements and, therefore, the effect of impact slosh pressure on structural requirements has not been studied to any extent.
A large percentage of the initial weight of boost or launch vehicles is fuel. A concern is that the dominant fuel-slosh frequencies are close to the control system frequencies and/or the elastic body bending frequencies. The consequence can be dynamic instabilities and large amplitude response of the launch vehicles. Vertical excitation of propellant tanks can be linked to Mathieu type of instabilities and Faraday waves.
The fact that spacecrafts orbiting around the Earth are in close to a weightless condition affects significantly sloshing in fuel tanks. Surface tension plays a dominant role instead of gravity. Spacecraft and rockets can be spinning as a gyroscope as a matter of stabilization and in order to moderate the effects of solar heating.
Sloshing induced loads on onshore tanks due to earthquake motions must be considered in their design. Acceleration spectra for vertical and horizontal accelerations define the tank excitation. Sloshing is a design consideration of closed marine salmon farms. The reason for using a closed fish cage instead of a net structure is to avoid salmon lice.
Sloshing of liquid cargo within tank trucks affects the lateral stability of the carrying vehicle. A tank vehicle with partially filled tank(s)may roll over due to sloshing because of a fast transverse maneuver(cornering)such as rapidly changing lanes on a highway. A sudden stop of the vehicle causes longitudinal sloshing in the tank. This is particularly critical if the tank is unbaffled or is not divided into compartments. The latter is the case for transportation of food(e.g., milk)due to sanitary cleaning reasons. Shallow liquid types of waves develop for such tanks at a sudden stop of the vehicle. When the waves hit the end of the tank, they push the vehicle in the wave direction. The consequence is, for instance, that they can shove a stopped truck out into an intersection. Commercial driver's manuals contain warnings about the sloshing phenomena described above. Sloshing in partially filled containers must also be considered in the dynamics of freight trains and can contribute to derailment and rollover when passing through tight turns.
Large scale sloshing in a lake with steep sides may be the result of a landslide or earthquake. During dam construction, such circumstances should be investigated. Large scale sloshing may also occur in harbors and lakes and even on an oceanic scale. Important natural periods are from a few minutes for artificial harbors to several hours for large natural bays. The corresponding flow is associated with shallow water conditions. Energy losses are due to waves propagating out from the harbor opening, bottom friction and flow separation at the opening. Resonance oscillations in harbors are associated with forced oscillations caused by external disturbances. Because storm waves may have periods up to 20 s, they cannot directly excite harbor resonance. However, nonlinear wave-wave interaction taking place in the shoaling zone matters. The vertical water surface motion may be one or several meters at certain points in the basin at harbor resonance. However, the main concern is the shallow water effect causing large horizontal motions on a moored ship near the nodal points of the harbor resonance. The consequence can be failure of the mooring system so that the ship comes adrift.
A partially filled ship tank can experience violent liquid motion when the wave-induced ship motions contain energy near the highest natural period for the liquid motion inside the tank. Ingress of water to a damaged ship and the resulting dynamics of the water on large deck areas can result in sloshing and affect the capsizing process. Sloshing in a partially filled ship tank may occur, for instance, because of collision between two ships, grounding or collision of a ship with ice.
There is a variety of ship tank shapes comprising rectangular, prismatic, tapered and spherical tanks as well as horizontal cylindrical tanks. The liquid may be oil, LNG, water or high-density cargoes like molasses and caustic soda. Even though a tank is completely filled with liquid, the angular ship motions cause liquid motion relative to the tank motion.
Because sloshing is a typical resonance phenomenon, it is not necessarily the most extreme ship motions or external wave loads that cause the most severe sloshing. This implies that external wave-induced loads can often be described with linear free-surface conditions. However, nonlinearities must often be accounted for when describing the tank liquid motions. Further, there is an interaction between sloshing and the ship motions in a seaway. Because it is the highest sloshing period(natural period)that is of prime interest, vertical tank excitation is of secondary importance.
The hydrodynamic loading inside a tank can be classified either as impact(slamming)loads or "dynamic", non-impulsive, loads. In this context, dynamic loads mean loads that have dominant time variations on the time scale of the sloshing period, while impact loads may last only from 10-3 s to 10-2 s. Sloshing loads must be considered in the context of structural stress response and are of significance for both ultimate limit state(ULS)and fatigue limit state(FLS)assessments. ULS is a limit state(collapse, tearing-off, etc.)due to one-time extreme loads while FLS is a limit state caused by repetitive loading resulting in fatigue.
Loads on any internal structures must be considered. Here the high-cycle fatigue may be of concern. Viscous flow separation is likely to occur and Reynolds number scale effects matter, in particular, when the separation does not occur from sharp corners, as in the case of pump towers in LNG tanks. Some internal structures may be in and out of the liquid so that impact loads as well as dynamic loads may matter. Total dynamic loads on the tank are of interest in order to estimate tank support reactions.
Environmental concerns have led to requirements for double hull tankers. Ship owners try to avoid internal structures in cargo tanks for cleaning reasons. The resulting wide and clean oil tanks increase the probability of severe sloshing. It is usual to have swash(wash)bulkheads in either center cargo tanks or wing cargo tanks. A swash bulkhead is a bulkhead with openings. The swash bulkhead is typically placed in the middle of the tank perpendicular to the main flow direction. If the ratio between the area of the holes and the area of the bulkhead is small, an important effect is the change in the highest natural sloshing period to a level where sloshing is less severe. The flow through the holes causes flow separation and thereby damping of resonant sloshing.
On floating oil and gas production platforms, sloshing will affect the efficiency of oil-gas separators. Sloshing can occur in an oil-gas separator on a floating offshore platform. Oil-gas separators are used to separate the oil, gas and water during oil production. The separation occurs as the liquids and gas flow through the separator. Because the density of water is higher than that of oil, there will be a lower layer of water with oil above. Waves will be generated both on the free surface between oil and gas and on the interface between oil and water. Wave-induced motions of the platform can excite sloshing. The consequence of sloshing is a mixing effect on the oil, water, and gas that delays the oil production. Sloshing damping devices are therefore commonly used to increase the operational time. Strategically placed perforated plates perpendicular to the flow direction is one way of doing this.
Both U-tube tanks and free-surface tanks are used as anti-rolling tanks. The sloshing-induced roll moment on the vessel due to a free-surface tank will cause roll damping if the highest natural sloshing period is tuned to be close to the roll natural period. Similar arguments can be used for the resonant liquid motion in a U-tube. A tuned liquid damper(TLD)is one possible damping device to avoid excessive wind and earthquake excited oscillations of tall buildings. It is the highest natural period of a building that is of concern. A TLD provides damping in a similar way as anti-rolling tanks. TLDs have also been used by civil engineers to damp vibrations of other tall constructions such as chimneys and bridge towers. If screens are used in connection with a TLD, the open water area ratios must be sufficiently small to not influence the resonance frequency of the water motion.
Resonant liquid motions can also occur in confined liquid spaces with a free surface and with external flow. An example is resonant oscillations in a moonpool with a large amplification of the free surface flow in the moonpool relative to the vertical ship motions. A moonpool is an opening in the middle of the ship used for marine operations. The most important resonance is called piston mode oscillation. The word "piston" refers to the liquid moving nearly one-dimensionally as a rigid body in the moonpool. The piston-mode resonance frequency occurs in a frequency range with relatively large vertical ship motions that act as an excitation by displacing the water outside the moonpool. A consequence of the fact that the confined space with resonance oscillations is part of the external water domain of the ship is generation of far-field waves. This causes a damping of the resonance oscillations. However, flow separation at sharp corners in the lower moonpool entrance is the most important damping mechanism. A general tendency is that the narrower the horizontal cross-section of the moonpool is, the larger the motion of the free surface in the moonpool for given vertical ship motions. Free surface nonlinearities are less important for piston mode resonance than for sloshing in a ship tank. Fredriksen et al.(2015)studied numerically and experimentally the moonpool problem in two dimensions in incident regular waves. A numerical domain decomposition method was applied. The flow near the hull with vorticity was described by Navier-Stokes equations. A high-order potential-flow method was used at a distance from the hull. Using a conventional Navier-Stokes solver for the whole water domain can lead to inaccuracies in describing surface wave propagation. Nonlinear body-boundary conditions played an important role in correctly predicting viscous roll damping due to flow separation. The heave motion of the hull is significantly affected by the presence of the moonpool. Good agreement between experimental and numerical values of piston mode amplitude as well as heave and roll of the hull was demonstrated. An interesting finding is that the maximum moonpool response does not occur at the piston-mode resonance frequency, but happens instead at a nearby heave natural frequency associated with small damping. A reason is cancelling of the forcing due to heave and wave diffraction at the moonpool resonance frequency.
Piston mode resonance occurs also in harbors associated with flow going in and out of a harbor opening. It can also happen in the water gap between a ship and a terminal with submerged vertical walls. The scenario is relevant for LNG terminals offshore. The LNG carriers off-load their cargo to the terminals where the LNG is re-gasified and transported to land by pipelines. Of particular importance in the design of the fender system and the mooring lines is the wave-induced horizontal ship motions, which are affected by the flow in the water gap.
3 Analytically-based global sloshing descriptionPotential flow theory of an incompressible liquid can often adequately describe global sloshing flow in a clean tank. There is an infinite number of eigenfrequencies and eigenmodes, i.e., non-trivial solutions satisfying the field equation(Laplace equation), liquid mass conservation and the boundary conditions with no tank excitation. Whilst these eigensolutions satisfy the linear free surface conditions, they play also an important role in the analytically based nonlinear multimodal method described in Faltinsen and Timokha(2009). Large amplification of the liquid motions occurs when the forcing frequency is near the lowest natural sloshing frequency of a clean tank. This leads in many ship applications to important nonlinear free-surface behavior inside the tank.
The highest natural period is of prime importance in assessing the severity of sloshing. The natural frequencies and corresponding modes for the liquid motion depend on the tank shape and the liquid depth-to-tank breadth(length)ratio. Let us exemplify for two-dimensional flow in a rectangular tank with liquid depth h and tank breadth(length)l. The liquid depth can have a significant influence on the natural period for a given tank breadth(length). However, the influence is small when h/l > 1.0, here defined as deep liquid conditions when the free-surface motions do not "feel" the tank bottom. Shallow liquid conditions are defined as h/l < 0.1. Intermediate and finite liquid depths correspond to 0.1< h/l < 0.2-0.25 0.1< h/l < 0.2-0.25 and 0.2-0.25 < h/l < 1.0, respectively. Strong changes and amplifications in the liquid behavior occur near the critical depth h/l = 0.3368… for excitation frequencies close to the lowest natural frequency.
A linear theory based on the potential flow of an incompressible liquid predicts infinite steady-state response for a forcing frequency equal to a natural frequency of the liquid motion. The reason is zero damping because the only possible damping source is due to radiated waves which, of course, are impossible for liquid in a container. If we consider the relatively small excitation amplitudes of a TLD, viscous damping may properly describe the resonance amplitude. However, for larger excitations the response will be limited at resonant conditions due to nonlinear transfer of energy associated, first of all, with nonlinear transfer of energy from the lowest(primary excited)to different higher sloshing modes of liquid motion as explained in Faltinsen and Timokha(2009)by the nonlinear multimodal method. The flow at resonant conditions will be clearly different for shallowintermediate and finite liquid depth conditions. The infinite depth case resembles the finite depth case when h/l>~0.4. Photos from experiments in Fig. 1 illustrate these facts. Hydraulic jumps traveling back and forth in the tank may occur in shallow liquid. When h/l>~0.4, the wave motion resembles a standing wave with largest free surface elevations at the tank walls. Even though the free surface elevation is smallest around the middle of the tank, there is not an exact node, i.e., a position with zero free surface elevation for all time instants. When h/l>~0.4, the damping is small and mainly associated with viscous boundary layer effects along the tank boundary for smooth tanks of practical interest. The consequence of small damping is that a very long time, e.g., 50 oscillation periods, is needed to reach steady-state(periodic)conditions. Breaking waves occur more easily in intermediate and shallow depths and at the critical depth than when h/l>~0.4. The consequence of breaking waves is greatly increased damping so that steady-state conditions are reached sooner. Large breaking waves may occur in the middle of the tank as illustrated in Fig. 1 for the shallow, intermediate and critical depth cases. This is because of several interacting natural sloshing modes. Many natural modes have, in particular, significant roles in the shallow liquid case. We can understand that many modes matter in shallow-liquid conditions by making a Fourier analysis of the free-surface profile in Fig. 1(a) and noting that each mode corresponds to a Fourier component.

|
| Fig. 1 Examples of typical periodic (steady-state) free-surface motions for shallow (a), intermediate (b), nearly critical (c), and finite (d) liquid depth conditions for forced horizontal oscillations with period T near the highest natural sloshing period T1 of two-dimensional flow in a rectangular tank. Shallow liquid conditions (a) are for h/l=0.125, h/l=0.125 , T/T1=1. The forcing amplitude to tank breadth ratio is 0.1. Nearly-critical depth conditions (c) are for h/l = 0.35, T/T1 = 0.787 |
The critical depth case illustrated in Fig. 1(c) needs special attention because a steady-state condition with the flow oscillating at the forcing period may not also be achieved. Sub-harmonic behavior can arise for particular forcing amplitudes and periods. The latter fact was first discovered by CFD and later experimentally confirmed.
Swirling(rotary)wave motions may occur during harmonic horizontal excitation of liquid motion in vertically axisymmetric or square-base tanks when the forcing frequency is near the lowest natural frequency. Examples of vertically axisymmetric tanks are spherical tanks and vertical circular cylinders. When the tank length-to-tank breadth ratio of a nearly square-base tank is approximately between 0.9 and 1.1, there are similarities with the sloshing behavior in a square-base tank(Faltinsen & Timokha 2009). A consequence of swirling is a lateral hydrodynamic force component that is perpendicular to the forced oscillation direction. We can easily observe swirling by doing experiments with a cup of coffee or a glass of water. The rotation direction depends on transient conditions, and the steady-state swirling motion could be clockwise or counter-clockwise. Swirling may change its rotation direction during transient conditions. Swirling is a nonlinear phenomenon. If linear theory were used, there could be in a square-base tank with longitudinal forcing parallel to a wall only be two-dimensional(planar)waves. The nonlinear effects may also cause diagonal waves in a longitudinally excited square-base tank, i.e., waves where the maximum wave elevations occur at diagonally opposite corners of the tank with small wave elevations at the other two corners. Again, the transient conditions determine the diagonal wave direction. There are conditions depending on the liquid depth and the forcing amplitude and frequency when no steady-state wave motions are possible in a square-base tank and vertically axisymmetric tanks. Faltinsen and Timokha(2009)denote this as irregular motions, or "chaos", and document experimentally and theoretically by the nonlinear multimodal method that chaos occurs in a certain excitation frequency domain near the lowest natural frequency for a square-base rectangular tank and an upright circular cylindrical tank. Faltinsen and Timokha(2012, 2013)present similar theoretical results for a spherical rigid tank. The frequency domain with chaos depends on the filling depth and the forcing amplitude. The wave regimes for different stable steady-waves have overlaps in 3D tanks, i.e., more than one type of stable steady-state waves is possible for a given condition. The wave type occurring depends on transient conditions. Figure 2 shows reasonable agreement between theoretical and experimental results for a spherical tank with filling depth-to-sphere radius ratio h/R0=0.6. The results are presented as a function of non-dimensional forcing frequency σ/σ11 for non-dimensional surge amplitude η1a/R0 below 0.03. Here σ11 means the lowest natural sloshing frequency. Chaos occurs according to theory between the lines T and S.

|
| Fig. 2 Experimental and theoretical stability boundaries T,S, and P for non-dimensional filling depth h/R0=0.6 and different longitudinal forcing amplitudes ε=η1a/R0 versus non-dimensional forcing frequency σ/σ11. Empty (stable) and solid (unstable) symbols are experimental bounds taken from Sumner and Stofan (1963) . The symbols related to S are covered by a shadow area. Theoretical stability boundaries are marked by the solid lines T, S, and P (Faltinsen & Timokha, 2013) |
How simple can we make the sloshing analysis? When we consider transient sloshing of short duration, linear sloshing theory is appropriate. Faltinsen and Timokha(2009)applied the linear multimodal method to study the transverse hydrodynamic force needed in rollover analysis of a tank vehicle with a partially filled horizontal circular cylindrical tank. A simplified analysis was made by considering only one mode that was approximated by an infinite-fluid horizontal dipole solution. A mass-spring system described the time-dependent generalized coordinate for the free-surface elevation. Satisfactory agreement with CFD calculations was obtained. The eigenmode and corresponding eigenfrequency were obtained by a variational formulation involving a Rayleigh quotient. The exact natural frequencies are given by the Rayleigh coefficient when eigenmodes are used. Instead, test functions are used in the variational formulation and the Rayleigh coefficient is minimalized. Actually, the Laplace equation and all the boundary conditions are natural, i.e., derivable from the corresponding variational equation. Faltinsen and Timokha(2009)used infinite-fluid horizontal dipole solutions as test functions and minimalized the Rayleigh quotient by varying the dipole singularity position in the center plane above the mean free surface. Very good agreement with benchmark numerical results for the lowest eigenfrequency as a function of filling depth was documented. Faltinsen and Timokha(2009)presented the same type of simplified transient hydrodynamic analysis in terms of an infinite-fluid horizontal dipole for a spherical tank with different filling ratios.
Faltinsen and Timokha(2009)analyzed resonant sloshing in a ship tank as a weakly nonlinear potential-flow problem of an incompressible liquid. Their analytically based nonlinear multimodal method reduces the original free-boundary problem to nonlinear-coupled ordinary differential equations with respect to generalized coordinates of the liquid motions in a tank. No overturning waves and infinite tank-roof height are assumed. The tank-wall surface must be vertical in the free-surface zone. The free-surface shape is represented as a Fourier series with time-dependent coefficients (generalized coordinates) and the velocity potential is expanded in terms of the linear eigenmodes for sloshing. The Fourier series representation implies that the free surface is perpendicular to the tank walls. The latter fact prevents adequate prediction of run-up in terms of a thin liquid layer along the walls. The series are substituted into the Bateman-Luke variational formulation. Ordinary nonlinear differential equations coupling the generalized coordinates of the free-surface elevation and the velocity potential are derived. All the coefficients in the differential equations are analytically expressed when the natural modes could be analytically determined such as for rectangular tanks, vertical cylindrical tanks, and upright annular tanks. However, dependent on the shape of the mean wetted tank surface, analytical continuation of the normal mode solutions outside of the liquid domain to the corresponding tank with analytical solution can be performed. In practice, the tank shape has small deviations from the previously mentioned tanks and the mean free surface areas must be the same. Examples on applications are for a chamfered tank bottom and an inclined tank bottom.
Asymptotic ordering of the generalized coordinates are required to truncate the system of differential equations of finite dimension by introducing a small parameter characterizing the tank excitation. In addition, a parameter characterizing the smallness of the liquid depth-to-tank length ratio is needed in the asymptotic analysis for intermediate and shallow depths. The multimodal methods are computationally very fast. The methods are more suitable than a CFD method to understand the many different flow configurations that can occur during sloshing. The equations can be used as a basis for analytical studies of steady-state response with possible multi-branched solutions and physical stability. Let us as an example consider 2D flow in a rectangular tank with finite water depth that is harmonically and horizontally forced with frequency near the lowest natural sloshing frequency. Only the lowest mode is considered dominant in the following. If a Moiseev (1958)-type of analysis is used, the amplitude A of the lowest-order steady-state solution follows from a secularity condition and is determined by a cubic equation, which may have either one or three real solutions for a given forcing frequency. When three real solutions exist, only two of the solutions are hydrodynamically stable. The characteristics of the solutions resemble the solutions of the Duffing equation describing a mass-spring system with a linear and cubic spring term. The hydrodynamic response has either a "hard spring" or a "soft spring" response, similar to the Duffing equation. The response changes from having a "hard spring" to a "soft spring" behavior at the so-called critical depth h = 0.3368…l. The perturbation scheme with one dominant mode fails at the critical depth and predicts an infinite response when the forcing frequency is equal to lowest natural sloshing frequency. Except for the critical depth, the maximum response occurs at a frequency different from the lowest natural frequency. However, we must account for damping in order to predict the frequency of maximum steady-state response. The behavior of steady-state response shows that jumps between solution branches and hysteresis effects are possible. A time-domain solution is needed to predict hysteresis and jumps between solution branches properly. This is possible with the multimodal method.
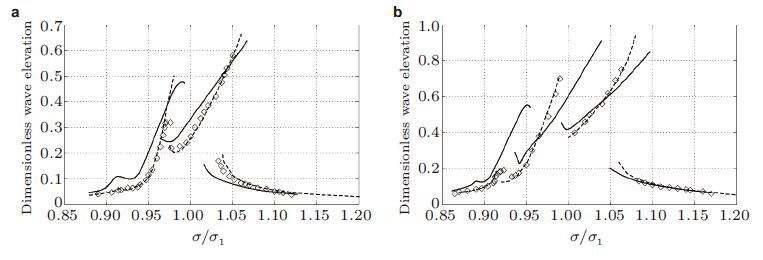
The lowest order term in the sloshing analysis is smaller order than the excitation, which expresses the fact that resonant liquid motion occurs. For instance, if the tank excitation is O(ε), the dominant sloshing modes are O(ε1/3) in finite and infinite liquid depths. The asymptotic interior flow analysis differs from the exterior flow problem for ships and offshore structures, where the lowest order term in a weakly nonlinear analysis is the same order as the wave slope. Damping due to viscous effects has to be added in the nonlinear ordinary differential equations of the generalized coordinates of the sloshing modes in order to reach steady-state oscillatory conditions in a time-domain analysis. The damping increases, in general, with increasing excitation amplitude and decreasing liquid depth because of breaking waves. The viscous damping associated with a laminar boundary-layer flow at the tank surface can be theoretically estimated. However, there is no theoretical mean to estimate damping due to breaking waves. Derivation of the asymptotic nonlinear modal system generally assumes resonant sloshing with the excitation frequency σ to be near the lowest natural sloshing frequency. However, the method is not limited to periodic excitation. When employing an asymptotic ordering, the methods are categorized as single-dominant, multi-dominant, and Boussinesq-type methods. The latter case refers to intermediate and shallow liquid depths. The assumption that only the lowest order is dominant fails due to(i)critical depth, (ii)large amplitude response, and(iii)secondary resonance. How many modes are dominant depend on secondary resonance excited by super-harmonic nonlinear flow effects. The necessary but not sufficient conditions for secondary resonance are that nσ=σn, n>1 and that σ/σ1 is close to one. Here σn means natural sloshing frequency. The probability of secondary resonance increases with decreasing liquid depth and increasing excitation amplitude. Secondary resonance in shallow-liquid conditions may be caused by the fact that the natural sloshing frequencies become commensurate. For instance, σn is nσ1 according to linear shallow-liquid theory of an inviscid liquid in a two-dimensional rectangular tank. The consequence is that many natural modes must be considered dominant in the corresponding shallow-liquid flow theory. However, the magnitude of damping is also a factor. The multimodal method is efficient and accurate in predicting the steady-state response in shallow-liquid conditions as long as the liquid depth-to-tank length ratio h/l is not too small and the experiments do not detect strongly breaking waves, run-ups and free-surface fragmentation. Comparisons were made with the experimental shallow-water results by Chester and Bones(1968)for wave amplitude response near the wall for harmonically sway-excited 2D sloshing in a rectangular tank with h/l = 0.083333 and 0.041667. The non-dimensional sway amplitudes were η2a/l=0.001254 and 0.002583. Results for h/l = 0.083333 and η2a/l = 0.001254 are presented in Fig. 3(a). The Boussinesq-type multimodal method agrees well with the experiments and gives clearly better theoretical results than those presented by Chester(1968). Figure 3(b) shows a good agreement between the multimodal theory and experiments with a forcing amplitude twice larger. Three jumps in the wave amplitude between solution branches associated with the primary resonance and secondary resonances of the second and third mode were detected. The secondary resonance of the fourth mode is predicted near σ/σ1=0.91, but we see a smooth curve instead of jumps. The reason is damping, which is larger for higher modes. When comparing with the experimental results by Chester and Bones(1968)conducted at a smaller depth of h/l = 0.0416667, there is reasonable agreement with the experiments with 8 modes. If the number of modes is further increased, convergence with relative error 10-4 was not reached.
|
| Fig. 3 Dimensionless steady-state wave elevation near the vertical wall =(fmax - fmin)/h (as proposed by Chester and Bones(1968) ) versus the excitation frequency. Rectangular tank with water depth-to-tank breadth ratio h/l = 0.08333 and 2D flow. Horizontal harmonic excitations. The calculated data are for fresh water with kinematic viscosity coefficient ν=1.1×10−6m2⋅s−1. ◊ = experiments by Chester and Bones(1968) , dashed line = Boussinesq-type multimodal theory and solid line = theory by Chester (1968) . (a) η2a/l=0.001254, (b) η2a/l = 0.002583 |
When the time-dependent generalized coordinates for the free-surface elevation are determined, integrated hydrodynamic force and moment components on the tank can be expressed in terms of the Lukovsky formulae. This fact facilitates coupling of sloshing with wave-induced ship motions in a seaway. The coupled sloshing-ship motion analysis is not limited to regular incident waves on a ship.
Time-domain simulations by the multimodal method show that many transient phases can occur before nearly steady-state conditions are achieved. The obtained results can be very sensitive to perturbations in both the transient and nearly steady state regimes. The latter fact has consequences for sloshing analysis in a ship in a stochastic sea state. A very large number of realizations of a given sea state are needed to obtain reliable probability density functions of response variables.
Most of the studies with the nonlinear multimodal method have been performed for lateral and angular tank excitations. However, it is shown in Faltinsen and Timokha(2009)for vertical tank accelerations how a system of Mathieu equation can be derived for the time-dependent generalized coordinates of the free-surface elevation. The spring term in the Mathieu equation is proportional to the sum of gravitational acceleration and the time-dependent vertical tank acceleration. When an instability occurs, it will lead to finite amplitude Faraday waves that, for instance, can be described by a numerical potential-flow method with exact boundary conditions. Vertical tank motions cannot excite sloshing according to linear theory.
4 Sloshing-induced slammingSlamming denotes the impact between a liquid and a solid boundary. When analyzing slamming, one must always have the structural reaction in mind. Sloshing-induced slamming in prismatic membrane tanks with LNG may be the most complex sloshing problem. The reasons are(a) sloshing involves violent liquid motions, (b) many flow parameters have to be recognized, (c) the membrane structure is far more complex than steel structures, (d) the fine details of an impacting free surface may matter for a membrane structure and lead to stochastic behavior even for deterministic tank motion. Thermodynamic effects may also matter for LNG and NG. Further, hydroelasticity is of concern. Hydroelasticity implies that the analysis of the hydrodynamic flow and structural reaction in terms of deflections and stresses cannot be separated. There is a mutual interaction whereby the structural vibrations cause hydrodynamic loads and vice-versa. If slamming is associated with the formation of gas pockets, the Euler number Eu=p0/ρlU2 matters. Here p0 is the ullage pressure, i.e., pressure in the ambient gas inside the tank. ρl and U are the mass density of the liquid and a characteristic tank velocity, respectively. Furthermore, the cavitation number (p0−pv)/(ρlU2/2) with pv as the vapor pressure matters for LNG. We note a similarity between the cavitation number and the Euler number. The basic mechanics of boiling and cavitation is similar. Boiling corresponds to p0=pv, i.e., zero cavitation number.
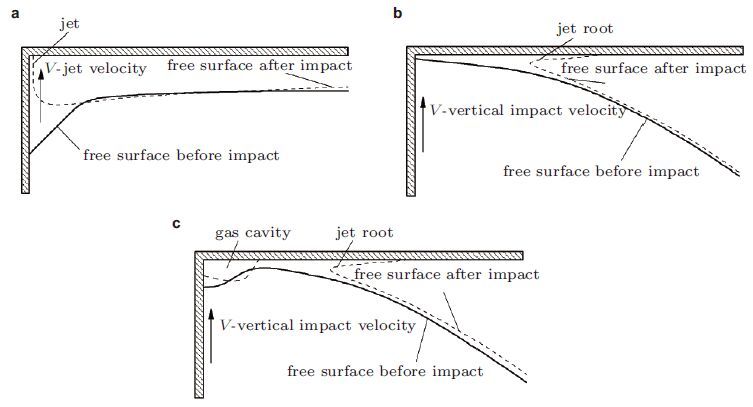
The inflow condition to slamming depends on the filling ratio. Three different scenarios from experimental studies with tank roof impact are illustrated in Fig. 4. All of them refer to cases where the flow in the tank is two-dimensional. Figure 4(a) illustrates a sudden flip-through of the free surface at the tank wall where a jet with high velocity impacts on the tank roof. The filling ratio is high, e.g., 0.98, and waves propagate towards the wall before the flip-through. Cases in Fig. 4(b) and Fig. 4(c) with flat impact and impact with oscillating gas cavity are associated with finite-liquid depth conditions, i.e., the filling does not need to be high. Slamming does not cause important loads only in the impact area. This is demonstrated in Faltinsen and Timokha(2009)where the liquid impacts with a nearly horizontal free surface on a rigid tank roof as in Fig. 4(b). Because the adjacent tank wall was more flexible than the tank roof, significant stresses with hydroelastic effects occurred in the wall due to tank roof impact. A gas cavity as illustrated in the impact scenario in Fig. 4(c) has a natural frequency associated with the compressibility of the gas and a generalized added mass due to the liquid oscillations caused by the gas cavity oscillations. Abrahamsen and Faltinsen(2012)presented formulas for the natural frequency of gas cushions at rigid tank walls and roofs based on an adiabatic pressure-density relation, i.e., boiling and condensation of relevance for LNG and NG are neglected. Transient damped pressure oscillations in the gas cavity are excited by the impact. The damping for a closed cavity is due to heat transfer to and from the gas cavity and dissipation of the boundary layer flow in the liquid(Abrahamsen and Faltinsen 2011). They also experimentally demonstrated that air leakage can significantly influence the decay of the pressure oscillations in the gas cavity.
|
| Fig. 4 Three different scenarios of impact against the tank roof considered by Rognebakke and Faltinsen (2005) : (a) high-curvature free-surface impact with a high velocity jet; (b) flat impact; (c) impact with oscillating gas cavity |
Steep wave impacting on a vertical tank wall is important for shallow and lower-intermediate liquid depths and influenced by the spatial evolution of the breaking wave and by its phasing with respect to the vertical wall. Lugni et al.(2006)studied nearly 2D flow in a rectangular tank partially filled with water and distinguished experimentally three modes:(a)Flip-through, i.e., impact of an incipient breaking wave without air entrapment.(b)Impact of an incipient breaking wave with air entrapment.(c)Impact of a broken wave with air/water mixing. In the last case, the wave breaks before the wall, and advances towards the wall as a breaking bore. The flow is governed by the turbulence of the wave front, characterized by air-water mixture with many small air bubbles in the water.
When the flip-through phenomenon occurs, the concave face of the wave approaches the wall with the crest moving forward and the trough rapidly rising at the wall. The presence of the wall delays breaking of the wave and causes the rise of the leading wave trough. The latter focuses with the wave front, giving intense acceleration to the flow and turning it in the focusing area to form a vertical jet. Very large pressures can occur in the flip-through condition. The high-pressure loading on the tank wall is sensitive to small changes of an impacting steep free surface.
Three dimensional effects, gas leakage, and ullage pressure in terms of Euler and cavitation numbers have fundamental roles in the kinematic and dynamic evolution of the flow in case(b)with air entrapment compressibility(Lugni et al. 2010a, 2010b). The cavity closes typically after the first or second oscillation of the cavity. A large increase in the pressure decay coefficient was observed in the vapor pressure regime, i.e., for ullage pressures close to the vapor pressure of the water.
Guo et al.(2011)carried out numerical simulations of the impact of the free surface with the entrapped air on the tank wall and reported a major computed oscillatory behavior of the impact pressure by comparison with the experimental data by Lugni et al.(2006). The computed leading peak pressure agrees well with the experimental data available, while the oscillation frequency of the pressure is underestimated. A reason may be three-dimensional effects in the experiments.
Wei et al.(2015)discovered experimentally a new wave system in shallow water conditions. Plunging breakers hit in the middle of the tank. Resulting pressures at the tank bottom need to be experimentally studied.
The time scale of a fluid dynamic phenomenon such as acoustic effects relative to natural periods of structural modes contributing to large structural stresses is important in judging if a particular fluid dynamic effect matters. Numerical studies of Graczyk(2008)give an idea about important structural natural periods. He examined the effect of slamming load on a part of the Mark III containment system. The hydrodynamic part of the analysis was strongly simplified while the structural modeling was complete. The maximum response values were of significance for the evaluation of the structural strength. There is a significant influence from structural modes with a range of natural frequencies from about 100 to 500 Hz. An important effect of these higher modes is compression of the foam and local bending of the plywood plate adjacent to the resin ropes. If the influence of bubbles in the liquid is neglected, the effect of liquid compressibility may matter for frequencies of the order of 1 000 Hz and higher. However, a mixture of gas and liquid can significantly lower the speed of sound and thereby increase the time scale of acoustic effects. On the other hand, the mixture of gas and liquid in an LNG tank is not homogeneous in space and takes place in a layer of the LNG next to the ullage space. If the ratios between the impact duration and important natural structural periods are very small, the fine details of the hydrodynamics are not needed in describing the maximum structural stresses, which occurred in a free-vibration phase after the slamming impact in the theoretical and experimental studies by Faltinsen(1997). The situation for the membrane structure considered by Graczyk(2008)is different. Significant response of the lower plywood occurs already during the slamming impact, i.e., before the free-vibration phase. This is both due to the slamming duration and due to the higher natural frequency of the lowest important mode(125-165 Hz).
Because presently there are no numerical methods that can fully describe the sloshing-induced slamming pressures, one has to rely on experiments, which means in practice model tests. The challenges are how to scale the model-test results to full scale and properly account for the structural elastic reactions(Faltinsen & Timokha 2009). Because sloshing is associated with gravity waves, we must require that the Froude number 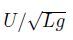

Model tests of slamming and sloshing are typically done with prescribed tank motion, which may be found by calculations as a realization of the ship motions in representative sea states. The calculations must account for the mutual interaction between ship motions and sloshing. Linear potential flow and empirical viscous roll damping can predict the external wave loads to a large degree. The latter depends on which sea conditions cause significant sloshing resonance. However, nonlinear free-surface effects play a dominant role for internal sloshing loads. Even though CFD is not recommended, in general, for sloshing-induced slamming, it may better describe the global effect of sloshing. However, the computational speed of CFD method makes it in practice unrealistic for long-time simulations in a sea state. The nonlinear multimodal method is time-efficient but limited in describing all flow conditions. Then we are left in practice with linear sloshing theories, which are fast and are commonly used. What errors are caused in slamming-induced structural stresses by using calculations of tank excitations based on linear theories as a basis for model tests should be investigated. An issue is also the statistical analysis of the response.
Examples on engineering recommendations to assess the dynamic structural response to sloshing loads are the following two calculation methods. The direct dynamic finite element analysis(FEA)uses the pressure loads measured during experiments carried out with a rigid model(scaled to prototype scale)as input of a dynamic FEA of the full structure. The indirect dynamic FEA uses the results from a static FEA multiplied by a correction factor obtained through the dynamic amplification factor(DAF)curve. The DAF is the ratio between the maximum dynamic response and the maximum static response for a considered sloshing pressure rise time. It is difficult with the two methods to account properly for the added mass effects associated with the slamming-induced wall vibrations, which depend on the time-dependent wetted structural area, free-surface position and possible presence of gas cavities. Lugni et al.(2014)illustrated the latter fact. Shallow-water sloshing with a flip-through event was experimentally studied with a rigid tank and the same tank with a flexible sidewall portion made by aluminum in the impact area. The ratio between the maximum strains measured in the two cases was 1.84 and clearly higher than obtained by using an approach similar to the direct dynamic FEA.
Since sloshing-induced slamming causes filling restrictions in prismatic membrane tanks, a natural question to ask is if there are ways to reduce the load level. Swash bulkheads are a possibility from a hydrodynamic point of view. However, it seems impossible to use in membrane LNG tanks. The Ishikawajima-Harima Heavy Indusies, Co., Ltd.(IHI)self-supported prismatic type B(SPB)tank with aluminum-alloy as material and used for LNG cargo is equipped with swash bulkheads. 2D calculations in Faltinsen and Timokha(2009)illustrate how the wave amplitude response depends on the sway excitation of a rectangular tank as a function of forcing frequency and opening-area ratio when a screen is in the middle of the tank. Linear free-surface conditions in combination with an empirical nonlinear pressure loss condition at the screen were used. Faltinsen et al.(2011a, 2011b)present comparisons between experiments and theory for non-shallow depths of rectangular tanks with nearly 2D flow and sway excitation for a wide range of opening-area ratios and frequencies. Minimum wave response for realistic tank excitation occurs for an opening-area ratio in the order of 0.2. However, conclusions from a hydrodynamic loading point of view require that realistic tank excitations be considered with focus on sloshing-induced slamming(Wei et al. 2015).
5 ConclusionsThe hydrodynamics of sloshing can be complicated. Its understanding requires a combination of theory, CFD and experiments. Resonant liquid motions in various engineering fields are exemplified. It is pointed out that nonlinearities associated with sloshing are important in describing coupled ship motions and sloshing. The multimodal methods are computationally very fast and easy to couple with the ship motions. The methods are more suitable than a CFD method to understand the many different flow configurations that can occur during sloshing.
Sloshing-induced slamming in prismatic LNG tanks is perhaps the most complicated slamming problem because many fluid mechanic and thermodynamic parameters as well as hydroelasticity may matter. Further, complicated in-flow scenarios of slamming may appear due to violent sloshing. The consequence is that both computational tools and model test scaling are limited.
| Abrahamsen B C, Faltinsen O M. 2011. The effect of air leakage and heat exchange on the decay of entrapped air pocket slamming oscillations. Physics of Fluids, 23:1–17. |
| Abrahamsen B C, Faltinsen O M. 2012. The natural frequency of the pressure oscillations inside an air pocket which is entrapped between a water-wave and a plane wall. J. of Fluids and Structures, 35:200–212. doi:10.1016/j.jfluidstructs.2012.07.004 |
| Chester W. 1968. Resonant oscillations of water waves. I. Theory. Phil. Trans. R. Soc. Lond. A, 306:5–22. |
| Chester W, Bones J A. 1968. Resonant oscillations of water waves. Ⅱ. Experiment. Phil. Trans. R. Soc. Lond. A, 306:23–30. |
| Faltinsen O M. 1997. The effect of hydroelasticity on slamming. Phil. Trans. R. Soc. Lond. A, 355:575–591. doi:10.1098/rsta.1997.0026 |
| Faltinsen O M.2005. Hydrodynamics of High-Speed Marine Vehicles. New York: Cambridge University Press, ) . |
| Faltinsen O M, Timokha A N.2009. Sloshing. New York: Cambridge University Press, ) . |
| Faltinsen O M, Firoozhkoohi R, Timokha A N. 2011a. Steady-state liquid sloshing in a rectangular tank with slat-type screen in the middle:Quasi-linear theory modal analysis and experiments. Physics of Fluids, 23:042101. doi:10.1063/1.3562310 |
| Faltinsen O M, Firoozhkoohi R, Timokha A N. 2011b. Effect of central slotted screen with a high solidity ratio on the secondary resonance phenomenon for liquid sloshing in a rectangular tank. Physics of Fluids, 23:062106. doi:10.1063/1.3602508 |
| Faltinsen O M, Timokha A N. 2012. Analytically approximate natural sloshing modes for a spherical tank shape. Journal of Fluid Mechanics, 703:391–401. doi:10.1017/jfm.2012.237 |
| Fredriksen A G, Kristiansen T, Faltinsen O M. 2015. Wave-induced response of a floating 2D body with moonpool. Philosophical Transactions of the Royal Society A Mathematical Physical & Engineering Sciences, 373:2033. |
| Guo X Y, Wang B L, Liu H. 2011. A numerical method for investigating free surface impact with air entrapment during sloshing. Journal of Marine Science and Technology, 19:651–659. |
| Lugni C, Brocchini M, Faltinsen O M. 2006. Wave impact loads:The role of the flip-through. Physics of Fluids, 18:122101. doi:10.1063/1.2399077 |
| Lugni C, Miozzi M, Brocchini M, Faltinsen O M. 2010a. Evolution of the air-cavity during a depressurized wave impact. Part I:The kinematic flow field. Physics of Fluids, 22:056101. |
| Lugni C, Brocchini M, Faltinsen O M. 2010b. Evolution of the air-cavity during a depressurized wave impact. Part Ⅱ:The dynamic field. Physics of Fluids, 22:056102. |
| Lugni C, Bardazzi A, Faltinsen O M, Graziani G. 2014. Hydroelastic slamming response in the evolution of a flip-through event during shallow-liquid sloshing. Physics of Fluids, 26:032108. doi:10.1063/1.4868878 |
| Moiseev N N. 1958. On the theory of nonlinear vibrations of a liquid of finite volume. Journal of Applied Mathematics and Mechanics (PMM), 22:860–872. doi:10.1016/0021-8928(58)90126-6 |
| Sauret A, Boulogne F, Cappello J, Dressaire E, Stone H A. 2015. Damping of liquid sloshing by foams. Physics of Fluids, 27:243–257. |
| Wei Z J, Faltinsen O M, Lugni C, Yue Q J. 2015. Sloshing-induced slamming in screen-equipped rectangular tanks in shallow-water conditions. Physics of Fluids, 27:032104. doi:10.1063/1.4913983 |



