2. 中国船舶工业系统工程研究院, 北京 100094
2. System Engineering Research Institute, Beijing 100094, China
1 引言
波动作为能量传播的一种方式在自然界普遍存在,如视觉感知的可见光是波长在纳米尺度的电磁波,语言交流是借助空气振动进行能量传递的声波,机械系统的振动是在结构中传播的弹性波,通过材料设计对波传播进行调控,无论对工程应用还是科学研究都有着重要意义. 例如,引导地震过程中危害最大的剪切波偏离建筑物传播,能够避免建筑损坏和人员伤亡; 精确控制电磁波绕过目标物体不产生散射,可实现目标对电磁波的隐身;通过材料和结构设计引导声波/弹性波按照预设方式传播,是工程结构减震降噪、能量收集、声波/弹性波隐身等诸多领域设计的基础.与传统已知材料性质分布求波传播轨迹不同,波传播调控设计是已知波传播的轨迹反求所需要的材料和结构分布,因此是一个典型的逆向设计问题,缺乏高效的设计方法.
2006年英国帝国理工学院Pendry等(2006)和圣安德鲁斯大学Leonhardt(2006)几乎同时提出的变换电磁学和变换光学理论,为上述波调控逆向设计提出了一种简洁高效的求解方法.该方法的基本原理是:如果波控制方程在曲线坐标变换下具有和笛卡尔坐标系下相同形式,则可建立空间变换与材料分布间的等价关系,用材料空间分布解释空间弯曲效应.该方法也被称为波调控设计的变换理论,它直接给出了功能与材料分布的对应关系,为波调控的逆向设计提供了分析手段. 变换电磁波学理论提出后,美国杜克大学Schurig等(Schurig et al. 2006)据此理论设计并制备了圆环形电磁隐身斗篷,在微波频段内证实了其有效性. 由于波动方程之间的相似性,该方法很快就被推广到声波、液体表面波、物质波、传热、扩散等领域(Schittny et al. 2013,Farhat et al. 2008,Han et al. 2013,Cummer&Schurig 2007,Chen&Chan 2007,Zhang et al. 2011,Zhang et al. 2008,Cummer et al. 2008),并得到了相应实验验证(Farhat et al. 2008,Chen et al. 2011,Stenger et al. 2012,Popa et al. 2011,Rohde et al. 2015,Zigoneanu et al. 2014,Bückmann et al. 2014). 结合同期发展起来的超材料技术,许多新奇的功能装置被提出并由实验验证. 例如,电磁波、声波黑洞装置(Climente et al. 2012,Chang&Hu 2012,Cheng et al. 2010)、多波束天线、定向天线(Tichit et al. 2009,Chang et al. 2011,Jiang et al. 2008,Ren et al. 2010)、波束分裂、旋转以及转弯等特殊功能装置(Rahm et al. 2008,Kwon&Werner 2008,Jiang et al. 2014,Schmiele et al. 2010).一般情况下弹性波控制方程不具有变换形式不变性(Milton et al. 2006,Norris&Shuvalov 2011),因此对弹性波调控的研究多集中在薄板弯曲波、高频近似、出平面剪切波等特殊情况(Farhat et al. 2009,Colquitt et al. 2014,Hu et al. 2011,Wu&Gao 2015),或者在非对称应力弹性介质框架下研究(Brun et al. 2009,Norris&Parnell 2012).
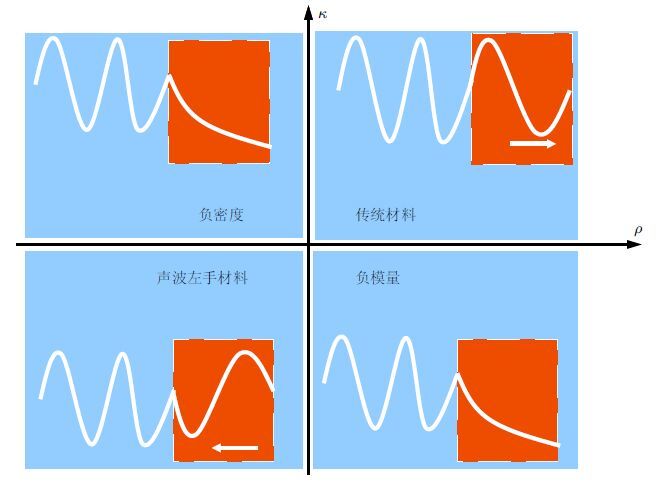
变换理论给出波传播路径与材料属性分布的关系,但所要求的材料属性往往比较苛刻,如急剧梯度化、强各向异性以及负等效参数等,须借助超材料技术实现.超材料是指人工周期结构组成的复合材料,通过对亚波长结构进行精心设计,其宏观等效性质具有天然材料不具备的物理性质(Pendry et al. 1996).以声学介质为例,传统介质密度和体积模量都大于零,取值位于图 1中第一象限,此时声波能在该介质传播且相速度与群速度方向一致.位于其他3个象限的材料要求密度或模量有一个或2个为负值(Fang et al. 2006,Lee et al. 2009),一般自然界材料很难具备上述负值属性,这里统称为声波超材料. 但通过适当设计复合材料微结构胞元,可实现位于这3个象限中任何一类材料. 对于具有单负材料,声波会快速衰减而无法传播; 对于双负介质,声波能正常传播,而其相速度与群速度方向相反(Li&Chan 2004,Lee et al. 2010).超材料的发展,极大地扩展了材料性质的可选择空间,为实现基于变换理论的波动控制提供了材料基础.
|
| 图1 传统声学介质和超材料密度、模量取值空间 |
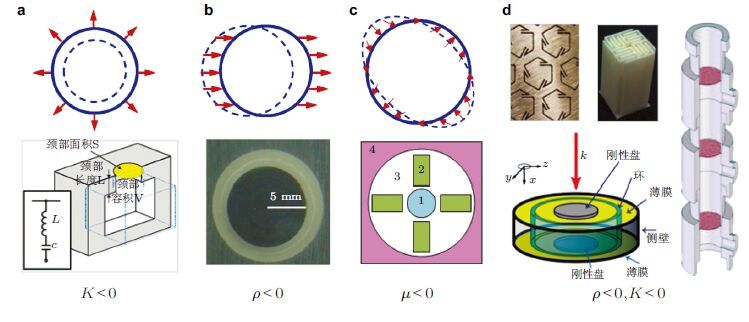
图 2 给出了谐振机理导致负参数的原理示意图和几种负参数超材料单胞.实现负参数的核心思想是,当胞元发生谐振时响应与激励反相. 例如,单极共振时施加于边界上的拉力使得介质缩小(如虚线所示),等效于介质此时具有负的体积模量.图 2(a)即为利用Helmholtz共振腔设计的负体积模量超材料(Ding et al. 2007). 偶极共振时,施加于代表单元上的载荷使其反向移动,等价于此时具有负的密度(Zhou&Hu 2009,Wu et al. 2007).图 2(b)为2000年首次基于局域共振设计的低频负密度超材料胞元(Liu et al. 2000),由橡胶包覆的铅颗粒和环氧树脂基体组成,高密度铅颗粒和低模量橡胶使其在低频出现负密度. 四级共振发生时,施加于胞元边界上的剪切应力与介质产生的剪应变反向,进而等效剪切模量为负值(Lai et al. 2011,Wu et al. 2011).图 2(c)中单胞由1代表的硬橡胶、3代表的软橡胶、2代表钢块和4代表的泡沫基体构成,四块钢块与软橡胶配合在低频发生四极共振而产生负的剪切模量.图 2(d)给出了利用手性介质偶极、旋转共振耦合(Liu et al. 2011,Zhu et al. 2014)、单偶极共振复合(Lee et al. 2010,Yang et al. 2013)、空间折叠机理设计的双负介质(Liang&Li 2012,Xie et al. 2013). 一些利用这类特殊属性的新概念,比如基于零质量的超分辨成像(Zhou&Hu 2011)、基于零折射率的波导、隐身(Wei et al. 2013,Li et al. 2014,Luo&Lai 2014,Zheng et al. 2014)、基于互补介质的外部隐身方案(Lai et al. 2009)等也相继出现.
|
| 图2 谐振机理产生负参数原理示意图及超材料单胞示例.(a)单极共振产生负体积模量,(b)偶极共振产生负密度,(c)四级共振产生负剪切模量,(d)基于不同谐振耦合设计的双负介质 |
超材料的奇特性质与变换方法相辅相成,为基于变换方法的波动控制提供了解决方案并拓展了超材料的应用领域.以基于各向异性密度声学介质的声波斗篷为例(Cummer&Schurig 2007,Chen&Chan 2007,Norris 2008),各向异性密度材料可由超材料技术实现,如流体中叠层和穿孔板技术(Torrent&Sanchez-Dehesa 2010,Smith 2011,Popa et al. 2011,Christensen&de Abajo 2012,Zigoneanu et al. 2014)、固体谐振单元在流体介质中周期排布技术(Zigoneanu et al. 2011,Wu et al. 2012). 需要指出的是,这些超材料技术实现的各向异性密度声学材料,由于需要流体介质为基体而不易在实际工程上应用. 另外,谐振机理使得有效性质为负值的频段较窄,不适应于工程上的宽频需求.随着声学斗篷研究的深入,五模材料因其固体特征和流体属性,并与变换方法完美结合而进入人们研究的视野.
|
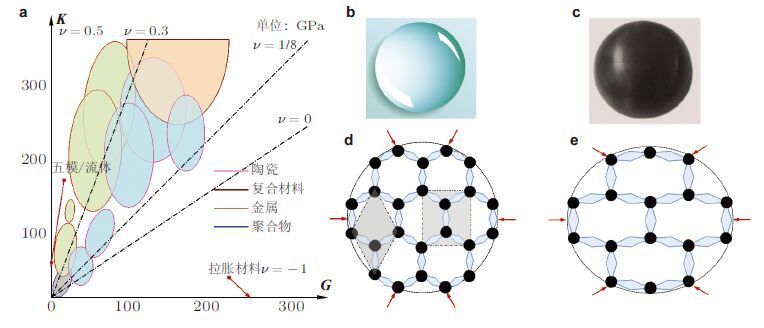
| 图3 (a)常见材料体积模量、剪切模量取值空间,(b)水$G/K=0$,(c)橡胶$G/K\ll 1$,(d)各向同性微结构五模材料,(e)各向异性微结构五模材料 |
五模材料(pentamode material,PM)最早由美国犹他大学Milton和Cherkaev(1995)提出,定义为弹性矩阵仅有一个特征值不为零的材料,是一种退化的弹性介质. 由于特殊的弹性张量形式$ C= K S \otimes S$,五模材料只能承受与特征应力 S成比例的应力状态,在其余应力状态下会像流体一样在剪应力下发生流动,因此五模材料也是一种具有固体形态的复杂流体. 图 3(a)给出了各向同性材料体积模量和剪切模量的取值空间.传统流体的剪切模量为零,位于纵轴上,只能承受静水压力,因此是五模材料的特例,如图 3(b)中所示的水. 固体材料中,橡胶(如图 3(c))的剪切模量远低于体积模量,可近似看作五模材料.通过对固体微结构设计可制备出近似各向同性的五模材料(如图 3(d)),或各向异性的五模材料(图 3(e)). 需要指出的是,由于结构稳定性的需要,固体五模材料的剪切模量不能严格为零,因此只是一种近似的五模材料. 固体五模材料不依赖于谐振机制,具有本质的宽频适用性,理论上如果微结构设计得无限小则有效性质适用频率可以无限宽. 2008年,Norris提出了基于五模材料的变换声学理论(Norris 2008),为通过五模材料控制声波奠定了理论基础,也引起了人们对五模材料本身(Kadic et al. 2012,Martin et al. 2012,Kadic et al. 2013,Schittny et al. 2013,Norris 2014,Kadic et al. 2014,Cai et al. 2015,Amendola et al. 2016,Huang et al. 2016)及其在声波控制领域(Norris 2009,Scandrett et al. 2010,Scandrett et al. 2011,Gokhale et al. 2012,Layman et al. 2013,Hladky-Hennion et al. 2013,Bückmann et al. 2014,Xiao et al. 2014,Zhang et al. 2015,Chen et al. 2015,Tian et al. 2015)中的研究热情. 特别是五模材料的固体形态、宽频等特点,被认为在水声环境中具有重要的潜在应用价值.
本文将分4节重点介绍五模材料的基本概念、微结构设计、声波调控和制备.在背景介绍后,第2节将根据材料易变形模式的数量对材料进行分类,在此基础上详细介绍五模材料的基本概念,从静和动力学2个方面介绍五模材料与传统固体和流体介质的差异、界面折反射及阻抗匹配条件;第3节将通过定义衡量微结构五模材料理想程度的特征指标,分析五模材料特殊力学行为的形成机理,并进一步介绍五模材料微结构的设计方法;第4节将重点介绍基于五模材料的声学变换方法、五模材料声学斗篷设计、非理想五模材料对隐身效果影响及五模材料在其他声学领域应用的研究进展;第5节将介绍有关五模材料制备的研究进展. 最后,对全文进行总结.
2 五模材料基本概念 2.1 依据易变形模式数量的材料分类方法通常情况下,弹性材料的分类是依据模量的大小或材料的对称性,比如,模量较大、较小的材料分别被称为硬材料、软材料;材料性质与方向无关称为各向同性材料等等. 对于一般性弹性介质,其弹性性质由一个四阶弹性张量$ C$描述,又可以表示为6阶的弹性矩阵.Milton和Cherkaev(1995)指出,一般情况下弹性材料的6阶弹性矩阵有6个不为零的特征值,以及相对应的特征向量,每个特征向量对应于一种变形模式(deformation mode). 如果某一个特征值退化为零,则称其对应的变形模式为易变形模式(easy deformation mode). 每种易变形模式,都对应于一个特殊的应变状态,这一应变状态不会引起应力. 因此,即使在没有外载荷作用的情况下,弹性体也能按照这一应变持续地变形,如同流体流动一样,"易变形模式"即由此变形特征而命名.
根据弹性矩阵零特征值的个数,可以对材料进行分类.常见的弹性材料由于弹性矩阵正定,没有零特征值和易变形模式,被划归为"零模材料";弹性矩阵仅有一个特征值为零的材料称为"单模材料"(unimode material),相应的有"双模材料"(bi-mode material)等;"五模材料"指弹性矩阵有5个特征值为零的材料,其英文名称为pentamode material(PM材料),penta-在希腊语中的含义即为五.天然流体可以看作是剪切模量为零的弹性介质,也是理想的各向同性五模材料.
为了讨论方便,我们将以二维五模材料作为讨论的对象,相关研究结论和方法可以很容易地推广到三维情形. 在讨论之前,我们将给出弹性力学理论的一些基本概念,用于完整刻画五模材料.在二维空间中,一般弹性介质的应力应变本构关系可以用如下矩阵形式表示 $$ \left({\begin{array}{l} \sigma_{11} \\ \sigma_{22} \\ \sigma_{12} \\ \end{array}} \right)= D \left({\begin{array}{l} \varepsilon_{11} \\ \varepsilon_{22} \\ 2\varepsilon_{12} \\ \end{array}} \right),D = \left({{\begin{array}{*{20}c} {C_{1111} } \quad& {C_{1122} } \quad& {C_{1112} } \\ {C_{2211} } \quad& {C_{2222} } \quad& {C_{2212} } \\ {C_{1211} } \quad& {C_{1222} } \quad& {C_{1212} } \\ \end{array} }} \right) \tag{1}$$ 其中,$\sigma_{\alpha \beta }$,$C_{\alpha \beta \gamma \rho }$,$\varepsilon_{\alpha \beta }$ (希腊字母取值1到2)分别是应力、弹性和应变张量的指标形式,$ D$代表材料的弹性矩阵. 由于弹性张量满足对称性$C_{\alpha \beta \gamma \rho }=C_{\beta \alpha \gamma \rho }=C_{\gamma \rho \alpha \beta }$,因此弹性矩阵是3 × 3的对称矩阵.对于一般非退化的2D弹性矩阵,应有3个正实数特征值和对应的3个相互正交的特征向量,分别记作,$\lambda ^{(p)}$和$ S ^{(p)}$ $(p=1,2,3)$ $$\sum\limits_{j = 1}^3 {D_{ij} S_j^{(p)} } = \lambda ^{(p)}S_i^{(p)}(i,j,p = 1,2,3) \tag{2}$$ 其中,$S_i^{(p)} $是特征向量$ S^{(p)}$的第$i$个元素,$D_{ij}$是弹性矩阵的元素. 根据以上表达式,弹性矩阵各元素$D_{ij}$可用其特征值和特征向量表示成如下形式 $$ D_{ij} = \sum\limits_{p = 1}^3 {K^{(p)}S_i^{(p)} S_j^{(p)} },K^{(p)} = \dfrac{\lambda ^{(p)}}{\vert S^{(p)}\vert ^2},\vert S^{(p)}\vert ^2 = \sum\limits_{ i = 1}^3 {S_i^{(p)} S_i^{(p)} } \tag{3}$$
由于特征向量$ S ^{(p)}$的选取不唯一,$K^{(p)}$的选取也不唯一.如果特征向量$ S^{(p)}$被归一化为单位向量,或者归一化为对应的特征值,上述表达式可以进一步简化为下述两种形式 $$ D_{ij} = \sum\limits_{p = 1}^3 {\lambda ^{(p)}S_i^{(p)} S_j^{(p)} },K^{(p)} = \lambda ^{(p)},\vert S^{(p)}\vert ^2 = 1 \tag{4}$$或 $$ D_{ij} = \sum\limits_{p = 1}^3 {S_i^{(p)} S_j^{(p)} } ,K^{(p)} = 1,\vert S^{(p)}\vert ^2 = \lambda ^{(p)} \tag{5}$$
为给出弹性张量$ C$的表达式,根据特征向量$ S ^{(p)}$定义如下二阶对称张量$ S^{(p)}$ $$ { S}^{(p)} = \left({{\begin{array}{*{20}c} {S_{11}^{(p)} } \quad& {S_{12}^{(p)} } \\ {S_{12}^{(p)} } \quad& {S_{22}^{(p)} } \\ \end{array} }} \right)= \left({{\begin{array}{*{20}c} {S_1^{(p)} } \quad& {S_3^{(p)} } \\ {S_3^{(p)} } \quad& {S_2^{(p)} } \\ \end{array} }} \right)\tag{6}$$
借助于上述定义,弹性张量可以改写为如下简洁的形式 $$ C = \sum\limits_{p = 1}^3 {K^{(p)}{ S}^{(p)} \otimes { S}^{(p)}} \tag{7}$$ 其中,符号$ \otimes $代表张量并乘.上述弹性张量的分解形式称为开尔文分解(Kelvin decomposition).根据弹性矩阵的特征向量分解可看出,如果某一个特征值等于零,比如 $\lambda ^{(1)}=0$,则任何与特征向量$S^{(1)} = \{S_1^{(1)},S_2^{(1)},S_3^{(1)} \}^{\rm T}$成比例的应变状态$\{ \varepsilon _{11},\varepsilon_{22},2 \varepsilon_{12}\}^{\rm T}$不会在弹性体中产生应力. 如以下方程所示 $$ \left({\begin{array}{l} \sigma_{11} \\ \sigma_{22} \\ \sigma_{12} \\ \end{array}} \right)= \left({{\begin{array}{*{20}c} {c_{1111} } \quad& {c_{1122} } \quad& {c_{1112} } \\ {c_{2211} } \quad& {c_{2222} } \quad& {c_{2212} } \\ {c_{1211} } \quad& {c_{1222} } \quad& {c_{1212} } \\ \end{array} }} \right)\left({\begin{array}{l} \varepsilon_{11} \\ \varepsilon_{22} \\ 2\varepsilon_{12} \\ \end{array}} \right)=$$ $$ \left({{\begin{array}{*{20}c} {c_{1111} } \quad& {c_{1122} } \quad& {c_{1112} } \\ {c_{2211} } \quad& {c_{2222} } \quad& {c_{2212} } \\ {c_{1211} } \quad& {c_{1222} } \quad& {c_{1212} } \\ \end{array} }} \right)\left({\begin{array}{l} \alpha S_1^{(1)} \\ \alpha S_2^{(1)} \\ \alpha S_3^{(1)} \\ \end{array}} \right)= \textbf{0} \tag{8}$$
因此,每一个零特征值都将给弹性介质引入一个易变形模式.根据开尔文分解,可以得到五模材料的弹性张量为 $$ C = K{ S} \otimes { S} \tag{9}$$ 如方程(4)所示,当$ S$被归一化为单位向量时,系数$K$等于弹性矩阵的特征值; 当$ S$被归一化其特征值时,系数$K$等于1,弹性张量可以更简洁地表示为$ C= S \otimes S$. 这两种表示形式在不同场合都有使用,后一种形式在接下来讨论中将被更多的用到.
由于五模材料内应力$ \sigma $始终与$ S$成比例,$\sigma = C: \varepsilon =K(S:\varepsilon)S$,$ S$被称为五模材料的特征应力张量,其在决定五模材料力学行为和传播特性方面起着关键作用.天然流体材料作为一种理想五模材料,其特征应力张量为$ S= I$,这类介质只能承受静水拉压的应力状态. 而更一般的五模材料,可以承受比静水压更复杂的应力状态,这一特性使其在控制声波方面更具潜力. 在静力学、动力学行为上,各向异性五模材料有着与传统各向同性流体不同的响应. 如Norris(2009)指出:当置于容器中的各向异性五模材料主轴方向与铅垂方向不一致时,重力作用下其自由表面将不再保持水平(图 4(a)),而呈现出看似不可能的倾斜自由表面. 图 4(b)给出了可能的五模材料微结构形式,该构型由六角形排布的光滑钢珠构成,来自于相邻钢珠的无摩擦相互作用力,使得钢珠在重力作用下保持平衡.

|
| 图4 (a)主轴非竖直各向异性五模材料在重力作用下的平衡状态,(b)由无摩擦接触钢球组成的可能微结构形式 |
五模材料的特征应力张量$ S$在主轴坐标下,具有最简单的对角矩阵形式$ S={\rm diag}\{(K_{x})^{1 / 2},\gamma(K_{y})^{1 / 2}\}$. 依据对角元素的正负符号关系,$\gamma $取$+1$或$-1$. 弹性矩阵在主轴坐标下也可简化为如下形式 $$ C = \left({{\begin{array}{*{20}c} {K_x } \quad& {\gamma \sqrt {K_x K_y } } \quad& 0 \\ \quad& {K_y } \quad& 0 \\ {\rm sym} \quad& \quad& 0 \\ \end{array} }} \right)\tag{10}$$ 根据参数$\gamma $的取值可将五模材料进一步细分为正型五模材料$(\gamma =+1)$或负型五模材料 $(\gamma =-1)$. 这两类五模材料(图 5)承载不同的应力状态: 对于$\gamma =+1$的正型五模材料,其在相互正交的2个主轴方向上,只能承受同为拉或压的应力状态;对于$\gamma = -1$的负型五模材料则只能承受一拉一压的相反应力状态.在后面的讨论中,还将深入地分析两种五模材料波传播的特性.

|
| 图5 (a)正型五模材料能承载同为拉或压的应力状态,(b)负型五模材料能承载一拉一压的应力状态 |
五模材料包含2个独立的弹性常数$K_{x}$和$K_{y}$,分别被称为五模材料$x$和$y$方向的体积模量,因为在这两主方向传播声波的相位速度分别为$c_{x}=(K_{x}/\rho)^{1 / 2}$和$c_{y}=(K_{y}/\rho)^{1 / 2}$,正好与流体中传声速度表达式$c=(K/\rho)^{1 / 2}$一致.在主轴坐标系下,由于联系剪应力和剪应变的剪切刚度$D_{33}$为零,五模材料在主方向上不能承受任何剪应力. 然而,旋转到其他坐标系下时,只要存在相应的正应力约束,五模材料允许剪应力存在.由于特殊的弹性矩阵形式,五模材料的应力主方向始终与材料主方向一致,而在一般弹性介质中,应力主方向可以随意选取.
2.3 五模材料动力学特征本节将讨论弹性波在五模材料中的传播特性,给出相应的频散关系.五模材料可看作各向异性弹性介质的一个特例,其动力学特性可由一般的弹性动力学方程来刻画.由于仅有一个特征值不为零,五模材料的应力状态可用伪声压(pseudo pressure)描述,$\dot {p}= - S: v \nabla $. 为便于讨论,伪声压在下面讨论中不加区分地简称为声压.将伪声压代入弹性介质本构方程和牛顿运动学方程$$ \sigma = - p{ S},\rho \dot { v} =\nabla \cdot \sigma \tag{11}$$
为了导出频散关系,考虑在五模材料内传播有波矢量为$ k$和角频率为$\omega $的平面波,并假定声压和粒子振动速度形式为$p=p_{0}\exp[{\rm i}(\omega t- k\cdot r)]$,$ v = v_{0}\exp[{\rm i}(\omega t- k\cdot r)]$. 将声压和速度的具体形式代入上述方程得到 $$ p_0 \omega = k \cdot { S} \cdot v_0,\rho \omega v_0 = p_0 { S} \cdot k \tag{12}$$
以上2个方程构成一个特征值问题,其中波矢量$ k $和角频率$\omega $作为既定变量,粒子振动速度$ v_{0}$和声压$p_{0}$为待定系数.为获得非退化的粒子速度和声压,假定其系数矩阵的特征值为零,这时角频率$\omega $与波矢量$ k $满足如下频散关系 $$ \rho \omega ^2 = k \cdot { S}^2 \cdot k\quad \mbox{或}\quad \omega ^2 = c_x^2 k_x^2 + c_y^2 k_y^2 \tag{13}$$ 其中,2个主方向波传播相速度定义为$c_{x}=(K_{x}/\rho)^{1 / 2}$和$c_{y}=(K_{y}/\rho)^{1 / 2}$. 该特征值系统仅有唯一非退化解,表明五模材料中只允许一种平面波传播.这是五模材料完全不同于传统固体介质的独特性质,在后者中可以同时允许横波和纵波两种平面波的存在.五模材料的等频率曲线,是一个主方向与材料主方向一致的椭圆.表征能量传播快慢的群速度,可由等频率曲线在波矢空间中的梯度给出$$ v_g = \omega \nabla_k = 1 /(\rho \omega){ S}^2 \cdot k,\tan \theta_g =(K_y / K_x)\tan \theta_k \tag{14}$$ 其中,$\theta_{k}$和$\theta _{g}$分别代表波矢量和群速度的方位角. 可以看出,由于材料的各向异性$K_{x} eq K_{y}$,能量流动方向不再与波矢量方向相同.各向异性弹性介质中关于能量流速的经典公式,$ k\cdot v _{g}=\omega $在五模材料中仍然适用.粒子振动速度和方向可以由公式(12)给出 $$ v_0 = p_0 /(\rho \omega){ S} \cdot k,\tan \theta_v = \gamma \sqrt {K_y / K_x } \tan \theta_k \tag{15}$$
对于负型五模材料,有趣的一点是,$\tan\theta_{v}$和$\tan\theta _{k}$的乘积在特殊方向 $\theta_{k}=\tan^{ - 1}(K_{x}/K_{y})^{1 / 4}$等于$-1$,表示粒子振动方向和波矢方向正好垂直,沿着这一特殊方向可以传输纯横波,如同各向同性介质中的剪切波.这一特殊的横波传播行为,有可能为设计波形模式转换装置提供新的思路.
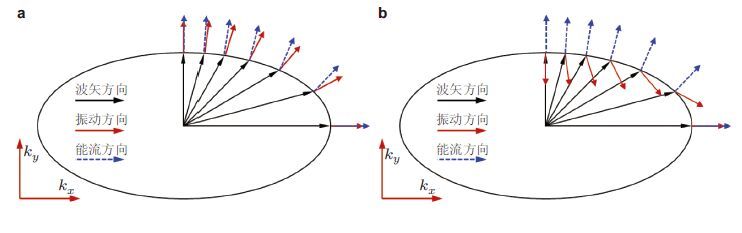
图 6给出了两种正负型五模材料的等频率曲线图,其材料参数分别为$K_{y}=4K_{x}$,$\gamma =+1$和$K_{y}=4K_{x}$,$\gamma =-1$. 如式(13)所述,各向异性五模材料等频率曲线为与材料主轴重合的椭圆. 正型五模材料中,材料主方向上存在纯纵波传播,其余方向均传播偏向刚性方向极化的纵波;负型五模材料中,能量流动方向与正型五模材料没有任何区别,均趋于向刚性方向流动. 然而,除了材料主方向传播纯纵波以外,负型五模材料还存在一个特殊方向,该方向只能传播纯横波.
|
| 图6 五模材料等频率曲线、粒子振动方向、能量流动方向与波矢量关系.(a)正型五模材料$(K_{y}=4K_{x}$,$\gamma =+1)$,(b)负型五模材料$(K_{y}=4K_{x}$,$\gamma =-1)$ |
与波在不同流体层界面处传输现象类似,波入射到不同属性五模材料层界面时,会因阻抗不匹配产生反射和折射现象.这节将重点探讨五模材料中波的折射和反射现象,给出五模材料在界面处满足无反射传播的阻抗匹配条件,并探讨其在调控声波方面的可能性.
如图 7所示,考虑上下半无限大区域的五模材料构成的水平界面,在界面处建立全局笛卡尔坐标系$xoy$.上下两部分五模材料主方向之一与界面平行,其五模材料参数分别为: ${ S}^{\rm I} = s_x^{\rm I} e_x e_x + s_y^{\rm I} e_y e_y $,$\rho ^{\rm I}$和${ S}^{\rm {Ⅱ}} = s_x^{\rm Ⅱ} e_x e_x + s_y^{\rm Ⅱ} e_y e _y $,$\rho ^{\rm Ⅱ}$,其中$s_x^{\rm I} =(K_x^{\rm I})^{1 / 2}$,$s_x^{\rm Ⅱ} =(K_x^{\rm Ⅱ})^{1 / 2}$,$s_y^{\rm I} = \gamma ^{\rm I}(K_y^{\rm I})^{1 / 2}$,$s_y^{\rm Ⅱ} = \gamma ^{\rm Ⅱ}(K_y^{\rm Ⅱ})^{1 / 2}$. 两种材料主方向的相速度分别为$c_x^{\rm I} = s_x^{\rm I}(\rho ^{\rm I})^{ - 1 / 2}$,$c_y^{\rm I} = \vert s_y^{\rm I} \vert(\rho ^{\rm I})^{ - 1 / 2}$和$c_x^{\rm Ⅱ} = s_x^{\rm Ⅱ}(\rho ^{\rm Ⅱ})^{ - 1 / 2}$,$c_y^{\rm Ⅱ} = \vert s_y^{\rm Ⅱ} \vert(\rho ^{\rm Ⅱ})^{ - 1 / 2}$.

|
| 图7 入射到不同五模材料层界面的波产生反射和折射现象,其中界面上下五模材料主方向之一与界面平行 |
入射、反射和折射角分别记作$\theta_{\rm i}$,$\theta_{\rm r}$和$\theta_{\rm t}$,对应的平面波声压假定为: $p_{\rm i}\exp(-{\rm i} k_{\rm i} \cdot r)$,$p_{\rm r}\exp(-{\rm i} k_{\rm r} \cdot r)$和$p_{\rm t}\exp(-{\rm i} k_{\rm t} \cdot r)$,其中的简谐项$\exp({\rm i}\omega t)$默认约去. 波矢可以用分量表示为$ k_{\rm i}=k_{{\rm i}x} e_{x} - k_{{\rm i}y} e_{y}$,$ k _{\rm r}=k_{{\rm r}x} e_{x} - k_{{\rm r}y} e_{y}$和$ k _{t}=k_{{\rm t}x} e_{x} - k_{{\rm t}y} e_{y}$. 根据上一节公式,材料I和材料Ⅱ中应力和速度分别为: $ \sigma ^{\rm I}= -(p_{\rm i}+p_{\rm r})S^{\rm I}$,$ \sigma ^{\rm Ⅱ}= - p_{\rm t} S^{\rm Ⅱ}$,$ v ^{\rm I}=p_{\rm i} S^{\rm I}\cdot k _{\rm i}/(\rho ^{\rm I} \omega)+ p_{\rm r} S^{\rm I}\cdot k _{\rm r}/(\rho ^{\rm I} \omega)$和$ v ^{\rm Ⅱ}=p_{\rm t} S^{\rm Ⅱ}\cdot k _{\rm t}/(\rho ^{\rm Ⅱ} \omega)$. 入射波声压及波矢为已知量,反射和折射波参数可以由界面处物理量连续条件确定,即界面两侧物质法向速度连续和界面力连续 $$ e_y \cdot { v }^{\rm I} = e_y \cdot { v }^{\rm Ⅱ},e_y \cdot \sigma^{\rm I} = e_y \cdot \sigma^{\rm Ⅱ} \tag{16}$$
由于式(16)在$y=0$界面处对于任意$x$都成立,可导出界面平行方向波数守恒结论: $k_{{\rm r}x}=k_{{\rm t}x}=k_{{\rm i}x}$. 从频散关系曲线得知,由于入射波和反射波$x$方向波数守恒,则$y$方向波数或者相同或者互为相反数.只有反射波和入射波在$y$方向的波数异号才符合物理实际,即有$\theta _{\rm i}=\theta_{\rm r}$. 声压的大小可由方程(17)确定 $$ p_{\rm r} = \dfrac{1 - \xi }{1 + \xi }p_{\rm i},p_{\rm t} = \dfrac{s_y^{\rm I} }{s_y^{\rm Ⅱ} }\dfrac{2}{1 + \xi }p_{\rm i} \tag{17}$$ 其中,阻抗比例系数$\xi =(\rho ^{\rm I}k_{{\rm t}y})/(\rho ^{\rm Ⅱ}k_{{\rm i}y})$. 可以看出,反射、折射声压主要由法向波数及密度决定.折射角度和折射波数$y$方向分量,可由两种介质中的频散曲线确定 $$ (c_x^{\rm I})^2k_{{\rm i}x}^2 +(c_y^{\rm I})^2k_{{\rm i}y}^2 = (c_x^{\rm Ⅱ})^2k_{{\rm i}x}^2 +(c_y^{\rm Ⅱ})^2k_{{\rm t}y}^2 \tag{18}$$ 将$k_{{\rm i}y}=k_{{\rm i}x}{\rm cot}\theta_{\rm i}$和$k_{{\rm t}y}=k_{{\rm t}x}{\rm cot}\theta_{\rm t}$代入上式可得折射角度为 $$ \theta_{\rm t} = \tan ^{ - 1}\dfrac{c_y^{\rm Ⅱ} }{\pm \sqrt {(c_x^{\rm I})^2 +(c_y^{\rm I})^2\cot ^2\theta_i -(c_x^{\rm Ⅱ})^2} } \tag{19}$$
根式前面正负号$\pm $的选取,应使得折射波数在$y$方向的分量$k_{{\rm t}y}$具有负虚部,以符合物理实际. 从声压表达式(17)可知,当$\xi =1$恒成立时,对于任意角度入射波反射声压始终为零,此时两侧五模材料满足界面阻抗匹配条件. 根据频散关系式(18),可以导出$\xi =1$的恒成立条件(阻抗匹配条件)为 $$ c_x^{\rm I} = c_x^{\rm Ⅱ},\rho ^{\rm I}c_y^{\rm I} = \rho ^{\rm Ⅱ}c_y^{\rm Ⅱ} \tag{20}$$
即五模材料界面阻抗匹配条件为: 两侧介质切向速度匹配且法向阻抗匹配.根据速度关系还可以导出: 当全透射现象发生时,界面两侧介质粒子振动速度完全连续,而不仅仅满足法向速度连续.以上公式同样适用于两侧五模介质均退化为传统各向同性声学介质情况,此时仅有当两侧介质为同一种声学介质时才始终满足全透射条件.
3 五模材料微结构设计 3.1 五模材料特征参数对于实际设计的微结构五模材料,其剪切模量很小但不为零,均质化后的宏观弹性矩阵与正交各向异性弹性介质一致,并在主轴坐标下具有最简单形式 $$ C = \left( {{\begin{array}{*{20}c} {K_x } \quad& {K_{xy} } \quad& 0 \\ {K_{xy} } \quad& {K_y } \quad& 0 \\ 0 \quad& 0 \quad& {G_{xy} } \\ \end{array} }} \right)\tag{21}$$
$K_{x}$和$K_{y}$分别是材料在$x$和$y$主轴方向的刚度,$K_{xy}$是材料2个主方向的耦合刚度,$G_{xy}$是材料的剪切模量.由理想五模材料的弹性矩阵仅有一个非零特征值得知,实际设计的微结构五模材料与理想五模材料的差别,由$K_{x}K_{y} - (K_{xy})^{2}$和$G_{xy}$趋于零的程度决定. 因此,可用如下2个无量纲五模特征指标,定量刻画所设计材料与理想五模材料的近似程度 $$ \pi = \dfrac{\vert K_{xy} \vert }{\sqrt {K_x K_y } },\mu = \dfrac{G_{xy} }{\sqrt {K_x K_y } } \tag{22}$$
可以看出当五模特征指标$\pi =1$和$\mu =0$时,所设计材料即成为理想五模材料. 对于实际设计的材料,由于需要满足结构静力学稳定性,其均质化弹性矩阵必须满足正定性,因此固体形态的五模材料必然有$\pi eq 1$和$\mu eq 0$.在设计材料微结构时,应使2个特征指标$\pi $和$\mu $尽可能分别接近1和0,而获得更好的近似五模材料. 对于各向同性情况,由于2个特征参数$\pi $和$\mu $具有关联$1/\pi =1+2\mu $,特征参数条件退化为一个: 只需剪切模量远小于体积模量,即可保证材料具有很好的五模材料特征. 然而,对于一般的各向异性介质,仅由剪切模量极小这一条件并不能确保五模材料特征,另一个特征参数$\pi $也需要同时考虑,才能保证所设计材料具有五模材料特性,而以往的研究往往忽略了这一点. 通常的经验表明,$\pi $和$\mu $分别满足$\pi \geq 0.99$和$\mu \leq 0.01$时,所设计微结构五模材料具有较好五模材料特征,并与理想五模材料一样可用于对声波进行调控.
传统弹性介质能够承受任意状态的应力,而五模材料只能承受与特征应力$ S$成比例的应力.以弹性介质为基材设计五模材料时,必须经过特殊的几何结构设计,来剔除基材的其他应力承载模式. 在具体设计时,可从五模材料的静力学行为特征得到启发: 在主轴坐标下,理想五模材料不能承受任何剪切应力,同时2个正应力必须保持一定比例关系. 据此可以推测,其微结构单胞可由具备轴向承载能力的部件,通过弱剪切方式连接构成.图 3中浅蓝色锥形杆为较硬材料,白色区域可以填充较软的材料,或者保持空腔,锥形杆通过细小部件与调节密度的配重圆连接.由几何构形的对称性可知,材料主轴为$x$和$y$方向.在虚线所示的矩形胞元中,由于锥形杆间的类铰链连接及其特殊的几何排布,只有当水平和竖直方向所受正应力满足一定比例关系,且不存在剪应力时,此结构才能保持稳定,这正是五模材料必备的特征.
需要指出的是,通过设计胞元的微结构来实现五模材料,是一个非常复杂的数学问题,至今还缺乏一些通用的指导原理.在后面的讨论中,我们将不涉及微结构胞元形成五模材料的深层机理,主要给出目前的一些五模材料微结构形式,并从中推测出一些适用的设计准则.
3.2 蜂窝结构五模材料解析均质化在构成二维蜂窝材料的梁单元具有很大的长细比时,蜂窝材料是五模材料很好的近似.以下将解析地给出蜂窝材料的等效弹性参数,并研究其与理想五模材料的近似规律.
蜂窝结构及其代表单胞如图 8所示,在非规则六边形单胞中,长度为$l$的两根斜梁和长度为$h$的竖直梁在顶点处相交,两根斜梁对称分布且与竖直方向成$\beta $角度. 角度$\beta $对蜂窝结构几何特征起主要作用,被称为蜂窝结构拓扑角度.单胞所占面积为,$V_{\rm cell}=2l^{2}(\xi +\cos\beta)\sin\beta $.等效密度可以将梁单元总质量在单胞内平均得到,$\rho ^{\rm eff}=\rho_{\rm s}V_{\rm s}/V_{\rm cell}$. 为简化分析,假设所有梁单元均为壁厚$t$的细长梁,且由同种基体材料组成,杨氏模量、泊松比和密度分别为$E_{\rm s}$,$v_{\rm s}$和$\rho_{\rm s}$. 在线弹性理论下考虑均质化,则等效弹性参数仅与拓扑角度 $\beta $、梁长度比$\xi =h/l$、梁的长细比 $\eta =t/l$这3个无量纲参数及基体属性相关.

|
| 图8 (a)梁单元组成的蜂窝材料,虚线区域代表单胞胞元,(b)非规则六边形代表单胞及几何参数 |
在此将采用基于应变能等效原理的均质化方法,即弹性参数可以由单胞应变能密度对应变求两次导数得出.该方法的关键点在于获得任意局部应变状态下单胞内存储的总应变能.由于假定所有梁单元为细长梁,在梁端点处的力偶作用可以忽略.在此假设下,细长梁的轴向变形由端部轴向载荷引起,横向变形由端部剪切力产生. 假定图 8(b)单胞中三根梁交点位于原点位置(0,0). 为了统一描述,三根梁的另一端分别编号为1,2和3,其位置矢量为$ R _{\rm i}$ $(i=1$,2,3),梁的长度分别记为$R_{\rm i}=\vert R _{\rm i}\vert $. 对每根梁$i$ $(i=1$,2,3),定义其轴向单位矢量和横向单位矢量为: $ e_i^n = R _i / R_i $,$ e_i^t = e_3 \times e_i^n $,其中,$ e_{3}$为指向纸面外的单位向量. 在外载荷作用下,假设单胞产生仿射变形,即各根梁单元边界点移动到新的位置$ r_{\rm i}= G \cdot R_{\rm i}$. 其中的变形梯度矩阵$ G$可以表示为 $$ G = \left({{\begin{array}{*{20}c} {\varepsilon_{11} } \quad& {\varepsilon_{12} + \phi } \\ {\varepsilon_{12} - \phi } \quad& {\varepsilon_{22} } \\ \end{array} }} \right)\tag{23}$$ 其中,$\varepsilon_{\alpha \beta }$ $(\alpha $,$\beta =1$,2)代表局部应变的各个分量,$\phi $代表剪应变 $\varepsilon_{12}$引起的单胞局部转动. 梯度矩阵总共包含4个变量,其中3个为局部应变,另外1个为局部转动. 局部应变作为已知参数,局部转动 $\phi $可由后面的平衡方程求出. 由于单胞变形,单胞中顶点从原点位置移动到新坐标$ X _{0}= \{ u_{0},v_{0} \} ^{\rm T}$,新坐标同样可由平衡方程求得.根据以上变形信息,每根梁端点产生轴向位移$u_i^n =(r _i - X _0)\cdot e_i^n $和横向位移$u_i^t =(r _i - X _0)\cdot e_i^t $.每根梁端点处分别承受轴向力$F_i^n $和横向力$F_i^t $.由于端点力偶已经忽略,轴向力和横向力可以通过梁理论由相应的轴向位移和横向位移得出 $$ F_i^n = \dfrac{E_{\rm s} t}{R_i }u_i^n,F_i^t = \dfrac{E_{\rm s} t^3}{4R_i^3 }u_i^t \tag{24}$$
以上端点力表达式适用于平面应力状态,即蜂窝结构在曲面厚度非常薄的情况.如果蜂窝结构在垂直于纸面方向很厚时,该2D问题应该考虑为平面应变问题,相应的杨氏模量$E_{\rm s}$只需要用$E_{\rm s} /(1 - v_s^2)$替代即可,其余参数均保持不变.为使得单胞在所受载荷下能保持平衡,必须满足力平衡和力矩平衡方程 $$ \sum\limits_{ i = 1}^3 {(F_i^n e_i^n + F_i^t e_i^t)} = \textbf{0},\sum\limits_{ i = 1}^3 { R _i \times(F_i^t e_i^t)} = \textbf{0} \tag{25}$$
以上3个平衡方程,正好能够求解出用局部应变表示的局部转动$ \phi $和顶点处位移$ X _{0}=\{u_{0},v_{0}\}^{\rm T}$,相应的梁端部载荷也可以用局部应变的形式给出,求解结果比较繁琐,就不在此列出. 得到以局部应变表示的各个局部变量之后,应变能密度可以由单胞内梁单元应变能求和再作面积平均得到 $$ w^{\rm e} = \dfrac{1}{V_{\rm cell} }\sum\limits_{ i = 1}^3 {\dfrac{1}{2}(F_i^n u_i^n + F_i^t u_i^t)} \tag{26}$$
将位移及载荷表达式代入上式,可以得到应变能密度最终关于局部应变 $\varepsilon_{\alpha \beta }$ $(\alpha $,$\beta =1$,2)的函数,通过将其对应变两次求导即可得到面内弹性常数 $$ K_x = C_{1111} = E_{\rm s} \eta \dfrac{(4\sin ^2\beta + \eta ^2\cos ^2\beta + 2\xi \eta ^2)\sin \beta }{2(\xi + \cos \beta)(2 + 4\xi \cos ^2\beta + \xi \eta ^2\sin ^2\beta)} \tag{27}$$ $$ K_y = C_{2222} = E_{\rm s} \eta \dfrac{(\xi + \cos \beta)(4\cos ^2\beta + \eta ^2\sin ^2\beta)}{2(2 + 4\xi \cos ^2\beta + \xi \eta ^2\sin ^2\beta)\sin \beta } \tag{28}$$ $$ K_{xy} = C_{1122} = E_{\rm s} \eta \dfrac{(4 - \eta ^2)\sin \beta \cos \beta }{2(2 + 4\xi \cos ^2\beta + \xi \eta ^2\sin ^2\beta)} \tag{29}$$ $$ G_{xy} = C_{1212} = E_{\rm s} \eta ^3\dfrac{4(\xi + \cos \beta)\sin \beta }{\eta ^2 + 4(1 + 2\xi)\xi ^2\sin ^2\beta +(2 + \xi \cos \beta)\eta ^2\xi \cos \beta } \tag{30}$$
可以看出,除了剪切刚度$G_{xy}$与长细比的立方$\eta ^{3}$线性相关以外,其余刚度参数基本都与梁长细比$\eta $线性相关.该蜂窝材料的2个五模特征参数分别为 $$ \pi = 1 - \dfrac{1 + 2\xi \cos ^2\beta }{2\sin ^22\beta }\eta ^2 + o(\eta ^2)\tag{31}$$ $$ \mu = \eta ^2\dfrac{(\xi + \cos \beta)(1 + 2\xi \cos ^2\beta)}{\xi ^2\sin ^2\beta \cos \beta(1 + 2\xi)} + o(\eta ^2)\tag{32}$$
从上式看出,蜂窝材料的2个五模特征参数与理想值偏离量是长细比 $\eta $的二阶小量. 因此由长细比 $\eta $很小的梁单元组成的蜂窝材料,可以作为理想五模材料的近似. 对于细长梁情况,通过忽略三阶小量$o( \eta ^{2})$,式(27)$\sim $式(30)中弹性常数可以简化为如下弹性矩阵 $$ D = E_{\rm s} \eta \dfrac{\sin \beta \cos \beta }{1 + 2\cos ^2\beta }\left({{\begin{array}{*{20}c} \alpha \quad& 1 \quad& 0 \\ 1 \quad& {1 / \alpha } \quad& 0 \\ 0 \quad& 0 \quad& 0 \\ \end{array} }} \right),\alpha = \dfrac{\sin \beta \tan \beta }{\xi + \cos \beta } \tag{33}$$
很明显,简化的等效刚度矩阵(Norris&Nagy 2011)与理想五模材料刚度矩阵完全一致. 忽略三阶小量$o(\eta ^{2})$在物理上对应的含义为,梁单元只能承受轴向载荷且顶点处连接为铰链形式.这一结构在主轴方向不能承受任何剪切力,承受的正应力也必须满足一定比例,因此具有和理想五模材料具有完全一样的静承载特征.微结构等效刚度与壁厚线性相关,与拓扑角度$\beta $及长度比$\xi $依赖关系复杂; 各向异性程度由参数$\alpha $表示,在长细比$\xi $降低或者拓扑角度$\beta $增加时,各向异性程度增大.鉴于细长梁蜂窝材料宏观有效性质近似于五模材料,目前复杂五模材料微结构都以蜂窝结构为基础,通过在不同位置附加不同几何形状的配重单元实现参数调节.
在图 9(a)和图 9(b)中,保持长度比为$\xi =1$,分别以4种不同长细比 $\eta =1/10$,1/20,1/25,1/50,给出了2个五模特征参数随拓扑角度$\beta $变化关系曲线. 参数$\pi $随$\beta $增大而降低,且在长细比 $\eta $较大时降低更加明显,另外在整个$\beta $取值范围$\pi $都小于1.对于所考察拓扑角度范围$60^{\circ}<\beta <85^{\circ}$,梁单元的长细比需要低于1/50 才能使得$\pi>0.99 $. 参数$\mu $随$\beta $的增大先缓慢降低随后增加,随长细比的减小而显著降低,在长细比小于1/20时,在整个$\beta $取值范围都小于0.01. 从图 9(a)和图 9(b)可以得出,为了能在拓扑角度$\beta $小于80$^{\circ}$的范围内,获得近似程度较高的五模材料$(\pi >0.99$和$\eta <0.01)$,梁单元的长细比必须小于1/25. 图 9(c)和图 9(d)中给出了长度比为$\xi =0.5$时,4种不同长细比时特征参数与角度关系. 特征参数$\pi $受长度比$\xi $的影响非常小,4种长细比的结果与$\xi =1$时几乎没有差别; 另一特征参数$\mu $随$\xi $减小而增大,尤其在长细比 $\eta >1/10$时增大非常明显.

|
| 图9 蜂窝结构的五模特征参数.(a),(b)长度比为$\xi =1$时和(c),(d)长度比$\xi =0.5$时,$\pi $和$\mu $随拓扑角度$\beta $和长细比 $\eta $变化关系曲线 |
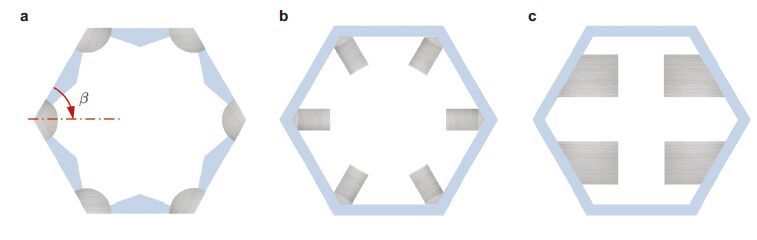
由于等效参数调节范围的需要,通常设计的五模材料单胞构形远比蜂窝结构几何复杂. 图 10给出了文献中报道的3种单胞构形,由基本的类蜂窝结构外框和深色配重单元构成.单胞等效密度可由配重单元调节,单胞的各向异性程度则主要由几何构型调节,主要是斜杆与水平方向之间的拓扑夹角$\beta $.
|
| 图10 不同配重单元构成的正六边形五模材料单胞.(a),(b)单胞顶点附加配重单元;(c)蜂窝壁中点附加配重单元 |
对于此类复杂几何形状的微结构,通过解析方式求解其等效参数几乎不可能,需要采用数值方法进行均质化.已有的数值方式验证表明,只要连接杆与配重块的连接部位非常窄,这类材料就可以在静态或者长波条件下近似看作五模材料.当波传播频率提高时,会出现一些由微结构导致的新现象,不再能由准静态参数描述,而必须采用动态均质化理论才能完整描述其波动行为(Norris et al. 2012,Srivastava&Nemat-Nasser 2014). 由于动态均质化方法发展较快,而且新的方法也不断被提出,我们在此不做详细讨论.对于具有复杂微结构的胞元,材料等效参数可以通过比较频散曲线得到.
在长波条件下一般不存在共振现象,单胞等效密度可由总质量作面积平均得到,$\rho ^{\rm eff}=\rho_{\rm s}V_{\rm s}/V_{\rm cell}$. 等效弹性常数则可从频散关系得到,而频散关系则由在单胞构型边界施加周期性Floquet-Bloch边界后求解特征频率问题得到.在主轴坐标下,假设对一个微结构单胞均质化后,等效弹性矩阵写为 $$ C = \left({{\begin{array}{*{20}c} {K_x^{\rm eff} } \quad& {K_{xy}^{\rm eff} } \quad& 0 \\ {K_{xy}^{\rm eff} } \quad& {K_y^{\rm eff} } \quad& 0 \\ 0 \quad& 0 \quad& {G_{xy}^{\rm eff} } \\ \end{array} }} \right)\tag{34}$$
将以上弹性矩阵代入动力学方程,并假定平面波解,即可得到介质在不同方向波传播的相速度 $$ \left.\begin{array}{l} x{\rm 方向},c_{{\rm L}x}^2 = K_x^{\rm eff} / \rho ^{\rm eff},\quad c_{{\rm T}x}^2 = G_{xy}^{\rm eff} / \rho ^{\rm eff} \\ y {\rm 方向},c_{{\rm L}y}^2 = K_y^{\rm eff} / \rho ^{\rm eff} \\ 45^{\rm \circ}{\rm 方向},c_{q{\rm L}}^2 = \dfrac{1}{4\rho ^{\rm eff}}\left( {K_x^{\rm eff} + K_y^{\rm eff} + 2G_{xy}^{\rm eff} + \sqrt {(K_x^{\rm eff} - K_y^{\rm eff})^2 + 4(K_{xy}^{\rm eff} + G_{xy}^{\rm eff})^2} } \right)\\ 45^{\rm \circ}{\rm 方向},c_{q{\rm T}}^2 = \dfrac{1}{4\rho ^{\rm eff}}\left( {K_x^{\rm eff} + K_y^{\rm eff} + 2G_{xy}^{\rm eff} - \sqrt {(K_x^{\rm eff} - K_y^{\rm eff})^2 + 4(K_{xy}^{\rm eff} + G_{xy}^{\rm eff})^2} } \right)\\ \end{array}\right\} \tag{35}$$
在主轴方向,$x$或者$y$方向,由于正剪应变不耦合,两种体波分别为纯纵波和纯横波. $c_{{\rm L}x}$,$c_{{\rm T}x}$和$c_{{\rm L}y}$分别代表$x$方向纵波波速、横波波速和$y$方向纵波波速.在其他方向,比如与$x$方向成45$^{\circ}$,两种体波分别是横向极化和纵向极化波,其波速分别记为$c_{q{\rm T}}$和$c_{q{\rm L}}$. 微结构内不在同方向波传播相速度,可由原点附近频散曲线的斜率计算得出.考虑到均质化后的介质相速度应该和微结构相速度一致,因此可以通过以下表达式得出微结构等效刚度参数 $$ \left.\begin{array}{l} K_x^{\rm eff} =\rho ^{\rm eff}c_{{\rm L}x}^2,K_y^{\rm eff} =\rho ^{\rm eff}c_{{\rm L}y}^2,G_{xy}^{\rm eff} = \rho ^{\rm eff}c_{{\rm T}x}^2 \\ K_{xy}^{\rm eff} = \rho ^{\rm eff}\left(\sqrt {(c_{q{\rm L}}^2 - c_{q{\rm T}}^2)^2 - (c_{{\rm L}x}^2 - c_{{\rm L}y}^2)^2 / 4} - c_{{\rm T}x}^2 \right)\\ \end{array}\right\} \tag{36}$$ 其中,$x$方向和$y$方向的体积模量由相应方向上的纵波分支确定,剪切模量$G_{xy}^{\rm eff} $则由$x$或$y$方向横波分支确定,在长波条件下两者数值相差很小,$K_{xy}^{\rm eff} $则由等效介质在45$^{\circ}$方向上的波传播特征决定.
以图 10(a)中给出的特定钛基单胞为例$(l=0.01$ m,$\beta =\pi /3$,$ r/l=0.296$,$t/l=0.016 3$,$\gamma =0^{\circ})$,其带结构如图 11(a)所示. 基材物理参数分别为杨氏模量$E_{\rm s}=110$ GPa、泊松比$v_{\rm s}=0.34$和密度$\rho_{\rm s}=4 400$ kg/m$^{3}$.内嵌图片给出了单胞构型和相应的第一布里渊区,其中灰色高亮区域代表不可约布里渊区(irreducible brillouin zone,IBZ),带结构曲线即由波矢量沿着不可约布里渊区边界一周时,所得各阶特征频率连接成的曲线.带结构图给出了单胞构型中允许传播的Bloch波的频率$\omega $和波矢量$ k $之间的组合.
在图 11(a)中,从原点$\Gamma $出发的黑、红色两阶频散曲线,分别代表横波和纵波模式分支,另外两阶绿、蓝色曲线则代表旋转模式分支,其中水的频散曲线用点划线给出. 微结构的前四阶分支所代表的传播模式,可以清晰地从水平方向小波数$(k = \Gamma M /20)$时的模态振型上加以区分(图 11(b)). 从图中可看出,在第一阶模态中,单胞整体有垂直于波矢方向的平动,表明其横波特征;第2阶模态中,单胞整体有平行波矢方向的平动,表示纵波特征.第三阶模式中,相邻的配重块向相反的方向旋转,梁单元则近似产生一阶C形弯曲; 而在第四阶模式中,所用配重块都沿相同方向旋转,梁单元则近似产生二阶S形弯曲.依据上述均质化方法可求得该单胞构型的等效参数,分别为密度$\rho =1 000$ kg/m$^{3}$,体积模量$K_{x}=2.269$ GPa和$K_{y}=2.268 $ GPa. 另一个弹性参数由45$^{\circ}$方向相速度得到,$K_{xy}=2.239$ GPa. 可以看到,即便单胞具有正六边形特征,水平和竖直方向上的体积模量仍然出现了轻微的各向异性,但相差小于0.03%. 等效剪切模量为$G_{xy}=0.030$ GPa,比体积模量低2个数量级,这也可从第一分支比第2分支斜率低很多这一点得到印证.

|
| 图11 (a)与水等效的五模材料单胞带结构曲线,(b)水平方向小波矢量$ k = \Gamma M/20$对应前四阶模态振型图 |
上述单胞等效参数与水很接近,因此其声学性质也应和水非常类似.为检验其与水声学特性匹配程度,将单胞在面内周期平移得到块体五模材料,随后用COMSOL Multiphysics中的声固耦合模块直接对其声学特性进行了仿真. 图 12(a)给出了平面波$(f=7.5$ kHz)从左侧以30$^{\circ}$角度入射到水中微结构五模材料上时,整个区域的声压分布图,背景介质中波长远大于单胞尺寸$(\lambda =20l)$. 可以看到,在五模材料以外的区域,平面波特征得到了很好的保持,且在入射声波一侧无明显反射,表明所设计微结构五模材料和水具有很好的匹配. 为便于对比,图 12(b)中给出了,相同平面波在均匀水域中传播时的声压分布.两幅图中声压场分布几乎完全一致,这也证实了上述均质化方法的有效性.将上述均质化方法与适当的优化算法结合,以几何参数作为优化变量,等效参数与所需五模材料参数之间的偏差作为优化目标,即可获得所需五模材料参数所对应的单胞微结构参数,该方法可用于波动调控装置设计中的五模材料的微结构设计.

|
| 图12 (a)平面波入射到水中微结构五模材料后声压分布图,(b)相同平面波在均匀水中时的声压分布 |
在基于五模材料声波调控器件的具体设计中,需要根据五模材料的宏观等效性质设计出相对应的胞元微结构参数,这个过程是均匀化方法的逆问题,往往需借助于优化等手段.由于常见五模材料胞元构型均至少包含4个几何调节参数,直接采用多变量优化算法迭代求解将变得非常耗时,也容易陷入局部极小而难以保证优化精度. 为克服以上困难,一般需要首先确定五模材料胞元的基本构型,使其具有较大的等效参数调节范围,满足调控功能的需要; 其次,需要建立适当的优化设计流程,加快优化设计过程并保证较高设计精度.
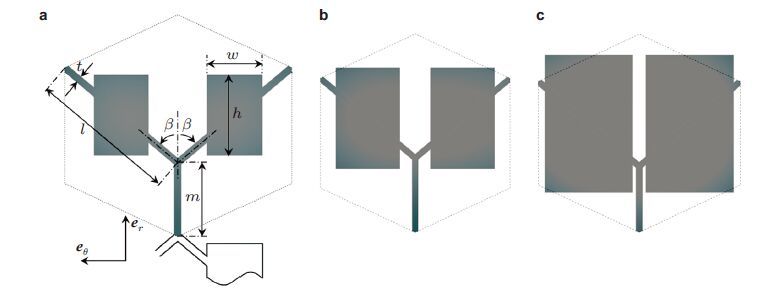
下面我们以图 13(a)所示的二维五模材料单胞构型为例,说明微结构设计优化过程.该六边形单胞由Y形杆及附着于两倾斜杆上的矩形配重构成,单胞等效性质由5个无量纲几何参数决定: Y形杆夹角$\beta $,竖直杆无量纲长度$\bar {m} = m / l$,梁单元长细比$\bar {t} = t / l$,矩形配重无量纲宽和高$\bar {w} = w / l$,$\bar {h} = h / l$.鉴于配重矩形块长宽的调节范围,该五模材料具有极大的等效密度调节能力(图 13(b)和图 13(c)),其等效密度在$\bar {w} \approx 0$,$\bar {h} \approx 0$时取极小值,在$\bar {w} \approx \sin \beta $,$\bar {h} \approx \bar {m} + \cos \beta $取近似基体密度的极大值.另外,通过非等长的竖直杆和斜杆设计,使得该构型各向异性程度可由$\beta $和$\bar {m}$同时调节,较通常五模胞元构型(图 10(a)和图 10(b)具有更大的各向异性调节能力.
|
| 图13 (a)斜梁中点附加矩形配重块的五模材料胞元构型;(b),(c)不同几何参数的胞元示意图 |
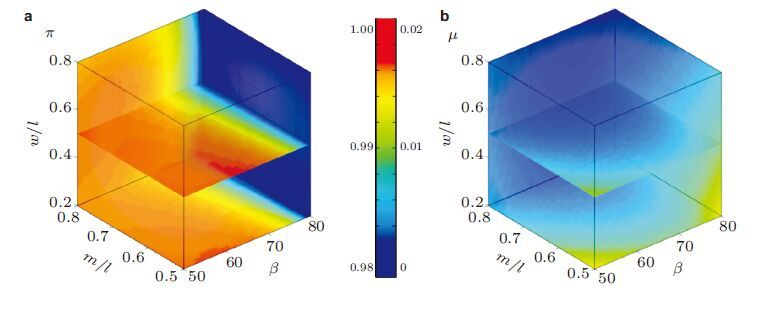
图 14 给出了上述铝基$(E_{\rm s}=69$ GPa,$\rho _{\rm s}=2 700$ kg/m$^{3}$,$v_{\rm s}=0.33)$胞元对应的2个五模特征参数随几何参数的分布图,图中3个几何参数取值范围为: 拓扑角$50^{\circ}<\beta <80^{\circ}$,竖斜杆长度比$0.5<\bar {m}<0.8$,矩形配重块宽度$0.2<\bar {w}<0.8$,高度固定为$\bar {h}=0.4$,梁长细比为$\bar {t}=0.04$. 可以看出,在绝大多数参数组合取值下,五模特征参数同时满足$\pi >0.99$和$\mu <0.01$,表明该微结构胞元等效性质具有非常好的五模材料特征.
|
| 图14 五模特征参数(a)$\pi $和(b)$\mu $随几何参数变化关系 |
图 15 给出了胞元对应的等效密度、模量随几何参数分布图.等效密度取值范围为$0.2<\rho /\rho_{0}<1.2$,且可通过调节矩形配重块高度进一步拓宽. 归一化模量$K_{x}(K_{\rm r})$主要与拓扑角度$\beta $以及配重块宽度$\bar {w}$相关,几乎不受竖斜杆长度比$\bar {m}$的影响,其中$\rho_{0}$和 $K_{0}$分别代表水的密度和体积模量.各向异性程度$K_{y}/K_{x}$主要由拓扑角度$\beta $及竖斜杆长度比$\bar {m}$决定,与矩形配重块宽度$\bar {w}$几乎无关. 壁厚比$\bar {t}$取0.05和0.08时,所得等效参数特征与上述结果类似.经具体定量分析得知,对于上述五模材料胞元构型,在保证特征参数$\pi >0.99$和$\mu <0.01$的前提下,能实现最大各向异性程度为$K_{y}/K_{x} \approx 26$; 在$\pi >0.98$和$\mu <0.01$的前提下,则能实现更强的各向异性程度$K_{y}/K_{x} \approx 66$.

|
| 图15 (a)等效密度,(b)等效模量,(c)各向异性程度与胞元微结构几何参数的依赖关系 |
对该基本胞元的分析结果表明,在根据有效性质设计胞元微结构几何参数时可分两步优化实现: 第一,调节拓扑角度$\beta $、竖斜杆长度比$\bar {m}$得到所需的各向异性程度$K_{y}/K_{x}$; 第二,调节梁单元长细比$\bar {t}$、矩形块宽$\bar {w}$得到所需的模量$K_{x}$; 最后,根据所需的密度$\rho $直接计算得到矩形块高$\bar {h}$.这一优化流程将原本5变量优化过程分解为2个双变量优化过程,明显降低了优化空间维数及复杂度. 而且,优化初值的选取可由扫描几何参数建立的等效参数数据库得出,以上方法能显著缩短优化时间且能保证优化结果精度. 然而,该优化算法用到了等效参数与几何参数之间的特殊关系,只针对当前五模胞元构形的优化问题. 对于更一般的情况,即由给定的五模材料宏观性能设计出相应的微观结构及几何参数,目前还没有普适的高效方法.
根据上述优化算法设计的与水声学参数相同的铝基五模材料 (俗称"金属水")胞元参数为: $\beta =60^{\circ}$,$\xi =1$,$\bar {t} = 0.060 5$,$\bar {w} = 0.8$,$\bar {h} = 0.188 6$,其等效性质与水差异小于1%: 密度$\rho ^{\rm eff}/\rho _{0}=1$,模量$K_{x}/K_{0}=1.001$,$K_{y}/K_{0}=1.009$,$K_{xy}/K_{0}=0.996$. 图 16(b)给出了该胞元的频散关系曲线,其中红色的纵波分支几乎与水的频散曲线重合. 图 16(a)给出了用图 10(a)中胞元设计的铝基"金属水"构形及频散曲线. 对比频散曲线图可以发现:在灰色区域所示的低频段,顶点附加圆形配重的胞元存在旋转波分支(蓝色和绿色曲线); 而中点附加矩形配重的胞元则不存在旋转分支,因此在低频应用时不会激发出其他传播模式,将具有更优的水声控制效果.这一特征主要由中点附加的配重块增强了连接杆抗弯能力,使得旋转分支向高频偏移所导致.

|
| 图16 两种"金属水"五模材料频散曲线.(a)顶点附加圆形配重单胞,(b)中点附加矩形配重单胞 |
该部分将介绍利用五模材料设计声波控制装置的基本方法.基于五模材料的变换声学理论最早由罗格斯大学Norris(2008)提出,该理论为基于五模材料的声隐身设计奠定了基础. 考虑如图 17(b)所示物理空间,由$\omega ^{\rm in}$,$\omega $和$\omega ^{\rm out}$三部分组成,其中背景区域$\omega ^{\rm out}$分布着密度为$\rho_{0}$和模量为$K_{0}$的声学介质.为实现中心区域$\omega ^{\rm in}$对声波隐身,需在区域$\omega $内设计特殊的材料参数分布引导声波绕过中心区域,使外部区域$\omega ^{\rm out}$内的声压场与整个空间均分布着背景声学介质时一致.为推导出区域$\omega $内需要的材料参数分布,考虑如图 17(a)中由相同背景介质覆盖的虚拟空间$\Omega $,$\Omega ^{\rm out}$,虚实空间区域$\Omega $和$\omega $具有相同的外边界,$\partial \Omega =\partial \omega ^{ + }$. 为简化公式推导,在虚实空间中分别建立直角坐标XOY和xoy以表示空间不同位置.

|
| 图17 五模材料变换声学示意图.(a)虚拟空间$\Omega $,$\Omega ^{\rm out}$及坐标XOY;(b)物理空间$\omega ^{\rm in}$,$\omega $和$\omega ^{\rm out}$及坐标xoy |
虚拟空间中流体声压控制方程为 $$ \dot{ v}(X)= - \rho_0^{ - 1} \nabla_ X p(X),\dot {p}(X)= - K_0 \nabla_ X \cdot { v }(X)\tag{37}$$
考虑虚空间位置$ X$到实空间位置$ x$之间的映射关系$ x = x(X)$,该函数关系分别将区域$\Omega ^{\rm out}$和$\Omega $映射至$\omega ^{\rm out}$和$\omega $.映射梯度定义为$ F= \partial x/ \partial X$,或以分量形式写为$F_{ij}=\partial x_{\rm i}/\partial X_{j}$,在$\Omega ^{\rm out}$上为恒等映射则有$ F = I$. 根据 $ x$和$ X$之间的映射,可以导出虚实空间算子映射关系: $\nabla_ X= F ^{\rm T} \cdot \nabla_ x$,$\nabla_ X \cdot = J\nabla _{x} \cdot(J^{ - 1} F \cdot)$,上式中应用了$\nabla_ x\cdot(J^{ - 1} F)={\bf 0}$,其中$J$为$ F$的雅克比行列式. 借助于算子映射,方程(1)可以重新用坐标$ x$表示为 $$ \left.\begin{array}{l} \dot {p}(X)= - K_0 J\nabla_x \cdot(J^{ - 1}{ S} \cdot { S}^{ - 1} \cdot F \cdot { v }(X))= - K_0 J{ S}:\nabla_x(J^{ - 1}{ S}^{ - 1} \cdot F \cdot { v }(X))\\ J^{ - 1}{ S}^{ - 1} \cdot F \cdot \dot{ v}(X)= -(\rho_0^{ - 1} J^{ - 1}{ S}^{ - 1} \cdot F \cdot F ^{\rm T} \cdot { S}^{ - 1})\cdot \nabla_x\cdot(p(X){ S})\\ \end{array}\right\} \tag{38}$$
上式中引入了实空间中的无源对称二阶张量$ S: S^{\rm T}= S$,$\nabla_x\cdot S={\bf 0}$. 定义$ x$坐标下的物理场量及材料参数,以上方程可以改写为标准五模材料声学控制方程形式 $$ {\rho '}^{ - 1} = \rho ^{ - 1}J^{ - 1}{ S}^{ - 1} \cdot F \cdot F ^{\rm T} \cdot { S}^{ - 1},{ C'}({ x})= {K'}{ S} \otimes { S},{K'} = K_0 J \tag{39}$$ $$ { v'}({ x})= J^{ - 1}{ S}^{ - 1} \cdot F \cdot { v }(X),{p'}({\rm x})= p(X)\tag{40}$$ $$ \dot {{p'}}({ x})= - {K'}({ x}){ S}:\nabla_x({ v'}({ x})\tag{41}$$ $$ \dot{ v'}({ x})= - {\rho'}^{ - 1}({ x})\cdot \nabla_x\cdot({p'}({ x}){ S})\tag{42}$$
因此,如果按照方程(39)的材料参数$\rho ^{ - 1}(x)$,$ C(X)$在$\omega $内布置五模材料,则区域$\omega $和$\omega ^{\rm out}$内的物理场可直接由虚空间物理场根据(40)映射得到.由于$\Omega ^{\rm out}$和$\Omega $的均匀性,$\Omega ^{\rm out}$区域不存在任何散射. 因此,对于相同的入射波,区域$\omega ^{\rm out}$也不存在任何散射,从而实现内部区域的隐身.由映射后物理量需要满足的连续性要求,还可导出$\omega $内特征应力张量$ S$应满足的额外限制条件: 即在边界$\partial \Omega =\partial \omega ^{ + }$有$[{ e}_{n}\cdot S]_{\vert \partial \Omega }=0$. 据此条件进一步分析表明,在隐身斗篷外边界$\partial \Omega $处特征应力张量$ S$的2个主轴方向分别与界面法向平行和垂直,且其法向分量满足$S_{nn}=1$,这正是前面给出的五模材料界面间的阻抗匹配条件. 值得指出的是,在以上变换公式中,将特征应力张量取作单位张量$ S={\bf I }$ (Norris 2008 ),可得到各向异性密度介质类型的隐身覆盖层参数.
由于$ S$需要满足多重限制,目前不存在$ S$的一般构造方法,这一难点限制了五模材料在设计任意形状隐身覆盖层中的应用.但当映射梯度为对称张量时,特征应力张量可以选为$ S= J^{ - 1} F $,此时特征应力张量满足所有的限制条件,目前成功设计的二维环形、三维球壳形五模材料隐身覆盖层即属于此类型.
4.2 五模材料环形声波斗篷设计为设计二维环形五模材料声波斗篷,可考虑虚拟空间中圆形区域 $(0<R<b)$到物理空间环形区域 $(a<R<b)$的径向映射关系: $R=f(r)$和$\varTheta =\theta $. 在上述径向映射关系下,映射梯度矩阵为 $$ F = \dfrac{1}{{f'}(r)} e_r e_r + \dfrac{r}{f(r)} e_\theta e_\theta,J = {\rm det} F = \dfrac{r}{{f'}(r)f(r)} \tag{43}$$
由于$ F $的对称性,特征应力张量可以选取为$ S=J^{ - 1} F $,代入式(39)并适当化简,可得到隐身覆盖层内所需五模材料性质分布为 $$ \rho = \rho_0 \dfrac{f(r){f'}(r)}{r},K_r = K_0 \dfrac{f(r)}{r{f'}(r)},K_\theta = K_0 \dfrac{r{f'}(r)}{f(r)} \tag{44}$$
根据密度分布公式可容易得出如下结论: 斗篷总质量与其排开的背景介质质量相等. 这表明,若在内部空腔区域额外放置其他需隐身目标,则隐身斗篷将不能悬浮于背景介质中. 考虑到在$r=b$处有$f(b)=b$,可以验证隐身斗篷在与背景介质界面处完美满足阻抗匹配条件,即法向阻抗与切向声速匹配,$\sqrt {\rho K_r } = \sqrt {\rho_0 K_0 } $,$\sqrt {K_\theta /\rho } = \sqrt {K_0 /\rho _0 } $.径向映射函数$f(r)$只需要满足边界条件$f(a)=0$,$f(b)=b$而没有额外限制,因而可以选择特殊的映射函数使隐身斗篷所需材料参数分布更加简单,更易于通过微结构设计实现. 根据式(44),显然$f(a)=0$会导致斗篷$r=a$处材料参数出现奇异,因此通常选取小参数$\delta \ll 1$使得$f(a)=\delta $以避免材料参数奇异. 据此设计的斗篷材料参数,物理上相当于将$0<r<a$的圆形区域映射为$0<r<\delta $的圆形区域,所设计的隐身斗篷将不再完美,具有与半径为$\delta $的散射体相同的散射特征,但相比半径为$a$的散射体散射强度大大降低.下面给出几种典型映射关系以及参数分布:
(1)常密度映射及材料参数分布 $$ f(r)= \sqrt {\xi r^2 + \eta },\xi = \dfrac{b^2 - \delta ^2}{b^2 - a^2},\eta = - \dfrac{b^2(a^2 - \delta ^2)}{b^2 - a^2} \tag{45}$$ $$ \rho = \rho_0 \xi,K_r = K_0 \dfrac{\xi r^2 + \eta }{\xi r^2},K_\theta = K_0 \dfrac{\xi r^2}{\xi r^2 + \eta } \tag{46}$$
(2)常模量映射及材料参数分布 $$ f(r)= b\left(\dfrac{r}{b}\right)^\xi,\xi = \dfrac{\ln(b/\delta)}{\ln(b/a)} \tag{47}$$ $$ \rho = \rho_0 \xi\left(\dfrac{b}{r}\right)^{2 - 2\xi },K_r = \dfrac{K_0 }{\xi },K_\theta = K_0 \xi \tag{48}$$
(3)线性映射及材料参数分布 $$ f(r)= \xi r + \eta,\xi = \dfrac{b - \delta }{b - a},\eta = b\dfrac{\delta - a}{b - a} \tag{49}$$ $$ \rho = \rho_0 \xi \dfrac{\xi r + \eta }{\xi },K_r = K_0 \dfrac{\xi r + \eta }{\xi r},K_\theta = K_0 \dfrac{\xi r}{\xi r + \eta } \tag{50}$$
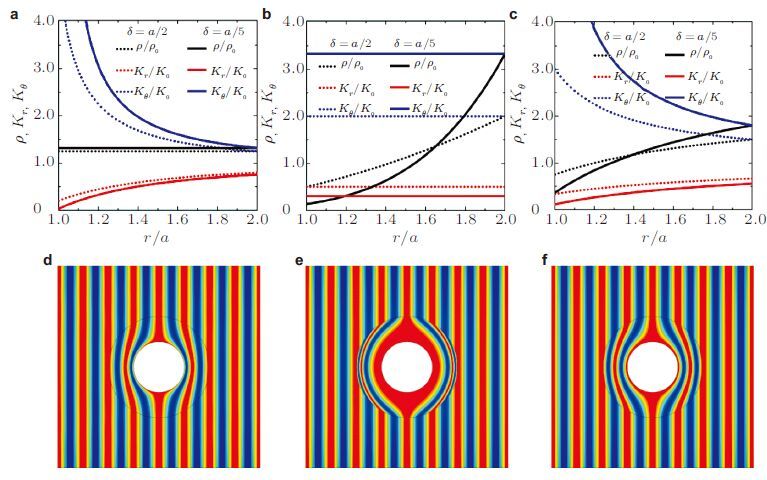
图 18为以上3种映射关系下隐身斗篷覆盖层内密度、模量沿径向的分布及声场模拟图,其中斗篷几何参数为$b=2a$,小参数$\delta $分别取$a/2$和$a/5$.根据材料参数的分布可以看出,在隐身斗篷内边界需要模量各向异性最强,其环向模量要远大于径向模量,以保证最内侧波传播时间与外侧一致.对比几种情况可以发现: 等密度映射需要的各向异性取值范围最宽;等模量映射需要的密度取值范围最宽;而线性映射对两者取值范围要求适中. 对以上3种情况,增加斗篷厚度(增大外半径$b)$或增大$\delta $均可减小斗篷内材料各向异性或密度取值范围.从3种映射隐身斗篷的直接声场模拟可看出,入射至隐身斗篷上的平面波能无反射地进入斗篷,并在内部梯度分布的五模材料引导下绕过中心区域从斗篷后方仍以平面波形式传出,斗篷外部区域几乎没有任何声散射,这也证实了基于变换声学设计的五模材料隐身斗篷的功能.从斗篷内等声压线压缩程度上看:等密度映射斗篷内边界处径向声速非常小,其等声压线压缩最明显;等模量映射斗篷中外侧径向密度极小,等声压线压缩也十分明显,而内侧等声压线则被显著地拉伸;线性映射斗篷对应的等声压线在内外边界处压缩程度处于两者之间.
|
| 图18 不同映射对应的斗篷材料参数分布及声隐身效果模拟图.(a),(d)等密度映射;(b),(e)等模量映射;(c),(f)线性映射 |
基于五模材料的变换声学理论提出后,研究者很自然地将其应用于声学覆盖层设计,并在隐身覆盖层性能分析和材料参数分布优化方面取得了相应进展.如Gokhale等(2012)研究了不同径向映射对应的材料参数分布,并推导出一种优化映射关系,使得斗篷内材料总体各向异性程度最小.Scandrett等(2010,2011)解析地研究了三维分层五模材料声学斗篷在平面波入射条件下的声散射.研究指出,通过优化各层材料参数分布,即使只有很少的几层五模材料也可以实现较好的宽频隐身效果,这一点体现了各向异性五模材料在声波控制上的明显优势. 然而,上述五模材料覆盖层研究都局限于均匀理想五模材料范畴,并没有考虑如何通过微结构设计来获得所需的五模材料参数.而通过调节几何参数来设计出不同位置所需五模材料胞元构型,并最终整合成微结构覆盖层,是五模材料覆盖层原理性验证及应用的关键一步.
4.3 五模材料声波斗篷的微结构设计根据3.4节提出的五模材料胞元(图 13(a))及分级优化算法,Chen等(2015)设计了微结构铝基五模材料声学隐身斗篷,并对微结构斗篷进行了声固耦合数值模拟,验证了预期的宽低频声学隐身性能.该微结构斗篷根据等密度映射关系设计,沿径向由12层不同属性的五模材料去逼近变换给出的连续材料分布,各层材料参数分布如图 19(a)所示,其中$a$为斗篷的内半径.除最内层介质由两层单胞构成外,其余各层介质均由一层单胞组成.可以看到,基于该胞元构型的五模材料能实现的模量各向异性程度大于64,因而可以很好地逼近斗篷最内层所需材料属性.在具体建立微结构斗篷模型时,首先构建由13层微结构单胞在径向组成的扇段,然后在环向复制100个周期即可最终得到环形五模材料微结构斗篷,整个斗篷共包含2 600个六边形五模材料胞元.由于采用含微结构分段逼近连续属性分布的原因,实际设计的微结构斗篷外半径$b_{1}=2.086a$,与变换方法中采用的外半径$b=2a$存在一定小偏差. 图 19(b)为所建立微结构隐身覆盖层几何模型的四分之一,斗篷内侧所需材料各向异性程度较大,因此胞元构型的拓扑角度也更大.

|
| 图19 (a)微结构斗篷各层材料参数分布与等密度映射的连续分布对比,(b)环形微结构五模材料斗篷四分之一模型,(c)从内至外第3,6,9,12层五模胞元构型,(d)微结构斗篷声固耦合数值模拟网格划分情况 |
图 20 给出半径为$a$的刚性圆柱体在有无五模材料隐身斗篷时总散射截面(其定义由式(66)给出)随频率 $(0<{ ka}<\pi)$的变化关系. 可以看出,微结构覆盖层直接模拟结果(蓝色曲线)与理想分层五模材料解析结果(红色曲线)整体趋势一致,随着频率增加而逐渐增大,相比于没有隐身覆盖层的刚性散射体(黑色粗点线)均减小很多.与理想五模材料斗篷不同的是,微结构斗篷的总散射截面在系列频点出现了峰值现象,低频峰值频率及强度与均质化的五模材料结果(黑色细点线)相吻合.在高频时峰值频率存在一定偏差,这是由等效参数在高频适用性变差所致.根据第4.4.1节所建立的正交各向异性环形弹性层声散射模型,这些峰值现象源于非理想五模材料的弱剪切引起的剪切波共振.

|
| 图20 (a)刚性圆柱体在有无3种斗篷时总散射截面随频率变化关系,(b)基体介质中引入0.5%黏弹性阻尼后微结构斗篷总散射截面随频率变化关系,两箭头所示频率$ka/\pi $分别为0.52和1.0 |
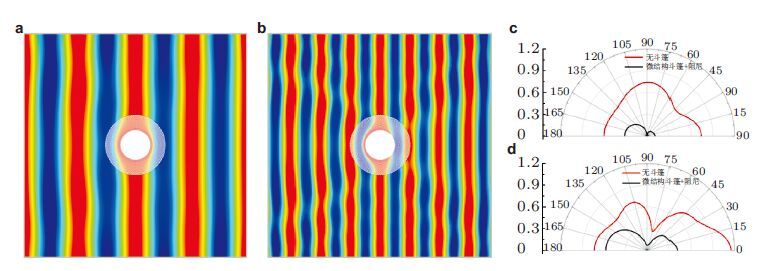
在基体中引入0.5%黏弹性阻尼后,微结构隐身斗篷中的高频共振散射得到了明显抑制(图 20),而低频共振散射由于衰减长度较大而受影响较小. 在频率$1<{ ka}<3$范围内,总散射截面比没有隐身斗篷覆盖时降低约4/5以上,基本实现了基于五模材料隐身斗篷预期的宽频隐身效果. 图 21(a)和图 21(b)给出了引入结构阻尼后在$ka/\pi $为0.52和1.02个频率点的声压场图,微结构斗篷使得总散射截面分别从1.26和1.53降低至0.09和0.37.从图中可以看出,左侧入射的平面波进入覆盖层后绕过中心区域,仍然保持平面波的形式从后方传出,覆盖层层外部区域的散射现象很弱,覆盖层具有非常明显的隐身效果. 图 21(c)和图 21(d)给出了$ka/\pi $取0.52和1.0的远场散射系数随方向的变化. 从图中可以看出:增加阻尼后的微结构斗篷前向散射系数,即0$^{\circ}$方向,降低更加明显; 而后向散射系数,即180$^{\circ}$方向,削弱不够明显.从数值上看,在$ka/\pi $为0.52和1.0时,前向散射系数降低分别达到了16.7 dB和9.0 dB,而后向散射系数分别只能降低5.7 dB和2.1 dB,表明五模材料斗篷在降低前向散射能力上比降低后向散射更加突出.
|
| 图21 (a),(b)频率$ka/\pi $分别为0.52和1.0时声压分布图;(c),(d)频率$ka/\pi $分别为0.52和1.0时有无斗篷覆盖的远场散射系数分布 |
由微结构五模材料斗篷的声固模拟结果可知,非理想五模材料对斗篷声隐身效果影响十分明显.为进一步分析其影响机理及调节方法,本节将建立相应的解析模型进行分析. 实际上,非理想五模材料覆盖层的声散射问题,本质上是柱坐标下正交各向异性梯度弹性介质的声散射问题,目前还不存在简单的封闭式解析解.利用处理分层复合材料圆筒问题常用的状态空间法(Chen et al. 2004,Fan 1996),Chen等(in preparation)建立了上述声散射问题的半解析模型.状态空间方法的关键在于:适当选取在材料属性间断处满足连续性的物理量构成状态空间矢量,并结合状态空间矢量的模态叠加方法,将原偏微分方程转化为状态空间矢量关于某一坐标的矩阵常微分方程.最后,通过数值离散方式求解该常微分方程,可得到内外边界处状态空间矢量的传递关系,再结合状态空间变量需要满足的边界条件,即可求解得出覆盖层中的状态空间变量.
考虑如图 22所示由$N$层均匀非理想五模材料构成的声学覆盖层,假定每一层均匀正交各向异性弹性层非常薄,这总可以通过将厚层离散为更多薄层而实现. 从最内层开始编号为1,直至最外层编号为$N$,背景流体介质编号为$N+1$.这种离散方式对于连续性材料参数分布覆盖层同样适应,只要将覆盖层沿径向划分足够多层以使每一层可近似作为均匀介质.考虑背景介质中有从左入射的平面波,则入射、散射声压可以分解为如下各阶波的叠加 $$ p_{{\rm i}n} = \sum\limits_{n = 0}^\infty {a_n J_n \left({k_0 r} \right)\cos(n\theta)},p_{\rm sc} = \sum\limits_{n = 0}^\infty {b_n H_n^{(1)}(k_0 r)\cos(n\theta)} \tag{51}$$ 其中,简谐项$\exp(-{\rm i}\omega t)$ 约定省略,$k_{0}=\omega /c_{0}$为背景介质波数,$c_{0}=(K_{0}/\rho_{0})^{1 / 2}$为背景介质声波相速度,$J_{n}(x)$和$H_n^{(1)} (x)$分别代表第一类Bessel和第一类Hankel函数.平面波分解后的入射波系数为已知量,$a_{n}=(2- \delta _{0n})i^{n }$ $(n\geq 0)$,$\delta_{\alpha \beta }$表示{Kronecker delta}符号,$\alpha $和$\beta $相等时为1,不等时为0. 对第$j$层非理想五模材料,其本构方程、几何方程及弹性动力学方程在柱坐标下可以表示为 $$ \left({\begin{array}{l} \sigma_{jr} \\ \sigma_{j\theta } \\ \sigma_{jr\theta } \\ \end{array}} \right)= \left({{\begin{array}{*{20}c} {K_{jr} } \quad& {K_{jr\theta } } \quad& 0\\ {K_{jr\theta } } \quad& {K_{j\theta } } \quad& 0 \\ 0 \quad& 0 \quad& {G_{jr\theta } } \\ \end{array} }} \right)\left({\begin{array}{l} \varepsilon_{jr} \\ \varepsilon_{j\theta } \\ 2\varepsilon_{jr\theta } \\ \end{array}} \right)\tag{52}$$ $$ \varepsilon_{jr} = \dfrac{\partial u_{jr} }{\partial r},\varepsilon_{j\theta } = \dfrac{1}{r}\dfrac{\partial u_{j\theta } }{\partial \theta } + \dfrac{u_{jr} }{r},\varepsilon_{jr\theta } = \dfrac{1}{2}\left(\dfrac{\partial u_{j\theta } }{\partial r} + \dfrac{1}{r}\dfrac{\partial u_{jr} }{\partial \theta } - \dfrac{u_{j\theta } }{r}\right)\tag{53}$$ $$ \dfrac{\partial \sigma_{jr} }{\partial r} + \dfrac{1}{r}\dfrac{\partial \sigma_{jr\theta } }{\partial \theta } + \dfrac{\sigma_{jr} - \sigma_{j\theta } }{r} = - \rho \omega ^2u_{jr},\dfrac{\partial \sigma_{jr\theta } }{\partial r} + \dfrac{1}{r}\dfrac{\partial \sigma_{j\theta } }{\partial \theta } + \dfrac{2\sigma_{jr\theta } }{r} = - \rho \omega ^2u_{j\theta } \tag{54}$$

|
| 图22 分层均匀非理想五模材料构成的声波覆盖层,从内到外各层均匀介质编号为1到$N$,外部均匀流体为$N+1$ |
$K_{jr}$,$K_{j\theta }$和$G_{jr\theta }$为第$j$层介质的弹性模量; $\varepsilon_{jr}$,$\varepsilon_{j\theta }$和 $\varepsilon_{jr\theta }$代表相应应变; $\sigma_{jr}$,$\sigma _{j\theta }$和$\sigma_{jr\theta }$代表应力.基于各阶入射声波的正交性以及层间物理量的连续性,第$j$层非理想五模材料中的应力和位移可用模态展开表示为 $$ u_{jr} = \sum\limits_{n = 0}^\infty {u_{jnr}(r)\cos(n\theta)},u_{j\theta } = \sum\limits_{n = 0}^\infty {u_{jn\theta }(r)\sin(n\theta)} \tag{55}$$ $$ \sigma_{jr} = \sum\limits_{n = 0}^\infty {\sigma _{jnr}(r)\cos(n\theta)},\quad \sigma_{jr\theta } = \sum\limits_{n = 0}^\infty {\sigma_{jnr\theta }(r)\sin(n\theta)},\quad \sigma _{j\theta } = \sum\limits_{n = 0}^\infty {\sigma_{jn\theta }(r)\cos(n\theta)} \tag{56}$$
选取第$n$阶位移、应力构成状态空间矢量$ D_{{\rm i}n}(r)=\{u_{{\rm i}nr}(r)$,$u_{{\rm i}n\theta }(r)$,$\sigma _{{\rm i}nr}(r)$,$\sigma_{{\rm i}nr\theta }(r)\}^{\rm T}$,并将应力和位移模态表达式代入方程(54),经过化简可以得到第$n$阶状态空间变量在径向满足的矩阵常微分方程 $$ \dfrac{\rm d}{{\rm d}r} D_{jn}(r)= P _{jn} (r)D_{jn}(r)\tag{57}$$ $$ P _{jn}(r)= \left( {{\begin{array}{*{20}c} { - \dfrac{1}{r}\eta_j } \quad& { - \dfrac{n}{r}\eta_j } \quad & {\dfrac{1}{K_{jr} }} \quad& 0 \\ {\dfrac{n}{r}} \quad& {\dfrac{1}{r}} \quad& 0 \quad & {\dfrac{1}{G_{jr\theta } }} \\ {\dfrac{1}{r^2}\xi_j - \rho_j \omega ^2} \quad& {\dfrac{n}{r^2}\xi_j } \quad& {\dfrac{1}{r}(\eta_j - 1)} \quad& { - \dfrac{n}{r}} \\ {\dfrac{n}{r^2}\xi_j } \quad& {\dfrac{n}{r^2}\xi_j - \rho_j \omega ^2} \quad& {\dfrac{n}{r}\eta_j } \quad& { - \dfrac{2}{r}} \\ \end{array} }} \right)\tag{58}$$
这里$\xi_{j}=[K_{jr}K_{j\theta } -(K_{jr\theta })^{2}]/K_{jr}$和$\eta_{j}=K_{jr\theta }/K_{jr}$. 由于矩阵$ P_{jn}(r)$与径向位置变量$r$相关,不能简单得到方程(57)的显式解.鉴于每一层材料已假定为足够薄,矩阵$ P_{jn}(r)$在每一层内可以认为是常数矩阵,其取值可为该层中点处的值,因此常微分方程(57)在单层内具有指数形式的解 $$ D_{jn}(r)= \exp \left[ {(r - r_{j - 1})P _{jn} \left(\dfrac{r_{j - 1} + r_j }{2}\right)} \right] D_{jn}(r_{j - 1})\tag{59}$$ 由于状态空间变量在层间处满足连续性条件,即$ D_{jn}(r_{j - 1})= D_{(j - 1)n}(r_{j - 1})$,则有第$N$层材料外侧状态空间变量$ D_{Nn}(r_{N})$,与第1层内侧状态空间变量$ D_{1n}(r_{0})$之间满足以下传递关系 $${D_{Nn}}({r_N}) = {T_n}{D_{1n}}({r_0}),{T_n} = \prod\limits_{j = 1}^{j = N} {\exp } \left[ {({r_j} - {r_{j - 1}}){P_{jn}}\left( {\frac{{{r_{j - 1}} + {r_j}}}{2}} \right)} \right] \tag{60}$$
在覆盖层最外侧处$r=r_{N}$,同时应该满足法向位移连续以及界面应力连续条件 $$\left.\begin{array}{l} u_{Nnr}(r_N)= \dfrac{1}{\rho_0 \omega ^2}[a_n {J'}_n(k_0 r_N)+ b_n {H'}_n^{(1)}(k_0 r_N)]\\ \sigma _{Nnr}(r_N)= - [a_n J_n(k_0 r_N)+ b_n H_n^{(1)}(k_0 r_N)]\\ \sigma_{nr\theta }(r_N)= 0 \end{array}\right\} \tag{61}$$
这样共有传递矩阵关系以及连续性条件(61)确定的7个方程,而第$n$阶物理场共有9个未知量:散射系数$b_{n}$、覆盖层最内侧以及最外层处状态空间矢量$ D_{Nn}(r_{N})$和$ D_{1n}(r_{0})$. 因此,还需要施加于覆盖层内侧的额外2个边界条件才可求解出全部9个未知物理量.对于最常见的内边界径向约束形式,有径向位移及切应力为零的条件:$u_{1r}(r_{0})=0$,$\sigma_{1r\theta }(r_{0})=0$,结合方程可得到背景介质中的散射系数. 其他内边界约束条件如,内边界完全约束、完全自由或填充有背景流体3种情况,也可类似得到各阶散射系数.
在求得各阶散射系数后,即可得到背景介质中的散射声场,其散射强度可通过总散射截面(total scattering cross section,TSCS)定量刻画,其基本定义为: 目标物体各方向的散射声能量与入射到其横截面积上能量之比,是定量表征五模材料斗篷声隐身性能的可信指标(Titovich&Norris 2014). 增加覆盖层后的目标体散射总散射能量,可用如下沿着包围斗篷的封闭路径积分计算 $${E_{{\rm{sc}}}} = - \frac{1}{{2{\rho _0}\omega }}{\rm{Im}}\oint_{_C} {{p_{{\rm{sc}}}}\frac{{\partial {{\bar p}_{{\rm{sc}}}}}}{{\partial n}}{\rm{d}}s} = \frac{1}{{{\rho _0}\omega }}\sum\limits_{n = 0}^\infty {(1 + {\delta _{0n}})|{b_n}{|^2}} \tag{62}$$
上式化简时用到了散射声压$p_{\rm sc}$的展开表达式(51).对于截面积为$S=2a$的圆柱散射体,入射到横截面上的能量为,$E_{{\rm i}n}=S/(2\rho_{0}c_{0})$. 根据定义得总散射截面表达式为 $$ \sigma_{tot} = \dfrac{E_{\rm sc} }{E_{{\rm i}n} } = \dfrac{1}{k_0 a}\sum\limits_{n = 0}^\infty {(1 + \delta_{0n} )\vert b_n \vert ^2} \tag{63}$$
从上述表达式可知,各阶散射系数幅值对于总散射截面均有贡献,仅当各阶散射系数均为零时,相应的总散射截面完全为零. 此时,斗篷外部声压场不存在任何散射,斗篷内部目标完全不能被声波探到.
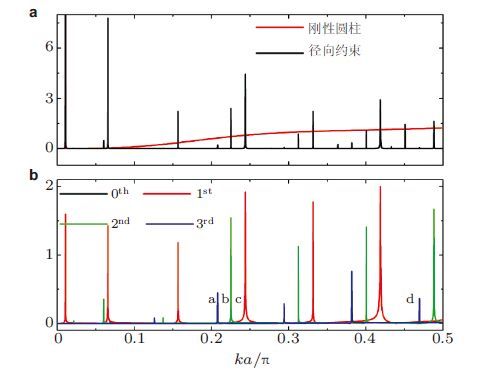
4.4.2 共振散射机理及五模特征参数分析为分析共振散射机理,考察由参数$(\delta =a/10$,$ b=2a$,$\pi =0.99$,$\mu =0.01)$构成的五模材料覆盖层在平面波入射下的声散射特性.斗篷内密度$\rho $和模量$K_{\rm r}$和$K_{\theta }$分别由等密度变换给出,模量$K_{r\theta }$和$G_{r\theta }$则根据五模特征参数计算得到$K_{r\theta }= \pi(K_{\rm r}K_{\theta })^{1 / 2}=\pi K _{0}$,$G_{r\theta }= \mu(K_{\rm r}K_{\theta })^{1 / 2}= \mu K _{0}$. 图 23给出了覆盖层内边界径向固定时,总散射截面TSCS及前四阶散射系数幅值$\vert b_{n}\vert $随频率变化关系. 在TSCS曲线中同样可以观测到共振峰现象,与以往发现的弹性圆柱体界面波导致的高频共振散射(Flax et al. 1978,Norris 1990)不同,该算例中的共振峰出现在很低的频率范围.如表达式(63)所示,每一个TSCS共振峰都与某一阶散射系数共振峰相对应,如图中a,b和c 3个位置标记所示. 注意到在所考察频率范围段$(\lambda >4a)$,零阶散射系数并不存在共振峰现象,表明上述共振峰可能是由斗篷内的剪切波引起,因为零阶模态对应入射声压不会在斗篷内激发起剪切波.
|
| 图23 非理想五模材料覆盖层总散射截面及前四阶散射系数幅值随频率变化 |
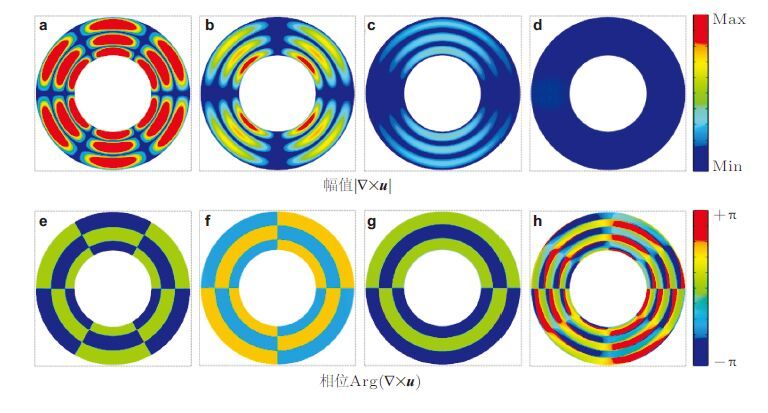
图 24 中给出了对应于三、二、一阶共振频率和一个非共振频率处的位移旋度幅值场以及位移旋度相位场分布.从图中可看出,归一化的旋度幅值在共振频率时强于非共振频率情况.相位的分布也明显地揭示了共振散射时对应的驻波现象特征,即相场中只有$\pi $相位的突变而不存在渐变.不同于共振频率处旋度相位场,图 24(h)中存在明显相位渐变,表明其中的剪切波具有行波的特征. 从以上两方面分析可知,共振散射由覆盖层内剪切波在径向产生干涉效应导致,这一剪切波由入射声波在覆盖层外侧界面处激发而被约束于覆盖层内部区域.这些共振散射出现在极低频率,本质上源于极小的剪切波速.
|
| 图24 (a),(b),(c),(d)三、二、一阶共振频率及非共振频率时覆盖层内位移旋度场幅值;(e),(f),(g),(h)位移旋度相位.频率分别对应于图 23中4个位置a,b,c和d,对应于波数${ka}/\pi =0.207 9$,$ka/\pi =0.225 2$,$ka/\pi =0.243 9$和$ka/\pi =0.455 0$ |
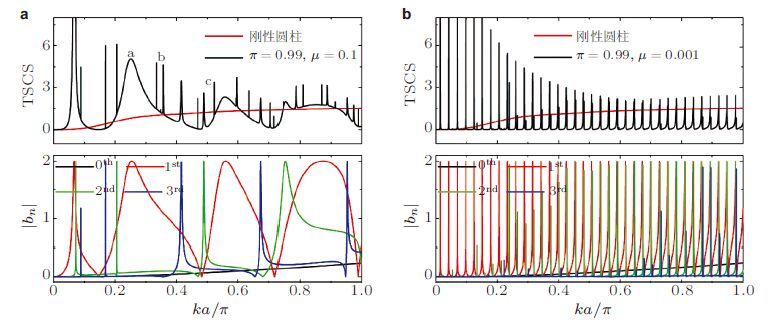
图 25 给出了内边界完全固定条件下,特征参数$\mu =0.1$与$\mu =0.001$对应结果. 可以看出,特征参数$\mu $的降低使得非理想五模材料的剪切刚度下降,从而将高频的共振峰向低频压缩,同时使得共振峰宽度变窄. 特征参数$\pi $对共振散射的影响类似,因为2个特征参数共同决定不同方向剪切波波速.可以自然地推断,当五模特征参数$\pi $和$\mu $同时趋近并最终等于1和0时,所有的剪切共振峰将被强烈压缩至零频率,共振峰宽度也随之消失,最终可以得到不存在剪切共振峰的平滑总散射截面曲线,也即是与由理想五模材料构成的覆盖层结果一致.其他3种约束边界条件也存在相似的结果.
|
| 图25 非理想五模材料覆盖层$(\delta =a/5$,$b= 2 a)$内边界完全固定时结果. 五模特征参数分别为:(a)$\pi =0.99$和$\mu =0.1$,(b)$\pi =0.99$和$\mu =0.001$ |
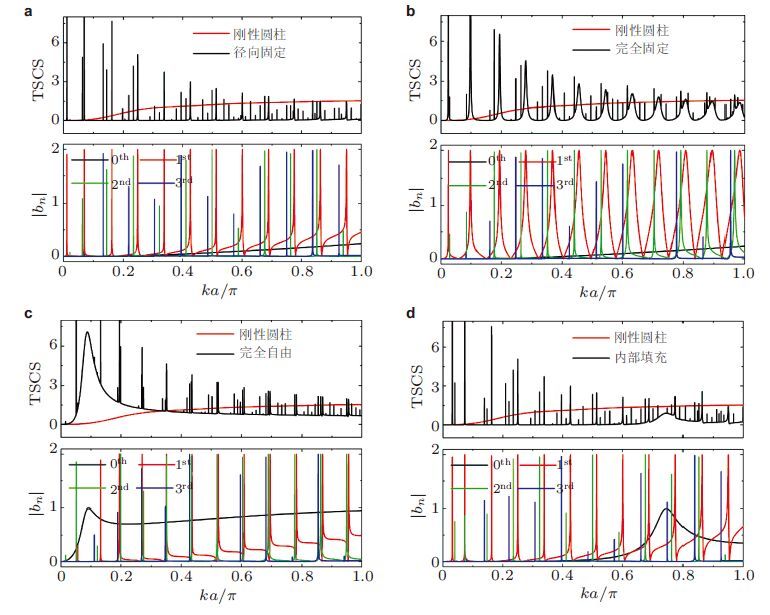
非理想五模材料覆盖层低频共振散射由剪切驻波引起,与覆盖层内边界条件密切相关,而且在实际应用时边界条件也不可能与理想情况一致,因此有必要对边界条件的影响作进一步分析.在此讨论内边界完全约束、径向约束、完全自由以及内部填充背景介质4种不同形式内边界条件的影响.图 26中给出了4种边界条件对应TSCS和前四阶$(n=0$,1,2,3)散射系数幅值$\vert b_{n}\vert $,以及红线曲线表示的刚性圆柱结果.
从图 26中可看出,对于内边界径向固定情况,总散射截面除了共振频率之外相比刚性圆柱大大降低,且零阶散射系数$\vert b_{0}\vert $在频率范围$0<ka/\pi <1$内得到了非常好的抑制. 对于内边界完全固定情况,由于非常宽的一阶共振散射影响,使得五模材料覆盖层的声波调控受到了严重破坏.
|
| 图26 非理想五模材料覆盖层$(\delta =a/5$,$ b=2a$,$\pi =0.99$,$\mu =0.01)$不同内边界约束时结果.(a)径向固定,(b)完全固定,(c)完全自由,(d)内部填充背景介质 |
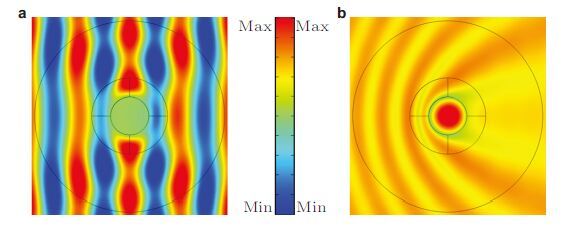
内边界完全自由、内部填充背景介质两种情形最显著的差别是,额外的零阶共振散射会在低频散出现. 对于内部填充背景介质情况,此现象由覆盖层内的纵波以及空腔内的纵波耦合所致,共振频率与覆盖层内的剪切模量无关,这一点也得到了数值结果的验证.在内部填充流体的传统各向异性密度流体覆盖层中,这种空腔共振现象同样被观察到(Cheng&Liu 2008). 图 26中零阶共振频点对应的瞬时声压场实部及幅值如图 27中所示.内腔中流体瞬时声压呈现高度同相特征,声压实部极小几乎完全为纯虚数,但声压幅值却非常大,相当于入射声压幅值的两倍,这很明显地表明了空腔内部流体的共振现象. 对于内边界完全自由情形,可以考虑成内部填充有模量极小的声学介质,因此,覆盖层内与空腔内纵波耦合导致的共振会向低频偏移.
|
| 图27 内部填充背景介质时零阶共振频率$(ka/\pi =0.746)$对应的声压分布.(a)声压实部,(b)声压幅值 |
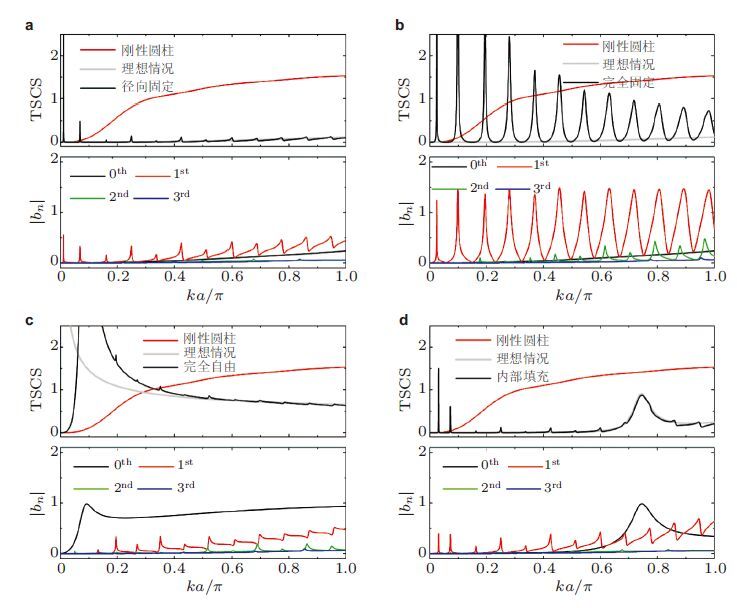
图 28 给出了在五模材料斗篷内引入1%黏弹性阻尼后4种内边界对应的结果,同时给出了理想五模材料斗篷结果以便于比较. 可以看出,非理想五模材料覆盖层引入阻尼后,其中的狭窄共振峰得到了明显的抑制,TSCS曲线也非常接近于理想五模材料覆盖层结果.在这几种不同内边界约束中,最具优势的情形为径向约束边界条件.以上结果表明,即便是在非理想五模材料中引入阻尼效应来抑制共振散射,覆盖层内边界约束形式也必须经过周全的考虑和设计才能实现预期的宽频段隐身效果.
|
| 图28 非理想五模材料覆盖层$(\delta =a/5$,$ b=2a$,$\pi =0.99$,$\mu =0.01)$存在黏弹性时结果.(a)径向固定,(b)完全固定,(c)完全自由,(d)内部填充背景介质 |
根据之前的分析,五模材料要应用于任意形状斗篷设计,需解决特征应力张量$ S$的选取问题. 可能的途径是,通过特殊方式构造对称的变形梯度场${ F}= F ^{\rm T}$,然后选取特征应力张量为$ S=J^{ - 1} F$,从而设计出各向同性密度的五模材料隐身斗篷,${\rho'}^{ - 1}({ x})= \rho_0^{ - 1} J^{ - 1}{ S}^{ - 1} \cdot F \cdot F ^{\rm T} \cdot { S}^{ - 1} = \rho_0^{ - 1} J{\rm {\bf I}}$.由于映射函数除了满足内外边界条件约束外没有其他的限制条件,因此可以借鉴变换电磁学中用到的数值算法(Chang et al. 2010),构造特殊的微分方程求解出对称或准对称的变形梯度矩阵(Chen et al., submitted). 下面针对任意形状斗篷设计问题,如图 29所示,将介绍如何求解出几乎完全对称的变形梯度矩阵. 记虚实空间映射关系 $ x= x(X)$的逆映射为$ X= x + u( x)$,其含义为,物理空间中一点$ x$经过位移$ u$移动至虚拟空间一点$ X$.

|
| 图29 任意形状五模材料斗篷设计.(a)由背景区域$\omega ^{\rm out}$、斗篷区域$\omega $和隐身区域$\omega ^{\rm in}$组成的物理空间,(b)虚拟空间 |
上述映射关系可以用分量形式写为$X(x,y)=x+u(x,y)$,$Y(x,y)=y+v(x,y)$,位移函数$u(x,y)$和$v(x,y)$要满足如下边界条件 $$ u _{\vert \partial \omega ^ + } = \textbf{0},u _{\vert \partial \omega ^ - } =(\varepsilon - 1){ x},u =(u(x,y),v(x,y))\tag{64}$$ 在上式中,与变换方法中常用的技巧一样,引入了小参量$0< \varepsilon \ll 1$以避免材料参数中出现奇异. 可以很容易地验证,当位移矢量满足无旋条件$\nabla \times u={\bf 0}$时,映射梯度矩阵$ F $即满足对称性. 然而,该一阶微分方程并不足以确定满足边界条件式(64)的位移场,对方程$\nabla \times u={\bf 0}$进一步取左旋度,则可给出位移场满足的二阶微分方程 $$ \nabla \times(\nabla \times u)= \nabla(\nabla \cdot u)- \nabla ^2 u = {\rm {\bf 0}} \tag{65}$$
这一方程形式与各向同性弹性介质的静力学方程类似,因此,可以用有限元软件中的弹性力学模块直接求解,其中材料参数按如下形式赋值 $$\lambda =(\xi - 2)\mu,|\xi | \ll {1} \tag{66}$$
在这里,引入了第2个小参量$\vert \xi \vert \ll {1} $避免弹性力学方程的退化. 这一组弹性常数对应的弹性力学方程可简化为 $$ \nabla \times(\nabla \times u)= \xi \nabla(\nabla \cdot u)\tag{67}$$
可以看出,当参量$\xi $足够小时,式(67)可以当作原方程(65)很好的近似. 需要指出的是,尽管方程(65)并不能反过来导出$\nabla \times u={\bf 0}$,但后面的数值算例表明,由方程(67)求解得出的位移场几乎完全无旋,相应的映射梯度矩阵也具有高度的对称性. 可以证明,由方程(67)和边界条件(64)求解的映射梯度矩阵的逆矩阵$ F ^{ - 1}$在整个斗篷区域$\omega $内的对称性偏差之和为零 $$\int \int_\omega {((} {F^{ - 1}}{)_{21}} - {({F^{ - 1}})_{12}}){\rm{d}}a = \int \int_\omega {(\nabla \times u)} \cdot {\rm{da}} = - (\varepsilon - 1)\oint_{_{\partial {\omega ^ - }}} {x \cdot {\rm{d}}r = 0} \tag{68}$$
在求解映射梯度矩阵后,只需选择特征应力张量$ S=J^{ - 1} F$即可根据变换方法给出声变换功能器件内所学的五模材料参数分布 $\rho ^{ - 1}(x)$,$ C(x)$.
下面以图 30所示的椭圆形斗篷为例,物理空间中斗篷外边界为半径 $r=2$ m的圆,内边界是长、短轴分别为$a_{\rm in}=1$ m和$b_{\rm in}=a_{\rm in}/1.5$的椭圆. 背景区域中的流体介质为水,其密度和体积模量为$\rho_{0}=1 000$ kg/m$^{3}$,$K_{0} =2.25$ GPa.映射梯度矩阵由方程(67)和对应的边界条件通过COMSOL求解得到,其中参数分别选择为$\mu =1$Pa,$\varepsilon =10^{ - 3}$和$\xi =10^{ - 4}$. 映射梯度矩阵的对称性偏差$\vert F_{12} - F_{21}\vert $如图 30(b)所示,其在绝大多数区域都小于10$^{ - 3}$,仅在内边界处由于变形比较明显而有较大值.

|
| 图30 (a)位移场幅值$\vert u\vert $;(b)映射梯度矩阵$ F$对称性偏差$(F_{12} - F_{21})$;(c)密度分布,(d)各向异性程度分布$K_{t}/K_{n}$;(e),(f)频率为$f = 1.5$ kHz的平面波从0$^{\circ}$和45$^{\circ}$方向入射时声压分布 |
可以看出,根据方程(67)求解的映射梯度矩阵$ F $具有很高的对称性,可以用来给出特征应力$ S=J^{ - 1} F $,并导出斗篷区域所需的五模材料参数分布.斗篷区域所需五模材料密度范围为$0<\rho_{\rm s}/\rho _{0} <2$,所需的模量各向异性程度,即2个主轴方向刚度比值,也不是很大$1< K_{t}/K_{n}<25$,同样可以比较容易地通过微结构设计而实现(Chen et al. 2015). 为了验证所导出的五模斗篷参数分布的有效性,图 30(e)和图 30(f)给出了频率为$f =1.5$ kHz的平面波从0$^{\circ}$和60$^{\circ}$方向入射时声压分布图,斗篷区域的颜色代表伪声压$p=- J \sigma_{x}/F_{xx}$的大小,其中斗篷内边界设置为法向约束以模拟刚性散射体. 可以看到,入射平面波在斗篷内部较完美地绕过了中心区域,表明所设计的斗篷具有近乎理想的隐身效果.
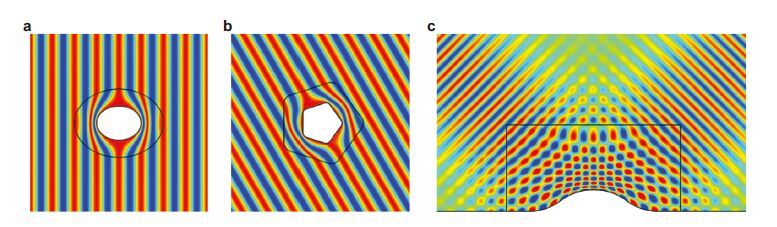
以上数值结果验证了算法所求变形梯度的高度对称性及所设计材料参数的有效性.图 31给出了相同算法设计的椭圆形、五边形、地毯式斗篷模拟结果,均显示出理想的隐身效果. 该对称梯度求解算法,极大地拓展了五模材料的声波变换器件设计能力,而不再局限于二维圆环形、三维球壳形等简单几何形状,为基于五模材料的复杂波动控制装置设计奠定了基础.
|
| 图31 五模材料应用于任意形状声学斗篷.(a)椭圆形,(b)带倒角五边形,(c)地毯式覆盖层隐身模拟结果 |
由于有效性质的可调节性及模量各向异性,五模材料不仅能于上述声学覆盖层设计,同时还可用于设计其他波动控制装置.
Laymen等(2013)最早将功能设计和材料微结构设计相结合,按照参数需求设计出了相应五模材料微结构(图 32),并对Norris(2009)理论上提出的声波蜃景现象做了数值模拟,验证了微结构五模材料在声波控制方面的有效性. 根据该胞元构型,Laymen等(2013)也设计了环形五模材料隐身斗篷不同位置所需的胞元构型,但并未将单胞构型集成为一个完整声学覆盖层.

|
| 图32 (a)五模材料微结构,(b)各向异性五模材料胞元带结构曲线,(c)声波蜃景模拟结果 |
Hladky-Hennion等(2013)基于Norris提出的"金属水"结构,设计了金属铝为基材的平板声波聚焦透镜.其单胞微结构由蜂窝状金属基构成(图 10(b)),宏观等效密度、体积模量与水高度一致,剪切模量$G$仅有0.065 GPa.该胞元第五、六阶带结构曲线(图 33(a))呈现出负的群速度,因此在与水频散(蓝线)曲线的交点频率可以实现负折射.在超声频率71.2 kHz处的数值模拟表明,多层微结构构成的平板透镜能实现负折射聚焦现象(图 33(b)).从模拟结果可以看到,透过平板的声波能量近乎降低了一个量级,这是由于模拟波长 $(\lambda =21.1$ mm)没有远大于单胞微结构尺寸$(2a=12.9$ mm),静态等效参数不再适用,平板透镜与水存在严重的阻抗适配所导致.实验测量中采用瞬态激励方式加载,并对测量结果进行了频谱分析得出不同频率下的结果.由于加工精度等原因导致的偏差,图 33(c)给出了81 kHz时焦点处声压分布,可以看到声波能量明显地聚焦到一点,证实了该"金属水"材料的声波聚焦功能,尽管测得声压强度与模拟类似仅有声源强度的20%.这种固体声聚焦透镜较流体聚焦器件具有便携、稳定的优势,可能在医学超声波聚焦成像领域具有潜在的应用价值.

|
| 图33 (a)"金属水"胞元带结构曲线,(b)平板透镜负折射聚焦仿真结果,(c)声聚焦点处声强分布实验测量结果 |
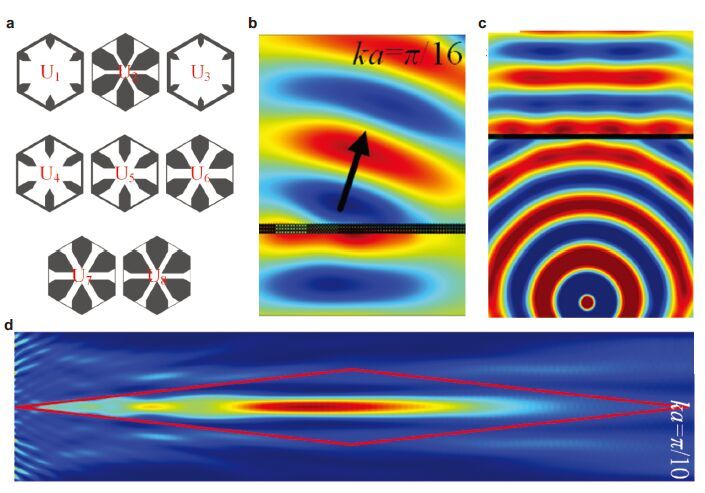
Tian等(2015)通过调节胞元几何参数,设计了阻抗与水匹配的系列各向同性五模材料胞元(图 34(a)),可以在远小于波长的几层单胞内实现明显声波相位累积.进一步将单胞用于实现基于相控的超表面,通过微结构声固耦合数值模拟验证了设计的有效性. 图 34(b)中垂直入射的波束经过超表面后,在横向产生明显的梯度分布相位,从而整个波束按一定倾斜角度传出; 图 34(c)中从点源发出的柱面波经过超表面后转换为平面波,根据声学互易原理,此超表面同样可用于将平面波聚焦至点源处; 图 34(d)中入射的平面波经过超表面后,在一定区域形成贝塞尔波束,具有保持一定传输距离而波束不扩散的非衍射特性.
|
| 图34 (a)阻抗与水匹配、声速小于水的系列各向同性五模材料胞元; (b),(c),(d)反常折射超表面、柱面波转平面波超表面、贝塞尔波束超表面数值模拟结果 |
以上研究表明,五模材料不仅可应用于设计复杂的声学覆盖层,还能应用于许多特定功能的声波控制器件,如上述介绍的声波聚焦透镜、波形转换超表面、特定波形发生器等.
5 五模材料及声学调控器件制备目前限制五模材料实验和应用的瓶颈之一是其制备加工技术.五模材料按基体材料可分为两类,聚合物基和金属基. 聚合物,如光敏高分子、塑料等基材五模材料一般采用激光固化或3D打印技术制备:激光固化主要利用光敏材料的光子吸收特性,这类加工技术具有非常高的加工精度,但加工的试样尺度一般都在微米量级,目前还很难直接应用于工程大构件制备;常规的3D打印技术可以制备塑料基宏观较大尺度五模材料,然而由于塑料基体材料模量较低,该类五模材料有效性质既不能与空气匹配,也无法适用于水声环境.
金属五模材料有效性质能比较容易实现与水匹配,且有钛、铝、铁等丰富金属基材可选择,被认为在水声中具有潜在应用前景.金属基五模材料有水枪切割、3D打印、慢走丝线切割及微细加工技术.水枪切割技术比较普遍,切割表面也较平整但不易于切割较厚板材;金属3D打印加工的样件表面较粗糙,且烧结后的金属也与理论弹性性质有一定差异;慢走丝线切割相对水枪切割、金属3D打印技术具有明显优势,包括加工精度更高、切割厚度较大、切割最薄壁厚小、样件表面平整等,是制备金属基五模材料的较好选择;微细铣削等微细加工技术拥有极高的加工精度及精细结构加工能力,然而在制备宏观分米以上尺度的试件时需要花费大量时间.
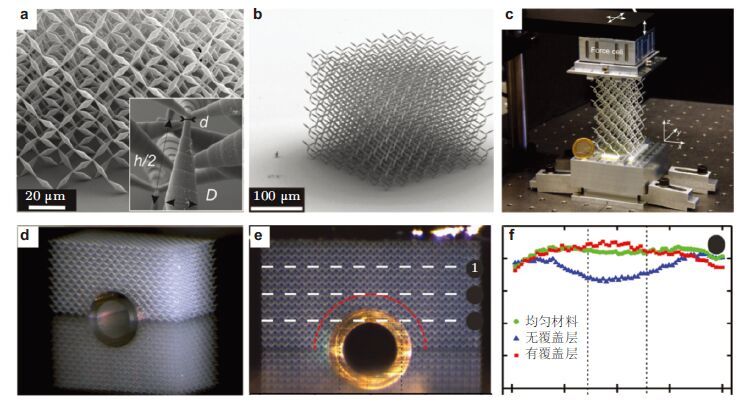
在高分子基五模材料制备方面,德国卡尔斯鲁厄尔大学Wegener课题组研究较多. 该课题组(Kadic et al. 2012,Martin et al. 2012,Kadic et al. 2013)首先通过数值仿真研究了Milton等(1995)提出的三维五模材料构型,发现在可接受的加工最小尺寸限制范围内,该微结构等效体积模量与剪切模量之比可以达到1 000,不同方向的体积模量可以相差100倍; 随后,利用激光直写技术(direct-laser-writing)加工聚合物,首次制备了微结构在微米级别的三维五模材料(图 35(a)和图 35(b)). 制备的材料样件由7 × 7 $\times $ 6个立方体单胞构成,整体尺寸为261 $\mu $m $\times $ 261 $\mu $m × 224 $\mu $m,胞元锥形杆最小直径$d =1 \mu $m,最大直径$D=3 \mu $m.这一微观五模材料样件的成功制备,将二十多年前提出的五模材料概念变为现实,因而引起了学界对五模材料制备和应用的广泛关注. 然而,由于聚合物承载能力较弱,样件中锥形杆间连接尺寸并不能做到太小,否则结构将在重力作用下坍塌,因而其等效剪切模量相对体积模量会比较明显,并不是一种非常理想的五模材料. 这也是五模材料制备中的普遍难点,亦即是如何制备胞元尺寸较小的五模材料时,使得最小连接点尺寸尽可能地小,从而获得更理想的五模材料特征.该课题组又利用3D打印技术制备了宏观聚合物基五模材料,其单胞晶格长度大致为10 mm,力学性能测试验证了其具有非常高的体积/剪切模量比$(B/G>1 000)$(Schittny et al. 2013). 利用五模材料剪切模量可以忽略,弹性参数调节比较简单的特点,该课题组制备了微结构在毫米量级的静力学隐身斗篷(Bückmann et al. 2014). 均匀五模材料内埋藏的近似刚性柱体(图 35(d))经覆盖较软五模材料斗篷后,在上表面施加压力时的响应与只有均匀五模材料时一致(图 35(f)),也即验证了其静力学"隐身"功能.该静力学实验主要利用五模材料剪切模量可以忽略的特点,实验中只需调节五模材料的体积模量即可实现对静力"隐身"的中性夹杂.
|
| 图35 激光加工技术制备的微观高聚物基五模材料.(a)扫描电镜图及微结构几何参数示意图,(b)斜视图,(c)3D打印制备的宏观聚合基五模材料,(d)五模材料静力学斗篷实验样件,(e)静力学加载测试,(f)位置1处变形曲线 |
在金属基五模材料制备方面,法国IEMN研究院、武汉第2船舶设计研究所及作者所在的课题组均取得了相应研究进展.法国IEMN研究院Hladky-Hennion等(2013)设计了铝基平板声波聚焦透镜,并通过水枪切割技术制备了试验样件(图 36(b)).由于水枪切割不便于加工较厚的铝板,实验样件由分别用水枪切割的15层5 mm厚铝板粘接而成,其长和高分别为265 mm和75 mm,宽为58.1 mm到60 mm.样件单胞为正六边形蜂窝结构,单胞边长$a=6.445$ mm,蜂窝薄壁厚度为0.5 mm.

|
| 图36 (a)"金属水"五模材料二维模型,(b)水枪切割技术制备的与水匹配的铝基五模材料样品 |
作者所在的课题组在五模材料理论、仿真研究基础上,采用金属3D打印制备了钛基"金属水"样件(图 37(a)),样件为截面直径$D=118$ mm、高为104 mm的圆柱体,六边形胞元边长$a=20$ mm,最薄壁厚$t=1$ mm.由于金属材料3D打印原理的限制,加工的钛基五模材料样件表面比较粗糙.图 37(b)为利用慢走丝线切割技术制备的铝基五模材料,2个样件中微结构五模材料所占区域长宽均为120.00 mm和34.64 mm,厚度分别为10 mm和50 mm,均采用板材整体切割而成.该五模材料胞元边长为10 mm,最薄壁厚为0.4 mm,其杨氏模量测试结果为85 MPa,与预测结果92 MPa基本接近. 图 37(c)为采用相同技术制备的梯度渐变环形五模材料斗篷试样,具有很高的加工精度.

|
| 图37 五模材料试件.(a)3D打印钛基五模材料,(b)线切割铝基五模材料样件,(c)线切割铝基五模材料斗篷,(d)微细铣削制备的环形铝基五模材料 |
图 37(d)为武汉第2船舶设计研究所采用微细铣削制备的环形铝基五模材料(Zhang et al. 2015,Xiao et al. 2014),该环形材料周向包含50个周期,径向包含13层相同等效性质的微结构.环形层内径、外径分别为75 mm和150 mm,最小连接点尺寸达到了0.1 mm. 微细铣削作为微细加工技术的一种,通过反复少量地切削基材而制备样件,通常加工的样件尺寸在厘米尺度,加工图 37(d)中分米尺度以上样件则需花费较长时间.
6 总结与展望本文从五模材料基本概念、材料微结构设计、声学应用及材料制备等方面对五模材料研究进展做了详细的介绍.五模材料作为微结构弹性材料,拥有宽频有效性、固体形态、基体介质选择多样等优点,是比各向异性密度声学超材料更理想的水声声波调控材料.鉴于其在水声环境中的潜在应用,近期受到了国内外研究关注. 目前,五模材料基本特性和优点已渐渐明晰,研究重点逐渐过渡到五模材料微结构优化设计、材料制备及实验方面的研究.需要指出的是,五模材料虽然在声波控制方面上有广阔的应用前景,但距离实际应用还有一系列关键技术需要解决:
新型五模材料胞元设计:现有的二维五模材料胞元均为蜂窝结构附加不同配重块构成,胞元整体构形差异不大,等效参数调节能力受到一定限制.该问题主要源于五模特征形成机理研究缺乏,新构型只能通过拓扑优化结合数值均质化等耗时方法设计.探究五模特征深层次形成机理,有助于设计出具有更大各向异性调节程度、更宽等效参数调节范围且易于加工制备的新构形.
高效微结构器件模拟算法: 鉴于五模材料功能器件的微结构复杂性,有必要首先通过微结构数值模拟,探明微结构精度、缺陷等对功能有效性的影响,再具体制备相应的微结构试件. 然而,一般的功能器件都包含上千的微结构单胞,采用直接有限元离散需要大量资源且耗时较长. 因此,建立快速、高效的微结构器件数值模拟方法显得尤为重要,尤是在复杂器件的迭代优化中.
微结构器件原理性验证:多种五模材料器件的声波调控功能已由数值模拟验证,然而其原理性验证还较缺乏. 实际制备的五模器件在具体应用中,面临微结构加工精度、弱剪切及复杂水声环境等问题,这些因素的影响需要通过实验加以分析验证.在多数五模器件的原理验证中,需要约束声波在面内传播的二维波导,这种约束在水声环境中非常难以实现,相关的近似方案还有待进一步研究.
最后,经过原理性验证的五模材料器件迈向实际应用时,还面临一些工程上的具体问题,比如微结构应力集中、耐压性差如何解决及高精度、大尺度微结构速制备工艺等.
致谢 国家自然科学基金资助项目(11472044,11521062,11372035).
| Amendola A, Smith C J, Goodall R, Auricchio F, Feo L, Benzoni G, Fraternali F. 2016. Experimental response of additively manufactured metallic pentamode materials confined between stiffening plates. Composite Structures, 142: 254. |
| Brun M, Guenneau S, Movchan A B. 2009. Achieving control of in-plane elastic waves. Applied Physics Letters, 94: 61903. |
| Bückmann T, Thiel M, Kadic M, Schittny R, Wegener M. 2014. An elasto-mechanical unfeelability cloak made of pentamode metamaterials. Nature Communications, 5 |
| Cai C X,Wang Z H, Li Q W, Xu Z, Tian X G. 2015. Pentamode metamaterials with asymmetric double-cone elements. Journal of Physics D: Applied Physics, 17: 175103. |
| Chang Z, Hu G K. 2012. Elastic wave omnidirectional absorbers designed by transformation method. Applied Physics Letters, 101: 54102. |
| Chang Z, Hu J, Hu G K, Tao R, Wang Y. 2011. Controlling elastic waves with isotropic materials. Applied Physics Letters, 98: 121904. |
| Chang Z, Zhou X M, Hu J, Hu G K. 2010. Design method for quasi-isotropic transformation materials based on inverse Laplace's equation with sliding boundaries. Optics Express, 18: 6089-6096. |
| Chen H Y, Chan C T. 2007. Acoustic cloaking in three dimensions using acoustic metamaterials. Applied Physics Letters, 91: 183518. |
| Chen W Q, Bian Z G, Ding H J. 2004. Three-dimensional vibration analysis of fluid-filled orthotropic FGM cylindrical shells. International Journal of Mechanical Sciences, 46: 159-171. |
| Chen X Z, Luo Y, Zhang J J, Jiang K, Pendry J B, Zhang S A. 2011. Macroscopic invisibility cloaking of visible light. Nature Communications, 2 |
| Chen Y, Liu X N, Hu G K. 2015. Latticed pentamode acoustic cloak. Scientific Reports, 5: 15745. |
| Chen Y, Liu X N, Hu G K. Low Frequency resonance scattering of acoustic cloak with imperfect pentamode material. In preparation |
| Chen Y, Liu X N, Hu G K. Design of arbitrary shaped pentamode acoustic cloak based on nearly symmetric mapping gradient algorithm. Submitted |
| Cheng Y, Liu X J. 2008. Resonance effects in broadband acoustic cloak with multilayered homogeneous isotropic materials. Applied Physics Letters, 93: 71903. |
| Christensen J, de Abajo F J G. 2012. Anisotropic metamaterials for full control of acoustic waves. Physical Review Letters, 108: 124301. |
| Climente A, Torrent D, Sáanchez-Dehesa J. 2012. Omnidirectional broadband acoustic absorber based on metamaterials. Applied Physics Letters, 100: 144103. |
| Colquitt D J, Brun M, Gei M, Movchan A B, Movchan N V, Jones I S. 2014. Transformation elastodynamics and cloaking for flexural waves. Journal of the Mechanics and Physics of Solids, 72: 131-143. |
| Cummer S A, Schurig D. 2007. One path to acoustic cloaking. New Journal of Physics, 9: 45. |
| Cummer S A, Popa B, Schurig D, Smith D R, Pendry J B, Rahm M, Starr A. 2008. Scattering theory derivation of a 3D acoustic cloaking shell. Physical Review Letters, 100: 24301. |
| Ding Y Q, Liu Z Y, Qiu C Y, Shi J. 2007. Metamaterial with simultaneously negative bulk modulus and mass density. Physical Review Letters, 99: 93904. |
| Fan J R. 1996. Exact theory of strongly thick laminated plates and shells. |
| Fang N, Xi D J, Xu J Y, Ambati M, Srituravanich W, Sun C, Zhang X. 2006. Ultrasonic metamaterials with negative modulus. Nature Materials, 5: 452-456. |
| Farhat M, Enoch S, Guenneau S, Movchan A B. 2008. Broadband cylindrical acoustic cloak for linear surface waves in a fluid. Physical Review Letters, 101: 134501. |
| Farhat M, Guenneau S, Enoch S, Movchan A B. 2009. Cloaking bending waves propagating in thin elastic plates. Physical Review B, 79: 33102. |
| Flax L, Dragonette L R, Überall H. 1978. Theory of elastic resonance excitation by sound scattering. The Journal of the Acoustical Society of America, 63: 723. |
| Gokhale N H, Cipolla J L, Norris A N. 2012. Special transformations for pentamode acoustic cloaking. The Journal of the Acoustical Society of America, 132: 2932-2941. |
| Han T C, Yuan T, Li B W, Qiu C W. 2013. Homogeneous thermal cloak with constant conductivity and tunable heat localization. Scientific Reports, 3 |
| Hladky-Hennion A C, Vasseur J O, Haw G, Croenne C, Haumesser L, Norris A N. 2013. Negative refraction of acoustic waves using a foam-like metallic structure. Applied Physics Letters, 102: 144103. |
| Hu J, Chang Z, Hu G K. 2011. Approximate method for controlling solid elastic waves by transformation media. Physical Review B, 84: 201101. |
| Huang Y, Lu X G, Liang G Y, Xu Z. 2016. Pentamodal property and acoustic band gaps of pentamode metamaterials with different cross-section shapes. Physics Letters A, 380: 1334-1338. |
| Jiang W X, Cui T J, Ma H F, Zhou X Y, Cheng Q. 2008. Cylindrical-to-plane-wave conversion via embedded optical transformation. Applied Physics Letters, 92: 261903. |
| Jiang X, Liang B, Zou X Y, Yin L L, Cheng J C. 2014. Broadband field rotator based on acoustic metama- terials. Applied Physics Letters, 104: 83510. |
| Kadic M, Bückmann T, Schittny R, Wegener M. 2013. On anisotropic versions of three-dimensional penta- mode metamaterials. New Journal of Physics, 15 |
| Kadic M, Bückmann T, Schittny R, Gumbsch P, Wegener M. 2014. Pentamode metamaterials with inde- pendently tailored bulk modulus and mass density. Physical Review Applied, 2: 54007. |
| Kadic M, Bückmann T, Stenger N, Thiel M, Wegener M. 2012. On the practicability of pentamode mechan- ical metamaterials. Applied Physics Letters, 100: 191901. |
| Kwon D, Werner D H. 2008. Polarization splitter and polarization rotator designs based on transformation optics. Optics Express, 16: 18731-18738. |
| Lai Y, Chen H Y, Zhang Z Q, Chan C T. 2009. Complementary media invisibility cloak that cloaks objects at a distance outside the cloaking shell. Physical Review Letters, 102: 93901. |
| Lai Y, Wu Y, Sheng P, Zhang Z Q. 2011. Hybrid elastic solids. Nature Materials, 10: 620-624. |
| Layman C N, Naify C J, Martin T P, Calvo D C, Orris G J. 2013. Highly anisotropic elements for acoustic pentamode applications. Physical Review Letters, 111: 24302. |
| Lee S H, Park C M, Seo Y M, Wang Z G, Kim C K. 2009. Acoustic metamaterial with negative density. Physics Letters A, 373: 4464-4469. |
| Lee S H, Park C M, Seo Y M, Wang Z G, Kim C K. 2010. Composite acoustic medium with simultaneously negative density and modulus. Physical Review Letters, 104: 54301. |
| Leonhardt U. 2006. Optical conformal mapping. Science, 312: 1777-1780. |
| Li J, Chan C T. 2004. Double-negative acoustic metamaterial. Physical Review E, 70: 55602. |
| Li Y, Wu Y, Mei J. 2014. Double Dirac cones in phononic crystals. Applied Physics Letters, 105: 14107. |
| Liang Z, Li J. 2012. Extreme acoustic metamaterial by coiling up space. Physical Review Letters, 108: 114301. |
| Liu X N, Hu G K, Huang G L, Sun C T. 2011. An elastic metamaterial with simultaneously negative mass density and bulk modulus. Applied Physics Letters, 98: 251907. |
| Liu Z Y, Zhang X X, Mao Y W, Zhu Y Y, Yang Z Y, Chan C T, Sheng P. 2000. Locally resonant sonic materials. Science, 289: 1734-1736. |
| Luo J, Lai Y. 2014. Anisotropic zero-index waveguide with arbitrary shapes. Scientific Reports, 4: 5875 |
| Martin A, Kadic M, Schittny R, Bückmann T, Wegener M. 2012. Phonon band structures of three- dimensional pentamode metamaterials. Physical Review B, 86: 155116. |
| Milton G W, Cherkaev A V. 1995. Which elasticity tensors are realizable? Journal of Engineering Materials and Technology, 117: 483-493. |
| Milton G W, Briane M, Willis J R. 2006. On cloaking for elasticity and physical equations with a transfor- mation invariant form. New Journal of Physics, 8: 248. |
| Norris A N. 2008. Acoustic cloaking theory. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 464: 2411-2434. |
| Norris A N. 2014. Mechanics of elastic networks. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 470: 20140522. |
| Norris A N. 2009. Acoustic metafluids. The Journal of the Acoustical Society of America, 125: 839. |
| Norris A N. 1990. Resonant acoustic scattering from solid targets. The Journal of the Acoustical Society of America, 88: 505-514. |
| Norris A N, Nagy A J. 2011. Metal water: A metamaterial for acoustic cloaking//Proceedings of Phononics, Santa Fe, New Mexico, USA: 112-113. |
| Norris A N, Parnell W J. 2012. Hyperelastic cloaking theory: transformation elasticity with pre-stressed solids. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science, 468: 2881- 2903. |
| Norris A N, Shuvalov A L. 2011. Elastic cloaking theory. Wave Motion, 48: 525-538. |
| Norris A N, Shuvalov A L, Kutsenko A A. 2012. Analytical formulation of three-dimensional dynamic homogenization for periodic elastic systems. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 468: 1629-1651. |
| Pendry J B, Holden A J, Stewart W J, Youngs I. 1996. Extremely low frequency plasmons in metallic mesostructures. Physical Review Letters, 76: 4773. |
| Pendry J B, Schurig D, Smith D R. 2006. Controlling electromagnetic fields. Science, 312: 1780-1782. |
| Popa B, Zigoneanu L, Cummer S A. 2011. Experimental acoustic ground cloak in air. Physical Review Letters, 106: 253901. |
| Rahm M, Roberts D A, Pendry J B, Smith D R. 2008. Transformation-optical design of adaptive beam bends and beam expanders. Optics Express, 16: 11555-11567. |
| Ren C Y, Xiang Z H, Cen Z Z. 2010. Design of acoustic devices with isotropic material via conformal transformation. Applied Physics Letters, 97: 44101. |
| Rohde C A, Martin T P, Guild M D, Layman C N, Naify C J, Nicholas M, Thangawng A L, Calvo D C, Orris G J. 2015. Experimental demonstration of underwater acoustic scattering cancellation. Scientific Reports, 5: 13175. |
| Scandrett C L, Boisvert J E, Howarth T R. 2010. Acoustic cloaking using layered pentamode materials. The Journal of the Acoustical Society of America, 127: 2856-2864. |
| Scandrett C L, Boisvert J E, Howarth T R. 2011. Broadband optimization of a pentamode-layered spherical acoustic waveguide. Wave Motion, 48: 505-514. |
| Schittny R, Bückmann T, Kadic M,Wegener M. 2013. Elastic measurements on macroscopic three-dimensional pentamode metamaterials. Applied Physics Letters, 103: 231905. |
| Schittny R, Kadic M, Guenneau S, Wegener M. 2013. Experiments on transformation thermodynamics: molding the flow of heat. Physical Review Letters, 110: 195901. |
| Schmiele M, Varma V S, Rockstuhl C, Lederer F. 2010. Designing optical elements from isotropic materials by using transformation optics. Physical Review A, 81: 33837. |
| Schurig D, Mock J J, Justice B J, Cummer S A, Pendry J B, Starr A F, Smith D R. 2006. Metamaterial electromagnetic cloak at microwave frequencies. Science, 314: 977-980. |
| Smith J D. 2011. Application of the method of asymptotic homogenization to an acoustic metafluid. Pro- ceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 467: 3318-3331. |
| Srivastava A, Nemat-Nasser S. 2014. On the limit and applicability of dynamic homogenization. Wave Motion, 51: 1045-1054. |
| Stenger N, Wilhelm M, Wegener M. 2012. Experiments on elastic cloaking in thin plates. Physical Review Letters, 108: 014301 |
| Tian Y,Wei Q, Cheng Y, Xu Z, Liu X J. 2015. Broadband manipulation of acoustic wavefronts by pentamode metasurface. Applied Physics Letters, 107: 221906. |
| Tichit P H, Burokur S N, de Lustrac A. 2009. Ultradirective antenna via transformation optics. Journal of Applied Physics, 105: 104912. |
| Titovich A S, Norris A N. 2014. Tunable cylindrical shell as an element in acoustic metamaterial. The Journal of the Acoustical Society of America, 136: 1601-1609. |
| Torrent D, Sanchez-Dehesa J. 2010. Anisotropic mass density by radially periodic fluid structures. Physical Review Letters, 105: 430117. |
| Wei Q, Cheng Y, Liu X J. 2013. Acoustic total transmission and total reflection in zero-index metamaterials with defects. Applied Physics Letters, 102: 174104. |
| Wu L Z, Gao P L. 2015. Manipulation of the propagation of out-of-plane shear waves. International Journal of Solids and Structures, 69-70: 383-391. |
| Wu Y, Lai Y, Zhang Z Q. 2007. Effective medium theory for elastic metamaterials in two dimensions. Physical Review B, 76: 205313. |
| Wu Y, Lai Y, Zhang Z. 2011. Elastic metamaterials with simultaneously negative effective shear modulus and mass density. Physical Review Letters, 107: 105506. |
| Wu Y, Mei J, Sheng P. 2012. Anisotropic dynamic mass density for fluid-solid composites. Physica B: Condensed Matter, 407: 4093-4096. |
| Xiao Q J, Wang L, Wu T, Zhao Z G. 2014. Research on layered design of ring-shaped acoustic cloaking using bimode metamaterial. Applied Mechanics and Materials, 687-691: 4399-4404. |
| Xie Y, Popa B, Zigoneanu L, Cummer S A. 2013. Measurement of a broadband negative index with space- coiling acoustic metamaterials. Physical Review Letters, 110: 175501. |
| Yang M, Ma G C, Yang Z Y, Sheng P. 2013. Coupled membranes with doubly negative mass density and bulk modulus. Physical Review Letters, 110: 134301. |
| Zhang S, Genov D A, Sun C, Zhang X. 2008. Cloaking of matter waves. Physical Review Letters, 100: 123002. |
| Zhang S, Xia C G, Fang N. 2011. Broadband acoustic cloak for ultrasound waves. Physical Review Letters, 106: 24301. |
| Zhang X D, Chen H, Wang L, Zhao Z G, Zhao A G. 2015. Theoretical and numerical analysis of layered cylindrical pentamode acoustic cloak. Acta Physica Sinica, 64: 134301-134303. |
| Zheng L Y, Wu Y, Ni X, Chen Z G, Lu M H, Chen Y F. 2014. Acoustic cloaking by a near-zero-index phononic crystal. Applied Physics Letters, 104: 161904. |
| Zhou X M, Hu G K. 2009. Analytic model of elastic metamaterials with local resonances. Physical Review B, 79: 195109. |
| Zhou X M, Hu G K. 2011. Superlensing effect of an anisotropic metamaterial slab with near-zero dynamic mass. Applied Physics Letters, 98: 263510. |
| Zhu R, Liu X N, Hu G K, Sun C T, Huang G L. 2014. Negative refraction of elastic waves at the deep- subwavelength scale in a single-phase metamaterial. Nature Communications, 5: 5510. |
| Zigoneanu L, Popa B, Cummer S A. 2014. Three-dimensional broadband omnidirectional acoustic ground cloak. Nature materials, 13: 352-355. |
| Zigoneanu L, Popa B, Starr A F, Cummer S A. 2011. Design and measurements of a broadband two- dimensional acoustic metamaterial with anisotropic effective mass density. Journal of Applied Physics, 109: 54906. |



