2. 浙江大学软物质科学研究中心, 杭州 310027;
3. 锡根大学土木工程系, 德国锡根 D57068
2. Soft Matter Research Center, Zhejiang University, Hangzhou 310027, China;
3. Department of Civil Engineering, University of Siegen, Siegen D57068, Germany
1 引言
电弹性材料(electroelastic materials)呈现出力电耦合特性,即在机械载荷作用下会产生内部电场/表面电荷,而在电场作用下又会产生机械变形(Yang 2005a). 电弹性材料包括压电陶瓷等脆性压电材料,也包括介电高弹体(dielectric elastomer)等具有力电耦合特性的软材料(soft electroelastic materials). 长期以来,压电材料或器件是构成许多力电耦合系统的核心,比如用于实现机械能和电能转换的换能器,用于频率控制、远程通信和精确记时的谐振器,以及声波传感器等(Uchino 1997,Campbell 1998,Hashimoto 2000,Rao & Sunar,1994,Sunar & Rao,1999,Chee et al. 1998),但其最明显的缺点是能够承受的变形较小. 而随着软物质科学的发展,成功制备出了许多新型的力电耦合软材料,其中包括在电场作用下能产生大变形的介电高弹体(Pelrine et al. 2000,Carpi et al. 2011)、电致伸缩聚合物(Zhang et al. 1998,Lehmann et al. 2001)、液晶高弹体(Thomsen et al. 2001,Camacho-Lopez et al. 2004)、电凝胶(Voltairas et al. 2003)和柔性驻极体(Bauer 2006,McCarty & Whitesides,2008,Deng et al. 2013)等. 这些软电弹性材料因其在生物工程、医疗、显示技术、传感器、机械控制等领域的广阔应用前景而引起研究者的普遍兴趣(Carpi et al. 2011,Halloran et al. 2008,赵晓鹏和尹剑波2011).
一般的非线性电弹性理论考虑了材料中的力电耦合效应. 早期用于较大机械变形和较高电场分析的非线性电弹性理论是由Toupin(1956,1963)提出的,其第一项工作针对静力学情形,第二项工作扩展到了动力学情形. 随着多功能力电耦合器件的快速发展及其高精度分析的需求,Tiersten(1971)进一步建立了考虑温度效应的非线性电弹性理论. 类似的工作还可参考Nelson(1978,1979). 20世纪80年代以来,由于各种智能材料与结构概念的提出及其广泛的应用前景,考虑力电磁耦合作用的非线性介质理论也得到很好的建立和完善(Maugin 1988,Eringen & Maugin,1990,Dorfmann & Ogden 2014b),这也为复杂问题的有限元计算、复合材料细观力学分析等奠定了良好的理论基础. 而随着具有巨大变形能力的软电弹性体的出现(Pelrine et al. 2000,Zhang et al. 2007,Fox & Goulboume,2008,Wang & Xiao et al. 2010,Rosset & Shea,2013),非线性电弹性理论又得到了重新的诠释和改善,至今仍在不断发展中(Dorfmann & Ogden2005,2006; McMeeking & Landis 2005; Ericksen 2007; Suo et al. 2008; Trimarco 2009;Bustamante et al. 2009a,2009b; Bustamante & Ogden,2013; Liu 2013a,2013b). 近几年,国内外学者在软电弹性体的非线性力电耦合分析方面取得了很多突破,为新型器件设计和各种工程应用奠定了良好的基础(DÍaz-Calleja et al. 2008; Bertoldi & Boyce,2008a,2008b; Bustamante 2009; Leng et al. 2009; Mannsfeld et al. 2010; Zhao & Suo,2010; He et al. 2011). 特别应该指出的是,基于非线性连续介质理论和电磁场论,Dorfmann和Ogden(2014b)在其专著中综述了考虑力电磁耦合作用的非线性理论框架,这为研究电敏感和磁敏感软材料的非线性力电磁耦合特性提供了坚实的理论指导. 但是,非线性电弹性理论十分复杂,基于此理论导出的控制方程往往是非线性、强耦合的偏微分方程组,其求解十分困难(Tiersten 1975,锁志刚2011).
另外,由电弹性材料构成的多功能力电耦合系统通常会受到初始预应力、初始预 应变或者初始电场(统称为偏场)的影响,偏场的存在可在很大程度上改变材料的物 理和力学特性. 一方面,偏场有可能导致力电耦合器件工作不稳定甚至失效(Tiersten et al. 1981,Gafka & Tani,1993,Kosinski et al. 2002,Bertoldi & Gei,2011,Li & Liu et al. 2011). 另一方面,正确地利用偏场也可能调制和改善力电耦合器件的工作性能(Gei et al. 2009,2011; Li & Chen et al. 2011; Chen & Dai,2012; Shmuel & deBotton,2012; Shmuel 2013b; Wang et al. 2015). 因此建立合理且精确的理论模型来研究偏场的影响对于多 功能力电耦合器件的设计至关重要.
现有文献中研究偏场作用下电弹性体的力电耦合特性通常是采用叠加于有限偏 场之上的小增量场理论(简称偏场理论)来描述(Yang 2005a; Maugin 1988; Eringen & Maugin,1990; Baumhauer & Tiersten,1972; Tiersten 1981; Baesu et al. 2003; Liu et al. 2003a,2003b; Ogden 2009; Dorfmann & Ogden,2010a,2010b; Yang 2009),但不同的 学者往往选取不同的数学列式进行具体的表述. 对电弹性体偏场理论的开创性研究 起源于Baumhauer和Tiersten(1972)以及Tiersten(1981)(后面简称Tiersten 偏场理 论),他们从一般的非线性电弹性理论出发,在连续介质力学框架下,通过建立具有自 然构型、初始构型及现时构型3 种构型的偏场模型,将场变量相对于初始构型进行 Taylor 级数展开,最终分别获得了以自然构型和初始构型作为参考构型的增量方程 及边界条件. Yang(2004)通过系统的级数展开方法推导了以自然构型为参考构型的 Tiersten 偏场理论的变分方程. 同时,Yang(2003)进一步推广了以自然构型为参考构 型的Tiersten 偏场理论,建立了考虑温度效应的电弹性偏场理论. 基于以自然构型为 参考构型的Tiersten 偏场理论,Sinha和Tiersten(1979)研究了弯曲偏场状态对压电弹 性体表面波速的影响; Tiersten(1995)给出了偏场作用下压电谐振器的精确描述; Yang(2001,2005b)分别研究了具有预应变的压电陶瓷中Bleustein-Gulyaev 波(简称BG 波)的传播特性以及无限小偏场作用下电弹性体的自由振动; Hu 等(2002,2004)分别研究 了偏场作用下电弹性壳体的拉伸和弯曲响应特性以及预置偏场下电致伸缩材料半空 间的表面波特性; Zhou 等(2011)研究了无限小偏场作用下连接于两块压电陶瓷板之 间的石英晶体板的厚度剪切振动; Huang和Zhang 等(2014)通过平面波展开法详细考 察了由压电夹杂和弹性各向同性基体组成的二维声子晶体在不同力电偏场作用下能 带结构的可调控性. 更多有关以自然构型为参考构型的Tiersten 偏场理论的深入讨论及其应用可参考专著(Yang 2005a)和综述论文(Yang & Hu,2004). 另外,Chai和Wu(1996)重新整理了以初始构型为参考构型的Tiersten 偏场理论,并进一步假设偏场无 限小,最终获得无限小偏场作用下的电弹性体偏场理论,最后给出了考虑预应力影响 的Lothe-Barnett 积分公式以计算半空间表面波速度.
Eringen和Maugin 在他们的专著中(Maugin 1988,Eringen & Maugin,1990)也利 用三构型的偏场模型,从一般的非线性电磁弹性理论出发,建立了以初始构型为参考 构型的电磁弹性偏场理论(后面简称E-M 偏场理论). Sóos(1996)对E-M 偏场理论进 行重新整理,给出了与E-M 偏场理论等效的以初始构型为参考构型的偏场理论(后 面简称Sóos 偏场理论). 而Baseu 等(2003)利用更新的拉格朗日方法(updated La-grangian method)重新用张量实体形式描述了Sóos 偏场理论,并考虑了非约束超弹性(unconstrained hyperelastic)介电和压电材料中平面波的传播问题. 基于Sóos 偏场理 论,Simionescu和Sóos(2001)研究了在初始变形和电场作用下压电晶体中波的传播; Simionescu(2000,2001,2002,2005,2007)对偏场作用下6mm 型和立方型压电晶体中波 的传播特性进行了大量研究; Simionescu和Ana(2009)还研究了压电半无限大平面中 平面导波传播的耦合条件. 更多有关Sóos 偏场理论的讨论及其应用可参见文献(Yang 2009).
利用三构型偏场模型,Liu 等2003a,(2003b)通过不同的定义和推导方式获得了以 自然构型为参考构型的电弹性偏场理论(后面简称Liu 偏场理论). 尽管Liu 偏场理论 适用于无限小偏场情形,但考虑了材料非线性(在能量密度函数的展开中包含三阶弹 性、压电和介电系数以及电致伸缩系数)和几何非线性(在增量控制方程中考虑了初 始位移梯度和增量位移梯度的点积); 当忽略预加电场和变形而仅考虑预应力的影响 时,Liu 偏场理论退化为通常的初始应力理论(Pao et al. 1984). 基于Liu 偏场理论,Liu 等(2003a)研究了预应力层合压电结构中BG 波的传播特性; Singh(2010)详细分析 了平面波在有预应力的压电半空间表面的反射,并研究了表面电学边界条件的影响; Lematre 等2006a,(2006b)采用传递矩阵法进一步分析了均匀和非均匀预应力场对波动特性的影响. 在他们的分析列式中,包含了三阶材料常数. 忽略三阶材料常数的影响,Qian 等2004a,(2004b)、Su 等(2005)、Du 等(2007b)、Son和Kang(2011)针对层状 压电介质详细地考察了预应力或预加电位移对各种波传播特性的影响; Du 等(2007a)分析了具有初应力的磁-电-弹层状介质中的Love 波传播特性; Zhou 等(2012)进一 步研究了初始应力和非完美界面对层合压电/压磁板中体波传播特性的影响.
从一般的非线性电磁弹性理论出发,Ogden(2009)也建立了不同形式的偏场理论(后面简称Ogden 偏场理论),其理论所使用的能量密度函数为总能量密度函数,其独 立的电学自变量为拉格朗日形式的电场矢量. 而基于Dorfmann和Ogden(2005)的工 作,Dorfmann和Ogden2010a,(2010b)又获得另一形式的电弹性偏场理论(后面简称Dorfmann 偏场理论),并建议了一个各向同性电弹性(isotropic electroelastic)材料的本 构关系,其所选取的能量密度函数的独立电学变量为拉格朗日形式的电位移矢量,并 分别考察了在均匀预变形作用下各向同性电弹性半无限体的稳定性问题以及无限体和半无限体中波动的传播问题. Dorfmann & Ogden(2014b)最近系统地整理归纳了他 们在电弹性材料偏场理论及其应用方面的研究(Ogden 2009; Dorfmann & Ogden,2010a,2010b). 基于Dorfmann 偏场理论,Shmuel 等(2012)研究了预加大变形对介电高弹体 层合介质中Rayleigh-Lamb 波传播特性的影响; 周伟建和陈伟球(2015)利用表面薄层 模型和Stroh 公式讨论了有限偏场作用下具有表面效应的可压缩介电高弹体中表面 波的传播特性; Chen和Dai(2012)考察了有限偏场对不可压缩软电弹性实心圆柱中 轴对称波频散特性的影响; 苏益品和陈伟球(2014)研究了均匀有限偏场和外电场对 不可压缩软电弹性圆柱壳中轴对称波频散特性的影响; Shmuel(2013a)则研究了非均 匀有限偏场作用下介电高弹圆柱管中轴对称波的传播特性. 另外,Shmuel和deBotton(2012)讨论了有限变形状态下无限大周期层合板的厚度剪切振动特性,获得了增量波 动场的色散关系,并指出波不能传播的频率范围(即带隙宽度)大大依赖于初始施加 的电偏场; Shmuel(2013b)还分析了有限预拉伸介电高弹体纤维复合材料的静电可调 带宽特性; Huang和Shen 等(2014)利用传递矩阵法并通过引进有效声阻抗差(effective acoustic impedance difference)进一步研究了有限机械偏场对可压缩两相软材料一维声 子晶体中纵波传播特性的调控.
对于初始应力作用下弹性体无限小增量运动不同形式的线性增量控制方程,Bazant(1971)已作了深入的比较和讨论. 对于电弹性体,Yang和Hu(2004)主要针对以自然 构型为参考构型(即拉格朗日描述下)的Tiersten 偏场理论,没有详细涉及和讨论以 初始构型为参考构型(即更新拉格朗日描述下)的偏场理论,也未对比不同偏场理论(如Tiersten 偏场理论、Sóos 偏场理论、Ogden 偏场理论等)之间的异同点. Yang和Hu(2004)的综述包含了偏场理论在一些领域内的应用,包括压电结构屈曲分析、压电谐 振器频率稳定性分析、测量力热场的声波传感器、非线性电弹性材料系数的测定以及 波传播等,研究对象主要是脆性电弹性材料及其器件结构. 随着力电耦合智能软材料 与结构的兴起以及微纳机电系统(MEMS和NEMS)的发展,了解力电耦合偏场理论 在不同领域中的最新应用具有十分重要的意义. 考虑到目前还没有文献对不同形式的 电弹性体偏场理论进行较深入的比较研究,而且许多最新文献仍然在利用不同的电弹 性体偏场理论对具体问题进行分析而未必明了相互之间的关联,本文首先将基于力电 耦合非线性连续介质理论的一般框架,利用3 个构型的表述方式,详细阐述拉格朗日 描述和更新拉格朗日描述下的力电耦合偏场理论. 重点对各种电弹性体偏场理论进行 深入的研究和探讨,甄别不同偏场理论之间的异同点,以理清不同偏场理论之间的关 系,既可为今后的相关理论研究提供指导和帮助,也可为力电耦合器件的设计提供必要的理论支撑. 最后,本文讨论了力电耦合偏场理论在不同研究领域的若干研究重点 及其未来发展趋势,其中包括非均匀偏场作用下波的传播特性、不同描述下偏场对电 弹性材料力电特性的影响、微纳米多晶薄膜中残余应力的表征和控制、纳米压电和铁 电材料的非线性力电特性、软材料声子晶体力电耦合调控、基于偏场方法的弹性波隐 身主动调控、软电弹性材料偏场状态的分叉和稳定性、生物软组织超声弹性成像等问题.
2 非线性电弹性理论如果电弹性体内部事先不存在力和电场(即无偏场),且材料变形与理想的参考状态偏离不远,那么线性电弹性理论就可以很好地描述此类小幅运动. 但由电弹性材料构成的力电耦合系统通常会受到偏场的影响,偏场的存在理论上将改变材料的力电特性,一般会使经典的线性电弹性理论失效(Yang & Hu,2004). 偏场作用下电弹性体的力电特性可以采用偏场理论来进行研究,而偏场理论的完整描述须基于三维非线性电弹性理论. 因此,本节将首先阐述电弹性体的非线性力学理论框架,而更详细的描述可参考专著(Yang 2005a,Dorfmann & Ogden,2014b). 为方便读者起见,附录A 给出了本文所采用的重要符号术语.
2.1 连续介质运动和变形图1 给出了可发生有限变形且可极化的电弹性体的构型及有限变形描述. 在初始时刻电弹性体不受外场作用,处于自然状态(即未变形状态),此构型定义为自然构型. 此时,电弹性体所占据的区域为Br,边界为∂Br,N 是∂Br上任意点的单位外法向矢量,微元面积和体积分别为dA和dV. 用X = XKIK 表示此构型下任意物质点的位置矢量,XK 表示任意物质点的自然坐标或物质坐标,基矢量IK 是沿着坐标XK的单位矢量. 此电弹性体在受到外场作用时将发生变形,定义在任意时刻t 处于变形状态的构型为现时构型,所占据的区域为B,边界为∂B,n 是∂B 上任意点的单位外法向矢量,微元面积和体积分别为dα和dν. 用y = y(X,t)= ykik 表示此构型下任意物质点X 在时刻t 的现时位置,yk表示任意物质点的现时坐标或空间坐标,基矢量ik是沿着坐标yk 的单位矢量. 矢量函数y(X,t)描述电弹性体与时间相关的变形运动,假设函数y(X,t)在每个时刻与X 都是一一映射的,且y(X,t)和它的逆函数皆为二次连续可微. 图1 中自然构型坐标系的原点O和基矢量IK 不同于现时构型坐标系的原点o和基矢量ik. 事实上,在电弹性体变形前后,有时可选取不同的坐标系来描述电弹性体的自然构型和现时构型. 例如,当矩形块变成圆柱体时,对于自然构型一般选用直角坐标系,而对于现时构型则宜选用圆柱坐标系,这样对边界条件的表达和问题的求解将带来方便.

|
| 图1 电弹性体的有限变形及其构型 |
在本文的公式推导中,用grad,div和curl 表示相对于现时构型y的微分算符,而用Grad,Div和Curl 表示相对于自然构型X 的微分算符. 梯度为右梯度,即T = gradu对应于Tkl = uk,l; 散度为左散度,即u= div T对应于ul= Tkl,k,指标前面的逗号表示对相关坐标求偏导.大多数情况下,将同时采用实体记法和指标记法来给出相关公式;在少数地方,为推导方便起见只采用笛卡尔指标记法. 将统一用分号“;”来分隔实质相同但形式不同的公式,而用逗号“,”来分隔不同的实体或指标公式. 另外,在使用指标记法时,采用两点张量记法,并约定对哑指标进行求和.
用ν和α分别表示物质点的速度和加速度,则
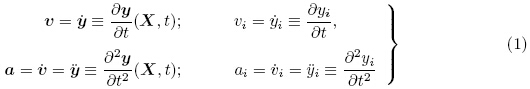
变形梯度张量(deformation gradient tensor)定义为
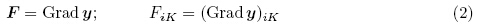

与变形梯度张量F有关的左、右柯西-格林变形张量(left,right Cauchy{Greentensor)分别定义为
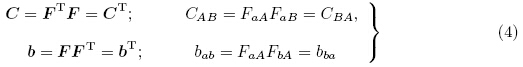
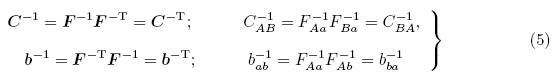
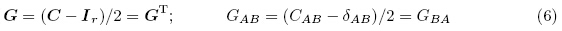
由式(2),现时构型和自然构型的线微元dy和dX 之间的关系为



利用高斯定理(Gauss theorem)、斯托克斯定理(Stokes theorem)和Nanson 公式(8)可得连续介质运动学恒等式如下(Ogden 2009)
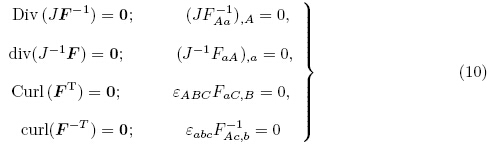
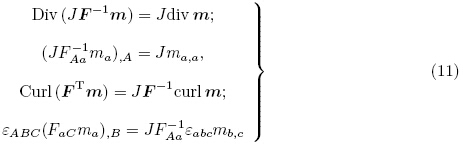
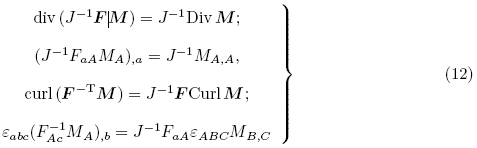
为方便后面的推导,参考Yang(2005a)和Holzapfel(2000),列出以下运动学恒等式
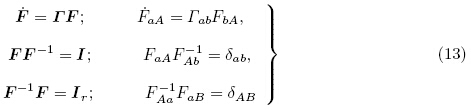
用E,D和P分别表示现时构型B 下的电场矢量、电位移矢量和电极化矢量,这些物理量都属于欧拉矢量场(Eulerian vector fields),即它们都定义在现时构型B 上,是y的函数.当不考虑磁场且电场为准静态时,电场E和电位移D 分别满足
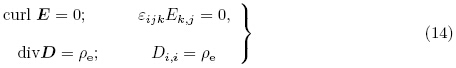
对于可极化材料,电极化矢量P 可表示为


可分别定义对应电场E和电位移D 的物质电场ε(material electric field)和电位移D(material electric displacement)如下
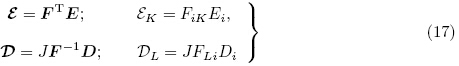
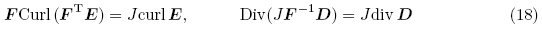
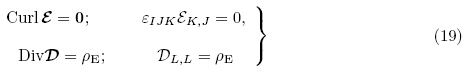

由连续体质量守恒定律可得

由于存在力电相互作用,现有文献中电弹性体的运动微分方程形式并不一致,也存在不同的“应力张量”定义. 正如Bustamante 等(2009a)所述,一般地,由线动量守恒定律可将运动微分方程统一写成以下形式

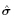 为类Cauchy 应力张量(Cauchy-type stress tensor),
为类Cauchy 应力张量(Cauchy-type stress tensor), 和f 分别为定义在现时构型B上的单位体积电场力和机械力. 另外,电体力矢量
和f 分别为定义在现时构型B上的单位体积电场力和机械力. 另外,电体力矢量 总是可以表示成如下形式
总是可以表示成如下形式
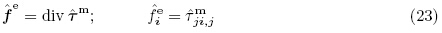
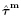 为对应于电体力矢量
为对应于电体力矢量 的电弹性体内部的Maxwell 应力张量. 很明显,电弹性体内部的类Cauchy 应力张量、电体力矢量和Maxwell 应力张量不是唯一确定的,也即对于不同的类Cauchy 应力张量,电体力矢量和Maxwell 应力张量是不一样的(Bustamante et al. 2009a). 对于电磁体力和Maxwell 应力的详细讨论,有兴趣的读者可参考Pao(1978)和Bustamante 等(2009b).
的电弹性体内部的Maxwell 应力张量. 很明显,电弹性体内部的类Cauchy 应力张量、电体力矢量和Maxwell 应力张量不是唯一确定的,也即对于不同的类Cauchy 应力张量,电体力矢量和Maxwell 应力张量是不一样的(Bustamante et al. 2009a). 对于电磁体力和Maxwell 应力的详细讨论,有兴趣的读者可参考Pao(1978)和Bustamante 等(2009b).
特别地,利用式(22)和(23),可以将运动微分方程写成
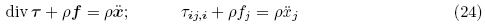
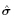 +
+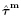 为总应力张量(total stress tensor),式(24)应该是现有文献中最简单的电弹性体的运动微分方程形式(Bustamante et al. 2009a,Dorfmann & Ogden,2014b),其中τ 是对称的,类似于弹性理论中的Cauchy 应力张量. 事实上,如果令式(22)中
为总应力张量(total stress tensor),式(24)应该是现有文献中最简单的电弹性体的运动微分方程形式(Bustamante et al. 2009a,Dorfmann & Ogden,2014b),其中τ 是对称的,类似于弹性理论中的Cauchy 应力张量. 事实上,如果令式(22)中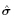 = τ 以及
= τ 以及 = 0,则式(22)变为式(24). 可见,总应力张量τ 已经考虑了电体力对电弹性体的影响.
= 0,则式(22)变为式(24). 可见,总应力张量τ 已经考虑了电体力对电弹性体的影响.
电场体力矢量的一种普遍定义为
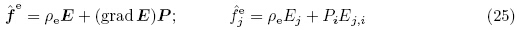
 可写成
可写成
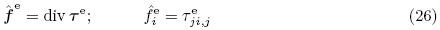
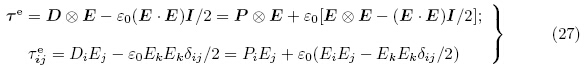
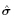 =σ,而运动微分方程式(22)变成
=σ,而运动微分方程式(22)变成
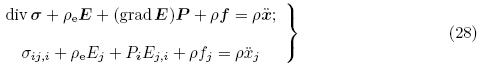
由式(24)~(28)可得σ与总应力张量τ 之间的关系为

式(24)和(28)是一般的运动微分方程式(22)的两种欧拉描述的特殊形式,也是现有文献中常用的两种形式. 更多的运动微分方程形式可参考Bustamante 等(2009a).总之,不同电体力矢量或者等效为不同Maxwell 应力张量对电弹性体影响的差别可以说是人为的,但它们都满足运动微分方程的一般形式(22). 正如Suo 等(2008)和Bustamante 等(2009a)所指出的,在任何情况下,尽管对于给定的电体力,相应的Maxwell应力张量只是相差一个附加的无散度应力张量,但是我们无法通过实验的直接测量来区分不同的电体力或者Maxwell 应力.
下面将推导对应于运动微分方程式(24)和(28)的拉格朗日描述形式. 类似于弹性理论中的名义应力张量,可定义对应于总应力张量τ 的第一类Piola-Kirchhoff 应力张量(the first Piola-Kirchhoff stress tensor,简称为第一类PK 应力张量)如下

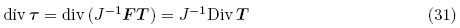
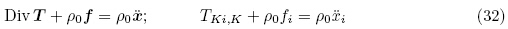
对应于类Cauchy 应力张量σ 的第一类PK 应力张量K 定义为
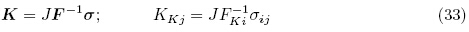



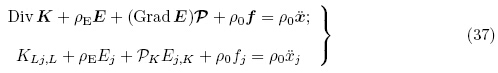
当不考虑本征力偶时,由角动量守恒定律可得

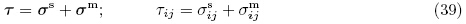


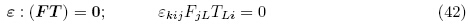
为方便后面推导,定义总应力张量τ 的第二类PK 应力张量为

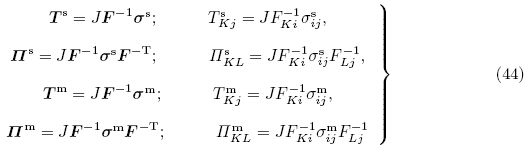

电弹性体本构方程的框架可通过能量守恒定律建立,而能量守恒定律中能量密度函数的选取是多样的,当选择的能量密度函数具有不同的独立力学变量和电学变量时,所获得的本构方程就不一样. 基于变形梯度张量F和不同电学变量的能量密度函数和本构方程可参考Bustamante 等(2009a)以及Dorfmann和Ogden(2014b). 本小节借鉴Bustamante 等(2009a)的方法,不仅考虑能量密度函数中的不同电学变量,也考虑不同力学变量.
首先,如果取单位质量的能量函数为x(F,  ),此时独立变量分别为变形梯度张量F和单位质量的电极化矢量
),此时独立变量分别为变形梯度张量F和单位质量的电极化矢量 ≡P/ρ. 按照Yang(2005a)的推导,由能量守恒定律可得
≡P/ρ. 按照Yang(2005a)的推导,由能量守恒定律可得
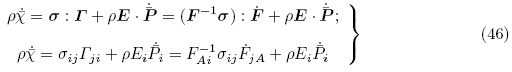
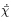 (F;
(F; 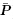 ),有
),有
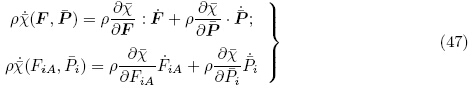
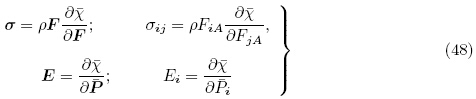
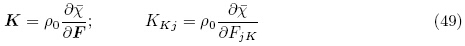
可通过对电学变量的勒让德变换定义能量密度函数ψ(F,E)为


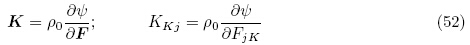
对于能量密度函数ψ(F,E),当利用关系式(17)1 时,可以等效地将能量密度函数ψ(F,E)看作F和ε的函数(Dorfmann & Ogden,2005),即
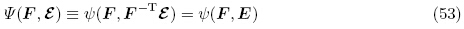

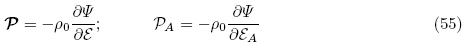
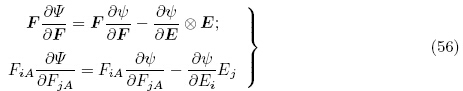

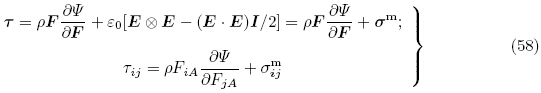
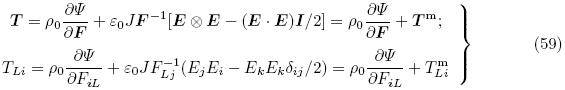


当利用关系式(4)1和(6)时,可以等效地将能量密度函数Ψ(F, ε)看作G和ε的函数 (G,ε),这样由式(4)1和(6)并利用链式求导法则可得两个能量密度函数Ψ(F, ε)和
(G,ε),这样由式(4)1和(6)并利用链式求导法则可得两个能量密度函数Ψ(F, ε)和 (G, ε)之间的关系为(Holzapfel 2000,Yang 2005a)
(G, ε)之间的关系为(Holzapfel 2000,Yang 2005a)
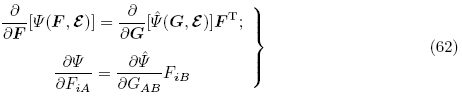

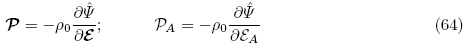

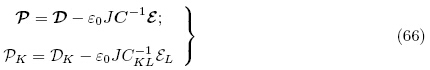
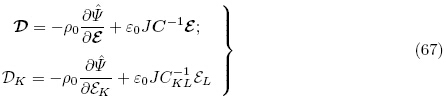
按照和DorfmannOgden(2005,2006)的推导方法引进以下增广能量密度函数Ω(F,ε)(augmented free energy density function)
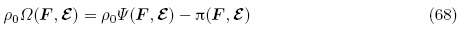
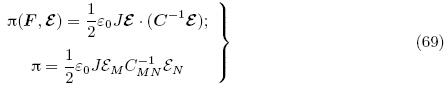
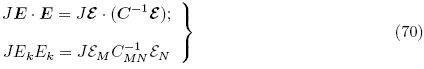
以下等式恒成立(Yang 2005a,Holzapfel 2000)
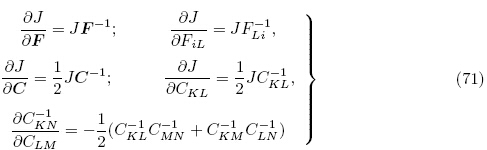
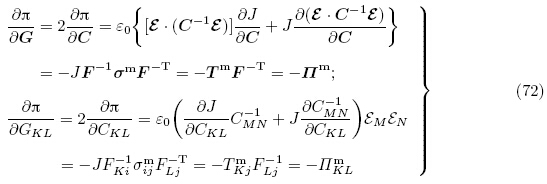

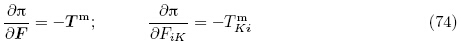

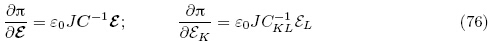
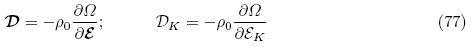
当将增广能量密度函数Ω(F,ε)中的独立变量F利用关系式(4)1和(6)变成G时,定义能量密度函数为 (G,ε),Yang(2005a)称其为总能量密度函数(total energydensity function),即
(G,ε),Yang(2005a)称其为总能量密度函数(total energydensity function),即
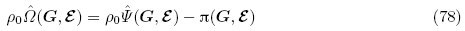
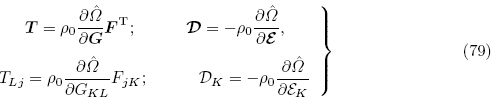
 (G,ε)表示的本构方程. 另外,由式(43),(78)和(79)2 可得
(G,ε)表示的本构方程. 另外,由式(43),(78)和(79)2 可得

最后,按照和DorfmannOgden(2005,2006),如果取拉格朗日形式的电位移矢量D作为独立的电学变量,那么通过对电学变量的勒让德变换可定义新的能量密度函数Ω*(F,D)为

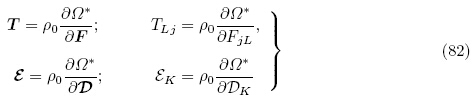
 *(G,D)如下
*(G,D)如下
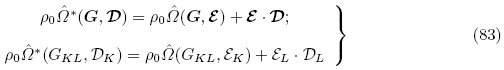

DorfmannOgden(2005,2006)指出,如果选择ε作为独立的电学变量,那么通过式(17)1 由ε计算得到的E必须满足式curlE = 0,然后通过本构方程式(77)或(79)2 得到对应D的拉格朗日电位移矢量D. 反过来,利用式(17)2 得到的电位移矢量D则必须满足方程式divD = ρe,对于给定的变形,此方程的满足可能会对能量密度函数Ω或 的形式施加某种限制条件.
的形式施加某种限制条件.
如果选择D作为独立的电学变量,那么通过式(17)2 由D计算得到的D必须满足式divD = ρe,然后通过本构方程式(82)2 或(84)2 得到对应E 的拉格朗日电场矢量ε. 反过来,利用式(17)1 得到的电场矢量E则必须满足方程式curlE = 0,同样地,依赖于给定的变形,此方程的满足可能会对能量密度函数Ω*或 * 的形式施加某种限制条件.
* 的形式施加某种限制条件.
总之,不同的能量密度函数所对应的独立力学变量和电学变量是不同的,从而根据能量密度函数所直接获得的功共轭力学因变量和电学因变量也是不同的,最终导致了本构方程形式的多样性. 但必须强调的是,如果所推导的本构方程式都是正确的,那么它们之间应该是等价的,可以通过相应的勒让德变换实现相互之间的转换. 表1给出了本节所提到的以不同力学变量和电学变量为独立自变量的能量密度函数,以及对应于不同能量密度函数中的力学变量和电学变量的功共轭力学因变量和电学因变量.
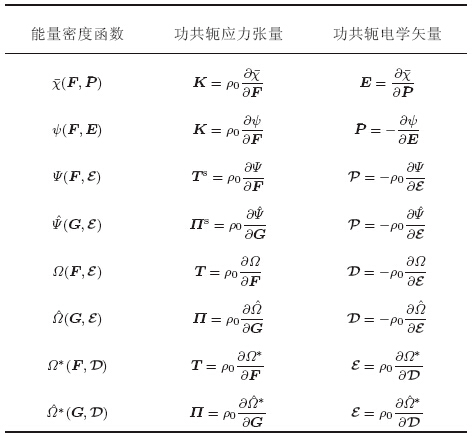 |
非线性电弹性体具体的本构关系必须通过给定能量密度函数如 (G,ε),Ω*(F,D),
(G,ε),Ω*(F,D), (G, ε)等的数学表达式而求出. 如果仅考虑电弹性材料的弱非线性(如压电陶瓷等脆性压电材料),可以将能量密度函数对其自变量在自然构型附近取泰勒展开近似.Baumhauer和Tiersten(1972),Tiersten(1981)和Yang(2005a)取能量密度函数为
(G, ε)等的数学表达式而求出. 如果仅考虑电弹性材料的弱非线性(如压电陶瓷等脆性压电材料),可以将能量密度函数对其自变量在自然构型附近取泰勒展开近似.Baumhauer和Tiersten(1972),Tiersten(1981)和Yang(2005a)取能量密度函数为 (G, ε),相应的多项式展开为
(G, ε),相应的多项式展开为
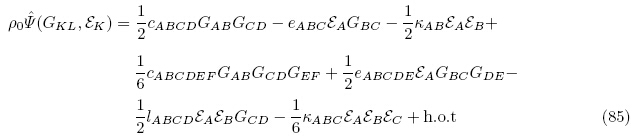
而Liu 等(2003a)选取能量密度函数为总能量密度函数 (G, ε),其多项式展开为
(G, ε),其多项式展开为
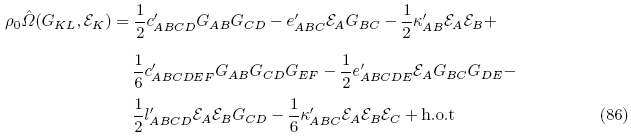
当不考虑偏场的影响且只考虑无限小应变和小电场变量时,对于极性材料(即非中心对称材料),能量密度函数依赖于电场方向的改变,因此能量密度函数必须保留电场变量的线性项,此时式(85)变成
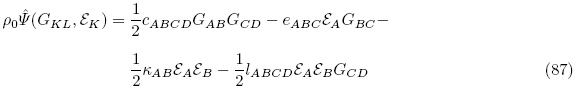
对于非极性材料(即中心对称材料),能量密度函数不依赖于电场的方向,因此能量密度函数中的每一项都应该是电场变量的偶函数,此时式(87)变成
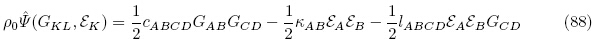
 (G,ε).
(G,ε).
此外,Suo 等(2008)取电场变量为电位移矢量,对能量密度函数 *(G,D)进行泰勒级数展开同样给出了无限小应变和小电位移近似下描述线性压电材料和电致伸缩材料的应变能函数形式,这里不再赘述.
*(G,D)进行泰勒级数展开同样给出了无限小应变和小电位移近似下描述线性压电材料和电致伸缩材料的应变能函数形式,这里不再赘述.
具有力电耦合特性的软材料(如介电高弹体)在电场作用下能产生大变形,呈现出较强的非线性,因此能量密度函数的形式较为复杂. 对于力柔性但电刚性材料(mechanically compliant but electrically stiff material),Suo 等(2008)建议了能量密度函数 *(G,D)的如下形式
*(G,D)的如下形式

 0*(G),αA(G)和βAB(G)是应变张量G的函数,可通过拟合实验数据得到. 式(89)可用于描述软电弹性体承受大变形但只考虑适度的电位移大小的响应,因此能量密度函数
0*(G),αA(G)和βAB(G)是应变张量G的函数,可通过拟合实验数据得到. 式(89)可用于描述软电弹性体承受大变形但只考虑适度的电位移大小的响应,因此能量密度函数 *(G,D)只保留到电位移矢量的二次项. 对于非极性材料,电位移矢量的线性项为零,即αA(G)= 0; 对于极性材料,αA(G)≠0.
*(G,D)只保留到电位移矢量的二次项. 对于非极性材料,电位移矢量的线性项为零,即αA(G)= 0; 对于极性材料,αA(G)≠0.  0*(G)是不存在电场时的弹性应变能函数,其形式可根据客观性原理及材料的对称性利用张量表示定理给出. Smith等(1963),Spencer(1971)以及Zheng(1994)对所有晶体材料的对称张量和矢量的标量值函数的基矢集已经进行了详细研究. 对于各向异性弹性固体材料对称性的讨论,读者也可参考Holzapfel(2000)和Ogden(1997)等专著. 例如,对于各向同性电弹性材料,
0*(G)是不存在电场时的弹性应变能函数,其形式可根据客观性原理及材料的对称性利用张量表示定理给出. Smith等(1963),Spencer(1971)以及Zheng(1994)对所有晶体材料的对称张量和矢量的标量值函数的基矢集已经进行了详细研究. 对于各向异性弹性固体材料对称性的讨论,读者也可参考Holzapfel(2000)和Ogden(1997)等专著. 例如,对于各向同性电弹性材料, 0*(G)是3 个应变张量不变量的函数,具体的应变能函数的形式可参考Holzapfel(2000). 而电刚度张量(或介电张量)βAB(G)在各向同性条件下可写成
0*(G)是3 个应变张量不变量的函数,具体的应变能函数的形式可参考Holzapfel(2000). 而电刚度张量(或介电张量)βAB(G)在各向同性条件下可写成
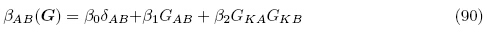
对于电柔性但力刚性材料(electrically compliant but mechanically stiff material),Suo等(2008)也给出了能量密度函数 *(G,D)的形式,此时的应变能函数普遍用于描述铁电材料,详细的讨论可参考Lines和Glass(1977),这里不再赘述.
*(G,D)的形式,此时的应变能函数普遍用于描述铁电材料,详细的讨论可参考Lines和Glass(1977),这里不再赘述.
其次,DorfmannOgden(2005,2006)利用式(4)1,将能量密度函数Ω(F,ε)看作对称二阶张量C和矢量ε的函数,也考虑了各向同性电弹性材料. 他们指出,各向同性电弹性材料中的电场矢量ε与自然构型Br 下横观各向同性弹性材料对称轴方向的单位矢量所扮演的角色类似,差别仅在于电场ε 一般不是单位矢量,因此除了与横观各向同性相关的两个不变量以外,电场ε还产生了额外的一个不变量. 故从本构观点来看,各向同性电弹性材料与经典横观各向同性弹性材料有许多相同之处. 因此Ω(F,ε)是张量C和ε⊗ε的各向同性函数,具体依赖于以下6 个C和ε⊗ε的联合不变量.
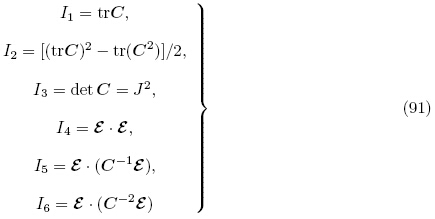

另外,Bustamante(2009)在非线性连续介质理论框架下考虑了横观各向同性的电弹性材料. 若以电场矢量ε作为独立的电学变量,则能量密度函数取为Ω(F, ε, α0),其中,α0代表横观各向同性电弹性材料在自然构型Br 下的对称轴方向的单位矢量,则|α0|=1. Ψ具体依赖于以下10 个不变量
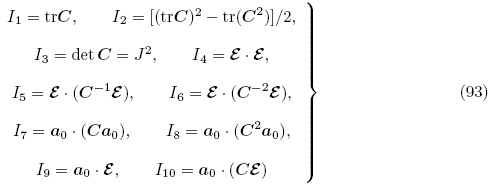
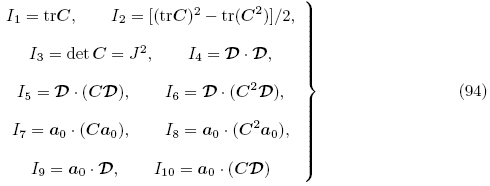
最后,特别值得一提的是,为描述软电弹性体的非线性力电耦合响应,能量密度函数实际形式的选择也是十分关键的问题. 正如Dorfmann和Ogden(2006)所指出的,具体形式的应变能函数的功效需要从多方面去考察,包括与控制方程性质有关的数学特征,稳定性不等式(如强椭圆性条件)的满足,以及从实验解释方面看数据边际效应的影响等等. 附录B 列举了文献中建议的一些各向同性软电弹性体能量密度函数的具体形式.
2.7 外场方程假设电弹性体外部空间为真空,则外部空间的电场方程为
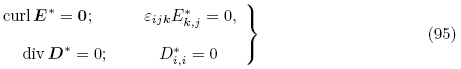

对于真空,由式(58)可知总应力张量τ 仅仅是真空中的Maxwell 应力张量τ*
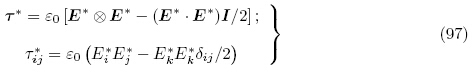

对于电弹性体材料的一般边值问题,在本构方程确定之后,还需在边界上给定电学量E和D 以及力学量τ(或σ)和y所满足的适当条件.
对于电弹性体在现时构型下的边界∂B,电场E和电位移D所满足的电学边界条件为(Kovetz 2000)


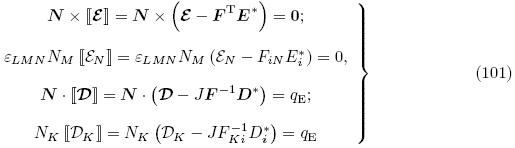

利用总应力张量τ,作用于现时构型B上微元面积的表面力矢量为τTnda. 如果ta 是施加于现时构型边界∂B上单位面积的机械表面力矢量,则电弹性体内总应力张量τ 所满足的力学边界条件为


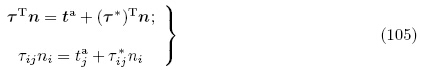
由于总应力张量τ 与类Cauchy 应力张量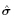 之间的关系为
之间的关系为

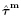 m为式(23)中对应于类Cauchy 应力张量
m为式(23)中对应于类Cauchy 应力张量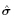 的Maxwell 应力张量. 正如Busta-mante 等(2009a)所述,不同的类Cauchy 应力张量
的Maxwell 应力张量. 正如Busta-mante 等(2009a)所述,不同的类Cauchy 应力张量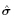 所满足的力学边界条件也是不同的. 利用式(105)和(106)可得
所满足的力学边界条件也是不同的. 利用式(105)和(106)可得

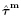 m分别是从电弹性体外部和内部在边界∂B 上进行计算的. 特别地,对应于式(28)中的类Cauchy 应力σ,电场体力和电弹性体内部的Maxwell 应力张量
m分别是从电弹性体外部和内部在边界∂B 上进行计算的. 特别地,对应于式(28)中的类Cauchy 应力σ,电场体力和电弹性体内部的Maxwell 应力张量 m= τe 的表达式分别为式(25)和式(27). 一般地,此Maxwell 应力τe 是非对称的,但是电弹性体外部的Maxwell 应力τ*却是对称的.当不考虑表面自由电荷密度时,利用式(27),(97)和式(100),可以得到由于电弹性体内部与外部Maxwell 应力的不同所产生的表面力矢量为
m= τe 的表达式分别为式(25)和式(27). 一般地,此Maxwell 应力τe 是非对称的,但是电弹性体外部的Maxwell 应力τ*却是对称的.当不考虑表面自由电荷密度时,利用式(27),(97)和式(100),可以得到由于电弹性体内部与外部Maxwell 应力的不同所产生的表面力矢量为


Baesu 等(2003)也获得了对应于类Cauchy 应力张量σ 所满足的边界条件,见该论文的公式(2.7),但是他们没有考虑到电弹性体内部与外部Maxwell 应力的不同所产生的表面力矢量的不同,即忽略了式(108). 最近,Rinaldi和Brenner(2002)从物理角度指出了不同的电磁体力和Maxwell 应力张量的差别,从而认为把电磁体力处理成Maxwell 应力可能会导致不正确的物理结果. 但是,Bustamante 等(2009a)指出Rinaldi和Brenner(2002)的分析过程是有缺陷的,因为后者并没有注意到不同的应力张量所需满足的边界条件一般是不同的. 例如,对比式(105)和式(109),可以看到总应力张量τ和类Cauchy 应力张量σ 所满足的边界条件是有区别的.
利用Nanson 公式(8)和式(30),总应力张量τ 所满足的面力边界条件(103)可以用拉格朗日形式写成



如果构型边界∂B 上的一部分受到空间约束或者给定运动形式y*,那么力学边界条件为

对于动力学或初边值问题,当然还需要给定电弹性体的初始条件,通常情况下是赋予初始位移和初始速度.
3 电弹性体偏场理论的增量线性方程在许多实际应用中,由电弹性材料构成的多功能力电耦合系统通常会受到偏场的作用,如残余应力或预应力、预拉伸、预加电场等. 本文仅限于考虑静态偏场. 对于某些偏场作用下的力学问题,电弹性体可通过以下两步达到最终状态: 一是在初始偏场作用下产生有限静态变形和有限电场; 二是在偏场之上叠加静态或动态的小增量场. 在此情况下,可以通过求解一系列线性偏微分方程而得到电弹性体的最终状态,只不过方程的系数(即所谓的有效材料常数)与初始变形和电场有关,这就是偏场方法(Yang & Hu,2004). 许多工程技术中非常重要的问题都可以利用这一方法来进行处理和分析.
3.1 电弹性体偏场理论的3 种构型
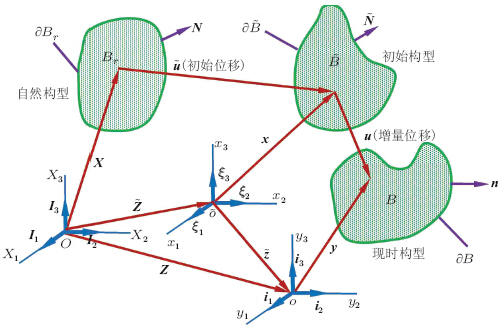
本小节我们将主要按照Tiersten(1981,1995),Yang和Hu(2004)以及Yang(2005a)的方法,通过如图 2所示的3 个构型来考虑电弹性体叠加于有限偏场之上的小增量场问题. 这里,3 个构型坐标系的选取可以不同,Z,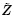 和
和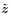 分别表示现时构型坐标系原点相对于自然构型坐标系原点的位置矢量、初始构型坐标系原点相对于自然构型坐标系原点的位置矢量和现时构型坐标系原点相对于初始构型坐标系原点的位置矢量.
分别表示现时构型坐标系原点相对于自然构型坐标系原点的位置矢量、初始构型坐标系原点相对于自然构型坐标系原点的位置矢量和现时构型坐标系原点相对于初始构型坐标系原点的位置矢量.
|
| 图2 电弹性体的自然构型、初始构型和现时构型 |
(1)自然构型Br. 物体在此构型下未发生变形而且不受电场作用,边界∂Br上任意点的单位外法向矢量为N. 自然构型中物质点的位置矢量用X=XKIK 表示,自然构型坐标系原点为O,基矢量为IK. 此构型下电弹性体的质量密度为ρ0.
(2)初始构型 . 此时电弹性体受到有限静电场作用,并且发生了有限静态变形,称这种预加的变形和电场为偏场. 边界∂
. 此时电弹性体受到有限静电场作用,并且发生了有限静态变形,称这种预加的变形和电场为偏场. 边界∂ . 上任意点的单位外法向矢量为Ñ,微元面积为dÃ. 电弹性体由Br到
. 上任意点的单位外法向矢量为Ñ,微元面积为dÃ. 电弹性体由Br到 的静态变形用x = x(X)= xγξγ 描述,xγ 表示任意物质点的初始坐标,基矢量ξγ是沿着坐标xγ 的单位矢量,坐标原点为õ,这里我们采用希腊字母下标表示与初始构型
的静态变形用x = x(X)= xγξγ 描述,xγ 表示任意物质点的初始坐标,基矢量ξγ是沿着坐标xγ 的单位矢量,坐标原点为õ,这里我们采用希腊字母下标表示与初始构型 有关的物理量分量. 另外,我们用置于物理量顶部的“~” 符号表示初始构型
有关的物理量分量. 另外,我们用置于物理量顶部的“~” 符号表示初始构型 下的场变量,即对应于x = x(X)的变形梯度张量为
下的场变量,即对应于x = x(X)的变形梯度张量为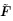 = Grad(x)和
= Grad(x)和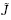 = det
= det 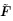 . 由于所考虑的偏场为静态偏场,此时所有的场变量都与时间t 无关,因此所有的场变量满足前一节所讨论的静态非线性电弹性力学方程
. 由于所考虑的偏场为静态偏场,此时所有的场变量都与时间t 无关,因此所有的场变量满足前一节所讨论的静态非线性电弹性力学方程

(3)现时构型B. 在初始构型 上再叠加与时间t 相关的小增量变形和电场,即可获得现时构型,此时边界∂B上任意点的单位外法向矢量为n. 物质点X 的最终位置由y= y(X, t)= ykik 确定,现时构型的坐标系原点为o,基矢量为ik. 令F(X, t)= Grad(y)表示电弹性体从自然构型Br 到现时构型B 的变形梯度张量,且J = detF(X, t).由于增量场是动态的,因此所有的场变量应满足前一节所给出的非线性电弹性体动力学方程
上再叠加与时间t 相关的小增量变形和电场,即可获得现时构型,此时边界∂B上任意点的单位外法向矢量为n. 物质点X 的最终位置由y= y(X, t)= ykik 确定,现时构型的坐标系原点为o,基矢量为ik. 令F(X, t)= Grad(y)表示电弹性体从自然构型Br 到现时构型B 的变形梯度张量,且J = detF(X, t).由于增量场是动态的,因此所有的场变量应满足前一节所给出的非线性电弹性体动力学方程
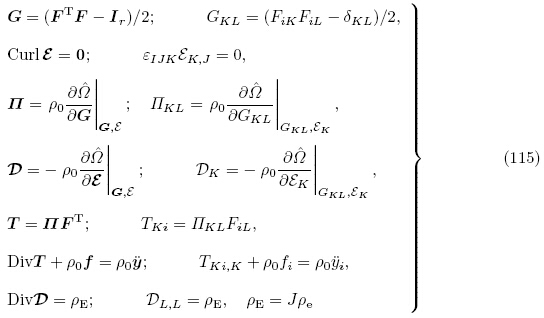
 (G, ε).
3.2 偏场理论的拉格朗日描述
3.2.1 基于$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Omega }$(G, ε)和Ω(F,ε)的拉格朗日描述
(G, ε).
3.2 偏场理论的拉格朗日描述
3.2.1 基于$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Omega }$(G, ε)和Ω(F,ε)的拉格朗日描述
按照Tiersten(1981,1995)和Yang(2005a)的方法,本小节将首先推导用总能量密度函数 (G, ε)表示的拉格朗日描述下的电弹性体偏场理论的增量线性方程. 令拉格朗日描述下的增量位移矢量和增量电场矢量分别为u(X, t)和
(G, ε)表示的拉格朗日描述下的电弹性体偏场理论的增量线性方程. 令拉格朗日描述下的增量位移矢量和增量电场矢量分别为u(X, t)和 (X, t),如图 2所示,并且认为u(X, t)和
(X, t),如图 2所示,并且认为u(X, t)和 (X, t)无限小,这里我们强调增量电场矢量
(X, t)无限小,这里我们强调增量电场矢量 (X, t)为拉格朗日描述,则
(X, t)为拉格朗日描述,则

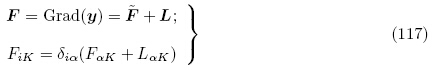
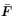 为
为
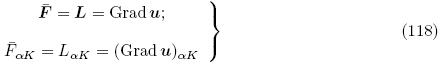
由于u(X, t)和 (X, t)无限小,可忽略L和
(X, t)无限小,可忽略L和 的二阶及以上项,由式(114)1,(115)1和式(117)可得
的二阶及以上项,由式(114)1,(115)1和式(117)可得

 为
为

 满足
满足

由于Π(G,ε)和D(G,ε)是格林-拉格朗日应变张量G和拉格朗日形式的电场矢量ε的函数,且增量物理量为小量,故可将Π(G,ε)和D(G,ε)对G和ε在初始应变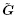 和初始电场
和初始电场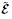 处进行Taylor 级数展开,略去
处进行Taylor 级数展开,略去 和
和 的二阶及以上项,利用式(114)3,4,(115)3,4,(116)2和(119)可得
的二阶及以上项,利用式(114)3,4,(115)3,4,(116)2和(119)可得
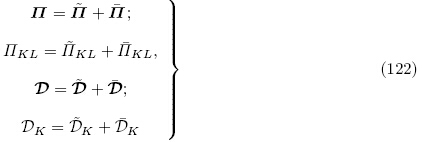
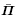 和增量电位移矢量
和增量电位移矢量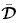 为
为
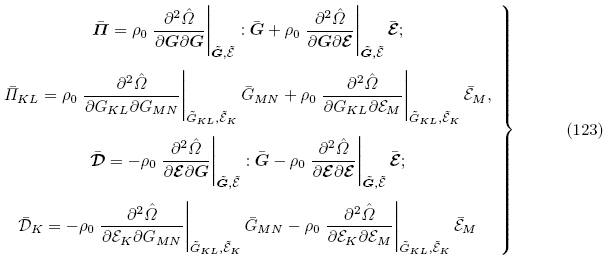
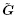 ,
,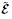 ” 表示总能量密度函数
” 表示总能量密度函数 的二阶偏导数在初始值
的二阶偏导数在初始值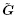 和
和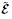 处的值. 因此,由式(114)5,(115)5,(117)和式(122)1 可得
处的值. 因此,由式(114)5,(115)5,(117)和式(122)1 可得

 为
为
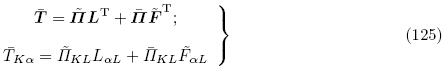


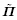 的对称性可得拉格朗日描述下的增量本构方程为
的对称性可得拉格朗日描述下的增量本构方程为
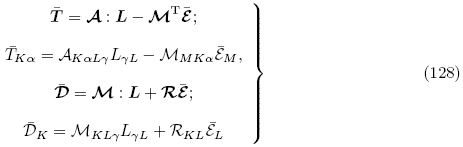
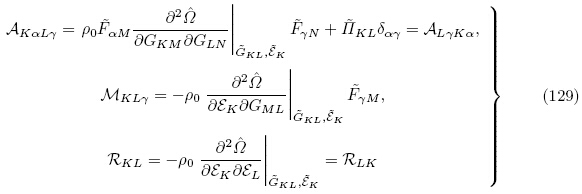
 点积就是M的第一个基矢量与
点积就是M的第一个基矢量与 的基矢量进行点积,指标记法为MMKα
的基矢量进行点积,指标记法为MMKα M.
M.
由于现时构型B下的T和D分别满足式(115)6,7,而初始构型 下的偏场满足式(114)6,7,注意到式(116)1 以及初始场变量与时间t 无关,则两式对应相减可得
下的偏场满足式(114)6,7,注意到式(116)1 以及初始场变量与时间t 无关,则两式对应相减可得 和
和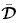 所满足的场方程为
所满足的场方程为
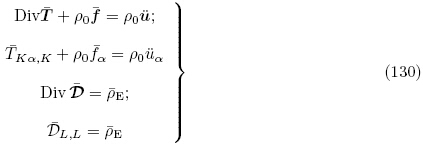
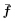 和增量自由电荷体密度
和增量自由电荷体密度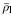 E 满足
E 满足
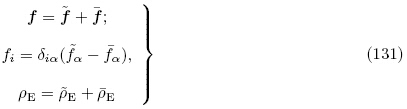
式(128)~(131)即为Yang(2005a)所获得的用总能量密度函数 (G,ε)表示的拉格朗日描述下的增量线性方程. 式(128)中的A,M和R 分别是有效弹性常数、有效压电常数和有效介电常数. 拉格朗日描述下的第一类PK 增量应力张量
(G,ε)表示的拉格朗日描述下的增量线性方程. 式(128)中的A,M和R 分别是有效弹性常数、有效压电常数和有效介电常数. 拉格朗日描述下的第一类PK 增量应力张量 和增量电位移矢量
和增量电位移矢量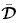 线性依赖于相对于自然构型Br的增量位移梯度L和增量电场
线性依赖于相对于自然构型Br的增量位移梯度L和增量电场 . 由式(129)可知,有效材料常数与初始变形
. 由式(129)可知,有效材料常数与初始变形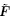 (或
(或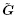 )和初始电场
)和初始电场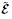 有关. 需要强调的是,即使所讨论的材料是线性的,即只含基本材料常数,式(128)中的有效材料常数仍然会随着偏场变化而变化. 一般来说,有效材料常数的对称性比基本的线弹性、压电和介电常数的对称性要低,这种情况称为偏场导致的各向异性(Yang 2005a). 在各向异性情况下,A 可以有45个独立分量,M可以有27个独立分量,而R可以有6个独立分量.由于有效材料常数对偏场的依赖性,一般来说有效材料常数是随位置变化而变化的(除非所施加的偏场为均匀偏场),这将导致对应问题求解的复杂性.
有关. 需要强调的是,即使所讨论的材料是线性的,即只含基本材料常数,式(128)中的有效材料常数仍然会随着偏场变化而变化. 一般来说,有效材料常数的对称性比基本的线弹性、压电和介电常数的对称性要低,这种情况称为偏场导致的各向异性(Yang 2005a). 在各向异性情况下,A 可以有45个独立分量,M可以有27个独立分量,而R可以有6个独立分量.由于有效材料常数对偏场的依赖性,一般来说有效材料常数是随位置变化而变化的(除非所施加的偏场为均匀偏场),这将导致对应问题求解的复杂性.
Ogden(2009)同样推导获得了拉格朗日描述下叠加在与时间无关有限变形和电磁场之上的小增量运动和增量电磁场的控制方程,但他没有使用三构型的描述方式,而是直接在初始构型上施加小的摄动以代表叠加于有限偏场之上的小增量运动. 另外,Ogden(2009)所使用的能量密度函数为增广能量密度函数Ω(F, ε). 当不考虑磁场作用且电场为准静态时,Ogden(2009)获得的增量电场变量 和
和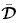 的控制方程和增量应力张量
的控制方程和增量应力张量 的控制方程与式(121),(130)2和(130)1 相同,而其获得的增量本构方程式(68)和(69)用本文的符号可表示为
的控制方程与式(121),(130)2和(130)1 相同,而其获得的增量本构方程式(68)和(69)用本文的符号可表示为
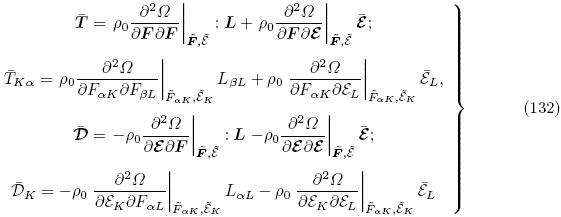
需指出的是,Ogden(2009)文中的L表示相对于初始构型 的增量位移梯度张量,即gradxu,而本文的L表示相对于自然构型Br 的增量位移梯度张量,即Gradu. Suo等(2008)通过在初始构型上施加小的摄动也推导获得了用增广能量密度函数Ω(F, ε)表示的拉格朗日描述下的增量本构方程(132).
的增量位移梯度张量,即gradxu,而本文的L表示相对于自然构型Br 的增量位移梯度张量,即Gradu. Suo等(2008)通过在初始构型上施加小的摄动也推导获得了用增广能量密度函数Ω(F, ε)表示的拉格朗日描述下的增量本构方程(132).
下面我们将利用指标记法来推导证明式(132)与式(128),(129)是等价的. 对于变形梯度张量F,有


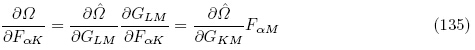
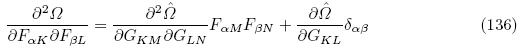

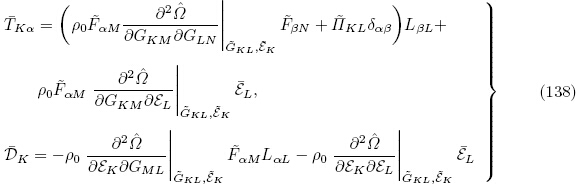
对比式(138)与式(128),(129)可以看出拉格朗日描述下的增量本构方程(132)与增量本构方程(128)和(129)等价,这表明Ogden(2009)和Suo 等(2008)获得的增量本构方程与Yang(2005a)获得的增量本构方程本质上是相同的,区别仅在于Ogden(2009)和Suo 等(2008)选取的能量密度函数为增广能量密度函数Ω(F, ε),其力学独立变量为变形梯度张量F,而Yang(2005a)选取的能量密度函数为总能量密度函数 (G, ε),以格林-拉格朗日应变张量G 为力学独立变量. 上述两个能量密度函数之间的关系通过式(4)1和(6)联系起来.
(G, ε),以格林-拉格朗日应变张量G 为力学独立变量. 上述两个能量密度函数之间的关系通过式(4)1和(6)联系起来.
由于在本构方程(114)3,4和(115)3,4中,选取了能量密度函数为总能量密度函数 (G, ε),因此所获得的拉格朗日描述下的增量本构方程(128)和(129)是用总能量密度函数
(G, ε),因此所获得的拉格朗日描述下的增量本构方程(128)和(129)是用总能量密度函数 (G, ε)表示的. 事实上,按照2.4和2.5 小节的描述,我们也可以选取其他的能量密度函数. Tiersten(1981)和Yang(2005a)选取能量密度函数为
(G, ε)表示的. 事实上,按照2.4和2.5 小节的描述,我们也可以选取其他的能量密度函数. Tiersten(1981)和Yang(2005a)选取能量密度函数为 (G, ε),利用本构方程(65)和(67),类似于增量本构方程(128)和(129)的推导,获得了以
(G, ε),利用本构方程(65)和(67),类似于增量本构方程(128)和(129)的推导,获得了以 (G, ε)表示的拉格朗日描述下的增量本构方程.
(G, ε)表示的拉格朗日描述下的增量本构方程.  (G, ε)与
(G, ε)与 (G, ε)之间的关系见式(78).
(G, ε)之间的关系见式(78).
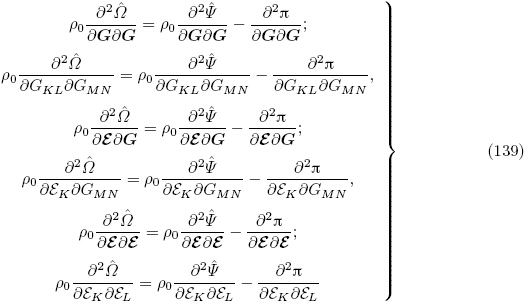
下面从另一个角度即直接从增量本构方程(128)和(129)出发推导Tiersten(1981)和Yang(2005a)所获得的以 (G, ε)表示的增量本构方程. 由式(80)可得
(G, ε)表示的增量本构方程. 由式(80)可得
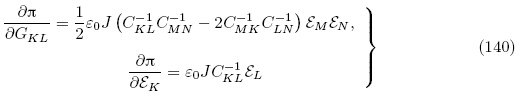
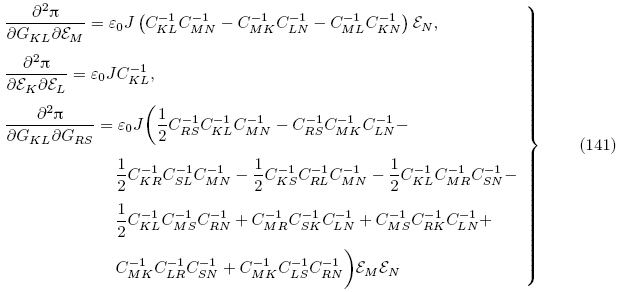


 上
上

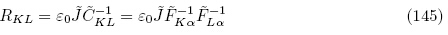
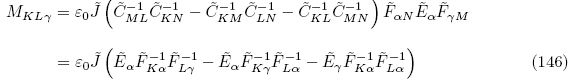
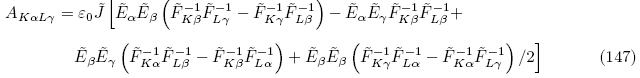
式(128),(142)和式(145)~(147)即为Tiersten(1981)和Yang(2005a)所获得的以能量密度函数 (G, ε)表示的拉格朗日描述下的增量本构方程. 可见,虽然能量密度函数
(G, ε)表示的拉格朗日描述下的增量本构方程. 可见,虽然能量密度函数 (G, ε)和
(G, ε)和 (G, ε)是不同的,即相差一个对应真空介质的电场能量密度π(G, ε);并且对于
(G, ε)是不同的,即相差一个对应真空介质的电场能量密度π(G, ε);并且对于 (G, ε),G 与Π功共轭,而对于
(G, ε),G 与Π功共轭,而对于 (G, ε)G 与Πs 功共轭,但基于
(G, ε)G 与Πs 功共轭,但基于 (G, ε)和
(G, ε)和 (G,ε)所得到的拉格朗日描述下的增量本构方程本质上是等价的,所定义的有效材料常数也相同,只是其表达形式不一样,见式(129)和式(142).
(G,ε)所得到的拉格朗日描述下的增量本构方程本质上是等价的,所定义的有效材料常数也相同,只是其表达形式不一样,见式(129)和式(142).
另外,Dorfmann和Ogden2010a,(2010b)选取拉格朗日形式的电位移矢量D 作为独立的电学变量定义能量密度函数为Ω*(F,D),获得了用Ω*(F,D)表示的拉格朗日描述下的增量线性方程. 当能量密度函数为Ω*(F,D)时,电弹性体本构方程为式(82),其自变量为F和D,因变量为T和ε. 由于T(F,D)和ε(F,D)是F和D的函数,故可将T(F,D)和ε(F,D)对F和D在初始状态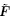 和
和 处进行Taylor 级数展开,略去增量
处进行Taylor 级数展开,略去增量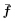 和
和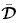 的二阶及以上项,由式(82)可得
的二阶及以上项,由式(82)可得 和
和 所满足的拉格朗日描述下的增量本构方程为
所满足的拉格朗日描述下的增量本构方程为
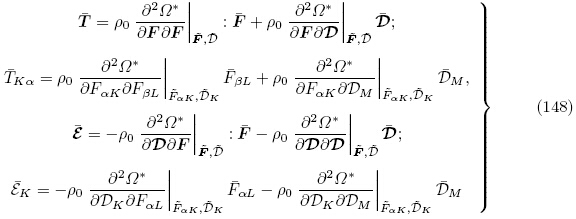
类似地,利用式(84)可以获得以能量密度函数 *(G,D)表示的拉格朗日描述下的增量本构方程.
*(G,D)表示的拉格朗日描述下的增量本构方程.
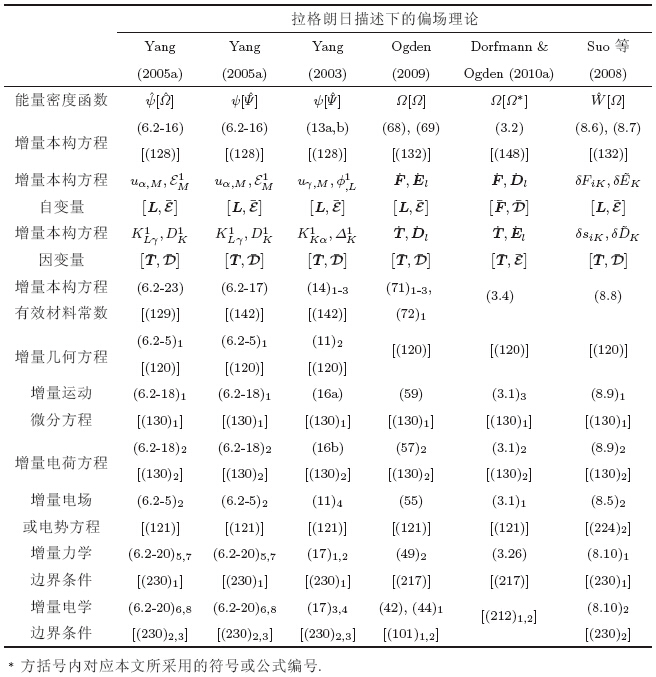
为方便读者查阅和比较,表 2 对不同文献中拉格朗日描述下的偏场理论进行了整理,给出了多种形式的偏场理论的增量控制方程和增量边界条件,并对比了不同文献中所定义的符号与本文定义的符号. 具体地,表 2 给出了不同文献中能量密度函数,增量本构方程及其自变量、因变量和有效材料常数,增量几何和电场或电势方程,增量运动微分方程和增量电荷方程,增量力学和电学边界条件的定义及控制方程式. 表 2 方括号内的符号和号码分别是本文所采用的符号与公式编号. 从表 2 可以看出,偏场理论可选取不同的能量密度函数来表述,而由表 1 可知不同的能量密度函数可能对应着不同的独立力学变量和电学变量,从而根据能量密度函数所直接获得的功共轭力学因变量和电学因变量也是不同的,这是导致增量本构方程形式及其自变量、因变量和有效材料常数形式不同的根本原因. 但必须强调的是,不同的能量密度函数之间是可以相互转换的,因此所获得的拉格朗日描述下的增量本构方程本质上也是等价的,所定义的有效材料常数也可以进行相互转换,只是其表达形式不一样. 另外,由表 2 可以看出,有些文献在增量力学和电学边界条件中未考虑外电场的影响(Yang 2003,2005a;Suo et al. 2008),而有些文献则考虑了外电场的影响(Ogden 2009,Dorfmann & Ogden2010a). 在某些情形下,外电场的影响可能不可忽略(苏益品& 陈伟球2014).
 |
上一小节给出了电弹性体偏场理论拉格朗日描述下的线性增量方程,但是在很多实际问题中,偏场状态已经存在,因此初始构型 是已知的,推导更新拉格朗日描述(updated Lagrangian description)下电弹性体偏场理论的线性增量方程就显得十分有必要. Baseu 等(2003),Yang(2009),Ogden(2009),Dorfmann和Ogden2010a,(2010b),Baumhauer和Tiersten(1972),以及Chai和Wu(1996)都获得了电弹性体偏场作用下更新拉格朗日描述的线性增量方程. 本节将推导证明以上文献中的线性增量方程相互之间都是等价的.
是已知的,推导更新拉格朗日描述(updated Lagrangian description)下电弹性体偏场理论的线性增量方程就显得十分有必要. Baseu 等(2003),Yang(2009),Ogden(2009),Dorfmann和Ogden2010a,(2010b),Baumhauer和Tiersten(1972),以及Chai和Wu(1996)都获得了电弹性体偏场作用下更新拉格朗日描述的线性增量方程. 本节将推导证明以上文献中的线性增量方程相互之间都是等价的.
本小节我们将利用Baesu 等(2003)的方法定义更新拉格朗日描述下的场变量和增量. 取电弹性体的初始构型 为参考构型,用下标“0” 表示更新拉格朗日描述下的场变量和增量,并且用gradx,divx和curlx 表示相应于初始构型
为参考构型,用下标“0” 表示更新拉格朗日描述下的场变量和增量,并且用gradx,divx和curlx 表示相应于初始构型 的微分算符. 因此,有
的微分算符. 因此,有

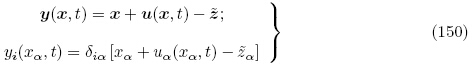

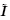 为初始构型
为初始构型 下的二阶单位张量,其分量为Kronecker 符号δαβ. 由于初始构型
下的二阶单位张量,其分量为Kronecker 符号δαβ. 由于初始构型 和现时构型B 相对于自然构型Br 的变形梯度张量分别为
和现时构型B 相对于自然构型Br 的变形梯度张量分别为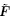 = Grad(x)和F= Grad(y),因此由式(149)和式(151)可得
= Grad(x)和F= Grad(y),因此由式(149)和式(151)可得
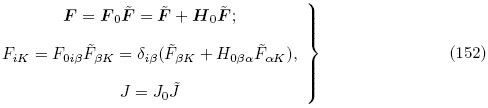
 (X, t)不同,用e = e(x,t)表示初始电场
(X, t)不同,用e = e(x,t)表示初始电场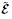 的小增量电场矢量,则现时构型B 状态下的电场为
的小增量电场矢量,则现时构型B 状态下的电场为

假设增量场H0和e无限小,忽略H0和e的二阶及以上项,有

式中,“tr” 表示二阶张量的迹,即trH0= H0αα. 因H0= gradxu 表示相对于初始构型 的增量位移梯度张量,而L = Gradu 表示相对于自然构型Br 的增量位移梯度张量,它们之间有如下关系
的增量位移梯度张量,而L = Gradu 表示相对于自然构型Br 的增量位移梯度张量,它们之间有如下关系



 表示为
表示为
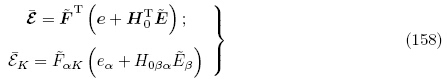
为方便起见,我们总结式(17),(30)和(36)如下
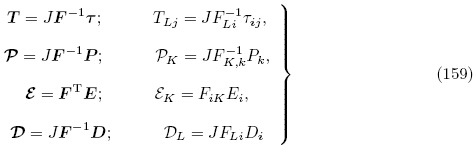
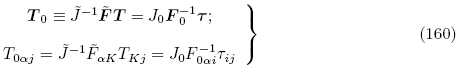
 时T 的值,因此,T0 被称为更新的拉格朗日场变量(updated Lagrangian ˉeld variables). 类似地,由式(159)2,3,4 并利用式(152),可定义更新拉格朗日描述下的电场极化矢量P0、电场矢量E0和电位移矢量D0 分别为
时T 的值,因此,T0 被称为更新的拉格朗日场变量(updated Lagrangian ˉeld variables). 类似地,由式(159)2,3,4 并利用式(152),可定义更新拉格朗日描述下的电场极化矢量P0、电场矢量E0和电位移矢量D0 分别为

当不存在增量场时,F0 = I0,J0 = 1. 因此对应于t = 0 时刻,由式(160)和(161)有

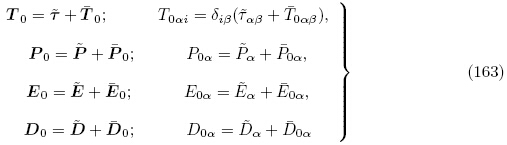
 0,
0,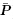 0,
0, 0和
0和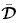 0 分别是对应于T0,P0,E0和D0 的增量. 另外,总结式(116),(122)和(124)并定义P的增量
0 分别是对应于T0,P0,E0和D0 的增量. 另外,总结式(116),(122)和(124)并定义P的增量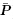 如下
如下
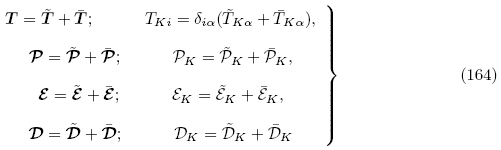
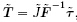 ,可得到增量
,可得到增量 0和
0和 之间的关系为
之间的关系为

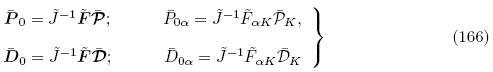
 0 可表示为
0 可表示为

 0和
0和 之间的关系为
之间的关系为

 0,
0,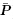 0,
0, 0和
0和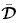 0 可以看作当参考构型由自然构型Br 更新成初始构型
0 可以看作当参考构型由自然构型Br 更新成初始构型 时拉格朗日描述下的增量
时拉格朗日描述下的增量 ,
,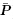 ,
, 和
和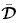 的值(Baesu et al. 2003,Ogden 2009),故
的值(Baesu et al. 2003,Ogden 2009),故 0,
0,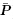 0,
0, 0和
0和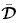 0统称为更新拉格朗日描述下的增量(updated Lagrangian field increments).
3.3.2 基于$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Omega }$(G, ε)和Ω(F,ε)的更新拉格朗日描述
0统称为更新拉格朗日描述下的增量(updated Lagrangian field increments).
3.3.2 基于$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Omega }$(G, ε)和Ω(F,ε)的更新拉格朗日描述
将式(11)2 用于自然构型Br和初始构型 之间物理量的转换,并利用式(168)可得
之间物理量的转换,并利用式(168)可得
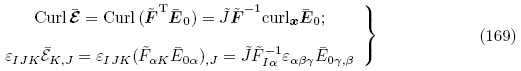
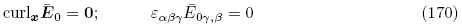
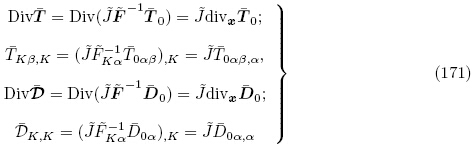
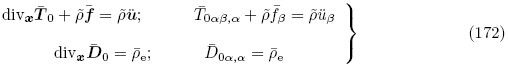
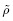 和增量自由电荷体密度
和增量自由电荷体密度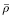 e 分别定义为
e 分别定义为

下面我们将推导T0 的增量 0和Π的增量
0和Π的增量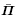 之间的关系. 由式(43)和(160)并利用式(152)有
之间的关系. 由式(43)和(160)并利用式(152)有
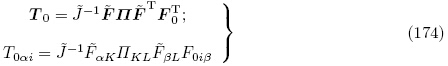
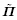 =
= 代入上式可得
代入上式可得
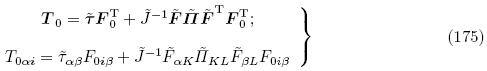
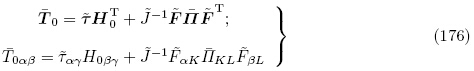
因此,在增量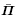 知道后,增量
知道后,增量 0 可由式(176)求得,而根据式(166)2 即可由增量
0 可由式(176)求得,而根据式(166)2 即可由增量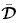 获得增量
获得增量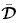 0. 注意到式(123)给出了增量
0. 注意到式(123)给出了增量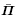 和
和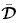 的表达式,因此将式(156)和(158)代入式(123)中可将以总能量密度函数
的表达式,因此将式(156)和(158)代入式(123)中可将以总能量密度函数 (G, ε)表示的拉格朗日描述下的增量本构方程写成
(G, ε)表示的拉格朗日描述下的增量本构方程写成

 0和
0和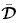 0 的表达式为
0 的表达式为

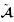 ,
,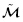 和
和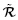 分别定义为
分别定义为
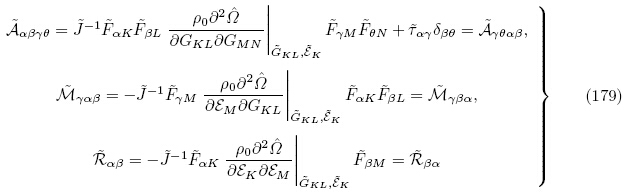
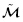 的转置符号“T” 类似于式(128)中M的转置符号.
的转置符号“T” 类似于式(128)中M的转置符号.
因此,类似于拉格朗日描述下的有效材料常数A,M和R,一般地,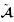 最多有45个独立分量,
最多有45个独立分量,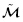 最多有18 个独立分量,而
最多有18 个独立分量,而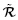 最多有6 个独立分量. 式(178)即为以总能量密度函数
最多有6 个独立分量. 式(178)即为以总能量密度函数 (G, ε)表示的更新拉格朗日描述下的增量本构方程,该方程以相对于初始构型
(G, ε)表示的更新拉格朗日描述下的增量本构方程,该方程以相对于初始构型 的增量位移梯度张量H0和增量电场矢量e为自变量,而因变量
的增量位移梯度张量H0和增量电场矢量e为自变量,而因变量 0和
0和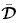 0线性依赖于H0和e.
0线性依赖于H0和e.
Ogden(2009)除了获得磁电体拉格朗日描述下的线性增量控制方程之外,还推导了更新拉格朗日描述下的线性增量方程. 正如3.2.1 小节所述,Ogden(2009)所使用的能量密度函数为增广能量密度函数Ω(F,ε). 当不考虑磁场作用且电场为准静态时,更新拉格朗日描述下的增量电场方程和增量运动微分方程为式(170)和(172),而Ogden(2009)所获得的更新拉格朗日描述下的增量本构方程用本文的符号可表示为
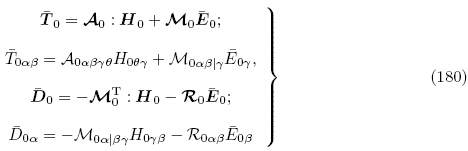

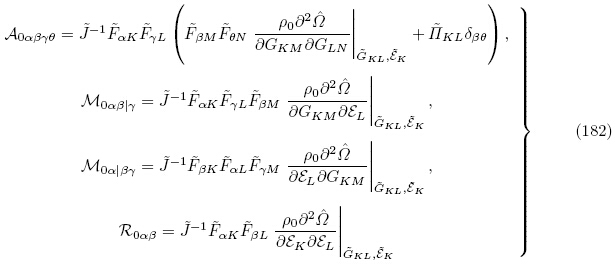
 (G, ε). 对比式(182)与式(179)可得
(G, ε). 对比式(182)与式(179)可得
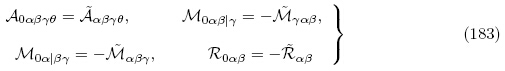
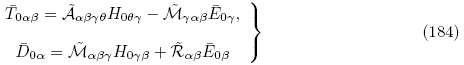
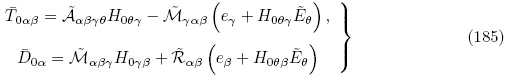
对比式(185)与式(178)可以看出式(180),(181)与式(178),(179)是等价的,这表明Ogden(2009)所获得的更新拉格朗日描述下的增量本构方程与本文给出的增量本构方程本质上是等价的,区别在于Ogden(2009)选取的能量密度函数为增广能量密度函数Ω(F,ε),其力学独立变量为变形梯度张量F,且增量本构方程式(180)以H0和 0 为自变量; 而本文中选取的能量密度函数为总能量密度函数
0 为自变量; 而本文中选取的能量密度函数为总能量密度函数 (G, ε),以Green-Lagrange 应变张量G为力学独立变量,且增量本构方程式(178)以H0和e 为自变量.两个能量密度函数Ω(F,ε)和
(G, ε),以Green-Lagrange 应变张量G为力学独立变量,且增量本构方程式(178)以H0和e 为自变量.两个能量密度函数Ω(F,ε)和 (G, ε)通过公式(4)1和(6)联系起来,两个增量电场矢量
(G, ε)通过公式(4)1和(6)联系起来,两个增量电场矢量 0和e 则通过式(167)联系起来.
0和e 则通过式(167)联系起来.
文献中,Baesu 等(2003)给出了另外一种更新拉格朗日描述下的线性增量方程形式,其选取的能量密度函数为 (G, ε). 下面对他们的增量线性方程进行简要推导.
(G, ε). 下面对他们的增量线性方程进行简要推导.
由式(33)和(44)1,并利用式(152),可以分别定义对应于σ和σs 的更新拉格朗日描述下的第一类PK 应力张量K0和T0s为


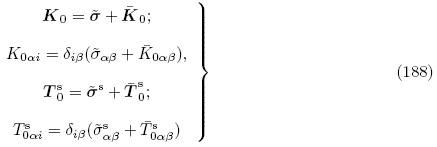

 0和Π的增量
0和Π的增量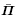 之间关系的推导,可知T0s的增量
之间关系的推导,可知T0s的增量 0s和Πs 的增量
0s和Πs 的增量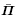 s之间的关系为
s之间的关系为

因此,在增量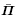 s知道后,增量
s知道后,增量 0s可由式(190)求得,而在增量
0s可由式(190)求得,而在增量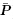 知道后,增量
知道后,增量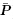 0 亦可由式(166)1 获得. 代替式(177)中的总能量密度函数
0 亦可由式(166)1 获得. 代替式(177)中的总能量密度函数 (G, ε),Baesu 等(2003)使用能量密度函数
(G, ε),Baesu 等(2003)使用能量密度函数 (G, ε). 类似于推导拉格朗日描述下的增量本构方程(177),由式(63)和(64),Baesu 等(2003)获得了以能量密度函数
(G, ε). 类似于推导拉格朗日描述下的增量本构方程(177),由式(63)和(64),Baesu 等(2003)获得了以能量密度函数 (G, ε)表示的更新拉格朗日描述下的增量本构方程为
(G, ε)表示的更新拉格朗日描述下的增量本构方程为

 (G, ε)表示的更新拉格朗日描述下的增量本构方程(177)获得. 由式(45)2和(66)可得
(G, ε)表示的更新拉格朗日描述下的增量本构方程(177)获得. 由式(45)2和(66)可得
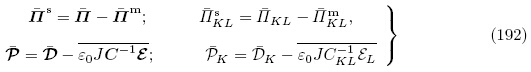
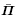 m和
m和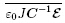 分别为Πm和ε0JC-1ε的增量,而拉格朗日描述下的增量应力
分别为Πm和ε0JC-1ε的增量,而拉格朗日描述下的增量应力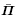 和增量电位移矢量
和增量电位移矢量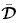 的表达式为式(177). 利用式(72)和(76),可得增量
的表达式为式(177). 利用式(72)和(76),可得增量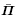 m和
m和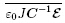 的表达式为
的表达式为

将式(191)1,2分别代入式(190)和式(166)1,并利用G和g的对称性,可得更新拉格朗日描述下的增量应力张量 0s和增量电极化矢量
0s和增量电极化矢量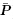 0的表达式为
0的表达式为

 ,
,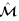 和
和 分别定义为
分别定义为
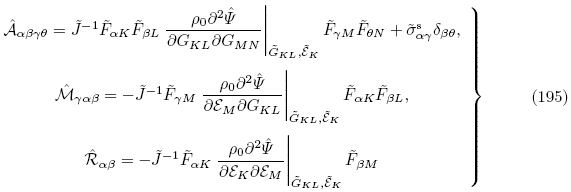
 ,
,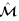 和
和 的对称性与
的对称性与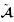 ,
,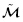 和
和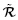 相同,但区别在于式(194)中的因变量为
相同,但区别在于式(194)中的因变量为 0s和
0s和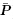 0,而式(178)中的因变量为
0,而式(178)中的因变量为 0和
0和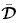 0. 另外,有效材料常数的表达式(195)基于能量密度函数
0. 另外,有效材料常数的表达式(195)基于能量密度函数 (G, ε),其数值大小依赖于对称的类Cauchy 初始应力张量
(G, ε),其数值大小依赖于对称的类Cauchy 初始应力张量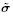 s,而式(179)基于总能量密度函数
s,而式(179)基于总能量密度函数 (G, ε),其数值大小依赖于总初始应力张量
(G, ε),其数值大小依赖于总初始应力张量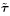 .
.
下面简要给出Baesu 等(2003)所获得的更新拉格朗日描述下的增量场方程的推导. 由式(15)和(161)1,3 可得D0和P0 之间的关系为
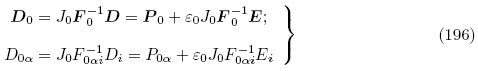
 =
=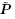 +ε0
+ε0 ,忽略高阶小量后可得
,忽略高阶小量后可得
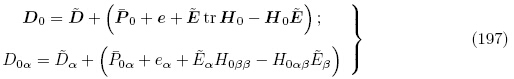
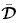 0和
0和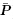 0之间的关系为
0之间的关系为

另外,将式(188)2,(153)和(163)2 代入式(189)中,并利用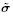 =
= 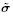 s-
s-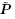 ⊗
⊗ ,忽略高阶小量后可得
,忽略高阶小量后可得

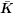 0和
0和 及
及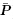 0 之间的关系为
0 之间的关系为
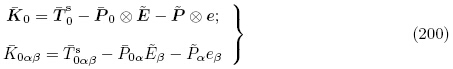
 0s和
0s和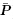 0 后,由式(198)和(200)可获得增量
0 后,由式(198)和(200)可获得增量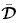 0和
0和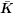 0.
0.
将欧拉描述下的运动微分方程式(28)应用于静态初始构型 可得
可得
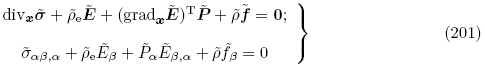
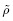 e =
e =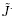 -1
-1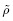 E. 由式(11)1和(186)1 可得
E. 由式(11)1和(186)1 可得

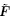 ,可得
,可得
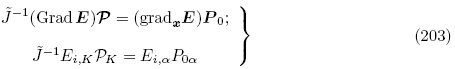

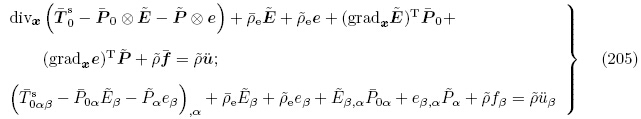
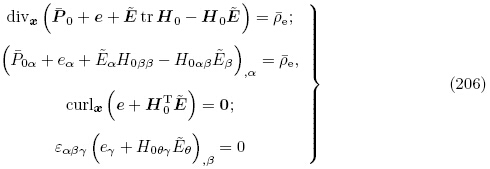
另外,Dorfmann和Ogden2010a,(2010b)不仅获得以能量密度函数Ω*(F,D)表示的拉格朗日描述下的线性增量方程,也推导了更新拉格朗日描述下的线性增量方程,其中增量运动微分方程和增量电场方程与式(170)和(172)相同,而增量本构方程选取的能量密度函数为Ω*(F,D),其自变量为H0和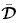 0,因变量为
0,因变量为 0和
0和 0. 更详细的讨论读者可参考Dorfmann和Ogden2010a,(2010b). 类似于式(178),我们也可以获得以能量密度函数
0. 更详细的讨论读者可参考Dorfmann和Ogden2010a,(2010b). 类似于式(178),我们也可以获得以能量密度函数 *(G,D)表示的更新拉格朗日描述下的增量本构方程.
*(G,D)表示的更新拉格朗日描述下的增量本构方程.
下偏场理论的比较同样,为方便读者查阅和比较,表 3整理了不同文献中更新拉格朗日描述下的偏场理论,给出了多种形式的增量控制方程和增量边界条件,并对比了不同文献中所定义的符号与本文定义的符号. 表 3的解释和说明类似于表 2,这里不再赘述.
 |
本小节按照Dorfmann和Ogden2010a,(2010b)的方法推导增量外场方程和不同描述下的增量力电边界条件. 假设电弹性体外部电场矢量和电位移矢量的增量分别记为 *和
*和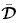 *,则由式(95)和(96)可知外部空间的增量电场控制方程为
*,则由式(95)和(96)可知外部空间的增量电场控制方程为
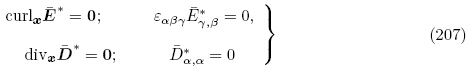

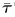 *为
*为
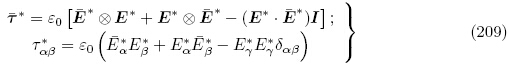
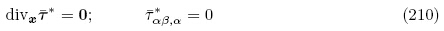
利用下面运动学恒等式(Dorfmann & Ogden,2010a,Dorfmann & Ogden,2010b)

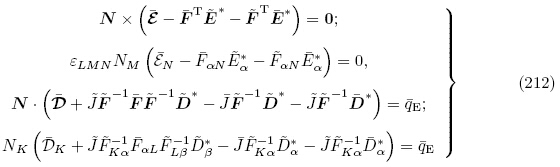
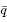 E 定义为
E 定义为

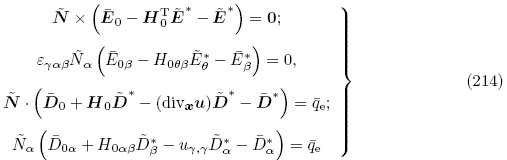
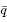 e 定义为
e 定义为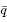 edà =
edà =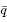 EdA.
EdA.
由式(104)和(111)2,利用Nanson 公式(8),定义单位自然构型Br 上由于电弹性体外部电场的存在产生的表面力矢量tE为
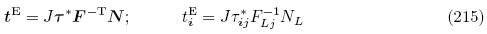
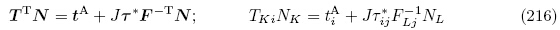
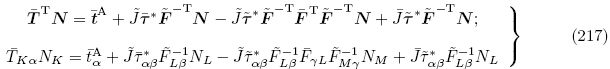
 A 为相对于自然构型Br 的表面力增量矢量. 利用Nanson 公式(8),(160)和式(211)2 可得更新拉格朗日描述下的力学边界条件为
A 为相对于自然构型Br 的表面力增量矢量. 利用Nanson 公式(8),(160)和式(211)2 可得更新拉格朗日描述下的力学边界条件为
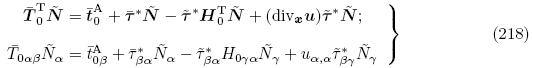
 0A定义为
0A定义为 0Adà =
0Adà = AdA.
AdA.
本节我们简要叙述了电弹性体偏场理论的两种构型描述,即拉格朗日描述和更新的拉格朗日描述,并且推导对比了本节所获得的结果与不同文献中偏场理论的增量控制方程和增量边界条件的异同点.本节的内容并没有涉及非线性电弹性体能量密度函数的具体形式,也没有讨论电弹性材料的对称性,因此本节所推导的公式和结果适用于任意的非线性电弹性材料(包括几何非线性和材料非线性).而正如2.6小节所述,非线性电弹性体的本构关系必须通过给定能量密度函数的具体形式才能得到其显式表达.
值得注意的是,根据偏场(即初始场)与叠加场(增量场)之间的大小关系可以定义不同类型的偏场理论.如果偏场是有限的,而叠加场是无限小的,则定义此偏场理论为“大+小”(small-on-large)偏场理论.以此类推,可定义“小+小”(small-on-small),“大+大”(large-on-large),“小+大”(large-on-small)等偏场理论.
本节所讨论的偏场理论即为“大+小”偏场理论,由于涉及有限偏场,因此,能量密度函数的形式应基于客观性原理和电弹性体材料的对称性,利用张量表示定理给出. 例如,当考虑的软电弹性材料为各向同性时,能量密度函数Ω(F,Σ)依赖于式(91)的6个联合不变量,或者能量密度函数Ω*(F,D)依赖于式(92)的6个联合不变量,各向同性软电弹性材料能量密度函数的若干具体形式可参见附录B. “大+小”偏场理论增量本构方程的具体表达式的详细推导可参考(Dorfmann和Ogden2005,Dorfmann和Ogden2006,Dorfmann和Ogden20010a,2010b). 此外,对于横观各向同性的电弹性材料,能量密度函数Ω*(F,Σ,α0)或Ω*(F,D,α0)分别依赖于式(93)或(94)的10 个联合不变量,与此对应的本构方程具体表达式的详细推导可参考Bustamante(2009).
如果仅考虑电弹性材料的弱非线性,可以将能量密度函数对其自变量进行多项式展开,如式(85)和(86). 下一节将考虑叠加于无限小偏场之上的小增量场情况(即“小+小” 偏场理论),此时能量密度函数一般取至三阶材料常数(即三次多项式)就已足够精确(Tiersten 1981,Liu et al. 2003a,Yang & Hu,2004,Yang 2005a). 值得一提的是,Ogden和Dorfmann 提出的电弹性体偏场理论是“大+小” 偏场理论,其主要的背景和应用是具有力电耦合的电敏感软弹性体(Dorfmann & Ogden,2014b),因此他们并没有将其“大+小”偏场理论退化为无限小偏场理论. 但是如果将Ogden和Dorfmann偏场理论中的能量密度函数取如式(85)和(86)所示的多项式展开,则也能得到下一节所讨论的无限小偏场理论.
对于“大+大”偏场理论,由于此时所涉及的偏场和叠加场都是有限的,因此可在非线性连续介质力学框架内直接处理,故“大+大” 偏场理论失去了其实际意义. 另外,残余应力普遍存在于心脏和血管等生物软组织中(Fung 1990,Rodriguez et al. 1994),同时因表界面松弛引起的初始应变也广泛存在于微纳米力电耦合材料中(见5.3 节及相关文献),为研究微纳米力电耦合材料和生物软组织的非线性力电特性,可以使用“小+大”的偏场理论. 对“小+大” 偏场理论感兴趣的读者可参考相关文献(Hoger A 1993,Rodriguez et al. 1994,Saravanan 2008,Shams et al. 2011,Shams & Ogden,2014).
4 无限小偏场 4.1 拉格朗日描述下的无限小偏场理论
本节将进一步考虑无限小偏场情形,即“小+小”偏场理论. 在许多实际应用中,偏场为足够小或无限小. 在此情况下,通常能量密度函数只需取至三阶材料常数(即三次多项式)即可. 对于无限小偏场,假设拉格朗日描述下初始变形的无限小位移矢量为 (X),如图 2所示,则
(X),如图 2所示,则

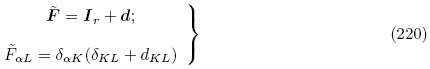
 (X)为相对于自然构型Br的初始位移梯度张量. 由式(114)1 并利用式(220)可得
(X)为相对于自然构型Br的初始位移梯度张量. 由式(114)1 并利用式(220)可得
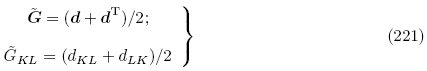

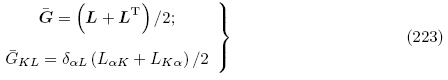
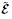 和增量电场
和增量电场 满足式(114)和式(121),即它们是无旋的,因此可引进初始电势
满足式(114)和式(121),即它们是无旋的,因此可引进初始电势 和增量电势
和增量电势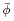 如下
如下

下面我们首先从总能量密度函数 (G, ε)式(86)出发推导无限小偏场作用下的线性增量本构方程. 由式(86),对于无限小偏场作用,总能量密度函数
(G, ε)式(86)出发推导无限小偏场作用下的线性增量本构方程. 由式(86),对于无限小偏场作用,总能量密度函数 (G, ε)取至三阶材料常数(即三次多项式),则有
(G, ε)取至三阶材料常数(即三次多项式),则有

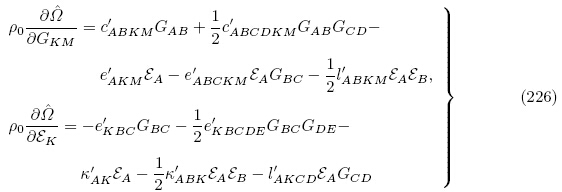
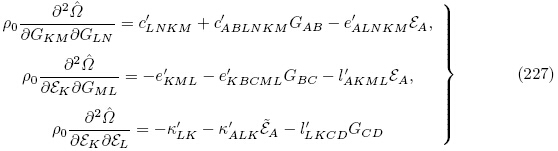
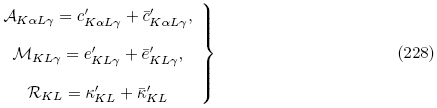
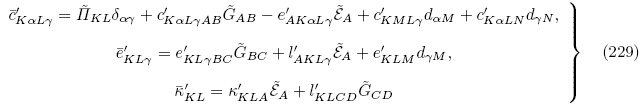
从式(228)可以看出当考虑无限小偏场作用时,有效材料常数必须由二阶材料常数按照式(229)修正得到. 因此,为了完整描述小偏场的线性效应,必须给出三阶材料常数(Yang & Hu,2004).
当不考虑电弹性体外部电场的影响时,拉格朗日描述下的增量边界条件为
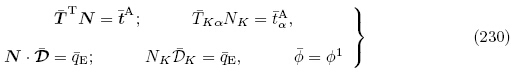
当考虑无限小偏场时,可统一采用小写罗马字母下标来进行描述,因此,由式(128)~(130),(223)~(224)2 以及(228)~(229),可将拉格朗日描述下叠加于无限小偏场之上的小增量场u和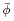 的线性控制方程改写如下:
的线性控制方程改写如下:
增量运动微分方程和增量电荷方程
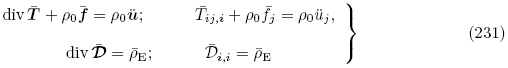
增量本构关系

增量机械应变-位移关系和增量电场-电势关系


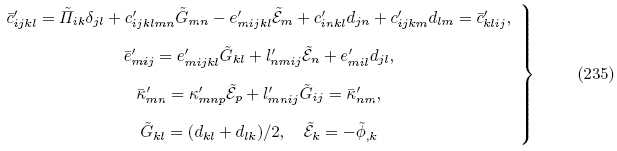
增量边界条件为
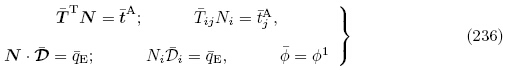
Liu 等(2003a)也通过对总能量密度函数 (G, ε)进行多项式展开并保留到三次多项式(即三阶材料常数)获得了拉格朗日描述下叠加于无限小偏场作用之上的小增量场的电弹性理论的基本方程和边界条件. Liu 等(2003a)获得的增量电荷方程为式(231)2,但没有考虑自由电荷体密度; 他们获得的增量机械应变-位移关系和增量电场-电势关系为式(233); 获得的增量电学边界条件为式(236)2,其自然构型Br上的表面自由电荷密度的定义与式(236)2 相反. 下面我们简要给出Liu 等(2003a)拉格朗日描述下的增量运动微分方程、增量本构方程和力学边界条件的推导,并将他们的结果与本文的结果进行比较.
(G, ε)进行多项式展开并保留到三次多项式(即三阶材料常数)获得了拉格朗日描述下叠加于无限小偏场作用之上的小增量场的电弹性理论的基本方程和边界条件. Liu 等(2003a)获得的增量电荷方程为式(231)2,但没有考虑自由电荷体密度; 他们获得的增量机械应变-位移关系和增量电场-电势关系为式(233); 获得的增量电学边界条件为式(236)2,其自然构型Br上的表面自由电荷密度的定义与式(236)2 相反. 下面我们简要给出Liu 等(2003a)拉格朗日描述下的增量运动微分方程、增量本构方程和力学边界条件的推导,并将他们的结果与本文的结果进行比较.
由式(125)和式(220)知拉格朗日描述下的第一类PK 增量应力张量 为
为
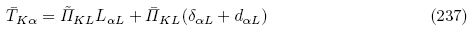

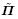 和
和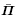 表示的增量运动微分方程. 注意到式(238)可适用于有限变形. 由式(230)1和(237)可将增量力学边界条件用第二类PK应力张量表示为
表示的增量运动微分方程. 注意到式(238)可适用于有限变形. 由式(230)1和(237)可将增量力学边界条件用第二类PK应力张量表示为
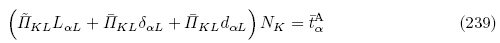

对于现时构型B,由本构方程(80)和总能量密度函数表达式(225)可得
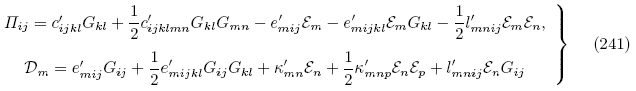
 ,有
,有
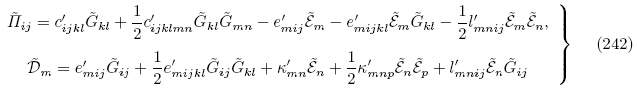
 以及无限小初始位移梯度d和初始电场矢量
以及无限小初始位移梯度d和初始电场矢量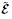 的高阶项,整理后可得
的高阶项,整理后可得
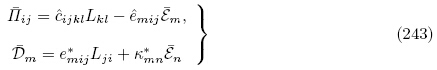

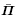 表示的无限小偏场作用下的增量本构方程. 由式(244)可见,尽管第二类PK 增量应力张量
表示的无限小偏场作用下的增量本构方程. 由式(244)可见,尽管第二类PK 增量应力张量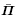 是对称的,但其材料常数ĉijkl 失去了主对称性,即ĉijkl ≠ ĉklij.事实上,从式(123)出发,利用式(126),(220)~(223)和(225)~(227)同样可以得到增量本构方程(243)和(244).
是对称的,但其材料常数ĉijkl 失去了主对称性,即ĉijkl ≠ ĉklij.事实上,从式(123)出发,利用式(126),(220)~(223)和(225)~(227)同样可以得到增量本构方程(243)和(244).
将增量本构方程式(243)代入增量运动微分方程式(240)1,利用式(244),并忽略无限小初始位移梯度d和初始电场矢量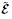 的高阶项,整理后可得
的高阶项,整理后可得
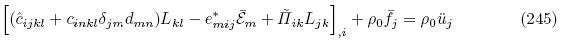


 ij 定义为
ij 定义为
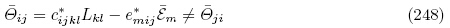
 ij 表示的拉格朗日描述下的增量本构方程为式(248)和(243)2,其中,cijkl*,emij*和Κmn*是Liu 等(2003a)所定义的有效弹性、压电和介电常数. 类似地,增量力学边界条件(240)2也可以写成
ij 表示的拉格朗日描述下的增量本构方程为式(248)和(243)2,其中,cijkl*,emij*和Κmn*是Liu 等(2003a)所定义的有效弹性、压电和介电常数. 类似地,增量力学边界条件(240)2也可以写成

对比增量本构方程式(243)2和式(232)2,并利用式(234),(235)和式(244)可得



 ij和
ij和 ij的关系为
ij的关系为

 ij既不是拉格朗日描述下的第一类PK 增量应力
ij既不是拉格朗日描述下的第一类PK 增量应力 ij,也不是第二类PK 增量应力
ij,也不是第二类PK 增量应力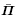 ij,它也没有对称性(Su et al. 2005).
ij,它也没有对称性(Su et al. 2005).
将式(248)代入式(253)可将 ij表示为
ij表示为

另外,对比式(248)和式(232)1,我们也可以注意到有效弹性常数cijkl*和Aijkl 与相对于自然构型的增量位移梯度张量L的指标缩并顺序不同,本文是按“内内外外”缩并,而Liu 等(2003a)是按\前前后后" 进行缩并,这也是导致Liu 等(2003a)有效弹性常数cijkl*不再具有本文有效弹性常数Aijkl主对称性的根本原因. Tiersten(1981)文中的公式(43)以及Yang(2005a)书中公式(6.2-16)都是按照“内内外外” 对有效弹性常数与相对于自然构型的增量位移梯度进行缩并的,因此相应的有效弹性常数具有主对称性.
总之,对比Liu 等(2003a)和本文所获得的拉格朗日描述下无限小偏场理论的基本方程和边界条件,增量机械应变-位移关系和增量电场-电势关系相同; 当不考虑自由电荷体密度时,增量电荷方程相同; 增量电学边界条件中相对于自然构型的表面自由电荷密度的定义相反; 有效压电常数相同且都不具有对称性,有效介电常数相同且都具有一般的对称性; 增量本构方程中的自变量都是相对于自然构型的增量位移梯度和增量电场强度,其电学因变量都是拉格朗日形式的增量电位移矢量. 但在Liu 等(2003a)的理论中,有效弹性常数不具有本文有效材料常数所具有的主对称性,原因见前所述; Liu 等(2003a)增量本构方程中所获得的增量应力张量既不是拉格朗日描述下的第一类PK 增量应力,也不是第二类PK 增量应力,且没有对称性. 最后,Liu 等(2003a)将第二类PK 初始应力张量直接纳入增量运动微分方程中,因此对增量本构方程中的有效弹性常数无影响,而本文中第二类PK 初始应力张量不出现在增量运动微分方程中,而是包含在有效弹性常数中,因此对有效弹性常数(即增量本构方程)有影响. 但是,本文和Liu 等(2003a)拉格朗日描述下的无限小偏场理论在本质上是一致的,只是形式不同. 本节推导表明,经过适当的变换整理,可以从一种理论转换到另一种理论.
4.1.2 基于$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Psi }$(G, ε)的拉格朗日描述
另外,通过式(85)取能量密度函数 (G, ε)至三次多项式(即三阶材料常数),利用式(142)和式(145)~(147),类似于推导有效材料常数式(228)和(229),Yang(2005a)也获得了拉格朗日描述下无限小偏场的增量本构方程为式(128),亦即式(232). Yang(2005a)给出了有效材料常数A,M和R 的另外一种表达式为
(G, ε)至三次多项式(即三阶材料常数),利用式(142)和式(145)~(147),类似于推导有效材料常数式(228)和(229),Yang(2005a)也获得了拉格朗日描述下无限小偏场的增量本构方程为式(128),亦即式(232). Yang(2005a)给出了有效材料常数A,M和R 的另外一种表达式为
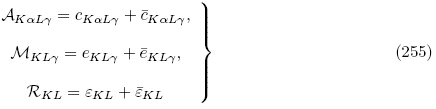
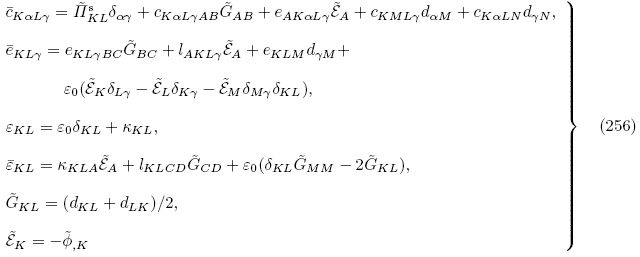
下面我们简要推导式(85)和式(86)中基本材料常数之间的关系. 将式(40)2和(44)4 应用于初始构型 可得
可得
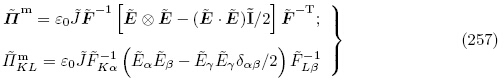
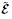 的二阶及以上项可得
的二阶及以上项可得

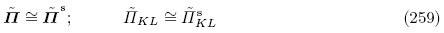
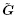 的对称性,经过整理后,有效材料常数A,M和R可写成
的对称性,经过整理后,有效材料常数A,M和R可写成


事实上,由式(69)并利用式(5)和式(221)~(223)以及G 的对称性,忽略高阶小量后可得能量密度函数π为
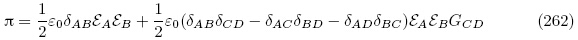
 (G, ε)和
(G, ε)和 (G, ε)之间的关系式(78)可得
(G, ε)之间的关系式(78)可得
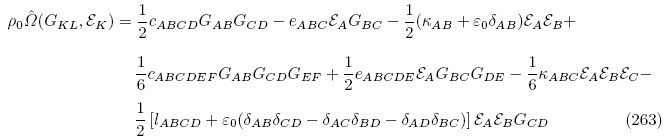
 (G, ε)中的电致伸缩系数l'AKLγ 等于电弹性材料存在时产生的相对电致伸缩效应(即能量密度函数
(G, ε)中的电致伸缩系数l'AKLγ 等于电弹性材料存在时产生的相对电致伸缩效应(即能量密度函数 (G, ε)中的电致伸缩系数lAKLγ)与真空中Maxwell 电应力张量产生的电致伸缩效应之和. 因此,尽管能量密度函数的选取不同,但其基本材料常数之间存在一定的关系. 在利用基本材料常数进行数值计算时,必须弄清楚该基本材料常数对应于何种能量密度函数; 如果能量密度函数与基本材料常数不对应,则必须通过式(261)或其他类似关系式对基本材料常数进行适当的转换.
4.2 更新拉格朗日描述下的无限小偏场理论
(G, ε)中的电致伸缩系数lAKLγ)与真空中Maxwell 电应力张量产生的电致伸缩效应之和. 因此,尽管能量密度函数的选取不同,但其基本材料常数之间存在一定的关系. 在利用基本材料常数进行数值计算时,必须弄清楚该基本材料常数对应于何种能量密度函数; 如果能量密度函数与基本材料常数不对应,则必须通过式(261)或其他类似关系式对基本材料常数进行适当的转换.
4.2 更新拉格朗日描述下的无限小偏场理论
Baumhauer和Tiersten(1972)以及Chai和Wu(1996)都推导获得了更新拉格朗日描述下叠加于无限小偏场作用之上的小增量场的线性增量方程. 下面我们简要推导他们所获得的增量控制方程和边界条件. 对于无限小偏场,假设更新拉格朗日描述下初始变形的无限小位移矢量为 (x),则
(x),则

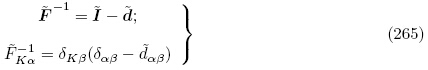
 = gradx
= gradx (x)为相对于初始构型
(x)为相对于初始构型 的初始位移梯度张量. 忽略
的初始位移梯度张量. 忽略 的二阶及以上项可得
的二阶及以上项可得

由式(170)和(172)可得更新拉格朗日描述下的增量电场方程和增量运动微分方程为

由式(184)和式(179)并利用式(43)1 可知以总能量密度函数 (G, ε)表示的更新拉格朗日描述下的增量本构方程如下
(G, ε)表示的更新拉格朗日描述下的增量本构方程如下
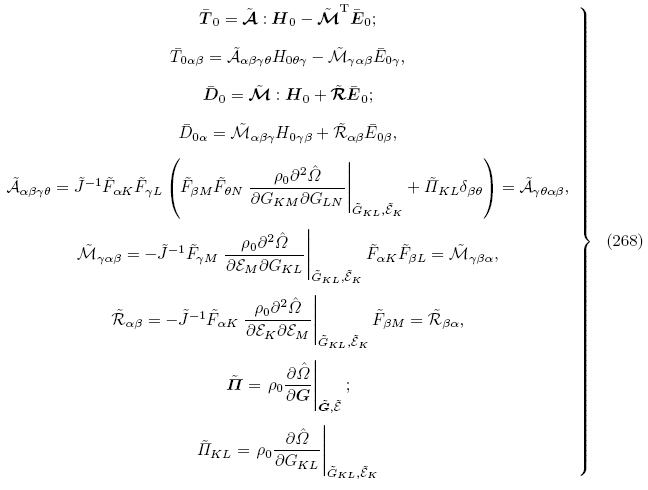
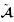 ,
,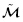 和
和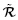 以能量密度函数
以能量密度函数 (G, ε)表示成
(G, ε)表示成

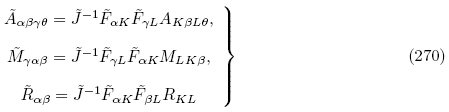



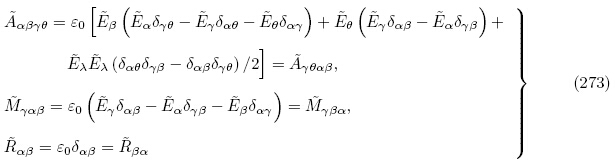
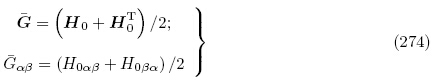
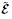 和更新拉格朗日描述下的增量电场
和更新拉格朗日描述下的增量电场 0 表示为
0 表示为
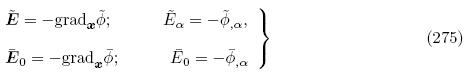
式(268)1,2,(269)和式(273)即为Baumhauer和Tiersten(1972)以及Chai和Wu(1996)所获得的用能量密度函数 (G, ε)表示的更新拉格朗日描述下叠加于有限偏场之上的线性增量本构方程. 通过仔细对比本小节的公式(268)1和(269)1和(273)1 与Baumhauer和Tiersten(1972)文中公式(75)和(77)1 及Chai和Wu(1996)文中公式(9)1和(11)1,可注意到Baumhauer和Tiersten(1972)以及Chai和Wu(1996)两文中的有效弹性常数不具有本文有效弹性常数Ãαβγθ所具有的主对称性(即Ãαβγθ= Ãγθαβ),其根本原因在于有效弹性常数与相对于初始构型的增量位移梯度张量的缩并顺序不同,即本文是按\内内外外" 进行缩并,而Baumhauer和Tiersten(1972)以及Chai和Wu(1996)都是按“前前后后”进行缩并. 这与4.1.1 小节所述情形类似. 文献中,Ogden(2009)是按照“内内外外” 对有效弹性常数与相对于初始构型的增量位移梯度进行缩并的,因此该文公式(84)所定义的有效弹性常数具有主对称性.
(G, ε)表示的更新拉格朗日描述下叠加于有限偏场之上的线性增量本构方程. 通过仔细对比本小节的公式(268)1和(269)1和(273)1 与Baumhauer和Tiersten(1972)文中公式(75)和(77)1 及Chai和Wu(1996)文中公式(9)1和(11)1,可注意到Baumhauer和Tiersten(1972)以及Chai和Wu(1996)两文中的有效弹性常数不具有本文有效弹性常数Ãαβγθ所具有的主对称性(即Ãαβγθ= Ãγθαβ),其根本原因在于有效弹性常数与相对于初始构型的增量位移梯度张量的缩并顺序不同,即本文是按\内内外外" 进行缩并,而Baumhauer和Tiersten(1972)以及Chai和Wu(1996)都是按“前前后后”进行缩并. 这与4.1.1 小节所述情形类似. 文献中,Ogden(2009)是按照“内内外外” 对有效弹性常数与相对于初始构型的增量位移梯度进行缩并的,因此该文公式(84)所定义的有效弹性常数具有主对称性.
通过式(85),取能量密度函数 (G, ε)至三次多项式(即三阶材料常数),类似于推导式(227)可得
(G, ε)至三次多项式(即三阶材料常数),类似于推导式(227)可得
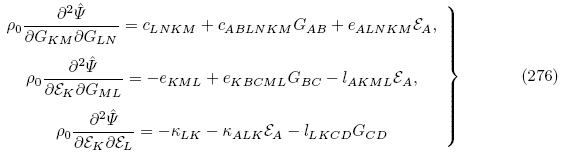
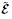 和
和 的点积,并利用基本材料常数的对称性,可以将式(269)中的二阶导数项写成
的点积,并利用基本材料常数的对称性,可以将式(269)中的二阶导数项写成

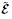 的二阶效应(即Ãαβγθ)和初始电场
的二阶效应(即Ãαβγθ)和初始电场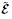 与相对于初始构型
与相对于初始构型 的初始位移梯度张量
的初始位移梯度张量 的点积(即式(277)),但只考虑了
的点积(即式(277)),但只考虑了 的一阶影响. 对比式(269)与式(255)可知,即使只考虑无限小偏场的线性效应,拉格朗日描述和更新拉格朗日描述下所获得的有效材料常数也是不同的,此时增量本构方程中的自变量和因变量也不相同,见式(232)和(268)1,2. 事实上,通过式(86),取总能量密度函数
的一阶影响. 对比式(269)与式(255)可知,即使只考虑无限小偏场的线性效应,拉格朗日描述和更新拉格朗日描述下所获得的有效材料常数也是不同的,此时增量本构方程中的自变量和因变量也不相同,见式(232)和(268)1,2. 事实上,通过式(86),取总能量密度函数 (G, ε)至三次多项式,将其代入式(268)3-5同样可以获得用
(G, ε)至三次多项式,将其代入式(268)3-5同样可以获得用 (G, ε)的基本材料常数表示的更新拉格朗日描述下无限小偏场理论的有效材料常数,这里不再赘述.
(G, ε)的基本材料常数表示的更新拉格朗日描述下无限小偏场理论的有效材料常数,这里不再赘述.
当不考虑电弹性体外部电场的影响时,更新拉格朗日描述下的边界条件为
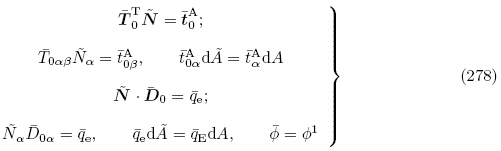
在某些应用如薄壁结构的屈曲分析中,考虑无初始变形的初始应力就足够精确了,这即对应于弹性理论中的初始应力理论. 由于无初始变形,则初始构型 和自然构型Br重合(即x = X),此时初始位移梯度d或
和自然构型Br重合(即x = X),此时初始位移梯度d或 为零,
为零,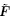 = I和
= I和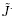 = 1,但有非零初始应力
= 1,但有非零初始应力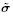 s和初始电场强度
s和初始电场强度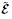 . 另外,对于屈曲等稳定性分析,只考虑能量密度函数
. 另外,对于屈曲等稳定性分析,只考虑能量密度函数 (G, ε)的二阶材料常数并忽略初始电场强度的二阶项已经足够精确(Yang 2005a). 因此由式(269),(273)和(277)可知,更新拉格朗日描述下的有效材料常数
(G, ε)的二阶材料常数并忽略初始电场强度的二阶项已经足够精确(Yang 2005a). 因此由式(269),(273)和(277)可知,更新拉格朗日描述下的有效材料常数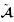 ,
,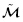 和
和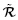 退化
退化
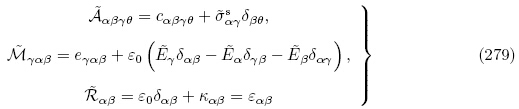
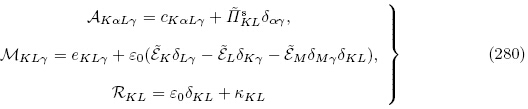


进一步,当不考虑偏场作用时,有效材料常数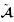 ,
,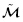 和
和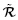 退化成
退化成
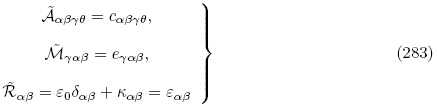
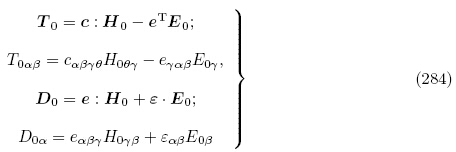
当考虑的材料是非电弹性材料(即力电不耦合),电场与弹性场解耦; 如只关心弹性变形,则所有关于电场的物理量都可以不予考虑. 这样,对于拉格朗日描述,由式(255)1和(256)1 可知有效弹性常数A 变成

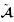 变成
变成

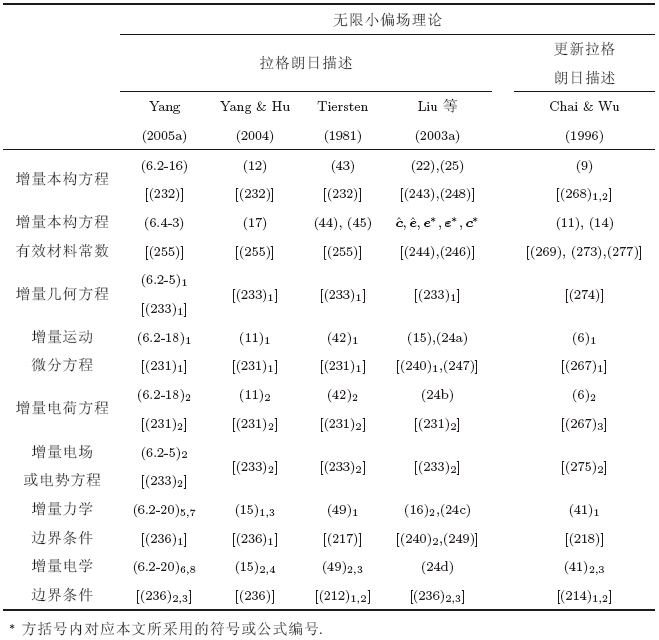
表 4对不同文献中拉格朗日描述和更新拉格朗日描述下的无限小偏场理论进行了整理,给出了多种形式的增量控制方程和增量边界条件,并与本文结果进行了对比.
 |
以下,我们结合自己的兴趣和理解,就偏场作用下力电耦合材料的若干当前研究重点作简单的阐述并指出其未来发展方向,供有兴趣的读者参考.
5.1 非均匀偏场对波传播的影响由于力电传感器、驱动器和换能器在不同领域的广泛应用以及工作状态下经常受到不同偏场的作用,因此偏场对电弹性材料中声波传播特性的影响已经被诸多学者所研究,包括表面声波(Gafka & Tani,1993,Palmieri et al. 1986,Liu et al. 2003b,Liu & Lee et al. 2004),Lamb 波(Palma et al. 1985a,1985b; Palmieri et al. 1988; Liu et al. 2002a,2002b; Shmuel et al. 2012),SH 波(Son & Kang,2011),B-G 波(Yang 2001,Liu et al. 2003a),轴对称波(Chen & Dai,2012,Shmuel 2013a)以及层合结构中波的传播(Liu & Shin et al. 2004; Du et al. 2007a,2007b,2008; Shmuel & deBotton,2012)等. 但很多研究仅限于考虑无初始变形的初始应力影响,如Du 等2007a,(2007b,2008),Son和Kang(2011). 若偏场较大,采用该假设可能无法精确描述真实的物理现象. 其次,在很多实际情况下,器件和结构所受到的偏场是非均匀的,而绝大多数已有研究考虑的都是均匀偏场的作用,因此研究非均匀偏场作用下波的传播特性也十分必要. 对于脆性压电材料,基于Liu 等(2003a)的偏场理论,Su 等(2005)利用传递矩阵法研究了层合压电结构中非均匀预应力场对Love 波传播特性的影响,但他们未考虑初始应变,因此忽略了高阶材料常数的影响. 而Lematre 等(2006a)利用Liu 等(2003a)的偏场理论,采用传递矩阵法分析了非均匀预应力场对LiNbO3 压电板以及LiNbO3 压电薄膜- 基体中波传播特性的影响,并考虑了高阶材料常数的影响. 但正如4.1.1 小节所述,Liu 等(2003a)偏场理论中的增量应力张量不是真实的应力张量且没有对称性(Su et al. 2005),只有在初始变形为小量时才能精确地描述偏场的影响,若偏场较大,其有效性有待进一步比较验证. 对于软电弹性材料,目前文献中主要考虑的仍然是均匀偏场的作用(Shmuel et al. 2012,Chen & Dai,2012,Shmuel & deBotton,2012). 最近,Shmuel(2013a)利用Dorfmann 偏场理论,结合数值求解算法,研究了不同状态的非均匀有限偏场作用下介电高弹圆柱管中轴对称波的传播特性. 由于研究非均匀偏场作用下波的传播特性需要将偏场理论和数值方法相结合,因此发展精确而高效的数值分析方法对于研究非均匀偏场作用下波的传播特性十分重要. 另外,正如2.6 小节所讨论指出的,对于弱非线性问题,能量密度函数可以采用多项式展开表示,此时偏场理论需要使用高阶材料常数,而对于强非线性问题,偏场理论需要知道能量密度函数对于不变量的具体表达式. 因此,通过精确有效的实验方法来确定所有高阶材料常数或能量密度函数的具体表达形式具有重要的实际意义和应用价值.
5.2 不同描述下偏场影响的理论预测与实验验证我们必须强调拉格朗日描述和更新拉格朗日描述下偏场理论研究结果的区别. 现有文献中关于偏场对压电结构力电特性影响的研究大都是基于拉格朗日描述,即选择自然构型作为参考构型,此时获得的波速为自然波速(natural velocity). 正如Thurston和Brugger(1964),Pao 等(1984)所述,自然波速在实验上可通过测量材料自然构型下的自然长度与预应力作用下波传播的时间之比获得,而真实波速(actual velocity)在实验上可通过测量材料在预应力作用下初始构型的真实长度与波传播的时间之比获得,此时所选择的参考构型为初始构型,即为更新的拉格朗日描述. 应当注意到,对于非力电耦合预应力材料中波传播的实验,大部分研究者都是利用更新拉格朗日描述来研究波的传播特性,所获得的波速为真实波速(Duquennoy et al. 1999a,1999b,2002; Junge et al. 2006). 因此,将不同描述下偏场理论的结果与实验结果对应比较十分关键. 最近,Lematre 等(2011)以及Domenjude 等(2013)基于Liu 偏场理论实验研究和比较了预应力压电材料在两种描述下电声特性的差异. 因此精确研究和对比两种描述下偏场对可实验测量的电弹性材料力电特性影响的差别显得尤为重要.
5.3 微纳米尺度力电耦合材料的响应特性首先,在微纳米多晶薄膜中残余应力普遍存在,其原因主要有两个: 一是晶界之间由于热处理工艺导致的本征残余应力; 二是当薄膜沉积于基体上,由于薄膜与基体之间热失配引起的外部残余应力(Lematre et al. 2006b). 因此建立合理的力学模型来描述残余应力对薄膜材料力学特性的影响就很关键,而偏场理论为我们提供了有效的方法. 此外,在微电子领域中,残余应力的存在既可能使材料产生“击穿现象”(Wang &Evans 1998),但也可以改善材料的力电性能(Narayanaswamy 1978),因此合理地控制力电耦合材料中的残余应力对实际应用来说是十分重要的. 最近,Duquennoy 课题组基于声弹理论,利用叉指换能器产生的高频表面声波从理论和实验上研究了材料中表面残余应力的大小和深度(Duquennoy et al. 2006,2012,2013). 总之,采用合理而精确的实验手段以获得力电耦合薄膜材料中残余应力的分布,并采用合适的理论模型分析预测其影响,不仅理论意义突出,也具有明确的实际应用价值.
其次,对于纳米晶体材料,正如Zhang 等(2010)所述,当沿着某个晶面切割晶体之后将产生自由表面,新产生的表面没有结构松弛,具有较高的表面能,因此分离的独立晶体不可避免的会发生能量最小化松弛. 在此过程中,独立晶体表面的原子位置重新排布以降低其总能量. 而表面原子的松弛也导致纳米尺寸材料内部晶格空间的改变,这个过程已经由原子模拟(Liang et al. 2005,Diao et al. 2006)和实验(Huang et al.2008)所观察到. 这种松弛引起的应变称为初始应变(Zhang et al. 2008,2010). 对于多相纳米材料,其界面相同样会发生类似的松弛现象,也会在纳米材料内部产生初始应变(Tiersten et al. 1981,Dingreville et al. 2014). 此外,在纳米压电和铁电材料中,表面自发极化和表面残余电场也会致使材料内部产生初始电场(Eliseev et al. 2009,2010;Pan et al. 2011; Xu & Shen,2012). 这些问题和现象用经典的线弹性理论已无法给予满意的解释. 我们可以尝试将纳米材料未松弛之前和松弛之后的状态分别看作自然构型和初始构型,在松弛状态上施加载荷或扰动之后的状态看作现时构型. 这样,就可以利用偏场理论去研究纳米材料的非线性力电特性. 为了精确描述纳米材料的非线性行为,必须首先通过数值模拟(比如分子动力学和第一性原理等)和实验确定纳米材料的高阶材料常数(包括块体和表面的高阶材料常数). 然而迄今为止只有少数研究工作致力于纳米材料高阶材料常数的确定(Dingreville 2007,Wang & Liu et al. 2010,Wang & Gu et al. 2014).
5.4 声子晶体与声波超材料中波的传播与调控最近十多年,利用声子晶体和声波超材料进行弹性波的主动调控得到了广泛的研究关注.然而,对于制作成型的结构如何实现材料参数或拓扑结构的灵活调节依然是个难题. 实现对波的实时、灵活、主动的可调控制,设计制作可调声学器件或装置已成为近几年的研究热点. 有研究者已开始尝试利用软材料周期结构开展波动调控的研究. 哈佛大学Bertoldi 教授和麻省理工Boyce 教授等首先注意到软材料周期结构因大变形和失稳屈曲可以导致丰富的构型变化,并指出了其在声子晶体声学功能调控中的前景(Bertoldi & Boyce,2008a,Bertoldi & Boyce,2008b; Wang et al. 2013; Shan et al. 2014). 大变形的引入使软材料结构的分析变得十分复杂,特别是涉及材料和几何双重非线性,须在非线性连续介质力学的框架下利用偏场理论对声子晶体的调控开展深入的研究. 值得一提的是,在软材料声子晶体的多场耦合效应调控研究方面,已开展了一些有趣的初步研究(Gei et al. 2011,Shmuel & deBotton,2012,Shmuel 2013b,Bayat & Gordaninejad,2015).最近,Parnell 等(2012)利用Neo-Hookean 超弹性材料的预应力实现了隐身,使得物体对于入射的反平面弹性波几乎不可见,不受入射波入射方向的影响. Parnell 等(2012)指出施加预应力偏场可以产生非均匀和各向异性的材料性质,因此利用超弹性材料预应力偏场方法有可能替代为达到隐身目的而要求非均匀和各向异性的超材料设计. 同年,Norris和Parnell(2012)提出了预应力固体的变换弹性理论(transformationelasticity),也称超弹性隐身理论(hyperelastic cloaking theory). 他们注意到变换弹性理论与本文所综述的叠加于有限变形之上的增量运动理论(即偏场理论)的相似性,证明了变换弹性理论的本构参数对应于偏场理论的密度和有效弹性常数,并数值研究了反平面和平面内弹性波的隐身. 利用变换弹性理论进行弹性波的主动调控隐身已成为最近的研究热点之一(Norris & Shuvalov,2011,Norris et al. 2014,Parnell 2012, Parnell &Shearer 2013,Brun et al. 2014,Colquitt et al. 2014),而进一步引入力电耦合特性无疑将极大地丰富弹性波隐身的调控手段,增加灵活性.
5.5 偏场作用下力电耦合材料的稳定性利用偏场理论可以研究初始构型的稳定性问题.静态时,可以通过研究增量能量密度函数的正定性来实现;而动态时,可以通过分析叠加于有限变形之上的增量波动特性(增长或衰减行为)来实现(Yang 2005a). Biot 在其专著(Biot 1965)中探讨了各向异性弹性体受初始应力的稳定性问题. Biogni 的专著(Biogni 2012)详细阐述了如何利用偏场理论对非线弹性和弹塑性材料的分叉(bifurcation)问题和材料失稳(instability)问题进行分析和研究. Dorfmann和Ogden(2010b)利用电弹性偏场理论研究了软电弹性体半空间在偏场作用下的稳定性问题. 相关研究工作也可参见Dorfmann和Ogden(2014b). Bertoldi和Gei(2011)讨论了在平面应变条件下力电有限偏场对软电弹性体层合结构稳定性的影响,给出了不同失稳模式的判别准则. 从传统观念来看,结构的设计应该使其工作于临界载荷以下,因为任意的失稳和分叉通常被认为是结构功能的不稳定和失效. 但大量研究发现软材料结构能在较大范围内承受超过屈曲或失稳临界值的变形和载荷,可充分利用其后屈曲阶段的变形特性和承载能力. 因此,利用软材料结构的屈曲或失稳可以实现很多过去无法想象的新奇科技与应用(Jang et al. 2009,Goncu et al. 2012,Rudykh & Boyce,2014,Wang & Casadei et al. 2014).
5.6 生物软组织超声弹性成像许多生物软组织是各向异性的,而横观各向同性是最简单也是最重要的一种各向异性,有明确的生物医学背景,如具有单一纤维排列方向的人体组织或者人造肌肉(Gennisson et al. 2010,Destrade et al. 2010a). 另外,许多疾病如癌症、肝硬化等通常会改变生物软组织的非线性力学特性(Jiang et al. 2015). 因此,确定各向异性生物软组织的非线性力学特性对于医学诊断至关重要. 而利用超声弹性成像技术(ultrasonicelastography technique)可以表征生物软组织的非线性力学特性,进而成为最近的研究热点之一(Ophir et al. 1991,1999; Gao et al. 1996; Sandrin et al. 2002a,2002b; Bercoff et al. 2004; O'Brien 2007; Khaled & Ermert,2008; Sarvazyan et al. 2011; Doyley 2012). 可通过两种方法确定生物软组织的非线性材料特性. 第一种是通过非线性(有限幅值)波动方法(Jacob et al. 2007,Réenier et al. 2008),但是非线性波在生物软组织中由于波的散射和由于波动强度变化而引起的温度变化使得非线性波的激励、控制和探测十分困难(Destrade et al. 2010b),而且非线性波将在生物软组织中产生较大的变形,不可避免地会造成生物软组织的损伤,至少在细胞水平上(Mironov et al. 2009),这也会影响非线性波的传播和探测. 另一种方法是通过声弹理论,即为本文所述的偏场方法.最近国际上有一些研究组利用偏场方法对软组织非线性材料特性的表征进行了研究(Gennisson et al. 2007; Destrade et al. 2010a,2010b; Latorre-Ossa et al. 2012; Jiang etal. 2015). 基于声弹理论,Gennisson 等(2007)利用声辐射力方法从理论和实验上确定了软物质的非线性剪切模量. Destrade 等(2010b)提出利用无限小声波(包括体波和表面波)与预加变形的耦合特性可从理论上确定不可压缩各向同性软物质中剪切波的非线性材料参数. Destrade 等(2010a)进一步利用偏场方法理论预测了不可压缩横观各向同性软物质中剪切波的非线性材料特性. 基于偏场理论,Latorre-Ossa 等(2012)结合静态弹性成像(static elastography)和超声剪切成像(supersonic shear imaging)技术实验测量了体外(ex vivo)生物软组织的三阶弹性常数; Jiang 等(2015)利用超声剪切成像技术数值确定和实验测量了体内(in vivo)生物软组织的非线性弹性性质. 生物软组织不仅是各向异性的,也具有力电耦合特性(Bassett & Becker,1962,Fukada 1968,Liu et al. 2012),因此研究偏场作用下力电耦合生物软组织中的波动特性将有助于获得高精度的超声弹性成像,从而为医学诊断提供有力的工具.
6 结论本文叙述了力电耦合固体非线性连续介质理论的一般框架,并重点推导和比较了现有的不同力电耦合偏场理论(或表述)之间的异同,具体体现在正文所列的4个表格中.可以看到,在现有各理论表述之间,事实上并没有实质性的区别,力电耦合固体非线性连续介质力学包括偏场理论的主要框架已经成熟.
尽管力电耦合偏场方法的理论框架已确立完成,但随着力电耦合智能软材料与结构的兴起以及微纳机电系统中非线性特性的出现,力电耦合偏场理论在不同领域中的应用将变得十分广泛.由于力电耦合软材料的潜在应用价值,并鉴于已有研究现状,今后的研究方向应该是针对具体应用中的问题进行建模与分析(如第5节所述),包括材料-结构-系统的一体化设计及相应的力学分析.由于常常涉及到强非线性和多场耦合,出现了一些新现象(包括失效破坏的新形式),而原有针对线性问题的方法或许也不再适用,需要发展新的理论、实验和计算方法,以推动多功能软材料的研究和工程应用.
本文只涉及到弹性变形与电场之间的耦合,没有考虑耗散,也没有考虑与其它物理、化学、生物等过程的耦合,对这方面感兴趣的读者可参考锁志刚(2011)和杨庆生等(2014)这两篇精彩的综述论文.
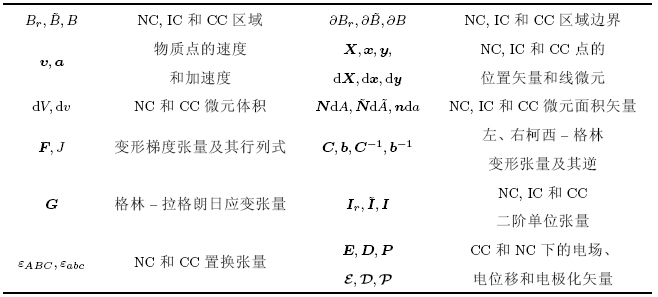
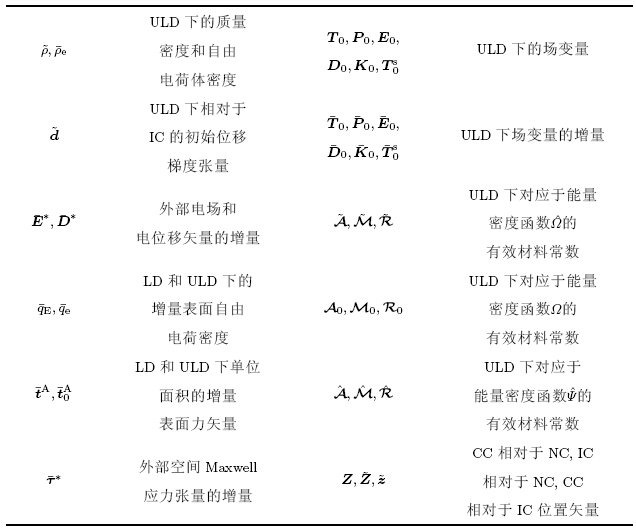
致谢 国家自然科学基金(11321202,11272281,11532001)和高等学校博士学科点专项科研基金(20130101110120)资助项目. 附录A 符号术语表以下表格中NC 表示自然构型(natural configuration),IC 表示初始构型(initial configuration),CC 表示现时构型(current configuration),LD 表示拉格朗日描述(Lagrangi and escription),ULD 表示更新拉格朗日描述(updated Lagrangian description).
符号术语表
 |
 |
 |
 |
本附录将列举一些文献中建议的若干具有代表性的各向同性软电弹性体能量密度函数的具体形式. 当不考虑温度的变化以及各种耗散和松弛机制时,假设软电弹性体的能量密度函数Ω*(F,D)可分解成两部分,即

(1)neo-Hookean 模型(Treloar 1975)

(2)Mooney-Rivlin 模型(Mooney 1940,Rivlin 1948)
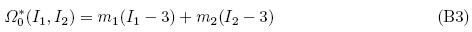
(3)Ogden 模型(Ogden 1997)

(4)Yeoh 模型(Yeoh 1990)
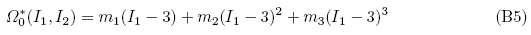
(5)Arruda{Boyce 模型(Arruda & Boyce,1993)
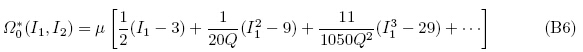
(6)Gent 模型(Gent 1996)
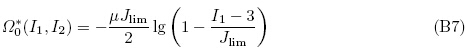
事实上,neo-Hookean 模型和Mooney-Rivlin 模型仅是Ogden 模型的两种特殊情况(Holzapfel 2000). Yeoh 模型、Arruda{Boyce 模型和Gent 模型可用于描述软材料在大应变时的刚化效应(Holzapfel 2000,锁志刚2011). neo-Hookean 模型和Arruda{Boyce 模型是统计力学模型,而其余4 种模型是连续介质力学的唯象模型(Holzapfel 2000,Boyce & Arruda 2000).
对电能密度函数Ω1*(F,D)的深入讨论可参考锁志刚(2011),这里将直接给出一些具体形式.
(1)线性的理想介电高弹体模型(Zhao et al. 2007,Zhao & Wang,2014)
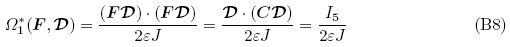
(2)非线性的理想电介质模型(锁志刚2011,Li & Liu et al. 2011)
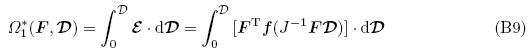
(3)准线性电介质模型(Zhao & Suo,2008,锁志刚2011)
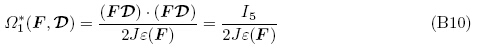
(4)准线性不可压缩电弹性模型(Dorfmann & Ogden,2010a,Dorfmann & Ogden,2010b)

 和
和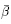 是力电耦合参数. 注意到,对于不可压缩材料,式(B8)~(B10)中J = 1.
是力电耦合参数. 注意到,对于不可压缩材料,式(B8)~(B10)中J = 1.
事实上,若假设电场和电位移的关系为E = D/ε(F),将其代入式(B9)中积分可获得准线性电介质模型(B10),进一步忽略介电常数与变形的依赖性即可得到线性的理想介电高弹体模型(B8). 另外,正如Dorfmann和Ogden(2014b)所述,准线性不可压缩电弹性模型(B11)中的参数 表征的是材料的电学性质对于变形的依赖性,而参数
表征的是材料的电学性质对于变形的依赖性,而参数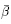 表征的是材料在电场作用下的刚度变化程度; 如果
表征的是材料在电场作用下的刚度变化程度; 如果 = 0,式(B11)退化为式(B8)所述的线性不可压缩理想介电高弹体模型.
= 0,式(B11)退化为式(B8)所述的线性不可压缩理想介电高弹体模型.
为模拟软电弹性体在工程实际中的力电耦合特性,还应该考虑诸多其它实际因素,包括材料可压缩性(Vertechy et al. 2012,Tagarielli et al. 2012)、各向异性(Huang et al. 2012,Yong et al. 2012)、热力耦合特性(Liu & Liu et al. 2011)、饱和极化(Li & Liu etal. 2011,Liu & Liu et al. 2012)、黏弹性或耗散特性(锁志刚2011,Hong 2011,Foo et al.2012)等的影响. 总之,对于能量密度函数具体形式的研究,还需要进行更为系统的实验验证和深入的理论分析.
| 苏益品, 陈伟球. 2014. 偏场作用下不可压缩软电弹性圆柱壳的轴对称波动. 应用力学学报, 31: 7-13 (Su Y P, Chen W Q. 2014. Axisymmetric waves in incompressible soft electroactive cylindrical shells subject to a biasing field. Chinese Journal of Applied Mechanics, 31: 7-13). |
| 锁志刚. 2011. 介电高弹聚合物理论. 力学进展, 41: 730-750 (Suo Z G. 2010. Theory of dielectric elastomers. Acta Mechanica Solida Sinica, 23: 549-578). |
| 杨庆生, 魏巍, 马连华. 2014. 智能软材料热-电-化-力学耦合问题的研究进展. 力学进展, 44: 201404. (Yang Q S, Wei W, Ma L H. 2014. Research advances in thermo-electro-chemo-mechanical coupling problem for intelligent soft materials. Advances in Mechanics, 44: 201404). |
| 赵晓鹏, 尹剑波. 2011. 电场调控的智能软材料. 北京: 科学出版社(Zhao X P, Yin J B. 2011. Smart Soft Materials Tuned by Electric Fields. Beijing: Science Press). |
| 周伟建, 陈伟球. 2015. 表面效应对偏场下介电高弹体表面波传播的影响. 应用数学和力学, 36: 119-127 (Zhou W J, Chen W Q. 2015. Surface effect on propagation of surface waves in a dielectric elastomer half space subject to biasing fields. Applied Mathematics and Mechanics, 36: 119-127). |
| Arruda E M, Boyce M C. 1993. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. Journal of the Mechanics and Physics of Solids, 41: 389-412. |
| Baesu E, Fortune D, Soós E. 2003. Incremental behaviour of hyperelastic dielectrics and piezoelectric crystals. Zeitschrift f&##196;ur angewandte Mathematik und Physik, 54: 160-178. |
| Bassett C A L, Becker R O. 1962. Generation of electric potentials by bone in response to mechanical stress. Science, 137: 1063-1064. |
| Bauer S. 2006. Piezo-, pyro-and ferroelectrets: Soft transducer materials for electromechanical energy conversion. IEEE Transactions on Dielectrics and Electrical Insulation, 13: 953-962. |
| Baumhauer J C, Tiersten H F. 1972. Nonlinear electroelastic equations for small fields superposed on a bias.Journal of the Acoustical Society of America, 54: 1017-1034. |
| Bayat A, Gordaninejad F. 2015. Bandgaps of a soft magneitorheological phononic crystal. Journal of Vibration and Acoustics, 137: 011011. |
| Bazant Z. 1971. A correlation study of formulations of incremental deformation and stability of continuous bodies. Journal of Applied Mechanics, 38: 919-928. |
| Bercoff J, Tanter M, Fink M. 2004. Supersonic shear imaging: A new technique for soft tissue elasticity mapping. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 51: 396-409. |
| Bertoldi K, Boyce M C. 2008a. Mechanically triggered transformations of phononic band gaps in periodic elastomeric structures. Physical Review B, 77: 052105. |
| Bertoldi K, Boyce M C. 2008b. Wave propagation and instabilities in monolithic and periodically structured elastomeric materials undergoing large deformations. Physical Review B, 78: 184107. |
| Bertoldi K, Gei M. 2011. Instabilities in multilayered soft dielectrics. Journal of the Mechanics and Physics of Solids, 59: 18-42. |
| Bigoni D. 2012. Nonlinear Solid Mechanics: Bifurcation Theory and Material Instability, Cambridge: Cam-bridge University Press. |
| Biot M A. 1965. Mechanics of Incremental Deformations: Theory of Elasticity and Viscoelasticity of Initially Stressed Solids and Fluids, Including Thermodynamic Foundations and Applications to Finite Strain. New York: Wiley. |
| Boyce M C, Arruda E M. 2000. Constitutive models of rubber elasticity: A review. Rubber Chemistry and Technology, 73: 504-523. |
| Brun M, Colquitt D J, Jones I S, Movchan A B, Movchan N V. 2014. Transformation cloaking and radial approximations for fiexural waves in elastic plates. New Journal of Physics, 16: 093020. |
| Bustamante R. 2009. Transversely isotropic non-linear electro-active elastomers. Acta Mechanica, 206: 237-259. |
| Bustamante R, Dorfmann A, Ogden R W. 2009a. Nonlinear electroelastostatics: A variational framework. Zeitschrift fÄur angewandte Mathematik und Physik, 60: 154-177. |
| Bustamante R, Dorfmann A, Ogden R W. 2009b. On electric body forces and Maxwell stresses in nonlinearly electroelastic solids. International Journal of Engineering Science, 47: 1131-1141. |
| Bustamante R, Ogden R W. 2013. Nonlinear magnetoelastostatics: Energy functionals and their second variations. Mathematics and Mechanics of Solids, 18: 760-772. |
| Camacho-Lopez M, Finkelmann H, Palffy-Muhoray P, Shelley M. 2004. Fast liquid-crystal elastomer swims into the dark. Nature Materials, 3: 307-310. |
| Campbell C. 1998. Surface Acoustic Wave Devices for Mobile and Wireless Communications. Boston: Academic Press. |
| Carpi F, Rossi D, Kornbluh R, Pelrine R, Sommer-Larsen P. 2011. Dielectric Elastomers as Electromechani-cal Transducers: Fundamentals, Materials, Devices, Models and Applications of an Emerging Electroactive Polymer Technology. New York: Elsevier. |
| Chai J F, Wu T T. 1996. Propagation of surface waves in a prestressed piezoelectric material. Journal of the Acoustical Society of America, 100: 2112-2122. |
| Chee C Y, Tong L, Steven G P. 1998. A review on the modelling of piezoelectric sensors and actuators incorporated in intelligent structures. Journal of Intelligent Material Systems and Structures, 9: 3-19. |
| ChenWQ, Dai H H. 2012. Waves in pre-stretched incompressible soft electroactive cylinders: Exact solution. Acta Mechanica Solida Sinica, 25: 530-541. |
| Cho Y, Yamanouchi K. 1987. Nonlinear, elastic, piezoelectric, electrostrictive, and dielectric constants of lithium niobate. Journal of Applied Physics, 61: 875-887. |
| Colquitt D J, Brun M, Gei M, Movchan A B, Movchan N V, Jones I S. 2014. Transformation elastodynamics and cloaking for fiexural waves. Journal of the Mechanics and Physics of Solids, 72: 131-143. |
| Deng Q, Liu L, Sharma P. 2013. Flexoelectricity and electrets in soft materials and biological membranes. Journal of the Mechanics and Physics of Solids, 62: 209-227. |
| Destrade M, Gilchrist M D, Ogden R W. 2010a. Third-and fourth-order elasticities of biological soft tissues. Journal of the Acoustical Society of America, 127: 2103-2106. |
| Destrade M, Gilchrist M D, Saccomandi G. 2010b. Third-and fourth-order constants of incompressible soft solids and the acousto-elastic effect. Journal of the Acoustical Society of America, 127: 2759-2763. |
| Diao J, Gall K, Dunn M L, Zimmerman J A. 2006. Atomistic simulations of the yielding of gold nanowires. Acta Materialia, 54: 643-653. |
| Díaz-Calleja R, Riande E, Sanchis M J. 2008. On electromechanical stability of dielectric elastomers. Applied Physics Letters, 93: 101902. |
| Dingreville R. 2007. Modeling and characterization of the elastic behavior of interfaces in nanostructured materials: From an atomistic description to a continuum approach. [PhD Dissertation]. Atlanta: Georgia Institute of Technology. |
| Dingreville R, Hallil A, Berbenni S. 2014. From coherent to incoherent mismatched interfaces: A generalized continuum formulation of surface stresses. Journal of the Mechanics and Physics of Solids, 72: 40-60. |
| Domenjoud M, Lematre M, Gratton M, Lethiecq M, Tran-Huu-Hue L-P. 2013. Theoretical and experimen-tal study of the electroacoustic behavior of lithium niobate under an initial mechanical stress. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 60: 2219-2224. |
| Dorfmann A, Ogden R W. 2005. Nonlinear electroelasticity. Acta Mechanica, 174: 167-183. |
| Dorfmann A, Ogden R W. 2006. Nonlinear electroelastic deformations. Journal of Elasticity, 82: 99-127. |
| Dorfmann A, Ogden R W. 2010a. Electroelastic waves in a finitely deformed electroactive material. IMA Journal of Applied Mathematics, 75: 603-636. |
| Dorfmann A, Ogden R W. 2010b. Nonlinear electroelastostatics: Incremental equations and stability. In-ternational Journal of Engineering Science, 48: 1-14. |
| Dorfmann L, Ogden R W. 2014a. Instabilities of an electroelastic plate. International Journal of Engineering Science, 77: 79-101. |
| Dorfmann L, Ogden R W. 2014b. Nonlinear Theory of Electroelastic and Magnetoelastic Interactions. New York: Springer. |
| Doyley M M. 2012. Model-based elastography: A survey of approaches to the inverse elasticity problem. Physics in Medicine and Biology, 57: R35-R73. |
| Du J, Jin X, Wang J. 2007a. Love wave propagation in layered magneto-electro-elastic structures with initial stress. Acta Mechanica, 192: 169-189. |
| Du J, Jin X, Wang J, Zhou Y. 2007b. SH wave propagation in a cylindrically layered piezoelectric structure with initial stress. Acta Mechanica, 191: 59-74. |
| Du J, Xian K, Wang J, Yong Y-K. 2008. Propagation of Love waves in prestressed piezoelectric layered structures loaded with viscous liquid. Acta Mechanica Solida Sinica, 21: 542-548. |
| Duquennoy M, Devos D, Ouaftouh M, Lochegnies D, Roméro E. 2006. Ultrasonic evaluation of residual stresses in fiat glass tempering: Comparing experimental investigation and numerical modeling. Journal of the Acoustical Society of America, 119: 3773-3781. |
| Duquennoy M, Ouaftouh M, Deboucq M, Lefebvre J-E, Jenot F, Ourak M. 2012. Infiuence of a superficial field of residual stress on the propagation of surface waves-Applied to the estimation of the depth of the superficial stressed zone. Applied Physics Letters, 101: 234104. |
| Duquennoy M, Ouaftouh M, Deboucq M, Lefebvre J-E, Jenot F, Ourak M. 2013. Characterization of micrometric and superficial residual stresses using high frequency surface acoustic waves generated by interdigital transducers. Journal of the Acoustical Society of America, 134: 4360-4371. |
| Duquennoy M, Ouaftouh M, Ourak M. 1999a. Determination of stresses in aluminium alloy using optical detection of Rayleigh waves. Ultrasonics, 37: 365-372. |
| Duquennoy M, Ouaftouh M, Ourak M. 1999b. Ultrasonic evaluation of stresses in orthotropic materials using Rayleigh waves. NDT&E International, 32: 189-199. |
| Duquennoy M, Ouaftouh M, Ourak M, Jenot F. 2002. Theoretical determination of Rayleigh wave acous-toelastic coe±cients: Comparison with experimental values. Ultrasonics, 39: 575-583. |
| Eliseev E A, Morozovska A N, Glinchuk M D, Blinc R. 2009. Spontaneous fiexoelectric/fiexomagnetic effect in nanoferroics. Physical Review B, 79: 165433. |
| Eliseev E A, Morozovska A N, Glinchuk M D, Zaulychny B Y, Skorokhod V V, Blinc R. 2010. Surface-induced piezomagnetic, piezoelectric, and linear magnetoelectric effects in nanosystems. Physical Review B, 82: 085408. |
| Ericksen J L. 2007. Theory of elastic dielectrics revisited. Archive for Rational Mechanics and Analysis, 183: 299-313. |
| Eringen A, Maugin G. 1990. Electrodynamics of Continua, Vol. 1: Foundations and Solid Media. New York: Springer-Verlag. |
| Foo C C, Cai S Q, Koh S J A, Bauer S, Suo Z. 2012. Model of dissipative dielectric elastomers. Journal of Applied Physics, 111: 034102. |
| Fox J W, Goulbourne N C. 2008. On the dynamic electromechanical loading of dielectric elastomer mem-branes. Journal of the Mechanics and Physics of Solids, 56: 2669-2686. |
| Fukada E. 1968. Piezoelectricity in polymers and biological materials. Ultrasonics, 6: 229-234. |
| Fung Y C. 1990. Biomechanics: Motion, Flow, Stress, and Growth. New York: Springer-Verlag. |
| Gafka D, Tani J. 1993. Sensitivity of surface acoustic wave velocity in lithium niobate to electric field or biasing stress. Journal of Applied Physics, 73: 7145-7151. |
| Gao L, Parker K J, Lerner R M, Levinson S F. 1996. Imaging of the elastic properties of tissue|A review.Ultrasound in Medicine & Biology, 22: 959-977. |
| Gei M, Movchan A B, Bigoni D. 2009. Band-gap shift and defect-induced annihilation in prestressed elastic structures. Journal of Applied Physics, 105: 063507. |
| Gei M, Roccabianca S, Bacca M. 2011. Controlling bandgap in electroactive polymer-based structures.IEEE/ASME Transactions on Mechatronics, 16: 102-107. |
| Gent A N. 1996. A new constitutive relation for rubber. Rubber Chemistry and Technology, 69: 59-61. |
| Gennisson J L, Rénier M, Catheline S, Barriμere C, Bercoff J, Tanter M, Fink M. 2007. Acoustoelasticity in soft solids: Assessment of the nonlinear shear modulus with the acoustic radiation force. Journal of the Acoustical Society of America, 122: 3211-3219. |
| Gennisson J L, De±eux T, Macé E, Montaldo G, Fink M, Tanter M. 2010. Viscoelastic and anisotropic mechanical properties of in vivo muscle tissue assessed by supersonic shear imaging. Ultrasound in Medicine & Biology, 36: 789-801. |
| Goncu F, Luding S, Bertoldi K. 2012. Exploiting pattern transformation to tune phononic band gaps in a two-dimensional granular crystal. Journal of the Acoustical Society of America, 131: 475-480. |
| Hashimoto K Y. 2000. Surface Acoustic Wave Devices in Telecommunications. Berlin: Springer. |
| He X, Yong H, Zhou Y. 2011. The characteristics and stability of a dielectric elastomer spherical shell with a thick wall. Smart Materials and Structures, 20: 055016. |
| Hoger A. 1993. The constitutive equation for finite deformations of a transversely isotropic hyperelastic material with residual stress. Journal of Elasticity, 33: 107-118. |
| Holzapfel G A. 2000. Nonlinear Solid Mechanics: A Continuum Approach for Engineering. Chichester:Wiley. |
| Hong W. 2011. Modeling viscoelastic dielectrics. Journal of the Mechanics and Physics of Solids, 59: 637-650. |
| Hu Y T, Yang J S, Jiang Q. 2002. On modeling of extension and fiexure response of electroelastic shells under biasing fields. Acta Mechanica, 156: 163-178. |
| Hu Y T, Yang J S, Jiang Q. 2004. Surface waves in electrostrictive materials under biasing fields. Zeitschrift fÄur angewandte Mathematik und Physik, 55: 678-700. |
| Huang J S, Lu T Q, Zhu J, Clarke D R, Suo Z. 2012. Large, uni-directional actuation in dielectric elastomers achieved by fiber stiffening. Applied Physics Letters, 100: 211901. |
| Huang W J, Sun R, Tao J, Menard L D, Nuzzo R G, Zuo J M. 2008. Coordination-dependent surface atomic contraction in nanocrystals revealed by coherent diffraction. Nature Materials, 7: 308-313. |
| Huang Y, Shen X D, Zhang C L, Chen W Q. 2014. Mechanically tunable band gaps in compressible soft phononic laminated composites with finite deformation. Physics Letters A, 378: 2285-2289. |
| Huang Y, Zhang C L, Chen W Q. 2014. Tuning band structures of two-dimensional phononic crystals with biasing fields. Journal of Applied Mechanics, 81: 091008. |
| Jacob X, Catheline S, Gennisson J L, Barriμere C, Royer D, Fink M. 2007. Nonlinear shear wave interaction in soft solids. Journal of the Acoustical Society of America, 122: 1917-1926. |
| Jang J H, Koh C Y, Bertoldi K, Boyce M C, Thomas E L. 2009. Combining pattern instability and shape-memory hysteresis for phononic switching. Nano Letters, 9: 2113-2119. |
| Jiang Y, Li G Y, Qiang L X, Hu X D, Liu D, Liang S, Cao Y P. 2015. Characterization of the nonlinear elastic properties of soft tissues using the supersonic shear imaging (SSI) technique: Inverse method, ex vivo and in vivo experiments. Medical Image Analysis, 20: 97-111. |
| Junge M, Qu J, Jacobs L J. 2006. Relationship between Rayleigh wave polarization and state of stress.Ultrasonics, 44: 233-237. |
| Khaled W, Ermert H. 2008. Ultrasonic strain imaging and reconstructive elastography for biological tissue.In: Artmann G M, Chien S. Bioengineering in Cell and Tissue Research, Springer, New York, 103-132. |
| Kosinski J, Pastore R A, Yang J S, Yang X M, Turner J A. 2002. Second-order frequency shifts in crystal resonators under relatively large biasing fields. In: Proc. of IEEE International Frequency Control Symposium, New Orleans LA, 103-110. |
| Kovetz A. 2000. Electromagnetic Theory. Oxford: Oxford University Press. |
| Latorre-Ossa H, Gennisson J L, De Brosses E, Tanter M. 2012. Quantitative imaging of nonlinear shear mod-ulus by combining static elastography and shear wave elastography. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 59: 833-839. |
| Lehmann W, Skupin H, Tolksdorf C, Gebhard E, Zentel R, KrÄuger P, LÄosche M, Kremer F. 2001. Giant lateral electrostriction in ferroelectric liquid-crystalline elastomers. Nature, 410: 447-450. |
| Lematre M, Domenjoud M, Tran-Huu-Hue L P. 2011. Exact second order formalism for the study of electro-acoustic properties in piezoelectric structures under an initial mechanical stress. Ultrasonics, 51: 898-910. |
| Lematre M, Feuillard G, Clézio E L, Lethiecq M. 2006a. Modeling of the infiuence of a prestress gradient on guided wave propagation in piezoelectric structures. Journal of the Acoustical Society of America, 120: 1964-1975. |
| Lematre M, Feuillard G, Delaunay T, Lethiecq M. 2006b. Modeling of ultrasonic wave propagation in inte-grated piezoelectric structures under residual stress. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 53: 685-696. |
| Leng J, Liu L, Liu Y, Yu K, Sun S. 2009. Electromechanical stability of dielectric elastomer. Applied Physics Letters, 94: 211901. |
| Li B, Chen H, Qiang J, Hu S, Zhu Z, Wang Y. 2011. Effect of mechanical pre-stretch on the stabilization of dielectric elastomer actuation. Journal of Physics D: Applied Physics, 44: 155301. |
| Li B, Liu L, Suo Z. 2011. Extension limit, polarization saturation, and snap-through instability of dielectric elastomers. International Journal of Smart and Nano Materials, 2: 59-67. |
| Liang H, Upmanyu M, Huang H. 2005. Size-dependent elasticity of nanowires: Nonlinear effects. Physical Review B, 71: 241403. |
| Lines M E, Glass A M. 1977. Principles and Applications of Ferroelectrics and Related Materials. Oxford: Clarendon Press. |
| Liu H, Kuang Z B, Cai Z M. 2003a. Propagation of Bleustein-Gulyaev waves in a prestressed layered piezoelectric structure. Ultrasonics, 41: 397-405. |
| Liu H, Kuang Z B, Cai Z M, Wang T J, Wang Z K. 2003b. Propagation of surface acoustic waves in prestressed anisotropic layered piezoelectric structures. Acta Mechanica Solida Sinica, 16: 16-23. |
| Liu H, Lee J J, Cai Z M. 2004. Analysis of nonlinear acoustoelastic effect of surface acoustic waves in laminated structures by transfer matrix method. Mechanics Research Communications, 31: 667-675. |
| Liu H, Shin K C, Lee J J, Cai Z M. 2004. Nonlinear acoustoelastic interactions of Lamb waves with LiNbO3 films deposited on sapphire substrates. Key Engineering Materials, 261: 263-268. |
| Liu H, Wang T J, Wang Z K, Kuang Z B. 2002a. Effect of a biasing electric field on the propagation of antisymmetric Lamb waves in piezoelectric plates. International Journal of Solids and Structures, 39: 1777-1790. |
| Liu H, Wang T J, Wang Z K, Kuang Z B. 2002b. Effect of a biasing electric field on the propagation of symmetric Lamb waves in piezoelectric plates. International Journal of Solids and Structures, 39: 2031-2049. |
| Liu L P. 2013a. An energy formulation of continuum magneto-electro-elasticity with applications. Journal of the Mechanics and Physics of Solids, 63: 451-480. |
| Liu L P. 2013b. On energy formulations of electrostatics for continuum media. Journal of the Mechanics and Physics of Solids, 61: 968-990. |
| Liu L W, Liu Y J, Li B, Yang K, Li T F, Leng J S. 2011. Thermo-electro-mechanical instability of dielectric elastomers. Smart Materials and Structures, 20: 075004. |
| Liu L W, Liu Y J, Luo X J, Li B, Leng J S. 2012. Electromechanical instability and snap-through instability of dielectric elastomers undergoing polarization saturation. Mechanics of Materials, 55: 60-72. |
| Liu Y M, Zhang Y H, Chow M J, Chen Q N, Li J Y. 2012. Biological ferroelectricity uncovered in aortic walls by piezoresponse force microscopy. Physical Review Letters, 108: 078103. |
| Mannsfeld S C B, Tee B C K, Stoltenberg R M, Chen C V H, Barman S, Muir B V O, Sokolov A N, Reese C, Bao Z. 2010. Highly sensitive fiexible pressure sensors with microstructured rubber dielectric layers. Nature Materials, 9: 859-864. |
| Maugin G A. 1988. Continuum Mechanics of Electromagnetic Solids. Amsterdam: North-Holland. |
| McCarty L S, Whitesides G M. 2008. Electrostatic charging due to separation of ions at interfaces: Contact electrification of ionic electrets. Angewandte Chemie International Edition, 47: 2188-2207. |
| McMeeking R M, Landis C M. 2005. Electrostatic forces and stored energy for deformable dielectric mate-rials. Journal of Applied Mechanics, 72: 581-590. |
| Mironov M A, Pyatakov P A, Konopatskaya I I, Clement G T, Vykhodtseva N I. 2009. Parametric excitation of shear waves in soft solids. Acoustical Physics, 55: 567-574. |
| Mooney M. 1940. A theory of large elastic deformation. Journal of Applied Physics, 11:582-592. |
| Narayanaswamy O S. 1978. Stress and structural relaxation in tempering glass. Journal of the American Ceramic Society, 61: 146-152. |
| Nelson D F. 1978. Theory of nonlinear electroacoustics of dielectric, piezoelectric, and pyroelectric crystals. Journal of the Acoustical Society of America, 63: 1738-1748. |
| Nelson D F. 1979. Electric, Optic, and Acoustic Interactions in Dielectrics. New York: Wiley. |
| Nelson D F, Lax M. 1976. Linear elasticity and piezoelectricity in pyroelectrics. Physical Review B, 13: 1785-1796. |
| Norris A N, Amirkulova F A, ParnellWJ. 2014. Active elastodynamic cloaking. Mathematics and Mechanics of Solids, 19: 603-625. |
| Norris A N, Parnell W J. 2012 Hyperelastic cloaking theory: Transformation elasticity with pre-stressed solids. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science, 468: 2881-2903. |
| Norris A N, Shuvalov A L. 2011. Elastic cloaking theory. Wave Motion, 48: 525-538. |
| O'Brien W D. 2007. Ultrasound-biophysics mechanisms. Progress in Biophysics and Molecular Biology, 93: 212-255. |
| O'Halloran A, O'Malley F, McHugh P. 2008. A review on dielectric elastomer actuators, technology, appli-cations, and challenges. Journal of Applied Physics, 104: 071101. |
| Ogden R W. 1997. Nonlinear Elastic Deformations. New York: Dover. |
| Ogden R W. 2009. Incremental elastic motions superimposed on a finite deformation in the presence of an electromagnetic field. International Journal of Non-Linear Mechanics, 44: 570-580. |
| Ophir J, Alam S K, Garra B, Kallel F, Konofagou E, Krouskop T, Varghese T. 1999. Elastography: Ul-trasonic estimation and imaging of the elastic properties of tissues. Proceedings of the Institution of |
| Mechanical Engineers, Part H: Journal of Engineering in Medicine, 213: 203-233. |
| Ophir J, Cespedes I, Ponnekanti H, Yazdi Y, Li X. 1991. Elastography: A quantitative method for imaging the elasticity of biological tissues. Ultrasonic Imaging, 13: 111-134. |
| Palma A, Palmieri L, Socino G, Verona E. 1985a. Acoustic Lamb wave-electric field nonlinear interaction in YZ LiNbO3 plates. Applied Physics Letters, 46: 25-27. |
| Palma A, Palmieri L, Socino G, Verona E. 1985b. Lamb-wave electroacoustic voltage sensor. Journal of Applied Physics, 58: 3265-3267. |
| Palmieri L, Socino G, Verona E. 1986. Electroelastic effect in layer acoustic mode propagation along ZnO films on Si substrates. Applied Physics Letters, 49: 1581-1583. |
| Palmieri L, Socino G, Verona E, Tran H T, Marini A. 1988. Nonlinear electroacoustic interaction between a bias electric field and acoustic Lamb modes in LiNbO3 plates. Journal of Applied Physics, 64: 1033-1039. |
| Pan X H, Yu S W, Feng X Q. 2011. A continuum theory of surface piezoelectricity for nanodielectrics. Science China Physics, Mechanics and Astronomy, 54: 564-573. |
| Pao Y H. 1978. Electromagnetic forces in deformable continua. In: Nemat-Nasser S, ed. Mechanics Today, Vol. 4, Pergamon Press, Oxford, 209-306. |
| Pao Y H, Sachse W, Fukuoka H. 1984. Acoustoelasticity and ultrasonic measurements of residual stresses. In: Mason W P, Thurston R N, ed. Physical Acoustics, Vol. XVII, Academic Press, New York, 61-143. |
| Parnell W J. 2012. Nonlinear pre-stress for cloaking from antiplane elastic waves. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science, 468: 563-580. |
| Parnell W J, Norris A N, Shearer T. 2012. Employing pre-stress to generate finite cloaks for antiplane elastic waves. Applied Physics Letters, 100: 171907. |
| Parnell W J, Shearer T. 2013. Antiplane elastic wave cloaking using metamaterials, homogenization and hyperelasticity. Wave Motion, 50: 1140-1152. |
| Pelrine R, Kornbluh R, Pei Q B, Joseph J. 2000. High-speed electrically actuated elastomers with strain greater than 100%. Science, 287: 836-839. |
| Qian Z, Jin F, Kishimoto K, Wang Z. 2004a. Effect of initial stress on the propagation behavior of SH-waves in multilayered piezoelectric composite structures. Sensors and Actuators A: Physical, 112: 368-375. |
| Qian Z, Jin F, Wang Z, Kishimoto K. 2004b. Love waves propagation in a piezoelectric layered structure with initial stresses. Acta Mechanica, 171: 41-57. |
| Rao S S, Sunar M. 1994. Piezoelectricity and its use in disturbance sensing and control of fiexible structures: A survey. Applied Mechanics Reviews, 47: 113-123. |
| Rénier M, Gennisson J L, Barrire C, Royer D, Fink M. 2008. Fourth-order shear elastic constant assessment in quasi-incompressible soft solids. Applied Physics Letters, 93: 101912. |
| Rinaldi C, Brenner H. 2002. Body versus surface forces in continuum mechanics: Is the Maxwell stress tensor a physically objective Cauchy stress? Physical Review E, 65: 036615. |
| Rivlin R S. 1948. Large elastic deformations of isotropic materials. IV. further developments of the gen-eral theory. Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 241: 379-397. |
| Rodriguez E K, Hoger A, McCulloch A D. 1994. Stress-dependent finite growth in soft elastic tissues. Journal of Biomechanics, 27: 455-467. |
| Rosset S, Shea H R. 2013. Flexible and stretchable electrodes for dielectric elastomer actuators. Applied Physics A, 110: 281-307. |
| Rudykh S, Boyce M C. 2014. Transforming wave propagation in layered media via instability-induced interfacial wrinkling.Physical Review Letters, 112: 034301. |
| Sandrin L, Tanter M, Catheline S, Fink M. 2002a. Shear modulus imaging with 2-D transient elastography. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 49: 426-435. |
| Sandrin L, Tanter M, Gennisson J L, Catheline S, Fink M. 2002b. Shear elasticity probe for soft tissues with 1-D transient elastography. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 49: 436-446. |
| Saravanan U. 2008. Representation for stress from a stressed reference configuration. International Journal of Engineering Science, 46: 1063-1076. |
| Sarvazyan A, Hall T J, Urban M W, Fatemi M, Aglyamov S R, Garra B S. 2011. An overview of elastography-An emerging branch of medical imaging. Current Medical Imaging Reviews, 7: 255-282. |
| Shams M, Destrade M, Ogden R W. 2011. Initial stresses in elastic solids: Constitutive laws and acoustoe-lasticity. Wave Motion, 48: 552-567. |
| Shams M, Ogden R W. 2014. On Rayleigh-type surface waves in an initially stressed incompressible elastic solid. IMA Journal of Applied Mathematics, 79: 360-376. |
| Shan S, Kang S H, Wang P, Qu C, Shian S, Chen E R, Bertoldi K. 2014. Harnessing multiple folding mechanisms in soft periodic structures for tunable control of elastic waves. Advanced Functional Materials, 24: 4935-4942. |
| Shmuel G. 2013a. Axisymmetric wave propagation in finitely deformed dielectric elastomer tubes. Proceed-ings of the Royal Society A: Mathematical, Physical and Engineering Science, 469: 20130071. |
| Shmuel G. 2013b. Electrostatically tunable band gaps in finitely extensible dielectric elastomer fiber com-posites. International Journal of Solids and Structures, 50: 680-686. |
| Shmuel G, deBotton G. 2012. Band-gaps in electrostatically controlled dielectric laminates subjected to incremental shear motions. Journal of the Mechanics and Physics of Solids, 60: 1970-1981. |
| Shmuel G, Gei M, deBotton G. 2012. The Rayleigh-Lamb wave propagation in dielectric elastomer layers subjected to large deformations. International Journal of Non-Linear Mechanics, 47: 307-316. |
| Simionescu P O. 2000. The infiuence of initial fields on wave propagation in piezoelectric crystals. Interna-tional Journal of Applied Electromagnetics and Mechanics, 12: 241-251. |
| Simionescu P O. 2001. Progressive wave propagation in the meridian plane of a 6 mm-type piezoelectric crystal subject to initial fields. Mathematics and Mechanics of Solids, 6: 661-670. |
| Simionescu P O. 2002. Wave propagation in cubic crystals subject to initial mechanical and electric fields. Zeitschrift fÄur angewandte Mathematik und Physik, 53: 1038-1051. |
| Simionescu P O. 2005. Attenuated wave propagation on a face of a cubic crystal subject to initial electro-mechanical fields. International Journal of Applied Electromagnetics and Mechanics, 22: 111-120. |
| Simionescu P O. 2007. Propagation of attenuated waves along an edge of a cubic crystal subject to initial electro-mechanical fields. Mathematics and Mechanics of Solids, 12: 107-118. |
| Simionescu P O, Ana I. 2009. On the coupling of guided waves propagation in piezoelectric crystals subject to initial fields. Mathematics and Mechanics of Solids, 14: 502-513. |
| Simionescu P O, Sos E. 2001. Wave propagation in piezoelectric crystals subjected to initial deformations and electric fields. Mathematics and Mechanics of Solids, 6: 437-445. |
| Singh B. 2010. Wave propagation in a prestressed piezoelectric half-space. Acta Mechanica, 211: 337-344. |
| Sinha B K, Tiersten H F. 1979. On the infiuence of a fiexural biasing state on the velocity of piezoelectric surface waves. Wave Motion, 1: 37-51. |
| Smith G F, Smith M M, Rivlin R S. 1963. Integrity bases for a symmetric tensor and a vector | The crystal classes. Archive for Rational Mechanics and Analysis, 12: 93-133. |
| Son M S, Kang Y J. 2011. The effect of initial stress on the propagation behavior of SH waves in piezoelectric coupled plates. Ultrasonics, 51: 489-495. |
| Sos E. 1996. Stability, resonance and stress concentration in prestressed piezoelectric crystals containing a crack. International Journal of Engineering Science, 34: 1647-1673. |
| Spencer A J M. 1971. Theory of invariants. In: Eringen A C, ed. Continuum Physics, Vol. 1, Academic Press, New York, 292-307. |
| Su J, Kuang Z B, Liu H. 2005. Love wave in ZnO/SiO2/Si structure with initial stresses. Journal of Sound and Vibration, 286: 981-999. |
| Sunar M, Rao S S. 1999. Recent advances in sensing and control of fiexible structures via piezoelectric materials technology. Applied Mechanics Reviews, 52: 1-16. |
| Suo Z, Zhao X, Greene W H. 2008. A nonlinear field theory of deformable dielectrics. Journal of the Mechanics and Physics of Solids, 56: 467-486. |
| Tagarielli V L, Hildick-Smith R, Huber J E. 2012. Electro-mechanical properties and electrostriction response of a rubbery polymer for EAP applications. International Journal of Solids and Structures, 49: 3409-3415. |
| Thomsen D L, Keller P, Naciri J, Pink R, Jeon H, Shenoy D, Ratna B R. 2001. Liquid crystal elastomers with mechanical properties of a muscle. Macromolecules, 34: 5868-5875. |
| Thurston R, Brugger K. 1964. Third-order elastic constants and the velocity of small amplitude elastic waves in homogeneously stressed media. Physical Review, 133: A1604. |
| Tiersten H F. 1969. Linear Piezoelectric Plate Vibrations. New York: Plenum. |
| Tiersten H F. 1971. On the nonlinear equations of thermo-electroelasticity. International Journal of Engi-neering Science, 9: 587-604. |
| Tiersten H F. 1975. Nonlinear electroelastic equations cubic in the small field variables. Journal of the Acoustical Society of America, 57: 660-666. |
| Tiersten H F. 1981. Electroelastic interactions and the piezoelectric equations. Journal of the Acoustical Society of America, 70: 1567-1576. |
| Tiersten H F. 1995. On the accurate description of piezoelectric resonators subject to biasing deformations.International Journal of Engineering Science, 33: 2239-2259. |
| Tiersten H F, Sinha B K, Meeker T R. 1981. Intrinsic stress in thin films deposited on anisotropic substrates and its infiuence on the natural frequencies of piezoelectric resonators. Journal of Applied Physics, 52: 5614-5624. |
| Toupin R A. 1956. The elastic dielectric. Journal of Rational Mechanics and Analysis, 5: 849-915. |
| Toupin R A. 1963. A dynamical theory of elastic dielectrics. International Journal of Engineering Science, 1: 101-126. |
| Treloar L R G. 1975. The Physics of Rubber Elasticity. Oxford: Oxford University Press. |
| Trimarco C. 2009. On the Lagrangian electrostatics of elastic solids. Acta Mechanica, 204: 193-201. |
| Uchino K. 1997. Piezoelectric Actuators and Ultrasonic Motors. Boston: Kluwer Academic Publishers. |
| Vertechy R, Frisoli A, Bergamasco M, Carpi F, Frediani G, De Rossi, D. 2012. Modeling and experimental validation of buckling dielectric elastomer actuators. Smart Materials and Structures, 21: 094005. |
| Voltairas P, Fotiadis D, Massalas C. 2003. A theoretical study of the hyperelasticity of electro-gels. Pro-ceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 459: 2121-2130. |
| Wang J S, Evans A G. 1998. Measurement and analysis of buckling and buckle propagation in compressed oxide layers on superalloy substrates. Acta Materialia, 46: 4993-5005. |
| Wang P, Casadei F, Shan S, Weaver J C, Bertoldi K. 2014. Harnessing buckling to design tunable locally resonant acoustic metamaterials. Physical Review Letters, 113: 014301. |
| Wang P, Shim J, Bertoldi K. 2013. Effects of geometric and material nonlinearities on tunable band gaps and low-frequency directionality of phononic crystals. Physical Review B, 88: 014304. |
| Wang S D, Xiao J L, Song J Z, Ko H C, Hwang K C, Huang Y G, Rogers J A. 2010. Mechanics of curvilinear electronics. Soft Matter, 6: 5757-5763. |
| Wang X Q, Gu Y S, Sun X, Wang H, Zhang Y. 2014. Third-order elastic constants of ZnO and size effect in ZnO nanowires. Journal of Applied Physics, 115: 213516. |
| Wang Y Z, Zhang C L, Dai H H, Chen W Q. 2015. Adjustable solitary waves in electroactive rods. Journal of Sound and Vibration, DOI: 10.1016/j.jsv.2015.04.023. |
| Wang Z J, Liu C, Li Z G, Zhang T Y. 2010. Size-dependent elastic properties of Au nanowires under bending and tension-surfaces versus core nonlinearity. Journal of Applied Physics, 108: 083506. |
| Xu Y, Shen S P. 2012. Surface electric Gibbs free energy and its effect on the electromechanical behavior of nano-dielectrics. Computers Materials and Continua, 28: 81-95. |
| Yang J S. 2001. Bleustein-Gulyaev waves in strained piezoelectric ceramics. Mechanics Research Commu-nications, 28: 679-683. |
| Yang J S. 2003. Equations for small fields superposed on finite biasing fields in a thermoelectroelastic body.IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 50: 187-192. |
| Yang J S. 2004. Variational formulation of the equations for small fields superposed on finite biasing fields in an electroelastic body. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 51: 1030-1034. |
| Yang J S. 2005a. An Introduction to the Theory of Piezoelectricity. New York: Springer. |
| Yang J S. 2005b. Free vibrations of an electroelastic body under biasing fields. IEEE Transactions on Ultrasonics Ferroelectrics, and Frequency Control, 52: 358-364. |
| Yang J S. 2009. Special Topics in the Theory of Piezoelectricity. New York: Springer. |
| Yang J S, Hu Y T. 2004. Mechanics of electroelastic bodies under biasing fields. Applied Mechanics Reviews, 57: 173-189. |
| Yang W, Suo Z. 1994. Cracking in ceramic actuators caused by electrostriction. Journal of the Mechanics and Physics of Solids, 42: 649-664. |
| Yeoh O H. 1990. Characterization of elastic properties of carbon-black-filled rubber vulcanizates. Rubber Chemistry and Technology, 63: 792-805. |
| Yong H D, He X Z, Zhou Y H. 2012. Electromechanical instability in anisotropic dielectric elastomers. International Journal of Engineering Science, 50: 144-150. |
| Zhang Q, Bharti V, Zhao X. 1998. Giant electrostriction and relaxor ferroelectric behavior in electron-irradiated poly (vinylidene fiuoride-trifiuoroethylene) copolymer. Science, 280: 2101-2104. |
| Zhang S H, Huang C, Klein R J, Xia F, Zhang Q M, Cheng Z Y. 2007. High performance electroactive poly-mers and nano-composites for artificial muscles. Journal of Intelligent Material Systems and Structures, 18: 133-145. |
| Zhang T Y, Luo M, Chan W K. 2008. Size-dependent surface stress, surface stiffness, and Young's modulus of hexagonal prism [111] fi-SiC nanowires. Journal of Applied Physics, 103: 104308. |
| Zhang T Y, Wang Z J, Chan W K. 2010. Eigenstress model for surface stress of solids. Physical Review B, 81: 195427. |
| Zhao X, Hong W, Suo Z. 2007. Electromechanical hysteresis and coexistent states in dielectric elastomers. Physical Review B, 76: 134113. |
| Zhao X, Suo Z. 2008. Electrostriction in elastic dielectrics undergoing large deformation. Journal of Applied Physics, 104: 123530. |
| Zhao X, Suo Z. 2010. Theory of dielectric elastomers capable of giant deformation of actuation. Physical Review Letters, 104: 178302. |
| Zhao X, Wang Q M. 2014. Harnessing large deformation and instabilities of soft dielectrics: Theory, exper-iment, and application. Applied Physics Reviews, 1: 021304. |
| Zheng Q S. 1994. Theory of representations for tensor functions. A unified invariant approach to constitutive equations. Applied Mechanics Reviews, 47: 545-587. |
| Zhou Y Y, Chen W Q, Yang J S. 2011. Thickness-shear vibration of a quartz plate connected to piezoelectric plates and electric field sensing. Ultrasonics, 51: 131-135. |
| Zhou Y Y, LÄu C F, Chen W Q. 2012. Bulk wave propagation in layered piezomagnetic/piezoelectric plates with initial stresses or interface imperfections. Composite Structures, 94: 2736-2745. |



