据文献记载，世界上已知隶属于鳞翅目(Lepidoptera)天蛾科(Sphingidae)的天蛾种类约有1 000种，我国天蛾种类约占世界种类的1/5(朱弘复等，1997)。天蛾科昆虫多为农林业重要害虫，对农林业造成了重要的危害和经济损失，准确地进行昆虫物种鉴定是害虫测报与防治的基础，同时动植物检疫和资源昆虫的保护及利用等方面也需要昆虫鉴定的工作。当前对蛾类昆虫鉴定还主要依靠传统的人工方法，这不仅要求鉴定人员具备一定的专业知识与长期的经验积累，而且鉴定工作耗时、主观性强。如何在生物分类学家人数减少的同时，能够对大量分类学资源进行快捷有效的信息提取和准确鉴定，是当今人们面临的一个重要挑战(Gaston et al., 2004；张蕾等，2011)。

几何形态测量学(Geometric morphometric)是关于生物形态结构定量比较的科学计算工具(白明等，2014a)，该方法通过在图形中设置具有生物学意义的同源标记点(Landmarks)或轮廓线而将图形引入二维或三维坐标系，并利用标记点的坐标值来捕获研究对象的形状信息(Slice, 2001；Adams et al., 2004；Zelditch et al., 2004；Mitteroecker et al., 2009)。同时，通过标记点间的相对位置使样本间形状差异变得更加直观(Adams et al., 2013)。一直以来，关于几何形态测量学的报道主要集中在医学(Slice，2007)、大型哺乳动物(Fureix et al., 2011；Baab et al., 2012)、古人类学(邢松等，2012；张亚盟等，2016；周蜜等，2016)和少数节肢动物(Gutierrez et al., 2011；Bai et al., 2012；Hübler et al., 2013；白明等，2014b)等领域。近十年，随着几何形态测量学日臻完善和成熟，其越来越多地应用在昆虫学的相关领域，如：昆虫的形态进化、系统发育和亲缘关系(潘鹏亮等，2008；闫宝荣，2011；Ge et al., 2011；Outomuro et al., 2013)；昆虫的雌雄二态性(白义等，2015)；种间或种下阶元昆虫的形态分化规律、地理环境因素对昆虫形态分化的影响(Hernández et al., 2010；Kitthawee et al., 2011；张秀秀等，2017)等。在国内，几何形态测量学方法在各个领域发挥着越来越重要的作用(詹庆斌，2014；佟一杰等，2016；李荣荣等，2016)，但是应用于昆虫数字化分类的研究还不多见。

针对天蛾成虫翅型极其相似，利用数学形态特征较难实现天蛾成虫数字化分类识别的问题，本研究以天蛾科10种天蛾成虫作为研究对象，对天蛾成虫前翅进行几何形态测量学分析，探讨利用几何形态测量方法实现天蛾成虫的数字化分类。若利用几何形态测量学对10种天蛾可取得较好的分类效果，便可进一步将其应用在更多种类的昆虫分类鉴定中。本文利用天蛾成虫右前翅进行研究，而不是利用昆虫的整个标本特征，这是考虑到：蛾类翅的翅脉特征不仅是蛾类等多数昆虫的主要鉴定特征之一，且其翅的翅脉图像便于获取，同时，具有同源性的标记点容易选取，并且保证了标记点的可重复选择，便于日后添加其他种类的蛾类昆虫。如果研究证实了本文提出的方法是可行的，则可将其扩展应用到其他蛾类昆虫成虫的分类鉴定中；同时，如果研究表明仅以右前翅翅脉特征鉴定蛾类昆虫的成虫仍有不足，还可考虑利用蛾类成虫其他部位的特征，以提高鉴定的准确性。

1 材料与方法 1.1 试验材料

本文选择天蛾科10种天蛾成虫作为试验材料，以它们的右前翅为研究对象，对天蛾成虫前翅脉图像进行标记点的选取，并获得相应的坐标数据，探讨标记点数据应用于天蛾成虫分类鉴定的可行性。试验所选10种天蛾隶属于4个亚科，其中面形天蛾亚科(Acherontiinae)1种、蜂形天蛾亚科(Philampelinae)1种、斜纹天蛾亚科(Choerocampinae)3种、云纹天蛾亚科(Ambulicinae)5种。这10种天蛾均为较常见的物种，并且物种间前翅翅脉的拓扑结构很相似，而几何形态测量学侧重于对生物形态的拓扑结构进行研究，这可帮助笔者从技术角度探明几何形态测量学方法在蛾类昆虫分类鉴定中应用的可行性。试验所用10种天蛾，每个种类取30个样本。10种蛾具体信息见表 1。

1.2 翅脉图像获取

由于鳞翅目成虫翅面上覆盖有大量鳞片，因此获取其翅脉图像首先要考虑去除蛾翅上的鳞片。本文利用化学浸泡法去除蛾翅面的鳞片和斑纹(蔡小娜，2013)，所采用药品、仪器和具体步骤如下。

药品和仪器：盐酸(质量分数36%~38%)，国药集团化学试剂有限公司；乙醇(质量分数95%)，国药集团化学试剂有限公司；次氯酸钠(有效氯≥10%)，国药集团化学试剂有限公司；大号培养皿(5套)、定性滤纸(中速)、水盆(2个)、镊子。

具体操作步骤：第1步，从蛾标本上取下完整的前翅，放入70%左右的乙醇溶液中约3 min或更长时间，使翅面充分浸润并具有一定的弹性，以免去鳞片不彻底或在以后的操作中折损蛾翅；第2步，用镊子把已浸润的蛾翅移入次氯酸钠溶液中1~3 min；第3步，再将翅移入盐酸溶液中约1~3 min，翅面的鳞片和斑纹会逐渐褪去。如果鳞片或斑纹没有去除干净，可重复第2和第3步，直到翅脉清晰可辨；第4步，将处理好的蛾翅移入水盆中，稀释掉残留的盐酸或次氯酸钠溶液；第5步，用纸条把翅从水中黏附出来，等翅面不再有流动的水时把其压在平整的纸层中，让其自然阴干，制成蛾翅脉标本。

蛾翅翅脉数字图像获取通过带有透扫功能的中晶Phantom v900 Plus型平板式扫描仪，在600 dpi分辨率下对翅脉标本进行负片扫描。图像保存为8位(8bit)的灰度图，在分析时使用原始图像，图像未压缩。

2 几何形态测量学 2.1 标记点选取

标记点的选择对于分析的结果有直接而且重要的影响，一般选择Bookstein分类(Bookstein，1991)中的第Ⅰ型或第Ⅱ型作为标记点的标准。这2种标记点的共同点是可以从解剖学特征上准确地在每一个标本上找到，而无不明确或复现困难的可能性。为了保证标记点的可重复选择，方便日后添加其他种类的蛾类昆虫，本研究选择第Ⅰ型标记点，即研究对象间其同源性有强烈证据支持的数学点(闫宝荣等，2010)，譬如结构上的交点、昆虫翅脉的交点和端点。

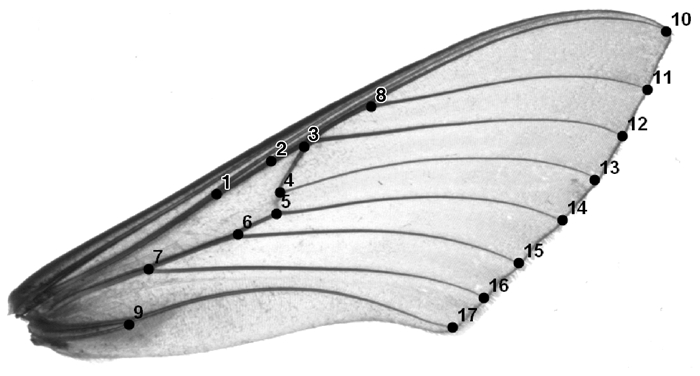
利用tpsDig软件对天蛾右前翅翅脉交点按特定次序进行标记(Rohlf，1998a；蔡小娜，2013)。翅面交点从径脉(R1)基部为起始点，顺时针方向依次取翅室周围所有翅脉交点，之后选取径脉R4和R5的交点和臀脉(A)基部分岔的交点，最后从径脉(R4)与翅外缘的交点开始顺时针方向选取所有翅外缘翅脉交点，共选择17个翅脉交点作为标记点，以深色白眉天蛾(Celerio gallii)为例给出所选取标记点的位置分布简图(图 1)。

2.2 普氏叠加

标记点的原始坐标数据包含了许多非形状因素，如获取图像时标本摆放的位置、方向、坐标系的选取(原点、刻度)及大小等(Rohlf，1999)。因此，利用软件tpsSuper(Rohlf，1998b)对样本数据进行普氏叠加分析，通过置中、旋转和缩放，以几何学上相应的线性代数作矩阵运算，所得运算结果消除了上述非形状因素等多余的信息，留下真正想要的形状。以深色白眉天蛾为例，进行普氏叠加分析可得到所有样本标记点的散点图和向量图(图 2)，从图中可以看出通过普氏分析相应的标记点都排列在质心的周围，这也从可视化角度验证了叠加后的标记点分布情况。

2.3 相对扭曲

由相对扭曲分析得到17个标记点的贡献率如表 2所示，由表 2可知，标记点2、4和5的贡献率相对较大，分别为34.54%、22.86%和11.85%，这也说明10种天蛾昆虫前翅基部的变异大于端部，或者可以说翅室周围的变异相对较大。

3 多元统计分析与结果 3.1 标记点差异显著性检验

单因素方差分析公式为$F = \frac{{{{\overline S }_{\rm{A}}}}}{{{{\overline S }_{\rm{E}}}}} = \frac{{{S_{\rm{A}}}}}{{s - 1}}/\frac{{{S_{\rm{E}}}}}{{n - s}}$(盛骤等，2001)，式中：S_A为效应平方和，S_E为误差平方和，n为样本总和，s为因素水平。

通过相对扭曲分析，可得到17个标记点的效应平方和S_A与误差平方和S_E(表 3)。由本文样本数据可知n=300，s=10。由单因素方差分析公式可计算得到各个标记点的F值(表 3)。根据F分布表，F_0.05(9, 290)=1.88、F_0.01(9, 290)=2.41。由此可知在显著性水平为0.05和0.01时F值均小于各个标记点的F值，所以10种天蛾的17个标记点间均具有显著甚至极显著的差异，即标记点在种间是有显著差异的，可以用于本文10种天蛾的分类鉴定。

3.2 主成分分析

利用软件SPSS13.0对10种天蛾300个样本经普氏叠加所得标记点坐标数据进行主成分分析，得到主成分的方差解释率(表 4)和主成分的得分系数矩阵。由表 4可知，第1个主成分的贡献率已达到86.01%，而一般认为若k个主成分达到85%，表明取前k个主成分基本包含了全部测量指标所具有的信息(于秀林等，1999)。

根据表 4的方差累计百分比，本文确定提取前3个主成分(累计贡献率为97.7%)，由主成分分析得到的前3个主成分的得分系数矩阵如表 5所示。根据该得分系数矩阵以及变量的观察值可计算出主成分得分，因通过表 4已确定提取3个主成分，此处将相应产生3个主成分得分，它们可作为对10种天蛾成虫进行分类鉴定的新变量。

3.3 判别分析

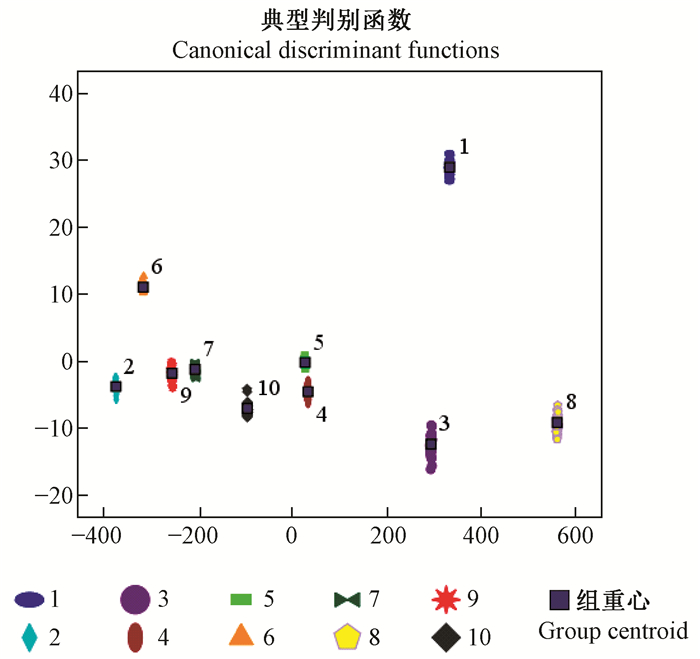
利用软件SPSS13.0对主成分分析所得的前3个主成分得分矩阵进行判别分析，得到10种天蛾300个样本的二维散点图(图 3)。从图 3中可知，10种天蛾明显地分为了10组，并且每种天蛾都很好地聚在了一起。300个样本的回归判别和交叉判别结果如表 6所示，回归判别和交叉判别的正确率均为100%，即利用几何形态测量学数据对10种天蛾成虫进行分类鉴定，达到了百分之百的准确率。

4 讨论

天蛾昆虫中有很多种类为害虫，以后可以利用几何形态测量学逐渐扩大对其种类的研究，实现常见天蛾害虫的数字化分类。但随着需要鉴别的天蛾种类的增加，可能需要在翅脉上选取更多标记点才能满足要求。此外，在今后的研究中，如果仅用前翅特征不能满足需求，还可将蛾后翅、头部、前胸背板、腹部、体躯等部位的数字化特征应用到昆虫分类中。昆虫自动分类鉴定的一个很重要的研究步骤就是对特征参数的选取，选取一组好的参数特征，既能方便提取和应用，又可使昆虫分类的准确率和有效性得以提高。随着自动分类系统中昆虫种类的不断增加，需要不断探索新的特征参数。

本文供试样本雌雄蛾均有，且是随机抽取个体，在分析过程中采用了与翅大小尺度和方向均无关的形态特征，因此虽然同一种蛾在雌雄之间会有一定差异，但是本文所用的这些特征对10种天蛾昆虫进行研究时并未受到影响。随着今后研究蛾类昆虫种类的不断增多，蛾翅在雌雄之间的差异会逐渐体现出来，这是需要注意与克服的问题。

由于天蛾科所属的鳞翅目其自身的特点，翅面上覆盖有大量鳞片，在生产实际中对于蛾翅的处理略显繁琐。为了便于处理试验所用的300个样本，本文采用了化学去鳞的方法且用扫描仪获取图像。在实际应用中，也可考虑采用毛笔刷去鳞片或漂白粉溶液使翅脱色等简便方法去除鳞片。将去鳞后的蛾翅脉标本放置在颜色较深的背景下，用普通相机即可获取蛾翅脉图像。相信随着获取图像的技术手段的不断改进，会有更简便的方法直接获取蛾翅脉图像，以便使昆虫翅脉特征更便捷地应用到蛾类昆虫的分类鉴定中。

本文利用几何形态测量学方法对10种天蛾进行数字化分类的准确率达到了100%，这说明几何形态测量学方法具有较高的分类准确率。但是，应用几何形态测量学方法对鳞翅目昆虫进行数字化分类也有其缺点：因鳞翅目昆虫翅面上覆盖有大量鳞片，研究翅脉的拓扑结构特征需要先去除翅面上的鳞片。在今后的研究中，可将数学形态学、几何形态测量学和颜色特征等多种数字化鉴定方法进行对比研究，明确这些方法的优缺点，同时积极探索新的方法，在保证较高准确率的前提下，更快、更简便地实现昆虫的数字化分类鉴定。

将几何形态测量学应用于昆虫系统发育研究已引起了大家的广泛兴趣(闫宝荣等，2010)，今后笔者也将进一步探索利用几何形态测量学对天蛾甚至更多种类的蛾类昆虫进行系统发育的研究。随着对昆虫系统发育研究的各种技术方法不断发展，可以将此方法和分子系统学以及传统分类学放到一起进行探讨，并最终将几种方法结合起来推进昆虫分类学的发展。

几何形态测量学分析主要是以二维数据为主，从二维数据到三维数据的分析也已经可行，由于三维数据具有维度高、信息量大等特点(白明等，2014b)，可帮助解决某些二维数据无法涉足的问题。在人类学研究和生物医学科学领域，三维地标点方法已成为公认的标准方法(Adamset al., 2004)。本研究中的蛾翅是平面结构，较易获取其二维图像，利用蛾翅二维标记点数据能够很好地实现10种天蛾的分类鉴定。三维数据的获取需要特殊且较昂贵的设备支持，数据处理也相对繁琐，但是随着计算机处理海量数据的能力不断提高以及研究昆虫种类的不断拓展，三维数据也将会被应用到昆虫的分类鉴定中，几何形态测量学方法可能会由二维数据为主的研究向三维的方向发展，并且三维数据将在分类鉴定、系统发育以及其他各个领域得到广泛应用。

几何形态测量学方法目前在医学、考古学、人类学和脊椎动物学等领域已有广泛应用，但由于昆虫个体相对较小，该方法在昆虫学领域的应用仍处于起步阶段。如今几何形态测量学方法通过与其他研究手段相结合，开始向其他研究领域渗透(白明等，2007)，如非对称性结构的研究、内部解剖对称结构的任意横向距离的研究、不定型非对称性结构的研究。随着几何形态测量学方法的不断改进和成熟，加之很多学者开发出大量免费的分析软件以及相关研讨培训活动的开展，此方法将会得到越来越广泛的应用。

5 结论

本文利用天蛾成虫右前翅翅脉的标记点数据实现了对试验所用10种天蛾成虫的数字化分类鉴定，回归判别和交叉判别的正确率均为100%，这表明利用标记点法来实现天蛾成虫的分类鉴定是可行的，为未来逐步实现蛾类成虫的自动识别鉴定提供了简便有效的方法。

本文所用10种天蛾成虫前翅翅脉拓扑结构极其相似，利用几何形态测量学方法对其进行分类研究，准确率达到了100%，这充分证明了此方法提取的特征可应用于蛾类成虫的分类鉴定。此外，几何形态测量学方法中的相对扭曲分析还可实现昆虫分类鉴定的可视化，可视化作为几何形态测量学的特点之一，能够使不同物种之间的形态差异清楚可见。今后，笔者将继续利用几何形态测量学对蛾类其他昆虫进行分类研究，将实现昆虫分类鉴定的可视化作为研究方向。

本文利用几何形态测量学对天蛾成虫进行分类鉴定，关于标记点的选取与分析须注意如下2点：1)标记点的选择对于分析的结果有直接而且重要的影响，为了方便以后添加其他种类的蛾类昆虫，一般会选择容易复现的标记点，即要保证标记点的可重复选择。2)标记点的原始坐标数据由于包含了许多非形状因素，如获取图像时标本摆放的位置、方向、坐标系的选取(原点、刻度)等，因此不能直接对其进行数据分析，要经过普世叠加分析消除这些非形状因素等多余的信息后才能进行相应的分析。