森林地上生物量(above-ground biomass，AGB)是森林生态系统发挥其生态功能的物质基础，是森林固碳能力的重要标志，在全球碳循环中扮演着重要角色(Chinembiri et al., 2013；Gara et al., 2014)，准确估测森林AGB及其变化对研究全球碳循环、气候变化具有重要意义(Güneralp et al., 2014；Lu，2006)。

遥感技术以其宏观、动态及可重复等优势，已成为当前区域森林AGB估测的主要方法(李德仁等，2012)。基于遥感的森林AGB估测，通常利用遥感数据结合森林资源调查数据进行统计回归，但该方法以大数定律为理论基础，只有当样本数量“足够多”时，样本的规律才能被统计出来；在实际应用中，森林资源调查数据往往难以获取，在样本数量有限的情况下模型会发生“过学习”现象。为了解决上述问题，一些学者采用非参数化方法估测森林AGB，如k最近邻法(k-nearest neighbor，k-NN)、决策树(decision tree，DT)、人工神经网络(artificial neural network，ANN)、支持向量机(support vector machine，SVM)等，其中k-NN法灵活、透明、泛化能力强，既不依赖于特定的函数分布(Franco-Lopez et al., 2001)，也无需样本测量值与遥感影像特征间的先验知识，不仅可用于若干森林参数的估计，还能融合各种空间数据到因变量估测中，尤其是在样本数量较少的情况下易于估算缺失值(Crookston et al., 2008；Troyanskaya et al., 2001)，在森林参数遥感估测领域得到了广泛应用(曹庆先等，2011；戚玉娇等，2015；Wilson et al., 2012；Reese et al., 2002；Tian et al., 2012；2014)。在森林参数估测方法不断发展的同时，多源遥感数据也被逐步应用于森林参数遥感估测，国内外众多学者研究表明，结合多源遥感数据及其派生的遥感特征因子(如纹理、植被指数、地形因子等)可有效提高森林AGB估测精度(曹庆先等，2011；李明阳等，2015；Dube et al., 2015；Eckert，2012；Kelsey et al., 2014；Lu，2005)。

综合利用多源遥感数据及其派生特征因子，在一定程度上提高了森林参数(如森林AGB、蓄积量等)的定量估测精度，但多源遥感数据通常伴随有数据维度高的特点，进而产生信息冗余和维度灾难，使分析和处理变得复杂，因此，如何从海量遥感特征组合中高效选取优化的特征进行建模成为森林AGB估测的首要问题。郭云等(2015)、李春梅等(2016)使用随机森林(random forest，RF)算法进行特征选择，并基于挑选后的特征建立森林AGB的k-NN估测模型，提升了森林AGB估测精度；但RF算法是通过对特征进行重要性度量的方式(Strobl et al., 2007)实现特征选择的，得到的只是特征得分由大到小排序的结果，并非“最优”特征组合。而且，RF算法的2个“随机性”(Breiman，2001)，即训练集抽取的随机性和节点候选分割特征集合的随机性，也在一定程度上增加了其用于特征选择时的不稳定性。在k-NN基础上，Li等(2011)提出了随机k最近邻法(random k-nearest neighbor，RKNN)，即在RF第一节点上，基于Bootstrap(Efron et al., 1986)抽取的样本，利用k-NN法进行一系列建模、优化，直到分类结果最佳。结果发现，RKNN大幅提高了基因识别效率，在一定程度上解决了“小样本 & 高维度信息”问题；但RKNN只应用于基因的定性分类识别，用于森林参数定量估测的相关研究未见报道。

针对如何从高维遥感数据产生的海量特征组合中高效选取相关特征进行森林AGB优化建模，本研究提出基于快速迭代特征选择的k最近邻法(k-nearest neighbor with fast iterative features selection，KNN-FIFS)，并以大兴安岭根河森林保护区为研究区，结合多源遥感及其派生数据进行森林AGB估测研究。

1 研究区概况与试验数据 1.1 研究区概况

大兴安岭根河森林保护区位于内蒙古自治区呼伦贝尔北部(图 1)，地理位置121°30′—121°31′E，50°49′—50°51′N，海拔800~1 100 m；保护区地处寒温带湿润气候区，气候寒冷湿润，年均温-5.3 ℃，年均日照时长2 594 h，无霜期90天左右，降水主要集中在7、8月，年降水量450~500 mm；保护区森林覆盖率达90%以上，以兴安落叶松(Larix gmelinii)构成的明亮针叶林为主，伴生树种有白桦(Betula platyphylla)、山杨(Populus davidiana)等。

1.2 森林资源调查数据

森林资源调查数据(图 1)包括2012年8月调查的38块样地(30 m×30 m)以及2013年8月调查的18块样地(45 m×45 m)。样地皆为正方形，边界沿东西—南北向分布，对样地内活立木进行每木检尺(胸径、树高、冠幅等)，胸径起测径级为5 cm。利用差分GPS(differential GPS，DGPS)定位样地4个角点坐标，其中基准站为Pro XRT，流动站为Geo XH 6000和Geo XT 6000，差分处理后定位平面误差大部分为1~2 m，最大误差小于10 m(胡凯龙等，2015)，并由角点坐标推算样地中心点坐标。

同时，本研究获取了研究区2012年小班数据，根据小班属性信息得到研究区主要地表覆盖类型(图 1)。由于本研究所用样地数目较少，所以后期的森林AGB估测并未分森林类型进行建模分析。

1.3 遥感数据及预处理

遥感数据包括Landsat-8 OLI数据、ASTER-GDEM V2(advanced spaceborne thermal emission and reflection radiometer global digital elevation model version2)数据以及机载合成孔径雷达(synthetic aperture radar，SAR)P-波段HV极化后向散射强度数据(P_HV)。

Landsat-8 OLI数据来源于美国地质调查局(http://glovis.usgs.gov/)，成像时间为2014年5月24日，影像无云层覆盖，产品级别Level 1T，即已进行了基于地形的几何校正，本研究所用B1—B7波段空间分辨率为30 m。在ENVI 5.3中将影像灰度值定标为辐亮度值，采用FLAASH(fast line-of-sight atmospheric analysis of hypercubes)大气校正模型(Anderson et al., 2002)对影像进行大气校正。虽然Landsat-8 OLI影像与样地调查时间未同步，但由于保护区地处高纬高寒，森林生长十分缓慢，且2012—2014年无自然(如冰雪灾害、火灾、虫害等)或人为(如植树造林、砍伐等)干扰，因此可以认为2012、2013年调查的样地数据可用于2014年该区域森林AGB的建模和反演。

ASTER GDEM V2数据来源于地理空间数据云(http://www.gscloud.cn/)，空间分辨率为30 m，较ASTER GDEM V1提高了数据的空间分辨率精度和高程精度。

P-波段机载合成孔径雷达数据来源于2013年9月13日在研究区开展的飞行试验。该试验以“奖状Ⅱ”为飞行平台，飞行高度5 80 7 m，航向由西向东，右视方向观测，中心入射角为55.058°，波长为0.5 m，距离向分辨率为0.666 m，方位向分辨率为0.625 m。对原始数据进行多视处理(3×3)、地理编码，并采用高精度LiDAR DEM数据进行正射校正，得到空间分辨率为2 m的HV极化后向散射强度数据(冯琦等，2016)。为与Landsat-8 OLI分辨率一致，在ENVI 5.3中采用像元聚合方法将P_HV重采样至30 m空间分辨率。

2 研究方法 2.1 样地生物量计算

采用陈传国等(1989)提出的幂函数一元方程计算不同树种单木生物量，累加得到林分水平样地生物量总量，除以样地面积得到单位面积生物量(t·hm^-2)。样地单木生物量计算公式如下：

$ W{\rm{ = }}a \times {\rm{DB}}{{\rm{H}}^b}。$

(1)

式中：W为地上部分生物量(kg)；DBH为实测胸径；a、b为系数(表 1)。

2.2 特征提取

遥感特征包括光谱信息、植被指数、纹理、地形因子和机载PolSAR 5种类型(表 2)，其中植被指数、纹理、地形因子在ENVI 5.3中提取完成。纹理基于灰度共生矩阵(gray-level co-occurrence matrix，GLCM)计算得到，一方面，纹理计算结果因GLCM参数([x, y]步距及窗口大小)设置不同而异；另一方面，纹理对于森林AGB的估测能力因地理条件、森林类型、传感器类型和遥感影像空间分辨率等不同而异(Bastin et al., 2014；Cutler et al., 2012；Dube et al., 2015；Sarker et al., 2011；2013)。本研究采用李春梅等(2016)研究得到的保护区森林AGB估测纹理参数，即以[x, y]步距为[1, 1]、窗口为5×5提取纹理特征。

2.3 KNN-FIFS方法森林参数估测

K-NN法通过搜索相似单元，待估像元的属性值${\hat V_{\rm{p}}}$由距离其最近的k个样地的属性值V_pi(1≤i≤k)加权求得，即：

$ {\hat V_{\rm{p}}} = \sum\nolimits_{i = 1}^k {{W_{{\rm{p, p}}i}}} \times {V_{{\rm{p}}i}}。$

(2)

式中：W_{p, pi}为权重，与待估像元特征向量(X_p)到样地所在像元特征向量(X_pi)的距离(D_{p, pi})呈反比，即：

$ {W_{{\rm{p, p}}i}} = \frac{{1/{D_{{\rm{p, p}}i}}}}{{\sum\nolimits_{i = 1}^k {\left({1/{D_{{\rm{p, p}}i}}} \right)} }}。$

(3)

D_{p, pi}可采用多种度量标准，而采用马氏距离(Mahalanobis distance)可以提高其估测精度(郭云等，2015；李春梅等，2016；Tian et al., 2012；2014)，因为马氏距离在一定程度上可克服变量量纲的影响，既考虑特征向量的离散度，也考虑向量分布的协相关，可以有效排除变量之间的相关性干扰。基于上述原因，采用马氏距离对D_{p, pi}进行度量，即：

$ {D_{{\rm{p, p}}i}} = \sqrt {{{\left({{X_{{\rm{p}}i}} - {X_{\rm{p}}}} \right)}^{\rm{T}}}{C^{ - 1}}\left({{X_{{\rm{p}}i}}{\rm{ - }}{X_{\rm{p}}}} \right)} 。$

(4)

式中：C为样本协方差矩阵；C^-1为样本协方差矩阵的逆矩阵；T为矩阵的转置。

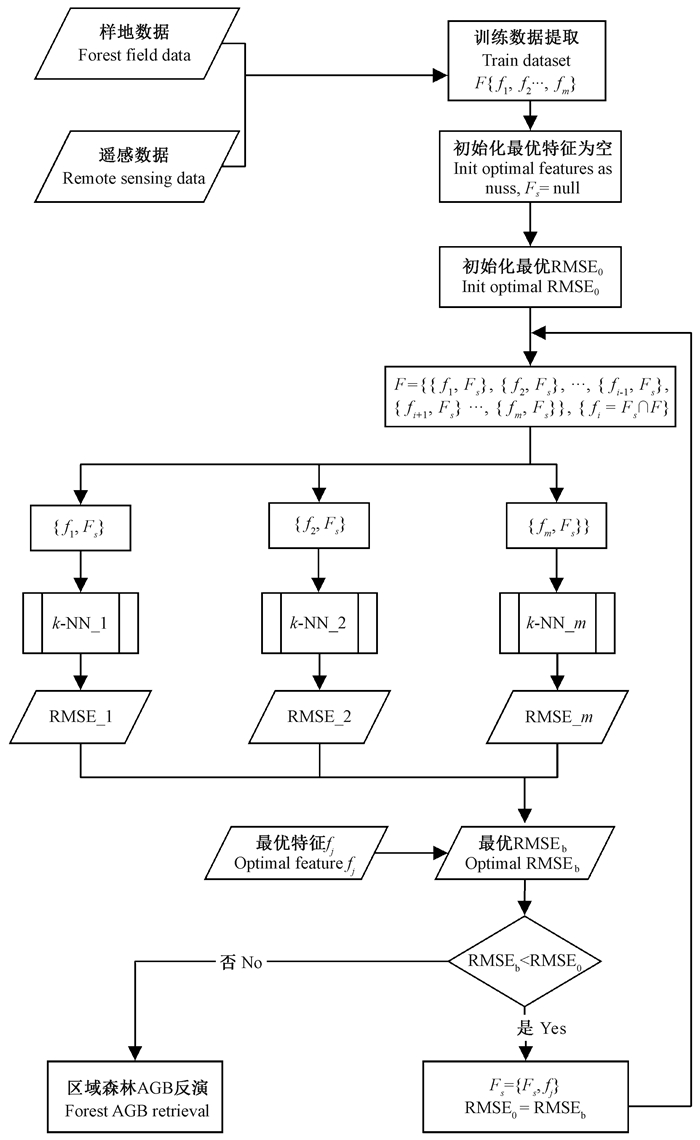
k-NN法虽然灵活、透明、泛化能力强，但是当特征维数较高时，会产生海量特征组合，降低模型预测效率和精度。为此，本研究提出KNN-FIFS方法用于森林AGB估测，其基本原理(图 2)如下(设样地数为n，特征数为m)：

1) 由样地数据和遥感特征提取训练数据F={f₁, f₂, …, f_m}，其中f_j=[x_j1, x_j2, …, x_jn]^T(1≤j≤m)，x_ji为第i块样地对应第j个特征所在像元的值；

2) 初始化最优特征子集F_s为空，即F_s=null；初始化最优模型均方根误差(root mean square error，RMSE)RMSE₀为理论上极大值用于对比迭代过程中得到的RMSE，本研究设置RMSE₀=255 t·hm^-2；

3) 基于k-NN法，依次利用特征{f₁, F_s}, {f₂, F_s}, …, {f_i-1, F_s}, {f_i+1, F_s}, …, {f_m, F_s}(其中f_i=F_s∩F)建立森林AGB估测模型，共得到m-s(s为最优特征子集的特征个数)个k-NN估测模型及每个模型对应的RMSE。RMSE采用留一法交叉验证计算得到，即每次从n块样地中不重复地抽取1个样地i，利用剩余的n-1块样地采用k-NN法估测样地i的森林AGB(${\hat y_i}$)，重复该过程n次。设样地i的森林AGB为y_i，n次共得到n对(${\hat y_i}$，y_i)，则RMSE计算公式为：

$ {\rm{RMSE = }}\sqrt {\frac{1}{n}\sum\nolimits_{i = 1}^n {{{\left({{y_i} - {{\hat y}_i}} \right)}^2}} }。$

(5)

4) 选取步骤3中得到的最优RMSE，即RMSE最小值，设该值为RMSE_b，若RMSE_b＜RMSE₀则将RMSE_b赋给RMSE₀, 并将RMSE_b对应的特征子集赋给F_s返回步骤3；反之迭代结束。

对于KNN-FIFS方法，当距离度量标准确定时，其估测结果受k的影响，而k最佳取值取决于样地数量、样地分布及待估森林参数实际变化程度等因素。Tokola等(1996)研究表明，k越大，估测结果越容易向平均值的方向平衡并呈集中分布趋势，此时估测结果与实测森林参数可能依然具有较高的相关性，但不能维持原有的森林参数统计分布特征。为了使森林参数估测结果能够保持原有的统计分布特征，k取值不宜过大，本研究设置k的变动范围为1~11，进行森林AGB估测。

2.4 多元线性逐步回归方法森林参数估测

多元线性逐步回归(stepwise multiple linear regression，SMLR)通过在设定的检验水平下交替引入和剔除变量，选取“最优”回归方程，探寻多个自变量与因变量之间的统计学意义。作为一种常用的特征变量筛选方法，已有诸多学者(国庆喜等，2003；郭志华等，2002；徐婷等，2015；Dube et al., 2015；Foody et al., 2001)利用其进行了森林参数估测研究，具体估测方法如下：

$ {\hat y_i} = {\beta _0} + {\beta _1}{x_{i1}} + {\beta _2}{x_{i2}} + \cdots + {\beta _i}{x_{ij}}。$

(6)

式中：${\hat y_i}$为待估森林参数；β_i为回归系数；x_ij为遥感特征因子。

本研究设置变量引入和剔除的显著性水平为P≤0.05和P≥0.10。为了最大程度减小分配训练、检验样本带来的随机误差并与KNN-FIFS精度验证方法一致，采用留一法交叉验证，即每次从n块样地中不重复地抽取1块样地i，利用剩余的n-1块样地建立回归方程，由此计算样地i的森林AGB估测值${\hat y_i}$，重复该过程n次，得到全部样地的森林AGB估测值。

3 结果与分析

遥感影像像元通常包含该像元周围地物信息，同时受阴影、树高和密度等因素影响，森林样地信息往往不能由其对应的某个像元精确反映出来。为了减小样地点定位、样地点与遥感影像匹配以及样地大小不一带来的误差，本研究以样地中心点对应遥感影像像元周围邻域3×3窗口内像元均值作为训练数据，分别利用KNN-FIFS和SMLR方法进行森林AGB估测，结果如图 3所示。

基于KNN-FIFS方法，当k为3，特征组合为P_HV、短波红外波段一均一性(H6)、短波红外波段二二阶矩(S7)、短波红外波段一二阶矩(S6)、海蓝波段相关性(Cr1)、近红外波段相关性(Cr5)、海蓝波段相异性(D1)、增强型植被指数(EVI)时，研究区森林AGB估测结果最优，其精度(R²=0.77，RMSE= 22.74 t·hm^-2)显著优于SMLR方法估测精度(R²=0.53，RMSE=32.37 t·hm^-2)。SMLR方法估测得到的森林AGB分布更为离散，尤其在实测高值区域，其估测值偏离实测值较大。这是因为SMLR方法以大数定律为理论基础，只有当样本数量“足够多”时，样本的规律才能被统计出来，其估测结果对数据中的异常值更为敏感，易造成估测值偏差较大；同时森林作为一种复杂的生态系统，森林AGB与遥感数据间存在着复杂的非线性关系，而SMLR并不能够很好地描述这种关系；对于KNN-FIFS方法，估测参数只与相邻的k个样本有关，利用k个样地点加权求值能够减小因影像噪声、林分变化引起的随机变化，可以有效避免样本不平衡问题，并能更好地描述森林参数与遥感影像间复杂的非线性关系。

此外，关于KNN-FIFS方法有2个重要的特性需要说明：1)设特征数为m，则共计可能产生的特征组合数为$\sum\nolimits_{n = 1}^m {C_m^n} $(其中C_mⁿ为从m个特征中取出n个不同特征进行组合)，而KNN-FIFS通过其迭代机制仅由至多$\sum\nolimits_{n = 1}^m {\sum\nolimits_{i = 1}^n {} } $次特征组合即可完成特征选择。如图 4所示，随特征数增加，特征组合数几何式急速增加，KNN-FIFS方法仍可以小数量级的特征组合数完成特征寻优，从而极大提升特征选择效率。2) Breiman(1996)研究指出，留一法交叉验证是一种较好的无偏估计方法，不存在分配训练、检验样本带来的随机误差，其产生的泛化误差估计结果相对真值较小。通过留一法交叉验证，每次验证过程中均有n-1个样本用于模型训练，使得训练样本最接近原始样本分布，得到的估测结果可信度高。KNN-FIFS通过留一法交叉验证，得到的结果更为可信，同时也使得整个过程是可重复性的，进而保证了KNN-FIFS特征选择结果的稳定性。

4 讨论

Landsat-8 OLI传感器在波段设置及对植被的敏感性上较之前的TM(thematic mapper)等传感器有较大提升(徐涵秋等，2013)，但光学遥感仍难以穿透森林冠层获得其垂直结构信息。而微波遥感因其电磁波波长较长，具有穿透树冠的能力，不仅能作用于树叶，而且与森林AGB的主体——枝和树干也发生作用。Ranson等(1994)研究认为，P-波段交叉极化数据是森林AGB制图的最佳波段，特别在森林AGB水平较高时，P-波段HV极化数据也可用于生物量的提取；同时，森林作为一种复杂的生态系统，对于相似的森林AGB结构而言，不同的土地类型、地理条件、森林类型会有不同的反射率，即“同物异谱”；对于不同的森林AGB结构而言，相似的土地类型、地理条件、森林类型也会有相同的反射率，即“异物同谱”。相较光谱特征，纹理可以更好地表征遥感影像的空间信息，在一定程度上抑制“同物异谱、异物同谱”现象的发生(Lee et al., 1991；Foody et al., 2001)；而植被指数能够定量光谱信息。以上因素可在一定程度上解释利用“P_HV+纹理+EVI”特征组合获得森林AGB估测结果最优的原因。

为了探究“最优”特征组合可能的作用机制，本文还进行了如下研究。

1) 计算各遥感特征与样地森林AGB之间的Pearson相关系数(Pearson correlation coefficient)。Pearson相关系数介于-1~1之间，1表示变量完全正相关，0表示无关，-1表示完全负相关。如图 5所示，P_HV与样地森林AGB相关性最强；光谱信息、植被指数、纹理、地形因子等与样地森林AGB相关性较弱，相关系数在-0.4~0.4之间。本研究选取相关性最强的前10个特征，即P_HV、H4、E4、H7、Slp、H6、D7、D6、S4和Co6，并建立全部特征组合的11 253种k-NN(k为1~11)估测模型，得到研究区森林AGB最优估测精度为R²=0.55，RMSE=31.39 t·hm^-2，明显低于KNN-FIFS估测精度(R²=0.77，RMSE=22.74 t·hm^-2)。

2) 利用KNN-FIFS方法估测黑河流域上游祁连山森林保护区森林AGB。依据各遥感特征与森林AGB的相关程度进行特征筛选，其实质是对每个特征和响应变量之间的线性相关性强弱进行特征优选。森林作为是一种复杂的生态系统，森林AGB与遥感特征之间的关系是复杂多样的，往往难以用简单的线性关系来描述。此时，则可以采用基于树的方法进行特征选择，如RF算法。郭云等(2015)结合黑河流域上游祁连山森林保护区133块森林样地调查数据和SCS+C地形校正后的Landsat-5 TM数据及其派生的纹理、植被指数等特征，首先利用RF算法进行特征选择，然后基于挑选出的特征建立森林AGB的k-NN估测模型，精度为R²=0.54，RMSE=26.62 t·hm^-2。基于相同遥感数据和样地数据，本研究利用KNN-FIFS方法估测黑河流域上游祁连山森林保护区森林AGB，精度为R²=0.63，RMSE=23.88 t·hm^-2，优于郭云等(2015)估测结果。该结果可以在一定程度上表明：1) KNN-FIFS方法适用于不同区域的森林AGB估测；2) KNN-FIFS优于“RF特征选择+k-NN建模”。

利用Pearson相关系数或RF算法均可剔除大部分无关或噪声特征，从而有效减小后续分析、计算的复杂度，提升森林参数估测效率和精度。但本研究发现，“最优”特征组合并非是各遥感特征与森林AGB相关性由强到弱排序的结果(Pearson相关系数特征选择+k-NN建模)，也不是各遥感特征重要性由大到小排序的结果(RF特征选择+k-NN建模)，即“最优+最优≠最优特征组合”。而对于“最优”特征组合作用机制，仍有待进一步研究，这对于森林参数多源遥感估测，尤其是大数据时代背景下的数据挖掘都具有重要意义。

5 结论

1) KNN-FIFS方法相比SMLR更适用于森林AGB多源遥感估测。SMLR方法以大数定律为理论基础，虽简单易行，但难以描述森林AGB与遥感数据间复杂的非线性关系，尤其在样本数量较少的情况下，易造成估测值偏差较大；而KNN-FIFS方法不依赖于特定的函数分布，利用已知样本建立非线性模型，估测参数只与最近邻的k个样本有关，有效避免了样本不平衡问题，在样本数量较少的情况下也可以估算缺失值。

2) KNN-FIFS方法可以实现高效特征选择。KNN-FIFS方法通过迭代特征选择，既保证了森林AGB估测精度，又极大提升了特征选择效率；采用留一法交叉验证，不存在分配训练和检验样本带来的随机误差，并且可以最大程度地利用样地数据，不仅使得估测结果更为可信，而且也保证了KNN-FIFS特征选择结果的稳定性。此外，KNN-FIFS方法的提出，为基于高维度遥感特征因子的其他森林参数(如蓄积量、叶面积指数等)估测提供了一种可能的有效方法。