文章信息
- 陈亮, 周国模, 杜华强, 刘玉莉, 毛方杰, 徐小军, 李雪建, 崔璐, 李阳光, 朱迪恩
- Chen Liang, Zhou Guomo, Du Huaqiang, Liu Yuli, Mao Fangjie, Xu Xiaojun, Li Xuejian, Cui Lu, Li Yangguang, Zhu Di
- 基于随机森林模型的毛竹林CO2通量模拟及其影响因子
- Simulation of CO2 Flux and Controlling Factors in Moso Bamboo Forest Using Random Forest Algorithm
- 林业科学, 2018, 54(8): 1-12.
- Scientia Silvae Sinicae, 2018, 54(8): 1-12.
- DOI: 10.11707/j.1001-7488.20180801
-
文章历史
- 收稿日期:2016-09-25
- 修回日期:2018-06-14
-
作者相关文章
在全球气候变化背景下,陆地生态系统碳循环对环境因子变化的响应是生态学研究的热点问题。作为陆地生态系统的主体,森林是一个巨大的碳库,其储存的碳量是大气的3倍,并且对全球气候变化极其敏感(王春林等,2006; Beer et al., 2010)。因此,准确测定和估算森林生态系统和大气间的碳交换量,对于评价区域碳源、汇功能以及深入研究森林生态系统对全球气候变化的反馈机制具有重要意义(王春林等,2006; Jha et al., 2013)。
目前,碳通量的观测主要有清单法、箱法和微气象法(王兴昌等,2015),其中,微气象法中的涡度相关技术法可以在半小时尺度上直接、连续地观测植被群落和大气之间的气体交换通量及其环境控制因子,现已广泛用于各个生态系统的通量观测研究中,成为了一种通用的标准方法(Baldocchi et al., 2001; Law et al., 2002)。研究表明,森林生态系统CO2通量易受温度、降水、光合有效辐射、林龄和树种组成等因子的影响, 且各因子之间交互作用对CO2通量的影响也不可忽视(Saigusa et al., 2002; Barr et al., 2007; Allard et al., 2008; Grossiord et al., 2013; Fernández-Martínez et al., 2014; Xie et al., 2015),因此,应用传统统计回归模型估测森林生态系统CO2通量时,难以克服诸多因子之间复杂的复共线性问题,且对数据中存在的噪声和缺失数据敏感,极易造成模型精度降低(张雷等,2014; Lopatin et al., 2016)。此外,一些学者运用人工神经网络模型(ANN)拟合森林生态系统CO2通量(He et al., 2006; Wen et al., 2014),该方法虽然有强大的自身学习能力和较强的非线性映射能力,但也存在一些不可避免的问题,如对训练数据依赖性较高、容易出现过度拟合等(李旭青等,2014)。随机森林模型是由Breiman (2001)提出的数据挖掘算法,该算法属于“灰箱”模型,其结果具有可解释性,并且可以有效解决过度拟合和复共线性等问题,在生态学领域具有广阔应用前景。
东亚季风区主要分布在20°—40°N之间,该区域森林林型多样、植被类型丰富,具有很高的净CO2吸收强度,每年的净生态系统生产力(NEP)达3.6 Mg C·hm-2,并且森林生态系统NEP总量约0.72 Pg C·a-1,占全球森林生态系统NEP的8%,在全球碳循环中扮演着重要角色(Yu et al., 2014;方精云等,2015)。毛竹(Phyllostachys edulis)作为该区域一种重要的林分类型,不仅具有可观的经济价值,而且具有巨大的固碳潜力,在减缓全球气候变化方面发挥了积极作用。在毛竹林生态系统固碳能力和碳分配方面,已有许多学者做了大量研究(Zhou et al., 2011; Tang et al., 2015),但毛竹林碳循环形成机制、CO2通量对环境因子的响应等方面还相对缺乏深入探讨。鉴于此,本研究基于浙江省安吉县山川乡2011—2014年毛竹林涡度相关数据,采用随机森林模型对毛竹林CO2通量进行模拟,并分析光合有效辐射(PAR)、大气温度(TA)、空气相对湿度(RH)、空气CO2浓度(CCO2)、土壤热通量(QS)、饱和水汽压差(VPD)、生态系统有效能量(AE)、风速(WS)和土壤5 cm深处温度(TS)9个环境因子对CO2通量的影响,以期为亚热带典型森林碳循环模拟提供技术和理论支撑。
1 研究区概况研究区位于浙江省安吉县山川乡毛竹林碳汇研究基地(119°40′25.7″ E,30°28′34.5″ N),海拔380 m,主要土壤类型为黄壤土。气候属典型的海洋性季风气候,四季分明,雨热同期,年均降水1 400 mm,年均气温16.6 ℃。2010年,浙江农林大学在该基地内建立了40 m涡度相关通量观测塔,以塔为中心1 km×1 km范围内主要森林类型为毛竹林,平均胸径为12~18 cm,平均高为13~20 m。此外,还有少量针阔混交林、农田、道路和建筑。
2 研究方法 2.1 数据来源及处理本研究采用2011—2014年毛竹林通量塔CO2通量和气象原始数据,时间分辨率为半小时,其中通量数据由于降水及传感器自身原因会出现异常值和缺失值。因此,本研究首先利用EdiRe软件(http://www.geos.ed.ac.uk/abs/research/micromet/EdiRe)对通量数据进行处理,包括WPL空气密度校正、二次坐标旋转和虚温订正(于贵瑞等,2006);然后进行冠层储存项校正和摩擦风速校正(于贵瑞等,2006);最后,对通量数据进行质量控制和插补。数据质量控制过程主要有:1)剔除摩擦风速小于0.2 m·s-1的数据;2)剔除超出仪器合理测量范围的观测数据,如水汽浓度超出0~40 g·m-3、CO2通量超出-2.0~2.0 mg·m-3。得到的有效数据比例如表 1所示,可以看出,除了2013年有效数据比例偏低,外其余各年有效数据均在正常范围内(50%~83%)(Katul et al., 2001)。
|
|
对于缺失数据,白天缺失数据利用Michaelis-Menten方程插补(Falge et al., 2001):
| $ {\rm{NE}}{{\rm{E}}_{\rm{d}}} = {R_{\rm{e}}} - {P_{\rm{m}}} \times \alpha \times {\rm{PAR}}/(\alpha \times {\rm{PAR}} + {P_{\rm{m}}})。$ | (1) |
式中:NEEd为白天缺失的CO2通量数据;Re为生态系统暗呼吸速率(mg·m-2s-1);Pm为冠层最大净光合速率(mg·m-2s-1);α为初始光能利用率。
夜间缺失数据利用基于温度响应的Lloyd & Taylor方程插补(Lloyd et al., 1994):
| $ {\rm{NE}}{{\rm{E}}_{\rm{n}}} = {\rm{R}}{{\rm{E}}_{{\rm{ref}}}}{\rm{exp}}[A(1/283.16 - {T_0} - 1/{T_t} - {T_0})]。$ | (2) |
式中:NEEn为夜间缺失的CO2通量数据;REref为参考温度(10 ℃)下生态系统呼吸速率;A为温度敏感参数(本研究取309 K);T0为温度常数(本研究取-46 ℃);Tt为土壤5 cm深处温度。
最后,对通量和气象数据求半小时观测值的月平均,得到本研究所用数据。
2.2 随机森林模型随机森林模型是一种基于决策树的组合模型,其回归过程如图 1所示。首先,对训练数据集利用自助抽样(Bootstrap)形成N个bootstrap样本;其次,对每个bootstrap样本分别建立回归树模型,且该样本对应回归树模型的全部训练数据和测试数据;最后,以N个回归树结果的平均值作为因变量的预测值。此外,该模型迫使每个二叉分裂点仅考虑预测变量的一个子集,从而使得弱相关性变量获得更多参与回归树模型构建的机会,因此所得到的回归树模型具有更高的可信度(Breiman, 2001)。为获得优化的随机森林模型,本研究以2011—2012年通量观测数据为模型训练样本,对随机森林模型进行训练;采用2013年观测数据作为测试样本,对通过训练的模型进行测试;用通过测试后的模型对2014年毛竹林CO2通量进行模拟,即2014年数据作为独立验证样本。随机森林模型构建通过R语言randomForest包实现。
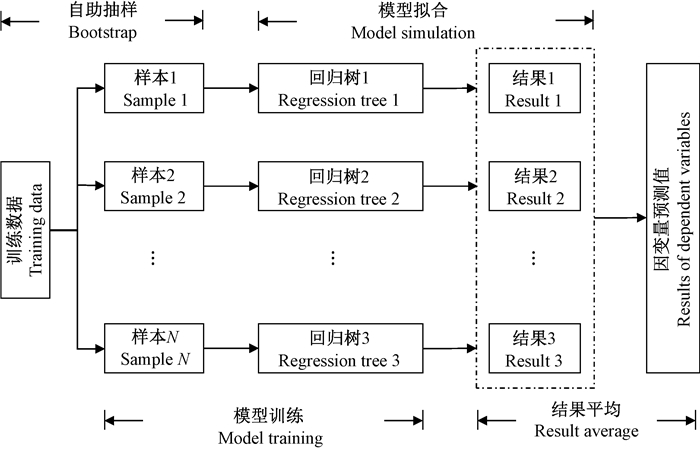
|
图 1 随机森林回归示意 Figure 1 Random forest regression principle |
随机森林模型输入环境变量包括PAR、TA、RN、CCO2、QS、VPD、AE、WS和TS,其中AE=RN-QS,RN为太阳净辐射(王兴昌等,2015),其余8个环境变量均由通量塔观测获取。Spearman相关分析表明,这9个环境变量与毛竹林CO2通量均极显著相关(P < 0.001)。
2.2.2 随机森林模型精度评价采用均方根误差(RMSE)、决定系数(R2)和林氏调和系数(LCCC)3个指标对训练、测试和验证数据集的随机森林模型模拟结果进行精度检验:
| $ {\rm{RMSE}} = \sqrt {\frac{1}{n}\sum\nolimits_{i = 1}^n {{{({p_i} - {o_i})}^2};} } $ | (3) |
| $ {R^2} = 1 - \sum\nolimits_{i = 1}^n {{{({p_i} - {o_i})}^2}} /\sum\nolimits_{i = 1}^n {{{\left({{o_i} - {{\bar o}_i}} \right.}^2};} $ | (4) |
| $ {\rm{LCCC}} = 2r{\sigma _{\rm{o}}}{\sigma _{\rm{p}}}/[{\sigma _{\rm{o}}}^2 + {\sigma _{\rm{p}}}^2 + \left({\bar o - \bar p} \right)]。$ | (5) |
式中:oi和pi分别为通量塔观测值(以下称观测值)和模型拟合值(以下称拟合值);σo和σp分别为观测值和拟合值的标准差;r为观测值和拟合值之间的皮尔逊相关系数;
为进一步检验模型泛化能力,基于2014年通量塔观测数据,利用十折交叉验证法(10-fold cross-validation)评价已构建好的随机森林模型的预测误差。十折交叉验证法是将所有数据随机分成大小相近的10组,先以第1组数据作为验证数据,剩下9组数据用作拟合模型;再以第2组数据作为验证数据,剩下9组数据用作拟合模型。依此类推,重复10次,以10次测试误差的平均值作为最后精度评价标准。
2.3 环境因子对模型的重要性随机森林模型中,在拟合或分类时会用到每个通过自助抽样形成的大约2/3 bootstrap样本数据,剩余1/3样本数据称为袋外样本数据(OOB),用于评估模型整体误差以及变量的重要性。若Xj为输入变量之一,则计算变量Xj在第n株树的重要性VIn时,首先利用自助抽样的样本数据建立回归树模型Tn,计算OOB的预测误差,然后随机置换变量Xj的观测值,再次建立回归树模型Tn′,计算OOB′ (随机置换变量观测后袋外数据)的预测误差,将2次袋外数据预测误差的差值进行标准化处理后,在所有回归树中取平均值即为变量Xj在第n株树的重要性VIn(Xj) (Delgado-Baquerizo et al., 2016),其计算公式如下:
| $ \begin{array}{l} {\rm{V}}{{\rm{I}}_n}({X_j}) = \{ \sum\nolimits_{i = 1}^{{{\rm{N}}_{{\rm{OOB}}}}} {I[f({X_i}) = {\rm{ }}{f_n}({X_i})]} -\\ \sum\nolimits_{i = 1}^{{{\rm{N}}_{{\rm{OOB}}}}} {I[f({X_i}) = {f_n}(X{\prime _i})]} \} /{{\rm{N}}_{{\rm{OOB}}}}。\end{array} $ | (6) |
变量Xj在整个随机森林模型中的重要性得分VI(Xj)为:
| $ {\rm{VI}}({X_j}) = \sum\nolimits_{n = 1}^{{N_{\rm{t}}}} {{\rm{V}}{{\rm{I}}_n}({X_j})/{N_{\rm{t}}}。} $ | (7) |
式中:NOOB为袋外样本数;f(Xi)为袋外数据中第i个观测值;fn(Xi)为在随机置换变量Xj的观测值前第n株树上袋外数据第i个观测值所对应的预测值;
本研究以输入参数对模型的重要性得分及其影响显著性为依据,评价环境因子对毛竹林CO2通量的影响。环境因子重要性得分及显著性检验通过R语言rfPermute包实现。
3 结果与分析 3.1 模型参数优化结果随机森林模型中有3个重要参数:一是随机森林模型中树的数量(Nt),在计算过程中,Nt取值足够大时,模型误差将趋于平稳,默认取值为500;二是分裂的变量个数M,即每个树节点上通过随机特征确定用于分裂的变量数, 默认为自变量数的1/3;三是终端节点最小样本数(NS),本研究采用模型默认取值,5。目前,随机森林模型中M大多基于经验公式判定,本研究采用逐次筛选确定最佳M,即遍历所有M的取值(输入变量数1~9),取模型误差最小时所对应的M。图 2显示,当M取值为4时,模型误差达到最小值,而Nt达到500以后模型误差趋于稳定,因此最终M、Nt和NS的取值分别为4、500和5。
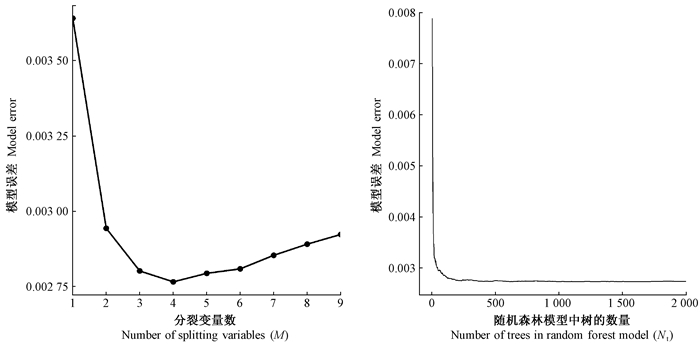
|
图 2 模型参数M和Nt对模型误差的影响 Figure 2 Influence of M and Nt to the model error |
图 3为2011—2014年模型输入变量变化特征。PAR、TA、QS、AE、WS和TS的日变化均为单峰型,在12:00—2:00达到极值。6月进入梅雨季,PAR开始下降,7月PAR又迅速增大,PAR极大值出现在2011年4月,为1 237.7 W·m-2;QS夜间为负值,表明土壤为热源,白天为正值,表明为热汇;2013年夏季出现极端高温现象,QS、TA和TS的极大值均出现在7月,分别为37.5 W·m-2、33.9 ℃和27.3 ℃。AE在-59.84~482.9 W·m-2之间;WS在各年夏季(6—8月)与同年其他月份相比均显著下降(P < 0.05);VPD主要受空气水热条件影响,在2013年波动最为剧烈,由于7、8月受极端高温胁迫影响,VPD显著高于同年其他月份(P < 0.05), 其最大值为23.4 hPa。RH和CCO2在日变化中均出现“谷峰交替”现象,由于夜间植被呼吸和土壤呼吸作用导致空气中CO2和水汽积累,在清晨5:00左右达到最大值,而后进行光合作用,CO2和水汽作为光合作用反应底物被消耗,其浓度逐渐下降并在14:30左右达到最小值,RH变化范围为36.7%~98.6%。
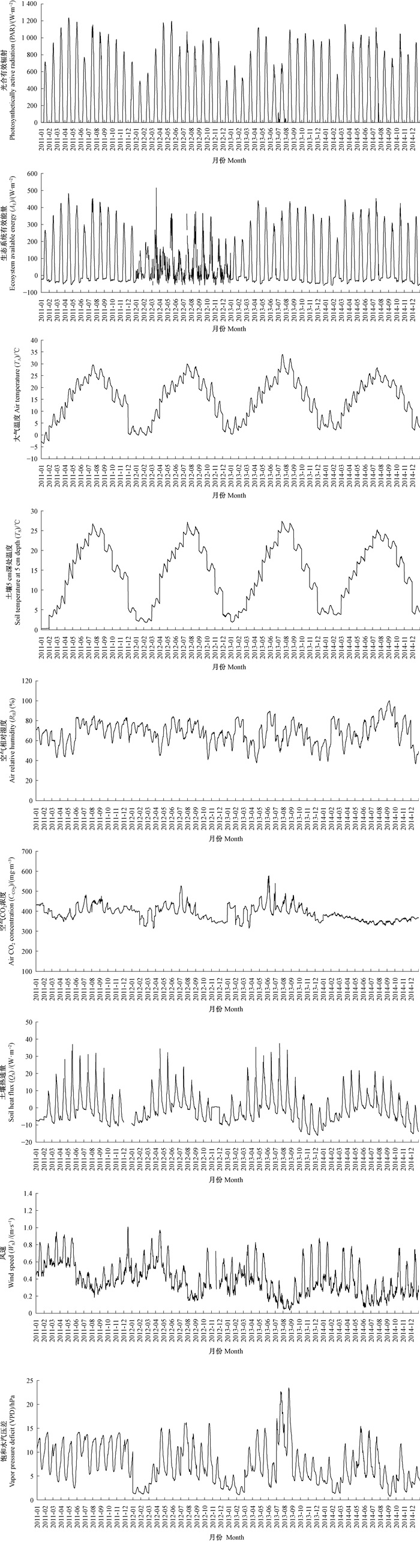
|
图 3 2011—2014年输入变量月平均日变化 Figure 3 Monthly diurnal variation of input variables from 2011 to 2014 |
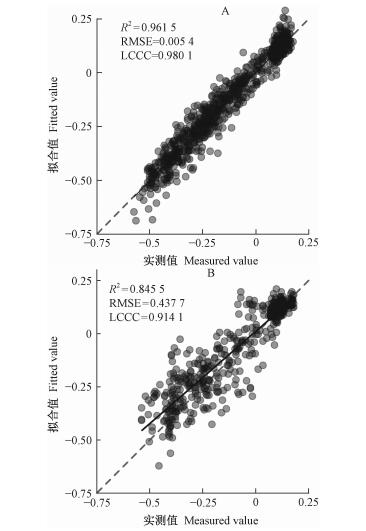
图 4为模型在训练和测试阶段的拟合结果,图 5为模型在训练和测试阶段的精度评价。可以看出,在2011—2012年模型训练阶段,R2=0.961 5,RMSE= 0.005 4 mg·m-2s-1,LCCC=0.980 1,模型拟合效果较好(图 5A)。而在模型测试阶段,R2下降至0.845 5,RMSE升高到0.437 7 mg·m-2s-1,LCCC下降至0.914 1(图 5B),并在2月12:00—14:00出现了低估情况,其极值低估了31.5%;在7月夜间,拟合值出现了较大波动,没有很好地体现该时段CO2通量真实变化趋势;在8和12月,CO2吸收峰值出现了明显高估,分别高估了57.3%和106%(图 4)。但总的来说,随机森林模型能较好地模拟CO2通量的数值大小和变化趋势。
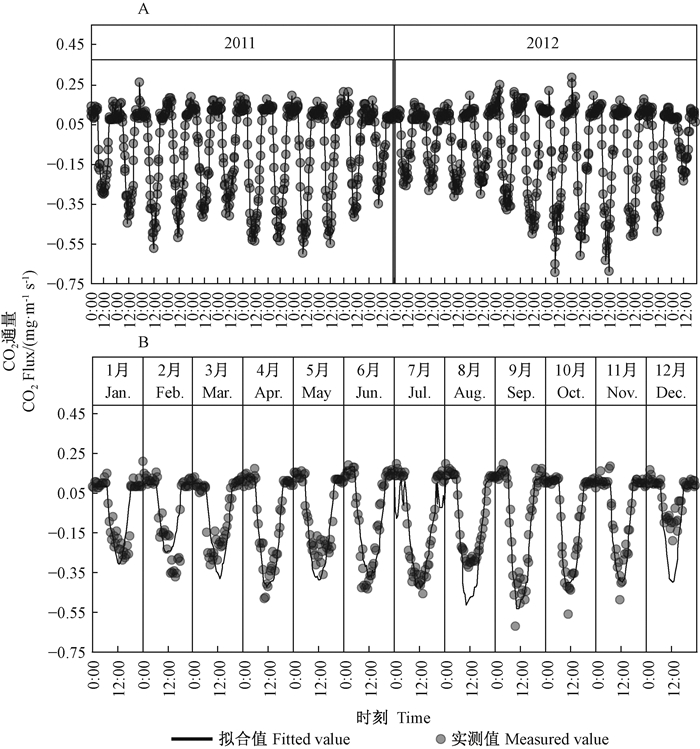
|
图 4 基于不同数据集的随机森林模型拟合效果 Figure 4 Performance of random forest model based on different datasets A:基于训练数据的随机森林模型拟合效果The performance of random forest model based on training dataset;B:基于测试数据的随机森林模型拟合效果The performance of random forest model based on testing dataset. |
|
图 5 训练(A)和测试(B)阶段随机森林模型精度评价 Figure 5 Accuracy evaluation for random forest model at training (A) and testing (B) phase |
为了验证随机森林模型的稳定性和泛化能力,首先,利用2014年独立验证数据对随机森林模型进行十折交叉验证,结果(表 2)表明,R2和LCCC较高,最大值分别为0.976 4和0.977 1,均值为0.970 5和0.974 1,而RMSE较小,为0.007 5~0.017 8 mg·m-2s-1,均值为0.011 6 mg·m-2s-1,这说明随机森林模型模拟精度高,在毛竹林CO2通量模拟中具有很好的稳定性。
|
|
其次,在日尺度上,选取2014年每月1日作为典型日,利用已训练的随机森林模型进行模拟,结果(表 3)表明,实测值与拟合值之间误差较小,R2为0.783 3,RMSE为0.010 6 mg·m-2s-1,线性关系也较为明显,LCCC为0.850 5,这说明随机森林模型在日尺度上也具有良好的拟合效果。
|
|
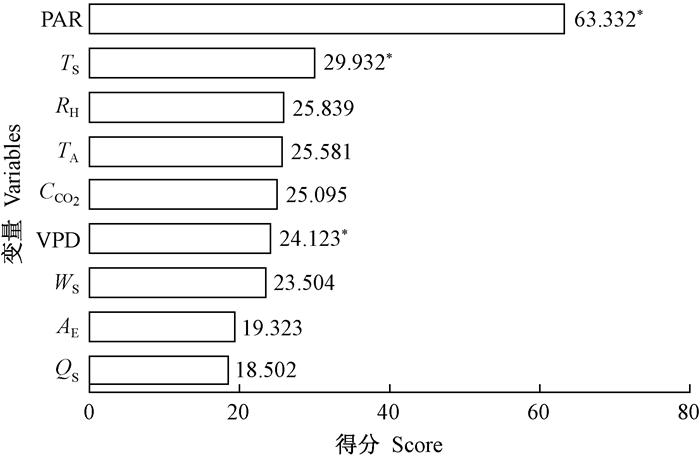
图 6为计算得到的环境因子对CO2通量影响的重要性得分。可以看出,环境因子对CO2通量影响的重要性得分表现为PAR(63.332) > TS(29.932) > RH(25.839) > TA(25.581) > CCO2 (25.095) > VPD(24.123) > WS(23.504) > AE(19.323) > QS(18.502),PAR在影响毛竹林CO2通量变化方面发挥了决定性作用。进一步分析表明,在0.05显著水平下,PAR、TS和VPD对毛竹林CO2通量的影响较为显著,说明这3个因子是影响CO2通量月尺度变化的重要因素。
|
图 6 输入变量重要性得分 Figure 6 Importance score of input variables |
虽然随机森林模型对输入参数间的共线性关系不敏感,但是该模型需要足够的样本容量来保证结果的合理性(张雷等,2014),因此模型精度除了与自身内部参数有关外,还与训练、测试和独立验证阶段的样本容量有关,当样本容量较多时,模型精度较高,反之则较低。本研究随机森林模型在训练、测试和独立验证阶段样本容量分别为1 152、576和576,样本容量较大。
模型误差与其内部参数M、Nt和NS有关,M过小,即在分裂节点上选择过少的变量特征,会使模型最终精度降低;过大,则减小模型的随机性,也会影响模型的最终精度(刘敏等,2015)。因此,M对模型精度的影响不能忽略。然而,对于M的选择,大多研究只是基于经验公式,如Yang等(2016)、Rahmati等(2015)的研究中M取值都为变量数的1/3,本研究选取的输入变量为9个,若取变量数的1/3,即3,根据图 4,显然不是最佳M取值,因此,本研究采用确定M的方法更为科学和严谨。Nt对随机森林模型的性能和可解释性具有重要意义(刘敏等,2015),Breiman(2001)早已证明当Nt足够大时,随机森林模型误差会逐渐收敛。根据图 2,本研究Nt取值为500时,模型误差已经收敛于一个极小值,达到稳定。随机森林模型对NS的取值并不敏感(刘敏等,2015),因此NS对模型误差的影响不予考虑,根据表 2和表 3结果,说明本研究随机森林模型参数设置合理,达到模型泛化要求。
4.2 环境变量对随机森林模型模拟的影响模型误差还与输入环境变量性质和通量数据质量有关,通量数据质量除易受降水、大气湍流及传感器自身噪声影响外,还受数据质量控制方法(数据剔除方法、数据插补方法)的影响,当缺失数据较多时,数据质量会下降,导致模型模拟值与实际值偏差大。本研究中9个输入变量为通量塔观测的气象因子,均属于非生物因素,而森林生态系统CO2通量还受其他生物因素的显著影响,如叶片气孔导度、水分利用效率、叶面积指数等(Wilson et al., 2001;张军辉等,2006; Keenan et al., 2013),生物因素在本研究并未充分考虑。此外,全球气候变化增加了极端气候出现的频率,利用模型拟合森林生态系统CO2通量时,往往难以刻画这种短时、强烈的干扰对CO2通量的影响(Campbell et al., 2009)。如在2013年夏季发生的极端高温干旱,使得模型拟合值没有很好地反映该年7、8月CO2通量真实值的大小和变化趋势,直接导致较大误差的产生,在模型测试阶段出现了精度下降现象。所以未来CO2通量拟合研究除应综合考虑生理因素和环境因素对森林生态系统碳通量的影响(Froelich et al., 2015)外,还应充分考虑极端气候的影响,增加模型物候参数,降低极端干扰对模型模拟的影响,以提高模型精度(Campbell et al., 2009; Richardson et al., 2012)。虽然模型误差来源多样,但随机森林模型总体上能够较好地拟合2011—2014年毛竹林CO2通量的数值大小和变化趋势。
4.3 CO2通量对主要环境因子的响应PAR是影响CO2通量的主导因子,而TS和VPD是重要的控制因子(图 6)。PAR是绿色植物生命活动、有机物质合成的重要能量来源,在一定范围内,PAR增大,植物光合作用增强,使植被固碳能力也相应增强;当伴随高温、高VPD出现时,为防止叶片失水过快,叶片气孔收缩甚至关闭,导致气孔导度下降;进而使CO2通量显著下降。尤其在夏季,由于高温干旱,毛竹林很容易出现“光合午休”现象(孙成等,2013),这导致2013年7、8月CO2通量比2011年同期分别小20.2%和40.1%,比2012年同期分别小15.7%和36.0%(图 5)。在不同时间尺度上,PAR和其他气象因子往往占据不同主导地位。在月尺度上,PAR对CO2通量的主导作用也出现在其他森林类型中,如Gonsamo等(2015)对北美洲东北部2种成熟林(温带落叶林和针阔混交林)碳通量的研究表明,PAR是影响2种成熟林碳通量的关键因子;Xie等(2015)对北京奥林匹克国家森林公园碳通量的研究表明,PAR是影响该森林在2012和2013年生长季碳通量变化的主导因子。而在年际间或更长时间尺度上,温度对CO2通量的影响比PAR更为显著(Yang et al., 2014)。此外,PAR和CO2通量之间的关系尚存在不确定性,在Xie等(2015)和Li等(2015)的研究中,PAR与CO2通量满足Michaelis-Menten关系式,而彭镇华等(2009)对安庆杨(Populus)树林生态系统碳通量与PAR关系的研究表明,在较低温度下,PAR和碳通量为线性关系。因此,准确揭示PAR对森林生态系统碳循环的影响,有利于更好认识植被对于全球气候变化的响应(Gonsamo et al., 2015)。本研究中,TS表示土壤5 cm深处温度,地表通常包含大量有机质(微生物、细根等),是异氧呼吸的主要来源,TS主要控制土壤呼吸进而影响森林生态系统CO2通量(Desai et al., 2005)。环境因子对CO2通量的影响具有时间尺度性(Yang et al., 2014),对于不同时间尺度下毛竹林CO2通量对环境因子变化的响应需要进一步研究。
5 结论本研究基于随机森林模型对毛竹林CO2通量进行模拟,结果表明,与BP人工神经网络模型相比,随机森林模型能够以致高精度模拟毛竹林CO2通量,说明随机森林模型在拟合毛竹林碳通量方面具有较好的适用性。在模型测试阶段,由于高温干旱使得模拟精度下降。十折交叉验证表明,随机森林模型内部3个参数(Nt、M和NS)设置合理,模型误差主要来源于输入数据。环境因子重要性得分表明,在0.05显著水平下,光合有效辐射、土壤5 cm深处温度和饱合水汽压差在月尺度上对毛竹林CO2通量变化的贡献显著,说明这3个因子在月尺度上对毛竹林CO2通量具有控制作用。为深入揭示毛竹林碳循环机制,今后应深入研究不同时间尺度下毛竹林碳通量对环境因子的响应。本研究结果可为深入了解亚热带典型森林生态系统碳通量控制机制及为区域生态系统过程模型参数调整提供科学依据。
方精云, 于贵瑞, 任小波, 等. 2015. 中国陆地生态系统固碳效应——中国科学院战略性先导科技专项"应对气候变化的碳收支认证及相关问题"之生态系统固碳任务群研究进展[J]. 中国科学院院刊, 30(6): 848-857. (Fang J Y, Yu G R, Ren X B, et al. 2015. Carbon sequestration in China's terrestrial ecosystems under climate change—progress on ecosystem carbon sequestration from the CAS strategic priority research program[J]. Bulletin of Chinese Academy of Sciences, 30(6): 848-857. [in Chinese]) |
李旭青, 刘湘南, 刘美玲, 等. 2014. 水稻冠层氮素含量光谱反演的随机森林算法及区域应用[J]. 遥感学报, 18(4): 923-945. (Li X Q, Liu X N, Liu M L, et al. 2014. Random forest algorithm and regional applications of spectral inversion model for estimating canopy nitrogen concentration in rice[J]. Journal of Remote Sensing, 18(4): 923-945. DOI:10.11834/jrs.20142329 [in Chinese]) |
刘敏, 郎荣玲, 曹永斌. 2015. 随机森林中树数量[J]. 计算机工程与应用, 51(5): 129-131. (Liu M, Lang R L, Cao Y B. 2015. Number of trees in random forest[J]. Computer Engineering and Applications, 51(5): 126-131. [in Chinese]) |
彭镇华, 王妍, 任海青, 等. 2009. 安庆杨树林生态系统碳通量及其影响因子研究[J]. 林业科学研究, 22(2): 237-242. (Peng Z H, Wang Y, Ren H Q, et al. 2009. Research on the variation of carbon flux and the relationship of environmental factors and carbon flux of populous forest[J]. Forest Research, 22(2): 237-242. [in Chinese]) |
孙成, 江洪, 周国模, 等. 2013. 我国亚热带毛竹林CO2变异特征[J]. 应用生态学报, 24(10): 2717-2724. (Sun C, Jiang H, Zhou G M, et al. 2013. Variation characteristics of CO2 flux in Phyllostachys edulis forest ecosystem in subtropical region of China[J]. Journal of Applied Ecology, 24(10): 2717-2724. [in Chinese]) |
王春林, 于贵瑞, 周国逸, 等. 2006. 鼎湖山常绿针阔叶混交林CO2通量估算[J]. 中国科学D辑:地球科学, 36(suppl.1): 119-129. (Wang C L, Yu G R, Zhou G Y, et al. 2006. CO2 flux evaluation over the evergreen coniferous and broad-leaved mixed forest in Dinghushan, China[J]. Science in China Series D:Earth Sciences, 36(suppl.1): 119-129. [in Chinese]) |
王兴昌, 王传宽. 2015. 森林生态系统碳循环的基本概念和野外测定方法评述[J]. 生态学报, 35(13): 4241-4256. (Wang X C, Wang C K. 2015. Fundamental concepts and field measurement methods of carbon cycling in forest ecosystems:a review[J]. Acta Ecologica Sinica, 35(13): 4241-4256. [in Chinese]) |
于贵瑞, 孙晓敏. 2006. 陆地生态系统通量观测的原理与方法[M]. 北京: 高等教育出版社: 222-218. (Yu G R, Sun X M. 2006. Principles of flux measuremnet in terrestrial ecosystems[M]. Beijing: Higher Education Press: 222-218. [in Chinese]) |
张军辉, 于贵瑞, 韩士杰, 等. 2006. 长白山阔叶红松林CO2通量季节和年际变化特征及控制机制, 中国科学[J]. D辑:地球科学, 36(S1): 60-69. (Zhang J H, Yu G R, Han S J, et al. 2006. Seasonal and annual variation of CO2 flux above a broad-leaved korean pine mixed forest[J]. Science in China Series D:Earth Sciences, 36(S1): 60-69. [in Chinese]) |
张雷, 王琳琳, 张旭东, 等. 2014. 随机森林算法基本思想及在生态学中的应用——以云南松分布模拟为例[J]. 生态学报, 34(3): 650-659. (Zhang L, Wang L L, Zhang X D, et al. 2014. The basic principle of random forest and its applications in ecology:a case study of Pinus yunnanensis[J]. Acta Ecologica Sinica, 34(3): 650-659. [in Chinese]) |
Allard V, Ourcival J M, Rambal S, et al. 2008. Seasonal and annual variation of carbon exchange in an evergreen mediterranean forest in southern France[J]. Global Change Biology, 14(4): 714-725. DOI:10.1111/gcb.2008.14.issue-4 |
Baldocchi D, Falge E, Gu L H, et al. 2001. Fluxnet:a new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities[J]. Bulletin of the American Meteorological Society, 82(11): 2415-2434. DOI:10.1175/1520-0477(2001)082<2415:FANTTS>2.3.CO;2 |
Barr A G, Black T A, Hogg E H, et al. 2007. Climatic controls on the carbon and water balances of a boreal aspen forest, 1994—2003[J]. Global Change Biology, 13(3): 561-576. DOI:10.1111/gcb.2007.13.issue-3 |
Beer C, Reichstein M, Tomelleri E, et al. 2010. Terrestrial gross carbon dioxide uptake:global distribution and covariation with climate[J]. Science, 329(5993): 834-838. DOI:10.1126/science.1184984 |
Breiman L. 2001. Random forests[J]. Machine Learning, 45(1): 5-32. DOI:10.1023/A:1010933404324 |
Campbell J L, Rustad L E, Boyer E W, et al. 2009. Consequences of climate change for biogeochemical cycling in forests of northeastern North America[J]. Canadian Journal of Forest Research, 39(2): 264-284. DOI:10.1139/X08-104 |
Delgado-Baquerizo M, Maestre F T, Reich P B, et al. 2016. Microbial diversity drives multifunctionality in terrestrial ecosystems[J]. Nature Communications, 7(10541): 10541. |
Desai A R, Bolstad P V, Cook B D, et al. 2005. Comparing net ecosystem exchange of carbon dioxide between an old-growth and mature forest in the upper midwest, USA[J]. Agricultural and Forest Meteorology, 128(1/2): 33-55. |
Falge E, Baldocchi D, Olson R, et al. 2001. Gap filling strategies for defensible annual sums of net ecosystem exchange[J]. Agricultural and Forest Meteorology, 107(1): 43-69. DOI:10.1016/S0168-1923(00)00225-2 |
Fernández-Martínez M, Vicca S, Janssens I A, et al. 2014. Spatial variability and controls over biomass stocks, carbon fluxes, and resource-use efficiencies across forest ecosystems[J]. Trees, 28(2): 597-611. DOI:10.1007/s00468-013-0975-9 |
Froelich N, Croft H, Chen J M, et al. 2015. Trends of carbon fluxes and climate over a mixed temperate-boreal transition forest in southern ontario, canada[J]. Agricultural and Forest Meteorology, (211/212): 72-84. |
Gonsamo A, Croft H, Chen J M, et al. 2015. Radiation contributed more than temperature to increased decadal autumn and annual carbon uptake of two eastern north America mature forests[J]. Agricultural and Forest Meteorology, 201(4): 8-16. |
Grossiord C, Granier A, Gessler A, et al. 2013. The influence of tree species mixture on ecosystem-level carbon accumulation and water use in a mixed boreal plantation[J]. Forest Ecology and Management, 298(3): 82-92. |
He H L, Yu G R, Zhang L M, et al. 2006. Simulating CO2 flux of three different ecosystems in China FLUX based on artificial neural networks[J]. Science in China, 49(S2): 252-261. DOI:10.1007/s11430-006-8252-z |
Jha C S, Thumaty K C, Rodda S R, et al. 2013. Analysis of carbon dioxide, water vapour and energy fluxes over an Indian teak mixed deciduous forest for winter and summer months using eddy covariance technique[J]. Journal of Earth System Science, 122(5): 1259-1268. DOI:10.1007/s12040-013-0350-7 |
Katul G, Lai C T, Schäfer K, et al. 2001. Multiscale analysis of vegetation surface fluxes:from seconds to years[J]. Advances in Water Resources, 24(9/10): 1119-1132. |
Keenan T F, Hollinger D Y, Bohrer G, et al. 2013. Increase in forest water-use efficiency as atmospheric carbon dioxide concentrations rise[J]. Nature, 499(7458): 324-327. DOI:10.1038/nature12291 |
Law B E, Falge E, Gu L, et al. 2002. Environmental controls over carbon dioxide and water vapor exchange of terrestrial vegetation[J]. Agricultural and Forest Meteorology, 113(1/4): 97-120. |
Li X L, Jia Q Y, Liu J M. 2015. Seasonal variations in heat and carbon dioxide fluxes observed over a reed wetland in northeast China[J]. Atmospheric Environment, 127: 6-13. |
Lin L I. 1989. A concordance correlation coefficient to evaluate reproducibility[J]. Biometrics, 45(1): 255-268. DOI:10.2307/2532051 |
Lloyd J, Taylor J A. 1994. On the temperature dependence of soil respiration[J]. Functional Ecology, 8(3): 315-323. DOI:10.2307/2389824 |
Lopatin J, Dolos K, Hernández H J, et al. 2016. Comparing generalized linear models and random forest to model vascular plant species richness using LiDAR data in a natural forest in central Chile[J]. Remote Sensing of Environment, 173(315): 200-210. |
Rahmati O, Pourghasemi H R, Melesse A M. 2015. Application of GIS-based data driven random forest and maximum entropy models for groundwater potential mapping:a case study at Mehran Region, Iran[J]. Catena, 137: 360-372. |
Richardson A D, Anderson R S, Arain M A, et al. 2012. Terrestrial biosphere models need better representation of vegetation phenology:results from the north American carbon program site synthesis[J]. Global Change Biology, 18(2): 566-584. DOI:10.1111/j.1365-2486.2011.02562.x |
Saigusa N, Yamamoto S, Murayama S, et al. 2002. Gross primary production and net ecosystem exchange of a cool-temperate deciduous forest estimated by the eddy covariance method[J]. Agricultural and Forest Meteorology, 112(2): 203-215. |
Tang X L, Fang S H, Qi L H, et al. 2015. Soil respiration and net ecosystem production in relation to intensive management in moso bamboo forests[J]. Catena, 137: 219-228. |
Wen X D, Zhao Z H, Deng X W, et al. 2014. Applying an artificial neural network to simulate and predict Chinese fir (Cunninghamia lanceolata) plantation carbon flux in subtropical China[J]. Ecological Modelling, 294: 19-26. DOI:10.1016/j.ecolmodel.2014.09.006 |
Wilson K B, Baldocchi D D, Hanson P J. 2001. Leaf age affects the seasonal pattern of photosynthetic capacityand net ecosystem exchange of carbon in a deciduous forest[J]. Plant Cell and Environment, 24(6): 571-583. DOI:10.1046/j.0016-8025.2001.00706.x |
Xie J, Jia X, He G M, et al. 2015. Environmental control over seasonal variation in carbon fluxes of an urban temperate forest ecosystem[J]. Landscape and Urban Planning, 142: 63-70. DOI:10.1016/j.landurbplan.2015.04.011 |
Yang R M, Zhang G L, Liu F, et al. 2016. Comparison of boosted regression tree and random forest models for mapping topsoil organic carbon concentration in an alpine ecosystem[J]. Ecological Indicators, 60: 870-878. DOI:10.1016/j.ecolind.2015.08.036 |
Yang Z, Chen J, Becker R, et al. 2014. Disentangling the confounding effects of PAR and air temperature on net ecosystem exchange in time and scale[J]. Ecological Complexity, 19(10): 74-75. |
Yu G R, Chen Z, Piao S L, et al. 2014. High carbon dioxide uptake by subtropical forest ecosystems in the east Asian monsoon region[J]. Proceedings of the National Academy of Sciences of the United States of America, 111(13): 4910-4915. DOI:10.1073/pnas.1317065111 |
Zhou G M, Xu X J, Du H Q, et al. 2011. Estimating aboveground carbon of moso bamboo forests using the k-nearest neighbors technique and satellite imagery[J]. Photogrammetric Engineering and Remote Sensing, 77(11): 1123-1131. DOI:10.14358/PERS.77.11.1123 |
 2018, Vol. 54
2018, Vol. 54

