圆锯片是切割固体材料的薄片圆形刀具的统称，广泛应用于金属、石材和木材等材料的机加工领域。圆锯片在锯切过程中，由于外缘与工件频繁接触，会导致外缘产生一定程度的温升，进而生成切向压应力。在切向压应力作用下，圆锯片一旦受到微小扰动，很容易产生失稳变形，导致锯切精度下降、锯片寿命缩短，严重时还会产生安全隐患(Li et al., 2015a；Heisel et al., 2014)。

为了避免上述现象的产生，一般需要对圆锯片进行适张处理，即通过机械手段使圆锯片局部区域产生塑性变形，进而使圆锯片外缘形成切向适张拉应力，以抵消切向压应力产生的不良影响。适张是圆锯片制造过程中最具技术含量的工艺，属于金属材料的弹塑性力学范畴。目前，应用最广泛的适张工艺主要有锤击和辊压2种。锤击适张能够获得一定的适张应力场，但由于其过于依靠工人操作经验，会导致锯片质量不稳定，且锤击力较小，锯片产生的塑性应变有限；辊压适张是圆锯片环形区域受上下轧辊的碾压，产生局部塑性变形和残余应力，在辊压环外侧，越靠近圆锯片外缘切向拉应力越小(Li et al., 2015b；2015c；2016)，而最大切向拉应力出现在圆锯片外缘才是理想的适张应力分布。

激光冲击强化技术是利用强激光束产生的等离子冲击波以高强度瞬间应力的方式作用在金属表面，提高金属材料抗疲劳、耐磨损和抗腐蚀能力的一种高新技术，具有非接触、无热影响区、可控性强及强化效果显著等突出优点(Rubio-González et al., 2006；Achintha et al., 2013；Zheng et al., 2010；Shadangi et al., 2015；Montross et al., 2002)，在航空、航天等制造领域有着潜在的重要应用(Cuellar et al., 2012；Achintha et al., 2014；Salimianrizi et al., 2016；Fu et al., 2016)。激光冲击强化技术能够使金属产生塑性变形，本质上与适张工艺具有共性。基于此，本研究利用激光冲击手段对圆锯片进行适张处理，以探寻圆锯片适张应力场的生成与调控机制，拓宽圆锯片的适张手段。圆锯片激光冲击适张过程为高度非线性力学过程，激光冲击波峰值压力和脉宽是重要的激光参数，因此探寻激光参数对圆锯片外缘切向拉应力的影响规律，对于优化圆锯片激光冲击适张工艺具有重要的理论和实用价值。

1 材料与方法

圆锯片：材质65Mn，硬度HRC42，外缘直径220 mm，中心孔直径30 mm，厚度2.2 mm。Nd:YAG型脉冲激光器：能量30 J，脉宽20 ns，圆形光斑，光斑直径3 mm。

圆锯片表面单个塑性变形区为圆形，且多个塑性变形区沿圆锯片中心轴呈循环轴对称分布，此时获得的适张应力分布较为理想(Li et al., 2015a；2015b；2015c)。本研究冲击区域半径为6 mm；铝箔贴附于圆锯片表面，作为吸收保护层，厚度约100 μm；流水作为约束层，厚度约1 mm。由于试验条件限制，本研究先对圆锯片一面进行激光冲击，然后再对另一面相对应的区域进行激光冲击(未来可通过光路调整等措施实现圆锯片双面对应区域同步激光冲击)。激光光斑的搭接形式如图 1所示。

采用静态应变采集仪和电阻应变花(双轴，90°)测量圆锯片表面生成的应力场，电阻应变花的贴附方式如图 1所示。电阻应变花中每个电阻应变片采用1/4桥的方式与静态应变采集仪连接，采集到的信号输入到计算机中进行处理。每个电阻应变花均用硅橡胶做防水隔热处理。在圆锯片激光冲击适张过程中，保持电阻应变花、静态应变采集仪与计算机一直处于联通状态。激光冲击适张过程结束后，静态应变采集仪记录下圆锯片指定区域的最终状态下的应变场。

对于电阻应变花①~⑧，其所在位置的应力场可由下式表示：

$ \begin{array}{l} {\varepsilon _r} = {\varepsilon _{{0^ \circ }}};\\ {\varepsilon _\theta } = {\varepsilon _{{{90}^ \circ }}};\\ {\sigma _r} = \frac{{E\left({{\varepsilon _r} + \mu {\varepsilon _\theta }} \right)}}{{1 - {\mu ^2}}};\\ {\sigma _\theta } = \frac{{E\left({\mu {\varepsilon _r} + {\varepsilon _\theta }} \right)}}{{1 - {\mu ^2}}}。\end{array} $

(1)

式中：ε_0^°和ε_90^°分别为电阻应变花两轴向的应变，由静态应变采集仪直接读取；以圆锯片中心点为坐标原点，ε_r和ε_θ分别为径向应变和切向应变，σ_r和σ_θ分别为径向应力和切向应力；E为圆锯片的弹性模量；μ为圆锯片的泊松比。

2 数学模型建立与分析 2.1 简化与假设

圆锯片激光冲击适张过程中，表面多个区域在冲击波作用下产生塑性变形。为建立能够满足理论计算分析的圆锯片激光冲击适张过程仿真分析模型，本研究作如下简化与假设：

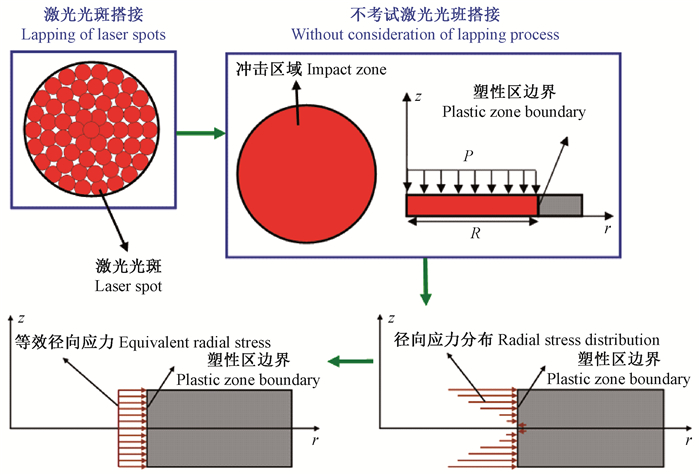
1) 多个激光光斑以不高于10%的搭接率进行连接，主要目的是扩大激光冲击区域面积，扩展塑性变形区。由激光光斑搭接形成的圆形冲击区域与不考虑搭接过程形成的圆形冲击区域，2种情况塑性区边界的应力状态近似相同，如图 2所示，单个冲击区域的形成过程可简化为轴对称力学模型，该轴对称模型也考虑了z方向上的对称性，因此厚度仅为圆锯片厚度的一半。

2) 圆锯片表面每个圆形冲击区域的塑性变形行为完全一致，忽略其相互影响。

3) 利用通孔替代圆锯片表面的圆形冲击区域，通孔内壁受均匀径向应力作用，如图 3所示，称为等效径向应力。图 3中最终形成的应力场等效于圆锯片激光冲击适张后冲击区域外侧弹性变形区所形成的应力场。

2.2 激光冲击波峰值压力的计算

激光冲击过程的冲击波压力在整个作用时间内总体呈先增大后减小的准高斯分布形式。压力随时间变化的最大值为峰值压力，冲击波作用时间通常为激光脉冲持续时间的2~3倍，激光冲击波的峰值压力和激光功率密度的关系为：

$ {P_{\max }} = 0.01{\left({\frac{\alpha }{{2\alpha + 3}}} \right)^{0.5}}{Z^{0.5}}I_0^{0.5}。$

(2)

式中：α为内能转化为热能的系数，取0.1；I₀为入射激光功率密度(GW·cm^-2)；Z为水约束层与金属试件合成的高压冲击波的声阻抗(Ding et al., 2006；Peyre et al., 1996)。

入射激光功率密度I₀可由下式表示：

$ {I_0} = \frac{{4E}}{{\pi {d^2}\tau }}。$

(3)

式中：E为激光能量(J)；d为激光光斑直径(cm)；τ为激光脉宽(ns)。

水约束层与金属试件合成的高压冲击波的声阻抗Z可由下式表示：

$ Z = 2\frac{{{Z_{t{\rm{arget}}}} + {Z_{{\rm{water}}}}}}{{{Z_{t{\rm{arget}}}} + {Z_{{\rm{water}}}}}}。$

(4)

式中：Z_water为水约束层的声阻抗，Z_water=0.165 ×10⁶g·cm^-2s^-1；Z_target为金属试件的声阻抗，Z_target=4.056 ×10⁶g·cm^-2s^-1。

经过计算可得冲击波峰值压力P_max=4.58 GPa，此压力用于理论分析模型的验证。

2.3 有限元模型的建立

单个冲击区域双面激光冲击的加载过程利用ABAQUS软件中的Dynamic/Explicit求解模块进行建模分析，卸载过程利用ABAQUS软件中的Static/General求解模块进行求解，最终获得冲击区域边界的等效径向应力。

圆锯片材料的本构关系模型设置为理想弹塑性。一般来说，金属材料的动态屈服强度是静态屈服强度的2~4倍(周南等，2002)。本研究用圆锯片的静态屈服强度约为430 MPa，故将其动态屈服强度设置为1 290 MPa。圆锯片材料的其他参数设置如下：厚度2.2 mm，密度7 800 kg·m^-3，泊松比0.3，弹性模量210 GPa。

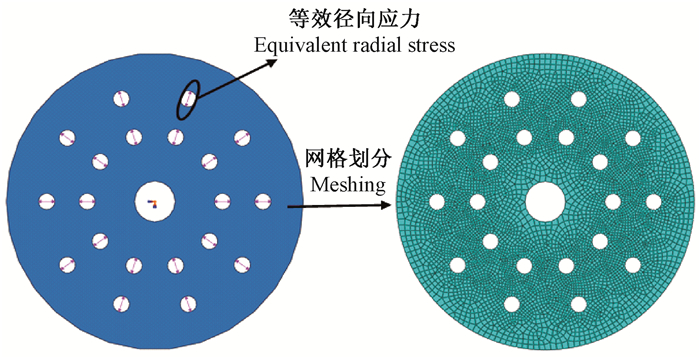
考虑模型z向的对称性，圆锯片厚度方向对称面施加z方向的对称约束，冲击区域表面施加冲击波载荷，这样即可反映双面激光冲击的效果。选择4节点轴对称减缩积分单元CAX4R对圆锯片进行网格划分。

激光冲击波作用时间一般为激光脉宽的2~3倍，本研究统一将激光冲击波作用时间设定为激光脉宽的3倍。选定4个等级的激光脉宽，分别为10、15、20和25 ns。激光冲击波压力幅值随时间呈先增大后减小的准高斯分布，如图 4所示。

利用ABAQUS软件中的Static/General求解模块建立圆锯片激光冲击适张过程适张应力场的仿真模型，此模型为二维平面应力模型，通孔内壁施加由图 4中模型计算得到的等效径向应力，选择4节点平面应力减缩积分单元CPS4R对圆锯片进行网格划分。

3 结果与讨论

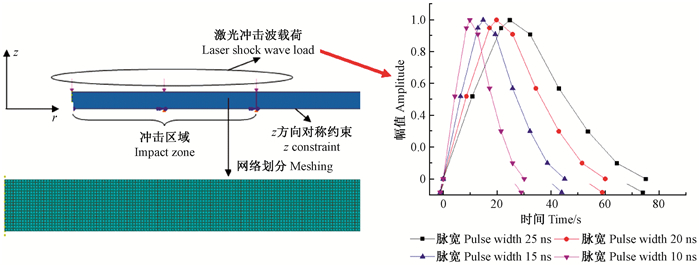
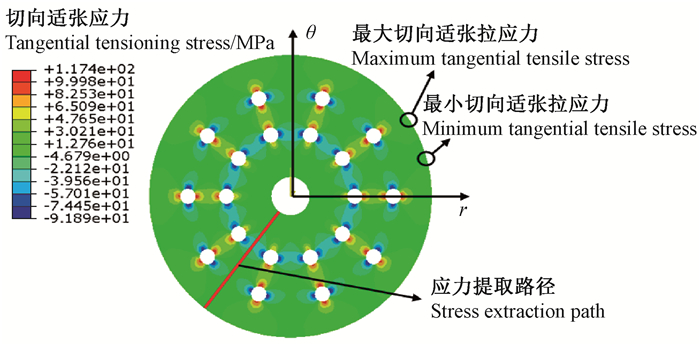
在等效径向应力作用下，每个通孔内壁均向四周扩展，在圆锯片表面形成沿中心轴呈循环轴对称分布的应力场，即适张应力场。图 5为利用本研究理论分析模型计算获得的圆锯片切向应力场，可见圆锯片外缘生成了一定的切向拉应力，用于抵消圆锯片在锯切过程中外缘由于温度升高而形成的切向压应力，有助于提高圆锯片动态稳定性。

利用电阻应变花与静态应变采集仪测试图 1中①~⑧位置的应变，按式(1)将应变转换为应力，转换后的应力即为圆锯片激光冲击适张后表面形成的径向和切向应力。利用前述建立的理论分析模型，提取图 1中路径上的径向和切向应力。

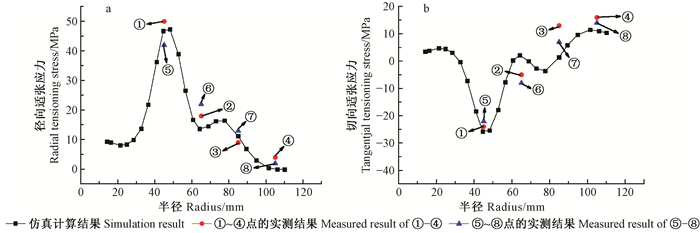
如图 6所示，径向、切向应力的仿真计算结果与实测结果均具有较好吻合度，表明本研究理论分析模型是正确的。在冲击区域以外，径向应力大部分呈拉应力状态，这是期望的应力状态，有助于提高圆锯片动态稳定性。最值得关注的是圆锯片的切向应力，即圆锯片经过激光冲击适张处理后，外缘所生成的具有一定数值并呈拉应力状态的切向应力，这种切向拉应力可以抵消或部分抵消锯切过程中圆锯片外缘由于温度升高而产生的切向压应力；并且，越靠近外缘，切向拉应力越大，这正是期望的适张应力分布状态。

限于试验条件，本研究在模型验证过程中，激光冲击区域半径仅为6 mm。依据圣维南原理，冲击区域向外扩展产生的应力衰减较多，因此在圆锯片外缘产生的切向拉应力只有10 MPa左右。在下面的分析中，将冲击区域半径统一设定为12 mm，提高冲击区域向四周的扩展效应，将圆锯片外缘的切向适张拉应力提升到一定量级。

如图 7所示，圆锯片外缘的切向拉应力与激光冲击区边界的等效径向应力呈正比例关系；圆锯片外缘的最大、最小切向拉应力均随激光冲击区边界等效径向应力的增加而线性增大。这说明，激光冲击区边界的等效径向应力对圆锯片的适张效果影响显著。

激光冲击波峰值压力、脉宽是影响激光冲击区边界等效径向应力的2个主要因素，也是表征激光束的重要参数。因此，本研究重点分析激光冲击波峰值压力、脉宽对冲击区边界等效径向应力的影响规律，再根据图 1计算结果间接预测激光参数对圆锯片激光冲击适张外缘切向拉应力的影响规律。

圆锯片激光冲击适张过程是一个高度非线性力学过程，如图 8所示，当激光脉宽为10和15 ns时，等效径向应力随激光冲击波峰值压力增加而增大。当激光脉宽为20和25 ns时，等效径向应力随激光冲击波峰值压力增加呈先增加后减小的趋势；当激光冲击波峰值压力在6~7 GPa范围内时，等效径向应力到达峰值，约140 MPa左右；当激光冲击波峰值压力继续增大时，等效径向应力不再增加，反而减小。

本研究结果可以参考文献(Peyre et al., 1996；Ballard，1991)来解释说明。激光冲击波在材料内部传播过程中，冲击波压力随传播距离增加而不断衰减。当激光冲击波峰值压力提高到一定大小后，会使冲击区表面以下一定深度范围内材料的塑性变形出现饱和；如果继续增加激光冲击波峰值压力，相应的残余应力会随冲击波峰值压力增加而下降；在塑性饱和区以下深度，峰值压力增加会导致未饱和区域进一步发生塑性变形，而使这一区域的残余应力进一步提高。本研究激光冲击的试件为圆锯片，厚度仅为2.2 mm，因此在整个厚度方向会出现塑性饱和的现象。

结合计算结果，当激光脉宽为10和15 ns时，等效径向应力随激光冲击波峰值压力增大而增加，说明圆锯片冲击区对应的厚度方向还未发生塑性变形饱和现象。这是因为激光冲击波作用时间短，冲击波压力传到圆锯片内部时，压力值已经衰减到一定量级，无法促使圆锯片内部区域达到塑形变形饱和状态，只有再进一步增大激光冲击波峰值压力才可使圆锯片整个厚度方向达到塑性变形饱和状态。当激光脉宽为20和25 ns时，等效径向应力在峰值压力为6~7 GPa时出现峰值，说明圆锯片冲击区对应的整个厚度区域在此范围内时呈现完全饱和状态；如果再进一步提高冲击波峰值压力，相应的等效径向应力会减小。

等效径向应力直接决定圆锯片外缘最终生成的切向适张拉应力大小，因此，在满足圆锯片不出现“过适张”现象的前提下，通过调整激光冲击波峰值压力大小，使等效径向应力趋近于峰值，能够使圆锯片的适张效果达到最优。

4 结论

1) 激光冲击能够诱导圆锯片多个局部区域产生塑性变形，冲击区域向四周扩张，在周围弹性区的约束作用下，导致圆锯片冲击区域外产生预应力场，特别是圆锯片外缘，生成期望的切向适张拉应力，即为适张效果。

2) 在本研究试验条件下，当激光脉宽小于20 ns时，圆锯片外缘的切向适张拉应力随激光冲击波峰值压力增加而增大；当激光脉宽大于等于20 ns时，圆锯片外缘的切向拉应力随激光冲击波峰值压力增加呈先增大后减小的趋势；当激光冲击波峰值压力为6 GPa左右时，圆锯片外缘的切向拉应力达到最大值。

3) 在满足圆锯片不出现“过适张”现象的前提下，通过调整激光冲击波峰值压力与脉宽能够使圆锯片的适张效果达到最优。