土壤有机质是土壤的重要组成部分，其含量是土壤肥力高低的重要指标，对土壤形成、农林业可持续发展起着重要作用，且其含量的时空变化信息在土壤数字制图和土壤资源调查中非常重要(Robin et al., 2010)。传统土壤养分测定方法速度慢且范围有限，而快速、便捷、大面积、低成本的高光谱技术为土壤有机质的时空动态变化监测提供了新的有效手段，并已逐渐成为高效获取土壤有机质含量的重要手段之一(高志海等, 2011; 于雷等, 2016a; 2016b; 袁征等, 2014)。

近年来，国内外不少学者开展了土壤有机质含量高光谱估算研究，如Baumgardner等(1970)的研究表明，有机质在一定含量范围会对其他土壤成分的光谱特征造成影响；Karneili等(1998)和Galvao等(2001)的研究发现，土壤反射光谱在550~700 nm范围的吸收峰主要受土壤有机质影响，且1 720、2 180和2 309 nm处是土壤有机质吸收特征光谱区；Al-Abbas等(1972)、Krishnan等(1980)和Gunsaulis等(1991)的研究发现，土壤光谱反射率与土壤有机质含量存在一定的相关性；刘磊等(2011)的研究发现，红壤土有机质的光谱响应波段为400~1 000 nm，与沈润平等(2009)认为的红壤有机质响应波段在540~1 000 nm接近；在建模方法上，传统的土壤有机质含量高光谱反演模型很多，主要有主成分分析(PCA)、多元逐步回归(MSLR)、偏最小二乘回归(PLSR)、人工神经网络(ANN)、回归树(RT)、支持向量机(SVM)及随机森林(RF)等(纪文君等，2012)。大量研究发现，在解决线性问题方面，PLSR方法能较好地分析土壤光谱特征，揭示光谱特征波段与土壤有机质含量的关系，是一种常用的线性方法；在解决非线性问题中，ANN是目前在高光谱数据挖掘中应用最广泛的一种方法(杨扬等，2015)。田永超等(2012)将逐步多元回归、主成分分析、偏最小二乘法、人工神经网络等用于构建土壤养分模型，发现估测精度存在一定差异。方少文等(2014)的研究发现，利用偏最小二乘回归模型建模的最优波段范围为560~710 nm；袁征等(2014)利用最常用的线性回归分析法、BP神经网络法和模糊识别法建立土壤有机质含量高光谱估测模型，对比后发现模糊识别模型的估测精度高于线性模型和BP神经网络模型。

当前研究表明，土壤反射光谱与土壤有机质含量之间存在一定的相关性，值得进一步研究、开发和应用。但现有研究中，反演模型只局限于某单一模型的研究，而传统的单一模型不能反映出事物的全面信息，信息的缺失又会对预测结果造成误差(黄仁东等，2015)，所以Bates等(1969)提出将多种单一模型结合起来构建组合模型以提高模型预测精度。因此，为了减少单一预测模型的随机影响因素、提高预测精度，本研究以赣北山地红壤为对象，在径向基函数(RBF)神经网络的基础上，探讨不同组合方式下组合模型在山地红壤有机质含量高光谱估算中应用的可行性, 以期为土壤有机质含量估测提供基础数据和科学依据。

土壤样品采集于江西省赣北的庐山(115°52′—116°8′E，29°26′—29°41′N)与湾里区(115°37′—115°49′E，28°40′—28°55′N)。该区属亚热带东部季风区，具有明显的山地气候特征，土壤以山地红壤为主，是典型的亚热带红壤区。采集0~30 cm土层土样，共采集318个土样，其中山地红壤248个(庐山143个，湾里105个)用于本试验。土样在室内进行风干、研磨、过0.25 mm筛处理后，每份样品分成2份，一份用于有机质含量测定，另一部分用于高光谱数据采集。有机质含量采用重铬酸钾容量法-外加热法测定(鲍士旦，1999)。

由于样本海拔跨度比较大，山地红壤有机质含量的差异也比较大，最小值为0.89 g · kg^-1，最大值为79.83 g ·kg^-1，平均含量为27.06 g ·kg^-1(表 1)。

表 1 山地红壤有机质含量统计特征 Tab.1 Statistics of organic matter content in mountain red soil

表 1 山地红壤有机质含量统计特征 Tab.1 Statistics of organic matter content in mountain red soil 土样类型 Soil sample type 样本数 Number of soil sample 有机质含量均值 Mean of organic matter content/ (g ·kg-1) 有机质含量最小值 Minimumof organic matter content/ (g· kg-1) 有机质含量最大值 Maximumof organic matter content/ (g ·kg-1) SD CV(%) 全体样本 Total dataset 248 27.06 0.89 79.83 15.78 58.34 建模样本 Modeling dataset 186 26.89 0.89 75.44 15.64 58.15 验证样本 Validation dataset 62 27.55 4.08 79.83 16.33 59.29

采用K-S(Kennard-Stone)算法计算各样本间的欧氏距离，选取山地红壤总样本数的75%作为建模样本(186个)构建模型，25%(62个)样本作为验证样本。从表 1的统计特征看，验证样本的标准差、变异系数与总样本接近，具有代表性。

将土壤样本进行风干、研磨、过筛，并采用美国ASD FieldSpec3地物光谱仪进行土壤光谱测定，光谱范围为350~2 500 nm，采样间隔为1.4 nm(350~1 000 nm)和2 nm(1 000~2 500 nm)，重采样间隔为1 nm。为减少外界光源等因素干扰，土壤光谱测定在暗室内进行，将土样装满平铺置于直径10 cm、深2 cm的盛样皿中，光源为50 W的平行光卤素灯，距土壤表面30 cm，天顶角15°，采用5°探头距离土样垂直上方15 cm处测量，测定前以白板定标，并每间隔20~30 min进行1次标准白板校正，每个土样测定5次，算术平均后得到的光谱值作为每个土样的实际反射光谱数据。每个土样重采样间隔为1 nm进行光谱输出，测定得到350~2 500 nm波长、波段数为2 151的反射光谱数据。

为消除光谱数据采集过程中的样本表面、环境和随机噪声等因素影响，利用ASD光谱仪自带的View Spec Pro Version 6.0软件进行断点校正，并考虑边缘波段存在较大的仪器噪声，去除边缘波段(350~399和2 451~2 500 nm)，保留了400~2 450 nm波段的反射光谱数据。为研究不同变换处理方法对山地红壤有机质含量估算的影响，对山地红壤原始光谱数据进行了倒数、一阶导数、对数、平方根、去包络线等处理，并与原始光谱比较，确定最优光谱变换方法。

本研究估测模型的建模思路为：1)计算分析不同光谱变换与山地红壤有机质含量的相关性；2)选择最优光谱构建模型；3)根据单项预测模型的选取原则，选择3种单项预测模型；4)以绝对误差和最小为目标，确定定权重及不定权重的组合模型权重值，再利用单项模型预测的相对误差值，进行训练数据的重构；5)构造基于径向基函数(RBF)神经网络的定权重与不定权重、数据重构与不重构山地红壤有机质含量估测组合模型；6)通过均方根误差(RMSE)、预测偏差比(RPD)和决定系数(R²)进行精度检验；7)确定最优组合模型。

径向基函数(RBF)神经网络属于前馈式神经网络，具有突出的函数逼近能力，并且在模式识别、函数逼近等领域均有着广泛应用，由输入层、隐含层和输出层组成的非线性函数，多输入单输出径向基函数(RBF)神经网络的输出为：

式中：n为隐含层神经元的个数；x (x₁, …, x_m)为输入向量；ω_i为第i个隐含层神经元与输出层神经元的联结权值；φ_i为径向基函数(RBF)高斯函数第i个隐含层神经元的输出；c_i为隐含层第i个神经元的基函数中心值；δ为高斯函数的方差(卫敏等，2012)。

目前土壤高光谱定量分析中，偏最小二乘回归(PLSR)方法是线性建模方法中的一种新型主流统计方法，在土壤有机质反演方面意义重大(于雷等，2015)；BP神经网络模型是应用较广的一种非线性人工神经网络(ANN)建模方法，具有很强的数学计算能力，能处理非线性问题(丁美青等，2012)，支持向量机回归分析(SVMR)方法是一类应用于各种分类和回归问题、可用于处理非线性系统的新型机器学习方法(曾胤等，2014)，并且BP神经网络与支持向量机回归分析(SVMR)在土壤养分含量的光谱反演中有较好的应用。综合考虑以上因素，本研究选用偏最小二乘回归(PLSR)、BP神经网络(BP)和支持向量机(SVMR)3种模型作为单一预测模型。

单一预测模型的加权系数是决定组合预测模型精度的关键。组合模型的加权系数的确定可分为固定权系数和变权系数两种方式，其中固定权系数方法在组合模型中一直占主导地位(代海波等，2012)。本研究以绝对误差和最小为目标，在数据重构与否的条件下，采用定权与不定权方法确定组合模型的系数。组合模型为：

其中：X为组合预测值；t为预测时段数；$ {{\hat x}_{{P_t}}}、{{\hat x}_{{B_t}}}、{{\hat x}_{{S_t}}}$和l_Pt、l_Bt、l_St分别为偏最小二乘回归(PLSR)、BP神经网络(BP)和支持向量机(SVMR)预测模型在第t时段的预测值及其相应的组合权系数。组合权系数l_P、l_B和l_S参考经验公式求取：

式中：l_k为第k种模型的组合权系数，满足$\sum\limits_i {{l_i} = 1;\;\;} {{\tilde d}_i}$为第i种模型在预测时段内的残差平方和。

数据重构是利用3种单一预测模型的预测值，分别计算各样本单一预测模型预测值的平均相对误差，对平均相对误差较大的模型预测值，取另2个模型同步预测值的平均值替换。

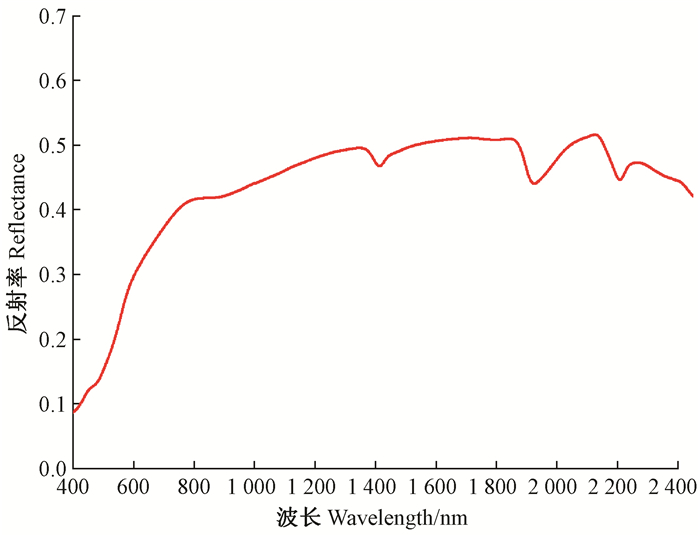
从图 1可见：山地红壤光谱曲线在可见光部分呈陡坎型。史舟等(2014)和徐彬彬等(1991)研究发现，黄淮以南的土壤中铁对光谱的贡献要大于有机质，推测本研究所得光谱曲线在900 nm附近较明显的吸收谷很大程度上是Fe³⁺的吸收谷；根据水对光谱的吸收作用及于雷等(2015)研究结果，本研究所得光谱曲线近红外1 400, 1 900和2 200nm附近明显的吸收谷应为水分吸收谷。

图 1 山地红壤光谱曲线 Figure 1 Reflectance spectra of mountain red soil

为探讨有机质含量对山地红壤光谱特征的影响，本研究将山地红壤有机质含量分为8个等级:＜6，6~10，10~20，20~30，30~40，40~50，50~60和>60 g ·kg^-1，每个等级求取对应的平均反射光谱曲线，得到不同有机质含量的山地红壤光谱曲线(图 2)。从图 2可看出，山地红壤有机质含量与光谱反射率呈负相关，即反射率随有机质含量升高而降低，并且有机质含量越低山地红壤的反射光谱特征越明显。

图 2 不同有机质含量的山地红壤光谱特征 Figure 2 Spectral characteristics of mountain red soil with different organic matter contents

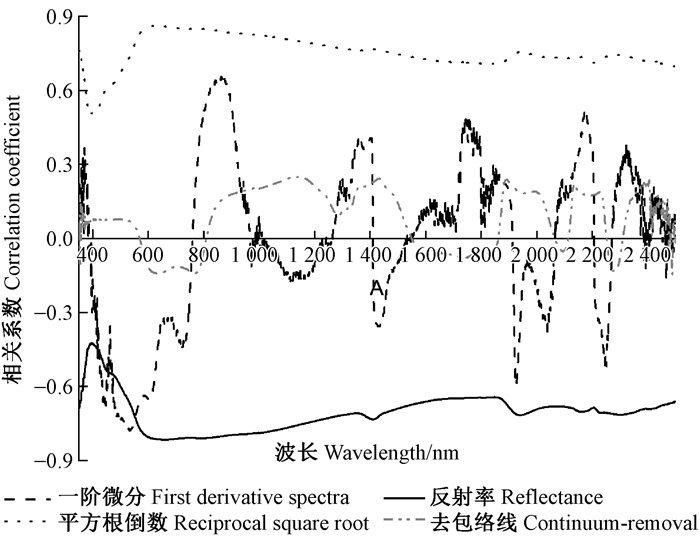
将山地红壤原始光谱及相关变换光谱与有机质含量进行相关性分析(图 3)，由图 3可看出，平方根倒数处理相关曲线与原始光谱相关曲线变化趋势呈对称性的一致，区别不明显；而一阶微分相关曲线在400~600 nm范围附近有明显提升，但在600~2 450 nm范围内相关性不如原始光谱显著。通过对比去包络线曲线可以发现，山地红壤有机质的光谱特征波段主要在600~2 450 nm处，在400~600 nm的可见光范围内特征波段并不明显。由此可见，山地红壤原始反射光谱存在与有机质含量连续的相关性，且波段范围较大。因此，本研究选用原始光谱的全波段(400~2 450 nm)与有机质含量进行建模。

图 3 山地红壤有机质含量与光谱反射率及其变换光谱的相关性 Figure 3 Correlations of reflectance and its variation spectra with mountain red soil organic matter content

根据单一预测模型的选择，分别建立山地红壤的偏最小二乘回归(PLSR)、BP神经网络(BP)和支持向量机(SVMR)3种预测模型，对比建模与验证结果(表 2)。支持向量机(SVMR)的建模、验证精度相对较高，并且非线性模型BP神经网络(BP)与支持向量机(SVMR)的山地红壤有机质含量估算效果明显优于偏最小二乘回归(PLSR)线性模型。

表 2 不同预测模型的山地红壤有机质含量预测结果 Tab.2 Prediction of the contents of organic matter in mountain red soil using different models

表 2 不同预测模型的山地红壤有机质含量预测结果 Tab.2 Prediction of the contents of organic matter in mountain red soil using different models 模型Model 建模精度Modeling accuracy 验证精度Verification accuracy R2 RMSEp/(g· kg-1) RPD R2 RMSEp/(g ·kg-1) RPD 偏最小二乘回归Partial least squares regression 0.30 13.05 1.20 0.28 13.82 1.18 BP神经网络Back propagation neural network 0.69 8.70 1.80 0.58 10.49 1.56 支持向量机Support vector machine regression 0.82 6.71 2.33 0.64 9.76 1.67 数据不重构定权重Data non reconstruction and definite weight 0.75 8.16 1.92 0.68 9.22 1.77 数据不重构不定权重Data non reconstruction and indefinite weight 0.79 7.64 2.05 0.72 8.70 1.88 数据重构定权重Data reconstruction and definite weight 0.86 6.27 2.49 0.76 7.91 2.06 数据重构不定权重Data reconstruction and indefinite weight 0.87 6.07 2.58 0.75 8.11 2.01

从单一模型与组合模型的对比可看出，组合模型的建模精度优势不明显，数据不重构的组合模型在建模精度上甚至不及支持向量机(SVMR)单一模型，仅数据重构的组合模型在建模精度和验证精度上均优于单一模型；但在对比验证精度时，组合模型均优于单一模型，说明组合模型不仅能解决PLSR线性模型高值低估的问题，也能很好地解决在BP神经网络(BP)、支持向量机(SVMR)模型中训练样本过拟合的问题，组合模型整体估测精度较高。

在组合模型中，预测数据重构以后的组合模型要优于不重构的组合模型。预测数据不重构条件下，不定权组合模型精度更高；预测数据重构的情况下，不定权组合模型估测精度要略低于定权组合模型。对预测数据重构的目的是减少单一模型间的误差，而不定权组合模型优势也是减少单一模型间的误差，因此，预测数据重构的条件下，不定权组合模型优势不明显，造成估测精度不如定权组合模型。对比发现，预测数据重构定权组合模型估测精度最高，效果最优，说明在山地红壤有机质含量估测中，由于3种单一预测模型的预测误差相差较大，数据重构将误差影响较大的因素去除，只考虑了在两种预测模型中精度高的模型的影响，因此，预测数据重构对组合模型的影响较大，大大提高了组合模型的估测精度。

山地红壤有机质含量的快速估测对红壤区林地质量评价、土壤数字化制图等方面有重要意义。目前土壤有机质含量光谱估测的方法较多，均仅局限于某单一预测模型的应用，而单一预测模型通常是按某种假设条件进行的，因此，单一模型无法全面反映土壤有机质含量与土壤光谱反射率的信息，且信息的缺失会影响预测结果。本研究通过多种单一预测模型进行加权组合，研究结果表明，组合模型在山地红壤有机质含量的光谱估测应用中是可行的，且与单一模型相比，组合模型的估测精度有所提升，但提升幅度与组合模型的权值及预测数据的重构与否有关。

单一预测模型的选择与权重系数的确定是组合模型减少误差、提升建模精度的关键。单一模型的确定与模型精度、模型相关度和模型数量有关，单一模型的预测精度会影响组合模型的估测结果，且单一预测模型间的相关性越小，组合模型的预测误差会越小。模型的数量并不是越多越好，模型数量过多会造成计算量过大，而模型精度却不一定增加(黄仁东等，2015)。综合以上因素，本研究选择了土壤有机质含量估测中精度较高的偏最小二乘回归(PLSR)线性模型、非线性神经网络模型中应用最广的BP神经网络模型和具有严格理论和数学基础的支持向量机(SVMR)模型。3种单一预测模型在土壤养分含量的估测中精度均较好，且考虑了不同类型的预测模型，模型相关性较小，单一预测模型数量也比较适中。

单一预测模型权重系数的确定，是组合模型的关键，组合预测模型中权系数的确定有定权和变权两种方法，目前主要研究方法为定权组合方法，但变权组合预测方法的预测精度较定权组合预测方法好，优势更明显(付华等，2013)。由于本研究3种单一预测模型在每个样本中的误差不同，为了提高组合模型的预测精度，将单一模型误差的影响减少到最小，因此，本研究根据3种单一预测模型的预测误差，对预测数据进行重构，以此降低单一模型误差的影响。结果表明，组合模型估测的预测偏差比(RPD)比单一模型提高了0.1~0.88，说明组合模型在山地红壤有机质含量的光谱估测中能得到有效提高。

综合对比，组合模型在估测精度方面有一定优势，可有效降低单一模型的误差、优化组合模型结构、提高估测精度，其中，预测数据重构组合模型估测效果最优，研究结果为赣北地区山地红壤有机质含量的光谱估测提供了新思路，并且具有一定可行性。与张娟娟等(2012)、于雷等(2016b)通过选取多个敏感波段并综合不同光谱处理方法提高单个模型估测精度不同，本研究探讨的组合模型选取土壤光谱的全波段信息，通过减少单一预测模型误差的方法提高估测精度，该方法对土壤光谱与土壤有机质含量的关系在模型中考虑比较全面，并且在土壤光谱建模数据预处理方面，更便于实现。但从表3中可看出，单一模型中的支持向量机(SVMR)模型与组合模型中定权不重构组合模型的估测精度相差不大，且单一模型具有模型简单、运算速度快等特点，说明定权不重构组合模型相对支持向量机单一模型优势并不明显，因此，权重的确定与预测数据的重构是影响组合模型估测精度的关键，如何快速确定最优权重、快速实现预测数据的重构和快速构建组合模型，是提高组合模型在土壤光谱估测中应用的关键。

本研究选用偏最小二乘回归(PLSR)、BP神经网络(BP)和支持向量机(SVMR)3种单一预测模型，在考虑预测数据重构及定权与不定权2种权系数方法下，建立径向基函数(RBF)神经网络组合模型，得到以下主要结论：

1) 支持向量机模型可用于土壤光谱估测研究。对比偏最小二乘回归(PLSR)、BP神经网络(BP)和支持向量机(SVMR)3种不同的单一预测方法模型，SVMR模型的建模效果最优，这与于雷等(2016)得出的支持向量机(SVMR)模型的土壤有机质估算精度高于偏最小二乘回归(PLSR)和BP神经网络的结论一致，可适用于山地红壤有机质含量的估测。

2) 组合模型估测精度要高于单一模型。在山地红壤有机质含量的光谱估测研究中，组合模型更能有效提高土壤有机质含量的估测精度，为土壤光谱估测提供了研究思路。

3) 组合模型的估测精度分别与权重的确定及预测数据的重构有关。组合模型的不同权重会影响组合模型的估测精度，一般情况下，因为不定权组合模型考虑了单一模型间的误差影响，因此不定权组合模型要优于定权组合模型；而在考虑预测数据重构的情况下，预测数据重构对提高组合模型的估测精度有较明显的优势，并且在预测数据重构的条件下，不定权组合模型估测精度并不如定权组合模型估测精度，说明在山地红壤有机质含量的估测中，预测数据重构对提高组合模型的估测精度的作用更明显。

4) 应提高组合模型在土壤光谱估测中的应用。与组合模型对比，单一模型具有计算简单、易于操作和推广性强的优势。因此，如何快速减小和消除单一预测模型误差的干扰，建立预测性能更高、推广性更好的组合模型在土壤光谱估测中的应用是今后的研究目标。