文章信息
- Hu Xingbo, Lu Xinjian, Yu Yang, He Kangning
- 胡兴波, 芦新建, 于洋, 贺康宁
- Simulation of Canopy Conductance of Qinghai Spruce (Picea crassifolia) Plantation based on Granier's Thermal Dissipation Probe Method
- 基于热扩散法的青海云杉冠层导度模拟
- Scientia Silvae Sinicae, 2018, 54(3): 8-18.
- 林业科学, 2018, 54(3): 8-18.
- DOI: 10.11707/j.1001-7488.20180302
-
文章历史
- 收稿日期:2017-02-08
- 修回日期:2018-01-31
-
作者相关文章
2. 北京市首发天人生态景观有限公司 北京 102600;
3. 中国水利水电科学研究院泥沙研究所 北京 100048
2. Beijing Shoufa Tianren Ecological Landscape Co., Ltd. Beijing 102600;
3. Department of Sediments Research, China Institute of Water Resource and Hydropower Research Beijing 100048
As an indispensable link in the soil-plant-atmosphere continuum, canopy transpiration (Ec) reflects the exchange and balance of material and energy between plants and environmental factors. Plant stoma not only transpire water into the atmosphere, but also uptake CO2 into the plant. The opening and closing statuses of stoma are largely controlled by the surroundings and directly affect the extent of plant photosynthesis and the strength of Ec.
In practical applications, a more useful variable is the canopy conductance (gc), which treats all stoma in parallel or considers the entire canopy as a big leaf. The gc is commonly used in ecological, meteorological and air quantity simulation models. Its value is usually computed by a scale transformation method that extends the stoma conductance of a single leaf over the canopy. The disadvantages of this method are the difficulty of acquiring long-term observations, and large errors may occur in the scale conversion processes. The errors are introduced by the inhomogeneous distribution of sunlight at the canopy level and the different chlorophyll contents of older and younger leaves (Alves et al. 1998; Green et al. 2003).
Sap flow can now be continuously and accurately monitored by Granier' s thermal dissipation probe (TDP) method (Granier 1985; 1987). With recent advances in micro-meteorological observation technology, we can also compute the canopy conductance from sap flow and meteorological data by inverting the Penman-Monteith (PM) equation. This method is popular, because it easily and accurately obtains the long-term canopy conductance. For example, the gcs of pine forest in Norfolk (Stewart 1988), Moso bamboo (Phyllostachys edulis) in western Japan (Komatsu et al. 2012), Douglas-fir forest in the Netherlands (Bosveld et al., 2001), and rain-fed citrus orchard under sub-humid tropical conditions (Oguntunde et al., 2007) have been determined by this method.
The opening and closing of gc mainly depends on environmental factors such as solar radiation, air temperature, humidity, and soil moisture (Jarvis 1976; Komatsu et al. 2012; Oguntunde et al. 2007; Whitley et al. 2009). To predict gc, multiple linear equations are advantaged by their simplicity, but non-linear Jarvis equations can better explain the mechanism of stomatal activity. However, most studies have focused on the applicability of gc prediction methods or modified the pre-existing equations to improve the correlation between predictions and observations. The physical and mathematical rationalities of the modeling approaches have been largely ignored.
Qinghai spruce (Picea crassifolia) is one of the main constructive species that is widely spread throughout Qinghai, Gansu, Inner Mongolia, and Ningxia. It inhabits altitudes between 1 600 m and 3 800 m. Chang et al. (2014)investigated the relationships between gc and environmental factors in a Qinghai spruce forest in the upper Heihe River Basin of arid northwestern China. However, classical gc models have yet to be applied to Qinghai spruce. To explore the mechanisms by which environmental factors affect the water use of forest eco-systems at the canopy level and to reveal the adaptabilities of different canopy conductance models, we simulate the changing canopy conductance in Qinghai spruce forest by implementing the PM formula in two models: multiple linear regression and the non-linear Jarvis model. We also hope to find a model to simulate gc simply and accurately, and to guide transpiration estimating and parameters calibrating with transportation models in high-cold region of western China.
1 Materials and Methods 1.1 Site descriptionQinghai spruce was a dominant species in Datong County (Xining, Qinghai Province, China), but was largely destructed in the 1950s. The damaged areas have since been occupied by the pioneer species Betula platyphylla (white birch). To promote natural regeneration, numerous Qinghai spruce seedlings were planted under white birch or in forest clearings in the 1980s. The study site (latitude 37°10′N, longitude 101°34.5′E, altitude 2 860 m above sea level) is located in a 30-year-old Qinghai spruce plantation in the Baoku forestry farm, Datong County. The tree spacing is 3 m × 4 m, giving a density of 833 trees·hm-2 at this site. The mean tree height is 11.35 m. The climate is a classic plateau continental climate characterized by abundant sunshine (2 553 h·a-1), long cold winters, short cool summers, and distinct wet (May-September) and dry (October-April) seasons. The total annual rainfall and annual mean air temperature is 523.3 mm and 4.9 ℃, respectively.

|
Fig.1 Location of study region and observation site |
Sap flow was monitored from June 1 to 30 in 2013 by a 32-stem flow measurement system (5 probes of 3 cm) based on Granier's TDP method (Dynamax Co., USA). Two cylindrical probes (single measurement set) were vertically implanted in the sapwood of the tree trunks. The downstream probe was continuously heated by a constant power source, and the unheated upstream probe provided a temperature reference. Temperature difference between the two probes was converted into a stem flow speed of the trunk by Eq. (1) (Granier 1985). The data logging internal was set to 15 min.
| $ f = 0.011\;9{\left({\frac{{\Delta {T_{{\rm{max}}}} - \Delta T}}{{\Delta T}}} \right)^{1.231}} $ | (1) |
where f is stem sap flux density (cm cm-2·s-1), ΔTmax is the maximum temperature difference between the two probes (℃, measured over a > 24 h period), and ΔT is the current temperature between the two probes (℃).
Five Qinghai spruce trees with diameters near the mean tree diameter (12.5 cm) of the experimental plot were selected as representative samples. The trees are relatively uniform in age and size. The sapwood area of the samples was determined by a power-law relationship between sapwood area (As) and trunk diameter (Dt) (Eq. (2); r2=0.99, n=20). Canopy transpiration (Ecm) was then calculated by Eq. (3).
| $ {A_s} = 0.14D_t^{2.44} $ | (2) |
| $ E_c^m = \frac{{3\;600 \cdot f \cdot {A_s}}}{{1\;000 \cdot {A_c}}} $ | (3) |
Where, Ecm is measured in mm h-1 and Dt, As and Ac denote the trunk diameter (cm), sapwood area and canopy projection area (m2) at the measured height (cm2), respectively.
1.3 Meteorological measurementsA portable automatic weather station (Weather link vantage pro2; Davis Co., US) was installed at a height of 2 m in a forest clearing and approximately 20 m from the sample area. The meteorological parameters, namely, rainfall, humidity, solar radiation (R, W·m-2), air temperature (T, ℃), air pressure (P, kPa) and wind speed (U, m·s -1) were synchronously logged with the data of TDP.
1.4 Calculation of canopy conductanceThe PM equation is popular because it clearly separates the influences of the atmosphere and the plant/soil system on transpiration process. Typically, gc is calculated from sap flow and meteorological data by inverting the PM equation (Eq. (4)) (Amp et al. 1994; Buckley et al. 2012; Chang et al. 2014; Granier et al. 2000; Komatsu 2004; Whitley et al. 2009):
| $ g_{\rm{c}}^{\rm{m}} = \frac{{\lambda E_{\rm{c}}^{\rm{m}}\gamma {g_{\rm{a}}}}}{{\Delta \left({{R_{\rm{n}}} - G} \right) + \alpha \rho {C_{\rm{p}}}D{g_{\rm{a}}} - \lambda E_{\rm{c}}^{\rm{m}}\left({\Delta + \gamma } \right)}} $ | (4) |
where gcm is the measured canopy conductance (m·s-1), Δ is the slope of a saturation vapor pressure versus temperature plot (kPa·℃-1), Rn is the net radiation above the forest canopy (MJ·m-2 h-1), and the soil heat flux G (MJ·m-2 h-1) is set to 0.1 Rn (Allen et al. 1998). α is a conversion factor (3 600 s·h-1) that converts Ecm to mm h-1, ρ is the air density (kg·m-3), Cp is the specific heat of air (1.013×10-3 MJ·kg-1 ℃-1), γ is the psychometric constant (kPa·℃-1), and λ is the latent heat of vaporization (MJ·kg-1 ℃-1). The aerodynamic conductance ga from the canopy to the reference level of the scalar quantities (m·s-1) is calculated by Eq. (5) (Rana et al. 2005; Kang et al. 1991).
| $ {g_{\rm{a}}} = \frac{{{k^2}{u_z}}}{{{\rm{ln}}\left({\frac{{z - d}}{{{z_0}}}} \right){\rm{ln}}\left({\frac{{z - d}}{{{h_c} - d}}} \right)}} $ | (5) |
where k is the Karman constant (0.41), uz is the wind speed at the reference height (m·s-1), hc is the height of the measured tree (m), and z is the reference height (m). The roughness length z0 and zero-plane displacement d were set to 0.1 hcm and 0.67 hc, respectively.
1.5 Prediction of canopy conductanceFrom the main meteorological factors, we computed gc by two common methods: (1) multiple linear regression analysis and (2) the non-linear Jarvis regression model. The multiple linear regression formula is given by Eq. (6) (Oguntunde et al. 2007).
| $ {\rm{ln}}\left({\mathit{g}_{\rm{c}}^{\rm{p}}} \right) = {\beta _0} + {\beta _1}\mathit{D} + {\beta _2}\mathit{T} + {\beta _3}\mathit{R} $ | (6) |
where gcp is the predicted value of gc, and the parameters β0-β3 are determined by multiple linear regression of D, T and R versus gcm.
Jarvis model is among the most widely used non-linear methods in gc predictions. The original Jarvis model is a product of five response functions with independent inputs of photon flux density, leaf water potential, vapor pressure deficit, leaf temperature and ambient CO2 concentration (Jarvis, 1976). To estimate gc from the commonly measured meteorological factors, researchers have revised Jarvis equation several times. In this study, we multiply the maximum canopy conductance (gcmax) by the response functions of vapor pressure deficit, air temperature and solar radiation (Oguntunde et al., 2007; Stewart, 1988). The values of the response functions range from 0 to 1, and the model is given by Eq. (7):
| $ g_{\rm{c}}^{\rm{p}} = {g_{{\rm{cmax}}}}f\left(D \right)f\left(T \right)f\left(R \right) $ | (7) |
where f(D) is computed as
| $ f\left(D \right) = {{\rm{e}}^{ - {k_1}D}} $ | (8) |
and f(T) is given by Eqs.(9) or (10).
| $ f\left(T \right) = \frac{{\left({T - {T_{\rm{L}}}} \right)\left({{T_{\rm{H}}} - T} \right){^{\frac{{{T_{\rm{H}}} - {k_2}}}{{{k_2} - {T_{\rm{L}}}}}}}}}{{\left({{k_2} - {T_{\rm{L}}}} \right){{\left({{T_{\rm{H}}} - {k_2}} \right)}^{\frac{{{T_H} - {k_2}}}{{{k_2} - {T_L}}}}}}} $ | (9) |
| $ f\left(T \right) = {{\rm{e}}^{ - {k_3}{T^2}}} $ | (10) |
Given that temperature can influence gc and Ec in the long-term, the optimal temperature (Topt) was incorporated into Eq. (10). The revised formula is given by Eq. (11):
| $ f\left(T \right) = {{\rm{e}}^{ - {k_4}{{\left({T - {T_{opt}}} \right)}^2}}} $ | (11) |
and f(R) is given by Eq. (12) or (13):
| $ f\left(R \right) = \frac{R}{{{R_{\rm{m}}}}}\frac{{{R_{\rm{m}}} + {k_5}}}{{R + {k_5}}} $ | (12) |
| $ f\left(R \right) = {k_6} + {k_7}R + {k_8}{R^2} $ | (13) |
where the high and low temperatures TH and TL are fixed at 45 ℃ and 0 ℃, respectively, and Rm is the radiation constant. Typically, Rm is arbitrarily assigned between 1 000 and 2 000 W·m-2 (Oguntunde et al., 2007). The maximum local R throughout the study period was measured as 1 145 W·m-2. Therefore, to constrain f(T) between 0 and 1, we set Rm to 1 200 W·m-2. The undetermined parameters gcmax, Topt and k1-k8 can be determined by multivariate nonlinear regression of the measured gc and the environmental factors.
Because both of f(T) and f(R) are not uniquely expressed, we investigated six Jarvis models with different forms of the response functions, as shown in Tab. 1.
|
|
The decoupling factor (Ω) quantifies the coupling between the evaporating surface and free airstream conditions. It varies between 0 (perfect coupling) and 1 (complete isolation) (Jarvis et al., 1986; Kumagai et al., 2004), as apparent from Eq. (14):
| $ \Omega = \frac{{1 + \frac{\Delta }{\gamma }}}{{1 + \frac{\Delta }{\gamma } + \frac{{{g_a}}}{{{g_c}}}}} $ | (14) |
Although the activity of leaf stoma is controlled by the external environment, it does not respond immediately to changes in the external environmental factors (Hu, 2010). In this paper, gc was calculated from sap flow data. Therefore, when cross-correlating Ec/gc with the external environment factors (D, T, R, Ep), we advanced or delayed the sap flow by 15-step intervals, up to the essential time lag (τ, ± 120 minutes). The correlation was calculated as the square of the Pearson coefficient (r2):
| $ {r^2} = \left\{ {\frac{{{\rm{Cov}}\left[ {X\left(t \right), Y\left({t + \tau } \right)} \right]}}{{{\delta _x}\delta _y}}} \right\}^2 $ | (15) |
In Eq.(15), Cov; ] denotes the covariance function, X and Y are series of environmental factors and gc (or Ec), respectively, and δx and δy represent the standard deviations of X and Y, respectively. t is the current time, and τ is the lag time (in minutes) between X and Y.
1.7 Statistics and validationTo validate the selected model, we divided the whole dataset into odd days (Database A) and even days (Database B), depending on their day date. The selected models were then fitted to Database A and validated on Database B (Han et al., 2012). The predicted gc (gcp) and Ec (Ecp) were separately compared against their own measured values.
Environmental factors such as rainfall, morning dew and fog will wet the leaves, causing errors in the calculated canopy conductance. To avoid such effects, we input only measurements collected from 10:00 to 18:00 (UTC+8). Data with R below 120 W·m-2 (the lowest R measured under sunny conditions by a standard meteorological station), data with obvious abnormalities (such as those introduced by voltage instability when replacing the TDP batteries), and data collected on overcast and rainy days, were also excluded.
The discrepancies between the predicted and the measured values were analyzed by statistical parameters, namely, the root mean square error (RMSE), mean absolute error (MAE) and mean relative error (MRE, %), respectively calculated by Eqs. (16), (17) and (18).
| $ {\rm{RMSE}} = \sqrt {\frac{1}{{n - 1}}\sum {{{\left({{y_i} - {x_i}} \right)}^2}} } $ | (16) |
| $ {\rm{MAE}} = \frac{1}{n}\sum {\left| {{y_i} - {x_i}} \right|} $ | (17) |
| $ {\rm{MRE}} = \frac{1}{n}\sum {\frac{{\left| {{y_i} - {x_i}} \right|}}{{{y_i}}}} $ | (18) |
Here, yi and xi denote the ith measured and predicted values, respectively, and n is the number of sample pairs.
To optimize the unknown coefficients, we ran 10 computations in 1st Opt software (Chinese version; the English version is Auto2Fit). For the numerical optimization calculation, we selected a software platform that solves non-linear regression and other mathematical problems without guessing the initial start values (http://www.7d-soft.com/en). We applied the Levenberg-Marquardt algorithm (Marquardt 1963), and the regression parameters that maximized r2 and minimized the RMSE. Most of the remaining statistical analyses were performed in Microsoft Excel, and all figures and fitted curves were generated by SigmaPlot software.
2 Results 2.1 Time lag and environmental conditionsBecause Ec modeling is subject to hysteresis the time lags (τ) between Ec and potential transpiration (Ep), estimated with the procedure outlined in FAO 5 (Allen et al., 1998), and other atmosphere variables (D, T and R) were determined by cross-correlation analysis. As shown in Fig. 2, Ec lagged R and Ep by 15 minutes (r2=0.49 and 0.41, respectively), D and T by 120 minutes (although the correlations with these variables were low; r2=0.17 and 0.22 respectively). Thus, when modeling the canopy conductance in the next subsection, we imposed a time lag of τ=15 behind the fluctuations in the meteorological parameters.
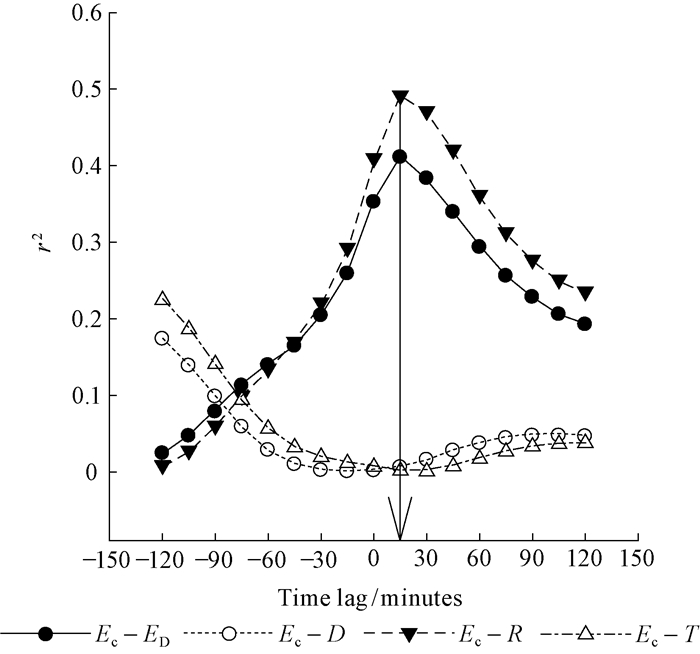
|
Fig.2 Correlations between environmental parameters and canopy transpiration at different time lags |
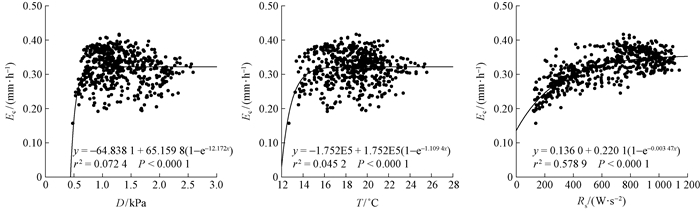
As shown in Fig. 3, the gc (which varied from 0.003 8 m·s-1 to 0.020 2 m·s-1) was a clearly decreasing function of vapor pressure deficit (D), which fluctuated from 0.48 to 2.59 kPa, and air temperature (T), which varied from 12.7 ℃ to 25.6 ℃. In contrast, gc was not obviously related to R.

|
Fig.3 Responses of canopy conductance to environmental factors |
The Ec displays opposite trends; that is, no significant correlations exist between Ec and D/T, but Ec clearly increases with R (Fig. 4).
|
Fig.4 Responses of canopy transpiration to environmental conditions |
Figure 5 plots the Ω values of the Qinghai spruce throughout the time series. The Ω vales ranged from 0.01 to 0.19, which indicated that the leaf surfaces were very strongly coupled to the surrounding air rather than to R.
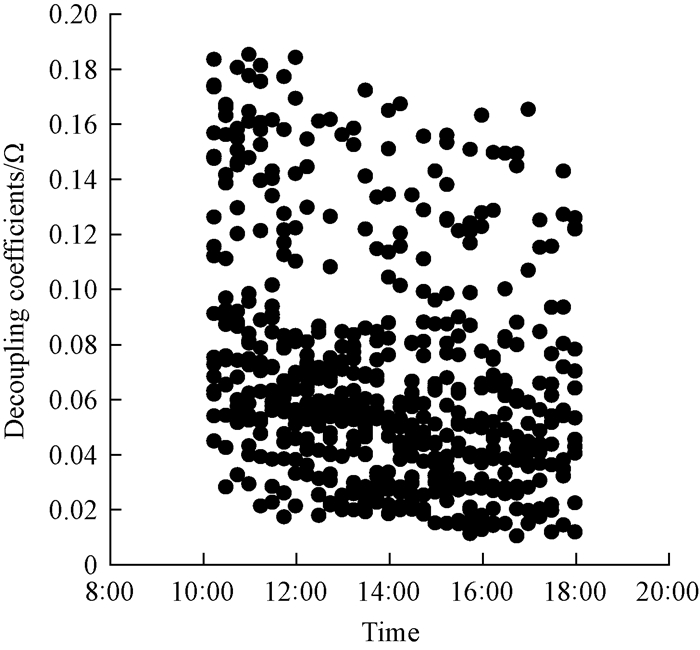
|
Fig.5 Distribution of decoupling coefficient in the time series |
The values of gcmax, Topt and k1-k8 in the different Jarvis models were optimized by a non-linear least-squares algorithm performed with 1stOpt software. Table 2(A) listed the obtained parameter values and their statistics. The six non-linear Jarvis functions explained at least 91% (0.91 < r2 < 0.92) of the variations, with an overall error of approximately 0.001 0 m·s-1. This indicates that all six equations can accurately simulate gc. The MREs vary from 7.86% (model 5) to 8.43% (model 1). In addition, the r2 calculations indicate that f(D) is best modeled by Eq. (10) and least well-modeled by Eq. (11). Eq.(9) yields an intermediate performance, whereas Eq. (13) better computes the f(R) than Eq. (12).
|
|
Parameters of the multiple linear model (Eq. (6)), which predicts the gc from meteorological variables, are presented in Tab. 2(B). This function yields a lower correlation (r2=0.90) and higher RMSE (0.001 1 m·s-1) among the three variables than the six Jarvis models, but the MRE (8.28%) is the third-highest of the seven evaluated functions. Therefore, the multiple linear model can also estimate gc with high accuracy.
2.3 Validation of canopy conductance modelsThe parameters of the gc functions determined from database A were validated on database B. As shown in Figure 6, all of the regression lines between the measured and predicted gc approximate the line y=x. In addition, the RMSE values of all seven models approximated 0.003 8 m·s-1 and the MREs varied from 7.17% (Jarvis model 5) to 8.42% (multiple linear model) (Tab. 3). Again, the best and worst predictors of f(D) were Eqs. (10) and (11), respectively, and Eq. (9) showed intermediate performance. Based on the fluctuations in the MRE values, Eq. (13) more accurately predicted the f(R) than Eq. (12).
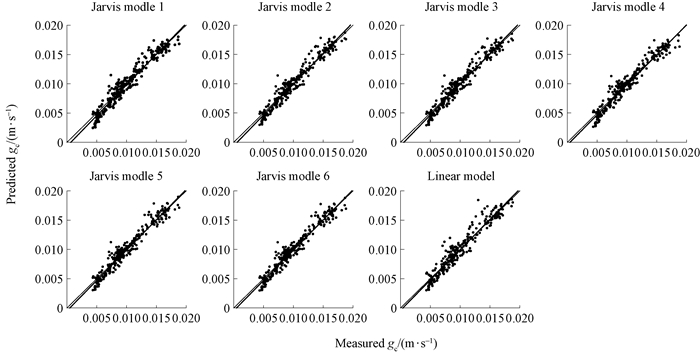
|
Fig.6 Comparisons between the measured and predicted gc values (calculated on database B) |
|
|
An objective of the gc models is to accurately estimate the Ec. Computations on database B reveal no statistical differences between the measured and predicted Ec (P > 0.01; Student's t-test), and the points on the predicted versus measured Ec plots distribute around y=x (Fig. 7). The errors between Ecp and Ecm are also presented in Tab. 3. The seven models estimated the 1/4-hourly Ec and daily Ec with MREs varying from 7.87% to 9.47% and from 5.46% to 7.39% respectively. The Ec prediction accuracies of the six Jarvis models followed the same trend as the gc prediction accuracies. The multiple linear method gave the second-worst performance in the 1/4 hourly Ec prediction, but the best performance (tying with Jarvis model 6) in the daily Ec prediction.
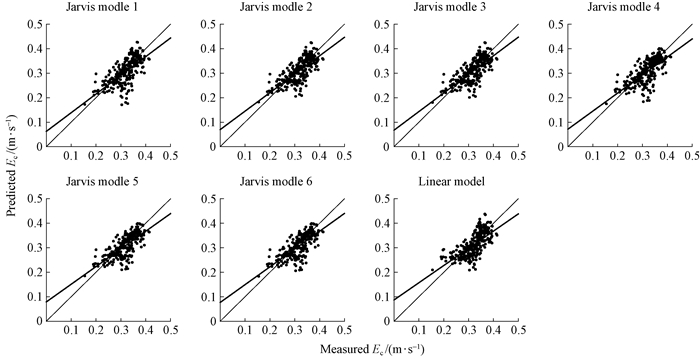
|
Fig.7 Comparisons between measured and predicted Ec values |
In this study, Ec (or measured sap flow) lagged behind R and Ep by 15 minutes. Similarly, Allen et al. (1998) reported a 30 minute lag of the Ec response to environmental factors in a rain-fed citrus orchard under sub-humid tropical conditions. Their data were logged at 30-minute intervals. Green et al. (2003) expected a response delay in apple trees at the Massey University research orchard near Palmerston North, New Zealand and at the Nelson Research Centre, Motueka in summer. However, Granier et al. (2000) reported no time lag in two beech stands inhabiting a rainy climate.
In this study, the gcm is a clearly decreasing function of vapor pressure deficit (D), while it was not obviously related to R. Similar results were presented by Chang et al. (2014), who investigated a Qinghai spruce forest in the upper Heihe River Basin in arid northwestern China. In a conifer study, Morén (1999) also reported a stronger dependence of canopy conductance on D than on R. The Ec displays opposite trends; that is, no significant correlations exist between Ec and D/T, but Ec exponentially increases with R(Fig. 3). The light appeared to saturate around 700 W·m-2, meaning that a further increase in R yielded no further increase in Ecm. Similarly, Oguntunde et al. (2007) reported that light saturates at approximately 400 W·m-2 under sub-humid tropical conditions. In summary, the Ec of the Qinghai spruces is mainly driven by R, but the opening and closing of the gc is mainly controlled by both D and T.
The Ω vales range from 0.01 to 0.19, similar to those obtained in two natural rainforests in French Guiana (NW of Kourou) during two successive dry seasons (0-0.2) and in the state forest of Hesse, France (0.05-0.2) (Granier et al., 1996). The Hesse forest comprises 90% beech trees, and experiences an annual precipitation and average annual temperature of 820 mm and 9.2 ℃, respectively (Granier et al. 2000). Ω values between 0 and 0.4 were reported in a natural forest in Lambir Hills National Park, which has a tropical climate (Kumagai et al. 2004). Jarvis et al. (1986) pointed out that Ω is very low in Pineceae plantations (normally below that of broad-leaved vegetation), indicating that the leaf surfaces are very strongly coupled to D rather than to R.
This study newly applied linear and non-linear gc prediction models to Qinghai spruce, and evaluated their accuracies. As demonstrated above, the non-linear Jarvis methods conferred no spectacular advantage over the multiple linear model. The multiple linear model was the best performer in the daily Ec prediction. Various forms of gc equations have been extensively evaluated. Although Oguntunde et al. (2007) also evaluated the accuracies of the Jarvis method and the multiple linear equation, they compared only the measured and predicted gc values in a citrus orchard. They concluded that the Jarvis model performs slightly better than the multiple linear equation, but both methods accurately determined the gc in their setting. The accuracy of Ec prediction was not verified. In a Populus pruinosa forest in Xinjiang of China, Wang et al. (2016) reported that the Jarvis method significantly outperforms the Ball model, a linear model advanced by Ball et al. (1987) and improved by Leuning (1995). Conversely, Wu et al. (2007) found that the Ball model outperformed the Jarvis method under urban conditions in north China in 2007. A similar conclusion was reached by Wang et al. (2012), who studied the winter wheat Lu 23 on the North China Plain.
For this Qinhai spruce, the canopy conductances (gc) obtained from the sap flow rates were up-scaled to represent the transpiration rates based on the quarter-hourly temporal scale. Their values ranged from 0.003 81 m·s-1 to 0.020 2 m·s-1, with a mean of (0.010 1 ± 0.003 7)m·s-1. Estimates of the same magnitude have been reported in other spruce stands. In 1998, Oltchev et al. (1998) reported a maximum canopy conductance of slightly under 0.001 2 m·s-1 for 114-year-old spruce (Picea abies) on a large plateau in the Soiling Hills in Central Germany. Chang et al. (2014) obtained 0.003-0.057 m·s-1 of gc for Qinghai spruce in the upper Heihe River Basin of arid northwestern China in 2014. Broad-leaved trees have also yielded gc values from 0 to 70 mm·s-1; for example, Oguntunde et al. (2005) obtained gc values of 0.004 0-0.021 2 mm·s-1 in young cashew trees, with a mean of (0.008 0 ± 0.003 3) mm·s-1. In western Japan, Komatsu et al. (2012) reported gc values from 0.005 m·s-1 to 0.015 m·s-1 and from 0.002 m·s-1 to 0.007 m·s-1 in bamboo and cypress forests, respectively. Kumagai et al. (2004) obtained a gc range of 0 mm·s-1 to 70 mm·s-1 in a lowland mixed dipterocarp forest in Sarawak, Borneo.
Throughout the study period (10:00-18:00 in June, 2013), the air temperature varied from 12.7 ℃ to 25.6 ℃. Consequently, the three temperature functions f(T) (Eqs. (9)-(11)) demonstrated a similar decline with increasing T. Equation (11) is modified from Eq. (10) and includes an additional unknown parameter Topt, defined as the optimum temperature of gc opening. In fact, Topt is a good correction because Eq. (10) is a monotonically decreasing function of temperature, whereas gc linearly increases or presents an inverted U-shaped curve with increasing air temperature. In this paper, Topt was approximated as 10 ℃. Moreover, Eq. (10) performed slightly better than Eq. (11) in our study.
Equation (13) yielded a slightly better f(R) than Eq. (12). Under the parameters listed in Table 2, Eq. (12) is an increasing function of R, whereas Eq. (13) presents an inverted-U quadratic curve with a maximum at R ≈ 700 W·m-2. This curve better fits the relationships between gc and R and between Ec and R, as shown in Figure 4, respectively.
Although the multiple linear equation yielded a slightly greater MRE than most of the Jarvis methods in the gc and 1/4-hourly Ec predictions, it produced the best result in the daily Ecpredictions. Consequently, the Jarvis and multiple linear models are both suitable for estimating the gc of Qinghai spruce. In the selected study site and period, Jarvis model 5 achieved the minimum MRE and maximum r2. However, the over fitting phenomenon precludes a unique solution for the optimal parameters in this model. Specifically, Eq. (13) in the Jarvis models includes three unknown parameters. For example, Jarvis model 6 estimates gc from Eqs. (11) and (13), so there are seven undetermined parameters (gcmax, Topt, k1, k4, k6, k7 and k8) in this function. In the curve-fitting by 1st Opt software, diverse solutions were obtained with r2 ≈ 0.92. An alternative set of fitted results is listed in Table 4. Apart from k1, the parameters are very different from the earlier case, but the validation results are as strong as those displayed in Table 3.
|
|
When too many parameters were input the multiple non-linear model, multiple solutions were output, which is undesirable. The overfitting phenomenon has two main causes (Hawkins, 2004); the application of an excessively flexible model; and a model with irrelevant components. In this study, the Jarvis models with too many undetermined parameters (introduced through Eq. (13)), were suboptimal for computing gc, owing to the over fitting problem.
4 ConclusionsThis study predicted the gc values in a Qinghai spruce plantation in northwest China. The gc is a critical parameter not only in Ec, simulations, but also in carbon cycle and other ecological models (Battaglia et al., 2004; Landsberg et al., 1997). Therefore, the study results could guide the transpiration estimating and parameters calibrating with transportation models in this region.
In the Qinghai spruce forest, the canopy transpiration lagged behind the meteorological factors by 15 minutes. R was the major influencer of Ec, but D and T chiefly controlled the opening and closing of stoma. The gc exhibited a declining trend with increasing D and T.
Comparing the measured and estimated gc, most of the Jarvis methods slightly outperformed the multiple linear model, but the linear model yielded the best predictions of daily Ec. Furthermore, no significant differences between the measured and predicted gc/Ec were observed, indicating that all of the methods accurately predicted the gc. However, when many variables were input into the Jarvis model, the overfitting problem occurred. Therefore, Jarvis model 1, Jarvis model 2 and the multiple linear method are suitable for evaluating the gc of Qinghai spruce. However, the multiple linear model is more recommended for its simplest expression and high accuracy.
Allen R G, Pereira L S, Raes D, et al. 1998. Crop Evapotranspiration: Guidelines for computing crop water requirements. Irrigation and Drainage Paper 56. Rome, Italy: Food and Agriculture Organization of the United Nations.
|
Alves I, Perrier A, Pereira L S. 1998. Aerodynamic and surface resistances of complete cover crops:How good is the 'big leaf'?[J]. Transactions of the ASAE, 41(2): 345-351. DOI:10.13031/2013.17184 |
Amp A, X e, Loustau G D. 1994. Measuring and modelling the transpiration of a maritime pine canopy from sap-flow data[J]. Agricultural & Forest Meteorology, 71(94): 61-81. |
Ball J T, Woodrow I E, Berry J A. 1987. A model predicting stomatal conductance and its contribution to the control of photosynthesis under different environmental conditions. Springer Netherlands.
|
Battaglia M, Sands P, White D, et al. 2004. CABALA:a linked carbon, water and nitrogen model of forest growth for silvicultural decision support[J]. Forest Ecology and Management, 193(1/2): 251-282. |
Bosveld F C, Bouten W. 2001. Evaluation of transpiration models with observations over a Douglas-fir forest[J]. Agricultural and Forest Meteorology, 108(4): 247-264. DOI:10.1016/S0168-1923(01)00251-9 |
Buckley T N, Turnbull T L, Adams M A. 2012. Simple models for stomatal conductance derived from a process model:cross-validation against sap flux data[J]. Plant Cell & Environment, 35(9): 1647-1662. |
Chang X X, Zhao W Z, Liu H, et al. 2014. Qinghai spruce (Picea crassifolia) forest transpiration and canopy conductance in the upper Heihe River Basin of arid northwestern China[J]. Agricultural and Forest Meteorology, (198/199): 209-220. |
Granier A. 1985. A new method of sap flow measurement in tree stems[J]. Annales Desences Forestieres, 42(2): 193-200. DOI:10.1051/forest:19850204 |
Granier A. 1987. Evaluation of transpiration in a Douglas-fir stand by means of sap flow measurements[J]. Tree Physiology, 3(4): 309-320. DOI:10.1093/treephys/3.4.309 |
Granier A, Biron P, Lemoine D. 2000. Water balance, transpiration and canopy conductance in two beech stands[J]. Agricultural & Forest Meteorology, 100(4): 291-308. |
Granier A, Huc R, Barigah S T. 1996. Transpiration of natural rain forest and its dependence on climatic factors[J]. Agricultural and Forest Meteorology, 78(1/2): 19-29. |
Green S, Mcnaughton K, Wünsche J N, et al. 2003. Modeling Light Interception and Transpiration of Apple Tree Canopies[J]. Agronomy Journal, 95(6): 1380-1387. DOI:10.2134/agronj2003.1380 |
Han L, He K, Hu X, et al. 2011. Characteristics and modelling of canopy conductance and transpiration of Platycladus orientalis (L.) Franco in Loess Plateau of China[J]. African Journal of Agricultural Research, 6(18): 4253-4260. |
Hawkins D M. 2004. The problem of overfitting[J]. Journal of Chemical Information and Computer Sciences, 44(1): 1-12. DOI:10.1021/ci0342472 |
Hu X B. 2010. Simulation study on transpiration of main tree species in Fangshan county Shanxi province. Beijing: Beijing Forestry University. [in Chinese]
|
Jarvis P G. 1976. The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field[J]. Philosophical Transactions of the Royal Society B Biological Sciences, 273(927): 593-610. DOI:10.1098/rstb.1976.0035 |
Jarvis P G, Mcnaughton K G. 1986. Stomatal control of transpiration:Scaling up from leaf to region[J]. Advances in Ecological Research, 15(15): 1-49. |
Kang S Z, Xiong Y Z, Liu X M. 1991. A Study of Penman-Monteith model to estimate transpiration from crops[J]. Journal of Northwest A&F University:Natural Science Edition, 19(1): 13-20. |
Komatsu H. 2004. A general method of parameterizing the big-leaf model to predict the dry-canopy evaporation rate of individual coniferous forest stands[J]. Hydrological Processes, 18(16): 3019-3036. DOI:10.1002/(ISSN)1099-1085 |
Komatsu H, Onozawa Y, Kume T, et al. 2012. Canopy conductance for a Moso bamboo (Phyllostachys pubescens) forest in western Japan[J]. Agricultural and Forest Meteorology, 156(4): 111-120. |
Kumagai T O, Saitoh T M, Sato Y, et al. 2004. Transpiration, canopy conductance and the decoupling coefficient of a lowland mixed dipterocarp forest in Sarawak, Borneo:dry spell effects[J]. Journal of Hydrology, 287(1/4): 237-251. |
Landsberg J J, Waring R H. 1997. A generalised model of forest productivity using simplified concepts of radiation-use efficiency, carbon balance and partitioning[J]. Forest Ecology and Management, 95(3): 209-228. DOI:10.1016/S0378-1127(97)00026-1 |
Leuning R. 1995. A critical appraisal of a combined stomatal-photosynthesis model for C3 plants[J]. Plant Cell & Environment, 18(4): 339-355. |
Marquardt D W. 1963. An algorithm for Least Square Estimation of Non-Linear Parameters[J]. Journal of the Society for Industrial & Applied Mathematics, 11(2): 431-441. |
Morén A. 1999. Modelling branch conductance of Norway spruce and Scots pine in relation to climate[J]. Agricultural and Forest Meteorology, 98-99(99): 579-593. |
Oguntunde P G, Nick V D G. 2005. Water flux measurement and prediction in young cashew trees using sap flow data[J]. Hydrological Processes, 19(16): 3235-3248. DOI:10.1002/(ISSN)1099-1085 |
Oguntunde P G, van de Giesen N, Savenije H H G. 2007. Measurement and modelling of transpiration of a rain-fed citrus orchard under subhumid tropical conditions[J]. Agricultural Water Management, 87(2): 200-208. DOI:10.1016/j.agwat.2006.06.019 |
Oltchev A, Ibrom A, Constantin J, et al. 1998. Stomatal and surface conductance of a spruce forest:Model simulation and field measurements[J]. Physics & Chemistry of the Earth Parts A/b/c, 23(4): 453-458. |
Progress in photosynthesis research: proceedings of Ⅶth International Congress on Photosynthesis. Providence, Rhode Island, USA: 4(4): 221-224.
|
Rana G, Katerji N, Lorenzi F D. 2005. Measurement and modelling of evapotranspiration of irrigated citrus orchard under Mediterranean conditions[J]. Agricultural & Forest Meteorology, 128(3): 199-209. |
Stewart J B. 1988. Modelling surface conductance of pine forest[J]. Agricultural & Forest Meteorology, 43(1): 19-35. |
Wang H Z, Han L, Xu Y, et al. 2016. Characteristics of stomatal conductance of Populus pruinosa and the quantitative simulation[J]. Scientia Silvae Sinicae, 52(1): 136-142. |
Wang H, He K N, Xu T, et al. 2015. Characteristics and simulation of the canopy conductance of Hippophae rhamnoides in Qaidam Region of northwestern China[J]. Journal of Beijing Forestry University, 37(8): 1-7. |
Wang Z H, Liu J D, Liu L, et al. 2012. Research on the applicability of Several stomatal conductance models on the North China Plain[J]. Chinese Journal of Agrometeorology, 33(3): 412-416. |
Whitley R, Medlyn B, Zeppel M, et al. 2009. Comparing the Penman-Monteith equation and a modified Jarvis-Stewart model with an artificial neural network to estimate stand-scale transpiration and canopy conductance[J]. Journal of Hydrology, 373(S1-2): 256-266. |
Wu D Q, Xu F, Guo W H, et al. 2007. Impact factors and model comparison of summer stomatal conductance of six common greening species in cities of Northern China[J]. Acta Ecologica Sinica, 27(10): 4141-4148. |
 2018, Vol. 54
2018, Vol. 54

