立木材积模型不但在编制立木材积表、计算森林蓄积量、提高森林资源调查工作效率等方面有着广泛应用(Fowler, 1997; Mäkelä et al., 2000;Xia et al., 2013), 而且也是木材生产、生物量和碳汇收益等研究的重要依据之一(Mason et al., 2012)。在林业中, 通常采用简单异速生长幂函数(V=aD^b)来建立立木材积模型。目前, 有2种常规方法拟合该模型:一是直接使用非线性回归来拟合; 二是通过对数转换的线性回归来拟合。在非线性回归中, 假设误差结构是相加的(additive error), 而在对数转换的线性回归中, 假设误差结构是相乘的(multiplicative error)。Xiao等(2011)提出的似然分析法确定误差结构已被用于很多领域, 一些研究者认为此方法更适合用来确定模型的误差结构(Packard et al., 2008a; Kerkhoff et al., 2009; Glazier, 2013; Lai et al., 2013; 董利虎等, 2015)。Ballantyne(2013)在Xiao等(2011)提出的似然分析法的基础上, 通过引入校正因子(σ²/2)将对数转换的线性模型误差分布进行了修正, 目的是确保误差满足正态分布, 即ε~N(0, σ²), 而不是服从对数正态分布。

在通常的立木材积模型研究中, 误差方差随着自变量、因变量或预测值的增大而增大, 即呈现明显的方差异质性, 如果仍采用普通最小二乘法估计模型的未知参数, 则会导致最小二乘法不再具有有效性、参数显著性检验不可靠以及立木材积模型预测失效等(Snorrason et al., 2006; Brooks et al., 2008; Case et al., 2008)。在统计上, 通常采用方差函数(固定方差、幂函数、指数函数和常数加幂函数等)来处理方差异质性问题(Pinheiro et al., 2000)。

目前, 国内外应用似然分析法对立木材积模型误差结构的研究还未见报道。鉴于此, 本文以兴安落叶松(Larix gmelinii)和樟子松(Pinus sylvestris var.mongolica)为研究对象, 以幂函数为基础模型, 分别对兴安落叶松和樟子松建立一元材积模型, 采用Ballantyne(2013)提出的似然分析法确定材积模型的误差结构(相加或相乘), 并对立木材积模型的误差方差函数进行研究, 最后对非线性模型(可加性误差结构)和对数转换线性模型(相乘误差结构)的拟合和检验评价指标进行对比分析。

1 数据与方法 1.1 数据

用来建立模型的数据来自大兴安岭西林吉、图强、阿木尔、呼中林业局和漠河林场。分别将每个树种的样木按径阶划分为6(4~8)、10(8~12)、14(12~16)、18(16~20)、22(20~24)、26(24~28)、30(28~32)、34(32~36)、38(36~40)、42(40~44)、46(44~48)和48(≥48) cm以上12个组, 每个径阶随机挑选40株样木, 每个树种均有480株样木用于建模; 剩余的287株兴安落叶松和214株樟子松作为模型的检验样本。每个径阶样木按树高级也接近均匀分布, 在大尺度范围内具有广泛的代表性。树木被伐倒后, 实测每株样木的胸径和树高等因子, 并通过区分求积法测定立木材积。建模样本和检验样本的数据统计量见表 1。

1.2 方法 1.2.1 幂函数及对数转换分析

通常用幂函数来描述胸径和材积的关系, 这种关系是非线性的, 误差项一般认为是相加的, 其表达式为:

$ Y = a{X^b} + \varepsilon, \varepsilon \sim N(0, {\sigma ^2})。$

(1)

经过对数转换, 非线性转换为线性, 其表达式为:

$ {\rm{ln}}Y = {\rm{ln}}a + b{\rm{ln}}X + \varepsilon, \varepsilon \sim N(0, {\sigma ^2})。$

(2)

这种转换会产生以下4方面问题:

1) 数据转换是非线性转换, 从本质上改变了因变量和自变量之间的关系(Osborne, 2002)。

2) 对数转换的直线拟合是基于隐含的假设, 即幂函数是拟合原始数据的最优模型(Packard et al., 2008b)。

3) 对数转换的直线拟合暗含了一个相乘误差结构的统计模型(Hayes et al., 2006), 其形式为:

$ Y = a{X^b}{{\rm{e}}^\varepsilon }, \varepsilon \sim N(0, {\sigma ^2})。$

(3)

4) 非线性和对数转换拟合都是最大限度地减少残差平方和, 因此对数转换能引起变换偏差(Warton et al., 2006)。

一些学者也相应提出了各种各样的对数转换偏差校正方法(Smith, 1993; Hayes et al., 2006), 主要用于降低对数转换引起的偏差。

1.2.2 误差结构分析

确定误差结构基于似然分析法, 幂函数在非线性模型中, 假设误差是服从正态分布、相加的。非线性相加误差结构的似然值为:

$ L(a, b, {\sigma ^2}) = \frac{1}{{{{(2{\rm{ π }}{\sigma ^2})}^{n/2}}}}{{\rm{e}}^{ - \sum\limits_{i = 1}^n {({{[{y_i} - a{x_i}^b]}^2}/2{\sigma ^2})} }}。$

(4)

而在对数转换的线性模型中, 假设误差是服从对数正态分布、相乘的(Packard, 2009; Xiao et al., 2011)。根据Ballantyne(2013), 无论是相加还是相乘的误差结构, 假设误差都满足ε~N(0, σ²), 那么在对数转换隐含模型中引入校正因子(σ²/2), 模型为:

$ Y = a{X^b}{{\rm{e}}^{\varepsilon - (\frac{{{\sigma ^2}}}{2})}}。$

(5)

该校正因子在参数a的解释和预测中发挥重要作用。经过对数变换可以看出该模型满足正态分布, 即: ${\rm{ln}}{y_i} - {\rm{ln}}a - b{\rm{ln}}{x_i} + \frac{{{\sigma ^2}}}{2} \sim N(0, {\sigma ^2})$。

对数转换线性相乘误差结构的似然值为:

$ L(a, b, {\sigma ^2}) = \frac{1}{{{{\left({2{\rm{ π }}{\sigma ^2}} \right)}^{n/2}}}}{{\rm{e}}^{ - \sum\limits_{i = 1}^n {({{[{\rm{ln}}{y_i} - {\rm{ln}}a - b{\rm{ln}}{x_i} + ({\sigma ^2}/2)]}^2}/2{\sigma ^2})} }}。$

(6)

由于对数转换数据与原数据不在同一尺度上, 因此必须将对数转换的似然值再除以y(Ballantyne, 2013), 似然值为:

$ L(a, b, {\sigma ^2}) = \frac{1}{{\prod\limits_{i = 1}^n {{y_i}{{\left({2{\rm{ π }}{\sigma ^2}} \right)}^{n/2}}} }}{{\rm{e}}^{ - \sum\limits_{i = 1}^n {({{[{\rm{ln}}{y_i} - {\rm{ln}}a - b{\rm{ln}}{x_i} + ({\sigma ^2}/2)]}^2}/2{\sigma ^2})} }}。$

(7)

一般有2种方法进行模型比较:1)如果是嵌套模型, 可以采用似然比法(likelihood ratio test); 2)如果不是嵌套模型, 则采用信息评价指标(AICc)进行比较(Burnham et al., 2002)。由于非线性相加误差结构和对数转换线性相乘误差结构模型不是嵌套模型, 因此选用第2种方法进行比较。具体包括如下步骤:

1) 分别拟合模型(1)和模型(2), 估计出每个模型的参数a、b和σ²; 然后, 用式(4)和(7)分别计算各模型误差结构的似然值L(a, b, σ²)。

2) 利用式(8), 计算非线性和对数转换模型的AICc:

$ {\rm{AICc}}=2k - 2{\rm{lg}}L + \frac{{2k\left({k + 1} \right)}}{{N - k - 1}}。$

(8)

式中:N为样本数; k为模型参数个数。

3) 如果AICc_nlr-AICc_lr < -2, 则幂函数的误差项是相加的; 如果AICc_nlr-AICc_lr>2, 则幂函数的误差项是相乘的; 如果|AICc_nlr-AICc_lr|≤2, 则2种误差结构的假设都不合适, 此时模型求平均值可能是最好的办法(Xiao et al., 2011)。

1.2.3 误差函数

采用普通最小二乘法拟合材积模型, 其误差项的方差一般都随自变量的变化有规律地增大, 即不满足等方差性, 称之为异方差(Uzoh et al., 2008)。求解模型参数时通常采用对数转换或加权回归来消除异方差的影响。本文选择固定方差、指数函数、幂函数和常数加幂函数来消除异方差, 并对求得的AIC和BIC进行比较以确定一个最适当的误差方差模型(Pinheiro et al., 2000)。

固定方差:

$ g({\mu _i}) = \sqrt {{\mu _i}} 。$

(9)

指数函数:

$ g({\mu _i}, \alpha) = {\rm{exp}}(\alpha {\mu _i})。$

(10)

幂函数:

$ g({\mu _i}, \beta) = {\left| {{\mu _i}} \right|^\beta }。$

(11)

常数加幂函数:

$ g({\mu _i}, \delta) = {\delta _1} + {\left| \mu \right|^{{\delta _2}}}。$

(12)

式中:μ_i为第i株林木的胸径(D)、材积观测值(V)或预测值(${\hat V}$); α、β、δ₁和δ₂为待估参数。

1.3 模型评价

拟合结果采用确定系数(R²)、均方根误差(RMSE)、绝对误差(Bias)3个指标来评价。模型检验利用检验样本计算均方根误差(RMSE)、绝对误差(Bias)和平均相对误差(MRE)等指标进行检验。相应的数学表达式为:

$ {R^2} = 1 - \left[ {\frac{{\sum\limits_{i = 1}^n {{{\left({{y_i} - {{\hat y}_i}} \right)}^2}} }}{{\sum\limits_{i = 1}^n {{{\left({{y_i} - \bar y} \right)}^2}} }}} \right]; $

(13)

$ {\rm{RMSE}} = \sqrt {\frac{{\sum\limits_{i = 1}^n {{{\left({{y_i} - {{\hat y}_i}} \right)}^2}} }}{{n - 1}}} ; $

(14)

$ {\rm{Bias}} = \frac{{\sum\limits_{i = 1}^n {\left| {({y_i} - {{\hat y}_i})} \right|} }}{n}; $

(15)

$ {\rm{MRE}} = \sum\limits_{i = 1}^n {({y_i} - {{\hat y}_i})/{{\hat y}_i}/n \times 100} 。$

(16)

式中:y_i为实测值; ${{{\hat y}_i}}$为模型预估值; n为样本数; k为自变量个数; y为实测值的平均值。

2 结果与分析 2.1 误差结构分析

为了深入分析立木材积模型的误差结构, 本文首先分别对兴安落叶松和樟子松数据进行随机抽样(120、240、360和480), 然后基于各树种的不同抽样, 利用S-PLUS软件的线性和非线性回归分别对模型(1)和模型(2)进行拟合, 得到每个模型参数a、b和σ²估计值。基于式(4)和(7)分别计算非线性相加误差结构和对数转换线性相乘误差结构的似然值(L_nlr和L_lr)。根据式(8), 分别计算各模型的AICc_nlr和AICc_lr, 然后用ΔAICc表示AICc_nlr和AICc_lr差值, 结果见表 2。可以看出, 随着样本数增加, 非线性和对数转换线性模型的似然值(L_nlr和L_lr)和AICc(AICc_nlr和AICc_lr)都在绝对的增大。每个树种不同抽样的立木材积模型的ΔAICc均为正数, 且都大于2。兴安落叶松的ΔAICc在192~809之间, 樟子松的ΔAICc在186~742之间, 所以兴安落叶松和樟子松立木材积模型的误差结构是相乘的。

2.2 误差方差函数

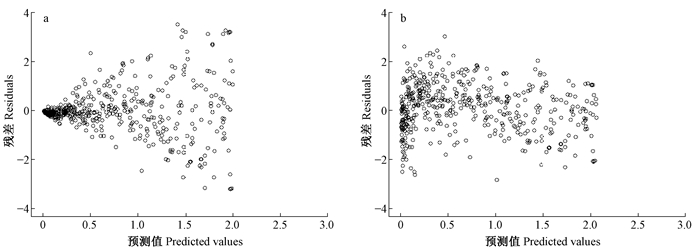
误差方差函数主要是为了消除立木材积模型的异方差现象。通常对数转换能消除异方差的影响, 因此模型(2)不需要引入方差函数。为了比较非线性模型(1)与对数转换的线性模型(2), 本研究利用S-PLUS软件的广义非线性GNLS模块对模型(1)进行拟合。从残差分布图 1a和图 2a可以看出:兴安落叶松和樟子松立木材积模型表现出极为明显的喇叭状, 即方差异质性。本研究分别利用固定方差、指数函数、幂函数和常数加幂函数对兴安落叶松和樟子松立木材积模型进行异方差校正。方差函数变量分别考虑材积观察值(V)、预测值(${\hat V}$)和胸径(D^0.5、D和D²), 结果如表 3所示。可以看出:兴安落叶松误差方差函数为固定方差时, 变量V对应的AIC和BIC最小; 为指数函数时, 变量D^0.5对应的AIC和BIC最小; 方差函数为幂函数和常数加幂函数时, 变量${\hat V}$对应的AIC和BIC最小。综合对比4种误差方差函数可以发现:幂函数中变量为${\hat V}$时, 所对应的AIC(-1 217.660)和BIC(-1200.970)最小。综上所述, 固定方差、指数函数、幂函数和常数加幂函数都能消除兴安落叶松立木材积模型异方差的影响, 而幂函数且在变量为${\hat V}$时消除异方差的效果最好。从残差分布图 1b可以看出:加入变量为${\hat V}$幂函数的兴安落叶松立木材积模型显示了均匀和随机的残差分布。

从表 3可以看出:樟子松方差函数为固定方差时, 变量V对应的AIC和BIC最小; 为指数函数时, 变量D^0.5对应的AIC和BIC最小; 方差函数为幂函数和常数加幂函数时, 变量V对应的AIC和BIC最小。经对比发现:常数加幂函数中变量为V时, 所对应的AIC(-1 389.620)和BIC (-1 368.750)最小。综上所述, 固定方差、指数函数、幂函数和常数加幂函数都能消除樟子松立木材积模型的异方差现象, 而常数加幂函数的效果最为显著, 且在变量为V时的常数加幂函数消除异方差的效果最好。从残差分布图 2b可以看出:在加入变量为V常数加幂函数的残差分布图中, 所有点都是随机散布的, 无任何明显规律。

2.3 模型拟合与检验评价

为了不改变立木材积与胸径的非线性关系, 本研究将对数转换线性(相乘误差结构)模型的参数估计值进行反对数转换。表 4给出了各树种非线性和反对数转换线性模型的参数估计值和拟合统计量。可以看出:对于两树种, 相加和相乘立木材积模型拟合评价指标非常接近, 具有相加误差结构的立木材积模型的拟合精度略高于相乘误差结构的立木材积模型。

利用兴安落叶松和樟子松的检验数据, 基于表 4的参数估计值, 分别计算相加和相乘立木材积模型的绝对误差(Bias)、均方根误差(RMSE)和平均相对误差(MRE)。为了减弱对数转换产生有偏估计的影响, 将对数转换线性模型的参数估计值进行反对数转换时, 在回归方程中加入了校正因子exp(s²/2)。结果见表 5。可以看出:兴安落叶松和樟子松检验结果与拟合数据的结果基本一致, 即相加和相乘误差结构材积模型的Bias和RMSE非常接近。相加误差结构的材积模型略优于相乘误差结构。兴安落叶松和樟子松相加和相乘误差结构材积模型的MRE均不超过±3%, 满足立木材积预测精度的要求(中华人民共和国林业部, 1990)。

3 讨论 3.1 误差结构

关于异速生长模型Y=aX^b的误差结构问题, 国内外存在2种争议:一是支持直接用非线性回归拟合, 即选择相加的误差结构(Fattorini, 2007; Packard et al., 2008b; 2010; Packard, 2009; Caruso et al., 2010); 二是建议进行对数转换, 即选择相乘的误差结构(Gingerich, 2000; Kerkhoff et al., 2009; Cawley et al., 2010; Ballantyne, 2013)。Xiao等(2011)提出似然分析法判断异速生长模型的误差结构。Lai等(2013)利用甜槠(Castanopsis eyrei)、木荷(Schima superba)和马尾松(Pinus massoniana)粗根生物量数据, 采用似然估计法研究异速生长模型的误差结构, 发现对数转换的线性回归更适合这些树种的粗根生物量。随后, Dong等(2014; 2015)利用不同树种的生物量数据, 采用相同方法得出对数转换的线性回归更适合这些树种的生物量。

Ballantyne(2013)在Xiao等(2011)提出似然分析法的基础上, 通过引入方差校正因子(σ²/2)将对数转换线性模型误差ε的假设由对数正态分布变换为正态分布, 目的是确保对数转换线性模型与非线性模型具有相同的误差假设, 即ε~N(0, σ²), 并采用似然分析法研究发现对数转换的线性回归适用于阐述生理学问题。本文基于Ballantyne (2013)提出的最大似然分析法对兴安落叶松和樟子松立木材积模型进行研究, 结果发现兴安落叶松和樟子松立木材积模型的误差结构都是相乘的。

3.2 误差方差函数

在广义模型中, 普通最小二乘估计一般不具有最小方差线性无偏估计等优良性质, 而加权最小二乘估计可以改进估计的性质, 消除异方差的影响。许多学者将误差方差函数作为权函数进行加权回归, 以消除异方差的影响, 提高拟合优度(Pan et al., 2003; Wang et al., 2005; 2010)。本研究将固定方差、指数函数、幂函数和常数加幂函数分别加入到兴安落叶松和樟子松立木材积模型中, 结果表明, 幂函数消除兴安落叶松立木材积模型的异方差效果最好, 而常数加幂函数消除樟子松立木材积模型的异方差效果最为显著。这与以往的研究基本一致, 即幂函数和指数函数都能消除模型的异方差。如Fang等(2001)对美国南部湿地松(Pinus elliottii)优势高生长模型研究时发现在参数个数相同的模型中, 引入幂函数和指数函数2个误差方差函数, 幂函数AIC最小, 可以更好地消除异方差的影响, 并提高模型的拟合效果。Budhathoki等(2008)对美国短叶松(Pinus echinata)单木断面积非线性模型研究发现, 幂函数可以有效地消除异方差的影响。姜立春等(2012a; 2012b)对落叶松枝条长度、基径和角度模型异方差进行研究时发现幂函数能显著消除枝条长度和基径的方差异质性, 而指数函数能显著消除枝条角度的方差异质性, 但其只比较了指数函数和幂函数, 忽略了固定方差和常数加幂函数, 也没有把观测值作为方差函数变量进行异方差校正分析。

以上分析表明, 非线性和对数转换的线性回归都能满足兴安落叶松和樟子松立木材积模型预测精度的要求。根据Ballantyne(2013)提出的方法, 兴安落叶松和樟子松立木材积模型的误差结构是相乘的, 应该选用对数转换的线性回归; 但是根据非线性和线性模型拟合和检验评价指标对比发现, 对数转换的线性模型并没有表现出绝对优势, 而非线性回归却略优于对数转换的线性回归。本文并没有给出绝对和一致的结论, 即相加和相乘误差结构应该选择哪一种。

不可否认模型的误差结构是异速生长模型的关键问题。Glazier(2013)指出, 关于异速生长模型是否进行对数转换, 应该从理论和实际上双重考虑, 并提出进行转换的3点建议: 1)异速生长基本上是关于比例变化的(而不是绝对变化); 2)大多数生物比例关系表现出相乘误差结构; 3)倾向于研究潜在生物比例关系的机制。这些建议似乎都不是立木材积模型研究的主要目的, 由于本研究构建的立木材积模型预测是最重要的, 因此建议直接对比非线性和对数转换的线性模型, 选择精度较高的误差结构, 或者采用Xiao等(2011)提出的基于非线性和对数转换线性模型的平均方法。

4 结论

本文比较了兴安落叶松和樟子松立木材积模型相加和相乘的误差结构。基于Ballantyne(2013)提出的似然分析法表明, 兴安落叶松和樟子松立木材积模型的误差结构都是相乘的, 而根据非线性(相加误差结构)和线性模型(相乘误差结构)拟合和检验评价指标对比发现, 非线性回归分析优于线性回归分析。本研究结论并不是否定Xiao等(2011)和Ballantyne(2013)提出的似然分析法, Ballantyne自己在结论中也指出该似然分析法不是定义, 对于实际数据的直接拟合比较永远是一个好的选择方法。