林业科学  2018, Vol. 54 Issue (12): 157-168 |
 PDF |
滴灌是根据植物需水规律进行局部灌溉的现代节水灌溉技术，由于植物会从滴灌产生的土壤湿润体内吸收大量的水分和养分，因而土壤湿润体的大小和形状能对植物生长产生重要影响(Charles, 2004; Barragn et al., 2006)。众多研究表明滴灌与其他灌溉方式相比能显著提高植物水分利用效率14%~35%(蒋桂英等, 2012; 聂紫瑾等, 2013; Bhunia et al., 2015; 李久生等, 2016)。因此，研究滴灌下土壤水分运移规律，揭示土壤湿润体时空变化特征，是制定高效灌溉策略的重要依据。
目前，滴灌下土壤水分运移规律的试验研究多集中在土壤湿润体特征参数(饱和区半径、水平和垂直湿润锋、湿润体内含水率)的时空变化规律上(李明思等, 2006; Wang et al., 2006; 王振华等, 2007; 王治军等, 2008; 傅建平等, 2013; McClymont et al., 2014)。通过田间试验虽可明确某一立地下的滴灌土壤水分运移规律，但周期长、耗费大、可研究情形有限。因此，利用田间试验资料，建立土壤水分运动模型，通过数值模拟获得优化的滴灌参数及模式，是较为经济、高效的研究手段(Bufon et al., 2012; Leterme et al., 2012; Zeng et al., 2014; Xi et al., 2016)。HYDRUS系列软件因能很好地模拟不同质地、灌溉水源、灌溉系统和作物条件下的土壤水分动态(Šimůnek et al., 2012; 余根坚等, 2013; Nakhaei et al., 2014; Naglič et al., 2014; Qin et al., 2016)，目前已广泛用于灌溉策略的制定和灌溉系统的设计。如黄凯等(2015)利用HYDRUS对赤红壤糖料蔗(Saccharum officinarum)田建模分析了滴头间距、流量对灌水均匀性的影响；王珍等(2013)利用HYDRUS-2D对砂壤土行播玉米(Zea mays)和棉花(Gossypium spp.)构建了滴灌水氮运移模型，研究了土壤水力参数、土壤初始含水率和初始氮浓度的空间变异对水分渗漏率和氮淋失率的影响；Naglič (2014)等利用HYDRUS-2D/3D针对不同质地土壤模拟了滴头流量和初始含水率对湿润体的影响。然而，利用HYDRUS模拟滴灌下土壤水分运动的研究多集中在玉米、棉花等产值较高的作物或裸地上(李久生等, 2005; Dabach et al., 2011; 王珍等, 2013; 黄凯等, 2015)，而在杨树(Populus)等人工林上类似的研究却几乎为空白。目前只有席本野等(2011)在验证HYDRUS可很好地模拟地下滴灌毛白杨(Populus tomentosa)纸浆林短期土壤水分动态的基础上，利用HYDRUS对林地的滴灌技术参数进行优化。但是，利用该模型研究地表滴灌下毛白杨人工林的土壤水分运移，并在此基础上通过情景模拟来筛选林地适宜灌溉策略的研究还未见报道。
毛白杨是我国华北地区主要用材树种，然而，目前其林地平均生产力12 m3·hm-2a-1(Xi et al., 2014)，尚不及国际中等水平20~30 m3·hm-2a-1(郑世锴, 2006)。因此，在华北黄泛平原毛白杨典型栽植立地砂壤土上，开展地表滴灌下毛白杨林地土壤水分运移的数值模拟研究，进而提出灌溉策略建议，对于毛白杨人工林生产力的快速提升具有重要意义。因此，本研究对地表滴灌下的毛白杨林地土壤水分运移规律开展系统研究，在华北黄泛平原砂壤土立地下，探讨地表滴灌毛白杨林地的土壤水分运移规律，结合田间试验，评估HYDRUS-2D/3D模拟林地土壤水分短期运移规律的精度和可行性，运用验证后的模型，通过情景模拟，得到不同初始土壤水分状况下土壤湿润体的变化特征，以期明确滴灌下林地土壤水分运移规律，为林分精准滴灌策略制定提供数据支撑和理论依据。
1 研究区概况试验地位于山东省高唐县国有旧城林场(116°5′25″E，36°48′47″N)，海拔30 m。该地属暖温带半干旱季风区域大陆性气候，具有显著的季节变化和季风气候特性，光照充足，热量丰富。年均降水量544.7 mm，降水主要集中在7—8月，年均蒸发量1 880 mm，年均气温12.0~14.1 ℃，极端最高气温41.2 ℃，极端最低气温-20.8 ℃。年日照总时数达2 651.9 h，全年无霜期204天，地下水位6 m左右。试验地土壤物理性质见表 1。
|
试验地于2015年春季采用三倍体毛白杨无性系B301植苗造林，林木均匀配置，株距2 m，行距3 m。2015年10月完成滴灌系统的安装及铺设，并于2016年4月投入使用。滴灌系统采用以色列耐特菲姆公司生产的滴灌管，滴头流量1.6 L·h-1，间距50 cm，置于地表，沿树行方向一行二带式(滴灌管位于树体两侧距树30 cm处)铺设。生长季内，根据毛白杨生长与土壤水分有效性间的定量关系(Xi et al., 2016)，设定当滴头正下方20 cm处的土壤水势达到-20 kPa时(即田间持水量θf的79%，土壤水分有效性rθ的73%)开始灌溉。此外，生长季内亦对林木进行常规施肥(穴施)，并定期用除草剂除去杂草。
2 研究方法 2.1 田间试验设计2016年于春(5月24日)、夏(8月7日)、秋(9月25日)季各选1个灌水周期开展田间试验，本研究中，春季和夏季的2个灌水周期的灌溉时长均为5 h，秋季为6.5 h。每个灌水周期内，在试验地随机选择3个布设滴灌的试验小区(共6个试验小区，即6个试验重复)，每个试验小区南北向长24 m，东西向长18 m，共含72株树。然后对土壤水势(ψs, kPa)、地表土壤水分饱和区半径、湿润锋运移距离和土壤体积含水率(θ，cm3·cm-3)等进行测定。
2.2 数值模拟情景设计为给不同初始土壤水分状况下的毛白杨林地提供灌溉策略建议，本研究以土壤水分有效性rθ为参考，rθ=(θ-θw)/(θf-θw)，θf和θw分别为-10和-1 500 kPa土壤水势对应的土壤体积含水率，设置土壤从干旱到湿润的3个初始土壤含水率梯度，即初始rθ分别为0.40，0.60和0.80，其分别对应θf的40.0%，51.7%和63.4%。此外，将田间试验中采用的灌溉起始阈值即-20 kPa(rθ=0.73，60%θf)设为第4个初始含水率梯度。上述4种初始含水率模拟情景下，灌水定额均设为12.8 L，即灌溉8 h。
2.3 测定项目和方法1) 土壤水势 2016年4月初，在1个试验小区中随机选择12个滴头，并在滴头正下方20 cm深处安装机械式张力计(7个滴头)或土壤水势传感器(TM2, Germany)(5个滴头)。然后，于2016年5月的一个灌水周期中，从灌水开始至停灌后6 h期间，每30 min读取1次张力计的土壤水势值。土壤水势传感器与数据自动采集器(G01014 i-Logger)相连，每隔10 min(春季和夏季)或30 min(秋季)自动记录土壤水势数据。
2) 地表饱和区半径 参考李久生等(2005)对线源滴灌下土壤水分运动模拟的方法，本研究在利用HYDRUS模拟水分运动时，假定进水面为不随时间变化的固定流量边界。因此，对灌溉过程中地表土壤水分饱和区的半径进行测定。2016年5月，于每个试验小区中随机选择10个滴头(共计30个滴头)，采用卷尺测量灌溉过程中每个滴头周围的饱和区半径，每5~20 min测定1次，直至灌溉结束。由图 1可知，本研究中饱和区半径在灌溉开始40 min后即稳定在4 cm左右，灌溉结束后积水区迅速消失。
|
图 1 地表土壤饱和区半径随时间的变化 Fig. 1 Variation of the soil surface saturation area radius with time |
3) 湿润锋运移距离 2016年5月，在各试验小区中选择用于地表饱和区半径测定的10个滴头(3个试验小区内共选30个滴头)，采用卷尺测量滴灌过程中以及停灌后的土壤水平湿润半径变化，本研究中将土壤水平湿润半径统称为湿润锋水平运移距离。灌溉过程中湿润锋水平运移距离每10或20 min测定1次，停灌后每1 h观测1次，停灌4 h后每12 h观测1次，直至停灌后48 h。
此外，每20 min测量1次湿润锋的垂直运移距离，测定方法为：在每个试验小区中随机选择3个滴头(3个小区内每次共选9个滴头)，挖取土壤剖面利用卷尺测量湿润锋的垂直湿润深度，观测至不能再明确观察出湿润锋运移深度为止。
4) 土壤体积含水率 2015年12月在1个试验小区中选择3株标准木，分别在每株样树旁距滴头5，20，70和120 cm处各布设1根3 m长的含水率测管，共计布设12根(图 2)。然后，采用管式TDR系统(TRIME-IPH, IMKO, Germany)测定θ，测定深度为1 m。其中，0~60 cm土层每10 cm为一层测定；60~100 cm土层每20 cm为一层测定。在2016年5月的灌水周期中，分别于灌溉前、灌溉中(每0.5 h测定1次)、灌溉结束12，24和48 h后测定土壤体积含水率θ。测定过程中，将所有含水率测管附近的地表区域进行覆膜处理，以避免降雨和蒸发对试验的影响。在2016年8和9月的2个灌水周期中，只测定灌溉前和停灌时的θ，且不对地表进行覆膜处理。
|
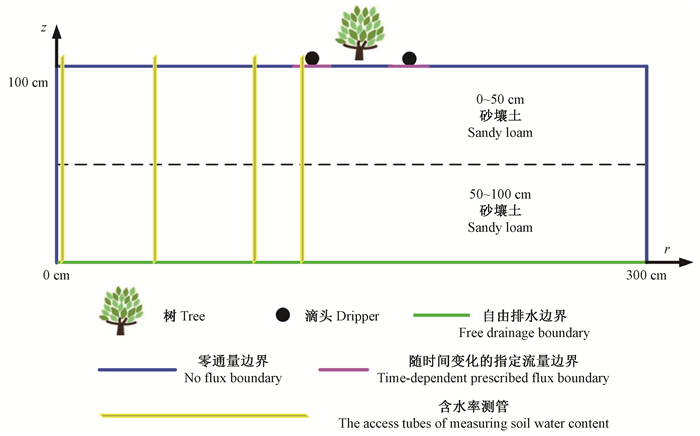
图 2 模拟区域及含水率测管布设示意 Fig. 2 Schematic diagram of the simulation area and installation of the access tubes |
1) 模型构建 选择由美国农业部国家盐土实验室开发的HYDRUS-2D/3D (Šimůnek et al., 2008)软件对地表滴灌下毛白杨林地的土壤水分运移进行模拟。由于本研究所采用滴灌管上的滴头间距较小，滴灌开始后相邻滴头的湿润峰在短时期内即可相接，从而使以滴灌管为中心形成一条湿润带，因此，本研究中滴灌下的土壤水分运动可简化为线源条件下的平面二维土壤水分运动(Skaggs et al., 2004)。假定土壤为均质、各向同性的刚性多孔介质，在不考虑气相和温度对土壤水分运动影响下，本研究中的土壤水分运动可用二维Richards方程来描述：
| $\frac{{\partial \mathit{\theta }}}{{\partial \mathit{t}}} = \frac{\partial }{{\partial \mathit{r}}}\left[ {\frac{{K\left(\mathit{h} \right)\partial h}}{{\partial r}}} \right] + \frac{\partial }{{\partial z}}\left[ {\frac{{K\left(h \right)\partial h}}{{\partial z}}} \right] + \frac{{\partial K\left(h \right)}}{{\partial \mathit{z}}} - S\left({r, z, t} \right)。$ | (1) |
式中：h为土壤负压水头(cm)；t为时间(h)；z为垂向距离(cm)，取向下为正；r为径向距离(cm)；K(h)为土壤非饱和导水率(cm·h-1)；S(r, z, t)为根系吸水项(cm3·cm-3h-1)，为简化模拟，本研究不考虑根系吸水。
方程(1)中的水力特性参数采用Van-Genuchten模型(Van-Genuchten, 1980)描述：
| $\mathit{\theta }\left(h \right) = \left\{ {\begin{array}{*{20}{c}} {{\mathit{\theta }_{\rm{r}}} + \frac{{{\mathit{\theta }_{\rm{s}}} - {\mathit{\theta }_{\rm{r}}}}}{{{{\left({1 + {{\left| {\mathit{\alpha h}} \right|}^n}} \right)}^\mathit{m}}}}}&{h < 0}\\ {{\mathit{\theta }_{\rm{s}}}}&{h \ge 0} \end{array}} \right.; $ | (2) |
| $K\left(\mathit{h} \right) = {K_{\rm{s}}}S_{\rm{e}}^1{\left[ {1 - {{\left({1 - S_{\rm{e}}^{1/m}} \right)}^m}} \right]^2}。$ | (3) |
式中：θ(h)为土壤持水力(cm3·cm-3)；θr为土壤残余含水率(cm3·cm-3)；θs为饱和含水率(cm3·cm-3)；Ks为饱和导水率(cm·h-1)；Se=(θ-θr)/(θs-θr)为土壤饱和度(cm3·cm-3)；l为孔隙连通性参数，一般取0.5；n和m为孔隙形状分布系数，m=1-1/n；α为土壤进气相关参数(cm-1)。
2) 模拟区域、初始和边界条件 模拟区域：本研究模拟区域设置为横向宽度300 cm、垂向深度100 cm的矩形区域(图 2)。
初始条件：以灌溉前测定的含水率剖面作为初始条件，并假设同一土层内的含水率均匀分布。
边界条件：滴头处采用变流量边界，假定滴头周围存在半径为W(本研究中实测饱和区半径为4 cm)的饱和区，且忽略饱和区半径随时间的变化，则该边界上的流量密度为(王珍等，2013)：
| $\mathit{\sigma }\left(\mathit{t} \right) = \frac{{\mathit{Q}\left(\mathit{t} \right)}}{{2W{L_{\rm{e}}}}}。$ | (4) |
式中：σ(t)为滴头周围饱和区变流量边界上的流量密度(cm·h-1)；Q(t)为滴头流量(L·h-1)；Le为滴头间距(cm)。
由于试验地地下水位较深(6 m左右)，所以模拟区域下边界设为自由排水边界；其余边界均设为零通量边界(图 2)。
3) 模型参数的率定 利用Rosetta软件(Schaap et al., 2001)，根据土壤颗粒组成和密度，通过人工神经网络预测得出各土层水力特性参数。然后，根据2016年5月测定的1个灌水周期内的含水率数据，利用HYDRUS-2D/3D软件中的反向求解功能对参数进行反演计算，得到的优化后的各土层水力特性参数见表 2。
|
|
4) 模拟结果评价 采用均方根误差(RMSE)和相对平均绝对误差(RMAE)定量评价HYDRUS-2D/3D模拟地表滴灌下毛白杨林地土壤水分运动的效果。
| ${\rm{RMSE = }}\sqrt {\frac{{\sum\nolimits_{i = 1}^N {{{\left({{S_\mathit{i}} - {M_\mathit{i}}} \right)}^2}} }}{N}} ; $ | (5) |
| ${\rm{RMAE = }}\frac{{\frac{1}{N}\sum\nolimits_{i = 1}^N {\left| {{S_\mathit{i}} - {M_\mathit{i}}} \right|} }}{{\frac{1}{N}\sum\nolimits_{i = 1}^N {{M_\mathit{i}}} }} \times 100\% 。$ | (6) |
式中：N为含水率的总观测点数；Si(cm3·cm-3)为第i个观测点的含水率模拟值；Mi(cm3·cm-3)为第i个观测点的实测值。
RMSE是对预测值与实测值偏差的总体估计，用来衡量二者之间的偏差，可定量描述模拟值与实测值的一致性，RMSE值越小表明模拟结果越接近于实测值；RMAE值为0~1，表示实测值与模拟值之间的吻合从“最优”到“最差”。
2.5 数据分析采用Excel 2013和Origin 9.0软件进行数据处理和图表绘制。
3 结果与分析 3.1 土壤水分运移规律1) 土壤水势变化规律 由图 3可以看出，灌溉开始1 h内，滴头正下方20 cm处的土壤水势(ψs)缓慢增加(增加幅度仅约1.6 kPa)；之后至灌溉开始后2.5 h，ψs快速升高，由(-19.0±1.6)kPa增高至(-9.9±1.2)kPa；但随后，随着灌溉时间的延长，ψs的升高速度逐渐变缓，至停灌时ψs达到(-7.9±1.0)kPa，较灌溉起始时升高约61.6%。整个灌水过程中，ψs随灌溉时长的变化规律可用Logistic函数描述，其决定系数R2为0.99。
|
图 3 灌溉过程中和停灌后滴头正下方20 cm处土壤水势动态变化 Fig. 3 Variation of soil water potential at 20 cm depth and 0 cm distance from a dripper during irrigation and after irrigation |
由图 3还可以看出，停灌后，ψs快速降低，在约4.5 h内可降低至(-12.7±1.2)kPa(降幅约60.2%)，之后至停灌6 h期间，ψs基本保持不变(其数值较停灌时降低4.8 kPa，较灌溉开始时升高7.9 kPa)。这期间，ψs随时间的变化规律可用二项式函数描述，其决定系数R2=0.97。
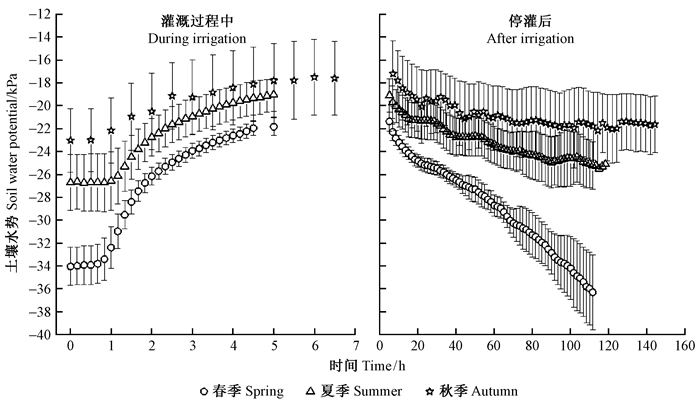
不同季节ψs在灌溉过程中均呈S型增长(“缓慢-快速-缓慢”增长)；停灌后至下次灌溉开始前ψs先快速下降后缓慢降低(图 4)。不同季节ψs在一个完整灌水周期(一次灌溉开始至下次灌溉启动；试验林分一个灌水周期约120 h)内虽然变化幅度不同，但趋势一致。
|
图 4 一个完整灌水周期中滴头正下方20 cm处土壤水势动态变化 Fig. 4 Variation of soil water potential at 20 cm depth and 0 cm distance from a dripper in a complete irrigation cycle |
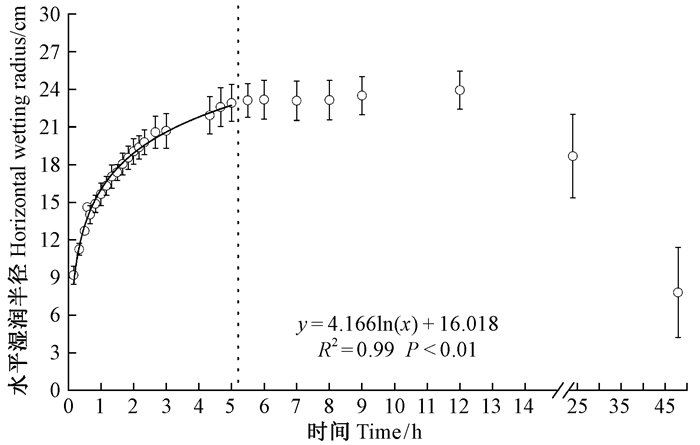
2) 湿润锋水平运移规律 如图 5所示，灌溉开始后，地表湿润锋的水平运移距离迅速增加，但灌溉2 h后，其增加速度逐渐变缓，到灌溉结束时刻平均可达约22.9 cm。湿润锋水平运移距离随灌水时长的变化规律可用对数关系式描述，其决定系数R2=0.99。从灌溉结束至停灌后7 h内，地表湿润半径并未减小，而是呈小幅缓慢增加趋势。但之后快速减小，至停灌43 h后，地表湿润半径平均仅为7.8 cm。
|
图 5 土壤水平湿润半径随时间的变化(虚线为停灌时刻) Fig. 5 Variation of soil horizontal wetting radius with time(dashed line indicates the end of irrigation) |
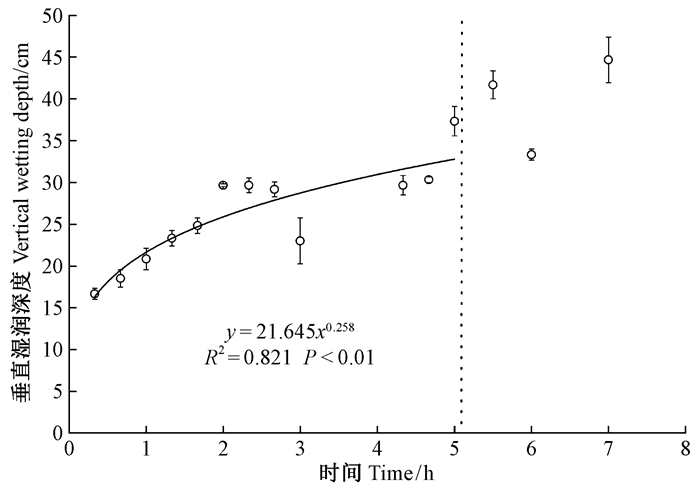
3) 湿润锋垂直运移规律 灌溉过程中，湿润锋的垂直运移距离逐渐增加，但其增加速度随灌水时间的延长而逐渐变缓，二者之间的定量关系可用幂函数描述，其决定系数R2 =0.82。停灌时土壤湿润深度平均可达37.3 cm。之后，其垂直运移距离继续增加，至停灌2 h后，土壤湿润深度较灌溉结束时刻平均增加7 cm(图 6)。
|
图 6 土壤湿润锋垂直运移距离随时间变化(虚线为停灌时刻) Fig. 6 Variation of the vertical movement distance of soil wetting front with time(dashed line indicates the end of irrigation) |
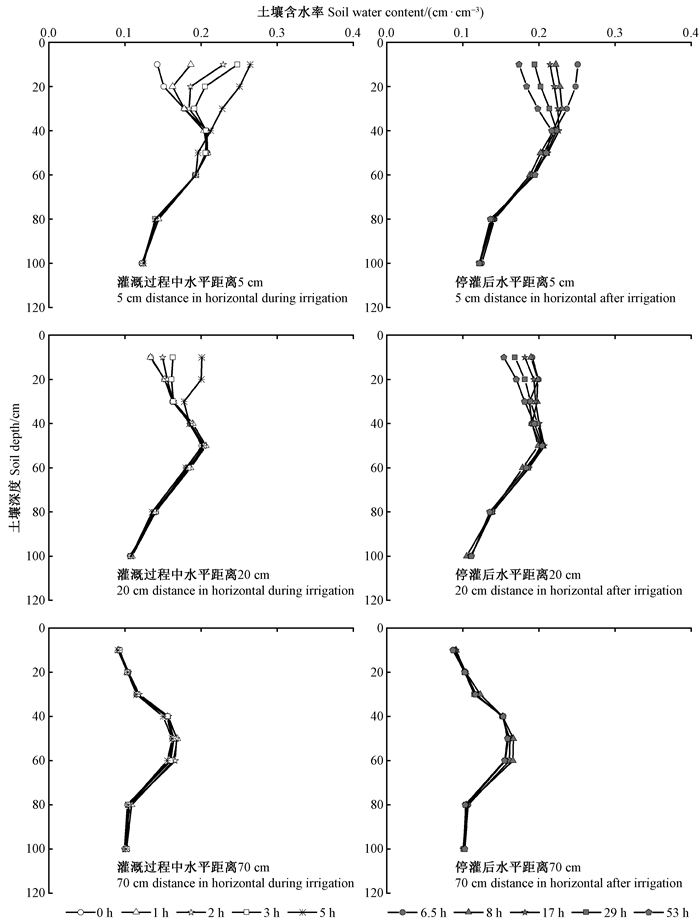
4) 土壤体积含水率变化规律 由图 7可以看出，一个灌溉周期内，水平方向上，滴灌能对距滴头5和20 cm处的θ产生明显影响，而对距滴头70 cm处θ无影响；垂直方向上，滴灌能明显提高0~40 cm土层水分，但随深度增加提高幅度逐渐减小。整体而言，灌溉5 h能使土壤湿润体内的平均θ(水平距滴头20 cm范围内、0~40 cm土层的平均值)提高30.9%，达到0.21 cm3·cm-3(θf的82%)，且湿润体内平均θ随灌水时长(t)的变化规律可用多项式函数描述(θ=0.000 5 t2+0.008 2 t + 0.162 5，n=8，R2=0.99)。停灌后土壤水分再分布过程中，40 cm以下土层中的θ仍无明显变化，而0~40 cm土层中的水分却逐渐降低，至停灌后48 h，土壤湿润体内的平均θ达到0.18 cm3·cm-3，较灌溉起始时高12.2%，较灌溉结束时降低14.3%。
|
图 7 距滴头不同距离处土壤含水率剖面动态变化 Fig. 7 Variation of soil water content profiles at different radial distances from dripper |
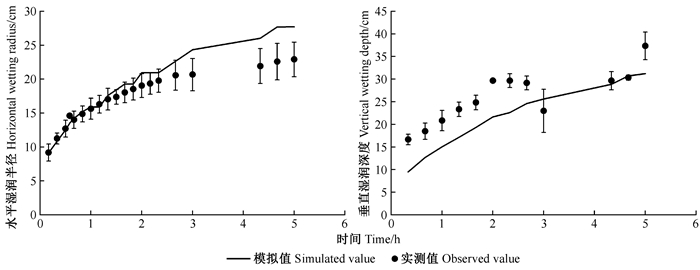
1) 土壤湿润锋运移距离模拟值与实测值对比 湿润锋水平和垂直运移距离的模拟值和实测值的整体变化趋势一致，但均存在一定偏差(图 8)。灌溉开始后1.5 h内，湿润锋水平运移距离的模拟值与实测值完全吻合，但随灌溉时间延长，二者之间偏差逐渐增大；湿润锋垂直运移距离的模拟值除个别时刻外均低于实测值。整个灌水过程中，HYDRUS模拟的湿润锋水平和垂直运移距离与实测值的平均偏差分别为1.3和4.5 cm。停灌时，水平运移距离的模拟值较实测值大4.8 cm，而垂直运移的模拟值较实测值小6.1 cm。
|
图 8 灌溉过程中土壤湿润锋模拟值与实测值对比 Fig. 8 Comparison of the simulated and observed soil wetting fronts during irrigation |
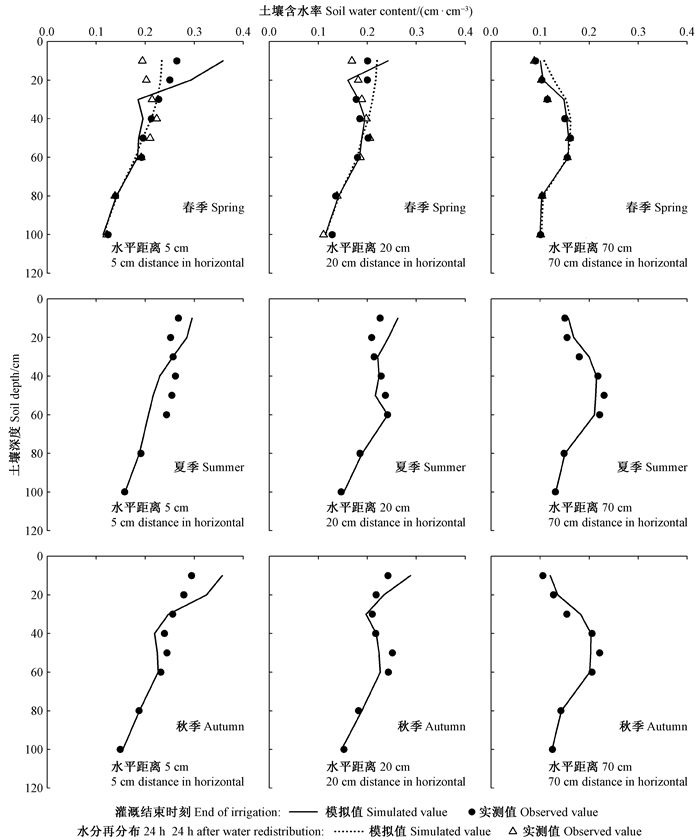
2) 土壤含水率模拟值与实测值比较 由图 9可知，HYDRUS对不同季节、距滴头不同位置处的θ模拟结果与实测值均非常接近，其RMSE为0.012~0.036 cm3·cm-3(平均为0.021 cm3·cm-3)，RMAE为6.5%~13.0%(平均为9.7%)(表 3)。但是，在距离滴头较近处(5和20 cm)的浅土层(0~30 cm)，θ的模拟值与实测值存在相对较大偏差，这可能是由于模拟过程中未考虑根系吸水和土壤蒸发所致。
|
图 9 灌溉结束时刻及水分再分布24 h后土壤含水率模拟值与实测值的对比s Fig. 9 Comparison of measured and simulated soil water content at the end of irrigation and 24 h later |
|
|
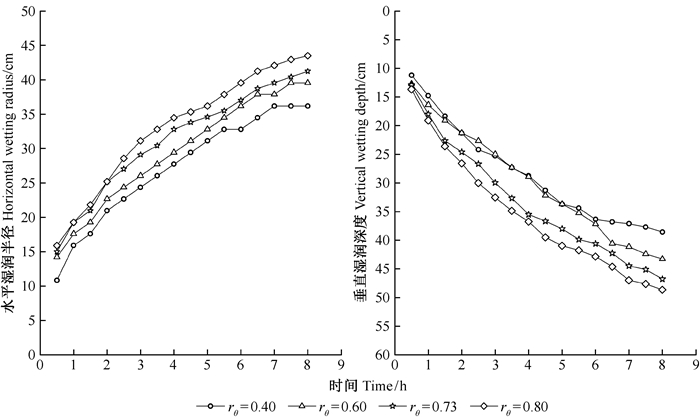
土壤初始含水率(θi)对湿润锋的垂直和水平运移距离均能产生较大影响(图 10)。在灌溉开始后的短时间内，不同θi下湿润锋垂直、水平运移距离间的差异相对较小，但随灌水时间的延长，差异逐渐增大。灌水结束时刻，θi越高，其湿润锋的水平和垂直运移距离均越大，而且不同θi下的湿润锋水平运移距离均略小于其垂直运移距离。图 10中的湿润锋模拟结果可帮助在与试验地类似立地下以及采用相近滴头流量时，根据林木根系的主要分布土层、土壤水分状况以及计划湿润土体大小等来确定合理的灌溉时长，同时亦能帮助设计滴灌系统的技术参数(滴头间距、滴灌管间距等)。例如，对于本研究中的2年生毛白杨林分(细根主要分布在0~30 cm土层)和滴灌系统，若想在停灌时只湿润细根的主要分布土层(使湿润锋的垂直运移深度达到30 cm)，则当rθ为0.40左右时(土壤较干旱情形)，通过查图 10可知适宜的灌溉时长为4.5 h；当采用本研究中的灌溉制度时(当土壤水势达到-20 kPa、rθ=0.73时开始灌溉)，适宜的灌溉时长为3.5 h。
|
图 10 不同初始含水率条件下湿润锋垂直和水平运移距离随时间的变化 Fig. 10 Variation of the soil wetting fronts in horizontal and vertical directions under different initial soil water content conditions |
试验地下，停灌时湿润锋水平和垂直运移距离分别达22.9和37.3 cm，其与灌水时长间分别呈对数和幂函数关系，与前人研究相似(付琳, 1983; 李明思等, 2006; 王治军等, 2008)。研究还发现，灌溉开始至停灌后48 h内，土壤湿润体形态变化范围(水平向20 cm和垂向40 cm内)与林分中细根主要分布范围(水平和垂直方向均30 cm)相一致，可满足主要根区的水分需求。停灌时及停灌后48 h湿润体内θ较灌溉开始时分别提高30.9%和12.2%，说明在停灌后48 h还无需启动下次灌溉，而ψs则在灌溉后120 h左右恢复到灌溉起始水平。同时结合试验林分全年灌溉制度可知，无降雨下，灌溉后4~7天ψs会再次降到-20 kPa。
由于田间试验耗费大、操作难、试验材料有限，众多学者多在室内有机玻璃箱中开展土壤水分运动研究(王振华等, 2007; Naglič et al., 2014; 黄凯等, 2015)。王治军等(2008)和傅建平等(2013)在田间只对湿润锋的运移进行了研究，而本研究是在大田条件下的人工林中，将土壤水分运动相关参数全部进行实测得到。尤其是湿润体内ψs的动态变化，在相关研究中至今未有学者开展类似工作。此外，本研究在不同试验小区测定了大量滴头周围的水分运动，所以测定结果能较好地反映田间平均水平。本研究结果相对室内试验研究而言，对田间实际操作的参考性更强。
4.2 HYDRUS模拟精度分析本研究利用湿润锋运移和土壤含水率的田间实测值，对HYDRUS模拟效果进行验证。对于水平湿润半径和垂直湿润深度，模拟值与实测值间存在偏差(图 7)。黄凯等(2015)认为造成这种偏差的原因是模拟初期取积水区半径为固定值，而实际初期地表积水区半径要略小。对于本研究，造成偏差的原因可能还与模拟时未考虑地表蒸发等因素有关。对于含水率，本研究整体模拟精度与前人研究相当(Skaggs et al., 2004; Siyal et al., 2009; 席本野等, 2011; 黄凯等, 2015; Xi et al., 2016)，但表土层(0~20 cm)的模拟精度比深土层差(图 9)，这可能是由于表土层中分布有密集细根，而本研究未考虑根系吸水造成。由此可见，HYDRUS可用于模拟试验地下毛白杨林分滴灌短期土壤水分动态。
本研究模拟时未考虑根系吸水和土壤蒸发等因素，因此，所建模型不足以模拟长期土壤水分运动。今后应在考虑根系吸水、土壤蒸发的前提下，进一步优化模型，以期得到砂壤土下毛白杨林分更为精确的土壤水分运动模型。
4.3 不同初始土壤含水率下湿润锋运移特征本研究对不同θi下湿润锋模拟结果表明，θi对湿润锋垂直和水平运移均产生较大影响，且θi越大，水平和垂直运移距离也越大(图 10)。Provenzano(2007)和Naglič等(2014)在砂壤土上也得到相同研究结果。停灌时，HYDRUS模拟湿润锋的水平和垂直运移距离偏差分别为4.8和6.1 cm，而这种偏差距离对应的田间灌溉时长小于0.3 h，为田间操作方便通常取整时长灌溉，因此可抵消该偏差。所以本研究结果可直接用于指导与试验地类似立地下以及采用相近滴头流量时的人工林灌溉。就本研究2年生毛白杨林分而言，当ψs达到-20 kPa时开始灌溉，结合试验地不同季节细根分布调查结果(春、夏和秋季细根主要分布在0~30，0~40和0~45 cm土层)，可初步得出本研究春、夏和秋季的参考灌溉时长分别为3.5，6和7.5 h。
湿润锋运移不仅受θi影响，土壤质地、滴头流量等对其影响也很大。如，砂土地湿润锋的水平运移距离小于壤土和黏土，而垂直运移距离则大于其他质地土壤(Siyal et al., 2009; Nagličet al., 2014)。Naglič(2014)等对粉壤土、黏土和砂土下不同滴头流量下湿润锋运移的研究结果表明：当流量大于1 L·h-1时，其对湿润锋运移影响较小，但小于0.5 L·h-1的滴头流量对湿润锋运移影响很大。由于地表滴灌模拟时流量边界需通过饱和区半径换算得到，而本研究受试验条件限制，未得到不同滴头流量及不同质地土壤下的饱和区半径，因此无法探究不同滴头流量及土壤质地下的湿润锋运移规律。然而，有学者通过数值模型得到不同土壤质地、滴头流量下饱和区半径的变化规律(李久生等, 2005; 李明思等, 2006; 赵晔等, 2014)，结果虽有一定局限性，但这也为笔者今后的研究指明了方向。
5 结论在研究田间土壤水分运动时，加入HYDRUS模拟对于有限田间试验材料的充分发挥及研究结果的推广应用极有必要。本研究通过大田试验，得到黄泛平原砂壤土下，地表滴灌及水分再分布过程中土壤湿润锋运移距离(水平、垂直)、水势和含水率的动态变化规律，其与灌水时长的定量关系可分别用对数函数(R2=0.99)、幂函数(R2=0.82)、Logistic函数(R2=0.99)和多项式函数(R2=0.99)描述。同时，对HYDRUS模拟湿润锋运移和θ变化的精度进行了评估，整体模拟效果较好，因此HYDRUS可用于模拟试验地短时间内的土壤湿润锋运移和θ动态。最后，运用所建模型通过情景模拟，得到砂壤土不同θi下湿润锋水平和垂直运移距离随灌溉时长的变化规律图，其不仅可用于确定不同干旱程度下毛白杨及其他相似树种人工林的合理灌溉时长，也可帮助设计滴灌系统技术参数。今后应在考虑根系吸水、土壤蒸发等条件下，建立更具普适性的土壤水分运动模型，并帮助构建更为通用的人工林灌溉制度检索表。
傅建平, 兰再平, 孙尚伟, 等. 2013. 滴灌条件下杨树人工林土壤的水分运移. 林业科学, 49(6): 25-29. (Fu J P, Lan Z P, Sun S W, et al. 2013. Soil water movement in a poplar plantation under drip irrigation. Scientia Silvae Sinicae, 49(6): 25-29. DOI:10.3969/j.issn.1672-8246.2013.06.004 [in Chinese]) |
付琳. 1983. 滴灌时的土壤浸润状况. 灌溉排水, 2(3): 36-45. (Fu L. 1983. Situation of the wetted soil in drip irrigation. Journal of Irrigation and Drainag, 2(3): 36-45. [in Chinese]) |
黄凯, 蔡德所, 潘伟, 等. 2015. 广西赤红壤甘蔗田间滴灌带合理布设参数确定. 农业工程学报, 31(11): 136-143. (Huang K, Cai D S, Pan W, et al. 2015. Determination of drip tapes layout parameters for irrigation of sugarcane in latosolic red soil in Guangxi Autonomous Region. Transactions of the Chinese Society of Agricultural Engineering, 31(11): 136-143. DOI:10.11975/j.issn.1002-6819.2015.11.020 [in Chinese]) |
蒋桂英, 魏建军, 刘萍, 等. 2012. 滴灌春小麦生长发育与水分利用效率的研究. 干旱地区农业研究, 30(6): 50-54. (Jiang G Y, Wei J J, Liu P, et al. 2012. Spring wheat growth and water use efficiency under drip irrigation. Agricultural Research in the Arid Areas, 30(6): 50-54. DOI:10.3969/j.issn.1000-7601.2012.06.008 [in Chinese]) |
李久生, 栗岩峰, 王军, 等. 2016. 微灌在中国:历史, 现状和未来. 水利学报, 47(3): 372-381. (Li J S, Li Y F, Wang J, et al. 2016. Microirrigation in China: history, current situation and prospects. Journal of Hydraulic Engineering, 47(3): 372-381. [in Chinese]) |
李久生, 张建君, 饶敏杰. 2005. 滴灌施肥灌溉的水氮运移数学模拟及试验验证. 水利学报, 36(8): 932-938. (Li J S, Zhang J J, Rao M J. 2005. Model verification of water and nitrate transport from a surface point source. Journal of Hydraulic Engineering, 36(8): 932-938. DOI:10.3321/j.issn:0559-9350.2005.08.007 [in Chinese]) |
李明思, 康绍忠, 孙海燕. 2006. 点源滴灌滴头流量与湿润体关系研究. 农业工程学报, 22(4): 32-35. (Li M S, Kang S Z, Sun H Y. 2006. Relationships between dripper discharge and soil wetting pattern for drip irrigation. Transactions of the Chinese Society of Agricultural Engineering, 22(4): 32-35. DOI:10.3321/j.issn:1002-6819.2006.04.007 [in Chinese]) |
聂紫瑾, 陈源泉, 张建省, 等. 2013. 黑龙港流域不同滴灌制度下的冬小麦产量和水分利用效率. 作物学报, 39(9): 1687-1692. (Nie Z J, Chen Y Q, Zhang J S, et al. 2013. Effects of drip irrigation patterns on wheat yield and water use efficiency in Heilonggang region. Acta Agronomica Sinica, 39(9): 1687-1692. [in Chinese]) |
席本野, 贾黎明, 王烨, 等. 2011. 地下滴灌条件下三倍体毛白杨根区土壤水分动态模拟. 应用生态学报, 22(1): 21-28. (Xi B Y, Jia L M, Wang Y, et al. 2011. Simulation of soil water dynamics in triploid Populus tomentosa root zone under subsurface drip irrigation. Chinese Journal of Applied Ecology, 22(1): 21-28. [in Chinese]) |
王治军, 雒天峰. 2008. 滴灌条件下侧柏林地根区土壤水分运动规律研究. 干旱地区农业研究, 26(4): 13-16. (Wang Z J, Luo T F. 2008. Soil water movement under drip irrigation of proscenia in Loess. Agricultural Research in the Arid Areas, 26(4): 13-16. [in Chinese]) |
王振华, 郑旭荣, 任杰, 等. 2007. 灌水频率对地下滴灌线源入渗土壤水分运动规律影响的试验研究. 水利学报, (s1): 299-302. (Wang Z H, Zheng X R, Ren J, et al. 2007. Study on effects of irrigation frequency on soil water-transport of line source permeation under subsurface drip irrigation. Journal of Hydraulic Engineering, (s1): 299-302. [in Chinese]) |
王珍, 李久生, 栗岩峰. 2013. 土壤空间变异对滴灌水氮淋失风险影响的模拟评估. 水利学报, 44(3): 302-311. (Wang Z, Li J S, Li Y F. 2013. Assessing the influence of soil spatial variability on water leakage and nitrate leaching under drip irrigation through simulation. Journal of Hydraulic Engineering, 44(3): 302-311. DOI:10.3969/j.issn.0559-9350.2013.03.009 [in Chinese]) |
余根坚, 黄介生, 高占义. 2013. 基于HYDRUS模型不同灌水模式下土壤水盐运移模拟. 水利学报, 44(7): 826-834. (Yu G J, Huang J S, Gao Z Y. 2013. Study on water and salt transportation of different irrigation modes by the simulation of HYDRUS model. Journal of Hydraulic Engineering, 44(7): 826-834. [in Chinese]) |
赵晔, 李明思. 2014. 点源滴灌地表积水区半径运移模型分析. 节水灌溉, (12): 16-19. (Zhao Y, Li M S. 2014. Analysis of soil surface ponding radius movement model under point source drip irrigation. Water Saving Irrigation, (12): 16-19. DOI:10.3969/j.issn.1007-4929.2014.12.004 [in Chinese]) |
郑世锴. 2006. 杨树丰产栽培. 北京: 金盾出版社. (Zheng S K. 2006. High yield cultivation of poplar. Beijing: Golden Shield Press. [in Chinese]) |
Barragn J, Bralts V, Wu I P. 2006. Assessment of emission uniformity for micro-irrigation design. Biosystems Engineering, 93(1): 89-97. DOI:10.1016/j.biosystemseng.2005.09.010 |
Bhunia S R, Verma I M, Sahu M P, et al. 2015. Effect of drip irrigation and bioregulators on yield, economics and water use of fenugreek (Trigonella foenum-graecum). Journal of Spices and Aromatic Crops, 24(2): 102-105. |
Bufon V B, Lascano R J, Bednarz C, et al. 2012. Soil water content on drip irrigated cotton: comparison of measured and simulated values obtained with the Hydrus 2-D model. Irrigation Science, 30(4): 259-273. DOI:10.1007/s00271-011-0279-z |
Charles M B. 2004. Rapid field evaluation of drip and microspray distribution uniformity. Irrigation and Drainage Systems, 18(4): 275-297. DOI:10.1007/s10795-004-2751-x |
Dabach S, Lazarovitch N, Šimunek J, et al. 2011. Numerical investigation of irrigation scheduling based on soil water status. Irrigation Science, 31(1): 27-36. |
Leterme B, Mallants D, Jacques D. 2012. Estimation of future groundwater recharge using climatic analogues and HYDRUS-1D. Hydrology and Earth System Sciences, 16(8): 2485-2497. DOI:10.5194/hess-16-2485-2012 |
McClymont L, Goodwin I. 2014. Effects of wetted soil volume on young pear trees. Acta Horticulturae, 1130: 479-484. |
Naglič B, Kechavarzi C, Coulon F, et al. 2014. Numerical investigation of the influence of texture, surface drip emitter discharge rate and initial soil moisture condition on wetting pattern size. Irrigation Science, 32(6): 421-436. DOI:10.1007/s00271-014-0439-z |
Nakhaei M, Šimůnek J. 2014. Parameter estimation of soil hydraulic and thermal property functions for unsaturated porous media using the HYDRUS-2D code. Journal of Hydrology and Hydromechanics, 62(1): 7-15. DOI:10.2478/johh-2014-0008 |
Provenzano G. 2007. Using HYDRUS-2D simulation model to evaluate wetted soil volume in subsurface drip irrigation systems. Journal of Irrigation and Drainage Engineering, 133(4): 342-349. DOI:10.1061/(ASCE)0733-9437(2007)133:4(342) |
Qin H P, Peng Y N, Tang Q L, et al. 2016. A HYDRUS model for irrigation management of green roofs with a water storage layer. Ecological Engineering, 95(2016): 399-408. |
Schaap M G, Leiji F J, Van Genuchten M T. 2001. ROSETTA: a computer program for estimating soil hydraulic properties with hierarchical pedotransfer functions. Journal of Hydrology, 251(3/4): 163-176. |
Šimůnek J, Van Genuchten M T, Šejna M. 2008. Development and applications of the HYDRUS and STANMOD software packages and related codes. Vadose Zone Journal, 7(9): 587-600. |
Šimůnek J, Van Genuchten M T, Šejna M. 2012. HYDRUS: Model use, calibration, and validation. Transactions of the Asabe, 55(4): 1561-1574. |
Siyal A A, Skaggs T H. 2009. Measured and simulated soil wetting patterns under porous clay pipe sub-surface irrigation. Agricultural Water Management, 96(6): 893-904. DOI:10.1016/j.agwat.2008.11.013 |
Skaggs T H, Trout T J, Šimůnek J, et al. 2004. Comparison of HYDRUS-2D simulations of drip irrigation with experimental observations. Journal of Irrigation & Drainage Engineering, 130(4): 304-310. |
Wang F X, Kang Y, Liu S P. 2006. Effects of drip irrigation frequency on soil wetting pattern and potato growth in North China Plain. Agricultural Water Management, 79(3): 248-264. DOI:10.1016/j.agwat.2005.02.016 |
Xi B Y, Li G D, Bloomberg M, et al. 2014. The effects of subsurface irrigation at different soil water potential thresholds on the growth and transpiration of Populus tomentosa in the North China Plain. Australian Forestry, 77(3/4): 159-167. |
Xi B Y, Bloomberg M, Watt M S, et al. 2016. Modeling growth response to soil water availability simulated by HYDRUS for a mature triploid Populus tomentosa plantation located on the North China Plain. Agricultural Water Management, 176(2016): 243-254. |
Zeng W, Xu C, Wu J, et al. 2014. Soil salt leaching under different irrigation regimes: HYDRUS-1D modelling and analysis. Journal of Arid Land, 6(1): 44-58. DOI:10.1007/s40333-013-0176-9 |
表1(Table 1)