20世纪60年代中期，中密度纤维板问世，随后取得了迅速发展。纤维是中密度纤维板的质量基础，研磨纤维是中密度纤维板制造的重要工序之一。热磨机研磨纤维的过程为蒸汽软化后的木片送入研磨室磨盘，使木片受压缩、拉伸、剪切、扭转、冲击、摩擦和水解等多次重复的外力作用，最终导致纤维分离，其实质是木片原料的断裂和解离(陈光伟，2012；徐大鹏，2012)。磨片是热磨机进行研磨分离的关键部件，直接参与研磨工作，磨片的结构参数设计是否合理，会直接影响纤维形态质量、热磨机能量耗散和磨片平均使用寿命(陈光伟等，2010)。多年来，国内外学者从不同角度研究热磨机磨片结构影响因素，并取得了不少研究成果(Berg, 2001; Chen et al., 2008; Resch et al., 2012; Fan et al., 1999; Hua et al., 2008; Li et al., 2007; Pelletier et al., 2013; Qin et al., 1999; Santos et al., 2009; Shida et al., 2010)。Olson等(2003)选用5种磨片采用建模法与试验法相结合对纤维分离强度和比能耗之间的关系进行研究，得出磨片齿刃比负荷与选择函数间具有显著相关性；Roux等(2009)运用建模法分析精磨机磨片磨齿对纤维的切断作用，得出纸浆研磨参数可以预测磨齿切断纤维的情况；Holmberg等(2009)通过试验对磨齿研磨木片和切断的过程进行研究，得出木材纤维的断裂特性，并分析了纤维分离中磨齿的作用；May(1973)研究磨片结构参数对木材研磨强度的影响，从理论角度分析了纤维长度的形成机制；沈立新(1999)对磨片齿形结构和选择理论依据进行研究，分析磨片的几何形状，并以扇形分区磨片和圆环分区直齿磨片的设计方法为例进行了详细阐述；李艳丽等(2008)设计扇块分区磨片的整体结构，通过仿真分析方法研究磨片在静载荷作用下的应力应变和热分布情况，并以降低磨片质量为优化目标对磨片结构进行了优化设计；邵贤林等(2013)研究磨片间隙变化量对制浆质量和磨片使用寿命的影响，并对常用磨片间隙调节方式的特点和应用进行了阐述。

总体来看，以往研究主要采用固体力学和流体力学等方法对磨片与木片原料之间的相互作用关系进行分析和建模，很难直接描述木片原料受力后逐步断裂的过程机制。鉴于此，本研究基于ADAMS和ABAQUS软件对热磨机研磨木片的断裂过程进行数值模拟，从理论上分析磨片破碎区域面积对纤维分离能耗的影响，以指导热磨机磨片的优化设计。

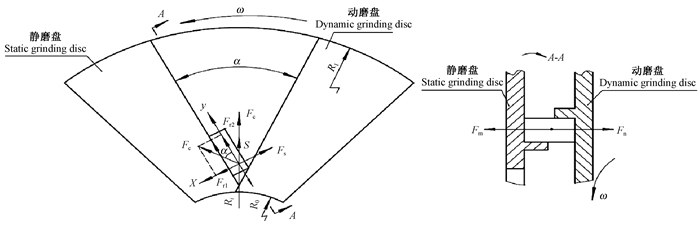
热磨机研磨木片时，木片断裂主要在研磨室内进行，磨片破碎区受力状况最为复杂，因此，本研究以热磨机研磨木片时的破碎区为例进行分析，如图 1所示。设热磨机工作时的输出功率为P(kW)，转速为n(r·min^-1)，木片尺寸为L×a×h(mm)(长×宽×高)，磨片内径为R₀(mm)，磨片外径为R₁(mm)，木片到主轴中心的距离为R_i(mm)；动磨盘随主轴高速旋转时，动、静盘磨齿间的夹角为α(锐角)，动盘磨齿对木片的剪切力为F_r(N)，方向垂直于动盘磨齿齿面指向木片一侧；静磨盘磨齿对木片的反作用力为F_s(N)，方向垂直于静盘磨齿齿面指向木片一侧；木片随着动磨盘高速旋转产生的离心力为F_c(N)，方向沿径向指向磨盘外侧；动磨盘对木片的研磨压力为F_m(N)，方向垂直于动磨盘面指向精磨盘；静磨盘对木片的反向支撑力为F_n(N)，方向与研磨压力方向相反；静盘磨齿对木片运动的摩擦阻力为F_f(N)，方向与木片运动方向相反，木片受到的蒸煮压力为S。

图 1 热磨机作用下木片的受力分析 Fig. 1 Mechanical analysis of wood chips under the action of hot mill

分析木片受力情况可知，使木片断裂的力主要是动盘磨齿对木片的剪切力F_r沿x轴方向的分力F_r1和动磨盘对木片的研磨压力F_m，而离心力F_c、蒸煮压力S和摩擦阻力F_f等主要与纤维的运动状态相关，促使木片向磨片外部运动，影响纤维在热磨区的停留时间，对木片断裂的影响很小。

热磨机研磨木片，是在动、静磨齿对木片的研磨压力F_m和剪切力F_r共同作用下，木片沿纤维结合力最弱的方向断裂，受离心力F_c、蒸煮压力S的影响很小。实际生产中，由于木片尺寸大小不一、研磨室内木片剪切面随机性很大以及研磨室内木片运动轨迹很难预测，对热磨机研磨木片的仿真分析存在一定难度；随动磨盘的高速旋转，木片在动、静磨片的挤压和剪切作用下被逐渐破碎和切断，由于木材横纹强度远小于顺纹强度，软化后更弱，因此木片沿横纹方向被剪切的可能性最大。本研究对单片木片沿横纹方向被剪切的情况进行分析。同时为了简化仿真模型，作以下假设：1)研磨室内被研磨木片与动磨盘磨齿接触瞬间木片处于静止状态；2)待研磨木片尺寸均匀，其磨片破碎区木片长度方向与磨齿侧面平行，宽度方向沿齿面的法向方向。

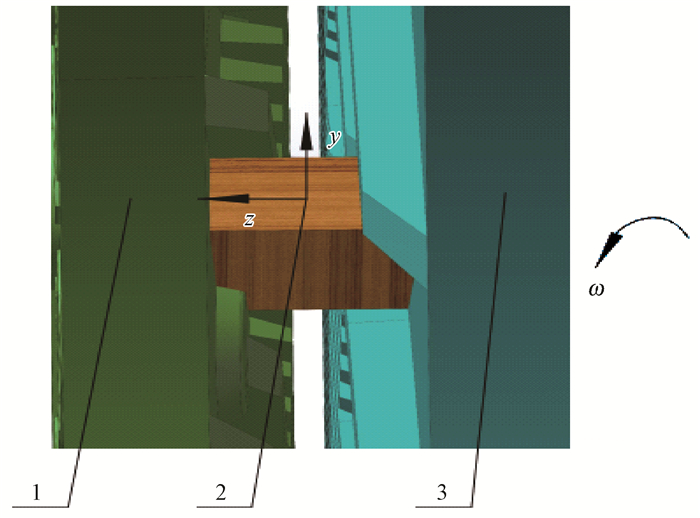
选取单片木片作为研究对象，热磨机研磨木片的状态简化为图 2所示。

图 2 热磨机研磨木片的仿真模型 Fig. 2 The simulation model of grinding wood chip in hot mill 1.静磨盘Static grinding disc; 2.木片Wood chip；3.动磨盘Dynamic grinding disc.

运用ADAMS软件模拟热磨机研磨本片的工作过程，首先在ADAMS软件中建立热磨机研磨木片的仿真模型，构建仿真工程环境，然后以热磨机实际工况对仿真模型添加约束条件、设置各运动副、定义动磨盘转速n=1 500 r·min^-1，进行仿真分析。α=15°(动、静盘磨齿间的夹角)、R=450 mm (木片到主轴中心的距离)时热磨机研磨木片的研磨压力F_m和剪切力F_r的仿真结果如图 3所示，可以看出由于动磨盘高速旋转，磨齿对单片木片的作用时间很短，剪切力F_r和研磨压力F_m呈先增大后减小的变化趋势。

图 3 α=15°、R=450 mm时木片所受的研磨压力Fm和剪切力Fr仿真结果 Fig. 3 The simulation results of grinding pressure(Fm) and shear stress (Fr) of wood chip at α=15°, R=450 mm a.木片所受剪切力Fr沿x方向的分力The shear force (Fr) along the x direction of wood chip; b.木片所受剪切力Fr沿y方向的分力The shear force (Fr) along the y direction of wood chip; c.木片所受研磨压力The grinding pressure (Fm) of wood chip.

木片进入研磨室后排列方向是随机的，很难预测，为了方便，本仿真限定在以下工况下进行：1)仿真针对磨片破碎区木片长度方向与磨齿侧面相平行、宽度方向沿齿面法向方向的情况进行研究；2)以单片木片主要沿横纹方向被剪切的情况进行研究。

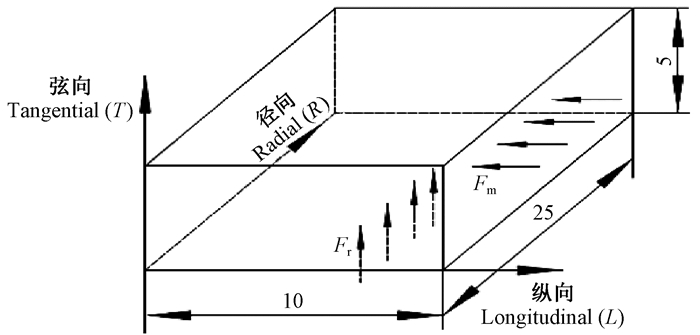
如图 4所示，以磨片上磨齿的F_r沿木片横纹方向被剪切、F_m沿木片顺纹方向被挤压的情况进行仿真分析。

图 4 木片仿真模型的弹性主轴方向 Fig. 4 The direction of elastic principal axis of wood chip simulation model

采用ABAQUS软件建立热磨机研磨木片的有限元模型，用于仿真的木材为杨木，其基本参数为：ρ=0.386 g·cm³，E_L= 5 352 MPa，E_R=1 204.7 MPa，E_T=1 039 MPa，G_RL= 621 MPa，G_TL=466.3 MPa，G_RT=94.3 MPa，μ_RT=0.452，μ_LR=0.64，μ_LT=0.66。进行网格划分，整个三维有限元模型均采用C3D8R，即八结点线性减缩积分六面体单元，结构化网格划分后得到57 702个单元83 753个节点。

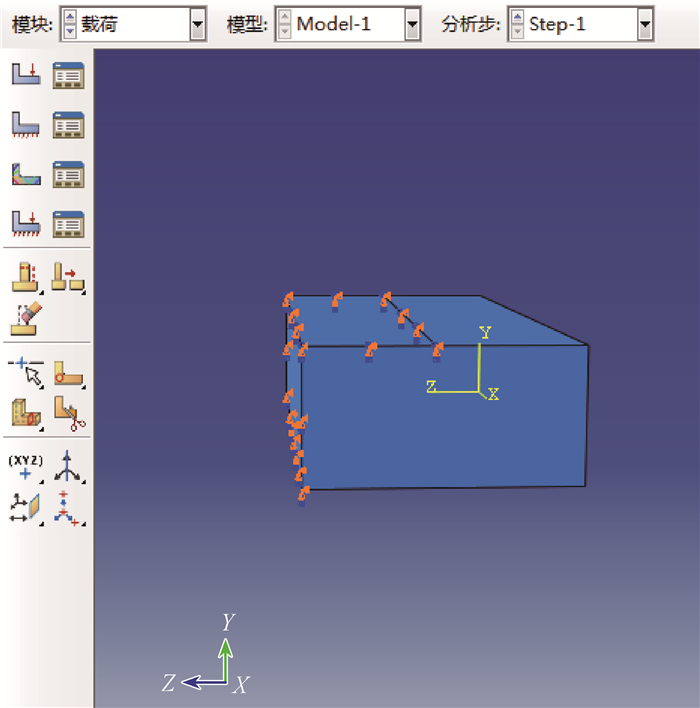
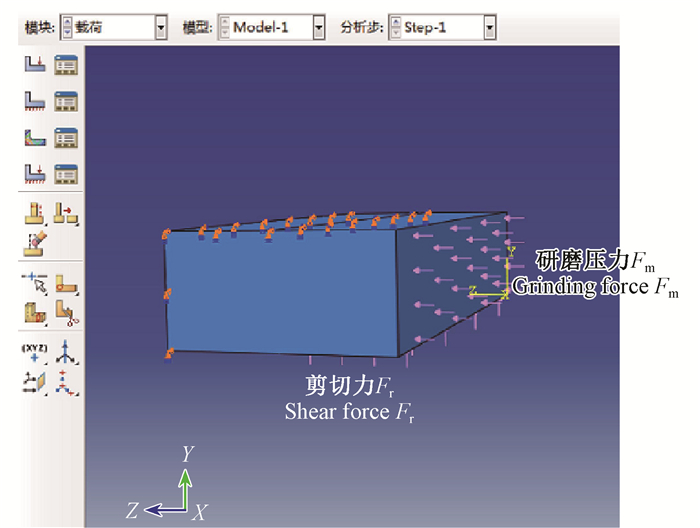
如图 5所示，热磨机研磨木片时木片侧面与磨片底面接触，在ABAQUS软件中定义木片侧面边界条件为U₂=0、U₃=0、U_R1=0；磨齿侧面与木片顶面的一部分接触，在ABAQUS软件中定义木片侧面边界条件为U₂=0、U₃=0、U_R1=0、U_R2=0。热磨机研磨木片时，木片断裂主要是由于动磨盘随主轴沿逆时针方向高速旋转对木片施加剪切力和挤压力作用，对木片添加载荷如图 6所示。

图 5 定义边界条件 Fig. 5 Defining boundary conditions

图 6 添加载荷 Fig. 6 Loading addition

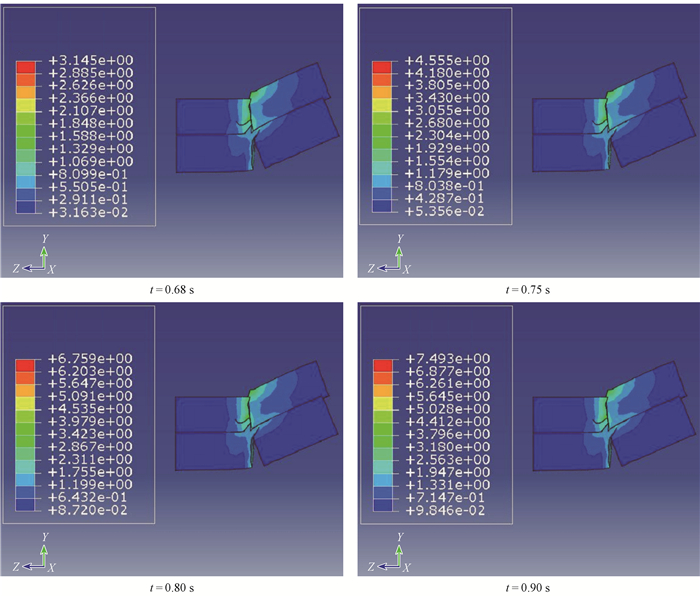
仿真木片长度(25 mm)方向为径向(R)，宽度(10 mm)方向为纵向(L)，高度(5 mm)方向为弦向(T)，热磨机研磨木片(10 mm×5 mm)时的断裂过程如图 7所示。木片被研磨过程中主要在剪切力F_r的作用下沿木片横纹方向被分离，随时间增加木片达到塑性破坏，裂纹附近区域的应力分布呈非对称现象，沿木片左右两侧依次减小。

图 7 裂纹扩展过程 Fig. 7 Crack propagation process

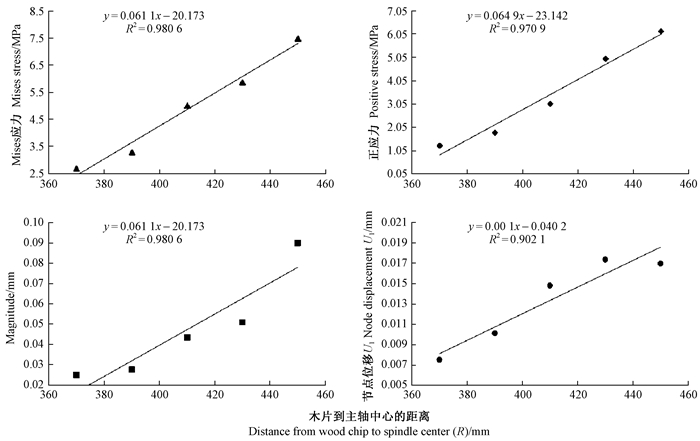
为了研究木片在磨片破碎区内不同位置时对木片断裂的影响，运用ADAMS求解木片到主轴中心的距离R分别为370、390、410、430、450 mm 5种情况时木片所变的研磨压力F_m和剪切力F_r，并将求得的研磨压力F_m和剪切力F_r分别加载在木片上，运用ABAQUS对热磨机作用下木片的裂纹扩展进行数值模拟。图 8所示为α=15°、R=450 mm时的场变量输出结果，不同条件下热磨机研磨木片时木片的Mises应力、正应力、Magnitude和节点位移的变化趋势利用Excel散点图作线性回归分析，如图 9所示。

图 8 α=15°、R=450 mm时场变量输出结果 Fig. 8 Field variables output results at α=15°, R=450 mm a.Mises应力云图Mises stress cloud image；b.第一主应变云图First principal strain cloud image; c.第三主应变云图Third principal strain cloud image；d.应变E23云图Strain E23 cloud image；e.节点位移U1云图Node displacement U1 cloud image；f.节点位移U3云图Node displacement U3 cloud image.

图 9 木片到主轴中心的距离R不相等时场变量输出线性回归 Fig. 9 Linear regression of field variables output when the distance between wood chip and spindle center is not equal

1) 在热磨机动、静磨齿研磨压力F_m和剪切力F_r作用下，木片发生断裂破坏，α=15°、R=450 mm时木片的Mises应力变化范围为9.846×10^-2 ~7.493 MPa，第一主应变变化范围为1.235×10^-5~ 2.546×10^-2，第三主应变变化范围为-1.231×10^-4~-1.853×10^-2，应变E₂₃变化范围为-3.481×10^-2~3.756×10^-3，较大的应力应变主要分布在裂纹附近，木片左右两侧的应力应变逐渐减小。α=15°、R=450 mm时木片节点位移U₁的变化范围为-7.605×10^-4~1.693×10^-3mm，节点位移U₃的变化范围为-3.334×10^-2~1.966×10^-2mm，U₃的变化范围大于U₁的变化范围，木片主要沿U₃方向被撕裂，即木片在被研磨过程中主要在剪切力F_r的作用下沿木片横纹方向被分离。因此，在对磨片进行结构设计和优化分析时，应尽可能增加磨齿对木片的剪切力F_r，使磨片破碎区木片的断裂程度更充分，降低粗磨区和精磨区的纤维分离能耗。

2) 在磨片破碎区，当动、静盘磨齿间的夹角α一定时，木片到主轴中心的距离R增大，木片的Mises应力、正应力、Magnitude、节点位移呈增大趋势。当木片到主轴中心的距离R越大，即破碎区面积越大时，木片所受应力应变增大, 木片断裂越容易。因此，合理设计磨片破碎区域面积对纤维分离质量和能耗具有重要影响。