木材密度是表示木材材质的重要指标，是木材内部因子综合性指标的外在反应，根据木材密度可以估计木材质量，判断木材的工艺性质和硬度、强度、干缩、湿胀等物理力学性质(徐明锋等，2016)。近红外光谱(near infrared spectrum，NIR)分析技术是近年来分析化学领域迅速发展起来的一门高新技术，具有操作简易、预测快捷、结果准确及对试样无损等优点(卢万鸿等，2015)，在国内外已广泛应用于检测木材密度、强度、含水率等物理性质，预测木材中的木质素、抽提物、糖类等化学性质(褚小立等，2014；Hein et al., 2010)。目前，木材近红外光谱预测主要有多元线性回归法(劳万里等，2015)、主成分回归法(李耀翔等，2010)、偏最小二乘法(李耀翔等，2012)等，但这些方法都是经典建立线性模型的方法，很难精确模拟出高度非线性的光谱数据。支持向量机(support vector machines，SVM)是现代智能算法的代表之一，相对于传统方法，其能根据数据建立更加准确的非线性模型，使模型具有较好的泛化能力，提高预测准确性(Djemai et al., 2016)。于仕兴等(2013)提出一种应用于木材近红外光谱分析的粒子群(PSO)-SVM回归模型，结果发现PSO-SVM回归模型在桉木(Eucalyptus)近红外光谱的木质素含量预测中具有较高的准确性和很好的稳定性。梁龙等(2016)将基于SVM的近红外特征变量选择(SVM-SCARS)算法用于树种快速识别，结果表明SVM-SCARS算法能够有效优化光谱特征变量，提高近红外在线分析模型在木材材性分析中的稳健性和适用性。但在实践中发现，经典SVM算法在参数选择过程中的随机性和主观性对预测结果影响很大，虽然目前也有一些优化算法对SVM参数进行优化选择，如粒子群算法、遗传算法等，但依然存在收敛速度慢、易陷入局部极值等缺点。灰狼优化算法(grey wolf optimizer，GWO)已被证明是相比于以上算法更为合理的全局最优解搜索机制，算法运行稳定性更强、收敛速度更快(Mirjalili et al.，2014)，因此，可以利用灰狼算法优化支持向量机(GWO-SVM)对木材密度进行预测。

杉木(Cunninghamia lanceolata)是我国特有的速生商品材树种，具有生长快、材质好、木材纹理通直、结构均匀等优点，广泛应用于建筑、造船、家具等领域(齐建文等，2014)。本研究利用主成分分析法对光谱数据进行降维处理，分别建立杉木密度多元线性回归模型、SVM模型和GWO-SVM模型，并比较分析3种模型的预测结果，以期为杉木性质定量分析提供理论依据。

1 材料与方法 1.1 样品来源与制备

杉木光谱数据由中国林业科学研究院木材工业研究所提供。近红外光谱仪采用美国ASD公司生产的LabSpec光谱仪，波长范围在350~2 500 nm之间。使用两分叉光纤探头采集杉木样品表面的近红外光谱，实验室温度为(22±1.5)℃，湿度50%±3%，对109个样品分别扫描10次全光谱(350~2 500 nm)，计算机显示每个样品的平均光谱，将得到的近红外光谱转换成Unscrambler R文件后保存。样本光谱图如图 1所示。

1.2 数据预处理

主成分分析(principal component analysis，PCA)的本质是对高维变量进行降维处理，其基本思路是将多维数据用少数几个相互独立的主成分表示，且这些主成分能够反映原始变量的绝大部分信息。给定一组相关变量X(x₁, x₂, x₃, …, x_n)，通过线性变换转成另一组不相关变量Z(z₁, z₂, …, z_n)，这些新的变量称为主成分，第i个主成分Z_i=l_i1x₁+l_i2x₂+l_i3x₃…+l_inx_n。将主成分按照方差递减顺序排列，方差越大，表示主成分所含原始变量信息越多；如果方差贡献率足够大，则可以用来反映原始变量的信息。

利用Matlab中的pca函数对109个样品数据进行主成分降维处理，将2 151维数据降至5维，累计贡献率达98%以上，可以用来解释原始变量，并将处理后的数据保存在Excel中。

1.3 多元线性回归法

利用主成分分析法处理杉木红外光谱数据，以得到的主成分Z₁、Z₂、Z₃、Z₄、Z₅作为自变量，以杉木密度y作为因变量，建立多元回归模型：

$\mathit{y = }{\mathit{b}_{\rm{0}}} + {b_{\rm{1}}}{Z_1} + {b_2}{Z_2} + {b_3}{Z_3} + {b_4}{Z_4} + {b_5}{Z_5} + e。$

(1)

式中：b₀为常数项，b₁，…，b₅为回归系数；e~N(0, σ²)为残差。

对求得的回归模型的可信度进行检验，判断自变量对y有无影响，一般P < 0.05，即说明自变量对因变量有显著影响。

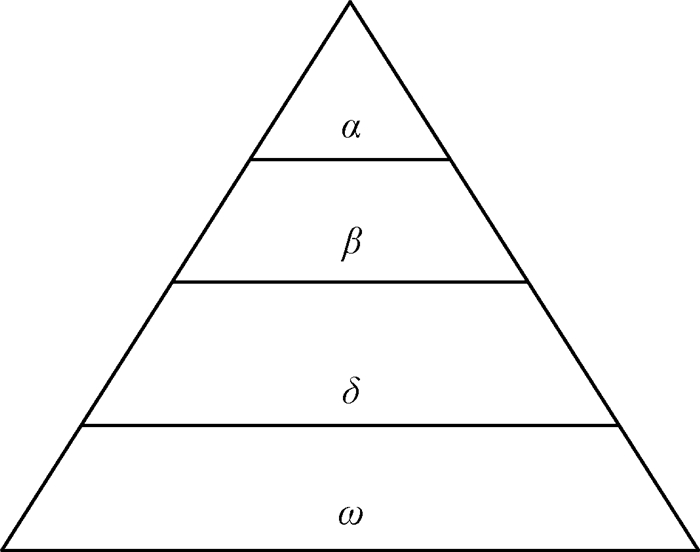
1.4 灰狼算法优化支持向量机

在灰狼算法中，狼群被分为4等，如图 2所示，其中等级最高的头狼标记为α狼，负责狩猎(寻优)过程中的决策制定，前3组依次是适应度最好的3组。

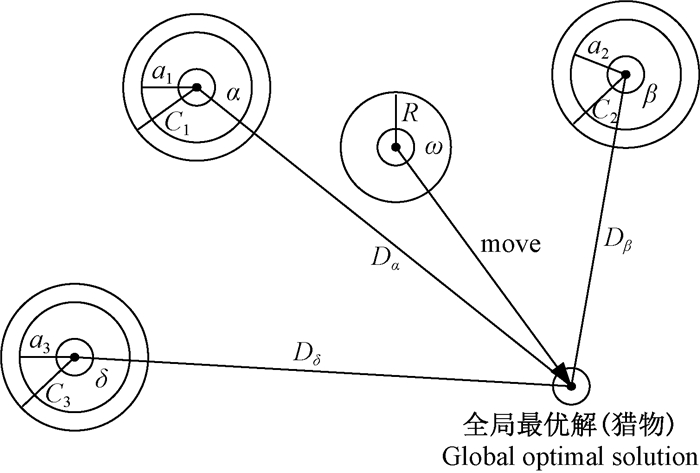
在优化过程中，各等级狼群通过不断更新自己的位置来寻找猎物。当狼群判断出猎物位置时，头狼α带领β、δ狼群对猎物进行包围，ω狼群根据前3个狼群的位置信息更新自己的位置，逐渐逼近猎物，灰狼算法位置更新过程如图 3所示。

灰狼算法优化支持向量机的基本思想是，用人工狼的位置代表支持向量机的惩罚参数C和径向基核函数参数σ。随机初始化人工狼位置，以均方误差(MSE)为适应度，适应度越小，越接近目标，人工狼位置更新，对支持向量机进行训练，并利用训练后的支持向量机模型进行预测。主要步骤如下：

1) 初始化参数，包括狼群数量、个体狼位置、最大迭代次数、参数C和σ取值的上下界。

2) 利用训练集计算每头狼相应的适应度，并选出前3个最好的狼分别作为α、β、δ狼。

3) 迭代更新ω狼的位置，直到达到最大迭代次数。

4) 输出α狼的位置，即最优参数C、σ。

5) 采用最优参数C和σ建模，对测试集进行预测，分析预测结果。

1.5 模型比较

使用决定性系数(R²)、均方误差(MSE)和平均绝对百分误差(MAPE) 3个指标对模型进行比较：

${R^2} = \frac{{{{\sum\limits_{i = 1}^n {\left({{{\mathit{\hat y}}_\mathit{i}} - \mathit{\bar y}} \right)} }^2}}}{{{{\sum\limits_{i = 1}^n {\left({{\mathit{y}_\mathit{i}} - \mathit{\bar y}} \right)} }^2}}}; $

(2)

${\rm{MSE = }}\frac{1}{n}{\sum\limits_{i = 1}^n {\left({{{\mathit{\hat y}}_\mathit{i}} - {y_\mathit{i}}} \right)} ^2}; $

(3)

${\rm{MAPE = }}\frac{1}{n}\sum\limits_{i = 1}^n {\left| {\frac{{{y_\mathit{i}} - {{\hat y}_\mathit{i}}}}{{{y_i}}}} \right|} 。$

(4)

式中：y为密度实测平均值；y_i为第i个样本密度实测值；${\mathit{\hat y}_\mathit{i}}$为第i个样本密度模拟值；n为样本个数。

决定系数(R²)越接近1，说明模型越好；均方误差(MSE)和平均绝对百分误差(MAPE)越小，说明模型预测效果越好。

2 结果与分析

利用Matlab对109个杉木样品的近红外光谱数据进行主成分分析，选择5个主成分，每个主成分的贡献率如表 1所示，累积贡献率达98.7%。

选取88个样品作为训练集，利用R软件对杉木密度数据和近红外光谱主成分建立多元线性回归模型，采用向后剔除法，按照AIC最小原则选出最优模型，当AIC=-574.21时，最优模型为：

$\begin{array}{l} y = 0.398{\rm{\;59 - 0}}{\rm{.021\;47}}{\mathit{Z}_{\rm{1}}} - 0.015{\rm{\;77}}{\mathit{Z}_{\rm{2}}} - \\ {\rm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;}}0.039{\rm{\;6}}{\mathit{Z}_{\rm{3}}} - 0.057{\rm{\;5}}{\mathit{Z}_{\rm{4}}}. \end{array} $

模型的偏回归系数Z₁、Z₂、Z₃和Z₄的P分别为2.3×10^-10、0.006 85、0.028 34和0.002 97，均满足P < 0.05，整个模型的P也小于0.05，说明该回归模型是有意义的。进一步，利用所建模型对测试集21个样品的密度进行预测。

SVM模型与GWO-SVM模型的运行环境是Matlab 2014b。SVM模型参数设置为默认值，核函数采用径向基函数。GWO-SVM模型的搜索参数：狼的数量为100，最大迭代次数为30，需要优化的参数为C和σ，故维数取2，参数取值下界为0.001、上界为1 000。对数据归一化后进行训练建模，其适应度变化曲线如图 4所示。

由图 4可知，当迭代到第3代时，均方误差大幅度减小，说明灰狼算法收敛速度快、收敛趋于稳定。经过寻优，获得的最优参数为C=18.366 6，σ=0.043 3。将训练后的模型用于测试集密度的预测，并对预测结果进行反归一化。

3种模型预测值与实际值的比较见表 2，GWO-SVM模型的预测值更接近实际值，预测效果更好。

3种密度预测模型的比较如表 3所示。从决定系数(R²)可以看出，MLR模型、SVM模型和GWO-SVM模型都能实现有效预测；但从模型具体参数分析，SVM模型的R²为0.923 8，稍优于GWO-SVM模型(R²=0.919 2)，且SVM模型和GWO-SVM模型的R²明显优于MLR模型(R²=0.771 4)。从均方误差(MSE)和平均绝对百分误差(MAPE)比较可知，GWO-SVM模型的MSE和MAPE最小，其次是SVM模型，且二者的MAPE均小于3%。这表明，在3种预测模型中，GWO-SVM模型结合红外光谱预测密度的效果最好，SVM模型次之，均优于现在应用最广的MLR模型，且GWO-SVM模型结合红外光谱预测杉木密度更精确、更有效。

3 结论

本研究提出基于灰狼算法支持向量机结合近红外光谱的杉木密度预测模型。结果表明，灰狼算法支持向量机模型在杉木密度预测中获得了良好效果，且预测精度优于传统多元线性回归和支持向量机方法。灰狼算法支持向量机预测模型结合了支持向量机的结构风险最小化和狼群全局优化算法的优点，预测模型准确度更高，在杉木密度近红外光谱的定量分析中有很好的应用和研究价值。探索近红外光谱数据去噪降维方法，并对灰狼算法进行改进，进一步提高其全局收敛速度和精度，将是今后的主要研究方向。