立地质量是指某一立地上既定森林或其他植被类型的生产潜力(孟宪宇，2006)，一个既定的立地，对于不同树种来说，可能会得到不同的立地质量评价结果。立地质量评价是森林经营的一项基础性工作，是研究森林生长规律、预估森林生长收获和科学制定森林经营措施的重要依据。200~300年前，欧洲人最早利用地学方法划分潜在生产力(Skovsgaard et al., 2008)；后来，人们采用林分蓄积量表示立地等级；到19世纪末，研究者们认识到一定年龄的林分高是一种评价潜在生产力的实用方法。1841年，德国科学家Heyer指出高生长和蓄积生长具有相关性，Baur首次根据林分高等级编制了收获表，之后按林分高划分的立地等级编制收获表在德国得到普遍认可。美国也在1920—1925年就立地质量评价方法进行了争论，并开始接受林分高作为立地生产力的指标。根据林分高评价同龄林立地质量的方法包括地位级法(site class)、地位指数法(site index)和立地形法(site form)(Vanclay et al., 1988；Vanclay, 1992)，分别依据林分条件平均高与林分平均年龄的关系划分等级、林分在标准年龄(亦称基准年龄)时优势木平均高的绝对值、基准胸径时的优势木高来表示立地质量。对于混交异龄林，由于年龄难以获得，限制了地位指数法的应用。虽然也有一些替代方法，如基于环境因子的地位指数法(Dǎnescu et al., 2017)和立地形法(Vanclay et al., 1988；Vanclay, 1992)等，但基于环境因子的地位指数法本质上仍需先建立地位指数方程，立地形法回避了年龄，可以反映林分长得好或不好，但不能回答达到或接近潜在生长量的时间，因此偏离了生产力的概念；且已有研究发现，立地形并不能很好地反映立地生产力(Wang，1998)。

我国对森林立地类型和立地质量评价的研究和实践始于20世纪50年代，当时主要采用前苏联立地学派和林型学派的方法进行宜林地立地类型划分，并编制了西南地区云杉(Picea asperata)、大兴安岭林区红松(Pinus koraiensis)等树种的地位级表。70年代中后期，吸收了德国、美国、加拿大和日本等国的先进经验，广泛开展立地分类和评价研究，如杉木(Cunninghamia lanceolata)产区区划、宜林地选择以及立地质量评价，并编制了多型地位指数表、建立了杉木林区立地分类系统和应用模型，也在华北石质山地、黄土高原、珠江三角洲、东北西部地区及华北中原平原地区等开展了大量森林立地研究工作。80年代以来，有关定量的立地质量评价研究逐渐增多，如《中国森林立地》(张万儒等，1997)的出版，东北山地林区、华北中原平原混农林区、南方丘陵山区的森林立地质量评价研究，形成了由多型地位指数表、数量化地位指数表、树种地位指数转换表等构成的森林立地质量评价体系(朱光玉等，2010；盛炜彤，2014)。近年来，还开展了用立地形(马建路等，1995；吴恒等，2015；张超等，2015；黄国胜等，2015；Fu et al., 2018)、去皮直径生长方程中的渐近线参数(孟宪宇等，1995)、综合立地指数(郭如意等，2016)等方法评价异龄林立地质量的研究。总的来看，目前国内仍缺乏立地潜在生产力的通用估计方法，无法对我国林地的立地潜在生产力进行有效估测，不能满足森林经营决策需要。

传统的立地质量评价方法，绝大多数基于现实林分调查数据，计算出的各项指标(如立地指数、地位级等)本质上反映的是立地的现实生产力。立地的现实生产力不等于立地能够达到的最高生产力，因为现实生产力受人为经营能力和其他非立地因素(如灾害、天然更新的不均匀、林木竞争等)的限制，因此在林业研究中早已出现立地潜力的概念(Paterson，1956；Skovsgaard et al., 2008)，如将林分最大年平均蓄积生长量作为潜在生产力的指标(Latta et al., 2009；Milner et al., 1996)。立地潜力的大致含义是在该立地上林分能够达到的最大年生产能力，评价立地质量需要评价其生产潜力以及现实生产力与生产潜力的差距。以往研究曾使用标准表建立年平均生长量与地位指数的关系(Hanson et al., 2002)、利用过程生长模型(Milner et al.，1996)等估计生产潜力，但关于生产潜力的确切含义并没有严格定义，这些方法也没有得到广泛应用。

当前，在我国日益重视森林经营、精准提升森林质量的背景下，回答我国林地的生产潜力尤为重要和迫切。无论是人工林还是天然林，只有明确了其潜在生产力，才能有针对性地制定经营和修复措施。为解决立地潜在生产力的预估问题，本研究提出一套立地质量评价的新方法学，首次严格定义潜在立地生产力概念，推导出潜在生产力和现实生产力的模型和计算方法，提出了立地元素-林分元素-林分生长类型-现实生产力和潜在生产力模型和数表-落实到地块的立地质量制图技术流程，并以吉林省中东部地区针阔混交林为例开展了案例研究。

1 基于林分潜在生长量的立地质量评价方法 1.1 基本假设和术语 1.1.1 基本假设

本研究基于下述基本假设：在同一立地条件下，相同的林分类型(树种组成接近)如果有相近似的林分结构和近似的密度，则有近似的生长过程，包括林分高生长、断面积生长和蓄积生长。

1.1.2 基本术语

1) 潜在生产力  某种确定的林分类型在同一种立地类型上可能达到的最大年生长量(蓄积、断面积或生物量生长量)，称为该林分类型在该立地类型上的潜在生产力，一般与年龄有关。与地位指数定义类似，用确定的林分类型在基准年龄时的潜在生产力作为评价立地质量的指标。在森林经营中，可以通过合理的森林经营措施(如调整林分密度和林分结构)提高林分现实生产力, 并逐渐接近或达到潜在生产力。

2) 最大生长量的定义域  最大生长量的定义域是指在同一立地类型上，影响某种确定的林分类型生长的可控林分因子(如密度、直径或树高结构等)取值的集合，不包括土壤、水肥等环境因子的调控，因为这相当于改变了立地类型。

3) 林分生长型和生长类型  不同林分的生长过程差异很大，有的早期生长快后期生长慢，有的反之，该生长过程可用不同的生长曲线来描述，称为林分生长型。林分生长型不同于生态学上的“生长型”(生物体在其遗传结构限度内在所遇环境条件下发育形成的一般形态或外表特征)或“种群增长模型”(J形和S形不能满足林分生长建模的精细要求)。同一树种的林分生长型，在不同立地上的生长规律也不相同，可用林分生长类型来描述。本研究将成子纯等(1991)对林分生长类型的定义扩展至混交林，定义为具有近似树种组成、起源相同、立地条件近似、具有相似生长过程的一类林分，即在固定立地条件下，相同年龄时有相似的林分高、断面积和蓄积，与同一自然发育体系概念类似，林分生长类型=林分类型+林分生长型+起源+立地等级。由于立地质量是指某一立地上既定森林或其他植被类型的生产潜力，因此同一林分生长类型具有近似的潜在生产力。在立地潜在生产力的实际计算中，将不同立地等级的林分生长类型(林分生长类型组)作为一个建模(编表)总体，一个具体林分的潜在生产力依赖于立地等级和生长过程2个属性。

4) 立地等级  同一林分生长类型组中的林分在不同立地上的潜在生产力不同，一般根据立地条件划分成若干等级，称为立地等级。本研究首先将同一林分生长类型组的立地条件划分成10个亚等级，以减少模型误差，然后将10个亚等级合并成5个等级，以便于应用。

1.2 潜在生产力估计方法 1.2.1 林分生长模型系统

基于上述基本假设和定义，对于某一个林分生长类型(林分生长型F和立地亚等级L)，可以建立林分高(H)、断面积(G)和蓄积生长(V)3个模型：

$H = {f_{\rm{h}}}\left( {T|L,\mathit{F}} \right); $

(1)

$G = {f_{\rm{g}}}\left( {T,S|\mathit{L},\mathit{F}} \right); $

(2)

$V = {f_{\rm{v}}}\left( {T,S|L,F} \right)。$

(3)

式中：S为林分密度或结构；T为林分年龄；f_h、f_g、f_v分别为林分高、断面积和蓄积的函数；|L, F表示一个固定的林分生长类型。

1.2.2 潜在生产力估计

1) 潜在生产力的数学表达  从模型(1)、(2)、(3)可以看出，S可能与年龄有关。设林分年龄T₁时的“密度/结构”为S₁，1年后林分年龄T₂(=T₁+1)时的“密度/结构”为S₂，林分由T₁到T₂的蓄积年生长量为：

$\begin{array}{l} \mathit{\delta V}\left( {T,S|L,F} \right) = {f_{\rm{v}}}\left( {{T_2},{S_2}|L,F} \right) - \\ {\rm{\;\;\;\;\;\;\;\;\;\;}}{f_{\rm{v}}}\left( {{T_1},{S_1}|L,F} \right)。\end{array} $

(4)

在L、F固定时，蓄积年生长量δV是T、S的函数，固定一个年龄T，蓄积生长量仅依赖于S。因此，应该有一个最合理的“密度/结构”S_opt使年龄T₁的|L, F林分蓄积生长量达到最大(潜在生产力)：

$\begin{array}{l} \mathit{\delta }{\mathit{V}_{{\rm{opt}}}}\left( T \right) = \mathit{\delta V}\left( {T,{S_{{\rm{opt}}}}|L,F} \right) = \\ {\rm{\;\;max}}\left\{ {\mathit{\delta V}\left( {T,S|L,F} \right):S} \right\}。\end{array} $

(5)

式(5)解决了由“密度/结构”控制的潜在生产力估计问题，是营林工作中“密度/结构”调整的理论基础。营林工作实践和林分培育模式研究，正是假定对具体的|L, F一定存在合理的“密度/结构”S_opt，通过试验寻找不同林龄T时的S_opt。利用式(5)，基于实际调查数据建立林分生长模型，可以从理论上推导出潜在生产力。

潜在生产力有2个重要性质：一是稳定性, 潜在生产力依赖于立地等级、林分类型、林分生长型和林分年龄，当这些属性固定后，立地潜在生产力随之确定；二是极大性，潜在生产力反映的是特定立地等级、林分生长型和林分年龄下的最大年生长量，现实中，在相同条件下林分年生长量(又称现实生长量)永远小于或等于潜在生产力，但是如果林分经营好，其现实生长量能接近或等于最大年生长量。

2) 基础生长模型的建立和参数估计  对某一林分生长类型组，利用式(2)、(3)建立每个立地亚等级的断面积和蓄积生长模型。本研究选用唐守正(1991a)提出的全林整体模型形式：

$\begin{array}{l} {G_\mathit{i}} = \mathit{a}_{i1}^{\left( G \right)}{\left\{ {1 - \exp \left[ { - a_2^{\left( G \right)}{{\left( {S/10\;000} \right)}^{a_3^{\left( G \right)}}}T} \right]} \right\}^{a_4^{\left( G \right)}}} + {\mathit{\varepsilon }_{\rm{g}}};\\ {V_\mathit{i}} = a_{i1}^{\left( V \right)}{\left\{ {1 - \exp \left[ { - a_2^{\left( V \right)}{{\left( {S/10\;000} \right)}^{a_3^{\left( V \right)}}}T} \right]} \right\}^{a_4^{\left( V \right)}}} + {\mathit{\varepsilon }_{\rm{v}}};\\ {\rm{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}}i = 1, \cdots ,m. \end{array} $

(6)

式中：i表示立地亚等级，其他变量同上。

模型评价指标要求：确定系数一般应大于0.9；系数a_i1^(G)、a_i1^(V)要有规律，接近一个等差数列，即随立地亚等级提高参数呈规律性增加；每个参数的估计范围不能包括0，即参数要显著不等于0；a₃、a₄小于但接近1。如果评价指标不理想，则重新划分林分生长类型，建立模型，直至满足评价指标。

3) 潜在生产力求解  以蓄积潜在生产力为例，对其求解方法进行说明。在已知林分生长类型、当前年龄T₁和立地亚等级L的条件下，从给定的林分密度指数SDI区间寻找一个$\widetilde {SDI}$，使目标函数达到最大，对应的MAI_v称为蓄积潜在生产力，此时的林分密度为最优密度:

$\begin{array}{l} {\rm{Max\;\;MA}}{{\rm{I}}_{\rm{v}}} = f\left( {L,{T_0},{\rm{SDI,}}{{\mathit{\hat \beta }}_{\rm{h}}},{{\mathit{\hat \beta }}_{\rm{g}}},{{\mathit{\hat \beta }}_{\rm{v}}}} \right),\\ {\rm{\;\;\;\;\;\;\;\;\;\;SDI}} \in \left[ {{\rm{SD}}{{\rm{I}}_{\min }},{\rm{SD}}{{\rm{I}}_{{\rm{max}}}}} \right]。\end{array} $

(7)

式中：${\mathit{\hat \beta }_{\rm{h}}}、{\mathit{\hat \beta }_{\rm{g}}}$和${\mathit{\hat \beta }_{\rm{v}}}$分别为林分高、断面积和蓄积生长模型对应的参数向量。

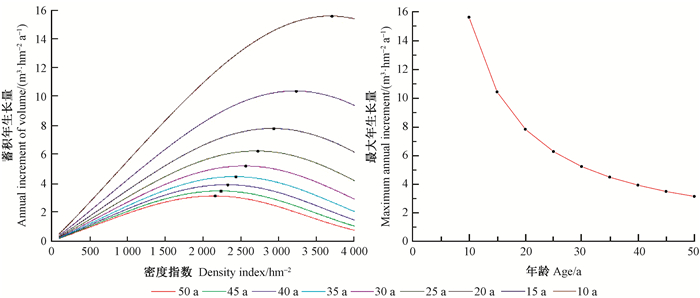
需要注意的是，同一林分不同立地等级在同一年龄时的最大年生长量并不相同，对应的密度也不相同，不同年龄时的最大年生长量形成一条潜在生产力曲线(图 1)。因此，对任一林分生长类型，最终会输出不同年龄时的最大年生长量Max MAI_v(包括基准年龄时的潜在生产力)、对应的林分密度、林分断面积和蓄积量。

为求解目标函数(7)，需给定下列已知条件：①林分生长类型；②$H{\rm{\; \; = }}{\mathit{f}_{\rm{h}}}\left({T, {{\mathit{\hat \beta }}_{\rm{h}}}} \right)$；③$G{\rm{\; \; = }}{\mathit{f}_{\rm{g}}}\left({T, {\rm{SDI, }}\mathit{H, }{{\mathit{\hat \beta }}_{\rm{g}}}} \right)$；④$V = {\mathit{f}_{\rm{v}}}\left({T, {\rm{SDI, }}\mathit{H, }{{\mathit{\hat \beta }}_{\rm{v}}}} \right)$；⑤基准年龄T₀；⑥密度指数SDI的可行区间，可在现有数据中获得最小(SDI_min)和最大(SDI_max)密度指数。采用黄金分割优选法和二分法，在SDI的可行区间找到MAI_v的最大值，即为不同年龄时的蓄积潜在生产力。Fu等(2017)详细给出了断面积潜在生产力计算方法，蓄积潜在生产力计算方法与断面积潜在生产力相似，不再详细介绍。

1.2.3 林分生长类型与立地等级划分

1) 林分生长类型划分  首先进行林分生长型划分。划分林分生长型旨在保证断面积和蓄积生长过程相似，即同一林分生长型使用相同的断面积和蓄积生长模型。目前，人们对什么样的林分具有相似生长过程的认识很不全面，只能从数据出发，从最接近相同的林分开始，逐步聚类，最后划分出林分生长类型组。现有林分类型划分标准，一般不满足上述基本假设，需要根据数据重新划分林分类型，为此，必须有一个基本单元，这个基本单元命名为林分元素。由于林分树种组成多样，林分元素的划分比较复杂，根据研究目的和基本假设可以采用以下原则：将树种组成和生长过程比较接近的样地划分成同一个林分元素。林分元素划分得越细，元素内的树种组成差异越小，精度越高；但是林分元素的细致程度受限于样地数量。根据经验，每个林分元素内有4个以上样地，则可保证作出一条回归曲线。在实际中，可先根据林分混交类型将全部林分分成针叶纯林、阔叶纯林、针叶混交林、针阔混交林和阔叶混交林，对于其中每一类型，再基于先验知识和树种组成给出一个初始分类，依据评价指标逐步合并修正。根据林分生长型和立地分级，最终形成包含多个立地等级的林分生长类型，即林分生长类型组。

2) 立地等级划分  从所有立地因子中筛选出K个与生长过程相关性较强的因子，包括定性因子(如坡向、坡位)和定量因子(如海拔、坡度)。为便于在实践中应用，将定量因子观测值划分为几个等级，按照定性因子处理。如第k因子，有L(k)个水平，共有

$KK = \prod\limits_{k = 1}^K {L\left( k \right)} $

个立地因子水平组合。每个立地因子水平组合称为一个立地元素，是对传统立地类型的进一步细分。

高生长模型[式(1)]不含“密度/结构”，相对比较容易，可以按高生长模型进行立地分级。对于某一林分生长型，首先，按哑变量F拟合树高生长曲线簇${\hat H_F} = {f_{\rm{h}}}\left({T, {\mathit{\beta }_\mathit{F}}} \right)$(T为年龄，F=1, …, m为哑变量)，建立m条同型或异型树高曲线。以异型曲线Richard公式为例，可得到m条树高生长曲线：

$\begin{array}{l} {\rm{\;\;\;\;\;\;\;\;\;\;\;\;}}{H_m} = 1.3 + \left[ {a + \left( {m - 1} \right){a_m}} \right]\\ F{\left\{ {\left( {1 - \exp \left[ { - b + \left( {m - 1} \right){b_\mathit{m}}} \right]F} \right)T} \right\}^{\left[ {c + \left( {m - 1} \right){c_m}} \right]F}}。\end{array} $

(8)

式中：a_m、b_m、c_m分别为参数a、b、c的级距，即任意2条树高生长曲线对应的参数差值。详细方法见Li等(2013)。

其次，按林分元素和立地元素构造建模单元，采用式(8)分级曲线簇的模型参数，计算每个单元的树高观测值与m条分级曲线产生的树高估计值的离差平方和，具有最小离差平方和的曲线即为该单元所属分级，反复迭代，直到每个单元的分级不再发生变化为止。由于立地元素由显著影响高生长的立地因子组合而成，单元中包含立地类型信息，因此该方法也称为立地约束的树高生长过程分级。

1.2.4 落实到小班的立地质量评价与制图

得到m个立地等级下不同年龄时的潜在生产力、对应的林分密度、林分断面积和蓄积量后，可以对森林经营单位的任一小班或地块进行立地质量评价。

1) 现有林的立地质量评价  对于现有林，已知林分平均(优势)高、林分年龄和立地元素，根据林分生长型划分方法，可以得到任一小班所属的林分生长类型组；按照立地等级划分方法，可以得到任一小班的立地等级；利用潜在生产力模型，可以得到任一小班不同年龄时的潜在生产力。

2) 任意林地(包括无林地)的立地质量评价  除现有林外，还可预估当前林分或无林地改造成其他类型或新造林的潜在生产力，且可以在多种林分类型中选择。这种方法类似于机器学习利用大量先验数据获得潜在生产力与林分类型和立地关系，从而预估任意林地任一林分类型的潜在生产力。

最终，可将森林经营单位内所有小班的潜在生产力、现实生产力、潜力提升空间进行制图，形成立地质量评价系列数表和图件，详见刘丹等(2018)。

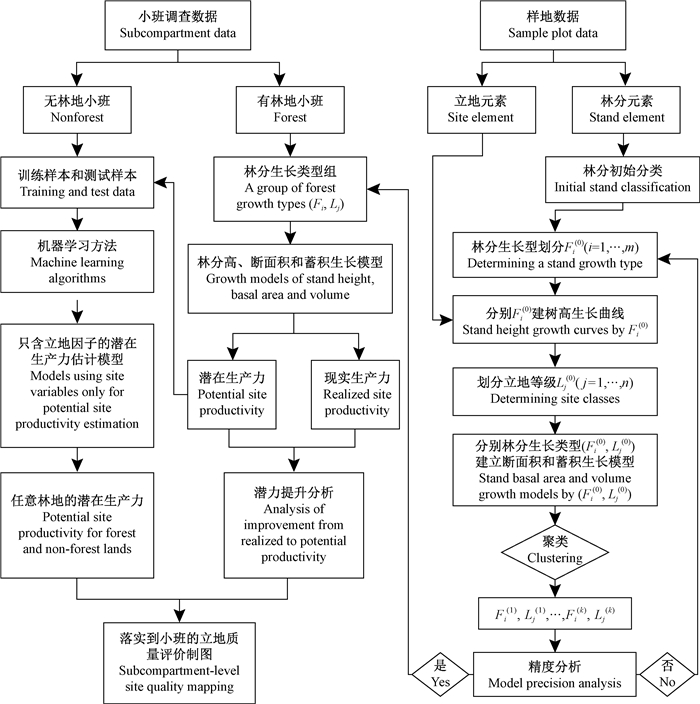
2 基于林分潜在生长量的立地质量评价流程

基于林分潜在生长量的立地质量评价流程见图 2。受数据和工作量限制，第1步，将样地分配给各立地元素和林分元素，形成一个数据集，这是划分立地等级和林分生长型、建模与评价的基本数据集；第2步，通过迭代方法将样地逐步聚类为林分生长类型组；第3步，分别建立各林分生长类型组的林分高、断面积和蓄积量生长模型，即现实(实际)生产力模型；第4步，通过优化模型中可控因子(本研究完成了优化林分密度因子)估计该立地等级可以达到的最大生长量，作为潜在生产力，即各林分生长类型的潜在生产力数表；第5步，根据地形和气象资料等环境因子将通过有林地样地得到的模型泛化(机器学习术语)到无林地和未设置样地的地区；第6步，立地质量评价制图(可视化)，将计算的数字结果用图形表达出来。

3 应用案例

以吉林省针阔混交林(林分生长类型组之一)为例，利用一类清查固定样地数据，基于林分潜在生长量的立地质量评价方法开展案例研究。

3.1 数据

数据来源于吉林省一类清查的480个针阔混交林样地，组成树种包括长白落叶松(Larix olgensis)、云杉、冷杉(Abies nephrolepis)、红松、白桦(Betula platyphylla)、枫桦(Betula costata)、椴树(Tilia amurensis)等。样地面积为0.06 hm²，分别于1994、1999、2004和2009年对部分或全部样地连续观测4次，共计1 127个观测值。主要调查因子包括样地的地理坐标、地形、坡度、坡向、海拔、土壤类型、土壤厚度、枯落物厚度、腐殖质层厚度、平均年龄、平均高及每木检尺(树种、胸径、立木类型、检尺类型)等。样地平均年龄为优势树种平均年龄，调查平均树高时根据平均胸径大小，在主林层优势树种中选择3~5株平均样木测定树高和年龄，采用算术平均法计算平均树高和平均年龄。林分密度指数SDI计算公式(Reineke，1933)为：

$SDI = N{\left( {D/20} \right)^{1.605}}。$

式中：N和D分别为林分活立木株数(tree·hm^-2)和样地平均直径(cm)。

数据统计信息见表 1。

3.2 立地元素及立地等级划分

一类清查数据中与立地相关的因子包括地貌、海拔、坡度、坡位、坡向、土壤类型、土壤厚度、枯落物厚度和腐殖质层厚度，将每个因子进行分级(分级标准如表 2示)，组合后便得到每个样地的立地元素。选用Richard模型：

${H_\mathit{i}} = {a_\mathit{i}}{\left[ {1 - \exp \left( { - bT} \right)} \right]^{{c_i}}} + \mathit{\varepsilon }。 $

(9)

式中：H_i和T分别为林分平均高(m)和平均年龄(a)；Φ_Hi=(a_i, b, c_i)为第i个立地亚等级对应的参数；ε为误差项。

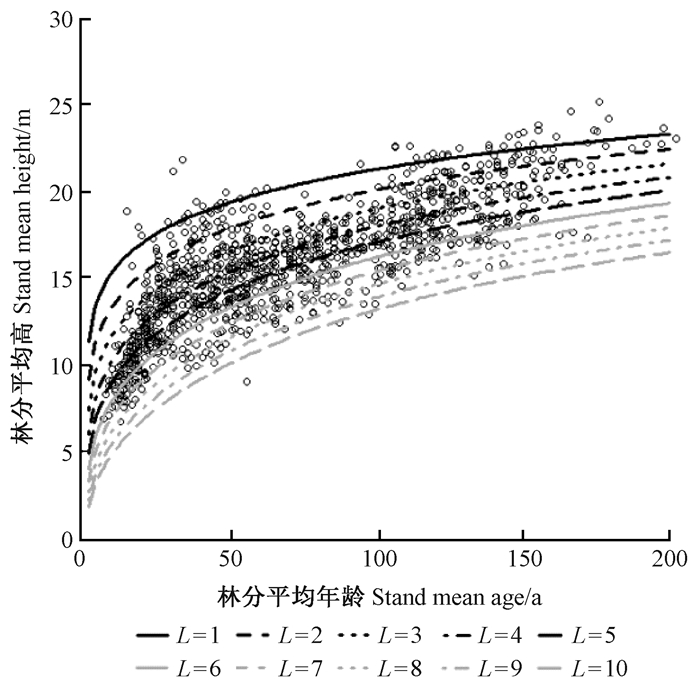
通过影响林分平均高生长曲线的立地因子筛选，最终确定海拔、坡向、坡度、坡位、土壤类型和腐殖质层厚度6个立地因子，将立地(高生长)分为10个亚等级。针阔混交林高生长分级对应的散点分布见图 3，1级为最高，10级为最低。

3.3 生长模型建立

选用唐守正等(1991a)提出的全林整体模型中的断面积生长模型：

$G = {b_{1i}}{\left\{ {1 - \exp \left[ { - {b_2}{{\left( {{\rm{SDI/10\;000}}} \right)}^{{b_3}}}T} \right]} \right\}^{{b_4}}} + \mathit{\varepsilon }。 $

(10)

式中：G为林分断面积(m²·hm^-2)；SDI为林分密度指数(tree·hm^-2)；T为林分平均年龄(a)；Φ_Gi=(b_1i, b₂, b₃, b₄)为模型参数，其中b_1i与立地等级有关(i=1, …, 10)；ε为误差项。

蓄积模型选用与断面积模型完全相同的模型形式：

$V = {b_{1i}}{\left\{ {1 - \exp \left[ { - {b_2}{{\left( {S/10\;000} \right)}^{{b_3}}}T} \right]} \right\}^{{b_4}}} + \mathit{\varepsilon }。 $

(11)

式中：V为林分蓄积(m³·hm^-2)。

表 3给出了针阔混交林10个亚立地等级的林分平均高、断面积和蓄积生长模型参数估计值及拟合统计量。可以看出，模型(9)—(11)都具有较高的拟合精度，决定系数(R²)分别为0.991 8、0.986 6和0.984 2。

3.4 潜在和现实蓄积生产力计算

根据蓄积潜在生产力的计算要求，针阔混交林对应的已知条件分别为：1)划分10个亚立地等级，分别用L=1, …, 10表示，见图 3；2)针阔混交林对应的林分平均高、断面积和蓄积生长模型，参数估计值见表 3；3)林分基准年龄假定为50年；4)林分密度指数SDI的搜索区间为(30，3 000)。据此可得到10个亚立地等级不同年龄的蓄积潜在生长量。为便于实践应用，将相邻2个亚立地等级合并，得到5个立地等级(L=1, …, 5)。

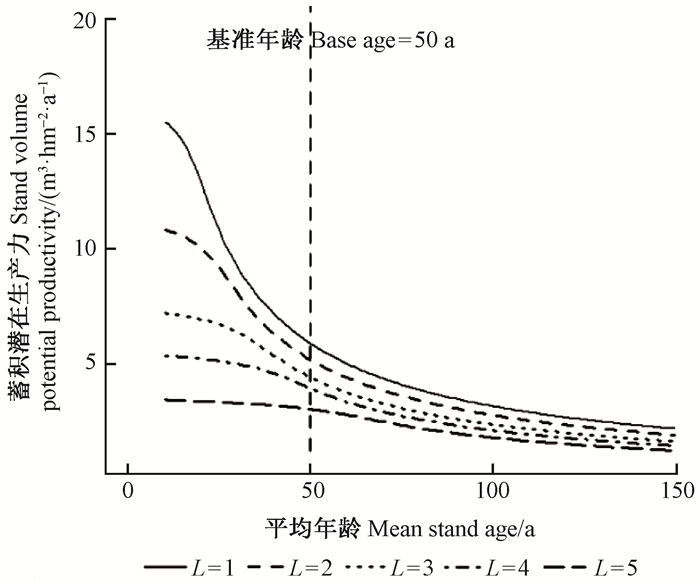
图 4为针阔混交林各立地等级(L=1, …, 5)在林分平均年龄为10~150年间对应的林分蓄积潜在生产力曲线。可以看出，对于所有L，林分蓄积潜在生产力都与林分平均年龄呈负相关，在幼龄、近成熟和过熟阶段，曲线下降较缓，在中龄阶段，曲线下降较快。在相同年龄下，各立地等级(L=1, …, 5)对应的潜在生产力呈逐渐下降趋势，与立地等级定义相一致(L=1表示立地等级最高，L=5表示立地等级最低)。针阔混交林各立地等级(L=1, …, 5)在基准年龄时对应的林分蓄积潜在生长量、蓄积量和林分密度见表 4。可以看出，立地等级1蓄积潜在生长量最大，为5.900 3 m³·hm^-2a^-1，相应的蓄积量最大，为375.18 m³·hm^-2。随着立地等级降低，相对应的蓄积潜在生长量逐渐减小，立地等级5的蓄积潜在生长量最小，为3.038 9 m³·hm^-2a^-1，是等级1的51.50%，相应的蓄积量最小，为170.03 m³·hm^-2。

通过蓄积潜在生产力和现实生产力的差异程度(ΔMI)可以对现实林分进行有效评价，从而定量掌握该林分的可提升空间。对于不同时间点林分的ΔMI由下式计算得到：

$\Delta {\rm{M}}{{\rm{I}}_\mathit{T}} = {\rm{PM}}{{\rm{I}}_T} - {\rm{RM}}{{\rm{I}}_T}。$

式中：ΔMI_T为T年林分蓄积年生长量可提升空间；PMI_T和RMI_T分别为T年时林分对应的蓄积潜在生产力和现实生产力。

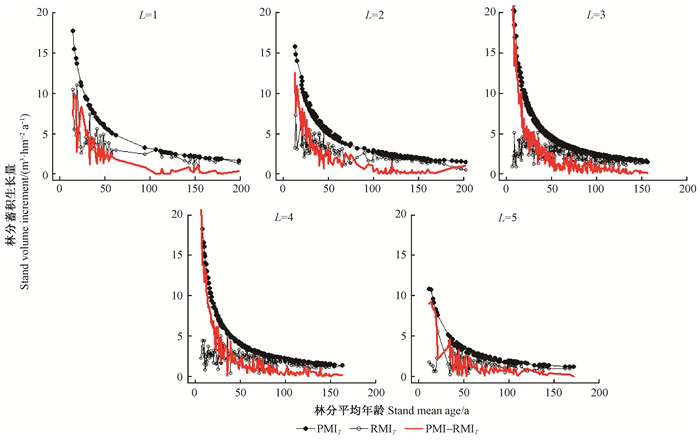
480个针阔混交林样地对应的各立地等级蓄积潜在生产力、现实生产力和蓄积年生长量可提升空间(ΔMI)见图 5。可以看出，对于不同年龄阶段的林分，各立地等级总体上都满足ΔMI随T的增大而减小。以基准年龄T=50为例，各立地等级L=1, …, 5对应的ΔMI分别为1.571 5、2.146 8、1.469 3、1.834 2和0.874 1 m³·hm^-2a^-1。

4 讨论

本研究提出一种基于林分潜在生长量的立地质量评价方法，将潜在生产力定义为某种确定的林分类型在同一种立地类型上(林分生长类型)、在给定的林分平均年龄下可能达到的最大生长量(蓄积、断面积或生物量)。利用该方法，可以得到某一林分生长类型基准年龄时的潜在生产力和对应的最优密度。以吉林省中东部地区针阔混交林为例开展案例研究，结果显示：1)目前几乎全部森林的现实生产力均低于其潜在生产力，尤其在中幼林阶段，森林的生产潜力远未得到充分发挥。以基准年龄50年为例，潜在生产力在3.591 1~5.793 0 m³·hm^-2a^-1之间，现实生产力在1.943 6~ 3.943 7 m³·hm^-2a^-1之间，为潜在生产力的54.12%~68.07%。2)森林在中幼林阶段表现出比成过熟林阶段更高的生长潜力，且现实生产力与潜在生产力差别较大，该阶段抓好森林抚育，会大大提高现实生产力，增加森林生长量和存量。3)模型结果与样地观测数据接近，并具有合理的林学解释。本研究完成了林分密度优化，下一步可优化林分结构，得到潜在生产力对应的最优林分结构。

基于林分潜在生长量的立地质量评价方法虽然需要林分平均年龄，但从本质上来说，立地生产力就是单位时间单位面积的生长量，无法回避年龄。对于人工林，林分平均年龄确定较为容易，对于天然林，尤其天然混交林，本研究将林分中主林层优势树种的平均年龄定义为林分平均年龄，如果林分中没有明显的优势树种，则通过树种组成占前几个树种的断面积加权平均年龄确定得到。随着新技术如树木微损测量技术的发展，树木年龄的准确测量有望解决，这将为本研究成果的广泛推广提供一个可行途径。对于混交林基准年龄的确定，目前尚未有统一方法，本研究基于主林层优势树种来确定，案例中根据吉林地区林分生长经验，暂将基准年龄假定为50年，需要进一步研究。此外，由于我国森林资源清查样地调查数据不调查林分优势高，因此为了保证所提方法与我国森林清查数据相兼容，本研究采用实测的林分平均高。混交林优势高的定义以及实地测量存在较大不确定性，如何定义和测量需要进一步研究(雷相东等，2018)；也有研究发现，林分平均高与优势高本身存在较强的相关性(唐守正，1991b；王忠诚等，2011；娄明华，2016)。

本研究将蓄积年生长量作为潜在生产力的指标，将来也可考虑出材率的影响。除蓄积生长量外，还可利用其他因子的生长量进行立地质量评价，如Hennigar等(2016)基于固定样地，采用林分生物量生长量模型的渐进线值作为最大值来评价立地质量。本研究提出的方法同样可以计算生物量潜在生长量或断面积潜在生长量(Fu et al., 2017)，并且可以得到达到最大生长量的林分密度，为通过调控林分密度发挥立地潜力提供了依据。

本研究以林分按等株生长作为前提条件计算蓄积年生长量。理论上讲，如果考虑林分自稀疏更能合理地描述林分生长过程，提高蓄积潜在生产力的估计精度；但是需要构建林分自稀疏模型，并且对试验数据要求更高，同时蓄积潜在生产力的计算也会变得更加复杂。未来在数据满足的情况下，将尝试围绕林分自稀疏模式对蓄积潜在生产力进行计算。基于树种组成和生长过程的林分类型划分也是本研究的一个关键内容，详见段光爽(2018)。此外，目前尚未考虑林分进界和更新过程，其会引起林分组成和结构变化，从而使林分生长类型的划分和潜在生产力计算更加困难。

立地质量评价需要同时回答某一立地能种什么树(或森林类型)和哪种树(或森林类型)的生产力最高2个问题。对于第1个问题，主要通过天然林树种分布模型确定树种的潜在分布适宜性来解决，详见刘丹等(2018)。本研究对既定森林类型的潜在生产力进行估计，解决了第2个问题，未来将把分布适宜性与潜在生产力相结合，更好地进行立地质量评价。

5 结论

本研究提出一种基于林分潜在生长量的立地质量评价方法, 首次严格定义潜在立地生产力的概念, 推导出潜在生产力和现实生产力的模型和计算方法, 提出立地元素-林分元素-林分生长类型-现实生产力和潜在生产力模型-落实到地块的立地质量制图的技术流程, 并以吉林省中东部地区针阔混交林为例, 利用4期一类清查固定样地数据, 基于林分潜在生长量的立地质量评价方法开展案例研究。结果表明, 基于林分潜在生长量的立地质量评价方法可行、可靠, 适用于纯林和混交林; 基于编制的立地质量数表, 可实现现有林的潜在立地生产力估计和落实到小班的立地质量制图; 基于机器学习方法, 可实现异林地的立地潜在生产力估计。下一步将考虑林分结构等特征的影响, 更准确地估计潜在生产力, 为精准提升森林质量提供科学依据。