文章信息
- 王建明, 吴保国, 梁其洋
- Wang Jianming, Wu Baoguo, Liang Qiyang
- 基于遗传算法的森林抚育间伐小班智能选择
- Forest Thinning Subcompartment Intelligent Selection Based on Genetic Algorithm
- 林业科学, 2017, 53(9): 63-72.
- Scientia Silvae Sinicae, 2017, 53(9): 63-72.
- DOI: 10.11707/j.1001-7488.20170908
-
文章历史
- 收稿日期:2016-04-01
- 修回日期:2016-06-28
-
作者相关文章
目前,我国森林经营方案编制以5年或10年为一个规划期(亢新刚,2011)。在经营方案中,抚育间伐是主要的经营技术措施。决策支持系统和专家系统作为一种必要工具,在森林资源管理、林火、生态保护、引种辅助决策、森林培育(造林)辅助决策、造林地选择等方面得到了广泛应用(吴保国等,2009a), 特别是在造林规划及造林地选择方面,建立了诸多决策支持系统及相关技术,如结合树种生长数学模型和计算机技术构建的辅助造林设计系统(俞新妥等,1986),采用遗传算法对小班进行两树种造林规划的造林决策技术(吴承祯等,1997),根据立地条件采用产生式规则进行适地适树决策推理并进行造林地选择的基于Web的森林培育专家系统(吴保国等,2009b),以经济效益最大化为目标并采用遗传算法对小班进行造林树种随机分配的造林决策技术(林晗等,2010),基于GIS、以森林生长率模型为基础的采伐决策支持系统(谢小魁等,2011),基于普通空间查询方式选择造林小班并进行造林设计的县级营造林管理系统(高飞,2013),采用决策论和空间规划用于造林树种选择、收获调整等的决策支持技术及系统等(Uhde et al., 2015;Dalemans et al., 2015;Segura et al., 2014;Lappi et al., 2013;Zambelli et al., 2012)。这些系统大多都提供了小班查询功能,通过输入查询条件即可得到满足条件的小班;但在经营管理中,如何根据给定的抚育间伐任务,选择满足空间和属性条件的小班集合有一定难度。传统给定条件的查询方式,经营者须了解选择抚育间伐小班需要的条件、如何进行条件组合及条件和条件值的增减,特别是空间属性与基本属性间的联合查询,在目前的系统中鲜有报道。
鉴于此,本文以人工林小班为对象,提出森林抚育间伐小班智能选择的概念,建立小班选择的数学模型并利用遗传算法进行求解,研究如何根据抚育间伐任务对人工林经营过程中需要进行抚育间伐的小班进行选择,以期为后续的经营活动提供决策支持。
1 研究区概况与研究方法 1.1 研究区概况选择内蒙古赤峰市克什克腾旗桦木沟林场为研究区。林场总经营面积68 667 hm2,有林地面积45 113 hm2,活立木总蓄积186.42万m3,灌木林面积1 922 hm2。用材林面积8 673 hm2,以华北落叶松(Larix principis-rupprechtii)为主。林场有2 612个小班,其中有林地小班2 251个,中龄林小班1 445个、幼龄林小班125个、近熟林小班143个、成熟林小班5个、过熟林小班63个,其他未标识龄组属性的有林地小班470个。
1.2 数据准备林场所有小班的属性数据和空间数据存储在森林资源数据库中,属性数据主要是赤峰市二类调查数据和桦木沟林场小班调查数据,调查因子包括林班、小班、林种、郁闭度、可及度、森林灾害等级、坡向、坡度、坡位、海拔、造林时间、土壤名称、年龄、龄级、平均直径、平均树高、株数、公顷蓄积、小班蓄积等;空间数据包括林场1:2.5万小班矢量数据和DEM数据。
1.3 小班选择问题的数学模型构建 1.3.1 选择规则人工林抚育间伐任务一般以面积为指标,要求设计面积大于任务面积,按照集中连片、整体推进的原则进行。抚育间伐对象为有林地幼龄林、中龄林和近熟林、林分郁闭度(疏密度)在0.7以上的林分,不可及或坡度26°以上不抚育间伐,南北方还需分别考虑坡向条件。在选择过程中,经营者可修改上述条件或额外限定年龄范围、株数密度范围、径阶范围等作为基本条件。
下达年度抚育间伐任务时,指定面积和上限值,为了便于控制并留有余地,上限值一般为5%,选择的小班总面积在二者之间。本文通过智能选择算法进行小班选择,先采用空间分析选择满足基本条件的小班作为初始小班集合,再使用改进的遗传算法进行求解,进一步选择出最符合任务目标的小班集合。
1.3.2 属性因子选择抚育间伐小班,需同时考虑其基本属性和空间属性。基本属性包括面积、地类、平均树高、龄组、郁闭度、疏密度、可及度、森林灾害等级、坡度、坡向、坡位等,可由经营者动态调整。
地类集合DL可用如下关系式表示:
| $ {\rm{DL}} = \left\{ {{\rm{d}}{{\rm{l}}_1},{\rm{d}}{{\rm{l}}_2},{\rm{d}}{{\rm{l}}_3}} \right\}。$ | (1) |
式中:dl1、dl2和dl3分别表示有林地、疏林地和灌木林地。
龄组集合G可用如下关系式表示:
| $ G = \left\{ {{g_1},{g_2},{g_3},{g_4},{g_5}} \right\}。$ | (2) |
式中:g1~g5分别表示幼龄林、中林龄、近熟林、成熟林和过熟林。
设集合R为初始小班集合,可表示为:
| $ R = \left\{ {t\left| {f\left( t \right) \in {\rm{d}}{{\rm{l}}_1} \cap g \cap y \cap u \cap x} \right.} \right\}。$ | (3) |
式中:t为符合基本条件的小班;y为郁闭度;u为坡度;x为其他控制变量;f表示通过空间分析选择符合基本条件的小班。
小班的空间属性主要是形状和距离。为便于集中作业,通常对某一区域内的小班进行选择,小班中心点与区域中心点间的距离是重要的决策变量。在大多数GIS分析工具中,面状要素中心点计算方式主要有3种:1) 计算要素外接矩形的中心点为要素中心点;2) 计算要素的重心作为要素中心点;3) 以一定角度的扫描线贯穿要素,取最长线的中点为要素中心点(沈立辉,2015)。但对于形状不规则的小班来说,以上方式计算的中心点有可能位于小班外,在计算距离时会造成偏差,因此须使用特定的算法使中心点始终位于小班内均匀分布的合适位置,本文采用小班标注点算法(SCLPA)进行中心点计算(沈立辉等,2014)。
1.3.3 数学模型表达为了衡量小班选择结果与任务目标的符合程度,需要对选择条件进行量化,构建评价指标。本文从抚育间伐迫切程度、作业难易程度和立地条件等方面进行讨论,构建了目标条件函数,以目标条件值衡量小班选择的符合程度(重要性)。最终选择的小班总面积应满足面积指标且在上限百分比控制之下,数学表达如下:
| $ \left\{ \begin{array}{l} {S_{{\rm{sel}}}} = \sum\limits_{\begin{array}{*{20}{c}} {i = 1}\\ {t \in R} \end{array}}^n {S\left( {{t_i}} \right)\left| {F\left( t \right)} \right.} \\ {S_{\rm{c}}} \le {S_{{\rm{sel}}}} \le \left( {1 + h\% } \right){S_{\rm{c}}} \end{array} \right.。$ | (4) |
式中:n为最终小班数;Ssel为选择的小班总面积;Sc为指定面积;h为面积上限值;F为限定条件。
1) 迫切程度 郁闭度(或疏密度)和森林灾害等级一定程度上反映了抚育间伐的迫切程度。在小班选择时,可指定郁闭度值或范围,若不指定,则按优先级默认选择郁闭度≥0.7以上的小班。数学表达如下:
| $ \max Y\left| {\left[ {{Y_1},1} \right] = f\left( t \right),t \in R} \right.。$ | (5) |
式中:Y为郁闭度;Yl表示在指定郁闭度范围时郁闭度下限值;f表示选择满足基本条件下郁闭度高的小班。
森林灾害等级分为无、轻、中和重4个等级,分别量化为1~4。以郁闭度和森林灾害等级构成抚育间伐迫切程度的量化指标值,其值越高表示越迫切,其中,森林灾害等级并不是抚育间伐的必要条件,等级低的小班也需要抚育间伐,故取其对数值。数学表达如下:
| $ \max {\rm{M}}{{\rm{u}}_t} = {Y_t} + \ln {Z_t},t \in R。$ | (6) |
式中:Mut为小班t的迫切程度指标值;Yt为小班t的郁闭度;Zt为小班t的森林灾害等级。
2) 难易程度 可及度和距离反映了作业的难易程度。对可及度进行量化,即可及为1、将可及为2、不可及为3。在小班选择时,可指定可及度范围,若不指定,则按优先级进行选择。数学表达如下:
| $ \max A\left| {\left[ {{A_1},{A_{\rm{u}}}} \right] = f\left( t \right),t \in R,A \in \left\{ {1,2} \right\}} \right.。$ | (7) |
式中:A为可及度值;Al为指定可及度范围时可及度下限值;Au为指定可及度范围时可及度上限值;f表示选择满足基本条件下可及度高(可及度值小)的小班。
根据由近及远的选择原则,小班中心点到指定中心点的距离D应尽量小。数学表达如下:
| $ \min D = f\left[ {d\left( {P,O} \right),t} \right],t \in R。$ | (8) |
式中:P为小班中心点;O为区域中心点(区域几何中心、自定义中心点或林场场部位置);d表示求取2点间距离;D为中心点P与O的距离(km);f表示选择满足基本条件下距离近的小班。
根据可及度、距离与抚育间伐任务的关系,以二者乘积的倒数作为默认难易程度指标值。数学表达如下:
| $ A{D_t} = \frac{1}{{{A_t} \times {D_t}}}。$ | (9) |
3) 立地因子 选择抚育间伐小班还需考虑立地因子,因子和分级指标的选择以经营地区的相关研究为准或由经营者指定。采用无林地立地质量评价方法和数量化理论思想对立地因子各分级指标值进行评分,采用专家打分并通过模糊层次分析法计算因子间的相互重要程度。本文以内蒙古赤峰市桦木沟林场为试验地,分级指标值和因子权重的默认值采用内蒙古东南部立地质量评价研究成果(温阳等,2011;韩焱云等,2014)。若用立地质量作为选择标准,选择立地条件好的小班时使用默认值,选择立地条件差的小班时则交换分级指标和因子权重的最大值和最小值。经营者还可根据实际需要,按任务需求的分级指标优先级从低到高分别重新赋值为[1, 2, …, n],因子权重ω按任务需求的因子优先级重新赋值并进行归一化处理。
如任务要求优先选择坡中、阴向的小班,并按坡向、坡度、坡位顺序考虑因子优先级,则进行如下设置:对于坡位,要求优先选择坡中,则坡中赋值为3,根据默认值大小设置坡下为2,坡上为1;对于坡向,要求优先选择阴坡,则阴坡赋值为3,同理,半阴半阳坡为2,阳坡为1;对于因子权重,根据参与计算的因子数赋值并进行归一化处理,坡向为0.5,坡度0.3,坡位0.2。
立地因子指标计算如下:
| $ {c_t} = \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^k {{X_t}\left( {i,j} \right){\omega _i}{b_{ij}}} } 。$ | (10) |
式中:ct为小班t的立地因子指标;Xt(i, j)为小班t的立地因子在第i个因子第j个分级指标的属性值,当小班属性值与指标相等时Xt=1,否则为0;bij为第i个因子第j个分级指标的得分值;ωi为第i个因子的权重值;m为立地因子数;k为分级指标数。
4) 目标条件函数 以迫切程度指标、难易程度指标和立地因子指标构建抚育间伐小班选择的目标条件函数。采用1-9标度法(陈迁等,1996),通过专家打分建立模糊判断矩阵并使用模糊层次分析法计算各指标的权重值,得到3个指标权重值为:ε1=0.648 3、ε2=0.229 7、ε3=0.122 0。经营者可根据任务需要重新赋值指标权重并进行归一化处理。
综合上述分析,本文构建了小班选择的目标条件函数,小班的符合程度由目标条件值进行量化。目标条件函数如下:
| $ {w_t} = {\rm{M}}{{\rm{u}}_t}{\varepsilon _1} + A{D_t}{\varepsilon _2} + {c_t}{\varepsilon _3}。$ | (11) |
式中:wt为小班t的权重值,即目标条件值;Mut为小班t的迫切程度指标;ADt为小班t的难易度指标;ct为小班t的立地因子指标;ε1为迫切程度指标权重值;ε2为难易程度指标权重值;ε3为立地因子指标权重值。
因此,经营者可根据需要灵活确定迫切程度、难易度和立地因子指标及对应权重值,对初始小班集合进行优选。以目标条件值最大为目标条件、指定面积及上限值为限制条件,则抚育间伐小班选择的数学模型为:
| $ \max\sum\limits_{i = 1}^n {{w_i} \times {x_i}} ,1 \le i \le n; $ | (12) |
| $ {\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{.}}\;{S_{{\rm{sel}}}} \ge {S_{\rm{c}}}; $ | (13) |
| $ {S_{{\rm{sel}}}} \le \left( {1 + h\% } \right){S_{\rm{c}}}。$ | (14) |
式中:xi=1表示小班i被选择;xi=0表示小班i未被选择;n为初始小班集合的小班数。
1.4 遗传算法选择小班 1.4.1 满足抚育间伐要求的初始小班集合生成根据抚育间伐任务和经营者指定的基本属性条件,基于空间查询和点缓冲区分析2种方式选择出空间分布连续的小班作为初始小班集合。空间查询通过几何运算直接获取空间几何体内及与其相交、相接的符合基本条件的小班组成初始小班集合;点缓冲区分析需设置初始缓冲区大小和步长,选择缓冲区内及与缓冲区相交、相接的符合基本条件的小班组成初始小班集合。对于普通的点缓冲区分析方式,如果初始半径和步长设置不当,会极大降低程序运行效率。
本文改进了点缓冲区分析方式,设计环带控制算法(annulus control algorithm,ACA)计算初始半径和步长。ACA算法通过读取林场所有小班的属性,计算所有小班平均面积和林场地图单位面积小班数,根据任务需求的基本条件,通过换算即可求出最优的初始半径和步长。算法步骤如下:
1) 计算所有小班平均面积:
| $ \bar S = \sum\limits_{i = 1}^n {{S_i}/n} 。$ | (15) |
式中:n为林场总的小班数;Si为第i个小班的面积;S为小班平均面积。
2) 计算整个林场地图区域内单位地图面积小班数:
| $ \bar N = \frac{n}{{{\rm{Are}}{{\rm{a}}_{{\rm{map}}}}}}。$ | (16) |
式中:n为林场总的小班数;Areamap为林场区域总面积;N为地图区域内单位面积小班数(个·hm-2)。
3) 根据任务指定的面积,计算初始地图区域面积和半径。假设任务指定的面积为Sc,则根据小班平均面积S计算出大概需要m个小班,根据单位面积小班数N,可估算出m个小班大概需要的地图面积Area′,将Area′看作圆形区域,则可以计算出初始缓冲区半径r′:
| $ m = \frac{{{S_{\rm{c}}}}}{{\bar S}}; $ | (17) |
| $ {\rm{Area'}} = \frac{m}{{\bar N}}; $ | (18) |
| $ r' = \sqrt {{\rm{Area'}}/{\rm{\pi }}} 。$ | (19) |
4) 在初始缓冲区内选择符合基本条件的小班,累加小班面积,若总面积S′大于指定面积Sc上限值,则生成初始小班集合;否则转到下一步。
5) 若总面积S′小于指定面积Sc,则需要扩增上一次缓冲区半径。先计算指定面积Sc和上一次查询面积S′的差S-,然后根据步骤3方法计算面积差值S-所需的小班数m-:
| $ {m^ - } = \frac{{{S^ - }}}{{\bar S}} = \frac{{{S_{\rm{c}}} - S'}}{{\bar S}}。$ | (20) |
再计算出m-个小班所需的地图面积Area-,将Area-看作与上一个圆形缓冲区为同心圆的环带面积,则上一个缓冲区面积Area′与环带面积Area-之和为较大同心圆面积Area*,即新的缓冲区面积。同时,还可求出环带宽度Δr作为缓冲区半径的步长,其值为较大同心圆半径(上界半径或外半径)r*与较小同心圆半径(下界半径或内半径)即上一个缓冲区半径r-之差:
| $ {\rm{Are}}{{\rm{a}}^ - } = \frac{{{m^ - }}}{{\bar N}}; $ | (21) |
| $ {\rm{Are}}{{\rm{a}}^ * } = {\rm{Are}}{{\rm{a}}^ - } + {\rm{Area'}}; $ | (22) |
| $ {r^ * } = \sqrt {{\rm{Area'}}/{\rm{\pi }}} 。$ | (23) |
| $ \Delta r = {r^ * } - r'。$ | (24) |
6) 确定新缓冲区后,转到步骤4,生成初始小班集合,进行后续计算,如果选择出符合要求的最优化小班集合则结束,否则重复上述步骤。
1.4.2 基于遗传算法的智能选择算法1) 智能选择算法流程 森林抚育间伐小班智能选择算法根据任务目标进行求解,先根据基本条件通过空间查询或点缓冲区分析并使用ACA算法选择出初始小班集合,通过式(11) 计算小班权重并利用贪婪策略对初始小班集合中的小班进行遗传算法编码,再对编码的染色体进行交叉、选择等遗传操作,直到得到最优解或达到迭代次数为止,算法流程如图 1所示。

|
图 1 森林抚育间伐小班智能选择算法流程 Fig.1 Flowchart of subcompartments intelligent selection algorithm |
2) 遗传算法染色体结构 传算法的基本思想是将问题的求解表示成“染色体”,即对问题进行编码操作(邱荣祖等,2010)。染色体的基本组成元素是“基因”,由不同的基因构成“染色体”(张国梁等,2016)。本文基因对应小班,用小班编号进行编码。以初始小班集合构成遗传算法的初始解空间,通过式(11) 计算小班权重(目标条件值),以面积指标和上限值为限制条件,求解出权重值最大、最符合任务目标的小班集合。
标准遗传算法(standard genetic algorithm,SGA)一般采用二进制编码,本文改进了标准遗传算法,形成新的算法IGSEGA(improved greedy strategy and encoding for genetic algorithm)。首先采用改进的贪婪策略以符号编码方式进行编码,然后改进遗传算法的操作算子,使用单基因交叉、基因段交叉和变长基因交叉方式进行交叉操作。编码时使用式(11) 分别计算初始小班集合内所有小班的权重值,按权重大小对小班进行降序排序,依次累加小班面积,若所有小班面积之和小于指定面积,则使用ACA算法调整缓冲区半径重新生成初始小班集合,否则当累加面积第1次大于或等于指定面积上限时,截取当前小班生成基础小班集合,对应“基础染色体”;剩余小班生成候补小班集合,对应“候补染色体”。由此,单个染色体由对应的基础小班集合和候补小班集合构成,染色体的每个基因对应初始小班集合中的每个小班,后续的遗传算子操作都在这2个子染色体之间进行。这是一种新的遗传算法染色体构造方式,这种改进是对遗传算法的一种优化,能使初始个体就具有较好的适应值,加快算法收敛速度。
如初始小班集合中有n个小班,假设计算权重并降序排序后小班编号顺序为1, 2, 3, …, n,依次累加面积,到第m个小班时总面积Ssel大于指定面积Sc上限值,则第1~m个小班构成“基础小班集合”,剩余的第m+1~n个小班构成“候补小班集合”。由此,智能化小班选择问题的染色体表示可描述为T[i](i=1, 2, …, n),其中T[i]是第i个遗传坐标位置上的遗传因子,取值为初始小班集合中小班编码值。染色体结构如图 2所示。
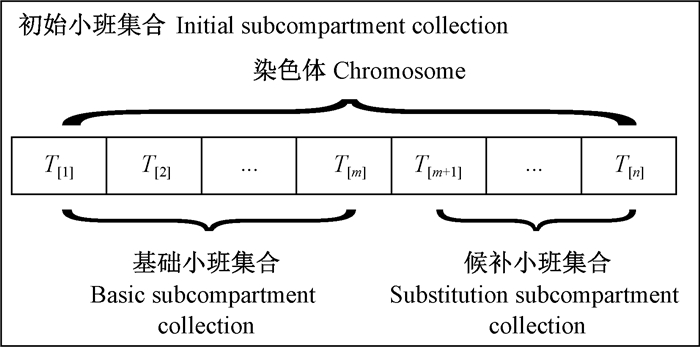
|
图 2 智能化小班选择的染色体结构 Fig.2 Architecture of chromosome for intelligent subcompartment selection |
3) 适应值函数 遗传算法的关键是适应值,其反映了个体适应环境的能力,本文中适应值反映的是最接近任务目标的小班集合能力。适应值函数与目标函数之间存在着对应关系,在此直接使用目标函数转换为适应值函数。小班智能化选择技术的遗传算法适应值函数为:
| $ W = \sum\limits_{i = 1}^n {{w_i} \times {x_i}} 。$ | (25) |
式中:W为个体的适应值;wi为初始解空间中第i个小班的权重值;xi为第i个小班的决策变量。
4) 交叉算子 本文构建的染色体由基础小班集合和候补小班集合2个子染色体组成,编码具有特殊性,故改进了标准遗传算法的交叉操作,在2个子染色体中进行,主要有单点交叉、多点交叉和变长交叉等。
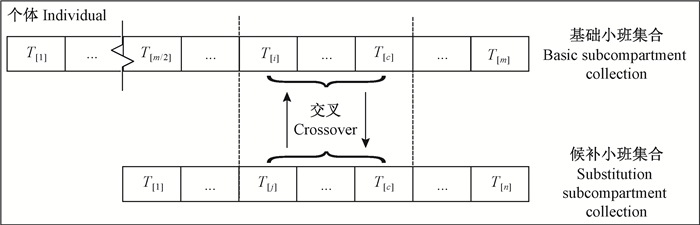
根据构建的染色体性质,生成的初代染色体是单一染色体,即一个小班集合,暂不能进行选择操作,须先进行交叉操作生成新的染色体。基础小班集合是通过贪婪策略构造的较为接近目标解的子染色体串,根据小班特性和本文构建的染色体结构,在对染色体进行交叉操作时截取其后半部分的基因位,以尽可能保留前段目标条件值较高的小班,主要有单基因交叉、基因段交叉和变长交叉。
(1) 单基因交叉 按一定的概率pc在基础小班集合后半部分基因中随机取一个基因(小班),同时在候补小班集合中随机取一个基因,二者进行交换,形成新的个体(小班集合)。如个体1中,基础小班集合和候补小班集合基因位数分别为m、n,随机在基础小班集合中取[m/2, m]间的一个基因T[i]与候补小班集合的随机基因T[j]进行交换,生成新的个体,如图 3所示。

|
图 3 单基因交叉 Fig.3 Single gene crossover |
(2) 基因段交叉 基因段交叉与单基因交叉类似,只是交换二者的一个基因段。如2个子染色体的基因位数分别为m、n,随机在基础小班集合中[m/2, m]间取一段长度为c的基因{[T1, T2, …, Tc], 2≤c≤n},在候补小班集合中截取等长的基因段进行交换,生成新的个体,如图 4所示。
(3) 变长交叉 变长交叉是对2个子染色体串以1对n或n对1的方式进行基因位交叉,对于基础小班集合同样是取后半部分的基因进行操作。如2个子染色体基因位数分别为m、n,在基础小班集合中[m/2, m]间随机取一段长度为c的基因,c∈{(0, n]∩(0, m/2)},在候补小班集合中截取β×c长度的基因进行交叉,生成新的个体,β为(0, k]之间的随机数,k为基因变长系数,取值为正整数。
|
图 4 基因段交叉 Fig.4 Gene segment crossover |
根据构造的染色体特征,进行的遗传操作主要是交叉,每次迭代时对每个个体分别进行单基因交叉、多基因交叉和变长交叉操作并生成新的个体,计算新个体的适应值,按照适应值大小降序排序,选择一定数量的高适应值个体生成种群(种群是由多个个体构成的小班集合矩阵),重复以上操作直到找到最优解或达到迭代次数为止。
2 结果与分析根据年度抚育间伐任务,指定面积300 hm2、面积上限值5%,选择郁闭度0.7以上的幼龄林和中龄林,坡度26°以上的小班不进行抚育间伐,径阶范围不考虑(默认全径阶范围)。为便于集中作业,拟定以林场场部为中心点,优先选择坡中、阴向的小班;同时,按坡向、坡度、坡位顺序考虑因子优先级,且在满足其他条件时,优先考虑迫切程度高的小班,其次为难易程度,在面积控制下选择出最符合任务目标的小班集合。
本文结合C#和ArcEngine,编程实现了空间分析功能模块和小班选择智能求解功能模块,并构建了森林经营决策支持系统。根据任务要求,指定基本条件参数如表 1所示。适应值函数各参数及权重值设置如下:迫切程度指标和难易程度指标对应的属性值通过读取小班属性和空间分析获取并计算;立地因子指标根据前文所述方法设置;对于迫切程度、难易程度和立地因子指标的权重值,根据任务要求,采用默认值。
|
|
根据基本条件,使用点缓冲区分析方式构建初始小班集合,对比普通点缓冲区分析和ACA优化算法,试验结果如表 2所示。经ACA算法优化得到初始缓冲区半径1 407 m,最终半径1 709 m,小班72个,通过1次半径变动即可构造出初始小班集合,根据算法原理,构建的初始小班集合是指定区域内的最小集合,便于后续求解计算。对于普通点缓冲区分析方式,当设置初始半径1 000 m、步长100 m时,首次分析得到的总面积小于指定面积,按步长扩增缓冲区,当总面积首次大于指定面积时,需进行8次扩增,最终半径为1 800 m,较ACA算法多91 m,最终小班数81个,比ACA算法多9个。这9个小班在最优半径以外91 m的环带周围,距离林场场址更远,对集中作业不利。当初始半径设置过大时,须进行更复杂的处理,按步长递减缓冲区半径,当获取的小班总面积首次小于指定面积时,以上次的半径作为最终半径。指定初始半径2 000 m、步长100 m,在第3次半径递减时,得到的小班总面积首次小于指定面积,以第2次的半径为最终半径。试验中虽然半径递减比递增的次数少,但属于特例情况,多数情况下由于初始缓冲区半径和步长设置的不确定性,半径递减为次数可能较递增更多。由试验结果可知,ACA算法的空间分析效率明显高于普通点缓冲区分析方式。
|
|
在ACA算法生成的初始小班集合基础上,分别使用SGA和IGSEGA算法进行求解。对于IGSEGA算法,迭代时对每个个体分别进行单基因交叉、基因段交叉和变长交叉操作并进行后续运算。经调试,SGA和IGSEGA算法的参数设置如表 3所示。为了进行多次测试和对比分析,在林场其他交通便利、具有设置生活点条件的适宜位置再指定2个中心点进行选择测试,基本条件值和各权重值不变,结果如表 4所示。以林场场部为中心点进行选择时,SGA迭代46次、IGSEGA迭代15次后算法收敛,得到小班总面积为311.48 hm2,最大权重值为74.47,IGSEGA效率明显高于SGA。通过分析小班属性可知,求解的小班符合要求,可作为当次任务的目标小班,为抚育间伐任务提供决策参考,而至于是否对小班进行抚育间伐及相应技术措施则由经营者决定。另外2个测试点的IGSEGA算法迭代次数分别为14和15次,收敛速度也较快,选择的小班同样符合任务目标要求。
|
|
|
|
在森林生产经营中,如何根据抚育间伐任务合理高效地选择小班,为后续森林经营活动做准备,是值得研究的问题。当前尚无森林抚育间伐小班智能选择的概念,普通的森林小班选择通常集成在造林决策系统中,且以一般的属性查询进行,不能满足日趋复杂的森林经营需求。同时,抚育间伐小班的选择条件多样,且经营者需求多变,如何综合权衡各种条件和需求间的关系,智能选择出最符合任务目标的抚育间伐小班有一定难度。本文提出了森林抚育间伐小班智能选择概念,针对森林经营管理中抚育间伐小班的选择问题,综合考虑小班空间属性与基本属性,结合任务目标和经营者主观需求,构建了目标条件函数,以目标条件值衡量小班与任务目标的符合程度。目标条件函数由迫切程度指标、难易程度指标和立地因子指标构成,可综合反映林分状态、作业难易程度和立地情况,在不同指标值和权重值控制下能适应不同任务和经营者需求,是对小班智能选择结果的有效评价指标。同时,使用改进的贪婪策略实现遗传算法编码,并构建了对应的染色体,设计了单基因、基因段及变长基因等遗传交叉算子,为小班的智能化选择提供了一种有效方法。通过智能选择方法选择的抚育间伐小班作为经营者的决策参考,至于是否对小班进行抚育间伐及相应技术措施则由经营者决定。
本文对森林抚育间伐小班进行智能选择的过程如下:1) 根据抚育间伐任务和目标,读取小班基本属性,结合GIS空间分析,动态生成满足基本条件、可供后续智能计算的初始小班集合。针对普通点缓冲区分析初始半径和步长设置的不确定性,研究设计了ACA算法进行优化,经ACA算法优化的点缓冲区分析通过任务面积动态计算初始半径和步长,具有智能特性,提高了空间分析效率。2) 对初始小班集合进行求解,智能选择出最符合任务目标的小班集合。通过构建的目标条件函数计算小班权重值,任务指定面积和上限值为限定条件,构建小班选择的数学模型并采用IGSEGA算法进行求解。IGSEGA算法因特殊的编码方式,构造出的初始个体适应值已较为接近最优解,收敛数度较SGA快,只需进行较少的有限次迭代即可求出最优解。试验结果表明,ACA算法通过智能计算初始缓冲区半径值和步长,提高了空间分析效率,且IGSEGA算法具有较高的求解效率。同时构建的目标条件函数能有效地对小班智能选择结果进行评价,其值越高越符合任务要求。
本文的智能选择方法还可以通过修改限定条件构造新初始小班集合、修改目标条件函数的方式应用于造林、林分改造等其他经营任务中对小班进行智能选择,具有较好的实用性和扩展性。当然,目标条件函数也存在着一定不足,本文主要针对抚育间伐任务和经营者对小班状态、立地情况等综合需求进行抚育间伐小班选择,所以函数的各指标还需要其他条件进一步完善,特别是迫切程度指标,可进一步考虑林分生长和收获等。同时,作业设备和人员可能会因作业方式和间伐强度而异,进而影响算法的优化结果,后续研究中需要考虑作业方式、间伐强度等条件并量化集成到目标条件函数中,进一步深化和完善基础理论。
| [] |
陈迁, 王浣尘. 1996. AHP方法判断尺度的合理定义. 系统工程, 14(5): 18–20.
( Chen Q, Wang H C. 1996. Proper definition of criteria in AHP. Systems Engineering, 14(5): 18–20. [in Chinese] ) |
| [] |
高飞, 刘波, 吴保国, 等. 2013. 县级营造林工程管理信息系统的研究与开发. 林业资源管理(3): 143–150.
( Gao F, Liu B, Wu B G, et al. 2013. Study and development of the county-level afforestation project management information system. Forest Resources Management(3): 143–150. [in Chinese] ) |
| [] |
韩焱云, 吴保国, 刘建成, 等. 2014. 不确定性推理在森林培育专家系统中的应用. 北京林业大学学报, 36(1): 88–93.
( Han Y Y, Wu B G, Liu J C, et al. 2014. Application of uncertainty inference in the forest cultivation expert system. Journal of Beijing Forestry University, 36(1): 88–93. [in Chinese] ) |
| [] |
亢新刚. 2011. 森林经理学. 北京, 中国林业出版社.
( Kang X G. 2011. Forest management. Beijing, China Forestry Publishing House. [in Chinese] ) |
| [] |
林晗, 洪滔, 陈辉, 等. 2010. 应用遗传算法的工业原料林多树种造林设计. 林业科学, 46(5): 92–101.
( Lin H, Hong T, Chen H, et al. 2010. Multi-species design in planting industrial forests by genetic algorithm. Scientia Silvae Sinicae, 46(5): 92–101. DOI:10.11707/j.1001-7488.20100515 [in Chinese] ) |
| [] |
邱荣祖, 林雅惠, 钟聪儿. 2010. 基于ArcGIS的木材物流中心选址. 林业科学, 46(6): 113–117.
( Qiu R Z, Lin Y H, Zhong C E. 2010. Location of timber logistics centers based on ArcGIS. Scintia Silvae Sinicae, 46(6): 113–117. DOI:10.11707/j.1001-7488.20100618 [in Chinese] ) |
| [] |
沈立辉, 吴保国, 杨乃. 2014. 面状要素主骨架线自动提取算法研究. 武汉大学学报:信息科学版, 39(7): 767–771.
( Shen L H, Wu B G, Yang N. 2014. Areal feature main skeleton extraction algorithm. Geomatics and Information Science of Wuhan University, 39(7): 767–771. [in Chinese] ) |
| [] |
沈立辉. 2015. 森林资源经营管理平台与经营决策服务子系统的研建. 北京: 北京林业大学硕士学位论文. ( Shen L H. 2015. The research and development of forest resources management platform and decision service subsystem. Beijing:MS thesis of Beijing Forestry University.) http://d.wanfangdata.com.cn/Thesis/Y2851075 |
| [] |
温阳, 高桂英, 杨跃文. 2011. 内蒙古主要造林树种立地质量评价研究. 呼和浩特, 内蒙古大学出版社.
( Wen Y, Gao G Y, Yang Y W. 2011. Study on site quality evaluation of main afforestation tree species in Inner Mongolia. Hohhot, Inner Mongolia University Press. [in Chinese] ) |
| [] |
吴保国, 李成赞, 马驰, 等. 2009a. 森林培育专家决策支持系统的研究. 北京林业大学学报, 31(S2): 1–8.
( Wu B G, Li C Z, Ma C, et al. 2009a. An expert decision support system for silviculture. Journal of Beijing Forestry University, 31(S2): 1–8. [in Chinese] ) |
| [] |
吴保国, 马驰. 2009b. 森林培育专家系统中造林决策知识库设计与推理机求解算法研究. 北京林业大学学报, 31(S2): 9–13.
( Wu B G, Ma C. 2009b. Design of afforestation and decision-making knowledge base and research of inference engine algorithm in the silviculture expert system. Journal of Beijing Forestry University, 31(S2): 9–13. [in Chinese] ) |
| [] |
吴承祯, 洪伟. 1997. 用遗传算法改进约束条件下造林规划设计的研究. 林业科学, 33(2): 38–46.
( Wu C Z, Hong W. 1997. An improved method of afforestation planning and design under restricted conditions using the genetic algorithm. Scintia Silvae Sinicae, 33(2): 38–46. [in Chinese] ) |
| [] |
谢小魁, 苏东凯, 代力民, 等. 2011. 森林经营决策支持系统的设计与实现及在采伐中的应用. 生态学杂志, 30(10): 2381–2388.
( Xie X K, Su D K, Dai L M, et al. 2011. Design and actualization of forest management decision support system and its applications in forest harvesting. Chinese Journal of Ecology, 30(10): 2381–2388. [in Chinese] ) |
| [] |
俞新妥, 林思祖. 1986. 计算机辅助造林设计系统. 林业科学, 22(4): 337–346.
( Yu X T, Lin S Z. 1986. A computer-aided design of forest culture. Scintia Silvae Sinicae, 22(4): 337–346. [in Chinese] ) |
| [] |
张国梁, 蔡小娜, 侯晓鹏, 等. 2016. 面向零件的人造板材矩形件锯切排样数学建模及遗传算法求解. 林业科学, 52(5): 150–159.
( Zhang G L, Cai X N, Hou X P, et al. 2016. Part-oriented cutting layout mathematical modeling and solving by genetic algorithm for rectangular wood based panel parts. Scintia Silvae Sinicae, 52(5): 150–159. [in Chinese] ) |
| [] | Dalemans F, Jacxsens P, Van Orshoven J, et al. 2015. Assisting sustainable forest management and forest policy planning with the Sim4Tree decision support system. Forests, 6(4): 859–878. DOI:10.3390/f6040859 |
| [] | Lappi J, Lempinen R. 2013. A linear programming algorithm and software for forest-level planning problems including factories. Scandinavian Journal of Forest Research, 29(sup1): 178–184. |
| [] | Segura M, Ray D, Maroto C. 2014. Decision support systems for forest management:a comparative analysis and assessment. Computers and Electronics in Agriculture, 101: 55–67. DOI:10.1016/j.compag.2013.12.005 |
| [] | Uhde B, Hahn W A, Griess V C, et al. 2015. Hybrid MCDA methods to integrate multiple ecosystem services in forest management planning:a critical review. Environmental management, 56(2): 373–388. DOI:10.1007/s00267-015-0503-3 |
| [] | Zambelli P, Lora C, Spinelli R, et al. 2012. A GIS decision support system for regional forest management to assess biomass availability for renewable energy production. Environmental Modelling & Software, 38: 203–213. |
 2017, Vol. 53
2017, Vol. 53

