树皮不仅是生物能源、单宁提取的重要原料，亦是景观覆盖物等的优良材料，而且树皮作为药材也比较常见，其经济价值高(Marshall et al., 2006; Williams et al., 2007)。树皮是树木有机体的组成部分，估测树皮厚度对于树木材积、出材量以及树皮蓄积量的估计至关重要(Gordon, 1983)。

树皮厚度往往因树种而异，如希腊北部白冷杉(Abies concolor)的平均树皮厚度为10.2~17.8 cm，白云杉(Picea glauca)和黑云杉(Picea mariana)的平均树皮厚度仅0.6~1.3 cm(Kitikidou et al., 2014)。而且随着林木直径增大，树皮亦相应增厚，如Paine等(2010)在研究法国圭亚那热带低地雨林阔叶树种的树皮厚度时发现，其直径每增加10 cm，树皮厚度约增加1.2 mm；陈东来等(1994)对白桦(Betula platyphylla)、山杨(Populus davidiana)的研究也显示其树皮随着直径、树高的增大而增厚。Richardson等(2015)研究指出，针叶树种树皮厚度受直径的影响程度小于常绿阔叶树种。目前，有关阔叶树种树皮厚度的文献报道相对较少。

许多学者应用胸径、树高或年龄拟合模型估算胸高处树皮厚度(Laasasenaho et al., 2005；Sonmez et al., 2007；Williams et al., 2007；王晓林等, 2011)，由于树皮厚度往往随着树干高度而变化，任意高度处树皮厚度的估计同样受到重视(Maguire et al., 1989; Laasasenaho et al., 2005; Brooks et al., 2009)。也有一些学者通过拟合相对树皮厚度(Johnson et al., 1987; Maguire et al., 1989; Laasasenaho et al., 2005)、树皮率(Cao et al., 1986; Li et al., 2010)以及去皮直径(Cole et al., 1972; Dolph, 1989; Li et al., 2010)的模型估计树皮厚度。

西南桦(Betula alnoides)是天然分布于东南亚以及我国南方的速生珍贵阔叶树种，其木材广泛应用于木地板、家具制作以及建筑装饰中(曾杰等, 2006)，树皮除了可作燃料、提取栲胶外，其提取物还具有抗炎、减肥及降血脂等功效(Sur et al., 2002；Raj et al., 2015; Velavan, 2014)。近10多年来，西南桦木材及其产品的市场需求量巨大，我国西南桦种植业发展迅速，其人工林面积已超过15万hm²(王春胜等, 2013)，预计未来10年内将有大量人工林进入成熟林阶段。西南桦树皮厚度估计无论对于树皮利用还是木材生产均至关重要，然而目前尚没有合适的模型估算其树皮厚度。鉴于此，本研究通过查阅文献收集及自建树皮模型，应用前期西南桦树干解析所获带皮直径、去皮直径、树皮厚度等数据进行模型拟合，比较分析不同模型的拟合效果，从而筛选出各类树皮因子估测的适宜模型，为估算西南桦材积、出材量以及树皮蓄积量奠定基础。

考虑不同年龄、海拔、坡向、坡位等因子，选取117株解析木，其中76株取自广西壮族自治区凭祥市中国林业科学研究院热带林业实验中心，41株取自广西壮族自治区百色市老山林场。解析木为西南桦人工林中的优势木或亚优势木，其所在样地基本信息见表 1。伐倒解析木之前，标明其南、北方向，伐根离地面0.2 m，用皮尺(精度为0.01 m)测量树高。去除枝丫后，以2 m为区分段，于树干上0.3、1.0、1.3、3.0、5.0 m等位置处依次截取圆盘，顶梢不足2 m时以1 m为区分段，圆盘厚度为2~3 cm。将圆盘带回实验室，分东、南、西、北4个方向应用游标卡尺(精度为0.01 cm)测量每个圆盘的树皮厚度、带皮及去皮直径。

表 1 解析木所在样地基本信息 Tab.1 Information of sample plots

表 1 解析木所在样地基本信息 Tab.1 Information of sample plots 调查因子 Regimes 最小值 Min. 最大值 Max. 平均值 Mean 海拔Altitude/m 190.0 670.0 461.6 坡度Slope gradient/(°) 15.0 42.0 27.9 林分年龄Stand age/a 10.0 24.0 14.9 胸径DBH/cm 6.7 26.3 16.9 树高Tree height /m 6.3 20.9 14.3

考虑到模型拟合和验证，将117株解析木按照约75%和25%的比例随机分为2部分，一部分用于模型构建(解析木90株，圆盘1 128个)，一部分用于模型检验(解析木27株，圆盘342个)。解析木数据的描述性统计结果如表 2。

表 2 西南桦人工林树皮厚度建模和检验数据^① Tab.2 Fitting and validating data for bark thickness models of Betula alnoides plantations

表 2 西南桦人工林树皮厚度建模和检验数据① Tab.2 Fitting and validating data for bark thickness models of Betula alnoides plantations 变量 Variable 建模数据Fitting data 检验数据Validating data 均值Mean 范围Range 标准差SD 均值Mean 范围Range 标准差SD t/a 13.5 10~24 3.18 13.7 10~24 4.29 H/m 18.8 11.0~27.2 3.61 18.1 12.2~26.9 3.40 DBH /cm 20.4 10.8~35.1 5.31 19.2 10.4~30.1 5.52 BBT /cm 1.52 0.68~3.10 0.49 1.46 0.60~2.90 0.51 dib/dob 0.93 0.75~0.97 0.02 0.92 0.82~0.98 0.02 DBHIB/DBHOB 0.93 0.87~0.96 0.02 0.92 0.89~0.96 0.02 RBT 0.80 0.06~2.22 0.35 0.80 0.05~1.95 0.35 ① t：年龄Tree age; H：树高Tree height; DBH：胸径Diameter at breast height of outside bark; BBT：胸高处树皮厚度Bark thickness at breast height; dib/dob：任意高度处树皮率(去皮直径/带皮直径)Bark r atio(inside bark diameter/outside bark diameter)at any height; DBHIB/DBHOB：胸高处树皮率Bark ratio at breast height; RBT：相对树皮厚度Relative bark thickness.下同The same below.

通过查阅文献收集和自行建模共获得13个模型，其中包含2个自建模型(表 3)，用于本研究的模型拟合。依据模型因变量将其归纳为以下几种：1) 胸高处树皮厚度(BBT)；2) 任意高度处树皮厚度(BT)；3) 相对树皮厚度(RBT)；4) 去皮直径(dib)。

表 3 模型形式及归类^① Tab.3 Model forms and classification

表 3 模型形式及归类① Tab.3 Model forms and classification 模型Models 模型表达式Model expression 来源文献Model source 胸高处树皮厚度模拟Modeling BBT (1) BBT=α+β1DBH Williams et al., 2007 (2) BBT=α+β1DBH +β2H 王晓林等, 2011 (3) lnBBT=α+β1lnDBH Laasasenaho et al., 2005 (4) lnBBT=α+β1lnDBH +β2lnt Sonmez et al., 2007 (5) lnBBT=α+β1lnDBH +β2lnH+ β2lnt Laasasenaho et al., 2005 任意高度处树皮厚度模拟Modeling BT (6) BT=α+β1dob Loetsch et al., 1973 (7) BT=α+β1t+β2RH+β3dob 自建The present study 相对树皮厚度模拟Modeling RBT (8) RBT=α+β1RH2+β2H+β3RD 自建The present study (9) RBT=α+β1RDβ2 Johnson et al., 1987 去皮直径模拟Modeling dib (10) dib=β1dob (11) dib=α+β1dob Li et al., 2010 (12) dib2=β1dob2 Cole et al., 1972 (13) dib=β1dobβ2 Dolph, 1989 ① H：全树高Total tree height; BT：任意高度处树皮厚度Bark thickness at any height; RD：相对直径Relative diameter; RH：相对高度Relative height; α：常数项Constant term; β1、β2、β3：模型参数Parameters estimated.

运用最小二乘法对13个模型进行拟合，并对模型参数进行显著性检验(显著性水平0.05)。针对所有参数均显著的模型，进一步应用偏差(B)、绝对偏差(AB)、均方误差(MSE)和决定系数(R²)4个统计指标进行综合评价，其计算公式如下：

式中：d_i为第i个实测值；${{{\hat d}_i}}$为第i个预估值；d为实测值的平均值；n为参与模型拟合的实测值数目；m为模型参数的数目。

应用相对排序法(Poudel et al., 2013)分别计算各模型B、AB、MSE及R²的相对排序值，其计算公式为：

式中：Rank_i为模型i的相对排序值(i=1, 2, …, w)，其值越小说明模型拟合效果越好；w为参与排序的模型数目；S_i为模型i的统计指标值(分别为B、AB、MSE和R²)；S_min和S_max分别为S_i的最小值和最大值。

由于偏差均值存在负值，故取其绝对值计算相对排序值；绝对偏差和均方误差越小，模型拟合效果越好；而R²则是值越大拟合效果越好，为了保证判断标准一致，取值1-R²，使之统一到值越小模型拟合效果越好。最后计算4个统计指标的平均相对排序值，通过比较其大小即可判断模型拟合的优劣。

应用配对t检验方法检验模型的有效性，若预估值和实测值之间存在显著差异(P＜0.05)，则说明此模型拟合效果不佳。进一步对预估值和实测值差异不显著(P≥0.05) 的模型进行共线性和异方差性诊断。应用条件指数评价共线性大小，条件指数是模型自变量相关矩阵最大特征根和最小特征根的比值，如果条件指数大于1 000^0.5，则认为具有共线性(Myers, 1990)。通过图形检验(Cellini et al., 2012)、怀特检验等方法检验模型中是否存在异方差；若模型中存在异方差，通过变量变换予以修正(何晓群等, 2015)。

上述数据分析均采用R软件(Ver.3.2.2) 完成。

应用90株解析木的相关数据对13个模型进行拟合，其参数显著性检验结果(表 4)表明，模型(2) 和(5) 均有一个参数预估值与零差异不显著(P≥0.05)，将不参与进一步分析。对照表 3和4可以看出，胸高处树皮厚度拟合模型(2) 和(5) 中不显著者为自变量树高(H)或lnH的参数，是因为胸高处树皮厚度与树高无明显相关性的缘故(图 1)。

表 4 模型参数及其显著性检验^① Tab.4 Model parameters and its significance test

表 4 模型参数及其显著性检验① Tab.4 Model parameters and its significance test 模型Models β1 β2 β3 (1) 0.066* (2) 0.077* -0.019ns (3) 0.840* (4) 0.586* 0.360* (5) 0.745* -0.335ns 0.430* (6) 0.066* (7) 0.013* -0.281* 0.054* (8) 0.419* -0.005* 1.327* (9) 0.942* 1.069* (10) 0.926* (11) 0.933* (12) 0.857* (13) 0.896* 1.011* ① *和ns分别表示模型参数预估值在5%水平与零差异显著和不显著。下同。* and ns refer to significant and non-significant differences from zero for estimated value of parameter at 5% level, respectively.The same below.

图 1 树高与胸高处树皮厚度关系 Fig.1 The plot of tree height and bark thickness at breast height

模型拟合效果直接影响其预测结果的准确性。由表 5可知，11个模型的偏差除了模型(10) 和(12) 约为-0.03外，其余9个模型均接近0。拟合胸高处树皮厚度的3个模型，模型(1) 的绝对偏差最大(0.27)，模型(3) 和(4) 略小于0.20；拟合任意高度处树皮厚度的2个模型以及去皮直径的4个模型，其绝对偏差均约为0.24；拟合相对树皮厚度的2个模型，其绝对偏差约为0.14。所有模型均方误差(MSE)大小顺序与绝对偏差(AB)顺序基本一致。R²以模型(10)、(11) 和(12) 为最高，均接近1；而模型(1)、(3) 和(4) 的R²则在0.5以下。

表 5 模型统计指标计算及排序 Tab.5 Values of the fitting statistics and their ranks, and average ranks of the models

表 5 模型统计指标计算及排序 Tab.5 Values of the fitting statistics and their ranks, and average ranks of the models 模型 Models B AB MSE 1-R2 排序均值 Mean rank 值 Value 排序 Rank 值 Value 排序 Rank 值 Value 排序 Rank 值 Value 排序 Rank (1) -0.000 1.000 0.270 11.000 0.124 11.000 0.530 10.133 8.283 (3) 0.000 1.000 0.193 5.279 0.061 3.784 0.580 11.000 5.266 (4) -0.000 1.000 0.191 5.168 0.059 3.591 0.557 10.605 5.091 (6) 0.000 1.000 0.235 8.407 0.091 7.284 0.262 5.506 5.549 (7) -0.000 1.000 0.233 8.288 0.090 7.080 0.257 5.409 5.444 (8) 0.000 1.000 0.135 1.000 0.036 1.000 0.292 6.029 2.257 (9) -0.000 1.000 0.140 1.364 0.038 1.250 0.306 6.271 2.471 (10) -0.029 11.000 0.236 8.526 0.096 7.773 0.002 1.002 7.075 (11) -0.000 1.000 0.235 8.407 0.092 7.398 0.002 1.000 4.451 (12) -0.029 11.000 0.236 8.526 0.096 7.773 0.002 1.002 7.075 (13) -0.002 1.625 0.233 8.273 0.091 7.284 0.002 1.000 4.546 ① B：偏差Bias; AB：绝对偏差Absolute bias; MSE：均方误差Mean standard error; R2：决定系数Determination coefficient.

综合4项统计指标的排序值可以看出，11个模型中，模型(8) 和(9) 的综合排序值最低(2.2~2.4)，模型(1)、(10) 和(12) 排序值最大(7.0~8.2)，其他模型居中(4.4~5.5)。同类模型比较，拟合BBT的3个模型，模型(1) 拟合度最低，模型(3) 和(4) 的拟合效果几乎相同；拟合BT的2个模型(6) 和(7)，其效果差异不大；拟合RBT的模型(8) 略优于模型(9)；模拟去皮直径的4个模型，模型(11) 和(13) 的拟合效果优于模型(10) 和(12)。

应用27株解析木的相关数据对11个模型的预估值和实测值进行配对t检验，其中模型(9)、(12) 和(13) 的预估值和实测值之间存在显著差异(表 6)，因而予以剔除。对剩余的8个模型进行共线性和异方差性诊断。

表 6 模型参数配对t检验 Tab.6 The results of the student's paired t test for validating data

表 6 模型参数配对t检验 Tab.6 The results of the student's paired t test for validating data 模型 Models 配对分析差异性Paired differences 显著性水平 Significance level(P) 平均值 Mean 标准差 SD 均数标准误 SEM t (1) 1.451 0.681 0.131 11.070 0.000* (3) 0.000 1.400 0.269 0.000 1.000ns (4) 0.000 1.386 0.266 0.000 1.000ns (6) 0.000 1.413 0.076 0.000 1.000ns (7) 0.000 1.411 0.076 0.000 1.000ns (8) 0.000 1.411 0.076 0.000 1.000ns (9) 0.783 0.355 0.019 40.754 0.000* (10) 0.047 1.344 0.072 0.652 0.515ns (11) 0.000 1.413 0.076 0.000 1.000ns (12) 13.736 6.836 0.369 37.160 0.000* (13) 13.708 6.891 0.372 36.785 0.000*

在8个模型中，(1)、(3)、(6)、(10) 和(11)5个模型只有1个自变量，无需考虑共线性问题。模型(4) 的条件指数略大于1 000^0.5(表 7)，存在微弱共线性，模型(7) 和(8) 的条件指数小于1 000^0.5，不存在共线性(Myers, 1990)。

表 7 模型(4)、(7) 和(8) 的共线性检验 Tab.7 Multicollinearity of Models(4), (7) and(8)

表 7 模型(4)、(7) 和(8) 的共线性检验 Tab.7 Multicollinearity of Models(4), (7) and(8) 模型Models 条件指数Condition index (4) 44.61 (7) 13.74 (8) 27.68

从8个模型的残差散点图(图 2)可以看出，模型(1)、(3) 和(4) 拟合胸高处树皮厚度(BBT)具有相似的残差分布，基本在零附近，经怀特检验表明不存在异方差性问题；其余5个模型均存在异方差性影响。模型(6)、(10) 和(11) 通过取对数后回归，模型(7) 和(8) 对因变量开方后回归，变换后模型的残差散点图(图 3)以及评价指标(表 8)均有明显改善。

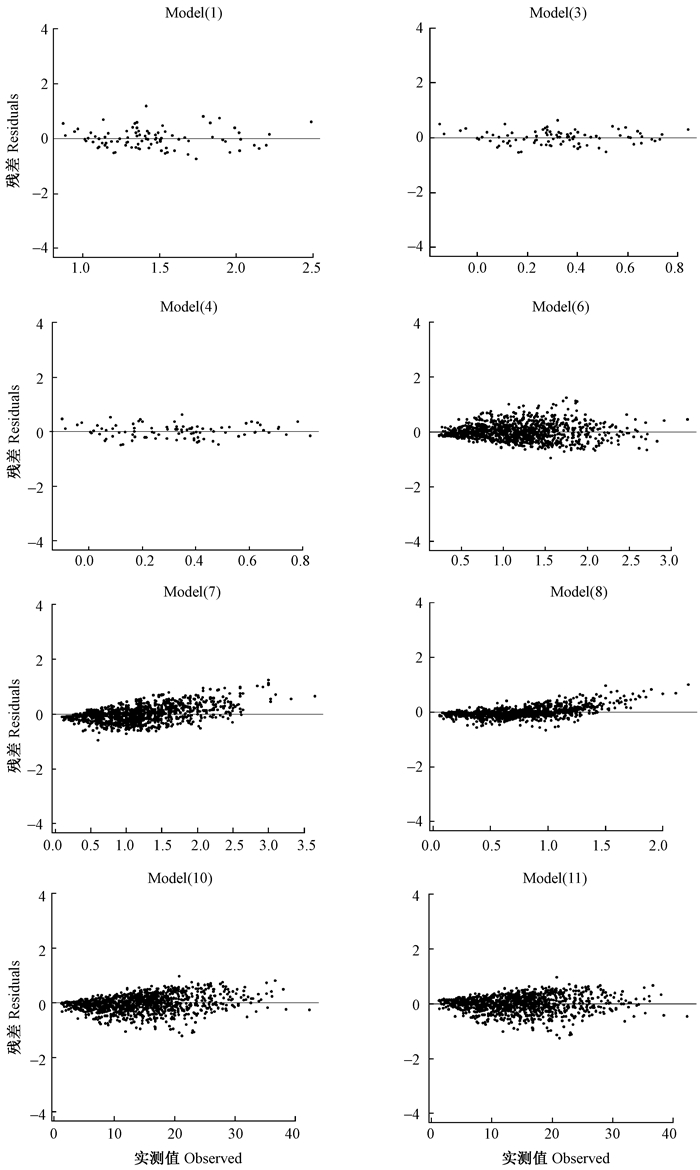
图 2 8个模型残差 Fig.2 Plot of residuals against observed values for 8 selected models

表 8 原模型与变换后模型统计指标对比 Tab.8 Statistics indices comparison between the original models and changed models

表 8 原模型与变换后模型统计指标对比 Tab.8 Statistics indices comparison between the original models and changed models 模型 Models 原模型Original model 变换后Changed model B AB MSE R2 B AB MSE R2 (6) 3.16e-18 0.234 8 0.091 3 0.737 8 -1.27e-17 0.215 2 0.071 7 0.798 8 (7) -1.39e-17 0.233 2 0.089 6 0.743 4 2.23e-18 0.113 1 0.019 4 0.754 8 (8) 9.56e-18 0.135 1 0.036 4 0.707 6 -3.4e-18 0.078 5 0.011 3 0.747 3 (10) -0.028 8 0.236 4 0.095 6 0.998 1 -0.006 0 0.026 7 0.001 2 0.999 9 (11) -1.6e-17 0.234 8 0.091 3 0.998 2 -3.6e-19 0.018 6 0.000 6 0.998 4

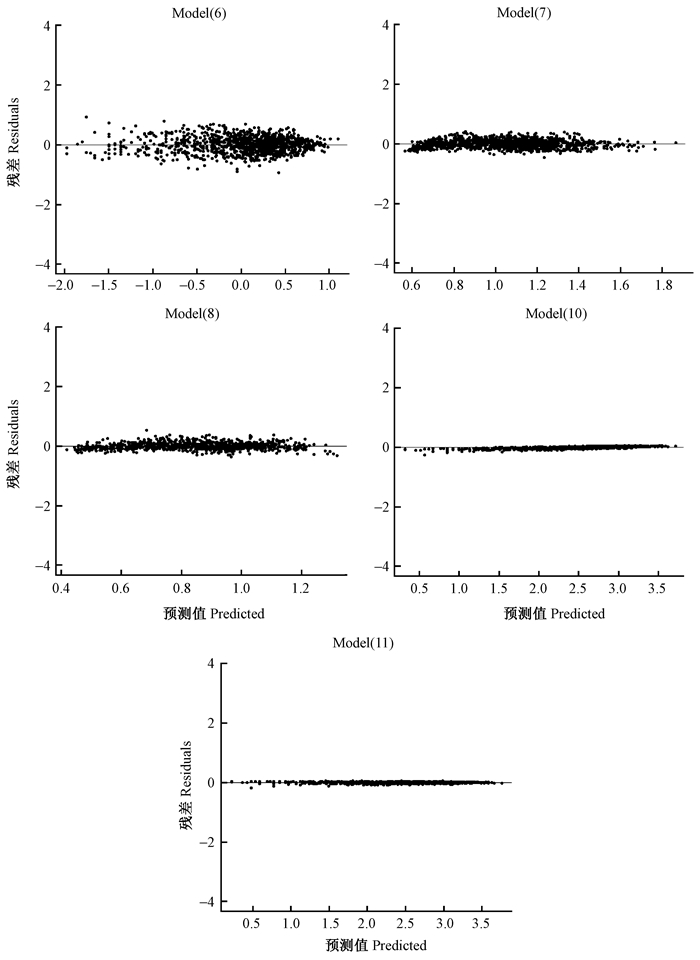
图 3 异方差修正后模型残差 Fig.3 Plot of residuals against fitted values for five models after correction of heteroskedasticity

模型评价既要考虑其拟合性能，又要兼顾其应用上简单可行。一些学者在拟合胸高处树皮厚度时通过增加自变量，如树高(王晓林等, 2011)、年龄(Sonmez et al., 2007)，或者通过自变量的对数转化(Laasasenaho et al., 2005; Sonmez et al., 2007)提高模型决定系数(R²)。本研究中，模型(4) 在模型(3) 的基础上增加年龄变量，提高了R²，模型(3) 对模型(1) 两边取对数却降低了R²；模型(1) 和(4) 增加树高项后分别转变为模型(2) 和(5)，但参数检验时树高项却不显著；模型(3) 和(4) 的拟合效果优于模型(1)，但模型(4) 存在微弱共线性。因此，选择模型(3) 预估西南桦胸高处树皮厚度。

对于同一株树而言，从基部到梢头，随着直径变小，其对应高度处树皮厚度亦减少(Laasasenaho et al., 2005)，模型(6) 和(7) 均反映了这种变化趋势。模型(7) 拟合后年龄与任意高度处树皮厚度呈正相关，亦符合生物学规律。2个模型均获得了较好的拟合效果，模型的异方差性亦得到修正，但从二者综合排序来看，模型(7) 略优于模型(6)。

Li等(2010)对7个针叶树种相对树皮厚度(RBT)的研究发现，其与RH²、H以及RD这些变量显著相关，本研究中模型(8) 拟合结果与此相一致。采用模型(9) 拟合相对树皮厚度，有学者认为β₂因树种而异，并不是固定的(Muhairwe, 2000；Li et al., 2010)。Johnson等(1987)对辐射松(Pinus radiata)的研究表明，β₂赋值4.0时拟合效果良好。对于西南桦而言，β₂约1.0时效果最好，但其预估值与实测值间差异显著。因此，选择模型(8) 用于西南桦相对树皮厚度的模拟，但从其残差散点图来看，当RBT>1时(多为胸径位置以下)，其残差均表现为正值，说明过低估计相对树皮厚度，可能与胸径以下树皮多翘起而难于准确测量有关，若建立分段方程或许模拟效果更好。

任意高度处的去皮直径是木材加工企业最关注的问题，预估给定树干高度处的去皮直径对于材积计算至关重要(Kozak, 2004)。利用带皮直径拟合去皮直径的4个模型中，当β₂等于1时，模型(13) 变为模型(10)，模型(12) 经两边开方处理亦变为模型(10)；模型(11) 是在模型(10) 的基础上增加了常数项。本研究中，模型(13) 中β₂=1.011≈1，模型(12) 中自变量的系数值开方即0.857 ≈0.926。通过综合排序、配对t检验分析，从4个模型中选择模型(11) 估算任意高度处去皮直径。实际应用时，2 m以下任意高度处树皮厚度通常容易测定，如利用打孔器即可取样测定，但高于2 m后树皮厚度则难以直接测定，可使用林分速测镜快速获取任意高度处带皮直径，亦可利用削度方程获取任意高度处带皮直径，进而利用模型(11) 拟合任意高度处去皮直径。

树皮厚度除了受林木年龄、树高、胸径等因子影响外，还受立地因子的影响。如阴坡的东方云杉(Picea orientalis)其胸径可以解释50%胸高处2倍树皮厚度变异，而阳坡则可以解释68%的变异(Sonmez et al., 2007)；生长于贫瘠山脊上的林木，树皮厚度往往大于生长在养分丰富山谷的林木(Jager et al., 2015)。本研究所选模型中未将立地因子作为解释变量，未来可考虑纳入立地因子，完善现有模型或新建模型，进一步研究树皮厚度变化规律。

本研究对胸高处树皮厚度、任意高度处树皮厚度、相对树皮厚度、去皮直径4个树皮厚度因子进行拟合，分别筛选出模型(3)、(7)、(8) 和(11)，这些模型拟合精度高，不存在共线性问题，异方差性不存在或通过变量变换可得到较好修正；且模型拟合所需基础数据，如年龄、胸径、树高在生产实践中易获取，任意高度处带皮直径则可通过林分速测镜快速测定。因此，上述模型颇具应用前景。