文章信息
- 邵卓平, 吴贻军, 黄天来, 王福利
- Shao Zhuoping, Wu Yijun, Huang Tianlai, Wang Fuli
- 风灾害下树木强度分析的理论、方法及应用
- Theory and Method of Tree Stem Strength Analysis Under Wind Disaster and Its Application
- 林业科学, 2017, 53(5): 170-178.
- Scientia Silvae Sinicae, 2017, 53(5): 170-178.
- DOI: 10.11707/j.1001-7488.20170520
-
文章历史
- 收稿日期:2015-10-30
- 修回日期:2017-02-25
-
作者相关文章
风灾害不仅会对森林生态系统的稳定性造成重大影响,也会给林业生产带来巨大的经济损失;城市行道树和园林古树在大风作用下可能发生断裂倒伏,对行人、游客的生命安全造成危害,对风载荷承受能力的研究是树木安全性评估和监测的重要内容之一。目前, 这方面的研究多集中于欧洲和美加等国,国内研究很少。常用的风载荷对树木破坏性的评估方法包括经验观察、统计学方法和力学方法。前期的大部分研究都依赖于经验观察和统计学方法,尽管能够定性描述风灾害的破坏程度,但却无法说明风载荷与树木强度之间的关系,对树木断裂风险性评估存在许多不确定性,因此,欧洲现在开始使用力学方法来评价风灾害对树木的破坏性。评价风载荷下树干弯曲断裂强度的准则是:σmax≤σultimate,即树干最外层的轴向应力σmax超过材料的极限应力σultimate时,树木就会发生破坏。已有很多学者采用拉力试验方法对此强度准则予以验证,并探索了影响树木断裂倒伏的因子(Petty et al., 1985;Peltola et al., 2000;James et al., 2006;Peltola,2006;Gardiner et al., 2008)。为了将上述准则用于研究风速与强度的关系,Mayer(1987)和Peltola等(1993)基于伯努力方程给出了计算风弯矩的公式:

|
(1) |
式中:Cd为树冠阻力系数;ρ为空气密度;v为高度z处的风速;A为树冠迎风面面积;h为风压中心高度。
应用材料力学公式σmax=M·32/πD3,即可建立树干弯曲正应力与风速之间的关系,再代入树木断裂强度准则,从理论上就可以得到树木能够承受的最大风速:

|
(2) |
但实际上,上述方法只是建立了树木强度与风速之间关系的一种概念,并不实用,因为在现实中树冠投影面积、风压中心高度和树冠阻力系数都是不便确定的量,因而很难获得真实的风载荷或风弯矩。在过去几十年里,已有很多学者试图通过在树上安装变形传感器测量树木变形来建立风速与最大应变之间的关系,但人们很快发现,通过固定安装的传感器来建立风速与最大应变之间的关系是很困难的,因为风的方向瞬息万变,只有当风向与传感器位于树的同侧时测得的才是最大变形量。也正是由于这个原因,多年来人们只能采用人工拉力模拟风载荷作用来研究树木变形与强度之间的关系(Peltola et al., 2000;Kane et al., 2008a),或以缩小的模型进行风洞试验(Vogel, 1989;Rudnicki et al., 2004;Vollsinger et al., 2005),或直接将树砍了绑在卡车上,以不同车速获得定向的大风来研究风速与树干应力之间的关系(Kane et al., 2008b)。
此外,目前树木力学测试技术较为单一,仅能测量树干弯曲的轴向线变形,但实际上,自然界中的树木多有偏冠,在风载荷作用下,其树干产生的是包括弯曲和扭转在内的组合变形。树干折断是风灾害中最常见的破坏类型,尤其在中龄林和成熟林中表现更为突出,但当树木偏冠严重时,树干在风力作用下会先发生扭转开裂使之丧失了整体刚度后再弯曲折断,而如何测量包括切应变在内的组合变形至今尚未解决。
鉴于此,本研究提出一种新的树木在风载荷下的强度测试方法,该方法不仅可以同时测量弯曲线应变和扭转切应变,而且所测得的最大应变仅取决于传感器测值而与风向无直接关系。由于该方法既不需要考虑树冠的面积大小和阻力系数,也不需要估算风压中心的高度和偏心距,只需在大风下应用该方法与风速仪相连,即可建立起树木最大应变或应力与风速之间的关系,因而为评估林区树木抗风害能力提供了一种直接、有效的方法。为了证明该方法的可行性,本研究先采用已知拉力模拟风载荷作用在树上,使树干同时产生弯曲与扭转组合变形,测得树干的轴向应变和扭转切应变后,再应用正交各向体虎克定律将应变转换至应力与理论计算结果相比较,最后应用该方法对实际风环境下的1株香樟(Cinnamomum camphora)树干进行实测,建立树干应力与风速平方之间的关系,并测算了该树可能发生断裂的临界风速以及破坏方式。
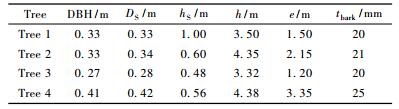
1 理论与方法 1.1 应变分析树木在大风作用下,树干或发生横弯变形(树冠不偏冠), 或发生弯扭组合变形(树冠偏冠)。所谓树干弯扭组合变形,即2个横断面之间的树干同时产生因弯矩导致的弯曲变形(图 1a)和由扭矩导致的扭转变形(图 1b),在弯曲与扭转复合变形作用下的树干应力分布如图 1c所示,当树干外层木质部处的最大弯曲正应力和扭转切应力达到树木极限应力时,树干就会发生弯曲断裂或扭转劈裂破坏。
|
图 1 树干变形和应力分布示意 Fig.1 Schematic diagram of the stem deformation a.弯曲变形Bending deformation;b.扭转变形Torsional deformation;c.弯曲正应力和扭转切应力分布方式The pattern of stresses in stem loaded in bending and torsion. |
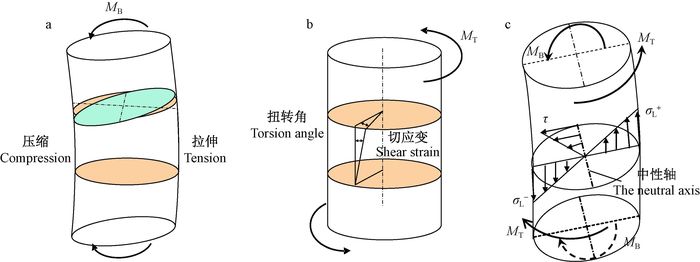
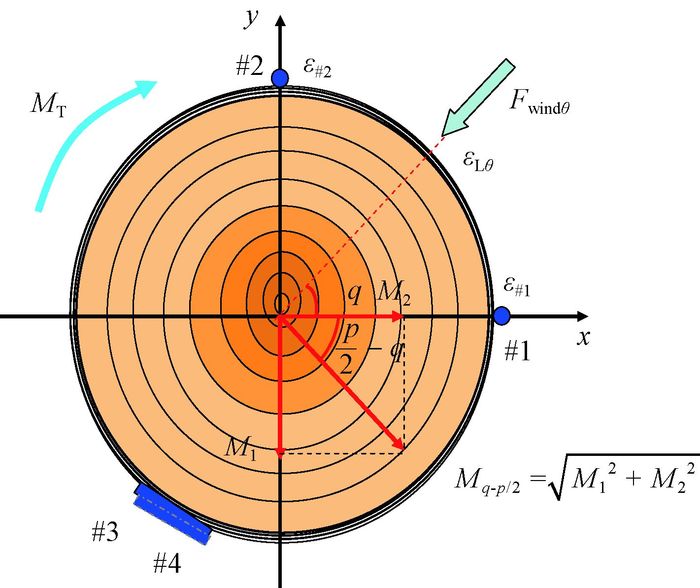
为了测试树木在风载荷作用下的弯扭组合变形,本研究采用4个位移传感器并设计了一套独特的布置方式,即将2个传感器#1、#2沿轴向安装在树干的正交直径上,另2个传感器#3、#4分别与轴向呈+45°、-45°交叉叠放安装,见图 2。
|
图 2 树干变形无损测量装置及安装方式示意 Fig.2 Non-destructive measurement method |
当立木受风向为θ的大风作用时(图 3),测得应变ε#1、ε#2、ε#3、ε#4,根据Mi=εiELDS3π/32推算弯矩M1、M2,再由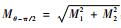
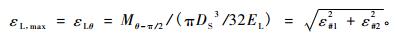
|
(3) |
|
图 3 风载荷与弯矩、扭矩及传感器位置的关系示意 Fig.3 Schematic diagram of the relationship among wind load, bending moment and sensor locations |
采用分离法计算树干扭转切应变,即将由正应力和切应力分别产生的形变分离并消除正应力的形变量。假设在树干外周木质部取一边长为a×a的单元体,其应力状态为如图 4a所示的在正应力和切应力共同作用下的应力状态,该应力状态可以分解为图 4b和图 4c 2种单一应力状态的叠加。

|
图 4 单元体在复合应力状态的变形(a)=轴向应力状态下的变形(b) +剪切应力状态下的变形(c) Fig.4 Analysis on stress state: the deformation of the cell cube under the state of combined stress(a)= the deformation under axial stress state(b) + the deformation under shear stress state(c) |
当树干上的传感器#3沿45°、#4沿-45°按“X”方式交叉安放时,2个传感器的应变测值由轴向正应力和扭转切应力共同引起,即:
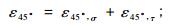
|
(4) |
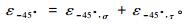
|
(5) |
并且,
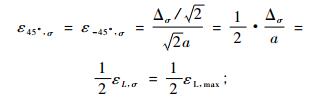
|
(6) |

|
(7) |
因此,
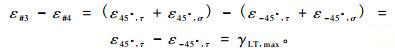
|
(8) |
式(3)、(8) 表明按照图 2所示方式布置传感器时,对于任意风向大风,最大应变仅与传感器测值有关,而与风向无直接关系。
需要说明的是,传感器两端的关节轴承是通过尼龙垫块安装在树干上的,所测得的传感器应变测值εsensor并非是树干外周木质部的应变值εwood,需作如下修正:
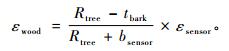
|
(9) |
式中:Rtree=DS/2为所测处树干半径;tbark为树皮厚度;bsensor为传感器中心线距树皮的距离。
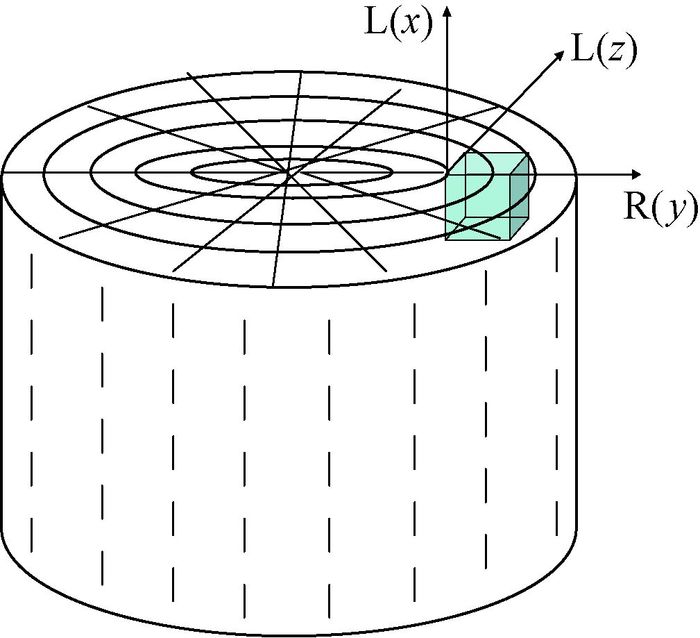
1.2 应力分析树干可视为圆柱对称弹性体,如果在距髓心一定距离处切取一小块矩形试样(图 5),并使其具有相互垂直的3个对称轴:L轴、R轴、T轴,即可近似视其为正交各向异性体。由于树干破坏是从最外层木质部开始的,因此该处应力单元体可视为平面应力状态,其应力与应变之间的关系如下:
|
图 5 树干的3个弹性主轴及立方单元体示意 Fig.5 Schematic diagram of the three elasticity principal axes and three mutually perpendicular planes of tree stem |

|
(10) |
式中:EL、ET、GLT、μTL、μLT是树木生材的5个弹性系数。
通常干燥木材的弹性系数可采用贴应变片的电测法测得,但电测法测试树木生材的弹性系数存在如下问题:1) 生材含水率高,不易涂胶贴片;2) 应变片树脂基的模量高于木材的模量,木材变形量传递到金属栅会有较大失真。因此生材弹性系数一般采用数字散斑法测定,即在试件表面制作人工散斑(喷漆),通过采集并计算试件变形前后2幅散斑图像上对应点在变形前后的几何位置获得点的变形信息,再通过计算机处理自动完成弹性系数的计算(邵卓平,2012)。本文香樟生材的弹性系数采用德国产Q-400数字散斑测试分析仪测得,结果为:EL=8 797 MPa(SD=244.437), ET=701 MPa(SD=63.786), GLT=804 MPa(SD=78.120), μTL=0.756, μLT=0.066。在弯扭组合变形下,树干外侧的周向应变εT=0,再略去μLT、μTL等小量,树干外围木质部的应力状态可简化为图 4a所示的平面应力状态,其应力与应变之间的关系可简化为σL=ELεL, τ=GLTγLT。于是,根据式(3)、(8) 即可得到由传感器应变测值计算树干外周上最大轴向应力和最大扭转切应力的表达式:
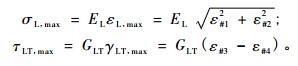
|
(11) |
树木拉力试验选择4株香樟树作为研究对象。使用的仪器有力传感器(2 t)、位移传感器(分辨率1 μm、量程±5 mm)和树木力学测试仪(自制,8通道,采样频率1~10 Hz)。
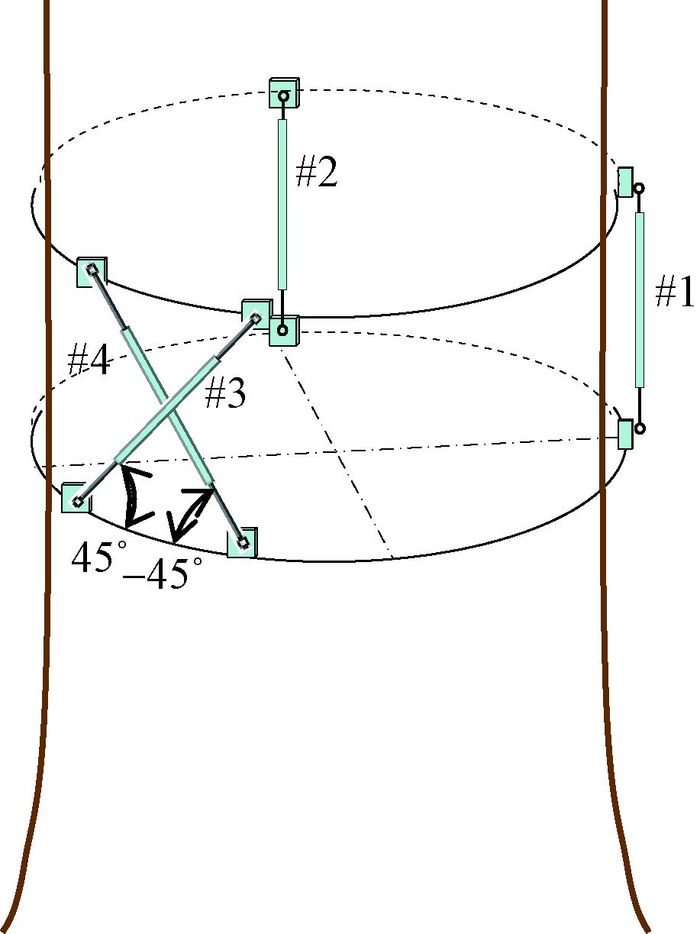
为了模拟偏冠树木在大风作用下产生的弯扭组合变形,在偏离树木主干中心的一根较粗枝干上系一接有力传感器的绳索,并通过力葫芦施加水平拉力,使树主干产生弯曲和扭转组合变形。设位移传感器在树干上的安装高度为hS(图 6),该处树干直径为DS,树皮厚为tbark。4株树的胸径DBH、施力点距所测树干截面的高度h、偏心距e等各参数值列在表 1中,拉力对应于所测树干截面所形成的弯矩M=Fh、扭矩MT=Fe,拉力值和传感器变形值由测试仪采集。
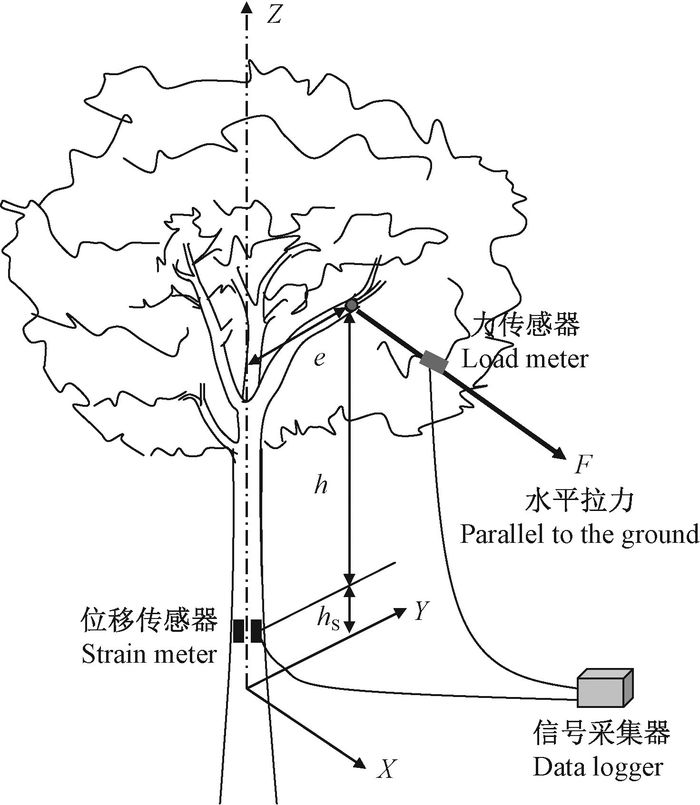
|
图 6 树木拉力试验示意 Fig.6 Schematic diagram of tree pulling test |
|
|
树木拉力试验中,Tree 1、Tree 2、Tree 3和Tree 4各重复做了7、4、4和16次,并且Tree 1、Tree 2、Tree 3上的传感器安装位置不变,以便于比较不同树干直径、测高h和偏心距e的测试结果;Tree 4则采用4种不同的传感器安装位置(图 7),类同于在一定的传感器安装方式下作用不同方向的拉力,以比较相对于传感器不同拉力方向对最大弯曲应变和扭转应变测试结果的影响,证明所测得的最大应变仅与传感器测值有关,而与风向无关。
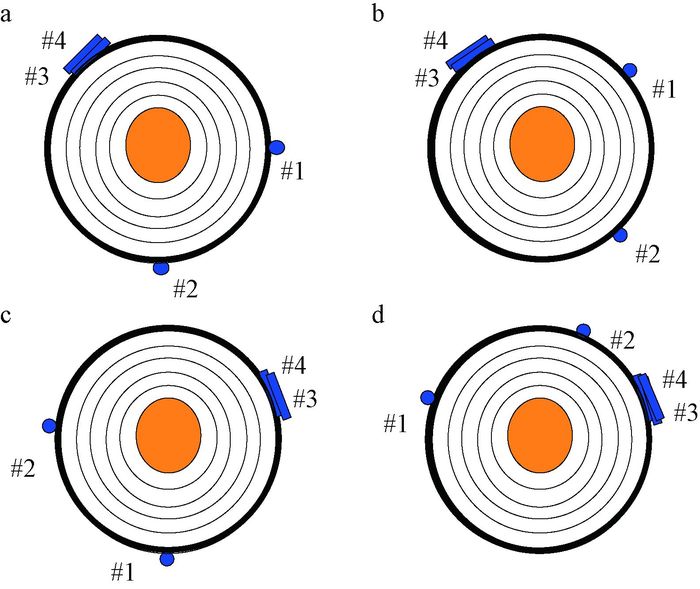
|
图 7 样树Tree 4的4种传感器布置位置 Fig.7 Four kinds of installation positions of strain meters on Tree 4 |
4株香樟树树干外周上的最大弯曲拉应变、最大扭转切应变与拉力之间的关系如图 8所示,可见均有很好的线性关系,而且,Tree 4的测试数据也表明相对于按图 2规则安装传感器,不同施力方向并不影响最大弯曲应变和最大扭转切应变的测量结果。
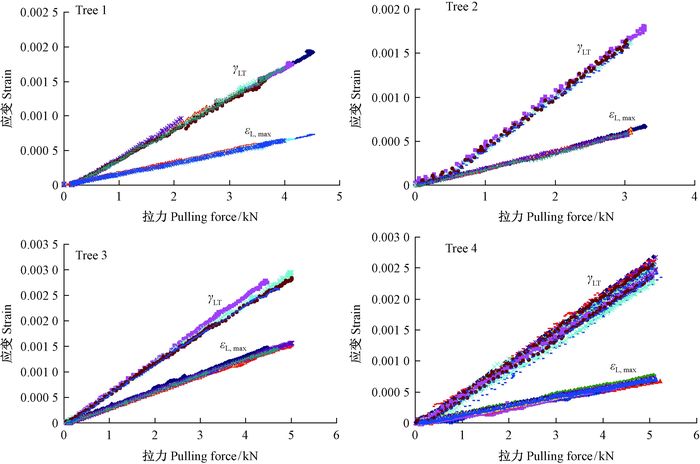
|
图 8 4株树树干外周上的最大弯曲拉应变、最大扭转切应变与拉力之间的关系 Fig.8 The relationships between maximum bending tensile strain, torsional shearing strain and the tension force at the periphery of the four trees |
根据材料力学知识,若已知立木所受的作用力或矩,则可从理论上计算传感器安装处树干木质部的最大轴向正应力和最大扭转切应力:
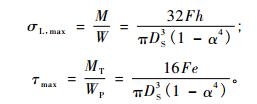
|
(12) |
式中:α=d/D为空洞树干的内外径比,当无空洞时α=0。传感器安装处的树干直径DS和施力点距所测树干截面的高度h、偏心距e见表 1。
按式(11) 计算的试验结果和按式(12) 计算的理论结果如图 9所示。由图 9可知:1) 不同粗细树干或不同载荷方向所得到的拉力与最大应力之间的关系与理论计算结果相符合,表明本试验方法用于测试树干的最大弯曲正应力与最大扭转切应力是可行的;2) 树干同一截面上的最大弯曲正应力和最大扭转切应力基本不受传感器安装位置的影响。如果说对最大弯曲正应力有点影响的话,那就是安装在压应力区的传感器测值会略高于安装在拉应力区的传感器测值,这是因为树木在弯曲过程中,当树体偏离原有平衡位置后所附加的重力弯矩导致的,这一现象与前人的研究结果(Petty et al., 1985;Mayer, 1987;Peltola et al., 1993)一致,由于该影响不大,可以忽略。
|
图 9 按式(11) 得到的试验结果和按式(12) 计算的理论结果 Fig.9 Experimental results calculated by Eq. (11) and theoretical results calculated by Eq.(12) |
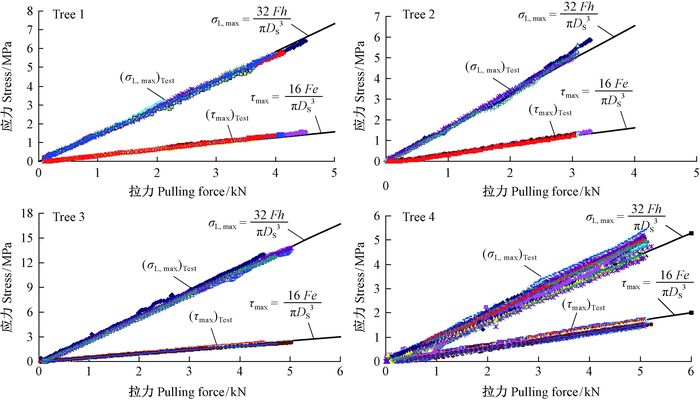
野外实地测试选择位于合肥市郊一处开阔地的香樟树,周边无建筑物,1号样树高8 m,胸径23.2 cm,偏冠,位移传感器安装在高0.5 m树干上,在1号样树迎风方向竖一风速风向仪,其探头高度与树冠中心高度大致相同,约5.5 m高,输出的风向系数从0—8—16—24—(32)0,分别代表北—东—南—西—北。依据风向测量数据,测试时的盛行风向系数在12~23之间(图 10)。
|
图 10 测试现场与风向系数示意 Fig.10 The prevailing wind coefficient and the spatial arrangement of the trees tested |
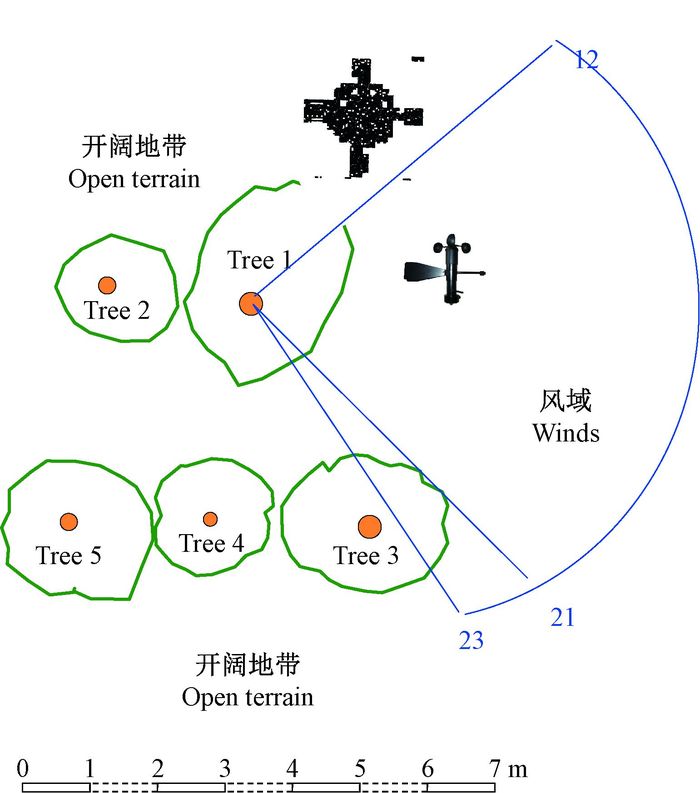
图 11是在某5 min时段上#1和#2传感器的应变关系曲线,可见随着风速风向变化,每个传感器的测值无时不在变化且毫无规律。但是按照图 2规则安装传感器所测得的最大弯曲正应变和扭转切应变与风速大小变化响应是一致的(图 12)。
|
图 11 5 min 1号样树干动态的摇摆行为 Fig.11 The dynamical sway motion of the trunk of Tree 1 in 5 min |

|
图 12 某5 min时段树干最大弯曲应变εLmax、扭转切应变γLT与风速的关系 Fig.12 The maximum bending strain εLmax and maximum torsional shear strain γLT plotted against wind speed in a certain 5 min |
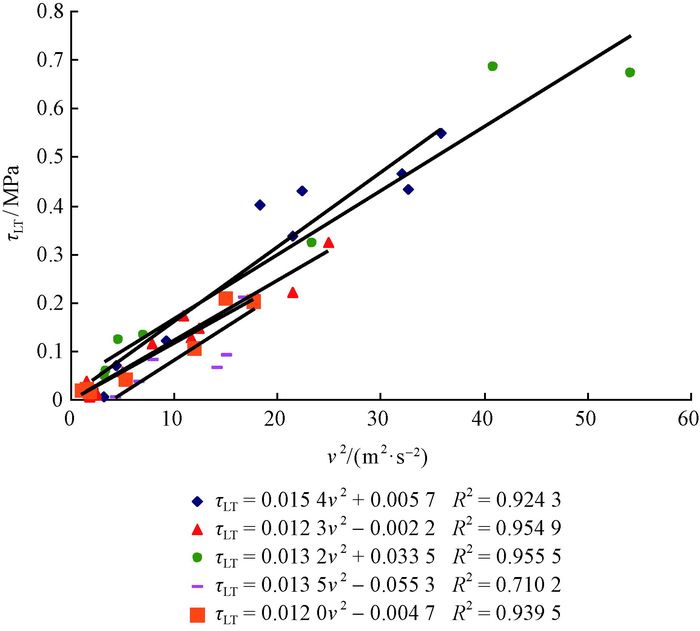
通常林木树干的自振频率在0.18~1.50之间(Hassinen et al., 1998;Baker, 1997;James et al., 2006),但由图 12所示风速时域曲线可以看出阵风的周期多在数十秒以上,因此,林木在大风作用下不会因共振导致树干破坏,而是在某次阵风中随着风速持续增大树干变形越来越严重,同时树冠的枝条枝叶会产生顺风势的剧烈抖动,直至风速达到临界值致使树干断裂。从风速时域图中找出若干组风速由小持续增大至最高后再逐渐变小的单波峰用来建立应力与风速平方的关系,结果发现最大弯曲应力、最大扭转切应力与风速平方之间具有明显的一致性线性关系(图 13、图 14),其斜率大致相等,且经差异性分析均不显著。线性关系式中的截距有一定差异性,其差异主要来源于分析时段的初应力值,但截距值与树木破坏应力值相比很小,可以忽略。于是,取系数的平均值即可得到该树干最大弯曲应力、扭转切应力与风速平方之间的关系:

|
图 13 5组单波峰阵风下的树干最大弯曲应力σL,max与风速平方之间的关系 Fig.13 The bending stresses σL, max plotted against the square of wind speed under 5 groups of single wave gust |
|
图 14 5组单波峰阵风下的树干最大扭转剪应力τLT与风速平方之间的关系 Fig.14 The torsional shear stresses τLT plotted against the square of wind speed under 5 groups of single wave gust |
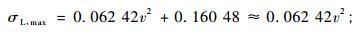
|
(13) |
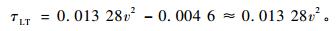
|
(14) |
将香樟生材的弯曲强度和顺纹剪切强度的试验值39.44 MPa(SD=7.36 MPa)和8.25 MPa(SD=0.63 MPa)代入上述关系式,即可得到1号样树发生弯曲破坏的临界风速为25.1 m·s-1,发生扭转破坏的临界风速为24.9 m·s-1。
按照风速等级划定标准,24.9 m·s-1为10级狂风,从8级大风起就会有树木折毁发生。可见作为内陆省份,预测该树发生断裂破坏的临界风速为10级狂风符合实情,并且在此临界条件下树干可能先发生扭转破坏。
4.2 讨论1) 其他波形时段上的应力与风速平方的关系 在风速时域图中,除了单波峰外,还有其他多种形态的波,如连续增强-减弱的多峰波形阵风等,通过对这些波形阵风时段上的应力与风速平方之间的关系进行分析,结果发现或线性相关性不明显,或有线性关系但不同时段内的斜率相差较大。这种差异性主要与树干的往复摇摆相关,如在风速增强过程中,恰遇树干回弹,由于惯性会使得这些时段上的树干变形与风速平方之间的关系存在较大的变异性甚至没有线性关系。所以,选择前期有一段无风或微风时段的单波峰,就能够获得斜率一致的应力与风速平方之间的线性关系。
2) 应力与风速一次方的关系 Kane(2008b)将立木捆绑在卡车上,通过改变车速来获得不同风速的定向风载荷,结果发现风速一次方与阻力和弯矩存在明显线性关系,据此推断立木树干上的弯曲应力与风速一次方呈正比。本研究发现,对于某一单波峰时段上的数据,也能够建立风速一次方与树干应力之间的线性关系,但不同组数据之间所获得的线性关系的斜率不同,且差异性较大,因此无法用于预测树木破坏的临界风速。
3) 其他统计参量 研究中也尝试了以一定时间间隔的众数、中位数、最大值以及风速平方关于时间的积分再开平方平均等参量来建立应力与风速之间的关系,但效果都不好。
4) 应用 基于本研究理论建立的强度分析技术,可以用来在线监测树木安全状况,也可以通过采集树木在大风中的响应信息,经分析软件评估林区树木能够承受的最大风速,并实现“只要经历一次,即可做出诊断”。当预报风速接近或大于树木的临界风速时,可以根据树木的破坏方式,指导人们采取相应的防护措施。因此,该技术对于保护森林资源、指导林业生产和防风林建设以及城市行道树与园林古树的安全防护都具有很好的应用价值。
5 结论本研究提出一种新的树木强度分析理论和方法,通过将4个位移传感器按一定规则布置,能够测量立木在风载荷作用下树干因弯扭组合变形所产生的最大弯曲线应变(应力)和扭转切应变(应力),并且最大应变(应力)测值仅取决于传感器测值而与风向无关。文中选用4株香樟树,采用可知力值的拉力试验对新方法进行了验证,结果证明试验与理论计算结果相符合,并且最大弯曲应变(或应力)和扭转切应变(或应力)的测值与施力方向无关。
由于新的树木强度分析方法不需要估算树冠面积、透风率以及树冠中心的高度、偏心距等许多难以确定的量,因而在实际风环境下应用本研究所建立的测试方法并与风速仪相连,即可建立起树木最大应变(应力)与风速之间的关系,为评估林区抗风灾害能力提供了一种直接、有效的方法。文章最后选择野外的1株香樟树进行了实际测试,建立了树干应力与风速平方之间的线性关系,并测算了树干发生破坏的临界风速以及破坏方式,测算结果符合实情。
| [] |
邵卓平. 2012. 植物材料断裂力学. 北京, 科学出版社: 22-25.
(Shao Z P. 2012. Fracture mechanics of plant material. Beijing, Science Press: 22-25. [in Chinese]) |
| [] | Baker C J. 1997. Measurements of the natural frequencies of trees. Journal of Experimental Botany, 48(5): 1125–1132. DOI:10.1093/jxb/48.5.1125 |
| [] | Gardiner B, Byrne K, Hale S, et al. 2008. A review of mechanistic modelling of wind damage risk to forests. Forestry, 81(3): 447–463. DOI:10.1093/forestry/cpn022 |
| [] | Haritos N, James K.2008.Dynamic response characteristics of urban trees. Proceeding of Australian Earthquake Engineering Society Conference. |
| [] | Hassinen A, Lemettinen M, Peltola H, et al. 1998. A prism-based system for monitoring the swaying of trees under wind loading. Agricultural and Forest Meteorology, 90: 187–194. DOI:10.1016/S0168-1923(98)00052-5 |
| [] | James K R, Haritos N, Ades P K. 2006. Mechanical stability of trees under dynamic loads. Americaan Journal of Botany, 93(10): 1522–1530. DOI:10.3732/ajb.93.10.1522 |
| [] | Kane B, Clouston P. 2008a. Tree pulling tests of large shade trees in the genus Acer. Arboriculture & Urban Forestry, 34(2): 101–109. |
| [] | Kane B, Pavlis M, Seiler J R, et al. 2008b. Crown reconfiguration and trunk stress in deciduous trees. Can J For Res, 38(6): 1275–1289. DOI:10.1139/X07-225 |
| [] | Mayer H. 1987. Wind induced tree sways. Trees, 1: 195–206. DOI:10.1007/BF01816816 |
| [] | Peltola H. 2006. Mechanical stability of trees under static loads. American Journal of Botany, 93(10): 1501–1511. DOI:10.3732/ajb.93.10.1501 |
| [] | Peltola H, Kellomäki S. 1993. A mechanistic model for calculating windthrow and stem breakage at stand edge. Silva Fennica, 27: 99–111. |
| [] | Peltola H, Kellomäki S, Hassinen A, et al. 2000. Mechanical stability of Scots pine, Norway spruce and birch:an analysis of tree pulling experiments in Finland. Forest Ecology and Management, 135: 143–153. DOI:10.1016/S0378-1127(00)00306-6 |
| [] | Petty J A, Swain C. 1985. Factors influencing stem breakage in conifers in high winds. Forestry, 58(1): 75–84. DOI:10.1093/forestry/58.1.75 |
| [] | Rudnicki M, Mitchell S J, Novak M D. 2004. Wind tunnel measurements of crown streamlining and drag relationships for three conifer species. Canadian Journal of Forest Research, 34(3): 666–676. DOI:10.1139/x03-233 |
| [] | Vogel S. 1989. Drag and reconfiguration of broad leaves in high winds. Journal of Experimental Botany, 40(8): 941–948. DOI:10.1093/jxb/40.8.941 |
| [] | Vollsinger S, Mitchell S J, Byrne K E, et al. 2005. Wind tunnel measurements of crown streamlining and drag relationships for several hardwood species. Canadian Journal of Forest Research, 35(5): 1238–1249. DOI:10.1139/x05-051 |
 2017, Vol. 53
2017, Vol. 53