文章信息
- 刘志理, 金光泽
- Liu Zhili, Jin Guangze
- 光学仪器法测定叶面积指数季节变化的误差分析
- Bias Analysis of Seasonal Changes of Leaf Area Index Derived from Optical Methods
- 林业科学, 2016, 52(9): 11-21
- Scientia Silvae Sinicae, 2016, 52(9): 11-21.
- DOI: 10.11707/j.1001-7488.20160902
-
文章历史
- 收稿日期:2015-07-25
- 修回日期:2016-06-27
-
作者相关文章
叶面积指数(leaf area index,LAI)是描述植被结构与功能特性的重要参数,也是量化植被对气候变化响应的关键因子(Dunn et al.,2015)。LAI通常定义为单位地面面积上总绿叶表面积的一半(Chen et al.,1992)。植被冠层的叶表面积与二氧化碳、水蒸气、氧气的交换息息相关(Law et al.,2001),总叶面积及其空间分布决定着冠层和大气间物质和能量的交换(Bréda,2003)。因此,LAI直接影响冠层中光合作用和蒸发散失的速率,也是模拟气候变化、生态系统生产力、碳、水循环的关键参数(Ryu et al.,2014)。
LAI的地面测定通常分为直接法和间接法。直接法主要包括: 破坏性取样法(Chen,1996)、异速生长方程法(Bréda,2003)和凋落物法(Eriksson et al.,2005)。直接法技术成熟、数据可靠,其测定值通常被认为是真实的LAI,经常用于校准其他方法测定值。然而,直接法测定费时费力,且仅依靠上述方法很难获得LAI的动态变化。间接法(光学仪器法)主要是借助光学仪器根据辐射传输定理,通过测定林冠结构参数反演得到LAI(Ross,1981),该方法方便、快捷,适于监测森林生态系统LAI的动态变化。其中,半球摄影法(digital hemispherical photography,DHP)和LAI-2000植物冠层分析仪(简称LAI-2000)被广泛应用于LAI测定(赵传燕等,2009; Thimonier et al.,2010)。但该方法由于自身局限性,其测量精度通常需要校准,因此,该方法测定的LAI通常认为是有效的LAI(effective LAI,Le)(Chen et al.,1992),而并非真实的LAI; 也有学者将光学仪器法直接测定的LAI称为有效植被面积指数(effective plant area index)(Fang et al.,2014),本研究中将光学仪器法直接测定的LAI称为Le。目前,影响光学仪器法测定LAI精度的误差源通常包括: 1)木质部(指树干和树枝),计算LAI时将木质部看作叶片而存在高估现象(Dufrêne et al.,1995); 2)集聚现象,计算LAI时假设林冠内的叶片随机分布,而多数林冠内的叶片存在一定的集聚现象,尤其针叶林,不仅存在冠层的集聚现象,还存在簇内集聚,忽略这种集聚效应会导致低估现象(Chen,1996); 3)相对于LAI-2000,自动曝光设置是造成DHP低估LAI的另一重要误差源,如在郁闭度较高的林分内设置为自动曝光,经常会因曝光过度而造成部分叶片颜色变白,使得光学仪器无法识别,进而低估LAI(Zhang et al.,2005)。
目前,多数学者通常用木质比例(α)来校正光学仪器因无法有效辨别木质部而产生的误差,测定α值的方法主要包括破坏性测量法(Chen,1996)、背景值法(Eriksson et al.,2005)以及基于Photoshop软件处理法(PS法)(Qi et al.,2013)等。破坏性测量法指通过砍伐树木来计算木质部的面积占总面积(包括木质部和叶片)的比例,该方法费时费力,且具有破坏性; 背景值法指将无叶期测定的LAI当作木质部产生的LAI,即木质指数(woody area index,WAI),将其当作背景值,然后利用有叶期测定的LAI直接减去该背景值来消除木质部对测定LAI的影响,该方法常用于落叶林,但不适用于常绿林; PS法是利用Photoshop软件将树干等木质部和树叶区分开,进一步计算α值,该方法同时适用于落叶林和常绿林(Qi et al.,2014)。集聚指数(ΩE)用来校正因忽略冠层水平上的集聚效应而产生的误差,通常基于Chen等(1995)提出的CC法来计算ΩE(Chen et al.,2006; Liu et al.,2015a)。针簇比(γE)用来校正因忽略针叶林内的簇内集聚效应而产生的误差,该参数主要通过实地采集样枝法获得(Chen,1996)。DHP测定LAI时因自动曝光设置产生的误差通常采用Zhang等(2005)建立的自动曝光状态下DHP与LAI-2000测定的LAI之间的相关关系来校正。
近年来利用不同方法测定LAI季节变化的研究越来越多。曾小平等(2008)对比分析CI-110冠层分析仪和异速生长方程法测定鹤山丘陵3种人工林LAI的季节变化; 童鸿强等(2011)利用LAI-2000测定华北落叶松(Larix principis-rupprechtii)人工林LAI的时空变化特征; 苏宏新等(2012)利用DHP,LAI-2000和CI-110冠层分析仪测定北京东灵山落叶阔叶林、华北落叶松林和油松(Pinus tabulaeformis)林LAI的季节变化; 郝佳等(2012)对比分析LAI-2000和凋落物法测定华北落叶松人工林落叶季节LAI的动态变化; Liu等(2015a)利用DHP,LAI-2000和直接法测定小兴安岭4种针阔混交林LAI的动态变化; Liu等(2015b)利用DHP和直接法测定帽儿山落叶阔叶混交林LAI的季节变化,并对影响DHP测量精度的误差源进行偏差分析。然而,如何量化影响DHP和LAI-2000测定针叶林LAI精度的误差源导致的偏差以及该偏差是否存在季节性差异的有待进一步研究。
红松人工林(常绿针叶林)和兴安落叶松(Larix gmelinii)人工林(落叶针叶林)是我国东北东部山区的主要人工林类型,本研究利用直接法和光学仪器法(DHP和LAI-2000)测定小兴安岭地区2种人工林LAI的季节变化(5—10月),并量化不同时期影响光学仪器法测定LAI精度的误差源(如: 木质部、集聚效应和自动曝光设置)导致的偏差,旨在为更系统、透彻地了解不同误差源对不同光学仪器法测定针叶林LAI季节变化产生的影响,为更准确地测定不同类型针叶林LAI季节变化提供参考和技术支持。
1 研究区概况野外调查在黑龙江省凉水国家级自然保护区(47°10′ 50″ N,128°53′ 20″ E)进行。保护区位于黑龙江省伊春市带岭区,地处小兴安岭南部达里带岭支脉的东坡,地形比较复杂,最高山脉海拔707 m。该区属温带大陆性季风气候,年均气温-0.3 ℃,最高年均气温7.5 ℃,最低年均气温-6.6 ℃; 年均降水量676 mm,降水集中在7月; 年积雪期130~150天,年无霜期100~120天(刘志理等,2014b)。
2 材料与方法 2.1 样地设置及数据采集分别设置3个20 m × 30 m的红松人工林和兴安落叶松人工林固定样地,物种组成见表 1。每个样地内随机设置6个凋落物收集器,其用径粗8 mm的铁丝和尼龙网围成(孔径1 mm,深0.5~0.6 m),网口为正方形,面积为0.5 m2,凋落网底离地面约0.5 m; 各凋落物收集器旁边固定3根30 cm长的PVC管,用于确保每次光学仪器在同一位置采集数据。
|
|
采用直接法和间接法测定2个林型样地2013年5月15日、6月1日、7月1日、8月1日、9月1日、10月1日及10月15日LAI的动态变化。其中,间接法在上述时期采集数据;直接法的数据采集分为展叶调查和凋落物收集: 展叶调查时期为2013年5月15日、6月1日、7月1日及8月1日,红松人工林内凋落物收集时期为2012年8月初—2014年8月初、兴安落叶松人工林内凋落物收集时期为2013年8月初—11月初,均在每月初收集1次。
2.2.2 直接法测定叶面积指数结合展叶调查和凋落物收集,直接测定红松人工林和兴安落叶松人工林LAI的季节变化,将该方法测定的LAI称为直接法测定的LAI。
展叶调查是对2个林型样地内主要树种的展叶情况进行定期监测,测定各树种不同时期的相对叶面积变化量。红松人工林内进行展叶调查的树种包括红松、云杉(Picea spp.)、兴安落叶松、白桦(Betula platyphylla)和水曲柳(Fraxinus mandshurica); 兴安落叶松人工林内包括兴安落叶松、色木槭(Acer mono)、水曲柳和紫椴(Tilia amurensis)。各阔叶树种分别选择3株样树,每株样树选择1个样枝,各调查时期测定样枝上所有叶片的叶长和叶宽,其乘积代替叶面积; 各针叶树种(包括常绿针叶和落叶针叶)也分别选择3株样树,每株样树上选择20个样枝,各调查时期测定样枝上所有针叶的叶面积,测定方案参照Liu等(2015a)。利用各时期样枝上的总叶面积除以样枝上最大时期的总叶面积即可得到各树种各时期的相对叶面积变化量。
利用落叶树种各时期相对叶面积变化量代替其LAI的相对变化量,该LAI的相对变化量再乘以叶面积最大时期(2林型均为8月初)的LAI(LAImax)即可得到5—8月初LAI的动态变化。累加8月初—11月初凋落物产生的LAI即可得到落叶树种的LAImax,同时能得到各时期的LAI。综合各树种LAI的动态变化即可得到兴安落叶松人工林5—10月LAI的季节变化。
常绿树种在展出新叶的同时,也存在叶凋落现象,因此,展叶调查测定的相对叶面积变化量只能代替1年中因展出新叶增加的总LAI(ΔLAI)的相对变化量,该相对变化量乘以ΔLAI即可得到常绿树种5—8月因展出新叶增加的LAI。因5月初和11月初,林冠中几乎不存在落叶树种的叶片,只存在常绿针叶,因此,各常绿针叶树种的ΔLAI可根据下式得到(刘志理等,2014b):
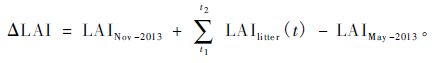
|
(1) |
式中,LAINov-2013和LAIMay-2013分别为2013年11月初和5月初常绿针叶树种林冠中的LAI,
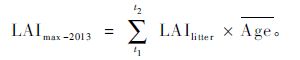
|
(2) |
式中,t1为2013年8月,t2为2014年8月,若计算LAImax-2012,t1为2012年8月,t2为2013年8月,Age为常绿针叶的平均存活周期(年)。红松人工林内的常绿针叶树种包括红松和云杉,其针叶平均存活周期分别为3.08年和3.91年(刘志理等,2014b)。
常绿针叶树种5月初的LAI加上各时期因展出新叶增加的LAI再减去期间因叶凋落减小的LAI,即可得到其5—8月LAI的动态变化; 利用LAImax减去8—11月各月因叶凋落减小的LAI,即得到8—10月LAI的动态变化。综合各树种即可得到红松人工林5—10月LAI的季节变化。
2.2.3 间接法(光学仪器法)测定叶面积指数采用DHP和LAI-2000 2种光学仪器测定红松人工林和兴安落叶松人工林LAI的季节变化。其中,DHP采用Winscanopy 2006冠层分析仪(Regent,Instruments,Quebec,Canada)采集图像。采集系统利用三脚架固定在离地面1.3 m处,为避免直射光对图像采集产生影响,每次图像采集在阴天或日出和日落前后进行,采集时相机保持水平,设置自动曝光状态。数据采用DHP 4.5.2软件处理,选取30°~60°天顶角。LAI-2000(LI-COR,Lincoln,USA)采集的数据与DHP采集时间、地点相同,采集数据时确保感应探头离地面1.3 m且保持水平,使用90°顶盖; 每次测量的初始值和结束值,即天空空白值均采自样地附近的防火瞭望塔上。数据采用C2000软件处理,选取3~4环(约30°~60°)天顶角。
光学仪器法测定的Le需要校准,以下公式常用于校准Le,以得到较为准确的LAI(Chen,1996):
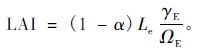
|
(3) |
式中,α为木质比例,即木质部的面积占总叶面积(包括木质部和叶片)的比率,用于校正木质部导致的误差; ΩE为集聚指数,用于校正冠层水平上的集聚效应; γE为针簇比(样簇内所有针叶的总叶面积与样簇投影面积的比率),用于校正针叶树种簇内的集聚效应,对于阔叶树种,通常γE=1.0。
红松人工林内常绿树种占较大比例,因此,利用PS法计算α值的季节动态,具体步骤参照Qi等(2013)。本研究忽略兴安落叶松人工林内常绿树种的影响,将其作为落叶林,采用PS法和背景值法计算α值的季节变化。背景值法是先利用DHP测定无叶期(5月初)的LAI,即WAI; 然后忽略木质部的季节性变异,WAI与DHP测定的有叶期LAI的比值即为α值。
红松人工林和兴安落叶松人工林采用相同的方法测定ΩE和γE的季节变化。ΩE值基于CC法,采用DHP-TRAC软件测定(Chen et al.,2006),选取40°~45°天顶角。通过实地采集样枝法测定2个林型的γE值,具体测定方法参照刘志理等(2014b)。
2.3.4 偏差分析对于红松人工林和兴安落叶松人工林,LAI-2000测定LAI的偏差主要源于α,ΩE和γE,即LAI=fLAI-2000(α,ΩE,γE),基于Topping(1972)的误差分析原理,各时期3个校正参数产生的偏差及其总偏差(δLAI)可由下式得到(Liu et al.,2015a):
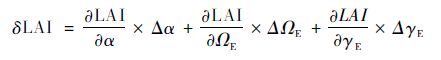
|
(4) |
式中,Δα=0-α,ΔΩE=1-ΩE,ΔγE=1-γE;其中α,ΩE及γE分别为不同时期各样点的均值。
相对于LAI-2000,DHP测定LAI的精度除受公式(3)中3个校正参数的影响外,还受自动曝光设置(其校正系数为AE,automatic exposure)的影响。因此,DHP测定LAI的偏差主要源于α,ΩE,γE和AE,即LAI=fDHP(α,ΩE,γE,AE),各时期4个参数产生的偏差及其总偏差(δLAI)可由下式得到(Liu et al.,2015a):
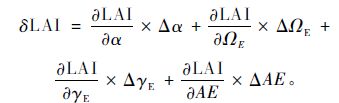
|
(5) |
式中,Δα,ΔΩE,ΔγE的计算方法同公式(4),ΔAE=1-AE,AE为不同时期各样点的均值,其值根据Zhang等(2005)建立的自动曝光状态下DHP测定的Le与LAI-2000测定的Le之间的相关关系(y=0.561 1x + 0.358 6,R2=0.77,x为LAI-2000测定的Le,y为自动曝光状态下DHP测定的Le)获得。此外,本研究采用PS和背景值2种方法测定兴安落叶松人工林α值的季节变化,而方法不同,各校正参数对DHP和LAI-2000测定LAI时产生的偏差存在差异,因此,对比分析了利用PS法和背景值法计算α值的情况下,不同参数产生偏差的变异情况。
将不同参数产生的总偏差(δLAI)能解释直接法和间接法测定的LAI间差异的比率称为解释率(explanation ratio,ER),根据下式计算:

|
(6) |
式中,Dif.为直接法测定的LAI-间接法测定的LAI; δLAI同公式(4)和(5)。
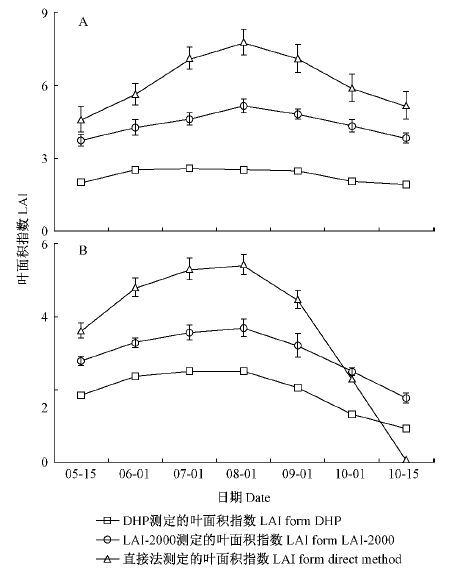
3 结果与分析 3.1 叶面积指数的季节变化由图 1可知,红松人工林内光学仪器法测定的LAI在不同季节均低于直接法测定值,其中DHP测定的LAI比直接法测定值低估55%~68%,LAI-2000的低估范围为19%~35%。兴安落叶松人工林内,DHP测定的LAI在5—10月初比直接法测定值低估43%~54%,但在10月中旬其测定值明显高于直接法; LAI-2000测定的LAI在5—9月比直接法测定值低估24%~28%,但在10月后明显高于直接法; 这主要源于在叶凋落末期光学仪器法测定LAI时误把林冠中的树干等木质部当作叶片而高估LAI。
|
图 1 不同方法测定红松人工林(A)和兴安落叶松人工林(B)叶面积指数的季节变化(平均值±标准偏差) Fig.1 The seasonal changes of LAI from different methods (mean ± SD) in Korean pine plantation (A) and Dahurian larch plantation ( B) |
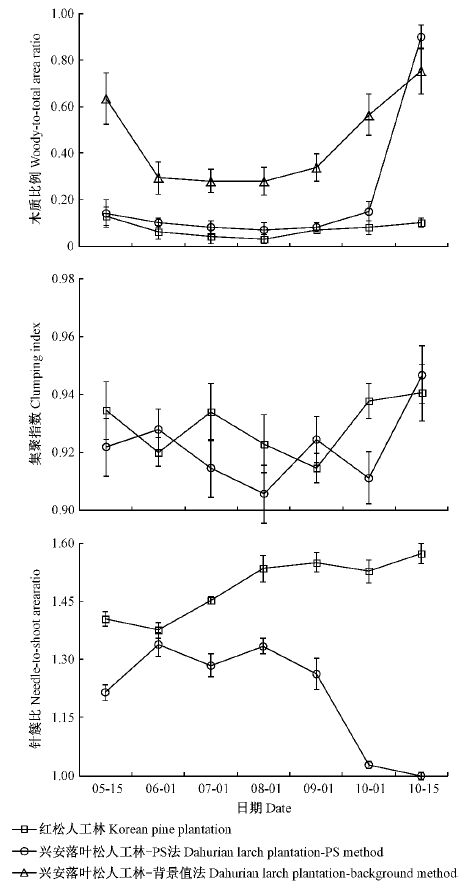
由图 2可知,基于PS法,红松人工林和兴安落叶松人工林内5—10月初的α值没有明显差异,其值均小于0.15,但在10月中旬兴安落叶松人工林内的α值为0.90明显高于红松人工林,主要源于该时期兴安落叶松人工林内叶凋落已几乎结束。兴安落叶松人工林内,基于背景值法测定的α值在5—10月初均高于PS法,整个调查周期内其值变化范围为0.28~0.75。红松人工林和兴安落叶松人工林内,ΩE值随季节变化波动范围较小,分别为0.91~0.94和0.90~0.95。红松人工林内γE值随季节变化波动较平缓,为1.38~1.57; 相对而言,兴安落叶松人工林内γE值随季节变化波动较大,范围为1.00~1.30,尤其9月后,γE值急剧下降,主要源于该时期兴安落叶松进入落叶高峰期,减小了计算林分水平上其γE值的权重。
|
图 2 红松人工林和兴安落叶松人工林内木质比例、集聚指数和针簇比的季节变化(平均值± 标准偏差) Fig.2 The seasonal changes of woody-to-total area ratio,clumping index and needle-to-shoot area ratio in Korean pine plantation and Dahurian larch plantation (mean ± SD) |
DHP和LAI-2000,木质部起到高估LAI的作用,而集聚效应和自动曝光设置的作用则相反(表 2和表 3)。红松人工林内,对于DHP,α值产生的偏差随季节变化其波动较平缓,范围为0.21~0.59,表明DHP在测定LAI时因无法有效辨别木质部导致最大高估0.59; 而对于LAI-2000,α值产生的偏差在不同时期差异较明显,波动范围为0.26~0.72。对于DHP,在不同时期,AE,γE和ΩE产生的偏差分别为-2.28~-1.29,-2.21~-1.13和-0.55~-0.26,表明DHP在测定LAI时因自动曝光设置、忽略簇内和冠层水平上的集聚效应而低估LAI的最大值分别为2.28,2.21和0.55,同时表明自动曝光设置和忽略簇内集聚效应均是造成DHP低估LAI的重要原因。对于LAI-2000,在不同时期,γE产生的绝对偏差大于ΩE,变化范围分别为-2.89~-1.41和-0.71~-0.34,表明簇内集聚效应是造成LAI-2000低估LAI的最重要因素。
|
|
|
|
兴安落叶松人工林内,对于DHP,在5—10月初,利用背景值法得到的α值产生的偏差明显大于PS法,其范围分别为1.26~2.31和0.33~0.51; 但在10月中旬,PS法计算的α值产生的偏差较大; LAI-2000也得到相似的结论(表 3)。对于DHP,在5—10月初,利用PS法计算α值的情况下,ΩE值产生的绝对偏差大于背景值法,其范围分别为-0.51~-0.18和-0.40~-0.09; 利用PS法γE值产生的绝对偏差大于背景值法,其范围分别为-1.05~-0.10和-0.82~-0.05; 而AE值产生的绝对偏差大于背景值法,其范围分别为-1.61~-0.57和-1.25~-0.29; 总体而言,利用PS法自动曝光设置是DHP测定LAI时最大的误差源,但采用背景值法时木质部是最大的误差源。对于LAI-2000,在5—10月初,利用PS法ΩE值产生的绝对偏差大于背景值法,其范围分别为-0.51~-0.24和-0.38~-0.12; 采用PS和背景值法γE值产生偏差的范围分别为-1.04~-0.14和-0.81~-0.07; 总体而言,在多数时期内,利用PS法γE值是LAI-2000测定LAI时最大的误差源,但背景值法下木质部是最大的误差源。
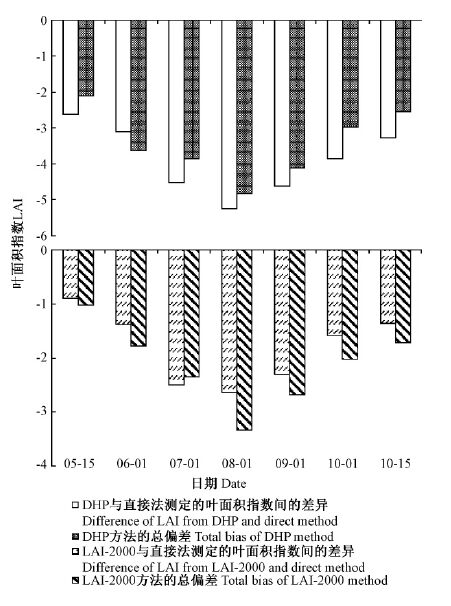
红松人工林内,不同时期4个参数(α,ΩE,γE和AE)产生的总偏差能解释DHP和直接法测定的LAI间差异的77%~92%,平均解释率为84%; 而考虑这些因素产生的总偏差后,在大部分时期(6月1日除外),仍存在低估LAI的现象(图 3),如10月1日低估程度最大,值为0.89,表明除α,ΩE,γE和AE是影响DHP测定LAI的因素外,仍最大有0.89的误差来自于其他不确定因素。相对而言,不同时期3个参数(α,ΩE和γE)产生的总偏差对LAI-2000和直接法测定的 LAI间差异的平均解释率为79%(范围为71%~94%); 而大部分时期(7月1日除外),总偏差的绝对值大于LAI-2000和直接法测定的LAI间差异的绝对值,如8月1日相差最大,值为0.70,表明考虑α,ΩE和γE对LAI-2000的影响后,其测定的LAI最多比直接法测定值高估0.70。
|
图 3 红松人工林内光学仪器法(DHP和LAI-2000)和直接法测定叶面积指数间的差异及光学仪器法产生的总偏差 Fig.3 The difference of LAI derived from both optical methods(DHP and LAI-2000)and direct method and the total bias of optical methods in Korean pine plantation 光学仪器法与直接法测定的叶面积指数间的差异=DHP/LAI-2000测定的有效叶面积指数-直接法测定的叶面积指数; DHP的总偏差指木质比例、集聚指数、针簇比和自动曝光设置产生偏差的总和; LAI-2000的总偏差指木质比例、集聚指数和针簇比产生偏差的总和。 The difference between optical LAI and direct LAI=DHP/LAI-2000 Le - direct LAI; Total bias of DHP equals the summation of the bias due to woody-to-total area ratio,clumping index,needle-to-shoot area ratio and automatic exposure setting; Total bias of LAI-2000 equals the summation of the bias due to woody-to-total area ratio,clumping index and needle-to-shoot area ratio. |
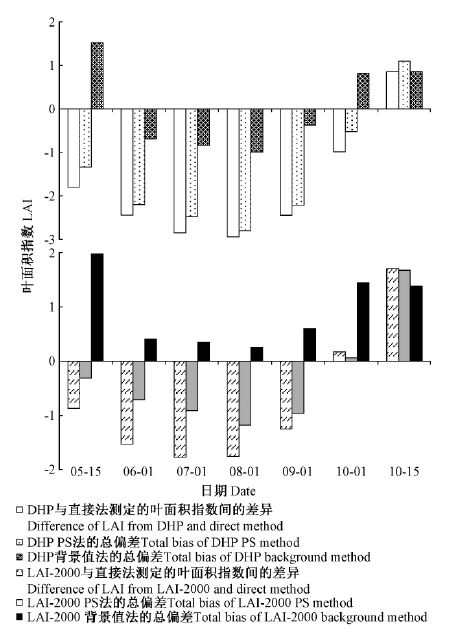
兴安落叶松人工林内,对于DHP和直接法测定的LAI间的差异,利用PS法不同时期不同参数产生总偏差的平均解释率为80%; 考虑这些偏差后,每个时期DHP测定的LAI仍存在一定程度的低估现象,如10月1日低估程度最大,值为0.46(图 4)。LAI-2000也得到类似结论,PS法下不同时期不同参数产生总偏差的平均解释率为65%,然而在7月1日,考虑总偏差后,LAI-2000测定的LAI比直接法最大低估0.86。相对而言,采用背景值法在不同时期不同参数产生的总偏差对DHP或LAI-2000与直接法测定的LAI间差异的平均解释率均低于5%,表明背景值法不适用于校正光学仪器法测定不同季节LAI时因无法有效辨别木质部而产生的误差。
|
图 4 兴安落叶松人工林内光学仪器法(DHP和LAI-2000)和直接法测定叶面积指数间的差异及光学仪器法产生的总偏差 Fig.4 The difference of LAI derived from both optical methods(DHP and LAI-2000)and direct method and the total bias of optical methods in Korean pine plantation 光学仪器法与直接法测定的叶面积指数间的差异=DHP/LAI-2000测定的有效叶面积指数-直接法测定的叶面积指数; DHP PS/背景值法的总偏差指PS/背景值法下木质比例、集聚指数、针簇比和自动曝光设置产生偏差的总和; LAI-2000 PS/背景值法的总偏差指PS/背景值法下木质比例、集聚指数和针簇比产生偏差的总和。 The difference between optical LAI and direct LAI=DHP/LAI-2000 Le- direct LAI; Total bias of DHP PS or background method equals the summation of the bias due to woody-to-total area ratio,clumping index,needle-to-shoot area ratio and automatic exposure setting using PS or background method; Total bias of LAI-2000 PS or background method equals the summation of the bias due to woody-to-total area ratio,clumping index and needle-to-shoot area ratio using PS or background method. |
近年来,结合叶生长季节的展叶调查和凋落物的收集来直接测定不同森林类型LAI季节变化的方法得到广泛地应用。如: Nasahara等(2008)通过该方法测定日本落叶阔叶林LAI的季节变化; Potithep等(2013)基于该方法分析日本落叶阔叶林不同季节LAI与植被指数(如NDVI)的相关关系; Liu等(2015a)以小兴安岭地区4种针阔混交林(常绿针叶和落叶阔叶混交)为例,在该方法的基础上进一步探讨了一种直接测定针阔混交林LAI季节变化的方法。这些研究结果为相对准确地测定不同森林类型LAI的季节变化奠定基础,尤其是可为校准不同光学仪器法测定的LAI提供参考标准。
本研究基于上述方法直接测定小兴安岭地区红松人工林和兴安落叶松人工林LAI的季节变化,并对比分析其与DHP和LAI-2000测定的LAI间的差异性。研究表明,在常绿针叶林(红松人工林)内,DHP和LAI-2000在不同季节测定的LAI均低于直接法测定值,分别低估55%~68%和19%~35%,且DHP测定值均低于LAI-2000。其他学者也得到类似结论,如: 曾小平等(2008)以马尾松(Pinus massoniana)和杉木(Cunninghamia lanceolata)为主的常绿针叶林内CI-110植物冠层分析仪测定的LAI明显低于异速生长方程法测定值; 刘志理等(2014a)发现在小兴安岭地区的谷地云冷杉林中DHP和LAI-2000在不同季节(5—11月)测定的LAI均低于直接法测定值,分别低估40%~48%和15%~26%; 苏宏新等(2012)发现在常绿针叶林内,DHP在7—10月测定的LAI均明显低于凋落物法测定值,且在5—10月,DHP测定值均低于LAI-2000测定值,然而LAI-2000测定值只是略低于凋落物法测定值,与本研究结果略有差异,可能源于LAI-2000计算LAI时选取的天顶角不以及林分的物种组成存在差异。
在落叶针叶林(兴安落叶松人工林)内,DHP和LAI-2000测定的LAI在整个生长季节的前期低于直接法测定值,但在叶凋落季节的后期出现相反趋势,主要源于凋落末期木质部对光学仪器法的干扰。Liu等(2015c)在帽儿山落叶阔叶林中也发现DHP测定的LAI在展叶初期和凋落末期高于直接法测定值,而其他时期出现相反趋势。这些研究表明,在落叶针叶林中,光学仪器法和直接法测定的LAI间的差异存在明显的季节性变异,但这种变异产生的原因国内报道尚少。
目前,影响DHP测定针叶林LAI精度的误差源通常包括: 木质部、冠层水平上的集聚效应、簇内水平上的集聚效应以及自动曝光设置; 相对而言,LAI-2000的误差源通常包括前3项。以往研究中多采用背景值法来校正落叶林内不同季节木质部(通常用α校正)对光学仪器法测定LAI时产生的误差(Dufrêne et al.,1995; Cutini et al.,1998)。随着叶片的生长和数量的增多,部分木质部被新生叶片遮挡,而后随叶片的凋落木质部重新暴露,若假设木质部对LAI的贡献率不存在季节性差异会带来一定误差,尤其是在叶茂盛期,背景值法会过高估计木质部对LAI的贡献率(Dufrêne et al.,1995; Barclay et al.,2000; Zou et al.,2009)。此外,背景值法不适用于常绿林,因此,本研究对比分析了背景值法和PS法量化木质部产生的误差。利用PS法计算α值,不仅适用于落叶林,而且适用于常绿林; 该方法能够相对有效地表明木质部对LAI贡献率的季节性变化,本研究结果也表明在红松人工林和兴安落叶松人工林内该方法均优于背景值法。
冠层水平上的集聚效应通常用集聚指数(ΩE)来校正,在2种针叶林内,其对DHP和LAI-2000测定LAI时产生的绝对偏差在大部分时期均小于其他误差源(表 2和表 3),表明冠层水平上的集聚效应对光学仪器法测定LAI的影响最小。相对而言,对于针叶林,忽略簇内水平上的集聚效应(通常用γE校正)会导致光学仪器法在测定LAI时的更大误差。尤其对于LAI-2000,在红松人工林内的每个时期,γE对LAI的贡献率远大于α和ΩE; 在兴安落叶松人工林的大部分时期也得到相同的结论,但在叶凋落末期(如10月中旬),γE产生的偏差为0,主要源于该时期兴安落叶松凋落几乎结束,致使整个林分的γE接近1.0(γE=1.0时,γE产生的偏差即为0)。这些研究结果表明,校正光学仪器法因忽略簇内集聚效应而产生的误差时,不仅要考虑针叶树种γE的季节性变异,而且要考虑林分的物种组成。
相对于LAI-2000,DHP测定LAI的精度还受曝光设置的影响(Zhang et al.,2005)。本研究中,在红松人工林和兴安落叶松人工林内的每个时期,DHP在自动曝光状态下测定的LAI均低于LAI-2000,这可能主要源于不正确的曝光方式。其他学者也得到类似结论,如: Zhang等(2005)报道在中高密度的林分内,DHP在自动曝光状态下测定的LAI比LAI-2000的测定值低估16%~71%。本研究结果还表明在红松人工林内的每个时期,自动曝光设置产生的绝对偏差高于其他误差源,而利用PS法计算α值时,在兴安落叶松人工林内的大部分时期也得到相同的结论(表 3); 只是在叶凋落末期(10月中旬)自动曝光产生的绝对偏差小于木质部,主要源于该时期大部分树种的叶凋落已基本结束,暴露了大部分木质部,增大了其对LAI的贡献率,这些结果表明在不同类型的针叶林内自动曝光设置均是影响DHP测定不同时期LAI精度的最大误差源。
5 结论在红松人工林内,经过校正后DHP比LAI-2000更适于测定LAI的季节变化,对于DHP,不同时期木质部、集聚效应及自动曝光产生的总偏差平均能解释DHP和直接法测定的LAI间差异的84%。兴安落叶松人工林内,利用PS法校正木质部产生误差的情况下,DHP比LAI-2000更适于测定LAI的季节变化,而背景值法并不适于校正DHP和LAI-2000测定LAI季节变化时木质部产生的误差。这些研究结果可为将来快速、准确地测定相似林型LAI的季节变化提供技术支持及参考方案。
| [1] |
郝佳, 熊伟, 王彦辉, 等. 2012. 华北落叶松人工林叶面积指数实测值与冠层分析仪读数值的比较和动态校正. 林业科学研究 , 25 (2) : 231–235.
( Hao J, Xiong W, Wang Y H, et al.2012. The comparison and dynamic calibration between the LAI values of a Larix principis-rupprechtii plantation determined by canopy scanner and littr-fall collection. Forest Research , 25 (2) : 231–235. [in Chinese] ) (  0) 0)
|
| [2] |
刘志理, 金光泽. 2014a. 基于光学仪器法测定谷地云冷杉林叶面积指数的季节变. 应用生态学报 , 25 (12) : 3420–3428.
( Liu Z L, Jin G Z.2014a. Estimation of seasonal changes in leaf area index based on optical methods in spruce-fir valley forest. Chinese Journal of Applied Ecology , 25 (12) : 3420–3428. [in Chinese] ) (  0) 0)
|
| [3] |
刘志理, 金光泽, 周明. 2014. 利用直接法和间接法测定针阔混交林叶面积指数的季节动态. 植物生态学报 , 38 (8) : 843–856.
( Liu Z L, Jin G Z, Zhou M.2014. Measuring seasonal dynamics of leaf area index in a mixed conifer-broadleaved forest withdirect and indirect methods. Chinese Journal of Plant Ecology , 38 (8) : 843–856. DOI:10.3724/SP.J.1258.2014.00079 [in Chinese] ) (  0) 0)
|
| [4] |
苏宏新, 白帆, 李广起. 2012. 3类典型温带山地森林的叶面积指数的季节动态:多种监测方法比较. 植物生态学报 , 36 (3) : 231–242.
( Su H X, Bai F, Li G Q.2012. Seasonal dynamics in leaf area index in three typical temperate montane forests of China:a comparison of multi-observation methods. Chinese Journal of Plant Ecology , 36 (3) : 231–242. DOI:10.3724/SP.J.1258.2012.00231 [in Chinese] ) (  0) 0)
|
| [5] |
童鸿强, 王玉杰, 王彦辉, 等. 2011. 六盘山叠叠沟华北落叶松人工林叶面积指数的时空变化特征. 林业科学研究 , 24 (1) : 13–20.
( Tong H Q, Wang Y J, Wang Y H, et al.2011. The Spatio-Temporal variation of LAI of the Larix principis-rupprechtii plantation ecosystems at Diediegou of Liupan Mountains of Northwest China. Forest Research , 24 (1) : 13–20. [in Chinese] ) (  0) 0)
|
| [6] |
ZengX P, ZhaoP, RaoX Q, 等. 2008. Measurement of leaf area index of three plantations and their seasonalchanges in Heshan hilly land. Journal of Beijing Forestry University , 30 (5) : 33–38.
( 0) 0)
|
| [7] |
赵传燕, 沈卫华, 彭焕华. 2009. 祁连山区青海云杉林冠层叶面积指数的反演方法. 植物生态学报 , 33 (5) : 860–869.
( Zhao C Y, Shen W H, Peng H H.2009. Methods for determining canopy leaf area index of Picea crassifolia forest in Qilian mountains,China. Chinese Journal of Plant Ecology , 33 (5) : 860–869. [in Chinese] ) (  0) 0)
|
| [8] |
Barclay H, Trofymow J, Leach R.2000. Assessing bias from boles in calculating leaf area index in immature Douglas-fir with the Li-Cor canopy analyzer. Agricultural and Forest Meteorology , 100 (2-3) : 255–260.
DOI:10.1016/S0168-1923(99)00091-X ( 0) 0)
|
| [9] |
Bréda N J J.2003. Ground-based measurements of leaf area index:a review of methods,instruments and current controversies. Journal of Experimental Botany , 54 (392) : 2403–2417.
DOI:10.1093/jxb/erg263 ( 0) 0)
|
| [10] |
Chen J M.1996. Optically-based methods for measuring seasonal variation of leaf area index in boreal conifer stands. Agricultural and Forest Meteorology , 80 (2/4) : 135–163.
( 0) 0)
|
| [11] |
Chen J M, Black T A.1992. Defining leaf area index for non-flat leaves. Plant,Cell and Environment , 15 (4) : 421–429.
DOI:10.1111/pce.1992.15.issue-4 ( 0) 0)
|
| [12] |
Chen J M, Cihlar J.1995. Plant canopy gap-size analysis theory for improving optical measurements of leaf-area index. Applied Optics , 34 (27) : 6211–6222.
DOI:10.1364/AO.34.006211 ( 0) 0)
|
| [13] |
Chen J M, Govind A, Sonnentag O, et al.2006. Leaf area index measurements at Fluxnet-Canada forest sites. Agricultural and Forest Meteorology , 140 (1/4) : 257–268.
( 0) 0)
|
| [14] |
Cutini A, Matteucci G, Mugnozza G.1998. Estimation of leaf area index with the Li-Cor LAI 2000 in deciduous forests. Forest Ecology and Management , 105 (1/3) : 55–65.
( 0) 0)
|
| [15] |
Dufrêne E, Bréda N.1995. Estimation of deciduous forest leaf area index using direct and indirect methods. Oecologia , 104 (2) : 156–162.
DOI:10.1007/BF00328580 ( 0) 0)
|
| [16] |
Dunn R E, Stromberg C A E, Madden R H, et al.2015. Linked canopy,climate,and faunal change in the cenozoic of Patagonia. Science , 347 (6219) : 258–261.
DOI:10.1126/science.1260947 ( 0) 0)
|
| [17] |
Eriksson H, Eklundh L, Hall K, et al.2005. Estimating LAI in deciduous forest stands. Agricultural and Forest Meteorology , 129 (1/2) : 27–37.
( 0) 0)
|
| [18] |
Fang H L, Li W J, Wei S S, et al.2014. Seasonal variation of leaf area index (LAI) over paddy rice fields in NE China:intercomparison of destructive sampling,LAI-2200,digital hemispherical photography (DHP),and AccuPAR methods. Agricultural and Forest Meteorology , 198-199 : 126–141.
DOI:10.1016/j.agrformet.2014.08.005 ( 0) 0)
|
| [19] |
Law B E, Cescatti A, Baldocchi D D.2001. Leaf area distribution and radiative transfer in open-canopy forests:implications for mass and energy exchange. Tree Physiology , 21 (12/13) : 777–787.
( 0) 0)
|
| [20] |
Liu Z L, Chen J M, Jin G Z, et al.2015a. Estimating seasonal variations of leaf area index using litterfall collection and optical methods in four mixed evergreen-deciduous forests. Agricultural and Forest Meteorology , 209 : 36–48.
( 0) 0)
|
| [21] |
Liu Z L, Wang C K, Chen J M, et al.2015b. Empirical models for tracing seasonal changes in leaf area index in deciduous broadleaf forests by digital hemispherical photography. Forest Ecology and Management , 351 : 67–77.
DOI:10.1016/j.foreco.2015.05.005 ( 0) 0)
|
| [22] |
Liu Z L, Wang X C, Chen J M, et al.2015c. On improving the accuracy of digital hemispherical photography measurements of seasonal leaf area index variation in deciduous broadleaf forests. Canadian Journal of Forest Research , 45 (6) : 721–731.
DOI:10.1139/cjfr-2014-0351 ( 0) 0)
|
| [23] |
Nasahara K N, Muraoka H, Nagai S, et al.2008. Vertical integration of leaf area index in a Japanese deciduous broad-leaved forest. Agricultural and Forest Meteorology , 148 (6/7) : 1136–1146.
( 0) 0)
|
| [24] |
Potithep S, Nagai S, Nasahara K N, et al.2013. Two separate periods of the LAI-VIs relationships using in situ measurements in a deciduous broadleaf forest. Agricultural and Forest Meteorology , 169 : 148–155.
DOI:10.1016/j.agrformet.2012.09.003 ( 0) 0)
|
| [25] |
Qi Y J, Jin G Z, Liu Z L.2013. Optical and litter collection methods for measuring leaf area index in an old-growth temperate forest in northeastern China. Journal of Forest Research , 18 (5) : 430–439.
DOI:10.1007/s10310-012-0370-1 ( 0) 0)
|
| [26] |
Qi Y J, Li F R, Liu Z L, et al.2014. Impact of understorey on overstorey leaf area index estimation from optical remote sensing in five forest types in northeastern China. Agricultural and Forest Meteorology , 198 : 72–80.
( 0) 0)
|
| [27] | Ross J.1981.The radiation regime and architecture of plant stands.Kluwer Academic Publishers,The Hague.391. |
| [28] |
Ryu Y, Lee G, Jeon S, et al.2014. Monitoring multi-layer canopy spring phenology of temperate deciduous and evergreen forests using low-cost spectral sensors. Remote Sensing of Environment , 149 : 227–238.
DOI:10.1016/j.rse.2014.04.015 ( 0) 0)
|
| [29] |
Thimonier A, Sedivy I, Schleppi P.2010. Estimating leaf area index in different types of mature forest stands in Switzerland:a comparison of methods. European Journal of Forest Research , 129 (4) : 543–562.
DOI:10.1007/s10342-009-0353-8 ( 0) 0)
|
| [30] | Topping J.1972.Errors of observation and their treatment.Chapman and Hall,London,England. |
| [31] |
Zhang Y, Chen J M, Miller J R.2005. Determining digital hemispherical photograph exposure for leaf area index estimation. Agricultural and Forest Meteorology , 133 (1/4) : 166–181.
( 0) 0)
|
| [32] |
Zou J, Yan G, Zhu L, et al.2009. Woody-to-total area ratio determination with a multispectral canopy imager. Tree Physiology , 29 (8) : 1069–1080.
DOI:10.1093/treephys/tpp042 ( 0) 0)
|
 2016, Vol. 52
2016, Vol. 52

