木材可视为正交各向异性材料，主向的材料弹性常数为E_L，E_R，E_T，G_LR，G_LT，G_RT，μ_LR，μ_LT，μ_RT，μ_RL，μ_TL和μ_TR。但是, 在这6个泊松比中只有3个是独立的, 即μ_LR，μ_LT和μ_RT, 而另外3个泊松比μ_RL，μ_TL和μ_TR可通过柔度矩阵对称性由主向弹性模量E_L，E_R，E_T和主向泊松比μ_LR，μ_LT，μ_RT计算得出。因此，木材只具有9个独立的主向弹性常数, 即弹性模量、剪切模量和泊松比各3个(谭守侠等，2007；孙友富，1999)，本文仅对μ_LR，μ_LT和μ_RT的测试进行探讨。泊松比是轴向拉伸(压缩)曲线在线性阶段的横向应变与纵向应变比值的绝对值(刘鸿文，1983)。从定义上看, 测定泊松比的试件是经受单向应力作用的, 而与之应力相对应的应变还应处于拉伸(压缩)曲线的直线段范围。

静态测试木材泊松比常用轴向拉伸或轴向压缩法。范文英等(1995)以应变片为传感器，采用轴向拉伸法测试了规格为200 mm×50 mm×10 mm定向刨花板(OSB)试件的弹性模量和泊松比，结果发现实测OSB试件泊松比的分散性大，其变异系数为18.5%～35%，并与试样的取向有关。龚蒙(1995)采用轴向压缩法测试了尺寸为30 mm×30 mm×60 mm马尾松(Pinus massoniana)试件的顺纹抗压弹性模量，结果发现顺纹径面和弦面试件抗压弹性模量测试值的分散性较大，其变异系数分别为30.9%和33.5%。由于采用轴向拉伸或轴向压缩法测试材料的泊松比需要在试验机上进行，因此存在着“加载对中”的问题；且采用轴向压缩法时还存在试验机压头与试件表面接触状态的问题。显然，采用轴向拉伸或轴向压缩法测试木材泊松比的试验条件要求苛刻，实现较为困难，难以保证其测试精度，这就是造成测试木材泊松比分散性大的因素之一。上述采用轴向拉伸或轴向压缩法测定实木、木质复合材料泊松比的工作属于静态测试范畴。鉴于寻求一种动态测试木材泊松比的方法为本文的宗旨，故本研究给出了动态测试木材泊松比的理论依据，并提出了一种简单易行且能提高测试精度的动态测试木材泊松比的方法。若根据悬臂板的一阶弯曲模态测定其泊松比，则首先要清楚悬臂板作一阶弯曲振动时，其内的应力除有沿板轴向的正应力σ_x外，还有横向正应力σ_y，即悬臂板作一阶弯曲振动时, 其内应力属于不均匀的二向平面应力。其次，板试件在作模态振动时，各点的应力或应变之间相差一个常数因子，而给出的应力或应变值本身又是没有实际工程意义的。通过对悬臂板一阶弯曲模态的应力和应变分析发现，板内的横向应力σ_y都很小，并且沿板中心线从正值单调减小到负值，即存在一个位置x₀，在这个位置上σ_y=0，也就是说悬臂板在作一阶弯曲振动时，板内存在一个区域，在这个区域内悬臂板近似处于单向应力状态，这一点正符合泊松比定义的条件。再次，悬臂板在作模态振动时，其内各点应变之间虽相差一个常数因子，但这并不妨碍用其测定泊松比，因为泊松比是横向应变与纵向应变的比值，相差一个常数因子在求其比值时也就约去了。因此，借助于悬臂板的一阶弯曲模态(傅志方，2002), 将应变花粘贴在适当位置测试泊松比亦是可行的。

本文将从木材的应力-应变关系(胡克定律)和悬臂板一阶弯曲模态的应力、应变分析2方面阐述动态测试木材泊松比的原理和方法，并且其测试结果的正确性还得到了静态试验的验证。值得一提的是，本文用于测试木材泊松比的原理和方法同样也适用于单向复合材料(马功勋，1996)，如典型复合材料0°单向板，只要调整应变花的粘贴位置即可。

1 测试原理 1.1 木材的应力-应变关系

悬臂板作一阶弯曲振动时，板内的应力处于二向平面应力状态。

对于悬臂的弦切面木板，L，T向应变ε_L, ε_T与应力σ_L, σ_T的关系可表示为：

$ \left\{ \begin{array}{l} {\varepsilon _{\rm{L}}}\\ {\varepsilon _{\rm{T}}} \end{array} \right\}=\left[ {\begin{array}{*{20}{c}} {\frac{1}{{{E_{\rm{L}}}}}}&{ - \frac{{{\mu _{{\rm{TL}}}}}}{{{E_{\rm{T}}}}}}\\ { - \frac{{{\mu _{{\rm{LT}}}}}}{{{E_{\rm{L}}}}}}&{\frac{1}{{{E_{\rm{T}}}}}} \end{array}} \right]\left\{ \begin{array}{l} {\sigma _{\rm{L}}}\\ {\sigma _{\rm{T}}} \end{array} \right\}. $

(1)

根据柔度矩阵对称性，有E_Tμ_LT=E_Lμ_TL。μ的下标第1个字母表示拉伸方向，第2个字母表示收缩方向，μ_TL表示沿T方向拉伸引起L方向收缩，μ_TL=-ε_L/ε_T。

从式(1)解出σ_L和σ_T，有：

$ \begin{array}{l} {\sigma _{\rm{L}}}=\frac{{{E_{\rm{L}}}}}{{1 - {\mu _{{\rm{LT}}}}{\mu _{{\rm{TL}}}}}}\left({{\varepsilon _{\rm{L}}}+{\mu _{{\rm{TL}}}}{\varepsilon _{\rm{T}}}} \right);\\ {\sigma _{\rm{T}}}=\frac{{{E_{\rm{T}}}}}{{1 - {\mu _{{\rm{LT}}}}{\mu _{{\rm{TL}}}}}}\left({{\varepsilon _{\rm{T}}}+{\mu _{{\rm{LT}}}}{\varepsilon _{\rm{L}}}} \right). \end{array} $

当σ_T=0时，-ε_T/ε_L=μ_LT，即μ_LT=-ε_T/ε_L。

同理，通过对径切面的L，R向应变ε_L, ε_R与应力σ_L, σ_R的关系分析可得，当σ_R=0时，μ_LR=-ε_R/ε_L。

从以上分析可知，沿主向L, T截取的板材(弦切面)，在σ_T=0的位置贴十字应变花可以测得μ_LT；而沿主向L, R截取的板材(径切面)，在σ_R=0的位置贴十字应变花可以测得μ_LR。

对于横切面泊松比μ_RT或μ_TR，相关的应力-应变关系为：

$ \left\{ \begin{array}{l} {\varepsilon _{\rm{R}}}\\ {\varepsilon _{\rm{T}}} \end{array} \right\}=\left[ {\begin{array}{*{20}{c}} {\frac{1}{{{E_{\rm{R}}}}}}&{ - \frac{{{\mu _{{\rm{TR}}}}}}{{{E_{\rm{T}}}}}}\\ { - \frac{{{\mu _{RT}}}}{{{E_{\rm{R}}}}}}&{\frac{1}{{{E_{\rm{T}}}}}} \end{array}} \right]\left\{ \begin{array}{l} {\sigma _{\rm{R}}}\\ {\sigma _{\rm{T}}} \end{array} \right\}. $

(2)

解之，

$ \begin{array}{l} {\sigma _{\rm{R}}}=\frac{{{E_{\rm{R}}}}}{{1 - {\mu _{{\rm{RT}}}}{\mu _{{\rm{TR}}}}}}\left({{\varepsilon _{\rm{R}}}+{\mu _{{\rm{TR}}}}{\varepsilon _{\rm{T}}}} \right), \\ {\sigma _{\rm{T}}}=\frac{{{E_{\rm{T}}}}}{{1 - {\mu _{{\rm{RT}}}}{\mu _{{\rm{TR}}}}}}\left({{\varepsilon _{\rm{T}}}+{\mu _{{\rm{RT}}}}{\varepsilon _{\rm{R}}}} \right). \end{array} $

当σ_R=0时，μ_TR=-ε_R/ε_T; 当σ_T=0时，μ_RT=-ε_T/ε_R。

由柔度矩阵对特性，有：弦切面E_Tμ_LT=E_Lμ_TL；径切面E_Rμ_LR=E_Lμ_RL；横切面E_Tμ_RT=E_Rμ_TR。故木材独立的泊松比只有3个，即μ_LT, μ_LR，μ_RT或μ_TR。

1.2 悬臂板一阶弯曲模态的应力、应变分析 1.2.1 ANSYS计算输入的材料常数

ANSYS计算采用shell 63单元，60×10，50×10，40×10，30×10网格划分分别用于l/b=6, 5, 4, 3的悬臂板试件。选择轻木(Ochroma lagopus)、云杉(Picea asperata)、欧洲赤松(Pinus sylvestris)、白蜡木(Fraxinus chinensis)和山毛榉(Fagus sylvatica)5个树种进行一阶弯曲模态的应力、应变分析，锯材的密度范围为200～750 kg·m^-3, 且其弦切面μ_LT、径切面μ_LR和横切面μ_RT的规范值及主向弹性模量和主向剪切模量均可查到(尹思慈，1996)。为了得到测试μ_LT的应变花粘贴位置，ANSYS计算输入的木材主向弹性常数如表 1所示(弦切面)。

ANSYS计算所用的坐标轴为x, y, z，与木材主向L, T, R的对应关系为:

径切面x→L, y→R, z→T；

弦切面x→L, y→T, z→R(对应表 1数据)；

横切面x→R, y→T, z→L。

对于木材径切面和横切面的9个弹性常数按上列的坐标轴x, y, z与木材主向对应关系输入。

1.2.2 ANSYS计算输出信息

从一阶弯曲模态应力数据中提取板试件中心线各节点的σ_x, σ_y，以计算板试件的σ_y/σ_x；从一阶弯曲模态应变数据中提取板试件中心线各节点的ε_x, ε_y, ε_z，以计算板试件的-ε_y/ε_x，-ε_z/ε_x。结果表明：-ε_y/ε_x随x/l增加而上升，而-ε_z/ε_x随x/l增加而下降。

通过计算发现：-ε_y/ε_x=μ_LT，-ε_z/ε_x=μ_LR处于同一位置x₀(x→L, y→T, z→R), 且在此位置上σ_y/σ_x改变符号，即满足σ_y/σ_x=0。因此，从测试原理可知，若将十字应变花粘贴在x₀位置上，则横向应变与纵向应变的比值绝对值即为板试件的泊松比。

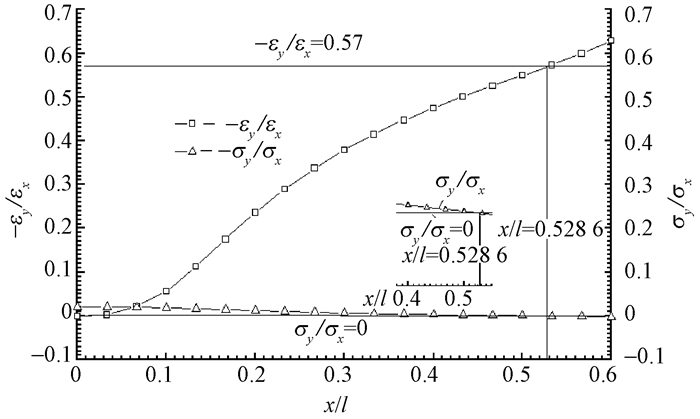
对于欧洲赤松弦切面悬臂试件，其l/b=5，由ANSYS模态程序计算出的一阶弯曲模态下的应力和应变数据可绘制出如图 1所示的σ_y/σ_x和-ε_y/ε_x曲线，由σ_y/σ_x=0确定的位置x₀，其-ε_y/ε_x恰好等于欧洲赤松的μ_LT。图 1显示的x₀=0.528 6l≈0.53l。

1.3 应变花粘贴位置 1.3.1 测试μ_LT应变花粘贴位置

对5个树种锯材悬臂板一阶弯曲模态的应力、应变进行分析(20个计算方案)，并根据σ_y/σ_x=0得到测试木材μ_LT的应变花粘贴位置，如表 2所示。计算时悬臂板的宽度取123 mm，而厚度取8，12.2和18 mm，结果发现，-ε_y/ε_x与板的厚度无关。

根据表 2数据特征，将计算得到的应变花粘贴位置x/l对ρ，l/b进行二元线性回归，可得测试木材弦切面μ_LT的应变花粘贴位置为：

$ x/l={\rm{0}}{\rm{.440 0}} - 0.0982\rho+0.6939l/b. $

(3)

$ \left({r=0.9897, n =20, \rho=0.2 \sim 0.75g \cdot c{m^{ - 3}}, l/b=3 - 6} \right) $

1.3.2 测试μ_LR应变花粘贴位置

输入木材径切面的主向弹性常数，进行悬臂板ANSYS一阶弯曲模态的应力、应变分析，再根据σ_y/σ_x=0得到测试木材μ_LR的应变花粘贴位置，如表 3所示。

从表 3可以看出，在锯材试件同一长宽比下，应变花粘贴位置不是随锯材试件的密度增加而单调减小，而是随锯材试件密度的增加有所波动；但对于同一树种而言, 其应变花粘贴位置仍随长宽比减少而增加。

根据表 3数据特征，拟定先对同一长宽比下5个树种锯材的应变花粘贴位置取平均值；然后根据ANSYS一阶弯曲模态应力、应变分析结果计算其在平均值位置的-ε_y/ε_x；最后计算在平均值位置上的-ε_y/ε_x与5个树种锯材径切面μ_LR规范值的相对误差。其结果为：当悬臂板长宽比l/b=6，5，4和3时, 平均值位置上计算的-ε_y/ε_x和5个树种锯材径切面μ_LR规范值的最大相对误差分别为1.4%，1.7%，1.9%和2.2%。

因此，先对表 3数据在同一长宽比下5个树种锯材的应变花粘贴位置x/l取其平均值，然后用该平均值对l/b进行一元回归，可得测试木材径切面μ_LR的应变花粘贴位置为：

$ \begin{array}{l} x/l=0.7709 - 0.0702l/b+0.00317{l^2}/{b^2}.\\ \left({r=1, n=4, l/b=3 \sim 6} \right) \end{array} $

(4)

1.3.3 测试μ_RT应变花粘贴位置

输入木材横切面的主向弹性常数，进行悬臂板ANSYS一阶弯曲模态的应力、应变分析，再根据σ_y/σ_x=0得到测试木材μ_RT的应变花粘贴位置，如表 4所示。

从表 4可以看出，与弦切面和径切面一样，保持同一树种锯材应变花粘贴位置随长宽比减小而增加的变化规律；但在同一长宽比下，5个树种锯材测试μ_RT的应变花粘贴位置随密度增加先剧烈下降后较快上升，其主要反映在云杉和欧洲赤松2个树种上。

根据表 4数据特征, 当拟定悬臂板长宽比l/b=6，5，4和3时, 5个树种锯材的应变花粘贴位置x/l分别取0.35，0.40，0.45和0.50。根据横切面ANSYS一阶弯曲模态的应力、应变分析结果分别计算x/l在0.35，0.40，0.45和0.50位置的-ε_y/ε_x, 然后计算-ε_y/ε_x与5个树种锯材横切面μ_RT规范值的相对误差。其结果为：当悬臂板长宽比l/b=6，5，4和3时, 在x/l=0.35，0.40，0.45和0.50位置计算的-ε_y/ε_x和5个树种锯材横切面μ_RT规范值的最大相对误差分别为0.8%，1%，2%和4%。

因此，用x/l=0.35，0.40，0.45和0.50与l/b=6，5，4和3进行一元回归，可得测试木材横切面μ_RT的应变花粘贴位置为：

$ \begin{array}{l} x/l={\rm{0}}{\rm{.65 - 0}}{\rm{.05}}l/b.\\ \left({r=1, n=4, l/b=3 \sim 6} \right) \end{array} $

(5)

2 测试方法 2.1 应变花粘贴和桥路接法

根据木材主向L，R和T制备弦切面(LT)、径切面(LR)和横切面(RT)试件；根据悬臂板试件的长宽比或宽长比，分别按式(3)、式(4)和式(5)计算出应变花的粘贴位置，并根据计算的应变花粘贴位置在板试件的上、下面各粘贴1枚十字应变花。结果发现，按1/4桥分别测量悬臂板试件上、下面的横向应变与纵向应变比值并不总是相同的，有时差异还较大，反映出木材随其板厚度的变化特性。因此，为了提高测试精度，测量木材泊松比时，悬臂板试件上、下面的横向应变片与纵向应变片应分别采用按互补偿的半桥接法。

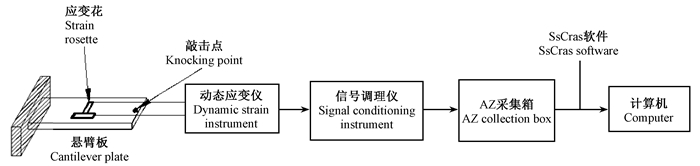
2.2 试验流程

动态测试木材泊松比的试验流程及其试验现场分别如图 2、图 3所示。

本研究采用黄岩应变计厂BX120-5AA型应变片(阻值120 Ω, 灵敏系数2.08%±1%, 应变栅长度和宽度分别为5 mm和3 mm)，应变片输出接上海华东电子仪器厂的YD-28A动态应变仪。试验采用双通道采集数据方式，其纵向片接第1通道，横向片接第2通道。敲击试件激发其自由振动，敲击点位于板中心线靠近自由端。根据悬臂板试件的一阶弯曲频率，设置低通滤波频率，滤掉2阶和2阶以上频率。采集的数据经软件进行频谱分析(王正，2007；Brancheriaul et al., 2002)，从频谱图上读取一阶弯曲频率横向应变和纵向应变的线性谱幅值(图 4)，横向应变幅值与纵向应变幅值之比即为木材泊松比测量值。每一试件重复测量3次，取其横向应变幅值与纵向应变幅值之比的平均值作为该试件的泊松比动态测量值。

由图 4(王正等，2008；Wang et al., 2012)一阶弯曲频率处的横向应变线性谱幅值与纵向应变线性谱幅值之比，得到蒙古栎(Quercus mongolica)4号试件计算的泊松比为0.577。

图 5显示了蒙古栎4号试件的波形，第1通道表示纵向应变波形，第2通道表示横向应变波形。从波形上看纵向应变与横向应变是反向的，其相位相差180°，即纵向应变与横向应变相差一个符号。在图 5波形图中，根据横向动应变峰峰值与纵向动应变峰峰值之比的平均值计算的蒙古栎4号试件泊松比为0.578，这表明不论从时域(波形的峰峰值)还是从频域(频谱图上一阶弯曲频率处的线性谱幅值)，均可得到相同的木材泊松比动态测量值，由此可从频域得出木材泊松比动态测量值。

3 木材泊松比的动态测试

考虑到同名树种生产地不同时材料常数存在差异，使得动态测试值不便于与表 1中给出的泊松比规范值相比较，故选择异于上述5个树种的其他树种，并将其动态测试泊松比结果与静态测试结果进行对比加以验证。需要说明的是，在验证动态测试木材泊松比的应变花粘贴位置式(3)、式(4)和式(5)的正确性时，不追求同一树种动态测试μ_LT，μ_LR和μ_RT3个泊松比的试验设计，而是重于式(3)、式(4)和式(5)本身的正确性及公式适用于多树种的验证。

3.1 油松μ_LT，μ_LR动态测试

油松(Pinus tabulaeformis)试件尺寸300 mm×60 mm×12.2 mm，夹持长度60 mm, 实现l/b=4的悬臂试件; 试件数量：径切面5块，弦切面5块；含水率为7.5%～7.8%。径切面应变花粘贴位置根据式(4)得x₀=0.544l，弦切面应变花粘贴位置根据式(3)得x₀=0.567l(计算气干密度取平均密度0.472 g·cm^-3)。

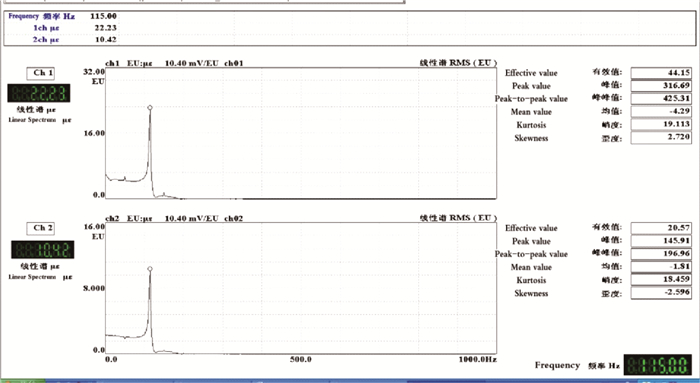
油松径切面μ_LR动态测量值为：均值0.41，标准差0.032，变异系数7.8%；弦切面μ_LT动态测量值为：均值0.48，标准差0.040，变异系数8.4%(表 5、图 6)。

3.2 西加云杉径切面μ_LR动态测试

西加云杉(Picea sitchensis)径切面试件尺寸625 mm×107 mm×12.2 mm，夹持长度143 mm，实现l/b=4.5的悬臂试件；试件数量11块；含水率为7.2%～7.6%。根据式(5)，得应变花粘贴位置x₀=0.52l。

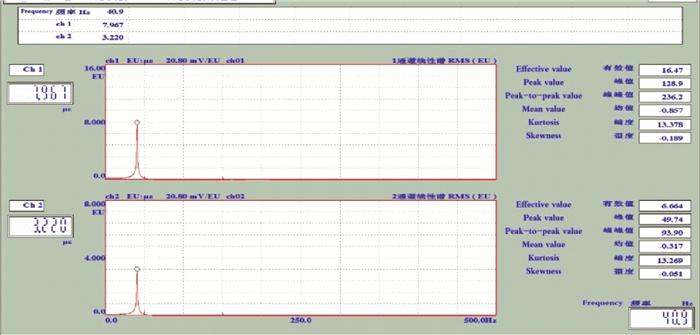
西加云杉径切面μ_LR动态测量值为：均值0.40，标准差0.033，变异系数8.1%(表 6、图 7)。

3.3 西加云杉横切面泊松比μ_RT动态测试

西加云杉横切面试件尺寸220 mm×60 mm×12.2 mm，夹持长度40 mm, 实现l/b=3的悬臂试件；试件数量4块；含水率为7.4%～7.6%。根据式(5), 得应变花粘贴位置x₀=0.5l。

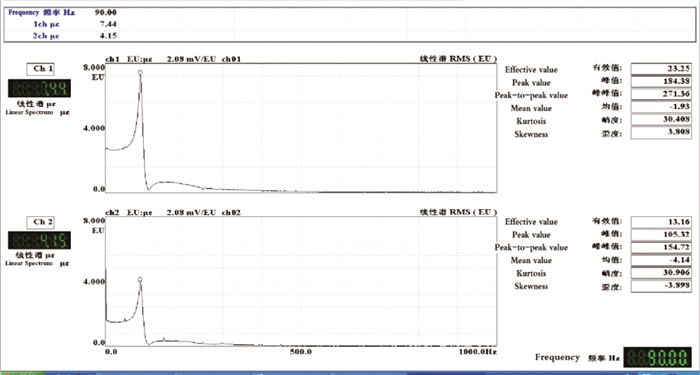
西加云杉横切面μ_RT动态测量值：均值0.57，标准离差0.042，变异系数7.4%(表 7、图 8)。

3.4 蒙古栎泊松比动态测试

蒙古栎试件尺寸710 mm×130 mm×18 mm，试件数量10块, 夹持长度60 mm，实现650 mm×130 mm×18 mm的悬臂板, l/b=5，含水率为7.6%～8.0%，平均气干密度800 kg·m^-3。

蒙古栎顺纹试件，来自于没有开槽口的地板毛坯，不是单一的径切面或弦切面试件，对于l/b=5的蒙古栎试件，根据式(3)和式(4)，其十字应变花粘贴位置皆为x₀=0.5l。

选用蒙古栎树种除验证动态测定泊松比的十字应变花粘贴位置正确性外，还有另一种考虑，对工程上的这种顺纹木材如何测定泊松比？选用蒙古栎动态测试其泊松比，正是这种测定工作的探索，使其满足于实用性的需要。

蒙古栎顺纹泊松比动态测量值为：均值0.48，标准离差0.073，变异系数15.2%(表 8)。

4 木材泊松比的静态测试

对于油松、西加云杉动态测试泊松比结果的正确性，采用从动态试件上下料制作轴向拉伸和四点弯曲试件，且进行轴向拉伸和四点弯曲试验加以验证。这种验证方法更能说明应变花粘贴位置式(3)、式(4)和式(5)的正确性。

4.1 轴向拉伸试验

在动态测试的宽度为107 mm的西加云杉大板试件上锯解3块尺寸为300 mm×40 mm×12.2 mm的锯材作为试件，其测试仪器为上海华东YD-28A动态应变仪和BX120-5AA型应变片、南京安正AZ308R型信号采集箱和SANS100N-300KN型万能力学试验机1台。测试前，试件两面各贴上1枚应变花, 两面纵向片和横向片分别作串联连接, 以消除拉伸过程中因加载不对中而产生的弯曲应变问题。应变仪纵向片、横向片的输出分别接采集箱的第1通道和第2通道，采用1/4桥接法，通过专用软件记录其纵向应变和横向应变数据。测试时试验机连续加载，加载速率为1 mm·min^-1。设定其下限载荷2 kN，上限载荷3.5 kN，并记录载荷区间的纵向应变和横向应变。在数据处理时，从采集数据的文本文件中读取下限载荷到上限载荷的横向应变和纵向应变。取若干组数据并验证其线性后, 从斜率可以确定木材的泊松比。亦可以简单地按下式计算木材的泊松比：

$ \mu=- \frac{{{\varepsilon _{横上限}} - {\varepsilon _{横下限}}}}{{{\varepsilon _{纵上限}} - {\varepsilon _{纵下限}}}}. $

4.2 四点弯曲试验 4.2.1 试件

油松和西加云杉试件取自于其动态测试泊松比试件，并取相同的试件编号。油松和西加云杉径切面尺寸300 mm×12.2 mm×12.2 mm，跨度240 mm，l/3 -l/3 -l/3加载方式；西加云杉横切面尺寸220 mm×12.2 mm×12.2 mm，跨度200 mm，l/4 -l/2 -l/4加载方式。

4.2.2 砝码加载

对于木材径切面和弦切面试件，设置下限载荷4.165 N，上限载荷16.66 N(ΔP=12.496 N)；对于木材横切面试件，设置下限载荷1.019 2 N，上限载荷2.744 N(ΔP=1.724 8 N)，其μ=-Δε_横向应变/Δε_纵向应变。

每一试件进行3次试验，取第2，3次试验值的平均值作为该试件的泊松比测量值(表 9)。

表 9中还列出了相同试件编号动态测试木材泊松比的结果。结果表明，用动态法与静态法测试木材试件的泊松比极为一致，且动态法测试木材泊松比的数据分散性与静态法相比有所改善。

5 结论

1) 悬臂板作一阶弯曲振动时, 其横向应变ε_y与纵向应变ε_x之比随距其悬臂端距离的增加而上升；横向应力σ_y与纵向应力σ_x之比随距其悬臂端距离的增加从正值下降到负值，存在一个σ_y等于零的位置，在此位置上横向应变与纵向应变之比的绝对值等于材料泊松比。

2) 对于悬臂板, 其横向应力与纵向应力之比在整个悬臂板内均很小，如山毛榉最大比值为0.043, 轻木、云杉、欧洲赤松和白蜡木等锯材最大比值在0.02左右。悬臂木板的这种应力分布特征不同于低碳钢和铝等各向同性材料, 即尽管木材的横向应力与纵向应力之比在整个悬臂板内均很小，但是由于木材主向弹性模量相异很大，故在测试木材泊松比时也不容忽视其横向应力σ_y与纵向应力σ_x的比值。

3) 动态测试木材泊松比时，十字应变花粘贴位置需在横向应力σ_y等于零的位置。对于木材弦切面悬臂板，其十字应变花粘贴位置与板长宽比和板材密度有关；对于木材径切面和横切面悬臂板，其十字应变花粘贴位置仅与板长宽比有关。

4) 动态测试木材泊松比方法的正确性得到轴向拉伸和四点弯曲静态试验的验证，并且动态测试木材泊松比的分散性相对于静态测试有所改善。